Lobbying, Time Preferences and Emission Tax Policy

Abstract

We develop a theoretical model to study the combined effect of lobbying and time preferences on emission tax policies. With a two-period model, we show that the influence of lobbying, by dirty industries and by environmental organizations, on the equilibrium tax decreases with the time horizon of the policymakers. An extension of the model to four periods shows that social welfare maximising policymakers may implement a tax higher than the marginal cost in the first period to speed up the transition to green technology. A policymaker influenced by lobby groups may, however, do the opposite, because future lobbying income will decrease if more firms invest in green technology. The results of this study indicate that countries with powerful lobby groups and a short-sighted policymaker are not likely to implement the optimal carbon tax. The influence of lobbying in combination with time preferences may explain some of the diversity in carbon taxes that we observe in practice. The results lead to the policy recommendation to combine carbon taxes with trade policies, which create an incentive for short-sighted governments to participate in carbon pricing policies.

Appendix

Equation (38), total Second-Period Profit (${\Pi }_{2}$)

Total second-period profit in the two-period model “Second Period” section is:

$${\Pi }_{2}=\phi {\Pi }_{G}-\sum_{0}^{\phi }{I}_{i}+(1-\phi ){\Pi }_{B}$$

(38)

The sum of investment cost is:

$$\sum_{0}^{\phi }{I}_{i}=0.5{\phi }^{2}=\frac{(2\tau -{\tau }^{2}{)}^{2}}{2}$$

(39)

Plugging (8), (9), (10) and (39) into (38) gives:

$$\begin{array}{c}{\Pi }_{2}=(2\tau -{\tau }^{2})-\frac{(2\tau -{\tau }^{2}{)}^{2}}{2}+(1-\tau {)}^{4}\\ =2\tau -{\tau }^{2}-(2{\tau }^{2}-2{\tau }^{3}+0.5{\tau }^{4})+(1-4\tau +6{\tau }^{2}-4{\tau }^{3}+{\tau }^{4})\\ =0.5{\tau }^{4}-2{\tau }^{3}+3{\tau }^{2}-2\tau +1\end{array}$$

Proof of Lemma 1

Lemma 1: Period 2 social welfare is maximised for $\uptau =\upeta$, i.e. when the tax is equal to the marginal damage costs (a Pigouvian tax).

To maximise the second period social welfare function in Eq. (13), we first take the derivative with respect to $\tau$. The second period social welfare function is equal to the second-period profit plus tax income minus damage costs. The derivative of ${W}_{2}$ is the sum of the derivatives of those three parts:

$$\frac{\partial {W}_{2}}{\partial \tau }=\frac{\partial {\Pi }_{2}}{\partial \tau }+\frac{\partial {T}_{2}}{\partial \tau }-\frac{\partial {D}_{2}}{\partial \tau }$$

(40)

Equation (38) specifies the second-period profit. The derivative of Eq. (38) with respect to $\tau$ is:

$$\frac{\partial {\Pi }_{2}}{\partial \tau }=2{\tau }^{3}-6{\tau }^{2}+6\tau -2=2({\tau }^{3}-3{\tau }^{2}+3\tau -2)=-2(1-\tau {)}^{3}$$

(41)

The second-period tax income is $\tau$ times the second-period emission, which leads to the derivative in Eq. (43):

$${T}_{2}=\tau (1-\phi ){x}_{B}=\tau (1-\tau {)}^{2}*2(1-\tau )=2\tau (1-\tau {)}^{3}$$

(42)

$$\frac{\partial {T}_{2}}{\partial \tau }=2(1-\tau {)}^{3}-6\tau (1-\tau {)}^{2}$$

(43)

For the damage function, we insert Eq. (7) and (10) into (5), leading to the derivative in Eq. (45):

$${D}_{2}=2\eta (1-\tau {)}^{3}$$

(44)

$$\frac{\partial {D}_{2}}{\partial \tau }=-6\eta (1-\tau {)}^{2}$$

(45)

Combining the above derivatives gives:

$$\begin{array}{c}\frac{\partial {W}_{2}}{\partial \tau }=-2(1-\tau {)}^{3}+2(1-\tau {)}^{3}-6\tau (1-\tau {)}^{2}+6\eta (1-\tau {)}^{2}\\ =6(\eta -\tau )(1-\tau {)}^{2}\end{array}$$

(46)

This first order derivative is equal to zero for $\eta =\tau$ and/or $\tau =1$. Analysing whether these points are a maximum requires taking the second order derivative:

$$\frac{{\partial }^{2}{W}_{2}}{{\partial }{\tau }^{2}}=-6(1-\tau )(1-3\tau +2\eta )$$

(47)

The second order derivative of ${W}_{2}$ is negative for $\tau =\eta$ and $\tau \in [\mathrm{0,1})$, so there is a local maximum at $\tau =\eta$. The second order derivative is zero for $\tau =1$. The first order derivative is negative just above and just below $\tau =1$ for $\eta <1$, which means that $\tau =1$ is a saddle point. Period 2 social welfare is thus maximised when the tax is equal to the marginal damage costs (a Pigouvian tax).

Proof of Proposition 2

Proposition 2 states that $\frac{\partial {C}_{I}(\tau )}{\partial \tau }\le 0$ and $\frac{\partial {C}_{E}(\tau )}{\partial \tau }\ge 0$ for $\tau \in \left(\mathrm{0,1}\right).$ We start with proofing that $\frac{\partial {C}_{I}(\tau )}{\partial \tau }\le 0$. In “Lobbying” section, we demonstrate that the derivative of the industry contribution function is the same as the derivative of the total brown firm profit. Since all firms are brown in the first period, total brown firm profit is the total profit in the economy ${(\Pi }^{TOT})$. The total profit is the discounted sum of the first- and second-period profits of all firms:

$$\frac{\partial {C}_{I}(\tau )}{\partial \tau }=\frac{\partial {\Pi }^{TOT}}{\partial \tau }=\frac{{\partial \Pi }_{1}}{\partial \tau }+\delta \frac{{\partial \Pi }_{2}}{\partial \tau }$$

(48)

Using $\frac{{\partial \Pi }_{1}}{\partial \tau }=\frac{{\partial \Pi }_{B}}{\partial \tau }=-2\left(1-\tau \right)$ and Eq. (41), $\frac{{\partial \Pi }_{2}}{\partial \tau }=-2(1-\tau {)}^{3}$, gives:

$$\frac{\partial {C}_{I}(\tau )}{\partial \tau }=-2(1-\tau )+\delta (-2(1-\tau {)}^{3})=-2(1-\tau )(1+\delta (1-\tau {)}^{2})$$

(49)

$-2\left(1-\tau \right)\le 0$ for $\tau \in \left(\mathrm{0,1}\right)$ and $(1+\delta \left(1-\tau {)}^{2}\right)\ge 0$, therefore $\frac{\partial {C}_{I}(\tau )}{\partial \tau }\le 0$

The derivative of ${C}_{E}$ with respect to $\tau$ is the derivative of the total damage function:

$$\frac{\partial {C}_{E}(\tau )}{\partial \tau }=-\frac{\partial D({x}_{B}^{1},{x}_{B}^{2})}{\partial \tau }=-\frac{\partial (\eta {x}_{B})}{\partial \tau }-\delta \frac{\partial (\eta (1-\phi ){x}_{B})}{\partial \tau }$$

Plugging in Eqs. (7) and (10) gives:

$$\begin{array}{c}\frac{\partial {C}_{E}(\tau )}{\partial \tau }=-\frac{\partial (2\eta (1-\tau )}{\partial \tau }-\delta \frac{\partial (2\eta (1-\tau {)}^{3})}{\partial \tau }\\ =2\eta -\delta (-6\eta (1-\tau {)}^{2})=2\eta (1+3\delta \left(1-\tau {)}^{2}\right)\ge 0\end{array}$$

Proof of Lemma 2

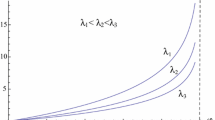
Lemma 2: When $\delta =1$, the equilibrium carbon tax rate is increasing in the degree of openness to lobby contributions $\left(\frac{\partial \tau }{\partial \lambda }>0\right)$ for $\eta =\frac{1}{2}$ and decreasing in the degree of openness to lobby contributions $\left(\frac{\partial \tau }{\partial \lambda }<0\right)$ for $\eta =\frac{1}{3}$ if $\lambda <2$.

Proof:

To proof the first part of Lemma 2 ($\eta =\frac{1}{2}$), we start with the FOC in Eq. (22). We plug in $\delta =1$ and for simplification we take $y=1-\tau$, which leads to the following rewritten FOC:

$$F\left(\eta ,\lambda ,\delta =1,y\right)=\eta -1+y+\left(3\left(\eta -1\right){y}^{2}+3{y}^{3}\right)+\lambda \left(-{y}^{3}-y+\eta +3\eta {y}^{2}\right)=0$$

(50)

Using Eq. (50) we can express $\lambda$ as a function of $y$ and $\eta :$

$$\lambda =\frac{3{y}^{3}+3\left(\eta -1\right){y}^{2}+y+\eta -1}{{y}^{3}-3\eta {y}^{2}+y-\eta }$$

(51)

If we take $\eta =\frac{1}{2}$ and let $z={y}^{-1}=\frac{1}{1-\tau }$ then the FOC in Eq. (50) can be simplified to:

$$F\left(\lambda ,y\right)=1-{z}^{2}+{\left(1-z\right)}^{3}-\frac{4}{\lambda -1}=0$$

(52)

To analyse the influence of the lobby group on the tax we want to calculate $\frac{\partial \tau }{\partial \lambda }$. Since $z={y}^{-1}=\frac{1}{1-\tau }$, we can calculate $\frac{\partial \tau }{\partial \lambda }$ by first calculating $\frac{\partial z}{\partial \lambda }$. Using the implicit function theorem and the FOC in Eq. (52), we get:

$$\frac{\partial z}{\partial \lambda }=-\frac{\frac{\partial F\left(\lambda ,z\right)}{\partial \lambda }}{\frac{\partial F\left(\lambda ,z\right)}{\partial z}}=-\frac{{F}_{\lambda }}{{F}_{z}}=\frac{4{\left(\lambda -1\right)}^{-2}}{2z+3{\left(1-z\right)}^{2}}>0$$

(53)

Recall: $z={y}^{-1}=\frac{1}{1-\tau }$, therefore:

$$\begin{array}{c}\frac{\partial z}{\partial \lambda }=\frac{\partial \left({y}^{-1}\right)}{\partial \lambda }=-{y}^{-2}\frac{\partial y}{\partial \lambda }=-\frac{1}{{\left(1-\tau \right)}^{2}}\frac{\partial \left(1-\tau \right)}{\partial \lambda }=\frac{1}{{\left(1-\tau \right)}^{2}}\frac{\partial \tau }{\partial \lambda }=\frac{4{\left(\lambda -1\right)}^{-2}}{2y+3{\left(1-y\right)}^{2}}>0\\ \Rightarrow \frac{\partial \tau }{\partial \lambda }=4\frac{{\left(1-\tau \right)}^{2}{\left(\lambda -1\right)}^{-2}}{2z+3{\left(1-z\right)}^{2}}>0\end{array}$$

To proof the second part of Lemma 2, we plug $\eta =\frac{1}{3}$ in Eq. (51), rewriting gives:

$$\lambda =2+\frac{{y}^{3}-y}{{y}^{3}+y-{y}^{2}-\frac{1}{3}}$$

(54)

$$\lambda -2=\frac{{y}^{3}-y}{{y}^{3}+y-{y}^{2}-\frac{1}{3}}$$

(55)

If $\lambda =2$, and $\eta =\frac{1}{3}$ then the left hand-side of the above equation is equal to zero. The right hand-side is equal to zero only if $y=0$ or $y=1$. Which leads to the conclusion that $\lambda \ne 2$.

With $\lambda \ne 2$, we can take the inverse of Eq. (55):

$${\left(\lambda -2\right)}^{-1}=\frac{{y}^{3}+y-{y}^{2}-\frac{1}{3}}{{y}^{3}-y}$$

(56)

Which leads to the following FOC:

$$F\left(y,\lambda \right)=\left({y}^{3}-y\right){\left(\lambda -2\right)}^{-1}-\left({y}^{3}+y-{y}^{2}-\frac{1}{3}\right)$$

(57)

Using the implicit function theorem, we can calculate $\frac{\partial y}{\partial \lambda }$:

$$\frac{\partial F}{\partial \lambda }=-{\left(\lambda -2\right)}^{-2}\left({y}^{3}-y\right)=-{\left(\lambda -2\right)}^{-2}y\left({y}^{2}-1\right)$$

(58)

$$\begin{array}{c}\frac{\partial F}{\partial y}={\left(\lambda -2\right)}^{-1}\left(3{y}^{2}-1\right)-\left(3{y}^{2}+1-2y\right)\\ =\left({\left(\lambda -2\right)}^{-1}-1\right)\left(3{y}^{2}-1\right)+2(y-1)\end{array}$$

(59)

$$\frac{\partial y}{\partial \lambda }=-\frac{\frac{\partial F}{\partial \lambda }}{\frac{\partial F}{\partial y}}=\frac{{\left(\lambda -2\right)}^{-2}y\left({y}^{2}-1\right)}{\left({\left(\lambda -2\right)}^{-1}-1\right)\left(3{y}^{2}-1\right)+2(y-1)}$$

(60)

To proof that $\frac{\partial \tau }{\partial \lambda }<0$, we need to proof that $\frac{\partial y}{\partial \lambda }>0$, because $\frac{\partial \tau }{\partial \lambda }=\frac{\partial (1-y)}{\partial \lambda }=-\frac{\partial y}{\partial \lambda }$. We have $y\in \left(\mathrm{0,1}\right)$ therefore, ${\left(\lambda -2\right)}^{-2}y\left({y}^{2}-1\right)\le 0$. Since the numerator in Eq. (60) is negative, the denominator, Eq. (59), should also be negative to make $\frac{\partial y}{\partial \lambda }>0$. We consider the case for $\lambda \le 2$, $\left({\left(\lambda -2\right)}^{-1}-1\right)<0$ and $2\left(y-1\right)<0$. We thus need $\left(3{y}^{2}-1\right)>0$, which is for $y>\sqrt{1/3}\approx 0.57735$ or $\tau <1-\sqrt{1/3}\approx 0.42265$

$$\frac{\partial F}{\partial y}=\underbrace{((\lambda-2)^{-1}-1)}_{<0}\underbrace{(3y^2-1)}_{>0\;if\;y>0.57735}+\underbrace{2(y-1)}_{<0}$$

We have proved that $\frac{\partial \tau }{\partial \lambda }=-\frac{\partial \mathrm{y}}{\partial \lambda }\le 0$ if $y>0.57735 \;\;{\text{or}} \;\; \tau <0.42265$ and $\lambda \le 2$.

Proof of Lemma 3

Lemma 3: For $\lambda =\frac{1}{2}$ , the equilibrium tax is increasing with the discount factor $\left(\frac{\partial \tau }{\partial \delta }>0\right)$ for both $\eta =\frac{1}{2}$ and $\eta =\frac{1}{3}$ . The equilibrium tax is at its maximum ( $\tau =1$ ) for $\eta \ge \frac{2}{3}$ .

Proof:

First, we plug in $\eta =\frac{1}{2}$ in the FOC in Eq. (25):

$$F\left(\eta =\frac{1}{2},\delta ,y\right)=5\delta {y}^{3}-\frac{3}{2}\delta {y}^{2}+y-\frac{1}{2}=0$$

(61)

When $\delta =0$, $y=\frac{1}{2}$ and $\tau =\frac{1}{2}$. When $\delta =1$, $5{y}^{3}-\frac{3}{2}{y}^{2}+y-\frac{1}{2}=0$, solving this nonlinear equation gives $y\approx \mathrm{0,409}$ and $\tau =1-y=0.591$. This gives us the range for $\tau \in \left[0.5, 0.591\right]$ or $y\in \left[\mathrm{0.409,0.5}\right]$.

Based on the range of y obtained above, we get:

$$\frac{\partial F}{\partial y}=15\delta {y}^{2}-3\delta y+1=3\delta y\left(5y-1\right)+1>0$$

(62)

$$\frac{\partial F}{\partial \delta }=5{y}^{3}-\frac{3}{2}{y}^{2}={y}^{2}\left(5y-\frac{3}{2}\right)={\delta }^{-1}\left(\frac{1}{2}-y\right)>0$$

(63)

Using the implicit function theory, we get:

$$\frac{\partial y}{\partial \delta }=-\frac{\frac{\partial F}{\partial \delta }}{\frac{\partial F}{\partial y}}<0$$

(64)

Since $\frac{\partial y}{\partial \delta }=-\frac{\partial \tau }{\partial \delta }$, we can conclude that $\frac{\partial \tau }{\partial \delta }>0$.

Second, we plug in $\eta =\frac{1}{3}$ in the FOC in Eq. (25):

$$F\left(\eta =\frac{1}{3},\delta ,y\right)=5\delta {y}^{3}-3\delta {y}^{2}+y-1=0$$

(65)

When $\delta =0, y=1, \tau =0$. When $\delta =1,$ solving $5{y}^{3}-3{y}^{2}+y-1=0$ gives $y\approx 0.713,$ and $\tau =1-y=0.287$. This gives us the range for $\tau \in \left[0, 0.287\right]$ or $y\in \left[\mathrm{0.713,1}\right]$.

We can again check the sign of $\frac{\partial \tau }{\partial \delta }$ by using the implicit function theorem:

$$\frac{\partial F}{\partial y}=15\delta {y}^{2}-6\delta y+1=3\delta y\left(5y-2\right)+1>0$$

(66)

$$\frac{\partial F}{\partial \delta }=5{y}^{3}-3{y}^{2}=\frac{1-y}{\delta }>0$$

(67)

$$\frac{\partial y}{\partial \delta }=-\frac{\frac{\partial F}{\partial \delta }}{\frac{\partial F}{\partial y}}<0\Rightarrow \frac{\partial \tau }{\partial \delta }>0$$

(68)

$$\frac{\partial \tau }{\partial \delta }>0$$

(69)

Proof of Lemma 4

Lemma 4: For $\lambda =1$ and $\eta =\frac{1}{3}$ the carbon tax is increasing in $\delta \left(\frac{\partial \tau }{\partial \delta }>0\right)\;\;{\text{for}} \;\; \delta >\frac{1}{3}$ and zero for $\delta \le \frac{1}{3}.$ The carbon tax is zero for $\eta =\frac{1}{4}$ and $\lambda =1$ , irrespective of the discount factor.

Plugging $\upeta =\frac{1}{3}$ and $y=1-\tau$ into the FOC in Eq. (26) gives:

$$F\left(\eta =\frac{1}{3},\delta ,y\right)=-\frac{1}{3}+2\delta {y}^{3}-\delta {y}^{2}=0$$

(70)

When $\delta =1$, solving $-\frac{1}{3}+2{y}^{3}-{y}^{2}=0$ gives $y=0.77645$ and $\tau =1-y=0.22355$, which is the upper bound for carbon tax when $\eta =\frac{1}{3}$. With $\delta =0$, the above equation does not hold ($=-\frac{1}{3}+2\delta {y}^{3}-\delta {y}^{2}\ne 0$). So, no carbon tax will be charged with $\eta =\frac{1}{3}$ and $\delta =0$ because future does not matter.

We know that that $y=0.77645$ is the lower bound of y. The term $2{y}^{3}-{y}^{2}$ is positive with $y>0.5$ and increases in y. Therefore, the maximum of $2{y}^{3}-{y}^{2}$ occurs when $y=1$. Then $2{y}^{3}-{y}^{2}=1$ and $\delta \left(2{y}^{3}-{y}^{2}\right)=\delta$. Plugging in $y=1$ in Eq. (70) gives:

$$F\left(\eta =\frac{1}{3},\delta ,y=1\right)=-\frac{1}{3}+\delta =0$$

(71)

Solving Eq. (71) gives $\delta =\frac{1}{3}$. At $y=1$, $\tau =0$, thus we can conclude that when $\eta =\frac{1}{3}$ and $\delta =\frac{1}{3}$ there will be no carbon tax charged as $y=1$ and $\tau =1-y=0$. The range the carbon tax can take is $[0, 0.2235]$ for $\eta =\frac{1}{3}$. Using the implicit function theorem, we get:

$$\frac{\partial y}{\partial \delta }=-\frac{\frac{\partial F}{\partial \delta }}{\frac{\partial F}{\partial y}}=-\frac{2{y}^{3}-{y}^{2}}{6\delta {y}^{2}-2\delta y}=-\frac{y}{2\delta }\frac{2y-1}{3y-1}<0$$

(72)

$$\frac{\partial \tau }{\partial \delta }>0 with \tau \le 0.2235$$

(73)

Plugging $\upeta =\frac{1}{4}$ and $y=1-\tau$ into the FOC in Eq. (26) gives:

$$F\left(\eta =\frac{1}{4},\delta ,y\right)=-\frac{1}{2}+2\delta {y}^{3}-\frac{3}{2}\delta {y}^{2}=0$$

(74)

This equation only holds when $\delta =1$ and $y=1$, which implies that $\tau =0$ for $\delta =1$ and $\eta =\frac{1}{4}$. For $\delta <1$, the equation is not well defined. To conclude, with $\lambda =1$ and $\eta =\frac{1}{4}$, the carbon tax will always be zero because the marginal damage is small, and the lobby power is not strong enough to make the carbon tax happen.

Social welfare maximising third-period tax

In “Social Welfare Maximising Policymaker” section, we claim that the social welfare maximising third-period tax is $\tau =\eta$. To get this tax we have to find the tax $\tau$ that maximises $S{W}_{3}={W}_{3}+\delta {W}_{4}$. For $2{\tau }_{3}-{\tau }_{3}^{2}\ge \phi$, ${W}_{3}={W}_{4}$ which is specified in (29). The derivative of (29) with respect to $\tau$ is:

$$\frac{\partial S{W}_{3}}{\partial \tau }=(1+\delta )\frac{\partial {W}_{3}}{\partial \tau }$$

(75)

Combining (26) with (7), (8) and (9) gives:

$${W}_{3}=\phi +(1-\phi )(1-{\tau }_{3}{)}^{2}+(1-\phi )({\tau }_{3}-\eta )2(1-{\tau }_{3})$$

(76)

$$\begin{array}{c}\frac{\partial {W}_{3}}{\partial {\tau }_{3}}=-2\left(1-\phi \right)\left(1-{\tau }_{3}\right)+2\left(1-\phi \right)\left(1-{\tau }_{3}\right)-2\left(1-\phi \right)\left({\tau }_{3}-\eta \right)\\ =-2(1-\phi )({\tau }_{3}-\eta )\end{array}$$

(77)

$$\frac{\partial S{W}_{3}}{\partial {\tau }_{3}}=(1+\delta )(-2(1-\phi )({\tau }_{3}-\eta ))$$

(78)

$$\frac{{\partial }^{2}S{W}_{3}}{{\partial {\tau }_{3}}^{2}}=-2(1+\delta )(1-\phi )$$

(79)

The first order derivative of $S{W}_{3}$ is zero for $\tau =\eta$ and the second order derivative is negative for $\phi >0$, thus we have a maximum at $\tau =\eta$.

For $2{\tau }_{3}-{\tau }_{3}^{2}>\phi$, $S{W}_{3}$ is specified in Eq. (30), the derivative of (30) is:

$$\frac{\partial S{W}_{3}}{\partial {\tau }_{3}}=\frac{\partial {W}_{3}}{\partial {\tau }_{3}}+\delta \frac{\partial {W}_{4}}{\partial {\tau }_{3}}$$

For this, we need to have the derivative of ${W}_{4}$ with respect to $\tau$. Combining (27) with (7), (8) and (9), and plugging in $\theta =2{\tau }_{3}-{\tau }_{3}^{2}$ and ${I}_{4}=\frac{1}{2}((2{\tau }_{3}-{\tau }_{3}^{2}{)}^{2}-{\phi }^{2})$ gives:

$${W}_{4}=2{\tau }_{3}-{\tau }_{3}^{2}+(1-{\tau }_{3}{)}^{4}-\frac{1}{2}((2{\tau }_{3}-{\tau }_{3}^{2}{)}^{2}-{\phi }^{2})+2(1-{\tau }_{3}{)}^{3}({\tau }_{3}-\eta )$$

(80)

$$\begin{array}{c}\frac{\partial {W}_{4}}{\partial {\tau }_{3}}=2-2{\tau }_{3}-4(1-{\tau }_{3}{)}^{3}-(2-2{\tau }_{3})(2{\tau }_{3}-{\tau }_{3}^{2})\\ -6(1-{\tau }_{3}{)}^{2}({\tau }_{3}-\eta )+2(1-{\tau }_{3}{)}^{3}\\ =-6(1-{\tau }_{3}{)}^{2}({\tau }_{3}-\eta )\end{array}$$

(81)

$$\frac{\partial S{W}_{3}}{\partial {\tau }_{3}}=\frac{\partial {W}_{3}}{\partial {\tau }_{3}}+\delta \frac{\partial {W}_{4}}{\partial {\tau }_{3}}=-2(1-\phi )({\tau }_{3}-\eta )-\delta 6(1-{\tau }_{3}{)}^{2}({\tau }_{3}-\eta )$$

(82)

$$\frac{{\partial }^{2}S{W}_{3}}{{\partial {\tau }_{3}}^{2}}=-2(1-\phi )+\delta (12(1-{\tau }_{3})({\tau }_{3}-\eta )-6(1-{\tau }_{3}{)}^{2})$$

(83)

$\frac{\partial S{W}_{3}}{\partial {\tau }_{3}}=0$ for $\eta =\tau$ and $\frac{{\partial }^{2}S{W}_{3}}{{\partial {\tau }_{3}}^{2}}(\tau =\eta )=-2(1-\phi )-6(1-\eta {)}^{2}<0$, thus this function is also maximised for $\tau =\eta$.

Proof of Eq. (36), Threshold Investment Costs ${I}_{l}^{*}$

Equation (36) follows from the inequality in Eq. (84):

$$(1+\delta +{\delta }^{2}){\Pi }_{G}-{I}_{i}\ge {\Pi }_{B}({\tau }_{1})+\delta {\Pi }_{B}({\tau }_{3})+{\delta }^{2}({\Pi }_{G}-{I}_{i})$$

(84)

Plugging in ${\Pi }_{G}=1$, ${\Pi }_{B}({\tau }_{1})=(1-{\tau }_{1}{)}^{2}$ and ${\Pi }_{B}({\tau }_{3})=(1-\eta {)}^{2}$ and solving the inequality gives the following:

$$\begin{array}{c}1+\delta +{\delta }^{2}-{I}_{i}\ge (1-{\tau }_{1}{)}^{2}+\delta (1-\eta {)}^{2}+{\delta }^{2}(1-{I}_{i})\\ 1-\delta +{\delta }^{2}-{I}_{i}\ge 1-2{\tau }_{1}+{\tau }_{1}^{2}+\delta (1-2\eta +{\eta }^{2})+{\delta }^{2}(1-{I}_{i})\\ \begin{array}{c}{I}_{i}\le 2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})+{\delta }^{2}{I}_{i}\\ {I}_{i}\le \frac{2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})}{1-{\delta }^{2}} \;\; {\text{for}}\;\; \delta <1\end{array}\end{array}$$

(85)

Which gives the threshold in Eq. (36):

$${I}_{l}^{*}=\frac{2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})}{1-{\delta }^{2}} \; {\text{for}} \; \delta <1$$

Proof of Eq. (37), First-Period Investment in Four-Period Model

Equation (37), states that the fraction of firms that invest in green technology in the first period is:

$$\begin{array}{c}\upphi =\mathrm{min}\left[1,\mathrm{ max }\left[2{\tau }_{1}-{\tau }_{1}^{2}+\left(\delta +{\delta }^{2}\right)\left(2\eta -{\eta }^{2}\right),2\eta -{\eta }^{2}\right]\right]\\ \; \text{if}\;\; 2{\tau }_{1}-{\tau }_{1}^{2}\ge (1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})\end{array}$$

(86)

And

$$\begin{array}{c}\upphi =\mathrm{min}[\frac{2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})}{1-{\delta }^{2}},2\eta -{\eta }^{2}]\\ \; \text{if}\;\; 2{\tau }_{1}-{\tau }_{1}^{2}<(1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})\end{array}$$

(87)

We show in the paragraphs before Eq. (37) that firms who will invest in the fourth period (${I}_{G}\le 2\eta -{\eta }^{2})$ will also invest in the second period if:

$${I}_{G}\le \frac{2{\tau }_{1}-{\tau }_{1}^{2}+\delta \left(2\eta -{\eta }^{2}\right)}{1-{\delta }^{2}} \; \text{if}\;\; \delta <1$$

(88)

All firms in this group will invest in the second period if:

$$\begin{array}{c}2\eta -{\eta }^{2}\le \frac{2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})}{1-{\delta }^{2}}\\ (1-{\delta }^{2})(2\eta -{\eta }^{2})\le 2{\tau }_{1}-{\tau }_{1}^{2}+\delta (2\eta -{\eta }^{2})\\ (1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})\le 2{\tau }_{1}-{\tau }_{1}^{2}\end{array}$$

(89)

Firms with higher investment costs $({I}_{G}>2\eta -{\eta }^{2})$ will invest in the second period if:

$${I}_{G}\le 2{\tau }_{1}-{\tau }_{1}^{2}+(\delta +{\delta }^{2})(2\eta -{\eta }^{2})$$

(90)

None of the firms in this group will invest if:

$$\begin{array}{c}2\eta -{\eta }^{2}>2{\tau }_{1}-{\tau }_{1}^{2}+(\delta +{\delta }^{2})(2\eta -{\eta }^{2})\\ (1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})>2{\tau }_{1}-{\tau }_{1}^{2}\end{array}$$

(91)

The indifferent firm is thus in the groups with lower investment costs if $2{\tau }_{1}-{\tau }_{1}^{2}<(1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})$ and in the group with higher investment costs if $2\tau -{\tau }^{2}\ge (1-\delta -{\delta }^{2})(2\eta -{\eta }^{2})$.

Increasing Marginal Damage

The social welfare maximising equilibrium tax in the two-period model stays constant when the discount factor increases. The literature on the social cost of carbon however shows that the social welfare maximising tax increases with the discount factor (e.g. Tol 2018). The reason that the optimal tax stays constant in our model is that we use a damage function with constant marginal damage. Constant marginal damage simplifies the analysis, but in reality, marginal damages are increasing with carbon emissions. Integrated Assessment Models of climate and the economy, such as Nordhaus’ DICE model, therefore use damage functions with increasing marginal damage (Nordhaus 2017). In this section, we analyse the impact of a damage function with increasing marginal damage and cumulative emissions on the equilibrium tax in our two-period model. The damage function we use is:

$${D}_{t}=\eta (\sum_{j=1}^{t}{e}_{j}{)}^{2}$$

(92)

The damage in each period is a quadratic function of the current emission and the emission in previous periods. First-period damage is thus equal to ${D}_{1}=\eta {e}_{1}^{2}=\eta {x}_{B}^{2}$ and second-period damage is ${D}_{2}=\eta ({e}_{1}+{e}_{2}{)}^{2}=\eta ({x}_{B}+(1-\phi ){x}_{B}{)}^{2}$. The total discounted sum of the damage is:

$$D=\sum_{j=1}^{2}{\delta }^{j-1}{D}_{j}=\eta {x}_{B1}^{2}+\delta \eta ({x}_{B1}+(1-\phi ){x}_{B2}{)}^{2}$$

(93)

$$\frac{\partial D}{\partial {x}_{B1}}=2\eta {x}_{B1}+2\delta \eta ({x}_{B1}+(1-\phi ){x}_{B2})>0$$

(94)

The discounted marginal damage increases with $\delta$, so the optimal social welfare maximising tax should also increase with $\delta$. Figure 10 indeed shows that the optimal social welfare maximising tax increases with the discount factor.

Fig. 10

Equilibrium tax as a function of the discount factor δ, λ = 0

The changing damage function has an influence on the lobby contribution. The contribution functions are still specified as follows:

$${C}_{I}(\tau )={\text{max}}[0,{\Pi }^{TOT}(\tau )-\overline{{W}_{I}}]$$

(95)

$${C}_{E}(\tau )={\text{max}}[0,\overline{{W}_{E}}-D({e}_{1},{e}_{2})]$$

(96)

The environmental lobby contribution depends on the damage. Another damage function thus influences the environmental lobby contribution. In “Lobbying” section, we assume that the industry lobby group decreases the tax to zero when there is no environmental lobbying. This assumption is less realistic with an increasing damage function, because the damage becomes very large when $\tau =0$ and the loss of social welfare can only be compensated by industry lobby contribution when $\lambda$ is very large. The equilibrium outcome with only industry lobby groups depends on $\eta$, $\delta$ and $\lambda$, and will be larger than zero in most cases. For simplicity, we can however assume that the environmental lobby group is naive and takes the worst-case scenario of $(\tau =0)$ as their baseline contribution $\overline{{W}_{E}}$:

$$\overline{{W}_{E}}=D(\tau =0)=\eta {2}^{2}+\delta \eta {4}^{2}=4\eta (1+4\delta )$$

(97)

For the industry lobby, we assume that they take the profit at $\tau =1$ as the baseline contribution, which is the same as in “Lobbying” section. Figure 11 plots the equilibrium tax as a function of $\delta$ with $\lambda =1$ using these lobby contributions. Compared to Fig. 10, this figure shows that, with lobbying, the equilibrium tax decreases for small $\eta$ and increases for larger $\eta$. Furthermore, the figure shows that the deviation from the optimal tax is larger when $\delta$ is smaller. These conclusions are the same as with the constant marginal damage in “Discount Factor” section. The impact of lobbying on the equilibrium tax is, however, less extreme. The figure also shows that lobbying already increases the equilibrium tax for relatively small values of $\eta$. This is both influenced by the fact that the chosen environmental lobby contribution schedule gives relatively big environmental lobby contributions, and the damage function increases relatively fast with $\eta$. This exploratory analysis, however, indicates that the direction of the lobby influence stays the same when increasing marginal damage functions are used. It can therefore be justified to focus on constant marginal damage costs for the purpose of this paper. Future research could try to analyse the influence of lobbying and time preferences on emission tax policies using different damage functions and baseline lobby contributions. The impact of damage functions becomes especially interesting when studying the impact of lobbying on long-term policy, using more time periods. Such an analysis, however, exceeds the scope of this paper.

Fig. 11

Equilibrium tax as a function of the discount factor δ, λ = 1