Abstract
Several recent business reports have described the global growth in demand for optical and photonic components, paralleled by technical reports on the growing shortage of skilled manufacturing staff to meet this demand. It is remarkable that producing ultraprecision surfaces remains so dependent on people, in contrast to other sectors of the economy, e.g., car manufacturing. Clearly, training can play some role, but ultimately, only process automation can provide the solution. This paper explores why automation is a challenge and summarizes multidisciplinary work aiming to assemble the building blocks required to realize automation.
Highlights
-
1.
Capturing polishing craft-expertise was academically successful, but commercially unviable due to personal privacy issues.
-
2.
Automating software communication between optical-design and manufacturing can minimise manufacturing cost and risk.
-
3.
Computational fluid dynamics of abrasive-slurries, plus real-time process-sensing, promises improved rocessconvergence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction—Defining the Problem
This paper considers the manufacture (and in particular, pre- and corrective polishing) of precision optical components, including lenses, mirrors, prisms, and windows (say, up to a nominal 400–500-mm aperture) for instrumentation, particularly astronomical instrumentation. These components may be individual bespoke optics or small production runs. In this paper, we are not encompassing the larger optics required for research telescopes but do include commercially manufactured optics for amateur telescopes. Our overall strategy is to implement incremental process advances, taking steps toward our long-term objective of an autonomous manufacturing cell requiring no human intervention. Admittedly, this goal is highly ambitious.
The starting point of manufacturing primarily comprises opto/mechanical design files and parent material purchased from a standard supplier. This material may comprise one of many optical glass types, ceramic (e.g., an ultra-low thermal expansion for mirrors), a crystalline material (e.g., for infrared transmission), an engineering polymer, or a metal or alloy (also for mirrors). Materials in common use present a huge dynamic range in materials properties, chemical and physical—reactive-to-inert, brittle-to-ductile, high-to-low values of Young’s modulus, with a wide range of thermal expansion coefficients, thermal diffusivity, and thermal conductivity.
The manufacturing task starts with defining a process chain to convert the input material into one or more finished products, meeting:
-
dimensional specifications and tolerances (size, shape, wedge, surface texture, and surface form)
-
and, in some cases, functional specifications (image size, encircled energy, modulation transfer function, power spectral density, near- and far-field stray light, infrared emissivity, laser damage threshold, etc.).
Assuming modern subtractive abrasive processes, the process chain may typically progress as follows:
-
1.
Coarse operations (e.g., sawing and milling) to achieve the specified overall geometry of the part, with some overage for subsequent processes. The blank supplier may undertake this task.
-
2.
Computer numerical control (CNC) diamond-milling of the optical surfaces, bevels, and edges.
-
3.
Depending on the output quality of point 2, loose abrasive smoothing to improve form, texture, and mid-spatial frequencies (MSFs).
-
4.
Fine loose abrasive polishing to achieve a specified texture.
-
5.
Differential material removal over the surface to rectify measured form errors (“figuring”) in the iterative/polish/measure cycles.
Other nonabrasive processes may be brought into play, such as ion or atomic plasma figuring.
In the special case of ductile metals and polymers, and following coarse machining to achieve overall geometry, single-point diamond turning may directly create the final optical surface (e.g., for more benign tolerances of infrared optics). For more critical applications, e.g., visible light, postpolishing may be used to remove turning features that degrade stray-light performance.
From this summary, we identify four key issues:
-
1.
The very large range of material properties in common use: glasses, metals, crystals, and ceramics.
-
2.
The diversity of surface forms: flat, concave, and convex spheres aspheres, and free form.
-
3.
The determination of the optimum process chain for a specific job.
-
4.
The pivotal role played by skilled technicians, even with modern CNC machines, particularly for bespoke, precision optics.
2 Modern Role of a Skilled Optics Technician
It is remarkable how much craft-based handwork is still used in optical manufacturing, including lapping and polishing and the local figuring of surfaces to mitigate measured defects. This manual approach is progressively giving way to CNC machines, and, as an example, we consider the Zeeko family of CNC polishing machines. These machines support a range of processes, principally shape adaptive grinding (SAG), smoothing (sometimes referred to by us as “grolishing”), prepolishing to improve texture, and form-corrective polishing in response to surface form metrology data.
Nevertheless, despite the automation, these machines depend on the expertise of skilled operators to optimize performance for each different part. This expertise may involve know-how in special techniques for different materials, geometries, and surface forms, including appropriate fixturing, abrasives, pads, tool pressures, machine speeds, and feeds. Then, the skilled operator will configure postprocess metrology and interpret measurement results, going on to plan the optimum approach to remedying remaining surface errors or unexpected surface anomalies.
3 Prospects for Capturing Human Expertise
3.1 Experimental Approach
We previously briefly described [1] some challenges in automating optical polishing and summarized attempts to capture craft expertise in a digital form. That work started with the definition of a representative case study: a 110-mm-diameter concave spherical glass part. Three skilled operators used a Zeeko IRP1200 CNC polishing machine to polish and form-correct the part, with a 4D simultaneous phase interferometer (Technologies Inc.) to provide metrology feedback.
Qualified psychologists then organized the capture, or “elicitation,” of knowledge. The machine operators wore neck microphones and were encouraged to use the “think aloud protocol,” i.e., to voice their actions and the reasoning behind them at each step in the process. Results were recorded with video footage of their activities.
Regarding corrective polishing, the key question was as follows: where particularly do the operators use their skills/knowledge? The psychologists assigned a case-based reasoning system to each process step. This system enables the reuse of concrete and relevant experience from the past when addressing a new task. Each case contains specific knowledge/expertise applied in a specific context to decide the next step. Some of the attributes of a case concern a part’s geometric and material characteristics, surface error map, etc. In a full implementation, the case base communicates with cross-referenced databases of material properties, optical design files, run-time process data, and before/after metrology data. Each case suggests parameters that the operator sets in a particular step, which serve as an input to the tool path generator software on the CNC machine.
A measure of similarity was used to determine which case from the case base was the most useful for polishing a new part. The k-nearest-neighbor similarity [2] is the standard simple similarity measure and measures the weighted difference between the attributes of a new case and cases from the case base. However, the project demonstrated the need for a better similarity measure representing how specific or general the relationships between case attributes are. In this regard, we define the specificity S and relationship R weights of 0–1. For example, the volumetric removal rate and texture are not specific but tightly coupled to abrasive grit size (S = 0, R = 1). “Orange peel” can be tightly coupled to surface speed for some substrate materials (S = 0.5, R = 1), but the texture will not normally be affected by polishing the spot size in the Zeeko process (S = 0, R = 0).
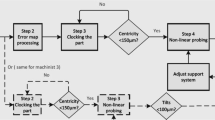
In practice, interviewing and monitoring the three operators required considerable prior negotiation with their commercial employer, reinforcing our view that we were treading on very sensitive ground. Personal privacy issues were particularly pressing with one of the interviewees, and all interviewees were possessive of their knowledge. We were required to edit video footage and delete any record of human faces, bespoke tooling, or anything else sensitive in the workshop. The request to delete background conversations from audio recordings proved impractical. Nevertheless, we could derive from the recorded information a process network for each operator. A very small but representative section of one network is shown in Fig. 1.
From an academic perspective, this attempt to capture craft expertise was a success in that a wealth of process details were consistently and usefully captured in the three network maps. From a commercial perspective, our view is that this method, as it stands, is not a viable approach because of personal privacy issues, the protection of commercial intellectual property, and the heavy workload in deriving useful digital content from recorded audio and video data. Nevertheless, we foresee opportunities and limitations for the automated reporting of machine setup, as described below:
-
1.
Part surface design, metrology data, and some tool path parameters are required as input to the software that generates the machine CNC tool path file for execution.
-
2.
Tooling provided with the machine, e.g., polishing bonnets and SAG tools, could be QR-coded so that the machine directly records the information.
-
3.
The machine’s graphical user interface could be programmed so that before an execution, other relevant process information can be manually input, such as the part’s glass (or other material) type and the slurry abrasive type.
-
4.
Bespoke tooling is more difficult, as each tool may be different. The strategy in the short term should focus on standard tooling, which can be QR-coded. The ultimate solution is foreseen as an automated version of our current manual practice: the development of the process optimization software to define any special tools required, which would be 3D-printed in a suitable polymer.
If such information as that above is to be auto-reported to the machine vendor to be incorporated into a global database, users must be given the option of opting out. This strategy will be effective only if the user community perceives that the benefits to them individually through enhanced process capability and efficiency exceed the perceived loss due to the auto-reporting of the data. This condition parallels how many Internet businesses operate.
3.2 Expert System Approach—PanDao
Through human evolution, survival has increasingly relied on technology for protection, well-being, and communication. To accommodate an increasing rate of change, our ability to manage knowledge has had to adapt to increasing diversity and specialization.
An important example is the development of optical systems, where many different technological areas (from surface physics to optical technologies and AI) and specialists (from astronomers to medical professionals to optical designers and manufacturing specialists) need to collaborate at the highest level while focusing on their respective specialist problems. In particular, the interface between the design of an optical system and the design of the subsequent optical manufacturing chain is a major stumbling block. The design and cost of such chains are strongly linked to the parameters and tolerances of the optical system design (by the use of dedicated optics design software tools). Nevertheless, at present, determining optimum optimal fabrication technologies and evaluating the cost impacts of design tolerances, other than through human-to-human communication, remain challenging. Consequently, establishing fabrication chains is still based on machining trial and error tests, which are high-risk and time-consuming.
We now report the results of our novel approach to optical design strategies, named PanDao [3, 4], which enables changes to a proposed fabrication chain to be investigated during, not just after, the design phase of an optical system. The difficulty in achieving this strategy is that there are > 360 known optical fabrication technologies (OFTs) and solutions available, which must be orchestrated into an optimized fabrication chain, depending only partially on lens optical design parameters and tolerances.
We assert that an optimized optics manufacturing chain must meet the “hexapod” challenge of the critical manufacturing parameters of the optical element: (a) fabrication cost (allowed), (b) throughput (required), (c) geometries (e.g., shapes, local radii of curvature, and the centering of optical surfaces and their peripheral cylinder design), (d) dimensions (diameters and sagittae ranging from microns to meters), (e) qualities (parameters and tolerances as described by the ISO10110 standards, e.g., shape, radii, diameter, and MSFs), and (f) materials (ranging from plastics through glasses up to semiconductor materials and crystals).
Given this challenge, the PanDao approach to optimizing entire optical fabrication chains, based on optical design data, has been developed along the following trajectory: (a) a rigorous differentiation between machining and processing [5] and (b) optical manufacturing technologies classified by a hexapod set of characteristic processing parameters that facilitate communication with the hexapod of the characteristic parameters of the optical element—see Fig. 2.
Although fabrication chains comprise single processes duly balanced against each other, a perception of the fabrication chain as one holistic process has been enabled by the above approach, leading to new insights and solutions. Thus, a methodological analysis on a processing level was applied, leading to a systematic and modular decomposition of OFTs into their partial functions, e.g., by dividing the process of surface smoothing into five physical and chemical submechanisms: (a) brittle cracking, (b) ductile flow, (c) chemical reaction, (d) heat, and (e) sputtering. Out of these submechanisms, we can assemble all existing smoothing processes, leading to a better methodological understanding of some 360 existing OFTs, e.g., fresh feed polishing (= a + c) [6], ductile grinding (= b) [7], chemical etching (= c) [8], float polishing (= b + c), [9], magnetorheological finishing (= b + c) [10], ion beam finishing (= e) [11], FJP (fluid jet polishing) (= b + c) [12, 13], laser polishing (= b + d) [14], laser-induced back etching (= c + d) [15], and plasma polishing (= c + d) [16].
In addition, the abrasion methods were classified according to five characteristic approaches: application of a two- or three-body approach, an abrasive jet [ranging from sandblasting through fluid jet polishing (FJP) to ion beam figuring (IBF)], pure energy (e.g., flame or a laser beam), or chemical agents, as per Fig. 3.
Based on a unique, expert-system-like algorithm, as well as know-how gained from decades of running academic and industrial manufacturing projects, PanDao considers all known OFTs to determine the optimal optical fabrication chain for a given lens design at minimum cost and risk. Therefore, PanDao enables the optimization of optical designs for producibility, minimum cost, and delivery times during the design stage and offers the possibility of replacing or supporting the human-to-human interaction between optical system designers and optical fabrication chain designers.
As an example, Fig. 4 shows an aspheric lens (featuring a spherical side 2) input into PanDao software. It also shows the corresponding results of PanDao’s analysis, containing detailed information on OFTs needed along the optimal fabrication chain, the fabrication cost, and the first-batch lead time (the time needed to deliver the first batch after receiving the order).
In addition, PanDao delivers information on the risk of setting up production, which is described, e.g., by the novel capability factor [4]. Capability is determined by the complexity and accuracies of the “hexapod” of the lens being analyzed. It describes the required capability level a machine, a tool, and the operator must have when the process is being installed along this particular fabrication chain. It is, so to say, a measure of the machining level needed for the process to be applied. With a capability of 100%, the machine must be applied at state-of-the-art processing levels. For the “hexapod” of this lens (see Fig. 4) (a.o.: smallest concave radius of curvature [ROC] 90 mm, 3/1 (0.25), Sq 1.5-nm rms, 5/0.016), the capability of aspherical side 1 reaches 100%, indicating that the modulated fabrication chain is at the state-of-the-art level, while the capability of spherical side 2 reaches 99.5%, indicating that its fabrication chain to be applied will not be at the state-of-the-art level.
Another risk parameter enabled by PanDao is chain uniqueness [4], measuring how many fabrication chains exist within a commercial tolerance band of 20% above the optimum fabrication chain: for the lens given in Fig. 4, the chain uniqueness is six chains for side 1 and three alternative technology chains for side 2.
The ability to analyze manufacturing costs and risk impacts for specific designs enables more complex analyses, such as optics life-cycle analyses (Fig. 5) or material-dependent Strehl-level cost analyses (Fig. 6).
To summarize, a novel methodical analysis of the critical parameters of optical elements and their relevant manufacturing parameters enables the modeling of entire fabrication chains during the design phase using a single “click.” This capability makes the current state of the art of human negotiations between designers and manufacturing personnel obsolete. The PanDao software application facilitates nonhuman communication between the optical design phase and the fabrication design of the required optical fabrication chain. In this way, optical designs can be optimized by smart algorithms in real time at minimum fabrication cost and risk rather than by human negotiation.
4 Real-Time Monitoring of Process Variables
4.1 Logic Behind Process Monitoring
For polishing, executed by hand, machine-assisted, or by a CNC machine, each process run is usually effectively conducted blind: the part’s surface characteristics are measured before the run, process variables are adjusted (manually or in software), the run is conducted, and the part is remeasured after the run ends and cleaned. In general, in-process measurements of surface form and texture are impossible because the part is flooded (or at least contaminated) with an abrasive slurry. One notable exception is the work reported by van der Bijl et al. [17], who succeeded in measuring the evolution of surface texture and subsurface damage during polishing. They illuminated the optical surface with a laser from the back through the material using a prism coupled to the rear surface with an index-matching fluid. This approach enabled them to measure the back reflected and scattered light from the front surface. Their method is a potentially powerful technique for investigating the mechanisms of polishing using flat witness samples, but its extension to the general case of lenses or mirrors with curved or free-form surfaces seems unlikely.
Therefore, the question arises in the general case as to whether any relevant diagnostic information can be collected as a run is executed, as presented in a previous report [1]. The basic idea was independently and almost concurrently presented by Schneckenburger et al. [18].
The objective would then be to infer something useful regarding progress in real time rather than explicitly measuring the characteristics of the surface. This work is currently in progress at Huddersfield’s laboratory at Daresbury, where the following sensors have been installed on an IRP600 CNC polishing machine:
-
A six-axis force table (on which the part is mounted)
-
Measurement of slurry conditions
-
o
pH
-
p
Temperature (T)
-
q
Particle size distribution (PSD)
-
o
Parenthetically, we note the ambiguity of the abbreviation “PSD.” In addition to particle size distribution, it is used for power spectral density (e.g., of a surface height error map) and position-sensitive detector (e.g., a CCD).
4.2 Measurement of Process Forces
The polishing rate depends on the applied force. However, we also wanted to measure the lateral components of force, which indicate the frictional coupling between the tool and the part. Friction should, in principle, be related to the material removal rate, as friction implies work performed due to the breaking of molecular bonds.
The detailed design optimization of the force table was conducted by an academic visitor to the University of Huddersfield, Dr. Chenhui An (Fine Optical Engineering Research Center, Chengdu, China), as part of an international collaboration. The key design requirements were as follows:
-
(1)
Three orthogonal axes of force measurement.
-
(2)
Forces along any axis must not damage another axis.
-
(3)
Capability of measuring torques and forces.
-
(4)
Long-term drifts and rapid changes are to be measured.
-
(5)
Mechanical overload protection is to be provided.
-
(6)
The first resonant frequency is sufficient to resolve the effects of imperfect sphericity (“tramping”) of a polishing bonnet, with a target of four measurements per revolution at 3000 rpm (200 Hz), requiring a first resonant mode of > 400 Hz.
The instrument is shown in Fig. 7 and was constructed under contract by McCales Science Ltd. in Chengdu.
The use of six preloaded compression load cells with overload protection springs differentiates the unit from some commercial cutting force dynamometers, e.g., marketed by Kistler, based on piezoelectric force transducers. Such instruments record dynamic forces, but the DC component required to track progress during a polishing run is lost.
The entire horizontal top plate was machined as a nested monolithic structure in stainless steel using wire-electro-discharge machining. It incorporates thin vertical flexure blades, providing lateral compliance in two axes (X, Y), and the workpiece holder is interfaced with the central square of the top plate. Lateral force components are measured by one load cell on X and two on Y, with the Y force given by the sum of the two load cell signals, and torque is given by the difference. The entire top plate is supported on three Z load cells, laterally constrained by three horizontal flexure blades. The entire unit is interfaced with the polishing machine through three kinematic mounts directly under the Z force load cells.
Figure 8 shows the finite element results of the optimized design, for which the resonant modes meet the design requirement.
A typical set of force measurement plots for raster polishing is shown in Fig. 9, where the direction of travel along the raster tracks and the inclination of the precessed bonnet were in the force table X direction. The short moves between adjacent rasters (conducted on the part) were in the force table Y direction. The cyclic signatures in the Y and Z directions proved to be synchronized with the time for each raster track across the part. Y cycling is attributed to the sudden decelerations, changes in direction, and accelerations between raster tracks. The cyclic Z forces may be due to the precessed bonnet moving in opposite (± X) leading and trailing directions for adjacent paths. The existence of some crosstalk between channels was demonstrated by applying a force on each axis and observing the load cell readings of the other axes. Even with nested designs such as ours, crosstalk is a common feature due to second-order twisting of the flexure, as discussed by Jin et al. [19]. Therefore, we conducted a comprehensive calibration campaign involving the capture of XYZ load cell readings for each of the following:
-
Construction of a dummy 100-mm metal square sample with an array of CNC-machined holes covering the top surface.
-
Pins were inserted in the holes one by one, with a range of horizontal and vertical (X, Y, Z) forces applied from different directions using a fine cord, pulley, and weights.
-
Further measurements were recorded with combined XYZ forces.
The total dataset comprised 400 5-s-long time series of digitized XYZ load cell readings for various combinations of static applied loads. Later, in the analysis, 20-ms time windows were extracted and averaged for each data sample. Data samples were collected at eight angles in 45° increments, as illustrated in Fig. 10, to cover as much of the sample space as practical and capture possible correlations between axes.
Force distributions Xcalc, Ycalc, and Zcalc were calculated for each data sample as a basis for the machining learning (ML) model ground truth. Table 1 presents the measurement results, Xmeas, Ymeas, and Zmeas, for loads of 3 kg and 5 kg in eight directions relative to the X, Y, and Z force sensor axes. Positive and negative signs represent opposite force directions relative to the force table. At certain positions, crosstalk is more evident, e.g., the positions of 90° and 270°.
With the calculated force distributions, a regression model was implemented to eliminate crosstalk and refine the analog-to-digital scaling of the force readings. The dataset was split into training and test samples with a ratio of 67:33. This approach facilitated assessing the performance of the model on data not used in its training.
Thus far, the initial results have demonstrated that a simple deep-learning multilayer perception with only one hidden layer can reduce the mean average error by more than a factor of five. This result provides a sound basis for further development.
The next stage in the project, now underway, is to optimize the deep learning model. One possible change would be to the architecture (e.g., one or more additional hidden layers). However, the first step will be to use “hyperparameter tuning,” such as optimizing the number of epochs in the model (which defines the number of complete passes through the training dataset) and the activation function [which controls the output(s) of a network node given its input(s)]. The functional performance will be evaluated in controlled tests with static and dynamic load changes. In parallel, the above deep learning approach will be compared with other less computationally intensive models, such as linear regression.
4.3 Measurement of Slurry Conditions
The slurry is supplied to the Zeeko IRP600 from a slurry management unit, which comprises a thermostatically controlled tank with a propeller for agitation and a pump to direct slurry onto the part through two flexible hoses. The slurry drained off the part is then collected and gravity-fed back to the tank. This setup was modified so that one of the hoses fed into a cylindrical container, and the overflow then continued its normal path onto the part. The cylindrical container could accommodate three sensors: (1) temperature, (2) pH, and (3) the probe for a Verder Microtrac Nanotrac FLEX PSD instrument. According to the specification, the PSD measurement ranged from 0.3 nm to 10 µm, which should have been well matched to measuring cerium oxide slurries and polishing debris. This setup enabled the PSD to be measured in two ways:
-
(1)
By inserting the probe in the cylindrical container, and hence in the continuous flow, using the Nanotrac flow guard.
-
(2)
By mounting the probe in the air with the window facing up and depositing a drop of slurry with a disposable pipette (changed for each sample).
A series of polishing runs were conducted on a 100-mm square, fused silica flat sample. An aqueous slurry of cerium oxide from Universal Photonics was used, specified to have a nominal particle size range of 1.1–1.9 µm. The specific gravity of the slurry was 1.02, and the slurry management unit provided a flow rate of 1405 ml per min.
In practice, the in-flow PSD measurements proved to be unreliable, with the peak PSD shown to be in the 100–200-nm region, incompatible with the nominal particle size. For this reason, subsequent measurements used sampling with disposable pipettes.
Each polishing run was of 20-min duration, and PSD was measured at the start and at 5-min intervals. Data were collected as an average of three 10-s measurements to reduce variance. Figure 11 shows a sample of the PSD measurements taken at the start and end of a 20-min run and 5 min into the next run after a gap without polishing of ~ 3.5 h. The results show that over time, the size distribution became larger, which is due to the addition of attritted materials mixing with the original aqueous suspension or to agglomeration of the cerium oxide.
Verder has kindly provided the following commentary for inclusion in this paper: the Nanotrac FLEX instrument that we used measures PSD using dynamic light scattering (DLS). As particles move under Brownian motion, the relationship between particle size and the Doppler change in frequency between the incident and scattered light is recorded. The larger the frequency difference, the faster a particle is moving and the smaller the particle size. Dispersion conditions such as temperature and viscosity are considered in the analysis. The Nanotrac flow guard allows for stabilizing the sample in a flowing system to facilitate DLS measurements.
An issue related to DLS measurement is its dependence on Brownian motion. For larger particles, sedimentation can occur, disrupting the Brownian motion. Theoretically, the method can measure particle sizes up to 10 µm, but only for particles with a low density in a viscous medium will the measurement be satisfactory. For the approximately micron-sized particles characteristic of cerium oxide slurries,
Verder advised that a better option for us would be an instrument measuring the angular distribution of laser light diffracted off the particles (an inverse dependence of angle on particle size). Provided that the slurry is diluted with deionized water, this technique can measure particles from ~ 10 nm up to 1 or 2 mm. This capability facilitates the measurement of a wider variety of samples (e.g., diamond or 5-, 9-, or 20-µm aluminum oxide abrasives) in wet or dry systems.
Given Verder’s commentary above, the company has replaced the DLS system with an ex-demo laser diffraction instrument with auto-dilution, currently under evaluation. Preliminary results on fresh cerium oxide slurry indicate an unexpected tail of larger particles, which Verder is currently investigating.
During the PSD measurements described above, slurry pH and temperature were also logged, as shown in Figs. 12 and 13, respectively, for a typical 20-min polishing run.
The conclusion is that in standard bonnet polishing, process conditions known to affect the volumetric removal rate do change substantially in process. This finding gives cause for optimism that, with real-time monitoring and techniques such as machine learning, improvement in process convergence should be possible, which will be explored in the next phase of this work. We see this improvement as an important part of our overall strategy leading toward autonomous manufacturing.
5 Vexed Question of Surface Metrology
5.1 Context for Metrology
Surface form measurement and MSF errors are required after each process run to compute the surface error map (the difference between design and measured surface maps). The error maps are required as input for the optimization of each subsequent run, in what is hoped will be a convergent series. As the surface evolves, surface texture measurements will also be needed. A final set of measurements supports the certification of the finished part. The range of available surface metrology techniques is extensive, as is the published literature and commercial technical data.
In this paper, we take a fresh view—what would be the appropriate metrology in terms of an ultimate autonomous manufacturing cell? The key issue here is the diversity of surfaces required in today’s optical systems, in particular
-
ROC varying from short to long concave, flat (∞), then long to short convex
-
Aspheres, off-axis aspheres, and true freeforms
-
Various shapes and sizes, sometimes with perforations.
5.2 Appropriateness of Traditional Form Metrology
Taking form metrology first, numerous traditional methods exist, based on the general principle of wavefront-sensing, e.g., a Fizeau or Twyman–Green interferometer, and slope-measuring technologies such as Hartmann, Shack–Hartmann, Ronchi, Foucault, and similar technologies, with slope data numerically integrated to provide the surface form. Each method must be individually configured for the optical prescription of the surface under test. These methods suffer dynamic range limitations (the ratio of the range of surface heights or slopes over the part to the required measurement accuracy). This limitation often makes the use of nulling optics indispensable when measuring substantial departures from a sphere or flat surface. A further complication arises when the part has significant errors such that even with null optics, the dynamic range requirements exceed what can be achieved. This complication can be mitigated by subaperture stitching but with an accumulation of stitching errors. The range of ROCs also provides an obstacle to incorporating optical tests within an autonomous cell, unless additional optics are included to compact long radii of curvature or measure convex surfaces; auxiliary optics must be designed and manufactured on a case-by-case basis. Commonly, the optical test configuration, once designed and toleranced, must then be aligned with tolerances sometimes down to microns.
The underlying issue with nulling is that the problem is “ill-conditioned” in the sense that the result is the difference between two large numbers:
-
1.
The aberrated wavefront off the surface under testing (SUT).
-
2.
The inverse nulling wavefront.
The Hubble Space Telescope provides informative insight [20] into how this can go disastrously wrong for apparently trivial reasons.
These traditional optical techniques, despite their potential for nanometer accuracies, do not sit well with the concept of an autonomous manufacturing cell because of the bespoke nature of the setup and the tight tolerances required.
5.3 Software Configurable and Scanning Long-Wave Optical Tests
Several “reflectometry” techniques are available, where the deflection of a beam of light reflected off the SUT is detected optically. Strictly speaking, these methods include the slope-measuring techniques in Sect 5.2 above, such as Ronchi and Hartmann. Here, we focus on a high-performance version—the University of Arizona software configurable optical test (SCOTS). SCOTS [21] is based on illuminating a mirror under testing with patterns generated on a computer display, which the mirror then images onto a digital camera. In this case, the patterns can be phase-shifted, and nulling is provided by defining appropriate patterns according to a ray-tracing optical design. Once again, the setup must be engineered according to the detailed prescription of the surface to be measured, and the integrity of form measurement depends critically on the geometric relationships between the display, mirror, and camera. Nevertheless, the method can be exploited in an autonomous cell for determining MSFs. Similar arguments apply to the Arizona scanning long-wave optical test [22], which uses a moving hot wire as a source to measure rough surfaces.
5.4 “Mechanical” Form Metrology Methods
Overall, we conclude that direct optical form metrology is ill-suited for an autonomous cell because of the complexity of reconfiguring for different SUTs and the challenging optomechanical tolerances often required. Therefore, we turn to mechanical systems, principally:
-
“Bed of nails”
-
Coordinate measuring machine (CMM)
-
Scanning profilometers for various types
5.4.1 “Bed of Nails”
The “bed of nails” comprises a 2D array of parallel linear displacement probes mounted on a common metrology frame. This frame is lowered to bring the probes into contact (or proximity) with the SUT. Badami et al. [23] described the performance of this instrument based on Zygo’s ZPS™ system, which offers a massively parallel arrangement of up to 64 small-footprint, noncontact, absolute sensors. The sensor resolution is given as 0.01 nm with ≤ 1 nm/day stability [24]. Badami et al. concluded that their results “show that an array of ZPS position sensors can measure changes in mirror shape to subnanometer levels for small mirror deformations (including low-order shape).” They then remark that “Calibration of the array against a known shape could also enable in situ metrology of the absolute mirror shape in its in-use mounted condition.”
This approach has a great advantage in that multiple measurements are conducted simultaneously, giving a “multiplex advantage.” The two main issues are, first, that the measurement range is limited by the sensor technology (1.2 mm for ZPS™). Second, if a fixed array were constructed and then deployed for a smaller or larger SUT, the surface would be under-sampled in both cases. Therefore, for optimal performance, the array must be constructed for each size of the part. This limitation points to measurement methods that scan the surface.
5.4.2 Coordinate Measuring Machine
CMMs rely on precise linear XYZ motions (almost always a hydrostatic or aerostatic bearing) to traverse a contact or noncontact probe over the SUT, usually sampling discrete points (“pick and poke”), typically in a rectilinear grid. Accuracy tends to be limited to the micron or marginally submicron regime in the highest-quality instruments. For example, the Zeiss PRISMO Ultra [25] claims a measurement error of 0.5 + L/500 µm, where L is the traverse length. This accuracy is insufficient to close the process loop in fine corrective polishing but is sufficient to assess the results of earlier process steps, such as CNC grinding.
5.4.3 Profilometry
Here, a probe (contact or noncontact) is mechanically scanned across the SUT, often using a hydrostatic or aerostatic linear bearing. However, ultraprecision linear bearing systems tend to be less accurate than equivalent rotational bearings. This lower accuracy is obtained because, in the linear case, the moving carriage is short compared with the fixed rail, and as it moves, it follows the rail’s height and slope errors. For a rotational system, the rotor remains in complete and constant contact with the full circumference of the stator, averaging bearing errors.
Given the advantages of a rotational system, the most attractive profilometer for an autonomous cell is the swing-arm profilometer conceived by the University of Arizona [26] (and in the context of this narrative, also confusingly described as an “optical CMM”). This profilometer uses an extended arm supported by a precision rotary air bearing (with a nominally vertical axis), with a probe at one end. The probe then scans the SUT in an arc across the center. In the Arizona implementation, the SUT is carried by a rolling-element rotary polishing table.
The axis of the air bearing may then be inclined to the vertical to compensate for the base ROC of the SUT, the probe then measuring aspheric departure, not the depth of the curve (“sag”). As reported [26], by rotating the mirror in fixed steps and scanning the mirror between each step, the 3D topography of the SUT can be synthesized using a maximum likelihood method. A refinement is to use two probes aligned to swing along the same trajectory on the part. Both probes see the same bearing errors while measuring different portions of the mirror, so they can be decoupled. Form accuracies can be down to the nanometer regime. Michal et al. described [27] a commercial swing-arm profilometer of the same geometry manufactured by Zeeko Ltd.
5.4.4 Huddersfield Profilometer at Daresbury
Figure 14 shows the Huddersfield instrument measuring a 1.6-m off-axis aspheric, lightweight aluminum mirror. The arm is mounted on a 685-mm diameter RPI combination turntable, which has an axial air bearing with a mechanical bearing for radial restraint, providing an extremely cost-effective solution. Nevertheless, compared with the PI bearing adopted by Arizona, the performance is inferior, with rotation errors < 5 μm, radial runout < 1 μm, and coning < 1 arcsec.
This instrument is also different in that the arm always swings precisely in the horizontal plane. The part is mounted on a mechanical rotary stage, which itself can be inclined on a massive tilt stage to compensate for the base ROC. This design has the advantage that the turntable, swinging arm, and probe are not subject to a varying gravity vector, which can cause mechanical flexure and hysteresis. Additionally, because the arm is horizontal, small tilt errors in the radial and lateral directions can be determined with clinometers. If the instrument is configured with the SUT also precisely horizontal, then the probe will measure the absolute form directly. Digital clinometers are readily available; for example, the Taylor Hobson Talyvel 6, based on a pendulum, has a range of 800 arcsecs, a resolution of 0.001 arcs, and the highest accuracy of 0.2 arcsecs. [28]. We purchased two rugged and much less expensive ACA826T two-axis micro-electromechanical system inclinometers from StrainSense with ranges of ± 15° and ± 1° (Fig. 15). The former inclinometer has a specified static accuracy of 3.6 arcsec and a resolution of 1.8 arcsec.
The simplicity of the horizontal arm and the possibility of measuring tilt errors comes at a price—potential gravity distortion of the SUT if it is inclined to compensate for the base ROC. Nevertheless, for the modest optics within the scope of this paper, and recognizing that they usually operate at different orientations, we consider that this distortion is a small price to pay. The decision on whether to tilt the SUT depends on whether the probe can accommodate the range of sags and local slopes. We currently use a SIOS displacement interferometer, CHRocodile chromatic aberration probes, and Solartron contact probes.
The swing-arm profilometer is our choice for form metrology within an autonomous cell because of its versatility for measuring different geometries and forms, avoidance of bespoke configurations, a wide range of available probes, and potential for accuracy. The key will be an investment in the highest-quality air bearing for the swinging arm.
5.5 Texture Metrology
The measurement of surface texture presents less of a challenge than that of surface form, as various companies produce texture interferometers that can measure down to subnanometer Sa. To illustrate how this measurement can be automated, Fig. 16 shows the measurement of the surface texture of a prototype mirror segment for the European Extremely Large Telescope. This study was conducted at the OpTIC Center in North Wales (where the Huddersfield group, now at Daresbury, was previously based). Figure 13 shows a simultaneous phase, vibration-insensitive texture interferometer provided by 4D Inc., mounted into the tool chuck of a Zeeko IRP1600 CNC machine used to polish the segments. The machine CNC control was then used to translate and incline the texture interferometer to conduct a spot test of a ~ 1-mm2 area over the segment.
5.6 Cleaning the Part
To implement form and texture metrology within an autonomous manufacturing cell, one complication would be the effective cleaning of the part after polishing and before measurement. Given the capability to incline the part, which is desirable in swinging arm profilometry to null the base radius, the most effective treatment is to flood the part with low-pressure jets of deionized water, with final drying using an air knife supplied from a clean, dry compressed air hose.
6 Computational Fluid Dynamics Modeling of Slurry Mobility in Bonnet Polishing
Computational modeling enables investigating and quantifying experimentally inaccessible parameters and process variables. Additionally, the mechanical polishing process includes a wide range of lengths and time scales, complicating the analysis. An example of these length scales is described in Eq. (1) below:
We consider here the polishing process, using a precessed, inflated bonnet rotating around its axis. The largest characteristic length scale corresponds to the bonnet diameter [29] and is 80 mm. Alternatively, the smallest length scale is the particle size and is in the range of a few μm. Therefore, similar to the processes identified in the introduction, computational fluid dynamics (CFD) can also be described in a process chain, starting with global flow field predictions and becoming increasingly more refined for local flow information. Each flow regime can be categorized by evaluating the Knudsen number, Kn, which is expressed in Eq. (2):
where \(\lambda\) is the mean free path of particles, and L is the representative length scale. The different computational methods available for these problems are as follows:
-
1.
Macroscopic—continuum assumption-based modeling, typically using a finite volume formulation of the Navier–Stokes equations (Kn < 1).
-
2.
Mesoscopic—a statistical representation of particle kinematics. Examples include the lattice Boltzmann method, smoothed particle hydrodynamics, and Monte Carlo methods (Kn < ~ 1).
-
3.
Microscopic—physically modeling the kinematics of molecules (Kn > 1).
Continuum-based modeling is therefore used to obtain information on the slurry flow characteristics, as resolving particle dynamics at this scale is computationally intractable and ultimately not very useful. Therefore, useful outputs of the velocity (illustrated in Fig. 17), volume fraction, and hydrodynamic force are extracted from these simulations.
A further illustration of the useful quantitative properties that can be extracted from continuum-based modeling is the shear stress on the glass surface. For example, in Fig. 18, the shear stress plot along the X axis (defined in Fig. 17) is extracted, highlighting the localized peak shear stress underneath the polishing tool.
Research interest in annular polishing is considerable, with numerous studies, experimentally and computationally, focusing on determining optimum polishing process parameters. Liu et al. [30] experimentally examined annular polishing to investigate the optimization of polishing parameters, such as the physical characteristics of polishing pad material, polishing time, and the rotation speed of the polishing disk. Terrell et al. [31] performed a hydrodynamic analysis based on wafer surface polishing to elucidate the importance of relevant parameters, including slurry film thickness distribution, pressure field, and shear rate, on the effectiveness of chemical–mechanical polishing.
Further research focused on experimentally developing a model based on the mechanical and chemical mechanisms proposed by Kaufman et al. [32]. Xin et al. [33] also developed a mathematical model to describe the aforementioned material removal mechanisms. They described how an understanding of the material removal rate based on the shear stress is useful in interpreting the edge and doming effect. Schneckenburger et al. [34] performed polishing operations with the application of a machine learning model for robot polishing to predict material removal at the nano-level. They combined the polishing process with artificial intelligence to optimize process technology, enabling better accuracy in glass polishing.
Numerical modeling of the polishing process depends heavily on being able to model the slurry flow accurately. Slurry flow modeling is a branch of macroscopic CFD, which has been extensively studied and has two distinct approaches, namely, multiphase modeling and discrete phase modeling—or, more generally, Eulerian- and Lagrangian-based techniques. For example, to model FJP [35,36,37,38], discrete phase (Lagrangian) techniques used for tracking particle trajectories are coupled with Eulerian solvers used to determine the flow characteristics. This approach offers a unique advantage, as particle trajectories are readily available and can be used as inputs for abrasion modeling and a subsequent prediction of the material removal rate. However, for Eulerian–Eulerian modeling, granular models [39, 40] can be used to simulate suspended particles. This technique has been used successfully to model the transport of slurries through pipes [41,42,43]. Furthermore, our previous studies focused on modeling slurry flows have investigated the impact of PSD in pipelines, quantifying flow velocity, particle concentration, pressure drop, wear characteristics, and hold-up ratio with good experimental agreement [44,45,46,47,48].
An example of the usefulness of the Eulerian–Eulerian approach for the modeling of annular polishing is the ability to determine, on a macroscopic basis, the volume fraction of particles at each point in the computational model, an example of which is illustrated in Fig. 19. This information coupled with additional information (described in the following section) may provide useful indications of the material removal rate on the glass surface. The rotational speed of a bonnet affects the concentration and the velocity fields of the slurry mixture, thus affecting the material removal rate on the glass surface. Here, the concentration fields corresponding to two rotational speeds of the bonnet are presented. The precession angle applied to the tool is 15°; therefore, the symbols “O” and “ + ” are used to mark the rotation axis and the model origin, respectively. Figure 19 shows that the rotational speed affects the distribution of particles, making concentration fields highly nonuniform, increasing concentration in the lower two quadrants. Furthermore, the extent of nonuniformity increases with rotational speed.
However, with this approach, to the authors’ knowledge, no mechanistic model has been formulated to predict the material removal rate directly. Therefore, in the following section, a novel process for predicting the material removal rate using the Eulerian–Eulerian-based CFD model coupled with a molecular dynamics (MD) model is presented.
7 Material Removal Modeling by the Interpretation of CFD Outputs Through Molecular Dynamics Models at the Nanoscale
The material removal in the polishing processes results from interactions between solid abrasive grains, slurry liquid, and solid glass. The modeling of material removal comprises a set of models at the macro-, micro-, and nanoscales. Although CFD facilitates modeling the polishing process at the macro- and microscales, providing useful information on fluid pressure, speed, and abrasive particle distribution, the material removal interactions require MD analysis to interpret the material removal mechanism at the nanoscale. MD can also simulate the chemical, physical, mechanical, and tribological phenomena of the polishing process and estimate the material removal rate at nanoscales [49]. The combination of the CFD modeling with MD simulation can predict the material removal rate at varying scales from the nanoscale to the macroscale. The idea is to take the results of CFD analysis as the inputs of MD simulation. The MD simulation will illustrate the material removal under the variation in abrasive motion in the polishing contact zone. The design of an adequate interface is essential to obtain a good combination of these two simulation methods. The definition of the inputs and outputs that link each simulation method, as well as total polishing process control and performance parameters, is vital for an appropriate interface design. The information flows between the CFD and MD simulation methods are illustrated below in Fig. 20.
The CFD simulation of fluid in and near the polishing zone provides information on fluid velocity, fluid pressure, and the abrasive slurry grain distribution volume fraction. This information may be further interpreted in terms of abrasive velocity distribution, hydrodynamic force, and abrasive grain distribution. An MD simulation can potentially provide the material removal rate per grain, which can be presented as a function of the sliding velocity, normal force, and grit size. The sliding velocity (\(\overrightarrow {{V_{{\text{S}}} }}\)) is a function of the bonnet velocity (\(\overrightarrow {{V_{{\text{B}}} }}\)) and fluid velocity (\(\overrightarrow {{V_{{\text{F}}} }}\)), as seen in Eq. (3):
Given that micron-sized grits can deliver nanometer or even subnanometer textures, a reasonable assumption is that grit sliding, not rolling, performs the material removal. Depending on the grit motion situation, the grit-sliding speed should be equal to the bonnet surface speed of the rotation when the grit is held by the bonnet or the fluid speed when the grit is floating with the fluid.
Another reasonable assumption is that the normal forces applied on grits in polishing are mainly exerted by the bonnet. The normal force (FN) applied on the grit that is held by the bonnet may then be estimated using Eq. (4):
where FB is the bonnet pressing force on the optical glass sample, FH is the hydrodynamic reaction force in the polishing contact area, and N is the number of grits that are held by the bonnet. FB was calculated using the experimental data of polishing, while FH was provided by a CFD simulation. N was estimated by combining the experimental data and CFD simulations. N was calculated with Eq. (5):
where VFrac is the volume fraction, VBonnet is the contact volume of the bonnet on the optical glass material, and VGrain is the volume of the grain. VFrac was obtained from CFD simulations, while VBonnet and VGrain were obtained from experimental data.
Notably, MD is performed with a Reax force field potential function, as this approach allows the simulation of several chemical reactions (e.g., redox, organic, and replacement reactions) of the materials at the same time as the physical processes [49,50,51,52]. Large-scale atomic/molecular massively parallel simulator (LAMMPS) software was employed to perform the MD simulations because of its versatility and availability [53]. The simulations were visualized using the open visualization tool (OVITO) [54].
The material removal (M.R.G) per grain in a polishing collision can be estimated using the interaction cross-sectional area between grit and workpiece, which can be determined by MD simulation (Fig. 16).
where De is the depth of the polishing by the grain, r is the grain radius, and l is the polishing distance.
Figure 21a provides the simulation results for fused silica polishing with a single α-alumina grain at a 4-piconewton normal force and 20 m/s sliding velocity. De can be estimated from the cross section of the polishing processing simulation (Fig. 21b). This parameter is defined with FN (Fig. 21c) and VS (Fig. 21d) according to the MD simulations. De increased with FN while the polishing length l increased with VS.
The total material removal rate (MRRT) was finally calculated with the following Eq. (7):
where Nu is the number of grits passed in a unit contact area and in a unit polishing time. Current work focuses on using CFD simulations to predict the flow rate of slurry through the contact area with the glass under the bonnet, and the volume fraction of cerium oxide can be calculated from the measured specific gravity. This information should be sufficient to predict the volumetric removal rate in mm3/min, which can be compared with the experiment.
Using the procedure described above, the gap between the macroscopic and microscopic modeling approaches for predicting the material removal rate under mechanical polishing can thus be bridged. Future work aims to use the physical insights at the macro- and microscales to optimize the polishing process to obtain the desired surface finish. Furthermore, the different numerical methods are to be used in conjunction to develop a generalized reduced-order model capable of predicting the material removal rate for different materials and surface topographies.
8 Conclusions and the Way Forward
Our ultimate objective of autonomous manufacture for fine optics and similar ultraprecision surfaces is extremely challenging and remains difficult to achieve. Nevertheless, we have taken steps in this direction. With the reported work, the ultimate realization is starting to take shape, and our goal will be to develop, apply, and integrate the different tools at our disposal. This undertaking is strategically critical, given the growth in demand for precision optics and the shrinkage in available skilled technicians and craftspeople to make them, even given modern CNC machine tools.
Clearly, the first step in tooling up for the industrial (or indeed scientific) manufacture of precision optical components to a new design is to identify the optimum process chain. We have observed the current situation, where the communication between the optical design and the fabrication chain design is conducted by humans, and noted that this should be minimized to eliminate skewing of the results by psychological and diplomatic factors. In this regard, the PanDao software we have described encapsulates a comprehensive knowledge base of available processes and selects individual process steps for maximum positive impact on the manufacturing chain.
Given the individual process steps, we then address the optimization of the process parameters. We have commented critically on our past work capturing master optician expertise through video and audio monitoring, noting the fatal flaw that this approach is unlikely to be viable in an industrial environment. This flaw has led us to change our approach, recognizing that various relevant processes, parts, and metrology data are naturally available to the machine software, as they are required to generate a CNC tool path file. We have also proposed the QR-coding of standard tooling. Presently, the principal missing information concerns the type of abrasive and the substrate material of the part, the combination of which profoundly impacts optimum polishing parameters and performance. The substrate material is easier to capture digitally, as it is resident in the optical design software and could be transferred to the process software in a more integrated system. Automatically capturing slurry abrasive composition is challenging; thus, we have proposed a workaround—the machine GUI demands manual input, the justification that the software automatically uses to optimize the process parameters. In a truly autonomous cell, different abrasive media would be automatically selected from cassettes, circumventing this problem. The comprehensive data then resident in the machine computer of an autonomous cell can be deployed to enhance a local database, providing input to machine learning algorithms.
In addition, the autonomous cell opens the door to automated data transmission for enhancing a substantially deeper and more diverse global process database representing the user community. We have drawn attention to the advantages and disadvantages to end-users and noted that auto-reporting must be subject to opt-out, as is common in internet businesses that garner customer data.
We have noted that any advance in process determinism will reduce the number of process iterations and the process risk, enhancing cost and time effectiveness. We acknowledge that the first purpose of our CFD/MD modeling is to enhance fundamental knowledge. From this purpose follows the second aim: to use that knowledge to aid the interpretation of real-time sensor data to detect drifts in the removal rate and the onset of defects and modify process parameters in real-time accordingly. In other words, the philosophy is not to rely on “blind” machine learning but to use modeling to inform and constrain it. For this philosophy to work in an industrial environment, we must extend the modeling to embrace a range of representative substrate materials.
This approach has required the development of sensor technologies, principally force and slurry conditions, and we have reported on preliminary results and arising issues. Although the reported work is only the start, we now have a clear direction on the way forward.
As is often said, “metrology is king,” and the concept of an autonomous cell is no exception. We have abandoned traditional null optical tests and subaperture stitching because of their bespoke nature. Rather, we have focused on profilometry to perform form measurements, supplemented by reflectometry (a version of SCOTS) to improve the resolution of mid-spatial frequency features.
Ultimately, we envisage an integrated software environment that brings together the PanDao preplanning of process chains with part descriptions, metrology data acquisition and analysis, process optimization, and tool path generation. This environment will be served by the databases of past job files, including process data and surface metrology data. Real-time process sensor data and their interpretation will then be feedback to modify appropriate process conditions to improve process convergence.
Overall, we recognize that, at present, attempting to build an autonomous manufacturing cell for fine optics is far too ambitious and most unlikely to succeed. Rather, we have adopted an incremental approach in which each separate advance is useful in itself and plays a role in taking us toward the final goal. In this way, our approach mirrors the one adopted by companies such as Tesla in striving for their ultimate ambition of autonomous driving.
Availability of Data and Materials
The data presented in this paper is preliminary, as the paper reports work currently in progress. Data can be provided on request. Publicly available data will await the completion of the work.
Abbreviations
- CFD:
-
Computational fluid dynamics
- CMM:
-
Coordinate measuring machine
- CNC:
-
Computer numerical control
- DLS:
-
Dynamic light scattering
- Hz:
-
Hertz
- IRP:
-
Intelligent robotic polisher
- MD:
-
Molecular dynamics
- ML:
-
Machine learning
- MRR:
-
Material removal rate
- OFT:
-
Optical fabrication technology
- PSD:
-
Particle size distribution
- QR:
-
Quick response
- Rpm:
-
Revolutions per minute
- ROC:
-
Radius of curvature
- SCOTS:
-
Software configurable optical test
- SUT:
-
Surface under testing
- T:
-
Temperature
- V :
-
Velocity
References
Walker D, Li H, Longstaff A, Pan W, Parkinson S, Petrovic S, Wilson K, Yu G (2018) Fully automating fine-optics manufacture—why so tough, and what are we doing?. In: European optical society biennial meeting 2018 (EOSAM 2018), Delft
Subramanian D (2019) A simple introduction to k-nearest neighbors algorithm. https://towardsdatascience.com/a-simple-introduction-to-k-nearest-neighbors-algorithm-b3519ed98e. Accessed 2022
Fahnle O, Rascher R, Tinner M (2021) Optical fabrication chain design. Photonics Rev 18(4):43–45
Faehnle O (2022) Modeling of optical fabrication chains during optics design. In: International conference on optics-photonics design & fabrication (ODF), Sapporo, Japan
Faehnle O (2016) Process optimization in optical fabrication. SPIE Opt Eng 55(3):035106–035106
Cook L (1990) Chemical processes in glass polishing. J Non-Cryst Solids 120(1):152–171
Faehnle O, Doetz M, Dambon O, Langenbach E (2018) Process controlling of surface roughness while ductile mode machining. In: Proceedings of SPIE conference on “precision optics manufacturing”, Deggendorf Institute of Technology, Deggendorf, Germany
Arnold T, Liebeskind T, Felli A, Faehnle O (2019) Reducing polishing time by previous subsurface damage removal applying wet chemical etching. In: Proceedings of SPIE conference on “Precision Optics Manufacturing”, Deggendorf Institute of Technology, Deggendorf, Germany
Faehnle O, Zygalsky F, Langenbach E, Frost F, Fechner R, Schindler A, Cumme M, Biskup H, Wunsche C, Rascher R (2015) Fabrication and qualification of roughness reference samples for industrial testing of surface roughness levels below 0.5 nm Sq. In: Optical manufacturing and testing XI, San Diego
Kordonski WI, Jacobs SD (1996) Magnetorheological finishing. Int J Mod Phys B 10:2837
Thomas F, Hansel T (2008) Ion beam figuring (IBF) solutions for the correction of surface errors of small high performance optics Optical Fabrication and Testing. In: Optical Society of America, 2008 frontiers in optics, optical fabrication and testing, no. Franz Thomas, and Thomas Hänsel
Fahnle O, van Brug H, Frankena H (1998) Fluid jet polishing of optical surfaces. Appl Opt 37(28):6771–6773
Fahnle O (2012) Abrasive jet polishing approaches to the manufacture of micro-optics with complex shapes. In: Proceedings of optical fabrication and testing, Monterey, CA, USA, in imaging and applied optics technical papers
Fahnle O, Rascher R, Vogt C, Kim D (2018) Closed-loop laser polishing using in-process surface finish metrology. Appl Opt 57:834–838
Kwon K, Song K, Seo J, Chu C, Ahn S (2021) Precise glass microstructuring with laser induced backside wet etching using error-compensating scan path. J Mater Process Technol 291:117046
Arnold T, Boehm G, Paetzelt H (2016) Optical freeform generation by laser machining and plasma-assisted polishing. J Eur Opt Soc Rapid 11:16002
van der Bijl RJ, Fähnle OW, van Brug H, Braat JJ (2000) In-process monitoring of grinding and polishing of optical surfaces. Appl Opt 39(19):3300–3303
Schneckenburger M, Garcia L, Boerret R (2019) Machine learning robot polishing cell. In: Fifth European seminar on precision optics manufacturing
Jin T, et al (2022) Design and analysis of a low crosstalk error nested structure two-dimensional micro-displacement stage. https://doi.org/10.1177/16878140211014061#bibr10-16878140211014061. Accessed 2022
NASA (2022) The Hubble space telescope optical system failure report, 990. https://ntrs.nasa.gov/api/citations/19910003124/downloads/19910003124.pdf. Accessed Oct 2022
Huang R et al (2014) Optical metrology of a large deformable aspherical mirror using software configurable optical test system. Opt Eng 53(8):085106
Yoo H, Smith GA, Oh CJ, Lowman AE, Dubin M (2018) Improvements in the scanning long-wave optical test system. In: Optical manufacturing and testing XII
Badami VG, Abruña E, Huang L, Idir M (2019) In situ metrology for adaptive x-ray optics with an absolute distance measuring sensor array. Rev Sci Instrum 90:021703
Zygo Corp. Absolute position sensors. https://www.zygo.com/products/nano-position-sensors/absolute-position-sensors
Zeiss. ZEISS PRISMO Family. https://www.zeiss.co.uk/metrology/products/systems/coordinate-measuring-machines/bridge-type-cmms/prismo.html. Accessed Oct 2022
Su P, Parks RE, Wang Y, Oh CJ, Burge JH (2012) Swing-arm optical coordinate measuring. Opt Eng 51(4):043604
Michal S, Horvath P, Hrabovsky M, Chytka L, Mundat D, Nozka L, Palatka M, Pech M, Shovanek P, Vacula M (2022) Swing arm profilometer as a tool for measuring the shape of large optical surfaces. Optik 264:169419
“Talyvel®6 and Clinometers,” Taylor Hobson. https://www.taylor-hobson.com/-/media/ametektaylorhobson/files/product-downloads/electronic-levels-and-clinometers/inclinometers-en.pdf?la=en&revision=774b6201-52c3-45de-bf01-84d43bd0ad8f
Choudhary S, Kumar Duvedi R, Singh Saini J (2022) Effect of material removal characteristics with varying incident angle in fluid jet polishing process. Mater Today: Proc 62:215–219
Liu Y, Han L, Liu H, Shi Y, Zhang J (2018) Experimental optimization of annular polishing parameters for silicon carbide. Adv Mater Sci Eng 2018
Terrell EJ, Higgs CF (2006) Hydrodynamics of slurry flow in chemical mechanical polishing: a review. J Electrochem Soc 1453(6):K15
Kaufman F, Thompson D, Broadie R, Jaso M, Guthrie W, Pearson D, Small M (1991) Chemical-mechanical polishing for fabricating patterned W metal features as chip interconnects. J Electrochem Soc 138(11):3460
Xin J, Cai W, Tichy J (2010) A fundamental model proposed for material removal in chemical–mechanical polishing. Wear 268(5–6):837–844
Schneckenburger M, Höfler S, Garcia L, Almeida R, Börret R (2022) Material removal predictions in the robot glass polishing process using machine learning. SN Appl Sci 4(1):33
Choudhary S, Duvedi RK, Saini JS (2022) Effect of material removal characteristics with varying incident angle in fluid jet polishing process. Mater Today: Proc 62:215–219
Buss L, Qi Y, Heidhoff J, Riemer O, Fritsching U (2022) Towards an understanding of multiphase fluid dynamics of a microfluid jet polishing process: a numerical analysis. Fluids 7(3):119
Cao Z-C, Cheung CF (2014) Theoretical modelling and analysis of the material removal characteristics in fluid jet polishing. Int J Mech Sci 89:158–166
Zhang L, Yuan Z, Qi Z, Cai D, Cheng Z, Qi H (2018) CFD-based study of the abrasive flow characteristics within constrained flow passage in polishing of complex titanium alloy surfaces. Powder Technol 333:209–218
Gidaspow D (1994) Multiphase flow and fluidization: continuum and kinetic theory descriptions. Academic Press, Cambridge
Lun C, Savage SB, Jeffrey D, Chepurniy N (1984) Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J Fluid Mech 140:223–256
Li M, He Y, Liu Y, Huang C. Computational fluid dynamics modelling of slurry transport by pipeline. https://www.sci-en-tech.com/ICCM2018/PDFs/3148-10999-1-PB.pdf. Accessed 2022
Gopaliya MK, Kaushal D (2016) Modeling of sand-water slurry flow through horizontal pipe using CFD. J Hydrol Hydromech 64(3):261
Sultan RA, Rahman MA, Rushd S, Zendehboudi S, Kelessidis VC (2019) Validation of CFD model of multiphase flow through pipeline and annular geometries. Part Sci Technol 37(6):685–697
Asim T, Mishra R, Kollar LE, Pradhan SR (2014) Optimal sizing and life-cycle cost modelling of pipelines transporting multi-sized solid–liquid mixtures. Int J Press Vessels Pip 113:40–48
Kumar U, Mishra R, Singh S, Seshadri V (2003) Effect of particle gradation on flow characteristics of ash disposal pipelines. Powder Technol 132:39–51
Mishra R, Singh S, Seshadri V (1998) Study of wear characteristics and solid distribution in constant area and erosion-resistant long-radius pipe bends for the flow of multisized particulate slurries. Wear 217(2):297–306
Mishra R, Singh S, Seshadri V (1998) Pressure drop across conventional and diverging-converging pipe bends in the flow of multi-sized particulate slurries. Indian J Eng Mater Sci 5:9–14
Seshadri V, Singh S, Fabien C, Mishra R (2001) Hold-up in multi-sized particulate solid-liquid flow through horizontal pipes. Indian J Eng Mater Sci 8:84–89
Aktulga HM, Fogarty JC, Pandit SA, Grama AY (2010) Parallel reactive molecular dynamics: numerical methods and algorithmic techniques. https://www.cs.purdue.edu/puremd/docs/Parallel-Reactive-Molecular-Dynamics.pdf. Accessed 2023
Ahuir-Torres J, et al (2022) Study of the normal force and velocity influence on the fused silica scratching mechanisms with α-alumina grit at atomic scale via reaxff reactive molecular dynamic simulations. In: Proceedings of the 24th international symposium on advances in abrasive technology, Guangzhou
Liu L, Jaramillo-Botero A (2012) Development of a ReaxFF reactive force field for ettringite and study of its mechanical failure modes from reactive dynamics simulations. J Phys Chem A 116(15):3918–3925
Agrawalla S, van Duin AC (2011) Development and application of a ReaxFF reactive force field for hydrogen combustion. J Phys Chem A 115(6):960–972
FrantzDale B, Plimpton SJ, Shepherd MS (2010) Software components for parallel multiscale simulation: an example with LAMMPS. Eng Comput 26:205–2011
Stukowski A (2009) Visualization and analysis of atomistic simulation data with OVITO—the open visualization tool. Modell Simul Mater Sci Eng 18(1):015012
Acknowledgements
We gratefully acknowledge several research grants from the UK EPSRC and STFC research councils and Innovate-UK, which financed various aspects of the research reported. We also appreciate Huddersfield University’s significant internal funding for equipment. We thank Professor S. Petrovic of Nottingham University and Drs. S. Parkinson and K. Wilson and colleagues of Huddersfield University for their invaluable contributions to the psychology and CBR aspects of capturing crafts expertise. This work would have been impossible other than for the cooperation of the OpTIC Centre in St Asaph, UK, operated by Glyndwr University, who provided access to their IRP1200 CNC polishing machine and three machine operators. The measurement of particle size distribution has proved to be a much deeper subject than we envisaged. We have been both impressed and appreciative of the support that Andy Winn and Jack Armitage of Verder Scientific have provided, including a critical commentary included in this paper on our preliminary results and recommendations for the best way forward. We gratefully acknowledge Chenhui An’s diligent work optimizing the force table design over many iterations, achieving the required dynamic performance, providing the FEA data in this paper, and arranging for the manufacture of the instrument.
Funding
Funding was provided by Engineering and Physical Sciences Research Council (Grant Nos. EP/V029304/1, EP/V029274/1, EP/V029266/1, EP/V029401/1) and Innovate UK (Grant No. 10029272).
Author information
Authors and Affiliations
Contributions
DW coordinated the paper and contributed Sects. 1, 2, and 4 and the Conclusion. XC and JA-T undertook molecular dynamics modeling. RM and YA undertook the computational fluid dynamic modeling with Frankie Jackson coordinating the interface with molecular dynamic. PB advised on the physics and chemistry underlying polishing processes. MD developed and executed the experimental methods to calibrate the Force Table and acquired the preliminary polishing force data. He is now working on full calibration using machine learning. OF contributed to the section on PanDao modeling. LM and PG provided access to and support for the use of high-performance computing for modeling. GL, HL and AS comprised a team that undertook the polishing experimental work reported in this paper. HL was also responsible for building, commissioning and using the swing arm profilometer described in Sect. 5. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethical Approval
Not applicable.
Consent for Publication
Not applicable.
Competing interests
David Walker declares he is a Director of Zeeko Ltd. The authors declare that they have no competing interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Walker, D., Ahuir-Torres, J.I., Akar, Y. et al. Bridging the Divide Between Iterative Optical Polishing and Automation. Nanomanuf Metrol 6, 26 (2023). https://doi.org/10.1007/s41871-023-00197-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41871-023-00197-3