1 Introduction

High-precision absolute distance measurement plays a key role in precision machining [1], advanced assembly [2], space detection [3], and other fields. Different from the traditional incremental laser interference, the point-to-point measurement ability and relative accuracy better than 10−6 of the high-precision absolute distance measurement give it a higher measurement efficiency, flexibility, and adaptability [4]. To realize the comprehensive perception from a one-dimensional length to a six-dimensional pose, multiple lengths are often required to be measured while keeping the accuracy of laser interference ranging. For example, in the semiconductor tracker (SCT) of a particle accelerator, hundreds of absolute rangefinders are laid to weave the length grid, and the length variation of the multichannel interferometer can reflect the three-dimensional deformation of SCT to achieve a continuous correction of the detector array alignment [5].

Commonly used high-precision absolute distance measurement methods include multiwavelength interference [6], optical frequency scanning interference (FSI) [7], and femtosecond optical frequency comb (OFC) interference [8]. Multiwavelength interference distance measurement needs to detect the interference phase of the interference wavelength to build the virtual synthetic wavelength and then expand the nonambiguity range. Hence, it is necessary to multiply the optical components and photoelectric detectors to perform a multichannel distance measurement. Subsequently, FSI can realize the absolute distance measurement by detecting the change in the interference phase during optical frequency scanning. The method is simple and does not depend on the initial distance value. It has a good integration degree when multiple channels are extended. However, the reading accuracy of the optical frequency directly determines the distance measurement accuracy, and it relies on the auxiliary interferometer, gas absorption cavity, and other additional devices for optical frequency calibration, which increases the complexity of the system to a certain extent [9].

The OFC is characterized by an ultrashort pulse sequence with an extremely stable pulse spacing in the time domain and numerous discrete, uniform, and traceable optical spectral lines in the wide spectrum in the frequency domain. Based on its unique time–frequency characteristics, in the past 20 years, various absolute distance measurement methods have been developed, such as pulse alignment interference [10], inter-mode beat interference [11], dispersive interference [12,13,14], and dual-comb interference [15]. A unique advantage appears when the OFC absolute distance measurement is used for multichannel expansion. Femtosecond-pulsed time-of-flight distance measurement, which takes pulse spacing as the scale, can realize the accuracy of the wavelength level under the nonambiguity range of the meter magnitude. When the pulse sequence is simultaneously applied to multiple targets, multiple delay pulses appear at the receiving end. Multichannel distance measurement signals can be simultaneously acquired by continuous optical sampling, and a multiobject parallel measurement can be realized. In 2015, Han et al. from the Korea Advanced Institute of Science and Technology combined the dual-comb balance detection technology with the multichannel distance measurement capability to achieve a simultaneous measurement with three degrees of freedom. With an absolute distance of approximate 3.7 m and multiple averaging of 0.5 s, the distance measurement accuracy reaches 17 nm, and the angular measurement accuracy reaches 0.073″ [16]. In 2018, Liu et al. from Tianjin University demonstrated the potential application of femtosecond-pulsed cross-correlation multichannel distance measurement in multilateral laser positioning. The four-channel parallel distance measurement was performed by a single interference system, and the repeated positioning accuracy at the micron level was experimentally obtained. In the frequency domain, the OFC contains extremely stable comb tooth spectral lines, which can greatly simplify the multiwavelength construction method when conducting a multichannel distance measurement [17]. In 2015, Weimann et al. from the Karlsruhe Institute of Technology, Germany, made a preliminary attempt to apply inter-mode beat interference ranging technology for multilateral positioning in space. At a distance of 1 m, the absolute distance measurement was conducted by microwave-assisted synthesis from the 240th to 241st harmonics of a 100-MHz repetition frequency of the OFC. Finally, a repeatable positioning accuracy of 24.1 μm was obtained [18]. In 2019, Kippenberg’s team at the Swiss Federal University of Technology proposed a parallel coherent LIDAR scheme based on a soliton microcavity OFC. Due to the large repetition frequency of the microcavity optical comb, each comb tooth can be used for FSI ranging when the optical frequency of the pump light source is linear modulation. The parallelization of the frequency-modulated continuous-wave LIDAR was realized, and the ranging accuracy of 30 detection channels were better than 1 cm [19].

Optical frequency comb dispersive interference (OFCDI) is a frequency-domain interference technique. Similar to white light spectral interference, a spectrometer receives interference signals. The measurement system does not contain mechanical moving parts, and the absolute distance measurement can be performed by the linear relationship between the interference phase and optical frequency. Different from an ordinary continuous spectrum, the OFC discrete comb tooth spectrum makes its dispersive interference signals with pulse spacing as a period. With the increase in the measured distance, the measured distance changes in the way of a triangle-shaped variation, so it can perform a long-distance high-precision absolute ranging. With the help of mode-locking technology and photonic crystal fiber spectrum spreading technology, the spectral width of the OFC can reach hundreds of nanometers. When its wide spectrum is divided into mutually separated multiband measurement channels, each frequency band can measure a distance independently. After receiving multiband interference signals by a single spectrometer, the interference signals of different frequency bands can be demodulated, corresponding to each distance. Therefore, the method is capable of frequency-division multiplexing. The single interference system can realize a synchronous multichannel distance measurement, which can reduce the complexity of the system and provide the multichannel distance measurement with a unified traceability benchmark.

On the basis of the OFCDI ranging technology, the wavelength-division multiplexer is used for frequency-division multiplexing (WDM). The distance measurement features of multichannel frequency-division multiplexing are studied. The influence of the spectrum width and shape on the multichannel distance measurement is analyzed. With the nonuniform discrete Fourier transform (NUDFT) algorithm and Hanning window, the ranging accuracy is optimized. Finally, the absolute distance measurement accuracy is better than ± 4 μm at a distance of 1.5 m in six measurement channels.

2 Measurement Principle

2.1 Multichannel Ranging Principle

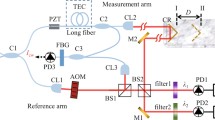
The layout of the experimental setup is shown in Fig. 1a. The light source is a femtosecond-pulsed laser (Menlo Systems_Germany, C-Fiber). The spectral pattern of the light source is presented in Fig. 1b, where the central wavelength and bandwidth are approximately 1582 and 170 nm, respectively. Its repetition frequency is locked to a rubidium atomic clock (Symmetricom_America, 8040C). The pulse train from the light source goes through the CIRC (Thorlabs_America, 6015–3-APC) and then is incident into the WDM (Flyin_China, WDM-1 × 6-(1510–1610)-900L-FA). The spectrum is divided into six probe channels (C1–C6). As depicted in Fig. 1c, each channel has its own filtered spectrum. The center wavelengths of the six-channel filtered spectrum are 1510, 1530, 1550, 1570, 1590, and 1610 nm, with a bandwidth of approximate 16 nm. To simplify the system structure, the optical-fiber end face of the WDM is coated with a beam splitter film (10:90). Here, the multiple detection channels uniformly use the fiber end face as the ranging zero point. The output light of the WDM is collimated through the FC (Thorlabs, F260PC-1550) toward the free space. Then, the interference signal is jointly sampled with a single OSA (Yokogawa_Japan, AQ6370D) after passing through the CIRC. As the spectrum is filtered by the WDM, the spectral interferogram of each probe can be isolated without crosstalk in the spectral domain. In theory, the acquired interference signal in the OSA can be expressed as

$$I\left( f \right) = \sum\limits_{i = 1}^{6} {S\left( {f_{i} } \right) \cdot \left[ {1 + \cos \left( {2\uppi f_{i} \cdot \tau_{i} } \right)} \right]}$$
(1)
Fig. 1
figure 1

Schematic of the multichannel parallel ranging approach. OFC: optical frequency comb, CIRC: optical circulator, WDM: wavelength-division multiplexer, FC1-FCN: fiber collimator, OSA: optical spectrum analyzer. a Optical setup of the multichannel parallel ranging. b Initial spectrum captured by the OSA. c Multichannel spectrum captured by the OSA

Full size image

where, \(i = 6\) indicates the number of detection channels, \(S\left( {f_{i} } \right)\) is the power spectral density (PSD) of each sensing channel, \(f\) represents the optical frequency sampled by the used OSA, \(\tau_{i} = 2nl{}_{i}/c\) is the delay time between two interference pulses, and \(n\) and \(c\) are the refractive index of air and speed of light in vacuum, respectively. As illustrated in Fig. 2, as the OFC performs ultrashort pulse trains with a stable pulse-to-pulse distance in the temporal domain, the distance \(L\) can be written as \(L = k \cdot L_{pp} /4 + l\). \(k\) is the number difference between the measurement pulse and reference pulse, \(L_{pp} = c/\left( {f_{r} \cdot n_{g} } \right)\) is the pulse-to-pulse temporal separation, and \(n_{g}\) is the group refractive index of air. \(l = c \cdot \tau /2n_{g}\) represents the fractional distance from the adjacent interference pulse. While the interference signal undergoes a fast Fourier transform (FFT), \(l\) can be obtained from the location of the peak in the Fourier domain. Because of the spectrum filtered by the WDM, the shape and bandwidth of the spectra are modified. To some extent, the time resolution in the Fourier domain will be reduced. Hence, the three-point peak curve-fitting (PCF) method is utilized to improve the extraction accuracy of the peak position. The three points at the left and right of the peak point are selected for quadratic function fitting, and the fitted peak point is used as the measurement result.

Fig. 2
figure 2

Architecture approach of the OFCDI. a Principle of the OFCDI. b Data processing for the measurement of the optical path difference (OPD). b1 Interference spectrum. b2 Fourier transform of the interferogram. b3 Extracting the peak position through the peak curve-fitting (PCF) method

Full size image

The dispersed spectrum in the OSA is evenly spread in the wavelength other than the optical frequency. Normally, additional resampling and interpolation before FFT are necessary. However, as the measured OPD increases, the sampling points of the single fringe gradually decrease, and then the interpolation error becomes obvious. Figure 3 shows that the simulation results originate from the FFT and interpolation (LIFFT) under different wavelength resolutions. For the whole path difference of 0.4 mm to 30.1 mm, the target mirror was moved at an incremental step of 0.3 mm. Under the same measured distance, as the wavelength resolution becomes larger, the interpolation error becomes increasingly obvious. While the wavelength resolution is equal to 0.005 nm, the ranging deviation still reaches 2 μm at a distance of 30 mm. Therefore, it is essential to further improve the data calculation accuracy of the interference signal.

Fig. 3
figure 3

Simulation results of the error introduced by spectral interpolation and reconstruction

Full size image

Here, the NUDFT algorithm is directly used to solve the above-mentioned problem through the Vandermonde matrix multiplication with the spectrum vector. The measured delay time can be directly reconstructed as

$$A\left( {\tau_{m} } \right) = \sum\limits_{s = 0}^{N - 1} {I\left( {f_{s} } \right)} \cdot \exp \left[ { - {\text{j}}\frac{2\uppi }{{\Delta f}}\left( {f_{s} \cdot m } \right) } \right]$$
(2)

where \({{N}}\) is the sampling point in the OSA and \(m = 0,1,...,N - 1\). \(I\left( {f_{s} } \right)\) is the intensity signal corresponding to the frequency sampling point \(f_{s}\), and \(\Delta f\) is the frequency sampling range. Equation (2) can be written in a matrix form as \({\varvec {A}} = {\varvec {DI}}\), where

$${\varvec A} = \left[ {\begin{array}{*{20}c} {A\left( {\tau_{0} } \right)} \\ {A\left( {\tau_{1} } \right)} \\ \vdots \\ {A\left( {\tau_{m} } \right)} \\ \end{array} } \right]$$
(3)
$$\begin{array}{*{20}c} {\varvec D = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ {p_{0}^{ - 1} } & {p_{1}^{ - 1} } & \cdots & {p_{N - 1}^{ - 1} } \\ \vdots & \vdots & \ddots & \vdots \\ {p_{0}^{{ - \left( {N - 1} \right)}} } & {p_{1}^{{ - \left( {N - 1} \right)}} } & \cdots & {p_{N - 1}^{{ - \left( {N - 1} \right)}} } \\ \end{array} } \right]} & , & {{\varvec {I}} = \left[ {\begin{array}{*{20}c} {I\left( {f_{0} } \right)} \\ {I\left( {f_{1} } \right)} \\ \vdots \\ {I\left( {f_{N - 1} } \right)} \\ \end{array} } \right]} \\ \end{array}$$
(4)

where, \(p_{n} = \exp \left( {{\text{j}} \cdot 2\uppi /\Delta f \cdot f_{s} } \right),s = 0,1,...,N - 1\) . The matrix D is the Vandermonde matrix, which can be precalculated by \(f_{s}\).

Immediately, the performances of different FT algorithms were evaluated by a numerical simulation. The interference spectrum was theoretically generated under a sampling condition, which is exactly identical to the actual measurement. The simulated OPD was set from 0.5 to 60.5 mm with an interval of 6 mm. Then, we compared different processing methods based on the LIFFT and NUDFT. As shown in Fig. 4a, as the NUDFT method directly uses nonuniform sampling data to implement the discrete FT, the interpolation error can be cleverly avoided, and then the calculated accuracy is optimal. Moreover, the wavelength accuracy of the used OSA will contribute much to the measurement uncertainty of the OPD. Therefore, we used the PSD collected by the OSA to further analyze the performance of the two algorithms. In Fig. 4b, the two algorithms are clearly affected by the wavelength accuracy of the used OSA, and the error amplitude is magnified. Fortunately, the residual-based NUDFT can still be controlled within ± 0.65 μm.

Fig. 4
figure 4

OPD solution for different FT processing methods: a Comparison between different FT algorithms b Comparison of the combined influence of the algorithm and wavelength accuracy

Full size image

Subsequently, we made a linear measurement comparison with a commercial laser interferometer (Renishaw, XL-80) to evaluate the above-mentioned methods. The target mirror HR was moved by ten steps at an increment of 3 mm at a distance of 1.5 m, and at each position, the spectral interferogram was repeatedly recorded five times. During the measurement, the temperature, humidity, and air pressure were recorded with the environmental parameter sensor (Renishaw, XC-80) to calculate the air refractive index [20]. As shown in Fig. 5a, when averaging the five measurement results and all distances, the measurement results have a good agreement with the theoretical simulation. For the NUDFT method, the agreement between the dispersive interferometry and commercial interferometer decreased to below 0.5 μm. In Fig. 5b, for each individual measurement, the agreement between the dispersive interferometry with the NUDFT and commercial interferometer is within 1.5 μm, except for the algorithm accuracy and wavelength accuracy of the used OSA. The tested differences were also caused by environmental conditions, such as turbulence and vibration.

Fig. 5
figure 5

a Measured difference between the dispersive interferometry using different FT algorithms and a commercial interferometer for a distance up to 30 mm. b Length comparison between the NUDFT dispersive interferometry and commercial interferometer. The error bar shows the standard deviation of the measurements. The red cross represents each measurement result

Full size image

2.2 Simulation Analysis

In this section, the performance of each channel is analyzed under the influence of the WDM. As shown in Fig. 6, the spectral shapes of the six channels are different, the envelope is not smooth enough, and the symmetry is poor. Hereafter, the variation of the spectral shape may affect the location accuracy of the interference peak.

Fig. 6
figure 6

Six measurement channel spectral shapes

Full size image

To precisely analyze the influence of the spectral shape on the absolute positioning accuracy, the spectrum of six detection channels was acquired separately by the OSA, and the ranging simulation was performed at a distance of 1 mm. As illustrated in Fig. 7a, the peak position corresponding to the interference peak of each channel is slightly different. Moreover, the spectrum of each channel is normalized, as shown in Fig. 7b, and the position accuracy of the interference peak is not significantly improved. Figure 7c shows the ranging deviation at a distance of 1 mm, and the ranging precision after the spectral normalization did not improve but slightly decreased.

Fig. 7
figure 7

Six measurement channel interference peak signals at a distance of 1 mm. a Initial six channel interference peak signals. b Normalized six channel interference peak signals. c Deviations of six measuring channel at a distance of 1 mm.

Full size image

Figure 8 shows the ranging deviation of different measurement channels. The simulated OPD was set from 0.5 to 20.5 mm with an interval of 1 mm, which covers the OPDs from the actual measurement. Compared to the initial spectral bandwidth, the residuals significantly increased, and the peak-to-valley value of residuals for each channel is different. Fortunately, the overall deviation was controlled within ± 15 μm in the six measurement channels. The main reason is that when the interference signal is intercepted by spectral division, it cannot be easily ensured that the signal is an integer with multiple periods of the interference fringe. Performing FT can easily cause spectral leakage. Subsequently, good spectral lines spread into a wide range of interference peak lines, which affects the peak localization accuracy. The spectral shapes in Figs. 6a and c and the residual curves of Figs. 8a and c show that the rounded spectral shape corresponds to a smaller error band.

Fig. 8
figure 8

Ranging simulation results of the six measurement channels

Full size image

To optimize the ranging accuracy, the Hanning window was added to the interference spectrum. It can smoothen the signal near the end point and weaken the influence of signal discontinuity. Figure 9 shows the shape of the spectrum after windowing. Compared with the spectral shape in Fig. 6, the spectral shape becomes rounded and symmetrical in the six measurement channels.

Fig. 9
figure 9

Different channel spectral shapes with the Hanning window

Full size image

The ranging simulation was performed with the window spectrum. As shown in Fig. 10, the shape of the residual curve has not significantly changed. Fortunately, ranging residuals were reduced from ± 15 μm to ± 3 μm. Based on the residual distribution law, the wavelength accuracy is different in different wavelength ranges of the used OSA.

Fig. 10
figure 10

Ranging simulation results of different channels with the Hanning window

Full size image

The effect of the spectral width on the ranging accuracy was analyzed. Under the initial spectral width, the ranging resolution can reach the submicron level with the PCF. The variation of the ranging resolutions was analyzed during the spectral width change. While the spectral bandwidth for the influence of the ranging accuracy was analyzed, within the spectral bandwidth of 1480–1600 nm, it was directly reduced from one side with a step of 20 nm, and the ranging residual curve was observed. As illustrated in Fig. 11, although the PCF can improve the ranging accuracy, the ranging deviation becomes larger as the spectral width continuously reduces. When the spectral bandwidth was reduced from 120 to 20 nm, the peak-to-valley value of the ranging residual also gradually increased from 1 to 5 μm.

Fig. 11
figure 11

Influence of the spectral width on the ranging accuracy

Full size image

3 Length Comparison

Finally, the length comparisons of the six channels were performed. Figure 12 shows the interference signals of the six channels, where the interference fringe quality of each channel was always good. Then, the target mirror was moved by ten steps at an increment of 1 mm. The commercial interferometer provide truth value to evaluate the multichannel ranging performance. The experimental results are in excellent agreement with the simulation results. Figure 13 shows the ranging residuals of the six channels, which can be effectively controlled within ± 4 μm.

Fig. 12
figure 12

Spectral interference patterns of the six channels

Full size image
Fig. 13
figure 13

Length comparison results

Full size image

4 Conclusions

This paper proposes an OFC frequency-division multiplexing dispersive interference multichannel distance measurement method. Based on the initial dispersive interference structure, the WDM was used to realize the multichannel expansion. The influence of the spectrum shape and width on the ranging accuracy was analyzed after a multichannel spectrum segmentation. With the NUDFT algorithm and Hanning window, the ranging accuracy was optimized. The design is simple and flexible and has a common optical path structure. The final six measurement channels can achieve an absolute distance measurement accuracy better than ± 4 μm at a distance of 1.5 m. With the increasement in the spectral bandwidth of the OFC and the detection bandwidth of the spectrometer, the measurement channels of frequency-division multiplexing can reach a dozen or more. Moreover, the high-precision multichannel parallel ranging technology has the potential to be applied to the deformation and posture measurement of large equipment.