1 Introduction

As result of a comprehensive literature survey, the majority of coordinate measuring machines with a repeatability in the nanometer range (nanopositioning and nanomeasuring machines, NPMMs) are based on three independent linear movements of up to 400 mm × 400 mm × 100 mm (xyz) in a Cartesian coordinate system [1,2,3,4,5,6]. This, in combination with the specific nature of sensors and tools (further on summarized as tool), limits the addressable part geometries. Depending on the tool in use, spherical and aspherical geometries as well as free-form surfaces cannot be measured or only to a certain limit. This article contributes to the enhancement of multiaxial machine structures by the implementation of rotational movements while keeping the precision untouched. Approaches are known that allow the movement with a degree of freedom of four or five, which is required for addressing freeform surfaces orthogonal to the surface [7,8,9]. These approaches do not achieve nanometer precision for working ranges of NPMMs. In comparison to this, the aim of this work is the extension of NPMMs with additional degrees of rotational freedom for multitool concepts and freeform manufacturing in working areas of up to 200 mm × 200 mm × 25 mm [10, 11]. Suitable concepts of the overall machine structure were investigated. A parameter-based evaluation system was created to identify solution concepts fulfilling given requirements [12]. The rotation of the tool in use showed a high application potential. This article contributes to the systematic development of multiaxial machine structures based on existing NPMMs [10, 11] in the early design state.

2 Overall Structural Concepts

2.1 Evaluation of Multiaxial NPMMs

To support the selection of machine structures for the development of a multiaxial nanopositioning machine, an evaluation system was developed in accordance with the VDI guideline 2225 [5, 13, 14]. This is based on modular arrangement variants of basic components, a dynamic evaluation system, and indications of the characteristics to be considered for the design process.

The fundamental structures of Cartesian nanopositioning and nanomeasuring machines are based on three modes of movement: the sample scanning mode (SSM), the mixed scanning mode (MSM), and the probe scanning mode (PSM). The movement of the object or the tool is measured on the base of a reference with highest thermal and geometric stability fulfilling the Abbe Comparator Principle.

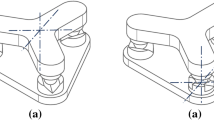
Suitable concepts of the extension of pure Cartesian structures with additional degrees of rotational freedom were investigated [5, 13]. In addition, compliance with the Abbe Comparator Principle has been an indispensable prerequisite for the design of the multiaxial NPMM. First evaluations for the overall structure show the highest degree of fulfilment for an SSM with additional rotations (turns and tilts) of the tool (Fig. 1b). Alternatively, rotations of the sample or of the sample and the tool have been considered, as shown in Fig. 1.

Fig. 1
figure 1

System configurations for the sample scanning mode with additional rotations of the object (a), the tool (b), or tool and object (c)

Full size image

The integration of additional rotary positioning systems near the respective end effector (object or tool) within the functional chain between the base and the end effector leads to:

  • Reduced masses to be moved and thus increased dynamic and reduced heat input.

  • Reduced complexity of the measuring system and the corresponding reference for comparatively large translational (≥ 10 mm) and rotational (≥ 10°) movements for the fulfilment of the Abbe Comparator Principle.

2.2 Sample Scanning Mode with Additional Tool Rotations

A central part of the fundamental structure of a positioning system is the underlying kinematic, which has a decisive influence on the design of the drive system.

In a first step, the rotation of a representative tool with a maximum mass of mT ≤ 2 kg, an overall extension in the measuring direction of lT ≤ 60 mm and rotation angles of 90° for φx,y and 360° φz are considered. For this purpose, a total of 21 suitable kinematic variants in order to address a hemisphere orthogonal to its surface are determined by means of a structural synthesis. The position of the instantaneous center of rotation, the number of joints, and the orientation of the rotary axes to the main axes of the NPMM have been varied.

In the following, kinematic variants are selected by use of a parameter-based evaluation system [5]. The evaluation criteria deployed are mainly based on quantitative characteristics. These include the complexity (number of joints), the position of the instantaneous center of rotation, expected masses and angles of rotation as well as the dependence of the axes of rotation to each other. To achieve this by means of commercially available positioning systems for ultra-precise rotations including multiaxial solutions such as hexapods [15], characteristic typical values of positioning systems are derived from comprehensive design catalogues [13]. Software-supported [16] parameter studies are used to derive typical dimensions and motion ranges. Figure 2 shows the kinematics with the highest degree of fulfilment.

Fig. 2
figure 2

Suitable kinematics for tool rotations

Full size image

These variants K1a–K4a describe rotations of the end effector (E) as a tool around the main axes of the Cartesian coordinate system with a common instantaneous center of rotation in the tool center point (TCP).

From the investigation it could be deduced that those kinematics are generally the most suitable. The tool rotation in form of a hemisphere is realized by rotation angles of 90° for φx,y and 360° φz. Linear corrective movements are not necessary since the tool center point coincides with the Abbe Point, thus avoiding first-order positioning errors.

2.3 Sample Scanning Mode with Additional Sample Rotations

In analogy to the rotation of the tool, possible kinematic variants are determined and evaluated for the rotation of the sample for addressing a hemisphere orthogonally to its surface. Since the sample has an unknown structure, linear correction movements are necessary to address the whole sample surface. As a result, the addressable sample points or the angle of rotation of the positioning system used, are considerably restricted. The sample dimensions are limited to a subset of the Cartesian volume. Depending on the kinematic variants, characteristical addressable volumes are showing the limits for given rotation kinematics (Fig. 3). If the sample fits to the dimensions derived from the given Cartesian volume, any hemisphere within the characteristic volume can be addressed.

Fig. 3
figure 3

Restrictions of object geometries due to the concept of object rotation

Full size image

The added mass and the necessary power supply of the rotary positioning systems must be taken into account for the design of the linear positioning systems. The deformation of the object when changing its orientation in the gravitational field remains as an undetermined influence. An adaptation of the object shape cannot be assumed, which is particularly important for nanofabrication processes.

In comparison with object rotations, the rotary positioning systems and corresponding coupling elements can be adapted to the tool design. This enables optimizations with regard to minimum mechanically and thermally induced deformations or their consideration within a tool-specific calibration process.

The solution variants for the rotation of the tool show in comparison the higher degree of fulfilment.

2.4 Sample Scanning Mode with Additional Sample and Tool Rotations

The restrictions of object geometries can be reduced to the level of one individual rotary axis (Fig. 3b), if rotations of the tool are implemented in addition to the object movements.

However, a higher degree of freedom influences the achievable uncertainty of the NPMM [7]. If the exact position of the tool center point (TCP) is not measured directly, the displacement as a consequence of the error motion can be calculated by geometric dimensions of the substructures. There are three translational and three rotational errors for every stage of rotation, which are dependent on the actuation angle. The movement of the TCP can be calculated by a superposition of the components resulting from those error motions. For tool rotation principles with an instantaneous center of rotation in the TCP, the resolution and measurement uncertainty of the rotation measurement system does not affect the position of the TCP.

The sample rotation can be described in the same manner as for the tool rotation. Since the TCP is fixed, the error motion of the positioning system now affects the position of the sample. Due to the dimension of the sample, the sample position is not independent from the properties of the angular measurement system. Although the characteristic lengths are much smaller for the sample rotation, the described systematic error leads to a comparable uncertainty for both approaches [17]. One approach to reduce the measurement uncertainty of the overall system is the in situ measurement of the respective translation and rotation errors of the rotation systems. This is simplified by the separation of the rotations to the object and tool, since only one positioning system has to be measured.

2.5 Investigation of the Positioning Repeatability

Best position repeatability is an indispensable prerequisite to secure the measurement uncertainty of the NPMM. If that is given, the remaining deviations can be corrected based on calibration data. A combination of a rotary stage [18] and a goniometer [19] for two independent rotations of the tool of an SSM-based NPMM has been chosen as the setup in specific (Fig. 4). This allows a tool (lT ≤ 60 mm; mT ≤ 2 kg) to be tilted horizontally by up to 90° and rotated 360° around the vertical axis of the NPMM.

Fig. 4
figure 4

NPMM [11] inside a climatic chamber with additional tool rotations; 1: linear stage of the NPMM (x, y, z), 2: glass sphere (n = 2) in the TCP, 3: tool adjuster (x, y, z) [20], 4: goniometer stage (φx,y) [19], 5: rotary stage (φz) [18], 6: metrological frame, (If) interferometer

Full size image

Measurement series are required to take the positioning repeatability of the rotation into account. The overall positioning repeatability of the tool can be derived by the combination of those of the individual axes or by measuring at the end effector (tool) directly. For this purpose, the positioning deviations of the rotation axes (Fig. 4) were measured with a universal autocollimator [21] along the respective axis with regard to the sensitivity to different stage setups (standing, hanging, single, or combined stages).

No significant changes of the repeatability caused by the arrangement were found. The repeatability depends on the angular position and the design of the positioning system. For the rotary stage in a setup equivalent to Fig. 4, the highest repeatability is ≤ ± 14.42 μrad within the positioning range. For the goniometer, the same conditions result in ≤ ± 17.95 μrad. These values are several orders of magnitude lower than the expected sensitivity of tools for surface inclinations of ≥ 1° to the tool axis, above which a significant increase in their measurement uncertainty can be expected [9].

For the measurement of the combined rotational movement around two axes, a glass sphere with a refractive index of 2 was used as a retroreflector placed in the TCP (Fig. 4) [22]. After removal of the linear stage, the three laser interferometers of the NPMM were used to determine the lateral deviations of the TCP while the tool was rotated over the full range. The goniometer is used to set the angular positions of the ball shaft to the vertical in steps of Δφx,y = 5°. In addition, the rotary stage rotates in steps of Δφz = 30° resulting in 91 measuring positions. The individual position is held for 60 s to reduce the influence of vibration. Long-term measurements of ten repetitions over 10 h are carried out for the entire series of positioning repeatability measurements inside the closed climate chamber of the NPMM.

The best-measured position repeatability over the entire rotation range and all measurement series is ± 100 nm for the x- and y-direction and ± 150 nm in the z-direction [5].

3 Tool Rotation with In Situ Deviation Measurement

The measurement and machining accuracy of the multiaxial NPMM depends on the positioning accuracy. The achievable accuracy is limited by the repeatability of the positioners. To overcome this, in situ measurement of the tool rotation based on a calibrated reference needs to be implemented. A parameter-based dynamic evaluation system with quantifiable technological parameters has been performed to identify general solution concepts [5, 14]. The number, arrangement, and operating principle of the measuring system and its reference were systematically investigated. Structural variants with a high degree of fulfilment consider the position detection at the coupling point of the end effector (reference) in order to reduce the number of necessary measuring systems and thus the total measurement uncertainty (Fig. 5).

Fig. 5
figure 5

System configurations for the SSM with additional tool rotations and in situ deviation measurement with rotations of the reference (a), or of the measuring system (b), (components see Figs. 1 and 4, interferometer carrier IC (9))

Full size image

Adapted from the design of Cartesian NPMM, the measuring beams are reflected at the corresponding reference, and intersect virtually at a point that coincides with the TCP thus fulfilling the Abbe Comparator Principle. Out of the evaluations, a system of three laser interferometers attached to the tool in correspondence to a hemispherical concave mirror as reference, attached to the metrological frame of the NPMM (Fig. 5b) has been chosen.

The developed design enables the strict separation of the force frame and the metrological frame. Further on, the thermal shielding of the rotary stage being the largest heat source (Fig. 6) can be realized. The hemisphere stands on a support made of Invar36 and can be adjusted in the main axes of the NPMM as well as subsequently fixed in position with minimized thermally induced stress. The three Fabry–Pérot interferometers are connected by a metrological frame and form a Cartesian coordinate system with their measuring axes, which are matching virtually in the TCP.

Fig. 6
figure 6

SSM-based NPMM [11] with additional tool rotations [18, 19] and in situ deviation measurement with rotations of three Fabry–Pérot interferometers [23] and a reference hemisphere as part of the metrological frame of the NPMM, (for components see Fig. 5)

Full size image

This way, the rotational positioning systems can be included in the metrological loop via an in situ measurement of the displacements of the TCP.

In addition, the positioning systems are connected to the base via a separate force frame, which reduces the mechanically induced deformations in the metrological frame. Alignment and subsequent position assurance of the positioning systems, the Fabry–Pérot interferometers, and the tool are done in each case via elements allowing adjustment along the main axes of the NPMM.

Since the hemisphere is used as a reference, the remaining unavoidable shape deviations must be determined. Due to the large diameter of the reference surface of 400 mm and the comparatively strong curvature, the shape deviations are determined in situ.

Using a glass sphere with a refractive index of two in the TCP, an in situ calibration is done by means of the three laser interferometers of the NPMM. The measured values of the Fabry–Pérot interferometers are assigned to the measured values of the NPMM laser interferometers simultaneously during the rotation of the tool. A first proof of concept has been realized on the basis of a none perfect but affordable reference hemisphere of polished stainless steel (Fig. 6).

Figure 7 shows an example of the measured values for the interferometers of the NPMM (Fig. 7a) and the corresponding values of the Fabry–Pérot interferometers (Fig. 7b) determined simultaneously during the rotation around the z-axis of the NPMM. The values are shown in the direction of the respective measurement axes for repeated forward and backward rotations (fwd/bwd).

Fig. 7
figure 7

Measured values of the six interferometers for the relative movements of the TCP with respect to the metrological frame

Full size image

The comparatively large measured values of the Fabry–Pérot interferometers are mainly caused by the shape deviations in the range of ± 350 µm of the stainless-steel hemisphere. For repeated measurements between individual positions of the rotary stage, the TCP could be determined with a deviation down to a maximum of 27 nm, which is already in the range of the periodic nonlinearities of the Fabry–Pérot interferometers (± 13 nm).

Within the framework of a detailed theoretical measurement uncertainty analysis for a setup with a hemisphere made of SiO2 (fused silica), the determination of the TCP could be proven with a maximum measurement uncertainty of ≤ 18 nm (p = 68%) in each direction (x, y, z) [24]. The largest contributions to the uncertainty budget are given by the thermal stability of the reference hemisphere and, after the material change to fused silica, by the orthogonality deviations and the nonlinearities of the Fabry–Pérot interferometers.

These compact interferometers allow measurements on both highly curved surfaces of high reflectivity, such as polished metals, and transparent surfaces of low reflectivity, such as fused silica [24].

As part of the static metrological frame, the hemisphere is to be designed as a reference for the interferometers with regard to highest long-term stability and thus minimal thermally and mechanically induced deformations (Table 1). The mechanically induced deformation can be reduced in particular by increasing the wall thickness in the area of the contact surface of the standing reference hemisphere (variants 1–2a and 2–2a in Table 1).

Table 1 Finite elements analysis (FEA) of the elastic deformation (ε) and eigen-frequencies (fe) of the reference hemisphere (RH) by gravity in relation to material and wall thickness variation for representative materials with a minimal coefficient of thermal expansion
Full size table

Reduced mechanically-induced deformations in turn decrease the creep of these structures, as an additional deformation ε(t), relative to the elastic start deformation ε0. For titanium silicate glass (ULE) and fused silica, for example, after t = 500 h values of ε(t) of ≤ 0.1%, for Invar36 ≤ 0.039% and for the glass ceramic Zerodur ≤ 0.7% can be assumed [6].

4 Nanofabrication with a Rotating Stamp of Nanoimprint Lithography

As was to be expected, the existing measurement uncertainties of the NPMM are slightly increased by additional rotary positioning systems. However, a scientific novelty is the possibility of addressing and processing three-dimensional bodies normal to their surface including undercuts. The alignment of a tool for nanoimprint lithography (NIL) normal to a strongly curved surface through the developed tool rotation of the NPMM opens up new application possibilities in the field of nanofabrication (Fig. 8).

Fig. 8
figure 8

NPMM [11] with rotating NIL tool; 1: linear stage of the NPMM (x, y, z), 2: plano-convex lens with substrate surface, 3: NIL tool, 4: goniometer stage (φx,y) [19], 5: rotary stage (φz) [18]

Full size image

The integrated NIL tool is developed based on the basic components of soft UV-NIL. It consists of a UV LED light source with a wavelength of 365 nm and an intensity of 148 mW/cm2 [25]. A fused silica plano-convex lens is used to focus the light on an area of approximately 20 mm2. The focused light is transmitted through the patterned area of 25 mm2 on the PDMS (polydimethylsiloxane, Sylgard 184 silicone elastomer) stamp. The stamp of 20-mm diameter has been fixed to the tip of the NIL tool. Combined movements of the axes are necessary to bring the tool in the printing position.

The object is uniformly coated with a substrate (AMONIL MMS4) [26] using the spray coating process [27]. The contact between the NIL tool and the substrate surface of the object is then made by a translational movement of the linear stage of the NPMM along the main tool axis. The contact of the stamp structures is followed by a resist filling time of 1 min for the stamp cavities, followed by a UV exposure time of 1 min. After subsequent translational demolding along the main tool axis, the process can be repeated at other points depending on the viscosity of the substrate (Fig. 9).

Fig. 9
figure 9

NIL: a NIL curing phase at 45° inclination to the horizontal, b multiple structured substrate on plano-convex lens, c image of structure 3 (45° NIL inclination to the horizontal) taken by means of a 3D laser scanning microscope [28], d profile of the structural cross section of the image c with optical profiling system [29]

Full size image

Due to the strong curvature of the surface, the analysis of the generated structures is performed only for the center of the replicated overall structure (Fig. 9c, d). A comparison of the central region of this replicated structure with the original of the stamp shows good fidelity. Thus, in images taken with a 3D laser scanning microscope [28], the measured difference in structure heights between the stamp and the replicated structure for steps in the central region is in a range of 25 to 35 nm.

The replication of structures over the entire object surface is not possible in a single printing process due to the strong curvature. Instead, the structuring of the entire object surface is carried out by a step and repeat printing process.

If continuous structuring is to be achieved, the partial structures must be linked to form an overall structure (stitching). For nanometer-precise stitching over the entire surface of the highly curved substrate, positioning with corresponding positioning accuracy of the stamp relative to the substrate is necessary.

Further investigations are therefore focused on the combination of the rotating NIL stamp with an in situ measurement of the displacements of the TCP, thus enabling the stitching of partial structures with nanometer precision.

5 Conclusions

A systematic parameter-based dynamic evaluation approach was developed for the creation and selection of adequate machine structures for multiaxial nanopositioning systems (DOF > 3). Out of these investigations, a rotation of the tool is a favorable solution. Kinematics with a high degree of fulfilment consider a common instantaneous center of rotation in the tool center point (TCP). Compared to a fixed tool position, this leads to shifting deviations of the TCP due to deformations of the frame, positioning errors of the rotational axes, vibrations, and thermal influences.

However, a scientific novelty for nanofabrication processes is given by the possibility of addressing and processing three-dimensional bodies with a strong curvature normal to their surface. As exemplified with the application of a developed nanoimprint tool, the positioning properties are sufficient for nanofabrication processes without stitching.

With the overall design developed, different tools (lT ≤ 60 mm; mT ≤ 2 kg) can be tilted horizontally by up to 90° and rotated 360° around the vertical axis of the NPMM.

A commercially available NPMM of 25 mm × 25 mm × 5 mm (x, y, z) [11] translational movement of the object was chosen for experimental investigations. The developed setup allows the transfer to an NPMM of 200 mm × 200 mm × 25 mm (x, y, z) [1] translational movement for future investigations.

The strict separation of the force frame and the metrology frame, thermal shielding, and direct measuring systems for the deviation of the TCP can be implemented to compensate the effects that are dependent on the selected overall structure and positioning system. The in situ deviation measurement of the TCP around two axes simultaneously can be achieved considering a hemispherical concave mirror as reference in combination with compact laser interferometers.

A new type of overall structure developed, in which Fabry–Pérot interferometers are used for the combined measurement of positioning deviations, ensures that the rotations are included in the closed control loop, thus increasing the measurement and machining accuracy. The interferometers measure the positioning errors against a hemispherical concave mirror that is an inherent part of the metrological frame of the NPMM. Using a glass sphere as a retroreflector with a refractive index of two in the TCP ensures the in situ calibration of the TCP position. Long-term dimensional stability is a prerequisite for the hemisphere and the interferometer carrier as part of the metrological frame.

Future investigations are therefore focused on a modification of the developed setup by a reference hemisphere made of fused silica with reduced shape deviations and an increase of the orthogonality of the measuring axes as the major influencing variables for the total measurement uncertainty.