Introduction

Power distribution networks are facing a dramatic transformation towards a more modern and practical structure, which is known as a smart grid (SG). Integrated distribution energy resources (IDER) including distribution generation (DG) and energy storage systems (ESS) become primary components of the SG scheme to contribute with the electric power generation delivered from the supply side, to meet the load demand and to enhance the system’s security, reliability, and efficiency.

Existing electric grid infrastructure that has been built with substantial investment costs is currently under pressure to increase its effectiveness and efficiency. The pressure grows as we seek more services from the electrical grid without the need for more huge investments. One of the technical limitations in the way is the real-time flow of energy from generators to end consumers without energy storage as supply is required to meet the demand at all time to maintain system stability. However, recent advancements in technologies and regulations drive the electrical energy sector toward exploring energy storage applications and benefits. Fortunately, there is a way forward as utility companies modernize their current infrastructure to become smart. A smarter grid implements advanced technologies, tools, and techniques that are available to enable the power grid to work far more efficiently, reliably, cleanly, and economically affordable. Toward this ambitious goal, utilities worldwide have embarked on several implementations of grid modernization projects at various levels. One of the main components of smart grids is energy storage systems (ESS) [1, 2].

Well-developed commercial low-energy ESS units are available in batteries, flywheels, superconducting magnetic storage, and compressed air storage [3]. Such promoted solutions are changing the direction which system planner used to follow for designing the expansion of the power generation capacity, transmission lines transfer capabilities, and new substation construction to serve the energy required of the future demand. Furthermore, the focus in the micro-grid planning and operation development is supporting the deferral of bulk power generation expansion in the short and midterms by utilizing demand-side management (DSM) programs along with ESS to manage the load demand during the peak time [3].

The distribution scale grid-connected ESS is examined for optimal online power operation for peak demand and load smoothing management [4]. The optimization framework considers the forecasted projected load demand and upcoming plans for renewable power generation integration. Optimizing the storage size decisions and quantifying the cost reduction of ESS comparing to DSM programs are evaluated in [5]. Two-stage stochastic programming is used to model the system and to represent its uncertainties represented in the DG. The sensitivity analysis validates the advantages of utilizing the central energy storage for load control. Further literature suggests the incorporating of several factors in the planning modeling such as the net present value of the ESS, the maintenance costs, interruption costs, system upgrade, and energy loss charge to evaluate the investment feasibility and its arbitrage benefit [6].

Optimal sizing and location placement of energy storage systems have received significant attention in the literature [6,7,8,9,10]. In [6], the authors proposed a planning framework for ES allocation in distribution networks, which can provide maximum benefits. The paper concluded that ES helped reduce the total costs of utilities due to improvement in network reliability and distribution system upgrade deferral.

The research done by Das et al. [11] investigated the impact of optimally placed energy storage in distribution networks. The installed energy storage was shown to improve the voltage profiles as well as the reduction of line losses. The test case was the IEEE-33 medium voltage test system with high penetration of renewable energy sources. Two heuristic optimization solvers were used to solve the problem, namely the artificial bee colony and the particle swarm optimization methods.

Energy storage technologies and applications

Energy storage systems are considered enabling technologies for different smart grids’ functionalities such as active management of network assets, network flexibility, improve power quality, self-healing, and resiliency. In addition, energy storage systems are essential components for integrating renewable energy resources [12]. Other applications for energy storage systems include micro-grids and electrification of remote areas, in which energy storage systems are used to minimize dependence on the main grid supply [13, 14].

Technologies

Different technologies have been adopted for energy storage in the industry, which can be generalized into three main themes, summarized in the following Table 1 [15, 16].

Table 1 Energy storage technologies
Full size table

There are several parameters that differentiate energy storage systems from each other. These parameters are defined in the following [2, 13, 17]:

Capacity Which represents the energy storage capability (Wh).

Specific energy It is defined as the electrical energy stored per mass (Wh/kg).

Specific power The amount of power that can be extracted from a kilogram of storage (W/kg).

Energy density The energy stored per unit volume (Wh/m3).

Electrical efficiency The measure for the amount of energy that can be converted into work (%).

Recharge rate The rate at which power can be pushed through the energy storage system (h).

Self-discharge The amount of time it takes for energy storage to discharge when unused due to current leakage and heat dissipation (h).

Depth of discharge (DOD) This term refers to the amount of utilized capacity of a battery energy storage system. Typically, expressed as a percentage of the battery’s full capacity. The DOD has an inverse relation with the lifetime of the battery.

C-rate The rate at which the battery is charged/discharged relative to its capacity. A 1 C discharge rate means that the battery will fully discharge in 1 h. 2 C means that the rate of discharge is twice the capacity. Thus, the battery will be fully discharged in half an hour.

State of charge (SOC) Represents the battery’s current capacity as a percentage of maximum capacity.

Lifetime The service life of the energy storage unit, which mainly depends on the technology and the intensity of usage (years).

Capital cost The investment cost for the design, specification, civil work, and installation ($/kW).

Operation cost The cost required for maintenance, fuel inspection, and part replacement ($/kWh).

Charge/discharge cycle The number of cycles the storage system can be charged and discharged without affecting the storage capabilities significantly (cycles).

The climate of the region for which the energy storage would be installed plays a significant role in the technology selection. With an extreme high temperature of Saudi Arabia, it is necessary to carefully choose an energy storage technology that can withstand such harsh environments.

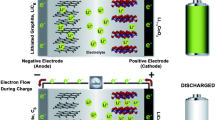
A high volume of energy storage projects worldwide is related to chemical battery energy storage systems. The three leading technologies are lithium-ion batteries, lead-acid batteries, and sodium–sulfur batteries.

Applications

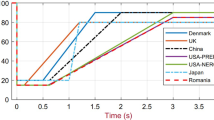
Many energy storage technologies are now available in the market with different capabilities and characteristics, which make them very useful in a wide range of applications. Also, energy storage systems can be designed and built in different sizes and capacities and can be placed at various locations throughout the grid ranging from being distributed at consumers’ levels to being located at transmission level as a utility-scale storage system. There are two major factors that characterize the type of application of an energy storage system: the amount of stored energy and the rate of energy transferred. [12, 18,19,20]. Figure 1 demonstrates different ESS technologies based on typical capacities and discharge rates, where the x-axis represents the size of the energy storage and the y-axis represents the possible discharge time for different storage technologies. The ESS size and charge/discharge rates depend on several factors, including the application for which the ESS is used. Table 2 summarizes different ESS applications and their technical requirements.

Fig. 1
figure 1

Energy management, power quality, and ride-through storage applications [4]

Full size image
Table 2 Technical considerations for grid applications of battery energy storage systems [8]
Full size table

Several energy storage demonstration projects are being conducted to evaluate various distribution-level storage technologies including batteries, compressed air and flywheels systems. These pilot projects are assessing its economic and technical performance for different system configuration and application like load management, frequency control, voltage regulation and solving the intermittency problem associated with renewable energy integration [21]. An example of a demonstrating project is reported in [22], the storage is used to provide ancillary services by responding to the regulation signals send by Independent System Operator (ISO). Details analysis of the energy storage project cost-effective along with the lessons learned are demonstrated [23].

The United States Department of Energy (DOE) has a database of energy storage projects worldwide which includes different energy storage technologies [21]. China, the United States of America and Japan are considered world leaders in regarding energy storage installation capacity. As reported by the DOE, the installation capacity of energy storage is approximately 187.8 GW divided over different technologies [24].

The role of energy storage in the energy transition process

The usage of variable renewable energy (VRE) resources will require high flexibility to be successfully integrated with the main grid. Fortunately, energy storage systems can be utilized to serve as a buffer for the inherency of VRE resources and allow for the dispatchability of such resources to some extent thus decoupling the supply–demand requirement [25]. EES can also enhance other levels of electricity value chain, which includes reducing the need for cycling of base load generation and increasing its average generation power. Also, EES could help enhancing the overall chain efficiency while reducing the operation of high cost peaking units. EES can relieve grid congestion and can smooth frequency and voltage fluctuations, ensuring grid reliability and security [26].

One of the biggest challenges for the transition from fossil fuels to sustainable energy sources is flexibility of the grid by meeting the ramping down of solar in the afternoon or when the wind speed reduces to lower than expected values. Energy storage in this situation can be used to provide the necessary flexibility required to maintain system balance, which would lower the burden of the ramping requirements for conventional generators.

Energy storage deployment could facilitate the electrification heating, and cooling sectors and support the roll-out of very fast charging infrastructure for electric vehicles, particularly in areas with weak grids. Industrial consumers can utilize storage to reduce consumption peaks, and to provide back-up power if there is a black-out.

Behind the meters, energy storage technologies can enable householders to contribute to the energy transition. In the sense that they provide householders the ability to store their energy for use at a later time, but are also an important element in enabling new energy practices and paradigms such as sharing and trading energy. The use of residential energy storage can help householders to become more autonomous in their energy supply with the integration of photovoltaic (PV) systems, in which reliance on grid power would be reduced. Domestic storage may also be used for demand response to help stabilize the grid [27].

System modeling

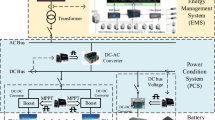
The modeling phase is the essence of being able to assess the feasibility of installing energy storage at the distribution level. Accurate models are of paramount importance to correctly quantify the impact, and potential benefits energy storage can provide to the system. In this paper, the distribution network and energy storage components are the major components of the simulation. Other elements such as the power electronics devices used as an interface between the energy storage and the network can be easily introduced in the model as a simple efficiency factor [11, 14, 28].

Network model

There are two major components representing the distribution network. The transformers and the distribution lines (cables/overhead). To model these two components, it is necessary to identify their impedances. The network is shown in Fig. 3, where it depicts a radial medium voltage distribution feeder (13.8 kV) with 12 distribution transformers.

BESS model

A generic model is used to represent the battery storage system. However, certain parameters within the model can be chosen to represent different battery technologies such as the efficiency of the batteries for charging and discharging, in this paper, lithium-ion batteries where assumed for all simulation. Thus, the charging/discharging efficiency was fixed [11, 28].

Load model

The load demand on each transformer is represented by an hourly time series of constant power values.

Cost functions

The cost functions are related to the net present cost of the batteries, transformers, and the cables [6, 29]. The operation and maintenance cost is assumed to occur each year of the components’ lifetime.

$$ \begin{aligned} C_{\alpha }^{\text{opex}} = c_{\alpha }^{o\& m} \mathop \sum \limits_{y = 1}^{Y} \left( {\frac{1 + \beta }{1 + \gamma }} \right)^{y} \hfill \\ \alpha \in \left\{ {{\text{EES}},{\text{ transformer}},{\text{ cables}}} \right\} \hfill \\ \end{aligned} $$
(1)
$$ C_{\text{ESS}}^{\text{rep}} = c_{\text{bat}}^{\text{rep}} \mathop \sum \limits_{r = 1}^{R} \left( {\frac{1 + \beta }{1 + \gamma }} \right)^{{rn_{\text{ESS}} }} , $$
(2)
$$ R = {\text{INT}}\left( {\frac{Y}{{n_{\text{ESS}} }}} \right), $$
(3)
$$ C_{\text{ESS,P}} = C_{\text{ESS,P}}^{\text{capex}} + C_{\text{ESS,P}}^{\text{opex}} + C_{\text{ESS,P}}^{\text{rep}} , $$
(4)
$$ C_{\text{bat,E}} = C_{\text{ESS,E}}^{\text{capex}} + C_{\text{ESS,E}}^{\text{opex}} + C_{\text{ESS,E}}^{\text{rep}} , $$
(5)
$$ \begin{aligned} C_{\lambda } = C_{\lambda }^{\text{capex}} + C_{\lambda }^{\text{opex}} \hfill \\ \lambda \in \left\{ {{\text{transformer,}}\,\,{\text{cables}}} \right\}. \hfill \\ \end{aligned} $$
(6)

Optimization formulation

The main objective of this project is to quantify and address the benefits provided by an energy storage system (batteries) for a distribution network. The optimization model is constructed to find the optimal capacity and location within the distribution network of the BESS. As such, the optimal solution will provide optimal kWh and kW of the battery to be installed as well as the transformer and cable expansion required. The complete optimization model is described below [30, 31]:

$$ \hbox{min} \mathop \sum \limits_{i \in I} C_{\text{ESS,P}} P_{{{\text{ESS}},i}}^{\text{R}} + C_{\text{ESS,E}} E_{{{\text{ESS}},i}}^{\text{R}} + \mathop \sum \limits_{{\begin{array}{*{20}c} {i \in I} \\ {i \ne j} \\ \end{array} }} \mathop \sum \limits_{j \in I} C_{\text{tf}} \delta_{{{\text{tf}},ij}} + C_{\text{c}} \delta_{{{\text{c}},ij}} . $$
(7)

Power balance constraints

$$ \mathop \sum \limits_{j} P_{ij,t} - \mathop \sum \limits_{k} P_{ki,t} = P_{{{\text{G}},i,t}} - P_{{{\text{L}},i,t}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j,\forall k} \\ \end{array} , $$
(8)
$$ \mathop \sum \limits_{j} Q_{ij,t} - \mathop \sum \limits_{k} Q_{k,i,t} = Q_{{{\text{G}},i,t}} - Q_{{{\text{L}},i,t}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j,\forall k} \\ \end{array} , $$
(9)
$$ \phi_{{{\text{c}},ij}} = \left( {\frac{1}{{1 + \delta_{{{\text{c}},ij}} }}} \right)\quad \forall i,\forall j, $$
(10)
$$ \phi_{{{\text{tf}},ij}} = \left( {\frac{1}{{1 + \frac{{\delta_{{{\text{tf}},ij}} }}{{S_{{{\text{tf}},ij}} }}}}} \right)\quad \forall i,\forall j, $$
(11)
$$ P_{{{\text{G}},i,t}} = P_{{{\text{g}},i,t}} + P_{{{\text{ESS}},i,t}}^{\text{dis}} \quad \forall t,\forall i, $$
(12)
$$ P_{{{\text{L}},i,t}} = P_{{{\text{l}},i,t}} + P_{{{\text{ESS}},i,t}}^{\text{ch}} \quad \forall t,\forall i, $$
(13)
$$ Q_{{{\text{G}},i,t}} = Q_{{{\text{g}},i,t}} \quad \forall t,\forall i. $$
(14)

Line flow constraints

$$ - (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \le P_{ij,t} \le (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(15)
$$ - (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \le Q_{ij,t} \le (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(16)
$$ - \sqrt 2 (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \le P_{ij,t} + Q_{ij,t} \le \sqrt 2 (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(17)
$$ - \sqrt 2 (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \le P_{ij,t} - Q_{ij,t} \le \sqrt 2 (1 + \delta_{{{\text{c}},ij}} )S_{{{\text{c}},ij}} \quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} . $$
(18)

Transformer flow constraints

$$ - \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right) \le P_{ij,t} \le \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right)\quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(19)
$$ - \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right) \le Q_{ij,t} \le \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right)\quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(20)
$$ - \sqrt 2 \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right) \le P_{ij,t} + Q_{ij,t} \le \sqrt 2 \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right)\quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(21)
$$ - \sqrt 2 \left( {S_{{{\text{tf}},ij}} + \delta_{tf,ij} } \right) \le P_{ij,t} - Q_{ij,t} \le \sqrt 2 \left( {S_{{{\text{tf}},ij}} + \delta_{{{\text{tf}},ij}} } \right)\quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} . $$
(22)

Energy storage system constraints

$$ 0 \le P_{ESS,i,t}^{dis} \le P_{ESS,i}^{R} u_{1,i,t} \quad \forall t,\forall i, $$
(23)
$$ - P_{{{\text{ESS}},i}}^{\text{R}} u_{2,t,i} \le P_{{{\text{ESS}},t,i}}^{\text{ch}} \le 0\quad \forall t,\forall i, $$
(24)
$$ u_{1,i,t} + u_{2,i,t} \le 1\quad \forall t,\forall i, $$
(25)
$$ E_{{{\text{ESS}},i,t + 1}} = E_{{{\text{ESS}},i,t}} - \left( {\frac{{P_{{{\text{ESS}},i,t}}^{\text{dis}} }}{{\eta_{\text{ESS}}^{\text{dis}} }} - \eta_{\text{ESS}}^{\text{ch}} P_{{{\text{ESS}},i,t}}^{\text{ch}} } \right)\Delta t\quad \forall t,\forall i, $$
(26)
$$ E_{{{\text{ESS}},i}}^{\hbox{min} } \le E_{{{\text{ESS}},i,t}} \le E_{{{\text{ESS}},i}}^{\text{R}} \quad \forall t,\forall i. $$
(27)

Voltage drop constraints

$$ \left| {V_{i,t} } \right| - \left| {V_{j,t} } \right| = \frac{{\left( {r_{ij} \phi_{c,ij} P_{ij,t} + x_{ij} \phi_{c,ij} \phi_{tf,ij} Q_{ij,t} } \right)}}{{\left| {V_{0} } \right|}}\quad \begin{array}{*{20}c} {\forall t,\forall i,} \\ {\forall j} \\ \end{array} , $$
(28)
$$ V_{i}^{\hbox{min} } \le V_{i,t} \le V_{i}^{\hbox{max} } \quad \forall t,\forall i, $$
(29)
$$ \delta_{{{\text{c}},ij}} \text{ } \in {\mathbb{N}}\quad \forall i,\forall j, $$
(30)
$$ P_{{{\text{ESS}},i}}^{\text{R}} ,\,\,E_{{{\text{ESS}},i}}^{\text{R}} ,\delta_{{{\text{tf}},ij}} ,\delta_{{{\text{c}},ij}} \ge 0\quad \forall i,\forall j. $$
(31)

The objective function (7) is to minimize the total net present cost of the installation of battery energy storage, additional transformers, and cables. The first two constraints represented by the equality constraints (8) and (9) are the power balance constraints, which is to ensure that the load demand is satisfied at each time instance for active and reactive power, respectively. Equations (13) and (14) define the factor for calculating the equivalent values of the resistive and reactive component of the network. Since the solution of the optimization problem involves the addition of new cables and transformers, the network topology will change, which will change the equivalent impedance of the network. The equality constraints (15) and (16) are the definition for the total power generation and load injection at bus i, respectively.

Inequality constraints (15)–(22) are for ensuring enough transformer and cable capacity are available to handle the active and reactive power flows through them. Constraints (23) and (24) are to limit the power discharge and charge from the battery at bus i in time t to its rated value. The inequality constraint (25) is to ensure that the battery status at bus i in time t is strictly either be charging, discharging, or idle. Equation (26) is to calculate the amount of energy available for the battery at bus i at the beginning of the next time step. Constraint (27) ensures that the capacity of the energy storage at bus i in time t does not exceed its rated energy capacity and provides a lower limit for energy capacity.

Constraint (28) is related to the voltage drop between bus i and j if they are connected at each time instant t. Constraint (29) ensures that the voltage at each bus is within a specific limit for each period t. Constraint (30) is to define the variable associated with cable capacity expansion to be integers. Finally, constraint (31) is to ensure all the variables are non-zero. A flowchart of the optimization algorithm is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the optimization algorithm

Full size image

Case studies

The models constructed were implemented in the General Algebraic Modeling System (GAMS) to solve the optimization problem. The test system is a distribution feeder part of a substation network in Riyadh, Saudi Arabia. The data in Table 3 were collected from several references including the Saudi Arabian Monetary Authority, documents from the Saudi Electricity Company (SEC) as well as references [32, 33] (Fig. 3).

Table 3 System economic parameters
Full size table
Fig. 3
figure 3

Test system

Full size image

Simulation results

Comprehensive simulations involved solving the optimization problem with 50 different scenarios. For the scenarios involving the current battery energy storage prices under different loading and transformer capacity schemes, the battery storage system was not a feasible solution. Meaning that the results of the optimization algorithm did not include energy storage as a solution. Since there are many simulation results to report, only the ones with feasible battery storage system is reported here.

  • Case A-1: Peak load is 120% of nominal transformer capacity

  • Case A-2: Peak load is 160% of nominal transformer capacity

  • Case B-1: Transformer capacity is reduced to 50% of nominal

  • Case B-2: Transformer capacity is reduced to 80% of nominal.

Discussion

The simulations were done to investigate the economic viability of utilizing battery energy storage systems at the distribution network. As stated previously in the paper, energy storage has the potential to serve various applications and provide different benefits to the network. From the many simulations that were carried out, it was noticeable that battery energy storage system with the current prices is not an economical choice for substation upgrade deferral or even for new construction of substations. The energy storage only became viable when the cost is only 20% (80% cost reduction) of the assumed current prices that is reported in Table 3. At this level of cost reduction, the energy storage prices are competitive with the cost of transformers, which is the reason for having a simulation solution that involved battery energy storage systems.

From the results section, Tables 4 and 5 shows the result of the simulation assuming the energy storage prices at 20% of current reported values. Two peak load scenarios were assumed 120% and 160% of each transformer nominal capacity. For example, transformers with a nominal capacity of 1000 kVA would have a peak load of 1200 kVA for the 120% peak load scenario. For the same scenario, the 1500 kVA transformers would have a peak load of 1800 kVA.

Table 4 Results for case A-1
Full size table
Table 5 Results for case A-2
Full size table

The peak load variation scenarios displayed an increase in energy storage capacity as the peak load increased. Transformers and cables expansion were still needed, although energy storage system in principle can be used to offset these components.

Tables 6 and 7 are the simulation results for the same energy storage cost assumption at 20% of current prices. The peak load for each transformer was fixed at 100% of each transformer nominal capacity as such a 1000 kVA and 1500 kVA transformers will have a peak load of 1000 kVA and 1500 kVA, respectively. Thus, the cost of energy storage as well as the peak load level are held constant, and the capacity of each transformer in the network is varied with two scenarios 50–80% of their nominal values. To clarify, the scenario reported in Table 6 represents a 50% of transformer capacity. This means that in this scenario, the transformer sizes were reduced to 50% of their nominal capacity thus, a 1000 kVA transformer will be reduced to 500 kVA and a 1500 kVA will be reduced to 750 kVA. This particular study was performed to investigate the viability for new construction of substations to be designed at a lower than peak load capacity for the transformers and utilize energy storage for the deficit in capacity.

Table 6 Results for case B-1
Full size table
Table 7 Results for case B-2
Full size table

For all the scenarios reported in Tables 4, 5, 6 and 7, the location of the energy storage system was always at the low side of the distribution transformers, which means that the energy storage is acting as a relief for the distribution transformers.

Conclusions

The paper discusses the feasibility of installing battery storage systems at the distribution level. The main application of the battery would be to provide peak shaving of the load in time of high demand. This has the potential to defer or even eliminate the need for the installation of new transformer and/or cables to handle the peak demand.

The simulations were done to investigate the economic viability of utilizing battery energy storage systems at the distribution network. As stated previously energy storage has the potential to serve various applications and provide different benefits to the network.

From the many simulations that were carried out, it was noticeable that battery energy storage system with the current prices is not an economical choice for substation upgrade deferral or even for new construction of substations. The energy storage only became viable when the cost is only 20% (80% cost reduction) of the assumed current prices reported in Table 3. At this level of cost reduction, the energy storage prices are competitive with the cost of transformers, which is the reason for having a simulation solution that involved battery energy storage systems.