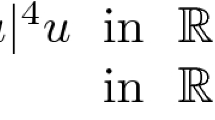Asymptotic formulas of the eigenvalues for the linearization of a one-dimensional sinh-Poisson equation

Abstract

We are concerned with a Neumann problem of a one-dimensional sinh-Poisson equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u''+\lambda \sinh u=0 &{} \text {for}\ 0<x<1,\\ u'(0)=u'(1)=0, \end{array}\right. } \end{aligned}$$

where $\lambda >0$ is a parameter. A complete bifurcation diagram of this problem is obtained. We also consider the linearized eigenvalue problem at every nontrivial solution u. We derive exact expressions of all the eigenvalues and eigenfunctions, using Jacobi elliptic functions and complete elliptic integrals. Then, we also derive asymptotic formulas of eigenvalues as $\lambda \rightarrow 0$. Exact eigenvalues and eigenfunctions for a Dirichlet problem are presented without proof. The main technical tool is an ODE technique.

1 Introduction and main results

We are concerned with a Neumann problem of a sinh-Poisson equation in an interval

$$\begin{aligned} {\left\{ \begin{array}{ll} u''+\lambda \sinh u=0 &{} {\text {for }} \, 0<x<1,\\ u'(0)=u'(1)=0, \end{array}\right. } \end{aligned}$$

(1.1)

where $\lambda >0$ is a parameter. The two-dimensional sinh-Poisson equation

$$\begin{aligned} \Delta u+\lambda \sinh u=0 \end{aligned}$$

(1.2)

appears as a vorticity equation in hydrodynamics [8] and it is also related to a constant mean curvature surface in geometry [18]. The Eq. (1.2) has received a considerable attention in recent years. See e.g. [2, 4, 5, 9, 10, 17] for previous studies. The solutions of (1.1) give one-dimensional solutions of a Neumann problem in a rectangle and of a problem in a two-dimensional flat torus. Though they are special solutions of (1.2), a solution structure of (1.1) and spectral properties for linearization problems will be studied in details in this paper. A one-dimensional Dirichlet problem is also considered in Sect. 5.

In this paper we extensively use the Jacobi elliptic functions $\textrm{sn}(x,k)$, $\textrm{cn}(x,k)$ and $\textrm{dn}(x,k)$ and the complete elliptic integrals of the first kind K(k), the second kind E(k) and the third kind $\Pi (\nu ,k)$. We recall definitions and basic properties in Appendix.

The first main result is about the exact solutions of (1.1) and a complete bifurcation diagram of (1.1). Let $\mathbb {R}_+:=\{x;\ x>0\}$ and $X:=C^2(0,1)\cap C^1[0,1]$.

Theorem 1.1

(Exact solutions) Let $\mathcal {S}\subset \mathbb {R}_+\times X$ denote the solution set of (1.1). Then,

$$\begin{aligned} \mathcal {S}=\mathcal {C}_0\cup \left( \bigcup _{n=1}^{\infty }\left( \mathcal {C}_n^+\cup \mathcal {C}_n^-\right) \right) , \end{aligned}$$

(1.3)

where

$$\begin{aligned} \mathcal {C}_0:= & {} \left\{ (\lambda ,u_0(x))\in \mathbb {R}_+\times X;\ \lambda >0\right\} ,\quad u_0(x)=0, \end{aligned}$$

(1.4)

$$\begin{aligned} \mathcal {C}^{\pm }_n:= & {} \{(\lambda _n(k),u_{n}^{\pm }(x,k))\in \mathbb {R}_+\times X;\ 0<k<1\}, \end{aligned}$$

(1.5)

$$\begin{aligned} \lambda _n(k):= & {} 4(1-k^2)K(k)^2n^2, \end{aligned}$$

(1.6)

$$\begin{aligned} u_{n}^{\pm }(x,k):= & {} \pm \left\{ 2\log \left( \textrm{dn}(2nK(k)x,k)+k\textrm{cn}(2nK(k)x,k)\right) -\log (1-k^2) \right\} .\nonumber \\ \end{aligned}$$

(1.7)

Let

$$\begin{aligned} \lambda _n:=\lambda ^+_n(0)=\pi ^2n^2,\ n=1,2,\ldots . \end{aligned}$$

(1.8)

The curve $\mathcal {C}^{\pm }_n$ is a graph of $\lambda$ and it is defined on $0<\lambda <\lambda _n$. In particular, the curve $\mathcal {C}^{\pm }_n$ bifurcates from $(\lambda _n,0)$ on the trivial branch $\mathcal {C}_0$ and the bifurcation is a subcritical pitchfork type. If $0<\lambda <\lambda _n$ for $n\ge 1$, then (1.1) has solutions $u^{\pm }_j$ for every $j\ge n$.

We call $u^{\pm }_n$ n-mode solutions. Figure 1 shows a bifurcation diagram given by (1.3).

Fig. 1

A complete bifurcation diagram given by Theorem 1.1. Every curve approaches to the u(0)-axis as $|u(0)|\rightarrow \infty$

Let $(\lambda ,u)$ be a nontrivial solution of (1.1). It follows from Theorem 1.1 that $(\lambda ,u)\in \mathcal {S}{\setminus }\mathcal {C}_0$ and $u=u^+_n$ or $u^-_n$ for some $n\in \{1,2,\ldots \}$. We consider the following linearized eigenvalue problem of (1.1) at u

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''+\lambda (\cosh u)\varphi =-\mu \varphi &{} {\text {for }} \, 0<x<1,\\ \varphi '(0)=\varphi '(1)=0. \end{array}\right. } \end{aligned}$$

(1.9)

Since $\cosh u^+_n(x,k)=\cosh u^-_n(x,k)$, the eigenvalues for $u^+_n$ are equal to those for $u^-_n$. Hence, $\{\mu ^n_j(k)\}_{j=0}^{\infty }$ denotes the eigenvalues for both $(\lambda _n(k),u^+_n(x,k))$ and $(\lambda _n(k),u^-_n(x,k))$. Moreover, eigenfunctions for both $(\lambda _n(k),u^+_n(x,k))$ and $(\lambda _n(k),u^-_n(x,k))$ are the same, and hence $\varphi ^n_j(x,k)$ denotes an eigenfunction for both $(\lambda _n(k),u^+_n(x,k))$ and $(\lambda _n(k),u^-_n(x,k))$.

In a general theory of functional analysis the spectrum for (1.9) consists only of real eigenvalues and the set of corresponding eigenfunctions is a complete orthogonal set in $L^2([0,1])$. Though it is not easy to obtain exact expressions for general differential operators, in the case of (1.9) exact eigenvalues and eigenfunctions are obtained as follows:

Theorem 1.2

(Exact eigenvalues and eigenfunctions) Let $\mathbb {N}_0:=\{0,1,2,\ldots \}$. The following hold:

• (i) The 0-th and n-th eigenvalues and eigenfunctions of (1.9) are given as follows:

  $$\begin{aligned} \mu ^n_0(k)= & {} -4K(k)^2n^2\ \ \text {and}\ \ \varphi ^n_0(x,k)=\textrm{dn}(2nK(k)x,k),\\ \mu ^n_n(k)= & {} -4k^2K(k)^2n^2\ \ \text {and}\ \ \varphi ^n_n(x,k)=\textrm{cn}(2nK(k)x,k). \end{aligned}$$

• (ii) [Eigenvalues] For $j\in \mathbb {N}_0\setminus \{0,n\}$, the j-th eigenvalue $\mu ^n_j(k)$ is a unique solution of

  $$\begin{aligned} \mathcal {A}(\mu ,k)=\frac{j\pi }{2n}. \end{aligned}$$

  (1.10)

  Here, $\mathcal {A}(\mu ,k)$ is defined for $\mu \in (\mu ^n_0(k),\mu ^n_n(k))\cup (0,\infty )$ and given by

  $$\begin{aligned} \mathcal {A}(\mu ,k):= & {} \mathcal {M}(\nu ,k),\ \ \nu :=\frac{4k^2K(k)^2n^2}{\mu }, \end{aligned}$$

  (1.11)
  $$\begin{aligned} \mathcal {M}(\nu ,k):= & {} \sqrt{\frac{(\nu +1)(\nu +k^2)}{\nu }}\Pi (\nu ,k), \end{aligned}$$

  (1.12)

  and K(k) and $\Pi (\nu ,k)$ are the complete elliptic integrals of the first and third kinds defined by

  $$\begin{aligned} K(k):=\int _0^1\frac{ds}{\sqrt{(1-s^2)(1-k^2s^2)}},\ \ \Pi (\nu ,k):=\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}. \end{aligned}$$

  Moreover, the Morse index of u, which is the number of negative eigenvalues, is $n+1$ and u is nondegenerate, i.e., 0 is not an eigenvalue. (Fig. 2 shows a graph of A$(\mu ,k)$.)

• (iii) [Eigenfunctions] For $j\in \mathbb {N}_0\setminus \{0,n\}$, a j-th eigenfunction $\varphi ^n_j(x,k)$ is given by

  $$\begin{aligned} \varphi ^n_j(x,k)= & {} \sqrt{\left| \mu ^n_j(k)-\mu ^n_n(k)\textrm{sn}^2(2nK(k)x,k)\right| }\nonumber \\{} & {} \times \cos \left( \int _0^x\frac{\sqrt{\mu ^n_j(k)(\mu ^n_j(k)-\mu ^n_0(k))(\mu ^n_j(k)-\mu ^n_n(k))}}{\left| \mu ^n_j(k)-\mu ^n_n(k)\textrm{sn}^2(2nK(k)y,k)\right| }dy\right) . \nonumber \\ \end{aligned}$$

  (1.13)

Fig. 2

A graph of $\mathcal {A}(\mu ,k)$ for $k=1/\sqrt{2}$ and $n=3$ which is defined for $\mu \in (\mu ^3_0(k),\mu ^3_3(k))\cup (0,\infty )$. For $j\in \mathbb {N}_0\setminus \{0\}$, the j-th eigenvalue $\mu ^3_j(k)$ is given by (1.10)

Remark 1.3

• (i) $\varphi ^n_0(x,k)$ can be formally obtained by substituting $j=0$ into (1.13). If we let the integral in (1.13) be 0 for $j=n$, then $\varphi ^n_n(x,k)$ can be also formally obtained from (1.13).

• (ii) The eigenfunction (1.13) can be also written as follows:

  $$\begin{aligned} \varphi ^n_j(x,k)= & {} C_0\sqrt{\left| \frac{1}{\nu _j}+\textrm{sn}^2(2nK(k)x,k)\right| }\\{} & {} \times \cos \left( \sqrt{\frac{(\nu _j+1)(\nu _j+k^2)}{\nu _j}}\right. \\{} & {} \left. \times \int _0^{\textrm{sn}(2nK(k)x,k)}\frac{ds}{(1+\nu _js^2)\sqrt{(1-s^2)(1-k^2s^2)}}\right) , \end{aligned}$$

  where $\nu _j:=4k^2K(k)^2n^2/\mu ^n_j(k)$.

In the studies of (1.2) a considerable attention has been attracted to the case $\lambda \rightarrow 0$. The third main result is about asymptotic formulas of eigenvalues for (1.9) as $k\rightarrow 1$. Note that $\lambda \rightarrow 0$ as $k\rightarrow 1$ because of (1.6) and Lemma A.3.

Theorem 1.4

(Asymptotic formulas) The following asymptotic formulas hold:

• (i) If $j\in \{1,2,\ldots ,n-1\}$, then

  $$\begin{aligned} \mu ^n_j(k)=\left\{ -4n^2+4n^2(1-k^2)\sin ^2\left( \frac{j\pi }{2n}\right) +o((1-k^2))\right\} K(k)^2 \quad {\text {as}} \ \ k\rightarrow 1. \end{aligned}$$

  In particular,

  $$\begin{aligned} \lim _{k\rightarrow 1}\frac{\mu ^n_j(k)}{K(k)^2}=-4n^2\ \ \text {for}\ \ j\in \{1,2,\ldots ,n-1\}. \end{aligned}$$

• (ii) If $j\in \{n+1,n+2,\ldots \}$, then

  $$\begin{aligned} \mu ^n_j(k)=\pi ^2(j-n)^2+o(1)\quad \text {as}\ \ k\rightarrow 1. \end{aligned}$$

Remark 1.5

By Theorem 1.2 (i) we have the exact eigenvalues $\mu ^n_0(k)$ and $\mu ^n_n(k)$. We can check that, for $j=0,n$,

$$\begin{aligned} \mu ^n_j(k)=\left\{ -4n^2+4n^2(1-k^2)\sin ^2\left( \frac{j\pi }{2n}\right) \right\} K(k)^2\quad \text {for all}\ \ 0<k<1. \end{aligned}$$

In Sect. 5 exact eigenvalues and eigenfunctions for a Dirichlet problem are presented without proof.

Let us mention technical details. A theory of exact expressions of eigenvalues and eigenfunctions associated to the linearization for one-dimensional elliptic problems was constructed in Wakasa–Yotsutani [11]. This theory can be applied to a general nonlinear term f(u). We recall the theory in Sect. 3 of the present paper. In the theory there is a key ODE (3.6) which is a linear ODE of third order with variable coefficients. In general it is difficult to obtain a solution h(u) of the key ODE (3.6). However, in the case of our nonlinearity $f(u)=\sinh u$ we can find a solution h(u) which is given by (3.14). In this case all the eigenvalues and eigenfunctions can be written in terms of h(u). Specifically, the following function becomes an eigenfunction:

$$\begin{aligned} \sqrt{h(u^{\pm }_n(x,k))}\cos \left( \sqrt{\frac{\lambda \rho }{2}}\int _0^x\frac{dy}{h(u^{\pm }_n(y,k))}\right) \ \ \text {for a certain constant}\ \rho . \end{aligned}$$

Since $h(u^{\pm }_n(x,k))$ and $\rho$ depend on $\mu$, the LHS of the equation

$$\begin{aligned} \sqrt{\frac{\lambda \rho }{2}}\int _0^{1/2n}\frac{dy}{h(u^{\pm }_n(y,k))}=\frac{j\pi }{2n}\quad \text {for}\ \ j\in \mathbb {N}_0\setminus \{0,n\}. \end{aligned}$$

becomes a function in $\mu$. A solution of the above equation gives the eigenvalue $\mu ^n_j(k)$ for $j\in \mathbb {N}_0\setminus \{0,n\}$. Two cases $j=0,n$ are exceptional and eigenvalues and eigenfunctions are given in a different way. Since $u^{\pm }_n(x,k)$ can be also written explicitly, we have exact expressions of all the eigenvalues and eigenfunctions. This method was applied to

• (1) a Neumann problem of $\varepsilon ^2u''+\sin u=0$ in [11, 13],

• (2) a Dirichlet problem of $\varepsilon ^2 u''+\sin u=0$ in [12],

• (3) a Neumann problem of the Allen-Cahn equation $\varepsilon ^2u''+u-u^3=0$ in [14, 15],

• (4) a Neumann problem of the scalar field equation $\varepsilon ^2u''-u+u^3=0$ in [6],

• (5) Dirichlet problems of $u''+\lambda e^{\pm u}=0$ in [7],

and it is applied to

• (6) a Neumann (and Dicrichlet) problem of $u''+\lambda \sinh u=0$ in the present paper.

Another interesting technical aspect of this paper is the modified complete elliptic integral of the third kind $\mathcal {M}(\nu ,k)$ defined by (1.12). The function $\mathcal {M}(\nu ,k)$ was introduced in [16]. In Theorem 1.2 and its proof we see that $\mathcal {M}(\nu ,k)$ plays a central role in the study of exact eigenvalues. It appears not only in our case (6) above but also in the cases (1), (2), (3) and (4) above, and hence $\mathcal {M}(\nu ,k)$ might be universal in some sense. Figure 3 in Appendix shows a graph of $\mathcal {M}(\nu ,k)$ in $\nu$. We will recall some limit formulas for $\mathcal {M}(\nu ,k)$.

This paper consists of six sections. In Sect. 2 we obtain the exact solutions $(\lambda ,u)$ of (1.1). We show that $d\lambda _n(k)/dk<0$ for $k\in (0,1)$ and that $0<\lambda _n(k)<\lambda _n$ for $k\in (0,1)$. Hence, $\mathcal {C}^{\pm }_n$ is a graph of $\lambda$ defined on $0<\lambda <\lambda _n$. We prove Theorem 1.1. In Sect. 3 we recall the theory for exact eigenvalues and eigenfunctions which was developed in [11]. In Sect. 4 we prove Theorems 1.2 and 1.4. Specifically, two exceptional eigenvalues and eigenfunctions are obtained in Lemma 4.1. We study a domain of $\mathcal {A}(\mu ,k)$, a monotonicity of $\mathcal {A}(\mu ,k)$ in $\mu$ and certain limits of $\mathcal {A}(\mu ,k)$. Using these properties of $\mathcal {A}(\mu ,k)$, we prove Theorem 1.2. Next, asymptotic formulas in Theorem 1.4 are proved. We will see that several limit formulas of complete elliptic integrals, which we recall in Appendix, are used in the proof. In Sect. 5 exact eigenvalues and eigenfunctions for a Dirichlet problem are presented without proof. Section A is an Appendix. We recall definitions and basic properties of $\textrm{sn}(x,k)$, $\textrm{cn}(x,k)$, $\textrm{dn}(x,k)$, K(k), E(k) and $\Pi (\nu ,k)$.

2 Proof of Theorem 1.1

Using a phase plane analysis, we obtain exact solutions of (1.1) and a complete bifurcation diagram of (1.1).

Lemma 2.1

All the nontrivial solutions of (1.1) can be expressed as

$$\begin{aligned} (\lambda ,u)=(\lambda _n(k),u^{\pm }_n(x,k))~\text { for some } n\in \{1,2,\ldots \}~\text {and some}~k\in (0,1), \end{aligned}$$

(2.1)

where $\lambda _n(k)$ and $u^{\pm }_n(x,k)$ are defined by (1.6) and (1.7), respectively.

Proof

Let us consider the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u'=v\\ v'=-\lambda \sinh u\\ \end{array}\right. } \end{aligned}$$

(2.2)

with $(u(0),v(0))=(\alpha , 0)$. We can easily see that (2.2) has only one equilibrium $(u,v)=(0,0)$ and that the other orbits are periodic. Since $\sinh (-u)=-\sinh (u)$, each periodic orbit is symmetric with respect to both the u and v axes. Hence, we can define a quarter period of each periodic orbit. A solution of (1.1) corresponds to an orbit of (2.2) that starts from $(\alpha ,0)$ and reaches a point on the u-axis, which is $(-\alpha ,0)$ or $(\alpha ,0)$, at $x=1$. Here, the orbit may rotate finitely many times around the origin. In summary, the orbit reaches the v-axis for the first time at $x=1/2n$ for some $n\in \{1,2,\ldots \}$, i.e.,

$$\begin{aligned} u \left( \frac{1}{2n}\right) =0\ \ \text {for some}\ n\in \{1,2,\ldots \}. \end{aligned}$$

(2.3)

In other words the quarter period is 1/2n. If (2.3) holds, then u(x) is an n-mode solution.

We consider (2.2) with $(u(0),v(0))=(\alpha , 0)$. Multiplying (1.1) by $u'$ and integrating it in x over [0, x], we have

$$\begin{aligned} \frac{1}{2}u'(x)^2+\lambda \cosh u(x)=\lambda \cosh \alpha . \end{aligned}$$

(2.4)

We consider the case $\alpha >0$. Then we have

$$\begin{aligned} x=\int _0^x\frac{-u'(y)dy}{\sqrt{2\lambda (\cosh \alpha -\cosh u(y))}}. \end{aligned}$$

(2.5)

We use the change of variables

$$\begin{aligned} s:=\sqrt{\frac{\cosh \alpha -\cosh u(y)}{\cosh \alpha -1}}. \end{aligned}$$

(2.6)

Since u(y) is monotone for $0\le y\le 1/2n$, the mapping $y\mapsto s$ defined by (2.6) for $y\in [0,1/2n]$ is one-to-one. Therefore, this change of variables is valid if $0\le x\le 1/2n$. Using (2.6), we see that (2.5) becomes

$$\begin{aligned} x&=\sqrt{\frac{2}{(\cosh \alpha +1)\lambda }}\int _0^{\sqrt{\frac{\cosh \alpha -\cosh u(x)}{\cosh \alpha -1}}} \frac{ds}{\sqrt{(1-s^2)(1-k^2s^2)}}\\&=\sqrt{\frac{2}{(\cosh \alpha +1)\lambda }} \textrm{sn}^{-1}\left( \sqrt{\frac{\cosh \alpha -\cosh u(x)}{\cosh \alpha -1}},k\right) , \end{aligned}$$

where $\textrm{sn}^{-1}$ denotes the inverse function of $\textrm{sn}$ and

$$\begin{aligned} k^2:=\frac{\cosh \alpha -1}{\cosh \alpha +1},\quad \text {and hence}\ \cosh \alpha =\frac{1+k^2}{1-k^2}. \end{aligned}$$

(2.7)

We have

$$\begin{aligned} \sqrt{\frac{\cosh \alpha -\cosh u(x)}{\cosh \alpha -1}}=\textrm{sn}\left( \sqrt{\frac{(\cosh \alpha +1)\lambda }{2}}x,k\right) , \end{aligned}$$

and hence

$$\begin{aligned} \cosh u(x)=\cosh \alpha -(\cosh \alpha -1)\textrm{sn}^2\left( \sqrt{\frac{(\cosh \alpha +1)\lambda }{2}}x,k\right) . \end{aligned}$$

(2.8)

Substituting $x=1/2n$ into (2.8), we see by (2.3) that

$$\begin{aligned} \sqrt{\frac{(\cosh \alpha +1)\lambda }{2}}\frac{1}{2n}=\textrm{sn}^{-1}(1,k)=K(k), \end{aligned}$$

(2.9)

which leads to

$$\begin{aligned} \lambda =4(1-k^2)K(k)^2n^2. \end{aligned}$$

Here we used (2.7). We denote $\lambda$ by $\lambda _n(k)$. Let

$$\begin{aligned} w(x):=\cosh \alpha -(\cosh \alpha -1)\textrm{sn}^2(2nK(k)x,k). \end{aligned}$$

By (2.8) and (2.9) we see that $\cosh u(x)=w(x)$. By a direct calculation we can check that

$$\begin{aligned} w(x)+\sqrt{w(x)^2-1} =\frac{1}{1-k^2}\left\{ \textrm{dn}(2nK(k)x,k)+k\textrm{cn}(2nK(k)x,k)\right\} ^2. \end{aligned}$$

(2.10)

By (2.10) we have

$$\begin{aligned} u(x)= & {} \cosh ^{-1}w(x)= \log \left( w(x)+\sqrt{w(x)^2-1}\right) \\= & {} 2\log (\textrm{dn}(2nK(k)x,k)+k\textrm{cn}(2nK(k)x,k))-\log (1-k^2), \end{aligned}$$

which is denoted by $u^+_n(x,k)$. In particular,

$$\begin{aligned} \alpha =u(0)=\log \frac{1+k}{1-k}, \end{aligned}$$

which is equivalent to (2.7). We can easily check that

$$\begin{aligned} u(x)=-u^+_n(x,k), \end{aligned}$$

which is denoted by $u^-_n(x,k)$, is a solution of (1.1) with $(u(0),u'(0))=(-\alpha ,0)$. We have proved (2.1). Because of this construction of solutions, we see that $(\lambda ,u^{\pm }_n(x,k))$ consist of all the nontrivial solutions of (1.1). The proof is complete. $\square$

Lemma 2.2

Let $\lambda _n(k)$ be defined by (1.6). Then, $\frac{d\lambda _n(k)}{dk}<0$ for $0<k<1$.

Proof

Because of Lemma A.2, we have

$$\begin{aligned} \frac{E(k)}{K(k)}-1<-\frac{k^2}{2}. \end{aligned}$$

(2.11)

By Lemma A.1 (i) and (2.11) we have

$$\begin{aligned} \frac{d\lambda _n(k)}{dk}&=-8kK(k)^2n^2+4(1-k^2)2K(k)\frac{dK(k)}{dk}n^2\\&=-8kK(k)^2n^2+4(1-k^2)2K(k)\frac{E(k)-(1-k^2)K(k)}{k(1-k^2)}n^2\\&=\frac{8K(k)^2n^2}{k}\left( \frac{E(k)}{K(k)}-1\right) <0. \end{aligned}$$

$\square$

Proof of Theorem 1.1

Let $\lambda _n(k)$ and $u^{\pm }_n(x,k)$ be defined by (1.6) and (1.7), respectively. Let $\mathcal {C}_0$ and $\mathcal {C}^{\pm }_n$, $n=1,2,\ldots$, be defined by (1.4) and (1.5), respectively.

First, every element of $\mathcal {C}_0$ is a trivial solution of (1.1). Next, we study nontrivial solutions. By Lemma 2.1, the solution set $\mathcal {S}$ can be written as (1.3). What we have to do is to prove a monotonicity of each nontrivial branch $\mathcal {C}^{\pm }_n$, $n\ge 1$, which indicates that $\mathcal {C}^{\pm }_n$ can be described as a graph of $\lambda$ for a certain interval. It is clear that

$$\begin{aligned} \lim _{k\rightarrow 0}\lambda _n(k)=\lambda _n, \end{aligned}$$

where $\lambda _n$ is defined by (1.8). By Lemma A.3 we have

$$\begin{aligned} \lim _{k\rightarrow 1}\lambda _n(k)=\lim _{k\rightarrow 1}4(1-k^2)\left( -\frac{1}{2}\log (1-k^2)+2\log 2+o(1)\right) ^2n^2=0. \end{aligned}$$

Because of Lemma 2.2, $\lambda _n(k)$ is a monotone function, and hence $\mathcal {C}^{\pm }_n$ can be described as a graph of $\lambda$ for $0<\lambda <\lambda _n$. All the other statements in Theorem 1.1 follow from this result. The proof is complete. $\square$

3 Preliminaries for proofs of Theorems 1.2 and 1.4

3.1 Sturm–Liouville theory

Let f be an arbitrary $C^1$-function. We consider the Neumann problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u''+\lambda f(u)=0, &{} \text {for}\ 0<x<1,\\ u'(0)=u'(1)=0. \end{array}\right. } \end{aligned}$$

(3.1)

Let $(\lambda ,u)$ denote a solution of (3.1), where $\lambda >0$. We define

$$\begin{aligned} \alpha :=u(0). \end{aligned}$$

(3.2)

The linearized eigenvalue problem at $(\lambda ,u)$ becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''+\lambda f'(u)\varphi =-\mu \varphi , &{} \text {for}\ 0<x<1,\\ \varphi '(0)=\varphi '(1)=0. \end{array}\right. } \end{aligned}$$

(3.3)

We recall basic properties about eigenvalues and eigenfunctions for (3.3).

Proposition 3.1

Let $\{\mu _j\}_{j=0}^{\infty }$ denote the eigenvalues of (3.3), and let $\varphi _j(x)$, $\varphi _j(x)\not \equiv 0$, be an eigenfunction corresponding to $\mu _j$. Then the following hold:

• (i) Each eigenvalue $\mu _j$ is real and simple, and $\mu _0<\mu _1<\mu _2<\cdots$.

• (ii) For $j\in \mathbb {N}_0$, the zero number of $\varphi _j(x)$ on [0, 1] is j, i.e.,

  $$\begin{aligned} \sharp \{x\in [0,1];\ \varphi _j(x)=0\}=j. \end{aligned}$$

See [3, Theorem 2.1 in p.212] for details of a proof of Proposition 3.1. We omit the proof.

3.2 General nonlinearity

First, we look for an eigenfunction of the form $\varphi (x)=\sqrt{\phi (x)}$. Substituting $\sqrt{\phi (x)}$ into the equation in (3.3), we see that $\phi (x)$ satisfies

$$\begin{aligned} 2\phi \phi ''-\phi '^2+4(\lambda f'(u)+\mu )\phi ^2=0. \end{aligned}$$

We define

$$\begin{aligned} \Phi (x):=2\phi ''\phi -\phi '^2+4(\lambda f'(u)+\mu )\phi ^2. \end{aligned}$$

Then,

$$\begin{aligned} \Phi '(x)= 2\phi \left\{ \phi '''+4(\lambda f'(u)+\mu )\phi '+2\lambda f''(u)u'\phi \right\} . \end{aligned}$$

We consider the equation

$$\begin{aligned} \phi '''+4(\lambda f'(u)+\mu )\phi '+2\lambda f''(u)u'\phi =0. \end{aligned}$$

(3.4)

If $\phi (x)$ satisfies (3.4), then $\Phi '(x)=0$, and hence $\Phi (x)$ is constant. In particular, $\Phi (x)=\Phi (0)$, i.e.,

$$\begin{aligned}{} & {} 2\phi ''(x)\phi (x)-\phi '(x)^2+4(\lambda f'(u(x))+\mu )\phi (x)^2\nonumber \\{} & {} \quad =2\phi ''(0)\phi (0)-\phi '(0)^2+4(\lambda f'(u(0))+\mu )\phi (0)^2. \end{aligned}$$

(3.5)

If $\Phi (0)=0$, then $\sqrt{\phi (x)}$ satisfies the equation in (3.3) and it is a candidate of the eigenfunction. We show that almost all the eigenfunctions can be constructed even if $\Phi (0)\ne 0$.

We look for a solution of (3.4) of the form $\phi (x)=h(u(x))$, where $h(u(x))>0$ for $0\le x\le 1$. Here, $h(\,\cdot \,)$ is an unknown function. In other words we construct an eigenfunction, using the shape of a solution u(x). Substituting h(u(x)) into (3.4), we see that h(u) satisfies the following key equation:

$$\begin{aligned}{} & {} 2(F(\alpha )-F(u))h'''(u)-3f(u)h''(u) \nonumber \\{} & {} \quad +\left( 3f'(u)+4\frac{\mu }{\lambda }\right) h'(u)+2f''(u)h(u)=0, \end{aligned}$$

(3.6)

where $F(u):=\int _0^uf(s)ds$ and we use the following relations:

$$\begin{aligned} u'(x)^2=2\lambda (F(\alpha )-F(u))\ \text {and}\ u''=-\lambda f(u). \end{aligned}$$

It is worth noting that the independent variable of (3.6) becomes u and that the explicit x-dependence disappears. Thus, (3.6) does not depend on each solution u of (3.1). Substituting h(u(x)) into (3.5), we have

$$\begin{aligned} (F(\alpha )-F(u))(2h''h-h'^2)-f(u)hh'+2\left( f'(u)+\frac{\mu }{\lambda }\right) h^2=\rho \end{aligned}$$

(3.7)

and

$$\begin{aligned} \rho :=-f(\alpha )h(\alpha )h'(\alpha )+2\left( f'(\alpha )+\frac{\mu }{\lambda }\right) h(\alpha )^2, \end{aligned}$$

(3.8)

where we use $u(0)=\alpha$ and $u'(0)=0$.

Hereafter, we construct an eigenfunction for (3.3). We assume that a solution h(u) of (3.6) that satisfies $h(u(x))>0$ for $0\le x\le 1$ is obtained. Then, we look for an eigenfunction of the form

$$\begin{aligned} \varphi (x)=\sqrt{h(u(x))}W(\theta (x)). \end{aligned}$$

(3.9)

The functions $W(\theta )$ and $\theta (x)$ are defined later. Using (3.7), we have

$$\begin{aligned}{} & {} \frac{d^2\sqrt{h(u(x))}}{dx^2}+\lambda f'(u)\sqrt{h(u(x))}+\mu \sqrt{h(u(x))}\nonumber \\{} & {} \quad =\frac{1}{4h\sqrt{h}}\left\{ 2\lambda (F(\alpha )-F(u))(2hh''-h'^2)-2\lambda f(u)hh'+4(\lambda f'(u)+\mu )h^2\right\} \nonumber \\{} & {} \quad =\frac{2\lambda \rho }{4h\sqrt{h}}. \end{aligned}$$

(3.10)

Substituting (3.9) into the equation in (3.3), by (3.10) we have

$$\begin{aligned} 0&= \frac{d^2\sqrt{h}}{dx^2}W+2\frac{d\sqrt{h}}{dx}W'\theta '+\sqrt{h}(W''\theta '^2+W'\theta '')+\lambda f'(u)\sqrt{h}W+\mu \sqrt{h}W\nonumber \\&=\sqrt{h}\theta '^2\left( W''+\frac{2\frac{d\sqrt{h}}{dx}\theta '+\sqrt{h}\theta ''}{\sqrt{h}\theta '^2}W'\right) + \left( \frac{d^2\sqrt{h}}{dx^2}+\lambda f'(u)\sqrt{h}+\mu \sqrt{h}\right) W\nonumber \\&=\sqrt{h}\theta '^2\left( W''+\frac{1}{h\theta '^2}\frac{d}{dx}(h\theta ')W'+\frac{\lambda \rho }{2h^2\theta '^2}W\right) . \end{aligned}$$

(3.11)

We assume that $\rho >0$, where $\rho$ is defined by (3.8). We consider the case where

$$\begin{aligned} h(u(x))\theta '(x)=\sqrt{\frac{\lambda \rho }{2}}. \end{aligned}$$

Since h(u(x)) is positive, $\theta (x)$ can be expressed as

$$\begin{aligned} \theta (x)=\theta _0+\sqrt{\frac{\lambda \rho }{2}}\int _0^x\frac{dy}{h(u(y))}\ \ \text {for some}\ \theta _0. \end{aligned}$$

Moreover, it follows from (3.11) that W satisfies $W''(\theta )+W(\theta )=0$. Therefore, $W(\theta )=C_1\cos (\theta +\theta _1)$ for some $C_1$ and $\theta _1$. By (3.9) we have

$$\begin{aligned} \varphi (x)=C_1\sqrt{h(u(x))}\cos \left( \sqrt{\frac{\lambda \rho }{2}}\int _0^x\frac{dy}{h(u(y))}+\theta _0+\theta _1\right) . \end{aligned}$$

Since $\varphi$ satisfies the Neumann boundary condition $\varphi '(0)=0$, we can take $\theta _0+\theta _1=0$, and hence a candidate of an eigenfunction becomes

$$\begin{aligned} \varphi (x)=C_1\sqrt{h(u(x))}\cos \left( \sqrt{\frac{\lambda \rho }{2}}\int _0^x\frac{dy}{h(u(y))}\right) . \end{aligned}$$

(3.12)

For each $j\in \mathbb {N}_0$, let us consider the equation

$$\begin{aligned} \sqrt{\frac{\lambda \rho }{2}}\int _0^1\frac{dy}{h(u(y))}=j\pi . \end{aligned}$$

(3.13)

Since $\rho$ and h(u(y)) depend on $\mu$, (3.13) is an equation for $\mu$. If $\mu$ satisfies (3.13) for some j, then $\varphi '(1)=0$. Since $\sqrt{h(u(x))}>0$ for $0\le x\le 1$, $\varphi (x)$ defined by (3.12) has exactly j zero(s) on $0\le x\le 1$. By Proposition 3.1 (ii) we see that the corresponding $\varphi (x)$ becomes a j-th eigenfunction, and hence $\mu$ becomes the j-th eigenvalue.

3.3 Hyperbolic sine case

We find an exact solution h(u) of (3.6) such that $h(u(x))>0$ for $0\le x\le 1$. When $f(u)=\sinh u$, (3.6) has an exact solution

$$\begin{aligned} h(u)=2\frac{\mu }{\lambda }+\cosh \alpha -\cosh u. \end{aligned}$$

Since $|u(x)|\le \alpha$ for $0\le x\le 1$, the following functions become positive for $0\le x\le 1$:

$$\begin{aligned} {\left\{ \begin{array}{ll} h_+(u(x)):=2\frac{\mu }{\lambda }+\cosh \alpha -\cosh u(x) &{} \text {if}\ \mu \in (0,\infty ),\\ h_-(u(x)):=-2\frac{\mu }{\lambda }-\cosh \alpha +\cosh u(x) &{} \text {if}\ \mu \in (-\infty ,\bar{\mu }^1), \end{array}\right. } \end{aligned}$$

(3.14)

where

$$\begin{aligned} \bar{\mu }^1:=-\frac{\cosh \alpha -1}{2}\lambda . \end{aligned}$$

(3.15)

Hence, (3.14) is a positive solution of (3.6). In the case $f(u)=\sinh u$ the LHS of (3.13) can be defined provided that

$$\begin{aligned} \mu \in (-\infty ,\bar{\mu }^1)\cup (0,\infty )\ \ \text {and}\ \ \rho >0. \end{aligned}$$

In Sect. 4 we will see that when $u(x)=u^{\pm }_n(x,k)$,

$$\begin{aligned} \begin{array}{l} \text {for }j\in \{1,2,\ldots ,n-1\},~(3.13)~\text {has a unique solution}~\mu _j~\text {in}~(-\infty ,\bar{\mu }^1),~\text {and}\\ \text {for}~j\in \{n+1,n+2,\ldots \},~(3.13)~\text {has a unique solution}~\mu _j~\text {in}~(0,\infty ). \end{array} \end{aligned}$$

Two cases $j=0,n$ are exceptional in our case $f(u)=\sinh u$.

4 Proof of Theorems 1.2 and 1.4

For simplicity we write $\lambda$ and u for $\lambda _n(k)$ and $u^{\pm }_n(x,k)$, respectively. In this section we study an exact expression of eigenvalues of (1.9) associated with an n-mode solution u. Let us recall $\alpha :=u(0)$ defined by (3.2). A family of solutions $(\lambda ,u)$ can be parametrized by k, and it can be also parametrized by $\alpha$. We use both k and $\alpha$. Note that k and $\alpha$ are related by (2.7).

4.1 Two exceptional eigenvalues

Lemma 4.1

The following hold:

• (i) The 0-th eigenvalue $\mu ^n_0(k)$ and a corresponding eigenfunction $\varphi ^n_0$ are given by

  $$\begin{aligned} \mu ^n_0(k)=-4K(k)^2n^2\ \ \text {and}\ \ \varphi ^n_0(x,k)=\cosh \frac{u^{\pm }_n(x,k)}{2}=\frac{1}{\sqrt{1-k^2}}\textrm{dn}(2nK(k)x,k). \end{aligned}$$

• (ii) The n-th eigenvalue $\mu ^n_n(k)$ and a corresponding eigenfunction $\varphi ^n_n$ are given by

  $$\begin{aligned} \mu ^n_n(k)=-4k^2K(k)^2n^2\ \ \text {and}\ \ \varphi ^n_n(x,k)=\sinh \frac{u^{\pm }_n(x,k)}{2}=\pm \frac{k}{\sqrt{1-k^2}}\textrm{cn}(2nK(k)x,k). \end{aligned}$$

Proof

(i) Let $\mu =-4K(k)^2n^2$ and $\varphi =\cosh \frac{u(x)}{2}$. Since

$$\begin{aligned} \varphi ''=\frac{1}{4}u'^2\cosh \frac{u}{2}+\frac{1}{2}u''\sinh \frac{u}{2} =\frac{\lambda }{2}\cosh \frac{u}{2}(\cosh \alpha -\cosh u)-\frac{\lambda }{2}\sinh u\sinh \frac{u}{2}, \end{aligned}$$

we have

$$\begin{aligned} \varphi ''+\lambda (\cosh u)\varphi +\mu \varphi&=\left( \mu +\frac{\lambda }{2}\cosh \alpha \right) \cosh \frac{u}{2}\\&\quad +\frac{\lambda }{2}\left( \cosh u\cosh \frac{u}{2}-\sinh u\sinh \frac{u}{2}\right) \\&=\left( \mu +\frac{\cosh \alpha +1}{2}\lambda \right) \cosh \frac{u}{2}, \end{aligned}$$

where we use $\cosh u\cosh \frac{u}{2}-\sinh u\sinh \frac{u}{2}=\cosh \frac{u}{2}$. Since

$$\begin{aligned} \mu +\frac{\cosh \alpha +1}{2}\lambda =-4K(k)^2n^2+\frac{1}{2}\left( \frac{1+k^2}{1-k^2}+1\right) 4(1-k^2)K(k)^2n^2=0,\nonumber \\ \end{aligned}$$

(4.1)

we have $\varphi ''+\lambda (\cosh u)\varphi +\mu \varphi =0$. We easily see that $\varphi '(0)=\varphi '(1)=0$. Since $\varphi (x)>0$ for $0\le x\le 1$, by Proposition 3.1 (ii) we see that $\mu$ is the 0-th eigenvalue and that $\varphi$ is a 0-th eigenfunction. We have

$$\begin{aligned} \cosh ^2\frac{u}{2}=\frac{\cosh u+1}{2}=\frac{1}{1-k^2}\left( 1-k^2\textrm{sn}^2(2nK(k)x,k)\right) =\frac{1}{1-k^2}\textrm{dn}^2(2nK(k)x,k). \end{aligned}$$

The proof of (i) is complete.

(ii) Let $\mu =-4k^2K(k)^2n^2$ and $\varphi =\sinh \frac{u(x)}{2}$. By a similar calculation we have

$$\begin{aligned} \varphi ''+\lambda (\cosh u)\varphi +\mu \varphi =\left( \mu +\frac{\cosh \alpha -1}{2}\lambda \right) \sinh \frac{u}{2}. \end{aligned}$$

Since

$$\begin{aligned} \mu +\frac{\cosh \alpha -1}{2}\lambda =-4k^2K(k)^2n^2+\frac{1}{2}\left( \frac{1+k^2}{1-k^2}-1\right) 4(1-k^2)K(k)^2n^2=0,\nonumber \\ \end{aligned}$$

(4.2)

we have $\varphi ''+\lambda (\cosh u)\varphi +\mu \varphi =0$. We see that $\varphi '(0)=\varphi '(1)=0$. Since u(x) has n zero(s) in $0\le x\le 1$, $\varphi (x)$ also has n zero(s) in $0\le x\le 1$. It follows from Proposition 3.1 (ii) that $\mu$ is the n-th eigenvalue and $\varphi$ is an n-th eigenfunction. We have

$$\begin{aligned} \sinh ^2\frac{u}{2}=\frac{\cosh u-1}{2}=\frac{k^2}{1-k^2}\left( 1-\textrm{sn}^2(2nK(k)x,k)\right) =\frac{k^2}{1-k^2}\textrm{cn}^2(2nK(k)x,k). \end{aligned}$$

Since an eigenfunction is smooth, we see that

$$\begin{aligned} \varphi ^n_n(x,k)=\sinh \frac{u(x)}{2}=\pm \frac{k}{\sqrt{1-k^2}}\textrm{cn}(2nK(k)x,k). \end{aligned}$$

The proof of (ii) is complete. $\square$

4.2 General eigenvalues

We define $\mathcal {A}(\mu ,k)$ by

$$\begin{aligned} \mathcal {A}(\mu ,k):=\frac{1}{2n}\sqrt{\frac{\lambda \rho }{2}}\int _0^1\frac{dy}{h(u(y))}, \end{aligned}$$

(4.3)

where $\rho$ is defined by (3.8) and h is given by (3.14) depending on $\mu$. We already saw in Sect. 3.3 that $\mathcal {A}(\mu ,k)$ can be defined provided that

$$\begin{aligned} \mu \in (-\infty ,\bar{\mu }^1)\cup (0,\infty ) \quad \text {and} \quad \rho >0. \end{aligned}$$

(4.4)

Lemma 4.2

Let $\mathcal {A}(\mu ,k)$ be defined by (4.3). Then,

$$\begin{aligned} \mathcal {A}(\mu ,k)~\text { is defined for}\ \mu \in (\bar{\mu }^0,\bar{\mu }^1)\cup (0,\infty ), \end{aligned}$$

(4.5)

where

$$\begin{aligned} \bar{\mu }^0:=-\frac{\cosh \alpha +1}{2}\lambda \end{aligned}$$

(4.6)

and $\bar{\mu }^1$ is defined by (3.15). Moreover,

$$\begin{aligned} \mathcal {A}(\mu ,k)=\mathcal {M}(\nu ,k), \end{aligned}$$

(4.7)

where $\mathcal {M}(\nu ,k)$ is defined by (1.12) and

$$\begin{aligned} \nu :=\frac{\cosh \alpha -1}{2\mu }\lambda =\frac{4k^2K(k)^2n^2}{\mu }. \end{aligned}$$

(4.8)

Proof

Since

$$\begin{aligned} 0<\rho =8\frac{\mu }{\lambda ^3}\left( \mu +\frac{\cosh \alpha +1}{2}\lambda \right) \left( \mu +\frac{\cosh \alpha -1}{2}\lambda \right) =8\frac{\mu }{\lambda ^3}(\mu -\bar{\mu }^0)(\mu -\bar{\mu }^1), \end{aligned}$$

by (4.4) we see that $\mathcal {A}(\mu ,k)$ can be defined for $\mu \in (\bar{\mu }^0,\bar{\mu }^1)\cup (0,\infty )$, and hence (4.5) is proved.

We consider the case $\mu \in (0,\infty )$. Since $\lambda >0$, we calculate $\int _0^1dy/h_+(u(y))$. We use the change of variables (2.6). Note that this change of variables is valid for $0\le x\le 1/2n$, since the n-mode solution u is monotone for $0\le x\le 1/2n$. By (2.6), we have

$$\begin{aligned} \frac{1}{\sinh u(y)}=\frac{1}{\sqrt{(1-s^2)(1-k^2s^2)}}\cdot \frac{k}{\cosh \alpha -1}. \end{aligned}$$

Using this equality, by a direct calculation we have

$$\begin{aligned} \int _0^{1/2n}\frac{dy}{h_+(u(y))} =\frac{1}{\mu }\sqrt{\frac{\lambda }{2(\cosh \alpha +1)}}\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)},}\qquad \end{aligned}$$

(4.9)

where

$$\begin{aligned} k^2:=\frac{\cosh \alpha -1}{\cosh \alpha +1}\quad \text {and}\quad \nu :=\frac{\cosh \alpha -1}{2\mu }\lambda . \end{aligned}$$

(4.10)

Note that $k^2$ given in (4.10) is equal to (2.7). We have

$$\begin{aligned} \sqrt{\frac{\lambda \rho }{2}} =\sqrt{\mu \left( 2\frac{\mu }{\lambda }+\cosh \alpha +1\right) \left( 2\frac{\mu }{\lambda }+\cosh \alpha -1\right) } =\frac{2}{\lambda }\sqrt{\mu (\mu -\bar{\mu }^0)(\mu -\bar{\mu }^1)}.\nonumber \\ \end{aligned}$$

(4.11)

Using (4.11) and (4.9), we have

$$\begin{aligned} \mathcal {A}(\mu ,k)= & {} \frac{1}{2n}\sqrt{\frac{\lambda \rho }{2}}\int _0^1\frac{dy}{h(u(y))} =\frac{2n}{2n}\sqrt{\frac{\lambda \rho }{2}}\int _0^{1/2n}\frac{dy}{h_+(u(y))}\\= & {} \sqrt{\frac{(\nu +1)(\nu +k^2)}{\nu }}\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}=\mathcal {M}(\nu ,k). \end{aligned}$$

Then, (4.7) holds for $\mu >0$ and (4.8) follows from (4.10).

Next, we consider the case $\mu \in (\bar{\mu }^0,\bar{\mu }^1)$. We have

$$\begin{aligned} \sqrt{\frac{\lambda \rho }{2}}\int _0^{1/2n}\frac{dy}{h_-(u(y))}&=-\sqrt{\frac{\lambda \rho }{2}}\int _0^{1/2n}\frac{dy}{h_+(u(y))}\\&=-\sqrt{\frac{\lambda \rho }{2}}\frac{1}{\mu }\sqrt{\frac{\lambda }{2(\cosh \alpha +1)}} \int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}\\&=\sqrt{\frac{(\nu +1)(\nu +k^2)}{\nu }}\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}, \end{aligned}$$

where $k^2$ and $\nu$ are defined by (4.10). Thus, $\mathcal {A}(\mu ,k)=\mathcal {M}(\nu ,k)$.

In both cases $\mu \in (0,\infty )$ and $\mu \in (\bar{\mu }^0,\bar{\mu }^1)$ we obtain (4.7). $\square$

Thanks to Lemma 4.2 the equation (3.13) becomes

$$\begin{aligned} \mathcal {A}(\mu ,k)=\frac{j\pi }{2n}. \end{aligned}$$

(4.12)

Therefore, the graph $\mu \mapsto \mathcal {A}(\mu ,k)$, which is defined for $\mu \in (\bar{\mu }^0,\bar{\mu }^1)\cup (0,\infty )$, becomes important.

Lemma 4.3

The following equalities hold:

• (i) $\displaystyle \lim _{\mu \downarrow \bar{\mu }^0}\mathcal {A}(\mu ,k)=0$.

• (ii) $\displaystyle \lim _{\mu \uparrow \bar{\mu }^1}\mathcal {A}(\mu ,k)=\frac{\pi }{2}$.

• (iii) $\displaystyle \lim _{\mu \downarrow 0}\mathcal {A}(\mu ,k)=\frac{\pi }{2}$.

• (iv) $\displaystyle \lim _{\mu \rightarrow \infty }\mathcal {A}(\mu ,k)=\infty$.

Proof

Because of (4.8), we have the following relations:

$$\begin{aligned} \mu \downarrow \bar{\mu }^0\ {}&\iff \ \nu \uparrow -k^2,\\ \mu \uparrow \bar{\mu }^1\ {}&\iff \ \nu \downarrow -1,\\ \mu \downarrow 0\ {}&\iff \ \nu \rightarrow \infty ,\\ \mu \rightarrow \infty \ {}&\iff \ \nu \downarrow 0. \end{aligned}$$

Since $\mathcal {A}(\mu ,k)=\mathcal {M}(\nu ,k)$, the assertions (i), (ii), (iii) and (iv) follow from Lemma A.7 (i), (ii), (iii) and (iv), respectively. $\square$

Lemma 4.4

The function $\mathcal {A}(\mu ,k)$ satisfies

$$\begin{aligned} \frac{d}{d\mu }\mathcal {A}(\mu ,k)>0\ \ \text {for}\ \ \mu \in (\bar{\mu }^0,\bar{\mu }^1)\cup (0,\infty ). \end{aligned}$$

(4.13)

Proof

We prove the following inequality instead of (4.13):

$$\begin{aligned} \frac{d}{d\mu }\log \mathcal {A}(\mu ,k)>0\ \ \text {for}\ \ \mu \in (\bar{\mu }^0,\bar{\mu }^1)\cup (0,\infty ). \end{aligned}$$

Since

$$\begin{aligned} \frac{d}{d\mu }\log \mathcal {A}(\mu ,k)=\frac{d\log \mathcal {M}(\nu ,k)}{d\nu }\frac{d\nu }{d\mu } =\frac{d\log \mathcal {M}(\nu ,k)}{d\nu }\left( -\frac{\cosh \alpha -1}{2\mu ^2}\lambda \right) , \end{aligned}$$

it is enough to show that

$$\begin{aligned} \frac{d}{d\nu }\log \mathcal {M}(\nu ,k)<0\ \ \text {for}\ \ \nu \in (-1,-k^2)\cup (0,\infty ). \end{aligned}$$

(4.14)

Here, $\bar{\mu }^0<\mu <\bar{\mu }^1$ corresponds to $-1<\nu <-k^2$ and $\mu >0$ corresponds to $\nu >0$. By Lemma A.1 (ii) we have

$$\begin{aligned} \frac{d}{d\nu }\log \mathcal {M}(\nu ,k)= & {} \frac{1}{2}\left( \frac{1}{\nu +1}+\frac{1}{\nu +k^2}-\frac{1}{\nu }\right) +\frac{1}{\Pi }\frac{\partial \Pi }{\partial \nu }\nonumber \\= & {} \frac{1}{2\nu (\nu +1)}\frac{K(k)}{\Pi }\left( \frac{\nu }{\nu +k^2}\frac{E(k)}{K(k)}-1\right) . \end{aligned}$$

(4.15)

Using Lemma A.2, we have

$$\begin{aligned} (4.15)< {\left\{ \begin{array}{ll} \frac{1}{2\nu (\nu +1)}\frac{K(k)}{\Pi }\left\{ -\frac{\nu }{\nu +k^2}\left( \frac{k^2}{2}+\frac{k^2}{\nu }\right) \right\} =-\frac{k^2(\nu +2)}{4\nu (\nu +1)(\nu +k^2)}\frac{K(k)}{\Pi }<0 &{} \text {if}\ \nu >0,\\ \frac{1}{2\nu (\nu +1)}\frac{K(k)}{\Pi }\left\{ -\frac{\nu }{\nu +k^2}\left( k^2+\frac{k^2}{\nu }\right) \right\} =-\frac{k^2}{2\nu (\nu +k^2)}\frac{K(k)}{\Pi }<0 &{} \text {if}\ -1<\nu <-k^2. \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.16)

The inequality (4.14) follows from (4.16). The proof is complete. $\square$

Remark 4.5

Let $\bar{\mu }^0$ and $\bar{\mu }^1$ be defined by (4.6) and (3.15), respectively. By (1.6), (4.10) and Lemma 4.1 we see that

$$\begin{aligned} \bar{\mu }^0&=-\frac{\cosh \alpha +1}{2}\lambda =-4K(k)^2n^2=\mu ^n_0(k),\\ \bar{\mu }^1&=-\frac{\cosh \alpha -1}{2}\lambda =-4k^2K(k)^2n^2=\mu ^n_n(k). \end{aligned}$$

Proof of Theorem 1.2

• (i) The assertion follows from Lemma 4.1.

• (ii) By Remark 4.5 we see that $\bar{\mu }^0=\mu ^n_0(k)$ and $\bar{\mu }^1=\mu ^n_n(k)$. Let $\mathcal {A}$ be defined by (4.3). Then, by (4.5) and (4.7) we see that $\mathcal {A}(\mu ,k)$ is defined in $\mu \in (\mu ^n_0(k),\mu ^n_n(k))\cup (0,\infty )$ and it can be written as (1.11). Since (3.13) is equivalent to (4.12), a solution of (1.10) gives a j-th eigenvalue. By Lemma 4.4 we see that $\mathcal {A}(\mu ,k)$ is increasing for $\mu \in (\mu ^n_0(k),\mu ^n_n(k))\cup (0,\infty )$. It follows from Lemma 4.3 that the range $\{\mathcal {A}(\mu ,k);\ \mu ^n_0(k)<\mu <\mu ^n_n(k)\}$ is $(0,\pi /2)$ and the range $\{\mathcal {A}(\mu ,k);\ \mu >0\}$ is $(\pi /2,\infty )$. This indicates that

  $$\begin{aligned}&\text {for }j\in \{1,2,\ldots ,n-1\},~(4.12)~\text {has a unique solution}~\mu ^n_j(k)~\text {in}\nonumber \\&\quad ~(\mu ^n_0(k),\mu ^n_n(k)),~and \end{aligned}$$

  (4.17)
  $$\begin{aligned}&\text {for}~j\in \{n+1,n+2,\ldots \},~(4.12)~\text {has a unique solution}~\mu ^n_j(k)~\text {in}~(0,\infty ). \end{aligned}$$

  (4.18)

  Since $\mu ^n_n(k)<0<\mu ^n_{n+1}(k)$, the number of the negative eigenvalues are $n+1$ and 0 is not an eigenvalue. All the assertions in (ii) hold. The proof of (ii) is complete.

• (iii) We consider the case $\mu _j>0$. Using (2.8), (3.14) and (4.11), we have

  $$\begin{aligned} h_+(u(x))= & {} 2\frac{\mu _j}{\lambda }+\cosh \alpha -\cosh u(x)\\= & {} \frac{2k^2}{1-k^2}\left( -\frac{\mu _j}{\mu ^n_n(k)}+\textrm{sn}^2(2nK(k)x,k)\right) ,\\ \sqrt{\frac{\lambda \rho }{2}}= & {} \frac{2}{\lambda }\sqrt{\mu _j(\mu _j-\bar{\mu }^0)(\mu _j-\bar{\mu }^1)}\\= & {} \frac{2k^2}{1-k^2}\frac{-1}{\mu ^n_n(k)}\sqrt{\mu _j(\mu _j-\mu ^n_0(k))(\mu _j-\mu ^n_n(k))}. \end{aligned}$$

  Substituting these equalities into (3.12), we have

  $$\begin{aligned} \varphi (x)= & {} C_1\sqrt{\frac{2k^2}{1-k^2}\left( -\frac{\mu _j}{\mu ^n_n}+\textrm{sn}^2(2nK(k)x,k)\right) }\\{} & {} \times \cos \left( \int _0^x\frac{\sqrt{\mu _j(\mu _j-\mu ^n_0(k))(\mu _j-\mu ^n_n(k))}}{\mu _j-\mu ^n_n(k)\textrm{sn}^2(2nK(k)y,k)}dy\right) . \end{aligned}$$

Let $C_1=\sqrt{(1-k^2)(-\mu ^n_n(k))/2k^2}$. We obtain (1.13). The case $\mu ^n_0(k)<\mu _j<\mu ^n_n(k)$ is almost the same. We omit the proof. $\square$

4.3 Asymptotic formulas

Proof of Theorem 1.4

• (i) We consider the case $j\in \{1,2,\ldots ,n-1\}$. We define

  $$\begin{aligned} \tilde{\mu }_j:=\frac{\mu ^n_j(k)}{K(k)^2}\quad \text {and}\quad \hat{\mu }_j:=\frac{\tilde{\mu }_j+4n^2}{1-k^2}. \end{aligned}$$

  (4.19)

  Then, $\mu ^n_j(k)$ can be written as

  $$\begin{aligned} \mu ^n_j(k)=\left\{ -4n^2+(1-k^2)\hat{\mu }_j\right\} K(k)^2. \end{aligned}$$

  (4.20)

  Because of (4.17), we see that a unique solution $\mu ^n_j(k)$ of (4.12) satisfies $\mu ^n_0(k)<\mu ^n_j(k)<\mu ^n_n(k)$. Since $\mu ^n_0(k)<\mu ^n_j(k)<\mu ^n_n(k)$, we see that $0<\hat{\mu }_j<4n^2$, and hence there is a sequence $k_i$, which is denoted by k for simplicity, and $\hat{\mu }^*_j\in [0,4n^2]$ such that $k\rightarrow 1$ as $i\rightarrow \infty$ and $\hat{\mu }_j\rightarrow \hat{\mu }^*_j$ as $i\rightarrow \infty$. Since

  $$\begin{aligned} \nu (k):=\nu =\frac{\cosh \alpha -1}{2\mu ^n_j(k)}\lambda =\frac{4k^2K(k)^2n^2}{\mu ^n_j(k)}=\frac{-4k^2n^2}{4n^2-(1-k^2)\hat{\mu }^j}, \end{aligned}$$

  recall (4.8), we have

  $$\begin{aligned} \nu ^*:=\lim _{i\rightarrow \infty }\frac{\nu +1}{1-k^2}=\lim _{i\rightarrow \infty }\frac{4n^2-\hat{\mu }_j}{4n^2-(1-k^2)\hat{\mu }_j}=1-\frac{\hat{\mu }^*_j}{4n^2}\in [0,1]. \end{aligned}$$

  By Lemma A.6 we have

  $$\begin{aligned} \frac{j\pi }{2n}=\mathcal {A}(\mu ^n_j(k),k)=\mathcal {M}(\nu (k),k)\rightarrow \frac{\pi }{2} - \tan ^{-1}\sqrt{\frac{1-\frac{\hat{\mu }^*_j}{4n^2}}{1-\left( 1-\frac{\hat{\mu }^*_j}{4n^2}\right) }}\ \ \text {as}\ \ i\rightarrow \infty . \end{aligned}$$

  Then,

  $$\begin{aligned} \tan \left( \frac{\pi }{2}-\frac{j\pi }{2n}\right) = \sqrt{\frac{1-\frac{\hat{\mu }^*_j}{4n^2}}{\frac{\hat{\mu }^*_j}{4n^2}}}. \end{aligned}$$

  (4.21)

  Solving (4.21) with respect to $\hat{\mu }^*_j$, we have

  $$\begin{aligned} \hat{\mu }^*_j=4n^2\sin ^2\left( \frac{j\pi }{2n}\right) . \end{aligned}$$

  (4.22)

  Note that the limit $\hat{\mu }^*_j$ does not depend on a sequence $k\rightarrow 1$. Substituting (4.22) into (4.20), we have

  $$\begin{aligned} \mu ^n_j(k)=\left\{ -4n^2+4n^2(1-k^2)\sin ^2\left( \frac{j\pi }{2n}\right) +o((1-k^2))\right\} K(k)^2 \ \ \text {as}\ \ k\rightarrow 1. \end{aligned}$$

  The proof of (i) is complete.

• (ii) We consider the case $j\in \{n+1,n+2,\ldots \}$. Because of (4.18), we see that a unique solution $\mu ^n_j(k)$ satisfies $\mu ^n_j(k)>0$. We have

  $$\begin{aligned} \frac{j\pi }{2n}= & {} \mathcal {A}(\mu ^n_j(k),k)=\mathcal {M}(\nu ,k)\\\ge & {} \sqrt{\frac{(\nu +k^2)(\nu +k^2)}{\nu }}\int _0^1\frac{ds}{(1+\nu )\sqrt{(1-s^2)(1-k^2s^2)}}\\= & {} \frac{1}{\sqrt{\nu }}\frac{\nu +k^2}{\nu +1}K(k) \ge \frac{k^2K(k)}{\sqrt{\nu }}=\frac{\sqrt{\mu ^n_j(k)}k}{2n}, \end{aligned}$$

  recall (4.8). Since $\mu ^n_j(k)$ is bounded as $k\rightarrow 1$ by $\sqrt{\mu ^n_j(k)}\le j\pi /k$, and since $K(k)\rightarrow \infty$ as $k\rightarrow 1$, we have

  $$\begin{aligned} \nu =\frac{4k^2K(k)^2n^2}{\mu ^n_j(k)}\rightarrow \infty \ \ \text {as}\ \ k\rightarrow 1. \end{aligned}$$

  We define

  $$\begin{aligned} J(\nu ,k):=\sqrt{\nu +1}\Pi (\nu ,k)-\frac{1}{\sqrt{\nu +1}}K(k). \end{aligned}$$

  (4.23)

  Multiplying (4.23) by $\sqrt{(\nu +k^2)/\nu }$, we have

  $$\begin{aligned} \sqrt{\frac{\nu +k^2}{\nu (\nu +1)}}K(k)= & {} \sqrt{\frac{(\nu +1)(\nu +k^2)}{\nu }}\Pi (\nu ,k) -\sqrt{\frac{\nu +k^2}{\nu }}J(\nu ,k)\nonumber \\= & {} \frac{j\pi }{2n}-\sqrt{\frac{\nu +k^2}{\nu }}J(\nu ,k). \end{aligned}$$

  (4.24)

  Since $\nu \rightarrow \infty$ as $k\rightarrow 1$, by Lemma A.5 we have

  $$\begin{aligned} \sqrt{\frac{\nu +k^2}{\nu }}J(\nu ,k)\rightarrow \frac{\pi }{2}\ \ \text {as}\ \ k\rightarrow 1. \end{aligned}$$

  (4.25)

  Since $\mu ^n_j(k)$ is bounded as $k\rightarrow 1$, there exists $\mu ^*_j$ such that $\mu ^n_j(k)\rightarrow \mu ^*_j$ as $k\rightarrow 1$. Then,

  $$\begin{aligned} \sqrt{\frac{\nu +k^2}{\nu (\nu +1)}}K(k) =\sqrt{\frac{1+\frac{\mu ^n_j(k)}{4n^2K(k)^2}}{4k^2n^2+\frac{\mu ^n_j(k)}{K(k)^2}}{\mu _j(k) }}\rightarrow \frac{\sqrt{\mu ^*_j}}{2n} \ \ \text {as}\ \ k\rightarrow 1. \end{aligned}$$

  (4.26)

  It follows from (4.24)–(4.26) that as $k\rightarrow 1$,

  $$\begin{aligned} \frac{\sqrt{\mu ^*_j}}{2n}=\frac{j\pi }{2n}-\frac{\pi }{2}. \end{aligned}$$

  Thus,

  $$\begin{aligned} \mu ^*_j=\pi ^2(j-n)^2. \end{aligned}$$

  Here, the limit $\mu ^*_j$ does not depend on a sequence $k\rightarrow 1$. Since $\mu ^n_j(k)=\mu ^*_j+o(1)$ as $k\rightarrow 1$, we have

  $$\begin{aligned} \mu ^n_j(k)=\pi ^2(j-n)^2+o(1)\ \ \text {as}\ \ k\rightarrow 1. \end{aligned}$$

The proof of (ii) is complete. $\square$

5 Dirichlet problem

In this section we consider the Dirichlet problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{u}''+\lambda \sinh \tilde{u}=0 &{} \text {for}\ 0<x<1,\\ \tilde{u}(0)=\tilde{u}(1)=0. \end{array}\right. } \end{aligned}$$

(5.1)

We present the results for the Dirichlet problem which correspond to Theorems 1.1, 1.2 and 1.4 in the Neumann problem. The proofs are almost the same, and hence we omit them.

Theorem 5.1

The solution set $\tilde{\mathcal {S}}$ of (5.1) is

$$\begin{aligned} \tilde{\mathcal {S}}=\mathcal {C}_0\cup \left( \bigcup _{n=1}^{\infty }\left( \tilde{\mathcal {C}}^+_n\cup \tilde{\mathcal {C}}^-_n\right) \right) , \end{aligned}$$

where $\mathcal {C}_0$ is defined by (1.4),

$$\begin{aligned} \tilde{\mathcal {C}}^{\pm }_n:= & {} \left\{ (\lambda _n(k),\tilde{u}^{\pm }_n(x,k))\in \mathbb {R}_+\times X;\ 0<k<1\right\} ,\\ \tilde{u}^{\pm }_n(x,k):= & {} \pm \log \left( \textrm{dn}(2nK(k)x,k)^{-1}+k\textrm{sd}(2nK(k)x,k)\right) , \end{aligned}$$

and $\lambda _n(k)$ is defined by (1.6). Here, $\textrm{sd}(\xi ,k):=\textrm{sn}(\xi ,k)/\textrm{dn}(\xi ,k)$.

Let $(\lambda _n,\tilde{u}^{\pm }_n)$ be a nontrivial solution of (5.1). We consider the linearized eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{\varphi }+\lambda _n(\cosh \tilde{u}^{\pm }_n)\tilde{\varphi }=-\tilde{\mu }\tilde{\varphi }&{} \text {for}\ 0<x<1,\\ \tilde{\varphi }(0)=\tilde{\varphi }(1)=0. \end{array}\right. } \end{aligned}$$

(5.2)

Let $\{\tilde{\mu }^n_j(k)\}_{j=1}^{\infty }$ denote the eigenvalues and let $\tilde{\varphi }^n_j(x,k)$ be an eigenfunction corresponding to $\tilde{\mu }^n_j(k)$. Here, $\tilde{\mu }^n_j(k)$ has no relation with $\tilde{\mu }$ defined by (4.19). Note that $\tilde{\mu }^n_1(k)$ is the principal eigenvalue in the Dirichlet problem, while $\mu ^n_0(k)$ is that in the Neumann problem.

Theorem 5.2

Let $\mathbb {N}:=\{1,2,\ldots \}$. The following hold:

• (i) The eigenvalues of (5.2) are given by

  $$\begin{aligned} \tilde{\mu }^n_j(k)=\mu ^n_j(k)\ \ \text {for}\ \ j\in \mathbb {N}. \end{aligned}$$

  Therefore, the same asymptotic formulas given by Theorem 1.4 and Remark 1.5 hold for $j\in \mathbb {N}$.

• (ii) An n-th eigenfunction of (5.2) is given by

  $$\begin{aligned} \tilde{\varphi }^n_n(x,k)=\sinh \frac{{\tilde{u}^{\pm }_n}(x,k)}{2}=\pm k\textrm{sd}(2nK(k)x,k), \end{aligned}$$

and, for $j\in \mathbb {N}\setminus \{n\}$, a j-th eigenfunction of (5.2) is given by

$$\begin{aligned} \tilde{\varphi }^n_j(x,k)= & {} \sqrt{|\tilde{\mu }^n_j(k)-\tilde{\mu }^n_n(k)\textrm{cd}^2(2nK(k)x,k)|}\nonumber \\{} & {} \times \sin \left( \int _0^x\frac{\sqrt{\tilde{\mu }^n_j(k)(\tilde{\mu }^n_j(k)-\bar{\mu }^0)(\tilde{\mu }^n_j(k)-\tilde{\mu }^n_n(k))}}{|\tilde{\mu }^n_j(k)-\tilde{\mu }^n_n(k)\textrm{cd}^2(2nK(k)y,k)|}dy \right) . \end{aligned}$$

(5.3)

Here, $\textrm{cd}(\xi ,k):=\textrm{cn}(\xi ,k)/\textrm{dn}(\xi ,k)$ and $\bar{\mu }^0$ is defined by (4.6).

Note that we use $\bar{\mu }^0$ in (5.3) since $\tilde{\mu }^n_0(k)$ is not defined in the Dirichlet problem.

Appendix A: Elliptic integrals and functions

1.1 A.1: Elliptic functions

Let $k\in (0,1)$. The Jacobi elliptic function $\textrm{sn}(x,k)$ is an odd, 4K(k)-periodic, 2K(k)-antiperiodic and analytic function for $x\in \mathbb {R}$ and the inverse function $\textrm{sn}^{-1}(y,k)$ is defined locally by

$$\begin{aligned} \textrm{sn}^{-1}(y,k)=\int _0^{y}\frac{ds}{\sqrt{(1-s^2)(1-k^2s^2)}} \end{aligned}$$

for $0\le y\le 1$. The function $\textrm{cn}(x,k)$ is an even, 4K(k)-periodic and 2K(k)-antiperiodic function defined locally by

$$\begin{aligned} \textrm{cn}(x,k):=\sqrt{1-\textrm{sn}^2(x,k)}, \end{aligned}$$

for $-K(k)\le x\le K(k)$ and $\textrm{dn}(x,k)$ is an even and 2K(k)-periodic function defined by

$$\begin{aligned} \textrm{dn}(x,k):=\sqrt{1-k^2\textrm{sn}^2(x,k)} \end{aligned}$$

for $x\in \mathbb {R}$. In particular,

$$\begin{aligned} \textrm{sn}^2(x,k)+\textrm{cn}^2(x,k)=1,\ \ k^2\textrm{sn}^2(x,k)+\textrm{dn}^2(x,k)=1 \end{aligned}$$

for $x\in \mathbb {R}$ and $k\in (0,1)$.

1.2 A.2: Complete elliptic integrals

Let $k\in [0,1)$ and $\nu \in \mathbb {C}{\setminus } (-\infty ,-1]$. The complete elliptic integral of the first kind K(k) is defined by

$$\begin{aligned} K(k):=\int _0^1\frac{ds}{\sqrt{(1-s^2)(1-k^2s^2)}}, \end{aligned}$$

and it satisfies $K(k)=\textrm{sn}^{-1}(1,k)$. The complete elliptic integrals of the second and third kinds are defined by

$$\begin{aligned} E(k):=\int _0^1\sqrt{\frac{1-k^2s^2}{1-s^2}}ds\ \ \text {and}\ \ \Pi (\nu ,k):=\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}, \end{aligned}$$

respectively. The function K(k) is monotonically increasing in k,

$$\begin{aligned} K(0)=\frac{\pi }{2},\ \ \lim _{k\rightarrow 1}K(k)=\infty \end{aligned}$$

and E is monotonically decreasing in k,

$$\begin{aligned} E(0)=\frac{\pi }{2},\ \ \lim _{k\rightarrow 1}E(k)=1. \end{aligned}$$

We give standard formulas for K(k), E(k) and $\Pi (\nu ,k)$ in Lemmas A.1–A.3 without proofs. See [1] for details.

Lemma A.1

Let $k\in (0,1)$ and $\nu \ne 0,-1,-k^2$. Then,

• (i) $\displaystyle \frac{dK}{dk}(k)=\frac{E(k)-(1-k^2)K(k)}{k(1-k^2)}$.

• (ii) $\displaystyle \frac{\partial \Pi }{\partial \nu }(\nu ,k)=-\frac{K(k)}{2\nu (\nu +1)}+\frac{E(k)}{2(\nu +1)(\nu +k^2)}+\frac{(k^2-\nu ^2)\Pi (\nu ,k)}{2\nu (\nu +1)(\nu +k^2)}$.

Lemma A.2

Let $k\in (0,1)$. Then,

$$\begin{aligned} (1-k^2)K(k)<E(k)<\left( 1-\frac{1}{2}k^2\right) K(k). \end{aligned}$$

Lemma A.3

Let $k\in (0,1)$. Then,

$$\begin{aligned} \lim _{k\uparrow 1}\left( K(k)-\log \frac{1}{\sqrt{1-k^2}}-2\log 2\right) =0. \end{aligned}$$

Lemmas A.4 and A.5 are formulas for $\Pi (\nu ,k)$. Proofs can be found in [14].

Lemma A.4

Let $k\in (0,1)$ and $\nu >-1$. Then,

• (i) $\displaystyle \lim _{\nu \downarrow -1}\sqrt{\nu +1}\Pi (\nu ,k)=\frac{\pi }{2\sqrt{1-k^2}}$.

• (ii) $\displaystyle \lim _{\nu \rightarrow \infty }\sqrt{\nu +1}\Pi (\nu ,k)=\frac{\pi }{2}$.

Lemma A.5

Let $J(\nu ,k):=\sqrt{\nu +1}\Pi (\nu ,k)-\frac{1}{\sqrt{\nu +1}}K(k)$. Then,

$$\begin{aligned} \lim _{\nu \rightarrow \infty ,\,k\rightarrow 1}J(\nu ,k)=\frac{\pi }{2}. \end{aligned}$$

1.3 A.3: Modified complete elliptic integral of the third kind

The modified complete integral of the third kind

$$\begin{aligned} \mathcal {M}(\nu ,k):=\sqrt{\frac{(\nu +1)(\nu +k^2)}{\nu }}\int _0^1\frac{ds}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}, \end{aligned}$$

was introduced in [16]. This function is defined for $k\in (0,1)$ and $\nu \in \mathbb {C}{\setminus } ((-\infty ,-1]\cup [-k^2,0])$, and hence on the real axis it is defined for $\nu \in (-1,-k^2)\cup (0,\infty )$. Figure 3 shows a graph of $\mathcal {M}(\nu ,k)$ as a real function in $\nu$ for $k=1/\sqrt{2}$. This function appears in Theorem 1.2 and its proof in Sect. 4. The following Lemmas A.6 and A.7 are important and useful in the study of exact eigenvalues and eigenfunctions.

Fig. 3

A graph of $\mathcal {M}(\nu ,k)$ for $k=1/\sqrt{2}$

Lemma A.6

Let $k\in (0,1)$. Suppose that $\nu$ is a continuous function on (0, 1) with $-1<\nu (k)<-k^2$ for $k\in (0,1)$. Assume that there exists $\nu ^*\in [0,1]$ such that

$$\begin{aligned} \lim _{k\uparrow 1}\frac{\nu (k)+1}{1-k^2}=\nu ^*. \end{aligned}$$

Then, for each $\nu ^*\in [0,1]$,

$$\begin{aligned} \lim _{k\uparrow 1}\mathcal {M}(\nu (k),k)=\frac{\pi }{2}-\tan ^{-1}\sqrt{\frac{\nu ^*}{1-\nu ^*}}. \end{aligned}$$

See [14] for a proof of Lemma A.6.

Lemma A.7

Let $k\in (0,1)$ and $\nu \in (-1,-k^2)\cup (0,\infty )$. Then, the following hold:

• (i) $\displaystyle \lim _{\nu \uparrow -k^2}\mathcal {M}(\nu ,k)=0$.

• (ii) $\displaystyle \lim _{\nu \downarrow -1}\mathcal {M}(\nu ,k)=\frac{\pi }{2}$.

• (iii) $\displaystyle \lim _{\nu \rightarrow \infty }\mathcal {M}(\nu ,k)=\frac{\pi }{2}$.

• (iv) $\displaystyle \lim _{\nu \downarrow 0}\mathcal {M}(\nu ,k)=\infty$.

See Fig. 3. Lemma A.7 (ii) (resp. (iii)) follows from Lemma A.4 (i) (resp. (ii)). Lemma A.7 (i) and (iv) are trivial.