Abstract
In this paper, we study the problem concerning the approximation of a rigid obstacle for flows governed by the stationary Navier–Stokes equations in the two-dimensional case. The idea is to consider a highly viscous fluid in the place of the obstacle. Formally, as the fluid viscosity goes to infinity inside the region occupied by the obstacle, we obtain the original problem in the limit. The main goal is to establish a better regularity of approximate solutions. In particular, the pointwise estimate for the gradient of the velocity is proved. We give numerical evidence that the penalized solution can reasonably approximate the problem, even for relatively small values of the penalty parameter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We are interested in approximation of rigid obstacle by highly viscous fluid. We prove that the weak solution to the approximate problem has some higher regularity. Moreover, we claim that the approximate problem tends to be a rigid obstacle problem in the high viscosity limit. Finally, we illustrate our claims using numerical simulations, showing that our approach is applicable in numerics. This approach should in particular enable us to approximate rough obstacles. We show numerical results for such case, leaving its theoretical analysis for future work.
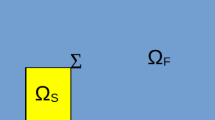
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\). Suppose that \(\Omega {\setminus } S \) filled with a homogeneous viscous incompressible fluid with an obstacle inside (Fig. 1). Denote by \( S \subset \Omega \) the domain occupied by the rigid obstacle, f is a given vector function. To simplify calculations we assume the density \(\rho =1\).
Our approach to the problem is based on the penalization method. We represent rigid obstacle as a highly viscous fluid. Consider an approximate stationary Navier–Stokes system
that satisfies the boundary condition
where the kinematic viscosity \(\nu (x)\) is a discontinuous function that has the following structure
and \({\textbf{D}}u\) is the deformation rate tensor with the components:
Since we interested in weak solutions, we introduce integral formulation of the problem: we say that a vector function \(u\in V(\Omega )\) is a solution to the problem if the following integral identity
holds true for arbitrary \(w \in V(\Omega )\), where V is defined at the beginning of Sect. 2.
In this paper, we want to prove that the gradient of the velocity field of the approximate problem (1.1)–(1.2) has a pointwise estimate in \(L^{\infty }\) norm.
The first method of our study is the penalty method that we gained from Starovoitov’s work [1].The method considers the rigid obstacles as fluids whose viscosity tends to infinity. The author presented the application of the method to the classical problem of rigid obstacles in a viscous incompressible fluid. In this direction, we mention here the papers [2] by Hoffmann and Starovoitov, [3] by San Martin, Starovoitov, and Tucsnak, [4] by Wróblewska-Kamińska, who used the penalty method to prove the global existence of weak solutions.
Also, we use tangential regularity techniques that are borrowed from Chemin [5], Danchin, Fanneli and Paicu [6]. They proved the existence and of weak solutions for the problem with the jump density for the barotropic compressible Navier–Stokes equations. In the case where the density has tangential regularity with respect to some non-degenerate family of vector fields, they also have uniqueness. Furthermore, this method helps us to approximate non-smooth domains with information about the geometry of the obstacle.
Moreover, we aimed to show that (1.1)–(1.4) may have some practical applications in numerics. We mention here Dryja’s work [7], where he analyzed the elliptic problem with highly discontinuous coefficients. The author shows that the convergence of the method (DG) presented in the work is almost optimal and only weakly depends on the jumps of coefficients.
The paper is organized as follows. In Sect. 2 we state our main results, Theorem 2.1 (existence of weak solutions), Theorem 2.2 (the limit case), Theorem 2.3 (higher regularity of approximate solution) and introduce some general notations. Section 3 is devoted to the analysis of the Stokes system. In Sect. 3.1 we introduce a regularity result for the model case, and the higher regularity of the Stokes system is proved in Sect. 3.2. Section 4 is the core of this paper. There we introduce the tangential regularity results that are needed in the proof of Theorem 2.3. In Sect. 5 we present numerical evidence that the approximate problem may have some practical applications.
The proof of existence of weak solutions and their high viscosity limit (Theorems 2.1 and 2.2) are postponed in the Appendix. These results are based on the Bogovskii type approach and general theory.
2 Notations and main results
In this section, we introduce some more general notation. In order to define spaces of divergence-free vector functions we introduce
According to classical result [8] for \(\Omega \) an open Lipschitz set we have
Next we define
The space H is equipped by scalar product \((\cdot ,\cdot )\), and the space V is the Hilbert space with the scalar product
By \(``\cdot ''\) we denote the scalar product of two vectors,
for \({\xi }=\{\xi _{1},\xi _{2},\ldots ,\xi _{n}\}\in {{\mathbb {R}}^n}\) and \({\eta }=\{\eta _{1},\eta _{2},\ldots ,\eta _{n}\}\in {{\mathbb {R}}^n}\) and “:” stands for scalar product for two tensors,
for \(\xi =\{\xi _{i,j}\}_{i=1,\ldots ,n,j=1,\ldots ,n}\in {{\mathbb {R}}^{n\times {n}}}\) and \(\eta =\{\eta _{i,j}\}_{i=1,\ldots ,n,j=1,\ldots ,n}\in {{\mathbb {R}}^{n\times {n}}}\).
Moreover, \(f\in L^2({\mathbb {R}}_{x_2};L^2({\mathbb {R}}_{x_1}))\) stands notation of 1-dimensional space in \(x_1\) and \(x_2\) directions respectively, and \(f\in H^1 ({\mathbb {R}}_{x_2};H^1 ({\mathbb {R}}_{x_1}))\) means that \(f, f_{x_2}\in L^2({\mathbb {R}}_{x_2};H^1 ({\mathbb {R}}_{x_1}))\) i.e.
Due to assumed regularity of \(\Omega \) and S, there exists a vector field \(X\in C^2\), such that
The first result concerns existence of weak solutions [8] reads
Theorem 2.1
(Existence) Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), let f be given in \(L^2(\Omega )\). Then Problem (1.5) has at least one solution \(u\in V(\Omega )\) and there exist a function \(p\in L^2(\Omega )\) such that (1.1) are satisfied.
The next result is about the limit \(m\longrightarrow \infty \).
Theorem 2.2
(The limit) Let assumptions of Theorem 2.1 hold and let \(m\longrightarrow \infty \), then \({\textbf{D}}u=0\) in the domain S.
When \({\textbf{D}}u=0\) in S we obtain rigid motion. The regularity of u implies that the trace of \(u\vert _{\partial S}= \phi \) is \(\phi \in H^{\frac{1}{2}}(\partial S)\). In situation when the obstacle touches the boundary, (1.3) together with Theorem 2.2 implies \(\Vert \phi \Vert _{H^{\frac{1}{2}}(\partial S)}\longrightarrow 0\).
The higher regularity of the approximate problem plays a crucial role in the proof of uniqueness. Generally, if the solution has tangential regularity with respect to some vector field, we get uniqueness. The main result of this paper is stated as follows
Theorem 2.3
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), \(S\subset \Omega \) with the boundary \(\partial {S}\in C^2 \), and let \({f}\in H^{1} (\Omega )\), then for every solution u of Navier–Stokes equations (1.1)–(1.2) we have \(\nabla u\in L^{\infty }(\Omega )\).
Due to technical difficulties, we split our analysis into two parts. We consider two approximate problems: Stokes and Navier–Stokes. The method of our proof relies on tangential regularity results for the approximate problem. The proof of tangential regularity differs from Danchin [6] and Chemin’ [5] works. The difficulty is that we propagate the whole approximate Navier–Stokes equations along the given vector field.
We prove tangential regularity for the Stokes system, that is stated in Lemma 3.1, where we derive energy estimate for \(\partial _{X} u\). In Lemma 3.3 we state the higher tangential regularity of Stokes system. In other words, we differentiate twice the whole system of equations along the given vector field X and prove that \(\nabla \partial _{X}^2 u\in L^2(\Omega )\). In the proof of tangential regularity results, we apply the Bogovskii type approach [9] to the ’pressure terms’ \(\partial _{X}p\), \(\partial ^2_{X} p\).
In Sect. 3.1, we consider a model case where the problem reduces to 1-dimensional functional spaces, which allows us to prove the higher regularity of a solution for the approximate Stokes system. The proof requires tangential regularity results and elementary tools like Hölder, Poincaré inequalities and embedding. We apply the model case idea in the proof of Theorem 2.3.
We establish tangential and higher tangential regularity results for the approximate Navier–Stokes system (1.1)–(1.2) in Lemmas 4.1 and 4.2. Proofs of these lemmas require Lemmas 3.1 and 3.3.
The interesting part of our approach is the viscosity jump area. Thus, in the proof of Theorem 2.3, we concentrate our analysis on \(\Sigma \) domain which is the neighbourhood of the approximate obstacle boundary. We straighten out the boundary using a transition to the curvilinear coordinate system [10]. We follow the model case idea. Tangential regularity results are the main steps in the proof of pointwise estimate for the gradient of the velocity field in \(L^{\infty }\) norm. We apply Lemmas 4.1, 4.2 and use tools like Hölder, Poincaré inequalities and embedding.
The proofs of Theorems 2.1 and 2.2 are the most standard and rely on known results (see Appendix).
3 Regularity for Stokes equations
In this section, we consider the approximate Stokes system of equations in a two dimensional case
Recall, that viscosity is a jump function (1.4). The system of Eqs. (3.1)–(3.2) appends the condition at the boundary, that is,
Definition 3.1
A vector field \(u:\Omega \longrightarrow {\mathbb {R}}^2 \) is called a weak (or generalized) solution to the Stokes problem (3.1)–(3.2) if and only if \(u\in V(\Omega )\) and it verifies the identity
The following lemma gives tangential regularity of the solution to Stokes problem, which will be useful in the proof of Lemma 4.1.
Lemma 3.1
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), \(S\subset \Omega \) with the boundary \(\partial {S}\in C^2 \). Assume X satisfies (2.3) and \(f,\partial _X f \in L^2 (\Omega )\). Then for every weak solution u of (3.1)–(3.2) we have
where \(C_1 := C_1 (\Omega ,X)\).
Proof
Assume that a given vector-field \(X=(X^1,X^2)\) is sufficiently smooth, and we are interested in the regularity of function u along X, i.e. in the quantity
We take the derivative along tangential vector-field from Stokes equation, that is
In order to get an equation for \(\partial _{X} u\), we are going to rewrite (3.6). After some calculations we get
We have
Using the above formula we rewrite the directional derivative of symmetric tensor as follows
Finally, using (3.8) and (3.7) we rewrite (3.6) in the following way
Multiplying the (3.9) by \(\psi \in C^{\infty }_0(\Omega ) \) and integrating by parts we obtain
We test (3.9) by function \(\partial _X v \in H^{1}_0 (\Omega )\) and get
Note that, \({\mathrm{div\,}}u=0\), but as we are differentiating the system of Stokes equations along the given vector field X we get
From the above equality we deduce that \({\mathrm{div\,}}(\partial _X u)=\sum _{k,j=1}^{2}\partial _{x_k} X^j \partial _{x_j} u^k\).
The pressure term. We are going to show that \(\partial _X p\in L^2 (\Omega ) \). In order to estimate \(\partial _X p \) we will use the Bogovskii type approach (see Lemma 6.2). Our aim is to show
where \(c_p \) is the constant from Poincaré inequality and \(c_{X''}, \,c_{X'}\) are constants depending only on X. In general, \(\partial _X p \) satisfies a following inequality
The above inequality we get via integrating by parts and using the condition on the boundary that is
Recall that (3.6) is equivalent to (3.9). Let us consider the functional
for all \(\psi \in H^{1}_{0} (\Omega )\). Recall (6.10), if take a test function \( \partial _{X}^{*}\psi \in C^{\infty }_0(\Omega )\), we get
where \( \partial _{X}^{*}\psi =-\partial _{x_i}(X^i \, \psi ) \). Therefore by Lemma 6.2 there exists a uniquely determined \(\partial _{X} p\in L^2 (\Omega )\) that \( \frac{1}{\vert \Omega \vert }\int _{\Omega } \partial _{X}p\) is bounded, and such that
Consider the problem
with \(\Omega \) bounded and satisfying the cone condition. Since
from [9, Theorem III.3.1] we deduce the existence of \(\psi \) solving the (3.16). We use such a \(\psi \) as a test function in (3.15), we obtain
Applying the Hölder and Poincaré inequalities to the above equation, we get
Using inequality (3.16) we reduce both sides of the above expression by the term \(\Vert \partial _{X} p\Vert _{L^2} \), and get the required estimate (3.13).
Now, we will examine the remaining terms of the Eq. (3.11), in order to estimate them. Recall that \(X\cdot n =0\), \(X\cdot \tau =1 \). We rewrite the directional derivative as
By assumptions and boundary condition (3.3), we get
Then Korn inequality holds
Using Hölder and Young’s inequalities to the 2nd term of (3.11), we get
The 5th term of the LHS of the (3.11) we could rewrite in the following way
Combining the above estimates of all terms of (3.11), we obtain
We take \(u=v\) in the above expression. Using the (3.13) and Young’s inequality with small \(\epsilon \) we get
where \((c_p c_{X''}+c_{X'}):=c_3,\, c_{X'}c_{\nu }=:c_2.\)
We apply the basic energy estimates (6.12) and (6.9) to get
For sufficiently small \(\epsilon \) we obtain
where \(A=1/(1-C_{b_1}\epsilon )\).
From (3.20) and (3.26) follows
The last term on the RHS we can put on the LHS, and for small enough \(\epsilon \) we obtain desired inequality (3.5). \(\square \)
3.1 The model case
In this section, we assume that \(\Omega \) is whole \({\mathbb {R}}^2\). In such a way that interior of the domain S is half-space \(x_2 <0\), and exterior is \(x_2 >0\), i.e.
In this case the derivative along the tangential vector field takes form
Obviously, viscosity (1.4) becomes a jump function along direction \(x_2\) :
One of the difficulties in proving higher regularity in the case with \(n=p=2\) is we do not have embedding \(H^1\nrightarrow L^{\infty }\). On the other hand, the jump function \(\nu (x)\) does not belong to space \(H^1\). Thus, we work in the spaces defined in (2.1)–(2.2), reducing our problem to space dimension one, where we have embedding \(H^1\hookrightarrow L^{\infty }\). Here we just show a formal estimate can be obtained for this particular case. This subsection gives us the crucial idea of proof of Theorem 2.3 and the following lemma reads
Lemma 3.2
Assume that domain \( \Omega ={\mathbb {R}}^2\) and let \(\partial _{x_1}^k {f}\in L^2({\mathbb {R}}^2)\) for some \(k\in {\mathbb {N}}\). Then for every solution u of Stokes equations (3.1)–(3.2) we have \(\partial _{x_1} u\in H^1({\mathbb {R}}_{x_2},H^k({\mathbb {R}}_{x_1}))\). Moreover, \(\nabla u\in L^{\infty }({\mathbb {R}}^2)\).
Proof
Let us propagate the Stokes equation over the given vector field
Multiplying by the test function \(\partial _{x_1} v\in H^1_0 ({\mathbb {R}}^2)\) and integrating by parts we get
Testing by function \(\partial _{x_1} u\), we could bound from below with Korn inequality
and we have
So, we get that \(\partial _{x_1}u\in H^1({\mathbb {R}}^2)\).
Now, we will follow the same procedure as above the for second time and assume \(\partial ^2_{x_1}{f}\in L^2({\mathbb {R}}^2)\). Differentiating (3.29) in \(x_1\), we get
We have
From the above estimates we deduce that
If \(\partial ^{k}_{x_1}f\in L^2 ({\mathbb {R}}^2)\), by iteration of the same procedure as above it follows that
for some \(k\in {\mathbb {N}}\). From standard theory [8, Ch. I, Proposition 2.2], for this weak solution u we can deduce an existence of pressure p, which is high regular in the \(x_1\) direction.
Let us rewrite the first row of Stokes equation in the following way
Because differentiation in \(x_1\) direction over \(\nu (x_2)\) is well defined, we transfer this term to the RHS. The fact that the weak derivative of p is in \(L^2\), can be proved by standard techniques like difference quotients in Evans [11].
Taking the \(L^2\) norm in the direction \(x_1\) we get
Now we differentiate (3.33) by \(x_1\) and take the \(L^2({\mathbb {R}}_{x_2};L^2({\mathbb {R}}_{x_1}))\) norm:
From (3.35), by differentiating in \(x_1\) direction, we have
which implies that \(\left[ \nu (x)(u_{,2}^{1}+u_{,1}^{2})\right] \in H^1 ({\mathbb {R}}_{x_2};H^1({\mathbb {R}}_{x_1}))\subset L^{\infty }.\)
From (3.2) we have \(u^1_{,1}=-u^2_{,2}\in H^1\) globally. It follows that \(u \in H^1 ({\mathbb {R}}_{x_2}; H^1({\mathbb {R}}_{x_1}))\).
From the above considerations we have an estimate
Due to embedding \(H^1({\mathbb {R}})\hookrightarrow L^{\infty }({\mathbb {R}})\), the following inequality holds
Using this, we could estimate LHS of (3.36) from below
We know that \(u^2_{,1}\in H^1({\mathbb {R}}_{x_2},H^k({\mathbb {R}}_{x_1}))\), so we can bound \(u^1_{,2}\) using triangle inequality
We could use the following inequality
Using triangle inequality and the above inequality we get
It follows that \(u^2_1\in L^{\infty } ({\mathbb {R}}_{x_2};L^{\infty } ({\mathbb {R}}_{x_1}))) \). Now, consider the second row of Stokes equation:
We take the \(L^2({\mathbb {R}}_{x_2};L^2({\mathbb {R}}_{x_1}))\) norm and differentiate (3.33) by \(x_1\) the above expression,
Because we know that differentiating in \(x_1\) direction is regular. We know that \(u^2_{,2}\in H^1 ({\mathbb {R}}_{x_2};H^1({\mathbb {R}}_{x_1}))\), so we could improve the regularity of the above inequality
and using embedding (3.37), we get
As in the previous case we obtain
It implies that \(u^2_2\in L^{\infty } ({\mathbb {R}}_{x_2};L^{\infty } ({\mathbb {R}}_{x_1}))) \). From estimates of u derivatives we conclude that
\(\square \)
3.2 The second derivative
In this subsection, we introduce a lemma that gives the higher tangential regularity of the solution to Stokes problem. We first study the tangential regularity of the Stokes system, which will be useful in the proof of Lemma 4.2. The result states
Lemma 3.3
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), \(S\subset \Omega \) with the boundary \(\partial {S}\in C^2 \), and let X be a vector field satisfying (2.3). Assume \(f, \partial _X f, \partial ^2_X f\in L^2 (\Omega )\), and let u solve (3.1)–(3.2). Then \(\partial ^2_{X} u\in H^1(\Omega )\), with an estimate
where \(C_2 :=C_2 (\Omega ,X)\).
Proof
Let us take the second derivative along tangential vector field from the Stokes equation, i.e. we take derivative \(\partial _{X}\) from (3.9).
We will rewrite the above expression term by term. Straightforward calculations of the 4th term of the LHS of (3.47) gives
For the 5th term we have
Also, the 6th term with pressure
Multiplying the Eq. (3.47) by \(\psi \in C^{\infty }_0(\Omega ) \) and integrating, we get
The weak formulation of (3.47), tested with \(\partial ^2_{X}v\in H^{1}_{0} (\Omega )\) gives
The pressure term: Bogovskii type estimate. We are going to estimate the pressure term \(\partial _X^2 p \) in the view of Lemma 6.2. We need to show that \(\partial _X^2 p\in L^2(\Omega ) \) such that Eq. (3.52) holds for every \(\psi \in C^{\infty }_0(\Omega ) \). Moreover, the pressure term is well defined
We’ve got the above inequality by knowing that \(\partial _{X}p\) is bounded in \(L^2(\Omega )\) according to the proof of Lemma 3.1, and also using integration by parts and Hölder inequality.
Let us consider the functional
For all \(\psi \in H^{1}_0 (\Omega )\). Thinking on the level of the weak formulation of Stokes system with a test function \((\partial _{X}^2)^{*}\psi \in C^{\infty }_0(\Omega )\) we get
where \((\partial _{X}^2)^{*}\psi := \partial _{x_k}(X^{k}\, \partial _{x_i}(X^{i}\, \psi ))\). We deduce by Lemma 6.2 there exists a uniquely determined \(\partial _{X}^2 p\in L^2 (\Omega )\) with bounded \(\frac{1}{\vert \Omega \vert }\int _{\Omega }\partial _{X}^2 p\), such that
for all \(\psi \in H^{1}_0 (\Omega )\). Consider the problem
with \(\Omega \) bounded and satisfying the cone condition. Since \(\frac{1}{\vert \Omega \vert }\int _{\Omega }\partial _{X}^2 p \) is bounded and
from [9, Theorem III.3.1] we deduce the existence of \(\psi \) solving the (3.55), using such a \(\psi \) as test function into the (3.51), we have
By applying Hölder, Poincaré inequalities to the above equation, we get
Then using the inequality from (3.55), we could reduce both sides of the above inequality by \(\Vert \partial _{X}^2 p\Vert \). Also, by applying (3.5) and (6.9) we deduce the estimate for the pressure term
Let us take the second directional derivative from the (3.12)
so we get
Now, we return to the (3.52) with \(u=v\), by applying Hölder inequality, we get
Here, using (3.60), (3.58) and applying Young’s inequality with small \(\epsilon \) to the above inequality, we get
Transferring the 1st term of the RHS of the above inequality to the LHS we get
In the same way as in (3.19), we deduce that \(\partial _{X}^2 u\vert _{\partial \Omega } =0\). Then Korn inequality holds
Implementing (3.64) to (3.63) gives required inequality (3.46). \(\square \)
4 Proof of Theorem 2.3
4.1 Tangential regularity
Tangential regularity result of approximate Navier–Stokes equations (1.1) reads
Lemma 4.1
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), \(S\subset \Omega \) with the boundary \(\partial {S}\in C^2 \), and let X be a vector field satisfying (2.3). Assume \(f, \partial _X f \in L^2 (\Omega )\), and let u solve (1.1)–(1.2). Then \(\partial _{X} u\in H^1(\Omega )\), with an estimate
where \(C :=C(\Omega ,X)\).
Proof
In this regard, we differentiate the stationary Navier–Stokes equation along the vector field
We are going to show estimates for the nonlinear part of the equation, as the rest has been proved in Lemma 3.1.
let us separately test the nonlinear part by \(\partial _{X}u\). We have
We use interpolation inequality for \(q > p\) of type
In our case \(p=n=2,\) \(q=4\)
where
We implement (4.5) to (4.4) and get that
From the property of trilinear form we have \(\int _{\Omega } b(v,u,u)\,dx=0\), so for the II term we obtain
To the next term we apply general Hölder and Poincaré inequalities
i.e.
Summing up all the above estimates and using Hölder, Young’ inequalities we get
From [9, Lemma IX 1.2] and the same way as in (3.15) we deduce that there exists a uniquely determined \(\partial _{X} p\in L^2 (\Omega )\) for Navier–Stokes system.
The estimate (3.27) for propagated Stokes equation combined with (4.2) give us an estimate
Taking \(\epsilon \) in such a way that \(C >C_8 \epsilon \), we have (4.1). \(\square \)
The higher tangential regularity is an important part of the proof of Theorem 2.3. It gives us higher regularity of solutions of Navier–Stokes problem (1.1)–(1.2). The following lemma states the result
Lemma 4.2
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), \(S\subset \Omega \) with the boundary \(\partial {S}\in C^2 \), and let X be a vector field satisfying (2.3). Assume \(f, \partial _X f, \partial ^2_X f \in L^2 (\Omega )\), and let u solve (1.1)–(1.2). Then \(\partial _{X}^2 u\in H^1(\Omega )\), with an estimate
where \(C:=C(\Omega ,X)\).
Proof
Consider
In order to prove the main estimate we just take the second directional derivative from the nonlinear term of (1.1), the rest has been proved in Lemma 3.3.
We test the above expression by \(\partial _{X}^2 u\) and consider more precisely the most problematic one
According to (4.5), we have
where
We implement (4.5) to (4.16) and get that
From the assumptions given vector field is smooth and we know that \(u\in H^1(\Omega )\), \(\partial _{X} u \in H^1(\Omega \)). So without loss of generality, we could estimate the rest terms of (4.15)
Using Young’s inequality with small \(\epsilon \) and Lemma 4.1, we get
From [9, Lemma IX 1.2] and the same way as in (3.54) we deduce that there exists a uniquely determined \(\partial _{X}^2 p\in L^2 (\Omega )\) for Navier–Stokes system.
The estimate (3.63) from the last step of the proof of Lemma 4.2 combined with the above estimate for nonlinear term give us an estimate of (4.13)
Taking \(\epsilon \) in (4.21) in such a way that \(C > \epsilon \), we obtain (4.12). \(\square \)
4.2 Proof of Theorem 2.3
In order to prove Theorem 2.3 we need results stated in Sect. 4.1. We assume that the approximate solution of problem (1.1)–(1.2) have tangential regularity (Lemma 4.1) and higher tangential regularity (Lemma 4.2).
Proof
In general, we want to change the global system of coordinates \((x_1 ,x_2)\) to the local normal and tangent vector coordinates system \((\tau , n)\) on \(\partial S\). The tangent vector direction becomes as \(y_1\) and the normal vector takes direction \(y_2\). The most problematic part is to transfer the Navier–Stokes equations from the closed domain into the whole space.
Thus consider, that Navier–Stokes equation is given in the neighbourhood \(\Sigma \) of the boundary \(\partial S\) s.t. there are open domains \(S\subset S^{\prime } \) and \(S^{\prime \prime }\subset S \) that is \(dist(x, x^{\prime })=\delta \) for \(x\in \partial S\), \(x^{\prime }\in \partial S^{\prime }\), and also \(dist(x,x^{\prime \prime })=\delta \) for \(x\in \partial S\), \(x^{\prime \prime }\in \partial S^{\prime \prime }\). Let us denote the neighbourhood of \(\partial S\) that is \(S^{\prime }{\setminus } S^{\prime \prime }:= \Sigma \), and \(\Omega ^{(1)}:= \Omega {\setminus } (S\cup \Sigma )\), \(\Omega ^{(2)}:= S{\setminus } \Sigma \) (Fig. 2). Without loss of generality, consider \( {{\mathcal {O}}}: = W \cap \Sigma \) where W is a plane that intersects with a part of \(\Sigma \). Let us fix \(\epsilon \) and introduce notations
There is a \(\Phi \) - \(C^2 \) diffeomorphism from \({{\mathcal {O}}}\) onto rectangle V, which is straightening out the boundary of obstacle S. In this regard, we apply a classical change of variables for the curvilinear system of coordinates (Fig. 3).
Change of variables takes form
such that
with \(\mathrm{det\,} J_{\Psi }(y)=1,\,\,\, \forall y \in {\mathbb {R}}^2 \).
i.e.,
The derivative along tangential field in the curvilinear system takes form
The jump of the viscosity field is transferred along \(y_2\) direction, so we get the dependence
We define the second order derivative operator as
and the convection term
Above, \(\Gamma ^i_{jk} \) are Christoffel symbols
with contravariant vectors tensor
and covariant vectors tensor
So, we have
by Corollary A.3. in [12].
Extending all the fields by Sobolev extension s.t. \(E U = U\) in V and \(E U=0\) in \({\mathbb {R}}^2 {\setminus } V^{\prime }\), \(V\subset V^{\prime }\), by Theorem II.3.3 in [9], we get Navier–Stokes equations in the curvilinear coordinates
We rewrite the first row of the above equation
Since \(\partial S \in C^2\) and compact, we have
Recall, the space dimension \(n=1\) and \(p=2\), we use an estimate for the convection term as follows
We know \(u\in H^1(\Omega )\), which implies \(U\in H^1({\mathbb {R}}^2)\). By Lemma 4.1 and (4.24) we deduce that \(\nabla \partial _{y_1} U \in L^2({\mathbb {R}}_{y_2};L^2({\mathbb {R}}_{y_2})) \). We take \(L^2({\mathbb {R}}_{y_2};L^2({\mathbb {R}}_{y_1})) \) norm of (4.27). Because the differentiation in \(y_1\) direction is well defined we transfer all terms of the LHS to the RHS, except the 2nd one. Also, using Cauchy–Schwartz, Poincaré inequalities, we get
where \( R:= 2\left[ g^{12}(\Gamma ^1_{11} U_1 +\Gamma ^1_{21} U_2)+g^{22}(\Gamma ^1_{12} U_1 +\Gamma ^1_{22} U_2)\right] \).
It’s obvious that the LHS of (4.29) \(\partial _{y_2}\left\{ \nu (y_2)\left( g^{21} \frac{ \partial U_1}{\partial {y_1}}+g^{22} \frac{ \partial U_1}{\partial {y_2}}+R \right) \right\} \in L^{2} ({\mathbb {R}}_{x_2};L^2 ({\mathbb {R}}_{x_1}))\).
In situation when we have \(\partial _{y_1}^2 F\in L^2({\mathbb {R}}_{y_2}; L^2 ({\mathbb {R}}_{y_1}))\) and \(\nabla \partial _{y_1} P \in L^2({\mathbb {R}}_{y_2}; L^2({\mathbb {R}}_{y_1}))\) from Lemma 4.2 it is obvious that \(\partial _{y_1}^2 (U\nabla U)\in L^2({\mathbb {R}}_{y_2};L^2({\mathbb {R}}_{y_1}))\)), we deduce that \(\nabla \partial _{y_1}^2 U \in L^2({\mathbb {R}}^2)\). If we differentiate by \(y_1\) both sides of (4.27), then obviously we get that
i.e. we have \(\partial _{y_2}\left\{ \nu (y_2)\left( g^{21} \frac{ \partial U_1}{\partial {y_1}}+g^{22} \frac{ \partial U_1}{\partial {y_2}}+R \right) \right\} \in L^{2} ({\mathbb {R}}_{x_2};H^1 ({\mathbb {R}}_{x_1}))\), that means
We split the above norm into two parts using the triangle inequality
and use it in (4.30). By embedding \(L^{\infty }({\mathbb {R}}_{y_2};H^1({\mathbb {R}}_{y_1}))\hookrightarrow L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1}))\), we could bound the above inequality from below and get
and it’s also true that we have
thus we have a priori estimate for \(U_{1,2}\)
So, we have that \(U_{1,2}\in L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1})) \), the same is true for \(U_{1,1}\in L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1}))\).
Now, we consider the second row of the Navier–Stokes equation
Let us denote \( R_1 := 2\left[ g^{12}(\Gamma ^2_{11} U_1 +\Gamma ^2_{21} U_2)+g^{22}(\Gamma ^2_{12} U_1 +\Gamma ^2_{22} U_2)\right] \).
From the above equation, we take the \(L^2({\mathbb {R}}_{y_2};L^2({\mathbb {R}}_{y_1}))\) norm and bound as in the previous case
Differentiating the above estimate by \(\partial _{y_1}\) it is obvious that,
Consequently, \(\nu (y_2)\left( g^{21} \frac{ \partial U_2}{\partial {y_1}}+g^{22} \frac{ \partial U_2}{\partial {y_2}}+R_1 \right) \in H^1 ({\mathbb {R}}_{y_2}; H^1({\mathbb {R}}_{y_1}))\hookrightarrow L^{\infty }({\mathbb {R}}_{y_2}; L^{\infty }({\mathbb {R}}_{y_1}))\).
In order to bound \(U_{2,2}\), we repeat the same procedure as in the first case
It follows that \(U_{2,2}\in L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1})) \), the same is true for \(U_{2,1}\in L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1}))\). So, we have that \(\nabla U \in L^{\infty }({\mathbb {R}}_{y_2};L^{\infty } ({\mathbb {R}}_{y_1}))\). By extension theorem and using (4.24) that is \(C_1\Vert \nabla U \Vert \leqslant \Vert \nabla u\Vert \leqslant C_2 \Vert \nabla U\Vert \), we conclude that \(\nabla u \in L^{\infty }({{\mathcal {O}}}) \). It’s obvious that for the other part of neighborhood we get the same, so we deduce that \(\nabla u\in L^{\infty }(\Sigma )\), the conclusion follows. \(\square \)
The next lemma gives a higher regularity of u in the \(\Omega ^{(1)}\cup \Omega ^{(2)}\)
Lemma 4.3
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\). And let u satisfy Navier–Stokes system of equations (1.1)–(1.2), \(q > n\). If \(f \in L^{q}(\Omega )\) then \(\nabla u\in L^{\infty }(\Omega ^{(1)}\cup \Omega ^{(2)})\) and there exists \(p\in W^{1,q}(\Omega ^{(1)}\cup \Omega ^{(2)})\) such that (1.1) is satisfies a.e.
Proof
We have
We localize the problem, take “cut off” function \(\eta \in C_0^{\infty }({\mathbb {R}}^2)\) such that
Putting \(w =u\eta ^{(1)}\), \(\pi =p\eta ^{(1)}\), and taking into account (1.4) we have that w and \(\pi \) satisfies the following problem
and
where
i.e.
Recalling the property of \(\eta \) that is
In some sense, we will repeat the proof according to Galdi [9]. We want to show that
We know that there is
that satisfies Navier–Stokes system (1.1). By the Lemma IX.2.1 [9] and Lemma 2.1, we deduce there is \(p\in L^2(\Omega ^{(1)}_{\epsilon })\). Furthermore, the embedding theorem, that furnishes recurrence relation for the exponents s.t. \(u\in L^{2 t_k\diagup (2-t_k)}(\Omega ^{(1)}_{\epsilon })\), and (4.42), allows us to conclude \(F\in L^{q}(\Omega ^{(1)}_{\epsilon })\), \(g\in W^{1,q}(\Omega ^{(1)}_{\epsilon })\) for \(q\in (1,2)\).
So that by Lemma IX.5.1 and (*) we want to prove (4.43). Assume next \(q\ge n\). Then, the (*) is satisfied for all \(q\in (1,n)\), and so, by the embedding theorem, we have
yielding,
From the interior estimates for the Stokes problem proved in [9, Theorem IV.4.1] follows that \(u\in W^{2,q}(\Omega ^{(1)}_{\epsilon })\) and \(p\in W^{1,q}(\Omega ^{(1)}_{\epsilon })\).
Denote \(F^{\prime }= F-u\cdot \nabla w\), for \(q\geqslant n\), \(1< q <\infty \). By the Hölder inequality and recalling the properties of \(\eta \) it follows that
So, we have \(F^{\prime } \in L^{q}(\Omega ^{(1)}_{\epsilon })\), using [9, Lemma IX.5.1], we deduce that \(w\in W^{2,q}(\Omega ^{(1)}_{\epsilon })\) , \(\pi \in W^{1,q}(\Omega ^{(1)}_{\epsilon })\) and satisfies an estimate
also, using the Theorem IX.5.1 and properties of \(\eta \) we derive
also, we could write
For the case \(q>n\), we have embedding \(W^{1,q}(\Omega ^{(1)}_{\epsilon })\hookrightarrow L^{\infty }(\Omega ^{(1)}_{\epsilon })\), thus \(\nabla u\in L^{\infty }(\Omega ^{(1)}_{\epsilon })\),
Let us now consider the other “cut off” function \(\eta ^{(2)}\) such that,
We localize the problem (4.2)–(4.3), and put \(v =u\eta ^{(2)}\), \(P=p\eta ^{(2)}\), using the properties of the function \(\eta ^{(2)}\) we get
and
The magnitude of the velocity for the half ball test problem. The a, b cases correspond to parameters from Table 1 (Test cases 1, 4). The c correspond to the real obstacle test case
The magnitude of the velocity for the wall test problem. The a, b cases correspond to parameters from Table 1(Test case 2, 5). The c correspond to the real obstacle test case
Comparison of the velocity magnitude for the half ball case. The velocity \(u_k\) correspond to test case number k from Table 1
Comparison of velocity magnitude for the wall case. The velocity \(u_k\) correspond to test case number k from Table 1
From the bounds of the first case, using that \(F\in L^q (\Omega ^{(2)}_{\epsilon })\), \(g\in W^{1,q}(\Omega ^{(2)}_{\epsilon }) \), and using [9, Lemma IX.5.1, Theorem IX.5.1] we get an estimate
using the embedding to \(W^{1,q}(\Omega ^{(2)}_{\epsilon })\hookrightarrow L^{\infty }(\Omega ^{(2)}_{\epsilon })\),
So, from (4.44) and (4.48) we conclude that \(\nabla u\in L^{\infty }(\Omega ^{(1)}_{\epsilon }\cup \Omega ^{(2)}_{\epsilon })\). \(\square \)
5 Numerical simulations
In this section, we will illustrate Theorem 2.2 with some numerical simulations, and show that our approximate problem (1.1–1.4) has a potential application in practice.
We conduct two numerical experiments, where we consider a smooth obstacle (a half ball) and an obstacle with edges (a wall). We do a number of tests with increasing value of viscosity m (see (1.4)). It turns out that for moderately high values of m the solutions are almost identical to the real rigid obstacle problem. We consider a rectangular channel flow problem in \(\Omega {\setminus } S\) with fixed rigid obstacle S touching the boundary of \(\Omega \) [13, 14]. We refer to it as a “real obstacle” problem and denote the velocity by \(u_r\) ( see Table 1). The experimental data and the geometry of channel flow are inherited from the Turek’s benchmark [13], test case 2D-2, with two exceptions the channel’s length equals \(L=1.2\), and the obstacles are of different shape and touch the boundary (Figs. 1, 2]). The experiments with half ball obstacle is illustrated in Fig. 4 with \(r=0.15\) and center at (0, 4; 0, 0). And the experiments with the wall obstacle is in Fig. 5 with height \(h=0,16\), width \(w=0,1\) and center of symmetry \(x=0,4\). We assume a parabolic velocity profile at the inlet and Dirichlet boundary condition on the boundary. We compare the solution of the real obstacle problem with the solution of the approximate problem (1.1)–(1.4), where the fixed obstacle domain S is filled with highly viscous fluid of viscosity m (see Table 1).
The results have been computed with the FEniCS package [15] using the incremental pressure correction scheme to solve the problem [16].
We compare solutions in a cross-section y at \(x=0.4\), along the vertical axis of symmetry of the obstacle. The comparison graphs of extracted solution of each test are given in Figs. 6 and 7, where the velocity \(u_k\) in graphs correspond to the test case number k from Table 1. The Figs. 6 and 7 show that the solution of the approximate problem approaches the solution of the real obstacle problem relatively fast. The solution of the approximate problem in the region S is really close to the solution of the rigid obstacle problem as predicted in Theorem 2.2.
These results establish that the regularized solutions can approximate the limiting case reasonably well even for small-scale penalty parameter. Moreover, we show that our approach has practical application in numerics.
References
Starovoitov, V.N.: Penalty method and problems of liquid–solid interaction. J. Eng. Thermophys. 18(2), 129–137 (2009)
Hoffmann, K.H., Starovoitov, V.N.: On a motion of a solid body in a viscous fluid. Two dimensional case. Adv. Math. Sci. Appl. 9, 633–648 (1999)
San Martin, A., Starovoitov, V.N., Tucsak, M.: Global weak solutions for the two dimensional motion of several rigid bodies in an incompressible viscous fluid. Arch. Ration. Mech. Anal. 161(2), 113–147 (2002)
Wróblewska-Kamińska, A.: Existence Result for the Motion of Several Rigid Bodies in an Incompressible Non-Newtonian Fluid with Growth Conditions in Orlicz Spaces. IOP Publishing Ltd and London Mathematical Society (2014)
Chemin, J.-Y.: Sur le mouvement des particules d’un fluide parfait incompressible bidimentionnel. Ann. Math. 103(3), 599–629 (1991)
Danchin, R., Fanneli, F., Paicu, M.: A well-posedness result for viscous compressible fluids with only bounded density. Anal. PDE 13(1), 275–316 (2020)
Dryja, M.: A Domain Decomposition Method for Discretization of Multiscale Elliptic Problems by Discontinuous Galerkin Method, PPAM 2013, Warsaw, Part II, pp. 461–468 (2013)
Temam, R.: Navier–Stokes Equations. Theory and Numerical Analysis. North-Holland Pub. Co, Amsterdam (1977)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Springer, Pittsburgh (2011)
Takahashi, T.: Analysis of strong solutions for the equations modeling the motion of a rigid-fluid system in a bounded domain. Adv. Differ. Equ. 8(12), 1499–1532 (2003)
Evans, L.C.: Partial Differential Equations. American Mathematical Society, Providence (1998)
Danchin, R., Mucha, P.B.: A Lagrangian Approach for the Incompressible Navier–Stokes Equations with Variable Density, Communications on Pure and Applied Mathematics, vol. LXV, pp. 1458–1480. Wiley Periodicals, Inc (2012)
Schäefer, M., Turek, S.: Benchmark computations of laminar flow around cylinder. In: Flow Simulation with High-Performance Computers II, Notes on Numerical Fluid Mechanics, vol. 52, pp. 547–566. Vieweg (1996)
Langtangen, H.P., Logg, A.: Solving PDEs in Python. The FEniCS Tutorial I. Springer Open (2016)
Logg, A., Mardal, K.A.: Automated Solution of Differential Equations by the Finite Element Method. The FEniCS Book, The FEniCS Project (2011)
Goda, K.: A multistep technique with implicit difference schemes for calculating two- or three-dimensional cavity flows. J. Comput. Phys. 30(1), 76–95 (1979)
Mucha, P.B.: On Navier–Stokes equations with slip boundary conditions in an infinite pipe. Acta Appl. Math. 76, 1–15 (2003)
Ladyzhenskaya, O.A.: The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach, New York (1966)
Acknowledgements
The author would like to thank Prof. Piotr Mucha, Dr. Piotr Krzyzanowski and Dr. Tomasz Piasecki for their invaluable help and remarks through the process of creating the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Theorem 2.1
Proof
The existence of u is proved by Galerkin method (Temam [8]: we construct the approximate solution of (1.5) and then pass to the limit.
From the definition of V space there exists a sequence \(w_1,w_2,\ldots ,w_n\ldots \) of linearly independent elements of \({{\mathcal {V}}}\) which is total in V. For each n we define an approximate solution \(u_n\) of (1.5) by
with unknown coefficients \(c_{jn}\in {\mathbb {R}} \), satisfying
for \(j= 1,2\ldots ,n\). The Eqs. (6.1) and (6.2) are a system of nonlinear equations for \(c_{1n},\ldots ,c_{nn}\), the existence of a solution of this system follows from the Lemma 1.4 [8, Ch. II, Lemma 1.4]), that is consequence of the Brouwer Fixed Point Theorem:
Lemma 6.1
Let X be finite dimensional Hilbert space with scalar product \(\left[ \cdot ,\cdot \right] \) and norm \(\left[ \cdot \right] \) and let P be a continuous mapping from X into itself such that for some \(k >0\)
Then there exists \(\xi \in X , \, \left[ \xi \right] \leqslant k \), such that
We apply this lemma for proving the existence of \(u_{n}\) as follows:
Let X be the space spanned by \(w_1,w_2,\ldots ,w_n\); the scalar product on X is the scalar product induced by V, and \(P=P_{m}\) is defined by
Let us check that scalar product \([\cdot ,\cdot ]\) is positive
In the last inequality were used the Korn and Cauchy–Schwartz inequalities. Therefore
It follows that \(\left[ P_{n} u,u\right] > 0\) for \(\Vert u \Vert =k\), and \(k>\frac{1}{c(\nu )}\Vert f \Vert \). It follows that, there exists a solution \({\textbf{u}}_{n}\) of (6.1)–(6.2). We multiply (6.2) by \(c_{jn}\), this gives
We know that, trilinear form \(b(u_n ,u_n ,u_n )=0\), and get
By Korn inequality we get a priori estimate
Hence the sequence remains bounded in V, there exists a subsequence \(k\longrightarrow \infty \) such that \(u_{n_k}\rightharpoonup u\) in V. From compact embedding of \(V\hookrightarrow L^2\), so we have also \(u_{n_k}\longrightarrow u\) in \(L^{2}(\Omega )\).
If \(u_n\) converges to u in \(W^{1,2}\) weakly and in \(L^2\) strongly, then we need to show that
Then we can pass to the limit in (6.2) with the subsequence \(k\longrightarrow \infty \), we find that
for any \(v= w_1,\ldots ,\, w_n\ldots \). The above equation is also true for any v which is the linear combination of \(w_1,\ldots ,\, w_n\ldots \). Since this combination are dense in V, a continuity argument shows that the above equation holds for each \(v\in V\) and that u is a solution of (1.5).
From the properties of trilinear form we have
We know that \(u_{mi}\rightarrow u_{i}\) converges strongly in \(L^{2}(\Omega )\), since \(\partial _{xi}v\in L^{\infty }(\Omega )\), so we have
Hence \(b(u_m ,v,u_m )\) converges to \(b(u,v,u)=-b(u,u,v)\). \(\square \)
Proof of Theorem 2.2
From (6.4) we could deduce that for the domain S we get
That is, if \(m\longrightarrow \infty \), then \({\textbf{D}}u\longrightarrow 0\) in S. Therefore, in the limit, as \(m\longrightarrow \infty \), we obtain the rigid motion. \(\square \)
1.2 Bogovskii type estimate
We need to derive some energy estimates for Stokes system of equations for the (3.1) case, to show that the velocity vector field is in Hilbert space.
From Korn inequality (6.15) for Stokes system (3.1) we have:
Using Hölder and Poincaré inequalities we get:
We get energy estimate:
The Definition 3.1 has no information about the pressure field. Since u is a weak solution, we know from [8, Lemma 2.1] that there exists \(p\in L^2(\Omega )\) such that
holds for \(\psi \in C_0^{\infty }(\Omega )\). So, to every weak solution we are able to associate a pressure p in such a way that (6.10) holds. We formulate the following result for our case.
Lemma 6.2
Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\), and let \(f\in L^2 (\Omega )\). A vector field \(u\in W^{1,2} (\Omega )\) satisfies (3.4) for all \(\phi \in {{\mathcal {V}}}(\Omega )\) if and only if there exists a pressure \(p\in L^2(\Omega )\) such that (6.10) holds for every \(\psi \in C_0^{\infty } (\Omega )\). Then
Finally, if we normalize p by the condition
The following estimate holds
Proof
The existence of pressure p follows from Temam [8, Lemma 2.1]. Let us consider the functional
for \(\psi \in H^{1}_0(\Omega ).\) By assumption, \({{\mathcal {F}}}\) is bounded in \(H^1_0 (\Omega )\) and is identically zero in \({{\mathcal {V}}}(\Omega )\). Consider the problem
with \(\Omega \) bounded and satisfying the cone condition. Since
from Theorem III.3.1 (in [9]) we deduce the existence of \(\psi \) solving (6.10). If we replace such a \(\psi \) into (6.10) and use (6.11) together with the Hölder inequality and Poincaré inequality we have
from (3.4) and Young’s inequality we obtain (6.12). The proof is therefore completed. \(\square \)
1.3 Korn inequality
Lemma 6.3
(Korn Inequality) Let \(\Omega \subset {\mathbb {R}}^2 \) be an open bounded domain of class \(C^2\). Then there exists constant \(c>0\) such that
for all \(u\in V\).
Proof
The proof is based on the results from [17, Lemma 2.1]. We will prove it in general case where viscosity is bounded \(\nu (x)\ge \nu _{0}\), where \(\nu _{0}\) is a fixed constant. Without loss of generality we could assume that \(u\in C^{2}_{c} (\Omega ) \). Consider,
Integration by parts of the last term on the RHS of (6.15) gives us
As u is compactly supported in \(\Omega \), it follows that the second term of the RHS of (6.17) is zero, so we get (6.16). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malikova, S. Approximation of rigid obstacle by highly viscous fluid. J Elliptic Parabol Equ 9, 191–230 (2023). https://doi.org/10.1007/s41808-022-00196-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41808-022-00196-3
Keywords
- Stationary Navier–Stokes system
- Stationary Stokes problem
- Weak solutions
- Tangential regularity
- Discontinuous viscosity
- Penalty method
- Bogovskii approach