Introduction

Transparent glass–ceramics, distinguished by their dual character, emit light as amorphous glasses, while their anisotropy, in addition to other physical and chemical properties, has given rise to their optical parameters, optical dielectric constant, and refractive index [1].

In recent years, scientists had investigated phosphate-based glasses for various technological applications including sealing materials, solid-state electrolytes [2, 3], radioactive waste containment [4], laser technologies, medical applications such as degradable tissue and bone scaffolds [5], and agro-fertilizers with controlled solubility [6, 7].

Phosphate glasses are suitable for a wide range of applications due to their low melting, softening temperatures, high electrical conductivity, high thermal expansion coefficient, optical characteristics, high thermal stability, and the possibility of adding many glass modifiers which in turn alter their chemical composition [8,9,10,11]. Also, phosphate glasses are widely used in high gain laser materials which are used in high-power laser systems due to its ability to be shaped in large-format production, the high solubility of rare-earth ions and transition metals, high damage threshold [12, 13].

Vitreous phosphate glass network is built by linkages between PO4 tetrahedra. These glasses have low chemical durability due to the presence of hygroscopic P–O–P bonds which limits the use of phosphate glasses in many fields. Fortunately, phosphate glasses properties and chemical durability can be improved by adding a modifying oxide such as transition metal oxide [14, 15]. Many reports have shown that the addition of transition metals (TM) replaces bridging P–O–P bonds with more moisture-resistant P–O–TM bonds. TM can mostly coexist in different oxidation states in the glass structure; both semiconducting and magnetic properties can be affected positively by the electronic transfer in between the low- and high-valence states [16].

The glasses containing 45P2O5 mol% can be melt easily and biocompatible in nature [17]. Na2O acts as network modifying oxide, which can depolymerize the glass network by forming nonbridging oxygen (NBO), and decreases the melting temperature.

The study of optical properties of the sodium phosphate glasses shows a wide range of transparency in IR and visible range [18] which candidate these glasses to be host materials for rare-earth elements and transition metals to produce laser cavities and optical filters.

The present study aims to prepare and investigate the effect of ZnO content and effect of annealing on crystallinity, structure, and optical properties for zinc sodium phosphate glass–ceramic nano composite to be used as a host material for rare-earth ions and/or transition metals used in solid-state lasers and other optical applications.

Experimental

Glass and glass–ceramics nano composite samples of composition (55-x) P2O5.(30 + x)ZnO.15Na2O where x = 0, 2.5, 5, 7.5, and 10 mol% were prepared by melting a pure regent of di-ammonium hydrogen orthophosphate, sodium carbonate, and zinc oxide with the proper ratios. The mixture was mixed and grinded in a mortar to produce a fine powder. The homogenous mixture was melted in porcelain coercible at 950 °C for 1 h and shacked regularly to insure the mixture homogeneity. To produce glass–ceramics nano composite, the molten mixture was poured in an oven at 350 °C. The furnace was cooled down to room temperature with a step of 1 °C/min, while the glass samples with the same composition were poured in air between two brass plates. Both group samples were annealed at 150 °C for 3 h to reduce the internal stresses and enhance the mechanical stability. The studied samples were grinded in agate-mortar pestle to obtain fine powders to be measured by X-ray diffraction (XRD) and FTIR.

XRD was used to confirm the crystal structure of the prepared samples. XRD patterns were recorded using a Brucker D8 Advanced, with a CuKα as radiation source (λCuKα = 0.1540600 nm) and operating at 40 kV. Data was taken in step mode, using intervals of 0.02°, over a 2θ range of 4–70°. The obtained experimental patterns of both glass samples, poured in air and the samples poured in furnace at 350 °C, were compared to standards compiled by Joint Committee on Powder Diffraction and Standards (JCDPS). The structure investigation was performed at room temperature using Bruker vertex 70 FTIR spectrometer in the wavenumber range 400–4000 cm−1. The spectrum of each sample represents an average of 20 scans. The IR spectra were analyzed using the deconvolution method [19, 20].

The glass heat treatment temperature that was chosen according to a previous published paper contains a similar phosphate glass composition prepared at the same conditions in our lab. Tg was found to be around 360 °C while Tc of such glasses was found to be around 480 °C [21]. In this work, the samples were poured around Tg and cooled at a slow rate of cooling, which allowed the crystalline phase to be formed. The annealing temperature was 150 °C to release any thermal stresses inside the formed glass–ceramic.

The density (ρ) was determined at room temperature by using the Archimedes method with toluene as an immersing liquid. The density of each glass sample was taken as the average of at least five samples, with a tolerance of about ± 1%. The relative error in the density measurements was found to be ± 0.02% g/cm3. The molar volume (Vm) was calculated using the formula.

$${V}_{\mathrm{m}}=\sum {n}_{\mathrm{i}}{M}_{\mathrm{i}}/\rho$$
(1)

where Mi is the molecular mass of the oxide i, and ni is the oxide molar fraction in the glass.

UV–Vis absorption spectra of the polished samples with a constant thickness (± 0.1 mm) were immediately measured using (JASCO V-570 Japan) with wavelength ranged between 190 and 2500 nm.

Result and dissection

X-ray diffraction results

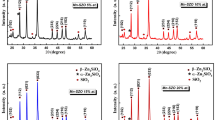
The X-ray patterns of the samples poured in furnace are shown in Fig. 1 for the samples x = 0 and 2.5 mol% showed a superposition of broad hump that characteristic the amorphous structure with some other peaks that characteristic to the crystalline phases referred to sodium zinc phosphate represents Na2Zn(P2O7) phase (card 87–0499). In order to identify the crystalline phases that appear in the diffraction patterns by using standard procedures, computer analysis is based on the powder diffraction file. This analysis permitted the identification of the crystalline phase present in the prepared samples. The crystallization increases at the expense of the amorphous structure with increasing ZnO mol%. Figure 1 shows the appearance of new diffraction peaks started in the composition range 5 ≤ ZnO < 10 mol% which are related to the crystalline phase Na2ZnP2O7.Zn2P2O7 (card 51–0349). The intensity of the second crystalline phase depends on the concentration of ZnO content up to 7.5 mol%. At ZnO = 10 mol%, the intensity decreases due to disillusion of the crystalline phase in the glass matrix and this means that the sample has tendency to form amorphous structure depending on ZnO content increment. The degree of crystallinity was found to suddenly increase with increasing ZnO concentration reaching a maximum value at ZnO = 7.5 mol%, then it starts to decrease at higher ZnO concentrations. The decrease in crystallinity at ZnO > 7.5 mol% gives good evidence that ZnO plays the role of glass modifier which forms NBOs in the glass network. The formation of NBOs will increase the disordered which leads to reducing the degree of crystallinity, see Fig. 2.

Fig. 1
figure 1

XRD patterns of glass–ceramics nano composite

Full size image
Fig. 2
figure 2

The degree of crystallinity and crystal size of glass–ceramics nano composite

Full size image

The crystalline size can be calculated by Scherrer’s formula: [22]

$$D=\frac{0.94 \lambda }{B\mathrm{ cos}\theta }$$
(2)

where D is the mean grain size, B is the full width at half maximum of the diffraction line radiant (broadening), θ is the diffraction angle for the diffraction line, and λ is the wavelength of the X-ray.

The calculated crystal sizes were found in the nano-meter range and varying by the variation of the ZnO content. By increasing the ZnO ratio, the crystal size increases up to 40 nm in the sample that contains 35 mol% ZnO followed by a decrease with increasing ZnO content to reach 29 nm in the sample that contains 45 ZnO. The relation between ZnO and crystal size is shown in Fig. 2.

FTIR results

Figure 3 shows the measured IR spectra of the samples under investigation. The spectra showed main peaks, based on visual judgment, and around 500, 731, 900, 1091, and 1245 cm−1. The IR spectra of the samples under investigation were normalized and deconvoluted. The analysis of the spectra demonstrates the existence of some peaks located around 480, 502, 548, 728, 785, 898, 989, 1083, 1156, 1252, and 1312 cm−1. Figure 4 shows the spectrum of the sample (55P2O5.30ZnO.15Na2O) after deconvolution analysis.

Fig. 3
figure 3

FTIR spectra of glass–ceramics nano composite

Full size image
Fig. 4
figure 4

The deconvolution of the IR spectrum of 30ZnO mol% sample

Full size image

Normally, the pentavalent of phosphate ion, PO4 tetrahedra shares three corners with the surroundings tetrahedra by sharing three oxygen atoms, bridging oxygen, forming branched polymer, long chains, or rings of interconnected PO4 tetrahedra, while the fourth oxygen atom double-bonded with the phosphate ion. The structure of PO4 tetrahedra can be found in many structural units described as Qn where n is the number of nonbridging oxygen in the PO4 [23]. The addition of modifier oxide, metal oxide (M), replaces P–O–P bond by M–O–P bond-forming single-bonded nonbridging oxygen.

By increasing the ratio of the modifier, the consistencies of the chains break down and depolymerize changing Q3, Q2, and Q1 units into Q0. Previous studies on sodium phosphate glasses (Na2O = 30–50 mol%) [24,25,26] proved that replacing P2O5 by Na2O changed the intermediate-range order of the glass matrix. Depolymerization increases by increasing Na2O content as a result; the compact glass matrix is gradually increased. Also, modifier cations (Zn, Na) are presumed to be located between the nonbridging oxygens forming considerably weak ionic bonds between the strong covalent bonds within the chains. Other (PO4)3 groups are cross-linked to these chains by sharing three corners by oxygen polyhedra containing the modifier ions [27]. The interpretation of the IR spectra of the samples under investigation can be summarized as the following [24,25,26, 28,29,30,31,32,33,34,35,36,37].

The band around 480 cm−1 is assigned to the bending vibration of O–P–O units, δ (PO4) modes of (PO2) in chain groups. The band centered at about 502 cm−1 is assigned to the fundamental frequency of (PO4)3− or harmonic of P = O bending vibrations. The band around 548 cm−1 is described as O = P–O bending vibrations. The peaks at 728 and 785 cm−1 may be due to symmetric stretching vibrations of P–O–P rings. The band at 898 cm−1 could be attributed to asymmetric stretching vibrations of P–O–P bonds linked with linear metaphosphate chain. The bands at 989, 1083, and 1156 cm−1 could be assigned to the asymmetric stretching vibration of P–O–P bonds linked with large metaphosphate ring, small metaphosphate rings, and bridges in pyrophosphate, respectively. 1252 cm−1 ascribed to the asymmetric stretch of doubly bonded oxygen modes, υas(P = O). The band at 1312 cm−1 is attributed to the stretching of P = O modes.

By increasing the ZnO content, the bands at 480 and 502 relative intensity increase in sample x = 2.5 then decrease with shifting towards lower frequency, which suggests the breakdown of the O–P–O bonds with the increment of ZnO content in the glass. The bands located between 400 and 600 cm−1 may be attributed to the bending vibrations of bridging phosphorous [26].

As seen from Fig. 3, there is a new absorption weak band around 500 cm−1. It is suggested that the band in the region below 600 cm−l is characteristic of Zn–O vibrations [38]. It is presumed that the stretching band corresponding to bridging oxygen P–O–Zn bonds might be located near 1100 cm−1 similar to that of S-P-O glasses proposed by Day et al. [39] and it may be buried in the dominant P-O− stretching band which is a broad region. The absorption band at 1260 cm−1 which is attributed to the nonbridging oxygen P = O decreased with the addition of Zn oxide as shown in Fig. 5. This decrease is associated with the increasing band at 1100 cm−1.

Fig. 5
figure 5

Relative area of bridging oxygen P–O–Zn bonds (1100 cm−1) and nonbridging oxygen P = O (1260 cm−1) as a function of ZnO content

Full size image

From this result, the zinc oxide may breakdown the nonbridging bonds P = O and convert to a bridging bond Zn–O-P which is more water-resistant than P-O-P and P-O−Zn+. This means that the ZnO can play the former role in this matrix in case of decrease in the P2O5 content, and this result agrees with the formation of crystalline phases with different formulas as discussed above in “X-ray diffraction results” section.

Density and molar volume

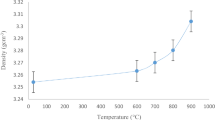
Figure 6 shows a slightly linear increase in density and a decrease in molar volume of (55-x)P2O5.(30 + x)ZnO.15Na2O glass–ceramics corresponding to the increase of ZnO mol%. The increase in density reflects the high packing of structural units when replacing P2O5 by ZnO. It is also revealed that the modified structural units related to Zn2+ ions such as P-O−Zn+ and Zn–O-P units are denser than P-O-P and the unit related to Na+ ions. This factor acts in the direction of decreasing the molar volume when increasing ZnO content. Another factor may cause the increase in density with increasing ZnO content, and this factor is related to the field strength of the Zn+2 ions.

Fig. 6
figure 6

Dependence of density and molar volume on the variation of ZnO content

Full size image

Optical band gap (direct and indirect) and Urbach energy

Optical absorption spectra of the prepared samples in infrared, optical, and UV range are shown in Fig. 7. The prepared zinc phosphate samples showed a wide range of transparency with no absorption peaks in the visible and infrared range, which is one of the main aspects of phosphate glasses [35, 40, 41]. The absorption edge, cut-off, near UV range is due to the transition between valance band and conduction band, i.e., energy gap. The cut-off has two regions with different slopes indicating the presence of two transitions of the samples, direct and indirect transitions. However, the absorption edge wavelength shows a red shift with increasing the ZnO content in the samples.

Fig. 7
figure 7

Optical density of the prepared samples as a function of ZnO content

Full size image

The absorption coefficient (α) can be calculated by the relation [42]:

$$\alpha \left(v\right)= \frac{1}{t}\mathrm{log}\frac{{I}_{0}}{I}$$
(3)

where \(\frac{{I}_{0}}{I}\) corresponds to the absorbance near the edge and t is sample thickness.

By calculating the absorption coefficient, the optical band gap can be calculated using Mott-Davis relation [43]:

$$\alpha \left(\upsilon \right)= B\frac{(hv-{E}_{\mathrm{opt}}{)}^{n}}{h\upsilon }$$
(4)

where Eopt is the optical band gap energy, B is energy independent constant, and n is a constant following the values 2, 3, ½, and ½ depending on direct and indirect intraband transitions. The indirect band gap is the common transition in glass material due to the amorphous nature of the glass composition, while the direct band gap transition is common in crystalline materials. Al-Ani and Higazy [44] show that phosphate-doped MgO glass has shown two-band transition direct and indirect with an indirect transition at lower energies ranging between 3.71 and 3.48 eV and a direct transition ranging between 4.6 and 3.92 eV which is suggested to be the case in this work due to the shape of the absorption edge regions.

Both direct and indirect band gaps were calculated for the prepared samples by extrapolating the linear part of the plots of (αhυ)2 and (αhυ)1/2, respectively, as a function of photon energy hυ, Tuac’s plot, the direct and indirect optical band gap can be obtained, as shown in Figs. 8 and 9, respectively. The calculated indirect band gap decreases with increasing zinc content as a general trend. This may be due to the addition of the zinc alters the internal glass–ceramic structure by reducing the cross-linking oxygen which increases the compactness of the system. Jlassi et al. [45] indicated that the increase in band gap energy of the phosphate glass by adding modifiers could be related to the increase of the cross-linking density in the glassy matrix. The band tail width of the absorption spectra can also provide information about a possible change in the glass structure [43]. At lower values of absorption coefficient band tail, ΔE is related to α(υ) by exponential relation [46]:

Fig. 8
figure 8

Tauc’s plot (indirect band gap) zinc sodium phosphate glass–ceramics nano composite

Full size image
Fig. 9
figure 9

Tauc’s plot (direct band gap) zinc sodium phosphate glass–ceramics nano composite

Full size image
$$\alpha \left(\upsilon \right)= {\alpha }_{0}\mathrm{exp}\left(\frac{h\upsilon }{\Delta E}\right)$$
(5)

where ΔE is the Urbach energy, αo is a constant, and hυ is the photon energy. Urbach energy indicates the width of the band tail of the localized states in the band gap. Figure 10 shows the relation between lnα and hυ, Urbach plot, for the prepared samples. ΔE can be determined by the reciprocal of the slope in the above relation. The calculated values are listed in Table 1.

Fig. 10
figure 10

Urbach energy for the prepared glass–ceramics nano composite

Full size image
Table 1 The optical band gap (direct and indirect), crystal size, and Urbach energy of the prepared glass–ceramic
Full size table

By increasing zinc content, the band tail width showed an opposite trend to band gap, i.e., increase with increasing the zinc content. The increase in band tail width indicates the addition of localized states by increasing the zinc content. This may be due to the creation of defects by adding modifiers to the glass–ceramics network, which increases the number of the localized states in the band gap due to the formation of crystalline phases, and this result agrees with the XRD and FTIR spectroscopy results [46,47,48].

Refractive index (n) is very important for optical applications of the glasses. The linearity of the refractive index is correlated to the energy band gap and the density of the oxide glasses in density range 1–3 gm/cm3, and n can be calculated by the relation [49, 50]:

$${n}_{r}= \frac{D+10.4}{8.6}$$
(6)

Optical dielectric constant can be calculated from refractive index (εo = n2) [50]. Hence, the expression of the Penn model can be formulated in relation with the refractive index [49, 50].

Figure 11 shows the variation of refractive index and optical dielectric constant of the prepared samples with ZnO content. The refractive index showed a linear increase with increasing ZnO content. (n) showed slightly increased between 1.53 for base glass and 1.55 for high ZnO content depending on the role of ZnO in the glass matrix. This is an indication of the increase of compactness of the system which agrees with increasing of crystallinity that observed in XRD results. On the other hand, the optical dielectric constant of all the samples is varying from 2.33 to 2.39, which is almost independent of the concentration of ZnO content. The slight increase in the optical dielectric constant causes a reduction in the optical band gap.

Fig. 11
figure 11

Refractive index (n) and optical dielectric constant as a function of ZnO content

Full size image

Visibility is transparent for all of compositions (X = 0–10 mol%) ZnO. Although nearly all compositions contain some specific crystalline nano structure, this means that the investigated samples lie in the region of transparent glass–ceramic (TGC). This argument is supported by the limited changes between refractive index with ZnO content, and (n) changes by only 0.04 for 10 mol% ZnO sample. Figure 12 shows UV/Vis transmission spectra for the prepared samples. All of composition is regard as transparent (⁓90%). This insures the phenomenon (TGC).

Fig. 12
figure 12

Optical transmission of zinc sodium phosphate glass–ceramics nano composite

Full size image

Conclusion

Phosphate-based glass system with the composition (55-x)P2O5.(30 + x)ZnO.15Na2O where x = 0, 2.5, 5, 7.5, and 10 was prepared with the conventional melt quenching method. The crystallinity of the samples increases with increasing the ZnO content up to 7.5 mol%. By increasing the ZnO content, the crystallinity decreases due to disillusion of the crystalline phase in the glass matrix. IR measurements show that the zinc oxide may breakdown the nonbridging bonds P = O and convert to a bridging bond Zn–O-P which is more water-resistant than P-O-P and P-O−Zn+. The density of the samples increases with increasing ZnO while molar volume decreases. The optical absorption of the samples under investigation shows a high range of transparency in the optical and IR range. The calculated optical band gap decreases with increasing ZnO content with the range 3.42 and 3.13 eV for indirect transition and ranging between 4.34 and 4.20 eV for direct transition. These results suggest the suitability of these samples for many glass–ceramics applications such as a host material for rare-earth ions and/or transition metals used in solid-state lasers and other optical applications.