Abstract
Pure (BNT) and iron-doped bismuth sodium titanate (Fe-BNT) ceramics were produced according to the formula Bi0.5Na0.5Ti1−xFexO3−0.5x, where x = 0 to 0.1. The addition of Fe2O3 enables decreasing the sintering temperature to 900 °C in comparison with 1075 °C for pure BNT, whilst also achieving lower porosities and greater densities. This is attributed to oxygen vacancy generation arising from substitution of Fe3+ onto the Ti4+ site of the BNT perovskite structure, and the resulting increase in mass transport that this enables during sintering. X-ray diffraction (XRD) analysis of Fe-BNT samples shows single-phase BNT with no secondary phases for all studied Fe contents, confirming complete solid solution of Fe. Rietveld refinement of XRD data revealed a pseudocubic perovskite symmetry (Pm-3m), and unit cell lengths increased with increasing Fe content. Scanning electron microscopy (SEM) showed that average grain size increases with increasing Fe content from an average grain size of ~ 0.5 μm in (x = 0) pure BNT to ~ 5 μm in (x = 0.1) Fe-doped BNT. Increasing Fe content also led to decreasing porosity, with relative density increasing to a maximum > 97% of its theoretical value at x = 0.07 to 0.1. The addition of Fe to BNT ceramics significantly affects electrical properties, reducing the remnant polarization, coercive field, strain and desirable ferroelectric properties compared with those of pure densified BNT. At room temperature, a high relative permittivity (ɛ′) of 1050 (x = 0.07) at an applied frequency of 1 kHz and a lower loss factor (tanδ) of 0.006 (x = 0.1) at an applied frequency of 300 kHz were observed by comparison with pure BNT ceramics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Lead zirconate titanate (PZT) ceramics have been extensively used in electronic applications such as transducers, capacitors and piezoelectric motors, due to their excellent ferroelectric and piezoelectric properties (coercive field of 1 kV/mm and remnant polarization of 35 μC/cm2) [1,2,3,4,5]. However, the use of PZT is under review in Europe, due to the high toxicity and evaporation of lead oxide (PbO) at higher sintering temperatures, which cause health and environmental hazards [3, 6,7,8]. Researchers have thus studied bismuth sodium titanate (BNT) ceramics [9], among others, as replacements for PZT. BNT plays an important role as a non-toxic electrical ceramic material and has thus been utilized in electronic applications such as resonators and filters, transducers, piezoelectric motors and actuators [10, 11]. Stoichiometric BNT has two main phase transitions: (i) a ferroelectric to anti-ferroelectric phase transition at approximately 200 °C and (ii) an anti-ferroelectric to paraelectric transition at approximately 320 °C [12]. BNT ceramics have thus been used for two reasons: they are non-toxic, and they have good piezoelectric properties [10, 11]. BNT has a good remnant polarization (38 μC/cm2), but drawbacks include evaporation during the processing of volatile Bi2O3 (melting temperature 817 °C) and Na2O (melting temperature 1132 °C) that can lead to porous ceramic products. Another limitation of BNT is a high coercive field (73 kV/cm) which results in difficulties with poling [13,14,15]. Many researchers have studied additions of flux materials and sintering aids to BNT as a potential means of solving this issue by reducing sintering temperatures. Such additions have included MgO [16], CuO [17], BiFeO3 [18] and Fe2O3 [19]. Watcharapasorn et al. [19] lowered the sintering temperature of BNT to 850 °C with a high densification of 95% relative density by adding 0.15 mol% Fe2O3. In addition, Chou et al. [17] reduced the sintering temperature from 1100 °C for pure BNT ceramics to 950 °C by adding 4 wt% CuO which also enhanced the relative density to 95%. Reducing energy consumption in BNT sintering through lower sintering temperatures was the primary aim of the present work.
Experimental procedures
A conventional solid-state processing route was used to prepare seven BNT ceramics, including pure BNT and BNT doped with Fe at different concentrations. The starting raw materials consisted of analytical-grade powders of Bi2O3 (> 99% purity), Na2CO3 (> 99.9% purity), TiO2 (> 99.9% purity) and Fe2O3 (> 99% purity). These were prepared as powder mixtures to manufacture ceramics according to the stoichiometric formula Bi0.5Na0.5Ti1−xFexO3−0.5x where x = 0, 0.025, 0.0375, 0.050, 0.070 and 0.100. The nominal compositions and the sintering temperatures of the samples prepared in this work are summarized in Table 1. The raw materials were dried at 110 °C for 24 h then weighed out using a three-decimal-place balance to provide batches for 20 g of each ceramic. Batches were wet-milled in 250-mL polyethene (PE) bottles containing propan-1-ol and yttria-stabilized zirconia (YSZ) milling media, on a roller-mill for 24 h. The milled powders were then removed and dried overnight at 110 °C in an oven placed in a fume cupboard. The dried powder was then placed in a recrystallized Al2O3 crucible and heated in an electric furnace at 5 °C/min to 700 °C and held for 2 h (samples BFe0.00 to BFe10.00) and 4 h (sample SB0), and then cooled to room temperature. The powders were then wet-milled again, in 250-mL polyethene (PE) bottles containing propan-1-ol and YSZ milling media, for 48 h. The milled powder was again removed and dried overnight at 110 °C in an oven placed in a fume cupboard. The dried powder was then pressed to form 10-mm-diameter pellets using a hydraulic press at 2 t force. The prepared pellets were sintered in one process as follows: (i) Heat from room temperature at 3 °C/min to 300 °C and hold at this temperature for 1 h; (ii) heat at 3 °C/min from 300 °C to 700 °C and hold at this temperature for 1 h; (iii) and finally heat at 5 °C/min from 700 °C to 900 °C (samples BFe0.00 to BFe10.00) or 1075 °C (sample SB0) and hold at this temperature for 2 h; then allow samples to cool slowly inside the furnace to room temperature.
Characterization
The crystalline structure of each sample was investigated using X-ray powder diffraction (XRD, PANalytical X’Pert Pro MPD) using Cu Kα radiation (λ = 1.5405 Å) over the range 10 to 80 °2θ. The structure was also analysed using Raman spectroscopy (DXR2 Raman Microscope, Thermo Fisher Scientific, USA) using a 532-nm laser, applied at room temperature. The microstructure was characterized by scanning electron microscopy (SEM, Nova NanoSEM). All samples were polished using SiC paper with water (100, 200, 400, 800, 1200 and 2500 grit size), then polished using diamond paste (1 μm). The polished samples were thermally etched at 800 °C in an oven for 1 h and then were coated with a thin layer of carbon. Silver paint was applied on three sides to provide electrical contact between the sample and SEM sample holder. Microstructural images were obtained using both secondary electron and backscattered electron imaging. Bulk density was measured according to the Archimedes principle. The relative density of ceramic samples was calculated according to the density of pure BNT using Eq. (1):
where ρm is bulk density and ρt is theoretical density (5.98 g/cm3 for Pure BNT) [17]. Bulk sample densities were measured using a four-decimal-place density balance and vacuum desiccator, where the dried sample pellet was weighed in the air (W1), then placed under vacuum to remove the air inside the vacuum desiccator for 30 min. The evacuated sample was then immersed in distilled water inside the vacuum desiccator for 10 min to allow the water to penetrate the open porosity. The wet sample was then weighed in water (W2) and in air (W3). The bulk density was calculated using Eq. (2) and theoretical density using Eq. (3):
where MBNT, MFe2O3, ρBNT and ρFe2O3 represent the mass of BNT composition, the mass of Fe2O3, the theoretical density of BNT, and the theoretical density of Fe2O3 (5.12 g/cm3, Powder Diffraction File Number 032-0469). Electrode samples were prepared using a coating instrument for electrical measurements. The electrodes were made using an Au sputter coater with sputtering current 10 mA, sputtering time 600 s and tooling factor 2.7. Polarization and strain as functions of electric field were analysed at 10 Hz using an AixACT system. The relative permittivity and loss factor were measured at three different frequencies (1, 10, 100 kHz) using an LCR meter (Agilent 4285A, Agilent Technologies Japan, Ltd.).
Results and discussion
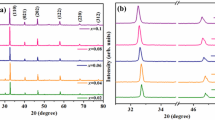
X-ray diffraction (XRD) analysis at room temperature shows pure rhombohedral perovskite phase (Powder Diffraction File Number 04-017-0216) for pure Bi0.5Na0.5TiO3 ceramics, and pure cubic perovskite phase (Powder Diffraction File Number 89-3109) for all iron-doped BNT ceramics, without measurable levels of any secondary phases or significant changes in the crystallographic structure, as shown in Fig. 1(a). This confirms that iron forms a complete solid solution in BNT for all compositions studied, i.e. up to x = 0.1. Also, the single-phase region has thus been demonstrated at higher Fe contents of doped BNT ceramics. By comparison, Aksel et al. suggested an upper limit of x = 0.050 [20] and Watcharapasorn et al. suggested an upper limit of x = 0.015 [19]. We have thus demonstrated a higher upper limit of solid solution (x ≥ 0.1) than was previously obtained by those authors.
For the <110> and <111> diffraction peaks at ~ 32.7 °2θ and 40.2°2θ, respectively, a slight shift to lower angles is observed with increasing additions of Fe (increasing x), as presented in Fig. 1(b and c). This slight shift, which shows increasing d-spacing with increasing Fe content (x), is due to the larger ionic radius of Fe3+ (0.645 Å) [21] by comparison with Ti4+ (0.605 Å) on the B-site of the perovskite structure, which causes changes in the unit cell dimensions and thus changes in d-spacings [22]. Similar peak shifts to lower angles upon addition of Fe to BNT were also reported by Watcharapasorn et al. [19].
Rietveld refinement [23] using FULLPROF [24] was carried out on XRD data to refine the crystal structure parameters. The Bi0.5Na0.5TiO3 structure [25] was used as a starting model for Rietveld refinement. For the Fe-doped samples, Fe and Ti were disordered over the same site. The Rietveld refinement outputs (Table 2) show pseudocubic cell symmetry (Pm-3m), in agreement with Vijayeta et al. [7] and Fukuchi et al. [26]. The pseudocubic phase results from rhombohedral distortion of perovskite lattice, and with shifting of the <110> peak position to lower angles. This is due to the substitution of Fe3+ (larger ionic radius 0.645 Å) on the Ti4+ (smaller ionic radius 0.605 Å) site, which generates oxygen vacancies. The observed intensity (measured, shown by blue lines in Fig. 2) shows slightly higher intensities than calculated intensity (red lines) for the <100>, <110>, <200> and <211> Bragg peaks. Quantitative analysis provides unit cell lengths (a=b=c), cell volumes, weighted residual factors (wRf), weighted residual expected (wRexp), d-spacing from the <110> Bragg peak, Bi-O/Na-O and Ti-O/Fe-O interatomic distances and X-ray densities, as shown in Table 2. The increase in unit cell lengths (a=b=c), from 3.8829 to 3.8893 Å with increasing Fe content, and accompanying increase in unit cell volume, from 58.618 Å3 for the Fe-free x = 0 sample to 58.832 Å3 for the x = 0.1 iron-doped sample, are consistent with the slight shift of the <110> Bragg peak as shown in Fig. 1(b), and are due to Fe (larger ionic radius, 0.645 Å) occupying the Ti (smaller ionic radius, 0.605 Å) site of the pseudocubic perovskite structure. The weighted residual parameters (wRf and wRexp) and chi-square (x2) show reasonable changes with increasing x. The d-spacing of the <110> Bragg peak increases with increasing Fe content, as do both the Bi-O/Na-O and Ti-O/Fe-O interatomic distances (Table 2).
Figure 3(a) shows room temperature Raman spectra for all samples. Spectra show six broad Raman peaks. The width of these peaks has been attributed to disorder on the A-site [27, 28]. The peak centred at low Raman shifts of ~ 140 cm−1 (labelled peak A) is attributable to A1 symmetry and vibrations of cations on the A-site in the ABO3 perovskite structure [27,28,29,30,31,32]. Wang et al. [27] and others have also suggested that this band implies the existence of local Na+TiO3 clusters of several unit cells. No Bi-O Raman bands are expected in this region since a Bi-O band should occur at < 100 cm−1 due to the large mass of Bi [27]; however, instrumental limitations meant that we could not provide robust data much below 100 cm−1 and therefore this spectral region was not considered further in this study. Raman results (Fig. 3(a)) show no significant changes in the Raman shift or intensity of peak A with increasing Fe content. This lack of change is thus consistent with Fe occupying the B-site, in light of the origin of peak A. Peak B, centred at ~ 280 cm−1, is assigned to Ti-O vibrations (A1 symmetry) [27,28,29,30,31,32]. Peaks C and D, at ~ 520 cm−1 and ~ 590 cm−1, respectively, are assigned to vibrations of TiO6 octahedra [27, 30, 31]. Peaks E and F at ~ 750 cm−1 and ~ 850 cm−1, respectively, whilst previously observed, were discussed in terms of their origins by Wang et al. [27], who stated that they are likely to be due to overlapping of A1 (longitudinal optical) and E mode (longitudinal optical) bands. As expected on the basis of similar spectral changes in Raman spectra when Mn3+ was substituted onto the B-site of BNT by Anthoniappen et al. [30], our Raman spectra show that the centroid position of peak B at ~ 280 cm−1 shifts slightly to lower Raman shift with increasing Fe3+ addition, as highlighted in Fig. 3(b). This shift may be due to structure disorder (structure transition from rhombohedral to pseudocubic) and existence of oxygen vacancies in the Fe-BNT system, as a result of substitution of Fe3+ onto the Ti4+ site of the BNT ceramics [32].
Secondary SEM imaging (Fig. 4) shows a distribution of grain sizes which increases with increasing Fe content, from ~ 200 nm in pure BNT to ~ 5 μm (x = 0.1). We observe that, for those samples with a 900 °C sintering temperature, SEM shows a porous microstructure and small average grain size, and as increasing amounts of iron are introduced into the material, the microstructure becomes progressively more densified (less porous), accompanied by a larger average grain size. This behaviour is analagous to the behaviour observed by Guo et al. [33] who added similar levels of Mn to BNT ceramics. SEM imaging is thus qualitatively in agreement with the relative density measurements of samples which shows increasing density with increasing Fe content, for samples sintered at 900 °C, as presented in Table 3. Undoped BNT (sample BFe0.00) exhibited a very low density at 900 °C sintering temperature; however, density rapidly increased with increasing Fe content, reaching a value of ~ 97% relative density at the highest Fe contents studied here. In addition, density increased with increasing sintering temperature, reaching ~ 93% relative density for the SB0 BNT sample sintered at 1075 °C. This is approximately the same density as the BFe3.75 sample which was sintered at 900 °C. Substituting Fe3+ onto the B-site in the BNT perovskite structure generates oxygen vacancies which aid mass transport during sintering and hence increase grain growth [19, 33,34,35].
Table 4 shows the measured remnant polarization and coercive field for selected samples. For the pure BNT sample sintered at 1075 °C (SB0, with increasing frequency from 1 to 5 to 10 Hz), significant reductions in both remnant polarization and coercive field were recorded. Similar magnitudes of reduction in both remnant polarization and coercive field were also observed with increasing Fe contents for the BFe series of samples sintered at 900 °C, within the range studied here.
The polarization-electric field response at 10 Hz in a bipolar field at room temperature is shown for the Fe-doped samples in Fig. 5(a) and for pure BNT in Fig. 5(b). A significant reduction of remnant polarization is displayed for the Fe-doped samples, compared with the high remnant polarization (38 μC/cm2) of pure BNT (Fig. 5(b)). The ferroelectric hysteresis response displays slimmed loops at the applied electric fields studied here, upon addition of Fe. Figure 5(b) shows the polarization versus electric field loops for densified pure BNT (SB0) ceramics at room temperature and three different (1, 5 and 10 Hz) frequencies. A lower remnant polarization (4.8 μC/cm2) was measured at 10 Hz, which then increased with decreasing frequency to reach a higher remnant polarization at 34.8 μC/cm2 at 1 Hz. The hysteresis loop shows a slimmed hysteresis (P–E) loop shape with relaxor behaviour at higher frequency (10 Hz), then the shape tends to be a broad shape typical of ferroelectric behaviour at a lower applied (1 Hz) frequency. The hysteresis loop exhibits ferroelectric shape with a maximum remnant polarization (34.8 μC/cm2) and coercive field (56.6 kV/cm) for the pure BNT SB0 sample at 1 Hz for an applied field of 70 kV/cm, in comparison with adding Fe to the BNT ceramics that made the hysteresis loop slimmer which significantly decreases remnant polarization and coercive field to 1.18 μC/cm2 and 21.92, respectively, for sample BFe2.5 at 10 Hz and applied field 60 kV/cm. This indicates that the ferroelectric behaviour of BNT ceramics is decreased by adding Fe dopants as the oxygen vacancies generated may assist in breakdown of the samples with broadly comparable behaviour observed in other ceramics [36,37,38,39]. The remnant polarization and coercive field for the pure BNT sample (SB0) are consistent with values for pure BNT ceramics reported in the literature (remnant polarization 38 μC/cm2 and coercive field 73 kV/cm) [13, 14, 40].
Figure 6 shows the strain versus electric field response at 70 kV cm−1 applied field and three different (1, 5 and 10 Hz) frequencies using bipolar measurement at room temperature for the pure BNT (SB0) sample. The lowest strain (0.018%) was measured at 10 Hz; it then increased with decreasing frequency to reach a maximum strain of 0.085% at 1 Hz. The strain loop shows a slimmed shape indicative of relaxor behaviour at 10 Hz, with no negative strain recorded, then changes to a butterfly shape indicative of ferroelectric behaviour at 1 Hz. The maximum strain (0.085%) obtained for the SB0 sample is in close agreement with the 0.08% previously reported for pure sintered BNT [36]. The strain-electric field curve collapsed upon additions of Fe, and so is not reproduced here. This may be attributed to the formation of structural defects or defect dipoles (FeTi′-VO●●) that produce oxygen O2− vacancies (O3−0.5x) in Bi0.5Na0.5Ti1−xFexO3–0.5x ceramics due to the replacement of Fe3+ by Ti4+ [20, 37, 38, 41].
The relative permittivity (ɛ′) and dielectric loss factor (tanδ) at different frequencies (1, 10, 100 kHz) and measured at 20 °C are shown in Table 5. The relative permittivity and dielectric loss factor decreased with increasing frequency from 1 to 100 kHz for all samples. Both parameters, ɛ′ and tanδ, generally tend to decrease relative to the SB0 sample, with increasing Fe content, although the data for the BFe0.00 sample may be unreliable due to the very low density/high porosity of this sample (Table 3).
Conclusions
Pure and iron-doped bismuth sodium titanate (BNT) ceramics were successfully produced using solid-state sintering. Substitution of Fe3+ onto the B-site occupied by Ti4+ can create oxygen vacancies which thereby enable lower sintering temperatures of 900 °C and higher densification at up to 97% of relative density. Iron concentrations ranged from x = 0.0 to x = 0.1 according to the formula Bi0.5Na0.5Ti1−xFexO3−0.5x. XRD analysis showed pure perovskite BNT phase for all studied Fe dopant levels. SEM imaging showed that increasing average grain size accompanied increasing iron content, from < 1 μm in pure BNT (x = 0.0) to ~ 5 μm at x = 0.1. The addition of iron to BNT enables a significant reduction in sintering temperatures whilst enhancing relative density, but this is accompanied by reductions in the remnant polarization, coercive field and the ferroelectric properties of BNT.
References
Wang, X.X., Murakami, K., Sugiyama, O., Kaneko, S.: Piezoelectric properties, densification behaviour and microstructural evolution of low temperature sintered PZT ceramics with sintering aids. J. Eur. Ceram. Soc. 21, 1367–1370 (2001)
Chu, S.Y., Chen, T.Y., Tsai, I.T., Water, W.: Doping effects of Nb additives on the piezoelectric and dielectric properties of PZT ceramics and its application on SAW device. Sensors Actuators A Phys. 113, 198–203 (2004)
Rödel, J., Jo, W., Seifert, K.T.P., Anton, E., Granzow, T., Damjanovic, D.: Perspective on the development of lead-free piezoceramics. J. Am. Ceram. Soc. 92, 1153–1177 (2009)
Bai, W., Hao, J., Fu, F., Li, W., Shen, B., Zhai, J.: Structure and strain behavior of textured BNT-based ceramics by template grain growth. Mater. Lett. 97, 137–140 (2013)
Xu, J., Yang, M., Gan, K., Qu, Y., Zhang, X., Ma, N., Wang, Y., Yang, J.: Enhanced piezoelectric properties of PZT ceramics prepared by direct coagulation casting via high valence counterions (DCC–HVCI). Ceram. Int. 42, 2821–2828 (2016)
Rahman, J.U., Hussain, A., Maqbool, A., Song, T.K., Kim, W.J., Kim, S.S., Kim, M.H.: Dielectric, ferroelectric and field-induced strain response of lead-free BaZrO3-modified Bi0.5Na0.5TiO3 ceramics. Curr. Appl. Phys. 14, 331–336 (2014)
Pal, V., Dwivedi, R.K., Thakur, O.P.: Synthesis and ferroelectric behavior of Gd doped BNT ceramics. Curr. Appl. Phys. 14, 99–107 (2014)
Lin, D., Kwok, K.W., Lam, K.H., Chan, H.L.W.: Structure and electrical properties of K0.5Na0.5NbO3-LiSbO3 lead-free piezoelectric ceramics. J. Appl. Phys. 101, 074111 (2007)
Zuo, R., Su, S., Wu, Y., Fu, J., Wang, M., Li, L.: Influence of A-site nonstoichiometry on sintering, microstructure and electrical properties of (Bi0.5Na0.5)TiO3 ceramics. Mater. Chem. Phys. 110, 311–315 (2008)
Yuan, Y., Zhao, C.J., Zhou, X.H., Tang, B., Zhang, S.R.: High-temperature stable dielectrics in Mn-modified (1-x)Bi0.5Na0.5TiO3-xCaTiO3 ceramics. J. Electroceram. 25, 212–217 (2010)
Priya, S., Nahm, S.: Lead-free piezoelectrics. Springer Science & Business Media (2011)
Chandrasekhar, M., Kumar, P.: Processing and characterizations of BNT-KNN ceramics for actuator applications. Proc Appl Ceram. 10, 73–77 (2016)
Li, H., Kang, J., Guo, F., Qu, Y., Yang, D.: Effect of the Nb2O5 content on electrical properties of lead-free BaTiO3–Bi0.5Na0.5TiO3 ceramics. Ceram. Int. 39, 7589–7593 (2013)
Panda, P.K., Sahoo, B.: PZT to lead free piezo ceramics: a review. Ferroelect. 474, 128–143 (2015)
Wu, L., Xiao, D., Zhou, F., Teng, Y., Li, Y.: Microstructure, ferroelectric, and piezoelectric properties of (1−x−y) Bi0.5Na0.5TiO3–xBaTiO3–yBi0.5Ag0.5TiO3 lead-free ceramics. J. Alloys Compd. 509, 466–470 (2011)
Chou, C.S., Chen, J.H., Yang, R.Y., Chou, S.W.: The effects of MgO doping and sintering temperature on the microstructure of the lead-free piezoelectric ceramic of Bi0.5Na0.5TiO3. Powder Technol. 202, 39–45 (2010)
Chou, C.S., Liu, C.L., Hsiung, C.M., Yang, R.-Y.: Preparation and characterization of the lead-free piezoelectric ceramic of Bi0.5Na0.5TiO3 doped with CuO. Powder Technol. 210, 212–219 (2011)
Fujii, I., Ito, Y., Suzuki, T., Wada, T.: Ferroelectric and piezoelectric properties of (Bi1/2Na1/2)TiO3–BiFeO3 ceramics. J. Mater. Res. 31, 28–35 (2016)
Watcharapasorn, A., Jiansirisomboon, S., Tunkasiri, T.: Sintering of Fe-doped Bi0.5Na0.5TiO3 at <1000°C. Mater. Lett. 61, 2986–2989 (2007)
Aksel, E., Erdem, E., Jakes, P., Jones, J.L., Eichel, R.-A.: Defect structure and materials “hardening” in Fe2O3-doped (Bi0.5Na0.5)TiO3 ferroelectrics. Appl. Phys. Lett. 97, 12903 (2010)
Shannon, R.D.: Revised effective ionic radii and systematic studies of interatomie distances in halides and chaleogenides. Acta Cryst. 5, 751–767 (1976)
Shannon, R.D., Prewitt, C.T.: Coordination and volume changes accompanying high-pressure phase transformations of oxides. Mater. Res. Bull. 4, 57–62 (1969)
Rietveld, H.M.: A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 2, 65–71 (1969)
Rodríguez-Carvajal, J.: Recent advances in magnetic structure determination by neutron powder diffraction. Physica B. 192, 55–69 (1993)
Anton, E.M., Schmitt, L.A., Hinterstein, M., Trodahl, J., Kowalski, B., Jo, W., Kleebe, H.-J., Rödel, J., Jones, J.L.: Structure and temperature-dependent phase transitions of lead-free Bi1/2Na1/2TiO3–Bi1/2K1/2TiO3–K0.5Na0.5NbO3 piezoceramics. J. Mater. Res. 27, 2466–2478 (2012)
Fukuchi, E., Kimura, T., Tani, T., Takeuch, T., Saito, Y.: Effect of potassium concentration on the grain orientation in bismuth sodium potassium titanate. J. Am. Ceram. Soc. 85, 1461–1466 (2002)
Wang, J., Zhou, Z., Xue, J.: Phase transition, ferroelectric behaviors and domain structures of (Na1/2Bi1/2)1−xTiPbxO3 thin films. Acta Mater. 54, 1691–1698 (2006)
Kreiselt, J., Glazer, A.M., Jones, G., Thomas, P.A., Abello, L., Lucazeau, G.: An x-ray diffraction and Raman spectroscopy investigation of A-site substituted perovskite compounds: the (Na1-xKx)0.5Bi0.5TiO3 (0≤x≤1) solid solution. J. Phys. Condens. Matter. 12, 3267–3280 (2000)
Lidjici, H., Lagoun, B., Berrahal, M., Rguitti, M., Hentatti, M.A., Khemakhem, H.: XRD, Raman and electrical studies on the (1-x)(Na0.5Bi0.5)TiO3-xBaTiO3 lead free ceramics. J. Alloys Compd. 618, 643–648 (2015)
Anthoniappen, J., Tu, C.S., Chen, P.Y., Chen, C.-S., Idzerda, Y.U., Chiu, S.-J.: Raman spectra and structural stability in B-site manganese doped (Bi0.5Na0.5)0.925Ba0.075TiO3 relaxor ferroelectric ceramics. J. Eur. Ceram. Soc. 35, 3495–3506 (2015)
Rout, D., Moon, K.S., Kang, S.J., Kim, I.W.: Dielectric and Raman scattering studies of phase transitions in the (100-x) Na0.5Bi0.5TiO3-x SrTiO3 system. J. Appl. Phys. 108, 084102 (2010)
Thangavelu, K., Asthana, S.: Monoclinic Cc-phase stabilization in magnetically diluted lead free Na1/2Bi1/2TiO3—evolution of spin glass like behaviour with enhanced ferroelectric and dielectric properties. Mater Res Exp. 9, 096301 (2015)
Guo, Y., Fan, H., Long, C., Shi, J., Yang, L., Lei, S.: Electromechanical and electrical properties of Bi0.5Na0.5Ti1−xMnxO3−δ ceramics with high remnant polarization. J. Alloys Compd. 610, 189–195 (2014)
Long, C., Fan, H., Ren, P.: Structure, phase transition behaviors and electrical properties of Nd substituted Aurivillius polycrystallines Na0.5NdxBi2.5-xNb2O9 (x=0.1, 0.2, 0.3, and 0.5). Inorg. Chem. 52, 5045–5054 (2013)
Long, C., Li, T., Fan, H., Wu, Y., Zhou, L., Li, Y., Xiao, L., Li, Y.: Li-substituted K0.5Na0.5NbO3-based piezoelectric ceramics: crystal structures and the effect of atmosphere on electrical properties. J. Alloys Compd. 658, 839–847 (2016)
Dong, G., Fan, H., Shi, J., Li, M.: Composition- and temperature-dependent large strain in (1−x)(0.8Bi0.5Na0.5TiO3–0.2Bi0.5K0.5TiO3)–xNaNbO3 ceramics. J. Am. Ceram. Soc. 98, 1150–1155 (2015)
Zhao, N., Fan, H., Ren, X., Gao, S., Ma, J., Shi, Y.: A novel ((Bi0.5Na0.5)0.94Ba0.06)1-x (K0.5Nd0.5)xTiO3 lead-free relaxor ferroelectric ceramic with large electrostrains at wide temperature ranges. Ceram. Int. 44, 571–579 (2018)
Shi, J., Fan, H., Liu, X., Li, Q.: Giant strain response and structure evolution in (Bi0.5Na0.5) 0.945− x(Bi0. 2Sr0.7□0.1)xBa0.055TiO3 ceramics. J. Eur. Ceram. Soc. 34, 3675–3683 (2014)
Hu, B., Fan, H., Ning, L., Gao, S., Yao, Z., Li, Q.: Enhanced energy-storage performance and dielectric temperature stability of (1-x)(0.65Bi0.5Na0.5TiO3–0.35Bi0.1Sr0.85TiO3)-xKNbO3 ceramics. Ceram. Int. 44, 10968–10974 (2018)
Kounga, A.B., Zhang, S.T., Jo, W., Granzow, T., Rödel, J.: Morphotropic phase boundary in (1−x)Bi0.5Na0.5TiO3–xK0.5Na0.5NbO3 lead-free piezoceramics. Appl. Phys. Lett. 92, 22290–22292 (2008)
Davies, M., Aksel, E., Jones, J.L.: Enhanced high-temperature piezoelectric coefficients and thermal stability of Fe- and Mn-substituted Na0.5Bi0.5TiO3 ceramics. J. Am. Ceram. Soc. 94, 1314–1316 (2011)
Funding
This study was financially supported by the Higher Committee for Educational Development in Iraq (HCED).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Muhammed, K.R., Scrimshire, A., Sterianou, I. et al. Physical properties and sinterability of pure and iron-doped bismuth sodium titanate ceramics. J Aust Ceram Soc 56, 1441–1449 (2020). https://doi.org/10.1007/s41779-020-00461-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41779-020-00461-5