Structural, optical and electrical properties of multiferroic BiFe_1-xNi_xO₃ ceramic

Abstract

BiFe_1−xNi_xO₃ (x = 0.7, 0.8 and 0.9) polycrystalline ceramics are synthesized by a solid-state reaction, and their structural, absorption, leakage current and electrical properties are investigated. The X-ray diffraction measurements show that the lattice parameter values increase with increasing the substitution of Ni²⁺ ions for Fe³⁺ ions. The optical absorption spectra indicate that the band gap energy increases with increasing Ni²⁺ ions. Leakage currents are much decreased by about three orders of magnitude with increasing Ni ions. The J-E hysteresis was also investigated. Both real and imaginary dielectric constants are investigated as a function of both frequency and temperature. The room temperature dielectric measurement with a wide frequency range of 1 KHz–1 MHz reveals that the real and imaginary dielectric constants are decreased with increasing frequency of BiFe_1−xNi_xO₃ (x = 0.7, 0.8, 0.9) ceramics. The real and imaginary dielectric constants are found to be increased with temperature. The temperature dependence of ε′ and ε″ exhibits an anomaly which shifted to lower temperature with increasing Ni²⁺. The anomaly indicates the possible existence of spin-glass states with Ni²⁺ ion substitution in places of Fe³⁺ ions.

Introduction

In multiferroic system, a coupling of at least two or all three of antiferroelectricity, antiferromagnetism and ferroelectricity characteristic are observed in the same phase [1,2,3]. The existence of both ferroelectric, ferromagnetism and elasticity in such a system will provide more degree of freedom in the field of new functional sensors and actuators [1, 4, 5]. BiFeO₃ represents one of such set of perovskite multiferroics family which has a ferroelectricity phase with cure temperature (T_c) that is around 820–850 °C [6, 7] and has an antiferromagnetic transition (T_N) around 370–380 °C [6, 8]. The leakage current represents the main problem for such material, this is due to its low resistivity which is reflected as its instability [9]. The co-existence of both vacancies and Fe²⁺ ions represents the main source of leakage current [10,11,12,13,14]. Several attempts were carried out to overcome such problems using doping techniques. This was done by substituting part of Bi⁺³ with dope ions at the side A of BiFeO₃ ceramic structure [15,16,17,18] or with substituting another type of dope ions (Nb⁺⁵, Mn⁺⁴, Ti⁺⁴ or Cr⁺³) at site B (Fe³⁺) [19,20,21]. The doping process leads to an improvement of ferroelectric properties and a reduction of the leakage current of BiFeO₃ ceramic to some extent.

As a photocatalytic material, BiFeO₃ had been examined in a visible region of light. Its photocatalytic degradation returns to its narrow optical band gap (~ 2.2 eV) and its chemical stability [22, 23].

In this work, we report the synthesis of BiFe_1−xNi_xO₃ ceramic with a composition of x = 0.7, 0.8 and 0.9 and study the influence of aliovalent ions of Ni²⁺ substitution, on structural, optical absorption, leakage current and dielectric behaviour of BiFe_1−xNi_xO₃ ceramic. The doping with Ni²⁺ may prevent the formation of Fe²⁺ and then reduce the oxygen vacancies which cause an improvement of the electrical properties of such multiferroic ceramic. The reduction of oxygen vacancies after the Ni²⁺ doping process which will prevent Fe²⁺ formation was expected.

Experimental

By using the solid-state reaction, BiFe_1−xNi_xO₃ (x = 0.7, 0.8 and 0.9) were synthesized from highly pure Bi₂O₃, (1 − x) Fe₂O₃ and 2xNiO powders. The weighed powders were milled mixed for half an hour at room temperature in air atmosphere. This milled powder was pressed into 16 mm diameter and 1 mm thickness discs under 1.5 Mpa pressure on a hydraulic press and then were rapidly heated to 750 °C and sintered for 30 min at atmospheric pressure. The calcined powder was milled again for half an hour. Then, they were pressed again into pellets of 16 mm diameter by applying a pressure of 1.5 Mpa. The pellets of the sample were found to be dark grey upon Ni substitution. For measurements of electrical properties, the ceramic pellets were coated on both surfaces with silver paint for good contacts.

The structure of the samples is characterized by X-ray diffractometer (X’Pert-Pro MPD, Philips) using CuKα radiation with λ = 1.541874 Å. The patterns were recorded in a 2θ interval of 20–60 with increments of 0.025 (2θ). The photo-absorption of BiFe_1−xNi_xO₃ was measured by UV-visible diffuse reflectance spectrophotometer ShimadzuUV-3600. The electric properties were measured using the semiconductor characterization system SCS4200 (Keithly). The electric data were carried out as a function of temperature and frequency during heating of the samples from room temperature up to 280 °C and frequency range from 5 kHz to 5 MHz.

Result and discussion

Structural

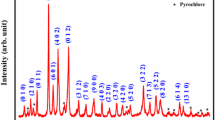
Figure 1a demonstrates XRD patterns of sintered BiFe_1−xNi_xO₃ ceramics, x = 0.7, 0.8 and 0.9. The patterns indicate that all samples have secondary phases (Bi₂FeO₉, Bi₂₅FeO₄₀, and NiFeO₄) in a perovskite structure. The secondary phase peaks Bi₂FeO₉ and Bi₂₅FeO₄₀ are usually observed in BiFeO₃ and its substituted samples because of the kinetic of their formation [24]. The new peak NiFe₂O₄ is observed corresponding to the phase associated with Ni ions which indicate that Ni ions are incorporated into the BiFeO₃ structure [25]. In addition, as a result of the highest Ni content in the samples, the reflection peaks of bismuth ferrite have disappeared which is in a good agreement with the previous results reported by Betancourt-Cantera et al. [25]. The lattice parameters are deduced from the XRD patterns at room temperature. The crystal structure of BiFeO₃ displays rhombohedral, while for high Ni²⁺ ions doping BiFe_1−xNi_xO₃ (x = 0.7, 0.8 and 0.9), the structure is found to be a triclinic unit cell (as reported before [26]). On the other hand, the data of cell parameters (Fig. 1b) were increased with the increasing of Ni²⁺ ion content because of the difference in ionic radius between the Ni²⁺ (ionic radius 0.69 Å) and the Fe³⁺ (0.64 Å).

Fig. 1

a The X-ray diffraction of BiFe_1−xNi_xO₃ samples. b Cell parameters as a function of x

Optical properties

The optical properties of BiFe_1−xNi_xO₃ samples with x = 0.7, 0.8 and 0.9 powder were investigated. Figure 2 illustrates the diffuse reflectance spectra (DRS) of BiFe_1−xNi_xO₃ samples in the wavelength range of 250 to 700 nm. Kubelka-Munk function [27, 28] is used to estimate the absorption coefficient from the DRS data. Kubelka-Munk function is defined as:

$$ F\left({R}_{\infty}\right)=\alpha /S={\left(1-{R}_{\infty}\right)}^2/2\ {R}_{\infty } $$

(1)

Fig. 2

The diffuse reflectance spectra of BiFe_1−xNi_xO₃ samples with different doping concentration

where R_∞ = R_sample/R_pref.

Here, “α is the absorption coefficient, S is the scattering coefficient and F(R_∞) is the KM function”. Near the absorption edge, the relation between photon energy (E = hν), absorption coefficient and band gap energy (E_g) for insulating substance is represented as:

$$ \upalpha\ E=K\ {\left(E-{E}_{\mathrm{g}}\right)}^n $$

(2)

K is a constant, and n is the exponent which depends on the type of transition [29].

The KM function can be used instead of the absorption coefficient a for the estimation of the optical energy gap (E_g) [21]. Figure 3 shows the method of calculating the optical gap in the case of a direct and an indirect transition of x = 0.9 sample as an example. It was noted that the calculation based on the direct transition shows more extended linear region as compared with the calculations based on indirect transition. For this reason, we consider the direct transition for all samples.

Fig. 3

Direct and indirect optical band gap for BiFe_1−xNi_xO₃ with x = 0.9

The direct band gap for BiFe_1−xNi_xO₃ can be predicted from the slope and intercept of the (αhν)² vs (hν) linear portion [30]. Figure 4 illustrates this relation for samples with different Ni content (x = 0.7, 0.8, 0.9). For samples with doping concentrations of x = 0.8 and 0.9, the band gaps were suddenly reduced to about 2.5 eV. Such a sudden decrease in optical band gap due to high doping concentration can be attributed to the Mott semiconductor-metal transition [31]. The value of the optical band gap energy of the samples with x = 0.8 and 0.9 is consistent with previous report [22, 32, 33]. However, the optical band gap exhibits an increase at x = 0.7 (E_g = 3.04 eV). This can be interpreted as the results of the molecular orbital rearrangements [34].

Fig. 4

(αhν)² versus hν (photon energy) plots of BiFe_1−xNi_xO₃ with different dopant concentrations

Electric properties

The leakage current represents one of the problems which hinder the ferroelectric and transport properties of multifarious ceramics. This leakage current is produced due to the existence of defects and nonstoichiometric in the bulk samples. The improvement of multiferroic properties requires a reduction of its leakage current. Hence, the study of the leakage current represents one of the important issues in this research. For this purpose, the J-E curve was measured for the present samples (BiFe_1−xNi_xO₃ ceramics) at room temperature. During the voltage change in positive and negative directions, the mean value of the leakage current (for five consecutive readings) was recorded automatically. We did not notice any significant differences between the two directions of applied voltage which supports our previous results [35]. As shown in Fig. 5a, the leakage current density of BiFe_1−xNi_xO₃ samples has a tendency to decrease with increasing of x (Ni contents), and the value is dramatically decreased when x = 0.9 (see Fig. 5b). This result shows a significant improvement in the properties of the prepared samples which represented as the lowering in the leakage current values with Ni co-doping content. As we know, the main source of the leakage current is the charge defects such as V³⁻_Bi (bismuth vacancies) and V_o²⁺ (oxygen vacancies). The oxygen vacancies are mostly generated from Bi volatility besides the changes from Fe³⁺ to Fe²⁺. The reduction in Fe³⁺ species to Fe²⁺ is possibly compensated by the substituted Ni²⁺ ion, and thus, it decreases the probability of oxygen vacancies formation, which may cause the initial reduction in leakage current as shown in the lattice parameters shown in Fig. 1.

Fig. 5

a Leakage current density as a function of applied electric field for BiFe_1−xNi_xO₃ ceramics. b Leakage current density as a function of x (Ni content). c The electrical hysteresis (I–V loop) for sample x = 0.9

The electrical hysteresis (IV loop) for sample x = 0.9 is represented in Fig. 5c. It is clearly noted that the area of the hysteresis decreases with decreasing Ni content, the symmetry of the curve behaviour (− 20 ➔ 0 ➔ + 20) increase with decreasing Ni content, and the shift between the two minima (m1 and m2 in Fig. 5c of the cycle becomes close to each other with decreasing Ni content. This behaviour can be attributed to the existence of trapping and detrapping process beside the cle bipolar resistive element which decreases the effect of the space charge carrier.

Figure 6 a and b represent the dependence of the real and imaginary dielectric constant ε′ and ε″ on frequency at room temperature. It is evident that for all samples, the ε′ and ε″ decrease with the increasing of frequency. In the starting low frequency range both ε′ and ε″ values decrease gradually as the frequency increases and then decrease slowly and become almost constant up to 1 MHz for all samples. These results can be attributed to the well-known dipole relaxation phenomena. At high electric field frequencies, the electric dipoles become enable to switch or rotate with the applied electric field frequency [36]. Furthermore, the real and imaginary parts of the dielectric constant are decreased as the concentration of Ni ions increases. The oxygen vacancies in BiFeO₃ materials, which are mostly generated during the heat treatment, are the major origin of the determination of the insulation and the formation of Fe, according to V_o^x + 2Fe³⁺ → V^t_o + 2Fe²⁺, where V^t_o is an oxygen vacancy and V_o^x is an oxygen position. Following Le Charelier principle, the concentration of Fe²⁺ would decrease if the content of Fe³⁺ is reduced. Therefore, doping at Fe site would suppress the formation of oxygen vacancies and reduce the concentration of Fe²⁺ [37].

Fig. 6

a Real (ε′) and b imaginary dielectric constants (ε″) as a function of frequency at room temperature for BiFe_1−xNi_xO₃ ceramics

The variation of the real and imaginary dielectric constants (ε′) and (ε″) of the BiFe_1−xNi_xO₃ (x = 0.7, 0.8 and 0.9) as a function of temperature measured at as elected frequencies is shown in Fig. 7. It shows a continuous increase with temperature up to the transition temperature T_c then it comes to be decreased. The exhibited anomaly has been detected in three samples around 260 °C, 255 °C and 240 °C. The existence of these anomalies in the temperature range 240–260 was reported previously by several authors [24, 38,39,40]. These anomalies seem to be related to magnetic transition (spin-glass-like behaviour) [41]. The position of the anomaly was shifted with doping of Ni in BiFeO3 towards to lower temperature side. The shift in the position of anomaly may be attributed to the increasing in the ionic radius of Ni²⁺ (0.69 Å) which is larger than Fe³⁺ (0.64 Å). These anomalies prove that the possibility of coupling between the electric and magnetic dipole moments of BiFe_1−xNi_xO₃, which attributed to the magneto-electric coupling.

Fig. 7

Real (ε′) and imaginary (ε″) dielectric constants as a function of temperature at selected frequencies for BiFe_1−xNi_xO₃ ceramics

Conclusion

The high nickel dopant induced changes in the structure, optical absorption and leakage current; the J-E hysteresis and dielectric properties of BiFe_1−xNi_xO₃ samples have been investigated. It is shown that the BiFe_1−xNi_xO3 crystallizes in the triclinic crystal structure. The cell parameters increase with increasing x doping, and optical band gaps decrease with increasing x. Leakage current were much reduced with Ni⁺² ion doping, it was decreased by about three orders of magnitude. The area of the hysteresis decreases with decreasing Ni doping. It is also found that the doping of Ni⁺² ions can effectively reduce the leakage current density and improve the ferroelectric properties. The dielectric constants ε′ and ε″ were found to be decreased with increased frequency. The real ε′ and imaginary ε″ dielectric constants were found to be increased with temperature. The temperature dependence of ε′ and ε″ exhibited an anomaly which shifted to lower temperature with increasing Ni⁺² ion doping. The anomaly indicates the possible existence of spin-glass states with Ni²⁺ ion substitution in the place of Fe³⁺ ions.