Modularity of Galois Representations and Langlands Functoriality

Abstract

This survey reports on some of the recent developments in the area of Galois representations and automorphic forms, with a particular focus on the author and Thorne’s work on symmetric power functoriality for modular forms.

1 Introduction

In this article, we survey some recent work on Langlands reciprocity and functoriality in which Galois representations play a central role. No attempt has been made to give a comprehensive, or historically minded account—for the recent history, Calegari’s survey²⁰ of modularity lifting theorems since the proof of Fermat’s last theorem is recommended.

The main goal of the final Sect. 5 of this article is to introduce the reader to some of the main ideas in the author’s work with Thorne on symmetric power functoriality^{73, 74}. For an alternative introduction to our work, see Thorne’s recent article⁹⁴.

Before we get there, in Sects. 2 and 3, we review the circle of ideas connecting Galois representations, automorphic forms and arithmetic geometry, and very briefly discuss recent developments in this area. In Sect. 4, we introduce modularity lifting theorems and the Taylor–Wiles method.

2 An Introduction to Galois Representations and Langlands Reciprocity

In this section, we introduce one of the main subjects of this article. We recommend Taylor’s article⁹⁰ to the reader for a more detailed survey on Galois representations and Emerton’s recent survey⁴³ for an introduction to Langlands reciprocity.

2.1 Notation and Preliminaries

We will be interested in continuous finite-dimensional representations of the profinite Galois group $G_{{{\mathbb {Q}}}} = {{\,\mathrm{Gal}\,}}({\overline{{{\mathbb {Q}}}}}/{{\mathbb {Q}}})$, where ${\overline{{{\mathbb {Q}}}}}$, the field of algebraic numbers, is the algebraic closure of the rational numbers.

For each prime p, we can embed ${\overline{{{\mathbb {Q}}}}}$ in the algebraic closure ${\overline{{{\mathbb {Q}}}}}_p$ of the field of p-adic numbers. Each choice of embedding identifies $G_{{{\mathbb {Q}}}_p} = {{\,\mathrm{Gal}\,}}({\overline{{{\mathbb {Q}}}}}_p/{{\mathbb {Q}}}_p)$ with a closed subgroup of $G_{{\mathbb {Q}}}$; for any two choices of embedding, we obtain conjugate subgroups.

There is a natural surjective homomorphism $G_{{{\mathbb {Q}}}_p} \rightarrow G_{{{\mathbb {F}}}_p}$ from $G_{{{\mathbb {Q}}}_p}$ to the absolute Galois group of the residue field ${{\mathbb {F}}}_p$. The kernel of this map is the inertia group $I_{{{\mathbb {Q}}}_p} \subset G_{{{\mathbb {Q}}}_p}$. The Galois group $G_{{{\mathbb {F}}}_p}$ is a free profinite group generated by the p-power map $\mathrm {Frob}_p(x) = x^p$.

If S is a finite set of primes, we can also consider the Galois group $G_{{{\mathbb {Q}}},S} = {{\,\mathrm{Gal}\,}}({{\mathbb {Q}}}^S/{{\mathbb {Q}}})$, where ${{\mathbb {Q}}}^S$ is the maximal subfield of ${\overline{{{\mathbb {Q}}}}}$ which is unramified at primes not in S. This means that the image in $G_{{{\mathbb {Q}}},S}$ of an inertia group $I_{{{\mathbb {Q}}}_p}$ is trivial when $p \notin S$ and we have an element $\mathrm {Frob}_p \in G_{{{\mathbb {Q}}},S}$. This element depends on the choice of embedding ${\overline{{{\mathbb {Q}}}}}\hookrightarrow {\overline{{{\mathbb {Q}}}}}_p$, but its conjugacy class is independent of this choice. It is a consequence of the Chebotarev density theorem that the union¹ of these Frobenius conjugacy classes is dense in $G_{{{\mathbb {Q}}},S}$ (for the profinite topology).

All of this generalizes in a straightforward way to Galois groups of number fields, or other global fields.

We can now say that a linear representation $(\rho , V)$² of $G_{{{\mathbb {Q}}}}$ is unramified at a prime p if the inertia subgroup $I_{{{\mathbb {Q}}}_p}$ acts trivially on V. Note that this notion depends only on p, not on the choice of embedding ${\overline{{{\mathbb {Q}}}}}\hookrightarrow {\overline{{{\mathbb {Q}}}}}_p$. We say $\rho$ is almost everywhere unramified if there is a finite set of primes S such that $\rho$ is unramified at all primes $p \notin S$. Equivalently, $\rho$ can be identified with a representation of $G_{{{\mathbb {Q}}},S}$.

When $\rho$ is unramified at p, we have a well-defined conjugacy class of endomorphisms $\rho (\mathrm {Frob}_p)$ and a polynomial $P_{\rho ,p}(t):= \det (1- t\rho (\mathrm {Frob}_p) | V)$ associated with it³. If $\rho$ is continuous and almost everywhere unramified, these characteristic polynomials determine the semisimplification of $\rho$ (by the Brauer–Nesbitt theorem and density of the Frobenius conjugacy classes).

At this point, we should say something about the fields over which our representations are defined. The most classical kind of Galois representation are Artin representations. These are continuous representations of $G_{{{\mathbb {Q}}}}$ on complex vector spaces. The matrix groups ${{\,\mathrm{GL}\,}}_n({{\mathbb {C}}})$ have ‘no small subgroups’. More precisely, there is an open neighborhood of the identity in ${{\,\mathrm{GL}\,}}_n({{\mathbb {C}}})$ which contains no non-trivial subgroup (this can be seen using the exponential map from the Lie algebra, for example). On the other hand, the identity has a neighborhood basis of open subgroups in the profinite topology on $G_{{{\mathbb {Q}}}}$. This means that an Artin representation necessarily has finite image and factors through the quotient $G_{{{\mathbb {Q}}}} \rightarrow {{\,\mathrm{Gal}\,}}(F/{{\mathbb {Q}}})$ for a finite Galois extension $F/{{\mathbb {Q}}}$.

A richer theory is obtained by considering p-adic Galois representations for a prime p. These are continuous representations of $G_{{{\mathbb {Q}}}}$ on vector spaces over the p-adic numbers ${{\mathbb {Q}}}_p$ (or an extension field $K/{{\mathbb {Q}}}_p$). Note that the p-adic matrix group ${{\,\mathrm{GL}\,}}_n({{\mathbb {Q}}}_p)$ is locally profinite (an open, profinite, subgroup is given by ${{\,\mathrm{GL}\,}}_n({{\mathbb {Z}}}_p)$), so unlike the case of Artin representations the image of a p-adic Galois representation can (and usually will) be infinite.

Here are some examples of Galois representations arising ‘in nature’:

• (1) Finite order characters By the Kronecker–Weber theorem, for any continuous finite order character $\chi : G_{{\mathbb {Q}}}\rightarrow {{\mathbb {C}}}^\times$ there is a positive integer N and a Dirichlet character ${\tilde{\chi }}: ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^\times \rightarrow {{\mathbb {C}}}^\times$ such that $\chi$ is given by composing ${\tilde{\chi }}$ with the map $G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{Gal}\,}}({{\mathbb {Q}}}(\zeta _N)/{{\mathbb {Q}}}) \cong ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^\times$ ($\zeta _N \in {\overline{{{\mathbb {Q}}}}}$ is a primitive N^th root of unity). These give all the continuous representations of $G_{{\mathbb {Q}}}$ on a one-dimensional complex vector space.

• (2) The p-adic cyclotomic character For any prime power $p^r$, we have a homomorphism $G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{Gal}\,}}({{\mathbb {Q}}}(\zeta _{p^r})/{{\mathbb {Q}}}) \cong ({{\mathbb {Z}}}/p^r{{\mathbb {Z}}})^\times$. Taking the limit over r gives a continuous homomorphism $\chi _p: G_{{\mathbb {Q}}}\rightarrow {{\mathbb {Z}}}_p^\times$, the p-adic cyclotomic character. It is characterized by the property that $\sigma (\zeta ) = \zeta ^{\chi _p(\sigma )}$ for any p-power root of unity $\zeta \in {\overline{{{\mathbb {Q}}}}}$. This gives a one-dimensional p-adic representation of $G_{{\mathbb {Q}}}$.

• (3) Tate modules of abelian varieties For an abelian variety $A/{{\mathbb {Q}}}$ of dimension g and a prime p, the Tate module $T_p(A) := \varprojlim _r A({\overline{{{\mathbb {Q}}}}})[p^r]$ defined using the p-power division points is a free rank 2g ${{\mathbb {Z}}}_p$-module with a continuous action of $G_{{\mathbb {Q}}}$. This gives us a 2g-dimensional p-adic Galois representation.

• (4) Cohomology of algebraic varieties If X is an algebraic variety defined over ${{\mathbb {Q}}}$, its p-adic étale cohomology groups $H^i(X_{{\overline{{{\mathbb {Q}}}}}},{{\mathbb {Q}}}_p)$ are p-adic Galois representations.

• (5) Automorphic Galois representations We will return to this example later!

We can apply all the standard representation-theoretic constructions to obtain more Galois representations: for example, tensor products of representations, duals, alternating or symmetric powers.

2.2 p-adic and Mod p Galois Representations

It is often very useful to consider the residual representation of a p-adic Galois representation. Suppose we start with a continuous representation

$$\begin{aligned} \rho : G_{{{\mathbb {Q}}}} \rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Q}}}}}_p). \end{aligned}$$

It is convenient to work with representations valued in ${\overline{{{\mathbb {Q}}}}}_p$, to avoid keeping track of coefficient fields. However, one thing which is good to know is that the image of $\rho$ is necessarily contained in ${{\,\mathrm{GL}\,}}_n(E)$ for $E/{{\mathbb {Q}}}_p$ a finite extension (see^{31, 86} for two different proofs). The compactness of $G_{{{\mathbb {Q}}}}$ implies that it moreover stabilizes an ${{\mathcal {O}}}_E$-lattice in $E^n$. So, a conjugate of $\rho$ has image contained in ${{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Z}}}}}_p)$, and we can reduce this conjugate mod ${\mathfrak {m}}_{{\overline{{{\mathbb {Z}}}}}_p}$ to give the residual representation

$$\begin{aligned}{\overline{\rho }}: G_{{{\mathbb {Q}}}} \rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {F}}}}}_p),\end{aligned}$$

whose isomorphism class is well defined up to semi-simplification (another application of the Brauer–Nesbitt theorem).

2.3 Compatible Systems

The examples of p-adic Galois representations introduced in the last section all naturally live in a family of representations, one for each prime p. To make this a bit more precise, we introduce a notion due to Taniyama⁸⁸ and Serre⁸⁴.⁴ Suppose E is a number field and we have a collection of continuous representations $(\rho _\lambda )_\lambda$ of $G_{{\mathbb {Q}}}$ on $E_\lambda$-vector spaces, one for each finite place $\lambda$ of E. We will write l for the residue characteristic of $\lambda$.

We say that $(\rho _\lambda )_\lambda$ is a compatible system (with coefficients in E) if there is a finite set S of primes such that:

• (1) For every $p \notin S\cup \{l\}$, $\rho _\lambda$ is unramified at p and the polynomial $P_{\rho _\lambda ,p}(t) \in E_\lambda [t]$ in fact has coefficients in E.

• (2) Moreover, for any two finite places $\lambda , \lambda '$ of E, we have $P_{\rho _\lambda ,p}(t) = P_{\rho _{\lambda '},p}(t)$ for all $p \notin S\cup \{l,l'\}$.

We say that a compatible system is irreducible if each $\rho _\lambda$ is absolutely irreducible (i.e., remains irreducible after extending coefficients to the algebraic closure ${\overline{E}}_\lambda$).

Note that the second condition implies that the dimension of a representation $\rho _\lambda$ in the compatible system is independent of $\lambda$.

The examples of Galois representations we listed above all give rise to compatible systems with coefficients in ${{\mathbb {Q}}}$, with the proviso that we assume the algebraic variety X in example (4) is proper and smooth.⁵

We might ask if all (irreducible) compatible systems are of geometric origin; to make this notion precise, we can say that a compatible system $(\rho _\lambda )$ is of geometric origin if each $\rho _\lambda$ appears as a subquotient of

$$\begin{aligned}H^i(X,r)_l:=H^i(X_{{\overline{{{\mathbb {Q}}}}}},E_{\lambda })\otimes {{\mathbb {Q}}}_{\ell }(\chi _l^r)\end{aligned}$$

for a proper smooth variety $X/{{\mathbb {Q}}}$, a cohomological degree i, and an integer r, all independent of $\lambda$. Assuming the Tate conjecture (in the form of Conjecture 1.2 in Taylor’s article⁹⁰) this is equivalent to the existence of a subspace W of the singular cohomology group $H^i(X({{\mathbb {C}}}),E)$ such that, having chosen an embedding⁶${\overline{{{\mathbb {Q}}}}}\subset {{\mathbb {C}}}$, for every $\lambda$, the $E_\lambda$-subspace

$$\begin{aligned} W\otimes _E E_\lambda \subset H^i(X({{\mathbb {C}}}),E_\lambda ) \cong H^i(X_{{\overline{{{\mathbb {Q}}}}}},E_{\lambda }) \end{aligned}$$

is $G_{{{\mathbb {Q}}}}$-stable and isomorphic to $\rho _\lambda \chi _l^{-r}$ as a representation of $G_{{{\mathbb {Q}}}}$.

Serre proved⁸⁴ that irreducible compatible systems are indeed of geometric origin when the representations in the compatible system factor through the abelianization of $G_{{\mathbb {Q}}}$. This result does not actually have much to do with compatible systems, it applies to a single $\rho _\lambda$ satisfying the rationality condition (1) above and relies on a result in transcendence theory due to Lang.⁷

2.4 Geometric Galois Representations

Compatible systems of geometric origin satisfy an additional subtle property: for each $\lambda$, the l-adic representation $\rho _\lambda |_{G_{{{\mathbb {Q}}}_{\ell }}}$ is de Rham in the sense of Fontaine. This reflects the remarkable fact that the Hodge filtration on algebraic de Rham cohomology of a proper smooth variety $X/{{\mathbb {Q}}}_{\ell }$ can be naturally recovered from the Galois action on the l-adic étale cohomology using the de Rham comparison theorem⁴⁴.

Following Fontaine and Mazur⁴⁵, we will say that a p-adic representation $\rho$ of $G_{{\mathbb {Q}}}$ is geometric if it is ramified at only finitely many primes and its restriction to $G_{{{\mathbb {Q}}}_p}$ is de Rham.⁸ We will usually denote the set of primes at which $\rho$ is ramified by S. Similarly to the case of compatible systems, we say that $\rho$ is of geometric origin if it appears as a subquotient of

$$\begin{aligned} H^i(X_{{\overline{{{\mathbb {Q}}}}}},{\overline{{{\mathbb {Q}}}}}_p)\otimes {{\mathbb {Q}}}_p(\chi _p^r) \end{aligned}$$

for a proper smooth variety $X/{{\mathbb {Q}}}$, a cohomological degree i, and an integer r.

Conjecture 2.4.1

(Fontaine–Mazur) Suppose $\rho : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Q}}}}}_p)$ is an irreducible geometric Galois representation. Then $\rho$ is of geometric origin.

In combination with the Tate conjecture, this also predicts that geometric Galois representations should lie in compatible systems.

Remark 2.4.2

Naturally, one might first consider the case $n = 1$. In this case, it follows from a theorem of Tate (as explained in⁸⁴, Ch. III]) that geometric Galois representations are locally algebraic. For representations of $G_{{{\mathbb {Q}}}}$ this simply means that the composition of $\rho$ with the Artin reciprocity map ${{\mathbb {Q}}}_p^\times \rightarrow G_{{{\mathbb {Q}}}_p}^{\mathrm {ab}}$ is given by $x \mapsto x^{r}$ for $r \in {{\mathbb {Z}}}$ and x in a sufficiently small open neighborhood of $1 \in {{\mathbb {Q}}}_p^\times$. Equivalently, $\chi _{p}^{-r}\rho$ is potentially unramified at p, which means that there is a finite extension $F/{{\mathbb {Q}}}$ such that $\chi _{p}^{-r}\rho |_{G_F}$ is unramified at every place of F dividing p. Finiteness of the class group now implies that $\rho$ is the product of $\chi _p^r$ and a finite order character. This gives the Fontaine–Mazur conjecture in this case, since finite order characters can be found in the cohomology of 0-dimensional varieties. The same strategy extends to one-dimensional p-adic representations of $G_F$ for number fields F, see⁷⁹, Theorem 2.3.13 for details. We note that the transcendence results used by Serre to show that rational representations are of geometric origin are not required here.

We say more about progress on this conjecture in dimension 2 in Sect. 3.3.

2.5 Langlands Reciprocity and the Fontaine–Mazur Conjecture

To continue the story, we need to say something about automorphic representations and their connection with Galois representations. Automorphic representations (for the algebraic group ${{\,\mathrm{GL}\,}}_n/{{\mathbb {Q}}}$) are representations of the adelic group ${{\,\mathrm{GL}\,}}_n({{\mathbb {A}}})$, where ${{\mathbb {A}}}$ is the ring of adèles ${{\mathbb {R}}}\times ({\widehat{{{\mathbb {Z}}}}}\otimes {{\mathbb {Q}}})$. Rather than explaining the definition of a cuspidal automorphic representation of ${{\,\mathrm{GL}\,}}_n({{\mathbb {A}}})$, we refer to⁹⁰, §3 for this, and restrict ourselves to mentioning some important features of a cuspidal automorphic representation $\pi$ which will play a role later in this survey:

• $\pi$ is determined by a collection of local factors $\pi _\infty$, $\pi _p$ (one for each prime p). The latter are irreducible smooth⁹ representations of ${{\,\mathrm{GL}\,}}_n({{\mathbb {Q}}}_p)$ on complex vector spaces.

• For all but finitely many p, the representation $\pi _p$ is unramified, i.e., it has a non-zero space of invariants under ${{\,\mathrm{GL}\,}}_n({{\mathbb {Z}}}_p)$. Unramified representations $\pi _p$ of ${{\,\mathrm{GL}\,}}_n({{\mathbb {Q}}}_p)$ are classified by semisimple conjugacy classes $c(\pi _p)$ in ${{\,\mathrm{GL}\,}}_n({{\mathbb {C}}})$ (Satake parameters).¹⁰ Such a conjugacy class is determined by the inverse characteristic polynomial: $P_{\pi ,p}(t) = \det (1-t c(\pi _p))$.

  When $c(\pi _p) = [\mathrm {diag}(\alpha _1,\alpha _2,\ldots ,\alpha _n)]$, we define a local L-factor: $L(\pi _p,t) = \prod _{i=1}^n(1-\alpha _it)^{-1} = P_{\pi ,p}(t)^{-1}$.

  Just as a Galois representation is determined by the characteristic polynomials of Frobenius elements at unramified primes, a cuspidal automorphic representation $\pi$ is determined by the polynomials $P_{\pi ,p}(t)$ (or equivalently, by the Satake parameters $c(\pi _p)$). This follows from the strong multiplicity one theorem of Piatetski-Shapiro, Jacquet and Shalika⁵⁶.

• $\pi$ has an L-function, a holomorphic function in a complex variable s defined for $Re(s) \gg 0$ by $L(\pi ,s) = \prod _p L(\pi _p,p^{-s})$. We have only defined the local L-factors at primes p where $\pi$ is unramified, but the definition can be extended to cover all primes.

• $L(\pi ,s)$ has an analytic continuation to an entire holomorphic function on ${{\mathbb {C}}}$, except if $n = 1$, when possibly it may have a simple pole.¹¹

A cuspidal Hecke eigenform f of weight k, level N and character $\epsilon : ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^\times \rightarrow {{\mathbb {C}}}^\times$ has an associated automorphic representation $\pi (f)$ of ${{\,\mathrm{GL}\,}}_2({{\mathbb {A}}})$.¹² For $p\nmid N$, the Satake parameter of $\pi (f)_p$ is given by $[\mathrm {diag}(\alpha _p/\sqrt{p},\beta _p/\sqrt{p})]$ where $\alpha _p, \beta _p$ are the roots of the polynomial $X^2-a_p(f)X+\epsilon (p)p^{k-1}$.

The connection with Galois representations is that an automorphic representation $\pi$ satisfying a certain algebraicity condition (defined by Clozel²⁸) is predicted to have an associated compatible system of geometric Galois representations. Particular examples of algebraic automorphic representations are given by the $\pi (f)$ coming from Hecke eigenforms. As we can already see in this special case, we need to do some kind of renormalization if we want the field of definition of the Satake parameters to reflect the rationality properties of $\pi$.¹³ So, our Galois representations will be directly related to the Satake parameters of the twisted automorphic representation $\pi ':=\pi |\det (\cdot )|^{\frac{1-n}{2}}$.

More precisely, the prediction is that there is a number field $E_\pi \subset {{\mathbb {C}}}$ containing the coefficients of the polynomials $P_{\pi ',p}(t)$ for all unramified p and a compatible system of semisimple Galois representations $(\rho _{\pi ,\lambda })$ with coefficients in $E_\pi$ such that

$$\begin{aligned} P_{\rho _{\pi , \lambda },p}(t) = P_{\pi ',p}(t) \end{aligned}$$

for all $\lambda$ and $p \notin S \cup \{l\}$.¹⁴

If a compatible system of Galois representations matches up with a cuspidal automorphic representation in this way, we will say that the compatible system is automorphic.

Thinking about individual Galois representations rather than compatible systems, for any choice of isomorphism $\iota : {\overline{{{\mathbb {Q}}}}}_p\cong {{\mathbb {C}}}$ we expect the existence of a geometric Galois representation $\rho _{\pi ,\iota }$ such that the polynomials $\iota P_{\rho _{\pi ,\iota },l}(t)$ match with the Satake polynomials $P_{\pi ',l}(t)$. If a p-adic Galois representation $\rho$ is isomorphic to $\rho _{\pi ,\iota }$ for some $\pi$ and $\iota$, we say that $\rho$ is automorphic.¹⁵ We can also associate an L-function to a geometric Galois representation and a choice of $\iota$. If $\rho$ is unramified outside S, we have

$$\begin{aligned} L(\rho ,s) = L_S(\rho ,s)\prod _{l \notin S\cup \{p\}} \iota P_{\rho ,l}(l^{-s})^{-1}, \end{aligned}$$

where the factor $L_{S}(\rho ,s)$ at the ramified primes is defined in⁹⁰, §2. When $\rho \cong \rho _{\pi ,\iota }$ is automorphic, we have $L(\rho ,s) = L(\pi ^\prime ,s)$.

Langlands’s reciprocity conjecture predicts that Galois representations of geometric origin are in fact automorphic (this prediction is also made precise in²⁸). Combining this with the Fontaine–Mazur conjecture, we obtain:

Conjecture 2.5.1

(Fontaine–Mazur–Langlands) Suppose $\rho : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Q}}}}}_p)$ is an irreducible geometric Galois representation. Then $\rho$ is automorphic.

In particular, the L-function $L(\rho ,s)$ has analytic continuation to the whole complex plane (when $n > 1$) and a functional equation.

2.6 Potential Automorphy and the Sato–Tate Conjecture

Langlands reciprocity is closely intertwined with Langlands functoriality—the transfer of automorphic representations from one group to another (along a homomorphism of Langlands dual groups). A particular example we will be discussing in this survey is symmetric power functoriality. For $n \ge 1$, the nth symmetric power of the standard representation of ${{\,\mathrm{GL}\,}}_2$ (and a choice of basis) gives a homomorphism

$$\begin{aligned} {{\,\mathrm{Sym}\,}}^n: {{\,\mathrm{GL}\,}}_2({\overline{{{\mathbb {Q}}}}}_p) \rightarrow {{\,\mathrm{GL}\,}}_{n+1}({\overline{{{\mathbb {Q}}}}}_p). \end{aligned}$$

Suppose we start with a cuspidal Hecke eigenform f. We have an associated two-dimensional geometric Galois representation¹⁶$\rho _{f,\iota } = \rho _{\pi (f),\iota }$ and composing with the symmetric power map, we get a geometric Galois representation ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ with dimension $n+1$.

When the eigenform f has weight at least 2 and is not a CM form,¹⁷ it follows from a result of Ribet⁸¹ that the representations ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ are irreducible for all n. Indeed, Ribet shows that under this assumption $\rho _{f,\iota }$ is irreducible on restriction to any open subgroup of $G_{{{\mathbb {Q}}}}$. It follows from the classification of algebraic subgroups of ${{\,\mathrm{GL}\,}}_2$ that the largest closed algebraic subgroup of ${{\,\mathrm{GL}\,}}_2/{\overline{{{\mathbb {Q}}}}}_p$ containing the image $\rho _{f,\iota }(G_{{{\mathbb {Q}}}})$ is ${{\,\mathrm{GL}\,}}_2$, and the irreducibility of ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is now a consequence of the irreducibility of ${{\,\mathrm{Sym}\,}}^n$ as an algebraic representation of ${{\,\mathrm{GL}\,}}_2$.

The Fontaine–Mazur–Langlands conjecture then predicts that the symmetric power representations are automorphic:

Conjecture 2.6.1

(Symmetric power functoriality) The Galois representation ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is automorphic for every $n \ge 1$.

In other words, for each n there should be a cuspidal automorphic representation $\pi$ of ${{\,\mathrm{GL}\,}}_{n+1}({{\mathbb {A}}})$ with $\rho _{\pi ,\iota } \cong {{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$. If the conjecture is proved for one choice of p and $\iota$, then it holds for all choices of p and $\iota$, since the compatible system of Galois representations associated with $\pi$ matches the compatible system coming from the symmetric powers.

The existence of the symmetric power lifting $\pi$ was proved for $n = 2$ by Gelbart and Jacquet⁴⁷, and for $n \le 4$ by Kim and Shahidi^{59, 65}. These results are proved using converse theorems and apply much more generally: they construct symmetric power liftings for cuspidal automorphic representations of ${{\,\mathrm{GL}\,}}_2({{\mathbb {A}}}_F)$ for arbitrary number fields F, without any algebraicity condition.¹⁸

Langlands’s seminal article⁶⁹ describes (in a more general context) how symmetric power functoriality can be used to deduce the Ramanujan–Petersson conjecture, which predicts that the roots $\alpha _p,\beta _p$ of the polynomial $X^2-a_p(f)+\epsilon (p)p^{k-1}$ have complex absolute values $p^{(k-1)/2}$. This was, of course, proved by Deligne as a consequence of the Riemann hypothesis over finite fields (with an idea inspired by Langlands’s method). Moreover, it is explained in Serre’s book⁸⁴ (cf. the Appendix to Chapter 1) that symmetric power functoriality can also be used to prove an equidistribution result for the Satake parameters $(\alpha _p,\beta _p)$, the Sato–Tate conjecture.

The Sato–Tate conjecture (for modular forms) was proved by Barnet-Lamb, Geraghty, Harris and Taylor¹³ (see also^{11, 26, 54, 91}), by proving something a little weaker than the symmetric power functoriality conjecture—potential automorphy of symmetric powers:

Theorem 2.6.2

¹³ For each $n \ge 1$, there is a Galois totally real number field $F/{{\mathbb {Q}}}$ and a cuspidal automorphic representation $\pi _F$ of ${{\,\mathrm{GL}\,}}_{n+1}({{\mathbb {A}}}_F)$ such that ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }|_{G_F} \cong \rho _{\pi _F,\iota }$ is automorphic.

The proof of this theorem involved significant developments in modularity lifting theorems, in the construction of automorphic Galois representations, and in the trace formula (including Laumon and Ngô’s work on the fundamental lemma)—we discuss the first two topics in a little more detail over the next few pages, but we refer the reader to Harris’s much more extensive survey⁵¹ of what goes into the proof of Theorem 2.6.2. The latter part of the present article will review part of the author’s proof with Thorne of Conjecture 2.6.1.

More recent developments in modularity lifting theorems²³ and the construction of automorphic Galois representations^{53, 82} have broadened the scope of the methods used to prove potential automorphy results. Using a crucial geometric breakthrough of Caraiani and Scholze³², it has been possible to establish potential automorphy of symmetric powers of certain two-dimensional representations of $G_F$ when F is a CM number field¹⁹¹. This gives a proof of the Sato–Tate conjecture for elliptic curves over CM fields. In this work, we also use Langlands’s method directly to prove the Ramanujan–Petersson conjecture for certain automorphic representations of ${{\,\mathrm{GL}\,}}_2({{\mathbb {A}}}_F)$ (again for a CM field F).

Another recent breakthrough, again using the work of Calegari and Geraghty²³, is the proof of the potential automorphy of the p-adic Galois representations given by the p-adic Tate modules of Abelian surfaces over totally real fields⁷.

3 Automorphic Galois Representations

We now say a little more about the construction of compatible systems of Galois representations associated with algebraic automorphic representations. We understand best the case of regular algebraic cuspidal automorphic representations. These are automorphic representations which contribute to the cohomology of arithmetic groups, or equivalently to the cohomology of arithmetic locally symmetric spaces which are quotients of contractible symmetric spaces by arithmetic groups.

What this means in practice is that for a regular algebraic cuspidal automorphic representation $\pi$ of ${{\,\mathrm{GL}\,}}_n({{\mathbb {A}}})$, we have the following objects which capture the Satake parameters of $\pi$:

• A locally symmetric space Y, a real manifold which is a disjoint union of quotients

  $$\begin{aligned}Y_\Gamma = \Gamma \backslash \left( {{\,\mathrm{SL}\,}}_n({{\mathbb {R}}})/{{\,\mathrm{SO}\,}}(n)\right) \end{aligned}$$

  for finite index subgroups $\Gamma$ of ${{\,\mathrm{SL}\,}}_n({{\mathbb {Z}}})$.

• A local system of abelian groups ${{\mathcal {V}}}$ on Y determined by an algebraic representation of ${{\,\mathrm{SL}\,}}_n({{\mathbb {Q}}})$ (for the trivial representation, we get the trivial coefficient system ${\underline{{{\mathbb {Z}}}}}$).

• A commutative ring ${{\mathbb {T}}}$ of endomorphisms of the finitely generated abelian group $H^*(Y,{{\mathcal {V}}}):=\oplus _i H^i(Y,{{\mathcal {V}}})$ (the ring of Hecke operators).

• Explicit polynomials $P_{{{\mathbb {T}}},l}(t) \in {{\mathbb {T}}}[t]$ for the primes l where $\pi$ is unramified.²⁰

• A ${{\mathbb {T}}}$-stable direct summand $H^*(Y,{{\mathcal {V}}})[\pi ] \subset H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {C}}}$ on which there is an identity $P_{{{\mathbb {T}}},l}(t) = P_{\pi ',l}(t)$ for all primes l where $\pi$ is unramified.

We can rephrase the final point as saying that the coefficients of the $P_{\pi ',l}(t)$ appear as eigenvalues of Hecke operators. A nice algebraicity result follows immediately; there is a number field $E_\pi$ which contains the coefficients of $P_{\pi ',l}(t)$ for all unramified l. Indeed, these coefficients are eigenvalues of a commuting family of operators on $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {C}}}$ which preserve the rational structure $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {Q}}}$.

When $n = 2$, the situation is quite classical. The locally symmetric spaces Y are modular curves, and Eichler and Shimura explained the relationship between the cohomology of these curves and modular forms of weight at least 2. This amounts to computing the cohomology groups $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {C}}}$ in terms of differentials on Y. Moreover, the action of ${{\,\mathrm{SL}\,}}_2({{\mathbb {R}}})$ on ${{\mathbb {P}}}^1({{\mathbb {C}}})$ by Möbius transformations identifies ${{\,\mathrm{SL}\,}}_2({{\mathbb {R}}})/SO(2)$ with the complex upper half-plane. The manifolds Y can therefore be equipped with a complex structure and moreover they can naturally be viewed as the set of complex points of an algebraic curve defined over ${{\mathbb {Q}}}$. This means that the construction of Galois representations can be done using the machinery of étale cohomology³⁷. If we fix $\iota : {\overline{{{\mathbb {Q}}}}}_p\cong {{\mathbb {C}}}$, then we have an isomorphism $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {C}}}\xrightarrow {\mathrm {id}\otimes \iota ^{-1}} H^*(Y,{{\mathcal {V}}})\otimes {\overline{{{\mathbb {Q}}}}}_p$ and the right hand side is equipped with a continuous action of $G_{{\mathbb {Q}}}$. The subspace $H^*(Y,{{\mathcal {V}}})[\pi ]$ is stable under the Galois action and this is the Galois representation $\rho _{\pi ,\iota }$.²¹

When $n > 2$, the construction of Galois representations is much more difficult, since the symmetric spaces have no natural complex structure. When $\pi$ is essentially self-dual²² it is possible, with a lot of work, to transfer the problem to automorphic representations of a unitary group. In this setting, there are complex structures and algebraic models (Shimura varieties) for the relevant locally symmetric spaces. This leads to the construction of Galois representations in the essentially self-dual case (which is due to many people, beginning with Clozel and Kottwitz, cf. Shin’s survey paper⁸⁵).

More recently, amazing progress was made on the construction of Galois representations in the general regular algebraic case. Harris, Lan, Taylor and Thorne⁵³ constructed these representations—in fact, their work extends to the case of automorphic representations of ${{\,\mathrm{GL}\,}}_n({{\mathbb {A}}}_F)$ for any totally real or CM field F. Scholze gave a different, but related, construction⁸² which goes further; if $H^*(Y,{{\mathcal {V}}})\otimes {\overline{{{\mathbb {F}}}}}_p$ contains a non-zero simultaneous eigenvector for all the Hecke operators, with eigenvalues given by a homomorphism $\theta : {{\mathbb {T}}}\rightarrow {\overline{{{\mathbb {F}}}}}_p$, then he constructs a continuous semisimple representation

$$\begin{aligned}\rho _\theta : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {F}}}}}_p)\end{aligned}$$

with the characteristic polynomial of Frobenius $\det (1 - t\rho _\theta (\mathrm {Frob}_l))$ given by applying $\theta$ to the polynomial $P_{{{\mathbb {T}}},l}(t) \in {{\mathbb {T}}}[t]$ for each prime l. The existence of such Galois representations had been conjectured by Ash⁴, and forms an essential input to Calegari and Geraghty’s extension of the Taylor–Wiles method²³. The existence of the Galois representations $\rho _{\theta }$ cannot be deduced directly from the construction of (characteristic 0) automorphic Galois representations, since in general the cohomology groups $H^*(Y,{{\mathcal {V}}})$ contain torsion elements whose Hecke eigenvalues are not the ‘reduction mod p’ of systems of Hecke eigenvalues in $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {C}}}$.

When $\pi$ is not essentially self-dual, the strategy to construct the representation $\rho _{\pi ,\iota }$ is to first construct the essentially self-dual representation $\rho _{\pi ,\iota }\oplus {\mathbf {1}} \oplus \rho _{\pi ,\iota }^\vee$ as a p-adic limit of Galois representations $\rho _{\Pi ,\iota }$ with $\Pi$ an automorphic representation of ${{\,\mathrm{GL}\,}}_{2n+1}({{\mathbb {A}}})$. The summand $\rho _{\pi ,\iota }$ can then be extracted from this larger representation. One point worth noting is that the representations $\rho _{\Pi ,\iota }$ can often be found in the étale cohomology of Shimura varieties, but the representation $\rho _{\pi ,\iota }$ cannot (except in certain degenerate situations)—this was observed by Clozel and Harris, and is expanded on in work of Johansson and Thorne⁵⁷.

The representations $\rho _{\pi ,\iota }$ are expected to be geometric. This has been verified in many cases¹. Work in progress of the author and Caraiani extends these methods to cover more cases, and there is also unpublished work of Varma using the construction of Harris, Lan, Taylor and Thorne⁵³. This gives us many geometric Galois representations which are known to be automorphic, but we seem very far from showing that they are of geometric origin—once we have left the world of Shimura varieties we have no systematic supply of algebraic varieties whose cohomology can be directly related to automorphic representations. At this point it seems fair to say that the evidence for the Fontaine–Mazur–Langlands conjecture is stronger than the evidence for the Fontaine–Mazur conjecture.

3.1 Reciprocity for More General p-adic Galois Representations?

One feature which makes the world of geometric Galois representations more flexible than the world of algebraic varieties and their cohomology is that, for a chosen prime p, we can consider geometric Galois representations inside the larger ambient category of p-adic Galois representations (we will always assume that our representations are unramified at almost all primes). A question which lies at the heart of the p-adic Langlands programme is to describe a comparable larger category of p-adic automorphic representations which contains the algebraic automorphic representations.

There is not yet a satisfactory definition of a p-adic automorphic representation, but there is a natural way to enlarge the p-adic part $H^*(Y,{{\mathcal {V}}})\otimes {{\mathbb {Z}}}_p$ of the cohomology groups which we considered above; this is Emerton’s theory of completed cohomology.

The interested reader will find an excellent introduction to this topic in Emerton’s ICM proceedings article⁴². We will be very brief here. The definition involves a tower $Y_{r+1} \rightarrow Y_r \rightarrow Y_{r-1}$ of locally symmetric spaces whose limit $Y_\infty = \varprojlim _r Y_r$ has an action of ${{\,\mathrm{GL}\,}}_n({{\mathbb {Q}}}_p)$ and is a ${{\,\mathrm{GL}\,}}_n({{\mathbb {Z}}}_p)$-torsor over the base locally symmetric space $Y = Y_0$. The mod $p^m$ coefficient systems ${{\mathcal {V}}}\otimes {{\mathbb {Z}}}/p^m{{\mathbb {Z}}}$ become trivial at some level in the tower, so for each m the group

$$\begin{aligned}{\widetilde{H}}^i(Y_\infty ,{{\mathbb {Z}}}/p^m{{\mathbb {Z}}}) = \varinjlim _r H^i(Y_r, {{\mathbb {Z}}}/p^m{{\mathbb {Z}}}) \end{aligned}$$

is a smooth representation of ${{\,\mathrm{GL}\,}}_n({{\mathbb {Q}}}_p)$ which interpolates the finite cohomology groups with varying coefficient systems.

Finally, the completed cohomology groups are defined by taking an inverse limit:

$$\begin{aligned} {\widetilde{H}}^i(Y_\infty ,{{\mathbb {Z}}}_p) = \varprojlim _m {\widetilde{H}}^i(Y_\infty ,{{\mathbb {Z}}}/p^m{{\mathbb {Z}}}). \end{aligned}$$

All these cohomology groups get a natural action of the ring of Hecke operators ${{\mathbb {T}}}$. It was proved by Scholze that the mod p or p-adic systems of Hecke eigenvalues $\theta : {{\mathbb {T}}}\rightarrow {\overline{{{\mathbb {F}}}}}_p$ or $\theta : {{\mathbb {T}}}\rightarrow {\overline{{{\mathbb {Q}}}}}_p$ appearing in completed cohomology have associated mod p or p-adic Galois representations $\rho _\theta$. In general, the p-adic Galois representations will not be geometric, as we can see in the following simple (but perhaps instructive) example:

Example 3.1.1

In the case of ${{\,\mathrm{GL}\,}}_1$, examples of the spaces $Y_r$ are the finite sets $({{\mathbb {Z}}}/p^r{{\mathbb {Z}}})^\times$. We then have ${\widetilde{H}}^0(Y_\infty ,{{\mathbb {Z}}}/p^m{{\mathbb {Z}}}) = {{\mathcal {C}}}_{cts}({{\mathbb {Z}}}_p^\times , {{\mathbb {Z}}}/p^m{{\mathbb {Z}}})$ and ${\widetilde{H}}^0(Y_\infty ,{{\mathbb {Z}}}_p) = {{\mathcal {C}}}_{cts}({{\mathbb {Z}}}_p^\times , {{\mathbb {Z}}}_p)$, where both source and target in the latter space of continuous functions have the profinite topology.

The Hecke operators are given by $\left( \langle l \rangle f\right) (z) = f(lz)$ for primes $l \ne p$, and their simultaneous eigenvectors in ${{\mathcal {C}}}_{cts}({{\mathbb {Z}}}_p^\times , {{\mathbb {Z}}}_p)\otimes {\overline{{{\mathbb {Q}}}}}_p$ are scalar multiples of continuous homomorphisms $\chi : {{\mathbb {Z}}}_p^\times \rightarrow {\overline{{{\mathbb {Q}}}}}_p^\times$. These homomorphisms are all of the form $\chi (z) = \chi _0(z)\left( z/[{\overline{z}}]\right) ^t$, where $\chi _0$ is a finite order character, $t \in {{\mathbb {Z}}}_p$ and $[{\overline{z}}]$ denotes the finite order element of ${{\mathbb {Z}}}_p^\times$ which is congruent to z modulo p.

Each such character $\chi$ has a corresponding Galois representation $\rho _\chi : G_{{\mathbb {Q}}}\rightarrow {\overline{{{\mathbb {Q}}}}}_p^\times$ which is the product of a finite order character corresponding to $\chi _0$ and $\left( \chi _p/[{\overline{\chi }}_p]\right) ^t$. Here, $[{\overline{\chi }}_p]:G_{{\mathbb {Q}}}\rightarrow {{\mathbb {Z}}}_p^\times$ is the finite-order character which is congruent to $\chi _p$ modulo p. The p-adic Galois representation $\rho _\chi$ is geometric if and only if t is an integer.

There seem to be only two restrictions on the Galois representations $\rho _\theta : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Q}}}}}_p)$ associated with Hecke eigenvalues appearing in completed cohomology:

• (1) The $\rho _\theta$ are continuous and unramified at all except finitely many primes.

• (2) If $c \in G_{{\mathbb {Q}}}$ is a complex conjugation²³, then $\mathrm {tr}\rho _\theta (c) = 0$ if n is even and $\mathrm {tr}\rho _\theta (c) \in \{-1,+1\}$ if n is odd²⁴. We call representations satisfying this condition odd (as in, e.g.,¹⁸, §6).

The fact that the second condition holds is a theorem of Caraiani and Le Hung²⁷ (and was proved by Taylor⁹² and Taïbi⁸⁷ in most essentially self-dual cases). The following version of p-adic Langlands reciprocity seems reasonable (and is suggested by Calegari and Emerton²²): all irreducible p-adic Galois representations satisfying conditions (1) and (2) are associated with Hecke eigenvalues appearing in completed cohomology. This is essentially completely known for $n \le 2$, but is wide open beyond that.

How might one approach this kind of reciprocity conjecture? We can first consider what kind of structure we can give to the collection of p-adic Galois representations. Looking back at the one-dimensional example, we have a discrete parameter, the finite order character $\chi _0$, and for each $\chi _0$ a continuous p-adic family in the variable t given by multiplying by $(\chi _p/[{\overline{\chi }}_p])^t$.

A similar parametrization, which works well in general, is to first fix a semisimple residual mod p Galois representation (continuous and unramified away from a finite set of primes S)

$$\begin{aligned} {\overline{\rho }}: G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {F}}}}}_p) \end{aligned}$$

and then consider the continuous representations

$$\begin{aligned} \rho : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Z}}}}}_p), \end{aligned}$$

which lift the fixed ${\overline{\rho }}$ mod ${\mathfrak {m}}_{{\overline{{{\mathbb {Z}}}}}_p}$ and which are also unramified away from S. Mazur’s fundamental work on the deformation theory of Galois representations shows that these lifts biject with local homomorphisms $R_{{\overline{\rho }}}^\square \rightarrow {\overline{{{\mathbb {Z}}}}}_p$ of local $W({\overline{{{\mathbb {F}}}}}_p)$-algebras ($W({\overline{{{\mathbb {F}}}}}_p)$ is a DVR with residue field ${\overline{{{\mathbb {F}}}}}_p$). The lifting ring $R_{{\overline{\rho }}}^\square$ is a complete Noetherian local $W({\overline{{{\mathbb {F}}}}}_p)$-algebra. We can therefore think of lifts as being parametrized by a geometric object: the formal scheme ${{\,\mathrm{Spf}\,}}(R_{{\overline{\rho }}}^\square )$ or, if we prefer, its rigid analytic generic fiber.

To give a little more feeling for these lifting rings, we mention that the reduced tangent space at the closed point of ${{\,\mathrm{Spec}\,}}(R_{{\overline{\rho }}}^\square )$, $\left( {\mathfrak {m}}_{R_{{\overline{\rho }}}^\square }/({\mathfrak {m}}_{{{\mathcal {O}}}_E} +{\mathfrak {m}}_{R_{{\overline{\rho }}}^\square }^2)\right) ^*$, can be identified with the group of continuous cocycles $Z^1(G_{{{\mathbb {Q}}},S},\mathrm {ad}({\overline{\rho }}))$ valued in the adjoint representation $\mathrm {ad}({\overline{\rho }})$.²⁵

3.2 Deformations of Galois Representations

It may seem more natural to parametrize isomorphism classes of representations, rather than matrix valued homomorphisms. This is perfectly reasonable, but the corresponding functor is not always representable by an affine formal scheme. Essentially, we want to take the quotient of ${{\,\mathrm{Spf}\,}}(R^\square _{{\overline{\rho }}})$ by the action of ${{\,\mathrm{PGL}\,}}_n$ corresponding to conjugation of lifts. When ${\overline{\rho }}$ is reducible, this action will usually have non-trivial stabilizers, and so this quotient is naturally a (formal algebraic) stack. On the other hand, if ${\overline{\rho }}$ is irreducible, the action is free and the quotient is representable by an affine formal scheme, ${{\,\mathrm{Spf}\,}}(R_{{\overline{\rho }}})$. The ring $R_{{\overline{\rho }}}$ is Mazur’s deformation ring. Its reduced tangent space $\left( {\mathfrak {m}}_{R_{{\overline{\rho }}}}/({\mathfrak {m}}_{{{\mathcal {O}}}_E}+{\mathfrak {m}}_{R_{{\overline{\rho }}}}^2) \right) ^*$ can be identified with the continuous cohomology group $H^1(G_{{{\mathbb {Q}}},S},\mathrm {ad}({\overline{\rho }}))$.

In the residually reducible setting, an important role is played by pseudorepresentations²⁶ which describe ‘representations up to semisimplification’ with general coefficient rings (in particular, there is a well-defined characteristic polynomial for every element of the group being pseudorepresented). The idea goes back to Wiles⁹⁸ and Taylor⁸⁹ and has been generalized by Chenevier²⁵ and Lafforgue⁶⁸. For a fixed ${\overline{\rho }}$, there is an associated pseudodeformation ring $P_{{\overline{\rho }}}$ parametrizing pseudorepresentations which lift the pseudorepresentation associated with (the semi-simplification of) ${\overline{\rho }}$. The pseudodeformation ring is closely related to the ring of invariants $(R_{{\overline{\rho }}}^{\square })^{{{\,\mathrm{PGL}\,}}_n}$⁹⁷.

3.3 Fontaine–Mazur–Langlands and p-adic Reciprocity in Dimension Two

Now we could try to establish p-adic Langlands reciprocity in two steps. The first is to show that each ${\overline{\rho }}$ is isomorphic to the residual representation of $\rho _{\pi ,\iota }$ for an automorphic representation $\pi$. Such a statement would be a generalization of Serre’s conjecture, proven by Khare and Wintenberger⁶⁶, that when $n=2$ every odd ${\overline{\rho }}$ arises from a modular form. The second step is to show that if one lift of ${\overline{\rho }}$ is automorphic, then every suitable lift of ${\overline{\rho }}$ is associated with Hecke eigenvalues appearing in completed cohomology. In the case $n = 2$, this is also known in most cases, using work of Böckle¹⁴ in the residually irreducible case, and work of Pan⁷⁶ in the residually reducible case.

Emerton went further and proved many cases of the Fontaine–Mazur–Langlands conjecture using completed cohomology⁴¹. He is able to compare the condition that the lift is geometric with the condition that its associated system of Hecke eigenvalues appears in the cohomology of a modular curve at finite level (not just in the limit which defines the completed cohomology groups). This uses work of Berger, Breuil and Colmez on the p-adic local Langlands correspondence. An alternative method, proving a similar result (with slightly different technical conditions), and also using the p-adic local Langlands correspondence, is due to Kisin⁶².

Recently, Pan⁷⁶ carried out a (very extensively) modified version of Emerton’s strategy using Paškūnas’s work on p-adic local Langlands⁷⁸, which includes the residually reducible case. This enables him to prove the Fontaine–Mazur–Langlands conjecture for all odd two-dimensional geometric p-adic representations $\rho$ of $G_{{\mathbb {Q}}}$ with distinct Hodge–Tate weights (this means that they will be associated with Hecke eigenforms of weight at least 2), when $p \ge 5$. Recent work of Paškūnas and Tung⁸⁰ should permit the extension of this result to small values of p.

The case of equal Hodge–Tate weights deserves its own survey, and is closely related to the strong Artin conjecture for two-dimensional complex representations of $G_{{\mathbb {Q}}}$. There are three different approaches here which have yielded almost complete results. First, Buzzard and Taylor’s approach using overconvergent modular forms¹⁶ (more recent developments have been surveyed by Kassaei⁵⁸), second Calegari and Geraghty’s application of their modified Taylor–Wiles method²³, and most recently Pan using a description of the contribution of weight 1 overconvergent modular forms to completed cohomology⁷⁷.

3.4 Beyond the Regular Algebraic Case

Beyond the regular algebraic case, we only know how to construct automorphic Galois representations in limited situations. The most classical is the case of weight 1 modular forms³⁹. Generalizing this, Galois representations have been constructed corresponding to Hecke eigenvalues appearing in the coherent cohomology of Shimura varieties^{15, 48}. This relies on finding congruences to Hecke eigenvalues for regular algebraic automorphic representations.

The simplest cases where a general construction of automorphic Galois representations is not known are for Maass wave forms (non-holomorphic modular forms). A certain family of these forms generate algebraic automorphic representations, conjecturally with algebraic Hecke eigenvalues and associated (geometric) Galois representations. In fact they should have associated even²⁷ Artin representations.

4 Modularity Lifting Theorems

First introduced as part of Wiles’s proof of Fermat’s last theorem, modularity lifting theorems and the Taylor–Wiles method^{96, 99} provide a robust technique for proving that geometric Galois representations are automorphic. The method was modified and significantly extended by Calegari and Geraghty²³, so that now it can, in principle, be applied whenever the target automorphic representations contribute to the cohomology of a locally symmetric space, or to the coherent cohomology of a Shimura variety (note that the Maass forms mentioned in Sect. 3.4 do not fall into either of these families of cases). We recommend Calegari’s recent survey²⁰ to the reader who is interested in the development of modularity lifting theorems and the Taylor–Wiles method since the proof of Fermat’s last theorem.

In this section, we will sketch what a modularity lifting theorem looks like, together with an outline of how the proofs of such theorems go. We incorporate ideas of Diamond, Fujiwara and Kisin which made the Taylor–Wiles method more flexible.

4.1 A Prototype Statement

The typical shape of a modularity lifting theorem is as follows:

Theorem 4.1.1

(Theorem prototype) Suppose $\rho : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {Q}}}}}_p)$ is a geometric Galois representation with residual representation ${\overline{\rho }}: G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n({\overline{{{\mathbb {F}}}}}_p)$. Suppose moreover that there exists an automorphic representation $\pi$ and $\iota : {\overline{{{\mathbb {Q}}}}}_p\cong {{\mathbb {C}}}$ with residual representation ${\overline{\rho }}_{\pi ,\iota }$ isomorphic to ${\overline{\rho }}$.

Assume various things about $\rho , {\overline{\rho }}, \pi , \ldots$

Then $\rho$ is automorphic: there exists an automorphic representation $\sigma$ of ${{\,\mathrm{GL}\,}}_n({{\mathbb {A}}})$ with $\rho _{\sigma ,\iota } \cong \rho$.

The ‘lifting’ part of the theorem is that we start from the assumption that the residual representation ${\overline{\rho }}$ is automorphic and then lift this to deduce automorphy of the p-adic representation $\rho$.

4.2 Modularity Lifting and ‘$R={{\mathbb {T}}}$’

In this subsection and the next, we try to explain the essence of the Taylor–Wiles method (as revised by Diamond and Fujiwara). For simplicity, we restrict to two-dimensional Galois representations, but the same ideas can be applied to higher dimensional cases with the proviso that we restrict to self-dual (up to twist²⁸) Galois representations²⁶. As we have mentioned, Calegari and Geraghty extended the scope of the method to go beyond the self-dual case. We will also assume that ${\overline{\rho }}$ is irreducible, so we have a deformation ring $R_{{\overline{\rho }}}$. It is now useful to fix a finite extension $E/{{\mathbb {Q}}}_p$ as a coefficient field. E is chosen so that the images of $\rho$ and $\rho _{\pi ,\iota }$ in Theorem 4.1.1 are contained in ${{\,\mathrm{GL}\,}}_n({{\mathcal {O}}}_E)$ (this is possible, at least after conjugating the representations) and reduction modulo the maximal ideal ${\mathfrak {m}}_E$ gives the same representation ${\overline{\rho }}: G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n(k_E)$.

We start out with a module M, finite free over ${{\mathcal {O}}}_E$, equipped with an action of a Hecke algebra ${{\mathbb {T}}}\subset {{\,\mathrm{End}\,}}(M)$, generated as an ${{\mathcal {O}}}_E$-algebra by a commuting family of Hecke operators. The set up will be such that applying $\iota$ to the eigenvalues of ${{\mathbb {T}}}$ on $M\otimes _{{{\mathcal {O}}}_E}{\overline{{{\mathbb {Q}}}}}_p$ gives (complex) Hecke eigenvalues for a collection of automorphic representations. For example, we could take $M = H^1(Y,{{\mathbb {Z}}}_p)$ for a modular curve Y, and we would then see Hecke eigenvalues for holomorphic modular forms of weight two and a fixed level.

We are assuming that we have a fixed residual Galois representation ${\overline{\rho }}$, which is automorphic, so it corresponds to a system of Hecke eigenvalues $\theta : {{\mathbb {T}}}\rightarrow k_E$. We, therefore, have a maximal ideal ${\mathfrak {m}}= \ker (\theta ) \subset {{\mathbb {T}}}$. We can take the localization $M_{\mathfrak {m}}$, which is a direct summand of M. The systems of Hecke eigenvalues in $M_{\mathfrak {m}}\otimes _{{{\mathcal {O}}}_E} {\overline{{{\mathbb {Q}}}}}_p$ come from automorphic representations whose residual Galois representation is isomorphic to ${\overline{\rho }}$. The existence of Galois representations associated with each of these automorphic representations gives a homomorphism $R_{{\overline{\rho }}} \rightarrow {{\mathbb {T}}}_{\mathfrak {m}}$ from a deformation ring (in this case, a complete Noetherian local ${{\mathcal {O}}}_E$-algebra), which is necessarily surjective because the characterizing property of the automorphic Galois representations (prescribed characteristic polynomials of Frobenius elements) implies that the Hecke operators which generate ${{\mathbb {T}}}$ appear in the image of $R_{{\overline{\rho }}}$.

Moreover, we know (or assume) that the Galois representations associated with Hecke eigensystems in $M_{\mathfrak {m}}$ are geometric.²⁹ This means that the map $R_{{\overline{\rho }}} \rightarrow {{\mathbb {T}}}_{\mathfrak {m}}$ will factor through a certain quotient $R_{{\overline{\rho }}}^\mathrm{{geo}}$ of $R_{{\overline{\rho }}}$ having the property that homomorphisms $R_{{\overline{\rho }}}^\mathrm{{geo}} \rightarrow {\overline{{{\mathbb {Q}}}}}_p$ correspond to geometric p-adic Galois representations.³⁰ The quotient is defined using work of Kisin⁶¹.

To prove a modularity lifting theorem, we need only to show that every such homomorphism factors through ${{\mathbb {T}}}_{\mathfrak {m}}$. Indeed, the Galois representations corresponding to homomorphisms $R^\mathrm{{geo}}_{{\overline{\rho }}} \rightarrow {\overline{{{\mathbb {Q}}}}}_p$ are geometric representations $\rho$ which lift ${\overline{\rho }}$ and satisfy some other conditions going into the definition of $R^\mathrm{{geo}}_{{\overline{\rho }}}$. The statement that every such representation is associated with a Hecke eigensystem $\theta : {{\mathbb {T}}}_{\mathfrak {m}}\rightarrow {\overline{{{\mathbb {Q}}}}}_p$, or in other words to an automorphic representation contributing to $M_{\mathfrak {m}}$, is precisely the statement of a modularity lifting theorem.

So we can re-phrase Theorem 4.1.1 as:

Theorem 4.1.1*. The ${{\mathcal {O}}}_E$-algebra homomorphism $R^\mathrm{{geo}}_{{\overline{\rho }}} \rightarrow {{\mathbb {T}}}_{{\mathfrak {m}}}$ induces a bijection between ${{\mathcal {O}}}_E$-algebra homomorphisms $R^\mathrm{{geo}}_{{\overline{\rho }}} \rightarrow {{\mathcal {O}}}_E$ and ${{\mathbb {T}}}_{{\mathfrak {m}}} \rightarrow {{\mathcal {O}}}_E$.

We immediately see that to prove this result it is sufficient to show that the map $R_{{\overline{\rho }}}^\mathrm{{geo}} \rightarrow {{\mathbb {T}}}_{\mathfrak {m}}$ is an isomorphism. We can get by with something a little weaker, for example that $R^\mathrm{{geo}}_{{\overline{\rho }}} \rightarrow {{\mathbb {T}}}_{\mathfrak {m}}$ has nilpotent kernel. This is equivalent to asking for the support of $M_{{\mathfrak {m}}}$ as an $R^\mathrm{{geo}}_{{\overline{\rho }}}$-module ($R^\mathrm{{geo}}_{{\overline{\rho }}}$ acts via ${{\mathbb {T}}}_{\mathfrak {m}}$) to be all of ${{\,\mathrm{Spec}\,}}(R^\mathrm{{geo}}_{{\overline{\rho }}})$.

In general, it seems hopeless to directly analyze $R^\mathrm{{geo}}_{{\overline{\rho }}}$ and compare it with ${{\mathbb {T}}}_{{\mathfrak {m}}}$. By construction, the Hecke algebra ${{\mathbb {T}}}_{{\mathfrak {m}}}$ is a finite local ${{\mathcal {O}}}_E$-algebra. On the other hand, at the moment the only general way to show that $R^\mathrm{{geo}}_{{\overline{\rho }}}$ has Krull dimension 1 (as it should, if it is to have a chance of being isomorphic to ${{\mathbb {T}}}_{{\mathfrak {m}}}$) is to first prove a modularity lifting theorem and then deduce this as a consequence.

4.3 The Taylor–Wiles Method

In a sentence, the goal of the Taylor–Wiles method is to ‘smoothen out’ the deformation ring $R_{{\overline{\rho }}}^\mathrm{{geo}}$ by allowing ramification at auxiliary sets of primes. In favorable circumstances, we will then be able to make a comparison with a similarly smoothened out version of the Hecke algebra ${{\mathbb {T}}}_{{\mathfrak {m}}}$. We will give a brief sketch of some of the details here. For the reader who has not previously been exposed to these ideas, two more recent texts we recommend are Gee’s Arizona Winter School notes⁴⁶ and Calegari’s CDM lecture¹⁹.

We recall that $R_{{\overline{\rho }}}^\mathrm{{geo}}$ classified geometric representations that are unramified outside a finite set of primes S. So for any finite set of primes Q, disjoint from S, we have a deformation ring $R_{{\overline{\rho }},Q}^\mathrm{{geo}}$ which admits $R_{{\overline{\rho }}}^\mathrm{{geo}}$ as a quotient and classifies the same representations as $R_{{\overline{\rho }}}^\mathrm{{geo}}$, except for allowing ramification at primes in Q.

In good situations, we will be able to choose sets of primes Q such that:

• The deformation rings $R_{{\overline{\rho }},Q}^\mathrm{{geo}}$ admit a surjective map from a fixed ring $R_\infty$ (independent of Q).

• Varying the set Q, we can ‘fill out’ all of $R_\infty$.

The first point is arranged by choosing primes Q so that a ‘dual Selmer group’, related to the reduced tangent space of $R_{{\overline{\rho }},Q}^\mathrm{{geo}}$ by global Tate duality, vanishes. This allows the dimension of the reduced tangent space to be computed by a local calculation. Being able to choose suitable primes requires an assumption that the image ${\overline{\rho }}(G_{{{\mathbb {Q}}}(\zeta _p)})$ is sufficiently large (usually it suffices for ${\overline{\rho }}|_{G_{{{\mathbb {Q}}}(\zeta _p)}}$ to be irreducible).

The second point is achieved by choosing different sets of primes $Q=Q_n$ for every $n \ge 1$ which satisfy

• $q \equiv 1$ mod $p^n$

• ${\overline{\rho }}(\mathrm {Frob}_q)$ has distinct eigenvalues

for each $q \in Q_n$, and then taking a limit over n to obtain a ring which we will call $R^{\mathrm {patch}}$. The limit has to be taken in a rather unnatural way, since there are no natural maps between the $R_{{\overline{\rho }},Q_n}^\mathrm{{geo}}$ as n varies. Scholze re-interpreted this in terms of ultraproducts⁸³. Since each $R_{{\overline{\rho }},Q_n}^\mathrm{{geo}}$ is quotient of $R_\infty$, $R^{\mathrm {patch}}$ is too. To show that we do indeed fill out all of $R_\infty$ requires a lower bound on the size of $R^{\mathrm {patch}}$—this is deduced from an input from the side of automorphic forms, which we will come back to.

The conditions on each set of Taylor–Wiles primes $Q_n$ make it easy to understand the difference between $R^\mathrm{{geo}}_{{\overline{\rho }},Q_n}$ and $R^\mathrm{{geo}}_{{\overline{\rho }}}$. For each $q \in Q_n$, when we restrict a representation lifting ${\overline{\rho }}$ to the local decomposition group $G_{{{\mathbb {Q}}}_q}$, we obtain a direct sum of characters $\chi _1\oplus \chi _2$ and the restriction to the inertia subgroup $I_q \subset G_{{{\mathbb {Q}}}_q}$ factors through the tame fundamental character $I_q \rightarrow {{\mathbb {F}}}_q^\times$. This means we can equip $R^\mathrm{{geo}}_{{\overline{\rho }},Q_n}$ with the structure of a $S_\infty = {{\mathcal {O}}}_E[[{{\mathbb {Z}}}_p^{r}]]$-algebra, where $r = 2|Q_n|$; this structure depends on a choice of generator of (the maximal p-primary quotient of) ${{\mathbb {F}}}_q^\times$ for each $q \in Q_n$. The ${{\mathcal {O}}}_E$-algebra $S_\infty$ (isomorphic to a power series ring over ${{\mathcal {O}}}_E$) comes with an augmentation $S_\infty \rightarrow {{\mathcal {O}}}_E$, and quotienting out by the kernel of the augmentation gives an ${{\mathcal {O}}}_E$-algebra $R^\mathrm{{geo}}_{{\overline{\rho }},Q_n}\otimes _{S_\infty }{{\mathcal {O}}}_E$ which is isomorphic to $R^\mathrm{{geo}}_{{\overline{\rho }}}$.

On the automorphic side, we can also allow ramification at auxiliary primes by modifying the level structure at these primes. It can be arranged that we have Hecke modules $M_{Q_n}$, for each n, which are simultaneously $S_\infty$-modules and $R_{{\overline{\rho }},Q_n}$-modules (the latter ring acts via a Hecke algebra, $S_\infty$ acts via Hecke operators at the primes $q \in Q_n$). In parallel to the isomorphism $R^\mathrm{{geo}}_{{\overline{\rho }},Q_n}\otimes _{S_\infty }{{\mathcal {O}}}_E \cong R^\mathrm{{geo}}_{{\overline{\rho }}}$ on the Galois side, we have $M_{Q_n} \otimes _{S_\infty }{{\mathcal {O}}}_E \cong M_{\mathfrak {m}}$. A crucial property of our Hecke modules is that when we take the limit over n, we get a finite free $S_\infty$-module $M_\infty$. This limit also has an action of $R^{\mathrm {patch}}$, coming from the action of $R^\mathrm{{geo}}_{{\overline{\rho }},Q_n}$ on $M_{Q_n}$ for each n. There is an isomorphism $R^{\mathrm {patch}}\otimes _{S_\infty }{{\mathcal {O}}}_E \cong R_{{\overline{\rho }}}^\mathrm{{geo}}$ and a commutative diagram:

Now, the crucial numerical coincidence we will need to arrange is

$$\begin{aligned} \dim (R_\infty ) = \dim (S_\infty ). \end{aligned}$$

Assuming this, we note that both the depth and dimension of $M_\infty$ as an $S_\infty$-module are equal to $\dim (S_\infty ) = \dim (R_\infty )$. The depth and dimension are unchanged by viewing $M_\infty$ as an $R_\infty$ module (the action is via $R^{\mathrm {patch}}$). So $M_\infty$ is a maximal Cohen–Macaulay $R_\infty$-module. In particular, it follows from a standard result contained in EGA⁴⁹ (cf. Chapter 0, Proposition 16.5.4) that its support in ${{\,\mathrm{Spec}\,}}(R_\infty )$ is a union of irreducible components.

Suppose we know that ${{\,\mathrm{Spec}\,}}(R_\infty )$ is irreducible. Then $M_\infty$ has full support in ${{\,\mathrm{Spec}\,}}(R_\infty )$ and the quotient map $R_\infty \rightarrow R^{\mathrm {patch}}$ has nilpotent kernel. We can deduce that $M\otimes _{S_\infty }{{\mathcal {O}}}_E = M_{\mathfrak {m}}$ has full support in ${{\,\mathrm{Spec}\,}}(R^\mathrm{{geo}}_{{\overline{\rho }}})$.

The situation is even better if $R_\infty$ is a regular local ring. We can then deduce from the Auslander–Buchsbaum theorem that $M_\infty$ is free over $R_\infty$, therefore $M_{\mathfrak {m}}$ is free over $R_\infty \otimes _{S_\infty }{{\mathcal {O}}}_E$. Since this ring acts on $M_{\mathfrak {m}}$ via its quotient $R_{{\overline{\rho }}}^\mathrm{{geo}}$, we deduce that $M_{\mathfrak {m}}$ is free over $R_{{\overline{\rho }}}^\mathrm{{geo}}$. In particular, we have an isomorphism $R_{{\overline{\rho }}}^\mathrm{{geo}} \cong {{\mathbb {T}}}_{\mathfrak {m}}$, and we deduce that $M_{\mathfrak {m}}$ is free over the Hecke algebra ${{\mathbb {T}}}_{\mathfrak {m}}$. If $R_{\infty }[1/p]$ is a regular domain, a similar argument shows that $R_{{\overline{\rho }}}^\mathrm{{geo}}[1/p] \cong {{\mathbb {T}}}_{\mathfrak {m}}[1/p]$.

4.4 Presenting $R^\mathrm{{geo}}_{{\overline{\rho }},Q}$ as a Quotient of $R_\infty$

We did not say anything about what we take for the ring $R_\infty$. For the original version of the Taylor–Wiles method, it is a power series ring ${{\mathcal {O}}}_E[[x_1,\ldots x_g]]$, with g equal to (an upper bound for) the dimension of the reduced tangent space of $R_{{\overline{\rho }},Q}^\mathrm{{geo}}$. Controlling the size of these tangent spaces, which are subspaces of the Galois cohomology group $H^1(G_{{{\mathbb {Q}}},S\cup Q},\mathrm {ad}({\overline{\rho }}))$, requires setting up the correct local conditions at primes in S and using the Greenberg–Wiles formula⁹⁹, (cf. Proposition 1.6). This is particularly delicate at p.

Kisin introduced a more flexible method⁶³, which instead considers $R_{{\overline{\rho }},Q}^\mathrm{{geo}}$ as an algebra over a local deformation ring and considers the relative tangent space.

For example, assume for simplicity that ${\overline{\rho }}_p := {\overline{\rho }}|_{G_{{{\mathbb {Q}}}_p}}$ is absolutely irreducible. We have a local deformation ring $R_{{\overline{\rho }}_p}$ which classifies lifts of ${\overline{\rho }}_p$ up to isomorphism, and a natural map $R_{{\overline{\rho }}_p} \rightarrow R_{{\overline{\rho }}}$ corresponding to restricting representations to $G_{{{\mathbb {Q}}}_p}$. The relative tangent space $\left( {\mathfrak {m}}_{R_{{\overline{\rho }}}}/({\mathfrak {m}}_{R_{{\overline{\rho }}_p}}+{\mathfrak {m}}_{R_{{\overline{\rho }}}}^2)\right) ^*$ can be identified with the kernel of the map

$$\begin{aligned} H^1(G_{{{\mathbb {Q}}},S},\mathrm {ad}({\overline{\rho }})) \rightarrow H^1(G_{{{\mathbb {Q}}}_p},\mathrm {ad}({\overline{\rho }}_p)).\end{aligned}$$

Supposing this kernel has dimension $g_p$, we deduce that $R_{{\overline{\rho }}}$ is a quotient of the ring $R_{{\overline{\rho }}_p}[[x_1,\ldots ,x_{g_p}]]$. By definition, $R_{{\overline{\rho }}}^\mathrm{{geo}}$ is a tensor product $R_{{\overline{\rho }}}\otimes _{R_{{\overline{\rho }}_p}}R_{{\overline{\rho }}_p}^\mathrm{{geo}}$, and therefore $R_{{\overline{\rho }}}^\mathrm{{geo}}$ is a quotient of $R_\infty =R^\mathrm{{geo}}_{{\overline{\rho }}_p}[[x_1,\ldots ,x_{g_p}]]$. We can then hope to deduce modularity lifting theorems from knowledge about $R^\mathrm{{geo}}_{{\overline{\rho }}_p}$. In particular, if ${{\,\mathrm{Spec}\,}}(R^\mathrm{{geo}}_{{\overline{\rho }}_p})$ is irreducible, then ${{\,\mathrm{Spec}\,}}(R_\infty )$ is irreducible and we are in good shape to apply the argument sketched in the previous subsection. This variant of the Taylor–Wiles method looks like some kind of ‘local-to-global’ principle.

4.5 Adjoint Selmer Groups

If $\rho : G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_n(E)$ is a geometric Galois representation with absolutely irreducible residual representation ${\overline{\rho }}$, it defines a prime ideal ${\mathfrak {p}}_{\rho }$ of the deformation ring $R^\mathrm{{geo}}_{{\overline{\rho }}}$, and the tangent space $\left( ({\mathfrak {p}}_{\rho }/ {\mathfrak {p}}_{\rho }^2)\otimes \kappa ({\mathfrak {p}}_{\rho })\right) ^*$ is a finite dimensional E-vector space, which can be identified with a subspace $H^1_g(G_{{{\mathbb {Q}}},S},\mathrm {ad}\rho ) \subset H^1(G_{{{\mathbb {Q}}},S},\mathrm {ad}\rho )$ of the Galois cohomology group. This subspace, defined by Bloch and Kato, corresponds to extensions of the trivial representation by $\mathrm {ad}\rho$ which are geometric. In fact, this subspace is expected to vanish: conjectures of Bloch and Kato predict that the dimension of this Selmer group is equal to the order of vanishing of an adjoint L-function at $s=1$. When $\rho$ is automorphic, this L-function is non-vanishing at $s=1$⁵⁵ (cf. Proposition 3.6).

Moreover, a non-split geometric extension of the trivial representation by $\mathrm {ad}\rho$ is also ruled out by the ‘yoga of motives’ (since there should be no non-trivial extensions between motives of the same weight).

If we can prove $R_{{\overline{\rho }}}^\mathrm{{geo}}[1/p]\cong {{\mathbb {T}}}_{{\mathfrak {m}}}[1/p]$ (as discussed above, this can be proved using the Taylor–Wiles method in certain cases), then it follows that $R_{{\overline{\rho }}}^\mathrm{{geo}}[1/p]$ is a finite E-algebra, and the tangent space $H^1_g(G_{{{\mathbb {Q}}},S},\mathrm {ad}\rho )$ vanishes for all representations corresponding to homomorphisms $R_{{\overline{\rho }}}^\mathrm{{geo}} \rightarrow E$. Allen² was able to generalize this to prove vanishing of an adjoint Bloch–Kato Selmer group for self-dual automorphic Galois representations $\rho$ with just an assumption that the image of ${\overline{\rho }}(G_{{{\mathbb {Q}}}(\zeta _p)})$ is sufficiently large.³¹ The author and Thorne recently proved a similar vanishing result replacing this large image assumption with a (much milder) large image assumption on the characteristic 0 representation $\rho$ itself⁷⁵. We use an idea due to Lue Pan (it appears in the work we have already mentioned on the Fontaine–Mazur conjecture in the residually reducible case) which allows us to carry out a version of the Taylor–Wiles method up to a bounded p-power torsion error term, which disappears when we invert p. Thorne subsequently improved our result to only require irreducibility of $\rho |_{G_{{{\mathbb {Q}}}(\zeta _{p^\infty })}}$⁹³. Vanishing of adjoint Selmer groups is an essential input to two different approaches to proving automorphy of Galois representations^{73, 74}, which are discussed in the next section.

5 Symmetric Power Functoriality

In what remains of this survey, we will discuss some of the ideas of the works^{73, 74} which establish symmetric power functoriality (Conjecture 2.6.1) for holomorphic modular forms. Crucial inputs come from some other works^{3, 5, 75}.

We recall that for a Hecke eigenform f (of weight $\ge 2$ and without CM), we want to show that ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is automorphic for some choice of p and $\iota$. Modularity lifting theorems (¹², for example) can be used to prove automorphy if we know that the residual representation ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }$ is automorphic, as long as this residual representation has big enough image. There is some tension here, because we have no idea how to prove that a ‘generic’ $(n+1)$-dimensional mod p representation of $G_{{{\mathbb {Q}}}}$ is automorphic. Potential automorphy (e.g., Theorem 2.6.2) involves dealing with this by finding an extension field $F/{{\mathbb {Q}}}$ over which a particular residual representation becomes automorphic.

However, often the representation ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }$ will not have big image. For example, when $p \le n$, it is always reducible³². In a series of three papers^33,34,35, Clozel and Thorne were able to exploit this reducibility to prove:

Theorem 5.0.1

(Clozel–Thorne) ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is automorphic for $n \le 8$.

For example, if we let $p = 7$, then we have an isomorphism

$$\begin{aligned} {{\,\mathrm{Sym}\,}}^8{\overline{\rho }}_{f,\iota } \cong ({}^{\sigma } {{\overline{\rho }}_{f,\iota }} \otimes {\overline{\rho }}_{f,\iota })\oplus (\det {\overline{\rho }}_{f,\iota })^2\otimes {{\,\mathrm{Sym}\,}}^4{\overline{\rho }}_{f,\iota }. \end{aligned}$$

Here, the subscript $^\sigma$ denotes composition with the Frobenius automorphism on the coefficients of the representation.

Tensor product functoriality (in this case due to Ramakrishnan), the ${{\,\mathrm{Sym}\,}}^4$ lifting, and Langlands’s theory of Eisenstein series now implies the automorphy of this residual representation. It is then possible to apply a modularity lifting theorem for a residually reducible representation, such as a theorem of Thorne⁹⁵ (and a later generalization³). To apply such a theorem, Clozel and Thorne must construct a congruence to a cuspidal automorphic representation (satisfying a ramification condition at an auxiliary place—this is the level raising congruence alluded to in their title). The strategy explained by them³³ establishes symmetric power functoriality as a consequence of a family of (still conjectural) cases of tensor product functoriality and the existence of suitable level raising congruences.

5.1 Relative Modularity Lifting

In each of our articles^{73, 74}, we introduce a new method for proving the automorphy of a symmetric power representation ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$. Crucially, neither method requires the $(n+1)$-dimensional residual representation ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }$ to be irreducible. We will start by explaining the method in the second article⁷⁴, because the main technical result of that paper can be stated as a modularity lifting theorem following the template of Theorem 4.1.1 and the idea of proof is a variation of the Taylor–Wiles method. We first state a version of this main technical result, for representations of $G_{{{\mathbb {Q}}}}$ (a similar statement for representations of $G_F$ with F totally real can also be proved⁷⁴).

Theorem 5.1.1

(N–Thorne) Suppose $f, f'$ are two cuspidal Hecke eigenforms of weight 2. Fix a prime p, an integer $n \ge 1$ and an isomorphism $\iota : {\overline{{{\mathbb {Q}}}}}_p\rightarrow {{\mathbb {C}}}$, and suppose the following conditions hold:

• (1) There is an isomorphism ${\overline{\rho }}_{f, \iota } \cong {\overline{\rho }}_{f', \iota }$.

• (2) Neither f nor $f'$ has CM and neither of the Hecke eigenvalues $\iota ^{-1}(a_p(f)), \iota ^{-1}(a_p(f'))$ is a p-adic unit.

• (3) For each prime l dividing the level of f or $f'$, $\pi (f)_l$ is a character twist of the Steinberg representation if and only if $\pi (f')_l$ is.

• (4) There exists $a \ge 1$ such that $p^a > 2n-1$ and there is a sandwich

  $$\begin{aligned} {{\,\mathrm{PSL}\,}}_2({\mathbf {F}}_{p^a}) \subset {\text {Proj}} {\overline{\rho }}_{f, \iota }(G_{{\mathbb {Q}}}) \subset {{\,\mathrm{PGL}\,}}_2({\mathbf {F}}_{p^a}), \end{aligned}$$

  up to conjugacy in ${{\,\mathrm{PGL}\,}}_2({\overline{{\mathbf {F}}}}_p)$.³³

• (5) ${{\,\mathrm{Sym}\,}}^n \rho _{f',\iota }$ is automorphic.

Then ${{\,\mathrm{Sym}\,}}^n \rho _{f,\iota }$ is automorphic.

Note that although this theorem includes the ‘big image’ condition (4) which depends on n, the representation ${{\,\mathrm{Sym}\,}}^n {\overline{\rho }}_{f,\iota }$ will be reducible for all $n \ge p$. Let’s indicate where each of the assumptions in this theorem comes from:

• Condition (1) is what we expect in any modularity lifting theorem. It also implies that ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f, \iota } \cong {{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f', \iota }$.

• Condition (2) allows us to work with a local deformation or lifting ring $R^\mathrm{{geo}}_{{\overline{\rho }}_p}$ which is a domain (thanks to a theorem of Kisin⁶³).

• Condition (3) ensures that we can work with deformation rings for p-adic representations of l-adic Galois groups which are also domains.

• Condition (4) ensures that ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f, \iota }(G_{{\mathbb {Q}}})$ contains a regular semisimple element of ${{\,\mathrm{GL}\,}}_{n+1}({\overline{{{\mathbb {F}}}}}_p)$. This is used when choosing sets of Taylor–Wiles primes.

• Condition (5) is again what we expect in any modularity lifting theorem. We are propagating automorphy along the congruence ${{\,\mathrm{Sym}\,}}^n\rho _{f, \iota } \cong {{\,\mathrm{Sym}\,}}^n\rho _{f', \iota }$ mod p.

To prove this theorem, we avoid applying the patching method directly to the $(n+1)$-dimensional representations lifting ${{\,\mathrm{Sym}\,}}^n {\overline{\rho }}_{f,\iota }$. Instead, we patch in the two-dimensional case, constructing a quotient $R^{\mathrm {patch}}$ of $R_\infty$ and a finite free $S_\infty$-module $M_\infty$ as described in §4.3. However, at the same time as doing this, we take compatible limits for deformation rings and modules of automorphic forms in the $(n+1)$-dimensional setting.

For the deformation rings, since ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }$ may be reducible, we have to work with a pseudodeformation ring $P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ (parametrizing self-dual geometric pseudodeformations). Going from a two-dimensional representation to its nth symmetric power naturally induces a map

$$\begin{aligned}{{\,\mathrm{Sym}\,}}^n: P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }} \rightarrow R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }}.\end{aligned}$$

The output of our ‘relative’ patching method is the following:

• (1) $S_\infty$-algebras $P^{\mathrm {patch}}$, $R^{\mathrm {patch}}$ with isomorphisms $P^{\mathrm {patch}}\otimes _{S_\infty }{{\mathcal {O}}}_E \cong P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ and $R^{\mathrm {patch}}\otimes _{S_\infty }{{\mathcal {O}}}_E \cong R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }}$.

• (2) A surjection $R_\infty \rightarrow R^{\mathrm {patch}}$, where $R_\infty$ is a domain with $\dim (R_\infty ) = \dim (S_\infty )$.

• (3) A $P^{\mathrm {patch}}$-module, $N_\infty$ and a $R^{\mathrm {patch}}$-module $M_\infty$, both finite free over $S_\infty$. The $P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$-module $N_\infty \otimes _{S_\infty }{{\mathcal {O}}}_E$ is isomorphic to a Hecke module $N_{{{\,\mathrm{Sym}\,}}^n{\mathfrak {m}}}$ which contains the Hecke eigenvalues of certain self-dual automorphic representations of ${{\,\mathrm{GL}\,}}_{n+1}({{\mathbb {A}}})$. The $R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }}$-module $M_\infty \otimes _{S_\infty }{{\mathcal {O}}}_E$ is isomorphic to $M_{\mathfrak {m}}$ as before.

• (4) The maps $P^{\mathrm {patch}} \rightarrow P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ and $R^{\mathrm {patch}} \rightarrow R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }}$ coming from (1) fit into a commutative square of ${{\mathcal {O}}}_E$-algebra maps:

  

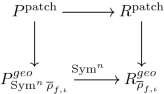  (1)

Note that we do not attempt to find a surjection from $P_\infty \rightarrow P^{\mathrm {patch}}$ with $\dim (P_\infty ) = \dim (S_\infty )$. This would involve controlling the dimension of the reduced tangent space of a pseudodeformation ring for ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f, \iota }$ (e.g by allowing ramification at auxiliary primes to force vanishing of a dual Selmer group), which is what we are trying to avoid.

We have $x, x' \in {{\,\mathrm{Spec}\,}}(R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }})$ prime ideals corresponding to the Galois representations $\rho _{f,\iota }, \rho _{f',\iota }$. Pulling back by ${{\,\mathrm{Sym}\,}}^n$, we get $y, y' \in {{\,\mathrm{Spec}\,}}(P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }})$. Since ${{\,\mathrm{Sym}\,}}^n\rho _{f',\iota }$ is assumed automorphic, we will be able to arrange things so that $y'$ is in the support of the ‘automorphic module’ $N_{{{\,\mathrm{Sym}\,}}^n{\mathfrak {m}}}$.

The localization ${P}_{y'}$ of $P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ at $y'$ is a Noetherian local E-algebra whose tangent space at the closed point is a subspace of a Galois cohomology group, and vanishing of an adjoint Selmer group⁷⁵ shows that this tangent space vanishes. In other words, ${P}_{y'}$ is simply E! Of course this is what we expect if $P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ is isomorphic to a Hecke algebra which acts semisimply on characteristic 0 vector spaces of automorphic forms.

These preparations leave us ready to explain the (rather simple) technical heart of the proof of Theorem 5.1.1. In a few words, we prove that the support of $N_\infty$ in ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$ contains the image of every irreducible component of ${{\,\mathrm{Spec}\,}}(R^{\mathrm {patch}})$ passing through $x'$ (thought of as a point of ${{\,\mathrm{Spec}\,}}(R^{\mathrm {patch}})$ using the closed immersion ${{\,\mathrm{Spec}\,}}(R^\mathrm{{geo}}_{{\overline{\rho }}_{f,\iota }}) \hookrightarrow {{\,\mathrm{Spec}\,}}(R^{\mathrm {patch}})$). In fact, the usual Taylor–Wiles method shows that ${{\,\mathrm{Spec}\,}}(R^{\mathrm {patch}})$ is irreducible, so we can move from $x'$ to x and deduce that y is also in the support of $N_\infty$. This shows that ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is automorphic.

The key step in the proof is to use vanishing of an adjoint Selmer group⁷⁵ to show that $y'$ defines a regular point of ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$.

Proposition 5.1.2

The prime ideal $y \in {{\,\mathrm{Spec}\,}}(P^\mathrm{{geo}}_{{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }})$ is in the support of $N_{{{\,\mathrm{Sym}\,}}^n{\mathfrak {m}}}$. As a consequence, ${{\,\mathrm{Sym}\,}}^n\rho _{f,\iota }$ is automorphic.

Proof

By the arguments we explained in Sect. 4.3, since $R_\infty$ is a domain, we know that $M_\infty$ has full support in ${{\,\mathrm{Spec}\,}}(R_\infty )$ and the quotient map $R_\infty \rightarrow R^{\mathrm {patch}}$ is an isomorphism.

The same argument tells us that $N_\infty$ is a Cohen–Macaulay $P^{\mathrm {patch}}$-module. This means that its support in ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$ is equidimensional of dimension $\dim (S_\infty )$. Writing $y'_\infty$ for the image of $y'$ in ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$, we know that $y'_{\infty }$ is in the support of $N_\infty$. We are going to show that $(P^{\mathrm {patch}})_{y'_{\infty }}$ is a regular local ring of dimension $\dim (S_\infty )-1$. On the one hand, we have a lower bound for the Krull dimension of $(P^{\mathrm {patch}})_{y'_{\infty }}$, as we now explain. Since $y'_{\infty }$ is in the support of $N_\infty$ it is contained in an irreducible subset of ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$ of dimension at least $\dim (S_\infty )$, corresponding to a minimal prime ${\mathfrak {p}}_{\min } \in {{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$.

As $P^{\mathrm {patch}}$ is a catenary local ring (it is a quotient of a power series ring over ${{\mathcal {O}}}_E$), we deduce that there is a chain of prime ideals refining ${\mathfrak {p}}_{\min } \subset y'_{\infty } \subset {\mathfrak {m}}_{P^{\mathrm {patch}}}$ of length at least $\dim (S_\infty )$. Since $y'_{\infty }$ has height 1, it follows that there is a chain of prime ideals joining ${\mathfrak {p}}_{\min }$ and $y'_{\infty }$ with length at least $\dim (S_\infty )-1$. This shows that $(P^{\mathrm {patch}})_{y'_{\infty }}$ has dimension at least $\dim (S_\infty )-1$.

On the other hand, quotienting out by the augmentation ideal of $S_\infty$ in $(P^{\mathrm {patch}})_{y'_{\infty }}$ (i.e., quotienting out by $\dim (S_\infty )-1$ variables) brings us to $P_{y'}$ which, as we remarked above, is just the coefficient field E. So the maximal ideal in $(P^{\mathrm {patch}})_{y'_{\infty }}$ can be generated by $\dim (S_\infty )-1$ elements. This shows that $(P^{\mathrm {patch}})_{y'_{\infty }}$ is a regular local ring of dimension $\dim (S_\infty )-1$.

It follows that there is a unique irreducible component of ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$ containing $y'_{\infty }$, and it has dimension $\dim (S_\infty )$. Since the support of $N_\infty$ is equidimensional of dimension $\dim (S_\infty )$, this irreducible component is contained in the support of $N_\infty$. Because ${{\,\mathrm{Spec}\,}}(R_\infty ) = {{\,\mathrm{Spec}\,}}( R^{\mathrm {patch}})$ is irreducible, the image of ${{\,\mathrm{Spec}\,}}( R^{\mathrm {patch}})$ in ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$, which contains $y'_{\infty }$, is contained in the support of $N_\infty$. This implies that the image $y_\infty$ of y in ${{\,\mathrm{Spec}\,}}(P^{\mathrm {patch}})$ is contained in the support of $N_\infty$. By Nakayama’s lemma, this is equivalent to y being in the support of $N_{{{\,\mathrm{Sym}\,}}^n{\mathfrak {m}}}$. $\square$

5.2 The Eigencurve

Our second method for proving automorphy of symmetric power representations is formally similar to Theorem 5.1.1, but propagates automorphy of symmetric powers along finite slope p-adic families of modular forms. We have already seen one way to p-adically interpolate systems of Hecke eigenvalues for modular forms—Emerton’s completed cohomology. Earlier work of Hida and Coleman used different methods to interpolate (respectively) ordinary and finite slope modular forms. A Hecke eigenform f is ordinary if $a_p(f)$ is a p-adic unit and finite slope if $a_p(f) \ne 0$.³⁴

Coleman and Mazur²⁹, and, in more generality, Buzzard¹⁷ constructed p-adic analytic spaces called eigencurves, interpolating Hecke eigenvalues arising from finite slope modular forms.

Fix a level N and a prime $p \nmid N$. An eigencurve is a p-adic analytic space ${{\mathcal {E}}}_p(N)$, equidimensional of dimension 1, containing a Zariski-dense set of points corresponding to pairs $(f,\alpha _p)$, $f \in S_k(\Gamma _1(N))$ a Hecke eigenform, $\alpha _p$ one of the roots of $X^2-a_p(f)X + \epsilon _f(p)p^{k-1}$.

More generally, if $f \in S_k(\Gamma _1(Np^r))$ is a Hecke eigenform, for some $r \ge 1$, with non-zero $U_p$ eigenvalue $\alpha _p = a_p(f)$, there is a corresponding point $(f,\alpha _p)$ of ${{\mathcal {E}}}_p(N)$. We call all these points coming from modular forms the classical points of ${{\mathcal {E}}}_p(N)$. The space ${{\mathcal {E}}}_p(N)$ comes with a map $w: {{\mathcal {E}}}_p(N) \rightarrow {{\mathcal {W}}}$ to a weight space ${{\mathcal {W}}}$ which parametrizes p-adic characters of ${{\mathbb {Z}}}_p^{\times }$. The image $w(f,\alpha _p)$ of a classical point is determined by weight and the p-part of the character of f:

$$\begin{aligned} w(f,\alpha _p)(x) = x^{k-2} \epsilon _{f,p}(x). \end{aligned}$$

The space ${{\mathcal {W}}}$ is very simple: it is a finite disjoint union of p-adic open unit discs. When p is odd the connected components correspond to the restriction of the character to $\mu _{p-1} \subset {{\mathbb {Z}}}_p^\times$ and a co-ordinate on the disc is given by evaluating a character at $1+p$.

To explain more about the eigencurve, we’ll describe its construction using deformation rings of Galois representations. We fix a mod p (semisimple) Galois representation ${\overline{\rho }}: G_{{{\mathbb {Q}}}} \rightarrow {{\,\mathrm{GL}\,}}_2({\overline{{{\mathbb {F}}}}}_p)$ which we assume arises from a Hecke eigenform of level N.

We have a pseudodeformation ring $P_{{\overline{\rho }}}$ parametrizing pseudodeformations of ${\overline{\rho }}$ which are unramified at primes not dividing Np, and we can construct from this a p-adic analytic space $X_{{\overline{\rho }}}$ (the construction is due to Berthelot³⁸³⁵). Considering a pair $(f,\alpha _p)$ as above, we get a ‘classical point’

$$\begin{aligned} (\rho _f,w(f,\alpha _p),\alpha _p) \in X_{{\overline{\rho }}}, \times {{\mathcal {W}}}\times {{\mathbb {G}}}_m \end{aligned}$$

if $\rho _f$ has mod p reduction isomorphic to ${\overline{\rho }}$. Taking the Zariski-closure³⁶ of the classical points gives a closed analytic subspace ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}} \subset X_{{\overline{\rho }}} \times {{\mathcal {W}}}\times {{\mathbb {G}}}_m$. Taking a disjoint union of the ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}}$ over modular (level N) residual representations ${\overline{\rho }}$ gives one construction of the eigencurve ${{\mathcal {E}}}_p(N)$. It is entirely unclear from this construction that ${{\mathcal {E}}}_p(N)$ has dimension one! This is proved using Coleman’s theory of families of overconvergent modular forms, which gives an automorphic construction of the space ${{\mathcal {E}}}_p(N)$ and in particular proves that ${{\mathcal {E}}}_p(N)$ is quasi-finite and flat over ${{\mathcal {W}}}$.

Each point $z \in {{\mathcal {E}}}_p(N)_{{\overline{\rho }}} \subset X_{{\overline{\rho }}}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m$ has an associated Galois pseudorepresentation, coming from the image of z in $X_{{\overline{\rho }}}$. Supposing that this pseudorepresentation is irreducible, we get a continuous representation

$$\begin{aligned} \rho _z: G_{{\mathbb {Q}}}\rightarrow {{\,\mathrm{GL}\,}}_2({{\mathbb {C}}}_p).\end{aligned}$$

Kisin proposed an extension of the Fontaine–Mazur conjecture which would characterize those Galois representations coming from points of the eigencurve. In particular, they should be points where the local Galois representation $\rho _z|_{G_{{{\mathbb {Q}}}_p}}$ is trianguline.

5.3 Trianguline Representations and the Eigencurve

To say something about these trianguline representations and their connection with the eigencurve, we first consider the p-adic analytic space $X_{{\overline{\rho }}_p}$ associated with the pseudodeformation ring $P_{{\overline{\rho }}_p}$ of the local residual representation ${\overline{\rho }}_p = {\overline{\rho }}|_{G_{{{\mathbb {Q}}}_p}}$. Each classical point $(f,\alpha _p)$ of ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}}$ gives us a point of $X_{{\overline{\rho }}_p}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m$, where $\alpha _p$ is an eigenvalue of the Frobenius operator on the crystalline Dieudonné module $D_{\mathrm {cris}}(\rho _f|_{G_{{{\mathbb {Q}}}_p}})$ and $w(f,\alpha _p)$ can be read off from $\det (\rho _f|_{G_{{{\mathbb {Q}}}_p}})$ using local class field theory. This means we can define (purely locally) a subset of points in $X_{{\overline{\rho }}_p}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m$ coming from certain de Rham lifts $\rho$ of ${\overline{\rho }}_p$ and a non-zero eigenvalue of Frobenius on $D_{\mathrm {cris}}(\rho )$; this subset will contain the image of all the classical points in ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}}$. Taking a Zariski-closure, we obtain a closed analytic subspace $X_{{\overline{\rho }}_p}^\mathrm{{tri}} \subset X_{{\overline{\rho }}_p}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m$ with a map ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}} \rightarrow X_{{\overline{\rho }}_p}^\mathrm{{tri}}$.

As with the eigencurve, the definition of the space $X_{{\overline{\rho }}_p}^\mathrm{{tri}}$ by a closure construction is not especially illuminating. With much more work the points of $X_{{\overline{\rho }}_p}^\mathrm{{tri}}$ can be intrinsically characterized as representations which are trianguline (in the sense of Colmez³⁰); this follows from a result of Kisin⁶⁰ on analytic continuation of crystalline periods. The simplest family of trianguline two-dimensional representations are those which are reducible. More generally, there are representations which are irreducible but which become reducible when passing to a category of $(\phi ,\Gamma )$-modules over a Robba ring.

Having constructed the local trianguline space, we can define a global version using a fiber product:

$$\begin{aligned} X^\mathrm{{tri}}_{{\overline{\rho }}} := (X_{{\overline{\rho }}}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m) \times _{X_{{{\overline{\rho }}}_p}\times {{\mathcal {W}}}\times {{\mathbb {G}}}_m} {{\mathcal {X}}}^\mathrm{{tri}}_{{{\overline{\rho }}}_p}. \end{aligned}$$

We then have a closed immersion ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}} \hookrightarrow X^\mathrm{{tri}}_{{\overline{\rho }}}$. This is the analogue of the closed immersion ${{\,\mathrm{Spec}\,}}({{\mathbb {T}}}_{\mathfrak {m}}) \hookrightarrow {{\,\mathrm{Spec}\,}}(R_{{\overline{\rho }}}^\mathrm{{geo}})$ which we consider when thinking about modularity lifting.

Kisin’s extension of the Fontaine–Mazur conjecture implies that ${{\mathcal {E}}}_p(N)$ is essentially isomorphic to $X^\mathrm{{tri}}_{{\overline{\rho }}}$—more precisely, it will be a union of irreducible components in $X^\mathrm{{tri}}_{{\overline{\rho }}}$ which we can describe by imposing extra conditions on the ramification at primes dividing N in the Galois representations parametrized by $X_{{\overline{\rho }}}$. Emerton’s approach to the Fontaine–Mazur conjecture also proves this statement in many cases⁴¹.

5.4 Analytic Continuation of Modularity

In this subsection, we will sketch the strategy used⁷³ to prove the following:

Theorem 5.4.1

(N–Thorne) Suppose $f, f'$ are two cuspidal Hecke eigenforms, both with weight at least two and a common level N. Fix a prime $p \nmid N$ and let $\alpha _p$ and $\alpha _p'$ be roots of $X^2-a_p(f)X + p^{k_f-1}\epsilon _f(p)$ and $X^2-a_p(f')X + p^{k_{f'}-1}\epsilon _{f'}(p)$ respectively. Fix an integer $n \ge 1$ and an isomorphism $\iota : {\overline{{{\mathbb {Q}}}}}_p\cong {{\mathbb {C}}}$, and suppose the following conditions hold:

• (1) $(f,\alpha _p)$ and $(f',\alpha '_p)$ lie on a common irreducible component of ${{\mathcal {E}}}_p(N)$.

• (2) Neither f nor $f'$ has CM and neither of the Hecke eigenvalues $\iota ^{-1}(a_p(f)), \iota ^{-1}(a_p(f'))$ is a p-adic unit.

• (3) The conjugacy classes ${{\,\mathrm{Sym}\,}}^n(\pi (f)_p)$ and ${{\,\mathrm{Sym}\,}}^n(\pi (f')_p)$ are regular (i.e., there are $n+1$ distinct eigenvalues).

• (4) ${{\,\mathrm{Sym}\,}}^n \rho _{f',\iota }$ is automorphic.

Then ${{\,\mathrm{Sym}\,}}^n \rho _{f,\iota }$ is automorphic.

A few remarks on the theorem:

• (1) The first condition automatically implies that ${\overline{\rho }}_{f,\iota } \cong {\overline{\rho }}_{f',\iota }$. So we can view this theorem as another ‘relative modularity lifting theorem’, but with a stronger condition on the relationship between $\rho _{f,\iota }$ and $\rho _{f',\iota }$. One significant gain, in comparison to Theorem 5.1.1, is that we have no condition on the image of ${\overline{\rho }}_{f,\iota }$.

• (2) To make condition (3) more explicit, note that ${{\,\mathrm{Sym}\,}}^n(\pi (f)_p)$ is regular if and only if, writing $\alpha _p$ and $\beta _p$ for the two roots of $X^2-a_p(f)X + p^{k_f-1}\epsilon _f(p)$, we have $(\alpha _p/\beta _p)^i \ne 1$ for $i = 1, \ldots , n$. An amusing argument with congruences mod 5 and 7 shows that a level 1 Hecke eigenform satisfies this condition for all n when $p=2$.

• (3) The precise statement in our paper corresponding to this result is a bit more general, allowing classical points with p dividing the level.³⁷ We also prove a version of the theorem where f and $f'$ are $\iota$-ordinary, in other words when $\iota ^{-1}(a_p(f))$ and $\iota ^{-1}(a_p(f))$ are p-adic units.

Proof

The idea of proof is formally similar to the proof of Theorem 5.1.1. However, we do not (directly) use Taylor–Wiles patching at all.³⁸ Instead the role of the patched deformation ring $R^{\mathrm {patch}}$ is played by the space of trianguline Galois representation $X^\mathrm{{tri}}_{{\overline{\rho }}_{f,\iota }}$ and the patched module $M_\infty$ is replaced by the eigenvariety ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}_{f,\iota }}$. The ring $S_\infty$ controlling ramification at auxiliary primes is replaced by the weight space ${{\mathcal {W}}}$.

In other words, instead of allowing ramification at auxiliary Taylor–Wiles primes and mapping the Galois representations $\rho _{f,\iota }$ and $\rho _{f',\iota }$ to points of an irreducible scheme ${{\,\mathrm{Spec}\,}}(R_\infty )$, we enlarge the class of local Galois representations we permit at the prime p and map $\rho _{f,\iota }$ and $\rho _{f',\iota }$ (with the extra data coming from the choice of refinements $\alpha _p$, $\alpha '_p$) to points of $X^\mathrm{{tri}}_{{\overline{\rho }}_{f,\iota }}$. Assumption (1) in the theorem means that these points lie in a common irreducible subspace.

We need versions of ${{\mathcal {E}}}_p(N)_{{{\overline{\rho }}}_{f,\iota }}$ and $X^\mathrm{{tri}}_{{{\overline{\rho }}}_{f,\iota }}$ which will interpolate self-dual automorphic representations and Galois representations lifting ${{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }$. We denote these by ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ and $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$, respectively. They fit into a commutative diagram with closed immersions for the vertical maps from the automorphic to Galois spaces:

There are several different ways to construct the eigenvariety ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$. For example, using Hansen’s general construction for cohomological automorphic representations of reductive groups⁵⁰. The construction which was most convenient for us was to change contexts so that we are working with automorphic forms on definite unitary groups of rank 2 and $n+1$, and then use Emerton’s representation-theoretic eigenvariety construction⁴⁰ as in the work of Breuil, Hellmann and Schraen⁹.

The trianguline space $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ parametrizes $n+1$-dimensional, (self-dual) p-adic representations of $G_{{\mathbb {Q}}}$, lifting the fixed pseudorepresentation ${{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }$. It is a closed analytic subspace of a product of spaces $X_{{{\,\mathrm{Sym}\,}}^n {{\overline{\rho }}}_{f,\iota }} \times {{\mathcal {T}}}$, where ${{\mathcal {T}}}$ parametrizes characters of the diagonal torus in ${{\,\mathrm{GL}\,}}_{n+1}({{\mathbb {Q}}}_p)$.³⁹ Its construction and the existence of a closed immersion from the eigenvariety in this higher rank case has been established in different contexts by people including Bellaïche and Chenevier⁶, Hellmann⁵², Kedlaya–Pottharst–Xiao.⁶⁴ and Liu⁷⁰. In fact, this is usually done under the assumption that ${{\,\mathrm{Sym}\,}}^n {\overline{\rho }}_{f,\iota }$ is irreducible (although Hellmann’s preprint⁵² does not include this assumption). For this reason, we do not literally use a space $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ , and instead work with an open neighborhood of $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ at a point with an irreducible associated Galois representation. This means that the difference between pseudorepresentations and representations can be safely ignored. The idea of the argument is easier to explain with a global space $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$, so we will do this here.

To complete the proof, following the pattern of the proof of Theorem 5.1.1, we first need to show:

• (REG) $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ is regular of dimension equal to $\dim ({{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }})$ at the point $y'$ associated to ${{\,\mathrm{Sym}\,}}^n \rho _{f',\iota }$ and the refinement $\alpha '_p$.

We will come back to the proof of this later. A consequence of (REG) is that there is a unique irreducible component C of $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ passing through $y'$, and it has dimension equal to $\dim ({{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }})$. It contains an irreducible component of ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$, and since the eigenvariety is equidimensional we see that the closed immersion ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }} \hookrightarrow X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ identifies C with an irreducible component of ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$. Since x and $x'$ are points of an irreducible subspace of ${{\mathcal {E}}}_p(N)_{{\overline{\rho }}_{f,\iota }}$, the image y of x in $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ is also contained in the irreducible component C. We deduce that y is a point of the eigenvariety ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$. To conclude, we need to show that y is in fact a classical point. If the slope $v_p(\alpha _p)$ is sufficiently small, this follows from a ‘small slope implies classical’ theorem generalizing Coleman’s theorem for overconvergent modular forms. However, since we are assuming f is non-ordinary, for big enough n we will not be able to apply this result. Instead we use a slightly more precise classicality theorem which follows from ideas of Chenevier and Breuil–Hellmann–Schraen^{9, 24}, and shows that a point of ${{\mathcal {E}}}_{p,{{\,\mathrm{Sym}\,}}^n{\overline{\rho }}_{f,\iota }}$ with a de Rham associated Galois representation which is sufficiently generic (‘every refinement in non-critical’) is classical. The idea goes back to Coleman, who proved that an overconvergent eigenform f of weight $k \ge 2$ which is not classical has a ‘companion form’ in weight $2-k$ with Hecke eigenvalues equal to a twist of those of f—more precisely, the eigenvalue of $T_l$ for $l \nmid Np$ is $l^{1-k}a_l(f)$. Supposing that $\rho _f$ is de Rham, the existence of the companion form forces the representation $\rho _{f}$ to have a special property: the local representation $\rho _{f}|_{G_{{{\mathbb {Q}}}_p}}$ is a direct sum of two characters.

Finally, we go back to the proof of (REG). This follows an idea due to Kisin in the two-dimensional case⁶⁰, which was generalized by Bellaïche and Chenevier⁶. Again the vanishing of a Bloch–Kato adjoint Selmer group is crucial. This is used to give an upper bound for the dimension of the tangent space of $X^\mathrm{{tri}}_{{{\,\mathrm{Sym}\,}}^n{{\overline{\rho }}}_{f,\iota }}$ at a classical point⁴⁰. On the other hand, the existence of the closed immersion j gives a lower bound on the dimension of the local ring at this point. Since these bounds coincide, we get regularity. $\square$

5.5 Symmetric Power Functoriality: the Rest of the Proof

Theorems 5.1.1 and 5.4.1 combine to allow us to prove:

Theorem 5.5.1

Let $n \ge 2$ be an integer and suppose that the nth symmetric power lifting exists for at least one cuspidal Hecke eigenform of level 1. Then the nth symmetric power lifting exists for every cuspidal Hecke eigenform without CM and of weight $k \ge 2$.

Proof

The argument proceeds in three steps. First, we show that automorphy of the nth symmetric power for one level 1 cuspidal Hecke eigenform implies automorphy of the nth symmetric power for all level 1 cuspidal Hecke eigenforms. To prove this, we are going to apply Theorem 5.4.1, but for this to be of any use we need some information about the irreducible components of an eigencurve. For this reason, we take $p = 2$ and use a beautiful explicit description, due to Buzzard–Kilford¹⁰, of a large part of the eigencurve ${{\mathcal {E}}}_2(1)$. This allows us to show that any two classical points on the eigencurve ${{\mathcal {E}}}_2(1)$ can be connected by a sequence of moves of two types:

• moving along an irreducible component

• jumping from a classical point $(f,\alpha )$ to $(f,\beta )$ when f has level 1 and $\alpha , \beta$ are the two roots of $X^2 - a_2(f)X+\epsilon _f(2)2^{k-1}$; more generally, we can jump from $(f,\alpha )$ to its ‘twin’ point $(f',\beta )$ where $f'$ is a character twist of f. In either case, $v_p(\alpha ) + v_p(\beta ) = k-1$, where k is the weight of f.

It is clear that the second kind of move preserves automorphy of symmetric powers. Moving along irreducible components preserves automorphy of symmetric powers by Theorem 5.4.1. So these moves allow us to propagate automorphy of the nth symmetric power to all level 1 eigenforms.

For the second step, we apply a version of Theorem 5.4.1 where p is allowed to divide the level N of the modular forms. This allows us to extend automorphy of the nth symmetric power to eigenforms of squarefree level, or more generally to those eigenforms whose associated automorphic representation has no supercuspidal local factor. These are precisely the eigenforms which (after possible twisting by a Dirichlet character) appear as classical points of eigencurves. A technical point arising here is that we need to deal with a version of the regularity condition in Theorem 5.4.1—in general, it is not known if the polynomial $X^2-a_p(f)X+p^{k_f-1}\epsilon _f(p)$ has distinct roots²¹. To do this, we use the Taylor–Wiles method to construct a congruence modulo a large auxiliary prime to an eigenform which does satisfy this regularity condition and then use an automorphy lifting theorem¹² to reduce to the regular case.

Finally, for the third step, we need to deal with eigenforms with supercuspidal local factors. We can reduce to the case of weight 2¹². Suppose p is a prime where our eigenform f has a supercuspidal local factor. We find a congruence mod p between f and a non-ordinary eigenform g with a (ramified) principal series factor at p. Using the modularity lifting Theorem 5.1.1, we can then deduce automorphy of ${{\,\mathrm{Sym}\,}}^n \rho _{f,\iota }$ from the automorphy of ${{\,\mathrm{Sym}\,}}^n \rho _{g,\iota }$. This time we need to ensure that the condition on the image of our mod p Galois representation in Theorem 5.1.1 is satisfied. To do this, we follow an idea of Khare and Wintenberger which they apply to deduce Serre’s conjecture in general from the level 1 case, using congruences (modulo a prime $l \ne p$) to modular forms with ‘good dihedral’ ramification at auxiliary primes which forces them to have large image. $\square$

With this theorem in hand, it remains to find one example (for each n) of a level 1 cuspidal Hecke eigenform for which the nth symmetric power exists. The strategy here is similar to Clozel and Thorne’s, but instead of using reducibility of the mod p Galois representations for small p, the idea (suggested by Clozel) is to consider modular forms which are congruent to a CM form $\theta$ mod p, which means that the associated mod p Galois representations are dihedral (induced from $G_K$ for $K/{{\mathbb {Q}}}$ the imaginary quadratic field relevant for $\theta$). In particular, the symmetric powers of these Galois representations decompose into 1- and 2-dimensional pieces, so it follows from Langlands’s theory of Eisenstein series that they are associated with a (non-cuspidal) automorphic representation $\pi _n(\theta )$. There is a great deal of work needed to complete the proof from here, but the ingredients include:

• Modularity lifting theorems allowing residually reducible Galois representations^95,3.

• A construction of congruences between the Eisenstein series $\pi _n(\theta )$ and cuspidal automorphic representations with appropriate ramification at an auxiliary prime. These level raising congruences are needed in order to apply our lifting theorem³. One family of level raising congruences comes from the work of Anastassiades and Thorne⁵.

• Another kind of level raising result established in our work⁷³ takes up a significant part of that paper. The construction is founded on the unipotent cuspidal representation of a finite unitary group in three variables, and a lot of results from the local and global theory of automorphic forms are applied, including Moeglin’s classification of discrete series representations of p-adic unitary groups⁷², base change for automorphic representations of unitary groups (proved using Arthur’s simple trace formula⁶⁷) and results of Lust and Stevens⁷¹ which allow us to understand some of the local behavior of this global base change in terms of Moeglin’s classification.