Heavy Metal Removal from Aqueous Solutions Using Fly-Ash Derived Zeolite NaP1

Abstract

Fly-ash derived zeolites have recently -received great attention as cheaper adsorbents to remove heavy metals from water since they can be synthesized from a waste product. In this study, we evaluated the single- and multi-cation adsorption efficiencies of fly-ash derived NaP1 for the removal of zinc (Zn), copper (Cu) and lead (Pb). We also determined precipitation and leaching from NaP1 during the adsorption. Results showed that the uptake capacities for Zn (34 mg/g) and Pb (192 mg/g) were higher than other fly-ash derived NaP1 and adsorbents such as clinoptilolite and activated carbon. The Cu uptake was estimated ~ 14.6 mg/g. Pb²⁺  > Cu²⁺  > Zn²⁺ is the order for the metal cation selectivity of NaP1. Langmuir adsorption isotherm and pseudo-second order kinetic model fitted best for all elements. The metal uptake occurred in 15 min. Diffusion of hydrated metals through microporous channels is the rate-determining step.

Article Highlights

• Fly-ash derived NaP1 adsorbed 34.2 mg g⁻¹ Zn²⁺, 14.6 mg g⁻¹Cu²⁺ and 192 mg g⁻¹ Pb²⁺.

• Ion selectivity of NaP1 is in the order of Pb²⁺  > Cu²⁺  > Zn²⁺.

• Langmuir and pseudo-second order kinetic models fitted best for all elements.

• The metal uptake occurred in 15 min for both single and multi-element adsorption.

• Leaching and precipitation were evaluated.

Introduction

Accelerated industrialisation and population growth in developing countries has generated vast quantities of wastewater effluents, comprising of wide variety of heavy metal ions into environment within the past decades. Direct disposal of these wastewater will impose serious threat to the environment and have lethal effects on the community due to their toxicity and carcinogenic nature (Timothy and Williams 2019). Industries such as electroplating, mines, pharmaceuticals, paint and textile, are the major point source, producing effluents constitute heavy metals (Tchounwou et al. 2012; Bazrafshan et al. 2015) such as zinc, lead, copper, nickel and cadmium, regardless of the economic benefits that these industries offer to the communities. Hence, there is a requirement to explore eco-friendly (Tokay and Akpinar 2021), sustainable, cost effective and efficient adsorbents while eliminating pollution (Klučáková and Pavlíková 2017).

Various heavy metal removal technologies have been explored to date. Adsorption is preferred to others such as reverse osmosis (Quadis and Moussa 2004), electrocoagulation (Bazrafsahn et al. 2015), ultrafiltration (Cao et al. 2020), filtration (Abdullah et al. 2019), coagulation and precipitation (Charerntanyarak 1999). The process is economically viable, highly efficient, easy to be operated and possesses great availability of adsorbent compared to other techniques. Designing and operation stage of adsorption processes are flexible, and the process can produce high-purity effluent (Perić et al. 2004; Asim et al. 2020). At present, the most widely applied porous adsorbents include activated carbon, carbon nanotubes, zeolite, clay minerals, biosorbent and biopolymers. However, most of these commercial adsorbents have become more expensive due to the increasing demand, high cost of production and regeneration (Zwain et al. 2014; Kołodyńsk et al. 2017; Erdem et al. 2004). Therefore, alternative adsorbents are crucial.

Zeolites are well known for their extensive ion exchange and adsorption capabilities (Margeta et al. 2013). Existing as both natural and synthetic, they have been used in petroleum refinery, water softening, heavy metal removal, separation of gases, dehumidifiers and many more applications (Li et al. 2019). Synthetic zeolites have been preferred over natural zeolites due to their tailorable properties, higher purity and high thermal stability (Li et al. 2019). However, synthetic zeolites are also becoming more expensive due to increasing demand, requiring cheaper precursors to promote sustainability.

Fly-ash from coal combustion power plants contains high amounts of quartz and mullite, composed of necessary precursors for the synthesis of zeolites (Yan et al. 2018). Thus, recycling waste from coal fly-ash to remove pollutants from water is a possible low-cost method for preparing synthetic zeolites, reinforcing sustainability, waste recycle, and thus industrial symbiosis. Fly-ash has mostly been used as construction material production (Ramesh et al. 2020), representing about 48% of the total amount, while most of the fly-ash was landfilled (Brännvall and Kumpiene 2016). To date, zeolite X, A, chabazite, sodalite and NaP1 have been synthesised from fly ash. Zeolite X and A are in high demand due to their uniform pore structure and larger pore size, compared to NaP1 (Alvarez-Ayuso et al. 2003), sodalite and chabazite. However, fly-ash derived zeolites X and A are more expensive to synthesize, compared to NaP1, through the conventional hydrothermal synthesis process as they require large quantities of raw materials (aluminate, silicon and NaOH) and a 2-step process (Czuma et al. 2019). Fly-ash derived NaP1 can be produced with a high yield (45–75%), compared to fly-ash derived zeolites X and A (16–18%) in a one-step process using low amount of raw materials (Moreno et al. 2001; Querol et al. 2001). Thus, fly-ash derived NaP1 is preferable due to its high yield, cost and duration of production and ease of preparation.

NaP1 has been tested for removal of heavy metals such as Zn, Cu, Ni and Cd in acid mine (Prasad and Mortimer 2011), electroplating wastewater (Steenbruggen and Hollman 1998; Alvarez-Ayuso et al. 2003) and synthetic water matrix (Lee et al. 2000; Nascimento et al. 2009). Lee et al. (2000) explored synthetic fly-ash derived NaP1 for zinc, copper and lead removal from water matrix of concentration (20–400 mg/l) using 0.1 g zeolite in a litre of solution at 25 °C. Although there is no record of pH adjustment and contact time. They reported 65.8 mg/g, 73.5 mg/g and 267 mg/g adsorptive capacities for zinc, copper and lead, respectively. Similarly, Moreno et al. (2001), Querol et al. (2002) and Prasad and Mortimer (2011) tested synthetic NaP1 on zinc removal from acid mine wastewater with initial concentrations of 65 mg/l, 54 mg/l and 174 mg/l, respectively. Contact time for all experiments was reported as 1 h with initial pH values of  > 4.6, 5.5 and 2.5–5.5, respectively, without further pH adjustment during the experiment. These experiments showed more than 94% removal efficiency for NaP1. Alvarez-Ayuso et al. (2003) treated zinc and copper from an electroplating wastewater finishing effluent (125 mg/l) at pH 6 in 1 h using 2.5 mg/l adsorbent. They obtained an adsorptive capacity of 32.6 and 50.5 mg/g for zinc and copper, respectively. Nascimento et al. (2009) tested NaP1 for lead, zinc and copper removal from water and reported adsorptive capacities of 195 mg/g, 59.2 mg/g and 76.9 mg/g, respectively. They conducted their experiments at pH of 4–5, with the metal concentrations in the range of 100–3000 mg/l using 10 g/l adsorbents over 2 h at 25 °C. These studies have limited scope since the removal conditions (i.e., pH, temperature and concentrations of metals) considered were either narrow to a localized wastewater (target specific) or not relevant to industrial conditions. In addition, they did not report on leaching or precipitation. Moreover, current research on NaP1 does not present a clear distinction of the heavy metal removal mechanism (i.e., ion exchange, adsorption and precipitation) at relevant industrial conditions, providing limited information to adopt NaP1 for industrial applications.

In this study, we evaluated the use of fly-ash derived zeolite NaP1 for the remediation of copper, zinc and lead from water, mimicking electroplating plant effluent. Adsorption selectivity, kinetics and adsorptive capacity of NaP1 were determined via single and multi-cation batch adsorption experiments. For the first time, we evaluated the precipitation and leaching from the adsorbent for a wide range of conditions. Various techniques including X-ray diffraction, scanning electron microscopy and X-ray fluorescence spectroscopy were used to characterise the samples.

Experimental

Materials

Zeolite NaP1 was provided by Lublin University of Technology, Poland, synthesized from class F fly-ash, obtained from a Polish coal power plant. Wdowin et al. (2014) described the method used to synthesise zeolites from fly-ash as one of the precursors. NaP1 is the synthetic form of the gismondine-type zeolite. The crystal structure is made up of 2-dimensional pore system 8-member oxygen ringed channels (0.31 × 0.44 mm) and (0.26 × 0.49 mm) in the (100) and (010) direction, respectively, connected by a double crankshaft chain made up of four rings (Sharma et al. 2016). The effective pore size of NaP1 is ~ 0.29 nm (Alvarez-Ayuso et al. 2003).

Copper nitrate (Cu(NO₃)₂·3H₂O, 98%), zinc nitrate (Zn(NO₃)₂·6H₂O, 98%), lead nitrate (Pb(NO₃)₂, 98%), sodium hydroxide pellets (NaOH, 99.9%), nitric acid (HNO₃, 68%), hydrochloric acid (HCl, 37%) and ammonium acetate (NH₄COOH, 98%) were purchased from Fisher Scientific.

Characterisation

Bruker D8 Advance X-ray diffractometer (XRD) was used to characterize the powder samples. Samples were measured with a 0.6 slit for 2 h at 25 ± 2 °C and scanned between 5° and –65° 2θ with increments of 0.05° in 2 s. Cu Kα radiation was used at 40 kV and 35 mA.

The qualitative and quantitative elemental composition of the zeolite samples were determined using a Panalytical Epsilon 3XL X-ray fluorescence analyser (XRF) before and after adsorption. Powder samples (~ 5 g) were ground, placed in a plastic cup (approx. 4.9 cm in depth) and covered with a plastic film at the bottom.

Philips XL30 scanning electron microscope, operated at 15 kV, was used to evaluate the shape and size of the NaP1 crystals. NaP1 crystals were sprinkled on sample stubs with carbon adhesives. Before use, crystals were carbon coated using Edwards E306A film coater (10 nm thin layer, high vacuum, 30 V/30 A).

The nitrogen adsorption/desorption isotherms were obtained using a Micromeritics ASAP 2420 V2.09. Samples were degassed in the chamber (at 250 °C) to remove any adsorbed gases and water prior to experiments. The pore size and the volume and BET surface area were reported.

Adsorption Experiments

For single metal cation adsorption experiments, Pb, Cu and Zn concentrations were set to 100, 150 and 250 mg/l, respectively, in purified water (at 18.2 MΩ.cm resistivity). The pH (Jenway 570 with temperature correction function) of the solutions was maintained at a range of 3–4 using 68% HNO₃ and 2% wt/v NaOH solutions to prevent precipitation of Cu ions. Approximately 5 g/l zeolite samples were used during the experiments. The solutions were mixed on a magnetic stirrer up to 3 h at 22 ± 2 °C. Preliminary multi-cation adsorption experiments were conducted using 1 g/l NaP1 at pH 3.5, 20 ± 2 °C with the same initial heavy metal concentrations (12.5 mg/l) for all heavy metals to eliminate the concentration effect.

For the determination of the adsorption isotherms, the concentrations of individual heavy metal solutions were adjusted in the range of 50–1000 mg/l, 50–3500 mg/l and 50–2800 mg/l for Cu, Zn and Pb, respectively. The pH, temperature and amount of adsorbent were the same as the multi-cation adsorption experiments. All experiments were repeated two times to observe errors associated. The sampling amount was not exceeded 5–10% of the solution amount.

The adsorption kinetics during the adsorption of heavy metal ions was determined by employing the pseudo-first (Eq. 1) and -second order (Eq. 2) kinetic models as follpws:

$$\mathrm{ln}\left({Q}_{e}-{Q}_{t}\right)=\mathrm{ln}\left({Q}_{e}\right)-{k}_{1}\times t,$$

(1)

$$\frac{t}{{Q}_{t}}=\frac{1}{{k}_{2}\times {{Q}_{e}}^{2}}+\frac{1}{{Q}_{e}},$$

(2)

where Q_t (mg/g) and Q_e (mg/g) are the adsorbed amount of metal ions at time t (min) and at equilibrium, respectively. k₁ (1/min) and k₂ (g/mg min) are the pseudo-first and -second order rate constants, respectively. t (min) represents the adsorption time.

Freundlich (Eq. 3) and Langmuir (Eq. 4) models were employed to determine the adsorption mechanism and the maximum adsorption capacity at equilibrium as follows:

$${Q}_{e}= {K}_{F}.{{C}_{e}}^\frac{1}{n},$$

(3)

where ${K}_{F}$ is the Freundlich isotherm constant, indicating the adsorption capacity of the adsorbent. C_e represents the adsorbate concentration in the solution at equilibrium and 1/n indicates the adsorption intensity between the NaP1 and metal ions.

$$\frac{{C}_{e}}{{q}_{e}}=\left(\frac{1}{b{q}_{m}}\right)+\frac{{C}_{e}}{{q}_{m}},$$

(4)

where q_e is the amount of solute adsorbed per unit mass of adsorbent. b (l/mg) is Langmuir constant. C_e represents the adsorbate concentration in the solution while q_m shows the maximum adsorption capacity of the adsorbent at equilibrium, estimated by the linear Langmuir adsorption model.

Zeolite NaP1 was also tested for leachates under the same adsorption conditions (pH 3.5, T = 22 ± 2 °C, 5 g/l NaP1) to determine the release of the elements into the purified water, in the absence of heavy metal ions. The experiments were repeated three times.

The effect of precipitation was quantified and deducted from the resulting metal uptake experiments. Precipitations of Cu, Zn, Pb were determined at pH 3.5, without zeolite, at 20 ± 2 °C. Initial Cu²⁺, Zn²⁺ and Pb²⁺ concentrations were set to approx. 12.5 mg/l for each element.

Sampling (12 ml) was conducted from the solutions at predetermined times for analyses using inductively coupled plasma atomic emission spectroscopy (ICP-AES, Perkin Elmer 300 DV). The NaP1 was separated from solutions using a centrifuge (Hettich, Rotofix 32 A) at 4000 rpm for 8 min. The supernatant was decanted and filtered (Minisart^® 0.2 μm, hydrophilic). Ten ml from the filtered solution was then pipetted in a 15-ml polypropylene conical tube, acidified with 5 ml of 30% (v/v) nitric acid and refrigerated to prevent metal precipitation and microbial degradation. Calibration standards were prepared using a multi-cation solution. Purified water was also tested in every batch.

Results and Discussions

Characterization

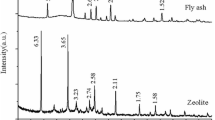
The XRD pattern of zeolite NaP1 confirmed the presence of NaP1 structure, represented by the characteristic peaks at 12.5°, 17.8°, 21.6°, 28.2°, 31°, 33.4° and 46° 2θ (Supplementary Information, (SI) Fig S1). The XRD pattern also shows the peaks of mullite and quartz.

The SEM image of NaP1 shows the agglomeration of cubes (min 0.2 micron) into larger particles in the size range of 4.5–6 μm, forming a rough heterogeneous surface (Fig. S2). Wdowin et al. (2014) described this appearance as lamellar aggregates of plate-like shapes as a characteristic feature of NaP1.

The chemical composition of zeolite NaP1 synthesized from coal fly-ash is presented in Table 1. Quantitative analysis using XRF showed that most of the zeolite constitutes SiO₂, Al₂O₃ and Na₂O, as expected. In addition, oxides of Mg, Ca and Fe accounted for ~ 7–8% of the remaining composition.

Table 1 Percentage composition of zeolite NaP1 obtained from XRF using 5 g sample

Silicon dioxide to aluminium oxide (SiO₂/Al₂O₃) ratio for NaP1 was estimated as 1.51. The SiO₂/Al₂O₃ ratio was used as an indicator of sorption properties (Ouki and Kavannagh 1997). Ramesh and Reddy (2011) reported that zeolites with Si/Al ratio between 1.0 and 1.5 represents the potential of higher sorption and ion exchange capability. This is due to the exchange of aluminium ions with silicon ions, providing a negative framework for that zeolite.

Nitrogen adsorption/desorption isotherms observed follow Type II IUPAC classification with an H3 hysteresis loop (Fig. 1). This is characteristic of a mesoporous material of pore size between 2 and 50 nm. The Type II isotherm (adsorption) indicates monolayer—multilayer adsorption while the H3 hysteresis loop (desorption) represents plate-like particles, forming slit-shaped pores. BET area and pore diameter were estimated as ~ 60 ± 0.1 m²/g and 11 ± 0.1 nm, respectively.

Fig. 1

Nitrogen adsorption–desorption isotherms for NaP1

The isotherms below P/P_o < 0.05 shows the presence of micropores, whereas the P/P_o > 0.06 demonstrates larger pores filled at higher pressure. The 0.01 < P/P_o < 0.06 region of the plot is also known as the knee, which shows the end of monolayer adsorption coverage of adsorbent surface. The micropore region of the isotherm indicates that the low-pressure uptake of nitrogen gas is limited. For 0.06 < P/P_o < 0.45 region, where larger pores are accessed, multilayer adsorption starts and thus the volume of nitrogen adsorbed was increased with increasing relative pressure. Capillary condensation, which was observed during the desorption, suggests the presence of mesopore structure that is also confirmed by the pore size diameter.

Leaching and Precipitation

Leaching tests from NaP1 was undertaken at the adsorption conditions (3 h, pH = 3.5 and T = 20 ± 2 °C) in the presence of zeolite (5 g/l) without heavy metals (Table S1, S2). The leaching experiments showed that, Cu²⁺ (13.6 µg/g), Zn²⁺ (61 µg/g) and Pb²⁺ (6 µg/g) ions leached into water from NaP1 only at microgram levels in the first 15 min and concentrations were constant until 60 min. These concentrations are below the allowed effluent discharge limits and thus negligible compared to initial heavy metal concentrations in the water. Similarly, Na⁺, (23 mg/g), Ca²⁺ (11.4 mg/g), K⁺ (2.8 mg/g) and Al⁺ (21.2 mg/g) released into water within the first 15 min and stayed at similar levels until 60 min. These leachates are negligible when the content of NaP1 compared with Table 1. Therefore, leaching from NaP1 is not considered as a problem during the adsorption experiments.

The effect of precipitation was quantified and deducted from the resulting adsorption experiments, where needed. Table 2 shows the heavy metal precipitation at pH (3.5, 6.5, 10.5) from control experiments when 1 L water matrix was stirred for 1 h without zeolite.

Table 2 Concentrations of heavy metal cations in water as a function of time at pH 3.5, 6.5 and 10.5 (T = 20 ± 2 °C, no zeolite, 1 h)

The highest percentage of precipitation for all the heavy metals (> 95%) was observed at pH 10.5 due to the formation of metal hydroxides of copper, zinc and lead. These metal hydroxides are not soluble in water above the pH values of 5.3, 7.5 and 6, for Cu, Zn and Pb, respectively (Marchioretto et al. 2005). Therefore, the lowest heavy metal precipitation (3%) was observed at pH 3.5, conforming the absence of precipitation. Copper (2.61 mg/l) and lead (2.89 mg/l) precipitated, representing approximately 23% of the starting concentration at pH 6.5. Zinc precipitation (1.2 mg/l) was lower than copper and lead and equals to 9.2% of the starting concentration at pH 3.5. Copper and lead hydroxide formation/precipitation begin from pH > 5.3 and pH > 6, respectively, while zinc hydroxide formation begins pH > 7.5. This explains the low zinc precipitation that was observed at pH 6.5.

Adsorption Experiments

Figure 2 shows the single cation adsorption and control experiments (without zeolite), conducted using NaP1 at pH 3.5. A steep decline in concentrations were observed within the first 15 min for all metals, followed by a slight decrease until 60 min. This trend indicates that most of the adsorption sites available were occupied in 15 min, followed by a slow diffusion of metal ions through the pores of zeolite NaP1 until further saturation was achieved (Motsi et al. 2009) Zinc, lead and copper concentrations were measured as 217, 4.11 and 115 mg/l at the end of the adsorption experiments. These represent approx. 14, 96 and 23% zinc, lead and copper removal, respectively. Percentage removals indicate that the adsorption preference for NaP1 is in the order of Pb²⁺  > Cu²⁺  > Zn²⁺.

Fig. 2

Concentrations of cations in water during single cation adsorption (1 g/l NaP1) and precipitation/control experiments (without zeolite) as a function of time. Conditions: Zn²⁺ = 250 mg/l, Cu²⁺ = 150 mg/l, Pb²⁺ = 100 mg/l, pH = 3.5,t = 3 h, T = 20 ± 2 °C, Error < 5%

The precipitation/control experiments performed without NaP1, under the same conditions as the adsorption experiments (Fig. 2), showed no reduction in metal concentrations. These demonstrate that the decreases in metal concentrations obtained during the adsorption experiments can only be due to the presence of zeolite NaP1 and not precipitation.

Preliminary multi-cation adsorption experiments were performed at pH 3.5, 20 ± 2 °C for 1 h. Figure 3 shows metal uptake of zeolite NaP1 in a multi-cation solution as a function of time and in the absence of precipitation. At pH 3.5, where the concentration of H⁺ ions is 3.16 × 10^–4 M (acidic medium), a low lead uptake (2.1 mg/g) was measured in comparison to zinc (4.9 mg/g) and copper (4.2 mg/g). The highest metal uptake at pH 3.5 in multi-cation system was observed for zinc that was the least adsorbed in the single-cationsystem (6.6 mg/g). In contrast, lead uptake was the highest in the single-cation system (19.2 mg/g) and the least in the multi-cation system. We conducted these experiments with the same initial heavy metal concentrations (12.5 mg/l). Therefore, we eliminated the effect of concentration on the removal.

Fig. 3

Concentrations of heavy metal cations in water as a function of time at pH 3.5 and T = 20 ± 2 °C using 1 g/l NaP1 during multi-cation adsorption experiments. Initial metal concentrations were maintained at 12.5 mg/l for each heavy metal

Adsorptive capacities of adsorbents are generally higher in single cation adsorption compared to multi-cation due to metal competition within the system (Mohan and Singh 2002). There is the possibility of metal/metal competition (Rao et al. 2007) and metal/H₃O⁺ competition at low pH, increasing the positive charge of the zeolite surface, influencing the removal efficiency. Therefore, lead uptake was most influenced by this competition.

Figure 4 shows the amount of heavy metals adsorbed per gram of zeolite over the range of concentrations. An increase in initial concentration of zinc from 50 to 600 mg/l increased the concentration gradient of zinc ions towards available sites, thereby increasing the uptake until the point of saturation, where further increase in zinc concentration (> 600 mg/l) did not change the metal uptake. The shape of the isotherm for zinc closely relates to Type 1 isotherm (Hinz 2001). Therefore, at lower concentrations, more zinc ions can be removed from solution using zeolite NaP1. This is one of the advantages of NaP1 over other adsorbents since most of the current adsorbents and methods are unable to remove metal cations at very low concentrations in large volumes of water (Lakherwal 2014). NaP1 has demonstrated better removal capabilities, in comparison to other adsorbentsincluding activated carbon and clinoptilolite (Koshy and Singh 2016). The heavy metal removal efficiencies for these adsorbents, tested under the similar conditions as NaP1, showed metal removal capacities < 10 mg/g for zinc and copper (Erdem et al. 2004) and < 24 mg/g for lead (Rahman et al. 2016).

Fig. 4

Lead and zinc (a) and copper (b) uptakes as a function of equilibrium concentration of cations in water. Conditions: 5 g/l NaP1, Zn²⁺ = 50–2300 mg/l, Cu²⁺ = 50–1000 mg/l, Pb²⁺ = 50–2800 mg/l, pH = 3.5, t = 1 h, T = 20 ± 2 °C. Error < 5%

The shape of the isotherms are similar to the Langmuir and Type 1 isotherm, as observed for zinc (Fig. 4a, b). However, the lead isotherm is relatively steeper than zinc isotherm, showing a higher affinity of NaP1 to lead than zinc and copper at lower concentrations, demonstrated in similar works for NaP1 (Querol et al. 2002). This implies that lead ions would be removed quicker from solution at lower concentrations, compared to zinc and copper (Hinz 2001).

Data from the adsorption isotherms were evaluated using Langmuir and Freundlich isotherm models to determine the model best fitting the experimental data (Table 3, Figure S3 and S4).

Table 3 NaP1 adsorptive capacities of heavy metal cations for Langmuir and Freundlich models

Langmuir model well represented the data for the heavy metal ions since the regression coefficients (R²) are in the range of 0.98–0.99. Although Freundlich model was also employed, the regression coefficients were lower than 0.95 (Table 3). Nascimento et al. (2009) used both the Langmuir and Freundlich isotherms in describing the experimental data for NaP1 as the R² for both models was above 0.91 for Cu²⁺, Pb²⁺ and Zn²⁺ metals. However, Alvarez-Ayuso et al. (2003) described their experimental data with Langmuir since R² values > 0.99. Similarly, Utami et al. (2019) reported Langmuir isotherm and physisorption (using Gibbs free energy) for NaP1 derived from natural zeolites. In contrast, Lee et al. (2000) showed better fit with Freundlich model (R² > 0.82) for NaP1. The maximum adsorption capacity for zinc (34.2 mg/g at pH 3.5) in this study is higher, compared to the other reports in literature (Alvarez-Ayuso et al. 2003) while maximum adsorption capacity for lead (192 mg/g) was similar to Nascimento et al. (2009). In contrast, maximum adsorption capacity for copper (14.6 mg/g) was the lowest, compared to literature, where up to 50–77 mg/g uptakes were reported at pH 4–5 (Alvarez-Ayuso et al. 2003; Nascimento et al. 2009). This is probably due to the source of the fly-ash used for preparation of NaP1, higher pH and concentrations. In contrast, NaP1 adsorbs copper up to five times more than other zeolites such as clinoptilotite (Motsi et al. 2009).

Cation selectivity of an adsorbent can be influenced by several factors including electrostatic forces, ion charge, hydrated radius and precipitate formation (Hendricks 2010). Among these properties, hydrated radius, enthalpy of hydration and sieve action were selected to explain the selectivity zeolite NaP1. Effects of cation charge and complex and precipitate formation were negligible since ions have the same charge and experiments were conducted at pH 3.5, avoiding complex formation and precipitation. The following order for cation selectivity Pb²⁺  > Zn²⁺  > Cu²⁺ was determined from maximum sorption capacity (q_m) (Table 3). However, this does not match the order (Pb²⁺  > Cu²⁺  > Zn²⁺), published in literature for fly-ash derived NaP1 samples (Steenbruggen and Hollman 1998; Lee et al. 2000), clinoptilolite (Sprynskyy et al. 2006), and sodalite (He et al. 2015).The difference may arise from the properties of adsorbent such as Si/Al ratio and experimental conditions, e.g., pH and solid/liquid ratio.

The Langmuir constants (b) for these heavy metals follow the order of Zn²⁺  > Cu²⁺  > Pb²⁺. A lower magnitude of Langmuir constant (b) indicates a higher affinity of the adsorbent for the metal. Therefore, results of the Langmuir constant (b) from this study follow the adsorption order of Pb²⁺  > Cu²⁺  > Zn²⁺, in line with Steenbruggen and Hollman (1998) and Lee et al. (2000).

Table 4 shows hydrated radius of metals in the order of Pb²⁺  < Cu²⁺  < Zn²⁺. A heavy metal ion with a smaller hydrated radius experiences a high electrostatic force of attraction to the surface of the NaP1, explaining the higher metal uptake and affinity of NaP1 for Pb²⁺ than the other metals. This also implies that less energy is required to attract Pb²⁺ than Cu²⁺ and Zn²⁺.

Table 4 Comparison of adsorption affinity of NaP1 and properties of heavy metals (Persson 2010)

Table 4 also shows that the hydrated radius of Cu²⁺ is smaller than Zn²⁺. This suggests that Cu²⁺ is preferred more than Zn²⁺, according to the size of the hydrated radius. However, the experimental results indicate the opposite since the Zn²⁺ uptake was 2.3 times more than the uptake of Cu²⁺ ions (Table 3). This may be related to the enthalpy of hydration for these metals, shown in Table 4. During metal uptake from NaP1, hydrated ions may need to lose their water of hydration in order to diffuse through NaP1 pores since their hydrated radii are closer to the pore dimensions (0.31 nm × 0.45 nm) and (0.28 nm × 0.48 nm) of the adsorbent (Alvarez-Ayuso et al. 2003). Enthalpy of hydration represents the affinity of metals to be in solution rather than the solute phase. Hence, a lower value for enthalpy of hydration indicates such cations will lose water and return to the solute phase easier than the others. Therefore, Zn²⁺ uptake was higher than Cu²⁺ since Zn²⁺ can return to the solute phase easier than Cu²⁺ with the ability to go through the NaP1 micropores. In addition, Table 4 shows Pb²⁺ with the smallest hydrated radius (0.401 nm) and enthalpy of hydration (− 1480 kJ/mol) amongst the heavy metal ions tested (Cu = 0.419 nm, Zn = 0.430 nm) (Persson 2010). When compared to pore dimensions (0.31 nm × 0.45 nm) and (0.28 nm × 0.48 nm) and active pore channel (0.29 nm) of NaP1 (Sharma et al. 2016), Pb²⁺ is most likely to be preferred to its counterparts. Although the un-hydrated radii of all the elements are below the accessible channels and could get through the zeolite pores, the metals do not exist as single cations in water but are bound to water molecules as hexa-aqua complexes, thus increasing their radii. Therefore, these metals would have to be stripped off the water in order to go through the narrow pores of NaP1 (Erdem et al. 2004). In conclusion, aqueous metal cations exist in water as hydrated ions with radii larger than the pore size of NaP1. The electrostatic forces of attraction between the surface of the zeolite and hydrated cations are influenced by the size of the heavy metals. Thus, smaller hydrated heavy metals are most attracted to the surface of the zeolite. Hence, heavy metals with a low enthalpy of hydration means that they can easily be stripped of water molecules and consequently removed by NaP1. Therefore, in describing the ion selectivity process, regarding the Langmuir sorption capacity, Pb²⁺  > Zn²⁺  > Cu²⁺ is in line with the study of Hendricks et al. and this is determined by the size of the hydrated cation and its enthalpy of hydration.

The single-cation adsorption data were tested against the pseudo-first and -second order kinetic models to further describe the kinetics of the uptake (Table 5) while the multi-cation adsorption data were only evaluated using pseudo-second order kinetic model, regarding the results of the data fit for single-cation. The pseudo-second order model best fitted the kinetic data with R² = 1 for all three heavy metals, using NaP1. multi-cationmulti-cation.

Table 5 Pseudo-second order kinetic model parameters for heavy metals, obtained from the single and multi-cation adsorption data

The pseudo-second order model suggests a heterogenous surface and either a chemisorption or an ion-exchange mechanism, depending on the functional group of the adsorbent. On the other hand, physisorption was proposed using clinoptilolite (Blanchard 1984). Zeolite NaP1 is closely related to clinoptilolite with a similar functional group, thus indicating physisorption as the main metal uptake mechanism. The rate controlling step is possibly particle diffusion through the porous channels of zeolite NaP1 (Erdem et al. 2004; Hendricks 2010). Metal cations are first attracted to the surface of the NaP1 through weak Van der Waal’s forces (electrostatic attraction) and diffuse through the pores of NaP1. Diffusion is fast (15 min) but becomes slow (30–180 min) as metals move through the porous structure since the pore dimensions are close to the molecular size of the metals (Erdem et al. 2004).

Conclusions

Fly-ash derived zeolites could be the possible solution for replacing expensive adsorbents for water and waste-water treatment industry. It is also another solution to utilizing coal fly-ash; waste from the coal power plants being dumped into landfills causing pollution of soil and water bodies. NaP1 displayed fast kinetics with all metals, removing > 80% of the total capacity in 15 min. Metal cation adsorption can be described by the Langmuir isotherm and fitted well to the pseudo-second order kinetic model. Lead removal (96%) was the highest amongst all three metals tested from single cation adsorption experiments. The rate determining step of the uptake mechanism was suggested as the diffusion of metal ions through the pores of NaP1. NaP1 is identified as a crystal structure with heterogenous surface for physical multilayer adsorption of metals while ion selectivity according to Langmuir’s constant (b) was in the order of Pb²⁺  > Cu²⁺  > Zn²⁺.