1 Introduction

1.1 Functionally graded concrete

As of 2019, the global construction sector accounted for 60% of resource consumption, 50% of waste and 30% of net CO\(_{2}\) emissions. In the light of the emerging climate crisis and a yet unbroken demand for new buildings, novel technologies addressing both resource consumption and pollution are in dire need. One such technology is functionally graded concrete, which aims at varying the typically isotropic material properties in the element. By the blended spraying of two different concrete mixtures, Wörner et al. (2016) showed that up to 25% mass can be saved in the fabrication of small-scale beams, whilst maintaining sufficient load-bearing capacity. However, the process is rather slow and dirty. Further developing the graded concrete idea, Schmeer and Sobek (2017) undertook research on the integration of hollow spheres in concrete elements, which yields up to 77% mass savings by the thus created cavities in a hexagonal packing. The more practical cubic packing was considered by Nigl et al. (2022), where it was shown that up to 46% mass can be saved in a slab, with a loss in load-bearing capacity of only 6%. See Frost et al. (2022) for an in-depth sustainability and quality analysis. Whilst this idea is not new, compare to the so called bubble-decks (Bubble Deck North America LLC 2018), the additional problem of recyclability was solved by using mineral hollow spheres, which are fabricated with a centrifuge. For a diameter of 10 cm, the fabricated spheres have a wall thickness of about 2 mm, and are thus quite fragile. The manual production of an FGC slab was performed successfully, see Fig. 1.

Fig. 1
figure 1

The centrifuge (top left) used for the production of hollow spheres (top right) and a manually fabricated FGC element (©Institute for Lightweight Structures and Conceptual Design, University of Stuttgart)

Full size image

In order to establish the automated fabrication of such elements, a prototypical production system is in development, consisting of a concrete pump, which delivers the slurry through a hose, mounted on the endeffector of a gantry crane, to an extrusion unit with a second screw pump, see Fig. 2.

Fig. 2
figure 2

Prototypical production system for FGC elements

Full size image

The fabrication for FGC elements does differ from 3D concrete printing, which is in focus of many researchers (Hahlbrock et al. 2022; Adams et al. 2022). Here, the endeffector path must cover the elements surface neatly, as the printed concrete is usually a structure the scale of the extruder nozzle. In our case, the concrete must be able to flow below the spheres to prevent cavities, for which reason a self compacting concrete is used. The challenge instead is to cover the element while avoiding extruding on the spheres.

1.2 Path planning and Hamiltonian triangulations

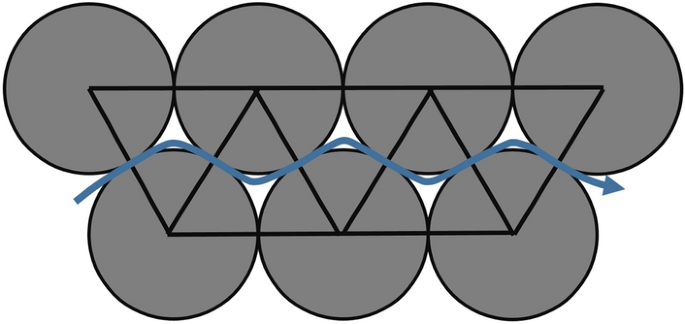
A major challenge in fabrication planning is the definition of a path for the extrusion unit. The path must avoid the spheres as best as possible in order to prevent damage/displacement, whilst neatly covering the entire element, such that the concrete slurry may evenly spread out and fill every cavity. Planning the production trajectories by means of optimal control was investigated in Blagojevic et al. (2021), with a simple path planning scheme for rectangular elements. The subject of this paper is a more general path planning scheme for FGC elements, based on a rigorous theoretical analysis of the problem. The challenges are sufficient coverage of the area, with a path avoiding the spheres. The idea pursued herein is a triangulation of the elements area, such that every sphere center is on the corner of a triangle, and that all edges only cut the spheres located on their corners, see Fig. 3.

Fig. 3
figure 3

Evading spheres by triangulation

Full size image

In order to cover an entire element, the triangulation must be Hamiltonian, i.e. a sequence in which all triangles can be visited exactly once. Note that this is similar to graph-based coverage path planning, as discussed in Cheng et al. (2019) and An et al. (2020). The main difference of our method compared to other work is guaranteed Hamiltonicity. Further, we address the issue of planning the actual path given the triangles, which is commonly done by planning splines throughout edge midpoints or triangle centers.

The question of Hamiltonian triangulations (HT) is deeply related to graph theory. There is a rich body of work on Hamiltonian paths (HP) on graphs stemming from the discretization of a 2D area, usually called planar. Deciding if a planar graph has a Hamiltonian cycle (HC), i.e. a HP with coinciding start/end, is NP-complete (Garey et al. 1976a). This also holds for the restricted case of finding a HP through the bigraph of a triangulation (Garey et al. 1976b). However, some classes of planar graphs allow a HP. For e.g. maximal planar graphs, a HP exists (Whitney 1931). Similar results can be found in Helden (2007) and Bagheri et al. (2020). Regarding triangulations, Arkin et al. (2005) introduced two algorithms defining a HT on a set of 2D points, but the result is convex. Given a triangulation (Gopi and Eppstein 2004) showed that triangle splitting allows for a HC. Similarly, Cardinal et al. (2018) proves that any triangulation on \(n\ge 6\) vertices can be transformed to a HT by edge flipping. However, both approaches are impractial for the given case: edge flipping can result in paths cutting the spheres, while the introduction of additional triangles might cause the path to pass a given cavity between spheres twice.

1.3 Contribution and structure

The contribution of this work are theoretical results on Hamiltonian triangulations, the design of an algorithm that creates such triangulations on FGC element geometries and the division of a thereon based path planning approach both evading the spheres and a smooth curvature trend. This work is structured accordingly to the contributions as follows.

In Sect. 2 the theoretical baselines for our path planning algorithm are layed out. Here, a new subclass of triangulations called truly layered triangulations (TLT) is identified, for which hamiltonicity is proven. This subclass is less restrictive compared to e.g. the one examined in Helden (2007), specifically as the number of separating triangles is not constrained.

In Sect. 3, we include the examined problem of path planning for FGC elements into the discussion. This is done by introducting the notion of sphere sets and finding a similar layered structure as introduced before by defining neighborness of two spheres. By exploiting this structure, an algorithm for triangulating a specific class of sphere sets is devised, alongside with a proof that it is a TLT and thus Hamiltonian.

With a HT thus defined, a path planning scheme within the triangles is presented in Sect. 4. For triangles where the in/outgoing edges only have one free point each, the tangential vectors are prescribed by the edge normals. This facilitates a polar coordinate approach for planning the path, which is constrained to the triangle, outside neighboring spheres and smooth in its endpoints. We define an appropriate ansatz for this problem, with two free parameters, whose values are shown to be determined by the geometry. The entire planning scheme is then applied on various elements.

This is followed by a discussion in Sect. 5 and a conclusion of the presented approach, including an outlook in Sect. 6.

2 Hamiltonian paths in truely layered triangulations

In this section, we introduce truly layered triangulations and give proof on their hamiltonicity. Due to their more direct geometric interpretation, triangles and polygons are used as basic entities of the proof, instead of their graph representation. We start by introducing the used notation.

2.1 Notation

We write \(P=\{p_1,\ldots ,p_{N}\}\) for an ordered set of 2D-points or even \(P=\{P_1,\ldots ,P_N\}\) with \(P_i=\{p_{i,1},\ldots ,p_{i,N_i}\}\) for a set of such sets. For a polygon, we write \(\mathcal {P} = \{P\}\) or \(\mathcal {P} = \{p_1,\ldots ,p_{N}\}\), where the last edge is between the last and the first points if not stated otherwise, and \(p\in \mathcal {P}\) if it agrees with any vertex of P. Further, \(p_{N+1}=p_1\) is used.

For triangulations two notations are used, that is \(T=(P_T,I_T)\) where \(I_T = \{t_{I,1},\ldots ,t_{I,N}\}\) denotes a triangle with \(t_i=\{i_1,i_2,i_3\}\), such that the indices are pointing towards a point set \(P_T\), or likewise \(T=\{t_1,\ldots ,t_N\}\) with \(t_i = \{p_{i_1},p_{i_2},p_{i_3}\}\) if the individual vertices are of interest.

2.2 Hulls in triangulations

Let \(\mathcal {P}_O = \{p_{O,1},\ldots ,p_{O,N}\}, N \ge 3\) be a pairwise-distinct (PWD) clockwise-sorted (CWS) set of 2D-points, representing a non-intersecting polygon that encloses the area of interest (AOI). Let \(\mathcal {P}_L = \{\mathcal {P}_{L_1},\ldots ,\mathcal {P}_{L_{M}}\}\) be a set of non-overlapping polygons with the same properties, representing holes inside \(\mathcal {P}_O\).

Definition 1

A proper triangulation \(T:=T(\mathcal {P}_O,\mathcal {P}_L)\) with \(T=(P_T,I_T)\) of a polygon \(\mathcal {P}_O\) with holes \(\mathcal {P}_L\) is given by a set of PWD 2D-points \(P_T = \{p_{T,1},\ldots ,p_{T,N_P}\}\) and an index set \(I = \{t_1,\ldots ,t_{N_T}\}\), where \(t_i = \{i_1,i_2,i_3,\}, i=1,\ldots ,N_T\) forms a triangle with CWS vertices \(P(t_i):=\{p_{T,i_1},p_{T,i_2},p_{T,i_3}\}\). Every point of \(P_T\) must be part of at least one triangle. All points of \(\mathcal {P}_O,\mathcal {P}_L\) are in \(P_T\), and no triangle edge of \(I_T\) or point of \(P_T\) may lie outside of \(\mathcal {P}_O\) or inside of \(\mathcal {P}_{L,i}~\forall ~i=1,\ldots ,M\). The triangulation must be connected, i.e. for every pair of non-adjacent triangles in T exists a sequence of adjacent triangles connecting them.

Similar to the vertex grouping of Cimikowski (1993), several types of triangles can be distinguished. By \(\mathcal {N}(T,i)\) the neighbors of the triangle \(t_i\) in T are denoted, i.e. triangles that share at least two common vertices with \(t_i\).

Definition 2

Given a proper triangulation \({T(\mathcal {P}_O,\mathcal {P}_L)=(P,I)}\), where \(P_L\) denotes the set of all vertices in \(\mathcal {P}_L\), the distinct sets

  • \(CN(T):= \{t_i| ~|P(t_i)\cap P_L|=0\wedge |\mathcal {N}(T,i)| = 1\}\) are called the corners of T,

  • \(TH(T):= \{t_i| ~|P(t_i)\cap P_L|\le 1~\wedge ~ |\mathcal {N}(T,i)| = 2\}\) is called the true hull of T,

  • \(PE(T):= \{t_i|~|\mathcal {N}(TH(T),i)| \ge 1 \wedge t_i \notin TH(T),CN(T)\}\) are called the primal entries of T,

  • \(DE(T):= \{t_i|~t_i \notin PE \wedge \exists t_j,t_k \in PE: t_i\in (t_j \cap t_k)\}\) are called the dual entries of T,

  • \(CR(T):= \{t_i|~|\mathcal {N}(T,i)| = 3\}\) are called the crossings of T.

Every triangle with an edge on the outer hull is a corner or a true hull triangle, if more than one triangle exists. Every triangle with a vertex on the outer hull is a primal or dual entry triangle, see Fig. 4.

Fig. 4
figure 4

Corners, true hull, primal and dual entries on the exterior edge

Full size image

These sets form a strip of triangles around the triangulation, called the hull, enclosing the remaining core.

Definition 3

The hull of a proper triangulation T with holes is defined as \(H(T):= (CN\cup TH \cup PE \cup DE)(T)\). The core of a proper triangulation T is defined as \(C(T):= T {\setminus } H(T)\).

Pursuing the idea of hull and core, it is straightforward to consider the hull of the core and so on, leading to a recursive definition of the core and the hull

$$\begin{aligned} \begin{aligned} C_0&:= T, \\ C_j&:= C_{j-1} {\setminus } H_j,\\ H_0&:= \emptyset , \\ H_j&:= (CN \cup TH \cup PE \cup DE)(C_{j-1}). \end{aligned} \end{aligned}$$
(1)

Further, a recursive definition of the set of hole vertices \({P_{L}^j=P_L(C_j)}\) is needed, since corners and true hull depend on it. Here, it is

$$\begin{aligned} \begin{aligned} P_{L}^0&:= P_{L}, \\ P_{L}^j&:= {P}_{L}^{j-1} {\setminus } \{{P}_{L,i}|~|P_T(H_j) \cap \in P_{L,i}|>0\}, \end{aligned} \end{aligned}$$
(2)

with \(j\in \mathbb {N}\). If a hole exists and wlog the first hull has a vertex on it, then they also share an edge. Removing the hull thus “opens” the hole, and the first core has it as part of the outer shape. If a second hull exists, this hole no longer appears as such, which justifies Eq. (2). The can be seen in Fig. 5.

Fig. 5
figure 5

Since the first hull (circles) touches the hole, the second hull (squares) has edges on it

Full size image

This allows the definitions of a subclass of triangulations, with the property of being separable into consecutive connected hulls, from the outside to the inside.

Definition 4

A proper triangulation T is called \({\bar{j}}\)-layered, if \(C_{{\bar{j}}} = \emptyset\) and \(C_{{\bar{j}}-1} \ne \emptyset\), for \({\bar{j}}=1,2,\ldots\), and if all hulls \(H_j\) are connected.

Note that the onion triangulation (Arkin et al. 2005) generates a layered triangulation. However, these triangulations have no holes, and the exterior shape of every core is convex, which is a more severe restriction. Inspired by the therein presented proof, a similar approach of finding a hamiltonian for every hull and connecting them is pursued herein.

2.3 Truely layered triangulations and Hamiltonian paths

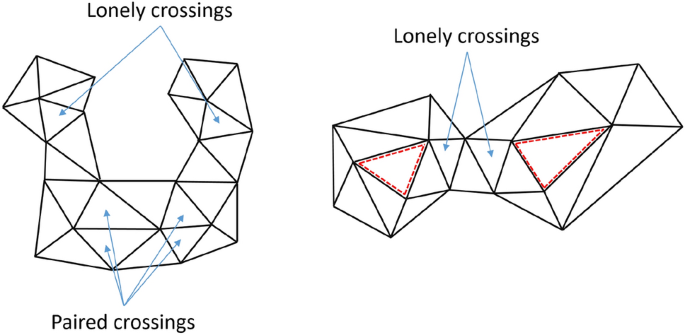
A HP in a hull cannot be found if more than two corners exist; indeed, since corners impose severe restrictions on where a path in a hull has to start/end, they are excluded altogether. However, even without corners a hull might not permit a HP, see Fig. 6.

Fig. 6
figure 6

Exemplary hulls which prevent a global hamiltonian path

Full size image

In the left example, a HP clearly cannot be found due to the two ears over the main body. In the right example, the hull itself has a HP. However, the remaining core, marked by two red-dashed triangles, is disconnected, which in general prevents a global hamiltonian path through all layers. As indicated in the figure, the problem stems from lonely crossings, i.e. crossings which are not paired with another crossing. While one such crossing might be permitted in a hull, two or more can lead to non-hamiltonian hulls. We thus extend the notion of a layered triangulation.

Definition 5

A triangulation T is called truly layered if

  1. 1.

    T is \({\bar{j}}\)-layered

  2. 2.

    No hull has a corner.

  3. 3.

    In every hull, all crossings have at least one neighboring crossing.

  4. 4.

    A sequence of neighboring triangles \((t_{s_1},\ldots ,t_{s_{2\cdot ({\bar{j}}-1)}})\) exists, where \(t_{s_1} \in TH_{{\bar{j}}}, t_{s_2} \in PE_{{\bar{j}}-1},t_{s_3} \in TH_{{\bar{j}}-1},\ldots\) and \(t_{s_{2\cdot ({\bar{j}}-1)}} \in (PE_1 \cup DE_1)\)

The fourth condition states, that a path from the inmost to the outmost layer throughout T exists, having exactly two triangles in every intermediate hull. Clearly, such a path exists if no hull has dual entries, but this is quite restrictive.

Theorem 1

Any truely layered triangulation T has a hamiltonian path.

Proof

First assume that no hull has a crossing. Thus, no triangle in the hull has three neighbors. Note that the hull is connected and no corners exist. Thus, every triangle in the hull has exactly two neighbors, i.e. the dual graph of \(H_j\) is a cycle, and every layer thus has a hamiltonian path on its own.

For the global hamiltonian path, start in the final hull \(H_{{\bar{j}}}\). Let \({\bar{j}}\ge 1\), otherwise the dual graph of T is a cycle and already hamiltonian. Given Definition 5, choose \(t_{s_1}\) as the end triangle in this hull, and one of its two neighbors as the start triangle. A hamiltonian path for this hull is obtained by going in the other direction of the start triangle, until the end triangle is reached. In hull \({\bar{j}}-1\), as start triangle choose \(t_{s_2}\), and as start triangle its neighbor \(t_{s_3}\). The hamiltonian path for this hull follows likewise. By definition, \(t_{s_2}, t_{s_3}\) are neighbors, and thus both hamiltonian paths are connected on their start/end triangles. Repeating this procedure for all hulls yields a hamiltonian path, where in the first hull any neighbor of \(t_{s_{2\cdot ({\bar{j}}-1)}}\) may be choosen as global end triangle.

Now consider the case \(\exists j \in \{1,\ldots ,{\bar{j}}\}: CR(H_j) \ne \emptyset\). The dual graph of \(H_j\) is no longer a cycle, there are \(|CR(H_j)|\) nodes with 3 edges instead. As before, the end triangle is a true hull element, and the start triangle is one of its neighbors. Traverse in the direction of the other neighbor and add triangles to the path, until the next triangle \(t_n,n \in I(H_j)\) is a crossing. Two cases are now possible:

  1. 1.

    Exactly one neighbor of \(t_n\) is a crossing.

  2. 2.

    Both neighbors \(t_{m,1},t_{m,2}\) of \(t_n\) are crossings.

In the first case, add the non-crossing neighbor to the path and continue. Since crossings only appear pairwise, the path will eventually encounter another crossing, that either is a neighbor of \(t_n\) or has one/two neighboring crossings. In the second case, one has to identify the correct crossing, as the other one would cut off parts of the hull. Note that wlog \(t_{m,1}\) is neighbored to another yet unknown crossing \(t_{l}\), which shares a vertex with \(t_n,t_{m,2}\). This is since two vertices of \(t_{m,1}\) are in the interior, forming an edge that bounds another triangle, which is \(t_{l}\). Now consider the triangulation \({\tilde{T}}_1\) that contains \(t_{n},t_{m,1}\) and all their consecutive neighbors in \(H_j\), i.e. neighbors of neighbors, except \(t_{l},t_{m,2}\). If \(|H_j|-|{\tilde{T}}_1|=2\), this triangulation contains the entire hull except \(t_{l},t_{m,2}\), i.e. taking \(t_{m,1}\) does not cut off the hull in two sets. If \(|H_j|-|{\tilde{T}}_1|>2\), some triangles are “behind” \(t_{l},t_{m,2}\) and thus cannot be reached when taking \(t_{m,1}\). Thus take \(t_{m,1}\) if \(|H_j|-|{\tilde{T}}_1|=2\) holds and \(t_{m,2}\) otherwise. By this, one can find a hamiltonian path for each hull, as no choice cuts off parts of the hull. With the start and end triangle as in the crossing-free case, a global hamiltonian path follows. \(\square\)

In Fig. 7, the definition and proof of hamiltonicity for a TLT is visualized.

Fig. 7
figure 7

Depiction of a TLT with the neighbor sequences of condition 4. (left), and the cut off path when encountering crossings (right)

Full size image

The triangulation on the left permits a hamiltonian path in each of the three hulls. However, to connect the individual paths, the start and end triangles in each hull must be neighbored with themselves and with the previous/next hull, which is not given for the red-dashed neighbor sequence. On the right, a non-cycle hull is depicted. When reaching \(t_n\), two paths are possible. When choosing \(t_{m,2}\), the triangles \(t_l,t_{m,1}\) cut off parts of the hull, indicated by the blue-dashed line. The path must thus lead to \(t_{m,1}\).

3 Hamiltonian triangulation of sphere sets in a polygon

In this section, the previously introduced notion of a truly layered triangulation is translated to the case of FGC elements, in order to establish an algorithm for generating a HT useable in path planning.

3.1 Hulls in sphere sets

The geometry of FGC elements is typically prismatic and described by the outer polygon \(\mathcal {P}_O\), without holes \(\mathcal {P}_L=\emptyset\) and a set of spheres S inside \(\mathcal {P}_O\).

Definition 6

A sphere set is a set \(S = \{s_i,\ldots ,s_n\}\) with 2-tuples \(s_i=(c_i,r_i), c_i \in \mathbb {R}^2,r_i\ge 0\) representing centers and radii of spheres on the 2D-plane, with the additional condition that \(||c_i-c_j||\le r_i+r_j \forall ~i,j\in [1,\ldots ,N]\).

Definition 7

The direct neighbors of a sphere \(s_i\) in a sphere set \(S = \{s_i,\ldots ,s_n\}\) are defined by

$$\begin{aligned} {e_{\textrm{dir},i}(S)=\{k|\ r_i+r_k=||c_i-c_k||, i,k \in S\}}. \end{aligned}$$

The diagonal neighbors are defined by

$$\begin{aligned} {e_{\textrm{diag},i}(S)=\{k|\ k\in e_{\textrm{dir},l}\cap e_{\textrm{dir},m},\forall l,m \in e_{\textrm{dir},i}(S)\}}. \end{aligned}$$

In order to simplify the analysis, we restrict the variety of possible sphere sets as follows.

Definition 8

A sphere set \(S = \{s_i,\ldots ,s_n\}\) is called proper if

  • all radii are equal \(r_1=\cdots =r_N>0\)

  • the centers are on a rectangular grid, i.e. \(\exists \Delta _x,\Delta _y > 0: ||c_{x/y,i}-c_{x/y,j}||=k\cdot \Delta _{x/y}, k\in \mathcal {N}\)

  • the graph \(G(S) = (V,E)\) with vertices \(V=\{1,\ldots ,n\}\) and edges \(E = \{e_{\textrm{dir},1},\ldots ,e_{\textrm{dir},n}\}\) is connected

These restrictions are motivated by the fabrication. One common diameter facilitates quick production and tailoring. The spheres are usually placed on a coinciding rectangular grid of reinforcement bars to ensure position stability. Further, a dense sphere layout maximizes mass savings, for which reason the spheres touch each other. We exclude the case of separate connected groups of spheres for simplicity.

Note that in a rectangular grid, every sphere can have at most four (direct) neighbors. This straightforwardly leads to a clear definition of the core and hull of a sphere set, similar to those of a triangulation.

Definition 9

The core of a proper sphere set \(S = \{s_i,\ldots ,s_n\}\) with graph \(G(S) = (V,E)\) is defined as

$$\begin{aligned} \mathcal {C}(S)=\{s_i| 4=|e_{\textrm{dir},i}(S)| \wedge 4=|e_{\textrm{diag},i}(S)|, i\in S\}. \end{aligned}$$

The hull of S is then defined as

$$\begin{aligned} \mathcal {H}(S) = \{s_i | s_i \in S{\setminus } \mathcal {C}(S)\}. \end{aligned}$$

Again, a recursive definition follows straightforwardly for the subsequent hulls

$$\begin{aligned} \begin{aligned} \mathcal {H}_0&= \emptyset ,\\ \mathcal {H}_j&= \mathcal {H}(\mathcal {C}_{j-1}), \end{aligned} \end{aligned}$$
(3)

the cores

$$\begin{aligned} \begin{aligned} \mathcal {C}_0&= S,\\ \mathcal {C}_j&= \mathcal {C}_{j-1}{\setminus }\mathcal {H}_{j}, \end{aligned} \end{aligned}$$
(4)

and the layeredness of triangulations.

Definition 10

A proper sphere set S is called \({\bar{j}}\)-layered, if

  • \(\mathcal {C}_{{\bar{j}}}=\emptyset \implies \mathcal {C}_{{\bar{j}}-1}\ne \emptyset\) for \({\bar{j}}\in \mathbb {N}\)

  • all spheres of \(\mathcal {H}_{j}\) have a direct or diagonal neighbor in \(\mathcal {H}_{j+1}\) and vice versa for \(j=0,\ldots ,{\bar{j}}-1\)

  • the graphs of all hulls \(G_j(\mathcal {H}_j)\) are connected.

3.2 Truely layered triangulation of layered sphere sets

With this analogy established, our approach aims at triangulating the centers of all pairs of subsequent sphere hulls, such that they form the hulls of a TLT. This algorithm must meet two conditions:

  1. 1.

    Each triangles edge must be drawn between two neighboring spheres

  2. 2.

    Each triangle must contain spheres from both hulls

The first condition is based on the requirement that no edge might cut any sphere not located on its corners. The second one follows from the insight that a triangle with all points on one hull would form either a corner or a lonely crossing, which is incompatible with a TLT.

Therefore, the edges in the triangulation consist of all edges in hull j and all edges in hull \(j+1\). Further, all edges between a pair of direct neighbors across the hulls are included. The respective diagonal neighbors don’t always form an edge, as intersection might occur. Additionally, all edges between a pair of direct or diagonal neighbors across the hulls are included. Before stating a proper triangulation algorithm, the following result is useful.

Lemma 1

Let \(\mathcal {H}_j\) be a hull of a layered sphere set S with \(j<{\bar{j}}\). Then, the graph \(G(\mathcal {H}_j)\) is a cycle.

Proof

If a sphere \(s_i\) has only one direct neighbor \(s_k\) in \(\mathcal {H}_{j}\), it cannot have a direct or diagonal neighbor in \(\mathcal {H}_{j+1}\), as the corresponding sphere \(s_l\) would then be in \(\mathcal {H}_{j}\), given that it cannot have four diagonal neighbors itself. Thus, this case is excluded.

Assume \(s_i \in \mathcal {H}_{j}\) has three direct neighbors \(s_k,s_l,s_m\), all in \(\mathcal {H}_{j}\). Let \(s_k\) be the common diagonal neighbor of \(s_l,s_m\). By definition, \(s_i\) must have at least one diagonal neighbor in \(\mathcal {H}_{j+1}\). Let this neighbor \(s_t\) be wlog the common direct neighbor of \(s_k,s_l\). If \(s_t\) is in \(\mathcal {H}_{j+1}\), then it is surrounded by four diagonal and four direct neighbors. Let further \(s_p\) be diagonal to \(s_t\) and direct to \(s_k\). If \(s_p\) is in \(\mathcal {H}_{j+1}\), then it is also surrounded by spheres, and one of its diagonal neighbors \(s_o\) is diagonal to \(s_i\) and direct to \(s_k\), causing the latter to have four direct and diagonal neighbors which is in contradiction to \(s_k \in \mathcal {H}_{j}\). If otherwise \(s_p \in \mathcal {H}_{j}\), then \(s_i,s_k,s_p\) form an edge of the sphere set. Since \(s_p\) must have more than one neighbor in \(\mathcal {H}_{j}\), it can be seen that a sequence of spheres in \(\mathcal {H}_{j}\) either connects to \(s_l, s_m\) or \(s_p\) again. In the first two cases, \(\mathcal {H}_{j+1}\) becomes disconnected as one set is enclosed by the connection line, and at least one sphere in \(\mathcal {H}_{j+1}\) neighbors \(s_m\) or \(s_l\). In the third case, the neighbor of \(s_p\) in \(\mathcal {H}_{j}\) not being neighbored to \(s_t\) must have a neighbor in \(\mathcal {H}_{j+1}\) by definition, which, as four direct and diagonal neighbors are needed, enforces the existence of a sphere \(s_o\) as defined before. Again, \(s_k\) is surrounded by spheres which is in contradiction to \(s_k\in \mathcal {H}_j\).

This can also be shown if \(s_i\) is enclosed by four neighbors in \(\mathcal {H}_j\). Thus, only two neighbors in \(\mathcal {H}_j\) are possible. Given that \(\mathcal {H}_j\) is connected by definition, it is a cycle. \(\square\)

In Fig. 8, the two scenarios are visualized. The thick line indicates the edges of \(\mathcal {H}_j\), the dashed line the direct/diagonal neighborness demanded by definition, and the dashed spheres follow from deduction in some cases.

Fig. 8
figure 8

A sphere \(s_i\) with one/three direct neighbors in \(\mathcal {H}_j\) yields contradictions

Full size image

The triangulation proceeds circlewise through the sorted hull \(\mathcal {H}_j\), and the per step defined triangles depend on the local structure of its neighbors of sphere i. There are always two direct neighbors in \(\mathcal {H}_j\) as it is a cycle. Thus, two, one or none direct neighbors in \(\mathcal {H}_{j+1}\) might exist. Only those diagonal neighbors in \(\mathcal {H}_{j+1}\) which are not a direct neighbor of \(i-1\) might be considered in order to prevent crossing edges. The triangulation algorithm is stated in Algorithm 1.

figure a

Here, \(\text {graphEdges}\) is a function returning the edges of a graph of a sphere set and \(\text {sortCirclewise}\) sorts the edges and centers accordingly. The neighbors of a sphere in a graph are computed by \(\text {directNeighbors}\), and the thereon based diagonal neighbors follow from \(\text {diagonalNeighbors}\). The five different triangulation cases are depicted in Fig. 9.

Fig. 9
figure 9

Triangulation cases between layered sphere hulls

Full size image

Lemma 2

Let \(\mathcal {H}_j,\mathcal {H}_{j+1}\) be two subsequent hulls of a layered sphere set S with \(j<{\bar{j}}\). The graph of the triangulation \(P_T,I_T\) yielded by applying Algorithm 1 is a cycle.

Proof

Regard the three cases to triangulate as in Algorithm 1 and note that all triangles defined in one step form a strip. Note that the last triangle of this strip contains \(i+1,e_{\textrm{diag}}\) in cases 1,2 and \(i+1,e_{\textrm{diag},2}\) in case 3. The first triangle of the next strip contains \(i, e_{\textrm{dir}}\) in cases 1,2 and \(i,e_{\textrm{dir},2}\) in case 3. Thus, the last and first triangles share an edge and the strips are connected. Further, the last strip is connected with the first strip as \(\mathcal {H}_j\) is a cycle, and thus \(P_T,I_T\) is a cycle itself. \(\square\)

Concerning the triangulation of an entire sphere set, it remains to be shown that a neighbor sequence exist. This follows from considering the “edges” of a hull, i.e. the spheres which are not aligned with the previous and next neighbors.

Theorem 2

Let S be a layered sphere set with \({\bar{j}}>1\) and hulls \(\mathcal {H}_1,\ldots ,\mathcal {H}_{{\bar{j}}}\). Then, the triangulation \(T=(P_T,I_T)\) obtained from fusing the subsequent triangulations \(T_1=(P_{T,1},I_{T,1}),\ldots ,T_{{\bar{j}}-1}=(P_{T,{\bar{j}}-1},I_{T,{\bar{j}}-1})\), stemming from applying Algorithm 1 on \(\mathcal {H}_j,\mathcal {H}_{j+1},j=1,\ldots ,{\bar{j}}-1\) is a TLT.

Proof

It is apparent that each hull of T is equivalent to the partial triangulation \(T_j\), and that T is thus \({\bar{j}}-1\)-layered. In \(\mathcal {H}_1\), choose any sphere \(s_{i,1}\) where the previous and next neighbor along its cycle are not aligned, and which only has a diagonal neighbor in \(\mathcal {H}_2\), called \(s_{i,2}\). Such a sphere must exist, as the hull must otherwise form a continued line with infinitely many spheres in order to meet the requirements.

Its diagonal neighbor in \(\mathcal {H}_2\) has two direct neighbors in \(\mathcal {H}_2\) by definition, and two more in \(\mathcal {H}_1\), namely the neighbors of \(s_{i,1}\). Thus, it only has one diagonal neighbor in \(\mathcal {H}_3\) and so on, yielding a sequence of diagonally neighbored spheres \(s_{i,1},\ldots ,s_{i,{\bar{j}}}\). Now, consider the triangulation, which is as in the first case of Fig. 9. Here, \(t_{1,1}=\{s_{i,1},s_{i+1,1},s_{i,2}\}\) is the triangle containing the diagonal edge, and the next triangle always is \(t_{2,j}=\{s_{i+1,j},s_{i+1,j},s_{i,j}\}\). This is necessitated by the existence of the neighbor sequence \(s_{i,1},\ldots ,s_{i,{\bar{j}}}\). Note that \(t_{2,j}\) and \(t_{1,j+1}\) are neighbored, such that \(t_{2,1},t_{1,2},t_{2,2},\ldots ,t_{1,{\bar{j}}-1}\) form a sequence of neighbored triangles with two each per intermediate hull, i.e. a neighbor sequence. As further all \(T_j\) form cycles, T is a TLT. \(\square\)

The diagonally neighbored spheres and the following neighbor sequence is depicted in Fig. 10.

Fig. 10
figure 10

Neighbor sequence between layered sphere hulls

Full size image

3.3 Layered triangulations in the remaining areas

Note that the triangulation of a sphere set as above does not include the area between the surrounding outer shape \(\mathcal {P}_O\) and the polygon \(\mathcal {P}_{O,T}\) of the circlewise sorted centers of \(H_1\). Given that the sphere pattern in FGC elements is usually dense as high mass savings are needed to legitimate the increased production effort, this outer area is typically a thin annulus, and it is assumed that a single revolution of the path around it suffices.

Let \(\tilde{\mathcal {P}}_{O,T}\) be \(\mathcal {P}_{O,T}\) without colinear vertices, i.e vertices whose associated edges are aligned. The following restriction is made for ensuring the existence of a global HT.

Assumption 1

For every point \(p_{O,r}\in \mathcal {P}_O\) there is at least one point in \(p_{O,T,j}\in \mathcal {P}_{O,T}\) such that the connecting line is inside \(\mathcal {P}_{O}{\setminus } \mathcal {P}_{O,T}\). Further, the same holds either for the pair \(p_{O,r},p_{O,T,j+1}\) or \(p_{O,r+1},p_{O,T,j}\).

This allows the definition of the following algorithm.

figure b

Here, \({\text{is\,Neighbor}}\) checks if the connection of vertices of the input polynoms is within the enclosed area. The function \(\text {findClosestNeighbor}\) finds the closest vertex in the second input polynom fulfilling this condition with respect to one vertex of the first polynom. The triangulation proceeds circlewise around both polygons, with the partial triangulations defined by \(\text {lineTriang}\) between two sets of colinear points, which are fused with \(\text {fuseTriang}\) subsequently. The thus defined triangulation is cyclic, as can be easily seen by regarding the three occuring cases which are depicted in Fig. 11.

Fig. 11
figure 11

Triangulation cases in the outer area

Full size image

Given that all points of \(\mathcal {P}_{O,T}\) are triangulated, any entry sequence in T can enter \(T_O\) and the fused triangulation is a TLT. The HP of a TLT \(T=(P_T,I_T)\) is straightforward to obtain by first finding one of possibly multiple neighbor series, followed by resorting of the hulls and a concatenation, yielding a sequence \({I_H=\{i_1,\ldots ,i_{N_T}\}}\) of triangle indices, which are then used for the local path planning. In Fig. 12, the application of the given procedure on a quadratic element is visualized. Here, the hulls of the sphere set and the respective hulls of the triangulation are indicated by different colors.

Fig. 12
figure 12

Hulls of the sphere sets and triangulation for a quadratic element

Full size image

4 Triangulation based path planning for FGC elements

4.1 Smooth, spatially constrained path planning through waypoints with tangential vectors

While path planning is a wide subject with numerous methods, the usual approach is a polynomial ansatz for the individual components of \(\mathcal {R}\), with the coefficients then obtained by solving a linear system. However, as discussed below, the given scenario prevents this, as it necessitates a condition resulting in a nonlinear coupling of the polynom parameters for the x/y component. For this reason, a specialized approach is required.

The problem of planning a local path \(\mathcal {R}_i(s_i)\in \mathbb {R}^2\) can now be stated as follows:

  1. 1.

    The path must interpolate two fixed endpoints. \({\mathcal {R}_i(0)=p^i_{1,F}},{\mathcal {R}_i(1)=p^i_{2,F}}\), called fixpoints, on the in/outgoing edge.

  2. 2.

    The path must be parallel to two fixed vectors, \({\mathcal{R}}^{\prime}_i(0)||v^i_{1,F},{\mathcal{R}}^{\prime}_i(1)||v^i_{2,F}\) called fixpoint vectors, which are further normal to the in/outgoing edge.

  3. 3.

    The paths curvature must be zero at the fixpoints and must have a constant sign.

  4. 4.

    The path must avoid all spheres nearby.

The fixpoints \(p^i_{1/2,F}\) are defined as the all points on the in/outgoing edge of the HP where the two spheres touch each other. Both the second and the zero-curvature condition allow for a straightforward concatenation of the local paths \(\mathcal {R}_i\) into a global one, as they are continous. Preventing a sign change of the curvature further forces the path to directly head towards the endpoint, facilitating a short length and overall smoothness. In the rectangular pattern of the sphere set, two cases can occur, as shown in Fig. 13.

Fig. 13
figure 13

The two cases for paths in layered sphere sets

Full size image

In the first case, \(v^i_{1,F},v^i_{2,F}\) are parallel to each other and the connecting line \(p^i_{2,F}-p^i_{1,F}\), for which reason the straight path \({\mathcal {R}_i(s)=p^i_{1,F}+s\cdot (p^i_{2,F}-p^i_{1,F})}\) is used, clearly fulfilling the above stated requirements.

We further only consider the second case. Here, the support points \(p^i_{K},p^i_{L}\) follow from the intersection of the vectors \(v^i_{1,F},v^i_{2,F}\) and their respective normals. The above requirements can be formally written as

$$\begin{aligned} \mathcal {R}_{i}(0)&= p^i_{1,F}, \end{aligned}$$
(5a)
$$\begin{aligned} \mathcal {R}_{i}(1)&= p^i_{2,F}, \end{aligned}$$
(5b)
$$\begin{aligned} \frac{\mathcal {R}'_i(0)}{||\mathcal {R}'_i(0)||}&= v^i_{1,F}, \end{aligned}$$
(5c)
$$\begin{aligned} \frac{\mathcal {R}'_i(1)}{||\mathcal {R}'_i(1)||}&= v^i_{2,F} , \end{aligned}$$
(5d)
$$\begin{aligned} \mathcal {C}(\mathcal {R}(0))&=0, \end{aligned}$$
(5e)
$$\begin{aligned} \mathcal {C}(\mathcal {R}(1))&=0, \end{aligned}$$
(5f)
$$\begin{aligned} \mathcal {C}(\mathcal {R}(s))&\lessgtr 0,s\in (0,1), \end{aligned}$$
(5g)
$$\begin{aligned} \mathcal {R}_i(s)&\in \{p^i_{1,F},p^i_{K},p^i_{2,F},p^i_{L}\} {\setminus } S, \end{aligned}$$
(5h)
$$\begin{aligned} ||\mathcal {R}_i(s)-p^i_{L}||&\ge ||p^i_{L}-p^i_{1,F}||. \end{aligned}$$
(5i)

The parallelity and curvature conditions are nonlinear and encompass a coupling of the x, y components of the path \(\mathcal {R}\), which exacerbates the use of a spline approach. Instead, the following form is used

$$\begin{aligned} \begin{aligned} \mathcal {R}_x(s)&=(r_0+r(s))\cos (\phi (s))+x_0,\\ \mathcal {R}_y(s)&=(r_0+r(s))\sin (\phi (s))+y_0. \end{aligned} \end{aligned}$$
(6)

Here, the subscript i is discarded for simplicity. This approach exploits the spherical nature of the geometry by turning the path about \(p_{1,L}=(x_0,y_0)\), with \(r_0\) being the respective radius. The angle \(\phi (s) = {\underline{\phi }}+s\cdot ({\overline{\phi }}-{\underline{\phi }})\) is shifted linear, with \({\underline{\phi }},{\overline{\phi }}\) being the angles of \(p_{1,F},p_{2,F}\) with respect to \(p_{L}\), and wlog \({\underline{\phi }}<{\overline{\phi }}\). The derivatives with respect to s are given by

$$\begin{aligned} \begin{aligned} \mathcal {R}_x'(s)&= -\Delta \phi (r_0+r)\sin (\phi )+r'\cos (\phi ),\\ \mathcal {R}_y'(s)&= \Delta \phi (r_0+r)\cos (\phi )+r'\sin (\phi ),\\ \mathcal {R}_x''(s)&= (r''-(r_0+r)\Delta \phi ^2)\cos (\phi )-2\Delta \phi r'\sin (\phi ),\\ \mathcal {R}_y''(s)&= (r''-(r_0+r)\Delta \phi ^2)\sin (\phi )+2\Delta \phi r'\cos (\phi ),\\ \end{aligned} \end{aligned}$$
(7)

with \(r:=r(s),\phi = \phi (s)\), yielding

$$\begin{aligned} \begin{aligned} \frac{\mathcal {R}_x'}{||\mathcal {R}'||}(s)&= \frac{-\Delta \phi (r_0+r)\sin (\phi )+r'\cos (\phi )}{\sqrt{r'^2+\Delta \phi ^2(r_0+r)^2}},\\ \frac{\mathcal {R}_y'}{||\mathcal {R}'||}(s)&= \frac{ \Delta \phi (r_0+r)\cos (\phi )+r'\sin (\phi )}{\sqrt{r'^2+\Delta \phi ^2(r_0+r)^2}}, \end{aligned} \end{aligned}$$
(8)

where \(\Delta \phi = {\overline{\phi }}- {\underline{\phi }}\). Based thereon, the first two conditions on \(r(\phi )\) are obtained as

$$\begin{aligned} \begin{aligned} r({\underline{\phi }})&=r({\overline{\phi }})=0,\\ r'({\underline{\phi }})&=r'({\overline{\phi }})=0, \end{aligned} \end{aligned}$$
(9)

which results in tangential vectors

$$\begin{aligned} \frac{\mathcal {R}'}{||\mathcal {R}'||}(0)&= (-\sin ({\underline{\phi }}),\cos ({\underline{\phi }})),\end{aligned}$$
(10)
$$\begin{aligned} \frac{\mathcal {R}'}{||\mathcal {R}'||}(1)&= (-\sin ({\overline{\phi }}),\cos ({\overline{\phi }})), \end{aligned}$$
(11)

that are clearly parallel with \(v_{1,F},v_{2,F}\). In order to restrict the path \(\mathcal {R}\) to the quadrilateral \(\{p_{1,F},p_{K},p_{2,F},p_{L}\}\) and outside the sphere centered at \(p_{L}\), the radius function r(s) must be bounded by

$$\begin{aligned} \begin{aligned} {\overline{r}}(s)&= {\left\{ \begin{array}{ll} r_0\left(\frac{1}{\cos (s\cdot \Delta \phi )}-1\right)&{} \quad 0\le s \le \frac{1}{2}\\ r_0\left(\frac{1}{\cos ((1-s)\cdot \Delta \phi )})-1\right)&{} \quad \frac{1}{2} < s \le 1 \end{array}\right. },\\ \underline{r}(s)&= 0. \end{aligned} \end{aligned}$$
(12)

The upper bound can be derived by the distance of the point \({\tilde{p}}(s)=p_{1,F}+2s \cdot (p_{K}-p_{1,F})\) to \(p_{L}\) for \(s\in [0,\frac{1}{2}]\) and mirroring it on the connecting line \(\{p_{K},p_{L}\}\). Inspired by the shape of the above derived bounds, the following form for r(s) is chosen

$$\begin{aligned} r(s) = r_0\cdot \Bigl (\frac{1}{f(s)}-1\Bigr ). \end{aligned}$$
(13)

The start/end condition on fixpoint interpolation and parallelity, as well as spatial boundeness and symmetry yield the transformed conditions

$$\begin{aligned} f(0)&=f(1)=1, \end{aligned}$$
(14a)
$$\begin{aligned} f'(0)&=f'(1)=0, \end{aligned}$$
(14b)
$$\begin{aligned} 1\ge f(s)&\ge \cos (s\cdot \Delta \phi ), s\in \left[ 0,\frac{1}{2}\right] , \end{aligned}$$
(14c)
$$\begin{aligned} f\left( s-\frac{1}{2}\right)&= f\left( s+\frac{1}{2}\right) . \end{aligned}$$
(14d)

Note that, due to the axis-symmetry of \({\overline{r}}(s)\) at \(s=\frac{1}{2}\), it is sufficient to guarantee all necessary conditions on f(s) in \(s\in [0,\frac{1}{2}]\), as long as f(s) is symmetric towards \(s=\frac{1}{2}\). The curvature follows to

$$\begin{aligned} \mathcal {C}(\mathcal {R})=f(s)^3\frac{\Delta \phi r_0^2\cdot (f(s)\Delta \phi ^2+f''(s))}{(r_0^2f'(s)^2+ f(s)^2\Delta \phi ^2)^{\frac{3}{2}}}, \end{aligned}$$
(15)

such that for the left curvature condition

$$\begin{aligned} f(0)\Delta \phi ^2+f''(0) = 0 \end{aligned}$$
(16)

must hold. Again, the conditions exacerbate the use of a polynomial; instead, we use the following form

$$\begin{aligned} f(s) = \left( \frac{\cos (s\cdot 2\pi )+\kappa }{\kappa +1}\right) ^{\lambda }, \end{aligned}$$
(17)

with two parameters \(\kappa \ge 1,\lambda > 0\). The \(2\pi\)-period is chosen as it guarantees symmetry towards \(s=\frac{1}{2}\). For the curvature at \(s=0\), the equation

$$\begin{aligned} (\kappa +1)^2\Delta \phi ^2 - (\kappa +1)\lambda 4 \pi ^2=0 \end{aligned}$$
(18)

is obtained after rearrangement, yielding the relation

$$\begin{aligned} \kappa = \lambda \frac{4\pi ^2}{\Delta \phi ^2}-1, \end{aligned}$$
(19)

which guarantees zero curvature at both ends. Note that the condition on \(\kappa\) translates to \(\lambda \ge \frac{\Delta \phi ^2}{2\pi ^2}\). Clearly, most conditions on f(s) are met regardless of the value of \(\kappa ,\lambda\), except for Eq. (5g) and the lower bound of \(f(s)\ge \cos (s\cdot \Delta \phi )\). Since an analytical solution of the latter could not be found, the “no-sign-change” condition in the curvature is regarded first. As apparent from Eq. (15), sign change is determined by the bracketed expression in the numerator. After rearrangement and elimination of factors with a constant sign in \(\mathcal {C}(\mathcal {R})\), the polynom

$$\begin{aligned} \begin{aligned} g(y)&=y^2\cdot \underbrace{(\Delta \phi ^2 -4\pi ^2\lambda ^2)}_{=:a}\\ {}&\qquad +y\cdot \underbrace{(\kappa (2\Delta \phi ^2-4\pi ^2 \lambda ))}_{=:b}\ldots \\&\qquad +\underbrace{(\kappa ^2\Delta \phi ^2+4\pi ^2\lambda (\lambda -1))}_{=:c}, \end{aligned} \end{aligned}$$
(20)

is yielded, where the bijective substitution \({y=\cos (s\cdot 2\pi )}, {s\in [0,\frac{1}{2}]}\) is employed, using \(\kappa\) instead of its derived expression for simplicity. Here, \(g'\) has a single root at \(y^*=-\frac{b}{2a}\), which is a extremum of g, and it is

$$\begin{aligned} g(y^*)=c-\frac{b^2}{4a}. \end{aligned}$$
(21)

By setting the extremum to zero, a sign change of \(\mathcal {C}(\mathcal {R})\) can be prevented, as g itself is a quadratic function. Solving for \(\lambda\) in \(g(y^*)=0\) yields

$$\begin{aligned} \lambda _{\textrm{min}} = \frac{3\Delta \phi ^2}{2\Delta \phi ^2+4\pi ^2}. \end{aligned}$$
(22)

Indeed, this result is equivalent to the lower bound condition Eq. (5g), as depicted in Fig. 14.

Fig. 14
figure 14

Minimal value for \(\lambda\), such that the path remains in the quadrilateral

Full size image

Here, \({\tilde{\lambda }}_{\textrm{min}}\) is computed by solving the problem

$$\begin{aligned} \begin{aligned} \min ~&\lambda \\ \text {s.t. }&\text {Eq }. (5g),\\&\lambda \ge \frac{\Delta \phi ^2}{2\pi ^2}. \end{aligned} \end{aligned}$$
(23)

on a grid \(s^*=[0,0.01,\ldots ,0.5]\). For the given case of \({\Delta \phi =\frac{\pi }{2}}\), a value of \(\lambda _{\textrm{min}}= \frac{1}{6}\) is obtained. The the paths resulting from the optimal and various other values of \(\lambda\) are depicted in Fig. 15 with \(r_0=1\,\text {m}\).

Fig. 15
figure 15

Paths corresponding to different values of \(\lambda\)

Full size image

Note that the increased distance to the sphere comes along with a higher curvature, especially at \(s=\frac{1}{2}\), see Fig. 16.

Fig. 16
figure 16

Curvature along s for various values of \(\lambda\)

Full size image

Depending on the kinematic of the applied manipulator, this directly translates into a higher velocity. In Fig. 16, both the curvature and the x-component of the velocity are shown, with the latter computed for an assumed constant path velocity of \(\dot{s}=1/\text {s}\). Indeed, the total travel time T for a path piece does not heavily depend upon \(\lambda\), which can be demonstrated for the simple case of linear kinematics \(p(q) = [q_x,q_y]\) with integrator chain dynamics \(\dot{q} = u\) and box constraints \(\dot{q}_{x/y}\in [-0.1,0.1]\text { m/s}\). Here, the path dynamics in the time-optimal case follow to

$$\begin{aligned} \dot{s} = {\left\{ \begin{array}{ll} \frac{0.1}{|\mathcal {R}_x'(s)|}&{}\quad 0\le s \le \frac{1}{2} \\ \frac{0.1}{|\mathcal {R}_y'(s)|}&{}\quad \frac{1}{2}< s \le 1 \end{array}\right. }, \end{aligned}$$
(24)

which allows computation of the total travel time by

$$\begin{aligned} \begin{aligned} \min \ {}&T\\ \text {s.t.}\ {}&s(T)=1,\\&\dot{s}(t) = {\text {Eq. }} (24), t \in [0,T]. \end{aligned} \end{aligned}$$
(25)

Indeed, the total travel time increases by less than \(10\%\) for the most outward path at \(\lambda =\frac{1}{6}\), compared to the minimum value for \(\lambda \rightarrow \infty\), see Fig. 17.

Fig. 17
figure 17

Total travel time for various values of \(\lambda\)

Full size image

In case of FGC fabrication, the production speed tends to be more heavily limited by the pumping system, for which reason we give preference to a greater path-sphere distance by choosing \(\lambda =\lambda _{\textrm{min}}\).

Fig. 18
figure 18

Application of the path planning procedure on a large floorplate

Full size image

4.2 Application and results

The presented path planning scheme was applied to several exemplary FGC elements, see Fig. 18, for a large scale floor plate. The path starts at the top of the central structure and loops around the outer shape down into the center, see Fig. 19. As the path performs an entire loop before coming into the vicinity of its start, there is an adequate amount of time for the concrete to spread out evenly, which is a necessary precondition for layerwise fabrication; otherwise, floating of spheres due to buoyancy forces might occur (Blagojevic et al. 2021). Further, every sphere is passed from at least two sides. This allows the concrete to spread evenly between the spheres, such that cavities are prevented.

Fig. 19
figure 19

The path loops around the shape towards the interior

Full size image

The planned paths for various other elements are depicted in “Appendix”. The time complexity of our algorithm is approximately linear in the number of spheres for our test elements, see Fig. 20.

Fig. 20
figure 20

Time required for the calculation of the triangulation

Full size image

5 Discussion

The given problem of path planning for FGC elements poses unique demands, for which existing methodologies from e.g. the field of 3D printing are not appropriate. There, the printing area is usually connected, while in our case it consists of a multitude of small areas in between four spheres, which share discrete points with each other.

Here, a triangulation approach allows to both account for evading the spheres and neatly covering the elements area. The problem can thus be dissected into defining the triangulation, finding a path through it and planning the actual spatial path in each triangle.

Hamiltonian triangulations clearly offer a substantial advantage, as no overlaps and thus an overall shorter length and easier concrete application results; the latter is important as, depending on the viscosity of the used concrete, enough time must pass for it to spread out evenly. For arbitrary sphere sets and element shapes, defining such a triangulation is a demanding task. The presented approach is based on theoretical findings on Hamiltonian triangulations, which can be applied to the given problem by restricting the elements geometries, but these restrictions comply with both requirements from fabrication and design, and are thus not deemed too limiting.

6 Conclusion and future work

The subject of this paper is a path planning method for FGC elements, which both cover the elements area and evades the therein present spheres. These specific requirements demand for special approaches, which are the main methodological contributions.

Triangulation was proposed as the baseline for path planning, since it allows a separation of the global planning problem in a sequence of smaller ones. This is desirable as a path evading the spheres in a triangle can be found quickly, as the geometric situation to consider is clear.

To this end, a new subclass of triangulations called truly layered triangulations (TLT) was presented, which is less restrictive than comparable work found in the literature. Some research recognized the notion of layeredness in triangulations; here, a formal definition of hull and core was given by recognizing several distinct subsets of triangles. For this subclass of triangulations, a proof on hamiltonicity was presented.

Applied to the problem at hand, transfering the properties of a TLT to sphere sets within an FGC elements allows for the straightforward definition of an algorithm to define such a triangulation.

The presented approach thus achieves path planning for FGC elements. It is thus mainly dependent on the elements geometry, with the only design parameter being \(\lambda\), controlling the paths curvature. Future work will thus focus on the actual motion planning for the manipulator, e.g. by offline solving the inverse kinematics problem in order to generate a feedforward reference trajectory for the joint velocities which is stabilized online by use of path deviation feedback. As the working space of the currently used portal robot is limited, we are planning to use a spidercrane (Lauer et al. 2023) for the fabrication of large-scale elements.

Future work will also include more advanced algorithms for triangulating broader classes of sphere sets. Key for this will be a broader definition of the hull and core of a sphere set. One approach might be a further generalization of allowed sphere sets by distributing additional virtual spheres, such that e.g. the combined set yields the desired properties. The latter seems especially promising in cases of elements with high load areas, where no spheres at all are placed. An alternative approach to a constructed Hamiltonian triangulation is the adjustment of a properly dense initial triangulation, e.g. based on the constrained Delaunay algorithm (Chew 1989). After finding a path covering the triangulation by solving the traveling salesman problem on its bigraph, triangles traveleled multiple times can be split up such that hamiltonicity is obtained. A difficulty with this approach however is, that the newly defined triangles must still allow the path to avoid the spheres.

Considering less restricted FGC geometries necessitates the generalization of the presented local path planning scheme, as subsequent fixpoints and their tangentials might not lie on a common sphere in more general sphere sets. While the given polar coordinate approach seems sufficient, the radius function r(s) will need adjustment.