Abstract
This study examined the impacts of price changes in fossil-energy resources on food prices across the world. We approached this issue with the input–output (IO) price model, which is suitable for evaluating the price effects due to cost-push (supply driven) processes through transaction linkages of intermediate goods. We employ an international interregional IO table comprising 14 regions and 57 industrial sectors, which is compiled from the global trade analysis project (GTAP) 9 database. The results revealed: (1) interregional price linkages are particularly strong between a wheat-producing region and energy producers in the adjacent regions; and (2) the world oil sector appears to exert the strongest effects on mechanized sectors (wheat, plant fibers and fishing) and regions practicing advanced agriculture (East Asia, the US, and Russia). Furthermore, a comparison with empirical observations suggests that approximately one tenth of observed 2-year price changes in US wheat in 2004–2016 can be explained by the cost-push processes derived from the world oil price changes.

Source modified and simplified after Peters et al. (2011). Note The figure shows an example of a 3-region table for simplicity. The shaded blocks indicate the diagonal blocks for intra-regional transactions (\(\varvec{Z}^{{\varvec{rr}}}\) and \(\varvec{y}^{{\varvec{rr}}}\))


Similar content being viewed by others
Notes
We may sometimes abbreviate the term “fossil energy” to “energy” for simplicity.
We use for convenience the term “food” to loosely indicate both edible and non-food agricultural produce or sectors supplying them. Likewise, we use the term “agriculture” to indicate all primary industries including forestry and fisheries (i.e., Sectors No. 1 to 14 in Table 1 presented later).
Among these, data of primary inputs and domestic/international taxes and subsidies can also be obtained from the GTAP, but these values are irrelevant in the context of this study.
A mathematical derivation of Eq. (6) is provided in “Appendix 1”.
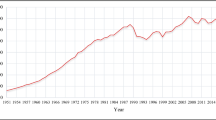
One must bear this in mind when referring to Fig. 2 later.
World crude oil price: Average import costs on c.i.f. basis in $US per barrel, which are volume-weighted averages for France, Germany, Italy, Spain, UK, Japan, Canada and USA. Although these values are not producer prices, we assume that they largely represent the trends in world oil market prices. US wheat price: producer prices in the USA extracted from the FAOSTAT database.
The existence of the relevant inverse matrix is assumed throughout.
References
Abbott PC, Hurt C, Tyner WE (2011) What’s driving food prices in 2011? Issue Report. Farm Foundation, IL, USA. https://www.farmfoundation.org/wp-content/uploads/2018/09/IR-2011-Final-FoodPrices_web.pdf. Accessed 17 Jan 2019
Aguiar A, Narayanan B, McDougall R (2016) An overview of the GTAP 9 data base. J Global Econ Anal 1:181–208. https://doi.org/10.21642/JGEA.010103AF
Baffes J (2007) Oil spills on other commodities. Policy research working paper WPS4333. World Bank, Washington, D.C. http://documents.worldbank.org/curated/en/897491468339553377/Oil-spills-on-other-commodities. Accessed 17 Jan 2019
FAO (2018) The state of world fisheries and aquaculture 2018—meeting the sustainable development goals. Food and Agriculture Organization of the United Nation, Rome. http://www.fao.org/state-of-fisheries-aquaculture/en/. Accessed 7 May 2019
FAO (2019) FAOSTAT. Food and Agriculture Organization of the United Nation, Rome. http://www.fao.org/faostat/en/#home. Accessed 17 Jan 2019
Fukuda Y, Kondo T (2009) The analysis of ripple effect of imported oil and cereals price hike. Rev Agric Econ Hokkaido Univ 64:53–57 (in Japanese)
Gilbert CL (2010) How to understand high food prices. J Agric Econ 61:398–425. https://doi.org/10.1111/j.1477-9552.2010.00248.x
Hanson K, Robinson S, Schluter G (1993) Sectoral effects of a world oil price shock-economywide linkages to the agricultural sector. J Agric Resour Econ 18:96–116
Headey D, Fan SG (2008) Anatomy of a crisis: the causes and consequences of surging food prices. Agric Econ 39:375–391. https://doi.org/10.1111/j.1574-0862.2008.00345.x
Hertel TW (1997) Global trade analysis: modeling and applications. Cambridge University Press, Cambridge
IEA (2018) Monthly oil price statistics. International Energy Agency, Paris. https://www.iea.org/classicstats/monthlystatistics/monthlyoilprices/. Accessed 17 Jan 2019
Miernyk WH (1976) Some regional impacts of the rising costs of energy. Pap Reg Sci 37:213–227. https://doi.org/10.1111/j.1435-5597.1976.tb00977.x
Miller RE, Blair PD (2009) Input–output analysis: foundations and extensions, 2nd edn. Cambridge University Press, Cambridge
Mitchell D (2008) A note on rising food prices, policy research working paper 4682. World Bank, Washington, D.C. http://hdl.handle.net/10986/6820. Accessed 17 Jan 2019
Miyazawa K (2002) Introduction to input–output analysis, new edition. Nikkei Bunko, Tokyo (in Japanese)
Oosterhaven J (1996) Leontief versus Ghoshian price and quantity. South Econ J 62:750–759. https://doi.org/10.2307/1060892
Peters GP, Andrew R, Lennox J (2011) Constructing an environmentally-extended multi-regional input–output table using the GTAP database. Econ Syst Res 23:131–152. https://doi.org/10.1080/09535314.2011.563234
Polenske KR (1979) Energy analyses and the determination of multiregional prices. Pap Reg Sci 43:83–97. https://doi.org/10.1111/j.1435-5597.1979.tb01077.x
Reboredo JC (2012) Do food and oil prices co-move? Energy Policy 49:456–467. https://doi.org/10.1016/j.enpol.2012.06.035
Steinhart JS, Steinhart CE (1974) Energy use in US food system. Science 184:307–316. https://doi.org/10.1126/science.184.4134.307
Tamamura C (2014) Foundations of the price model and its applications to the Asian international input–output tables. In: Tamamura C, Kuwamori H (eds) International input–output analysis: theory and application. IDE Research Series 609, Institute of Developing Economies, Chiba, pp 199–229 (in Japanese)
Timmer MP, Dietzenbacher E, Los B, Stehrer R, de Vries GJ (2015) An illustrated user guide to the world input–output database: the case of global automotive production. Rev Int Econ 23:575–605. https://doi.org/10.1111/roie.12178
Yakushiji T, Sato K (2000) Factors of cost changes in agricultural sectors. Nogyo Sogo Kenkyu 54(4):25–55 (in Japanese)
Acknowledgements
We acknowledge with gratitude that this work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI 16KT0036.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Mathematical derivation of Eq. (6)
Appendix 1: Mathematical derivation of Eq. (6)
This appendix explains a mathematical derivation for Eq. (6) in the main text, on the basis of Tamamura (2014). Assume an economy with n goods (sectors) and one region for notational simplicity. We set to describe a situation in which the price of the nth good is exogenously increased from \(p_{n}\) to \(p_{n} + \Delta p_{n}\), which induces price increases in the other n − 1 goods in response, via cost-push processes, from \(p_{i}\) to \(p_{i} + \Delta p_{i} (i = 1, \ldots ,n - 1)\).
We begin by partitioning the input coefficient matrix A into four sub-matrices:
where
Notice when A is transposed, the corresponding sub-matrices become:
First, using these sub-matrices, we rearrange Eq. (4) with respect to goods 1 to n − 1:
where \(\varvec{p}_{1}\) and \(\varvec{v}_{1}\) are the vectors of price and value-added of goods 1 to n − 1, respectively.
When the price of the nth good is raised, the prices of the other goods are increased in response, as mentioned above, and the economy will reach another price equilibrium:
Subtracting Eq. (10) from (11) gives:Footnote 8
Second, we define the transposed Leontief inverse matrix in four sub-matrices corresponding to Eq. (9):
where the sub-matrices B11 to B22 are defined in correspondence with A11 to A22 in Eq. (8).
Multiplying \(\left( {\varvec{I} - \varvec{A}^{{\prime }} } \right)\) and \(\varvec{B}^{{\prime }}\) (Eq. 13) gives:
where In is the n-dimensional identity matrix and On is the n-dimensional zero vector.
Hence, we have:
Finally, inserting Eq. (15) into (12) gives:
This proves Eq. (6).
About this article
Cite this article
Ueda, T., Kunimitsu, Y. Interregional price linkages of fossil-energy and food sectors: evidence from an international input–output analysis using the GTAP database. Asia-Pac J Reg Sci 4, 55–72 (2020). https://doi.org/10.1007/s41685-019-00124-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41685-019-00124-9