FormalPara Key Points for Decision Makers

Over a long-term time horizon, the NHS DPP was shown to be cost-saving and generate more QALYs compared with usual care.

Policymakers should use this as evidence to support the continued investment in diabetes prevention programmes.

1 Introduction

Type 2 diabetes is a chronic condition that affects insulin function and production, leading to high blood glucose levels; symptoms include tiredness and excessive thirst. It is also associated with an increased risk of developing other problems, such as cardiovascular disease, nerve and eye damage [1]. Worldwide, it is estimated that diabetes is the sixth leading cause of disability [2]. Whilst there are genetic risk factors, such as a family history of the disease and being of South-Asian, African-Caribbean or black African descent, the majority of risk factors are lifestyle based. These include being overweight, smoking, poor diet and physical inactivity [3]. Patients with type 2 diabetes are usually prescribed medications, such as metformin, to regulate their blood sugars, although it can sometimes be managed with weight loss, diet or exercise alone [4].

In the United Kingdom (UK), the prevalence of type 2 diabetes is increasing, with prevalence rates more than doubling between the years of 2000 and 2013 (2.39–5.32%) [5]; exacerbated by an increase in average weight, sedentary lifestyles, and an ageing population. As well as the patient and carer burden, type 2 diabetes also places a considerable burden on health care systems, with a study estimating direct costs to the NHS each year of approximately £8.8 billion (price year 2011–2012) [6].

Before developing type 2 diabetes, many patients first develop non-diabetic hyperglycaemia, characterised by elevated blood glucose levels that are below the threshold of type 2 diabetes but above normal ranges [7]. It is possible for individuals in this state to progress to type 2 diabetes or return to normal glucose tolerance levels. It is estimated that 11% of individuals with obesity and non-diabetic hyperglycaemia will progress to type 2 diabetes annually [7], with an estimated conversion rate of 7% within the first year of non-diabetic hyperglycaemia diagnosis [8].

Studies have shown that targeting this high-risk group of non-diabetic hyperglycaemia patients with interventions that combine diet and exercise advice can delay or prevent the progression to type 2 diabetes [9]. A recent systematic review identified 29 studies evaluating a lifestyle intervention to prevent type 2 diabetes (Chapter 2, [10]); and conducted a meta-analysis (using 25 studies). This meta-analysis found that lifestyle interventions resulted in a mean weight loss at 12 months of 2.31 kg (95% confidence interval [CI] –2.87 to –1.76), and a reduction of 0.11% (95% CI –0.19 to –0.03) in blood glucose levels, measured with HbA1c (using eight studies).

1.1 NHS Diabetes Prevention Programme

The NHS Diabetes Prevention Programme (DPP) was established as part of a major new emphasis in England on the need for targeted prevention strategies. The programme targets individuals with non-diabetic hyperglycaemia, with the aim of preventing these individuals from going on to develop type 2 diabetes.

Participants are primarily referred to the programme by a healthcare professional, during an NHS health check, or opportunistically during a consultation. To be referred, participants require a blood test to show that they are within the non-diabetic hyperglycaemic range (HbA1c 42–47 mmol/mol [6.0–6.4%]). HbA1c is a measure of average blood sugar over 8–12 weeks, with normal glucose tolerance considered to be a HbA1c concentration of below 42 mmol/mol.

The full programme comprises 13 group-based behaviour change sessions (one provider delivered 18 sessions), incorporating structured education on nutrition, physical activity and weight loss and typically lasts 9–12 months. It began in 2016 and was rolled out across England in a series of waves, covering the whole of England by April 2018. A diagram showing the rollout of the programme across English clinical commissioning groups is shown in Fig. 1 of the electronic supplementary material (ESM), and Fig. 2 of the ESM shows an example of a participant pathway through the programme. To avoid placing additional burden on frontline NHS services, NHS England decided to procure the programme from external contractors. As part of the first framework, four commercial providers were selected in a national competition. Only these providers were able to bid to provide the programme at each site.

NHS England conducted an impact assessment in 2016, which estimated the costs associated with implementing the NHS DPP in England from 2016 to 2021, along with the expected outcomes of the programme in the short- and long-term [11] using estimates from the literature along with expert opinion. This report estimated that by 2021, a total of 18,000 cases of diabetes would have been prevented or delayed amongst a cohort of 390,000 participants. It also found that the programme was likely to be cost-effective, and by the year 2033/34 cost saving (when applying discounting), assuming a cost of £270 per participant.

This paper aims to update these estimates of cost-effectiveness, for the first time using observed data from the programme on participant retention and health outcomes, along with provider contract information.

2 Methods

A Markov cohort model was developed in R [12, 13] to evaluate the cost-effectiveness of the NHS DPP compared with usual care, from the perspective of the English NHS. A model was developed as it is likely that many of the benefits of the NHS DPP occur in the long-term, beyond that which can be observed using routinely collected data. The model code is available via the author’s GitHub repository [14].

2.1 Interventions Analysed

Two strategies were considered: (1) usual care and (2) referral to the NHS DPP, in addition to usual care. In this instance, usual care was defined as what existed prior to the introduction of the NHS DPP. Guidance from the National Institute for Health and Care Excellence (NICE), first published in 2012, recommends that individuals with non-diabetic hyperglycaemia be offered a blood test and assessment of their body mass index at least once a year [15]. The intervention evaluated was a referral to the NHS DPP. An individual referred to the programme is free to take up as much or as little of the programme as they wish. The usual programme pathway comprises of first, an initial assessment and then a series of group-based sessions. Depending on the provider, there are either 13 or 18 total sessions. Further details about the programme can be found in Barron et al. [16].

2.2 Model Structure

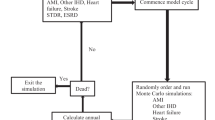
A Markov model was used due to the chronic nature of type 2 diabetes, which involves recurring events and continuous risk over time [17]. The model comprises the following states: ‘Normal glucose tolerance’ (HbA1c <42 mmol/mol [6.0%]), ‘Non-diabetic hyperglycaemia’ (HbA1c within the range of 42–47 mmol/mol [6.0–6.4%]), ‘Type 2 diabetes’ (HbA1c >47 mmol/mol [6.4%]) and ‘Death’. These states are mutually exclusive and exhaustive. A diagram of the model and the possible transitions between each of the states is shown in Fig. 1.

Fig. 1
figure 1

Markov model structure

Full size image

In the model, it is possible for individuals in the ‘Non-diabetic hyperglycaemia’ state to transition to the ‘Normal glucose tolerance’ state, remain in ‘Non-diabetic hyperglycaemia’, progress to ‘Type 2 diabetes’ or ‘Death’. Individuals in the ‘Type 2 diabetes’ state can remain in the state, return to ‘Non-diabetic hyperglycaemia’ or die (‘Death’). However, individuals in the ‘Type 2 diabetes’ state cannot directly transition to ‘Normal glucose tolerance’ and likewise, it is not possible for individuals in the ‘Normal glucose tolerance’ state to directly transition to ‘Type 2 diabetes’.

The model structure was developed by reviewing existing model structures and in collaboration with a clinical expert. This structure is also used elsewhere [18,19,20,21]. Roberts et al. [18] also state that this structure was developed following a review and in collaboration with a multi-disciplinary clinical team. It is believed that this structure captures the clinical reality of the disease.

2.3 Model Parameters

The transition probabilities from and to each of the model states are described in Table 1, in terms of the point estimates and sampling distributions used. Where possible, age-specific transition probabilities were sought for the following age groups: <40, 40–49, 50–59, 60–69, 70–79 and 80+ years, although this was not possible for all parameters.

Table 1 Transition probabilities and distributions used
Full size table

The NHS DPP-specific parameters were obtained from data used for the national evaluation of the programme. Other parameter values were obtained from peer-reviewed literature. The way these parameters were sourced and derived, as well as justifying where choices were made between sources, are described fully in the ESM (1.2. Transition Probabilities).

2.4 Costs and Outcomes

Table 2 shows the costs used for each of the model states along with the sources for these values. Costs considered were from the perspective of the NHS and with a price year of 2020. Whilst there is not a state associated with type 2 diabetes-related complications in this model, the cost distribution used for the ‘Type 2 diabetes’ state was sourced from two studies which costed the healthcare resource use of a population of individuals with type 2 diabetes. As such, it is expected that they will have incorporated a range of disease severity, including those experiencing diabetes-related complications, which will then be reflected in the cost distribution used in this model. Model outcomes were in terms of quality-adjusted life-years (QALYs). To calculate these, each of the model states were assigned utility scores, which were then used to calculate QALYs depending on the time spent in that state. Table 3 shows the values used along with the sources of these. Further information on how these sources were selected is available in the ESM (1.3. Costs and 1.4. Utility Scores).

Table 2 Costs associated with each state of the model (2020 price year)
Full size table
Table 3 Utility scores associated with each state of the model
Full size table

To derive the cost of the NHS DPP, data collected by providers on programme session attendance up to April 2019 was used along with commercially sensitive contract data provided by NHS England to determine the average cost of each referral made to the programme. Briefly, providers were paid according to five milestones of programme attendance. Each milestone included a set number of programme sessions and providers received a percentage of the total programme cost for a milestone met, if an individual attended at least 60% of sessions within that milestone. The percentage reimbursement attributed to each milestone and the total programme cost could vary depending on the contract of that provider, as providers competitively bid to deliver the programme. The programme data collected by providers was subject to validation checks by NHS England. Implementation costs for the NHS DPP were provided to regions by NHS England as part of a wider diabetes agenda and therefore how these costs were used varied. NHS England stated that the exact amount used towards NHS DPP implementation could not be estimated, and as such, estimates for the implementation costs of the programme were sourced from the original impact assessment [11]. Further detail on the reimbursement of providers is provided in McManus et al. [22]. Analysis of the provider attendance data and information on the provider contracts showed that the average cost per referral received up until April 2019 was £118.98 (standard deviation [SD] 117.54), weighted by provider, with an additional £22.79 per referral estimated due to implementation costs of the programme [22]. This was based on the 384,611 referrals received prior to April 2019, which had attended on average 3.0 sessions (SD 4.6). The time point of April 2019 was used to allow for all referrals to theoretically have the time to complete all programme sessions based on the follow-up data available (April 2020).

As a probabilistic version of the model was implemented, point estimates were transformed into distributions using their respective means and standard errors. Beta distributions were used for transition probabilities and utility estimates, and Gamma distributions for costs. The formulas used to derive the shape parameters for each of these distributions are detailed in the ESM (1.5. Distributions).

2.5 NHS DPP Effectiveness

The effect of the NHS DPP was modelled in two ways. The first considered the utility gains obtained directly from individuals participating in the programme, which were attributed to all individuals for the first cycle of the model. Previous regression analysis using EQ-5D responses recorded at initial assessment and final programme sessions showed that for each session attended, an individual gains a 0.0042 increase in utility (95% CI 0.0025–0.0059) [22]. Provider data was used to determine the average number of sessions attended for all referrals up until April 2019 within the age categories of <40, 40–49, 50–59, 60–69, 70–79 and 80+ years, to then calculate the average utility benefit. These estimates were then applied to the starting cohort of the NHS DPP in the model according to the proportion of the cohort in each age category.

The second measure of NHS DPP effect considered the long-term effect of the programme in terms of delaying or preventing type 2 diabetes. For this, analysis conducted as part of the wider NHS DPP evaluation was used, which estimated the impact of being referred to the NHS DPP compared with not being referred, using a matched analysis. This analysis found an adjusted hazard ratio of 0.80 (95% CI 0.73–0.87) for developing type 2 diabetes within 36 months [23]. There was also no evidence of a ‘rebound’ effect, which may have been expected after an individual left the programme and returned to previous lifestyle habits. When modelling the cohort exposed to the NHS DPP, this hazard ratio was applied to the transition probability for transitioning from ‘Non-diabetic hyperglycaemia’ to ‘Type 2 diabetes’. In the base case, it was assumed that this effect was maintained for three model cycles, akin to the time horizon of effect within the observed analysis.

For both costs and outcomes, a discount rate of 3.5% was used as recommended by the NICE Reference Case [24]. A common price year of 2020 for all costs was used and where applicable, costs were inflated using the annual Office for National Statistics Consumer Price Index (All items) [25]. The price year of 2020 was used as this study evaluates the first framework of the NHS DPP which ran from 2016 to 2020, and so the most up-to-date costs relative to this time were used.

2.6 Cost-Effectiveness Analysis

A cohort of 1000 individuals was simulated, all of whom began in the ‘Non-diabetic hyperglycaemia’ state. A model cycle length of 1 year was used, and the model was run over a total of 35 cycles. To better reflect the reality of individuals referred to the NHS DPP, six age groups were considered (<40, 40–49, 50–59, 60–69, 70–79 and 80+ years) within this cohort based on the observed age composition of individuals referred to the programme prior to April 2020. As such, 5.8% of this cohort began at an age of 34 years, 12.2% started at 45 years, 21.9% started at 55 years, 26.7% started at 65 years, 24.4% started at 75 years and 9.0% started at 84 years.

The annual cycle length is consistent with the natural history of type 2 diabetes and is commonly used in other modelling studies in this disease area. A within-cycle correction [26, 27] was also applied to account for the fact that transitions could occur at any point during the cycle and not at a discrete point in each cycle.

For the primary analysis, a probabilistic analysis with 10,000 Monte Carlo simulations was run. Running a probabilistic analysis as the base case of the model is in line with current recommendations by NICE [24] and academic debate [28, 29].

Using the 10,000 Monte Carlo simulations, the expected costs and QALYs accrued for usual care and for the NHS DPP were calculated. From this, the incremental costs and QALYs gained by the programme were estimated, averaged across the Monte Carlo simulations. The average incremental cost and QALYs associated with each individual for each of these simulations were plotted in a scatter plot to display the uncertainty around the simulation estimates.

The NHS DPP was considered cost-effective if the incremental cost per additional QALY gained was below the currently accepted willingness-to-pay threshold. For this analysis, two thresholds of £20,000 and £30,000 were considered, as these are the commonly used thresholds by NICE [24]. The NHS DPP was considered to dominate usual care if it incurred less costs and generated more QALYs over the course of the model (or be dominated if the converse was true).

The incremental net monetary benefit was also calculated, estimated as the average incremental benefit, multiplied by the willingness-to-pay threshold, minus the incremental cost of the programme. Here, a positive net monetary benefit amount would mean that the NHS DPP would be considered cost-effective, with higher values being more cost-effective than lower values. The probability of the NHS DPP being cost-effective compared with usual care was calculated at £20,000 and £30,000 per QALY by counting the proportion of simulations for which the incremental net benefit was positive.

Lastly, a cost-effectiveness acceptability curve (CEAC) was plotted. The CEAC shows the probability that the NHS DPP is cost-effective compared with usual care for a range of willingness-to-pay thresholds.

2.7 Impact of the NHS DPP

The results of the simulated cohort of 1,000 were then used along with the number of actual referrals received by the NHS DPP (526,283 referrals received by 31st March 2020) to estimate the total incremental costs and benefits incurred for the whole of the programme.

2.8 Sensitivity Analyses

Finally, the sensitivity of the analyses were explored according to several scenarios. Firstly, different levels of effectiveness of the NHS DPP were considered, in terms of the length of time for which the probability of transitioning to ‘Type 2 diabetes’ from ‘Non-diabetic hyperglycaemia’ was reduced. In the base-case analysis, a hazard ratio of 0.80 was applied to this transition probability for three cycles of the model. This effectiveness was based on what has been observed from analysis of routinely collected data. In sensitivity analyses, two different scenarios were considered for the continued effectiveness of diabetes prevention. The first scenario was based on evidence from the US Diabetes Prevention Programme (US DPP), a large clinical trial evaluating three different treatment groups: placebo, metformin and a lifestyle programme. This study found that there was still an observable effect in diabetes incidence at 10 years following the lifestyle programme (a hazard ratio of 0.66 at 10 years from 0.42 after 3 years) in comparison with placebo [30]. Calculating the equivalent proportional change for the 0.80 hazard ratio observed in the NHS DPP base case, this would be equivalent to an effect of 0.88, assumed to be maintained for 7 years, after which there was no lasting effect of the programme.

The second sensitivity analysis used subsequent analysis of the US DPP which showed that after 15 years there was still an observable difference between the lifestyle programme arm and placebo, with a hazard ratio of 0.73 [31]. As above, the equivalent proportional change was calculated and it was assumed that this effect would be observed for the subsequent 5 years, with the hazard ratio going from 0.80 (3 cycles) to 0.88 (7 cycles) to 0.91 (5 cycles), after which the risk of diabetes returned to normal.

There were also several sources for model parameters that could have been selected. As such, an alternative source for the costs associated with each of the model states was used, which was used in another published model [18]. In this modelling study, the authors assumed an annual cost of £773.00 (standard error [SE] 102.63) for normal glucose tolerance, a cost of £869.00 (SE 104.56) for non-diabetic hyperglycaemia and an annual cost of type 2 diabetes which increased linearly over 15 years from £1179.00 to £2939.00 (SE 270.00). These costs used a price year of 2015. As in the current study a Markov cohort model was implemented, it was not possible to determine how long an individual had remained in the ‘Type 2 diabetes’ state, and so instead the average of this range was used, £2059. These estimates were inflated to the 2020 price year using Shemilt et al. [32] to obtain the following annual cost estimates: £853.48 (SE 113.32) for ‘Normal glucose tolerance’, £959.47 (SE 115.45) for ‘Non-diabetic hyperglycaemia’ and £2273.37 (SE 298.11) for ‘Type 2 diabetes’.

The uncertainty surrounding the parameters of transition to ‘Type 2 diabetes’ from ‘Non-diabetic hyperglycaemia’ was also explored. In the base case, this was sourced from analysis of routinely collected primary care data and produced a probability of 0.0249. However, this produced a lower probability than what has been reported in other studies (particularly clinical trials), and therefore what has been used in other modelling studies. Therefore, the impact of using two higher rates was explored, the first reported by Herman et al. [33], who used data from the US DPP data to obtain a transition probability of 0.108, and the second used by Leal et al. [34], who reported an event rate of 80.4 per 1000 person-years for their base case (equivalent to a transition probability of 0.077). Neither of these estimates presented the different transition rates across age categories, and as such it was assumed to be the same rate across all ages modelled.

Finally, the uncertainty around utility scores was also explored. An alternative source to estimate the utility score of individuals with type 2 diabetes was used. In the base case, the utility scores were estimated from data obtained from the Health Survey for England, using responses from 491 individuals. Whilst using data from the survey enabled utility estimates for different age categories to be obtained, this sample size was relatively low and there was no information about the length of time an individual was diagnosed with diabetes or if they were suffering from any diabetes-related complications. Instead, estimates presented by Keng et al. [35] detailing the health utility score of 11,683 individuals with established diabetes (93.9% with type 2 diabetes and 6.1% with type 1 diabetes) were used in a sensitivity analysis. This population had a mean diabetes duration of 16.4 years and 14.7% were recorded as having at least one comorbid adverse event. The utility scores presented by Keng et al. [35] were not broken down by diabetes type or age category, and thus the mean utility score presented (after imputation) of 0.771 (SD 0.221) was used to derive the Beta distribution, which was used for all age categories in the model. The final sensitivity analysis considered there to be zero utility benefit from the programme session attendance. Whilst the utility benefits associated with session attendance included in the base case analysis of the model were sourced from analysis of EQ-5D data from referrals to the NHS DPP, this regression analysis was conducted only on a reduced sample of individuals who had attended both the initial assessment and final planned programme session (where the EQ-5D was recorded) and who had provided responses to the EQ-5D questionnaire. As such, there is some uncertainty surrounding these estimates and so a conservative assumption that zero benefit was derived from session attendance was made in this sensitivity analysis.

The different sensitivity analyses conducted are described in Table 4.

Table 4 Different probabilistic sensitivity analyses conducted
Full size table

2.9 Validation

The mathematical programming of the model was validated by double programming a deterministic version of the model using the point estimates described, in both Microsoft Excel and R, to ensure the same results were obtained. The parameters used in the distributions were checked by plotting the distributions and ensuring that they clustered around the point estimate they were based upon. The model outputs were also compared against results from other modelling studies in the same disease area by comparing state memberships over time to ensure the same general trends were observed.

3 Results

3.1 Base Case – Effectiveness observed for 3 years

Table 5 presents the costs and QALYs generated according to the two strategies: NHS DPP and usual care. Over the course of the 35 model cycles, the cohort referred to the NHS DPP incurred less costs on average than usual care, and generated more QALYs. This suggests that the NHS DPP dominates usual care. Across the 10,000 Monte Carlo simulations, on average the NHS DPP resulted in cost savings of £135,755 with QALY gains of 40.8, compared with usual care alone (for the cohort of 1000).

Table 5 Model results for base case and sensitivity analyses (cohort of 1000 with 10,000 Monte Carlo simulations)
Full size table

A scatterplot of the incremental costs and QALY pairs from the 10,000 Monte Carlo simulations comparing the NHS DPP to usual care is shown in Fig. 2. This plot illustrates the uncertainty surrounding the estimates of expected costs and expected effects, compared with the willingness-to-pay threshold of £20,000 per QALY (shown by the black line). The majority of these points fall within the south-east quadrant (86.1%) which indicates that the NHS DPP was both cost-saving and generated more QALYs.

Fig. 2
figure 2

Base case analysis. Scatter plot of incremental cost and quality-adjusted life-year (QALY) pairs from 10,000 Monte Carlo simulations, on average, for an individual in the modelled cohort. The black line represents a willingness-to-pay threshold of £20,000 per QALY gained. The number of points in each quadrant are: North-East: 1295, North-West: 91, South-East: 8614, South-West: 0. Percentage cost-effective at £20,000 willingness to pay (£30,000): 98.1% (98.4%)

Full size image

The CEAC is presented in Fig. 3. This plot shows the likelihood of the NHS DPP being cost-effective at different willingness-to-pay thresholds. This plot begins at 86.1% due to the number of simulations that both generate additional QALYs and incur less costs. The probability of the NHS DPP being effective at a willingness-to-pay threshold of £20,000 per QALY generated was 98.1%, which increased to 98.4% with a willingness-to-pay threshold of £30,000.

Fig. 3
figure 3

Cost-effectiveness acceptability curve for the strategy of NHS DPP compared with usual care (base case analysis). DPP Diabetes Prevention Programme, NHS National Health Service, QALY quality-adjusted life-year

Full size image

Scaling up these cost savings to the number of referrals actually received by the NHS DPP by the end of March 2020 (526,283) would equate to an additional 21,472 QALYs generated and cost savings of £71.4 million over the course of the 35-year time horizon.

An example of a cohort trace from one of the Monte Carlo simulations is shown in the ESM (Table 6).

3.2 Sensitivity Analyses

The results of the sensitivity analyses conducted are also shown in Table 5 and the respective scatter plots of incremental cost and QALY pairs from the 10,000 Monte Carlo simulations shown in the ESM (Figs. 3–9), alongside the number of simulations that fell within each of the scatterplot quadrants. Across all scenarios modelled, the NHS DPP dominates usual care. The scenario which resulted in the highest on average cost savings was when the transition probability from ‘Non-diabetic hyperglycaemia’ to ‘Type 2 diabetes’ was updated with the transition probabilities reported in the US DPP trial [33] (SA4), which had a higher probability than that used in the base case. This resulted in an average cost saving of £321,383 and an average increase of 90.2 QALYs across the cohort of 1000. Indeed, 99.7% of the 10,000 Monte Carlo simulations were shown to fall within the south-east quadrant of the scatter plot, equivalent to the NHS DPP being cost-saving and generating additional utilities when compared with usual care (Fig. 6, ESM). Across the seven sensitivity analyses, the scenario which resulted in the highest uncertainty and therefore the lowest probability that the NHS DPP was cost-effective at a willingness-to-pay threshold of £20,000 occurred when zero benefit from session attendance was assumed. This was the most conservative scenario modelled, assuming only a benefit from type 2 diabetes prevention over 3 years, however, it still found that the NHS DPP dominated usual care, with 96.4% of simulations finding the NHS DPP cost-effective at a willingness-to-pay of £20,000 (96.9% at £30,000). The sensitivity analysis with the second lowest estimates of cost-effectiveness was when the lower state costs were used (SA3). In this instance, 97.9% of the 10,000 Monte Carlo simulations were cost-effective at a willingness to pay of £20,000, which increased to 98.4% when using a willingness to pay of £30,000. There were three sensitivity analyses in which all of the Monte Carlo simulations fell below the willingness-to-pay threshold of £20,000; these were when the effect was maintained for 15 years (SA2), and in the two instances (SA4 and SA5) when the transition probability from ‘Non-diabetic hyperglycaemia’ to ‘Type 2 diabetes’ was updated using trial data.

4 Discussion

4.1 Main Findings

This paper sought to evaluate the long-term cost-effectiveness of the NHS DPP in comparison to usual care using a decision-analytic model. A Markov cohort model was developed, run over a 35-year time horizon, with a cohort representative of the different age groups referred to the programme. A total of 10,000 Monte Carlo simulations were used to assess the uncertainty of the results, as well as several sensitivity analyses. These sensitivity analyses considered different effectiveness estimates of the programme, different cost and utility sources for the model states, as well as varying the transition probability from the ‘Non-diabetic hyperglycaemia’ state to the ‘Type 2 diabetes’ state.

In the base case, the NHS DPP was found to likely dominate usual care, by generating on average 40.8 additional QALYs at a reduced cost, with average cost savings being £135,755. At a willingness to pay of £20,000 per QALY, 98.1% of simulations were on or under the willingness-to-pay threshold. Inflating these findings to the number of referrals actually received by the NHS DPP by April 2020, it can be estimated that over the course of 35 years, the programme will have saved a total of £71.4 million in comparison with usual care and generated an additional 21,478 QALYs. The results of the base case use the assumption that the effectiveness of the programme only lasted for the period of time for which an effect has actually been observed amongst referrals to the programme [23]. As such, it is likely that this estimate of cost-effectiveness is conservative, given that the effects of the programme may continue on after 3 years.

These findings were robust to several sensitivity analyses conducted, with all of these analyses finding the NHS DPP to dominate usual care. The sensitivity analyses which resulted in the lowest potential cost-effectiveness results occurred when no utility benefit from session attendance was assumed, followed by when the cost estimates for each of the model states were changed, leading to cost savings of £26,703. The cost estimates used in this sensitivity analysis were used in a modelling study by Roberts et al. [18]. The costs were based on estimates from the NICE costing template and a study by Hex et al. [6], which used a top-down costing approach to estimate the cost of type 2 diabetes, using aggregated data sets and secondary sources. This study found that type 2 diabetes had an average cost of £2499 (2020 prices). This annual estimate is lower than the estimate used in the base case of this modelling study, which combined data from Morgan et al. [36] (which used routinely collected data on 15,258 individuals with type 2 diabetes) and Currie et al. [37] (which used routinely collected data on 114,752 individuals with type 2 diabetes) estimating an annual average healthcare resource use cost of £3717 (equivalent to £4421 in the 2020 price year) for individuals with type 2 diabetes.

In another of the sensitivity analyses, published findings from the 10-year follow-up of the US DPP [30] were used to model how effectiveness may change over time. If the NHS DPP follows the same trajectory as the US DPP’s effectiveness, in that diabetes prevention or delay is observed up to 10 years, it is likely that it will be even more cost-saving than the base case analysis suggests, with results of the sensitivity analysis showing it as being cost-effective in 99.9% of simulations at a willingness to pay of £20,000 per incremental QALY. However, it should be noted that there were some key differences between the NHS DPP and the US DPP. Firstly, the US DPP recruited participants to a randomised controlled trial, which may mean that there was greater adherence to the programme than what could realistically be observed in the real-world roll out of the NHS DPP. The length and format of the programme was also different, in that the US DPP was delivered as an individual programme which involved 16 visits in the first 6 months, with subsequent face-to-face visits at least once every 2 months thereafter for the remainder of the trial (average follow-up 2.8 years). In contrast, the NHS DPP delivered a maximum of 13 or 18 (depending on provider) group-based sessions over a period of 9–12 months. These differences may reduce the likelihood that the longer-term effectiveness of the NHS DPP will follow the trajectory observed in the US DPP 10-year follow-up.

The results of these analyses should be used by NHS England policy makers as evidence for the continued investment in type 2 diabetes prevention programmes. Whilst short-term needs often take precedence in budget allocation, this modelling study has shown that investment in prevention initiatives now will lead to substantial cost savings in the future, along with quality-of-life improvements. These findings can also be used by policymakers in other countries where prevention programmes are yet to be established.

4.2 Other Modelling Studies

Prior to rolling out new legislation or implementing new policies, it is customary for the Department of Health and Social Care to conduct an impact assessment, with the purpose of identifying the costs associated with the new policy as well as the potential benefits [38]. An impact assessment was conducted for the NHS DPP [11]. This assessment used a model to estimate the potential long-term cost-effectiveness of the programme. In the absence of programme data, the model was parameterised using estimates from other prevention programmes and expert opinion. It found that over a time horizon of 20 years the NHS DPP would result in cost savings of £35 million (excluding implementation, support and local costs), whilst generating 18,000 QALYs. In contrast, the analysis presented here, which used actual data from the programme in terms of overall effectiveness and impact on utility score, estimated a total of £71.4 million in cost savings over a 35-year time horizon (which includes implementation costs of £22.79 per referral), which suggests that the original impact assessment may have underestimated the cost-effectiveness of the programme. A source of these differences may have been that in the impact assessment, the primary analysis estimated the average cost of referral to the programme to be £270, which was based on a tariff of approximately £435 if an individual attended all sessions. However, analysis which used actual provider contract data and observed participation rates showed that the average cost per referral was actually lower at £141.77 per referral (including implementation costs) due to lower average provider tariff prices and different retention rates [22], reasons for variable attendance rates are discussed in Howarth et al. [39].

In terms of health outcomes, the estimated total QALYs generated within the impact assessment were 18,000 QALYs over 20 years, whereas this model estimates 21,472 additional QALYs generated over 35 years. Another preliminary evaluation of the potential impact of the NHS DPP is reported in Thomas et al. [40]. This evaluation used a patient-level simulation model as described in Breeze et al. [41], where the programme effectiveness was sourced from a literature review of pragmatic lifestyle interventions [42] and the programme cost was assumed to be the same as in the impact assessment (an average cost of referral of £270). This model assumed in the base case that the programme effect lasted for 5 years. It found that the programme was likely to be cost-effective within 6 years and cost-saving within 12 years. These findings are slightly more conservative than the cost-effectiveness estimates presented here, which as described above, may be due to the lower actual average referral cost and the observed QALY gains from session attendance which were not originally considered.

There have also been several literature reviews of decision-analytic models in the prevention of type 2 diabetes [43,44,45,46,47]. These reviews identified the following modelling studies with a UK focus: Palmer et al. [21], Gillies et al. [48], Gillett et al. [49] and Breeze et al. [41]. Since these reviews were conducted, there have also been three more modelling studies focusing on the UK setting: Roberts et al. [18], Leal et al. [34] and Frempong et al. [19]. The majority of these studies estimated that prevention programmes of type 2 diabetes are cost-effective. The model structure used in this analysis is consistent with existing models and the use of a 1-year cycle length is also consistent with the review findings of Leal et al. [46], which found that 90% of studies included used this length.

4.3 Strengths and Limitations

This is the first modelling study to use data directly from the NHS DPP, which includes commercially sensitive cost data from providers, estimates of observed effect in terms of type 2 diabetes progression and utility values from individuals referred to the programme. In using this data, some elements of uncertainty in the modelling results presented here were removed, as the programme-specific parameters are based on real-world evidence of the NHS DPP. The cohort modelled was also tailored to reflect the age profile of referrals made to the programme, and where possible the model was parameterised using age-specific parameters. This analysis focused on the cost-effectiveness of the NHS DPP amongst individuals with elevated HbA1c levels (the criteria for a referral to the NHS DPP), which is something that another modelling study had previously identified as a suggestion for future research [18].

In addition to programme-specific data, this study utilised access to two extracts of the National Diabetes Audit. This audit data contains information on when an individual was diagnosed with non-diabetic hyperglycaemia and/or type 2 diabetes along with other basic sociodemographic characteristics, between 1st April 2017 and 31st March 2020. This audit covered 99.3% of practices in England in 2019/20 [50]. This data was used to generate the transition probability from ‘Non-diabetic hyperglycaemia’ to ‘Type 2 diabetes’, rather than relying on clinical trial data which were found to report substantially higher rates of transition than observed in the real world (which may reflect selection bias of more high-risk individuals into clinical trials).

The model was also run using probabilistic analyses in the base case, which is in line with current methodological debate [28]. It has been shown that using deterministic analysis on non-linear models (such as Markov models) with each input at its mean will not generate the expected value of the outputs and hence may produce misleading results. The majority of existing studies identified used a deterministic model in their base case analysis.

There are also some limitations of this study. The first is that despite being clinically validated and used in other published studies, the Markov model structure used in this analysis is relatively simple. Other modelling methods, such as individual-level simulation models, may be better placed to capture the physiological nuances of both non-diabetic hyperglycaemia and type 2 diabetes; however, the level of data required to parameterise these models is high. In particular, type 2 diabetes is associated with several comorbidities and complications which can lead to increased healthcare costs [51] and utility decrements [35]. The model structure in this analysis does not include a state explicitly for diabetes-related complications. Instead, these were indirectly considered by using population estimates of costs and utilities for the ‘Type 2 diabetes’ state. The original studies upon which these were sourced incorporated individuals with a range of disease severity and progression, and thus were likely to capture those with diabetes-related complications. This paired with the fact that parameters are sampled from a distribution to help capture the range of potential values should help to mitigate the absence of a specific complications state. Furthermore, by not having a diabetes-related complications state, an inherent assumption was made that rates of diabetes-related complications were the same across both treatment arms. There is currently no evidence regarding the NHS DPP to suggest whether rates of complications are reduced in individuals who go on to develop type 2 diabetes after the programme, although if this were the case, the analysis presented here would likely underestimate the potential cost savings.

There was substantial choice about the source of cost and utility data for the modelling states. An attempt to identify all possible sources of data and assess the quality of these studies was made, however not all estimates were directly applicable to the population modelled. Some estimates were taken from studies conducted outside of England and therefore may lack generalisability. Others may relate to differential methods of measuring blood glucose (such as impaired fasting glucose or impaired glucose tolerance) where it was then necessary to make an assumption that they also applied to individuals with raised HbA1c. However, the effect of this was mitigated by running probabilistic analyses which inherently capture some uncertainty around parameters and also by running several sensitivity analyses. Furthermore, in this model, the choice was made to focus on stratifying parameters according to different age categories. This was done as there was evidence in the data that the size of the difference between health-related quality of life scores for individuals with non-diabetic hyperglycaemia compared with normal glucose tolerance changed according to age. With this being said, there are other sociodemographic characteristics that may also have been important to consider and parameterise by, which were not considered in this model.

Finally, as an English NHS perspective was adopted, the potential financial costs borne by individuals participating in the programme were not considered, which may have included travel to the course venue, and the opportunity cost of time lost whilst they were participating in sessions.

5 Conclusion

A decision-analytic model was developed to determine the long-term cost-effectiveness of the NHS DPP. The results show that this prevention programme is highly likely to be a cost-effective initiative, with 98.1% of simulations coming on or under the willingness-to-pay threshold of £20,000 per QALY. Indeed, in the majority of the simulations, the NHS DPP was cost-saving in comparison with usual care and generated more QALYs. These findings can be used by policymakers as evidence in support of the likely cost-saving nature of such prevention programmes and thus their future roll-out and recommissioning.