FormalPara Key Points for Decision Makers 

Mixture cure rate models may be a suitable way to estimate long-term survival outcomes for patients with relapsed or refractory diffuse large B-cell lymphoma (R/R DLBCL), as they account for the presence of ‘cured’ and ‘non-cured’ patients within a population.

We used a mixture cure rate model to estimate long-term survival of patients with R/R DLBCL treated with polatuzumab vedotin plus bendamustine and rituximab (Pola+BR) using data from the Phase Ib/II GO29365 study.

The estimated proportion of long-term survivors was 23.0% of patients treated with Pola+BR versus 0% of patients treated with BR alone.

1 Introduction

For some patients with relapsed or refractory (R/R) diffuse large B-cell lymphoma (DLBCL), achieving long-term survival (and potential cure) is possible with the use of high-dose chemotherapy combined with rituximab, followed by autologous stem cell transplantation (ASCT) [1, 2]. However, the majority of patients are ineligible for transplant, due to advanced age, concomitant conditions, or inadequate stem cell harvest [3, 4]. For these patients, salvage treatment options are limited, and the prognosis is relatively poor [1, 3, 5]. Patients who relapse following ASCT are expected to survive for only a few months [4].

With advances in treatment for R/R DLBCL, such as the introduction (in the third- or later-line settings) of CD19-directed chimeric antigen receptor (CAR)-T cell therapy [6,7,8,9] and the approval of the antibody–drug conjugate, polatuzumab vedotin, in combination with bendamustine and rituximab (Pola+BR) [10, 11], the proportion of patients who survive with durable, long-term remissions will likely increase. In clinical trials of new therapies, initial response rates are often observed shortly after patients receive treatment; however, events for patients with long-term response may not yet have occurred and availability of predictive long-term survival data for new therapies will help to ensure that patients are receiving the most effective treatments as early as possible.

Long-term survivors (LTS) introduce heterogeneity into the data on the overall survival (OS) of a patient population, and OS in a heterogeneous population may not be adequately described using the traditional standard parametric survival models [12]. Mean OS is most important to healthcare payers as it estimates the average lifespan of patients (rather than the time for which the average [median] patient lives) but it requires the survival times of all patients to be known. The mean OS of ‘cured’ patients is often much longer than that of ‘non-cured’ patients. Additionally, it has been shown that DLBCL-related mortality rates plateau over time, particularly at five or more years following treatment [13]. As such, OS may exceed the observation period of most clinical studies as many patients are still alive at the time the trial results are made public (i.e., at readout), which means that data for LTS are not available at trial readout.

To account for patients who die from their primary disease, and also for LTS who may die later from other causes, a mixture cure rate model can be used to predict mean survival time [12, 14,15,16]. Mixture cure rate models are extensions of standard parametric models, which explicitly model a blend of ‘cured’ and ‘non-cured’ patients to estimate the probability that a patient is ‘cured’, and also predict the survival of patients who are ‘not cured’. In this setting, the term ‘cure’ refers to those cured of the disease of interest (otherwise known as the ‘cure fraction’, according to the statistical model).

Primary results from a randomised Phase II study demonstrated that, compared with BR, Pola+BR provided clinically meaningful benefit in transplant-ineligible patients with R/R DLBCL. With a median follow-up duration of 22.3 months, the complete response (CR) rate as assessed by independent review committee (IRC) was significantly improved with Pola+BR versus BR (40.0% vs 17.5%, respectively; p = 0.026), with longer IRC-assessed progression-free survival (PFS; median 9.5 vs 3.7 months; HR 0.36; 95% confidence interval [CI] 0.21, 0.63; p = 0.0002) and OS (median 12.4 vs 4.7 months; HR 0.42; 95% CI 0.24, 0.75; p = 0.002) [17].

The aim of this analysis was to use PFS as an intermediate endpoint to estimate long-term survival with Pola+BR treatment; these survival estimates will be utilised to inform future economic analyses. We use a mixture cure rate model and standard parametric extrapolation approaches to estimate the OS benefit associated with Pola+BR compared with BR alone in patients with R/R DLBCL and compare the findings with actual (observed) data from the GO29365 clinical trial (NCT02257567) [17], which supported the approved indication for Pola+BR.

2 Materials and Methods

2.1 Clinical Setting and Data for Extrapolations

GO29365 (NCT02257567) is an international, multicentre, open-label, randomised, Phase Ib/II trial, comparing the safety and efficacy of Pola+BR versus BR alone in patients with R/R DLBCL. Detailed methodology for GO29365 are published elsewhere [17].

We fitted standard parametric as well as mixture cure rate models to OS data from the randomised arms of GO29365 (Pola+BR vs BR) for patients dying from DLBCL and for LTS (i.e., patients who had not died from this disease, informed by life tables given patients’ age/sex/nationality [18]). The GO29365 data cuts for the model extrapolations were taken from March 2019 (29.5 months). To validate these results, survival was also estimated using data from April 2018 (22.3 months) and October 2018 (27.6 months).

The proportion of LTS was estimated from standard parametric model and mixture cure rate model extrapolations, with mean OS calculated by estimating the area under the curve.

2.2 Standard Parametric Models

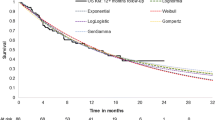
OS extrapolation beyond the GO29365 clinical follow-up period was performed by fitting standard parametric distributions (exponential, Weibull, log-normal, generalised gamma, log-logistic and Gompertz) to the observed data from the randomised Phase II DLBCL cohort of Study GO29365, comparing Pola+BR (N = 40) with BR (N = 40) [17]. These parametric distributions were assessed for their goodness-of-fit to the data using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (Supplementary Table 1), as well as visual assessment of the observed Kaplan–Meier curves. Although AIC values are a measure of the goodness-of-fit for the observed period, it has been shown that they do not necessarily reflect long-term behaviour [19]; thus, we opted to use the generalised gamma distribution due to plausible results on the PFS and OS convergence.

Cure models were adjusted for age, sex, and country; it is particularly vital to adjust for age as the relationship between mortality and age is non-linear (Fig. 1). The OS for a treated population with a cure fraction is calculated as the weighted average of OS among the ‘cured’ and ‘non-cured’ patients. Standard parametric survival distributions may not accurately represent the mean in a heterogeneous population because the majority of the events observed will be from the patients who are at higher risk of those events. In contrast, mixture cure rate models incorporate different patient populations based on their survival, which may allow predictions to better match clinical trial data (Fig. 2). As such, we explored the use of a mixture cure rate model to estimate long-term survival.

Fig. 1
figure 1

How differences in age may influence survival curves; a impact of age on mortality in the general population; b distribution of age in Study GO29365. a The relationship between age and mortality is non-linear [20]; b age adjustment is necessary due to the distribution of age in the GO29365 study [Roche data on file]

Full size image
Fig. 2
figure 2

How mixture cure rate models incorporate different patient populations based on their survival. a At 0% LTS, the mixture model (orange line) aims to estimate the trial data (green line) but fails to do so; b At 20% LTS, there is improved prediction but it is still far off the trial data (green line); c At 40% LTS, the proportion of LTS (blue line) is increased and the disease model mortality is decreased (purple)—the mixture cure prediction (orange) better matches the trial estimate (green); Note: the mixture model (orange line) is a mixture of the disease model mortality (i.e., the parametric extrapolation model fitted on the OS data of the non-cured fraction; purple) and background LTS mortality (blue). BR bendamustine-rituximab, LTS long-term survivors, KM Kaplan–Meier, OS overall survival, Pola polatuzumab vedotin

Full size image

2.3 Mixture Cure Rate Model

Standard mixture cure methods [15] use external information such as the hazards linked to background mortality to estimate the proportion of LTS, by applying Machine Learning methods such as clustering using the expectation–maximisation algorithm [21]. The data presented here were analysed using R software with code: Felizzi/Cure_Models: Cure_Models_Tutorial. 2018: Zenodo [22]. A tutorial and practical guidance on this methodology has been reported separately [23].

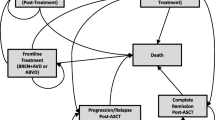
Clustering algorithms typically split the patient population into two subgroups: one representing the LTS, and the other representing those who die from their primary disease. In the presence of an intervention and control arm, clustering into these subgroups can be further differentiated by arm, creating four possible outcomes (Fig. 3A). Patients who are not LTS in the intervention and control arms have a background mortality rate that is related to their status as cancer survivors (which can be thought of in terms of hazards, or survival function). Previous studies demonstrate that cancer survivors do not have the same mortality as the general population; this increased risk has been estimated as an additional 10–40% [24, 25 ,26]. However, if the estimation of the relative benefit (intervention vs control) incorporates all four possible outcomes, as described above, there is the risk of artificially overestimating the cure proportion (LTS) in the intervention arm. In parallel, an accelerated (or higher) mortality rate may be artificially estimated for non-LTS patients in the intervention arm versus the control arm, as study treatment is more likely to have a positive effect on the proportion of LTS in the intervention arm, compared with the effect of the control on LTS in the other arm. This issue can be overcome by merging the non-LTS of the intervention and control arms (i.e., assuming no between-arms difference in the mortality hazard rate for non-LTS; Fig. 3B). Clustering into LTS and non-LTS can be based on a number of baseline characteristics; Fig. 3C is a simplified illustration of the model output, showing the relation of the estimated probability of long-term survival to two of the variables in the model, age and PFS. Probability of long-term survival is based on a generalised gamma distribution, and is estimated independently of the treatment arm.

Fig. 3
figure 3

Schematic figure of clustering approach: a Assuming non-LTS proportion (mortality hazard) may vary between intervention and control arm; b Assuming no difference in mortality hazard between arms for non-LTS; c Classification of PFS into long-term survivor based on a generalised gamma distribution. a non-long-term survivors analysed individually in each arm; b non–long-term survivors in both arms merged to avoid overestimation of the cure proportion in the intervention arm; c Simplified example of using clustering to separate patients from study GO29365 (March 2019 data cut) into long-term survivors (green) and non–long-term survivors (orange), with probability of cure calculated using PFS, assuming a generalised gamma distribution. The shapes denote the treatment arm, a triangle indicates Pola+BR and circle indicates BR, the colour of the shapes indicates the probability of the patient being a LTS. The plot does not depict the censoring status hence shapes higher up on the y-axis (i.e., longer survival time) may already have experienced an event. BR bendamustine-rituximab, LTS long-term survivors, PFS progression-free survivor, Pola polatuzumab vedotin

Full size image

The mixture cure rate model considers the population as a mixture of cured patients (the cure fraction) and non-cured patients who are at a risk of death as defined by a parametric survival model. The cure fraction can therefore be interpreted as the proportion of the overall population that is normally subject to a background mortality risk. In line with the reported non-cancer mortality risk in cancer survivors [26], a background mortality risk hazard ratio of 1.41 was assumed for ‘cured’ patients in this analysis. Adjustment for age, gender, and country was incorporated in construction of the background mortality risk.

Two variations of the mixture cure rate model were explored, using OS [14] or OS extrapolation informed by the observed PFS data. There is a close association between PFS and OS; as progression events always occur either before or at the same time as death, we often see more progression events, which can then be used to inform OS predictions. The clear relationship between OS and PFS in R/R DLBCL can be observed using evidence extracted from the UK health technology appraisal of the CAR-T therapy, tisagenlecleucel [26]. As progression events precede OS events, the distance between the PFS and the OS curves tend to diminish as time progresses in this patient population (Fig. 4).

Fig. 4
figure 4

Comparison of standard parametric extrapolations and mixture cure rate model extrapolations for patients treated with Pola+BR in the GO29365 study. OS overall survival, PFS progression-free survival, Pola+BR polatuzumab vedotin + bendamustine + rituximab. Mixture cure rate models were calculated assuming a generalised gamma distribution

Full size image

Goodness-of-fit criteria and visual inspection were used to determine how closely aligned each model was to the clinical data; these methods were previously reported [23].

2.4 External Validation

In order to utilise the totality of available long-term follow-up data, six patients from the safety run-in part of GO29365 (Phase Ib) were pooled with the 40 patients randomised to Pola+BR (Phase II), so that the maximum follow-up time reached 45.9 months. This data set was used to validate the mixture cure rate model predictions, along with data from 39 patients with R/R DLBCL who received Pola+R in a Phase II trial (ROMULUS; NCT01691898; maximum follow up 49.5 months) [27].

3 Results

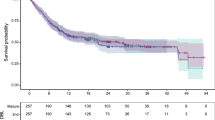
Kaplan–Meier estimations of OS based on observed data (showing a plateau in the curves with longer-term follow-up) and extrapolation estimates of OS for the Phase II randomised cohort of patients with R/R DLBCL who were treated with Pola+BR in GO29365 are shown in Fig. 4. Pola+BR treatment for R/R DLBCL in GO29365 led to a proportion of patients who could be considered LTS, as shown by the plateauing of Kaplan–Meier OS curves with prolonged follow-up. Most disease progression events occurred within 12 months of treatment initiation, after which fewer events were observed (Fig. 5); this also caused the Kaplan–Meier estimate of PFS to plateau (Fig. 4). Mixture cure rate model extrapolations were more closely aligned with the observed clinical data than standard parametric extrapolations, suggesting that this is a more reliable method to estimate long-term survival. When calculated using the mixture cure rate model (OS informed by PFS, generalised gamma distribution), estimated mean OS was 4.00 years for Pola+BR versus 1.02 years for BR.

Fig. 5
figure 5

Cumulative incidence of progressions (investigator-assessed) from GO29365: a Pola+BR; b BR (March 2019 data cut). CI confidence interval, Pola+BR polatuzumab vedotin + bendamustine + rituximab

Full size image

Using the mixture cure rate methods to model OS using PFS data from the Phase II randomised DLBCL cohort of GO29365, the estimated proportion of LTS ranged from 22.0 to 26.6% for Pola+BR versus 0 to 4.3% for BR (Table 1), depending on the assumed distribution.

Table 1 LTS rates for OS informed by IRC-assessed PFS
Full size table

Extrapolation model results were consistent across all assessed data cuts. Of the extrapolation methods tested, mixture cure rate model predictions were better aligned with pooled Phase Ib/II Pola+BR survival data than the parametric model OS estimates. Pola+BR OS predictions were also consistent with the pooled GO29365 dataset and ROMULUS Pola+R data, validating the mixture cure rate model (Fig. 6).

Fig. 6
figure 6

Comparison of Kaplan–Meier OS estimates and extrapolation models for Pola+BR, BR (Phase II GO29365 data) and Pola+R (ROMULUS data). BR bendamustine + rituximab, OS overall survival, Pola polatuzumab vedotin. Mixture cure rate models were calculated assuming a generalised gamma distribution

Full size image

4 Discussion

The plateau in PFS and OS curves observed in GO29365 suggests that some patients achieved sustained, long-term survival benefit with Pola+BR (or BR) treatment and may be considered cured, particularly if still in remission beyond 24 months [28]. A similar plateau in survival curves was shown with CAR-T cell therapy in the JULIET and ZUMA-1 studies of patients with R/R DLBCL [14, 26, 28, 29, 30] .

Traditional standard parametric models (i.e., those typically used in cost-effectiveness analyses) have limited scope to capture variations in the clinical course of disease, or to account for heterogeneity among populations that contain a mixture of those patients who are progression-free in the long term (and may be considered ‘cured’, with a background mortality level similar to the general population) and those who experience disease progression (in the current study, DLBCL) [12, 14, 15]. As the treated patient population with R/R DLBCL contains both ‘cured’ and ‘non-cured’ patients, the mixture cure rate model is most appropriate for estimating mean OS.

We compared mixture cure rate model extrapolations of OS with standard parametric models using data from the Phase II randomised R/R DLBCL cohort of GO29365 in which OS and PFS outcomes with Pola+BR were compared with BR. The mixture cure rate model provided the best fit for survival curves when compared with the actual (observed) survival data from the clinical trial.

Supporting our findings, another analysis compared the utility of standard parametric models with mixture cure rate models for estimating long-term OS in patients with R/R DLBCL, based on data from the Phase I/II ZUMA-1 trial of axicabtagene ciloleucel [14]. Using Weibull and generalised gamma distributions, extrapolated mean survival using the mixture cure rate model was found to be 15.7 years (95% CI 9.3, 21.1) and 17.5 years (95% CI 12.0, 22.8) respectively, compared with just 2.0 years (95% CI 1.5, 3.0) and 3.0 years (95% CI 1.7, 5.6) for standard parametric models. The authors concluded that in a situation where many patients can achieve long-term remission with potentially curative therapy and sufficient follow-up, mixture cure models may provide a more accurate estimate of OS compared with standard parametric approaches. Ouwens et al. [31] also found that standard parametric models underestimated OS of patients treated with immuno-oncology therapies compared with alternative methodologies including flexible parametric, cure and landmark models. Flexible parametric models, such as spline models, represent an alternative approach that can be used to characterise hazard functions that may be too complex to be fully captured by standard parametric models. An advantage with the mixture cure rate model used in the current analysis is that this approach allows the incorporation of OS informed by PFS.

In the current analysis, in addition to OS-only estimates, we also utilised a variation of the mixture cure rate model that extrapolates OS estimates informed by PFS. The rationale for this approach was that basing the mixture cure rate on OS only would also include progressed patients as LTS, which has not been favoured in previous evaluations of treatment for R/R DLBCL [28]. As progression events preclude OS events, these can be used to predict future survival; the more PFS event data that are available, the more robust these predictions are. Supporting the association between PFS and OS, the Kaplan–Meier curves for these two outcomes converge as the duration of follow-up increases.

The estimated proportions of LTS derived from the parametric model and mixture cure rate model extrapolations showed that, in R/R DLBCL, the proportion of LTS with Pola+BR were 20.8–25.4% higher versus BR alone depending on the assumed distribution. The model predicted that 35.3% and 21.9% of patients with R/R DLBCL who received Pola+BR would be expected to still be alive at 2 and 5 years, respectively, compared with 12.7% and 3.5% of those who received BR. Limitations in this analysis must be noted. As estimates were based on data from a small patient sample with limited follow-up, there is an intrinsic degree of uncertainty within the results of both the parametric and mixture cure rate models. Additionally, regarding visual validation of the results with additional data from the Phase Ib safety run-in and the ROMULUS study, it must be acknowledged that some differences in the baseline characteristics of these patients may be expected, particularly between the different studies. Such differences may be accounted for using a propensity score methodology. However, as the ROMULUS study used a different treatment combination (Pola+R rather than Pola+BR) the efficacy from these studies cannot be directly compared; rather, these validation data sets serve to demonstrate that the mixture cure rate model follows the same general trend of survival as has been shown with clinical data from patients treated with polatuzumab vedotin.

Life-years (and quality-adjusted life-years) gained are currently being utilised in cost-effectiveness models of Pola+BR, based on survival and safety data from GO29365 and published utility estimates for patients with R/R DLBCL. These models have shown that Pola+BR is cost effective compared with BR for the treatment of patients with transplant-ineligible R/R DLBCL, from the perspective of third-party healthcare payers in the USA [32]. Based on the available data, our analyses demonstrate that mixture cure rate models may more accurately reflect the long-term outcomes of patients than standard parametric models. As such, their use to extrapolate OS and estimate the proportion of LTS has the potential to provide more reliable cost-effectiveness evaluations of new treatments, particularly where survival durations are considerable and treatment is potentially curative in the long-term.

5 Conclusions

When applying standard parametric extrapolation methods and a mixture cure rate model to data from the Phase II randomised R/R DLBCL cohort of GO29365, the results of our study showed that compared with BR alone, Pola+BR shows a higher proportion of LTS; however, the estimated proportion is still subject to high uncertainty and the statistical significance of the comparison is dependent on the assumed standard parametric assumption. Mixture cure rate models may offer more reliable prediction of survival compared with standard parametric measures that do not incorporate cure modelling. This analysis provides further evidence that mixture cure rate models are a valuable tool to be used in health technology assessments, supporting utility and cost-effectiveness analyses in heterogeneous patient populations.