Abstract
Introduction
HFE-associated haemochromatosis, the most common monogenic disorder amongst populations of northern European ancestry, is characterised by iron overload. Excess iron is stored in parenchymal tissues, leading to morbidity and mortality. Population screening programmes are likely to improve early diagnosis, thereby decreasing associated disease. Our aim was to develop and validate a health economics model of screening using utilities and costs from a haemochromatosis cohort.
Methods
A state-transition model was developed with Markov states based on disease severity. Australian males (aged 30 years) and females (aged 45 years) of northern European ancestry were the target populations. The screening strategy was the status quo approach in Australia; the model was run over a lifetime horizon. Costs were estimated from the government perspective and reported in 2015 Australian dollars ($A); costs and quality-adjusted life-years (QALYs) were discounted at 5% annually. Model validity was assessed using goodness-of-fit analyses. Second-order Monte-Carlo simulation was used to account for uncertainty in multiple parameters.
Results
For validity, the model reproduced mortality, life expectancy (LE) and prevalence rates in line with published data. LE for C282Y homozygote males and females were 49.9 and 40.2 years, respectively, slightly lower than population rates. Mean (95% confidence interval) QALYS were 15.7 (7.7–23.7) for males and 14.4 (6.7–22.1) for females. Mean discounted lifetime costs for C282Y homozygotes were $A22,737 (3670–85,793) for males and $A13,840 (1335–67,377) for females. Sensitivity analyses revealed discount rates and prevalence had the greatest impacts on outcomes.
Conclusion
We have developed a transparent, validated health economics model of C282Y homozygote haemochromatosis. The model will be useful to decision makers to identify cost-effective screening strategies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
This is the first validated economic model to be published for C282Y homozygote haemochromatosis for the Australian setting utilising utilities and costs from a haemochromatosis cohort. |
From the government perspective, mean discounted lifetime direct medical costs for C282Y homozygote males were estimated to be more than 1.5 times that of females ($A22,737 vs. $A13,840). |
The model estimated mean discounted quality-adjusted life-years associated with the current screening approach were 15.654 for males and 14.390 for females. |
This model can be used by decision makers to identify cost-effective screening and treatment strategies for C282Y homozygote haemochromatosis. |
1 Introduction
HFE-associated hereditary haemochromatosis is the most common monogenic disorder amongst populations of northern European ancestry [1–3]. Whilst several mutations of the HFE gene have been identified, C282Y homozygotes account for between 80 and 90% of the burden of disease [4, 5]. The prevalence of this genotype has been estimated to be between 1 in 150 and 1 in 200 in populations of northern European ancestry (i.e. UK, Ireland and Scandinavian countries) [6–9]. Prevalence in populations of other ancestries is far lower, with estimates in the range of 1 in 1000 for both First Nation and African Americans [10] and 1 in 1 million amongst Asian populations [11].
Clinically, haemochromatosis is characterised by iron overload, with excess iron stored in the parenchymal tissues of the liver, heart and pancreas [2, 12, 13]. Early symptoms of iron overload are non-specific, including fatigue, lethargy and arthropathy of the metacarpophalangeal joints. As iron overload progresses, liver disease, heart disease and type 2 diabetes mellitus can occur. Clinical penetrance is incomplete: a further genetic mutation is thought to play a role in this process [14, 15]. Whilst age of onset of iron overload varies, males typically develop overload at an earlier age as menstruation assists in reducing iron stores in females [6].
Both diagnosis and treatment of haemochromatosis are straightforward. The former involves iron studies, most importantly transferrin saturation (TfS) and ferritin, with confirmatory HFE genotyping. Treatment involves regular therapeutic venesection. When treatment is commenced prior to organ damage and maintained, the patient will not experience any long-term health problems related to haemochromatosis and retains normal life expectancy (LE). However, as the early symptoms of haemochromatosis are non-specific, timely diagnosis is often missed until organ damage has occurred [16, 17]. In order to increase early diagnosis, population screening programmes have been suggested [18–21].
Screening programmes are typically resource intensive, and therefore decision makers need to be confident that such interventions are likely to be cost effective prior to their introduction. Economic modelling is a method that assists decision makers to evaluate the cost effectiveness of a given intervention [22]. Long-term costs and consequences of the disorder with or without screening can be predicted by using existing clinical, epidemiological and cost data combined in a suitable model. However, to date, no health economic model based on costs and utilities from a haemochromatosis cohort has been published. To address this lack of evidence, we have developed a model to assess screening strategies for the Australian setting for people homozygous for the C282Y mutation. The aim of this paper is to describe the construction and validation of our haemochromatosis screening model and to present model predictions for LE, quality-adjusted life-years (QALYs) and total lifetime costs associated with haemochromatosis.
2 Methods
2.1 Model Structure
We constructed a cost-effectiveness model using a Markov approach allowing for modelling of multiple disease states over a lifetime horizon. The cycle length was 1 year, which continued to run until the death of all simulated subjects. A lifetime horizon was selected to reflect the chronic nature of haemochromatosis. The perspective taken was that of the government. This perspective was adopted as funding decisions are based, in part, on these government costs. Both costs and effectiveness were discounted annually by 5%, in line with the Australian guidelines [23]. The structure of the model is detailed in “Appendix 1”. The model was constructed using TreeAge Pro Suite 2014 (TreeAge Software, Williamstown, MA, USA). Validation was conducted using TreeAge Pro and SPSS® version 22.0.0.0 (IBM Corp., Armonk, NY, USA). Modelled output data were exported into SPSS® allowing for calculation of correlation coefficients and fitting linear curves for goodness-of-fit analyses.
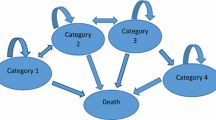
Markov states were categorised according to the European Association for the Study of the Liver’s (EASL) recommendations pertaining to how research on haemochromatosis is reported (Table 1) [18]. The four categories represent increasing severity of haemochromatosis and iron overload. For the Markov model, an absorbing ‘Death’ state was also included. Figure 1a, b provide an overview of the possible transitions between these states (“Appendix 1” provides a more detailed flowchart showing the steps in the screening process). Simulated participants could move in either direction between the four categories of haemochromatosis for all disease states except Category 4, as this included irreversible organ damage, and could also move to the absorbing state of ‘Death’. Clinical pathways that were incorporated into the model (screening, diagnosis and treatment) were based on current guidelines and input from an expert clinician (KCY). The model structure was designed by a health economist/clinician (AJP) and three health economists (BdG, LS, ALN).
Probabilities were calculated for each possible transition through the model, as outlined in Fig. 1. These annual probabilities were calculated based on data from an epidemiological study [6] (Table 2). Transition probabilities were mediated by adherence to treatment, i.e. non-adherence led to a higher probability of a participant moving to a more severe category of haemochromatosis. Transition probabilities for the ‘Death’ state were set at age- and sex-specific mortality rates for the Australian population [24] for all states with the exception of Category 4. As Category 4 is characterised by irreversible organ damage, a higher probability of death was assumed, as discussed in Sect. 2.1.5.
2.1.1 Base-Case Populations
Two base-case populations were selected for analysis: males 30 years of age and females 45 years of age, both of northern European ancestry. The rationale for this decision was based on prevalence and penetrance estimates. Northern European ancestry was chosen as the prevalence of C282Y homozygosity is far higher than reported for populations of other ancestries [6, 10]. Amongst males, iron overload and related complications typically occur from the age of 30 years onwards, and this has been the preferred age in other haemochromatosis models [25–27]. The second base-case population consisted of females 45 years of age, as females tend to experience iron overload following commencement of menopause [28].
2.1.2 Screening
A single screening strategy was modelled for validation purposes, which was based on the status quo approach in Australia. Screening was assumed to occur at age 30 years for males and 45 years for females. Screening occurs either through a cascade approach, in which first-degree relatives of a homozygote are offered genotyping, and iron studies reimbursed by the Medical Benefits Scheme (MBS). Alternatively, screening occurs incidentally, consisting of a three-step process: two consecutive elevated TfS tests followed by HFE genotyping. In our model, when a participant tested negative to the genotype test, a referral to a specialist medical practitioner for further investigation was assumed (“Appendix 1”). Genetic counselling was assumed to take place during the medical consultations conducted before and after HFE genotyping. At present, this combined approach is estimated to diagnose 31% of C282Y homozygotes in Australia (L. Gurrin, Principal Investigator, HealthIron study, personal communication, 16 March 2015).
As no data were available to inform uptake of cascade and incidental screening in Australia, expert opinion and literature were relied on to inform this. The uptake rate for any screening for a population of northern European ancestry was estimated to be 5% [29]. This group was then equally divided as to whether they were screened via a cascade or incidental approach.
Estimates for adherence to treatment were taken from a longitudinal study describing this over a 9-year period [30]. Based on this study, patient adherence was set at 90.5% in year 1, decreasing linearly to 29.3% in year 9. For the purposes of the model, the estimate of adherence plateaued at 29.3% from year 10 onwards. Adverse events associated with treatment were not included in the model as venesection is considered a safe treatment, with adverse events typically limited to dizziness and/or syncope subsequent to treatment [30, 31]. In Australia, the clinician providing venesection typically provides care to the patient.
2.1.3 Costs
Costs were reported from the government perspective, and were limited to direct medical costs, although other costs (indirect and direct non-medical costs) can also be included in the model. The costs were screening and state (category) costs, both of which were reported in 2015 Australian dollars ($A) (0.75 US dollars). Costs were deflated to constant prices using the price index for Government final consumption expenditure on hospitals and nursing homes for 2013/2014 [32].
Direct medical costs associated with screening were sourced from the 2015 MBS [33]. Specific costs related to genetic counselling were not included, as this was assumed to be provided by the medical practitioner during the consultations conducted before and after HFE genotyping. Costs were based on the assumption that repeat testing, related to either collection or analysis errors, was not required.
The costs associated with haemochromatosis states were sourced from our previous cost-of-illness study [34]. This study estimated the costs of haemochromatosis on the basis of a national survey using a bottom-up approach. To date, these are the only published cost estimates for haemochromatosis. Costs were reported for each of the four EASL categories of haemochromatosis and are defined in Table 2. These costs were used for hypothetical participants who were diagnosed and received treatment. For participants either not diagnosed or not adhering to treatment, treatment costs, i.e. therapeutic venesection, were subtracted from the total costs for each category. Further, costs for undiagnosed Category 1 patients (either not screened or a false-negative test) were set a zero. A brief description of the costing methodology is included here, but readers are directed to the original paper for a more detailed description [34].
Costs included were limited to resources funded by federal or state and territory governments. Pharmaceutical costs were based on the subsidy from the 2015 Pharmaceutical Benefits Scheme (PBS) Price Schedule of 1 January 2015 [35]—the difference between the dispensed price and the co-payment, if the dispensed price is greater. Unit costs for medical consultations and investigations (blood tests, liver biopsies, X-rays, etc.) were derived from the Medicare Benefits Schedule Book [33]. The National Hospital Cost Data Collection cost weights for Australian Refined Diagnosis-Related Group (AR-DRG) version 6.0 × (2011–2012) were used to estimate public hospital events [36]. Costs for public outpatient admissions were costed as reported by the Independent Hospital Pricing Authority [37].
2.1.4 Effectiveness
Health state utility values (HSUVs) were used to calculate QALYs. Utility values were taken from a recently published study by our group, the only study to date that has assessed utility values directly in people with haemochromatosis [38]. This study reported HSUVs amongst a sample of Australian adults with haemochromatosis, using the Assessment of Quality of Life 4D (AQOL-4D) instrument [38]. Mean utilities and their distributions were calculated for each of the four EASL categories (Tables 1, 2).
2.1.5 Mortality
Mortality associated with haemochromatosis was assumed to be the same as the Australian population age- and sex-adjusted rates, with the exception of Category 4. Age- and sex-adjusted mortality was sourced from Australian life tables [24], which are based on demographic data collected by the Australian Government for the entire population (Table 2). For Category 4, as irreversible organ damage (e.g., liver cirrhosis, heart disease) characterises this category, an elevated probability of death was assigned to this state reflecting current literature. A multiplier of 2.45 (95% confidence interval [CI] 2.27–2.64) was applied to the age- and sex-specific mortality rates for the Australian population, based on an estimate from an epidemiological study [39].
2.1.6 Bayes’ Revision
As with almost all diagnostic tests, the sensitivity and specificity of TfS and HFE genotyping as diagnostic tools for haemochromatosis are imperfect, i.e. both less than 100%. To address this, the Bayes’ revision function within the TreeAge model structure was used. This function, based on Bayes’ theorem [40], combines prior and posterior probabilities (or, alternatively, combines a prior odds with a likelihood ratio to generate a posterior odds for a given hypothesis) as per the following formula (Eq. 1):
where P(Hypothesis) is the prior probability of the hypothesis of disease (usually taken to be the unadjusted population prevalence if we are considering a diagnostic test for a binary outcome) and P(Evidence) is the marginal probability of the evidence given that the hypothesis is true, usually derived from a ‘sampling model’ for the probability of the observed data given values of the sensitivity and specificity consistent with the hypothesis. The model incorporated four posterior probabilities in both the incidental and cascade screening sub-branches, specific to the tests ordered. The estimates of sensitivity and specificity for genotyping [41] and TfS tests [42] are displayed in Table 2.
2.2 Sensitivity Analyses
Probabilistic decision analysis with simultaneous sampling from distributions of key input parameters was used to address uncertainty. Tornado diagrams were produced for both populations to identify parameters with the greatest individual impact on costs and effectiveness. Prevalence of C282Y homozygosity, adherence to treatment, transition probabilities, Category 4 mortality rates, utility values and costs were varied by ±20% of the values used in the base-case analysis [43]. Screening uptake was varied by ±50% of the values used in the base-case analysis, reflecting the greater uncertainty given reliance on expert opinion. Discounting of both costs and effectiveness was varied between zero and 7%, from the base-case of 5%. Based on these results, one-way sensitivity analysis of all key input parameters was performed. For variables that were defined by a distribution, probabilistic sensitivity analysis was conducted to incorporate multiple parameter uncertainties simultaneously.
2.3 Model Validity
Validation of the model followed the recommendations of the International Society of Pharmacoeconomics and Outcomes Research (ISPOR) Task Force-7 [44]. Face and internal validity were addressed; however, as no long-term data were identified that could be used to assess external validity, this was not conducted. Face validity is a subjective approach involving people with clinical expertise in the disease area, thus ensuring the model incorporates the highest level of clinical evidence. The overall structure of the model, population, screening approaches, outcomes and assumptions were reviewed and validated by a hepatologist (KCY), biostatistician (LCG) and four health economists (AJP, LS, BdG, ALN).
Internal validity involved assessments to ensure the correct mathematical calculations were implemented. This was conducted by validating equations and parameters against their sources (BdG, LS). Modelled mortality rates, LE and prevalence for C282Y homozygosity for males and females at various ages were compared with the mortality data that were used to populate the model [24] and prevalence estimates [10, 42, 45]. One-way sensitivity analyses were conducted, as previously discussed, to ensure the results changed as expected when input parameter values were varied.
3 Results
3.1 Results of Validity Assessment
3.1.1 Face Validity and Internal Validation
For face validity, the model structure was found to represent all clinical aspects of haemochromatosis correctly [7, 17, 46, 47]. To assess internal validity, mortality rates and LE generated by the model were compared with the published rates used to build the model (Table 3) [24]. The modelled predictions for mortality rates for males (at ages 30, 40, 50, 60, 70 and 80 years) and females (at ages 45, 55, 65, 75 and 85 years) were plotted against the published rates and the goodness of fit for the linear relationship assessed (Fig. 2a). The correlation coefficient (R 2) was 1.00, indicating the model accurately reproduced the inputted mortality rates. Similarly, for the overall cohort, the model predicted LE of 30-year-old males to be 51.0 years, identical to the data reported in the Australian Bureau of Statistics’ (ABS) Life Tables (51.0 years) (Table 3) [24]. For females aged 45 years, the model predicted LE of 40.4 years, consistent with the data from the ABS Life Tables (40.4 years). These findings were as expected, given the relatively low prevalence of C282Y homozygotes. Further, the penetrance of Category 4—the only state with elevated mortality rates—is very low, ranging between 0 and 0.01% (Fig. 4a, b). R 2 was 1.00, indicating the model accurately calculated LE (Fig. 2b). The model also predicted prevalence of C282Y homozygosity for male and female cohorts (Table 3). The model predicted a prevalence rate of 0.62%, similar to the rate reported from a large prevalence study of northern Europeans (0.75%) [42], and R 2 was 0.905.
3.2 Model Predictions
Table 4 displays the results of the base-case Monte-Carlo simulations, calculated from age 30 years for males and 45 years for females. LE was estimated specifically for C282Y homozygotes: for 30-year-old males, LE (standard deviation) was estimated to be 49.9 years (0.04), 1.1 years less than the Australian LE for 30-year-old males (51.0 years). The projected LE for female C282Y homozygotes aged 45 years was 40.2 years (0.01), 0.3 years less than the Australian LE for females of the same age (40.4 years). The mean (95% CI) discounted QALYs associated with screening were 15.7 (7.7–23.7) for males and 14.4 (6.7–22.1) for females. Figure 3a, b illustrate the dispersion of the cost and effectiveness results in scatterplots. The model also predicted mean lifetime direct medical costs (95% CI) for male C282Y homozygotes as $A22,737 (3670–85,793) and $A13,840 (1335–67,377) for females.
3.3 Time in States
The model projected the time spent in each disease state (Table 4). The low rates of uptake of screening and adherence to treatment were the drivers of transition to Categories 3 and 4, the states in which co-morbidities related to iron overload occur. Males spent a mean of 23 years in Category 3 and 3 years in Category 4, whilst females, with lower clinical penetrance, spent a projected mean of 6 years in Category 3 and less than 1 year in Category 4.
The model predicted the probabilities of both the male and female cohorts being in each of the five Markov states for each stage of the model, until all hypothetical participants were in the absorbing ‘Death’ state (Fig. 4a, b). For both sexes, the probability of being in Category 1 increased between the first two stages, and, conversely, the probability of being in Category 2 decreased. This result is a function of screening, in that 90.5% of Category 2 patients access treatment subsequent to screening. Therefore, most Category 2 participants transition to Category 1, the impacts of haemochromatosis being potentially reversible until Category 4. This effect is less dramatic for females as fewer females than males are in Category 2 at the time of screening (80 and 95%, respectively).
For both sexes, the probability of being in Category 1 decreased over time, reflecting reduced adherence to treatment: from 90.5% in the first year to 29.3% in the tenth year and thereafter [30]. In turn, the probability of being in Categories 2, 3 or 4 increased. Participants in Category 4 had a higher probability of moving into the ‘Death’ state than other participants. In addition, the probability of transitioning into the ‘Death’ state increased with the advancing age of the cohort, in line with population data [24].
3.4 Sensitivity Analysis
One-way sensitivity analyses were carried out by varying the value by ±20% for all key parameters, with the exception of uptake of screening (±50%) and discounting (varied between 0 and 7%) (“Appendix 2”). Tornado diagrams were constructed to identify parameters with the greatest effect on costs and effectiveness. The five parameters with the greatest impact (discount rate, prevalence, probability of starting in Category 1, transition from Category 1 to 2 and costs associated with Categories 2 and 3) are included in “Appendix 2”.
For males, varying the discount rate had the most notable effect on both costs and effectiveness. With no discounting, mean costs increased from the base-case estimate of $A145 to $A497 and effectiveness increased from 15.7 to 42.2 QALYs. When the discount rate was set at 7%, mean costs decreased to $A101 and effectiveness reduced to 11.9 QALYs. Varying the prevalence also had an impact on costs: increasing the estimate by 20% increased mean costs to $A185, and decreasing the estimated by 20% reduced costs to $A126. Varying uptake of screening (±50%) marginally impacted costs and effectiveness. Decreasing uptake reduced costs to $A143, and increasing uptake increased costs to $A146. No notable impact on effectiveness was observed (<0.001 QALY). Varying the mortality multiplier had negligible effects on cost and effectiveness for males (<$A1 and < 0.001 QALY, respectively). For LE, varying the multiplier for mortality by ±20% (1.96–2.94) resulted in small changes. For males aged 30 years, decreasing the multiplier increased LE to 50.2 years from a base-case LE estimate of 40.1 years, and, conversely, increasing the multiplier decreased LE to 49.7 years. One-way sensitivity analysis on other variables showed small impacts on costs and effectiveness (“Appendix 2”).
For females, the parameter with the most effect on costs and effectiveness was the discount rate. Decreasing this to zero resulted in costs increasing to $A264 from the base-case estimate of $A91, and increasing this rate to 7% decreased costs to $A64. Similarly, effectiveness increased from the base-case estimate of 14.4 to 33.1 QALYs gained with no discounting and decreased to 11.3 QALYs gained when the discount rate was set at 7%. Increasing the prevalence estimate increased costs to $A114; when this was decreased, costs reduced to $A79. Decreasing the uptake estimate by 50% reduced costs to $A89, and increasing this estimate increased costs to $A93. No notable change in effectiveness was observed (< 0.001 QALY). Similar to males, varying the mortality multiplier had negligible effects on costs and effectiveness (<$A1 and <0.001 QALY gained, respectively). The LE of females aged 45 years increased by <0.01 years when the multiplier was decreased by 20% (40.2 years), and, conversely, LE decreased to 40.1 years when the multiplier was increased. All other sensitivity analyses revealed minor changes from the base-case estimate (“Appendix 2”).
4 Discussion
This is the first economic model to be published using utility and cost data from a haemochromatosis cohort to populate a Markov model with probabilistic decision analysis—the approach best suited to this chronic, progressive disease. Just one other model has evaluated the cost effectiveness of population screening for haemochromatosis, using a Markov model with probabilistic decision analysis [25]. Our model has built on this previously published model by incorporating multiple disease states as recommended by the EASL, along with disease-specific cost and utility data derived from people living with haemochromatosis. Previous models used estimates of costs and utilities based on expert opinion [5, 26, 48, 49].
The number of health technology assessments being conducted has increased over the past two decades and, with an increasing focus on value in healthcare, this is likely to continue. Whilst clinical studies are ideally placed to assess the short- to medium-term costs and effectiveness of interventions, long-term costs and effectiveness are most feasibly and efficiently assessed through modelling. Important considerations for modelling studies include use of the highest quality clinical and epidemiological data available, transparency, and acceptability to patient groups, expert clinicians, decision makers and healthcare payers. The model for haemochromatosis that we have constructed has aimed to address all of these issues.
The model was assessed for internal validity using linear regression. The R 2 values of the slopes indicated the modelled projections closely correlated with the inputted and external data. All key input parameters, results of one-way sensitivity analyses and the structure of the model have been provided to enhance transparency. A limitation of this study was that external validation of the model was not conducted. To date, limited data on the long-term clinical and health economic outcomes of haemochromatosis have been published. As a result, where these data were available, they were used in the construction of the model, thereby rendering external validation not possible.
The base-case analyses estimated the mean direct medical costs associated with screening and consequential treatment for those identified was $A145 for males and $A91 for females. The higher costs incurred by males than females are expected given the higher rate of clinical penetrance for males. One-way sensitivity analysis identified no parameters which altered this. Increasing the penetrance for females by increasing the probability of commencing in Category 2 (rather than Category 1) had a negligible effect on costs and effectiveness in comparison to the base-case results. Another factor contributing to the lower costs for females is the low sensitivity of TfS as a screening test for females. This results in missed diagnoses and lower total screening costs (two consecutive elevated TfS tests followed by confirmatory genotype) as fewer females than males will go on to have the second TfS test and genotype. In turn, potential venesection treatment costs are not accrued. Whilst in our model female C282Y homozygotes who are not diagnosed, and therefore not receiving treatment, still accrue costs (with the exception of Category 1), these costs are smaller as venesection costs are excluded. Further, treatment costs accrue in the future, and are thus subject to discounting. Overall, the trade-off for this lower cost screening strategy is the reduced identification of female homozygotes. The trade-off between any cost savings versus the greater burden of disease generated is an issue that requires careful consideration.
Our model, consistent with other published studies, reported relatively high levels of uncertainty as evidenced by large standard deviations and 95% CIs reported in the base-case analyses [4, 25, 41, 50, 51]. However, these uncertainties were addressed in our one-way sensitivity analyses and, with the exception of discounting, were found to have little impact on the base-case results. Our primary avenue to minimise uncertainty was by utilising patient-derived information on costs and utilities associated with EASL categorisations.
One-way sensitivity analyses were conducted by varying the base parameter values by ±20%, with the exception of uptake of screening (±50%). For these parameters, the 95% CIs were within the ±20% ranges adopted. Whilst conducting one-way sensitivity analyses by varying the base parameter values by ±20% is an approach recommended by ISPOR [44], using the 95% CIs for each parameter represents an alternative, useful approach.
Projected LE for C282Y homozygotes was marginally lower than for the general population. The mortality multiplier applied to Category 4 of 2.45 [39] was in-line with other recent epidemiological work on mortality associated with haemochromatosis [52]. Whilst higher mortality rates were adopted for Category 4, the low penetrance rate for this category resulted in marginal impacts on overall mortality in both the base-case and sensitivity analyses.
Our model has been developed to allow for comparisons between the status quo approach of screening for haemochromatosis and alternatives, such as population-level genetic or neonatal screening [53]. Our model is well-placed to assist decision makers in Australia to assess different screening strategies for haemochromatosis. Further, it is flexible enough that alternative parameters may be used to allow for cost-effectiveness analyses in different jurisdictions.
5 Conclusion
A transparent and validated health economics model of screening for C282Y homozygote haemochromatosis based on Australian economic, epidemiological and clinical data has been developed. The model will be useful to decision makers to identify cost-effective screening and treatment strategies for C282Y homozygote haemochromatosis.
References
Worwood M. Inborn errors of metabolism: iron. Br Med Bull. 1999;55(3):556–67.
Allen K. Hereditary haemochromatosis—diagnosis and management. Aust Fam Physician. 2010;39(12):938–41.
Wood MJ, Skoien R, Powell LW. The global burden of iron overload. Hepatol Int. 2009;3(3):434–44.
Gagné G, Reinharz D, Laflamme N, Adams PC, Rousseau F. Hereditary hemochromatosis screening: effect of mutation penetrance and prevalence on cost-effectiveness of testing algorithms. Clin Genet. 2007;71(1):46–58.
Adams PC, Valberg LS. Screening blood donors for hereditary hemochromatosis: decision analysis model comparing genotyping to phenotyping. Am J Gastroenterol. 1999;94(6):1593–600.
Allen KJ, Gurrin LC, Constantine CC, Osborne NJ, Delatycki MB, Nicoll AJ, et al. Iron-overload-related disease in HFE hereditary hemochromatosis. N Engl J Med. 2008;358(3):221–30.
Whitlock EP, Garlitz BA, Harris EL, Beil TL, Smith PR. Screening for hereditary hemochromatosis: a systematic review for the US Preventive Services Task Force. Ann Intern Med. 2006;145(3):209–23.
Asberg A, Hveem K, Thorstensen K, Ellekjter E, Kannelønning K, Fjøsne U, et al. Screening for hemochromatosis: high prevalence and low morbidity in an unselected population of 65,238 persons. Scand J Gastroenterol. 2001;36(10):1108–15.
Allen KJ, Gurrin LC, Osborne NJ, Constantine CC, Delatycki MB, Nicoll AJ, et al. Healthiron: a longitudinal population study defining the burden of disease in HFE-associated hereditary hemochromatosis. Am J Hematol. 2007;82(6):537.
Adams PC, Reboussin DM, Barton JC, McLaren CE, Eckfeldt JH, McLaren GD, et al. Hemochromatosis and Iron Overload Screening (HEIRS) Study Research Investigators. Hemochromatosis and iron-overload screening in a racially diverse population. N Engl J Med. 2005;352(17):1769–78.
Cullen LM, Gao X, Easteal S, Jazwinska EC, et al. The hemochromatosis 845 G - > A and 187 C - > G mutations: prevalence in non-Caucasian populations. Am J Hum Genet. 1998;62(6):1403–7.
Barton J, Edwards CQ. Hemochromatosis: genetics, patholphysiology, diagnosis and treatment. Cambridge: Cambridge University Press; 2000.
Byrnes V, Coughlan B, Flanagan AM, Ryan E, Crowe J. The underdiagnosis of hereditary haemochromatosis: lack of presentation or penetration, expectations based on a study of relatives of symptomatic probands. Gastroenterology. 2000;118(4):A997.
Handa P, Kowdley KV. Glyceronephosphate O-acyltransferase as a hemochromatosis modifier gene: another iron in the fire? Hepatology. 2015;62(2):337–9.
McLaren CE, Emond MJ, Subramaniam VN, Phatak PD, Barton JC, Adams PC, et al. Exome sequencing in HFE C282Y homozygous men with extreme phenotypes identifies a GNPAT variant associated with severe iron overload. Hepatology. 2015;62(2):429–39.
Adams P, Barton JC, McLaren GD, Acton RT, Speechley M, McLaren CE, et al. Screening for iron overload: lessons from the hemochromatosis and iron overload screening (HEIRS) study. Can J Gastroenterol. 2009;23(11):769–72.
Gasser B, Courtois F, Hojjat-Assari S, Sauleau EA, Buffet C, Brissot P. Hereditary hemochromatosis: presenting manifestations and diagnostic delay [in French]. Rev Med Int. 2014;35(3):160–5.
Adams P, Brissot P, Powell L. EASL International Consensus Conference on Haemochromatosis—part II. Expert document. J Hepatol. 2000;33(3):487–96.
Mundy L, Merlin T. Population genetic screening for haemochromatosis: identifying asymptomatic “at risk” homozygous individuals. Adelaide Health Technology Assessment (AHTA). Horizon Scanning Prioritising Summary—vol 1. Adelaide: AGDHA; 2004.
Allen KJ. Population genetic screening for hereditary haemochromatosis: are we a step closer? Med J Aust. 2008;189(6):300–1.
Delatycki MB, Allen KJ, Nisselle AE, Collins V, Metcalfe S, du Sart D, et al. Use of community genetic screening to prevent HFE-associated hereditary haemochromatosis. Lancet. 2005;366(9482):314–6.
Drummond MF, Sculpher MJ, Torrance GW, O’Brien BJ, Stoddart GL. Methods for the economic evaluation of health care programmes. Oxford: Oxford University Press; 2005.
Australian Government Department of Health and Ageing. Technical Guidelines for preparing assessment reports for the Medical Services Advisory Committee—service type: therapeutic (version 1.2). Canberra: Australian Government Department of Health and Ageing: Canberra; 2013.
Australian Bureau of Statistics. Life table, states, territories and Australia, 2011–2013. 2014. http://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/3302.0.55.001Main+Features12011-2013?OpenDocument. Accessed 5 Jul 2015.
Rogowski WH. The cost-effectiveness of screening for hereditary hemochromatosis in Germany: a remodeling study. Med Decis Mak. 2009;29(2):224–38.
Asberg A, Tretli S, Hveem K, Bjerve KS. Benefit of population-based screening for phenotypic hemochromatosis in young men. Scand J Gastroenterol. 2002;37(10):1212–9.
Phatak PD, Guzman G, Woll JE, Robeson A, Phelps CE. Cost-effectiveness of screening for hereditary hemochromatosis. Arch Intern Med. 1994;154(7):769–76.
Moirand R, Adams PC, Bicheler V, Brissot P, Deugnier Y. Clinical features of genetic hemochromatosis in women compared with men. Ann Intern Med. 1997;127(2):105–10.
Stuhrmann M, Strassburg C, Schmidtke J. Genotype-based screening for hereditary haemochromatosis. I: technical performance, costs and clinical relevance of a German pilot study. Eur J Hum Genet. 2005;13(1):69–78.
Hicken BL, Tucker DC, Barton JC. Patient compliance with phlebotomy therapy for iron overload associated with hemochromatosis. Am J Gastroenterol. 2003;98(9):2072–7.
Morand C, Coudurier N, Rolland C, Thoret S, Legrand D, Tiberghien P, et al. Prevention of syncopal-type reactions after whole blood donation: a cluster-randomized trial assessing hydration and muscle tension exercise. Transfusion. 2016;56(10):2412–21.
Australian Institute of Health and Welfare. Health expenditure Australia 2013–14. Health and Welfare Expenditure Series No. 54. Canberra: Australian Institute of Health and Welfare; 2015.
Australian Government Department of Health. Medicare Benefits Schedule Book. Canberra: Australian Government Department of Health; 2014.
de Graaff B, Neil A, Sanderson K, Yee KC, Palmer AJ. Costs associated with hereditary haemochromatosis in Australia: a cost of illness study. Aust Health Rev 2016. doi:10.1071/AH15188 (Epub 2016 Jul 22).
Australian Government Department of Health. Schedule of pharmaceutical benefits 1 January 2015-31 January 2015. Canberra: Australian Government Department of Health; 2015.
Independent Hospital Pricing Authority. National hospital cost data collection Australian public hospitals cost report 2011–2012, round 16. Sydney: Independent Hospital Pricing Authority; 2014.
Independent Hospital Pricing Authority. National non-admitted and subacute admitted costing study. Sydney: Independent Hospital Pricing Authority; 2014.
de Graaff B, Neil A, Sanderson K, Yee KC, Palmer AJ. Quality of life utility values for hereditary haemochromatosis in Australia. Health Qual Life Outcomes. 2016;14:31.
Crooks CJ, West J, Solaymani-Dodaran M, Card TR. The epidemiology of haemochromatosis: a population-based study. Aliment Pharmacol Ther. 2009;29(2):183–92.
Spiegelhalter D, Abrams M, Myles J. Bayesian approaches to clinical trials and health-care evaluation. Chichester: Wiley; 2004.
Bryant J, Cooper K, Picot J, Clegg A, Roderick P, Rosenberg W, et al. A systematic review of the clinical validity and clinical utility of DNA testing for hereditary haemochromatosis type 1 in at-risk populations. J Med Genet. 2008;45(8):513–8.
Thorstensen K, Kvitland MA, Irgens WØ, Hveem K, Asberg A. Screening for C282Y homozygosity in a Norwegian population (HUNT2): The sensitivity and specificity of transferrin saturation. Scand J Clin Lab Invest. 2010;70(2):92–7.
Briggs AH, Weinstein MC, Fenwick EA, Karnon J, Sculpher MJ. Paltiel AD; ISPOR-SMDM Modeling Good Research Practices Task Force. Model parameter estimation and uncertainty analysis: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group-6. Med Decis Mak. 2012;32(5):722–32.
Eddy DM, Hollingworth W, Caro JJ, Tsevat J, McDonald KM, Wong JB, ISPOR-SMDM Modeling Good Research Practices Task Force. Model transparency and validation: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force–7. Value Health. 2012;15(6):843–50.
Jackson HA, Carter K, Darke C, Guttridge MG, Ravine D, Hutton RD, et al. HFE mutations, iron deficiency and overload in 10 500 blood donors. Br J Haematol. 2001;114(2):474–84.
McLaren GD, Gordeuk VR. Hereditary hemochromatosis: insights from the Hemochromatosis and Iron Overload Screening (HEIRS) study. Hematology Am Soc Hematol Educ Program. 2009:195–206. doi:10.1182/asheducation-2009.1.195.
McLaren GD, McLaren CE, Adams PC, Barton JC, Reboussin DM, Gordeuk VR, et al. Hemochromatosis and Iron Overload Screen (HEIRS) Study Research Investigators. Clinical manifestations of hemochromatosis in HFE C282Y homozygotes identified by screening. Can J Gastroenterol. 2008;22(11):923–30.
Adams P, Gregor JC, Kertesz AE, Valberg LS. Screening blood donors for hereditary hemochromatosis: decision analysis model based on a 30-year database. Gastroenterol Clin North Am. 1995;109(1):177–88.
Adams P, Kertesz A, Valberg L. Screening for hemochromatosis in children of homozygotes: prevalence and cost-effectiveness. Hepatology. 1995;22(6):1720–7.
Schoffski O, Schmidtke J, Stuhrmann M. Cost-effectiveness of population-based genetic hemochromatosis screening. Community Genet. 2000;3:2–11.
Adams PC, Gregor JC, Kertesz AE, Valberg LS. Screening blood-donors for hereditary hemochromatosis—decision-analysis model-based on a 30-year database. Gastroenterology. 1995;109(1):177–88.
Elmberg M, Hultcrantz R, Ebrahim F, Olsson S, Lindgren S, Lööf L, et al. Increased mortality risk in patients with phenotypic hereditary hemochromatosis but not in their first-degree relatives. Gastroenterology. 2009;137(4):1301–9.
de Graaff B, Si L, Neil A, Yee KC, Sanderson K, Gurrin L, Palmer AJ. Population screening for hereditary haemochromatosis in Australia: construction and validation of a state-transition cost-effectiveness model. (in press).
Gurrin LC, et al. The natural history of serum iron indices for HFE C282Y homozygosity associated with hereditary hemochromatosis. Gastroenterology. 2008;135(6):1945–52.
Australian Medical Association. List of Medical Services and Fees. Canberra: Australian Medical Association; 2014.
Acknowledgements
Author contributions
Barbara de Graaff planned, constructed and validated the model, and prepared the manuscript. Lei Si assisted with construction and validation of the model and assisted with preparation of the manuscript. Amanda Neil and Kristy Sanderson contributed to constructing the model and assisted with preparation of the manuscript. Kwang Chien Yee assisted with assessing the model for face validity and assisted with preparation of the manuscript. Lyle Gurrin assisted with the construction and validity of the model, and assisted with preparation of the manuscript. Andrew Palmer assisted with planning, constructing and validating the model, and assisted with preparation of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
Barbara de Graaff was supported by a PhD Australian Postgraduate Research Award scholarship provided by the Australian Government: this body did not have any role in the study.
Conflicts of interest
Barbara de Graaff, Amanda Neil, Kristy Sanderson, Lei Si, Kwang Chien Yee, Lyle Gurrin and Andrew J. Palmer have no conflicts of interest to declare that are directly relevant to the content of this study.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
de Graaff, B., Si, L., Neil, A.L. et al. Population Screening for Hereditary Haemochromatosis in Australia: Construction and Validation of a State-Transition Cost-Effectiveness Model. PharmacoEconomics Open 1, 37–51 (2017). https://doi.org/10.1007/s41669-016-0005-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41669-016-0005-0