Shapley-Shubik Agents Within Superstructure-Based Recycling Model: Circular Economy Approaches for Fish Waste Eco-Industrial Park

Abstract

The tremendous production of fish has resulted in an increased fish waste generation, which ultimately led to the current triple planetary crises on climate, biodiversity, and pollution. In this study, a Fish Waste-based Eco-Industrial Park (FWEIP) model is developed in an attempt to convert the linear economy in existing fish waste management into a circular economy model. Process Graph (P-graph) is used for combinatorial optimization to synthesize optimal FWEIP with the consideration of economic and environmental aspects. The model favors the production of biofuel using the gasification process (Rank 1) with a promising economic benefit of $2.28 million/y without proposing circular synergy within the FWEIP ecosystem. On the other hand, suboptimal solutions—suboptimal 1 (black soldier fly (BSF)) and suboptimal 2 (pyrolysis and gasification) solutions—exhibit gross profit of 17.98% and 24.12% lower than that of the optimal solution. Both suboptimal solutions offer greater circularity with self-sustaining resources (e.g., fish feed, chitosan, and energy). The sensitivity analysis indicates the potential debottlenecking of suboptimal 2 with the use of a catalyst to improve the conversion of bio-oil in the pyrolysis pathway and exhibits a gross profit of 22.54% higher than that of the optimal solution. Following the Shapley-Shubik power index analysis, the hydroponics facility is identified as the pivotal player for both optimal and suboptimal 2 cases with the exception of suboptimal 1 indicating both BSF and hydroponics as a pivotal player. In brief, this research provides the fish waste-based industry with insights and strategies for the implementation of a circular economy as a step toward sustainable development.

Introduction

In recent decades, fish-based product consumption has risen dramatically as it has been recognized as an important constituent of a nutrient-rich diet and a robust lifestyle. Global fisheries and aquaculture production has a total production of 177.8 million metric tons in 2021, which is a 20.05% growth compared to 2010 production (Coppola et al. 2021). Meanwhile, in the year 2018, the total global capture fisheries production hit 178.1 million tons, i.e., the highest level ever recorded, increased by 5.4% from the previous 3-year average. On the other hand, world fish consumption increased from 9.0 kg per capita in 1961 to 20.5 kg in 2018 and is expected to rise to 21.2 kg per capita in 2030 (Osawa 2014). Owing to this high amount of fish consumption, a significant amount of fish waste (i.e., approximately 17.9 to 39.5 million tons per year (Wallace et al. 2014)) is generated every year due to its putrescible nature and the presence of inedible fractions (e.g., bones, skin, scales, gut, as shown in Fig. 1).

Fig. 1

Composition of fish waste biomass (Coppola et al. 2021)

Given that the unavoidable fish waste generated is high in organic content, the waste management associated with environmental concerns becomes a matter of issue (Arvanitoyannis and Kassaveti 2008). Therefore, over the years, the management of fish waste has been a pressing issue. There is a need for sustainable waste management strategies. In light of this, conventional methods have been employed to extract additional value from fish wastes such as converting them into low-profit fish meals, fertilizers, and fish oils, or as a raw material for direct aquaculture feeding with a focus on sustainability (Nederlof et al. 2019).

In this context, the current surge in interest in alternative uses of fish wastes is critical for waste management development and long-term economic growth. The conventional linear economy, i.e., “take-make-use-dispose” paradigm in the fish supply chain results in resource loss, which is, therefore, termed as an inefficient method due to the omittance of potential economic gains. This necessitates the transition of the linear fish supply chain toward a circular economy. In contrast to the linear economy, the circular economy creates a closed-loop system that aims to minimize natural resource consumption and waste generation through reuse, restoration, re-purpose, reprocessing, and recycling (Korhonen et al. 2018). On that account, by embedding the circular economy principles, the generated wastes can be repurposed to realize cost savings and make the entire fish supply chain more resilient. In this regard, the valorisation of fish wastes into bioprocessing to produce value-added products is critical in advocating a sustainable circular economy through the eco-industry park (Ciriminna et al. 2019).

The notion of establishing eco-industrial parks (EIP), especially in the supply chain, is gaining a lot of attention in various countries as it narrows the gap between industries, cities, or even regions by promoting resource efficiency and circular economy (CE) practices (Andiappan et al. 2016). The whole idea of an EIP is to achieve better performance in terms of environmental, economic, and social compared to industries operating in “silos” (Laso et al. 2018). The establishment of EIP offers chances to minimize net material and energy consumption, add value to industrial waste, and reduce pollution throughout the processes, which is aligned and complemented with the concept of the circular economy. Thus, a novel fish-waste-based eco-industrial park (FWEIP) model with the incorporation of fish waste conversion and recycling pathways is developed in this study.

It is still a great challenge to synthesize an EIP that is economically competitive and environmentally sustainable. In real-case scenarios, both economic and environmental issues may conflict with each other. It could be strenuous that a single solution generated can satisfy all objectives. To overcome this, a multi-objective mathematical optimization technique is proposed to formulate the FWEIP model more realistically. For example, Tiu and Cruz (2017) formulated a multi-objective optimization model that incorporates the economic costs (e.g., capital and operating costs) and environmental impact (e.g., volume and quality of water consumed and disposed of) within the EIP infrastructures. Note that the mathematical approaches usually generate a single global optimal solution. However, the practicability of the “optimal” solution suggested by the model is subject to the list of constraints and assumptions set by the decision-makers, which may be erroneous in real-world situations (i.e., not guaranteed to be practical for implementation). To overcome such limitation, P-graph is proposed in this study to synthesize the FWEIP model as it has the capability to generate multiple solutions (optimal and suboptimal) simultaneously which gives insights to the decision makers for de-bottlenecking study (How and Lam 2019).

The development of the P-graph started in the late 1970s and it was first used for biochemical reactor network pathway establishment (Friedler et al. 2022). It can be described as a bipartite graph that is made up of O-type vertices (horizontal bars) and M-type vertices (dots) that represent processes or operational units (Friedler et al. 1992, 1993). Since then, P-graph has been widely used in systematic optimal design, such as the industrial processes synthesis and supply chain network synthesis, (How et al. 2016), synthesis of heat exchanger networks (Nagy et al. 2001), and resource conservation networks (Fan et al. 2008). Recently, machine learning algorithms have been embedded within P-graph(Teng et al. 2022), allowing more flexible usage within various applications. Our previous work also demonstrated the usage of P-graph and process monitoring techniques for aquaponics(Ondruška et al. 2022), however, fish waste recycling remains a problem to be solved. Table 1 shows the penetration of the P-graph in various Process Systems Engineering (PSE) fields. To the best of the authors’ knowledge, none of the existing works has attempted to synthesize an optimal FWEIP using P-graph thus far.

Table 1 P-graph applications

Further in developing an EIP, failure to determine the system bottleneck that has the greatest impact on system performance for flowsheet advancement may result in unfavorable outcomes such as resource waste. To this end, Shapley-Shubik Power Index (SSI) is proposed in this particular study to determine pivotal players (facilities) and identify the optimal allocation of resources in FWEIP. The SSI was first found to determine the power of each voter in affecting the outcome of the voting system and the permutations of all voters in the game are used to evaluate sequential coalitions (Shapley and Shubik 1954; Arnell et al. 2020). To win the alliance, the total number of votes supplied by each player must exceed the defined quota. The power index of each member in the sequential coalition is described as his or her proclivity to be the decisive voter (i.e., pivotal player) in winning the coalition, in which his or her vote flips the coalition from losing to winning (Mizuno et al. 2020). To date, SSI has been widely used to determine the bottleneck facilities of a defined system. For instance, Tan, et al. (2021a, b) developed an internal system bottleneck identification using SSI for the palm oil complex. Furthermore, in the study conducted by Yahya et al. (2021), SSI has been utilized to allocate the power of each process in achieving or failing the palm oil-based complex (POBC) performance target, before identifying the system bottleneck (SB) in terms of process stage.

To-date, there has been a lack of studies that simultaneously discuss the feasibility of FWEIP and identify pivotal players involved in the FWEIP. The inclusion of SSI analysis is vital for decision-making later, especially in terms of resource allocation (e.g., more budget should be allocated to the unit that plays to pivotal spot given its influencing nature). The main objective of this study is to provide decision-makers with a proposed research framework to: (i) optimize the FWEIP using the P-graph approach; (ii) identify the bottleneck and study the impact of various parameters on the optimality of the solutions using sensitivity analysis; and (iii) identify the pivotal technology of the FWEIP using SSI.

Problem Statement

The disposal and recycling of fish waste biomass have become critical issues that must be addressed. The utilization of unused or abandoned fish wastes can constitute a sustainable strategy for the implementation of a circular fish waste-based economy, with the manufacture of materials with high added value. To address this issue, this work proposes the implementation of FWEIP which cooperates through infrastructural, material, water, and energy exchange initiatives due to their close proximity. As a result, the total benefit of an EIP is expected to be greater than the sum of individual benefits obtained without forming any symbiotic relationship. The main objective of this research project is to generate an optimal design for FWEIP by analyzing fish waste technologies to acquire parameters (e.g., price, yield, emissions rate) that aid in the construction of the FWEIP.

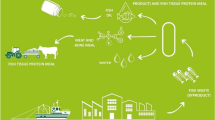
As for the first step, the optimal mathematical model in selecting the re-refining pathway and supply chain network is constructed via P-graph. The next step is to conduct a sensitivity analysis on the optimized model to evaluate the robustness of the developed FWEIP. At the end of the analysis, SSI is used to determine the pivotal facility of the FWEIP to conduct the multi-stakeholder analysis. Figure 2 depicts a simplified superstructure that shows the major components of a Fish Waste Eco-Industrial Park (FWEIP), including fish waste supply, the conversion technologies, the intermediate products, the final products and their supply pathway to customers. Accordingly, the overall superstructure is divided into four sections: a, the fish producing site; b, the fish waste conversion; c, recycling; and d, the consumer. The Sector a symbolizes the fish processing plant, which uses imported resources and generates fish wastes. Sector b contains a list of fish waste conversion routes, each of which generates products through a sequence of conversion technologies. Sector c represents a list of possible recycling routes (e.g., Fish processing wastewater from fish tank can be treated into clean water and recycled back into the tank) to produce recyclable products (p′) that can be consumed in sites a, b or sold directly to consumer (d). The intermediates (i) and products (p) are then produced from these wastes (w) through a series of technologies (t and t′). Next, there are two potential usages for the products (p). It can either be exported to clients or sold to gain profit. Alternatively, it can be sent to the recycling c for additional processing using a number of technologies (r and r′) to form intermediates (j) and regenerated products (p′). The regenerated products (p′) can be utilized for energy generation (m) for regenerated energy e′, which are subsequently used at the waste conversion technologies (t and t′) to keep the operation running. The energy (e) can also be imported externally and consumed by each technology together with the regenerated energy e′. Finally, Section (d) represents the customers that purchase products either from recycled pathways or direct pathways from fish waste biomass. The following superstructure can be modeled and optimized through P-graph model.

Fig. 2

Generic superstructure of the sustainable FWEIP based on circular economy

Methodology

Figure 3 depicts the research flowchart employed in the present study for the optimization of the FWEIP. It begins with gathering data, information, and parameters pertaining to the available technology for fish waste conversion to develop an FWEIP. In addition, the corresponding information, such as product yield, capital (CAPEX) and operational (OPEX) expenses, and environmental impact for each entity are collected. This is followed by the development of a generic superstructure depicting the formulation of the FWEIP as shown in Fig. 2. The discussed FWEIP problem in the previous section was reflected in the formulated model in P-graph and was optimized for the optimal and promising suboptimal solutions. Furthermore, sensitivity analysis was carried out to identify the possible debottlenecking solutions of the suboptimal pathways. Moreover, a multistakeholder analysis called the Shapley-Shubik power index has been employed to determine the pivotal facility of the FWEIP system. This provides useful insights for stakeholders to identify critical facilities to maintain the functionality of the FWEIP supply chain in the case of disruption or facility failure.

Fig. 3

Research flowchart toward optimal FWEIP design via P-graph modeling

Model Constraints

The mathematical model was formulated considering various decision criteria (e.g., CAPEX, OPEX, and carbon penalty) in choosing the optimal pathway for FWEIP. The economic performance of the conversion and recycling paths is the main emphasis of this study. Equation (1) is used to ensure the total flowrate (${F}_{w,a,b}$) of fish waste (w) delivered from the fish processing site ($a$) to the fish waste conversion plant (b) are constrained by the availability limit at each fish processing site ($a$) (${F}_{w,a})$:

$$\begin{array}{cc}{\sum }_{b}{F}_{w,a,b}\le {F}_{w,a}& \forall w\in W,\forall a\in A \end{array}$$

(1)

Equation (2) is used to constrain the amount of fish waste (${F}_{w,b})$ collected at each fish waste conversion plant ($b$) is equal to the sum of the amount delivered (${F}_{w,a,b}$) from fish processing site ($a$).

$$\begin{array}{cc}{F}_{w,b}={\sum }_{a}{F}_{w,a,b}& \forall w\in W,\forall b\in B\end{array}$$

(2)

Equations (3) and (4) define the mass balance of input fish waste (${F}_{w,b,t}$) and intermediate (${F}_{i,b,{t}{\prime}}$) to respective waste conversion technologies ($t$, ${t}{\prime}$) are constant.

$$\begin{array}{cc}{\sum }_{t}{F}_{w,b,t}={F}_{w,b}& \forall w\in W,\forall b\in B\end{array}$$

(3)

$$\begin{array}{cc}{\sum }_{{t}^{\mathrm{^{\prime}}}}{F}_{i,b,{t}^{\mathrm{^{\prime}}}}={F}_{i,b}& \forall i\in I,\forall b\in B \end{array}$$

(4)

The total production rates of intermediate ($i$) (${F}_{i,b}$) and product ($p$) (${F}_{p.b}$) at fish waste conversion plant ($b$) are constrained using Eqs. (5) and (6) respectively, where ${X}_{w,t,i}$ and ${X}_{i,{t}{\prime},p}$ refer to the conversion ratios of fish waste ($w$) to intermediate ($i$) and intermediate ($i$) to product ($p$) through technology ($t$) and (${t}{\prime}$), respectively. It is worth noting that not all pathways produce intermediate materials. In such cases, the conversion rate of waste to intermediate (${X}_{w,t,i}$) is set to 1 so the produced intermediate is equal to the waste flowrate (${F}_{i,b}=\sum_{w}\sum_{t}\left({F}_{w,b,t}\right)$).

$$\begin{array}{cc}{F}_{i,b}=\sum_{w}\sum_{t}\left({F}_{w,b,t}\times {X}_{w,t,i}\right)& \forall i\in I,\forall b\in B\end{array}$$

(5)

$$\begin{array}{cc}{F}_{p,b}=\sum_{i}\sum_{t{\prime}}\left({F}_{i,b,t{\prime}}\times {X}_{i,t{\prime},p}\right)& \forall p\in P,\forall b\in B\end{array}$$

(6)

The produced product ($p$) from the fish waste conversion plant is then either sold to the consumer ($d$) for profit or sent to the recycler ($c$) for future use. Equation (7) constrains the total distribution of products ($p$) to recyclers (${F}_{p,b,c}$) and consumers (${F}_{p,b,d}$) does not exceed the amount of product available (${F}_{p,b}$).

$$\begin{array}{cc}{\sum }_{c}{F}_{p,b,c}+{\sum }_{d}{F}_{p,b,d}={F}_{p,b}& \forall p\in P,\forall b\in B\end{array}$$

(7)

From there, Eqs. (8) and (9) describe the amount of product ($p$) received at recycler (${F}_{p,c}$) and customer (${F}_{p,d}$) respectively through the fish conversion site ($b$):

$$\begin{array}{cc}{F}_{p,c}={\sum }_{b}{F}_{p,b,c}& \forall p\in P,\forall c\in C\end{array}$$

(8)

$$\begin{array}{cc}{F}_{p,d}={\sum }_{b}{F}_{p,b,d}& \forall p\in P,\forall d\in D\end{array}$$

(9)

At recycle ($c$), Eqs. (10) and (11) describe the mass balance of input feed using product (${F}_{p,c,r}$) and intermediate (${F}_{j,c,{r}{\prime}}$) to the respective recycling technologies ($r$, ${r}{\prime}$) are constant, while Eq. (12) describes the mass balance of regenerated products (${p}{\prime}$) for energy generation (${F}_{{p}{\prime},c,m}$) and sold for profit (${F}_{{p}{\prime},c,d}$) to energy generation technology ($m$) and consumer ($d$) is equal to the amount of regenerated products (${p}{\prime}$) produced.

$$\begin{array}{cc}{\sum }_{r}{F}_{p,c,r}={F}_{p,c}& \forall p\in P,\forall c\in C \end{array}$$

(10)

$$\begin{array}{cc}{\sum }_{{r}^{\mathrm{^{\prime}}}}{F}_{j,c,{r}^{\mathrm{^{\prime}}}}={F}_{j,c}& \forall j\in J,\forall c\in C\end{array}$$

(11)

$$\begin{array}{cc}{\sum }_{m}{F}_{{p}^{\mathrm{^{\prime}}},c,m}+{\sum }_{d}{F}_{{p}^{\mathrm{^{\prime}}},c,d}={F}_{{p}^{\mathrm{^{\prime}}},c}& \forall {p}^{\mathrm{^{\prime}}}\in {P}^{\mathrm{^{\prime}}},\forall c\in C\end{array}$$

(12)

The total recycle production rate of intermediate ($j$) (${F}_{j,c}$) and regenerated products (${p}{\prime}$) (${F}_{{p}{\prime},c}$) at the product recycling facilities ($c$) are constrained using Eqs. (13) and (14) where ${X}_{p,r,j}$ and ${X}_{j,{r}{\prime},{p}{\prime}}$ refer to the conversion ratios of the products ($p$) to intermediates ($j$) and intermediate ($j$) to regenerated products (${p}{\prime}$) at the respective technology ($r$) and (${r}{\prime}$).

$$\begin{array}{cc}{F}_{j,c}={\sum }_{p}{\sum }_{r}\left({F}_{p,c,r}\times {X}_{p,r,j}\right)& \forall j\in J,\forall c\in C \end{array}$$

(13)

$$\begin{array}{cc}{F}_{{p}^{\mathrm{^{\prime}}},c}={\sum }_{j}{\sum }_{{r}^{\mathrm{^{\prime}}}}\left({F}_{j,c,{r}^{\mathrm{^{\prime}}}}\times {X}_{j,{r}^{\mathrm{^{\prime}}},{p}^{\mathrm{^{\prime}}}}\right)& \forall {p}^{\mathrm{^{\prime}}}\in {P}^{\mathrm{^{\prime}}},\forall c\in C \end{array}$$

(14)

Furthermore, the produced regenerated products (${F}_{{p}{\prime},d}$) can be sold to consumers for profit (see Eq. (15)).

$$\begin{array}{cc}{F}_{{p}^{\mathrm{^{\prime}}},d}={\sum }_{c}{F}_{{p}^{\mathrm{^{\prime}}},c,d}& \forall {p}^{\mathrm{^{\prime}}}\in {P}^{\mathrm{^{\prime}}},\forall d\in D \end{array}$$

(15)

Equation (16) describes the recycled energy (${e}{\prime}$) (${F}_{{e}{\prime}}$) from energy generation facility ($m$) where, ${X}_{{p}^{\mathrm{^{\prime}}},m,{e}{\prime}}$ denotes the conversion rations of regenerated products (${p}{\prime}$) from the respective recycling facilities ($c$) to recycled energy (${e}{\prime}$).

$$\begin{array}{cc}{F}_{{e}^{\mathrm{^{\prime}}}}={\sum }_{{p}^{\mathrm{^{\prime}}}}{\sum }_{c}{\sum }_{m}\left({F}_{{p}^{\mathrm{^{\prime}}},c,m}\times {X}_{{p}^{\mathrm{^{\prime}}},m,{e}^{\mathrm{^{\prime}}}}\right)& \forall {e}^{\mathrm{^{\prime}}}\in {E}^{\mathrm{^{\prime}}} \end{array}$$

(16)

Equation (17) denotes the total energy demand (${F}_{z}$) of the FWEIP is represented as the summation of the imported energy (${F}_{e}$) and the recycled energy (${F}_{{e}{\prime}}$). Whereby, z is a set of energy resources that are materially identical to the energy set of e and e′.

$$\begin{array}{cc}{F}_{z}={F}_{e}+{F}_{{e}^{\mathrm{^{\prime}}}}& \forall z\in Z,\forall e\in E,\forall {e}^{\mathrm{^{\prime}}}\in {E}^{\mathrm{^{\prime}}} \end{array}$$

(17)

Equations (18) and (19) depict the energy demand ($z$) at the respective fish processing (${F}_{z,a}$) and fish waste conversion plant (${F}_{z,b}$), where, ${k}_{w\to z,a}$, ${k}_{w\to z,b,t}$ and, ${k}_{i\to z,b,{t}{\prime}}$ denotes the conversion of feed to energy demand ($w\to z$, $i\to z$) associated with the rate of feedstock processed (${F}_{w,a}$, ${F}_{w,b,t}$, ${F}_{i,b,{t}{\prime}}$) at the respective processing sites ($a$ and $b$).

$$\begin{array}{cc}{F}_{z,a}={\sum }_{w}{F}_{w,a}{k}_{w\to z,a}& \forall z\in Z,\forall a\in A \end{array}$$

(18)

$$\begin{array}{cc}{F}_{z,b}=\sum_{w}\sum_{t}({F}_{w,b,t}{k}_{w\to z,b,t})+\sum_{i}\sum_{t\mathrm{^{\prime}}}({F}_{i,b,{t}^{\mathrm{^{\prime}}}}{k}_{i\to z,b,{t}^{\mathrm{^{\prime}}}})& \forall z\in Z,\forall b\in B \end{array}$$

(19)

The total energy demand (${F}_{z}$) can be expressed using Eq. (20) as the summation of energy required from fish processing (${F}_{z,a}$) and fish waste conversion plant (${F}_{z,b}$).

$$\begin{array}{cc}{F}_{z}={\sum }_{a}{F}_{z,a}+{\sum }_{b}{F}_{z,{\text{b}}}& \forall z\in Z \end{array}$$

(20)

Objective Function

The FWEIP gross profit (${C}^{GP}$) is calculated using Eq. (21) where, ${C}^{EP}$ denotes the sales of exported goods, ${C}^{IR}$ denotes the cost of imported resources, ${C}^{CX}$ and ${C}^{OX}$ denotes the capital and operational cost, and ${C}^{EM}$ denotes the carbon penalty.

$${C}^{GP}={C}^{EP}-{C}^{IR}-{C}^{CX}-{C}^{OX}-{C}^{EM}$$

(21)

The economic gains from sales of exported goods (${C}^{EP}$) is calculated as the amount of product exported (${F}_{p,d}$, ${F}_{{p}^{\mathrm{^{\prime}}},d}$) to customer ($d$) multiplied by the price of the respective products (${C}_{p}$, ${C}_{{p}^{\mathrm{^{\prime}}}}$) (see Eq. (22)).

$${C}^{EP}={\sum }_{p}{\sum }_{d}\left({F}_{p,d}\times {C}_{p}\right)+{\sum }_{{p}^{\mathrm{^{\prime}}}}{\sum }_{d}\left({F}_{{p}^{\mathrm{^{\prime}}},d}\times {C}_{{p}^{\mathrm{^{\prime}}}}\right)$$

(22)

Equation (24) denotes the cost of imported resources (${C}^{IR}$) is based on the amount of imported resources (${F}_{w,a}$, ${F}_{e}$) and the cost of imported resources (${C}_{w}$, ${C}_{e}$) (see Eq. (23)).

$${C}^{IR}={\sum }_{w}{\sum }_{a}\left({F}_{w,a}\times {C}_{w}\right)+{\sum }_{e}\left({F}_{e}\times {C}_{e}\right)$$

(23)

The total capital (${C}^{CX}$) and operational (${C}^{OX}$) cost accounts for the waste conversion plant ($b$), recycling facility ($c$), and energy generation ($m$) (see Eq. (24) and (25)).

$${C}^{CX}=\sum_{b}{C}_{b}^{CX}+\sum_{c}{C}_{c}^{CX}+\sum_{m}{C}_{m}^{CX}$$

(24)

$${C}^{OX}=\sum_{b}{C}_{b}^{OX}+\sum_{c}{C}_{c}^{OX}+\sum_{m}{C}_{m}^{OX}$$

(25)

Equations (26) and (27) represent the capital cost (${C}_{b}^{OX}$, ${C}_{c}^{OX}$, ${C}_{m}^{OX}$) while Eq. (29) to (31) operation cost (${C}_{b}^{OX}$, ${C}_{c}^{OX}$, ${C}_{m}^{OX}$) of the respective processing plant ($b$, $c$, $m$). Both capital and operating costs are calculated via the rate of processed feedstock (${F}_{w,b,t}$, ${F}_{i,b,{t}^{\mathrm{^{\prime}}}}$, ${F}_{p,c,r}$, ${F}_{j,c,{r}{\prime}}$, ${F}_{{p}^{\mathrm{^{\prime}}},m}$), the respective technology capital (${CX}_{t}$, ${CX}_{{t}^{\mathrm{^{\prime}}}}$, ${CX}_{r}$, ${CX}_{{r}{\prime}}$, ${CX}_{m}$) and operation cost factor (${OX}_{t}$, ${OX}_{{t}^{\mathrm{^{\prime}}}}$, ${OX}_{r}$, ${OX}_{{r}{\prime}}$, ${OX}_{m}$).

$$\begin{array}{cc}{C}_{b}^{CX}=\sum_{w}\sum_{t}\left({F}_{w,b,t}\times {CX}_{t}\right)+\sum_{i}\sum_{{t}^{\mathrm{^{\prime}}}}\left({F}_{i,b,{t}^{\mathrm{^{\prime}}}}\times {CX}_{{t}^{\mathrm{^{\prime}}}}\right)& \forall b\in B \end{array}$$

(26)

$$\begin{array}{cc}{C}_{c}^{CX}=\sum_{p}\sum_{r}\left({F}_{p,c,r}\times {CX}_{r}\right)+\sum_{j}\sum_{{r}^{\mathrm{^{\prime}}}}\left({F}_{j,c,{r}{\prime}}\times {CX}_{{r}{\prime}}\right)& \forall c\in C \end{array}$$

(27)

$$\begin{array}{cc}{C}_{m}^{CX}=\sum_{{p}^{\mathrm{^{\prime}}}}\left({F}_{{p}^{\mathrm{^{\prime}}},m}\times {CX}_{m}\right)& \forall m\in M \end{array}$$

(28)

$$\begin{array}{cc}{C}_{b}^{OX}=\sum_{w}\sum_{t}\left({F}_{w,b,t}\times {OX}_{t}\right)+\sum_{i}\sum_{{t}^{\mathrm{^{\prime}}}}\left({F}_{i,b,{t}^{\mathrm{^{\prime}}}}\times {OX}_{{t}^{\mathrm{^{\prime}}}}\right)& \forall b\in B \end{array}$$

(29)

$$\begin{array}{cc}{C}_{c}^{OX}=\sum_{p}\sum_{r}\left({F}_{p,c,r}\times {OX}_{r}\right)+\sum_{j}\sum_{{r}^{\mathrm{^{\prime}}}}\left({F}_{j,c,{r}^{\mathrm{^{\prime}}}}\times {OX}_{{r}^{\mathrm{^{\prime}}}}\right)& \forall c\in C \end{array}$$

(30)

$$\begin{array}{cc}{C}_{m}^{OX}=\sum_{{p}^{\mathrm{^{\prime}}}}\left({F}_{{p}^{\mathrm{^{\prime}}},m}\times {OX}_{m}\right)& \forall m\in M \end{array}$$

(31)

The environmental performance of the FWEIP has been incorporated by introducing the concept of carbon penalty as an objective function for optimizing the FWEIP. The carbon penalty is employed when the owner of the facility has to pay a certain amount of penalty for missing the carbon emissions target. The carbon penalty (${C}^{EM}$) is calculated using Eq. (32) for the respective processing plant ($b$, $c$, $m$) which is composed of the emission rate (${EM}_{b}$, ${EM}_{c}$, ${EM}_{m}$) and the cost per kg of carbon emitted (${C}^{emi}$). Equation (33) to (35) denotes the emission rate of the respective processing plant (${EM}_{b}$, ${EM}_{c}$, ${EM}_{m}$) based on the processed feedstock (${F}_{w,b,t}$, ${F}_{i,b,{t}^{\mathrm{^{\prime}}}}$, ${F}_{p,c,r}$, ${F}_{j,c,{r}{\prime}}$, ${F}_{{p}^{\mathrm{^{\prime}}},m}$) and the respective technology emission factor (${EM}_{t}$, ${EM}_{{t}^{\mathrm{^{\prime}}}}$, ${EM}_{r}$, ${EM}_{{r}{\prime}}$, ${EM}_{m}$).

$${C}^{EM}=\sum_{b}\left({EM}_{b}\times {C}^{emi}\right)+\sum_{c}\left({EM}_{c}\times {C}^{emi}\right)+\sum_{m}\left({EM}_{m}\times {C}^{emi}\right)$$

(32)

$$\begin{array}{cc}{EM}_{b}=\sum_{w}\sum_{t}\left({F}_{w,b,t}\times {EM}_{t}\right)+\sum_{i}\sum_{{t}^{\mathrm{^{\prime}}}}\left({F}_{i,b,{t}^{\mathrm{^{\prime}}}}\times {EM}_{{t}^{\mathrm{^{\prime}}}}\right)& \forall b\in B \end{array}$$

(33)

$$\begin{array}{cc}{EM}_{c}=\sum_{p}\sum_{r}\left({F}_{p,c,r}\times {EM}_{r}\right)+\sum_{j}\sum_{{r}^{\mathrm{^{\prime}}}}\left({F}_{j,c,{r}^{\mathrm{^{\prime}}}}\times {EM}_{{r}^{\mathrm{^{\prime}}}}\right)& \forall c\in C \end{array}$$

(34)

$$\begin{array}{cc}{EM}_{m}=\sum_{{p}^{\mathrm{^{\prime}}}}\left({F}_{{p}^{\mathrm{^{\prime}}},m}\times {EM}_{m}\right)& \forall m\in M \end{array}$$

(35)

Hence, the objective function is formulated as the maximization of the gross profit (see Eq. (36)).

$${\text{Objective}}={\text{max}}\left({C}^{GP}\right)$$

(36)

P-Graph Modeling of FWEIP

Figure 4 illustrates the generic FWEIP superstructure from Fig. 2 reflected in the form of P-graph framework. This FWEIP network can be divided vertically into 6 sections based on the intermediate material produced. Section A represents the generation of fish wastes, which corresponds to site $a$ in the superstructure. Section B address the decision-making process for selecting the appropriate waste conversion technologies into the desired products denoted as “$b$,” whereas section C denotes the decision-making process for the fish waste-based product’s outcome, which is either to sell or recycle. Section D, on the other hand, constitutes the recycle phase “$c$,” which represents the conversion of products into recyclable products such as fish feed, clean water, heat, and electricity. Finally, section E represents the resource management of importing the required resources to maintain the functionality of the FWEIP system. These resources, in the same case, would be fish feed, steam, clean water, and electricity. Electricity, steam, and fish feed can all be considered exportable products or recyclable resources. By observing the material flow, the FWEIP model can produce both linear and circular models, similar to the generic superstructure. For example, if the material flows from E → A → B → C and all products are exported without recycling, the model is termed as linear economy. Circularity, on the other hand, is observed when a resource loop is formed such as steam and electricity are regenerated resulting in the flow from E → A → B → C → D → E.

Fig. 4

Generic FWEIP modeled using P-graph framework

Sensitivity Analysis

Following the P-graph optimization of the FWEIP, a sensitivity analysis is performed as illustrated in Fig. 5 to determine the degree of change in the optimal solution with respect to changes in the problem parameters. The analysis starts with the design of a scenario, from which the concept of the scenario is used to predetermine the intended solution. The Accelerated Branch-and-Bound (ABB) algorithm typically determines a list of optimal and near-optimal solutions. Then, a range of numerical values is allocated to one or more specific parameters related to the scenario developed. The parameters are adjusted either by incrementing or decrementing depending on the base value, followed by performing optimization via P-graph to obtain the revised result. This process is then repeated until the expected optimal solution is reached.

Fig. 5

Sensitivity analysis flow chart

Shapley-Shubik Power Index (SSI) Analysis

The FWEIP has to meet the minimum profit to ensure the economic feasibility of the eco-industrial park so that there is no significant loss in operating the eco-industrial park. The Shapley-Shubik power index (SSI) is used to assess the vitality of each entity and achieve power distribution based on the weighted voting systems. According to the cooperative game theory, the SSI was found to determine the power of each voter in affecting the outcome of the voting system and the permutations of all voters in the game are used to evaluate sequential coalitions. To win the alliance, the total number of votes supplied by each player must exceed the defined quota. Each internal process within a plant can be thought of as a weighted player in a binary game with operation and failure options. SSI allocation could be effective in expressing the dominant influence of each process in achieving the FWEIP’s benchmark objective-based performance by analyzing consecutive coalitions of plant processes. In this work, the fish waste conversion facilities are deemed as the “stakeholder” of the FWEIP, whereas $n$ denotes the total number of stakeholders in the optimal solution of the FWEIP. Their respective power outputs (${F}_{n}$) and quota ($q$) is represented in Eq. (37). The term $q$ refers to a goal of minimum requirements that have been the benchmark that the FWEIP must meet.

$$\begin{array}{cc}\left[q:{F}_{n=1},{F}_{n=2},{F}_{n=3},\dots {F}_{n}\right]& n\in N \end{array}$$

(37)

This provides insight to decision-makers on the significance of each FWEIP entity to meet the minimum benefits to the cost ratio (BCR) (see Eq. (38)). The subsequent step is to identify the possible number of permutations of the technologies selected in the optimal and suboptimal solutions of the FWEIP. The permutations (factorial of N or N!) show the various possibilities in which each technology can close in the FWEIP system while satisfying the required minimum BCR.

$$BCR=\frac{\mathrm{Revenue}\;\mathrm{generated}-\mathrm{Operating}\;\mathrm{cost}}{\mathrm{Total}\;\mathrm{capital}\;\mathrm{cost}}$$

(38)

For example, considering the BCR quota > 80% of the base case at BCR = 10, the absence of each subsequent power player: P1 (BCR=9), P2 (BCR=5), and P3 (BCR=2) will influence the overall system performance. In this case, P1 is the first to leave the supply chain, followed by P2 and P3. As P1 leave the supply chain system, the overall BCR is reduced to 9 which, still satisfies the quota > 80% of the base case BCR value. As P2 leaves the system, the overall BCR drops below the quota at 5 where P2 is indicated as the pivotal player in this permutation. The pivotal player would alter depending on the order of facility failure in the supply chain system. As such, all permutation of the supply chain technology ($N!$) is iterated to identify the respective pivotal player in each case. The frequency of the technology being pivotal is recorded and utilized to calculate the Shapley-Shubik power index (${\alpha }_{P}$) is calculated using Eq. (39).

$${\alpha }_{P}=\frac{{\mathrm{Pivotal}}\;{\mathrm{Frequency}}}{N!}$$

(39)

Case Study Description

Figure 6 illustrates the FWEIP case study adapted in this work where various fish waste conversion technologies are considered (e.g., black soldier fly (BSF), Fischer Tropsch (FT), pyrolysis, gasification, anaerobic digestion, hydrotreating, and combined heat and power (CHP)). Detailed information on the conversion technologies and respective parameters adapted in the model is documented in the Supplementary Materials (see Tables S1 to S5). As such, Fig. 7 illustrates the maximal structure of the P-graph model and reflects the formulated FWEIP case study superstructure from Fig. 6. This represents the base case scenario in which further adjustments are made to the model parameters (e.g., price, yield, emission rate) to evaluate the sensitivity of the formulated model.

Fig. 6

FWEIP superstructure of the case study

Fig. 7

Maximal structure of the base case study in P-graph framework

Results and Discussion

The Accelerated Branch and Bound (ABB) algorithm is used to determine the optimal (and suboptimal) FWEIP pathway. Figure 8 illustrates the economic revenue and cost comparison between the optimal and suboptimal technology pathways. The model favors the production of syngas using gasification followed by the FT upgrading process into biofuel as the optimal FWEIP solution. This is attributed to the higher annual profit of gasification with FT pathway (Optimal, $2.28 million) compared to BSF (suboptimal 1, $1.87 million) and pyrolysis with gasification (suboptimal 2, $1.73 million) pathway. However, this pathway does not promote any form of circular economy within the FWEIP system as all resources are imported with heavy reliance on the economic gain of selling biofuel. In contrast, the BSF pathway (suboptimal 1) offers resource circularity which has reduced (14.55%) the dependence on imported fish feed. As a trade-off, the resultant revenue potential has been reduced by 16.43% since there is no additional economic benefit of biofuel production. On the other hand, for the second alternative (suboptimal 2), pyrolysis is proposed alongside gasification with FT process for energy and biofuel productions. With such intervention, the process can be self-sustainable as the energy generated from pyrolysis can be used for the FWEIP, whereas the cost can be compensated by the revenue generation from selling the biofuel through gasification and FT upgrading process. Contradictory, this resulted in the lowest revenue potential (18.17%) compared to gasification and BSF pathway with major resources (fish waste) allocated to pyrolysis for energy generation (84.91%) rather than gasification for biofuel production (15.09%). Considering the potential of suboptimal solutions, further analysis is performed to provide useful insights to debottleneck the technology pathway.

Fig. 8

Economic comparison between optimal and suboptimal solutions

Sensitivity Analysis

In this section, sensitivity analysis is performed on the base case model to study the variation of optimal technology pathways for FWEIP under different scenarios. These scenarios are developed by taking into account the key parameters that promote the circularity of resources within the system. As discussed in the previous section, potential pathways to achieve a circular economy in FWEIP involve the recycling of four resources—fish feed, chitosan, steam, and electricity. Owing to the fact that the application of gasification offers a higher revenue opportunity that overweighs the economic contribution of the recycling pathway, debottlenecking is demonstrated specifically on the production pathway of these resources.

Scenario 1—Price Inflation in Imported Resources

The first scenario is created by varying the price of imported chitosan, fish feed, electricity, and steam to study the sensitivity of the FWEIP model toward the reliance on imported resources. The price is increased gradually by 10% of the base value until the recycling pathway of the respective resources is observed at Rank 1. The values from the previous optimal solution have been considered as the benchmark. The imported resources are then compared and reported as a percentage of the benchmark’s value, for example, $\frac{\mathrm{Scenario I }}{{\text{Benchmark}}}\times 100\%$. After a series of tests, it is noticed that the model is more sensitive toward the price of chitosan and fish feed in stimulating the recycling pathway. In contrast, the recycle flow of steam and electricity is not favored even at a price increment of + 400% (which is less likely to have such fluctuation). The parameter setting and the resultant optimized results are summarized in Table 2. By analyzing the changes in the consumption of imported resources with respect to the increment in price, it can be seen that the FWEIP is more responsive to chitosan than fish feed. This could be owing to the high conversion ratio of chitosan (0.56 t/t input) compared to fish feed (0.35 t/t input), which further leads to a greater influence caused by the chitosan sales compared to that of the fish feed. This also shows that the revenue gained from the fish feed production is insufficient to compensate for the profit loss if biofuel is no longer generated for exportation.

Table 2 Parameter setting and the results of P-graph optimization for imported resources price inflation

Scenario 2—Debottlenecking on the Pyrolysis Pathway

While implementing the strategies of regenerating and recycling resources can drastically reduce production costs, it is revealed that the proposed model is inclined toward exporting biofuel to generate income. Hence, to further maximize the economic benefits of the model and to achieve sustainable development at the same time, it is suggested to introduce an additional route with a recycling flow of resources to the existing optimal solution. As demonstrated in the base case study, the conversion pathway chosen for biofuel production is through the use of syngas via the FT process rather than the hydrotreating of bio-oil in the pyrolysis pathway. This can be explained as the FT process facility has a lower CAPEX and OPEX compared to the hydrotreating facility. However, products generated from pyrolysis can contribute to promoting circular economy, i.e., bio-char for the regeneration and recycling of electricity and heat; and profit generation, i.e., syngas and bio-oil to be further processed to produce biofuel for exportation.

Additional scenario analysis is performed to analyse processing debottlenecking potential on the pyrolysis pathway. The first scenario focuses on the economic parameter, where the CAPEX and OPEX of the hydrotreating facility gradually decrease by 10% to its base value. However, after a series of tests, such a solution is not observed even at zero cost. This is owing to the higher conversion ratio of fish waste to syngas with the application of gasification (i.e., 88.89% higher than that of pyrolysis). The second scenario is to study the impact of this conversion ratio on the favorability of pyrolysis. Such change in conversion ratio can be realized by the incorporation of the use of a catalyst (Wang et al. 2022). In this case, a mixture of Al₂O₃ and Na₂CO₃ is chosen for its high bio-oil yield (0.72 t bio-oil/t input) characteristic of fish fat (Mrad et al. 2013). Along with that, the OPEX of pyrolysis is increased by 30% of the base value to account for the additional catalyst used in the process. As a result, the pyrolysis conversion pathway has become the Rank 1 solution (as presented in Fig. 9).

Fig. 9

Rank 1 solution structure with an improved conversion ratio of bio-oil from fish waste

The results of P-graph optimization are summarized in Table 3. It is revealed that despite the increment in the operating cost for the pyrolysis process and the increment of steam demand for the hydrotreating facility, a significant increment in gross profit is observed. Aside from the high revenue potential of exporting biofuel produced via hydrotreating and FT process, this can be explained as the import of electricity in the model is diminished to 44.62% of the base value due to the recycle flow implemented. With that, the conversion pathway that offers a circular economy accounting for both resource circularity and exporting of sustainable products is debottlenecked.

Table 3 Results of P-graph optimization by improving the conversion ratio of bio-oil in the pyrolysis process

Estimation of Pivotal Player Using Shapley-Shubik Power Index

The Shapley-Shubik power index approach is utilized to identify the possible bottleneck of the proposed optimal and suboptimal solutions. Three cases were considered with respect to the technologies selected in the gasification with FT (optimal), BSF (suboptimal 1), and pyrolysis and gasification (suboptimal 2) solution with the respective power index calculated based on Eq. (29). Detailed outcome of Shapley-Shubik power index is documented in the Supplementary Materials section (see Tables S6 and S7). Based on the SSI results (see Fig. 10), the hydroponics plant represents the pivotal player for the first (optimal) and third (suboptimal 2) cases. This is attributed to the high revenue potential from vegetable production ($1,679,790/y) and relatively lower operating cost ($555,976/y), in which the absence of this facility will result in a significant decrease in BCR of the whole system for the respective cases (optimal = 49.25%; suboptimal 1 = 60.16%; suboptimal 2 = 65.11%). In the case of gasification for biofuel production (optimal), hydroponics (41.67%) remains the pivotal player despite both gasification (29.17%) and FT process (29.17%) contributing significantly to the power index. Although, the absence of hydroponics incurs a significant decrease (18.47%) in the total operating cost compared to gasification and FT combined (7.51%) should contribute positively to the BCR. The loss of sales (31.75%) from hydroponics compared to biofuel (21.40%) from gasification and FT process is significant in offsetting the lower operating cost. This highlights the dominance of hydroponics facility’s detrimental impact on the overall BCR in the case of failure compared to gasification and FT process combined. This is highlighted in the pyrolysis and gasification case (suboptimal 2) where the feedstock resources are divided for both pyrolysis for energy generation and gasification for biofuel production. This further reduces the revenue potential (84.91%) of the gasification facility compared to the optimal solution, empowering hydroponics as the pivotal player with a power index of 96.67%. Alternative to the hydroponics facilities, in the case of BSF (suboptimal 1), the BSF facility is equally as important as the hydroponics facility with a power index of 50% respectively. The BSF facility offers 14.55% worth of self-sustained fish feed production and 5.95% of revenue from chitosan production. The identification of the pivotal player in the FWEIP will enable the allocation of precious resources to other facilities ensuring the functionality of the FWEIP supply chain (satisfying demand) in the case of disruption or alterations to any facilities. Furthermore, this can provide crucial information to stakeholders to plan and strategize the maintenance schedule based on the pivotal players (Tan et al. 2021a, b).

Fig. 10

Shapley-Shubik power index on the FWEIP

Implication and Limitation of the FWEIP Model

The formulated FWEIP model using the P-graph framework offers essential insights for stakeholders in designing a sustainable CE eco-industrial park system. The suitability of gasification and FT process favored by the model indicates the high annual profit potential of biofuel production to establish a circular FWEIP system. The sensitivity analysis is performed to showcase the robustness of the optimal solution as well as possible debottlenecks of suboptimal solutions. This enables policymakers to formulate policy strategies such as subsidies and tax reductions to encourage investors to drive the FWEIP system toward a more sustainable industry. Furthermore, the estimation of pivotal players in the FWEIP system using Shapley-Shubik Power Index highlights the importance of respective processes in maintaining the desired economic goal. This provides stakeholders with crucial information to allocate limited resources to key processes in ensuring the functionality of the FWEIP system in achieving the desired outcome. On the other hand, in case when the FWEIP is formed by multiple individual entities, the outcome of the SSI can be used as a guide for further cooperative negotiations. For example, despite not covered in the scope of this work, the index can be used as a referenced indicator for fair distribution of profit sharing (e.g., greater share of profit is allocated for entity that play a more pivotal role) among multiple involved parties (e.g., shown in the work conducted by Fadzil et al., (2022)).

Conclusion

In this work, a novel model based on a graph theoretic approach is developed to propose the integration and optimization of fish waste conversion technologies to establish circularity within the FWEIP. The optimal solutions of the FWEIP have been identified using P-graph and the results favors the economic gains ($2.28 million/y) of gasification pathway for biofuel production (optimal) without promoting circular synergy within the FWEIP ecosystem. To achieve circular relation within the FWEIP ecosystem, the BSF pathway (suboptimal 1) is favored as it offers self-sustaining resources from the production of fish feed and chitosan for the fish farm and wastewater treatment facilities respectively, but offering lower economic gain (17.98%) compared to the gasification pathway (optimal). Furthermore, the pyrolysis pathway (suboptimal 2) also promotes circular relation by offering self-sustaining energy generation from the produced biofuel. However, this hindered the economic potentials of this solution (84.91%) compared to the gasification pathway (optimal) which favors the marketing of biofuel produced instead for energy generation.

As such, debottlenecking is performed to identify the pyrolysis pathway (suboptimal 2) potential of increasing the conversion ratio of fish waste to biofuel with the use of catalyst. The analysis indicates a significant increase in the conversion ratio (from 0.4 to 0.72 wt%) of the pyrolysis pathway is expected for the model to favor it as the optimal solution. Overall, the BSF pathway (suboptimal 1) is favored to promote circular relation which the SSI (41.67%) suggest the importance of hydroponic facility impact on economic goal. Suggesting the significance of maintaining the functionality of the hydroponic facility to ensure the welfare of the FWEIP supply chain. Hence, these findings serve as guidelines for policymakers and decision makers in governing the FWEIP ecosystem ensuring the interest of both economic and environmental are achieved.

Throughout the study, the aforementioned research gap has been successfully addressed with the presented FWEIP framework. However, several potential works can still be extended from this study. For instance, the developed FWEIP supply chain can adopt digital twin technologies to ensure the sustainability of the fish-waste supply chain by enhancing resource utilization, real-time monitoring of the availability of fish waste and optimizing the supply chain design. On the other hand, future work can also be extended by taking into account the combined water and heat integration problems in the FWEIP model to meet the trade-offs of the energy consumption costs and technologies investment costs. Furthermore, the proposed FWEIP model can be further extended by considering a multi-period operation to cater for uncertainties in terms of waste quality and flowrate and thus generating more promising results for the decision-makers. Lastly, the findings can be extended toward game theory model to access the strategic interactions between each party of the FWEIP ecosystem and provide useful insights on the bargaining powers to facilitate effective and systematic negotiations.