A Practical Approach to Estimate the Min-Entropy in PUFs

Abstract

Helper data algorithms reliably extract secrets from physical unclonable functions. The necessary helper data can leak information, though. One state-of-the-art approach to assess the remaining min-entropy is limited to homogeneous bias or correlation, not both. Another one extends this to only local bias without correlation but is limited to short code lengths. This work presents a new approach for determining the min-entropy based on convolving histograms. It provides a better bound and good approximation given arbitrary bias, more realistic correlation effects, and practically relevant code sizes. Experiments on real-world and synthetic data show the benefit of the new method compared with state-of-the-art ones. This work also facilitates a better understanding of how the error correction as post-processing impacts the min-entropy.

1 Introduction

The technology of physical unclonable functions (PUFs) deriving secrets unique to each device from minuscule and unavoidable process variations promises security in low-cost devices. This is important for many applications on the Internet of Things and can help protect future supply chains. A secure way of using a PUF is to derive a key encryption key from it.

Therefore, the currently only PUF standard [1, 2] requires PUFs to be sufficiently unique.¹ The standard suggests testing this property with statistical tests or entropy estimations targeting the PUF response. However, real-world PUF designs usually do not provide responses that can be modeled as drawn from unbiased, independent and identically distributed (IID) random sources. Instead, a certain amount of imperfection in the PUF response is accepted and compensated by post-processing, which usually includes two steps: increasing the reliability of the output, e.g., through correction by an error-correcting code (ECC), and increasing the entropy per bit, e.g., by compression.

Helper data algorithms (HDAs) can correct a PUF response. They map the PUF response to a code word using public helper data. Good HDAs are designed such that the helper data do not leak about the secret as long as the PUF response bits correspond to unbiased IID random variables [3]. If the PUF response deviates from this requirement, though, helper data and information regarding the PUF’s statistical properties start leaking and reduce the effective entropy of the PUF. Since the helper data generated for a specific design also depend on the ECC, the ECC influences how information leaks. This phenomenon, called helper data leakage, is currently not considered in the standard, as mentioned earlier, and might lead to incorrect assumptions: After error correction, the entropy left for a key might be lower than expected when only considering the entropy in the PUF response. Besides, selecting an ECC must not only target the efficiency when implementing the required decoder but also the helper data leakage given the PUF in a specific design. In other words, if PUF designs with biased or non-IID responses are used to generate a secret, methods are necessary to estimate the remaining key entropy.

Contribution

Based on preliminary works providing a bound for the min-entropy after error correction in the light of helper data leakage [4, 5], which are discussed below, this work significantly improves and makes applying these bounds practically feasible. In particular, the contributions of this work are as follows:

• As a base for computing the min-entropy of PUF-derived secrets after error correction, we introduce the response mass function (RMF).

• Based on it, we introduce the convolution of histograms [6] into the domain of PUFs. This results in the first feasible approach to approximate the min-entropy in PUF-derived secrets in a wide range of practically relevant scenarios. In previous works, the practical relevance was limited due to unrealistic assumptions about the PUF behavior or due to only being feasible for very short ECCs.

• We demonstrate the practical relevance of our work using data from real-world SRAMs. Nevertheless, the proposed bound and approximation are independent of the PUF primitive.

• We demonstrate the influence of ECC parameters and conclude that short codes with a high rate are preferable regarding helper data leakage.

• We also show for synthetic correlated data that the leakage is significant for an overlapping comparison of ring oscillator (RO) frequencies.

• The source code to compute the bound is available at [7].

Structure

The rest of this paper is structured as follows: After providing the necessary background in Sections 2 and 3 introduces the RMF and the approach to compute the expected conditional min-entropy. Section 4 presents and discusses the results when applying our approach. A conclusion is drawn in Section 5.

2 Background

2.1 Helper Data Algorithms

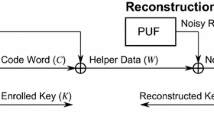
In a practical context, PUF responses are subject to noise. Hence, error correction is necessary if, e.g., the PUF should provide a secret key. For this error correction, so-called HDAs first compute public helper data, which can then reconstruct the original secret together with a noisy PUF response. This work focuses on HDAs employing a linear error-correcting code. Pointer-based approaches are out of scope for this work because they significantly differ in their vulnerability: Other than the schemes considered in this work, they are susceptible to helper data manipulation attacks and they leak about the PUF through reliability information exploitable by machine learning [8]. In the following, we explain why for the considered HDAs—fuzzy commitment scheme, code-offset fuzzy extractor, and syndrome construction—the conditional min-entropy of the secret given the PUF response is equivalent, and distinguishing these cases is not necessary, as presented in [4, 9].

During the enrollment phase, the fuzzy commitment scheme [10] encodes the secret into a code word, which is then XORed with the PUF response X to compute the helper data Y. During reproduction, the ECC can derive the correct original secret by decoding the XOR-sum of the noisy PUF response and the helper data if not too many errors have occurred.

The code-offset fuzzy extractor [11] is similar to the fuzzy commitment [10]. However, the hashed PUF response specifies the secret, and a random code word is XORed to facilitate error correction. The conditional min-entropy is the same because this XOR is the same as for the fuzzy commitment scheme. The hash function serves as a randomness extractor. It can be based on universal [12] or cryptographic hash functions. Hereby, universal hash functions are good randomness extractors, but they result in a larger min-entropy loss $L\ge 2\log (1/\epsilon )$ if the input to the hash function is not perfectly uniform [13, 14]. A measure for this distance to uniformity is $\epsilon$.

A syndrome-based approach in general [11] or for polar codes [15] can be reformulated by mapping the syndrome to a corresponding code word. Thus, the conditional min-entropy can be computed equivalently for all three cases [4, 9].

2.2 ECCs for PUFs

An overview of commonly used ECCs in the PUF domain is given in [16]. In summary, concatenations of linear block codes are the most common choice for error correction. Of those, concatenations of repetition and BCH codes seem to be favored due to their efficiency. Additionally, current research considers polar codes as a stand-alone solution for PUFs [15]. Therefore, our experiments focus on these three codes individually and on a concatenation of a repetition and a BCH code. This work denotes codes as tuples (n, k, t) where n is the code word length, k is the message length, and t is the number of correctable errors. We omit t below if not relevant at that point.

2.3 Expected Conditional Min-Entropy

For most real-world designs, the probability distribution of PUF responses is not uniform, i.e., the probability is not equal for each possible response $\underline{x}$. An attacker might combine knowledge about a PUF design’s imperfections with the helper data of a particular device under attack to guess the corresponding PUF response and hence the key more easily. In this scenario, the expected conditional min-entropy $\bar{H}_\infty (X\vert Y)$ is a measure for the expected chance that an attacker finds the correct key with the first guess given the helper data. Therefore, it is a measure of the security of the construction, which incorporates deficiencies of the PUF and the HDA. We now explain the previous work of Delvaux et al. [4] in detail because it is a prerequisite to comprehending our approach. The PUF entropy estimation in [17] follows the so-called $n-k$ bound, which is overly pessimistic [4, 5] and thus inefficient. A shorter PUF response would already suffice.² The findings in [4] also refute [18], which tries to determine the entropy loss when the error correction for a PUF utilizes repetition codes. Delvaux et al. [4] simplified the approach in [11] using two assumptions:

• 1. The input to the ECC encoder, a random number $\underline{u}\in \mathcal{U}$, $\underline{u}{{\,{\leftarrow}\,}}{U}$, is uniformly distributed. Hence, all code words $\underline{v}\in \mathcal{V}$ are equally probable.

• 2. The space of PUF responses $\mathcal{X}$ can be partitioned into a limited number of subsets $\varphi _j$ with $j \in [0,J]$, where each subset contains PUF responses with equal probability of occurrence $p_{\varphi ,j}$ and $p_{\varphi ,j} > p_{\varphi ,j+1}$.

Two examples of distributions that fulfill these assumptions are given in [4]:

• (a) All n bits of the PUF response are IID from a Bernoulli source, i.e., ${{\,\textrm{P}\,}}(x_i=1) = p$ for $i \in \{1,\dots ,n\}$. The probability of a response then only depends on its Hamming weight (HW), but not on which bits are 1 or 0.

• (b) The first bit is uniform, and all following bits are equally correlated to their predecessor, i.e., ${{\,\textrm{P}\,}}(x_{i} = x_{i-1}) = r$ with $i \in \{2,\dots ,n\}$. Here, the probability of a response only depends on its amount of transitions, but not their direction ($1\rightarrow 0$ vs. $0\rightarrow 1$) or where they happen. Both examples are illustrated for a response with three bits in Table 1.

Table 1 Examples of partitioning for IID ($p<0.5$) and correlated ($r > 0.5$) distribution

The first assumption, combined with Bayes’ rule, leads to

$$\begin{aligned} \bar{H}_\infty (X\vert Y) = -\log _2\left( \frac{1}{|\mathcal {{V}}|} \sum _{\underline{y}\in \mathcal{Y}} \max _{\underline{v}\in \mathcal{V}} {{\,\textrm{P}\,}}\left({X}= \underline{y}\oplus \underline{v}\right) \right) \end{aligned}$$

(1)

for a general ECC. For linear ECCs, it can be further simplified to

$$\begin{aligned} \bar{H}_\infty (X\vert Y) = -\log _2\left( \sum _{\underline{\epsilon }\in \mathcal {E}} \max _{\underline{v}\in \mathcal{V}} {{\,\textrm{P}\,}}\left({X}= \underline{\epsilon }\oplus \underline{v}\right) \right) \text {,} \end{aligned}$$

(2)

where $\underline{\epsilon }\in \mathcal {E}$ is a coset leader. Coset leaders are bit strings of minimum HW so that $\{\underline{v}\oplus \underline{\epsilon }\vert \underline{v}\in \mathcal{{V}}, \underline{\epsilon }\in \mathcal {E}\} = \mathcal{{Y}}$ with $\mathcal {{Y}}$ being the space of all possible helper data. Note that $|\mathcal {{U}}| = |\mathcal {{V}}| = 2^k$, and $|\mathcal{{V}}||\mathcal {E}| = |\mathcal{{Y}}| = |\mathcal {{X}}| = 2^n$. A 3-repetition code, for example, has code word space $\mathcal {{V}}= \{000, 111\}$ and $\mathcal {E}= \{000,001,010,100\}$.

In both formulae, the $\max$ operator selects for given helper data $\underline{y}$ the most probable PUF response that is reachable by any valid code word $\underline{v}$. For linear codes, this produces the same response for all elements of a coset, so it is sufficient to consider the coset leader $\underline{\epsilon }$. Since all code words are equiprobable, the expectation boils down to a sum. In this form, the computational cost is $|\mathcal {{V}}|\cdot |\mathcal {{Y}}|$ operations for (1) respectively $|\mathcal {{Y}}|$ operations for (2). Therefore, usage is limited to ECCs with $n$ approximately up to 60 with today’s computing resources.

The computational cost can be further reduced by considering that the $\max$ operator in (1) and (2) always selects the most probable $\underline{x}$ that is reachable by adding any $\underline{v}$ for the given $\underline{y}$ or $\underline{\epsilon }$. Since all $\underline{v}$ are assumed equally probable, the same $\underline{x}$ is selected for every $2^k$ elements in $\mathcal {{Y}}$.

For example, if $\underline{x}=100$ is more probable than $\underline{x}=011$, the former is chosen for $\underline{y}=100$ and $\underline{y}=011$, by an XOR with $\underline{v}=000$ and $\underline{v}=111$, respectively. It is thus sufficient to consider $\nicefrac {|\mathcal {{X}}|}{|\mathcal {{U}}|} = 2^{n-k} = |\mathcal {E}|$ elements of $\mathcal{{X}}$ in (1) and (2). Which $|\mathcal {E}|$ elements of $\mathcal{{X}}$ to consider depends on the probability distribution of ${X}$ and the specific ECC. For example, for a repetition code with odd $n$, which can correct up to t bit errors, and an IID distribution, the set of coset leaders $\mathcal {E}$ either equals the $|\mathcal {E}|$ most probable elements of $\mathcal{{X}}$ or the coset leaders can be derived from the bitwise inverse of the most likely responses.

$$\begin{aligned} \mathcal {E}= {\left\{ \begin{array}{ll} \bigcup _{j=0}^t \varphi _j &{} p < 0.5\\ \{\underline{x}\oplus 1\dots 1 \vert \underline{x}\in \bigcup _{j=0}^t \varphi _j\} &{} p > 0.5\end{array}\right. } \end{aligned}$$

(3)

For correlated distributions, as depicted in Table 1, the elements of $\mathcal {E}$ are instead distributed among all $\varphi _j$ for repetition codes. For ECCs that are not maximum distance separable (MDS), some elements of $\mathcal {{X}}$ with HW larger than t have to be considered because the ECC can still correct them. Neglecting this and instead always choosing the $|\mathcal {E}|$ most likely $\underline{x}$ overestimates the sum in (1). Hence, this overestimation results in a lower bound for $\bar{H}_\infty (X\vert Y)$. The bound holds with equality for MDS ECCs and uncorrelated distributions.

Since $|\mathcal {E}|$ operations may still be infeasible to compute, it is necessary to utilize that all $\underline{x}$ in a subset $\varphi _j$ have the same probability. Therefore, the contribution of a subset $\varphi _j$ to the sum equals $|\varphi _j|\cdot p_{\varphi ,j}$. This allows processing $\vert \varphi _j\vert$ elements of $\mathcal {{X}}$ at once so that for a linear (n, k, t), block code t or $t+1$ operations suffice. However, this requires the second assumption to hold, i.e., $\mathcal {{X}}$ can be partitioned into several subsets $\varphi _j$, which are feasible to iterate. This partitioning has previously been shown only for the types of distribution depicted in Table 1.

The grouping bound [5] achieved such a partitioning for local bias, i.e., each bit of the response may have a different probability to turn out as 1, but still required the assumption of independence between the bits. It rounded each bias value to a chosen granularity, so bits with similar bias were approximated to have equal bias. Then, the partitioning by Delvaux et al. can be performed within each group of bits with equal bias. The partitions are combined to find the $|\mathcal {E}|$ most probable PUF responses.

These state-of-the-art methods have multiple drawbacks: First, assumptions about the PUF, such as an IID bias, do not hold in practice, and dropping these assumptions results in an infeasible long computation time. Second, the grouping bound still ignores correlation among response bits, and the combination of partitions becomes infeasible for long code words. This work closes the gap such that we can compute the conditional min-entropy for more realistic ECCs and distributions of PUF responses.

3 Min-Entropy Estimation Through Histogram Convolution

In this section, we propose a method that can deal with arbitrary biases like the grouping bound [5]. However, it produces a tighter bound with less computational effort. For this purpose, the response is considered a bit string partitioned into substrings, possibly each with a different number of bits. Additionally, our new approach requires independence only between substrings, not between all bits. If the substrings are not independent, our metric is no longer a bound but an estimation of the conditional min-entropy.

3.1 Response Mass Function

In this work, we use the RMF to find the $|\mathcal {E}|$ most likely PUF responses and their probability but are not interested in their values since this is not relevant for (1) and (2). The RMF $f_{{X}}$ [19] maps a log-probability to the share of outcomes of random variable (RV) ${X}$ that occurs with this log-probability. It can be seen as the inverse of the probability mass function (PMF), which maps outcomes to (log-)probability values. For the security assessment of PUFs, it is usually relevant that there are one or more PUF responses with at least a specific probability. This does not mean we need to know which responses have these specific probabilities. Thus, the RMF is also a potential metric for the quality of a PUF.

The support of the RMF is $]-\infty ,0]$ and has similar axioms as a PMF, i.e.,

$$\begin{aligned} f_X(l)\ge 0 \quad \forall l \in \; ]-\infty ,0] \quad \textrm{and}\quad \int _{-\infty }^0 f_X(l)dl = 1 \text {.} \end{aligned}$$

(4)

The RMF is a series of Dirac impulses $\delta (\cdot )$, whose weights depend on how many outcomes occur with the same probability. Figure 1 illustrates the RMF for the distributions from Table 1 and selected values of p, r.³

The RMF of a sequence of independent RVs is found by convolving the marginal RMFs because the joint probability of independent events equals the product of their marginal probabilities, respectively the sum of their marginal log-probabilities. This holds for any discrete distribution, even if the log-probabilities or the number of events differ. Figure 2 exemplifies this for a single-bit and a two-bit substring. Iterating over all Dirac impulses (right to left, i.e., most likely PUF response to least likely one) results in the ranking of PUF responses necessary for (1) and (2).

Fig. 1

RMF of the distributions in Table 1 for selected values of $p,\;r$. The dashed line indicates the RMF for $p,\;r=0.5$

3.2 Convolution of Histograms for RMF

With longer substrings, i.e., more events per marginal distribution or many substrings being convoluted, the number of Dirac impulses can become inefficient to handle. However, accepting some reduction in accuracy, the RMF of each substring can be approximated by a histogram, as also shown in Fig. 2. Then, all outcomes whose log-probability falls into the same bin are approximated to occur with this bin’s central value. Designing the bin width allows us to adjust the approximation error. As Glowacz et al. [6] showed, the convolution of these histograms—more precisely the vectors of bin counts—approximates the histogram of the entire string if all histograms use the same bin width.

The example in Fig. 2 uses bin width $w=0.5$, and bins of marginal histograms are located to have an edge at an integer value. For the first substring, this produces the vector $\begin{pmatrix}1/2&0&0&0&1/2\end{pmatrix}$ with a central value of $-0.25$ for the rightmost bin. For the second substring, the vector is $\begin{pmatrix}\nicefrac {1}{4}&\nicefrac {1}{2}&0&\nicefrac {1}{4}\end{pmatrix}$ with a central value of $-1.25$ for the rightmost bin.⁴ After the convolution, the vector is $\begin{pmatrix}1/8&1/4&0&1/8&1/8&1/4&0&1/8\end{pmatrix}$ with a central value of $-1.5$ for the rightmost bin. Note that the bin width does not change by convolution, and the central value of the rightmost bin of the convoluted histogram equals the sum of the central values of the rightmost bins in the marginal histograms. Since the output vector grows linearly with the number of convoluted histograms, not exponentially as the number of Dirac impulses would, this approach remains feasible even for thousands of substrings, e.g., 1024 single-bit substrings that are necessary to evaluate the conditional min-entropy for polar codes.

Compared to a histogram after the convolution of the RMFs, which is shown by Dirac impulses in Fig. 2, the convolution of histograms in this example differs in the bin of the least probable event. This is because every event is approximated to occur with a log-probability equal to the corresponding bin’s central value. As shown by Glowacz et al. [6], the maximum error by this approach is $\nicefrac {j}{2}$ bins into each direction if j histograms have been convoluted.

Fig. 2

Convolution of RMF and histograms for a one-bit substring ($p_1=0.19$) and a two-bit substring ($p_2=0.36$)

3.3 Expected Conditional Min-Entropy Based on the RMF

The approximated RMF of the entire response string—obtained through the convolution of histograms of assumed independent substrings—provides a partitioning of $\mathcal {{X}}$ into a selectable number of bins. This is equivalent to the partitioning by Delvaux et al. [4], but more generally applicable. Each bin constitutes a group $\phi _j$ with $|\phi _j|$ events that—approximately—occur with log-probability $q_j$ respectively probability $p_j$. Therefore, the groups $\phi _j$ can be used the same way as the groups $\varphi _j$ from Section 2.3 to calculate the expected conditional min-entropy. So starting from the rightmost bin, as many bins as necessary are processed until $|\mathcal {E}|$ elements of $\mathcal {{X}}$ are collected. The negative logarithm of their sum then is the expected conditional min-entropy. This corresponds to (1) and (2). Note that this approach only requires knowledge about the statistics of individual bits or substrings of the response, where substrings may comprise an arbitrary number of possibly correlated bits. It is entirely independent of the PUF primitive.

3.4 Optimization of Error Bound

Convolving histograms rather than exact RMFs is an approximation. It is, therefore, crucial to consider the resulting error. Glowacz et al. [6] provided a general bound that assumes an error of half the bin width, but we can improve upon it. Only the rightmost bins are of interest for the expected conditional min-entropy. It is thus beneficial to minimize the approximation error in this area, even if it would cause larger errors in the leftmost bins. Histogram convolution only requires bins of equal width but not equal bin location. Thus, without restricting the applicability, the bins of each marginal histogram can be located so that the most probable event coincides with the central value of the rightmost bin. This reduces the approximation error to zero for each marginal distribution’s most probable event and the entire distribution’s most probable event. The error for less probable events increases the more events with non-zero approximation error contribute to them. For single bits, the maximum error increases proportionally to the response’s Hamming distance (HD) to the most probable response. To demonstrate this, we choose an example where an exact calculation is feasible, and the error is known. Figure 3 shows the difference in log-probability between exact calculation and histogram convolution for an exemplary 8-bit response, where $p_i\;\forall i \in \{1,\dots ,8\}$ is drawn independently from a uniform distribution between 0.1 and 0.9 and bin width $w=0.25$. Without bin alignment, the general error bound [6] holds, which is, in this case, $\pm 1$ for every response; hence, it is not depicted in Fig. 3. With our proposed alignment, the error bound decreases from the general case in the least probable bin toward zero for the most probable bin. Additionally, the actual observed errors are reduced.

Fig. 3

Difference in estimated log-probability between convolution of histograms and exact calculation, sorted by the HD to the most probable response. Dashed lines indicate the improved error bound by the alignment of bins

4 Results

In this section, we apply the concept of Section 3.3 to different linear ECCs. We incorporate the error term discussed in Section 3.4 to achieve a lower bound. If possible, we compare the results in this work with [4] and [5]. We also give results for the $n-k$ bound as a reference. Advancing over the results in [4, 5], this is the first work that can additionally analyze large codes in a scenario with locally biased PUF response bits. Therefore, it illustrates the impact of code selection when the underlying PUF exhibits bias effects. The problem with the methods in [4, 5] is the infeasibility of sorting sufficiently many PUF responses by their probability. This is because the respective groups become too small, and naively sorting, e.g., $2^{1024}$ PUF responses for the polar code is impossible in practice.

Experiments on Real Data with Local Bias Effects

The PUF data for the experiments are from SRAM PUFs on commercial XMC4500 microcontrollers [20, 21]. We assume that local bias is the predominant deficiency in this data set, and correlations, as illustrated in Table 1, are negligible [19]. Note that our approach does not depend on the PUF primitive or the amount of PUF data per device. It only requires information about the probability for single bits or small groups of correlated bits (cf. Section 3.3). For all codes, the bias for 10,240 bits is evaluated. The information about the bias stems from averaging each bit at a specific position over 144 devices.

As many code words as possible are fit into these 10240 bits, and the conditional min-entropy is computed for each one of them. For comparison, the average conditional min-entropy per message bit of all code words (of the same code) is taken for comparison.

Table 2 Conditional min-entropy for different error-correcting codes (n, k, t) as in [4, 5] and the convolution of histograms (bin width 0.001). The data is taken from SRAM PUFs ($\bar{H}_\infty (X)=0.74$) on commercial microcontrollers [20, 21]. A dash indicates that the method is not computationally feasible for the respective code length based on our own experiments. For a comparison, the results according to the $n-k$ bound [11] are included as well normalized to k

Table 2 summarizes the findings. The bin width for the convolution is set heuristically to 0.001. A smaller bin width would result in a higher accuracy of the entropy estimation at the cost of a longer runtime. A larger bin width would only be beneficial to speed up the computation if even longer codes than $n=1024$ would be considered. Each row represents an error-correcting code with its corresponding conditional min-entropy. The top part of the table evaluates the impact of different code parameters, such as the rate or overall length of the code. Note that these codes do not have the same error correction capability. In the context of code concatenation, evaluating one of its components (e.g., a (7, 1, 3) repetition code) is insufficient, but the resulting code has to be analyzed. Primarily, it is based on a serial code concatenation as in [22]. The lower part thus presents the findings for codes that are tailored toward PUF applications. They can derive a 128-bit key with an error probability of $<10^{-6}$ even if the bit error rate on the input side is $15\%$. These numbers are common when comparing error correction for PUFs [16].

The table features a (1024, 128) polar code as proposed in [15] and a concatenation of a (127, 64, 10) BCH code with a 7-repetition code as in [23]. In the latter case, two code words form one 128-bit key. (815, 128, 173) are theoretic code parameters with a code rate of 0.16 according to the Griesmer bound [24]:

$$\begin{aligned} n \ge \sum ^{k-1}_{i=0}\left\lceil \frac{d}{2^i} \right\rceil \end{aligned}$$

(5)

For a message length of $k=128$ and the constraints regarding bit error probability and desired key error probability, we find the smallest possible n. While not every error-correcting scheme is based on linear block codes, and by utilizing reliability information error correction beyond $d_{min}$ might be possible, this code rate still serves as a reference point and indicator of a PUF’s quality.

Table 2 shows the largest approximated min-entropy values for the approach in [4]. This is because by falsely assuming IID PUF bits, the approach by [4] does not hold for the given data set. It hence overestimates the min-entropy. Compared to [5], the min-entropy estimation based on the convolution of histograms results in slightly larger values. However, assuming that no correlations are in the data set, it is still a lower bound and thus closer to the actual value. Most importantly, it is also feasible for larger codes and thus codes relevant in the PUF context. In [5], computing the conditional min-entropy for a (127,8,31) BCH code required about 20 min on a commodity computer compared to 5 s with histogram convolution (with an Intel^® Core^™ i7-7600U CPU @ 2.8GHz × 4 cores and 16 GB RAM). For larger codes such as the (1024, 128) polar code, our approach requires 30 s whereas [4, 5] do not provide a bound for the min-entropy in feasible time based on our experiments re-implementing their methods for local bias effects. Even for smaller codes than $n=1024$, several days of computing [4, 5] did not provide a result on our commodity computer, and the computation was aborted. Furthermore, the results show that the $n-k$ bound is too pessimistic regarding the remaining entropy given helper data.

Fig. 4

Estimated $\bar{H}_\infty$ for different codes and rates. PUF-ECC denotes codes that achieve a 128-bit key error rate of less than $10^{-6}$: C for code concatenation of repetition and BCH code, P for polar code, and G for Griesmer bound

To put the results in a larger context and for a better comparison of the impact of code parameters, Fig. 4 visualizes the conditional min-entropy over the code rate for different codes. As a reference, the data on a bit level have an average min-entropy $\bar{H}_\infty (X)=0.74$, as indicated by the black horizontal line. It is computed by summing the min-entropy of each bit divided by the total amount of bits. Beyond what is provided in Table 2, repetition codes of lengths 3, 5, 7, and 21 are shown. The code parameters for the BCH codes are (7, 4, 1), (15, 5, 3), (31, 6, 7), (63, 7, 15), and (127, 8, 31). The figure also shows the results for the following (n, k) polar codes: (8, 3), (16, 4), (64, 12), (128, 16), (256, 32), (512, 64), (1024, 90), (1024, 128). Note that several polar codes have a rate of 0.125 and form a stack of blue lines close to marker P in Fig. 4. Of these codes with the same rate, the one with the shortest overall length, the (128, 16), has the highest $\bar{H}_\infty$.

While a higher $\bar{H}_\infty$ is beneficial, sufficient error correction capability is necessary. Therefore, Fig. 4 does not imply that, e.g., a 3-repetition code is more suitable for PUFs than, e.g., a (128, 16) polar code. Instead, Fig. 4 includes three exemplary codes labeled as PUF-ECC that achieve said error correction capability. They are the same codes as in the lower part of Table 2.

Experiments on Synthetic Data with Independent Groups of Correlated Bits

Illustrating the efficiency and efficacy of our approach to correlated data requires a large data set with known correlation effects. We enforce such correlation effects for a simulated PUF scenario by sampling RO frequencies and deriving the responses as the sign bit of an overlapping comparison: Instead of comparing RO frequencies as differences A–B, C–D, and E–F, in the overlapping comparison, differences like A–B, B–C, C–D, D–E, and E–F are taken. This way, more bits are derived from the same oscillators. However, neighboring bits are likely different, which corresponds to a negative correlation. This correlation effect has been studied for real data by Maiti et al. [25] in [26]. Unfortunately, the data set in [25] is too small to derive 1024 bits for a polar code (1024, 128). Hence, for this experiment, we replicate the effect of overlapping comparisons with synthetic data.

First, we sample random frequencies from a standard normal distribution. We then define the number of correlated bits $b=\#ROs-1$, i.e., how many bits are derived from a group of $\#ROs$ ring oscillators. $b=1$ means, e.g., that two ROs are compared, and no correlation exists; $b=4$ corresponds to comparing five frequencies in an overlapping manner so that four neighboring bits are pairwise correlated. To derive probability data as input to the convolution, we repeat this experiment as a Monte Carlo simulation and observe the $2^b$ probabilities for every possible resulting bit sequence. Asymptotically, each bit group has the same probability distribution regarding its bit sequences. However, to not necessitate each bit group having the same probability distribution, we determine the probability distributions individually for each bit group.

For the experiment, we set $b\in {1,2,4}$, and the amount of Monte Carlo simulations is $2^b \cdot 1000$ to ensure sufficient accuracy for the empirically determined probabilities. We evaluate our method using the aforementioned (1024,128) polar code as an ECC.

Table 3 Conditional min-entropy for independent subgroups of b correlated bits and a (1024,128) polar code

Table 3 compares the conditional min-entropy per message bit after the convolution of histograms with the actual min-entropy in the PUF. The deviation for $b=1$ from the ideal value of 1.0 appears by chance since there are extreme cases where the resulting zero/one probability is not exactly 0.5 for a bit. However, these extreme cases are the ones that determine the min-entropy. The results of this experiment provide three insights: First, the convolution of histograms is possible for a realistic setting of partially correlated PUF bits and practical code sizes. Second, as to be expected, the entropy per bit decreases already in the original PUF response the more overlapping comparisons are made, i.e., for increasing b. Third, this decrease in entropy is even more significant in the experiment after considering the helper data for the conditional min-entropy.

To put the results about overlapping comparisons into perspective, this means, e.g., for a (theoretical) array of 10,240 ring oscillators, that different amounts of effective entropy can be extracted. For $b=1$, we can extract $5\cdot (1024,128)$ codes; for $b=4$, we have more bits and thus more codewords: $8\cdot (1024)$. However, the remaining conditional min-entropy in the overall messages is nonetheless higher for $b=1$ (576bit) than for $b=4$ (102bit).

Discussion

From the experiments, we draw several conclusions. A higher code rate leads to an increased conditional min-entropy. This means that the smaller implementation complexity of concatenated codes comes at the price of a possibly lower security level: Due to combining two simpler individual codes, the resulting code rate is smaller than for a stand-alone code such as the polar code or optimally for the code based on the Griesmer bound. For the exemplary data, the average conditional min-entropy for a polar code is approximately twice the one for the code concatenation due to having a higher code rate (point P in Fig. 4 vs. point C). A higher code rate means an attacker has less knowledge (in the form of helper data) about the underlying secret. This shows that when designing a code for a practical scenario, the choice of the code significantly impacts the entropy given helper data and a non-ideal PUF.

If the code rate is the same for two codes, but they have different lengths (such as for the exemplary polar codes), this effect is similar. The additional attacker knowledge due to more helper data outweighs the additional information due to a longer underlying message. Thus, in principle, it might also be advantageous not only for a reduced implementation complexity but also for a higher min-entropy to split the key into several smaller chunks. But this does not necessarily result in improved security with regard to other attack vectors such as side-channel attacks. It might be easier for an attacker to focus on two 64-bit chunks instead of a single 128-bit one. While in other PUF scenarios, a different number of key bits might be required; the general observations remain the same as for our case with 128-bit: Regarding the conditional min-entropy, a higher code rate as provided by stand-alone codes is preferable.

Furthermore, based on the new approach of convolving histograms, we show that overlapping comparisons of ring oscillator frequencies exhibit a high decrease regarding conditional min-entropy. So, although an overlapping comparison is beneficial for extracting more bits in theory, the effectively extracted entropy is less than for a non-overlapping comparison.

5 Conclusion

Within this work, we have introduced an approach to bound and approximate the conditional min-entropy in a PUF-derived key given the helper data. Our approach is the first one which is feasible for practical code lengths and realistic PUF weaknesses. Such an evaluation method is essential to ensure security and for future certification approaches, which also have to support PUFs with non-ideal response statistics. The results of this work show that the approach can evaluate the key entropy in realistic scenarios. The results also point to a general finding: Concerning helper data leakage, short codes with a high rate are preferable. Both aspects emphasize that our approach is important to assess the security of constructions based on PUFs.