Description of magnetic field lines without arcana

Abstract

This work is based on the variational principle for magnetic field lines introduced in 1983 by Cary and Littlejohn. The action principles for magnetic field lines and for Hamiltonian mechanics are recalled to be analogous. It is shown that the first one can be rigorously proved from first principles without analytical calculations. Not only the action principles are analogous, but also a change of canonical coordinates is recalled to be equivalent to a change of gauge. Furthermore, using the vector potential makes obvious the freedom in the choice of “time” for describing Hamiltonian dynamics. These features may be used for a new pedagogical and intuitive introduction to Hamiltonian mechanics. In the context of confined magnetic fields, the action principle for magnetic field lines makes practical calculations simpler and safer, with an intuitive background and allowing to keep a high degree of generality, as shown in the practical example of the calculation of the width of a magnetic island, analytically derived without any need of abstract Fourier components and independently of the choice of coordinates. Moreover, a new formula provides explicitly the Boozer and Hamada magnetic coordinates from action-angle coordinates.

1 Introduction

Magnetized plasmas are ubiquitous in space and astrophysics, and are also artificially produced for the development of thermonuclear fusion by magnetic confinement. If the Larmor radius may be neglected, a low-energy charged particle follows a magnetic field line (B-line) in the absence of other forces. For finite Larmor radius, B-lines still strongly constrain the dynamics, especially if they wrap on nested toroidal magnetic surfaces, as usually wanted in developing fusion devices. This fact has generated a huge literature about these lines to describe both the case where they do lie on such surfaces, providing good confinement, and the case where they do not, bringing magnetic chaos and a related transport. In the fusion context, this topic is in particular of paramount interest for the control of edge localized modes by magnetic chaos in tokamaks (Kim et al. 2010; Canik et al. 2010; Kirk et al. 2010; Orlov et al. 2010), a relaxation phenomenon susceptible to harm ITER plasma facing components.

In this frame, this review paper shows how Hamiltonian mechanics tools can be applied to the study of magnetic fields principally in toroidal geometry. This is important, since a natural tendency for people interested in B-lines in a given device, is to describe them by using directly the magnetic field (D’haeseleer et al. 2012; Boozer 2005; White 2013, chapter 3 of Hazeltine and Meiss 1992), instead of the vector potential, that permits to deal with the magnetic field line problem in the frame of Hamiltonian mechanics. Unfortunately, overlooking the genuine Hamiltonian character of these lines often led to wrong results (8 wrong papers quoted in Park et al. 2008 and 6 in Kaleck 1999).

To the contrary, the review paper shows that working with the vector potential ${\textbf{A}}$ is very efficient, and, maybe surprisingly, simpler than using the magnetic field, which means also the use of general coordinate systems, and their covariant and contravariant representations of vectors in physical space, as done in D’haeseleer et al. (2012), Boozer (2005), White (2013), in chapter 3 of Hazeltine and Meiss (1992), and in section 3.4 of Kikuchi (2011) (also in an ICTP course (Kikuchi 2012) by the same author). This simplicity stems from the fact that the variational principle for B-lines is written with the vector potential (the Aharonov-Bohm effect in quantum mechanics further indicates the importance of ${\textbf{A}}$). The review starts with an innovative pedestrian, yet rigorous, derivation of B-line equations from this variational principle. Indeed, the action principle for B-lines can be proved from Stokes theorem applied to the circulation of ${\textbf{A}}$. This principle was sketched in equation (1.3) of the chapter by Morozov and L. S. Solov’ev in Sagdeev and Leontovich (1966). It was introduced four decades ago Cary and Littlejohn (1983) in the very educated language of noncanonical Hamiltonian mechanics, which probably did not help making it very popular, with the above-quoted negative consequences (for a more recent introduction, see chapter 9 of Hazeltine and Meiss 1992; Viana et al. 2023). This type of principle had already proved to be useful for the description of magnetohydrodynamics (Newcomb 1962)

Then the paper recalls the analogy of the action principle for B-lines and of that for Hamiltonian mechanics (Pina and Ortiz 1988). With beautiful formal aspects: not only the action principles are analogous, but also a change of canonical coordinates is shown to be equivalent to a change of gauge (Elsasser 1986). Furthermore, using the vector potential makes obvious the freedom in the choice of “time” for describing Hamiltonian dynamics. After introducing the above basic concepts, the paper proposes a methodology to minimize the work necessary to answer a theoretical or modeling problem about B-lines, analytically or numerically.

The tools introduced in the first part of the review are used in a second one to solve typical problems faced by people in the fusion community, as calculating the width of a magnetic island. The above-mentioned errors on treating resonant magnetic perturbations are explicitly corrected using an invariant magnetic flux, which is proportional to the magnetic flux through a ribbon whose edges are the B-lines related to the O and X points of the corresponding magnetic island. In turn, the island width can be expressed in terms of the latter flux, which provides the first expression of this width avoiding abstract Fourier components and obviously independent of the choice of coordinates. Simplifications result from substituting heavy approximate analytical calculations by simple numerical estimates provided by any validated computer code computing B-lines; in particular to compute the width of a magnetic island in a simpler way than previous work (Cary and Hanson 1991; Kaleck 1999; Bécoulet et al. 2008; Cahyna et al. 2009). Moreover, the action-angle formalism enables the derivation of a new simple formula providing explicitly the Boozer and Hamada coordinates, well-known in the fusion community.

While relying upon conceptual tools of modern theoretical physics, the review paper uses elementary mathematics, so as to be accessible to non-specialists and to experimentalists wanting to model their results; in particular, the symplectic structure underlying Hamiltonian mechanics (Arnol’d 2013) is only alluded to. Furthermore, most calculations are set in a series of appendices, so as to make the body of the review short and easily readable.

In contrast with other action principles, that for B-lines can be proved without any calculation. This suggests a natural spinoff. Thanks to the above-mentioned beautiful formal aspects and a generalization of the above method, the review paper proposes an alternative, intuitive, way to introduce Hamiltonian mechanics from B-lines “mechanics”. In particular, using the vector potential makes obvious the freedom in the choice of “time” and “energy” in the Hamiltonian description of mechanics.

In conclusion, this review paper promotes overlooked treasures about B-lines (essentially references (Cary and Littlejohn 1983; Pina and Ortiz 1988; Elsasser 1986)) to enable simple and safe practical calculations. There is some beauty in the approach, which may provide a new pedagogical and intuitive introduction to Hamiltonian mechanics. This review paper is organized as follows. Section 2 recalls the variational principle for magnetic field lines, and introduces a new derivation of it from first principles. Section 3 provides a translation of the principle into a Hamiltonian description by recalling that the action principles for magnetic field lines and for Hamiltonian mechanics are analogous. It also suggests a new pedagogical and intuitive introduction to these mechanics based on magnetic lines “mechanics”. Section 4 introduces action-angle coordinates for magnetic systems, which correspond to the classical magnetic coordinates. It derives a new explicit formula for those of Boozer and Hamada. Section 5 shows that the variational principle makes practical calculations about magnetic field lines simpler and safer, with an intuitive background. In particular, with a new analytical result: the width of a magnetic island is proportional to the square root of an invariant flux related to this island, the magnetic flux through a ribbon whose edges are the field lines related to the O and X points of the island. The same analytical calculation provides a simple way to compute numerically the width of a magnetic island. Also to apply Chirikov resonance overlap criterion. Section 6 provides the conclusion.

2 Variational principle for magnetic field lines

Magnetic field lines are usually viewed as a whole, possibly parametrized by a curvilinear abscissa. However, when computing one, it is convenient to consider this abscissa as a time, and the line as the orbit of a flow. A corresponding variational principle was introduced (Cary and Littlejohn 1983), which uses the action

$$\begin{aligned} S({\textbf{x}};{\textbf{x}}_0,{\textbf{x}}_1)& = {} \int _{{\textbf{x}}_0}^{{\textbf{x}}_1} {\textbf{A}}({\textbf{x}}) \cdot {\textrm{d}}{\textbf{x}}, \end{aligned}$$

(1)

$$\begin{aligned}& = {} \int _{\lambda _0}^{\lambda _1} \Big ( {\textbf{A}}[{\textbf{x}}(\lambda )] \cdot \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}\lambda } \Big ) {\textrm{d}}\lambda , \end{aligned}$$

(2)

where the integral runs between points ${\textbf{x}}_0$ and ${\textbf{x}}_1$ of a magnetic field line; Eq. (2) uses a curvilinear abscissa $\lambda$ and $\lambda _0$ and $\lambda _1$ are the abscissas of the end points ${\textbf{x}}_0$ and ${\textbf{x}}_1$.

In previous papers (Cary and Littlejohn 1983; Elsasser 1986), the variational principle for magnetic field lines was first postulated, and then proved to be right by showing one can derive from it the usual equations defining these lines; this is recalled in Sect. 2.2. However, Sect. 2.1 first provides a new intuitive, yet rigorous, proof of the principle using Stokes theorem, which avoids any calculation.

2.1 New intuitive physical approach using Stokes theorem

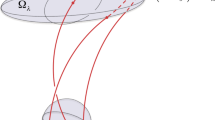
Figure 1a displays a blue segment L of magnetic field line bounded by points ${\textbf{r}}_1$ and ${\textbf{r}}_2$. It is weakly distorted into the green segment $L'$. The difference $\delta S$ between the actions computed for L and $L'$ corresponds to the circulation of the potential vector along the oriented circuit C indicated by red arrows. Stokes theorem implies that $\delta S$ is the magnetic flux across this circuit.

Fig. 1

A physical intuitive approach to the variational principle for magnetic field lines

Figure 1a also displays a flux tube $T_{\epsilon }$ with a small radius $\epsilon$ about L enclosing the weakly distorted segment $L'$. We assume this segment to make at most N turns about L. Since $L'$ is confined into $T_{\epsilon }$, the magnetic flux $\delta S$ across circuit C is smaller than N times the flux across $T_{\epsilon }$. The latter is of order $\epsilon ^2$. So is $\delta S$. Since $L'$ corresponds to a variation of L of order $\epsilon$, $\delta S$ is the second order in this variation. Therefore, S is stationary along any magnetic field line.

Figure 1b displays a blue segment L, which is not a magnetic field line. It intersects a magnetic field line at a point here named P. The segment $[{\textbf{r}}_3,{\textbf{r}}_4]$ of L includes P. Q is a point of the straight line passing per P and perpendicular to the plane defined by L and the tangent at P of the magnetic field line. The length of segment PQ (perpendicular to both L and the B-line) is assumed to be of order $\epsilon$. We define the green path made of the straight segment going from ${\textbf{r}}_3$ to Q and of the straight segment going from Q to ${\textbf{r}}_4$. The difference $\delta S$ between the actions computed for L and for its small perturbation going along the green path is again the circulation of the potential vector along the oriented circuit C indicated by red arrows. Stokes theorem implies that $\delta S$ is the magnetic flux across this circuit. Since L is not tangent to the field line at P, this flux is of order $\epsilon$, i. e. of the same order as the variation of L. Therefore, the action S is not stationary along any curve that does not coincide with a magnetic field line.

As a result of these discussions, action S is stationary on a path, if and only if it is a segment of a magnetic field line. This defines the stationary-action principle for magnetic field lines. We stress that the above discussions of Fig. 1a, b were performed with the usual assumption that the variation of the integration path vanishes at end points.

The first part of the proof is performed with a typical deformation $L'$. Some exceptional ones come with a vanishing $\delta S$ that does not give any information on the field line trajectory and are therefore not interesting for the proof of the variational principle. As an example, this is the case for a purely toroidal magnetic field and an $L'$ inside a surface made up of neighboring field lines. Such a vanishing $\delta S$ can also occur in the usual derivation of Euler–Lagrange equations by specific choices of displacements. Indeed, one can write

$$\begin{aligned} \delta S& = {} \int _{t_0}^{t_1} \delta L(\dot{{\textbf{q}}},{\textbf{q}},t) \, {\textrm{d}}t \end{aligned}$$

(3)

$$\begin{aligned}& = {} \int _{t_0}^{t_1} \Big [\frac{\partial L}{\partial {\textbf{q}}} \cdot \delta {\textbf{q}} + \frac{\partial L}{\partial \dot{{\textbf{q}}}} \cdot \delta \dot{{\textbf{q}}} \Big ] \, {\textrm{d}}t \end{aligned}$$

(4)

$$\begin{aligned}& = {} \int _{t_0}^{t_1} \Big [\frac{\partial L}{\partial {\textbf{q}}} \cdot \delta {\textbf{q}} + \frac{{\textrm{d}}}{{\textrm{d}}t} \Big (\frac{\partial L}{\partial \dot{{\textbf{q}}}} \cdot \delta {\textbf{q}} \Big ) - \frac{{\textrm{d}}}{{\textrm{d}}t} \frac{\partial L}{\partial \dot{{\textbf{q}}}} \cdot \delta {\textbf{q}} \Big ] \, {\textrm{d}}t \end{aligned}$$

(5)

$$\begin{aligned}& = {} \Big [ \frac{\partial L}{\partial \dot{{\textbf{q}}}} \cdot \delta {\textbf{q}} \Big ]_{t_0}^{t_1} + \int _{t_0}^{t_1} \Big [\frac{\partial L}{\partial {\textbf{q}}} - \frac{{\textrm{d}}}{{\textrm{d}}t} \frac{\partial L}{\partial \dot{{\textbf{q}}}} \Big ] \cdot \delta {\textbf{q}} \, {\textrm{d}}t \end{aligned}$$

(6)

$$\begin{aligned}& = {} \int _{t_0}^{t_1} \Big [\frac{\partial L}{\partial {\textbf{q}}} - \frac{{\textrm{d}}}{{\textrm{d}}t} \frac{\partial L}{\partial \dot{{\textbf{q}}}} \Big ] \cdot \delta {\textbf{q}} \, {\textrm{d}}t, \end{aligned}$$

(7)

where the fully integrated term in the penultimate equation vanishes because the displacements vanish at $t_0$ and $t_1$. The last equation shows that an appropriate choice of $\delta {\textbf{q}}$ can make the integral vanish even if the bracket is non-zero. However, the bracket must vanish if the integral is zero for any $\delta {\textbf{q}}$. This leads to Euler–Lagrange equations.

2.2 Previous derivations

The variational principle for magnetic field lines was first intuitively introduced without a proof in a 1966 paper by Morozov and L. S. Solovèv (equation (1.3) of Sagdeev and Leontovich 1966). The rationale was that a mass-less particle in a vanishing electric field follows magnetic field lines. Now, the action for this motion is the integral over time of ${\textbf{A}}.{\textbf{v}}$, where ${\textbf{v}}$ is the particle velocity. Setting ${\textrm{d}}{\textbf{x}} = {\textbf{v}} {\textrm{d}}t$ yields the action integral (1). Therefore, the principle can be intuitively deducted, while this is not generally the case for other variational principles.

Subsequent derivations introduce a curvilinear abscissa $\lambda$ and write the action as in Eq. (2),

$$\begin{aligned} S({\textbf{x}};{\textbf{x}}_0,{\textbf{x}}_1) = \int _{\lambda _0}^{\lambda _1} \Big ( {\textbf{A}}[{\textbf{x}}(\lambda )] \cdot \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}\lambda } \Big ) {\textrm{d}}\lambda , \end{aligned}$$

(8)

where $\lambda _0$ and $\lambda _1$ are the abscissas of the end points of the first integral.

The stationary action principle for the field line flow can then be written as

$$\begin{aligned} \delta S& = {} \delta \int _{{\textbf{x}}_0}^{{\textbf{x}}_1} {\textbf{A}}({\textbf{x}}) \cdot {\textrm{d}}{\textbf{x}} = 0 \end{aligned}$$

(9)

$$\begin{aligned}& = {} \delta \int _{\lambda _0}^{\lambda _1} \Big ( {\textbf{A}}({\textbf{x}}(\lambda )) \cdot \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}\lambda } \Big ) \, {\textrm{d}}\lambda = 0 \end{aligned}$$

(10)

with the usual requirement that the arbitrary variation $\delta {\textbf{x}}(\lambda )$ of the trajectory vanishes at the end points ${\textbf{x}}_0={\textbf{x}}(\lambda _0)$ and ${\textbf{x}}_1={\textbf{x}}(\lambda _1)$. If the stationary action principle holds, then magnetic field line equations must be derived from Eq. (10).

Cary and Littlejohn (1983) focused on the important practical case where $\lambda$ is one of the coordinates. Using general coordinates $x^i=(x^1,x^2,x^3)$, say $\lambda = x^3$ (for instance the toroidal angle in a tokamak). Then, (10) becomes

$$\begin{aligned} 0& = {} \delta \int _{x^3_0}^{x^3_1} {\textrm{d}}x^3 \, L\left( {\textbf{x}}, \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}x^3}, x^3\right) \end{aligned}$$

(11)

$$\begin{aligned} L\left( {\textbf{x}}, \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}x^3}, x^3\right)& = {} A_{1}({\textbf{x}}) \, \frac{{\textrm{d}}x^{1}}{{\textrm{d}}x^3} + A_{2}({\textbf{x}}) \, \frac{{\textrm{d}}x^{2}}{{\textrm{d}}x^3} +A_{3}({\textbf{x}}) = A_i({\textbf{x}}) \, \frac{{\textrm{d}}x^{i}}{{\textrm{d}}\lambda }, \end{aligned}$$

(12)

where the form of the Lagrangian of the magnetic system is emphasized. The last expression of Eq. (12) writes the Lagrangian in a more compact form using the covariant components $A_i={\textbf{A}} \cdot {\textbf{e}}_i$ of the vector potential and Einstein’s convention of summation over repeated indices. The corresponding Euler–Lagrange equations, solution of the stationary principle $\delta S =0$, are

$$\begin{aligned} \frac{\partial L}{\partial x^j} - \frac{{\textrm{d}}}{{\textrm{d}}x^3} \frac{\partial L}{\partial ({\textrm{d}}x^{j}/ {\textrm{d}}x^3)}=0, \quad j=1,2. \end{aligned}$$

(13)

If the $x^i$’s are Cartesian coordinates, these equations yield

$$\begin{aligned} \frac{{\textrm{d}}x^{1}}{B^1}= \frac{{\textrm{d}}x^{2}}{B^2}=\frac{{\textrm{d}}x^3}{B^{3}}, \end{aligned}$$

(14)

which are the equations defining the magnetic field lines from the contravariant components of the magnetic field, defined as $B^i={\textbf{B}} \cdot \nabla x^i$, since Eq. (14) are equivalent to the condition of collinearity between the velocity vector ${\textrm{d}}{\textbf{x}}/ {\textrm{d}}\lambda$ and ${\textbf{B}}$. This proves that magnetic field line equations can indeed be derived from principle (9) or (10). Equations (14) are valid in any coordinate system, not only in Cartesian coordinates. In deriving them from Eqs. (12) and (13), the general relation that links the covariant components $A_i$ of the vector potential and the contravariant ones of the magnetic field in any coordinate system must be used. Extended calculations can be found in Appendix 1.

Elsasser (1986) proved again the validity of the variational principle for magnetic field lines showing in an algebrical way that Eq. (10) is true if and only if

$$\begin{aligned} \Big ( \nabla \times {\textbf{A}} \Big ) \times \frac{{\textrm{d}}{\textbf{x}}(\lambda )}{{\textrm{d}}\lambda } = 0 \end{aligned}$$

(15)

which means that ${\dot{\textbf{x}}} \equiv {\textrm{d}}{\textbf{x}} / {\textrm{d}}\lambda$ is parallel to ${\textbf{B}}=\nabla \times {\textbf{A}}$, as required for magnetic field lines. Following his proof, and considering the fields always taken at ${\textbf{x}}={\textbf{x}}(\lambda )$ even when this is not explicitly stated,

$$\begin{aligned} 0& = {} \delta \int _{\lambda _0}^{\lambda _1} {\textrm{d}}\lambda \; \Big [ {\textbf{A}}(\mathbf {x(\lambda )}) \cdot {\dot{\textbf{x}}(\lambda )} \Big ] \end{aligned}$$

(16)

$$\begin{aligned}& = {} \int _{\lambda _0}^{\lambda _1} {\textrm{d}}\lambda \; \Big [ \Big (\delta {\textbf{x}}\cdot \nabla \Big ) \Big ( {\textbf{A}} \cdot {\dot{\textbf{x}}} \Big ) + {\textbf{A}} \cdot \delta {\dot{\textbf{x}}} \Big ]_{{\textbf{x}}={\textbf{x}}(\lambda )} \end{aligned}$$

(17)

$$\begin{aligned}& = {} \int _{\lambda _0}^{\lambda _1} {\textrm{d}}\lambda \; \Big [ \nabla ({\textbf{A}} \cdot {\dot{\textbf{x}}}) - ( {\dot{\textbf{x}}} \cdot \nabla ) {\textbf{A}} \Big ]_{{\textbf{x}}={\textbf{x}}(\lambda )} \cdot \delta {\textbf{x}}(\lambda ) \end{aligned}$$

(18)

Therefore, for arbitrary variations $\delta {\textbf{x}}(\lambda )$,

$$\begin{aligned} 0& = {} \Big [ \nabla ({\textbf{A}} \cdot {\dot{\textbf{x}}}) - ({\dot{\textbf{x}}} \cdot \nabla ) {\textbf{A}} \Big ]_{{\textbf{x}} = {\textbf{x}}(\lambda )}\end{aligned}$$

(19)

$$\begin{aligned}& = {} {\dot{\textbf{x}}} \times \Big [ \nabla \times {\textbf{A}} \Big ]_{{\textbf{x}} = {\textbf{x}}(\lambda )} \end{aligned}$$

(20)

This shows that the variational principle stated in Eq. (10) leads to Eq. (15) as Euler equation, ending the proof. The function ${\textbf{A}}({\textbf{x}})$ is considered fixed, but the argument ${\textbf{x}}$ must be varied independently of $\lambda$ with vanishing variations $\delta {\textbf{x}}(\lambda )$ at the end points $\lambda =\lambda _1, \lambda _2$. A partial integration brings from Eqs. (17) to (18), considering also interchanging $\delta$ and the derivative with respect to $\lambda$.

3 Translation into a Hamiltonian description

In Sect. 2 the existence of a variational principle for magnetic field lines was proved. Here, Sect. 3.1 recalls the equivalence between the variational principle for magnetic field lines and that for their Hamiltonian mechanics showing that magnetic field lines in physical space are analogous to the flow of a dynamical system with one degree of freedom in phase space. The identification between canonical variables (p, q, t) and magnetic ones follows, intending for magnetic variables the space coordinates ${\textbf{x}}$ and the covariant components of the vector potential ${\textbf{A}}$. Section 3.2 recalls then the equivalence between canonical and gauge transformations. To conclude, going beyond the physical meaning of magnetic fluxes and field lines, Sect. 3.3 proposes a way of teaching Hamiltonian mechanics from magnetic lines “mechanics”.

3.1 Equivalence between the variational principles for magnetic field lines and for their Hamiltonian mechanics

The possibility of a Hamiltonian description of magnetic field line is intuitively natural, since the conservation of magnetic flux is analogous to that of phase space volume (Liouville theorem). It was introduced more than 70 years ago (Kruskal 1952; Kerst 1962; Gelfand et al. 1962; Whiteman 1977; Boozer 1983; Cary and Littlejohn 1983). It is at the root of a large contribution of plasma physics to Hamiltonian mechanics (Escande 2018).

This section shows the equivalence between the variational principle for magnetic field lines in physical space expressed in Eq. (9) and that for their Hamiltonian dynamics in phase space, obtaining the identification between canonical and magnetic variable as proved by Pina and Ortiz (1988).

The canonical equations of a N degree of freedom mechanical system can be derived from the variational principle, where $\dot{{\textbf{q}}}={\textrm{d}}{\textbf{q}} / {\textrm{d}}t$,

$$\begin{aligned} 0& = {} \delta \int _{t_0}^{t_1} L(\dot{{\textbf{q}}},{\textbf{q}},t) {\textrm{d}}t = \delta \int ({\textrm{d}}S) \end{aligned}$$

(21)

$$\begin{aligned} L(\dot{{\textbf{q}}},{\textbf{q}},t)& = {} \Big [{\textbf{p}} \cdot \dot{{\textbf{q}}} - H({\textbf{p}},{\textbf{q}},t) \Big ] \end{aligned}$$

(22)

Or, equivalently,

$$\begin{aligned} 0& = {} \delta \int _{t_0}^{t_1} \Big [{\textbf{p}} \cdot {\textrm{d}}{\textbf{q}} - H({\textbf{p}},{\textbf{q}},t) {\textrm{d}}t \Big ] \end{aligned}$$

(23)

where $({\textbf{p}},{\textbf{q}})$ are the canonical variables (N-vectors), $L(\dot{{\textbf{q}}},{\textbf{q}},t)$ the Lagrangian and $H({\textbf{p}},{\textbf{q}},t)$ the Hamiltonian of the system. The differential of the action, $dS = [{\textbf{p}} \cdot {\textrm{d}}{\textbf{q}} - H({\textbf{p}},{\textbf{q}},t) {\textrm{d}}t]$ is called Poincaré-Cartan integral invariant (Arnol’d 2013). Indeed, the corresponding Euler–Lagrange equation, solution of (21) or (23),

$$\begin{aligned} \frac{\partial L}{\partial {\textbf{q}}} - \frac{{\textrm{d}}}{{\textrm{d}}t} \frac{\partial L}{\partial \dot{{\textbf{q}}}} =0 \end{aligned}$$

(24)

yields the canonical equations of motion in phase space:

$$\begin{aligned} \frac{{\textrm{d}}{\textbf{q}}}{{\textrm{d}}t}& = {} \frac{\partial H}{\partial {\textbf{p}}} \end{aligned}$$

(25)

$$\begin{aligned} \frac{{\textrm{d}}{\textbf{p}}}{{\textrm{d}}t}& = {} - \, \frac{\partial H}{\partial {\textbf{q}}}. \end{aligned}$$

(26)

In the same way, as proved in Sect. 2, magnetic field line equations can be derived from the variational principle (9), that we now write in an arbitrary coordinate system ${\textbf{x}}=(x^1, x^2, x^3)$ as

$$\begin{aligned} 0 = \delta \int A_i {\textrm{d}}x^i \quad . \end{aligned}$$

(27)

This expression uses the classical covariant expression of the dot product and Einstein convention of summation over repeated indexes ($i = 1,2,3$). The vector potential is always defined up to a gauge transformation defined by $A_i \mapsto A'_i = A_i+\partial _iG$ (or ${\textbf{A}} \mapsto \mathbf {A'}={\textbf{A}} + \nabla G$) where G is an arbitrary scalar function of the spatial coordinates, being ${\textbf{B}}=\nabla \times {\textbf{A}}=\nabla \times \mathbf {A'}$. Since an axial gauge, for which $A_i=0$ for one of the indexes, can be always chosen, one term in the sum of Eq. (27) can be killed. Here we take $A_1=0$. Then, principle (27) becomes

$$\begin{aligned} {\textrm{d}}S& = {} A_2 \, {\textrm{d}}x^2 + A_3 \, {\textrm{d}}x^3, \end{aligned}$$

(28)

$$\begin{aligned} 0& = {} \delta \int ({\textrm{d}}S) \quad . \end{aligned}$$

(29)

With the choice of an axial gauge, principle (27) for magnetic field lines has the same structure as principle (23) for $N=1$ degree of freedom mechanical system. Therefore, one can identify canonical and magnetic variables. Going back to the particular choice $A_1=0$, from $p {\textrm{d}}q - H {\textrm{d}}t = \alpha (A_2 {\textrm{d}}x^2 + A_3 {\textrm{d}}x^3$) the identifications result:

$$\begin{aligned} p& = {} \alpha \, A_2(x^1,x^2,x^3) \end{aligned}$$

(30)

$$\begin{aligned} q& = {} x^2 \end{aligned}$$

(31)

$$\begin{aligned} H(p,q,t)& = {} - \, \alpha \, A_3(x^1,x^2,x^3) \end{aligned}$$

(32)

$$\begin{aligned} t& = {} x^3 \end{aligned}$$

(33)

where $\alpha$ is an arbitrary constant. The relation $p = \alpha \,A_2(x^1,x^2,t)$ must be inverted (possibly only locally) in order to write $x^1 = x^1(x^2, p, t)$, and therefore the Hamiltonian as a function of the canonical variables, $H=H(p,q,t)$.

A mere change of the indices of the coordinates enables us to deal with gauge $A_2=0$ or $A_3=0$. Therefore, we anticipate the important result discussed in the next section, that different choices of gauge correspond to different sets of canonical variables. Moreover, the freedom in the definition of a Hamiltonian for magnetic field lines is even larger since coordinates 2 and 3 can be exchanged in Eq. (28) defining a dynamics where the new Hamiltonian corresponds to the previous $- p$, the new p is the previous $-H$, the new time is q, and the new q is t. This highlights an aspect of the freedom in the definition of a Hamiltonian for magnetic field lines: the canonical momentum p and the Hamiltonian can exchange their role, which corresponds to inverting the roles of $p \, {\dot{q}}$ and $- H$ in Eq. (22) or of $p \, {\textrm{d}}q$ and $H \, {\textrm{d}}t$ in Eq. (23). With a caveat, yet: an arbitrary choice of time does not guarantee magnetic field lines to be fully parametrized by such a time. A full parametrization requires a “reasonable” choice of coordinates, for instance some kind of toroidal angle in a tokamak or a stellarator, and of poloidal angle in a reversed field pinch must be used as a time. This limits the freedom in the choice of the Hamiltonian and therefore in the identifications between canonical and magnetic coordinates.

This derivation of a Hamiltonian for B-lines is shorter and simpler than the standard one in Boozer (2005). Indeed, the latter requires to compute with coordinates, to introduce a symplectic form of the magnetic field for specific ones, and to prove orthogonality properties of the covariant and contravariant basis vectors. Finally, the present derivation uses a variational principle with an intuitive physical basis, while providing a way of generating a Hamiltonian for field lines in very general coordinates.

3.2 Equivalence between change of gauge and of canonical transformation

The previous section shows that different choices of gauge correspond to different sets of canonical variables. In reality, the link between gauge and canonical variables is stronger. This section shows that gauge transformations are nothing but canonical transformations, as proved by Elsasser (1986).

First of all, we show that Hamiltonian flows are independent not just of canonical transformation of coordinates, but also of gauge transformation. Identification (30)–(33) implies a new way to write the Lagrangian in (22):

$$\begin{aligned} \alpha (A_2 \, \dot{x^2} + A_3 \, \dot{x^3}) = p {\dot{q}} - H(p,q,t). \end{aligned}$$

(34)

where $\dot{x^i}= {\textrm{d}}x^i / {\textrm{d}}t$ with the identification $t=x^3$. We remind that identifications (30)–(33) assume the gauge $A_1=0$, so in the left-hand side of the last equation $A_1$ is absent because of the chosen axial gauge. Note moreover that $\dot{x^3}= {\textrm{d}}t / {\textrm{d}}t =1$. Under a gauge transformation, the vector potential transforms as

$$\begin{aligned} {\textbf{A}}\mapsto & {} {\textbf{A}}+\nabla G \end{aligned}$$

(35)

$$\begin{aligned} A_{i}\mapsto & {} A_{i} + \frac{\partial G}{\partial x^{i}} \end{aligned}$$

(36)

where function $G({\textbf{x}})$ is a scalar, and $\nabla G$ is its gradient. Then, if a change of gauge is applied, the Lagrangian in Eq. (34) becomes

$$\begin{aligned} \alpha (A_2 \, \dot{x^2} + A_3 \, \dot{x^3} + \frac{\partial G}{\partial x^i} \dot{x^i}) = p {\dot{q}} - H(p,q,t) + \alpha \frac{{\textrm{d}}G}{{\textrm{d}}t}, \end{aligned}$$

(37)

where the summation over partial derivatives of G of the left-hand side is written in a more compact form on the right-hand side. So a gauge transformation adds to the Lagrangian the total derivative of a scalar function G, and to the Poincaré-Cartan form the total differential ${\textrm{d}}G$ of the same function. Both variational principles (23) and (27) are therefore not affected by gauge transformations (due to the vanishing variation of the position at the boundaries, $\delta G =0$), and so are not canonical equations of motion and magnetic field line equations.

To show the equivalence between gauge and canonical transformations, we now apply the same gauge transformation, defined by the function $G({\textbf{x}})$, before and after the canonical transformation $(p,q,t) \mapsto (P,Q,t)$ defined by

$$\begin{aligned} p=\frac{\partial F}{\partial q} , \; P=\frac{\partial F}{\partial Q} , \; H'=H+\frac{\partial F}{\partial t} \quad , \end{aligned}$$

(38)

where F is an arbitrary function of (q, Q, t) (see Appendix 2 for the definition of a canonical transformation). This means performing the gauge transformation in the (p, q) coordinates with G(p, q, t) and the gauge transformation in the (P, Q) coordinates with G(P, Q, t):

$$\begin{aligned} p {\dot{q}} - H(p,q,t) + \alpha \frac{{\textrm{d}}G(p,q,t)}{{\textrm{d}}t} = P {\dot{Q}} - H'(P,Q,t) +\frac{{\textrm{d}}F(q, Q, t)}{{\textrm{d}}t} + \alpha \frac{{\textrm{d}}G(P,Q,t)}{{\textrm{d}}t}. \end{aligned}$$

(39)

We now link the canonical transformation and the subsequent gauge transformation by

$$\begin{aligned} F(q,Q,t) + \alpha G[P(q,Q,t), Q, t] =0 \end{aligned}$$

(40)

where P(q, Q, t) is defined by Eq. (38). Equation (39) becomes

$$\begin{aligned} p {\dot{q}} - H(p,q,t) + \frac{{\textrm{d}}G(p,q,t)}{{\textrm{d}}t} = P {\dot{Q}} - H'(P,Q,t). \end{aligned}$$

(41)

This means that G[P(q, Q, t), Q, t] is the generating function of the reciprocal canonical transformation

$$\begin{aligned} (P,Q)\mapsto & {} (p,q) \end{aligned}$$

(42)

$$\begin{aligned} H'\mapsto & {} H. \end{aligned}$$

(43)

Therefore, Eq. (40) enables the two-way translation of any gauge transformation into a canonical one.

3.3 Teaching Hamiltonian mechanics from magnetic lines “mechanics”

A typical textbook of classical mechanics starts with Newton’s laws, introduces the energy as the sum of a kinetic and a potential part, and then the variational principle with a Lagrangian, which is the difference between these two parts. Then the Hamiltonian is introduced as energy, the sum of these two parts, and the canonical equations of motions are derived from the corresponding expression of the Lagrangian (Eqs. (21) and (22)). This sets in the mind of students that, in Hamiltonian mechanics, the Hamiltonian is the energy, and ${\textbf{p}}$ is a momentum. In reality, the version of the variational principle provided by Eq. (23) uses the Poincaré-Cartan integral invariant

$$\begin{aligned} {\textbf{p}} \cdot {\textrm{d}}{\textbf{q}} - H({\textbf{p}},{\textbf{q}},t) {\textrm{d}}t, \end{aligned}$$

(44)

whose scalar components may be swapped (Arnol’d 2013). Therefore, any $p_i$ may be taken as the Hamiltonian and $q^i$ as the time. Furthermore, another invariant can be obtained by subtracting ${\textrm{d}}({\textbf{p}} \cdot {\textbf{q}})$ to the first one, $- {\textrm{d}}({\textbf{p}} \cdot {\textbf{q}}) - H {\textrm{d}}t$, which enables any $q^i$ to be taken as the Hamiltonian and $p_i$ as the time. This flexibility is very useful. For instance for the description of the motion of electrons in a traveling wave tube, where it is convenient to use the position along the tube as time (Ruzzon et al. 2012). It was essential to the development of neo-adiabatic theory, which deals with the jumps of an adiabatic invariant at slow separatrix crossings (see section 8.1 of Escande 2018 and references therein).

If, in contrast with what is done in Sect. 3.1, the variational principles for magnetic field lines is introduced first, and then that for their Hamiltonian mechanics, the above flexibility for the choice of Hamiltonian is obvious, since it stems from the arbitrariness in the choice of coordinates for describing the vector potential. Furthermore, the action principle for the magnetic field lines can be introduced in the pedestrian way of section 2.1 without calculations, while that for Hamiltonian mechanics is more abstract and requires analytical calculations. Finally, the somewhat abstract change of canonical coordinates can be made more concrete by showing it is nothing but a change of gauge (Sect. 3.2).

This suggests teaching Hamiltonian mechanics from magnetic lines “mechanics”. The Poincaré-Cartan integral invariant would be first introduced for a one-degree-of-freedom time-dependent Hamiltonian and then generalized to higher dimensions.

4 Action-angle coordinates for magnetic systems

This section focuses on toroidal magnetic configurations for magnetic confinement like the tokamak, the stellarator and the reversed field pinch. We first introduce a general expression of the potential vector using the toroidal and poloidal fluxes, whose complete derivation can be found in Appendix 4. Then, we specify the case where the magnetic field is regular, i.e. where there are conserved magnetic flux surfaces on which magnetic field lines flow. This corresponds to the case of a time-independent Hamiltonian and bounded energy surfaces. We introduce corresponding action-angle variables, called magnetic coordinates in the fusion context. For the sake of completeness, a general derivation of action-angle variables for any one-degree-of-freedom Hamiltonian system is provided in Appendix 3. We then show that the Boozer and Hamada magnetic coordinates used to describe MHD equilibria can be explicitly computed using the action-angle formalism.

4.1 Explicit magnetic fluxes

For the tokamak, the stellarator and the reversed field pinch, one can use the natural cylindrical coordinates $(r, \theta , \varphi )$, but other poloidal and toroidal angles may be more convenient to emphasize the symmetries of the system. For instance, if there is a helical symmetry or quasi-symmetry with poloidal and toroidal periodicity ($m_0,n_0$), the helical angle $u=m_0 \theta - n_0 \varphi$ may be used instead of $\theta$. In the general ${\textbf{x}}=(r, \theta , \varphi )$ coordinates, the potential vector can be written as

$$\begin{aligned} {\textbf{A}} = \psi _t \, \nabla \theta / 2 \pi - \psi _p \, \nabla \varphi / 2 \pi . \end{aligned}$$

(45)

and the corresponding magnetic field, ${\textbf{B}} =\nabla \times {\textbf{A}}$, as

$$\begin{aligned} {\textbf{B}} = \nabla \psi _t \times \nabla \theta / 2 \pi - \nabla \psi _p \times \nabla \varphi / 2 \pi , \end{aligned}$$

(46)

which is a formulation, called canonical form, valid for any divergence-free field on a torus. Here $\psi _t$ is a toroidal magnetic flux, i. e. the magnetic field integrated over the cross section of a constant-$\psi _t$ torus; $\psi _p$ is a poloidal magnetic flux, i. e. the poloidal flux that goes through the hole in a constant-$\psi _p$ torus. These two types of tori do not need to be identical and in general $\psi _t=\psi _t({\textbf{x}})$ and $\psi _p=\psi _p({\textbf{x}})$ can define different surfaces for a constant $\psi _t$ and a constant $\psi _p$. These fluxes define the same flux surfaces if the magnetic field is regular (i.e. if there are magnetic flux surfaces), and magnetic field lines wrap on sets of nested tori. In this case $\psi _t=\psi _t(\psi _p)$ and each of the two magnetic fluxes can be used as the radial variable which identifies magnetic flux surfaces, instead of the generic cylindrical coordinate r. The definition of the coordinate system in which $\psi _t=\psi _t(\psi _p)$ (named action-angle system) is given in the next section and more discussion on the physical meaning of magnetic fluxes can be found in Appendix 4, as well as the way to go from a classical formula for tokamak magnetic field to our Eq. (45). From here on, the case of a one to one relation between fluxes will be emphasized by the use of capital letters in indices, $\psi _T$ and $\psi _P$.

In the following, we take the toroidal flux as the radial coordinate, playing the role of the canonical momentum, as generally done for the tokamak and the stellarator. Then the poloidal flux is intended as a function of $(\psi _t, \theta , \varphi )$ (or $\psi _T$ in the case of a regular magnetic field configuration), implying a change of coordinates from $(r, \theta , \varphi )$. $\theta$ and $\varphi$ are arbitrary poloidal and toroidal angles, except for the requirement ${\textbf{B}} \cdot \nabla \varphi \ne 0$, in order to be able to use $\varphi$ to follow a given magnetic field line. Note that this condition is also required to define a good change of coordinates, with a non-zero Jacobian, from the $(r, \theta , \varphi )$ to $(\psi _t, \theta , \varphi )$ coordinates. Indeed, from Eq. (46), $2 \pi {\textbf{B}} . \nabla \varphi = \nabla \psi _t . (\nabla \theta \times \nabla \varphi )$, and the latter quantity is the inverse of the Jacobian of the change of coordinates from Cartesian ones to $(\psi _t, \theta , \varphi )$, as can be shown for instance by using successively equations (A4), (A7), and (A2) of Boozer (2005).

We note that, because of toroidal field reversal, the choice of the toroidal flux as a radial coordinate is not a good choice for the magnetic field of a reversed field pinch: the opposite choice must be done, choosing the poloidal coordinate as the radial coordinate, but all the following calculations can be trivially rephrased.

4.2 Magnetic or action-angle coordinates

Conserved flux surfaces have their equivalent in the bounded constant energy surfaces of a time-independent Hamiltonian. In the case of a regular magnetic field, therefore, new angle variables can be defined exploiting the symmetries of the system, having their equivalent in the action-angle coordinates of a Hamiltonian system. We remind here that in the following we use the toroidal flux as radial coordinate, and the general poloidal and toroidal $(\theta , \varphi )$ angle coordinates to start with.

We use equivalence (30)–(33), coming from the choice of the axial gauge $A_1=0$, between canonical and magnetic coordinates, and here reported using also the magnetic fluxes according to expression (45),

$$\begin{aligned} p& = {} \alpha A_2 = \psi _t \end{aligned}$$

(47)

$$\begin{aligned} q& = {} x^2 = \theta \end{aligned}$$

(48)

$$\begin{aligned} H& = {} - \alpha A_3 = \psi _p(\psi _t, \theta , \varphi ) \end{aligned}$$

(49)

$$\begin{aligned} t& = {} x^3 = \varphi \end{aligned}$$

(50)

where we assume $\alpha = 2\pi$. We now assume that the $A_i$’s (i.e. the fluxes) do not depend on $x^3 = \varphi$, which makes the Hamiltonian time-independent. In agreement with the Eqs. (47)–(50), we take $x^2 = \theta$, and $H(\psi _t, \theta ) = \psi _p(\psi _t, \theta )$. Then, this enables us to define $\psi _t(E,\theta )$ by inverting $E = H(\psi _t, \theta )$.

Then, we define action-angle variables $(\psi _T,\zeta )$ for the magnetic system, using their definition given by Eqs. (110) and (118), which yields

$$\begin{aligned} \psi _T (E)& = {} \frac{1}{2 \pi } \oint \psi _t(E, \theta ) \, {\textrm{d}}\theta \end{aligned}$$

(51)

$$\begin{aligned} G(\theta , \psi _T)& = {} \int _{\theta _0}^{\theta } \psi _t[E(\psi _T ), \theta '] \, {\textrm{d}}\theta ' \end{aligned}$$

(52)

$$\begin{aligned} \zeta (\theta , \psi _T)& = {} \frac{\partial G}{\partial \psi _T} = \int _{\theta _0}^{\theta } \frac{\partial \psi _t[E(\psi _T ), \theta ']}{\partial \psi _T} \, {\textrm{d}}\theta '. \end{aligned}$$

(53)

Identifications (47)–(50), valid for the general $(p,q,t)=(\psi _t, \theta , \varphi )$ toroidal coordinates, can now be written for action-angle variables $(P,Q,t)=(\psi _T, \zeta , \varphi )$:

$$\begin{aligned} P& = {} \alpha A_{\zeta } = \psi _T \end{aligned}$$

(54)

$$\begin{aligned} Q& = {} x^2 = \zeta \end{aligned}$$

(55)

$$\begin{aligned} H& = {} - \alpha A_{\varphi } = \psi _P(\psi _T) = E(\psi _T) \end{aligned}$$

(56)

$$\begin{aligned} t& = {} x^3 = \varphi \end{aligned}$$

(57)

again assuming $\alpha = 2\pi$.

Equation of motion (119) defines the constancy of $\psi _T$ on each flux surface, whereas Eq. (120) provides the equation defining the magnetic field lines:

$$\begin{aligned} \frac{{\textrm{d}}\psi _T}{{\textrm{d}}\varphi }& = {} 0 \end{aligned}$$

(58)

$$\begin{aligned} \frac{{\textrm{d}}\zeta }{{\textrm{d}}\varphi }& = {} \iota (\psi _T) = \frac{{\textrm{d}}\psi _P}{{\textrm{d}}\psi _T}. \end{aligned}$$

(59)

This implies that, when using action-angle coordinates, both magnetic fluxes (the action and the Hamiltonian of the system) are constant  of the motion, i.e. are constant on magnetic flux surfaces. Moreover, magnetic field lines written in action-angle coordinates are straight lines in the $(\zeta , \varphi )$ plane. Therefore, action-angle coordinates are the well-known magnetic coordinates, named also flux or straight-field-line coordinates in the fusion community. The frequency $\iota$ is called the rotational transform. Its inverse is called safety factor, usually indicated with the symbol q (we avoid using it to avoid any confusion with a canonical variable). Both $\iota$ and its inverse, as well as the magnetic fluxes, can be used to label magnetic flux surfaces.

According to identifications (54)–(57), the vector potential can be written in a way similar to (45), but for magnetic coordinates ${\textbf{x}}=(\psi _T, \zeta , \varphi )$

$$\begin{aligned} 2 \pi \, {\textbf{A}} = \psi _T \, \nabla \zeta - \psi _P \, \nabla \varphi \end{aligned}$$

(60)

where $\psi _P=\psi _P(\psi _T)$. With respect to Eq. (45), constant fluxes on magnetic flux surfaces are used, the toroidal angle $\varphi$ is kept fixed, but the poloidal angle $\theta$ is substituted for the “straight” poloidal angle $\zeta$.

We are now interested in a change in magnetic coordinates from $(\psi _T, \zeta , \varphi )$ to $(\psi _T, \zeta _N, \varphi _N)$. For convenience for the following calculations, we define it implicitly by

$$\begin{aligned} \zeta& = {} \zeta _N + f(\psi _T,\zeta _N, \varphi _N), \end{aligned}$$

(61)

$$\begin{aligned} \varphi& = {} \varphi _N + g(\psi _T,\zeta _N, \varphi _N), \end{aligned}$$

(62)

where both poloidal and toroidal angle are transformed and f and g are arbitrary functions on each flux surface. The toroidal flux coordinate is therefore kept constant in this change. Setting these expressions for $\zeta$ and $\varphi$ into Eq. (60), we find the relations between the functions f and g so that $(\zeta _N, \varphi _N)$ are magnetic coordinates, which means ${\textbf{A}}$ can be written as in (60) also in the new coordinates. It results in

$$\begin{aligned} 2 \pi {\textbf{A}}& = {} \psi _T \, \nabla \zeta _N - \psi _P \, \nabla \varphi _N + F, \end{aligned}$$

(63)

$$\begin{aligned} F& = {} \nabla (f \psi _T - g \psi _P) + (\iota g - f) \nabla \psi _T. \end{aligned}$$

(64)

Of course ${\textbf{A}}$ is defined up to a gauge, defined in Eq. (35). In order for F to be a gradient, $\iota g - f$ must be a function of $\psi _T$. We call it $h(\psi _T)$. If F is a gradient, a change of gauge can be performed by adding its opposite in Eq. (63), which yields Eq. (60) written for the $(\zeta _N, \varphi _N)$ magnetic coordinates. Therefore, Eqs. (61)–(62) define a change of magnetic coordinates if and only if

$$\begin{aligned} f = \iota g - h(\psi _T), \end{aligned}$$

(65)

with $h(\psi _T)$ an arbitrary function. Since there is a lot of freedom in the definitions of g and h, there are infinitely many systems of magnetic coordinates. In Appendix 5 extended calculations proving these results are provided.

It is worth noting that the change of magnetic coordinates (61)–(62) is not a change of canonical coordinates. According to Eq. (63) with F a gradient, the Hamiltonian stays the same in the new coordinates. In particular Eq. (65) shows that Eq. (59) stays correct in these coordinates.

Among the most common sets of magnetic coordinates used in the fusion community are the Hamada (1962), Boozer (1981) and PEST (Grimm et al. 1983) coordinates. PEST coordinates are defined as the straight-B-line coordinates in which the toroidal angle corresponds to the geometrical one. Therefore, straight-B-line coordinates obtained from Eqs. (51)–(53) are the PEST coordinates if the ignorable coordinate $\varphi$ coincides with the geometrical toroidal angle. Any other set of magnetic coordinates needs to change both the angular coordinates, as shown in Eqs. (61)–(62). A clear definition of the symmetry angle $\varphi$ in an axisymmetric system can be found for instance in chapter 6 of D’haeseleer et al. (2012), where the symmetry flux coordinates in a tokamak are described: the $\varphi =\text{ constant }$ surfaces are vertical surfaces so that $\nabla \varphi$ points in the symmetry direction and the $\varphi$-coordinate curves (produced when only $\varphi$ is allowed to vary while the other two coordinates are held fixed) are circles whose tangents points in the symmetry direction requires $e_\varphi \propto \nabla \varphi$. Being R the distance from the major symmetric axis to a point on flux surface, $|\nabla \varphi |=1/R$. Hamada and Boozer coordinates are defined in the next section.

For people aware of action-angle variables, the proof of existence of magnetic coordinates as action-angle variables of the Hamiltonian defining magnetic field line is a lot shorter than the specific proof using the Clebsch representation of the magnetic field (see for instance section 4.B.1 of Cary and Brizard 2009; with the caveat that a minus sign must be added in the right-hand side of its equation (4.43)). Using action-angle variables also puts magnetic coordinates in a wider and more fundamental perspective.

4.3 Boozer and Hamada coordinates—a new formulation

We now focus on magnetic coordinates used to describe MHD equilibria. Such equilibria are defined by

$$\begin{aligned} {\textbf{j}} \times {\textbf{B}} = \nabla p, \end{aligned}$$

(66)

where ${\textbf{j}}$ is the current density, and p in this context indicates the kinetic pressure. Because of this equation, $\nabla p$ is perpendicular to both ${\textbf{B}}$ and ${\textbf{j}}$, so the pressure p is constant along both B and j-lines. Magnetic field lines, where the rotational transform $\iota$ is irrational, wrap densely on the corresponding magnetic surfaces. Therefore, p is constant over such surfaces. If p is a smooth function, this property carries over to all real numbers. Because p is constant along both B and j-lines, magnetic surfaces coincide with current-density surfaces. Considering force-free equilibria, i. e. $\nabla p=0$, magnetic field lines are parallel to current-density lines; when $\nabla p \ne 0$ they are not, but still lie on flux surfaces.

Two types of magnetic coordinate systems are commonly used to describe MHD equilibria: Hamada coordinates (Hamada 1962) and Boozer coordinates (Boozer 1981). In Hamada coordinates, both the magnetic field lines and current lines corresponding to the considered MHD equilibrium are straight. In Boozer coordinates, both the magnetic field lines corresponding to the MHD equilibrium are straight and the diamagnetic lines, i.e. the integral lines of $\nabla p \times {\textbf{B}}$. The derivation of these two kinds of magnetic coordinates can be found for instance in appendix B of Cary and Brizard (2009), where these coordinates are defined also from the specific form of their Jacobian ($J \propto 1$ defines Hamada coordinates, whereas $J \propto B^{-2}$ defines Boozer ones). Analytical calculations involving these coordinates are simplified by the technique introduced in Pustovitov (1998a, b, 1999).

We now show that the action-angle approach enables a simple explicit definition of these specific coordinates from Eq. (65), that does not use at all the magnetic field or magnetic differential equations.

4.3.1 Hamada coordinates

Equation (46), written for the magnetic field, is said canonical form and can be generalized to any divergence-free field on a torus. In MHD, the divergence of ${\textbf{j}}$ vanishes, as does that of the magnetic field. This makes natural the application of the above formalism to ${\textbf{j}}$. Because ${\textbf{j}} \sim \nabla \times {\textbf{B}}$, now ${\textbf{B}}$ plays the previous role of ${\textbf{A}}$. Naturally, there is no gauge invariance for ${\textbf{B}}$, but if we are interested in the current lines only, we do not care about the exact magnetic field producing $\textbf{j}$, and we may again use the freedom of adding a gradient, now to ${\textbf{B}}$, which makes ${\textbf{j}}$ invariant. It is worth noting that this fact is implicit in the Clebsch representation of the current in equation (B2) of Cary and Brizard (2009). Moreover, to define action-angle coordinates, the Hamiltonian of the magnetic system (the component $B_3$ of the magnetic field when studying j-lines) needs to be time independent, which is true in toroidal systems when the canonical time is associated with the toroidal angle $\varphi$. The gauge transformation to define the axial gauge $B_1=0$ is “time” independent, so that action-angle formalism can indeed be applied to look for straight j-lines. Hamada coordinates can be defined following a list of steps.

• On magnetic flux surfaces, straight magnetic field lines coordinates $(\psi _T, \zeta , \varphi )$ are defined in Eqs. (51)–(53) from the action-angle formalism. Hamada coordinates can then be defined from general magnetic coordinates $(\psi _T, \zeta , \varphi )$ using Eqs. (61)–(62) and (65):

  $$\begin{aligned} \zeta _H(\psi _T,\theta )& = {} \zeta (\theta ,\psi _T) + \iota (\psi _T) \, g(\psi _T,\zeta (\theta ,\psi _T),\varphi ) - h(\psi _T), \end{aligned}$$

  (67)
  $$\begin{aligned} \varphi _H(\theta ,\varphi ,\psi _T)& = {} \varphi + g(\psi _T,\zeta (\theta ,\psi _T),\varphi ). \end{aligned}$$

  (68)

• Exploiting the canonical form for ${\textbf{j}}$, the equivalent of Eqs. (51)–(53) can be used to define action-angle variables for the current line “dynamics” on magnetic flux surfaces (when magnetic flux surfaces exist, we remind the equivalence of magnetic and current density flux surfaces due to Eq. (66)). Adding a prime to all quantities related to the current dynamics, and noting that ${\textbf{B}}$ plays the previous role of ${\textbf{A}}$, the canonical form for ${\textbf{j}}=\nabla \times {\textbf{B}} / \mu _0$ can be written as

  $$\begin{aligned} (2 \pi / \mu _0) \, {\textbf{B}}& = {} \psi '_t \, \nabla \theta - \psi '_p \, \nabla \varphi \end{aligned}$$

  (69)
  $$\begin{aligned} 2 \pi \, {\textbf{j}}& = {} \nabla \psi '_t \times \nabla \theta - \nabla \psi '_p \times \nabla \varphi \end{aligned}$$

  (70)

  where quantities $\psi '_t$ and $\psi '_p$ define the “current density fluxes” in the general toroidal coordinates ${\textbf{x}}=(\psi '_t, \theta , \varphi )$:

  $$\begin{aligned} \psi '_i = \int {\textbf{j}} \cdot {\textrm{d}}\mathbf {\Sigma } = \frac{1}{\mu _0} \int _{\Sigma (l)} (\nabla \times {\textbf{B}}) \cdot {\textrm{d}}\mathbf {\Sigma } = \frac{1}{\mu _0} \oint _{l} {\textbf{B}} \cdot {\textrm{d}}{\textbf{l}} = \left\{ \begin{array}{l} \frac{2 \pi }{\mu _0} B_\theta \;\;\; (i=t)\\ \frac{2 \pi }{\mu _0} B_\varphi \;\;\; (i=p)\\ \end{array} \right. \end{aligned}$$

  (71)

  where the definition of the flux of ${\textbf{j}}$ through a surface $\Sigma$, Ampère’s law and Stokes theorem have been used in Eq. (71). Last equality uses $B_1=0$ and the definition of poloidal or toroidal surface, as done for the derivation of the magnetic fluxes in Appendix 4.1. We now use the equivalence of magnetic and current density flux surfaces and we keep in mind that we use the same ${\textbf{x}}$ spatial coordinates for magnetic and current lines; in particular $x^3 = \varphi$. The definition of straight current density lines on magnetic flux surfaces and their rotational transform follow from Eqs. (51)–(53) and (58)–(59) :

  $$\begin{aligned} \psi '_T(E)& = {} \frac{1}{2 \pi } \oint \psi '_t(E, \theta ) \, {\textrm{d}}\theta \end{aligned}$$

  (72)
  $$\begin{aligned} \zeta '(\theta , \psi '_T)& = {} \int _{\theta _0}^{\theta } \frac{\partial \psi '_t[\theta ,x^2(\theta ,\psi '_T)]}{\partial \psi '_T} \, {\textrm{d}}\theta \end{aligned}$$

  (73)
  $$\begin{aligned} \iota '(\psi '_T)& = {} \frac{{\textrm{d}}\zeta '}{{\textrm{d}}\varphi } = \frac{{\textrm{d}}\psi '_P}{{\textrm{d}}\psi '_T} \end{aligned}$$

  (74)

  The fluxes $\psi '_T(\psi '_P)$ define the “current surfaces”.

• Because Hamada coordinates define both straight ${\textbf{B}}$ and ${\textbf{j}}$-lines, equations similar to (67)–(68) can be written to define the same Hamada coordinates from straight current lines coordinates $(\zeta ', \varphi )$. We distinguish the new definition of Hamada coordinates from the previous one by adding a prime to $\psi _T$, $\zeta$, $\iota$, g, and h.

• Equating the two formulations of Hamada coordinates yields an expression of these coordinates as a function of general straight magnetic field and straight current density lines, here indicated by the symbols $(\psi _T, \zeta , \varphi )$ and $(\psi '_T, \zeta ', \varphi )$, respectively. Equating the right-hand sides of the two sets of equations for Hamada coordinates, and remembering that $\zeta =\zeta (\psi _T, \theta )$, $\iota =\iota (\psi _T)$, $g = g(\psi _T,\zeta (\theta ,\psi _T),\varphi )$, $h=h(\psi _T)$, and the same for prime quantities, yields

  $$\begin{aligned} \zeta + \iota \, g - h& = {} \zeta ' + \iota ' \, g' - h' \end{aligned}$$

  (75)
  $$\begin{aligned} g& = {} g' \end{aligned}$$

  (76)

  where we used that the initial toroidal angle is the same in both cases. The second equation enables substituting $g'$ for g in the first one, which yields

  $$\begin{aligned} (\iota ' - \iota ) \, g = \zeta - \zeta '+ h- h'. \end{aligned}$$

  (77)

  This enables the calculation of g which is found independent of the toroidal angle,

  $$\begin{aligned} g(\psi _T,\zeta (\theta ,\psi _T)) = \frac{\zeta - \zeta '+ h- h'}{(\iota ' - \iota )} \,. \end{aligned}$$

  (78)

  Setting g in Eqs. (67) and (68), gives a simple explicit expression for Hamada coordinates $(\psi _T, \zeta _H, \varphi _H)$ as a linear combination of action-angle coordinates for B and j:

  $$\begin{aligned} \zeta _H(\theta ,\psi _T)& = {} \frac{\iota ' (\zeta - h) - \iota (\zeta '- h')}{\iota ' - \iota }, \end{aligned}$$

  (79)
  $$\begin{aligned} \varphi _H(\theta ,\varphi , \psi _T)& = {} \varphi + \frac{\zeta - \zeta ' - h+ h'}{\iota ' - \iota }. \end{aligned}$$

  (80)

  These coordinates have some freedom due to the arbitrary functions $h(\psi _T)$ and $h'(\psi '_T)$. This freedom corresponds to the integration constants present when using magnetic differential equations to define Hamada coordinates.

4.3.2 Boozer coordinates

Boozer coordinates can be computed in the same way. Indeed, diamagnetic lines are the integral lines of $\nabla \psi _T \times {\textbf{B}}$, which is colinear to ${\textbf{q}} = \nabla p \times {\textbf{B}}$, since the gradient of the scalar pressure p is colinear with that of $\psi _T$ ($\nabla p \parallel \nabla \psi _T$). Now, ${\textbf{q}}$ is a divergence-free vector like ${\textbf{B}}$ (Pustovitov 1999). Indeed, $\nabla . (\nabla p \times {\textbf{B}}) = {\textbf{B}} \,. \nabla \times \nabla p - \mu _0 \nabla p \, . \,{\textbf{j}} = 0$, since $\nabla p = {\textbf{j}} \times {\textbf{B}}$ and ${\textbf{j}} = \nabla \times {\textbf{B}} / \mu _0$. Furthermore, ${\textbf{q}} \times {\textbf{B}} = - \textbf{B}^2 \nabla p$ which is similar to Eq. (66), which implies that p is constant along ${\textbf{q}}$ lines. Therefore, ${\textbf{q}}$ can be dealt with like we did previously with $\textbf{B}$ and ${\textbf{j}}$. Naturally, to fit with diamagnetic “dynamics”, in this calculation all primes become double primes, and index H becomes index B for “Boozer”. In this way $\psi {''}_T$ and $\psi {''}_P$ are the fluxes defining the surfaces where diamagnetic ${\textbf{q}}$-lines lays. Again, a one-to-one correspondence between $\psi {''}_T$ and $\psi _T$ is expected, so Boozer coordinates define a frame of reference in which both ${\textbf{B}}$ and ${\textbf{q}}$ lines are straight.

5 Calculations made easier with the action principle: the perturbative approach and a new derivation of the magnetic island width

This section deals with the effect of a small resonant perturbation to a regular magnetic field. Section 5.1 defines the corresponding perturbed Hamiltonian. Subsection 5.2 introduces an invariant flux related to a magnetic island, useful to express its width as shown in Sect. 5.3. Subsection 5.4 shows how to compute numerically a magnetic island width from experimental data, and Sect. 5.5 how to derive from this Chirikov overlap parameter when several resonant perturbations are present.

5.1 Small resonant perturbation of a regular magnetic field

We now consider the effect of a small resonant perturbation of a regular magnetic field, associated with a “time” independent Hamiltonian $H_0$. Such a field is defined by the existence of magnetic flux surfaces and by a one-to-one relation between $\psi _T$ and $\psi _P$ when using action-angle coordinates. Using $\psi _T$ as the radial coordinate identifying magnetic flux surfaces, we take $\psi _P = \psi _P(\psi _T)$, or $H_0=H_0(p)$. In the following we use the notation ${\textbf{x}} = (\psi _T, \theta , \varphi ) = (p,q,t)$ for the action-angle coordinates defined on $H_0$ flux surfaces. It is worth noting that these are not magnetic coordinates for the perturbed Hamiltonian.

The perturbation $\delta {\textbf{B}}(\psi _T, \theta , \varphi )$ of the regular magnetic field is provided by a perturbation $\delta {\textbf{A}}(\psi _T, \theta , \varphi )$ of both components of the potential vector. However, in Appendix 6, it is shown that, whatever be the perturbation of the toroidal flux, an appropriate redefinition of this variable enables considering the magnetic perturbation to bear only on the poloidal flux. Then, using Eq. (45), the perturbation to the vector potential is defined by

$$\begin{aligned} \delta {\textbf{A}} = - \delta \psi _P \, \nabla \varphi / 2 \pi , \end{aligned}$$

(81)

where $\delta \psi _P$ is a function of $(\psi _T, \theta , \varphi )$, or, equivalently, of the canonical variables (p, q, t). This perturbation to the vector potential turns out to be a perturbation to the Hamiltonian (49), which is defined by

$$\begin{aligned} H& = {} H_0 + H_1 \end{aligned}$$

(82)

$$\begin{aligned} H_0& = {} \psi _P(\psi _T) \end{aligned}$$

(83)

$$\begin{aligned} H_1& = {} \delta \psi _P(\psi _T, \theta , \varphi ). \end{aligned}$$

(84)

In the following we consider the case where $H_1$ consists in a single helical Fourier component, $\delta \psi _P = H_{1,m_0,n_0}(p) \cos (m_0 \theta - n_0 \varphi )$, which is resonant at a value of $p = \psi _T$ defined by $\iota (p_0) = n_0/m_0$. The classical local reduction of the Hamiltonian to a pendulum Hamiltonian close to $p_0$ is performed in Appendix 7. It proves the existence of a magnetic island that develops around the unperturbed resonant flux surface defined by $\iota (p_0)$. Defining the helical angle $u=m_0 \theta - n_0 \varphi$, its X-point corresponds to $u_X = 0$ and its O-point to $u_O = \pi$ if $\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) >0$, and the opposite otherwise. In the following, results from Appendix 7 will be used also to compute the magnetic island width.

The following calculations are rephrased in Appendix 8 in the case of a perturbation bearing on both magnetic fluxes.

5.2 Invariant flux related to a magnetic island

Physical quantities, like the width of a magnetic island, cannot depend on the choice of the coordinates. They must therefore be related to invariants under change of coordinates or gauge transformations. In this section, we use the definition of the action for magnetic field lines and Stokes theorem, that implies the equivalence between the action along a closed circuit (circulation of ${\textbf{A}}$) and the magnetic flux through any surface having the oriented circuit as a boundary. This mathematics will be used to prove the existence of a magnetic flux, defined for each magnetic island through the ribbon defined by the O and X points, which is invariant under change of coordinates and named $\Phi _{OX}$ in the following. This flux is the analogous of the flux $\Phi$ defined in Park et al. (2008), or, better, to its resonant Fourier components that are proved to be the same in each set of magnetic coordinates, and the island width results $\sim \sqrt{(}|\Phi _{mn}|)$. The explicit definition of $\Phi$ is given in Appendix 8.1.

We compute the action along the closed orbit O, corresponding to the center of the magnetic island. According to Eqs. (28) and (47)–(50), it is

$$\begin{aligned} S_O = \frac{1}{2 \pi } \int _O [p {\textrm{d}}\theta - H(p,q,\varphi ) {\textrm{d}}\varphi ]. \end{aligned}$$

(85)

Since the perturbation is small, along O and X it is true to lowest order that $p= p_0$, ${\textrm{d}}\theta / {\textrm{d}}\varphi = \iota (p_0)=m_0/n_0$, and $u_0=m_0 \theta - n_0 \varphi =\pm \pi$ (see Appendix 7). Assuming that $m_0$ and $n_0$ are mutually relatively prime, $\varphi$ varies by $2 m_0 \pi$ along O and $\theta$ varies by $2 n_0 \pi$. Assuming (82)–(84), this yields

$$\begin{aligned} S_O = m_0 [p_0 \iota (p_0) - H_0(p_0) - H_{1,m_0,n_0}(p_0) \cos (u_O)]. \end{aligned}$$

(86)

Its geometrical meaning is explained in Appendix 8 to be the helical flux through the surface defined by the O-point. Similarly, the action $S_X$ along the closed orbit corresponding to the X-point of the magnetic island is given by Eq. (86) where $\cos (u_O)$ becomes $\cos (u_X)= - \cos (u_O)$. Consequently,

$$\begin{aligned} S_O - S_X= - 2 \cos (u_O) m_0 H_{1,m_0,n_0}(p_0) = 2 m_0 \textrm{sgn}\left[ \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p}\right] |H_{1,m_0,n_0}(p_0)|, \end{aligned}$$

(87)

where the last expression results from Eq. (160).

Fig. 2

Helical ribbon defining the $\Phi _{OX}$ flux. In red and blue the closed orbits defined by the O and X-point of a $(m_0=1,n_0=1)$ magnetic island, respectively. Their intersections o and x in a poloidal section are indicated. The magnetic island separatrix is indicated in green

The geometrical meaning of the $S_O-S_X$ flux can be understood from Figure 2, which displays the closed orbits O, in red, and X, in blue, for a $(m_0=1,n_0=1)$ magnetic island whose separatrix is indicated in green. It displays their intersections o and x in a poloidal section. We now compute the action corresponding to the closed path starting at o, following O with a growing $\varphi$ up to reaching back o, then going from o to x in the poloidal section along the red segment ox, then following X with a decreasing $\varphi$ up to reaching back x, then finishing by going from x to o in the poloidal section along blue segment ox. Stokes theorem implies that this action is nothing but the magnetic flux $\Phi _{OX}$ through any oriented ribbon whose edges are the oriented closed orbits corresponding to the O and X-point. Since the two contributions to this action corresponding to ox cancel because they are opposite, this magnetic flux is

$$\begin{aligned} \Phi _{OX} = S_O - S_X. \end{aligned}$$

(88)

As a consequence, as expected, the width of the magnetic island is not related to the specific choice of toroidal coordinates but is defined by a coordinate-independent magnetic flux with a simple geometrical definition. In particular, it does not depend on the choice of the radial coordinate. The single helical Fourier component introduced above verifies $|H_{1,m_0,n_0}(p_0)| = |\Phi _{OX}|/2 m_0$.

By inverting the roles of $\psi _T$ and $\psi _P$, Eq. (87) becomes

$$\begin{aligned} S_O - S_X = - 2 \cos (u_O) n_0 H'_{1,m_0,n_0}(\psi _{P0}) = 2 n_0 \textrm{sgn}\left[ \frac{{\textrm{d}}q_s(\psi _{P0})}{{\textrm{d}}\psi _{P}}\right] |H'_{1,m_0,n_0}(\psi _{P0})|, \end{aligned}$$

(89)

where $\psi _{P0}$ is the resonant value of $\psi _{P}$ defined by $q_s (\psi _{P0}) = m_0/n_0$ with $q_s = 1/\iota$ the safety factor, and $H'_{1,m_0,n_0}(\psi _{P})$ is the resonant contribution in the Hamiltonian with the inverted roles of $\psi _T$ and $\psi _P$. This shows that $m_0 H_{1,m_0,n_0}(p_0) = n_0 H'_{1,m_0,n_0}(\psi _{P0})$.

The existence of a coordinate-independent magnetic flux related to a magnetic island that correctly estimates its width was already proved in Park et al. (2008) by using a magnetic differential equation and by performing explicit changes of magnetic coordinates with the corresponding Jacobians. The above path, based on the action for magnetic field lines, avoids using coordinates and Jacobians, and leads to an expression for the invariant flux in terms of a magnetic flux through an explicit surface: the ribbon defined by the periodic orbits related to the O and X points. Appendix 8 discusses previously introduced coordinate-independent fluxes and shows their interpretation as helical fluxes.

Reference Park et al. (2008) quotes eight papers (its references 11–13 and 15–19) where the resonant Fourier components of the magnetic field were mistakenly considered as almost invariant when going to magnetic coordinates. Its abstract states: when replacing the Fourier components of the perturbation vector potential by those of the magnetic field finite aspect ratio effects have been neglected so far. For present tokamaks with $B = r/R \sim 0.3$ this can lead to an error in the field line diffusion of one to two orders of magnitude. Reference Kaleck (1999) quotes six papers (its references 5, 7–9, 12, 13) where the same mistake was made. Above its equation (15), it states that a number of papers have discussed the resonant Fourier harmonics of the magnetic field [...] instead of the [Fourier harmonics of the flux], assuming the Fourier spectrum is little changed by going to magnetic coordinates. But this assumption can be very inaccurate in toroidal plasmas. Figure 4 of Park et al. (2008) shows this can be wrong by a factor 3, leading to a factor 9 for a quasilinear estimate of a corresponding diffusion coefficient. This shows how useful is the use of the potential vector and of the corresponding Hamiltonian description of magnetic field lines to find out the right invariants.

If on top of the single helical component considered at the end of Sect. 5.1 there is another non-resonant one, say $H_{1,m,n}(p) \cos (m \theta - n \varphi )$, when performing the integral of Eq. (85), this component adds a non-vanishing contribution to $S_O$. In this case, therefore, $S_O$ cannot be estimated by an integration over a single period of O, as done in Eq. (85). When performing the integration over N periods of O, we get $N S_O$, plus an oscillating term, that stays bounded when N grows. Dividing by N the integral over N periods of O, we get $S_O$, plus a contribution vanishing for N large. Therefore, in an experimental case where there is more than one component in the Fourier series of $H_1$ in $\theta$ and $\varphi$, $S_O$ can be estimated by this method.

5.3 Width of a magnetic island

We refer to Appendix 7 for the calculation of the island width in terms of the Hamiltonian perturbation, and to the results of the previous section to express it in terms of the invariant island flux defined by Eqs. (87) and (88).

Equation (159) of Appendix 7 shows that the magnetic island half-width in units of $p_0$ (i.e. of a flux) is

$$\begin{aligned} \Delta p = \Delta \psi _T = 2\sqrt{\left| \frac{H_{1,m_0,n_0}(p_0)}{\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p}} \right| } = 2\sqrt{\left| \frac{\Phi _{OX}}{2 m_0 \frac{ {\textrm{d}}\iota (p_0)}{{\textrm{d}}p}} \right| }, \end{aligned}$$

(90)

where the last expression is obtained through Eqs. (87) and (88). It is worth noting that this width is defined even if the island is washed out by chaos.

The equivalent expression in units of $\psi _{P0}$ (i.e. of the poloidal flux), valid when the poloidal flux $\psi _P$ is taken as radial coordinate and obtained by inverting the roles of $\psi _T$ and $\psi _P$ in Eq. (45) and by replacing factor $1/2 \pi$ in the latter expression, yields

$$\begin{aligned} \Delta \psi _P = 2\sqrt{\left| \frac{ H'_{1,m_0,n_0}(\psi _{P0})}{\frac{{\textrm{d}}q_s(\psi _{P0})}{{\textrm{d}}\psi _P}} \right| } = 2\sqrt{\left| \frac{\Phi _{OX}}{2 n_0 \frac{ {\textrm{d}}q_s(\psi _{P0})}{{\textrm{d}}\psi _P}} \right| }, \end{aligned}$$

(91)

where the last expression is obtained through the Eq. (89). For instance, Eq. (91) must be used for the reversed field pinch in the domain where the toroidal field reverses, since $\psi _T$ does not evolve monotonically radially there, which invalidates the derivation leading to the Eq. (90).

It is worth noting that the above second expressions of island widths involve an explicit magnetic flux instead of an abstract Hamiltonian perturbation.

The calculations of Appendix 7 assume the magnetic shears $\frac{ {\textrm{d}}\iota (p_0)}{{\textrm{d}}p}$ and $\frac{ {\textrm{d}}q_s(\psi _{P0})}{{\textrm{d}}\psi _P} = - \frac{1}{\iota (p_0)^2} \frac{ {\textrm{d}}\iota (p_0)}{{\textrm{d}}p}$ do not vanish. When these quantities diminish, the island width increase. The above calculations make sense only when the island domain does not overlap a flux surface with a vanishing shear. It is worth mentioning that magnetic shear vanishes at q-minimum radius of reversed shear plasma of tokamaks.

Finally, the island width computed in terms of flux can be translated into the geometric width of a pendulum-like eye-of-cat through the equations defining magnetic surfaces. Formula (90) agrees with equation (1.44) of White (2013) and with equation (7.2.8) of Wesson and Campbell (2011); equation (20) of chapter 9 of Hazeltine and Meiss (1992) yields a result $\sqrt{2}$ larger.

5.4 Numerical calculation of a magnetic island width from experimental data

The calculation of a magnetic island width from experimental data can be done using Eqs. (90) or (91), where the actions along the closed orbit O and X are computed by performing the integration over several periods of these orbits, as indicated in the last paragraph of Sect. 5.2. Furthermore, the $\Phi _{OX}$ flux can also be computed directly from formulas (87) or (89) when the resonant components of the perturbation are known. An example is given in Appendix 8.2 using data from the RFX-mod Reversed Field Pinch experiment (Sonato et al. 2003).

Previously, the calculation of this width from experimental data was performed in at least two ways. A first one starts with the calculation of ${\textbf{A}}$ by a Biot-Savart calculation in cylindrical coordinates $(R,Z,\varphi )$ (Kaleck 1999; Bécoulet et al. 2008; Cahyna et al. 2009). Then, the toroidal spectra of the three cylindrical components of ${\textbf{A}}$ is calculated, and from them are computed the corresponding components of the magnetic field perturbation so as to satisfy numerically the condition $\nabla \cdot {\textbf{B}} = 0$. Then, the radial component of ${\textbf{B}}$, and its poloidal and toroidal Fourier spectra are computed, before making calculations involving metric coefficients, which provide finally the island width.

A second type of calculation of magnetic island width is performed by computing numerically magnetic field lines from the knowledge of the magnetic field (Cary and Hanson 1991). First the O-point of the island of interest is identified. The full-orbit tangent map related to the O-point of the island of interest is then computed by integrating the differential equations for the derivative of the “equations of motion” of the field line. Two eigenvectors are then computed by diagonalizing matrices obtained from this map. This yields the rotation frequency in the center of the island, and then the shear of magnetic field lines. This is finally set into a formula providing the island width.

In view of the many steps of these techniques, it might be worthwhile checking the accuracy of the simple estimate in terms of action integrals indicated above. This could be done by dealing with synthetic magnetic data produced from a Hamiltonian enabling an analytical calculation of island widths from Eqs. (90) or (91).

5.5 Resonance overlap

If several resonant perturbations are present in an experiment, Chirikov resonance overlap criterion (Chirikov 1979) can be applied from the experimental data about the magnetic field. One can use engineer coordinates like $(z,R,\phi )$ or $(r,\theta ,\phi )$, and choose $\phi$ as time when dealing with the tokamak. Then, magnetic field lines can be numerically computed by using a symplectic code and the Hamiltonian description of field lines provided by Eqs. (30)–(33).

If possible, first plot the Poincaré map without perturbation to make sure there is no spurious chaos due to the algorithm (in particular due to time discretization). Then, plot the Poincaré maps including the successive resonant perturbation you want to analyze. Measure the normalized width of the resonances. Then Chirikov overlap parameter can be computed for any couple of resonance amplitudes. There is no need for a high precision, since the criterion is approximate, and only gives an order of magnitude estimate.

Chirikov criterion can be applied in the following way: plot the Poincaré map corresponding to the experimentally measured magnetic field, and identify the location of the periodic orbits corresponding to the resonances whose overlap is to be checked. Then, compute the width of the resonances from the technique of the preceding subsection. Then Chirikov overlap parameter can be computed for any couple of resonances.

Chirikov criterion is a very useful rule of thumb. In reality, the threshold for large-scale chaos (or “stochasticity”) depends on two features of the overlapping resonances; the ratio of their amplitudes and that of the number of island chains. This was shown in figure 2.19 of Escande (1985). We use the notations of this reference where k is the ratio of the number of island chains, M and P are the normalized amplitudes of the resonances, such that Chirikov overlap parameter is $s= 2 \sqrt{(}M) + 2 \sqrt{(}P)$. The smallest threshold corresponds to $s=0.7$ for $k=1$ and $\rho =1$ with $\rho = \sqrt{(}M/P)$. The threshold corresponds to $s=1$ for $k=1$ and $\rho \simeq 3$, and for $\rho =1$ and $k \simeq 4$. The increase of the threshold when $\rho$ becomes large or small is natural. Indeed, if one of the resonances has a vanishing amplitude, no chaos will occur whatever big is s. The increase of the threshold when k becomes large or small is natural too. Indeed, if a resonance has many islands along a single one of the other resonance, the effect of the former on the dynamics of the latter is a fast perturbation, which can be averaged out.

Chirikov criterion can be interpreted as a criterion of heteroclinic intersection, i. e. of intersection of the stable manifold of an X-point of the first resonance with the unstable manifold of an X-point of the second resonance, and vice-versa (see section 7 of Escande 2018). Indeed, the part of these manifolds close to the corresponding X-point can be approximated by the separatrix corresponding to the resonance alone. Therefore resonance overlap is an approximation of heteroclinic intersection.

Section III of reference (Elsasser 1986) points out the difficulty of choosing relevant resonances to use Chirikov criterion when many resonances with close values of m/n are present. Empirically, one can apply it to the largest islands in Poincaré maps. This choice can be often justified by the Hamiltonian version of renormalization theory for Kolmogorov-Arnold-Moser tori (Escande 1985). Indeed, the largest islands often correspond to the dominant current perturbations. Then islands with higher values of m or n turn out to be the “daughters” of the large ones, and belong in the large islands of the smaller scales of phase space exhibited by the renormalization “microscope”. A pedagogical introduction to these concepts can be found in section 5 of Escande (2018). Finally, it is worth noting, that when the amplitude of a magnetic perturbation increases, there may be a collision of the O and X-points of the corresponding magnetic island (inverse saddle-node bifurcation) canceling the separatrix and leading to a strong resilience to chaos (Escande et al. 2000).

Finally, it is worth noticing that numerical calculations are so handy, that it may be more reliable to compute a threshold of chaos this way than to compute it by applying the Chirikov criterion numerically, or analytically after painstaking uncontrolled approximations.

6 Conclusion

This review paper proceeded as follows. It recalled the variational principle for magnetic field lines and showed it can be intuitively deducted. It introduced a new derivation of it from first principles, using Stokes theorem and avoiding analytical calculations, and recalled previous ones using such calculations. It was recalled that the action principles for magnetic field lines and for Hamiltonian mechanics are analogous. Also that a change of gauge is equivalent to a canonical transformation. Action-angle coordinates were introduced for magnetic systems, which correspond to the so-called magnetic coordinates. A new formula was derived providing explicitly the Boozer and Hamada magnetic coordinates from action-angle coordinates. Then practical calculations about magnetic field lines were shown to be simpler and safer, with an intuitive background. In particular, with a new analytical result: the width of a magnetic island is proportional to the square root of an invariant flux related to this island, the magnetic flux through a ribbon whose edges are the field lines related to the O and X points of the island. This is the first expression of this width avoiding abstract Fourier components and obviously independent of the choice of coordinates. The same analytical calculation provides a simple way to compute numerically the width of a magnetic island. Also to apply Chirikov resonance overlap criterion.

It was also shown that the pedestrian derivation of the action principle for magnetic field lines suggests a new pedagogical and intuitive introduction to Hamiltonian mechanics: teaching it from magnetic lines “mechanics”. There would be some beauty in the approach, in particular because of the equivalence of change of gauge and of canonical transformation. Also because it provides a natural unification of the many Hamiltonians describing the same dynamics, which broadens the freedom for practical applications. As a result, this review brings a further element of the contribution of plasma physics to nonlinear dynamics and chaos (Escande 2016, 2018). Also, more generally to mechanics, when including the capability of the N-body description of the plasma to enable a reductionist approach to kinetic problems, in contrast to most of the rest of physics (Escande et al. 2018).

The review shows that important simplifications are brought by working with the vector potential, i.e. in a geometrical way avoiding the use of specific coordinates, and respecting the symplectic background of the dynamics. This philosophy is also present in the description of particle dynamics with the Lagrangian derivation of a guiding center equation of motion (Littlejohn 1983), which involves the use of the Lie transform technique (Littlejohn 1982), which is also at the basis of the modern derivation of gyrokinetic theory (Hahm 1988; Hahm et al. 1988; Brizard and Hahm 2007), and of the development of various gyrokinetic simulation codes (Garbet et al. 2010). Further developments along these lines are noncanonical guiding-center theory (Cary and Brizard 2009), Hamiltonian formulations of quasilinear theory for magnetized plasmas (Brizard and Chan 2022), with an extension for inhomogeneous plasmas (Dodin 2022). Also a gauge-free electromagnetic gyrokinetic theory where the gyrocenter phase-space transformation are expressed in terms of the perturbed electromagnetic fields, instead of the usual perturbed potentials (Burby and Brizard 2019). Finally, Tronko and Chandre (2018) shows how to account for various orderings of the small parameter associated with spatial inhomogeneities of the background magnetic field and that characterizing the small amplitude of the fluctuating fields. This review paper and the above references contribute to making plasma physics a fundamental science.

Appendices

Appendix 1: Euler–Lagrange equations for magnetic field lines

In Sect. 2 it has been shown that the Euler–Lagrange equations yield the equations defining the magnetic field lines when the Lagrangian of the magnetic system is used. In this appendix we explicitly derive the magnetic field line equations from the Euler–Lagrangian ones, recalling first the Lagrangian of the system:

$$\begin{aligned} L({\textbf{x}}, \frac{{\textrm{d}}{\textbf{x}}}{{\textrm{d}}x^3}, x^3) = A_{1}({\textbf{x}}) \, \frac{{\textrm{d}}x^{1}}{{\textrm{d}}x^3} + A_{2}({\textbf{x}}) \, \frac{{\textrm{d}}x^{2}}{{\textrm{d}}x^3} +A_{3}({\textbf{x}}) = A_i({\textbf{x}}) \, \dot{x}^{i} , \end{aligned}$$

(92)

where ${\textbf{x}}=(x^1, x^2, x^3)$ are the spatial coordinates, $x^3$ being the coordinate that parametrizes the magnetic field line, and the $A_i$’s the covariant components of the vector potential. The last expression of Eq. (92) writes the Lagrangian in a more compact form using the Einstein’s convention of summation over repeated indices and $\dot{x}^i = {\textrm{d}}x^i/ {\textrm{d}}x^3$. The corresponding Euler–Lagrange equations are

$$\begin{aligned} \frac{\partial L}{\partial x^j} - \frac{{\textrm{d}}}{{\textrm{d}}x^3} \frac{\partial L}{\partial \dot{x}^j}=0, \quad j=1,2. \end{aligned}$$

(93)

With L given by Eq. (92),

$$\begin{aligned} \frac{\partial L}{\partial x^j}& = {} \frac{\partial A_i}{\partial x^j} \, \dot{x}^i \end{aligned}$$

(94)

$$\begin{aligned} \frac{\partial L}{\partial \dot{x}^j}& = {} A_i \, \delta _j^i \end{aligned}$$

(95)

where $\delta _j^i =1$ when $i=j$ and null otherwise. The second term of the left hand side of Eq. (93) can then be written as

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}x^3} \frac{\partial L}{\partial \dot{x}^j} = \frac{{\textrm{d}}A_i}{{\textrm{d}}x^3} \, \delta _j^i = \frac{\partial A_i}{\partial x^k} \frac{{\textrm{d}}x^k}{{\textrm{d}}x^3} \, \delta _j^i = \frac{\partial A_j}{\partial x^k} \frac{{\textrm{d}}x^k}{{\textrm{d}}x^3} \quad j=1,2 \end{aligned}$$

(96)

so the Euler–Lagrange equations (93) assume the form

$$\begin{aligned} \frac{\partial A_i}{\partial x^j} \, \frac{{\textrm{d}}x^i}{{\textrm{d}}x^3} - \frac{\partial A_j}{\partial x^k} \frac{{\textrm{d}}x^k}{{\textrm{d}}x^3}=0 , \quad j=1,2. \end{aligned}$$

(97)

Expanding the summations over repeated indexes, Eq. (97) yields

$$\begin{aligned} 0 = \frac{\partial A_1}{\partial x^j} \, \frac{{\textrm{d}}x^1}{{\textrm{d}}x^3} + \frac{\partial A_2}{\partial x^j} \,\frac{{\textrm{d}}x^2}{{\textrm{d}}x^3} + \frac{\partial A_3}{\partial x^j} - \left ( \frac{\partial A_j}{\partial x^1} \frac{{\textrm{d}}x^1}{{\textrm{d}}x^3} + \frac{\partial A_j}{\partial x^2} \frac{{\textrm{d}}x^2}{{\textrm{d}}x^3} + \frac{\partial A_j}{\partial x^3} \right ) , \quad j=1,2. \end{aligned}$$

(98)

To recognize the magnetic field line equations in Eq. (98), one needs the general relations linking the covariant components $A_i$ of the vector potential and the contravariant ones of the magnetic field from the definition of the curl in generic curvilinear coordinates:

$$\begin{aligned} B^i = \frac{1}{\sqrt{g}} \, \epsilon _{ijk} \, \frac{\partial A_k}{\partial x^j} \end{aligned}$$

(99)

where $\epsilon _{ijk}=\pm 1$, depending on the order of the indexes, and $1/\sqrt{g}$ is the Jacobian of the coordinate system. Using definitions (99) we can explicitly write the contravariant components of the magnetic field, as

$$\begin{aligned} \sqrt{g} B^1 = \Big ( \frac{\partial A_3}{\partial x^2} - \frac{\partial A_2}{\partial x^3}\Big ) \, , \quad \sqrt{g} B^2 = \Big ( \frac{\partial A_1}{\partial x^3} - \frac{\partial A_3}{\partial x^1}\Big ) \, , \quad \sqrt{g} B^3 = \Big ( \frac{\partial A_2}{\partial x^1} - \frac{\partial A_1}{\partial x^2}\Big ) \end{aligned}$$

(100)

Using Eq. (100) in Eq. (98) yields

$$\begin{aligned} \frac{{\textrm{d}}x^{1}}{B^1}& = {} \frac{{\textrm{d}}x^3}{B^{3}} \quad \text{ for } \,\, j=1 \end{aligned}$$

(101)

$$\begin{aligned} \frac{{\textrm{d}}x^{2}}{B^2}& = {} \frac{{\textrm{d}}x^3}{B^{3}} \quad \text{ for } \, \, j=2 \end{aligned}$$

(102)

which are Eq. (14) defining the magnetic field lines. Note that these relations are valid in any coordinate system, and that one does not really need to compute the related Jacobian. This finally proves that magnetic field line equations can indeed be derived from a stationary action principle.

Appendix 2: Canonical transformations

Here we recall a classical way of defining a canonical transformation. The variational principle expressed by Eqs. (21) and (22) for the one-degree-of-freedom case related to magnetic field lines yield

$$\begin{aligned} 0& = {} \delta \int _{t_0}^{t_1} \, [p {\dot{q}} - H(p,q,t)] {\textrm{d}}t \end{aligned}$$

(103)

where ${\dot{q}} = {\textrm{d}}q / {\textrm{d}}t$. For the same lines and another set (P, Q) of canonical coordinates, this equation becomes

$$\begin{aligned} 0& = {} \delta \int _{t_0}^{t_1} \, [P {\dot{Q}} - H'(P,Q,t)] {\textrm{d}}t, \end{aligned}$$

(104)

where $H'$ is the corresponding Hamiltonian and ${\dot{Q}} = {\textrm{d}}Q / {\textrm{d}}t$. One way for both variational principles to be satisfied is to have

$$\begin{aligned} p {\dot{q}} - H(p,q,t) = P {\dot{Q}} - H'(P,Q,t) + \frac{{\textrm{d}}F}{{\textrm{d}}t}, \end{aligned}$$

(105)

where F is an arbitrary function of the coordinates, called generating function of the canonical transformation. We now specify it by considering F as a function of (q, Q, t). Then, Eq. (105) becomes

$$\begin{aligned} p {\dot{q}} - H(p,q,t) = P {\dot{Q}} - H'(P,Q,t) + \frac{\partial F}{\partial q} {\dot{q}}+ \frac{\partial F}{\partial Q} {\dot{Q}} +\frac{\partial F}{\partial t} \end{aligned}$$

(106)

so

$$\begin{aligned} \Big ( p - \frac{\partial F}{\partial q} \Big ) {\dot{q}} - \Big ( P + \frac{\partial F}{\partial Q} \Big ) {\dot{Q}} + \Big ( H' - H - \frac{\partial F}{\partial t} \Big ) =0 , \end{aligned}$$

(107)

which implies

$$\begin{aligned} p=\frac{\partial F}{\partial q} \;, \; P=-\frac{\partial F}{\partial Q} \;, \; H'=H+\frac{\partial F}{\partial t} \quad . \end{aligned}$$

(108)

By subtracting $\frac{{\textrm{d}}(pq)}{{\textrm{d}}t}$ in the left hand side of Eq. (105), and/or $\frac{{\textrm{d}}(PQ)}{{\textrm{d}}t}$ in the right-hand side of the same equation, one can define three other generating functions with arguments (p, Q, t), (P, q, t), or (p, P, t). The above canonical transformations extend naturally to Hamiltonians with more degrees of freedom.

It is worth noting that Hamiltonian motion may be considered as a canonical transformation. Indeed, consider the transformation from [p(t), q(t)], to $[p(t+T),q(t+T)]$ where T is an arbitrary time. It is canonical, since there is a Hamiltonian describing the dynamics of $[p(t+T),q(t+T)]$: the same as that for [p(t), q(t)]. This is the basis of Lie perturbation theory where T is considered as infinitesimal (Cary 1981).

Appendix 3: Action-angle variables for one-degree-of-freedom Hamiltonians

Canonical equations of motion, ${\textrm{d}}{\textbf{q}}/{\textrm{d}}t = \partial H / \partial {\textbf{p}}$ and ${\textrm{d}}{\textbf{p}} / {\textrm{d}}t = - \, \partial H / \partial {\textbf{q}}$, imply that the total time derivative of a one-degree-of-freedom time-independent Hamiltonian H(p, q) vanishes, ${\textrm{d}}H / {\textrm{d}}t =0$. Therefore, H(p, q) is a constant of the motion and defines constant energy surfaces in phase space: $H(p,q)=E$. In this case it is always possible defining new canonical coordinates (P, Q) such that the new momentum is some function of E, $P=f(E)$, and a constant of the motion too. In such a case, $H'=H'(P)$: the evolution of P is ruled by

$$\begin{aligned} \frac{{\textrm{d}}P}{{\textrm{d}}t} = \frac{{\textrm{d}}f}{{\textrm{d}}E} \frac{{\textrm{d}}E}{{\textrm{d}}t} = - \frac{\partial H'}{\partial Q}, \end{aligned}$$

(109)

where the last expression results from the canonical equation of motion for P. Since E is a constant, the second expression vanishes, which implies $H'$ does not depend on Q. This means that $H'=H'(P)$, ending the proof.

If energy surfaces $H(p,q)=E$ are bounded in phase space, so is the range of variation of q on any of them, defining a periodic motion. In this case the new $(P,Q)=(I, \zeta )$ canonical variables defined by $H'=H'(P)$ are called action-angle variables. For a given value of E, we define the corresponding action as

$$\begin{aligned} I(E) = \frac{1}{2 \pi } \oint p(q, E) \, {\textrm{d}}q, \end{aligned}$$

(110)

where the integration runs over the related whole range of variation of q. Because of the conservations of the area in canonical transformations, this definition of I is independent from the choice of canonical coordinates. The conjugate variable, $\zeta$, can be defined from the relation between canonical variables using Eq. (105), by setting $Q=\zeta$, $P=I$, and $F= - \zeta I + G(q,I)$, where G is the generating function of the canonical transformation. Then, Eq. (105) becomes

$$\begin{aligned} p {\dot{q}} - H(p,q) = - \zeta {\dot{I}} - H'(I,\zeta ) + \frac{\partial G}{\partial q} {\dot{q}}+ \frac{\partial G}{\partial I} {\dot{I}} , \end{aligned}$$

(111)

so

$$\begin{aligned} \Big ( p - \frac{\partial G}{\partial q} \Big ) {\dot{q}} + \Big ( \zeta - \frac{\partial G}{\partial I} \Big ) {\dot{I}} + H' - H =0 , \end{aligned}$$

(112)

Which implies

$$\begin{aligned} p& = {} \frac{\partial G}{\partial q} \;, \end{aligned}$$

(113)

$$\begin{aligned} \zeta& = {} \frac{\partial G}{\partial I} \;, \end{aligned}$$

(114)

$$\begin{aligned} H'& = {} H \quad . \end{aligned}$$

(115)

Equation (113) implies

$$\begin{aligned} G(q, I) = \int _{q_0}^q p(q', I) \, {\textrm{d}}q', \end{aligned}$$

(116)

which provides the transformation rules

$$\begin{aligned} p(q,I)& = {} \frac{\partial G}{\partial q} = \int _{q_0}^{q} \frac{\partial p}{\partial q}(q, I) \, {\textrm{d}}q \end{aligned}$$

(117)

$$\begin{aligned} \zeta (q, I)& = {} \frac{\partial G}{\partial I} = \int _{q_0}^{q} \frac{\partial p}{\partial I}(q, I) \, {\textrm{d}}q \qquad . \end{aligned}$$

(118)

Equation (115) implies that the change of canonical variables $(p,q) \mapsto (I,\zeta )$ is a change of coordinates that does not perturb the constant energy surfaces in phase space.

Canonical equations of motion are very simple in action-angle coordinates. Because of Eq. (110), the action is constant along any orbit of constant energy E

$$\begin{aligned} \frac{{\textrm{d}}I}{{\textrm{d}}t} = - \frac{\partial H}{\partial \zeta } =0 \quad . \end{aligned}$$

(119)

The motion of $\zeta$ is ruled by

$$\begin{aligned} \frac{{\textrm{d}}\zeta }{{\textrm{d}}t} = \frac{ {\textrm{d}}H}{ {\textrm{d}}I} \equiv \omega (I) = const \quad . \end{aligned}$$

(120)

Equations (110) and (113) imply the range of $\zeta$ is

$$\begin{aligned}{} & {} \Delta \zeta = \frac{\partial }{\partial I} \int p(q, E) \, {\textrm{d}}q = 2 \pi , \end{aligned}$$

(121)

where the integral runs over the range of q, and the right hand side results from the definition of I, Eq. (110). Because of this range, $\zeta$ is called angle. It evolves linearly in time with the frequency $\omega (I)$.

A word of caution is of order for systems with a separatrix. Indeed the partial derivative with respect to I is not defined at the X-point. So does $\zeta$. In reality, a separatrix separates orbits with different topologies, which implies a discontinuity of the definition of the action when crossing it. Away from a separatrix, the integral in Eq. (110) turns out to be a curvilinear integral on a closed orbit.

We conclude by mentioning that the action defined in Eq. (21) and the one in Eq. (110) defining the canonical momentum in action-angle coordinates are not physically related, except for their dimensions.

Appendix 4: Intuitive physical approach to the vector potential

Any divergence free field (like the magnetic field ${\textbf{B}}$) in a torus can be written in its canonical form, as showed in Sect. 4.1,

$$\begin{aligned} {\textbf{B}} = \nabla \psi _t \times \nabla \theta / 2 \pi - \nabla \psi _p \times \nabla \varphi / 2 \pi , \end{aligned}$$

(122)

where ${\textbf{x}}=(\psi _t, \theta ,\varphi )$ are general toroidal coordinates. A similar form can be used for the vector potential ${\textbf{A}}$,

$$\begin{aligned} {\textbf{A}} = \psi _t \, \nabla \theta / 2 \pi - \psi _p \, \nabla \varphi / 2 \pi \, + \nabla G \, , \end{aligned}$$

(123)

that can be always defined up to a gauge, which means up to the gradient of a scalar function here named G, irrelevant for the corresponding magnetic field, ${\textbf{B}}= \nabla \times {\textbf{A}}$.

Here we show the equivalence between the covariant components of the vector potential and the magnetic fluxes. We first remind the definition of covariant components of a vector, defined by ${\textbf{A}}=A_i \nabla x^i$, where the $\nabla x^i$ are the gradients of the spatial coordinates. We use an intuitive physical approach, and in particular Stokes theorem that states the equivalence between a circulation and a flux:

$$\begin{aligned} \oint _{l} {\textbf{A}} \cdot d{\textbf{l}} = \int _{\Sigma } (\nabla \times {\textbf{A}}) \cdot d \mathbf {\Sigma } \end{aligned}$$

(124)

being $\Sigma$ any surface having the oriented circuit l as a boundary. If ${\textbf{A}}$ is the vector potential, the circulation of ${\textbf{A}}$ along l immediately implies the flux of the magnetic field ${\textbf{B}}=\nabla \times {\textbf{A}}$ through $\Sigma$.

In different frames of references, fluxes assume different physical meaning depending on the definition of the surface $\Sigma$ through which they are computed, see for example (Predebon et al. 2016). In the more general definition, poloidal and toroidal fluxes are the fluxes across some surface $\Sigma$ defined by fixed values of the chosen angle $\theta$ or $\varphi$. We anticipate that only in magnetic (or action-angle) coordinates $\Sigma$ represents the magnetic flux surfaces.

In Sect. D.1 we prove that function $A_i({\textbf{x}})$ is a measure of the poloidal/toroidal flux across the surface defined by $\Sigma =A_i({\textbf{x}})=\text{ constant }$, which in general does not correspond to a magnetic flux surface, and without a clear geometric interpretation. In particular, in general toroidal coordinates $(x^1, x^2, x^3)=(r, \theta , \varphi )$ and choosing the axial gauge $A_1=0$, it is true that:

• $A_2 = \psi _t/2\pi$: the $A_2=A_\theta$ component is a measure (up to $2 \pi$) of the toroidal flux $\psi _t$ across the surface defined by $\Sigma = A_\theta (r, \theta , \varphi )=\text{ constant }$ at $\varphi =\text{ constant }$.

• $A_3 = -\psi _p/2\pi$: the $A_3=A_\varphi$ component is a measure (up to $-2 \pi$) of the poloidal flux $\psi _p$ across the ribbon bounded by the magnetic axis and the surface defined by $\Sigma = A_\varphi (r, \theta , \varphi )=\text{ constant }$ at $\theta =\text{ constant }$. Equivalently, the $A_3$ component can be defined as a measure (up to $2 \pi$) of the poloidal flux across the disk outside surface $\Sigma$ at $\theta =\text{ constant }$.

When magnetic flux surfaces exist, they are defined by function $\Sigma =H(p,q)=\psi _p(r,\theta )=\text{ constant }$, but not by $\Sigma =\psi _t(r, \theta )$, as shown in Sect. D.1. Only choosing magnetic (or action-angle) coordinates, defined in Sect. 4.2, magnetic flux surfaces are well-defined by both magnetic fluxes, $\Sigma =H(I)=\psi _P(\psi _T)$, that can be used as flux-surface labels. Following the method described in section D.1, and choosing the axial gauge $A_1=0$ and magnetic coordinates ${\textbf{x}}=(\psi _T, \zeta , \varphi )$, one can prove that:

• $A_2 = \psi _T/2\pi$: $I(\psi _T)=A_\zeta (\psi _T)$ is a measure (up to $2 \pi$ for the $A_\zeta$ component of ${\textbf{A}}$) of the toroidal flux $\psi _T$ across magnetic flux surfaces at $\varphi =\text{ constant }$.

• $A_3 = -\psi _P/2\pi$: $H(I)=A_\varphi (\psi _T)$ is a measure (up to $- 2 \pi$ for $A_\varphi$) of the poloidal flux $\psi _P$ across the ribbon bounded by the magnetic axis and the magnetic flux surfaces at $\zeta =\text{ constant }$.

Magnetic coordinates therefore define the only coordinate systems in which the magnetic fluxes assume the usual meaning of fluxes through magnetic flux surfaces. In addition to the results reported in this review, knowing the relationship between magnetic fluxes and the $A_i$ components allows to tackle the study of physical problems in a geometrical way. The transformation rules of the covariant components of a vector have been used for example to study the relationship between the Fourier spectra of the magnetic fluxes in different frame of reference defined by magnetic coordinates (Predebon et al. 2016).

1.1 Appendix 4.1: Magnetic fluxes in general toroidal coordinates

Let us compute the toroidal flux $\psi _t(r, \theta )$ using its general definition for a time-independent Hamiltonian system, for which the $A_i$’s components do not depend on time (here identified by the toroidal angle $\varphi$):

$$\begin{aligned} \psi _t& = {} \int _{\Sigma (\varphi )} \, {\textbf{B}} \cdot {\textrm{d}}\mathbf {\Sigma (\varphi )} = \int _{\Sigma (\varphi )} \, (\nabla \times {\textbf{A}}) \cdot {\textrm{d}}\mathbf {\Sigma } = \oint _{\partial \Sigma (\varphi )} {\textbf{A}} \cdot {\textrm{d}}{\textbf{l}} \end{aligned}$$

(125)

$$\begin{aligned}& = {} \int _0^{2 \pi } A_{\theta }(r, \theta ) \, {\textrm{d}}\theta \end{aligned}$$

(126)

$$\begin{aligned}& = {} \, 2 \pi \, A_{\theta }(r, \theta ) = \psi _t(r, \theta ) \end{aligned}$$

(127)

The definition of the toroidal flux and Stokes theorem have been used in the first line. The symbol $\Sigma (\varphi )$ defines the surfaces at $\varphi =\text{ constant }$, and the elementary surface element is ${\textrm{d}}\Sigma (\varphi )=\sqrt{g} \, \nabla \varphi \, {\textrm{d}}r \, {\textrm{d}}\theta$, where $\sqrt{g}$ is the inverse of the Jacobian of the coordinate system. The line element is defined by ${\textrm{d}}{\textbf{l}}={\textrm{d}}x^i {\textbf{e}}_i$, where the ${\textbf{e}}_i$’s are the tangent basis vectors. Because of the constancy of the toroidal angle $\varphi$ and of the choice $A_1=A_r=0$ for the axial gauge, we obtain Eq. (126). Equation (127) can be true if and only if we consider the flux through surface $\Sigma = A_{\theta }(r, \theta )= \text{ constant }$. This ends the explanation of the physical meaning of $A_{\theta }$.

The poloidal flux can be written in the same way:

$$\begin{aligned} \psi _p^d& = {} \int _{\Sigma (\theta )} \, {\textbf{B}} \cdot {\textrm{d}}\mathbf {\Sigma (\theta )} = \int _{\Sigma (\theta )} \, (\nabla \times {\textbf{A}}) \cdot {\textrm{d}}\mathbf {\Sigma } = \oint _{\partial \Sigma (\theta )} {\textbf{A}} \cdot {\textrm{d}}{\textbf{l}}\end{aligned}$$

(128)

$$\begin{aligned}& = {} \int _0^{2 \pi } A_{\varphi }(r, \theta ) \, {\textrm{d}}\varphi \end{aligned}$$

(129)

$$\begin{aligned}& = {} \, 2 \pi A_{\varphi }(r, \theta ) = \, - H(p,q) \end{aligned}$$

(130)

where symbol $\psi _P^d$ has been introduced for the poloidal flux through a disk defined outside surface $\Sigma (\theta )$ (w.r.t the magnetic axis). Symbol $\Sigma (\theta )$ defines the surfaces at $\theta =\text{ constant }$, and ${\textrm{d}}\Sigma (\theta )=\sqrt{g} \, \nabla \theta \, {\textrm{d}}r \, {\textrm{d}}\varphi$. Equivalences in Eq. (130) are written reminding identification (32), and are true if and only if in Eq. (129) we consider the flux through surface $\Sigma = A_{\varphi }(r, \theta )= \text{ constant } = -H(p,q)$, defining magnetic flux surfaces.

It is worth noting that the circulation in ${\textrm{d}}\varphi$, at the $\theta =\text{ constant }$ angle, defines the ribbon outside the $\Sigma (\theta )$ surface, and that is why symbol $\psi _p^d$ has been introduced. The relation with the poloidal flux $\psi _p$ inside the flux surface can be found in chapter 4 of D’haeseleer et al. (2012), which states the complementarity of the two poloidal fluxes with respect to the total one. In the case where magnetic coordinates are used, each of the two fluxes can be chosen to label magnetic flux surfaces, but $\psi _p^d$ has the disadvantage of decreasing radially outward. Therefore, calling $\rho$ any label of magnetic flux surfaces, it is natural to choose $\rho =\psi _P$ or $\rho =-\psi _P^d$.

1.2 Appendix 4.2: Using a classical tokamak formula for the magnetic field

A classical formula for tokamak magnetic fields is

$$\begin{aligned} {\textbf{B}}=\nabla \varphi \times \nabla \psi + I(\psi ) \nabla \varphi \end{aligned}$$

(131)

where $\psi =\psi _p/2\pi$ is the radial variable proportional to the poloidal flux, $I(\psi )$ is a flux function that will be better defined in the following, and $\varphi$ is the symmetry angle. The axisymmetry of the system is used in the choice of poloidal and toroidal angles satisfying the orthogonal relations $\nabla \psi \cdot \nabla \varphi =0$ and $\nabla \varphi \cdot \nabla \theta =0$, as shown in section 6.2 of D’haeseleer et al. (2012).

When magnetic coordinates are used, by taking into account that for magnetic flux surfaces, $\psi _P=\psi _P(\psi _T)$ and $\nabla \psi _T = ({\textrm{d}}\psi _T/{\textrm{d}}\psi _P) \nabla \psi _P$, it is easy to see that Eq. (46) for the magnetic field is equivalent to the Clebsch relation

$$\begin{aligned} {\textbf{B}} = \nabla \psi \times \nabla (q \theta - \varphi )\, \end{aligned}$$

(132)

where $q=1/\iota ={\textrm{d}}\psi _T/{\textrm{d}}\psi _P = {\textrm{d}}\varphi / {\textrm{d}}\theta$, as defined in (59). Section 6.2 of D’haeseleer et al. (2012) shows (131) and (132) are equivalent when the orthogonal coordinates are magnetic coordinates too. Therefore (131) preserves the Hamiltonian structure defined by Eqs. (45)–(46).

Section 6.3 of D’haeseleer et al. (2012) shows that Eq. (131) can be recovered even in non-magnetic coordinates. In this case, however, Clebsch relation (132) can be recovered only for a particular choice of the poloidal angle such that the Jacobian of the coordinate system $\sqrt{g} \propto R^2$, where R is the radial coordinate in a cylindrical coordinate system ($R,\varphi ,Z$). This yields

$$\begin{aligned} I(R,Z) = \frac{q R^2}{\sqrt{g}} , \end{aligned}$$

(133)

which is valid in magnetic coordinates too. I(R, Z) can be written as $I=R B_T$ in cylindrical coordinates. Sections 6.2 and 6.3 of D’haeseleer et al. (2012) show that I is a flux function for an isotropic pressure plasma equilibrium and it is physically related to the poloidal flux external to the $\psi$-constant flux surfaces (including plasma and coils currents).

When Eq. (133) holds, for a given I(R, Z), one can derive q(R, Z). Because of the symmetry in $\varphi$, $\psi _p = \psi _p(R,Z)$. To $(R,Z=0)$ corresponds q(R, 0) and $\psi _p = \psi _p(R,0)$. The latter expression can be inverted to yield $R(\psi _p)$ on the flux surface $\psi _p=constant$ that contains point (R, 0). Because of the existence of magnetic surfaces, this expression can be set into q(R, 0), which yields $q(\psi _p)$. Then, $\psi _T$ can be computed from Eq. (59) with $\iota = 1/q$. Therefore, the vector potential can be computed from Eq. (45), and (131) preserves again the Hamiltonian structure defined by Eqs. (45)–(46).

In the case of general orthogonal (with respect to the toroidal angle) coordinate systems, expression (131) preserves the very general Hamiltonian structure given by Eq. (46), for which only the divergence null of the magnetic field on the torus is required. However, there is no simple way to compute $\psi _T$.

Appendix 5: Change of coordinates between magnetic coordinates

We showed in Appendix 4 the equivalence between the covariant components of the vector potential and the magnetic fluxes, as introduced also in Sect. 4. In general, $\psi _t=\psi _t({\textbf{x}})$ and $\psi _p=\psi _p({\textbf{x}})$ are poloidal and toroidal fluxes that do not define magnetic flux surfaces. Magnetic flux surfaces exist only in integrable systems, and are defined by $H(p,q)=\text{ constant }$. Only when using magnetic (or action-angle) coordinates to describe the system, magnetic flux surfaces are equivalently defined by both magnetic fluxes, for which $\psi _P=\psi _P(\psi _T)$ holds. Capital letters in indices are used to distinguish them from the more general $\psi _p({\textbf{x}})$ and $\psi _t({\textbf{x}})$ fluxes with a less geometrical intuitive definition (see Appendix 4).

Here we prove the relations defining the change of coordinates between magnetic coordinates, considering that the vector potential can be written in the form

$$\begin{aligned} {\textbf{A}} = \psi _T \, \nabla \theta / 2 \pi - \psi _P \, \nabla \varphi / 2 \pi \, , \end{aligned}$$

(134)

where $\psi _P=\psi _P(\psi _T)$, if and only if a set of magnetic coordinates is chosen.

In particular, we prove that Eqs. (61)–(62), here reported

$$\begin{aligned} \zeta& = {} \zeta _N + f(\psi _T,\zeta _N, \varphi _N), \end{aligned}$$

(135)

$$\begin{aligned} \varphi& = {} \varphi _N + g(\psi _T,\zeta _N, \varphi _N), \end{aligned}$$

(136)

define the change of coordinates between magnetic coordinates, from $(\zeta , \varphi )$ to $(\zeta _N, \varphi _N)$, if and only if functions f and g are linked by Eq. (65):

$$\begin{aligned} f = \iota g - h(\psi _T). \end{aligned}$$

(137)

We prove it showing that if ${\textbf{A}}$ can be written in its general form (123) for the fluxes $\psi _P(\psi _T)$, both in $(\psi _T, \zeta , \varphi )$ and $(\psi _T, \zeta _N, \varphi _N)$ coordinates, then Eq. (137) must be valid: the following equations are derived simply using Eq. (123) in the magnetic coordinates $(\psi _T, \zeta , \varphi )$, their relation with the $(\psi _T, \zeta _N, \varphi _N)$ coordinates, and the definition of the gradient of a function:

$$\begin{aligned} 2\pi {\textbf{A}}& = {} \psi _T \nabla \zeta - \psi _P \nabla \varphi = \end{aligned}$$

(138)

$$\begin{aligned}& = {} \psi _T \Big ( \nabla \zeta _N + \nabla f \Big ) - \psi _P \Big ( \nabla \varphi _N + \nabla g \Big ) = \end{aligned}$$

(139)

$$\begin{aligned}& = {} \psi _T \Big ( \nabla \zeta _N + \frac{\partial f}{\partial \psi _T} \nabla \psi _T + \frac{\partial f}{\partial \zeta _N} \nabla \zeta _N + \frac{\partial f}{\partial \varphi _N} \nabla \varphi _N \Big ) +\end{aligned}$$

(140)

$$\begin{aligned}- & {} \psi _P \Big ( \nabla \varphi _N + \frac{\partial g}{\partial \psi _T} \nabla \psi _T + \frac{\partial g}{\partial \zeta _N} \nabla \zeta _N + \frac{\partial g}{\partial \varphi _N} \nabla \varphi _N \Big ) = \end{aligned}$$

(141)

$$\begin{aligned}& = {} \psi _T \nabla \zeta _N - \psi _P \nabla \varphi _N + F \end{aligned}$$

(142)

where

$$\begin{aligned} F = \Big ( \psi _T \frac{\partial f}{\partial \psi _T} - \psi _P \frac{\partial g}{\partial \psi _T} \Big ) \nabla \psi _T + \Big ( \psi _T \frac{\partial f}{\partial \zeta _N} - \psi _P \frac{\partial g}{\partial \zeta _N} \Big ) \nabla \zeta _N + \Big ( \psi _T \frac{\partial f}{\partial \varphi _N} - \psi _P \frac{\partial g}{\partial \varphi _N} \Big ) \nabla \varphi _N \end{aligned}$$

(143)

In order to reduce Eq. (142) - written in the $(\psi _t, \zeta _N, \varphi _N)$ coordinates - to the general form in Eq. (123), function F must be the gradient of some function G: let us say $F = \nabla G(\psi _T, \zeta _N, \varphi _N)$, with F given in Eq. (143). Therefore it results:

$$\begin{aligned} \frac{\partial G}{\partial \psi _T}& = {} \frac{\partial }{\partial \psi _T} \big ( \psi _T f - \psi _P g) - f + \iota g \end{aligned}$$

(144)

$$\begin{aligned} \frac{\partial G}{\partial \zeta _N}& = {} \frac{\partial }{\partial \zeta _N} \big ( \psi _T f - \psi _P g) \end{aligned}$$

(145)

$$\begin{aligned} \frac{\partial G}{\partial \varphi _N}& = {} \frac{\partial }{\partial \varphi _N} \big ( \psi _T f - \psi _P g) \end{aligned}$$

(146)

where $\iota ={\textrm{d}}\psi _P / {\textrm{d}}\psi _T$ is the rotational transform of the configuration and the fluxes depend on the radial variable only. For Eqs. (144)–(146) to be compatible, $(\iota g - f)$ in Eq. (144) must be a function of $\psi _T$ only: $\iota g - f = h(\psi _T)$, which ends the first part of the proof.

Vice versa (only if), one can prove that if Eq. (137) holds, then ${\textbf{A}}$ can be written in its canonical form. Applying Eqs. (135)–(136) together with Eq. (137) in Eq. (138), one obtains the canonical form for ${\textbf{A}}$ in $(\psi _T, \zeta _N, \varphi _N)$ coordinates with

$$\begin{aligned} G = \big ( \iota \psi _T - \psi _P \big ) g - \int \psi _T \frac{\partial h}{\partial \psi _T} {\textrm{d}}\psi _T \end{aligned}$$

(147)

This is in agreement with what already found in Eq. (144) and ends the proof.

Appendix 6: Perturbation of the vector potential

A perturbation to a regular magnetic field involves the perturbation of both poloidal and toroidal magnetic fluxes through magnetic flux surfaces. Using expression (45) for ${\textbf{A}}$, its perturbation can be written as

$$\begin{aligned} \delta {\textbf{A}} = \delta \psi _T \, \nabla \theta / 2 \pi - \delta \psi _P \, \nabla \varphi / 2 \pi , \end{aligned}$$

(148)

where we consider both $\delta \psi _T$ and $\delta \psi _P$ are function of the coordinates ${\textbf{x}}=(\psi _T, \theta , \varphi )$.

Here we prove that whatever the perturbation to the toroidal flux $\delta \psi _T$, there exists an appropriate redefinition of this variable that permits to consider the perturbation to be only on the Hamiltonian of the system (the poloidal flux), as written in Eq. (82).

Let $\psi '_T = \psi _T + \delta \psi _T$ and define $\delta \psi '_T(\psi '_T, \theta , \varphi ) = \psi _T - \psi '_T$, which leads to the redefinition of the radial coordinate $\psi _T = \psi '_T + \delta \psi '_T$. The perturbed potential vector ${\textbf{A}}+\delta {\textbf{A}}$, written as a function of $\psi '_T$, is

$$\begin{aligned} {\textbf{A}}' = \psi '_T \, \nabla \theta / 2 \pi - \psi '_P(\psi '_T + \delta \psi '_T, \theta , \varphi ) \, \nabla \varphi / 2 \pi , \end{aligned}$$

(149)

where $\psi '_P = \psi _P(\psi '_T + \delta \psi '_T) + \delta \psi _P(\psi '_T + \delta \psi '_T, \theta , \varphi )$. We now define $\Delta \psi _P(\psi '_T, \theta , \varphi ) = \psi '_P(\psi '_T, \theta , \varphi ) - \psi _P(\psi '_T)$, in order to write an expression for ${\textbf{A}}'$ that highlights a perturbation only of the poloidal flux

$$\begin{aligned} {\textbf{A}} ' = \psi '_T \, \nabla \theta / 2 \pi - [\psi _P(\psi '_T) + \Delta \psi _P(\psi '_T, \theta , \varphi )] \, \nabla \varphi / 2 \pi . \end{aligned}$$

(150)

This shows the perturbed magnetic field can always be defined by a perturbation of the poloidal flux only. The memory of the change in $\psi _T$ is lost when going to the Hamiltonian and using canonical coordinates, where it corresponds to a conjugate momentum with the same name p. In the literature, for practical purposes, often people perturb directly the Hamiltonian, which hides the actual change in the potential vector, as done in Eq. (82).

Appendix 7: Magnetic island width

Small perturbations of an integrable magnetic field open magnetic islands around the magnetic flux surface where the perturbation is resonant. By definition, resonant magnetic flux surfaces are identified by a rational value of the rotational transform, $\iota (\psi _T)=n_0/m_0$. Magnetic perturbations resonant on this surface have the form $H_{1,m_0,n_0}(p_0) \cos (m_0 \theta -n_0 \varphi )$. Using identities (47)–(50) between magnetic fluxes and canonical coordinates, we define $p_0$ as the value of the canonical momentum (or toroidal flux) on the resonant flux surface defined by $\iota (p_0)=n_0/m_0$, the canonical variable q as the poloidal angle $\theta$ and the canonical time as the toroidal angle $\varphi$.

We recall here that any small resonant magnetic perturbation can be described by a Hamiltonian formally identical to the Hamiltonian of a simple pendulum. Two equivalent demonstrations of this fact are provided in the next subsections.

1.1 Pedestrian calculation

In this subsection the pendulum Hamiltonian is derived from the canonical equations of motion.

Let p be the value of the toroidal flux (canonical momentum) of a magnetic flux surface very near to the resonant one defined by $p_0$. Let $\delta p = p - p_0$, and expand Hamiltonian (82) in $\delta p$ next to $p_0$. Since the width of the magnetic island in $\delta p$ will turn out to scale like $\sqrt{H_{1,m_0,n_0}(p_0)}$, considered as small, this expansion must be done up to order 2 in $\delta p$. This yields the reduced Hamiltonian

$$\begin{aligned} H_r(\delta p,\theta ,\varphi ) = H_0(p_0) + \iota (p_0)\delta p + \frac{1}{2}\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} \delta p^2 + H_{1,m_0,n_0}(p_0) \cos (m_0 \theta - n_0 \varphi ), \end{aligned}$$

(151)

from which we deduce the canonical equation of motion by using identities (25,26)

$$\begin{aligned} {\dot{\theta }}& = {} \frac{{\textrm{d}}\theta }{{\textrm{d}}t} = \frac{\partial H_r}{\partial p} = \iota (p_0) + \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} \delta p \end{aligned}$$

(152)

$$\begin{aligned} {\dot{p}}& = {} \frac{dp}{dt} = - \frac{\partial H_r}{\partial q} = m_0 H_{1,m_0,n_0}(p_0) \sin (m_0 \theta - n_0 \varphi ) \end{aligned}$$

(153)

$$\begin{aligned} \ddot{\theta }& = {} m_0 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) \sin (u), \end{aligned}$$

(154)

$H_r$ does not depend separately on $\theta$ and $\varphi$, but only on their helical composition. In order to recognize the Hamiltonian $H_p$ of the pendulum, the helical angle $u=m_0 \theta - n_0 \varphi$ must be introduced.

This yields $\ddot{u} = m_0 \ddot{q} = m_0^2 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) \sin (u)$, which results from the combination of the canonical equations

$$\begin{aligned} \dot{u}& = {} p' \end{aligned}$$

(155)

$$\begin{aligned} \dot{p'}& = {} m_0^2 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) \sin (u), \end{aligned}$$

(156)

of the pendulum Hamiltonian

$$\begin{aligned} H_p(p',u) = \frac{1}{2}p'^2 + m_0^2 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) \cos (u). \end{aligned}$$

(157)

For the general pendulum Hamiltonian $H=G p^2/2- F$, where G and F characterize the kinetic and potential energy respectively, the half-width of the separatrix of the pendulum in phase space is $W/2 = 2 \sqrt{F/G}$. The half-width of the separatrix of the pendulum in Eq. (157) is

$$\begin{aligned} \Delta p' = 2\sqrt{\left| m_0^2 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) \right| }. \end{aligned}$$

(158)

Equations (152) and (157), together with the definition of the helical angle u and of the toroidal angle $\varphi$ as canonical time t, imply $p' = m_0 {\dot{q}}- n_0 = m_0 (\iota (p_0) + \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} \delta p) \, - \, n_0$. Therefore the width in $p'$ translates in an island width in units of p, which is $m_0 \frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p}$ smaller, and given by Eq. (90) here recalled

$$\begin{aligned} \Delta p = \Delta \psi _T = 2\sqrt{\left| \frac{H_{1,m_0,n_0}(p_0)}{\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p}} \right| } . \end{aligned}$$

(159)

Note that this is the formula for the half width of a magnetic island. Note moreover that the island width is proportional to the square root of the perturbation of the Hamiltonian, and therefore of the perturbation of a magnetic flux, and not to a perturbation of a component of the magnetic field.

The X and O points correspond to the extrema of the perturbation of the Hamiltonian respectively. The X-point corresponds to $u_X = 0$ and the O-point to $u_O = \pi$ if $\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} H_{1,m_0,n_0}(p_0) >0$ and the opposite otherwise. This implies

$$\begin{aligned} \cos (u_O) H_{1,m_0,n_0}(p_0) = - \textrm{sgn}[\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p}] |H_{1,m_0,n_0}(p_0)| . \end{aligned}$$

(160)

1.2 Calculation with a canonical change of variables

In this subsection, the Hamiltonian of the pendulum is obtained through a canonical change of coordinates, that highlights the helical symmetry of the system. We transform Hamiltonian (82) by a canonical change of variables from $(p,\theta )$ to (P, u) defined by the generating function $G(P,\theta , \varphi ) = P (m_0 \theta - n_0 \varphi ) + p_0 \theta$. This yields

$$\begin{aligned} u& = {} \frac{\partial G}{\partial P} = m_0 \theta - n_0 \varphi \end{aligned}$$

(161)

$$\begin{aligned} p& = {} \frac{\partial G}{\partial \theta } = m_0 P + p_0 , \end{aligned}$$

(162)

which implies $P = (p-p_0)/ m_0$ and the new Hamiltonian

$$\begin{aligned} H'(P,u,\varphi ) = H + \frac{\partial G}{\partial \varphi } = H_0(p_0) + \frac{m_0^2}{2}\frac{{\textrm{d}}\iota (p_0)}{{\textrm{d}}p} P^2 + H_{1,m_0,n_0}(p_0) \cos (u), \end{aligned}$$

(163)

which is again a pendulum Hamiltonian with other units for P, except for the dynamically irrelevant $H_0(p_0)$ term. This yields again the magnetic island width Eq. (90) with the same values of u as above for the O-point and X-point respectively.

Appendix 8: Generalization of the magnetic island width formula

Perturbation $\delta {\textbf{B}}(\psi _T, \theta , \varphi )$ of a regular magnetic field is provided by a perturbation $\delta {\textbf{A}}(\psi _T, \theta , \varphi )$ of both components of the vector potential (the third one being killed by choosing an axial gauge). Section 5.1 considers the case where an appropriate redefinition of the toroidal flux enables considering the magnetic perturbation to bear only on the poloidal one, as shown in Appendix 6. Here we obtain the same results as Sect. 5.2, but considering the perturbation on both fluxes. Covariant components of ${\textbf{A}}$ and magnetic fluxes are identified remembering the results of Appendix 4, $\psi _t=2\pi A_\theta$ and $\psi _p=-2\pi A_\varphi$.

A general perturbation can be decomposed in a whole spectrum of Fourier components. We consider the case of a single Fourier component perturbation to the equilibrium magnetic field whose magnetic flux surfaces are defined by the equilibrium fluxes $\psi _P(\psi _T)$. We consider that ${\textbf{x}}=(\psi _T, \theta , \varphi )$ are magnetic coordinates for the equilibrium field, so the perturbed fluxes can be written as

$$\begin{aligned}{} & {} \psi _t(\psi _T, \theta , \varphi ) \simeq \psi _T + \psi _t^{m_0,n_0}(\psi _T) \, e^{i u} + c.c. = 2 \pi A_\theta \end{aligned}$$

(164)

$$\begin{aligned}{} & {} \psi _p(\psi _T, \theta , \varphi ) \simeq \psi _P(\psi _T) + \psi _p^{m_0,n_0}(\psi _T) \, e^{i u} + c.c.=- 2 \pi A_\varphi \end{aligned}$$

(165)

where $m_0$ and $n_0$ define, respectively, the poloidal and toroidal periodicity of the single perturbation and $u = m_0 \theta - n_0 \varphi$ defines the helical angle. Being Fourier components, $\psi _t^{m_0,n_0}(\psi _T)$ and $\psi _p^{m_0,n_0}(\psi _T)$ are complex functions and c.c. means the complex conjugate. Note moreover that capital letter T is used to indicate the equilibrium toroidal flux, used as radial coordinate, whereas the lowercase letters t and p are used for the perturbed fluxes. Clearly, Eq. (165) correspond to Eq. (82).

Using both Eqs. (164)–(165), we compute the $S_O$ flux introduced in Sect. 5.2, as

$$\begin{aligned} S_O = \frac{1}{2 \pi } \int _O [p {\textrm{d}}\theta - H(p,q,\varphi ) {\textrm{d}}\varphi ] = \int _O [A_\theta {\textrm{d}}\theta + A_\varphi {\textrm{d}}\varphi ] \end{aligned}$$

(166)

which is a line integral along the line defined by the O-point of the $(m_0, n_0)$ island developed around the resonant surface defined by $\iota (\psi _T)={\textrm{d}}\psi _P / {\textrm{d}}\psi _T= n_0/m_0$. The $S_X$ flux is defined in an analogous way along the line defined by the X-point. We show that they are the helical fluxes through the flux surface defined by the O and X-point respectively. Their difference, the $\Phi _{OX}$ flux, can be written in terms of the perturbation to the helical flux at the resonant surface, and is defined as the flux through the ribbon defined by the extremal points of the island.

In computing $S_O$, we assume that $m_0$ and $n_0$ are mutually relatively prime, $\varphi$ varies by $2 \pi m_0$ along O and $\theta$ varies by $2 \pi n_0$, while $u_O=\text{ constant }$. This yields

$$\begin{aligned} S_O& = {} \frac{1}{2\pi } \Big [ \psi _T + \psi _t^{m_0,n_0}(\psi _T) \, e^{i u_O} \Big ] \int _O {\textrm{d}}\theta - \frac{1}{2\pi } \Big [ \psi _P + \psi _p^{m_0,n_0}(\psi _T) \, e^{i u_O} \Big ] \int _O {\textrm{d}}\varphi +c.c. \end{aligned}$$

(167)

$$\begin{aligned}& = {} \Big [ n_0 \psi _T - m_0 \psi _P \Big ] + \Big [n_0 \psi _t^{m_0,n_0} - m_0 \psi _p^{m_0,n_0}\Big ] \, e^{i u_O} +c.c. \end{aligned}$$

(168)

where all radial functions must be evaluated on the rational surface defined by $\iota =n_0/m_0$. Introducing the helical flux

$$\begin{aligned} \psi _h(\psi _T, u)= m_0 \psi _p - n_0 \psi _t \, , \end{aligned}$$

(169)

$S_O$ in Eq. (168) can be written in terms of this flux through the O-point orbit as

$$\begin{aligned} -S_O& = {} \psi _H (\psi _T) + \psi _h^{m_0,n_0}(\psi _T) \, e^{i u_O} + c.c. = \psi _h(\psi _T, u_O) \end{aligned}$$

(170)

where $\psi _H$ is related to the equilibrium fluxes. To compute correctly the amplitude and phase of the Fourier component of the helical flux, $\psi _h^{m_0,n_0}(\psi _T)=\left| \psi _h^{m_0,n_0} \right| \, e^{ i\,\phi _h^{m_0,n_0}}$, as a function of the poloidal and toroidal ones, formulas for the sum of complex numbers must be used.

The computation of the $S_X$ flux follows the same steps, with $u_O$ being substituted by $u_X$ and remembering that $u_X$ is shifted by $\pi$ with respect to $u_O$: $u_O+\phi _h^{m_0,n_0}=0,\pi$ and $u_X+\phi _h^{m_0,n_0}=\pi ,0$ depending on the sign of the magnetic shear (see Appendix 7). Here $\phi _h^{m_0,n_0}$ is the phase of the resonant Fourier component of the helical flux. This yields

$$\begin{aligned} S_O-S_X = 4 \, sgn \Big [ \frac{{\textrm{d}}\iota }{{\textrm{d}}\psi _T} \Big ] \left| \psi _h^{m_0,n_0} \right| \end{aligned}$$

(171)

where, again, all radial functions must be evaluated on the resonant surface.

Let us now compare Eqs. (87) and (171) for $\Phi _{OX} = S_O-S_X$, the first obtained considering the perturbation to the vector potential to bear on the poloidal flux only as defined by Eq. (81), the latter considering perturbations (164)–(165) to both the fluxes. One can immediately note a simple change in the notation between the two equations, where $p = \psi _T$ and $p_0$ is the equilibrium toroidal flux on the resonant surface. Moreover, to derive Eq. (87) the phase of the single Fourier components of the perturbation has been neglected. This cannot be done in the case where both fluxes are perturbed.

More interesting is to note that both equations express the $\Phi _{OX}$ flux in terms of the perturbation to a helical flux evaluated at the resonant surface. Expressing the helical flux perturbation in terms of the perturbation to the poloidal and toroidal fluxes using definition (169), and formulas for the sum of complex numbers, it is straightforward to see that

$$\begin{aligned} \left| \psi _h^{m_0,n_0}\right| (\psi _T) = m_0 \left| \psi _p^{m_0,n_0}\right| \end{aligned}$$

(172)

if the perturbation is considered to the Hamiltonian $\psi _p$ only. This shows that Eq. (171) reduces to Eq. (87) in this case, considering also that $|H_{1,m_0,n_0}|=2 \, |\psi _p^{m_0,n_0}|$ for the chosen definitions of the perturbations, and this ends the proof.

1.1 Appendix 8.1: Previously introduced coordinate-independent fluxes

Equation (14) of reference (Boozer 2005) considers the Fourier component

$$\begin{aligned} \sqrt{g} \, \delta {\textbf{B}} \cdot \nabla \psi = b_{mn} \sin (n \varphi - m \theta ), \end{aligned}$$

(173)

written in our notations for the magnetic coordinates ${\textbf{x}}=(\psi , \theta , \varphi )$ with Jacobian $1/\sqrt{g}$. It computes from it the corresponding island half-width (16), which is exactly Eq. (90), if one identifies $|b_{mn}|$ and $2 |\Phi _{OX}|$. This proves $|b_{mn}|$ to be a coordinate-independent flux (and not a component of the magnetic field, despite the notation).

Another example can be found in reference (Park et al. 2008) which considers under equation (12) the single Fourier component

$$\begin{aligned} \sqrt{g} \, \delta {\textbf{B}} \cdot \nabla \psi = \Phi _{mn} \exp \mathrm{(m \theta - n \varphi )} +c.c. \end{aligned}$$

(174)

of a flux $\Phi$, written in our notations. It proves the resonant $|\Phi _{mn}|$ to be coordinate independent, being the same in each set of magnetic coordinates. It is straightforward to show that $|\Phi _{mn}| = |b_{mn}|/2 \pi = |\Phi _{OX}| / \pi$.

The definition of the curl in generic curvilinear coordinates, $B^i = \frac{1}{\sqrt{g}} \, \epsilon ^{ijk} \, \frac{\partial A_k}{\partial x^j}$, permits to express the flux $\Phi$ through the covariant components of the potential vector or, equivalently, the magnetic fluxes. Einstein’s convention has been used in the expression for the curl of ${\textbf{A}}$, where $\epsilon ^{ijk}=\pm 1$, depending on the order of the indexes. This yields

$$\begin{aligned} \Phi = \sqrt{g} \, \delta B^\psi = - \Big ( \frac{\partial A_\theta }{\partial \varphi } - \frac{\partial A_\varphi }{\partial \theta } \Big ) = -\frac{1}{2 \pi } \Big ( \frac{\partial \psi _t}{\partial \varphi } + \frac{\partial \psi _p}{\partial \theta } \Big ) \end{aligned}$$

(175)

Using definitions (164) and (165) for the fluxes around the resonant surfaces and the definitions $\psi _h = m_0 \psi _p - n_0 \psi _t$ of the helical flux and $u=m_0 \theta - n_0 \varphi$ of the helical angle, Eq. (175) can be written as

$$\begin{aligned} \Phi \simeq \Phi _{m_0,n_0}(\psi ) \, e^{i\,u} + c.c. = - \frac{i}{2 \pi } ( m_0 \psi ^{m_0,n_0}_p - n_0 \psi ^{m_0,n_0}_t ) \, e^{i\,u} + c.c. \end{aligned}$$

(176)

showing that, as the $\Phi _{OX}$ flux defined in this review, the flux $\Phi$ defined in Park et al. (2008) can be defined through the perturbation to the helical flux, i. e. the flux due to the radial perturbation to the magnetic field. The definition of $\Phi _{OX}$ through the helical flux perturbation is proved in Eqs. (88) and (171).

1.2 Appendix 8.2: An example: numerical calculation of a magnetic island width from RFX-mod experimental data

RFX-mod device (Sonato et al. 2003) is a large toroidal RFP device with major radius 2 m and minor radius of about 0.5 m operating in Padova, Italy. RFX-mod experimental data have been used here to compute the width of a $(m_0, n_0) = (1,7)$ core magnetic island applying the formula given by the last equality of Eq. (90) which involves the computation of the $\Phi _{OX}$ flux.

In RFX-mod, many Fourier components of a perturbation can be reconstructed for both the poloidal and toroidal magnetic fluxes from the solutions of Newcomb-like equations in toroidal geometry (Zanca and Terranova 2004). Considering just the single helical deformation related to the island periodicity, perturbed magnetic fluxes can be written as in Eqs. (164)–(165), with $p=\psi _t$ and $H=\psi _p$. The $\Phi _{OX} = S_O-S_X$ flux in Eq. (90) is here calculated using Eq. (171), derived in Appendix 8 considering the perturbation to both the fluxes, and not just on the Hamiltonian as done in deriving the analogous Eq. (87). The equilibrium fluxes, $p_0=\psi _T(r)$ and $H_0=\psi _P(r)$, are known as a function of the radius r of the unperturbed circular magnetic flux surfaces and this is used to get the final island width in units of lengths:

$$\begin{aligned} \Delta r = \Big ( \frac{{\textrm{d}}\psi _T}{{\textrm{d}}r} \Big ) ^{-1} \, \Delta p \end{aligned}$$

(177)

As a practical example we choose an island whose width can be also measured from the Poincaré plot in figure 6 of Predebon et al. (2018) and here reported in Fig. 3 on a horizontal plane. Both, the island width computed from Eq. (177) and with a ruler from the Poincaré plot, give an island width of about 12 cm, confirming the applicability and the correctness of the method proposed in Sect. 5.3.

Fig. 3

Poincaré plot of a $(m_0,n_0)=(1,7)$ magnetic island from RFX-mod experimental data