Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant

Ding, Siye; Garofalo, Andrea M.

doi:10.1007/s41614-022-00106-z

Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant

Special Topics
Open access
Published: 26 December 2022

Volume 7, article number 4, (2023)
Cite this article

Download PDF

You have full access to this open access article

Reviews of Modern Plasma Physics Aims and scope Submit manuscript

Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant

Download PDF

2764 Accesses
9 Citations
Explore all metrics

Abstract

The high poloidal-beta ($\beta _{\textrm{P}}$) regime was first proposed as a high bootstrap current scenario for a steady-state fusion pilot plant (FPP) in the 1990s (Kikuchi in Nucl Fusion 30:265, 1990). Since then, there have been many theoretical, modeling, and experimental research activities on this topic. A joint DIII-D/EAST research team began exploring the high-$\beta _{\textrm{P}}$ regime in 2013, focusing on addressing the needs of attractive FPP design by taking advantage of the extensive diagnostic set and sophisticated plasma control system on DIII-D and the well-developed integrated modeling capability at General Atomics. The ultimate goal is to demonstrate such a scenario on EAST with truly long pulse and metal wall compatibility. This paper summarizes the highlights of the research results on DIII-D by the joint team in the past decade. Experimental evidence and modeling analysis show the high-$\beta _{\textrm{P}}$ scenario has great advantages in addressing key needs for an attractive FPP design, such as high-energy confinement quality at low rotation, excellent core-edge integration, high line-averaged density above the Greenwald limit, low disruption risk, and high bootstrap current fraction for steady-state operation. This provides a relatively safe and economical option to base an FPP design on that will lead to commercial fusion energy.

DIII-D Research to Prepare for Steady State Advanced Tokamak Power Plants

Article Open access 03 September 2018

The Princeton Field-Reversed Configuration for Compact Nuclear Fusion Power Plants

Article 31 January 2023

A high-density and high-confinement tokamak plasma regime for fusion energy

Article Open access 24 April 2024

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

1 Introduction

Sustained toroidal plasma current is required in tokamaks and is a major challenge for steady-state tokamak reactor design. There are two approaches to generate non-inductive plasma current in a tokamak. One relies on external auxiliary current drive (Fisch 1987), including neutral beam current drive, electron cyclotron current drive, lower hybrid wave current drive, fast wave current drive (Wesson 2004) and helicon current drive (Pinsker 2015). The other is the so-called “bootstrap current”, a self-generated plasma current due to the existence of trapped particles and density and temperature gradients between magnetic surfaces (Wesson 2004). In the high density conditions expected in a fusion reactor, the external current drive efficiency will be low. This means that a lot of power will be needed for external current drive, which would reduce the fusion gain ($Q=P_{\textrm{fus}}/P_{\textrm{aux}}$), in a fusion reactor. Here, $P_{\textrm{fus}}$ is the fusion power and $P_{\textrm{aux}}$ is the total auxiliary power. Therefore, a high poloidal-beta scenario aimed at maximizing bootstrap current fraction ($f_{\textrm{bs}}$) in a reactor was proposed in 1990 (Kikuchi 1990). Bootstrap fraction $f_{\textrm{bs}}\sim \epsilon ^{0.5}\beta _{\textrm{P}}\sim \epsilon ^{0.5}\beta _{\textrm{N}}q_{95}$, where $\epsilon$ is inversed aspect ratio, $\beta _{\textrm{P}}$ is poloidal beta, $\beta _{\textrm{N}}$ is normalized beta, and $q_{95}$ is safety factor at the 95% poloidal flux surface. For a given reactor design, $\epsilon$ is fixed. Two approaches for high $f_{\textrm{bs}}$ are high $\beta _{\textrm{N}}$ and high $q_{95}$. Since $\beta _{\textrm{N}}$ could be limited by MHD stability with a typical value around 3.5 (Troyon et al. 1984), increasing $q_{95}$, i.e., decreasing plasma current, becomes a standard choice for accessing this high $f_{\textrm{bs}}$ regime. Based on this concept, a steady-state reactor scenario with $\beta _{\textrm{P}}\ge 2.0$, $f_{\textrm{bs}}$ up to 70% and $Q\sim 30$ was proposed in Kikuchi (1990).

Experimentally, multiple tokamaks explored the high-$\beta _{\textrm{P}}$ scenario. Soon after the proposal of a high-$\beta _{\textrm{P}}$ steady-state reactor design, such a regime was achieved and studied on the TFTR tokamak using a fast current ramp-down technique (Sabbagh et al. 1991; Kesner et al. 1993). Later, experiments on ASDEX Upgrade showed high-density operation at the Greenwald limit with high $\beta _{\textrm{P}}$ (Hobirk et al. 2001). In 2002, the JET team reported exciting progress on quasi-steady operation with internal transport barriers (ITBs) (Litaudon et al. 2002). The ITB has been maintained up to 11 s with a large fraction of non-inductive current (above 80%) in a high-$\beta _{\textrm{P}}$ plasma “...which is the longest duration of sustainment of this regime on JET. The duration of the discharges is close to the technical operational limits fixed by the maximum duration of (i) the application of the full NBI power and (ii) the high toroidal field operation ($B_0$ = 3.45 T).” [quote from Litaudon et al. (2002)]. The authors also proposed several important aspects that need to be addressed, including the compatibility of the ITB performance at high triangularity, $\beta$ limits in this highly non-inductive operation, exploration of a stationary regime at high normalized density, compatibility of the ITB with good plasma exhaust edge and a mild edge localized mode (ELM) activity, and investigation of impurity behavior in the ITB plasmas. Some of these have been investigated and addressed in the more recent DIII-D and EAST joint research activities, which are the main subject of this paper and will be discussed later. Another set of pioneering research was performed by the JT-60U team in the 1990s (Koide et al. 1994; Kamada et al. 1994). High-performance-sustained high-$\beta _{\textrm{P}}$ plasmas were demonstrated in JT-60U (Fujita et al. 2001; Sakamoto et al. 2005). One example shows $\beta _{\textrm{N}}\sim 2.4$, $\beta _{\textrm{P}}\sim 1.7$, $f_{\textrm{bs}}\sim 43$–50% for 5.8 s, i.e. $26\times \tau _{\textrm{E}}$ or $2.8\times \tau _{\textrm{R}}$ and another discharge has $\beta _{\textrm{N}}\sim 1.7$, $\beta _{\textrm{P}}\sim 2.4$, $f_{\textrm{bs}}\sim 75$% for 7.4 s, i.e., $16\times \tau _{\textrm{E}}$ or $2.7\times \tau _{\textrm{R}}$. Here, $\tau _{\textrm{E}}$ is the energy confinement time and $\tau _{\textrm{R}}$ is the current profile relaxation time defined as $\mu _0\langle \sigma \rangle a^2/12$, where $\langle \sigma \rangle$ is the volume average of plasma conductivity and a is the plasma minor radius. The high-performance plasmas on JT-60U have an ITB at large radius, e.g., $\rho \sim 0.65$ in $T_{\textrm{e}}$, $T_{\textrm{i}}$ and $n_{\textrm{e}}$ channels (Sakamoto et al. 2009). Many normalized parameters of this plasma, such as $H_{\textrm{98y2}}$, $f_{\textrm{Gr}}$, $\beta _{\textrm{N}}$, $f_{\textrm{bs}}$, and $f_{\textrm{CD}}$, meet or exceed the requirement for ITER’s $Q=5$ steady-state operation. Here, $H_{\textrm{98y2}}$ is the normalized thermal energy confinement factor defined by the ratio of experimental thermal energy confinement time and the scaling based on an international tokamak database (ITER Physics Expert Groups on Confinement and Transport and Confinement Modelling and Database et al. 1999), $f_{\textrm{Gr}}=n_{\textrm{e}}/n_{\textrm{Gr}}$, is the Greenwald fraction, where $n_{\textrm{Gr}}$ ($10^{20}$ m$^{-3}$) = $I_{\textrm{p}}$ (MA)/$\pi a^2$ and $f_{\textrm{CD}}$ is the non-inductive driven current fraction. High-$\beta _{\textrm{P}}$ scenario was also explored on DIII-D in 2000s (Politzer et al. 2005). ITBs were observed at large radius in the experiments. $H_{\textrm{98y2}}>1.5$ and $f_{\textrm{bs}}\sim 65$–85% were achieved at $q_{95}\sim 10$. Since 2013, intensive joint research activities by the DIII-D and EAST teams have successfully applied this scenario to both tokamaks. More importantly, various aspects of this scenario has been individually extended to reactor relevant conditions, but not yet simultaneously, e.g., stationary operation, low toroidal rotation, intermediate $q_{95}\sim 6$, line-averaged density above Greenwald limit, high core confinement quality ($H_{\textrm{98y2}}$) with fully detached divertor, etc., with deepened physics understandings (Garofalo et al. 2015, 2018; Ren et al. 2016; Ding et al. 2017a, b, 2020a, 2021a; Staebler et al. 2018; Jian et al. 2019, 2021a; McClenaghan et al. 2019; Huang et al. 2020; Wang et al. 2021a, b; Qian et al. 2021). There is also recent active high-$\beta _{\textrm{P}}$ related research on EAST (Garofalo et al. 2017; Gong et al. 2022), KSTAR (Na et al. 2015; Park et al. 2019; Kwak et al. 2020; Kim et al. 2022) and HL-2A (Chen et al. 2022).

The purpose of this paper is to summarize progress developing and understanding the high-$\beta _{\textrm{P}}$ scenario in the last decade. DIII-D results will be used as examples. The rest of this paper will be organized as follows: Sect. 2 discusses the key needs for an attractive reactor scenario and shows how the high-$\beta _{\textrm{P}}$ scenario addresses those needs. Other features of the high-$\beta _{\textrm{P}}$ scenario are communicated in Sect. 3. Section 4 introduces the efforts on operational space expansion in the joint DIII-D/EAST high-$\beta _{\textrm{P}}$ experiments on DIII-D. Predictive high-$\beta _{\textrm{P}}$ modeling studies for current and future devices are introduced briefly in Sect. 5. Finally, Sect. 6 summarizes this paper and discusses the outlook of the high-$\beta _{\textrm{P}}$ scenario as a promising advanced scenario for a fusion reactor.

2 Key needs for an attractive reactor scenario design and the high-$\beta _{\textrm{P}}$ solutions

A tokamak plasma is a complicated physical system. A good tokamak fusion reactor design needs to include physics and engineering considerations. Usually, capital cost is an important additional consideration when making decisions in the real world. A recent paper discusses the most critical areas in reducing the capital cost risk for a compact tokamak pilot plant (Wade and Leuer 2021). The conclusion is that these areas are confinement quality, tritium breeding multiplier, thermal efficiency, divertor heat flux, and neutron wall loading. The confinement quality and the divertor heat flux are the two areas that the recent research in high-$\beta _{\textrm{P}}$ scenario can address.

In this section, high-$\beta _{\textrm{P}}$ solutions on the topics of high confinement quality, high density operation, and core-edge solution will be presented. Last but not least, the advantages of high-$\beta _{\textrm{P}}$ scenario on low disruptivity for machine safety and steady-state operation for high duty-cycle will be discussed as well. These two are also important considerations in fusion reactor design.

2.1 High-energy confinement quality and its low rotation compatibility

As discussed in Wade and Leuer (2021), energy confinement quality, in terms of $H_{\textrm{98y2}}$, is the highest leverage parameter for fusion capital cost. There are high $H_{\textrm{98y2}}$ (e.g. $\ge 1.5$) operational scenarios in present experiments. However, many of them suffer confinement quality degradation at low toroidal rotation (Solomon et al. 2013; Ding et al. 2020b, 2021b; Garofalo et al. 2022; Thome et al. 2021). This is a very important research topic, because large tokamak plasmas like ITER’s will have high inertia, and therefore possibly low rotation. It is critical to identify a physics regime that can provide excellent energy confinement quality (e.g., $H_{\textrm{98y2}}\sim 1.5$) at low toroidal rotation and achieve it in experiments. The high-$\beta _{\textrm{P}}$ regime is such an example.

DIII-D high-$\beta _{\textrm{P}}$ plasmas usually have an upward-biased double-null configuration (green line in Fig. 1), but recently, an ITER-similar true single-null shape has been used (blue line in Fig. 1) (Wang et al. 2021d). Modifications to the upper triangularity and the X-point location were needed for effective pumping. Typically, the scenario is produced using relatively strong early heating and an early L-to-H-mode transition before $I_{\textrm{p}}$ flattop.

Figure 2 shows waveforms and profiles of a typical high-$\beta _{\textrm{P}}$ discharge on DIII-D. Since $\beta _{\textrm{P}}\sim I_{\textrm{p}}^{-2}$, it is relatively easy to establish a well-developed ITB plasma at low plasma current. A two-part experimental strategy is used in DIII-D high-$\beta _{\textrm{P}}$ experiments. First, $I_{\textrm{p}}$ is programmed to have two flattop steps in it. The first $I_{\textrm{p}}$ flattop is relatively low and the typical value is between 0.6 and 0.75 MA. This results in a relatively high $q_{95}$ value, e.g., $\sim 10$. To access the medium $q_{95}$ regime (6–8), which is more reactor relevant, the discharges usually have a second $I_{\textrm{p}}$ ramp-up phase. Typical target of the second $I_{\textrm{p}}$ flattop is between 0.8 and 1 MA. Second, since too much $I_{\textrm{p}}$ ramp-up causes MHD instability, a toroidal field ramp-down is also applied. Therefore, a toroidal field ramp-down technique in combination with $I_{\textrm{p}}$ ramp-up is used in the experiments to alleviate the problem by targeting lower $I_{\textrm{p}}$ value while keeping the desired $q_{95}$, as shown in Fig. 2a. $\beta _{\textrm{N}}$ feedback control of NBI power is used, as shown in Fig. 2b. This offers two benefits: (1) a high enough $\beta _{\textrm{N}}$ ensures $\beta _{\textrm{P}}$ is also high enough to access this desired regime; (2) when an ITB is developed, the energy confinement would be improved substantially, e.g., 50%. The $\beta _{\textrm{N}}$ feedback mechanism prevents an overshoot of $\beta _{\textrm{N}}$ to too high a value, which may cross an MHD stability boundary, by decreasing NBI power as shown in Fig. 2c. The typical line-averaged $f_{\textrm{Gr}}$ is around 1.0, with an absolute line-averaged density reaching $0.7\times 10^{20}$ m$^{-3}$ or higher (Fig. 2d). Feedback control of the pedestal density is used instead of the line-averaged density, which is different from most other experiments. This technique ensures enough freedom in the density profile evolution for an ITB to form by providing sufficient fueling when a density ITB is developing. It also prevents too much fueling when confinement is not good enough. It is important to note that MHD stability and avoiding disruptions are prerequisites for sustained high confinement quality in experiment.

An ITB in all channels (temperatures, densities, and toroidal rotation) at large radius (e.g., $\rho \sim 0.7$) is the signature characteristic of high-$\beta _{\textrm{P}}$ scenario plasmas on DIII-D. Typical profiles are shown in Fig. 2e–g. Shaded areas show the location of the ITBs in temperature and density. The location of minimum q is well within the ITB region. Therefore, there is no “current misalignment” issue; this topic will be discussed further in Sect. 3.1. A strong gradient of toroidal rotation is observed in Fig. 2g. However, it is not well aligned with the ITB region in temperature and density. The toroidal rotation shear at $\rho \sim 0.7$, which is the foot of the ITB in temperature and density, is almost zero. The role of toroidal rotation on the high confinement quality and ITB formation will be further discussed in the next subsection.

2.1.1 Experimental observations and modeling analysis on high confinement quality at different toroidal rotation

DIII-D high $\beta _{\textrm{P}}$ experiments had shown high $H_{\textrm{98y2}}$ ($>1.5$) at wide range of toroidal rotation (from 10 to 120 krad/s measured at $\rho =0.5$) as reported in Ding et al. (2017b) and Huang et al. (2020). Investigations on DIII-D of the role of toroidal rotation shear on ITBs in the high $\beta _{\textrm{P}}$ scenario have been summarized in previous papers (Ding et al. 2017b; Garofalo et al. 2018). Two high $\beta _{\textrm{P}}$ discharges with similar $\beta _{\textrm{N}}$ and $H_{\textrm{98y2}}$ but different NBI torque are presented in Fig. 3a–c. Measurement shows two almost identical electron temperature profiles with ITB at large radius (Fig. 3d), while the high-gradient region of the toroidal rotation profile has very different radial location in the high and low rotation cases. This is a clear experimental demonstration of the minor role of rotation shear played in the ITB formation in high $\beta _{\textrm{P}}$ plasmas.

It is worth mentioning that there shows a $\beta$ collapse at around 3.2 s in #164538 in Fig. 3b. It was caused by a transient MHD event. $\beta _{\textrm{N}}$ and $H_{\textrm{98y2}}$ transiently dropped from 3 to 2 and from 1.5 to 1, respectively. However, both $\beta _{\textrm{N}}$ and $H_{\textrm{98y2}}$ recovered in a few hundred milliseconds. $\beta _{\textrm{N}}$ reached the same level before collapse and $H_{\textrm{98y2}}$ became even higher. This discharge is also discussed in McClenaghan et al. (2019). This example shows robustness of high $\beta _{\textrm{P}}$ scenario in plasma operation. More similar experimental observations are presented in Huang et al. (2020).

Further transport modeling analysis supports the experimental observations (Ding et al. 2017b; Pan et al. 2017; Garofalo et al. 2018). The TGYRO (Candy et al. 2009) transport solver, combining TGLF (Staebler et al. 2007) for turbulence and NEO (Bellie and Candy 2008) for neoclassical transport predictions, was used to simulate the temperature profile in high-$\beta _{\textrm{P}}$ plasmas with high and low rotation as shown in Fig. 3. Figure 4 shows results from the high rotation case. An interesting finding is that with or without E $\times$ B physics, TGYRO can reproduce the experimental ion temperature profile, suggesting different working mechanism for turbulence suppression in this plasma. Neoclassical transport is dominant inside the ITB, while turbulence transport can play a role outside the ITB. Note that plasma density and electron temperature profiles are kept unchanged in this set of modeling. Similar results were obtained using the low rotation case. In addition to the modeling analysis, turbulence measurement (beam emission spectroscopy, BES) found no low-k turbulence inside of the ITB for both the high and low rotation discharges shown in Fig. 3 (Ding et al. 2017b).

2.1.2 Understanding of $\alpha$-stabilization physics in high Shafranov shift, high $\beta _{\textrm{P}}$ plasmas

Even though experimental results and analysis support the compatibility of high-energy confinement quality with low toroidal rotation, it is still important to understand the physics of turbulence suppression in the high $\beta _{\textrm{P}}$ regime. Progress understanding this came in two phases. Phase one was focused on the major experimental parameters that lead to strong turbulence suppression and low transport. Gyrokinetic modeling and gyrofluid modeling suggested that Shafranov shift, $\alpha _{\textrm{MHD}}$ and the related parameter $\beta _{\textrm{P}}$ (Shafranov shift $\sim \beta _{\textrm{P}}$, $\alpha _{\textrm{MHD}}=-q^2R\textrm{d}\beta /{\textrm{d}}r\sim \textrm{d}\beta _{\textrm{P}}/\textrm{d}r$) are the key (Ding et al. 2017b; Pan et al. 2017; Garofalo et al. 2018). In linear GYRO (Candy and Waltz 2003) modeling, the effect of $\alpha$-stabilization can be tested by artificial scan of $\beta$ in the formula. The results show that the growth rate of the most unstable low-k mode is reduced as $\alpha _{\textrm{MHD}}$ is increased. The micro-turbulence mode can be completely suppressed beyond a certain value of $\alpha _{\textrm{MHD}}$. To better evaluate this effect in real geometry, a modeling study combining EFIT (Lao et al. 1985), NEO, and TGLF was performed. Based on experimental data, this exercise reconstructed a series of equilibrium with scaled plasma pressure in EFIT with constant q-profile. Transport analysis on these equilibria shows a clear decreasing trend of large radius turbulence energy fluxes in both ion and electron channels when $\beta _{\textrm{P}}$ is increased (Fig. 5). Please note that this scan has fixed q-profile and scale lengths of temperature and density. Therefore, it is not self-consistent and the purpose of this exercise is to show the effect of $\alpha$-stabilization qualitatively.

A dedicated $\beta$ ramp-down experiment was performed (Ding et al. 2017b). At fixed $I_{\textrm{p}}$ and $B_{\textrm{T}}$, a feedback controlled, decreasing $\beta _{\textrm{N}}$ results in a decreasing $\beta _{\textrm{P}}$ as shown in Fig. 6a. The experimental observation is that a well-developed temperature ITB at high $\beta _{\textrm{P}}$ is weakened at lower $\beta _{\textrm{P}}$, and finally disappears when $\beta _{\textrm{P}}$ is lower than a certain value (Fig. 6b). The threshold is identified at about 1.9 in this experiment. Turbulence measurement from BES at large radius confirms the increasing low-k turbulence in the $\beta$ ramp-down phase (Fig. 6c). Figure 6d shows the effective ion and electron thermal diffusivities at $\rho =0.5$ calculated by the TRANSP code (Hawryluk 1979). The increasing trend of $\chi$s implies higher energy transport, when $\beta _{\textrm{P}}$ is decreasing. This is consistent with the predicted trend by transport models shown in Fig. 5. This experiment demonstrated the essential role that $\beta _{\textrm{P}}$ plays in this turbulence suppression regime. Later, further experiments discovered that such $\beta _{\textrm{P}}$ thresholds for strong ITB is closely related to the structure of the q-profile at large radius (Huang et al. 2020). Figure 7 compares two examples with different $\beta _{\textrm{P}}$ thresholds from DIII-D high $\beta _{\textrm{P}}$ experiments. It is found that if there is a deeper ‘well’, i.e., a stronger negative local shear, in the q-profile at large radius, the strong-ITB state is sustainable to lower $\beta _{\textrm{P}}$ in a $q_{95}$ scan. This finding suggests that lower/negative magnetic shear either directly suppresses turbulence or plays a role in the physics of $\alpha$-stabilization.

The experimental observations motivate further investigation of the deeper detailed physics of large radius ITB formation in the high-$\beta _{\textrm{P}}$ regime. This is phase two of the joint research activities. Theoretical and modeling analysis points out that a high-density gradient can enhance the $\alpha$-stabilization effect on turbulence suppression (Kotschenreuther et al. 2019; Qian et al. 2021). First of all, it is important to understand how high $\alpha _{\textrm{MHD}}$ stabilizes turbulence. The physics was elucidated in Bourdelle et al. (2005) based on an analytic equilibrium for large aspect ratio and circular flux surface. At low $\beta$, the curvature and the $\nabla B$ drift frequencies can be expressed as:

$$\begin{aligned} \begin{aligned} n\omega _{\nabla B}&=n\omega _K=k_{\theta }\cdot \frac{T}{eB}\cdot \frac{1}{R}\cdot \left( \cos \theta +\frac{k_r}{k_{\theta }\sin \theta }\right) \\&=k_{\theta }\cdot \frac{T}{eB}\cdot \frac{1}{R}\cdot (\cos \theta +(s\theta -\alpha \sin \theta )\sin \theta ) \end{aligned} \end{aligned}$$

(1)

where $\theta$ is the poloidal angle, $k_r$ and $k_{\theta }$ are the radial and poloidal wave vectors, s is the magnetic shear. Results of three combinations of s and $\alpha$ values are shown in Fig. 8 to demonstrate how s and $\alpha$ affect the curvature drift. Note that if the flux surface average of the curvature and $\nabla B$ drift is reduced or reverses sign, the drive for the dominant curvature micro-instability is reduced or even suppressed. One can see negative s is able to suppress the micro-instability and so is high $\alpha$ (maybe more effective). The important fact is that high $\alpha$ narrows the eigenfunction of the instability and results in a poor coupling to the relatively wide trapped electrons orbits in the bad curvature region. Therefore, the trapped electron mode (TEM) cannot feed on the free energy from the high-density gradient when this physics dominates. Regarding the ion temperature gradient (ITG) mode, it loses free energy drive due to the decrease of $\eta _{\textrm{i}}$ ($=n\nabla T_{\textrm{i}}/T_{\textrm{i}}\nabla n$), when the density gradient fraction of the pressure gradient ($F_{\textrm{p}}$) increases. Recent studies indicate a huge turbulence reduction of over 2 orders of magnitude from a low $\alpha$ (= 0.18) case to a high $\alpha$ (= 3.0) case at $F_{\textrm{p}}\sim 0.5$, but only a small reduction ($\sim 4{{\times }}$) at $F_{\textrm{p}}\sim 0$ (Kotschenreuther et al. 2019; Qian et al. 2021). Note that $\alpha \ge 3.0$ is commonly seen in the ITB region of DIII-D high-$\beta _{\textrm{P}}$ plasmas, while $\alpha \sim 0.18$ is typical at large radius in a standard H-mode plasma. This result suggests that high-density gradient amplifies turbulence suppression and confinement gains from high $\alpha$.

The leading model of large radius ITB formation in the DIII-D high-$\beta _{\textrm{P}}$ scenario is the bifurcation around the kinetic ballooning mode (KBM) mountain (Staebler et al. 2018). The modeling study uses TGLF to calculate the linear growth rate of a standard case, which has the following parameters: $k_{\theta }=0.2$, $T_{\textrm{e}}=T_{\textrm{i}}$, $n_{\textrm{e}}=n_{\textrm{i}}$, $q=2$, $a/L_{\textrm{n}}=1$, $a/L_{\textrm{T}}=3$, $r/a=0.6$ and $R/a=3$. Here, $L_{\textrm{n}}$ and $L_{\textrm{T}}$ are scale lengths of density and temperature, respectively. By scanning magnetic shear and $\alpha _{\textrm{MHD}}$, a landscape of KBM instability mountain is revealed as shown in Fig. 9. A high linear growth rate region is located at high magnetic shear and mid-$\alpha _{\textrm{MHD}}$ area. Two regions of low linear growth rate, implying low turbulence transport, can be found next to the instability mountain. The 1st stability regime is a low transport regime with low pressure gradient, in terms of $\alpha _{\textrm{MHD}}$. The 2nd stability regime on the other side of the instability mountain enables high-pressure gradient together with low transport. This is where an ITB state can exist. A stable pass, making a “low shear detour” from 1st to 2nd stability regime is sketched out in Fig. 9. Similar instability mountain results were also reported in Bourdelle et al. (2005) using a linear local gyrokinetic code, with JET-like and ITER-like parameters. Due to the electrostatic nature of the modeling, this study reported unstable ITG–TEM instead of KBM at low-k. Nevertheless, these independent studies both suggest a low transport regime with high-pressure gradient in the high-$\beta _{\textrm{P}}$ scenario. Now, the question is if the transition from low pressure gradient, non-ITB state to high-pressure gradient, ITB state, i.e. from 1st stability regime to 2nd stability regime, can be identified in experiment.

Two confinement states in DIII-D high-$\beta _{\textrm{P}}$ experiments were identified and analyzed (Ding et al. 2017c; Staebler et al. 2018; Staebler 2018; McClenaghan et al. 2019). One is an H-mode confinement state with a high edge pedestal. The other is an enhanced confinement state with a low pedestal and an ITB. One example of the two states is summarized in Fig. 10a. A physics picture of two self-organized states was proposed (Staebler et al. 2018; Staebler 2018). The two current density peaks are driven by (i) the ITB at large radius and (ii) the pedestal fight for control of the magnetic shear in the pedestal region ($\rho \sim 0.9$). In the strong-ITB state, the ITB current peak dominants and results in a positive magnetic shear in the pedestal, which destabilizes the KBM there. The pedestal pressure gradient is limited by the KBM-induced transport. The lowered pedestal pressure keeps the pedestal bootstrap current peak lower than the ITB peak. This is a self-organized loop that enhances the strong-ITB state. On the other hand, if the pedestal current peak is strongest, it weakens the magnetic shear in the pedestal, opening up access to the KBM stable pass. The consequence is the low transport in pedestal due to the drift-wave transport suppression by the large Shafranov shift in pedestal. Low transport facilitates higher pedestal pressure. Therefore, this is also a positive feedback loop that enhances the high-pedestal state. But this state is limited by ELMs in DIII-D discharges. A connection between these two states—a fast transition by ELMs, was reported (McClenaghan et al. 2019). Figure 10b shows the waveform of $n=1$ magnetic field perturbation during an ELM. Before the ELM crash, $T_{\textrm{e}}$ is about 0.55 keV in the pedestal as shown in Fig. 10c. The $T_{\textrm{e}}$ gradient at $\rho =0.6$ is low. However, the ELM reduces $T_{\textrm{e}}$ by a factor of three at $\rho =0.8$ and increases the $T_{\textrm{e}}$ gradient at mid-radius, $0.5<\rho <0.75$. This event pushes the plasma into the positive feedback, self-organized state of strong ITB and low pedestal as discussed above. The experimental observation was that the plasma developed a sustained strong ITB at large radius since then, as shown in yellow and green profiles in Fig. 10a.

Another slow transition by gas puffing was recently discovered in DIII-D high-$\beta _{\textrm{P}}$ experiments (Wang et al. 2021a, b). The slow process enables multiple profile measurements during the transition in the experiment, and thus gives a great opportunity to understand the physics in detail. One example is shown in Fig. 11. The experiment uses D$_2$ gas puffing to study detachment. As expected, pedestal pressure decreases during strong gas puffing (Fig. 11b). Consequently, the pedestal current density decreases. Due to current redistribution, the current density at large radius, e.g., $\rho =0.6$, is increasing (Fig. 11c), resulting in reduced magnetic shear at large radius. Sometime later, pressure gradient at $\rho =0.6$ starts to increase, indicating a developing ITB (Fig. 11b). The experimental trajectory of magnetic shear and $\alpha _{\textrm{MHD}}$ at $\rho =0.6$ is shown in red dots in Fig. 11d. The color contours of this figure show the 2D scan of linear growth rate versus magnetic shear and $\alpha _{\textrm{MHD}}$ based on experimental equilibrium and profiles at 2.75 s (shown in yellow star) using the CGYRO code (Candy et al. 2016). A KBM instability mountain, which is similar to the previous finding (Staebler et al. 2018), is found in the simulations using experimental parameters. A high growth rate region is located at high magnetic shear and medium $\alpha _{\textrm{MHD}}$. Evolution of experimental data is shown by the red dots and the red arrows. Before ITB formation, experimental data are all clustered on the low-pressure gradient side of the KBM mountain, i.e., the 1st stability regime. As time goes by, the decreasing magnetic shear brings the plasma to a “low shear detour” around the high growth rate region of KBM mountain. Then the plasma can access the other side of the KBM mountain with high-pressure gradient and low transport, i.e., the 2nd stability regime, without climbing up the mountain. This observation suggests that the fundamental reason of ITB formation in this scenario is the access of 2nd stability regime, while a “low shear detour” is what triggers the access. The “low shear detour” identified in this experiment is an example of the so-called “stable pass” illustrated in Fig. 9. Furthermore, this physics picture also supports the experimental observations described in Fig. 7. Lower magnetic shear deflects the boundary of the 2nd stability regime from high $\alpha _{\textrm{MHD}}$. This implies sustained low transport at lower $\beta _{\textrm{P}}$, i.e., the lower $\beta _{\textrm{P}}$ threshold discussed in the previous subsection.

From the physics picture of bypassing KBM instability mountain, one can see high enough $\alpha _{\textrm{MHD}}$ is a key parameter that leads to the 2nd stability regime. $\alpha _{\textrm{MHD}}\sim q^2\textrm{d}p/\textrm{d}r$, which means high local safety factor and high pressure (and its gradient) are essential to high $\alpha _{\textrm{MHD}}$. Another key of bypassing KBM mountain is the reduced magnetic shear. Therefore, the physics creates a few constraints when developing this sceanrio. (1) Low $q_{95}$ will generally lower the whole q-profile at large radius. This reduces $\alpha _{\textrm{MHD}}$, unless higher pressure (or $\beta$) can compensate the decrease in $\alpha _{\textrm{MHD}}$. This is the major difficulty of operating this scenario at high plasma current at certain toroidal field. Besides, operating very high $\beta$ (or $\beta _{\textrm{N}}$) at high plasma current is always challenging in present tokamaks. (2) High $q_{\textrm{min}}$ is very important for reducing magnetic shear at large radius. To achieve high $q_{\textrm{min}}$, present tokamaks either use operational techniques, such as early strong central heating, early H-mode, to facilitate transient off-axis Ohmic current, or employ auxiliary systems for external-driven off-axis current. Too high initial density may limit the capability of creating sufficient off-axis current, either transient Ohmic current or external-driven current. Careful planning in experimental gas puffing (or density feedback target) waveforms is required to access high-density regime.

In summary, the strong turbulence suppression and the high-energy confinement quality in high-$\beta _{\textrm{P}}$ scenario mainly come from the $\alpha$-stabilization physics at large Shafranov shift. This is a separate physics from the E $\times$ B shear turbulence suppression. Therefore, such physics and the high-confinement quality regime is able to be extended to a reactor-relevant low toroidal rotation condition, expecting very limited contribution of toroidal rotation shear in the E $\times$ B shear turbulence suppression physics. When entering the 2nd stability low transport regime, it should be noticed that it is not very magnetic shear sensitive, unless the plasma state is too close to the instability mountain. The benefit is that one does not need to carefully control the current profile to maintain a favorable magnetic shear for low transport. The ITB state is robust with a wide range of magnetic shear as demonstrated in Fig. 7. Nevertheless, other turbulence suppression mechanisms, such as E $\times$ B shear, etc., are always helpful in the turbulence suppression in the high-$\beta _{\textrm{P}}$ scenario. On the other hand, $\alpha$-stabilization effect is weakened in a lower q plasma (other than high-$\beta _{\textrm{P}}$ regime) assuming similar pressure profile. It needs to compete with the destabilization effect of pressure-driven modes as pressure gradient increases. A well-documented analysis on this topic can be found in Na et al. (2020).

2.2 Edge solution: detached divertor and small/no ELMs

Tokamak reactors will have hundreds of MW of power flowing from plasma core to edge. The state-of-the-art material choice for a tokamak first wall is tungsten. It is reported that the upper limit of heat loads could be 10–15 MW/m$^2$ (Pitts et al. 2019). No first wall material will be able to withstand such high power flux in long pulse operation without dissipation. In H-mode discharges, ELMs could cause sudden edge collapse. As a result, transient very high energy flux towards the wall could happen in a very short time, e.g., 1 ms. Therefore, how to deal with the stationary and the transient heat loads becomes a critical task when designing a tokamak reactor. Scientists developed particle (either fueling or impurity) injection technique to achieve a so-called ‘detachment’ state, which enables low temperature (below a few eV) and low particle flux on divertor plates (Stangeby 2000). In most present experiments, it is commonly found that divertor detachment significantly reduces the plasma performance, as the detachment front cools the core plasma through a degrading of the H-mode pedestal (Asakura et al. 2009; Kallenbach et al. 2015; Leonard et al. 2015). An experimental approach for a promising edge solution and with high-core performance compatibility is highly desired.

The high-$\beta _{\textrm{P}}$ approach shows great potential in this research topic. As shown in Fig. 11, a slow transition from the no-ITB high-pedestal state to the ITB weak-pedestal state was identified in a strong D$_2$ gas puffing high-$\beta _{\textrm{P}}$ experiment on DIII-D. The purpose of this experiment was to study divertor detachment in the high-$\beta _{\textrm{P}}$ scenario. With detached divertor, enhanced atomic processes, such as radiation, neutral ionization, charge-exchange and recombination, move the plasma boundary interaction off the divertor target. The benefit of low divertor temperature ($T_{\textrm{e}}<5$–10 eV) is the suppression of physical erosion on the divertor plates. When particle flux is also limited to a low level, chemical erosion on the material is reduced as well. This is called full detachment. Indeed, very good recent progress was achieved in the series of investigations on high-$\beta _{\textrm{P}}$ scenarios.

In the experiments, excellent integration of full divertor detachment with improved confinement was observed for the first time in a tokamak (Wang et al. 2021a, b). Figure 12 shows details of one example. With active feedback control of $I_{\textrm{sat}}/I_{\textrm{roll}}$ via N$_2$ seeding from a main chamber valve (Fig. 12b), the plasma successfully enters a full divertor detachment state. Here, $I_{\textrm{sat}}$ is the ion saturation current around the outer strike point. This quantity can be measured by divertor Langmuir probes. The maximum $I_{\textrm{sat}}$ at its rollover is called $I_{\textrm{roll}}$. As shown in Fig. 12d, both divertor temperature and $J_{\textrm{s}}$ are sustained at very low level in the shaded area, indicating a full detachment state. When starting N$_2$ puffing via feedback control, pedestal pressure decreases as expected. However, the on-axis pressure does not decrease at all. Instead, some increase can be observed from 3000 to 5000 ms in Fig. 12a. As discussed in Sect. 2.1.2, this is due to the development of the ITB at large radius. It greatly elevates the core profiles and compensates the loss in pedestal. Therefore, high globe performance ($\beta _{\textrm{N}}$, $\beta _{\textrm{P}}$ and $H_{\textrm{98y2}}$) is maintained during detachment (Fig. 12b).

Sustained excellent confinement quality during detachment is a unique feature of the high-$\beta _{\textrm{P}}$ scenario. In Fig. 13, comparisons between several operational scenarios reveal many other scenarios, including open divertor H-mode, close divertor H-mode, and super H-mode-like, have reduced $H_{\textrm{98y2}}$ associated with increased degree of detachment ($\textrm{DoD}=I_{\textrm{s,roll}}/I_{\textrm{sat}}$) and decreased normalized electron $\beta$ at pedestal top ($\beta _{\textrm{N,ped,e}}=\beta _{\textrm{ped,e}}/(I_{\textrm{p}}/aB_{\textrm{T}})$). Note that the peak $I_{\textrm{sat}}$ in the profile across outer divertor and the peak value before the rollover ($I_{\textrm{s,roll}}$) is used for the calculation of DoD. Since pedestal degradation seems to be inevitable during detachment (including high $\beta _{\textrm{P}}$ scenario), the key approach to maintain core performance is breaking core stiffness and developing ITBs, if possible. The observed self-organized regime with ITB and weak pedestal (as discussed in Sect. 2.1.2) in high $\beta _{\textrm{P}}$ scenario exhibits advantages on core-edge integration compared to other H-mode scenarios.

Further investigations along this line suggest a greater demonstration on core-edge integration with simultaneous full divertor detachment, ELM mitigation/suppression, and an ITB core (Wang et al. 2021d). Neon impurity gas puffing is applied in the experiment. Similar to the discussion above, the experimental observation during neon injection is $T_{\textrm{e,div}}<5$ eV and very low $J_{\textrm{s}}$ level, indicating full detachment (Fig. 14c). Pedestal pressure decreases, while on-axis pressure increases, due to the development of the ITB (Fig. 14b). Global parameters, such as $\beta _{\textrm{N}}$, $\beta _{\textrm{P}}$ and $\tau _{\textrm{E}}$, slightly increase or remain unchanged (Fig. 14a). Different from the discharge shown in Fig. 12, which is still ELMy, this example shows very clear and steady ELM mitigation or suppression, depending on the definition (Fig. 14d shaded area). The physics behind the observation is under investigation. In addition, this discharge is operated with ITER-like true single null configuration similar to the blue case in Fig. 1. In summary, high-$\beta _{\textrm{P}}$ scenario shows great advantages in coping with core-edge integration, realizing a hot and dense core plasma surrounded by a radiation mantle and a cool edge.

It is worth pointing out that studies of the grassy ELM regime in DIII-D and EAST plasmas have identified similar operational spaces for this regime (Wang et al. 2021c; Yang et al. 2020). DIII-D results suggest that grassy ELMs are obtained with $q_{95}\ge 5.9$ and $\beta _{\textrm{P}}\ge 1.7$, while EAST results indicate $q_{95}\ge 5.2$ and $\beta _{\textrm{P}}\ge 1.2$. Therefore, the high-$\beta _{\textrm{P}}$ scenario is compatible with grassy ELM operation based on these two important parameters, although future studies are required to investigate the potential of integration between these two attractive operating modes.

2.3 High density

Thermonuclear power density $p=n^2\langle \sigma \nu \rangle E/4$, where n is the total ion density with equal parts deuterium and tritium, $\langle \sigma \nu \rangle$ is the normalized reaction rate, and E is the energy released per reaction (Wesson 2004). Since $\langle \sigma \nu \rangle$ is mainly a function of temperature, high fuel density is desired for high thermonuclear power density.

There are attractive fusion pilot plant (FPP) designs around the world that use high density for high fusion power (Yeom et al. 2013; Federici et al. 2018; Kessel et al. 2015; Wade and Leuer 2021; Buttery et al. 2021). However, for H-mode plasmas, there is a hard limit for pedestal (electron) density, i.e., an empirical “Greenwald density limit” defined as $n_{\textrm{Gr}}$ [$10^{20}$ m$^{-3}$] = $I_{\textrm{p}}$ [MA]/$\pi$(a [m])$^2$ (Kamada et al. 1991; Greenwald 2002). Note that all the FPP designs mentioned above require the averaged density to be above the Greenwald limit. To access high density, especially when exceeding the Greenwald limit, one needs to develop a peaked density profile. In a fusion reactor, large machine size and high density make it difficult to have effective fueling in the deep core region. It is realized that low collisionality is beneficial to a peaked density profile (Angioni et al. 2009). At ITER relevant $\nu _{\textrm{eff}}$, a peaking factor of 1.4–1.6 is expected as stated in Angioni et al. (2009). Here, $\nu _{\textrm{eff}}=0.1\times Z_{\textrm{eff}}\langle n_{\textrm{e}}\rangle R/\langle T_{\textrm{e}}\rangle ^2$, where symbol $\langle \dots \rangle$ stands for volume average. $T_{\textrm{e}}$ is in keV, $n_{\textrm{e}}$ in $10^{19}$ m$^{-3}$ and R in m. The peaking factor is defined as $n_{\textrm{e}}(\rho _{\Psi }=0.2)/\langle n_{\textrm{e}}\rangle$. However, it is unclear if the natural peaking effect by low collisionality is sufficient for the desired high density in a reactor. Using this approach, one may need to maximize pedestal density as close to the Greenwald limit as possible. A degradation in energy confinement quality, i.e., a ‘roll-over’, happens when the density approaches the Greenwald limit (Zohm et al. 2013). Work on ASDEX Upgrade (Lang et al. 2012) describes the reduced confinement quality, in terms of $H_{\textrm{98y2}}$, at line-averaged Greenwald fraction between 0.75 and 1.5. $H_{\textrm{98y2}}$ above 1.0 is not observed in these high-density plasmas by pellet core fueling. As discussed, $H_{\textrm{98y2}}$ is the highest leverage parameter of fusion pilot plant capital cost (Wade and Leuer 2021). This is a dilemma and an obvious gap between present experiments and the attractive FPP designs. The high-$\beta _{\textrm{P}}$ scenario offers an effective and robust approach to address this important issue.

The approach is to develop a density ITB at large radius. A strong ITB can greatly elevate the plasma density in the core region, while leaving pedestal density below the Greenwald limit. The averaged (either line-averaged or volume-averaged) density benefits even more from an ITB at large radius, because high density exists in a greater volume than in plasmas with a small-radius ITB or peaked density profile, assuming similar densities on-axis. One example from DIII-D is shown in Fig. 15. The experimental approach for high density used in this case is impurity gas puffing. Note that impurity injection is not required for developing a density ITB in the high-$\beta _{\textrm{P}}$ scenario. Line-averaged $f_{\textrm{Gr}}$ about 1.0 is observed without impurity injection on DIII-D. However, neon injection facilitates a strong density ITB with even higher $f_{\textrm{Gr}}$, e.g., line-averaged $f_{\textrm{Gr}}\sim 1.3$ as shown in Fig. 15. This figure shows the developing ITB during neon injection phase. It also shows the sustained ITB for almost one second after turning off the injection (red and cyan lines). Note that this high $f_{\textrm{Gr}}$ plasma does not require high pedestal density. The case shown in Fig. 15 has almost constant pedestal density below 70% of its Greenwald limit in both no-ITB and strong-ITB states. The physics of strong-density ITB with neon injection is not very clear so far. Detailed analysis has not been launched. One working hypothesis is that partially ionized neon penetrates deeper and releases electrons at large radius, i.e., near the potential location of the ITB foot. When turbulent transport is suppressed by the physics described in the previous subsection, such electron sources at large radius can easily fuel the ITB. A higher $f_{\textrm{Gr}}$ target may require stronger fueling. It is not clear if higher $Z_{\textrm{eff}}$ induced by impurities also plays a role in this process as discussed in Staebler et al. (1999).

The high-density phase with $f_{\textrm{Gr}}$ above unity is not transient in DIII-D high-$\beta _{\textrm{P}}$ discharges. Figure 16 shows the time histories of two examples. One of them is #180264, the same discharge discussed in Fig. 15. $f_{\textrm{Gr}}$ above unity is observed for 1–2 s in the experiments. Specifically, $f_{\textrm{Gr}}\sim 1.3$ is sustained up to $8\tau _{\textrm{E}}$ in 180264 and $f_{\textrm{Gr}}>1.0$ for up to $21\tau _{\textrm{E}}$ in 180303. The absolute density is also high ($>7\times 10^{19}$ m$^{-3}$), reaching the expected level for future devices, such as ITER. $q_{\textrm{95}}$ is about 8.0. $\beta _{\textrm{N}}$ is around 3.0 and up to 3.5. The energy confinement quality stays above unity. The lower density case shows a well-sustained $H_{\textrm{98y2}}\sim 1.4$, while the higher density case shows $H_{\textrm{98y2}}$ reduction. It is believed to be related to the experimental approach used in these experiments, i.e., impurity gas puffing as mentioned in the previous paragraph. High puffing rate of impurity gas indeed increases $Z_{\textrm{eff}}$ and the core radiated power. This jeopardizes the energy confinement quality. Different fueling approaches—pellet injection, super-sonic molecular beam injection and high field side gas puffing, may be able to alleviate or solve this problem. Even with high impurity content, on-axis impurity peaking is not observed. This is discussed further in a later subsection. Figure 16e, f also show $D_{\alpha }$ data for the two discharges discussed here. As density increases, low ELM amplitude is observed. This phenomenon is being analyzed and will be reported separately in the future. Note that this particular discharge #180264 has a radiative collapse, i.e., radiated power exceeding injected power. It happens at 5.06 s in the plasma shut-down phase, which started at 5 sec, while NBI power steps down at 5.05 s. If NBI power can be maintained at a high level, such collapse can be avoided.

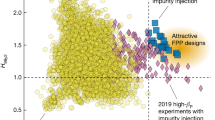
In addition to case-by-case analysis, statistical results show how the high-$\beta _{\textrm{P}}$ scenario extends operational parameter space toward high $f_{\textrm{Gr}}$ and high $H_{\textrm{98y2}}$. Figure 17 shows the highest $H_{\textrm{98y2}}$ and $f_{\textrm{Gr}}$ in each discharge in the 2019 DIII-D campaign. For each discharge, data pairs of ($f_{\textrm{Gr}}$, $H_{\textrm{98y2}}$) from two time slices are recorded: (1) highest $H_{\textrm{98y2}}$ and the corresponding $f_{\textrm{Gr}}$ at the same time, (2) highest $f_{\textrm{Gr}}$ and the corresponding $H_{\textrm{98y2}}$ at the same time, unless the two time slices are the same. The following filters are applied to all discharges: $I_{\textrm{p}}\ge 0.55$ MA, $P_{\textrm{tot}}\ge 5$ MW and $(\textrm{d}W/\textrm{d}t)/P_{\textrm{tot}}\le 0.1$. Data are also smoothed in a time window of 40 ms and truncated at $H_{\textrm{98y2}}=0.5$. There are more than 1300 discharges in Fig. 17. Only high-$\beta _{\textrm{P}}$ discharges show data in a regime with simultaneous $f_{\textrm{Gr}}$ above unity and $H_{\textrm{98y2}}$ above unity. Unlike the experimental observations of reduced $H_{\textrm{98y2}}$ at high density from the other experiments as discussed above, it is important to recall the theory/modeling results in Sect. 2.1.2, showing high-density gradient (a consequence of high density) amplifies the effect of $\alpha$-stabilization and inherently leads to high-energy confinement quality in the high $\beta _{\textrm{P}}$ scenario. Although there is still a gap between what has been achieved in experiment and the attractive FPP design, one would see the potential of extending the parameter space of the high $\beta _{\textrm{P}}$ scenario to a high $f_{\textrm{Gr}}$ and high $H_{\textrm{98y2}}$ regime via improved physics understanding and experimental techniques. More dedicated research efforts including experiments on DIII-D are planned to close this gap.

2.4 Low disruptivity and operation near $\beta _{\textrm{N}}$ limit

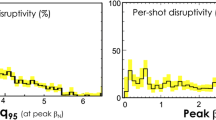
Disruptions and their consequences pose significant design and plasma operation challenges for reactor-regime tokamaks (Hender et al. 2007). A scenario with low disruptivity is needed. Disruptivity is observed to decrease with increasing $q_{95}$ (Gerhardt et al. 2013; Garofalo et al. 2014; de Vries et al. 2014). Figure 18 presents analysis of the flattop disruptivity database from DIII-D (Garofalo et al. 2014). Only disruptions not caused by operator error or power supply failures are counted as disruptions in this database of about 6000 cases. In the parameter range with a lot of data (un-shaded area in Fig. 18), there is a decreasing trend of disruptivity when $q_{\textrm{95}}$ is increasing. This paper also shows that disruptivity does not increase with achieved maximum $\beta _{\textrm{N}}$ value. Statistical results from a spherical tokamak (NSTX) show similar trends (Gerhardt et al. 2013). It is worth pointing out that JET metal wall results also support the trend of higher $q_{\textrm{95}}$ having lower “likelihood of disruption” as described in Fig. 8b of de Vries et al. (2014).

Since $q_{\textrm{95}}\sim \epsilon \beta _{\textrm{P}}/\beta _{\textrm{N}}$, higher $\beta _{\textrm{P}}$ would have higher $q_{\textrm{95}}$ for a given $\epsilon$ and $\beta _{\textrm{N}}$, so the high-$\beta _{\textrm{P}}$ scenario is advantageous for disruptivity. Disruption damage is known to be proportional to $I_{\textrm{p}}^2$ (Wesson 2004). That means that the high-$\beta _{\textrm{P}}$ scenario, which usually runs at reduced plasma current at a given toroidal field, also has an advantage of relatively lower disruption damage, in addition to the low disruptivity.

The scenario requires sufficient $\beta _{\textrm{P}}$ to enable strong $\alpha$-stabilization to suppress turbulence, and therefore increase confinement quality. For a given plasma current, this requires a certain value of $\beta _{\textrm{N}}$, especially when the target $q_{95}$ is lower. Since $\beta _{\textrm{P}}\sim \beta _{\textrm{N}}q_{95}$, high $\beta _{\textrm{N}}$ is the key to maintain sufficient $\beta _{\textrm{P}}$ for high confinement quality when $q_{95}$ is lowered to an FPP-relevant range (4–9). Therefore, the high-$\beta _{\textrm{P}}$ scenario inherently requires high $\beta _{\textrm{N}}$. Naturally, the challenge of MHD issue at high $\beta _{\textrm{N}}$ is unavoidable in this scenario. The $n=1$ kink mode and its stabilization by a resistive wall in the presence of slow plasma rotation are an outstanding issue.

Efforts have been made to understand requirements for achieving high $\beta _{\textrm{N}}$ and understanding stability limits in this scenario. As summarized in Ren et al. (2016), it is observed that maintaining a controlled smaller outer gap maximizes achievable $\beta _{\textrm{N}}$. Outer gap is the distance between the plasma surface and the low-field-side limiter surface at the midplane. The plasma shape is kept similar when the outer gap is changed between discharges. In these experiments, plasmas disrupt at a certain value of $\beta _{\textrm{N}}$, as $\beta _{\textrm{N}}$ is ramped up. Note that they are minor disruptions with $\beta _{\textrm{N}}$ collapses instead of dangerous full current disruptions. The $\beta _{\textrm{N}}$ threshold varies as the outer gap changes. As shown in Fig. 19a, the trend is consistent with the increased ideal wall $n=1$ kink $\beta _{\textrm{N}}$ limit when the plasma is closer to the wall. The prediction of the ideal wall limit is done by the GATO code (Bernard et al. 1981). The experimental cases show pressure peaking factor ($P_0/\langle P\rangle$)$\sim 2.4$–2.5. Two sets of calculations have been performed using pressure peaking factors of 2.4 and 2.6. The experimental observations of maximum $\beta _{\textrm{N}}$ agree well with the predictions using similar pressure peaking factors. These plasmas not only have passed the no-wall limit, but also are approaching the ideal wall limit. It is important to note that broader pressure profiles, i.e., lower peaking factors, are observed at higher $\beta _{\textrm{N}}$. The physics reason can be concluded that ITB foot tends to be at higher radius at higher $\beta _{\textrm{N}}$ as shown in Ren et al. (2016). As pointed out in Turnbull et al. (1998), broader pressure profiles have a higher ideal wall limit. Indeed, the decrease of pressure peaking increases the predicted ideal wall limit at small outer gap as shown in Fig. 19a. However, it is also worth pointing out that higher peaking factor is favorable to high fusion reactivity, which is proportional to $n_{\textrm{i}}^2T_{\textrm{i}}^2$, in near-axis region of an FPP.

Although the analysis above is based on transient experimental observations, there is also evidence to show the sustainability of high-$\beta _{\textrm{P}}$ discharges with high $\beta _{\textrm{N}}$. Figure 19b shows an example for a few seconds (few $\tau _{\textrm{R}}$) with $\beta _{\textrm{N}}\sim 6l_{\textrm{i}}$, which far exceeds $4l_{\textrm{i}}$, the empirical estimation of no-wall limit (Howl et al. 1992; Strait 1994). This plasma maintained $H_{\textrm{98y2}}\sim 1.5$ during the high-$\beta _{\textrm{N}}$ phase (Fig. 19c). The termination of this high-$\beta _{\textrm{N}}$ phase is due to the limit of NBI operation in this particular discharge.

As shown in Figs. 2h, 7b and 21a, the high-$\beta _{\textrm{P}}$ plasmas have high $q_{\textrm{min}}$ above 2.0. Therefore, this feature avoids many deleterious MHD modes, such as the $m/n=1/1$ sawteeth and the 2/1 neoclassical tearing mode (NTM). Instead, high-order modes, such as $m/n=5/1$ and 6/1, may still occur in the experiments. Nevertheless, they may produce less confinement degradation than lower-order NTMs. Observations of $n=1$ mode in DIII-D high $\beta _{\textrm{P}}$ plasmas have been documented in Garofalo et al. (2015) and Ren et al. (2016), showing a feature of ideal kink mode that can be stabilized by a wall close to the plasma.

2.5 Fully non-inductive operation

It is straightforward that the high-$\beta _{\textrm{P}}$ scenario is beneficial for 100% non-inductive current fraction for the purpose of steady-state operation. This is because $f_{\textrm{Oh}}=1-f_{\textrm{bs}}-f_{\textrm{CD}}$ and $f_{\textrm{bs}}\sim \epsilon ^{0.5}\beta _{\textrm{P}}$, where $f_{\textrm{Oh}}$ is the Ohmic current fraction, $f_{\textrm{bs}}$ is the bootstrap current fraction, $f_{\textrm{CD}}$ is the external current drive fraction. High-$\beta _{\textrm{P}}$ regime naturally has high $f_{\textrm{bs}}$ for a given $\epsilon$. On one hand, a high $f_{\textrm{bs}}$ will help reduce $f_{\textrm{Oh}}$ to access fully non-inductive operation when $f_{\textrm{Oh}}$ is zero. On the other hand, a high enough $f_{\textrm{bs}}$ will further reduce the requirement of $f_{\textrm{CD}}$ and the corresponding external power that is required to maintain the $f_{\textrm{CD}}$. This is an important and effective approach toward a high Q ($=P_{\textrm{fus}}/P_{\textrm{aux}}$) solution for steady-state FPP by reducing the required auxiliary power. This approach is particularly suitable for a small/medium-size compact FPP (CFPP) that does not pursue very high fusion power output.

DIII-D has demonstrated fully non-inductive operation with $f_{\textrm{bs}}$ up to 85% in high-$q_{95}$ ($>10$), high-$\beta _{\textrm{P}}$ discharges (Garofalo et al. 2015). This discharge, DIII-D #154406, has constant current in the transformer coils after 1.6 s, when the plasma current reaches its flattop. The current components shown in Fig. 20 are calculated by the TRANSP code, showing $f_{\textrm{bs}}\sim 80$–85%, $f_{\textrm{NBI}}\sim 15$–20% and $f_{\textrm{EC}}<5$%, where $f_{\textrm{NBI}}$ and $f_{\textrm{EC}}$ are the current fraction driven by neutral beam injection and electron cyclotron wave, respectively. Although surface voltage has reached zero at 2.6 s, there is residual Ohmic current decaying over time. An exponential fit to the calculated Ohmic current yields a time constant of $\sim 1.06$ s. This is consistent with the estimated current profile relaxation time 1–2 s based on experimental data between 2–6 s. This evidence showcases the non-inductive sustainment of such high-$f_{\textrm{bs}}$ scenario. It may also be worth mentioning that this plasma has maintained $\beta _{\textrm{N}}\sim \beta _{\textrm{P}}\ge 3$, $f_{\textrm{Gr}}\ge 0.9$ and $H_{\textrm{98y2}}\sim 1.5$. Recent progress on high-$\beta _{\textrm{P}}$ scenario development on DIII-D shows $f_{\textrm{bs}}$ up to 80% at medium $q_{95}\sim 7$–8 (Wang et al. 2021d). Note that $f_{\textrm{bs}}$ is expected to be higher at lower collisionality expected in a reactor.

3 Other features of the high-$\beta _{\textrm{P}}$ scenario

This section introduces several aspects of the high-$\beta _{\textrm{P}}$ scenario based on DIII-D experimental and modeling studies, including ITB sustainment, dominant turbulence, impurity accumulation, pedestal features, $\beta _{\textrm{N}}$ limit, and fast ion instabilities.

3.1 Current alignment in ITB

ITB shrinkage, i.e., when the foot location of an ITB moves radially inwards over time, is an issue for some ITB plasmas (Sarazin et al. 2002; Hogeweij et al. 2002; Houlberg et al. 2005). The physics can be described as following: “the bootstrap current naturally peaks where the pressure gradient is maximum, i.e., at the ITB, which in turn is due to a current that peaks outside the ITB itself” (García et al. 2008). This is the current alignment problem. ITBs with this problem are usually associated with negative magnetic shear $\hat{s}$, which is an important physics mechanism of turbulence suppression that can be applied in reactor-relevant conditions. In this case, external control of current profile becomes essential to sustain such ITBs for long pulse operation.

However, experimental evidence of sustained ITBs exist in multiple devices. JT-60U experiments indicate that the shrinkage of the reversed shear region can be suppressed, and a large radius ITB sustained, by having a sufficiently large bootstrap current peak at the ITB peak gradient region (Fujita et al. 2001). Later, JT-60U extended the duration of the sustained ITB to 7.4 s, which is about $16\tau _{\textrm{E}}$ and $2.7\tau _{\textrm{R}}$ (Sakamoto et al. 2005). Analysis using JT-60U data (Litaudon et al. 2011) discussed the self-sustained reversed magnetic shear by bootstrap current and broader NBCD. ITBs can be also sustained with LHCD in JET as discussed in Baranov et al. (2005) and in Tore Supra for up to 2 min as shown in Litaudon (1996). These results reveal an important fact that the high local bootstrap current density can develop its own minimum q and can suppress the shrinkage of the ITB. This effect is recognized in multiple review papers (Gormezano et al. 2007; Ida and Fujita 2018).

It is clear that the ITB shrinkage phenomenon or the current alignment problem is not something universal in ITB plasmas. It strongly depends on the governing physics of ITB formation and only happens in a specific category of ITBs, i.e., reversed magnetic shear (RS)-driven ITB. The reference (Litaudon 2006) summarizes several approaches or physical mechanisms that could be responsible for ITB formation. In addition to that, recent studies from both modeling and experiment indicate that fast ions can also play an important role in turbulence suppression and ITB development (Citrin et al. 2013; Di Siena et al. 2021; Han et al. 2022).

The high-$\beta _{\textrm{P}}$ scenario large-radius ITB belongs to the $\alpha$-stabilization category, which is different from the RS-driven ITB category in Litaudon (2006). It states in Litaudon (2006): “ITBs could be self-sustained in certain conditions thanks to a positive feedback loop between pressure and the $\alpha$-stabilizing parameters.” Indeed, the high-$\beta _{\textrm{P}}$ experiments on DIII-D do show stable ITBs at large radius for a few seconds, i.e., a few $\tau _{\textrm{R}}$. Figure 21a, b shows the profiles for DIII-D #154406 at 5.17 s. A striking feature is the dominant bootstrap current density in the total current density in the ITB region. Therefore, a local minimum in q-profile is within the ITB and aligns with peak bootstrap current. Consequently, such alignment leads to stable ITB in experiments as shown in Fig. 21c, d. $\beta _{\textrm{N}}$ and $\beta _{\textrm{P}}$ stay around 3 from 1.7 to 5.7 s and $H_{\textrm{98y2}}$ sustains above 1.5. The ITB foot location remains at $\rho \sim 0.75$ during the high performance phase. As discussed in Sect. 2.1.2, the physics of ITB formation in the high-$\beta _{\textrm{P}}$ scenario gives some flexibility in magnetic shear compatible with the ITB. This is an important factor that ensures ITB robustness against transient events, such as minor $\beta$ collapses due to MHD instability.

3.2 Dominant residual turbulence in high confinement state with ITB

The presence of an ITB in high-$\beta _{\textrm{P}}$ plasmas greatly suppresses micro-turbulence at large radius and elevates temperature and density in the core and global confinement quality. Analysis has been performed to understand the residual turbulence in the high confinement state with an ITB. The dominant remaining turbulence is a slab-like micro tearing mode (slab-MTM) at high $q_{95}$, and ballooning modes at lower $q_{95}$ (Jian et al. 2019, 2021a; Ding et al. 2020a).

Gyrokinetic analysis based on DIII-D high-$\beta _{\textrm{P}}$ experimental data using CGYRO code shows that all ballooning modes can be fully suppressed when the $\alpha$-stabilization effect is strong, leaving an $\alpha$-destabilized slab-MTM as the dominant and unique micro-instability in the ITB region (Jian et al. 2019, 2021a). It is likely to happen with high q since $\alpha \sim q^2\textrm{d}p/\textrm{d}r$. The structure of the eigenfunction is shown in Fig. 22. Unlike ballooning modes, the slab-MTM has narrow, peaked, and ballooning extended eigenfunctions. The difference can be better visualized when the eigenfunctions are plotted in R-Z space as shown in Fig. 22c, d. While a ballooning mode has a dominant peak $\phi$ at low field side with a large radial width (Jian et al. 2020), the peak eigenfunctions of a slab-MTM are located at the high field side and the radial extent is relatively small. Such eigenfunctions are difficult for reduced transport models like TGLF to capture. As Fig. 23 shows, TGLF can reproduce the $\alpha$-stabilization of the TEM but fails to find the MTM solutions at higher q. This could be a fundamental reason for the systematic overprediction of electron temperature in the high-$q_{95}$ high-$\beta _{\textrm{P}}$ plasmas on DIII-D (Pan et al. 2017; McClenaghan et al. 2017). Comparisons between TGLF results on low-$q_{95}$ and high-$q_{95}$ can be found in Pan et al. (2017) and McClenaghan et al. (2017) as well.

Figure 23 reveals an important q dependence of the dominant mode in high-$\beta _{\textrm{P}}$ plasmas. As q decreases, a branch of the ballooning mode is identified as the dominant mode, e.g., TEM in this particular case, by CGYRO. This is within the capability of TGLF, although TGLF may have quantitative differences when calculating the linear growth rate compared with CGYRO in this particular case. This explains the much better temperature and density prediction results compared to experimental data at lower $q_{95}$ (McClenaghan et al. 2017). Gyrokinetic modeling using GYRO code based on lower $q_{95}$ DIII-D high-$\beta _{\textrm{P}}$ discharge data confirms that the residual turbulence is all ballooning modes from the ITB shoulder to the ITB foot (Ding et al. 2020a). Figure 24 shows a 2D contour of linear growth rate of the most unstable micro-instability from ITB shoulder to ITB foot, i.e. $0.3\le \rho \le 0.7$ and from low-k to high-k, i.e., $0.1\le k_{\theta }\rho _{\textrm{s}}\le 100$. Three kinds of dominant instabilities are identified in this parameter region. They are collisional TEM (CTEM), ITG, and electron temperature gradient (ETG) mode as shown in Fig. 24. This finding strengthens the confidence of predictive application of the TGLF model in high-$\beta _{\textrm{P}}$ regime based on the fact that TGLF behaves very well in capturing the ballooning-type drift-wave instability. Ding et al. (2020a) gives a test case using the same set of parameters used in Fig. 24, except the q-profile. By doubling the q-profile, the test case indicates slab-MTM as the most unstable mode, confirming the existence of dominant mode conversion and its q dependence.

3.3 Impurity transport in an ITB core

Excessive impurity concentration in an FPP core will dilute the fuel and reduce fusion power output. Since the existence of an ITB increases energy and particle confinement in the core, two questions naturally arise: (1) does impurity confinement also increase? (2) If so, is the impurity density peaked on-axis?

The primary impurity in DIII-D high-$\beta _{\textrm{P}}$ plasmas is carbon, since DIII-D has a carbon wall. The carbon density profile in a typical high-$\beta _{\textrm{P}}$ ITB plasma is shown in Fig. 25. As expected, the presence of an ITB at large radius indeed increase carbon confinement. A clear carbon density ITB developed at large radius. However, the carbon density profile is very flat inside the ITB. The peaking factor is far less than the NEO prediction based on the neoclassical transport theory. Therefore, $Z_{\textrm{eff}}\sim 2.0$ for most of the DIII-D high-$\beta _{\textrm{P}}$ discharges without impurity injection (Wang et al. 2021d). In this case, the ratio of core radiated power to total injected power is usually 15–20%. For strong impurity gas puffing high-$\beta _{\textrm{P}}$ discharges, e.g., the case discussed in Sect. 2.3, the line-averaged $Z_{\textrm{eff}}$ can reach 4 or higher. However, the profiles of impurity density, e.g., neon, are still similar to the electron density profiles shown in Fig. 15b. That means although neon density builds up an ITB at large radius, it is still pretty flat inside the ITB. The peaking factor is actually not high. A working hypothesis is that the dominant turbulence inside the ITB, e.g., CTEM in Fig. 24, plays a role in regulating impurity transport in the near-axis region. More analysis and experiments of impurity transport are planned in the near future.

3.4 Features of the pedestal

As discussed in Sect. 2.1.2, there are two types of self-organized states in DIII-D high-$\beta _{\textrm{P}}$ plasmas. One is the high-pedestal weak/no-ITB state. The other is the low-pedestal strong-ITB state. Analysis has been performed of the pedestal and ELM behaviors in these two states (Li et al. 2017; McClenaghan et al. 2020).

The EPED model (Snyder et al. 2011) is employed to predict the pedestal pressure height for both states and in both high $q_{95}$ ($\sim 12$) and lower $q_{95}$ ($\sim 6$) cases (Li et al. 2017). The results show that the pedestal heights agree well with EPED predictions when the pedestal is high. However, the low-pedestal cases have much lower pedestal pressure values than their EPED predictions. The phenomena are the same for both $q_{95}$ cases. In the transition from a high-pedestal state to a low-pedestal state, the pedestal width does not change. ELMs with high frequency and low amplitude are observed in the low-pedestal state, while type-I or compound ELMs are observed in the high-pedestal state.

Further pedestal analysis on the two states are performed using the ELITE code (Snyder et al. 2002) to understand the different heights (McClenaghan et al. 2020). Figure 26 shows the stability analysis of the two states. In the high-pedestal case (Fig. 26a), the pink–red region on the top represents the current gradient peeling stability limit. The pink region on the right shows the pressure gradient ideal ballooning mode limit. The experimental data are located in the gap between these two limits, but near the peeling stability limit. This result suggests that the high-pedestal state is limited by the peeling mode, while the low-pedestal state shows a different situation. The low-pedestal state has a lower value in both pressure gradient and current gradient. Thus, it is far from the peeling-ballooning stability limit as shown in Fig. 26b. When interpreting this modeling result, a caveat is that the ELITE model uses a derived criteria in the limit of constant diamagnetic frequency ($\omega _{*}$) to consider the diamagnetic stabilization. However, $\omega _{*}$ actually varies significantly over the pedestal. The plasma may shift closer to the ballooning stability limit, if a more realistic diamagnetic stability model is used and the uncertainty in the experimental edge current and pressure gradient are considered.

Transport analysis by TGLF near the pedestal top ($\rho =0.9$) shown in Staebler et al. (2018) gives a possible explanation to the lower pedestal pressure in the strong-ITB state. The analysis applied on both states indicates that the low-pedestal case has large turbulent transport as it appears on top of the KBM mountain, while the high-pedestal case is in the stable pass. It is believed that the very different magnetic shear, positive for low-pedestal case and negative for high-pedestal case, plays important role in this picture. Magnetic shear is determined by the local bootstrap current density, which is affected by the pressure profile. Again, this is related to the state self-organization described in Sect. 2.1.2. Another recent analysis in Jian et al. (2021b) supports a similar picture. In this study, a boundary of KBM instability, defined by the linear growth rate, is calculated by the CGYRO code using high $\beta _{\textrm{P}}$ experimental data in the strong-ITB low-pedestal state. The result indicates that the ITB region is in the 2nd stability regime and is far away from the KBM mountain, while moving towards the pedestal top makes it closer to the instability. This gyrokinetic analysis is qualitatively consistent with the TGLF results in Staebler et al. (2018). Furthermore, in this dedicated work using CGYRO, the general conclusion is that the whole pedestal stays in a regime with higher ballooning drive due to the high magnetic shear, suggesting that not only KBM, but actually all the ballooning-type drift-wave instabilities have higher growth rate (Jian et al. 2021b). There is ongoing work along this line that will be published separately. Therefore, the latest understanding of the low-pedestal state is that it could be induced by the enhancement of turbulent transport across the whole pedestal. Enhanced pedestal transport may open an avenue for ELM mitigation in the high-$\beta _{\textrm{P}}$ scenario. DIII-D experiments along this line are planned, including turbulence mode verification and effects on ELM mitigation.

3.5 Alfvén eigenmode instabilities

Investigations on DIII-D show that Alfvén eigenmode (AE) activity degrades fast-ion confinement in many high $\beta _{\textrm{N}}$, high $q_{\textrm{min}}$, steady-state scenario discharges (Heidbrink et al. 2014). The increased fast-ion transport in discharges with strong AE activity accounts for most of the observed reduction in global confinement with increasing $q_{\textrm{min}}$. In scenarios with $q_{\textrm{min}}$ above 2, AEs usually cause greater fast-ion transport than classical models predict (Holcomb et al. 2015).

As mentioned in Sect. 2.4, high-$\beta _{\textrm{P}}$ scenario has $q_{\textrm{min}}$ above 2 due to the broad current density profile dominated by the large-radius bootstrap current and ITB. The AE activities have been compared in a standard high-$q_{\textrm{min}}$ case and a high-$\beta _{\textrm{P}}$ case, both of which have $q_{\textrm{min}}>2.0$ (Holcomb et al. 2015). The high-$\beta _{\textrm{P}}$ case actually has $q_{\textrm{min}}\sim 5.0$. Here, the “standard high $q_{\textrm{min}}$” regime has $q_{\textrm{min}}\sim 2$–2.5, $q_{95}\sim 5$–7, $I_{\textrm{p}}\sim 0.8$–1 MA, line-averaged density $\sim 3.5$–$4.5\times 10^{19}$ m$^{-3}$ and density Greenwald fraction near 0.5. These conditions were chosen to target fully non-inductive operation with a significant fraction of externally driven current. This is a regime aimed at the same steady-state goal but using a different approach, i.e., low density, compared to high density in the high-$\beta _{\textrm{P}}$ scenario. Figure 27a, b compares the frequency spectrum of the electron temperature fluctuations measured by the electron cyclotron emission diagnostic. The standard high-$q_{\textrm{min}}$ plasma has many more coherent modes inside of $\rho \sim 0.5$, while the high-$\beta _{\textrm{P}}$ case has strong modes around 60 and 70 kHz only outside of $\rho \sim 0.6$, which is the location of the ITB. Both cases have a fast-ion profile peaked on-axis. However, the high-$\beta _{\textrm{P}}$ case has much shorter slowing-down time, and therefore a lower classically predicted $\nabla \beta _{\textrm{fast}}$ on axis, due to the very high density and the relatively low temperature. This may be consistent with the “critical $\nabla \beta _{\textrm{fast}}$” picture described in Heidbrink et al. (2013), which suggests a rapid increase of fast-ion transport when $\nabla \beta _{\textrm{fast}}$ exceeds a critical value. AEs near the magnetic axis are more likely to cause enhanced fast-ion transport than AEs at large radius. Indeed, TRANSP analysis on the high-$q_{\textrm{min}}$ discharge indicates a $\sim$ 15% stored energy overestimate, which means higher calculated stored energy assuming classical fast ions compared to the observed stored energy. This implies a necessary anomalous fast-ion diffusivity in the calculation. On the other hand, the same analysis on the high-$\beta _{\textrm{P}}$ plasma shows a stored energy overestimate of $\sim$ 3%, which means a near classical fast-ion transport level. Modeling analysis on the toroidal Alfvén eigenmode (TAE) gap using NOVA code (Cheng and Chance 1987; Gorelenkov et al. 1999) shows a wide TAE gap near axis in the high-$q_{\textrm{min}}$ case, while the gap only widens at the large radius in the high-$\beta _{\textrm{P}}$ case (Fig. 27c, d). This is qualitatively consistent with the experimental observations discussed above.

A recent independent study gives an alternative mechanism on beta-induced Alfvén eigenmode (BAE) in regulating the mode location. The new analysis is performed based on another representative high-$\beta _{\textrm{P}}$ shot with lower $q_{95}$ (Jian et al. 2022a, b). The mode peaks at large radius, ($\rho \sim 0.75$), which is consistent with the observation above. Density fluctuation measurements from BES and CO$_2$ interferometer show that the mode has a dispersion relation consistent with BAE theory. The free energy for BAE excitation consists of two parts, the background thermal plasma drive ($\delta W_{\textrm{th}}$) and the kinetic drive from fast ions ($\delta W_{\textrm{k}}$) (Chen and Zonca 2016). Since BAE shares the same thermal drive with KBM (Zonca et al. 1999), which is closest to the stability boundary near the edge (Sect. 3.4), this suggests that the free energy of thermal drive is highest there. Although the fast-ion population (and the kinetic drive) is low near the edge, it is sufficient to destabilize BAE on top of the high $\delta W_{\textrm{th}}$ there. Moving toward the plasma core or the ITB, the plasma is getting father away from the BAE instability due to the increased $\alpha$-stabilization effect. For the high-$q_{\textrm{min}}$ case, the edge region is not close to the KBM boundary. Such low $\delta W_{\textrm{th}}$ and low $\delta W_{\textrm{k}}$ are not able to excite BAE. Therefore, the plasma is stable to BAE at large radius as observed experimentally. Unlike the high-$\beta _{\textrm{P}}$ case, the high $q_{\textrm{min}}$ inner plasma does not have an ITB and high $\alpha$. Therefore, $\alpha$-stabilization is weak in the inner core and the BAE will be excited when $\delta W_{\textrm{k}}$ is high enough, which can be satisfied in the inner core region. This picture is also a candidate explanation on the observed localized AEs in the outer core region in high-$\beta _{\textrm{P}}$ experiments and the AEs in the inner core region in high-$q_{\textrm{min}}$ experiments (Jian et al. 2022a, b). Additionally, nonlinear gyrokinetic modeling of high-$\beta _{\textrm{P}}$ plasma suggests that BAE is responsible for almost all of the electron particle transport and one third to one half of electron energy transport in the outer core region. Neoclassical transport accounts for most ion energy transport, while ETG provides the residual electron thermal transport. Therefore, BAE plays an important role in recovering the missing transport in addition to drift-wave modeling in gyrokinetic simulations at the outer core region in high-$\beta _{\textrm{P}}$ plasmas.

4 Efforts on operational space expansion in the high-$\beta _{\textrm{P}}$ regime

In the past decade, significant effort has been spent by the Joint DIII-D/EAST team to extend the operational space of the high-$\beta _{\textrm{P}}$ scenario toward higher normalized performance. As discussed in Sect. 2, an attractive FPP design requires: (1) high $H_{\textrm{98y2}}$ for high fusion gain and low capital cost; (2) high density for high fusion power. These are also the key physics that the joint research team would like to address. Another focus in the research is to reduce $q_{95}$. Historically, high-$\beta _{\textrm{P}}$ plasmas were usually operated at low plasma current, i.e., very high $q_{95}$ ($\sim 10$), on DIII-D (Politzer et al. 2005). This was also the starting point of the research by the Joint DIII-D/EAST team. However, this range of $q_{95}$ may be too high for an FPP. It limits the normalized performance, such as $\beta _{\textrm{T}}$. Here, $\beta _{\textrm{T}}$ is the toroidal beta defined by the ratio of averaged plasma pressure to toroidal magnetic field pressure. This is because for a given $\beta _{\textrm{N}}\sim \beta _{\textrm{T}}/I_{\textrm{p}}$, lower $I_{\textrm{p}}$ means lower $\beta _{\textrm{T}}$ and lower fusion reactivity in FPP. A trade-off between $\beta _{\textrm{P}}$ and $\beta _{\textrm{T}}$ at constant $\beta _{\textrm{N}}$ exists. Therefore, development of high-$\beta _{\textrm{P}}$ scenario toward lower $q_{95}$ (higher $I_{\textrm{p}}$) on DIII-D is also a major task for the joint team. It is worth noting that the key to achieving high $\beta _{\textrm{P}}$ and high $\beta _{\textrm{T}}$ at lower $q_{95}$ is high enough $\beta _{\textrm{N}}$.

Figure 28 shows the development of parameters in the high-$\beta _{\textrm{P}}$ scenario over years following the major tasks described above (Wang et al. 2021d). The best $\beta _{\textrm{T}}\times H_{\textrm{98y2}}$ value in each year and the corresponding $q_{95}$ at the same time in the same discharge are summarized in Fig. 28a, while the highest line-averaged $f_{\textrm{Gr}}$ in each year and the corresponding density are shown in Fig. 28b. Note that data in Fig. 28a and data in Fig. 28b in the same year may come from different discharge/time slice. Same filter is applied to these data as described in Sect. 2.3 when introducing Fig. 17. Therefore, these data are not transient due to the 40 ms averaging time window and the constraint of $(\textrm{d}W/\textrm{d}t)/P_{\textrm{tot}}\le 0.1$. However, some of them may keep evolving in a longer period. As one can see, $q_{95}$ has been reduced to 6–8, which is a suitable range for an FPP design. The normalized parameter $\beta _{\textrm{T}}\times H_{\textrm{98y2}}$, which is proportional to the triple product $n_{\textrm{i}}\times T_{\textrm{i}}\times \tau _{\textrm{E}}$, increases steadily and is approaching a value of 6. Those cases all have $H_{\textrm{98y2}}\ge 1.5$. Note that the prediction of ITER steady-state has $\beta _{\textrm{T}}\times H_{\textrm{98y2}}\sim 3.7$ (Poli et al. 2014) and the value for the predicted high-$\beta _{\textrm{P}}$ version of ITER steady-state scenario is about 3.97 (McClenaghan et al. 2020). Although high-$\beta _{\textrm{P}}$ plasmas on DIII-D are usually operated at line-averaged $f_{\textrm{Gr}}\sim 1.0$ or slightly below 1.0, the best cases for each year actually exceed unity. As lower $q_{95}$ and higher plasma current are reached, the achieved absolute density is gradually increasing to maintain or improve Greenwald fraction. In 2019, the record $f_{\textrm{Gr}}$ is up to 1.4 and line-averaged $n_{\textrm{e}}$ up to $9.5\times 10^{19}$ m$^{-3}$. It is important to note that high density is not achieved by elevating the pedestal. Instead, pedestal densities are usually under feedback control at a moderate level, e.g., $f_{\textrm{Gr,ped}}\sim 0.6$. The substantial increase of density comes from the development of a density ITB with or without impurity injection. Figure 15b in Sect. 2.3 shows such an example with impurity injection. This development towards high normalized parameters enables the potential of operational point demonstration for FPP designs. Recent work on a CFPP design, which is also called compact advanced tokamak (CAT) DEMO, proposes several target scenarios for an output electric power of 200 MW with a $B_{\textrm{T}}=6$–7 T, $R\sim 4$ m compact device (Buttery et al. 2021). One of the candidates, case D in table 2 of this reference, shows features achievable by the high-$\beta _{\textrm{P}}$ scenario: $q_{95}=6.5$, $\beta _{\textrm{N}}=3.6$, $H_{\textrm{98y2}}=1.51$. The modeling was performed by 1.5D FASTRAN code (Park et al. 2017, 2018) using TGLF as the transport model. As pointed out in the reference, “...Indeed, recent work on DIII-D has already shown similar normalized performance ($H_{\textrm{98}}\sim 1.5$, $q_{95}\sim 6$, $\beta _{\textrm{N}}\sim 3.5$) at Greenwald density fractions approaching those used here (line average value $\sim 1$ vs. 1.3 in the $f_{\textrm{GW}}^{\textrm{ped}}=1$ cases of table 2)...”.

The latest “parameter pushing” experiments with the DIII-D high-$\beta _{\textrm{P}}$ scenario achieved $\beta _{\textrm{N}}\sim 4.2$, $\beta _{\textrm{T}}\sim 3.3$%, $H_{\textrm{98y2}}\sim 1.8$, $f_{\textrm{Gr}}\sim 1$ (Fig. 29). This is corresponding to the highest $\beta _{\textrm{T}}\times H_{\textrm{98y2}}$ data point in Fig. 28a. The bootstrap current fraction is up to 80%. $q_{95}$ is about 7–8 and $q_{\textrm{min}}$is about 3. This discharge sustained the high-performance phase for about one $\tau _{\textrm{R}}$, then evolved to an MHD-unstable state, which is believed to be due to the Ohmic current penetration induced by a slow current ramp up started at 2 s. Further optimizations, including applying extra non-inductive current drive, are being considered for future DIII-D experiments. Specifically, the planned additions of ECCD, helicon, and high field side lower hybrid wave may allow elimination of all Ohmic current and $I_{\textrm{p}}$ ramps to sustain the high-performance phase with $q_{\textrm{min}}>2$, limited only by available NBI capability or coil limits. This high-performance state, in terms of the normalized parameters shown in Fig. 30, is actually within the parameter range of a FPP design called A-SSTR [KIKUCHI00]. Such an experimental basis would be very helpful in predictive model validation and build better confidence on further FPP designs.

The ultimate goal of scenario research is to develop a fully integrated scenario that can be used in the future. Although it still needs time to reach such goal, this paper provides latest partially integrated experimental results on high $\beta _{\textrm{P}}$ scenario on DIII-D. At present, there are two main research topics in the joint research team: (1) fully non-inductive operation with high $\beta _{\textrm{T}}$; (2) detached divertor with ELM mitigation. One good example of partially integrated results on high non-inductive current fraction and high $\beta _{\textrm{T}}$ is #185959 (Fig. 29) as shown earlier in this section. In the high-performance phase of this discharge, features like high $\beta _{\textrm{T}}$, high $H_{\textrm{98y2}}$, high $f_{\textrm{Gr}}$, medium $q_{95}$, and high $f_{\textrm{bs}}$, have been integrated together. Although bootstrap current fraction is high (up to 80%), this discharge is still not fully non-inductive due to limited external current drive capability on DIII-D. However, it is important to note that such scenario on FPP will have lower collisionality because of much higher plasma temperature. Hence, fully non-inductive operation is anticipated on FPP with similar dimensionless parameters, such as $H_{\textrm{98y2}}$, $f_{\textrm{Gr}}$, $\beta _{\textrm{T}}$, $\beta _{\textrm{P}}$, etc. For future demonstration on DIII-D, more external-driven current is required. Prediction shows additional $\sim$ 100 kA from helicon current drive or LHCD would be able to meet the experiment goal of non-inductive operation. Recent DIII-D upgrade on helicon wave and high field side lower hybrid wave project provides excellent opportunity for this development. Impurity injection is also considered in the experiment seeking possible core-edge integration in the very high-performance phase. Related high $\beta _{\textrm{P}}$ experiment has been scheduled in 2023. The other type of partially integrated scenario focuses on edge solution and core-edge integration. One typical example is #186027 (Fig. 14) discussed in Sect. 2.2, which shows good confinement quality, fully detached divertor, and simultaneously suppressed ELM. What are not mentioned in that subsection include medium $q_{95}\sim 7.5$ and high $f_{\textrm{Gr}}>0.9$ in this discharge. This result has been achieved in an ITER-like shape (Fig. 1), which is new to the high $\beta _{\textrm{P}}$ scenario development on DIII-D and has not been well explored. The future direction on developing high $\beta _{\textrm{P}}$ scenario along this path will be improving $\beta _{\textrm{N}}$ and non-inductive current fraction, studying effect of divertor closure on performance of divertor and core plasma using the unique SAS divertor on DIII-D and investigating tungsten transport from divertor to plasma core taking advantage of the tungsten ring in SAS divertor. Related experiments will be performed in 2022 and 2023.

5 Projections to present and future devices

This section briefly introduces high-$\beta _{\textrm{P}}$ scenario development efforts for present and future devices mainly by 1.5D self-consistent modeling.

The goals of the Joint DIII-D/EAST research team are: (1) to develop an FPP scenario and understand its physics, taking advantage of the well-equipped diagnostics and sophisticated plasma control on DIII-D; and (2) adapt the prototype scenario to EAST and demonstrate truly long-pulse operation with a metal wall. Since the team has many accomplishments in DIII-D on scenario development and physics understanding as discussed in the paper, the experimental and modeling explorations have been actively launched on EAST to realize high-$\beta _{\textrm{P}}$ scenario with large-radius ITB. However, the high-$\beta _{\textrm{P}}$ plasmas on EAST always have electron temperature profiles very peaked near the axis (Gong et al. 2022) instead of a broadened profile with ITB at large radius, even if $\beta _{\textrm{P}}$ exceeds DIII-D’s empirical threshold around 2.0. Using the same physics picture for large-radius ITB development described in Sect. 2.1.2, gyrokinetic modeling based on EAST high $\beta _{\textrm{P}}$ experimental data provides a possible explanation for the observations (Ding et al. 2021c). The analysis shows that on EAST, plasma at large radius is trapped on an “ITG mountain”. In other words, the gradients of profiles are limited by the ITG mode. The modeling work also provides insight into the potential approaches for breakthrough: (1) apply strong external off-axis current drive or use strong early heating to reduce magnetic shear at large radius; (2) pause $I_{\textrm{p}}$ ramp-up at higher $q_{95}$ to obtain stronger $\alpha$-stabilization before proceeding to the main $I_{\textrm{p}}$ flattop; (3) increase ion heating at large radius or increase pedestal ion temperature for higher $T_{\textrm{i}}/T_{\textrm{e}}$; (4) inject impurity at large radius for higher density gradient. Both high $T_{\textrm{i}}/T_{\textrm{e}}$ and high-density gradient are beneficial to ITG suppression. In addition to the single-mode linear gyrokinetic analysis, TGLF modeling on heat fluxes across a wide spectrum of $k_{\theta }\rho _{\textrm{s}}$ (from 0.1 to 25) confirms such a physics picture. Further profile predictions by TGYRO indicate that more central heating power (up to $3{\times}$) is not able to significantly increase pressure gradient at large radius, e.g., $\rho =0.55$, when q-profile is monotonic as shown in EAST experimental data. Adding an artificial reversed q-profile in the simulation gives a boost of predicted pressure gradient at large radius. At high power, the result suggests a threefold increase in the pressure gradient. Further applying Gaussian-like particle source (e.g., pellet) at $\rho =0.6$ will increase the pressure gradient to 4–5 times its experimental value. These modeling results clearly point out important strategies that need to be considered in future EAST experiments: (1) create and maintain high $q_{\textrm{min}}$ with low or reversed magnetic shear at large radius; (2) fuel the large radius region effectively.

As summarized in Marinoni et al. (2021), DIII-D has made good experimental progress in the negative triangularity (NT) configuration since 2016. A dedicated NT mini-campaign is planned on DIII-D in 2022 with a new armor installed in the low field side vacuum vessel. With the new armor, it is possible to develop an NT plasma with strong shaping in the core and high-power handling capability at the edge. Many important physics as well as advanced scenario development will be explored in the coming campaign. It has been decided that developing high $\beta _{\textrm{P}}$ scenario in NT configuration is a part of the experimental goals. Preliminary modeling work using STEP code (Meneghini et al. 2021) and TGLF as transport model shows the possibility of developing a large-radius ITB within current heating capability of DIII-D at reduced plasma current. A reduced plasma current at relatively high $q_{95}$ is important to high-$\beta _{\textrm{P}}$ scenario development, especially for the initial attempt. This is to ensure sufficient $\alpha$-stabilization effect at large Shafranov shift. From scenario development point of view, development of an ITB core in NT configuration is a great advance in core-edge integration, where ITB further enhances the global confinement quality [previous no-ITB cases show $H_{\textrm{98y2}}\sim 1.0$–1.2 (Austin et al. 2019; Marinoni et al. 2019)] and the L-mode edge resolves the ELM challenge in H-mode. It may also provide a new path for future FPPs.

At present, ITER uses a standard H-mode approach for its $Q=10$ goal. This approach requires very high plasma current $\sim 15$ MA, which is corresponding to $q_{95}\sim 3.0$ (ITER Organization 2018). The high plasma current leads to several challenges, such as high disruption risk and high transient heat load on divertor plates induced by Type-I ELMs. As shown in Fig. 18, statistical analysis shows a per-shot disruptivity of 20–50% at $q_{95}$ around 3.0 (Garofalo et al. 2014). Regarding the transient heat load issue, research shows that mitigation of Type-I ELMs by several factors is still required if melting of the monoblock surface is to be avoided in the 15 MA ITER baseline scenario (Pitts et al. 2019; Eich et al. 2017). These are strong motivations for an investigation of a scenario solution at lower plasma current, i.e., higher $q_{95}$. The DIII-D database shows a per-shot disruptivity close to zero at $q_{95}\sim 6$ or higher (Garofalo et al. 2014). Although the other two references (Gerhardt et al. 2013; de Vries et al. 2014) mentioned in Sect. 2.4 do not show exact percentage of disruptivity, there is little doubt that higher $q_{95}$, e.g., $\sim 6$–8, would have much lower disruption risk than $q_{95}\sim 3.0$, according to trends shown in the references. Furthermore, ITER may not require ELM mitigation if the plasma current is maintained below 10 MA (Pitts et al. 2019).

The Joint DIII-D/EAST research team explored the possibility of developing a high-$\beta _{\textrm{P}}$ scenario for ITER’s $Q=5$ steady-state mission (McClenaghan et al. 2020). Using 1.5D self-consistent STEP modeling, $Q=5.5$ is predicted at $I_{\textrm{p}}=8.25$ MA with only the day-one heating and current drive with a modification to the upper EC launcher. Some other parameters are $f_{\textrm{Gr,ped}}=0.97$, $f_{\textrm{Gr}}=1.3$, $\beta _{\textrm{N}}$=3.0, $P_{\textrm{aux}}=73$ MW with $P_{\textrm{NBI}}=33$ MW, $P_{\textrm{EC}}=20$ MW, $P_{\textrm{IC}}=20$ MW, and a fast-ion fraction contribution to pressure of 5%. The q-profile has reversed shear at large radius and is flatter near the axis, similar to that of DIII-D experiments. The magnetic shear reversal is driven almost entirely by the ITB, and not by the injected off-axis current drive sources. This is consistent with the requirements for sustaining an ITB described in Gormezano et al. (2007), Litaudon et al. (2011) and Ida and Fujita (2018). Based on the $Q=5$ result, the team explored a high-$\beta _{\textrm{P}}$ solution to ITER’s $Q=10$ goal (Ding et al. 2021a). The philosophy is that since $Q=P_{\textrm{fus}}/P_{\textrm{aux}}$, there exists two path toward higher Q. One is greatly pushing $P_{\textrm{fus}}$ at constant or further increased $P_{\textrm{aux}}$. This is what ITER chooses in the present plan. The other path is to reduce $P_{\textrm{aux}}$ in the denominator, while maintaining a moderate $P_{\textrm{fus}}$. Due to the high-energy confinement quality in the high-$\beta _{\textrm{P}}$ scenario, it is an excellent candidate to follow this second path, a path with better fusion economy. Indeed, the 0D study using the ITER $Q=5$ high-$\beta _{\textrm{P}}$ solution as a starting point shows an increasing trend of Q at reduced Paux. The key is to maintain a similar $H_{\textrm{98y2}}$. 1.5D simulations are performed to evaluate the confinement quality at reduced $P_{\textrm{aux}}$ and provide more detailed plasma performance in that condition. A similar modeling approach using STEP confirms the results. ITER $Q\sim 10$ is predicted at $I_{\textrm{p}}\sim 7.5$–9 MA with $\beta _{\textrm{N}}\sim 2.8$ and $f_{\textrm{Gr}}$ up to 1.5. $H_{\textrm{98y2}}$ is predicted between 1.6 and 1.8. Although $P_{\textrm{fus}}$ is about 300 MW at $I_{\textrm{p}}\sim 7.5$ MA and $\beta _{\textrm{N}}\sim 2.8$, another ITER goal of $P_{\textrm{fus}}\sim 500$ MW can still be met at higher $\beta _{\textrm{N}}$, e.g. 3.2–3.4. Q exceeds 10 at higher $\beta _{\textrm{N}}$. Increase of toroidal field is another effective approach to enhance both Q and $P_{\textrm{fus}}$. Although ITER may not consider operation at higher toroidal field, this exercise would still shed light on the application of high-$\beta _{\textrm{P}}$ scenario to future high field devices. Experiments on DIII-D that support the ITB development at such high density, or vice versa, developing high $f_{\textrm{Gr}}$ using an ITB approach are also reported in Ding et al. (2021a). Such experimental results are described in Sect. 2.3 in this paper. It is worth pointing out that compared with some ITER $Q=10$ high $\beta _{\textrm{P}}$ modeling cases, the experimental electron density profiles not only share the same density value in the core, but also have similar profile shape with large-radius ITB. Experimental electron temperature profiles also have similar profile shape. Yet, the core temperature is much lower than the ITER prediction, due to the very different toroidal field, heating power, etc.

There are more published and ongoing modeling studies based on the high-$\beta _{\textrm{P}}$ scenario. One example is the CAT-DEMO design (Buttery et al. 2021) discussed in Sect. 4. In China, a next-generation machine named Burning Experimental Superconducting Tokamak (BEST) is being designed. This new device will be slightly larger than JET with high field and D-T capability. There will be two main scenarios aiming at different missions. One is $Q>1$ steady-state operation. The other is $Q>5$ pulsed operation. The design of the $Q>1$ steady-state scenario is considering using the high-$\beta _{\textrm{P}}$ concept. It is also important to mention the aggressive tokamak design, ARIES-AT, showing the “ultimate potential” of a tokamak (Jardin et al. 2006). Some parameters are $\beta _{\textrm{T}}\sim 9.1$%, $\beta _{\textrm{N}}\sim 5.4$, $H_{\textrm{98y2}}\sim 2$, $Q\sim 40$. The work on ARIES-AT shows that an equilibrium with self-consistent profiles exists and is stable, at very high $\beta$ and confinement quality. It has been pointed out that “the Shafranov shift is the main cause of the improved transport in this case” and “the high beta-poloidal regime is the most similar to ARIES-AT” (Jardin et al. 2006). The reference also expects “experiments on the physics of the Shafranov shift effect on turbulence in tokamaks are needed to test the theory” (Jardin et al. 2006). The series of experimental and modeling results from the Joint DIII-D/EAST research team in the past decade address this issue.

6 Summary

Since the proposal of the high-$\beta _{\textrm{P}}$ regime as a high bootstrap current scenario in the 1990s, there have been many theoretical, modeling, and experimental research activities in this field. Based on the results and the experience of previous research from around the world, the Joint DIII-D/EAST research team started the exploration in this regime in 2013. This paper summarizes the highlights of the research results on DIII-D by the joint team in the past decade.

Due to the high bootstrap current, the high-$\beta _{\textrm{P}}$ scenario is envisioned to serve the FPP as a candidate for steady-state operation. Therefore, the joint research is focusing on addressing the needs of an attractive FPP design by taking advantage of the well-equipped diagnostics and sophisticated plasma control on DIII-D and the well-developed integrated modeling capability at General Atomics. The ultimate goal is to demonstrate this scenario on EAST with truly long pulse and metal wall compatibility. In the past decade, high-$\beta _{\textrm{P}}$ scenario on DIII-D has been developed from high $q_{95}$ ($>10$) to medium $q_{95}$ (6–8), from high rotation to low rotation, from $f_{\textrm{Gr}}$ around 1.0 to above 1.0 (e.g. 1.3), from attached plasma to fully detached and ELM mitigated/suppressed plasma. During this journey, many modeling validation and application studies have been done. In some trophy discharges, the normalized parameters, e.g., $\beta _{\textrm{N}}$, $\beta _{\textrm{P}}$, $\beta _{\textrm{T}}$, $H_{\textrm{98y2}}$, $f_{\textrm{Gr}}$, etc., already support operational points in some FPP designs. Beyond the key parameter values, several important and FPP-relevant issues and physics are addressed in the research:

1.
The high-energy confinement quality in the high-$\beta _{\textrm{P}}$ regime is experimentally confirmed at low toroidal rotation. The underlying physics is understood to be $\alpha$-stabilization at high Shafranov shift, independent of E $\times$ B shear stabilization provided by plasma rotation. Detailed physics of how plasma evolves from a weak/no-ITB state to a strong-ITB state is also illustrated based on experimental observation and gyrokinetic modeling. This confirms the physics picture of bypassing the KBM instability mountain and entering the 2nd stability regime for low transport. Two self-organized core-edge states, i.e., weak/no-ITB high-pedestal state and strong-ITB low-pedestal state, are identified in experiment.
2.
Leveraging the physics of interplay between pedestal and ITB at large radius in the high-$\beta _{\textrm{P}}$ regime, full divertor detachment with excellent global energy confinement quality ($H_{\textrm{98y2}}\sim 1.5$) is achieved in a tokamak for the first time. Detachment indeed degrades pedestal pressure. The growing ITB compensates the loss by the lowered pedestal and maintains the overall stored energy or $\beta$, resulting in an unchanged or slightly improved global confinement. Later experiment shows an integration of full divertor detachment, ELM mitigation/suppression, and un-degraded global energy confinement quality.
3.
An experimental approach aiming at achieving high line-average density above the Greenwald limit is developed in the high-$\beta _{\textrm{P}}$ scenario. Experimentally, sustained $f_{\textrm{Gr}}\sim 1.3$ and $f_{\textrm{Gr}}>1.0$ with $H_{\textrm{98y2}}>1.0$ are achieved by developing strong density ITB for $8\tau _{\textrm{E}}$ and $21\tau _{\textrm{E}}$, respectively. Sufficient particle source near the ITB foot is believed to be the key to such achievement. High-$\beta _{\textrm{P}}$ scenario expands the operational space toward high confinement quality ($H_{\textrm{98y2}}>1.0$) and high density ($f_{\textrm{Gr}}>1.0$) in a statistical analysis based on more than 1300 DIII-D discharges in 2019.
4.
Disruptivity analysis on multiple machines suggests that higher $q_{95}$ reduces the risk of disruption in tokamak operation. DIII-D results show that the disruptivity is approaching zero when $q_{95}$ is 6 or higher, i.e, the typical high-$\beta _{\textrm{P}}$ scenario operating space. Dedicated high-$\beta _{\textrm{P}}$ experiments on DIII-D demonstrate that a reduced outer gap, i.e., moving plasma closer to the low field side wall, increases the ideal wall $\beta _{\textrm{N}}$ limit, which is actually reached in experiments. These experiments also show stable operation at $6l_{\textrm{i}}$ for a few seconds.
5.
DIII-D high-$\beta _{\textrm{P}}$ experiments show $f_{\textrm{bs}}$ up to 80% at medium $q_{95}\sim 7$–8. The value of $f_{\textrm{bs}}$ is expected to be higher at the same $\beta _{\textrm{P}}$ in a reactor with lower collisionality.

Several other features of the high-$\beta _{\textrm{P}}$ plasmas on DIII-D are also summarized in this paper:

1.
Current alignment is not an issue in high-$\beta _{\textrm{P}}$ ITB plasmas. The primary turbulence suppression mechanism is $\alpha$-stabilization instead of negative magnetic shear by external current drive. In ITB region, the bootstrap current component is much larger than external current component. The bootstrap current density maximum is aligned with $\rho _{\textrm{qmin}}$ inside the ITB. DIII-D experiments have demonstrated stable ITB operation for a few seconds, limited only by NBI duration limits.
2.
In high-$\beta _{\textrm{P}}$ plasmas with an ITB, the dominant micro-instability varies and depends strongly on the local q value. Gyrokinetic modeling shows that a slab-MTM dominates at high q, while the dominant modes become ballooning modes at lower q. Although the local q value depends on the detailed structure of the q-profile, $q_{95}$ plays an important role in determining the overall q value when the shape of q-profile is similar, assuming similar pressure profile in the same type of scenario. Therefore, high $q_{95}$, e.g., $\sim 10$, high-$\beta _{\textrm{P}}$ plasmas on DIII-D could be slab-MTM dominant in general and lower $q_{95}$, e.g., 6–7, discharges could be ballooning mode dominant. This explains why TGLF results match experimental data much better at lower $q_{95}$, while it overpredicts experimental electron temperature at high $q_{95}$. This is because the current version of TGLF cannot capture the narrow, peaked and ballooning extended eigenfunctions of slab-MTMs.
3.
It is observed that low-Z impurity density develops a similar ITB at large radius in DIII-D high-$\beta _{\textrm{P}}$ plasmas. However, the overall impurity content is in a well-controlled condition with $Z_{\textrm{eff}}\sim 2$, assuming no strong impurity injection. The impurity density profile inside the ITB is flat rather than peaked. Its value near the magnetic axis is much lower than the neoclassical prediction. More experiments with high-Z impurity are planned soon.
4.
Comparisons between experimental pedestal pressure and EPED show that the strong-ITB low-pedestal state has lower pedestal pressure than EPED predicts, while the weak/no-ITB high-pedestal state matches the prediction. The high-pedestal state may be limited by peeling modes. The low-pedestal state could be induced by the enhancement of turbulent transport across the whole pedestal. This also may be consistent with the experimental observation of reduced ELM amplitude in the low-pedestal state.
5.
With similar $q_{95}$ and high $q_{\textrm{min}}$, high-$\beta _{\textrm{P}}$ plasmas and high-$q_{\textrm{min}}$ steady-state plasmas have very different AEs and AE-induced fast-ion transport. Most experimental observed AEs are near the magnetic axis in the high-$q_{\textrm{min}}$ steady-state plasmas, while they are in the outer half of plasma (outside the ITB) in the high-$\beta _{\textrm{P}}$ cases. Multiple explanations are proposed. One is related to the TAE gap opening. The high $q_{\textrm{min}}$ steady-state case has a wide gap near the axis, while the gap only widens at large radius in the high-$\beta _{\textrm{P}}$ case. Another explanation is that high-$\beta _{\textrm{P}}$ plasma has lower $\nabla \beta _{\textrm{fast}}$, due to a shorter slowing-down time in the core. AE activities would be quiet, if $\nabla \beta _{\textrm{fast}}$ does not exceed the critical value. A latest analysis suggests that the AE activities in high-$\beta _{\textrm{P}}$ plasmas could be BAE. Since the high-$\beta _{\textrm{P}}$ plasma outside ITB is in the 1st stability regime, it is vulnerable to the BAE instability. The plasma in the ITB region stays in the 2nd stability regime and it also stays away from the BAE instability. The same analysis applied on the high $q_{\textrm{min}}$ state-state case shows the plasma near axis is also close to the 1st stability regime, and therefore is vulnerable to the BAE instability.

DIII-D is not designed as a long pulse machine, compared with current diffusion time. At high $q_{95}$, i.e., low $I_{\textrm{p}}$, DIII-D high $\beta _{\textrm{P}}$ plasmas usually have 4–5 s with sustained ITB. One example has been shown in Fig. 21c, d. This is corresponding to 4–5$\tau _{\textrm{R}}$s. However, at lower $q_{95}$, DIII-D high $\beta _{\textrm{P}}$ plasmas have shorter available $I_{\textrm{p}}$ flattop, due to a second $I_{\textrm{p}}$ ramp-up phase. Indeed, the experiments only show sustained ITB and the related q-profile about 1–2 $\tau _{\textrm{R}}$s in this condition. Therefore, sustained ITB and stationary q-profile in high $\beta _{\textrm{P}}$ scenario have not been fully demonstrated in the present DIII-D experiments. Although the underlying physics on the ITB sustainment is encouraging, it still needs to be demonstrated in a long pulse experiment. This is also one of the main goals of the international collaboration between DIII-D and EAST. Development of such scenario has been discussed and becomes one of the main tasks in EAST experiment.

It is important to point out that there are other dimensionless parameters, such as normalized collisionality and Larmor radius, that cannot be varied in a wide range in DIII-D high $\beta _{\textrm{P}}$ experiments, due to the limits of machine operation. Hence, their roles on the energy confinement quality and stability in high $\beta _{\textrm{P}}$ scenario have not been fully demonstrated in experiment. Future machines with higher magnetic fields and better external current drive capability will be perfect for the investigations. Besides, modeling research on the applications of high $\beta _{\textrm{P}}$ scenario on future devices may also provide insight on this topic.

There are also intensive 1.5D self-consistent modeling studies on the high-$\beta _{\textrm{P}}$ scenario. The goal has been to project this scenario to a different configuration, e.g., negative triangularity, or a different present machine, e.g., EAST, or future devices, e.g., BEST, ITER. Although the high-$\beta _{\textrm{P}}$ scenario has been robustly reproduced on DIII-D, JT-60U, etc., it is still very important to understand its performance in long pulses, i.e., 100 s or longer, and its compatibility with metal walls. The successful adaption of the scenario to EAST is vital for this step. Modeling studies of future devices suggest a high-energy confinement quality (in terms of $H_{\textrm{98y2}}$) and low plasma current approach toward high fusion gain. This is a different approach than what ITER is currently pursuing for its $Q=10$ mission. However, it is a safer approach with better fusion economy towards an FPP and commercial fusion energy, which requires fusion gain far greater than 10. Modeling shows that higher magnetic field will be able to amplify the fusion power output and further enhance fusion gain.

In conclusion, joint DIII-D/EAST research in the past decade has advanced the physics understanding of the high-$\beta _{\textrm{P}}$ scenario and shown it to be an excellent candidate for supporting an attractive FPP and commercial fusion energy. Experiment and modeling show that the high-$\beta _{\textrm{P}}$ scenario has great advantages in addressing several key needs: high-energy confinement quality at low rotation above the Greenwald density limit for high fusion gain, excellent core-edge integration, high bootstrap current fraction for steady-state operation, and low disruption risk for improved machine safety. There are ongoing and future studies to further understand the physics and further develop this scenario.

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

C. Angioni et al., Plasma Phys. Control. Fusion 51, 124017 (2009)
ADS Google Scholar
N. Asakura et al., Nucl. Fusion 49, 115010 (2009)
ADS Google Scholar
M.E. Austin et al., Phys. Rev. Lett. 122, 115001 (2019)
ADS Google Scholar
Y.F. Baranov et al., Plasma Phys. Control. Fusion 47, 975 (2005)
ADS Google Scholar
A. Bellie, J. Candy, Plasma Phys. Control. Fusion 50, 095010 (2008)
ADS Google Scholar
L.C. Bernard et al., Comput. Phys. Commun. 24, 377 (1981)
ADS Google Scholar
C. Bourdelle et al., Nucl. Fusion 45, 110 (2005)
ADS Google Scholar
R.J. Buttery et al., Nucl. Fusion 61, 046028 (2021)
ADS Google Scholar
J. Candy, R.E. Waltz, J. Comput. Phys. 186, 545 (2003)
ADS MathSciNet Google Scholar
J. Candy et al., Phys. Plasmas 16, 060704 (2009)
ADS Google Scholar
J. Candy et al., J. Comput. Phys. 324, 73 (2016)
ADS MathSciNet Google Scholar
L. Chen, F. Zonca, Rev. Mod. Phys. 88, 015008 (2016)
ADS Google Scholar
W. Chen et al., Phys. Lett. A 440, 128141 (2022)
Google Scholar
C.Z. Cheng, M.S. Chance, J. Comput. Phys. 71, 124 (1987)
ADS Google Scholar
J. Citrin et al., Phys. Rev. Lett. 111, 155001 (2013)
ADS Google Scholar
P.C. de Vries et al., Phys. Plasmas 21, 056101 (2014)
ADS Google Scholar
A. Di Siena et al., Phys. Rev. Lett. 127, 025002 (2021)
ADS Google Scholar
S. Ding et al., Nucl. Fusion 57, 022016 (2017a)
S. Ding et al., Phys. Plasmas 24, 056114 (2017b)
S. Ding et al., “Mutually exclusive relation between high pedestal and large radius internal transport barrier in high $\beta _{{\rm P}}$ scenario on DIII-D” (GP11.00070), in 59th Annual Meeting of the APS Division of Plasma Physics, Milwaukee, USA, October 23–27 (2017c)
S. Ding et al., Nucl. Fusion 60, 016023 (2020a)
S. Ding et al., Nucl. Fusion 60, 034001 (2020b)
S. Ding et al., “A low plasma current ($\sim 8$ MA) approach for ITER’s $Q=10$ goal” (EX/1-3R), in 28th IAEA Fusion Energy (Conference, Remote Conference, May (2021a), pp. 10–15
S. Ding et al., Phys. Plasmas 28, 112504 (2021b)
S. Ding et al., “Strategy for developing internal transport barriers at large radius in high poloidal beta plasmas on EAST” (CP11.00012), in 63rd Annual Meeting of the APS Division of Plasma Physics, Pittsburgh, USA, November 8–12 (2021c)
T. Eich et al., Nucl. Mater. Energy 12, 84 (2017)
Google Scholar
G. Federici et al., Fusion Eng. Des. 136, 729 (2018)
Google Scholar
N.J. Fisch, Rev. Mod. Phys. 59, 175 (1987)
ADS Google Scholar
T. Fujita et al., Phys. Rev. Lett. 87, 085001 (2001)
ADS Google Scholar
J. García et al., Phys. Rev. Lett. 100, 255004 (2008)
ADS Google Scholar
A.M. Garofalo et al., Fusion Eng. Des. 89, 876 (2014)
Google Scholar
A.M. Garofalo et al., Nucl. Fusion 55, 123025 (2015)
ADS Google Scholar
A.M. Garofalo et al., Nucl. Fusion 57, 076037 (2017)
ADS Google Scholar
A.M. Garofalo et al., Plasma Phys. Control. Fusion 60, 014043 (2018)
ADS Google Scholar
A.M. Garofalo et al., Nucl. Fusion 62, 056008 (2022)
ADS Google Scholar
S.P. Gerhardt et al., Nucl. Fusion 53, 043020 (2013)
ADS Google Scholar
X. Gong et al., Nucl. Fusion 62, 076009 (2022)
ADS Google Scholar
N.N. Gorelenkov et al., Phys. Plasmas 6, 2802 (1999)
ADS Google Scholar
C. Gormezano et al., Nucl. Fusion 47, S285 (2007)
Google Scholar
B.J. Green for the ITER International Team and Participant Teams, Plasma Phys. Control. Fusion 45, 687 (2003)
M. Greenwald, Plasma Phys. Control. Fusion 44, R27 (2002)
ADS Google Scholar
H. Han et al., Nature 609, 269–275 (2022)
ADS Google Scholar
R.J. Hawryluk, An empirical approach to tokamak transport, in Proceedings of the Course on Physics of Plasmas Close to Thermonuclear Conditions, Varenna, Italy, vol. 1, p. 19 (1979)
W.W. Heidbrink et al., Nucl. Fusion 53, 093006 (2013)
ADS Google Scholar
W.W. Heidbrink et al., Plasma Phys. Control. Fusion 56, 095030 (2014)
ADS Google Scholar
T.C. Hender et al., Nucl. Fusion 47, S128 (2007)
Google Scholar
J. Hobirk et al., Phys. Rev. Lett. 87, 085002 (2001)
ADS Google Scholar
G.M.D. Hogeweij et al., Plasma Phys. Control. Fusion 44, 1155 (2002)
ADS Google Scholar
C.T. Holcomb et al., Phys. Plasmas 22, 055904 (2015)
ADS Google Scholar
W.A. Houlberg et al., Nucl. Fusion 45, 1309 (2005)
ADS Google Scholar
W. Howl et al., Phys. Fluids B 4, 1724 (1992)
ADS Google Scholar
J. Huang et al., Nucl. Fusion 60, 126007 (2020)
ADS Google Scholar
K. Ida, T. Fujita, Plasma Phys. Control. Fusion 60, 033001 (2018)
ADS Google Scholar
ITER Organization, ITER research plan within the staged approach (2018). https://www.iter.org/doc/www/content/com/Lists/ITER%20Technical%20Reports/Attachments/9/ITER-Research-Plan_final_ITR_FINAL-Cover_High-Res.pdf
ITER Physics Expert Groups on Confinement and Transport and Confinement Modelling and Database et al., Nucl. Fusion 39, 2175 (1999)
S.C. Jardin et al., Fusion Eng. Des. 80, 25 (2006)
Google Scholar
X. Jian et al., Phys. Rev. Lett. 123, 225002 (2019)
ADS Google Scholar
X. Jian et al., “Destabilization of high-field-side modes by large Shafranov shift in present and future devices” (BI02.00005), in 62nd Annual Meeting of the APS Division of Plasma Physics, Virtual Meeting, November 9–13 (2020)
X. Jian et al., Phys. Plasmas 28, 042501 (2021a)
X. Jian et al., “Role of beta-induced Alfvén eigenmode in DIII-D high $\beta _{{\rm P}}$ scenario” (CP11.00080), in 63rd Annual APS Meeting Division of Plasma Physics, Pittsburgh, USA, November 8–12 (2021b)
X. Jian et al., Role of beta-induced Alfvén eigenmode in DIII-D high $\beta _{{\rm P}}$ scenario, in US-EU Joint Transport Taskforce Workshop, Santa Rosa, USA, April 5–8 (2022a)
X. Jian et al., submitted to Nucl. Fusion (2022b)
A. Kallenbach et al., Nucl. Fusion 55, 053026 (2015)
ADS Google Scholar
Y. Kamada et al., Nucl. Fusion 31, 1827 (1991)
Google Scholar
Y. Kamada et al., Plasma Phys. Control. Fusion 36, A123 (1994)
ADS Google Scholar
J. Kesner et al., Phys. Fluids B 5, 2525 (1993)
ADS Google Scholar
C.E. Kessel et al., Fusion Sci. Technol. 67, 1 (2015)
ADS Google Scholar
M. Kikuchi, Nucl. Fusion 30, 265 (1990)
Google Scholar
M. Kikuchi et al., Fusion Eng. Des. 48, 265 (2000)
Google Scholar
J. Kim et al., Nucl. Fusion 62, 026029 (2022)
ADS Google Scholar
Y. Koide et al., Phys. Rev. Lett. 72, 3662 (1994)
ADS Google Scholar
M.T. Kotschenreuther et al., “Regimes of weak ITG/TEM modes for transport barriers without velocity shear” (UP10.00020), in 61st Annual Meeting of the APS Division of Plasma Physics, Fort Lauderdale, USA, October 21–25 (2019)
J.-G. Kwak et al., IEEE Trans. Plasma Sci. 48, 1388 (2020)
ADS Google Scholar
P.T. Lang et al., Nucl. Fusion 52, 023017 (2012)
ADS Google Scholar
L.L. Lao et al., Nucl. Fusion 25, 1611 (1985)
Google Scholar
A.W. Leonard et al., J. Nucl. Mater. 463, 519 (2015)
ADS Google Scholar
G.Q. Li et al., “ELM behavior and pedestal structure in high-$\beta _{{\rm P}}$ plasmas on DIII-D” (NP11.00092), in 59th Annual Meeting of the APS Division of Plasma Physics, Milwaukee, USA, October 23–27 (2017)
X. Litaudon, Plasma Phys. Control. Fusion 38, A251 (1996)
Google Scholar
X. Litaudon, Plasma Phys. Control. Fusion 48, A1 (2006)
ADS Google Scholar
X. Litaudon et al., Plasma Phys. Control. Fusion 44, 1057 (2002)
ADS Google Scholar
X. Litaudon et al., Nucl. Fusion 51, 073020 (2011)
ADS Google Scholar
A. Marinoni et al., Phys. Plasmas 26, 042515 (2019)
ADS Google Scholar
A. Marinoni et al., Rev. Mod. Plasma Phys. 5, 6 (2021)
ADS Google Scholar
J. McClenaghan et al., Nucl. Fusion 57, 116019 (2017)
ADS Google Scholar
J. McClenaghan et al., Nucl. Fusion 59, 124002 (2019)
ADS Google Scholar
J. McClenaghan et al., Nucl. Fusion 60, 046025 (2020)
ADS Google Scholar
O. Meneghini et al., Nucl. Fusion 61, 026006 (2021)
ADS Google Scholar
Y.-S. Na et al., Exploration of advanced tokamak operation and its control in KSTAR, in 8th IAEA TM on “Steady State Operation of Magnetic Fusion Devices”, Nara, Japan, May 26–29 (2015)
Y.-S. Na et al., Nucl. Fusion 60, 086006 (2020)
ADS Google Scholar
C. Pan et al., Nucl. Fusion 57, 036018 (2017)
ADS Google Scholar
J.M. Park et al., Comput. Phys. Commun. 214, 1 (2017)
ADS MathSciNet Google Scholar
J.M. Park et al., Phys. Plasmas 25, 012506 (2018)
ADS Google Scholar
H.K. Park et al., Nucl. Fusion 59, 112020 (2019)
ADS Google Scholar
R.I. Pinsker, Phys. Plasmas 22, 090901 (2015)
ADS Google Scholar
R.A. Pitts et al., Nucl. Mater. Energy 20, 100696 (2019)
ADS Google Scholar
F.M. Poli et al., Nucl. Fusion 54, 073007 (2014)
ADS Google Scholar
P.A. Politzer et al., Nucl. Fusion 45, 417 (2005)
ADS Google Scholar
J.P. Qian et al., Phys. Plasmas 28, 042506 (2021)
ADS Google Scholar
Q.L. Ren et al., Phys. Plasmas 23, 062511 (2016)
ADS Google Scholar
S.A. Sabbagh et al., Phys. Fluids B 3, 2277 (1991)
ADS Google Scholar
Y. Sakamoto et al., Nucl. Fusion 45, 574 (2005)
ADS Google Scholar
Y. Sakamoto et al., Nucl. Fusion 49, 095017 (2009)
ADS Google Scholar
Y. Sarazin et al., Plasma Phys. Control. Fusion 44, 2445 (2002)
ADS Google Scholar
P.B. Snyder et al., Phys. Plasmas 9, 2037 (2002)
ADS Google Scholar
P.B. Snyder et al., Nucl. Fusion 51, 103016 (2011)
ADS Google Scholar
W.M. Solomon et al., Nucl. Fusion 53, 093033 (2013)
ADS Google Scholar
B.N. Sorbom et al., Fusion Eng. Des. 100, 378 (2015)
Google Scholar
G.M. Staebler, Nucl. Fusion 58, 115001 (2018)
G.M. Staebler et al., Phys. Rev. Lett. 82, 1692 (1999)
ADS Google Scholar
G.M. Staebler et al., Phys. Plasmas 14, 055909 (2007)
ADS Google Scholar
G.M. Staebler et al., Phys. Plasmas 25, 056113 (2018)
P.C. Stangeby, The Plasma Boundary of Magnetic Fusion Devices (IOP Publishing, Bristol, 2000)
Google Scholar
E.J. Strait, Phys. Plasmas 1, 1415 (1994)
ADS Google Scholar
K.E. Thome et al., Nucl. Fusion 61, 036036 (2021)
ADS Google Scholar
F. Troyon et al., Plasma Phys. Control. Fusion 26, 209 (1984)
ADS Google Scholar
A.D. Turnbull et al., Nucl. Fusion 38, 1467 (1998)
ADS Google Scholar
M.R. Wade, J.A. Leuer, Fusion Sci. Technol. 77, 119 (2021)
ADS Google Scholar
H.Q. Wang et al., Phys. Plasmas 28, 052507 (2021a)
L. Wang et al., Nat. Commun. 12, 1365 (2021b)
Y.F. Wang et al., Nucl. Fusion 61, 016032 (2021c)
H.Q. Wang et al., “Extending the operational space of the high bootstrap current fraction scenario on DIII-D towards ITER steady-state” (GO08.00003), in 63rd Annual APS Meeting Division of Plasma Physics, Pittsburgh, USA, November 8–12 (2021d)
J. Wesson, Tokamaks, 3rd edn. (Oxford University Press, Oxford, 2004)
MATH Google Scholar
Q.Q. Yang et al., Nucl. Fusion 60, 076012 (2020)
ADS Google Scholar
J.-H. Yeom et al., Fusion Eng. Des. 88, 742 (2013)
Google Scholar
H. Zohm et al., Nucl. Fusion 53, 073019 (2013)
ADS Google Scholar
F. Zonca et al., Phys. Plasmas 6, 1917 (1999)
ADS Google Scholar

Download references

Acknowledgements

The authors thank the DIII-D team and the Joint DIII-D/EAST research team for their support in the machine operation and the data analysis/modeling. The author, Siye Ding, would like to thank Dr. Xiang Jian, Dr. Huiqian Wang, Dr. Wilkie Choi of General Atomics and Dr. Chris Holcomb of Lawrence Livermore National Laboratory, for helpful discussions. This work is supported by the US Department of Energy under DE-SC0010685, DE-FC02-04ER54698.

Author information

Authors and Affiliations

General Atomics, P.O. Box 85608, San Diego, CA, 92186-5608, USA
Siye Ding & Andrea M. Garofalo

Authors

Siye Ding
View author publications
You can also search for this author in PubMed Google Scholar
Andrea M. Garofalo
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Siye Ding.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Ding, S., Garofalo, A.M. Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant. Rev. Mod. Plasma Phys. 7, 4 (2023). https://doi.org/10.1007/s41614-022-00106-z

Download citation

Received: 15 June 2022
Accepted: 21 November 2022
Published: 26 December 2022
DOI: https://doi.org/10.1007/s41614-022-00106-z

Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant

Abstract

Similar content being viewed by others

DIII-D Research to Prepare for Steady State Advanced Tokamak Power Plants

The Princeton Field-Reversed Configuration for Compact Nuclear Fusion Power Plants

A high-density and high-confinement tokamak plasma regime for fusion energy

1 Introduction

2 Key needs for an attractive reactor scenario design and the high-\(\beta _{\textrm{P}}\) solutions

2.1 High-energy confinement quality and its low rotation compatibility

2.1.1 Experimental observations and modeling analysis on high confinement quality at different toroidal rotation

2.1.2 Understanding of \(\alpha\)-stabilization physics in high Shafranov shift, high \(\beta _{\textrm{P}}\) plasmas