Abstract
Dynamic stochastic general equilibrium (DSGE) models are the common workhorse of modern macroeconomic theory. Whereas story-telling and policy analysis were in the forefront of applications since its inception, the forecasting perspective of DSGE models is only recently topical. In this study, we perform a post-mortem analysis of the predictive power of DSGE models in the case of Austria’s Great Recession in 2009. For this purpose, eight DSGE models with different characteristics (small and large models; closed and open economy models; one and two-country models) were used. The initial hypothesis was that DSGE models are inferior in ex-ante forecasting a crisis. Surprisingly however, it turned out that not all but those models which implemented features of the causes of the global financial crisis (like financial frictions or interbank credit flows) could not only detect the turning point of the Austrian business cycle early in 2008 but they also succeeded in forecasting the following severe recession in 2009. In comparison, non-DSGE methods like the ex-ante forecast with the Global Economic (Macro) Model of Oxford Economics and WIFO’s expert forecasts performed comparable or better than most DSGE models in the crisis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is common knowledge that the economic community was not able to forecast the Great Recession in 2009. The crisis evolved in a sequence of crises (see Breuss 2016): it started with the US subprime crises, followed by a banking crisis triggered by the Lehman Brothers’ crash on 15 September 2008 which induced a collapse of the interbank market. Then the stock market plunged and caused the Great Recession in 2009. Starting in the United States it spread to most industrial countries. Europe, in particular the Euro area generated its unique “Euro (debt) crisis”. As an excuse, one argued that because of the specificity of the crisis, the economic models then used were not able to forecast it.
In the forecasting business, a variety of models are used, but primarily traditional macro econometric models. The now common workhorse of modern macroeconomic theory, however, are DSGE (Dynamic stochastic general equilibrium) models.Footnote 1 They are used to predict (forecast) and explain (story-telling) co-movements of aggregate time series over the business cycle (real business cycle theory) and to perform policy analysis (policy experimentsFootnote 2: IRF implications of shocks of fiscal and monetary policy and of technical changeFootnote 3). Whereas the two latter applications were in the forefront of applications since its inception, based on the work by Kydland and Prescott (1982),Footnote 4 the forecasting perspective is only recently topical.
Most forecasting evaluations with DSGE models so far were executed for the US economy and for the Euro area (at the ECB). In the following we perform a post-mortem of DSGE model forecasts of the Great Recession (2009) in Austria. For this purpose, we use eight DSGE models with different characteristics (closed and open economy models; one and two-country models). Primarily, the development of the Austrian real GDP during the Great Recession of 2009 and thereafter is evaluated ex-ante with out-of-sample forecasts.
The paper is structured as follows. Chapter 2 gives a brief overview of the literature on forecasting with DSGE models. Chapter 3 describes the eight DSGE models used for this forecasting exercise. In chapter 4 the forecasting performance of the different models for Austria during the Great Recession is evaluated. Additionally, in chapter 5 we check the forecasting performance of non-DSGE methods (Global Economic (Macro) Model of Oxford Economics and WIFO’s expert forecasts). Conclusions are drawn in the last chapter.
2 Review of Literature on Forecasting with DSGE Models
DSGE models are micro founded, based on optimizing agents: consumers and firms maximizing utility and profits respectively. Technology drives output via a production function. Institutions (fiscal and monetary) are modelled by budget constraints and some policy rule (e.g. Taylor rule). At present there exist two competing schools of DSGE modelling which end in a synthesis:
-
Real business cycle (RBC) theory of neoclassical growth models with flexible prices. Real shocks cause business cycle fluctuations.Footnote 5 The fathers of RBC models are Kydland and Prescott (1982).
-
New Keynesian DSGE models (NK) build on a structure similar to RBC models, but assume that prices and wages are set by monopolistically competitive firms, adjusting not instantaneously and costlessly (price and wage rigidity). The first who introduced this framework were Rotemberg and Woodford (1997).
-
New Keynesian Synthesis (NKS) models.Footnote 6 Goodfriend and King (1997) and Clarida et al. (1999) introduced a framework mixing RBC features with nominal and real rigidities.
In empirical work,Footnote 7 DSGE models are primarily estimated with Bayesian methods,Footnote 8 if the goal is to track and forecast macroeconomic time series (e.g. GDP, consumption, investment, prices, wages, employment and interest rates). Bayesian inference delivers posterior predictive distributions that reflect uncertainty about latent state variables, parameters, and future realizations of shocks conditional on the available information. The models, applied to make forecasts with DSGE models as well as the models we have selected for the same exercise for Austria are all estimated with Bayesian methods.
DSGE models are widely applied in academic research but also in international institutions (European Commission, IMF, ECB), in particular in central banks. More and more DSGE models are also used for forecasting purposes.Footnote 9 The literature so far dealt firstly with general aspects of the forecasting performance of DSGE models and with comparisons with other times series techniques (mostly VARs and BVARs), in recent attempts the predictive power of DSGE models were applied to understand the GFC 2008/09.Footnote 10 The hitherto forecasting exercises were concentrated on the USA and the Euro area.
2.1 USA
The forecasting exercise of Del Negro and Schorfheide (2007) is an early attempt to evaluate the forecasting quality of DSGE models. First, they develop a set of tools that is useful for assessing the time series fit of a DSGE model. They systematically relax the implied cross coefficient restrictions of the DSGE model to obtain a VAR specification that is guaranteed to fit better than the DSGE model. Then they use this specification as a benchmark to characterize and understand the degree of misspecification of the DSGE model. Second, they apply these tools to a variant of the model of Smets and Wouters (2007) and document its fit and forecasting performance based on postwar U.S. data over the period 2Q1974 to 1Q2004.
The first comprehensive analysis of the forecasting capability of DSGE models during the Great Recession 2009 in the USA is done by Del Negro and Schorfheide (2013). They demonstrate the forecasting performance of the Smets and Wouters (2007) DSGE model with data up to 2011, compare it with professional forecasts published in the “Blue Chip” survey and the forecasts by the Federal Reserve Board of Governors (the so-called “Greenbook”). Firstly, the DSGE models used to ex-ante forecast the Great Recession 2009 do not perform better than the Blue Chip and the Greenbook forecasts. Secondly, the examination of DSGE model’s forecasts during the 2008–2009 US recession suggests that the DSGE models with financial frictions are preferable to the original Smets and Wouters model.
Kolasa and Rubaszek (2014) compare the quality of forecasts from DSGE models with and without financial frictions. The exercise is done for the US economy with data, covering the period 1Q1970 to 4Q2010. They find that accounting for financial market imperfections does not result in a uniform improvement in the accuracy of point forecasts during non-crisis times while the average quality of density forecast even deteriorates. In contrast, adding frictions in the housing market proves very helpful during the times of financial turmoil, over performing both the frictionless benchmark and the alternative that incorporates financial frictions in the corporate sector.
Merola (2014) analyses ex-post the relevant factors for the recent banking crisis of the US economy in 2008. The analysis is done by comparing the original Smets and Wouters model (2007) with an alternative version augmented with the financial accelerator mechanism à la Bernanke et al. (1999). Both versions are estimated using Bayesian techniques over the sample period: 1967 to 2012. The Smets and Wouters model, augmented with the financial accelerator mechanism, is suitable to capture much of the historical developments in U.S. financial markets that led to the financial crisis. The model can account for the output contraction in 2008, as well as the widening in corporate spreads and supports the argument that financial conditions have amplified the U.S. business cycle and the intensity of the recession.
2.2 Euro Area
Christoffel et al. (2011) make n-step ahead and out-of-sample forecasts for the Euro area with the “The New Area-Wide Model (NAWM) of the Euro Area” and compared its performance with vector autoregressions (VARs), Bayesian vector autoregressions (BVARs), a random walk, and a location parameter, namely the mean. The out-of-sample forecast evaluation exercise covers the period after the introduction of the euro up to the pre-crisis year 2006. Overall, the results suggest that the NAWM performs quite well when compared with the reduced-form forecasting tools. In particular, the model compares favourably when forecasting real GDP growth, the trade variables, employment, the real exchange rate, and the short-term nominal interest rate. However, the NAWM is less successful when forecasting certain nominal variables, e.g. nominal wage growth.
Smets et al. (2013) analyze the real-time forecasting performance of the New Keynesian DSGE model of Galí et al. (2012) estimated on Euro area data. They investigate to what extent forecasts of inflation, GDP growth and unemployment by professional forecasters improve the forecasting performance over the period 1Q1999 to 4Q2010. The authors consider two approaches for conditioning on such information. Under the “noise” approach, the mean professional forecasts are assumed to be noisy indicators of the rational expectations forecasts implied by the DSGE model. Under the “news” approach, it is assumed that the forecasts reveal the presence of expected future structural shocks in line with those estimated over the past. The forecasts of the DSGE model are compared with those from a Bayesian VAR model and a random walk. Overall, the authors find that the GSW model outperforms the random-walk model and has similar performance as the non-structural BVAR model. Adding one to two-year-ahead professional forecasts of real GDP growth, inflation, and the unemployment rate does not significantly improve the overall performance of the GSW model, although it does help to reduce some of the bias in the forecasts of wage growth in the news models.
3 DSGE Models Applied to the Austrian Business Cycle
Austria is a small open economy and since its EU accession in 1995 deeply integrated into EU’s Single Market. Therefore, DSGE models with an international nexus should be more suitable to describe the Austrian business cycle.
On the other hand, under the basic assumption that theoretical DSGE models are micro founded, they should describe any market economy, not only that for which the model was originally designed. Because this implies an uncertainty concerning the model selection, we make a compromise. We use DSGE models originally applied for other countries (USA, Portugal, Euro Area etc.) as well as such designed for Austria in order to track the development of Austrian macroeconomic data. We have selected eight different types of models: closed and open economy DSGE models, models for small and medium-sized models as well as large open economy models; some are one, others are two-country models.
In the application of the eight models we used the original calibration and adjusted it to the Austrian case where necessary (e.g. in the open economy and two-country models) we used the respective parameters for Austria’s export and import shares).
3.1 Small and Medium-Sized Closed and Open Economy Models
We start with the description of a small closed economy DSGE model and then advance to more complex models (see the overview in Table 1).
3.1.1 A Small Closed Economy 3-Equation DSGE Model
The simplest possible example of a DSGE modelFootnote 11 is the “Baby” DSGE model of An and Schorfheide (2007).Footnote 12 With this small benchmark monetary policy analysis model, the authors studied monetary policy aspects of the USA. The theoretical economy in the An and Schorfheide model consists of a final goods producing firm, a continuum of intermediate goods producing firms, a representative household, and a monetary and a fiscal authority. It has six equations describing the behaviour of output, consumption, government spending, technology, inflation, and a short-term nominal interest rate (Taylor rule). When substituting consumption and government spending into the output equation and technology into the Euler consumption equation the model reduces to three endogenous variables (GDP, inflation and interest rate). Three shocks (fiscal, monetary and productivity) are applied. Except of the interest rate, all variables are detrended.Footnote 13 The measurement equation linking the data on quarter-to-quarter GDP growth (differences of the natural logarithm, annual quarter-to-quarter inflation rates, and annual nominal interest rates. The model is estimated in YADAFootnote 14 and Austrian data over the period 1Q1992 to 4Q2016. The primary database for this and the following models is those of Oxford Economics which are mainly based on Eurostat data.
3.1.2 A Small Open Economy DSGE Model
Lubik and Schorfheide (2007)Footnote 15 extended the closed economy An and Schorfheide model to a small open economy DSGE model. It consists of a forward-looking IS-equation and a Phillips curve. Monetary policy is also given by a Taylor-type interest rate rule, where the exchange rate is introduced via the definition of consumer prices and under the assumption of PPP. The model uses five shocks (three shocks of the An and Schorfheide model) plus two external shocks (foreign GDP and foreign inflation). In log-linearized form the model is estimated in YADA and with Austrian data over the period 1Q1999 to 4Q2016.
3.1.3 The Most Cited DSGE Model of a Closed Economy
A well-known example of a medium-sized DSGE model is that of Smets and Wouters (2007).Footnote 16 Although the authors study shocks and frictions in US business cycles the model is designed for a closed economy. The Smets and Wouters (SW) model uses basically a sticky price and wage system, followed by a flexible-price based output gap measure in the monetary policy rule.
The SW model is consistent with a balanced steady-state growth path driven by deterministic labour augmenting technological progress. The observed variables are given by quarterly data of the log of real GDP per capita, the log of real consumption per capita, the log of real investment per capita, the log of hours per capita, the log of quarterly GDP deflator inflation, the log of real wages, and the federal funds rate (in the application for Austria, ECB’s Main Financing Operations (MFO) interest rate). All observed variables except hours, inflation, and the MFO rate measured in first differences of the natural logs. Consistent with the number of endogenous variables, the SW model uses seven shocks to describe the business cycle development: shock to fiscal, monetary, consumption, investment, technology, inflation and wages. The model is estimated in YADA with Austrian data over the period 1Q1995 to 4Q2016.
3.1.4 The SW DSGE Model with Financial Frictions
Del Negro and Schorfheide (2013)Footnote 17 presents a small-scale version of the Smets and Wouters model by removing several features, such as capital accumulation. It is also assumed that there is no wage stickiness in the small-scale model. Consequently, the marginal cost is equal to the real wage, and the latter is equal to the marginal rate of substitution between consumption and leisure. In addition, Del Negro and Schorfheide (2013) introduce financial frictions into their variant of the SW model based on the financial accelerator approach of Bernanke et al. (1999). The set of measurement equations is augmented by an equation explaining the spread of Moody’s seasoned Baa corporate bond yield spread over the 10-year treasury note yield at constant maturity by the interest rate difference (real interest rate minus real rent on capital). In the Del Negro and Schorfheide model the eight endogenous variables are driven by eight shocks: In addition to the seven shocks in the SW model, one financial shock is introduced. In the estimation for Austria, the spread is measured by the 10-year Austrian government bond yield over those of Germany. The model is estimated in YADA with Austrian data over the period 1Q1992 to 4Q2016.
3.2 Large Open Economy Models
3.2.1 The NAWM DSGE Model for the Euro Area
In the following we describe large-sized open economy DSGE models, used to estimate the Austrian business cycle. These models should be able to better track the development of the Austrian economy than small and often closed economy DSGE models. The reason is that Austria since its EU accession in 1995 became more and more integrated into the Single Market of the EU. The economic development of the EU neighbours (in particular that of the major trading partner Germany) primarily determine the path of the business cycle in Austria.
Christoffel et al. (2008), authors at the European Central Bank (ECB) designed the “The New Area-Wide Model (NAWM) of the Euro Area”, a micro-founded open-economy DSGE model. The NAWM is for use in the (Broad) Macroeconomic Projection Exercises regularly undertaken by ECB/Eurosystem staff and for policy analysis. The NAWM is neo-classical in nature and centred around intertemporal decisions of households and firms which are maximising expected life-time utility and the expected stream of profits, respectively.
The NAWM models the domestic economy (the Euro area) existing of four types of economic agents: households, firms, a fiscal authority, and a monetary authority (Taylor rule). Firms are distinguished between producers of tradable differentiated intermediate goods and producers of three non-tradable final goods: a private consumption good, a private investment good, and a public consumption good. In addition, there are foreign intermediate-good producers that sell their differentiated goods in domestic markets, and a foreign retail firm that combines the exported domestic intermediate goods. International linkages arise from the trade of intermediate goods and international assets, allowing for limited exchange-rate pass-through on the import side and imperfect risk sharing.
The NAWM consist of 18 endogenously explained macro-economic variables (GDP, private consumption, government consumption, investment, employment, wages, interest rate, effective exchange rate, exports, imports, foreign demand, foreign prices, inflation (GDP and consumption deflator), foreign interest rate, export prices of competitors, import deflator, oil prices). These 18 variables are driven by the same number of shocks. For our exercise the model is estimated with Austrian data in YADA over the period 1Q1995 to 4Q2016.
3.2.2 A Two-Regions Euro Area DSGE Model with Banking
Poutineau and Vermandel (2015) develop a two-country DSGE model to document how the transmission of asymmetric shocks in the Eurozone has been affected with a banking system that provides cross-border interbank and corporate lending facilities. This solution is original with respect to the existing literature of monetary policy issues in a monetary union. The authors try to overcome with their specification missing elements in pre-crisis models by considering phenomena which have contributed to the GFC 2008, the Great Recession 2009 and the following Euro crisis. The two-country model considers EMU (the Euro area) as consisting of two regions: the periphery and the core. The number of shocks is higher (or equal) to observable variables (15) to avoid stochastic singularity issues.
We estimate this DSGE model with 15 endogenous variables for a two-country setting (Austria and Euro Area) in DynareFootnote 18 over the (Euro area) period 1Q1999 to 4Q2016.
3.2.3 A NK DSGE Model for Portugal
Almeida (2009) developed a New-Keynesian DSGE model for a small open economy integrated in the Economic and Monetary Union (EMU of the EU), estimated for the Portuguese economy, using a Bayesian approach. The model features five types of economic agents namely households, firms, aggregators, the rest of the world and the government. It is assumed that monetary policy is decided by the ECB and that the domestic economy’s size is negligible, relative to those of the EMU, and therefore Portugal cannot influence EMU’s economy but the EMU is determining Portugal’s business cycle. The model contains 13 endogenous variables with the same number of shocks.
This prototype model for a small member of the Euro area should also fit well for the Austrian economy. The estimation of this DSGE model with Austrian data (13 endogenous variables) is executed in Dynare over the period 1Q1995 to 4Q2015.
3.2.4 A Two-Country DSGE Model of Austria and the Euro Area
Breuss and Rabitsch (2009) were the first to model a DSGE model for Austria. Although the approach is theoretically similarly to those of the SW model, its novel feature consists in modelling a two-country DSGE model. It is a DSGE model in the style of New Keynesian/New Open Economy Macroeconomics for the small open economy of Austria as a member of the European Economic and Monetary Union (EMU).Footnote 19 The model was originally estimated using Bayesian methods on quarterly data covering the period of 1Q1975-1Q2005. Because Austria entered the EMU on 1 January 1999 we considered this regime switch by partitioning into two periods: a pre-EMU and a post-EMU period. For our purpose, the evaluation of the forecast quality in the Great Recession 2009 we re-estimated the model (with 17 endogenous variables and an equal number of shocks) from 1Q1995 to 4Q2015. The estimation is executed in Dynare with Austrian and Euro area data.
4 Which Model Would Have Best Predicted the Recession 2009?
In the following we examine ex-ante (or out-of-sampleFootnote 20) forecasts of Austria’s Great Recession in 2009 with the models described in Table 1. The forecasts of real GDP growth are obtained at two different junctures of the crisis that lead to the recessionFootnote 21:
-
(i)
Before the default of Lehman Brothers (bLB). The models are estimated until 1Q2008 (the peak of the business cycle) and the out-of-sample forecasts run from 2Q2008 to 4Q2016.
-
(ii)
After the default of Lehman Brothers (aLB). The models are estimated until 3Q2008 (the peak of the business cycle) and the out-of-sample forecasts run from 4Q2008 to 4Q2016.
Out-of-sample forecast can be executed conditionalFootnote 22 on specific knowledge at the inception of a crisis or unconditional (without side knowledge). In the following we evaluate the models with unconditional forecasting methods. In our analysis, we take the mean forecasts.Footnote 23
The forecasting quality of the DSGE models during the Great Recession and thereafter are evaluated with the measure Root Mean Square Error (RMSE). Because the eight DSGE models have different measures of GDP (mostly the annual growth rate of real GDP, but some use also GDP Gaps) we take the normalized RMSE (NRMSEFootnote 24) to be able to compare the forecasting performance of the different models. The results are collected in Table 2.
The common interpretation of the causes of the past crisis is that it started with a sub-prime housing crisis, leading to a financial (banking) crisis in the USA (default of Lehman Brothers on 15 September 2008) and spread then globally to a global financial crisis and a Great Recession in 2009 (see Breuss 2016). The Austrian economy was hit primarily by external forces via trade and capital movements. Of course, the shock of Lehman Brothers led also to a freeze of interbank lending. However, in contrast to the USA as well as Ireland and Spain Austria had no housing crisis.
Austria is a prototype of a small open economy. Therefore, models designed for closed economies should a priori not fit very well when it comes to reproduce and forecast its business cycle. Interestingly, in turned out that this first presumption is not quite true. A further conjecture is, that a two-country DSGE model approach (Austria and Euro area) should be better suitable to reproduce Austria’s business cycle because Austria—as a member of EU and the Euro area—is economically heavily integrated into the Euro area. Therefore, shocks in the Euro area determine heavily Austria’s business cycle.
4.1 Turning Point of the Austrian Business Cycle in 2008
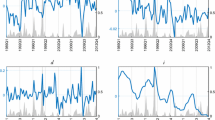
Before evaluating the predictive power of the DSGE models let’s have a look on their ability to catch the turning point of the business cycle in 2008. The pre-crisis peak of the Austrian business cycle was reached in 1Q2008. After that real GDP began to decline until the trough was reached in 2Q2009. Whereas—with the exception of An and Schorfheide—all eight DSGE models got the turning point correctly after the information of the default of Lehman Brothers, only five models realized the break of the business cycle in their pre-Lehman Brothers estimations (see Table 2). In 1Q2008 the models of An and Schorfheide, Smets and Wouters, Poutineau and Vermandel, Almeida and Breuss and Rabitsch got the turn already right. The models of Lubik and Schorfheide, Del Negro and Schorfheide and the NAMW did not realize the turning point early in 2008 (see also the Figs. 1, 2).
Post-mortem of DSGE model forecasts of the Great Recession in Austria. Out-of-sample forecast of real GDP with small and medium-sized models. Three out of the four DSGE models measure the business cycle in quarterly growth rates of real GDP (the Smets and Wouters model uses real GDP per capita) by taking the differences of the logs of real GDP (GDP_qoq%): \( \left( {lnY_{t} - lnY_{t - 1} *100} \right) \). For the graphical representation the development of (actual and estimated) real GDP is displayed in this figure as annual growth rates in % (GDP_yoy%) by summing up the differences of the logs of real GDP over four quarters: \( \sum\nolimits_{1}^{4} {(lnY_{t} - lnY_{t - i} )} \). GDP_b(a)LB = is GDP estimated before (after) the default of Lehman Brothers
Post-mortem of DSGE model forecasts of the Great Recession in Austria. Out-of-sample forecast of real GDP with large models. The NAWM model and those of Poutineau and Vermandel measure the business cycle in quarterly growth rates of real GDP. As explained in the note to Fig. 1, for the graphical representation the development of real GDP is displayed in annual growth rates in %. The Almeida model and those of Breuss and Rabitsch use the GDP gap in % of real GDP. GDP(GDP_Gap)_b(a)LB = the estimated GDP (GDP Gap) before (after) the default of Lehman Brothers
4.2 Ex-ante Forecasting the Great Recession in 2009
4.2.1 Before Lehman Brothers (1Q2008)
At the beginning of 2008 (before the default of Lehman Brothers) one could already have known the burst of the subprime sector in the USA evolving already in 2007.Footnote 25 At that point in time only a few DSGE models could realize that the Austrian business cycle passed the peak and began to turn into a recession. At the beginning of 2008, the closed economy models of Smets and Wouters and that of Del Negro and Schorfheide (see Fig. 1) as well as the open economy model of Almeida and the two-country models of Poutineau and Vermandel as well as those of Breuss and Rabitsch realized that a recession is under way (see Fig. 2).
Measured by NRMSE, Poutineau and Vermandel (the two-region Euro area model with banking) wins the trophy with the best score (see Table 2). The second-best performer in ex-ante forecasting the recession was the SW model. Although catching the turning point early in 2008 the two-country model of Breuss and Rabitsch did not get the upswing following the Great Recession in 2009 (see Fig. 2). Similarly, the Almeida model performed badly after the Great Recession (see Fig. 2). Quite bad was the NAWM model in realizing the turning point and catching the recession at the beginning of 2008.
4.2.2 After Lehman Brothers (3Q2008)
During 2008 the financial crisis broadened and reached its climax with the default of Lehman Brothers on 15 September 2008. After that unique event the inter-bank market crashed, a credit squeeze stopped new real investments, the financial crisis turned into a real recession, called the Great Recession. By hindsight we understand the mechanics of the emergence of the Great Recession in 2009. At the end of 2008, after the Lehman Brothers crash only few forecasters realized which consequences this event might have. Therefore, they were not able to forecast properly the recession.
Nevertheless, all eight DSGE models were able to detect the turning point of the Austrian business cycle after Lehman Brothers (see Table 2; Figs. 1, 2). Again, the best performer with the least forecasting errors was the two-country DSGE model with banking of Poutineau and Vermandel. Closely at the second place comes the SW model. The SW is a surprise in the case of Austria, because it was designed for a closed economy and estimated with US data (although the USA are also a closed economy). The explanation may be due to the sticky price and wage system, followed by a flexible-price based output gap measure in the monetary policy rule which can describe quite properly the Austrian institutional wage bargaining process with its strong trade unions. The worst performer at the end of 2008 was the simplest model of An and Schorfheide.
4.3 Ex-ante Forecasting the Great Recession in 2009 and the Recovery Thereafter
Measured by the normalized RMSE before and after Lehman Brothers, the best performer over the period 2008–2016 was the small-scale SW DSGE model with financial frictions by Del Negro and Schorfheide. However, also the SM model and those of Poutineau and Vermandel performed quite well. The worst score (highest NRMSE) produced the DSGE model of Almeida (see Table 2; Figs. 1, 2).
4.4 Inflation
Making the same forecasting exercise for nominal variables, more precisely for the ex-ante forecast of the performance of inflation during the Great Recession produces the following results (see Table 3):
-
The best inflation performance (the lowest NRMSE figures) exhibits the Pouteneau and Vermandel model during the Great Recession 2008–2010; the best inflation performer in the post-recession period (2010–2016) was the Almeida model. The worst performance delivered the NAWM model.
-
Comparing the predictive power of real GDP with those for inflation the results were as follows:
-
During the Great Recession 2009 the models of Del Negro and Schorfheide and that of NAWM forecasted GDP better than inflation before and after Lehman Brothers. Poutineau and Vermandel as well as Breuss and Rabitsch forecasted inflation better than GDP after Lehman Brothers. The small (An and Schorfheide, Lubik and Schorfheide) and medium-sized DSGE models (Smets and Wouters) were better in forecasting ex-ante the inflation than real GDP.
-
In the post-recession period 2009–2016 five out of the eight DSGE models forecasted ex-ante real GDP better than inflation. Only the models An and Schorfheide, Almeida, as well as Breuss and Rabitsch forecasted inflation better than real GDP.
-
5 How Performed Non-DSGE Methods?
The primary goal of this paper was to test the ex-ante forecasting quality of DSGE models in case of a severe recession. For purposes of comparison, we take two Non-DSGE methods to evaluate post-mortem the Austrian Great Recession. One is a global macro model of Oxford Economics, the other is the expert forecasting of WIFO.
5.1 OEF Global Economic Model
Oxford Economics forecasts monthly the economic development of 80 countries in its Global Economic (Macro) Model. The OEF Global Economic ModelFootnote 26 is the only macroeconomic model that fully integrates 80 global economies plus the Eurozone. The Oxford model is an eclectic model designed to capture the key relationships in the global economy: (i) Keynesian in the short run; (2) Monetarist in the long run. In the short run, shocks to demand will generate economic cycles that can be influenced by fiscal and monetary policy. But over the long run, output is determined by supply side factors: investment, demographics, labour participation and productivity.
We evaluate the forecast of Austrian real GDP growth executed at two different junctures of the crisis:
-
(i)
Before the default of Lehman Brothers (bLB). We take the OEF database as of 3M2008 and forecast the further development of the Austrian GDP in the coming years up to the end of 2012.
-
(ii)
After the default of Lehman Brothers (aLB). Here we take the OEF database as of 11M2008 and execute with it a forecast of the following years up to the end of 2013.
As one can see from Fig. 3, at the beginning of 2008 the OEF model did not realize that a recession is advancing. Only after Lehman Brothers the growth rate of real GDP was forecasted slightly negative (− 0.2%) for the year 2009. Then the Oxford Economics forecaster gradually approached the Great Recession in 2009. Nevertheless, measured by NRMSE, the ex-ante forecasting performance of the OEF Global model was not the worst in comparison with DSGE models (see Table 2).
Post-mortem of Non-DSGE model forecasts of the Great Recession in Austria. Out-of-sample forecast of real GDP. GDP = realized real GDP growth in %; F_3M08 = Forecast in March 2008 etc. The Oxford Economics model uses real GDP (quarterly) growth rates in %; the WIFO forecast is based on annual real GDP growth rates in %
5.2 WIFO’s Expert Forecasts
The Austrian Institute of Economic Research (WIF0) makes quarterly forecasts (or revisions of previous forecasts), however, it does not forecast quarterly variables but only yearly macro variables, like real GDP. WIFO always forecasts only 1 year in advance. The forecast is done by a team of experts. Only afterwards the forecast is translated into the WIFO macro model for policy simulation purposes.
Before Lehman Brothers, in March 2008 WIFO already anticipated a turning of the business cycle due to gloomy news about the development (subprime and banking crises) in the USA. After Lehman Brothers in December 2008, WIFO already forecasted a slight decline of real GDP for 2009 (− 0.5%). Then the GDP growth was corrected downwards step by step: March 2009 (− 2.2%). In June 2009 (− 3.4%), WIFO forecasted nearly correctly the final decline of real GDP (− 3.7%) in the year 2009 (see Fig. 3).Footnote 27
6 Conclusions
DSGE (Dynamic stochastic general equilibrium) models are the common workhorse of modern macroeconomic theory. They are widely applied in academic research but also in international institutions (IMF, European Commission, ECB), in particular in central banks. DSGE models serve three purposes: They are used to predict (forecast) and explain (story-telling) co-movements of aggregate time series over the business cycle (real business cycle theory) and to perform policy analysis (policy experiments: IRF implications of shocks of fiscal and monetary policy and of technical change). Whereas the two latter applications were in the forefront of applications since its inception, the forecasting perspective is only recently topical.
Most forecasting evaluations with DSGE models so far were executed for the US economy and for the Euro area (at the ECB). In this study, we performed a post-mortem of DSGE model forecasts of the Great Recession (2009) in Austria. For this purpose, eight DSGE models with different characteristics (closed and open economy models; one and two-country models) were used.
The initial hypothesis that DSGE models might be less suitable to forecast a severe recession than macro models could be partly falsified. The forecasts of real GDP growth for Austria are obtained at two different junctures of the crisis that led to the recession: At the beginning of 2008 and at the end of this year (after the default of Lehman Brothers). Whereas early in 2008 only five of eight models detected the turn into recession, after Lehman Brothers seven out of eight DSGE models correctly saw the Austrian business cycle turning into recession. With respect to the predictive power measured by RMSE values those models which already included factors which led to the Great Recession, namely financial frictions and inter-bank features performed the best. This is true for the Poutinau and Vermandel model. Surprisingly, the most cited Smets and Wouters model, a closed economy DSGE model also performed for Austria—a prototype open economy—quite well in ex-ante forecasting the crisis.
With exception of the best performing DSGE models (Poutineau and Vermandel as well as Smets and Wouters) ex-ante forecast of real GDP with non-DSGE models like the Global Macro Model of Oxford economics and WIFO’s expert forecasts performed comparable or better than the other DSGE models in the crisis. Inflation during the crisis was better predicted by the Oxford model than by most DSGE models.
Notes
Although DSGE modelling is mainstream in modern macroeconomics, there are many critics of DSGE modelling. Blanchard (2016) questions the future of DSGE models as a proper instrument of modern macroeconomics. Romer (2016) fundamentally criticises the flaws of DSGE models in properly explaining the fluctuations of economic development. Also, Stiglitz (2017) attacked DSGE modelling because of the wrong microfoundations, which—from his point of view—failed to incorporate key aspects of economic behaviour.
A recent example is the analysis of the implication of the EU-Banking Union with the DSGE model QUEST of the European Commission (2 two-regions Euro area model) by Breuss et al. (2015).
Volker Wieland (see Wieland et al. 2012) heads an EU-sponsored project of DSGE model comparison to analyse fiscal and monetary policy shocks under different rules, executed with a common algorithm. The models used are collected in “The Macroeconomic Model Database (MMB)” (see the MMB-Website: http://www.macromodelbase.com/download/).
A short history of DSGE modelling can be found in Fernández-Villaverde (2010).
A basic RBC DSGE model with monopolistic competition can be found in Griffoli (2013), pp. 11–14.
Poutineau et al. (2015) demonstrate the working of a NKS DSGE model using the benchmark “New Keynesian 3-equation Model” consisting of a New Keynesian Phillips curve (inflation), a dynamic IS curve (output) and a monetary policy (Taylor) rule (interest rate).
Fernández-Villaverde (2010) calls the research of formal estimation of DSGE models (the cornerstone of modern macroeconomics)—the combination of rich structural models, novel solution algorithms, and powerful simulation techniques—which allows researchers to transform the quantitative implementation of equilibrium models from ad hoc procedures to a systematic discipline, the New Macroeconometrics.
For a literature review, see Del Negro and Schorfheide (2013), p. 35.
A critical assessment of the usefulness of theory-base forecasts with estimated DSGE models can be found in Giacomini (2015).
Another similarly simple model would be the “New Keynesian 3-equation Model” presented by Poutineau et al. (2015).
A short description of the An and Schorfheide model can be found in Warne (2015).
The method of detrending varies in this study. In the Smets and Wouters model we use their method, in the other models we use Hodrick-Prescott filtering to detrend the variables.
A short description of the Lubik and Schorfheide model can be found in Warne (2015).
A short description of the Smets and Wouters model can be found in Warne (2015).
A short description of the Del Negro and Schorfheide model can be found in Warne (2015).
Dynare is used together with Matlab. See Griffoli (2013) and the DYNARE website: http://www.dynare.org/.
A three-country version (Austria, Euro area and USA) of this NK DSGE model was developed in Breuss and Fornero (2009).
The ex-post or within-sample forecast of the eight DSGE models used to capture the business cycle in Austria can be found in the Annex.
Six out of the eight DSGE models are estimating the business cycle in quarterly growth rates (differences of the logs of the respective variables). The Almeida and the Breuss-Rabitsch models are estimated in gaps of real GDP.
Conditional forecasting concerns forecasts of endogenous variables conditional on a certain path and length of path for some other endogenous variables. This is important when one uses real-time data vintages. The values for all observed variables for period T, the last “historical” time period, have often not been released by the statistical authority yet and are therefore missing from the relevant data vintage, i.e., the data set is unbalanced. Accordingly, some of the time T values need to be forecasted and the forecasts of these variables need to take into account that values for other variables are available for the same time period (see Warne, 2015, p. 173).
The ex-ante forecasts of the eight models also show the confidence intervals (from 50% to 90%). In some cases, where the mean forecast results bLB and aLB are very close, there may be no significant difference in both forecast. Candidates for this conjecture would be the outcome of the well performing models of Smets and Wouters, Del Negro and Schorfheide as well as Poutineau and Vermandel.
The RMSE of a model prediction with respect to the estimated variable \( X_{model} \) is defined as the square root of the mean squared error: \( RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{obs,i} - X_{model,i} } \right)^{2} }}{n}} \). Non-dimensional forms of the RMSE are useful because we want to compare RMSE of DSGE models with different GDP metrics. There are two approaches: normalize the RMSE to the mean of the observed data or normalize to the range (maximums minus minimum) of the observed data. The latter is used in Table 2: \( NRMSE = \frac{RMSE}{{X_{obs,max} - X_{obs,min} }} \).
After it reached the peak in 2006, since early 2007 the Case-Shiller Home Price Index began to decline dramatically.
See the website of Oxford Economics: http://www.oxfordeconomics.com/.
A numerical comparison of the goodness of WIFO’s forecast with the other models (DSGE and OEF model) in Table 2 is difficult, because WIFO makes only annual forecasts. If however, one calculates the normalized RMSE (NRMSE) values for the WIFO forecast of real GDP growth made before LB (March 2008) and after LB (December 2008) over the forecast period 2007–2010, one gets the following NRMSE values: before LB 0.4304, after LB 0.2361. Hence, WIFO forecasted the Great Recession 2009 nearly as good as the OEF model.
References
Almeida, V. (2009). Bayesian estimation of a DSGE model for the Portuguese economy. Master Thesis, Universidade Técnica de Lisboa, June 2008.
An, S., & Schorfheide, F. (2007). Bayesian analysis of DSGE models. Econometric Reviews, 26(2–4), 113–172. (with discussion, 173–219).
Bernanke, B. S., Gertler, M., & Gilchrist, S. (1999). The financial accelerator in a quantitative business cycle framework. In J. B. Taylor & M. Woodford (Eds.), Handbook of macroeconomics (Vol. 1C, pp. 1341–1393). Amsterdam: North Holland.
Blanchard, O. (2016). Do DSGE models have a future? Policy brief PB 16-11, Peterson Institute for International Economics (PIIE), August 2016.
Breuss, F. (2016). The crisis in retrospect: Causes, effects and policy responses. In Harald Badinger & Volker Nitsch (Eds.), Routledge handbook of the economics of european integration (pp. 331–350). London and New York: Routledge.
Breuss, F., & Fornero, J. A. (2009). An estimated DSGE model of Austria, the Euro area and the U.S.: Some welfare implications of EMU, FIW working paper, no. 34, August 2009.
Breuss, F., & Rabitsch, K. (2009) An estimated two-country DSGE model of Austria nd the Euro area. Empirica—Journal of European Economics, 36(1), 123–158 (based on EI working paper, no. 78, June 2008; Europainstitut WU-Wien).
Breuss, F., Roeger, W., & in’t Veld, J. (2015). The stabilising properties of a European Banking Union in case of financial shocks in the Euro Area. European Economy—Economic Papers, no. 543, February 2015.
Canova, F. (2007). Methods for applied macroeconomic research. Princeton: Princeton University Press.
Christoffel, K., Coenen, G., & Warne, A. (2008). The new area-wide model of the Euro Area: A micro-founded open-economy model for forecasting and policy analysis. ECB working paper series no. 944, October 2008.
Christoffel, K., Coenen, G., & Warne, A. (2011). Forecasting with DSGE models. In M. P. Clements & D. F. Hendry (Eds.), The oxford handbook of economic forecasting (pp. 89–127). New York: Oxford University Press.
Clarida, R., Galí, J., & Gertler, M. (1999). The science of monetary policy: A new Keynesian perspective. Journal of Economic Literature, 37(4), 1661–1707.
DeJong, D. N., Ingram, B. F., & Whiteman, C. H. (2000). A Bayesian approach to dynamic macroeconomics. Journal of Econometrics, 98(2), 203–223.
Del Negro, M., & Schorfheide, F. (2013). DSGE model-based forecasting. In G. Elliott & A. Timmermann (Eds.), Handbook of economic forecasting (Vol. 2, pp. 57–140). Amsterdam: North Holland.
Del Negro, M., Schorfheide, F., Smets, F., & Wouters, R. (2007). On the fit of new Keynesian models. Journal of Business & Economic Statistics, 25(2), 123–143.
Fernández-Villaverde, J. (2010). The econometrics of DSGE models, SERIEs, Journal of the Spanish Economic Association, 1(1–2), 3–49 (CEPR discussion paper, no. 7157, February 2009).
Galí, J., Smets, F., & Wouters, R. (2012). Unemployment in an estimated new Keynesian model. In D. Acemoglu & M. Woodford (Eds.), NBER macroeconomics annual 2011 (Vol. 26, pp. 329–360). Chicago: University of Chicago Press.
Giacomini, R. (2015). Economic theory and forecasting: lessons from the literature. Econometric Journal, 18(2), C22–C41.
Goodfriend, M., & King, R. (1997). The new neoclassical synthesis and the role of monetary policy. In B. S. Bernanke & J. Rotemberg (Eds.), NBER macroeconomics annual 1997 (Vol. 12, pp. 231–296). MIT Press.
Griffoli, T. M. (2013). DYNARE user guide: An Introduction to the solution and estimation of DSGE models. DYNARE Website http://www.dynare.org/. Accessed 23 Feb 2018.
Kolasa, M., & Rubaszek, M. (2014). Forecasting with DSGE models with financial frictions. Dynare working paper series, working paper, no. 40, June 2014.
Kydland, F. E., & Prescott, E. C. (1982). Time to build and aggregate fluctuations. Econometrica, 50(6), 1345–1370.
Lubik, T. A., & Schorfheide, F. (2007). Do central banks respond to exchange rate movements? A structural investigation. Journal of Monetary Economics, 54(4), 1069–1087.
Merola, R. (2014). The role of financial frictions during the crisis: An estimated DSGE model. Dynare working paper series, working paper, no. 33, January 2014.
Poutineau, J-Ch., & Vermandel, G. (2015). Cross-border banking flows spillovers in the Eurozone: Evidence from an estimated DSGE model. Journal of Economic Dynamics & Control, 51, 378–403.
Poutineau, J.-Ch., Sobczak, K., & Vermandel, G. (2015). The analytics of the new Keynesian 3-equation model. In HAL-01194642, 7 September 2015.
Romer, P. (2016). The trouble with macroeconomics. https://paulromer.net/wp-content/uploads/2016/09/WP-Trouble.pdf. Accessed 23 Feb 2018.
Rotemberg, J. J., & Woodford, M. (1997). An optimization-based econometric framework for the evaluation of monetary policy. In B. S. Bernanke & J. Rotemberg (Eds.), NBER macroeconomics annual (Vol. 12, pp. 297–346). MIT Press.
Smets, F., Warne, A., & Wouters, R. (2013). Professional forecasters and the real-time forecasting performance of an estimated new Keynesian model for the Euro Area. ECB working papers series, no. 1571, August 2013.
Smets, F., & Wouters, R. (2007). Shocks and frictions in US business cycles: A Bayesian DSGE approach. The American Economic Review, 97(3), 586–606.
Stiglitz, J. E. (2017). Where modern macroeconomics went wrong. NBER working paper, no. 23795, September 2017.
Warne, A. (2015). YADA manual—Computational details. http://www.texlips.net/download/yada.pdf. Accessed 23 Feb 2018.
Wieland, V., Cwik, T., Mueller, G. J., Schmidt, S., & Wolters, M. (2012). A new comparative approach to macroeconomic modeling and policy analysis. Journal of Economic Behavior & Organization, 83(3), 523–541.
Acknowledgements
Open access funding provided by Vienna University of Economics and Business (WU).
Author information
Authors and Affiliations
Corresponding author
Annex: Ex-post (Within-Sample) DSGE Model Forecasts of Austria’s GDP (See Figs. 4, 5)
Annex: Ex-post (Within-Sample) DSGE Model Forecasts of Austria’s GDP (See Figs. 4, 5)
Small and Medium-Sized DSGE Models. 1-Step ahead mean forecasts, executed with YADA: With the exception of the Smets and Wouters model (which uses real GDP per capita), all models measure the business cycle in the development of real GDP (graphically represented in annual growth rates in %). GDP = realized GDP; GDP_f = ex-post forecast of GDP
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Breuss, F. Would DSGE Models Have Predicted the Great Recession in Austria?. J Bus Cycle Res 14, 105–126 (2018). https://doi.org/10.1007/s41549-018-0025-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41549-018-0025-1