Rigorous computation in dynamics based on topological methods for multivector fields

Abstract

Motivated by the theoretical results of Mrozek et al. (Commun Nonlinear Sci Numer Simul 108:106–226, 2022) we present an algorithmic construction of a transversal cellular decomposition for a planar ODE. We then use the associated combinatorial multivector field to algorithmically detect the existence of an isolated invariant set with the Conley index of a periodic orbit and admitting a combinatorial Poincaré section. This construction combined with the theoretical results of Mrozek et al. (2022) leads to a method for automatized computer assisted proofs of the existence of periodic solutions in ODE’s.

1 Introduction

1.1 Background and motivation

Differential equations are among the most frequently used mathematical tools in modeling physical processes in science and engineering. Unfortunately, in most cases the equations cannot be solved analytically and numerical methods may provide only approximate solutions for a finite number of initial values and over a bounded time interval. Getting a global, asymptotic view of the dynamics associated with a general ordinary differential equation remains a challenge. Significant progress has been achieved in the last 2 or 3 decades by means of topological methods combined with rigorous numerical analysis. Such a combination has been fruitfully used in constructing computer-assisted proofs of the existence of various dynamical phenomena including bounded trajectories, heteroclinic connections (Wilczak 2009), equilibrium and periodic solutions (Kapela and Zgliczyński 2003; Lessard et al. 2016), and chaotic invariant sets (Mischaikow and Mrozek 1995; Tucker 1999; Arioli and Zgliczyński 2001). However, most of these proofs, particularly proofs of recurrent behavior, must be preceded by a substantial number of numerical experiments. They are needed to locate the objects of interest and properly prepare the actual computer assisted proof.

A remedy to this situation might be the recently developed theory of combinatorial dynamical systems based on combinatorial multivector fields (Mrozek 2017; Lipiński et al. 2022). The theory has been already equipped with several concepts and results of classical topological dynamics, including Morse decomposition and Conley index theory (Lipiński et al. 2022), providing tools for the analysis of combinatorial systems. In Mrozek and Wanner (2021) authors show that a combinatorial vector field gives rise to a semi-flow admitting the same Conley–Morse graph as the combinatorial system. Conversely, it is proved in Mrozek et al. (2022) that, under certain assumptions, a multivector field properly constructed on top of a continuous vector field can be used to infer some properties of the flow. In particular, a combinatorial isolated invariant set of the multivector field implies the existence of an isolated invariant set for the flow (Mrozek et al. 2022, Theorem 5.28) and, moreover, the existence of a combinatorial periodic solution implies the existence of a periodic solution of the differential equation (Mrozek et al. 2022, Theorem 5.37). These results are based on the concept of an admissible flow with respect to a given cellular decomposition of the space which guarantees that trajectories of the flow cross the facets of the decomposition transversally. A multivector field associated with the cellular decomposition can be further used for finding some isolated neighborhoods in the original flow. By (McCord et al. 1995, Corollary 1.4) if an isolating neighborhood N with the Conley index of a hyperbolic periodic orbit admits a Poincaré section, then there is a periodic trajectory in N. As indicated by Mrozek et al. (2022), there is a combinatorial counterpart of the concept of Poincaré section which, when applied to a combinatorial multivector field derived from an admissible flow, gives rise for a Poincaré section of the flow.

Due to its finite, combinatorial nature, the theory of multivector fields enables an automatized search for dynamically interesting objects, in particular periodic solutions. However, the approach presented in Mrozek et al. (2022) does not include the construction of the required cellular decomposition. Such transversal polygonal decompositions of flows have been also studied by Boczko et al. (2007), but an explicit algorithm also has not been presented. Hence, all what is missing to turn the methods of Mrozek et al. (2022) into an automatized computer-assisted proof of the existence of periodic orbits is an algorithmic construction of a cellular decomposition transversal with respect to the flow and a strategy for finding a combinatorial Poincaré section for a Morse set with the Conley index of a hyperbolic periodic orbit.

The main aim of the present paper is to solve these algorithmic tasks and to compose them into a complete procedure leading to the proof. We emphasize that although the presented results concern planar flows, the used techniques are not specifically planar. Therefore, we believe that they may be adapted to problems in dimensions three and above. We leave this for further investigation.

1.2 Overview of main results

The paper provides a full algorithmization of the approach presented in Mrozek et al. (2022) leading to a computer assisted proof of the existence of a periodic orbit. A complete pipeline is presented in Sect. 5.2. Here, we provide a simple demonstration of the outcome of its key steps which are the main subject of this paper.

Fig. 1

Left: selected trajectories of the dynamical system induced by the vector field (1). Right: transversal polytope with 12 edges and radius 0.2 around a equilibrium point at the origin for that vector field

Let f be a vector field given by:

$$\begin{aligned} f(x,y) = (ay - x(x^2 + y^2 - 4), -ax - y(x^2 + y^2 - 4)), \end{aligned}$$

(1)

with parameter $a=1$. The equation induces a flow shown in Fig. 1 (left). This system has a repelling equilibrium point at (0, 0) and an attracting periodic orbit forming a circle of radius 2 with a center at the origin.

To automatically prove the existence of the orbit we need to construct a flow-transversal cellular decomposition of the region containing it. In the example the considered region is $X:=[-3,3]\times [-3,3]$. The main algorithm, $\texttt{AdmissibleMVF}$, presented in Sect. 3.1, transforms the input triangulation (Fig. 2 left) into a desirable, transversal cellular decomposition (Fig. 2 right) by properly combining simplices into larger cells. In fact, it also provides an associated multivector field used for further analysis. Computations involve a rigorous interval arithmetic guarantying the transversality of edges with respect to the flow.

Fig. 2

Left: a triangulation of the rectangular region of interest. Solid lines corresponds to the transversal edges of the triangulation. Dotted lines represent edges that cannot be rigorously confirmed as transversal. Right: an f-admissible cellular decomposition computed from the triangulation in the left panel. Dashed-lines represent internal edges of cells

We proved (Corollary 3.10) that the construction leads to a cellular decomposition with respect to which the input vector field give rise to an admissible flow. Nevertheless, there is no guarantee that it will be useful from the perspective of the proof. In particular, one may end up with a low-resolution representation containing large cells (see Fig. 3 right). The main culprit is a strong rotation of a flow (often around equilibrium points) causing an expansion of cells. To prevent it we employ an additional preprocessing. Specifically, we construct polytopes around equilibrium points with faces transversal to the flow (see Fig. 1 right) using algorithm ${} \texttt{TransversalPolytope}$ described in Sect. 4.1. Panels in Fig. 3 provide a comparison of the cellular decompositions for system (1) with parameter $a=3$ for a triangulation with and without the preprocessing.

Fig. 3

Both panels show admissible cellular decomposition with respect to the vector field (1) with parameter $a=3$. The left panel shows the outcome for a triangulation with a transversal polytope around the equilibrium point at the origin. The right panel shows the outcome for the same triangulation, but with some random points at the origin instead of the polytope. The second case results in a strong inflation of a cell in the process of constructing cellular decomposition

The cellular decomposition produced by ${} \texttt{AdmissibleMVF}$ induces a combinatorial multivector field ${{\mathcal {V}}}$ for which, in the next step, we compute a Morse decomposition. Figure 4 shows the extracted Morse sets; the yellow set, containing the equilibrium point and the red-blue set, containing the periodic orbit. For the red Morse set, admitting Conley index of a hyperbolic periodic orbit, we construct a combinatorial Poincaré section using algorithm PoincaréSection described in Sect. 3.3. The obtained Poincaré section for the example is highlighted in Fig. 4 as a blue region.

After successfully computing all the elements we can conclude from (Mrozek et al. 2022, Theorem 5.37) the existence of the periodic orbit contained in the polytope of the red-blue region.

Fig. 4

Morse sets and Poincaré section for periodic orbit of the multivector field shown in the Fig. 2 (right)

1.3 Organization of the paper

In Sect. 2 we introduce basic concepts and notation used later in the paper. Section 3 is dedicated to the main algorithms of the paper. It contains the procedure for constructing a transversal cellular decomposition from a given triangulation and the algorithm for finding a combinatorial Poincaré section. Section 4 provides the algorithm for constructing a transversal polytope around an equilibrium point of a dynamical system. In Sect. 5 we outline a complete pipeline for the computer assisted proof based on multivector fields theory and, as a proof of concept, we demonstrate its outcome for two planar systems: a flow with two periodic orbits and the Van der Pol oscillator. Lastly, we gather final remarks regarding computations and further research in Sect. 6.

2 Preliminaries

2.1 Relations and posets

A pair $(X, \le )$ of a set and a partial order relation is called a poset. A set $A \subset X$ is an upper set if $\{ z \in X \mid \exists _{x\in A}\, x \le z \} \subset A$. Analogously, $A\subset X$ is a lower set if $\{ z \in X \mid \exists _{x\in A}\, z \le x \} \subset A$. A set $A\subset X$ is convex with respect to poset $(X,\le )$ if for every $x,z\in A$ and $y\in X$ such that $x\le y\le z$ it follows that $y\in A$. Equivalently, a convex set is an intersection of a lower set and an upper set.

A partition of a space X is a family ${{\mathcal {V}}}$ of non-empty subsets of X such that for every $A,B\in {{\mathcal {V}}}$ we have $A \cap B = \emptyset$ and $\bigcup {{\mathcal {V}}}= X$. In particular, a partition ${{\mathcal {V}}}$ induces an equivalence relation R defined by xRy if there exists $A\in {{\mathcal {V}}}$ such that $x,y\in A$. We denote the equivalence class of a point $x\in X$ induced by partition ${{\mathcal {V}}}$ by $[x]_{{{\mathcal {V}}}}$.

2.2 Topological spaces

Given a topology ${\mathcal {T}}$ on X, we call $(X, {\mathcal {T}} )$ a topological space. When the topology ${\mathcal {T}}$ is clear from the context, we also refer to X as a topological space. We denote the interior, closure, and boundary of a $A\subset X$ with respect to ${\mathcal {T}}$ by ${\text {int}}_{\mathcal {T}}A$, ${\text {cl}}_{\mathcal {T}}A$, and ${\text {bd}}_{\mathcal {T}}A$, respectively. The mouth of A is defined as $\textrm{mo}_{\mathcal {T}} A:= \textrm{cl}_{\mathcal {T}} A {\setminus } A$. If the topology is known from the context, we write, e.g., ${\text {cl}}_X A$, or we skip the subscript completely. Let $Y\subset X$. The induced topology on Y is defined as ${\mathcal {T}}_Y:=\{U\cap Y\mid U\in {\mathcal {T}}\}$. The closure of $A\subset Y$ with respect to the induced topology on Y will be denoted by ${\text {cl}}_{{\mathcal {T}}_Y} A$ or simply by ${\text {cl}}_Y A$. Similarly, for the interior, boundary, and mouth.

A set $A\subset X$ is $locally~closed$ if A is an intersection of an open and a closed set. Equivalently, A is locally closed if and only if ${\text {mo}}A$ is closed (Engelking 1989, Problem 2.7.1).

We will be particularly interested in $T_0$ finite topological spaces. By the Alexandroff theorem (Alexandrov 1937) we can identify them with partial orders.

Theorem 2.1

(Alexandrov 1937) For a finite poset $(P,\le )$ the family ${\mathcal {T}}_{\le }$ of upper sets of $\le$ is a $T_0$ topology on P. For a finite $T_0$ topological space $(X,{\mathcal {T}})$ the relation $x \le _{{\mathcal {T}}} y$ defined by $x \in {\text {cl}}_{{\mathcal {T}}} \{ y \}$ is a partial order on X. Moreover, the two associations that relate $T_0$ topologies and partial orders are mutually inverse.

It follows that in this setting all topological concepts can be expressed in the terms of partial order concepts and vice versa. In particular, given a finite $T_0$ topological space $(X, {\mathcal {T}})$ with the associated poset $(X,\le )$, we get for $A\subset X$

$$\begin{aligned} {\text {cl}}_{\mathcal {T}}A&:= \{x\in X\mid \exists _{a\in A}\ x\le a\}, \end{aligned}$$

(2)

$$\begin{aligned} {\text {bd}}_{\mathcal {T}}A&:= \{x\in X \mid \exists _{a\in A,\ b\in X{\setminus } A}\ x\le a \text { and } x\le b\}. \end{aligned}$$

(3)

We emphasize that in the setting of finite topological spaces local closedness and convexity coincide (Lipiński 2021, Proposition 1.4.10). Hence, A is a locally closed set in a $T_0$ topology iff it is convex with respect to the associated poset. We will use these two concepts exchangeably throughout the paper; locally closed when we try to emphasize the topological context and convex when we focus on the algorithmical or the combinatorial aspect.

2.3 Cellular decompositions

Let X be a topological space. A d-$dimensional~ cell$ (or a d-cell) is a subset $\sigma \subset X$ which is a homeomorphic image of the closed unit ball in ${\mathbb {R}}^d$. The associated open cell and cellular boundary of the cell $\sigma$ are defined as the image in the same homeomorphism restricted to the open unit ball and the unit sphere in ${\mathbb {R}}^d$, respectively. The open cell is denoted by $\overset{\circ }{\sigma }$.

A finite family ${\mathcal {X}}$ of cells in a topological space X is a $cellular ~decomposition$ (Mrozek et al. 2022, Sect. 5.1) of X if:

• (i) $\overset{\circ }{\sigma }\cap \tau \ne \emptyset \Rightarrow \sigma \subset \tau$ for all cells $\sigma , \tau \in {\mathcal {X}}$, and

• (ii) $X=\bigcup \{\overset{\circ }{\sigma }\ \mid \sigma \in {\mathcal {X}}\}.$

Given two cells $\tau ,\sigma \in {\mathcal {X}}$ such that $\tau \subset \sigma$ we say that $\tau$ is a $face$ of $\sigma$, and that $\sigma$ is a $coface$ of $\tau$. The face or coface is called $proper$, if $\sigma \ne \tau$. A face $\tau$ of $\sigma$ is a $facet$ of $\sigma$, if $dim \,\sigma = dim \,\tau + 1$. We write ${\text {Cbd}}_{\mathcal {X}}\sigma$ to denote the family of all proper cofaces of $\sigma$ with respect to cellular decomposition ${\mathcal {X}}$. For ${\mathcal {A}}\subset {\mathcal {X}}$, by ${\text {Cbd}}_{\mathcal {X}}{{\mathcal {A}}}$ we understand $\bigcup \{{\text {Cbd}}_{\mathcal {X}}\sigma \mid \sigma \in {\mathcal {A}}\}$.

The inclusion relation among cells, known as the face relation, is a partial order in ${\mathcal {X}}$. By Theorem 2.1 this partial order induces $T_{0}$ topology in ${\mathcal {X}}$. We denote this topology by ${\mathcal {T}}_{{\mathcal {X}}}$. We will be often using topological operators in the context of cellular decomposition. Thus, if ${\mathcal {A}}\subset {\mathcal {X}}$ then we can rephrase (2) and (3) as

$$\begin{aligned} {\text {cl}}{\mathcal {A}}&:= \{\tau \in {\mathcal {X}}\mid \exists _{\sigma \in {\mathcal {A}}}\ \tau \subset \sigma \}, \end{aligned}$$

(4)

$$\begin{aligned} {\text {bd}}{\mathcal {A}}&:= \{\sigma \in {\mathcal {X}}\mid \exists _{\tau \in {\mathcal {X}},\,\mu \in {\mathcal {X}}{\setminus } {\mathcal {A}}}\ \sigma \subset \tau \ \text {and}\ \sigma \subset \mu \}. \end{aligned}$$

(5)

Given a collection of cells ${\mathcal {A}}\subset {\mathcal {X}}$ we denote its support by $\left| {\mathcal {A}}\right|:=\bigcup _{\sigma \in {\mathcal {A}}} \overset{\circ }{\sigma }$ and by $\left|{\mathcal {A}}\right|_G:=\bigcup _{\sigma \in {\mathcal {A}}}\sigma$ its geometric realization. In particular, if ${\mathcal {A}}$ is a closed set with respect to ${\mathcal {T}}_{\mathcal {X}}$ then $\left|{\mathcal {A}}\right|=\left|{\mathcal {A}}\right|_G$. We denote the collection of all top-dimensional cells of ${\mathcal {X}}$ by ${\mathcal {X}}_\text {top}$. By the frame of ${\mathcal {X}}$ we will understand set ${\text {Fr}}(X):=\left| {\mathcal {X}}{\setminus }{\mathcal {X}}_\textrm{top}\right|$.

Later on we will work with a 2-dimensional cellular decomposition ${\mathcal {X}}$, that is, a decomposition with cells of at most 2 dimension. Let ${\mathcal {A}}\subset {\mathcal {X}}$. We adopt the following notation:

$$\begin{aligned} \texttt{Verts}({\mathcal {A}})&:= \{\sigma \in {\mathcal {A}}\mid \dim \sigma = 0\}, \\ \texttt{Edges}({\mathcal {A}})&:= \{\sigma \in {\mathcal {A}}\mid \dim \sigma = 1\}, \\ \texttt{Tops}({\mathcal {A}})&:= \{\sigma \in {\mathcal {A}}\mid \dim \sigma = 2\}. \end{aligned}$$

In this case ${\mathcal {X}}_\textrm{top}=\texttt{Tops}({\mathcal {X}})$.

A d-cell which is a convex hull of $d+1$ affinely independent points in ${\mathbb {R}}^n$ is called a d-simplex (or just simplex). A cellular decomposition ${\mathcal {X}}$ consisting only of simplices in ${\mathbb {R}}^n$ such that:

• (i) Every face of a simplex of ${\mathcal {X}}$ is in ${\mathcal {X}}$, and

• (ii) The intersection of any two simplices of ${\mathcal {X}}$ is a face of each of them,

is denoted as a simplicial complex.

Let ${\mathcal {A}}\subset {\mathcal {B}}\subset {\mathcal {X}}$ be a topological pair of two closed sets with respect to ${\mathcal {T}}_{\mathcal {X}}$. Then, the singular homology in a finite topological spaces is isomorphic to singular homology of the corresponding supports (Mrozek et al. 2022, Proposition 5.15). In particular, $H({\mathcal {A}},{\mathcal {B}})\cong H(\left| {\mathcal {A}}\right|, \left| {\mathcal {B}}\right|)$.

2.4 Flows

Let $\varphi :X\times {\mathbb {R}} \rightarrow X$ be a flow on a topological space X. Given a set $A \subset X$ the invariant part of A with respect to $\varphi$ is the set

$$\begin{aligned} Inv (A, \varphi ):=\{x \in A \mid \varphi (x, {\mathbb {R}}) \subset A \}. \end{aligned}$$

If ${\text {Inv}}(S,\varphi )=S$ then we say that S is invariant set. Let $N\subset X$ be a compact nonempty subset. It is called an isolating neighborhood if $Inv (N, \varphi ) \subset \text {int } N$. If invariant set S admits an isolating neighborhood such that $S = Inv (N, \varphi )$ then S is an isolated invariant set. The strong exit set and the strong entry set of a compact $B \subset X$ are given respectively by

$$\begin{aligned} B^-&:=\{x\in {\text {bd}}B \mid \exists \epsilon >0 \text { such that } \varphi (x,(0,\epsilon ))\cap B=\emptyset \} \\ B^+&:=\{x\in {\text {bd}}B \mid \exists \epsilon <0 \text { such that } \varphi (x,(\epsilon , 0))\cap B=\emptyset \} \end{aligned}$$

2.5 Transversality

By a $hyperplane$ we mean an affine subspace of ${\mathbb {R}}^d$ of dimension $d{-}1$. For a hyperplane H we denote by $\overrightarrow{H}$ the associated linear vector subspace $\{p-q: p,q \in H\}$. We have $H = p + \overrightarrow{H}$ for any $p \in H$.

Let $\sigma$ be a $(d{-}1)$-dimensional cell contained in some $d{-}1$ hyperplane. We say that a vector field $f:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}^{d}$ is transversal to $\sigma$ if for each $x \in \sigma$ the space ${\mathbb {R}^d}$ is a direct sum of the linear space $\overrightarrow{H}$ and the one-dimensional space spanned by f(x). In practice, to check transversality we compute $v_\sigma$, a normal vector to $\sigma$, and check that $\langle f(x),v_\sigma \rangle \ne 0$ for all $x\in \sigma$. Through this paper, we use the standard scalar product in ${\mathbb {R}}^d$.

A vector field is transversal to a d-dimensional polytope P if it is transversal to each of the facets of that polytope.

2.6 Combinatorial multivector fields

In this section, we provide a brief overview of the multivector fields theory for finite topological spaces. For the comprehensive introduction see (Lipiński et al. 2022; Lipiński 2021).

Let X be a finite topological space. A combinatorial multivector or briefly a multivector is a locally closed subset $V \subset X$. A combinatorial multivector field on X, or briefly a multivector field, is a partition ${\mathcal {V}}$ of X into multivectors. We denote by $[x]_{{\mathcal {V}}}$ the unique multivector in ${{\mathcal {V}}}$ that contains $x\in X$. If the multivector field ${{\mathcal {V}}}$ is clear from the context, we write briefly [x]. We say that a set $A \subset X$ is ${{\mathcal {V}}}$-compatible if for every $x \in X$ either $[x] \cap A = \emptyset$ or $[x] \subset A$. We say that a multivector $V\in {{\mathcal {V}}}$ is critical if the relative homology $H({\text {cl}}V, {\text {mo}}V)$ is non-trivial. A multivector V which is not critical is called regular. The distinction of multivectors into critical and regular ones is inspired by the Ważewski’s theorem (Mrozek et al. 2022, Proposition 3.4). Intuitively, a multivector can be thought of as a finite model of an isolating block, then, its mouth represents the exit part of its boundary. By Ważewski’s theorem, a nontrivial $H({\text {cl}}V, {\text {mo}}V)$ indicates a nonempty invariant set within the block.

Multivector field ${\mathcal {V}}$ on X induces a multivalued map $\Pi _{{\mathcal {V}}}: X \multimap X$ given by

$$\begin{aligned} \Pi _{{\mathcal {V}}}(x)=[x]_{{\mathcal {V}}}\cup {\text {cl}}x~. \end{aligned}$$

(6)

We consider a combinatorial dynamical system given by the iterates of $\Pi _{{\mathcal {V}}}$. A solution of such combinatorial dynamical system in $A\subset X$ is a partial map $\varphi :{\mathbb {Z}}\nrightarrow A$ whose domain, denoted ${\text {dom}}\varphi$, is a ${\mathbb {Z}}$-interval and for any $i,i+1\in {\text {dom}}\varphi$ the inclusion $\varphi (i+1)\in \Pi _{{\mathcal {V}}}(\varphi (i))$ holds. If ${\text {dom}}\varphi$ is a bounded interval in ${\mathbb {Z}}$ then we say that $\varphi$ is a path. If ${\text {dom}}\varphi ={\mathbb {Z}}$ then we call $\varphi$ a full solution.

A full solution $\varphi : {\mathbb {Z}} \rightarrow X$ is left-essential (respectively right-essential) if for every regular multivector $[x]_{{\mathcal {V}}}$ such that $x \in {\text {im}}\varphi$ the set $\{ t \in {\mathbb {Z}}\mid \varphi (t) \notin [x]_{{\mathcal {V}}} \}$ is left-infinite (respectively right-infinite). We say that $\varphi$ is essential if it is both left- and right-essential. The collection of all essential solutions $\varphi$ such that ${\text {im}}\varphi \subset A$ is denoted by $eSol (A)$.

A solution $\varphi$ is an extension of solution $\gamma$ if ${\text {dom}}\gamma \subset {\text {dom}}\varphi$ and $\gamma (i)=\varphi (i)$ for all $i\in {\text {dom}}\gamma$. We say that $\varphi$ is a maximal solution in $A\subset X$ if it is either an essential solution in A or a path in X that cannot be extended neither to a left- nor right-essential solution in A.

The invariant part of a set $A\subset X$ is ${\text {Inv}}A:= \bigcup \{{\text {im}}\varphi \mid \varphi \in {\text {eSol}}(A)\}$. In particular, if $Inv A = A$ we say that A is an invariant set for a multivector field ${\mathcal {V}}$. A closed set $N\subset X$ isolates invariant set $S \subset N$ if the following conditions are satisfied:

• (i) Every path in N with endpoints in S is a path in S,

• (ii) $\Pi _{{\mathcal {V}}}(S) \subset N$.

In this case N is an isolating set for S. If an invariant set S admits an isolating set then we say that S is an isolated invariant set. The Conley index of an isolated invariant set S in this setting can be computed by ${\text {Con}}(S)=H({\text {cl}}S,{\text {mo}}S)$ (see Lipiński et al. 2022, Proposition 5.3 and Theorem 5.16). It may be considered as an algebraic signature of S capturing its dynamical nature.

Let $A \subset X$. By $\bigl \langle A \bigl \rangle _{{\mathcal {V}}}$ we denote the intersection of all sets locally closed and ${{\mathcal {V}}}$-compatible in X containing A. We call this set the ${\mathcal {V}}$-hull of A. The combinatorial $\alpha$-limit set and $\omega$-limit set for a full solution $\varphi$ are defined as

$$\begin{aligned} \alpha (\varphi )&:= \Bigl \langle \bigcap \limits _{t \in {\mathbb {Z}}^-}\varphi ((-\infty ,t]) \Bigl \rangle _{\mathcal {V}}\ , \\ \omega (\varphi )&:= \Bigl \langle \bigcap \limits _{t \in {\mathbb {Z}}^+}\varphi ([t, \infty )) \Bigl \rangle _{\mathcal {V}}\ . \end{aligned}$$

Let $S\subset X$ be a ${{\mathcal {V}}}$-compatible, invariant set. Then, a finite collection ${\mathcal {M}}=\{M_p\subset S\mid p\in {\mathbb {P}}\}$ is called a Morse decomposition of S if there exists a finite poset $({\mathbb {P}},\le )$ such that the following conditions are satisfied:

• (i) ${\mathcal {M}}$ is a family of mutually disjoint, isolated invariant subsets of S,

• (ii) For every $\varphi \in {\text {eSol}}(S)$ either ${\text {im}}\varphi \subset M_r$ for an $r \in {\mathbb {P}}$ or there exist $p, q \in {\mathbb {P}}$ such that $q > p$, $\alpha (\varphi )\subset M_q \text {, and } \omega (\varphi )\subset M_p$.

We refer to the elements of ${\mathcal {M}}$ as Morse sets.

2.7 Graphs induced by a multivector field

The dynamics $\Pi _{{\mathcal {V}}}$ might be additionally analyzed via graphs. In Lipiński et al. (2022) authors consider graph $G_{{\mathcal {V}}}$ consisting of nodes given by points in X and edges $(x,y)\in X\times X$ such that $y\in \Pi _{{\mathcal {V}}}(x)$. In particular, a collection of all strongly connected components of $G_{{\mathcal {V}}}$ with non-empty invariant part forms the minimal Morse decomposition (Lipiński et al. 2022, Theorem 7.3). However, for algorithmic purposes, it is also convenient to consider a simplified graph $G_{{{\mathcal {V}}}}^*:=({{\mathcal {V}}}, E)$ with nodes given by multivectors and the set of edges defined by

$$\begin{aligned} \begin{aligned} E:=&\left\{ (V,W)\in {{\mathcal {V}}}\times {{\mathcal {V}}}\mid W\cap {\text {mo}}V\ne \emptyset \right\} \cup \\&\left\{ (V,V)\in {{\mathcal {V}}}\times {{\mathcal {V}}}\mid V \text { is critical} \right\} . \end{aligned} \end{aligned}$$

(7)

In particular, if $(V,W)\in E$, then there exist $v\in V$ and $w\in W$ such that $w\in \Pi _{{\mathcal {V}}}(v)$.

A walk in graph $G_{{{\mathcal {V}}}}^*$ is a sequence of vertices $\varrho =\{\varrho _i\}_{i\in I}\subset {{\mathcal {V}}}$ such that $(\varrho _i,\varrho _{i+1})\in E$ and I (denoted ${\text {dom}}\varrho$) is a ${\mathbb {Z}}$-interval containing 0. A walk $\varrho$ is infinite if ${\text {dom}}\varrho ={\mathbb {Z}}$. We define a map $\pi _{{\mathcal {V}}}$ translating every solution $\varphi$ in ${{\mathcal {V}}}$ with $0\in {\text {dom}}\varphi$ into a walk in $G_{{{\mathcal {V}}}}^*$. To achieve this, we first introduce partial maps $n_+,n_-$:

$$\begin{aligned} n_+(\varphi , t)&:= \min \{s>t \mid [\varphi (t)]_{{\mathcal {V}}}\ne [\varphi (s)]_{{\mathcal {V}}}\text { or } [\varphi (s)]_{{\mathcal {V}}}\text { is critical}\}, \\ n_-(\varphi , t)&:= \max \{s<t \mid [\varphi (t)]_{{\mathcal {V}}}\ne [\varphi (s)]_{{\mathcal {V}}}\text { or } [\varphi (s)]_{{\mathcal {V}}}\text { is critical}\}. \end{aligned}$$

In particular, $n_+$ (respectively $n_-$) is not defined if $t=\max {\text {dom}}\varphi$ ($t=\min {\text {dom}}\varphi$) or $[\varphi (t)]_{{\mathcal {V}}}$ is a regular multivector and for all $s\ge t$ ($s\le t$) we have $[\varphi (s)]_{{\mathcal {V}}}=[\varphi (t)]_{{\mathcal {V}}}$. Now, we can recursively construct a partial map $\tau _\varphi$:

$$\begin{aligned} \tau _\varphi (i):= {\left\{ \begin{array}{ll} n_-\left( \tau _\varphi (i+1)\right) &{}\text {if } i<0,\\ 0 &{}\text {if } i=0,\\ n_+(\tau _\varphi (i-1)) &{}\text {if } i>0, \end{array}\right. } \end{aligned}$$

defined for $i\in {\mathbb {Z}}$ whenever the corresponding value of $n_\pm$ is defined. In particular, $\tau _\varphi$ indicates time steps at which solution $\varphi$ escapes a current regular multivector. Finally, $\pi _{{\mathcal {V}}}(\varphi ):= \left\{ \varrho _i:=[\varphi (\tau _\varphi (i))]_{{\mathcal {V}}}\mid i\in {\text {dom}}\tau _\varphi \right\}$. Intuitively, $\pi _{{\mathcal {V}}}$ translates $\varphi$ into a sequence of visited multivectors leaving only a single occurrence of a regular multivector if repeated on consecutive positions.

Proposition 2.2

Map $\pi _{{\mathcal {V}}}$ is well defined, that is, for every solution we get a proper walk in $G_{{{\mathcal {V}}}}^*$.

Proof

Let $\pi _{{\mathcal {V}}}(\varphi )=\{V_i\}_{i\in I}$. Fix $i\in I$. By the definition of $n_+$ and $n_-$, it follows that either (a) $V_i=V_{i+1}$ and $V_i$ is critical, or, (b) $V_i\ne V_{i+1}$ and $\Pi _{{\mathcal {V}}}(V_i)\cap V_{i+1}\ne \emptyset$. In both cases $(V_i,V_{i+1})\in E$; thus, $\pi _{{\mathcal {V}}}$ is well defined. $\square$

Proposition 2.3

Let $\varphi$ be a full solution for ${{\mathcal {V}}}$. Then, $\varphi$ is essential if and only if $\pi _{{\mathcal {V}}}(\varphi )$ is an infinite walk.

Proof

Note that $\varrho$ is an infinite walk if and only if $n_\pm (\varphi ,t)$ is well defined for all $t\in {\mathbb {Z}}$. In particular, $n_+(\varphi , t)$ is not defined if and only if $[\varphi (t)]_{{\mathcal {V}}}=[\varphi (s)]_{{\mathcal {V}}}$ for all $s>t$ and $[\varphi (t)]_{{\mathcal {V}}}$ is a regular multivector. This cannot be the case if $\varphi$ is right-essential. Similarly, $n_-$ is defined for all $t\in {\mathbb {Z}}$ if and only if $\varphi$ is left-essential. Thus, $\pi _{{\mathcal {V}}}(\varphi )$ is an infinite walk if and only if $\varphi$ is an essential solution. $\square$

Corollary 2.4

If $S\subset X$ is an isolated invariant set and ${{\mathcal {W}}}$ is a multivector field restricted to S then every walk in $G_{{{\mathcal {W}}}}^*$ admits an extension to an infinite walk.

Proposition 2.5

Let S be a ${{\mathcal {V}}}$-compatible, invariant set and ${{\mathcal {W}}}$ be the multivector field restricted to S. If $G_{{\mathcal {W}}}$ is strongly connected (in particular, S is a minimal Morse set), then $G_{{{\mathcal {W}}}}^*$ is a strongly connected graph.

Proof

If S contains only a single multivector then it follows that S is a critical multivector; thus, $G_{{{\mathcal {W}}}}^*$ has a single node with a self-loop.

For all the other cases let $W,W'\in {{\mathcal {W}}}$, $W\ne W'$, $w\in W$ and $w'\in W'$. Since $G_{{\mathcal {W}}}$ is strongly connected we can find paths $\rho$ and $\rho '$ in S from w to $w'$ and from $w'$ to w, respectively. Clearly, a composition $\varphi :=\rho \cdot \rho '$ is a path such that $\pi _{{\mathcal {W}}}(\varphi )$ is a cycle containing W and $W'$. It proves that $G_{{{\mathcal {W}}}}^*$ is a strongly connected graph. $\square$

Proposition 2.6

Let $S\subset X$ be an isolated invariant set for ${{\mathcal {V}}}$ consisting of only regular multivectors and let $P\subset A$ be a ${{\mathcal {V}}}$-compatible set. Let ${{\mathcal {W}}},{{\mathcal {W}}}'\subset {{\mathcal {V}}}$ be multivector fields restricted to S and P respectively. If $G_{{{\mathcal {W}}}}^*$ is a strongly connected graph and $G_{{{\mathcal {W}}}{\setminus }{{\mathcal {W}}}'}^*$ and $G_{{{\mathcal {W}}}'}^*$ are acyclic then every maximal solution in ${\text {cl}}S$ passes through ${\text {mo}}_X S\cup {\text {mo}}_X P$.

Proof

By the assumption, for every node in $G_{{{\mathcal {W}}}}^*$ we can find a cycle going through it. Thus, since $G_{{{\mathcal {W}}}{\setminus }{{\mathcal {W}}}'}^*$ is acyclic we get that P has to be non-empty.

Let $\varphi$ be a maximal solution in ${\text {cl}}S$. Suppose first that $\varphi$ is essential and ${\text {im}}\varphi \cap {\text {mo}}S=\emptyset$. It follows that ${\text {im}}\varphi \subset S$. By Proposition 2.3 we know that $\varrho :=\pi _{{\mathcal {W}}}(\varphi )$ is an infinite walk in $G_{{{\mathcal {W}}}}^*$. Every walk in $G_{{{\mathcal {W}}}{\setminus }{{\mathcal {W}}}'}^*$ is finite; therefore, we necessarily get $\varrho _i\in {{\mathcal {W}}}'$ for some $i\in {\mathbb {Z}}$ and, consequently, $\varphi (t)\in P$ for some $t\in {\mathbb {Z}}$. Since $G_{{{\mathcal {W}}}'}^*$ is acyclic we will find an $s\in {\mathbb {N}}$ such that $\varphi (s)\in P$ and $\varphi (s+1)\not \in P$. Hence, $\varphi (s+1)\in {\text {mo}}P$ by (6), what we needed to prove.

On the other hand, if $\varphi$ is a non-extendable finite path in ${\text {cl}}S$ with ${\text {dom}}\varphi =[a,b]$ then it follows that $\varphi (a),\varphi (b)\in {\text {mo}}S$. Otherwise, if $\varphi (a)\in S$, then by Corollary 2.4 we could extend $\varphi$ to a left-essential solution, which contradicts the assumption that $\varphi$ is maximal in ${\text {cl}}S$. Similarly, if $\varphi (b)\in S$ then $\varphi$ is right-extendable. $\square$

2.8 Admissible flow

Now, let X denote a topological space with a cellular decomposition ${\mathcal {X}}$, and let $\varphi :X\times {\mathbb {R}}\rightarrow X$ denote a flow on X. A cell $\sigma \in {\mathcal {X}}$ is called immediate future of a point $x\in X$ (see Mrozek et al. 2022, Sect. 5.1), if we have $\varphi (x,(0,\epsilon ))\subset \overset{\circ }{\sigma }$ for some $\epsilon >0$. In this case, it is written ${\text {ift}}_{\mathcal {X}}(x)=\sigma$. Symmetrically, a cell $\sigma \in {\mathcal {X}}$ is the immediate past for a point $x\in X$ if $\varphi (x,(-\epsilon , 0))\subset \overset{\circ }{\sigma }$ for some $\epsilon >0$. In this case, it is written ${\text {ipt}}_{\mathcal {X}}(x)=\sigma$. If for every point $x \in \overset{\circ }{\tau }$ we have that ${\text {ift}}_{\mathcal {X}}(x) = \sigma$ then we write ${\text {ift}}_{\mathcal {X}}(\tau ) = \sigma$. Similarly for ${\text {ipt}}_{\mathcal {X}}(\tau ) = \sigma$. We skip the subscript ${\mathcal {X}}$ if the cellular decomposition is clear from the context.

Definition 2.7

(Mrozek et al. 2022, Definition 5.17) We say that $\varphi$ is an admissible flow with respect to ${\mathcal {X}}$ if the following three conditions are satisfied:

• (i) For every point in X the immediate future and the immediate past are well-defined;

• (ii) For every point x in ${\text {Fr}}({\mathcal {X}})$ the immediate future of x is different from the immediate past of any backward solution through x;

• (iiii) For every $\sigma \in {\mathcal {X}}$ the strong exit and entry sets $\sigma ^-$ and $\sigma ^+$ are closed.

If, in addition, for every cell $\sigma$ its invariant part is empty unless $H_*(\sigma ,\sigma ^-)$ is nontrivial, then we say that $\varphi$ is strongly admissible. Conversely, we say that cellular decomposition ${\mathcal {X}}$ is (strongly) $\varphi$-admissible whenever the above conditions are satisfied (or f-admissible if we work with a vector field f inducing the flow $\varphi$).

Let ${\mathcal {X}}$ be a $\varphi$-admissible cellular decomposition of X. Define $V_\sigma := \{ \tau \in {\mathcal {X}}\mid {\text {ift}}(\tau ) = \sigma \}$. Then, there is a naturally induced multivector field (see Mrozek et al. 2022, Proposition 5.25):

$$\begin{aligned} {{\mathcal {V}}}:= \{V_\sigma \mid \sigma \in {\mathcal {X}}_{\text {top}}\}. \end{aligned}$$

We call ${{\mathcal {V}}}$ a $\varphi$-admissible multivector field on ${\mathcal {X}}$.

Definition 2.8

Let ${{\mathcal {V}}}$ be a $\varphi$-admissible multivector field on a strongly $\varphi$-admissible cellular decomposition of ${\mathcal {X}}$ and assume that ${\mathcal {A}}\subset {\mathcal {X}}$ is a combinatorial isolated invariant set. Then, we can define a combinatorial Poincaré section (Mrozek et al. 2022) as a non-empty, locally closed, and ${{\mathcal {V}}}$-compatible set ${\mathcal {P}}\subset {\mathcal {A}}$ satisfying the following conditions:

• (i) ${\mathcal {H}}={\text {cl}}_{{\mathcal {X}}}({\mathcal {A}}\cap {\text {mo}}_{\mathcal {X}}{\mathcal {P}})$ is non-empty and connected,

• (ii) ${\mathcal {R}}=({\text {cl}}_{\mathcal {X}}{\mathcal {A}}){\setminus } {\mathcal {H}}$ is connected,

• (iii) every maximal solution in ${\text {cl}}{{\mathcal {A}}}$ reaches ${\mathcal {H}}\cup {\text {mo}}_{\mathcal {X}}{\mathcal {A}}$,

• (iv) ${\mathcal {H}}\cap {\text {cl}}_{\mathcal {X}}{\text {bd}}_{\mathcal {R}}{\overline{{\mathcal {P}}}}=\emptyset$ where ${\overline{{\mathcal {P}}}}={\text {cl}}_{\mathcal {R}}{\mathcal {P}}$.

Recall that subscripts in the above topological operators specify the topology, e.g., ${\text {cl}}_{\mathcal {R}}$ is the closure with respect to topology induced by face relation within cells of ${\mathcal {R}}$, i.e., ${\mathcal {T}}_{\mathcal {R}}$. The intuition behind some sets constructed in the above definition are presented in Fig. 5.

Fig. 5

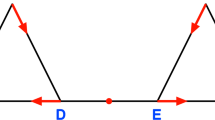
The gray region in the pictures represents a fragment of a Morse set containing a repelling periodic orbit. The simplices in the boundary of the Morse set (dashed lines) are not a part of the Morse set. Three marked multivectors $V_1=\{C, AC, CE, CD, ACD, CDE\}$, $V_2=\{AD, ABD\}$, and $V_3=\{DE, DEF\}$ form a combinatorial Poincaré section ${\mathcal {P}}=V_1\cup V_2\cup V_3$. The red region in the left panel shows the mouth of ${\mathcal {P}}$, i.e., ${\text {mo}}_{\mathcal {X}}{\mathcal {P}}$. The yellow and purple region in the right panel show sets ${\mathcal {H}}$ and ${\text {cl}}_{\mathcal {X}}{\text {bd}}_{\mathcal {R}}{\overline{{\mathcal {P}}}}$, respectively (colour figure online)

3 Construction of a flow-admissible cellular decomposition for a closed 2-manifold

Let X be a 2-dimensional closed manifold with a continuous vector field $\texttt{f}$ defined on it and let $\varphi$ be the flow on X induced by $\texttt{f}$. In this section we present the construction of an $\texttt{f}$-admissible cellular decomposition ${\mathcal {X}}$ of X and the related $\texttt{f}$-admissible multivector field. Moreover, we address the problem of finding a combinatorial Poincaré section for an isolated invariant set. These two procedures are the main computational steps leading to the automatic proof of the existence of a periodic orbit with respect to $\texttt{f}$ on X.

The starting point for the construction is a simplicial model of X, denoted by $\texttt{T}$. In particular, since X is a 2-dimensional manifold we assume that

$$\begin{aligned} \texttt{e}\in \texttt{Edges}(\texttt{T})\ \Rightarrow \ \#{\text {Cbd}}(\texttt{e})=2. \end{aligned}$$

(8)

3.1 Construction of the flow compatible multivector field

The main algorithm, ${\texttt{AdmissibleMVF}}$, constructs a multivector field $\texttt{mvf}$ on $\texttt{T}$ which can be directly used to produce an $\texttt{f}$-admissible cellular decomposition. Before moving to the algorithm let us introduce two auxiliary procedures. First of them, the IFT algorithm, determines the immediate future of an input transversal edge. The second algorithm, ${\texttt{FixConvexity}}$, helps us guarantee that the constructed partition is in fact a multivector field and implicitly controls the closedness of strong entry and exit sets of the created cells.

We aim to construct a multivector field that reflects the features of the continuous vector field on input. To this end, we rigorously, with the use of the interval arithmetic (Moore 1966) implemented in Kapela et al. (2021), verify the transversality of the edges of $\texttt{T}$ with respect to $\texttt{f}$. Transversal edges will constitute boundaries of the cells in the final cellular decomposition (some of them may end up in the interior of cells, though). Algorithm 1 ($\mathtt IFT$) returns a triangle that represents the direction of the flow for an input transversal edge $\texttt{t}\in \texttt{Edges}(\texttt{T})$. Note that the algorithm checks the direction of a single vector attached to the input edge $\mathtt e$ (line 6), but this is enough given that $\mathtt e$ is indeed transversal.

Algorithm 1

IFT—the immediate future of a transversal edge.

Further algorithms operate on a partition $\texttt{P}$ of a finite topological space $\mathtt X$ on input. In most cases, $\mathtt X$ is a finite topological space corresponding to a simplicial complex $\texttt{T}$, or its subspace, e.g., an isolated invariant set. We equip the partition object with method $\mathtt merge(V, W)$ that merges two elements $\mathtt V,W\in P$ into a single set. More precisely, calling $\mathtt merge(V, W)$ on partition $\mathtt P$ gives $\mathtt P.merge(V,W):=\{V\cup W\}\cup P{\setminus }\left\{ V,W\right\}$.

Algorithm 2 (FixConvexity) takes as input a partition $\mathtt P$ of a finite topological space $\mathtt X$ and an element of that partition $\mathtt V\in P$. In every loop of the algorithm, set $\mathtt U$ gathers elements of $\mathtt X$ that violate the convexity of $\mathtt V$ with respect to the poset induced by the topology of $\mathtt X$. Then, partition elements related to simplices in $\mathtt U$ get merged with $\mathtt V$. The procedure continues until $\mathtt V$ becomes convex (or $\mathtt V$ becomes locally closed, in topological terms). Note, that since we consider here at most 2-dimensional complexes only edges may fall into the set $\mathtt U$.

Proposition 3.1

Let $\mathtt P$ be a partition of a finite topological space $\left( \texttt{X}, \le \right)$ and let $\mathtt V\in P$. Algorithm $\mathtt FixConvexity$ stops. Moreover, let $\mathtt P' = FixConvexity(P, V)$. Then, there exists a locally closed element of partition $\mathtt W\in P'$ such that $\mathtt V\subset W$ and for every $\mathtt x\in P'{\setminus }\{W\}$ we get $\mathtt x\in P$.

Proof

Since elements of partition $\mathtt P$ only get merged there exists $\mathtt W\in P'$ such that $\mathtt V\subset W$. In particular, $\mathtt W$ is created as a result of merging $\mathtt V$ with other partition elements in lines 4–8. Since $\mathtt P'$ is initialized as a copy of $\mathtt P$ after each iteration of the loop in lines 4–8 another element of partition $\mathtt P$ is merged with $\mathtt V$. The loop stops when the resulting element $\mathtt W$ is convex, which occurs when $\mathtt U$ is empty (there is no edge that violates convexity). In the worst-case scenario, we get $\mathtt W = X$ when the algorithm stops, but the entire space is convex as well.

If an element from $\mathtt P'$ wasn’t merged during the loop, then it remains unchanged. Hence, it is also an element of $\mathtt P$. $\square$

Algorithm 2

FixConvexity—fix the convexity of a partition element.

The main algorithm, ${} \texttt{AdmissibleMVF}$, constructs a multivector field modeling the input vector field $\texttt{f}$. It starts with a trivial multivector field—a partition of $\texttt{T}$ into singletons, i.e., every singleton forms its own multivector, and then, it gradually expands multivectors to reflect the behavior of $\texttt{f}$. The algorithm consists of two major steps. The first part (lines 2–11) is focused on assigning edges to triangles according to the direction of the vector field and the transversality of edges. Then, we assign vertices to multivectors (lines 12–26). In this step we make sure that the resulting elements of the partition are indeed convex. Moreover, as we prove in the next Section, the multivector field will lead to a flow admissible cellular decomposition.

Algorithm 3

AdmissibleMVF

Proposition 3.2

After completing for loops in lines 3–11 of Algorithm $\texttt{AdmissibleMVF}$ partition $\texttt{mvf}$ of $\texttt{X}$ is a multivector field.

Proof

Before entering the first for loop in line 3 variable $\texttt{mvf}$ is a partition of $\texttt{T}$ into singletons. Variable $\texttt{mvf}$ is modified only by merging of two partition elements into one. Thus, $\texttt{mvf}$ is still a partition.

Throughout lines 3–11 only elements of the partition containing edges or triangles get merged. Hence, after finishing the second for loop every element $\mathtt V\in \texttt{mvf}$ is either a singleton consisting of a single vertex or a collection of edges and triangles. However, the only possibility to violate convexity in the case of 2-dimensional simplicial complex is to have a vertex and a triangle in $\texttt{V}$ without a certain edge. Consequently, $\texttt{mvf}$ is a partition of $\texttt{T}$ into a convex subsets, and therefore, a multivector field. $\square$

Theorem 3.3

Algorithm ${} \texttt{AdmissibleMVF}$ stops and returns a multivector field $\texttt{mvf}$ of $\texttt{X}$. Moreover, every multivector contains at least one 2-dimensional simplex.

Proof

Algorithm 3 stops, because all for loops are over finite collections. Method $\mathtt FixConvexity$ contains an additional inner loop, but, by Proposition 3.1, it also stops.

From Proposition 3.2 we know that mvf is a multivector field when entering the outer for loop in lines 12–26. We will show that through this loop mvf remains a partition and its elements remain convex sets.

Variable $\texttt{mvf}$ is a partition, because its elements are modified only in lines 16, 22 and 24. In lines 16 and 22 they are modified explicitly by merge operation which preserves partitions properties. In line 24, Algorithm 2 acts on $\texttt{mvf}$ also only via merge operation. Hence, we still get a partition.

Elements of $\texttt{mvf}$ are merged either in the for loop in lines 14–19 or in the if block in lines 20–25. In the first case we guarantee that the result of merging will be convex by checking the condition in line 15. In the second case, element $\mathtt [v]$ is first enlarged in the for loop in lines 21–23 by being merged with other elements of the partition, but then, by Algorithm 2 in line 24 and Proposition 3.1 we guarantee that $\mathtt [v]$ is convex ultimately. Hence the output of the algorithm is a multivector field on $\texttt{X}$.

The first part of the algorithm (for loops in lines 2 and 7) puts every edge to a multivector containing a triangle. The second part (for loops in line 12) provides that every vertex is assigned to some multivector with a triangle in it. Thus, it is impossible to have a multivector consisting only of edges and vertices. $\square$

Proposition 3.4

Let $\texttt{mvf}$ be a multivector field returned by Algorithm $\texttt{Admissible}$$\texttt{MVF}$. Every edge $\mathtt e\in {\text {bd}}V$ for $\mathtt V\in \texttt{mvf}$ is $\mathtt f$-transversal.

Proof

By contradiction, assume that there exists a multivector $\mathtt V\in mvf$ such that there exists an edge $\mathtt e\in {\text {bd}}V$ and e is not $\mathtt f$-transversal. If $\mathtt e\in {\text {bd}}V$ then by (5) there exist two triangles $\sigma \in V$ and $\tau \in T{\setminus } V$ such that $\mathtt e\in {\text {cl}}\sigma$ and $\mathtt e\in {\text {cl}}\tau$. It follows by (8) that $\{\sigma , \tau \}={\text {Cbd}}(\texttt{e})$. Lines 7–11 of Algorithm 3 provide that for every $\mathtt t \in {\text {Cbd}}(e)$ we have $\mathtt [e] = [t]$. Thus, $[\tau ]=[\texttt{e}]=[\sigma ]$ which contradicts that $\sigma \in \mathtt V$ and $\tau \not \in \mathtt V$. $\square$

3.2 Flow admissible cellular decomposition

Let $\texttt{mvf}$ be a multivector field returned by algorithm $\texttt{AdmissibleMVF}$. The necessary condition to construct a cellular decomposition of X based on $\texttt{mvf}$ is that every multivector $\texttt{V}\in \texttt{mvf}$ has a geometric realization $\left|\texttt{V}\right|_G$ homeomorphic to a 2-dimensional ball. In our settings, as a consequence of the Schoenflies theorem (Brown 1960) it is enough to check if $|{\text {bd}}_\texttt{T}\texttt{V}|$ is homoemorphic to a 1-sphere. This is algorithmically trivial as it is enough to verify that ${\text {bd}}\texttt{V}$ is connected and

$$\begin{aligned} \#({\text {Cbd}}{\texttt{v}}\cap {\text {bd}}\texttt{V})=2 \end{aligned}$$

(9)

for every $\texttt{v}\in \texttt{Verts}({\text {bd}}\texttt{V})$. It may happen, though, that this property does not hold. In that case, it is necessary to repeat the procedure with a different simplicial model $\texttt{T}$ of X. We recommend trying a finer resolution of $\texttt{T}$.

After the above verification, we are ready to construct an $\texttt{f}$-admissible cellular decomposition ${\mathcal {X}}$ of X. In particular, every multivector $\mathtt V\in \texttt{mvf}$ induces a 2-cell defined by $\left|\texttt{V}\right|_G$. Then, the induced cellular decomposition of X can be defined as

$$\begin{aligned} {\mathcal {X}}:= \bigcup _{\texttt{V}\in \texttt{mvf}} \{\left|\texttt{V}\right|_G\} \cup {\text {bd}}_\texttt{T}\texttt{V}, \end{aligned}$$

(10)

where by ${\text {bd}}_\texttt{T}\texttt{V}$ we get all 1- and 0-cells of ${\mathcal {X}}$. Clearly, we also have

$$\begin{aligned} \texttt{Edges}({\mathcal {X}})\subset \texttt{Edges}(\texttt{T}) \qquad \text {and}\qquad \texttt{Verts}({\mathcal {X}})\subset \texttt{Verts}(\texttt{T}). \end{aligned}$$

Proposition 3.5

Let ${\mathcal {X}}$ be a cellular decomposition of X induced by a multivector field $\texttt{mvf}$ returned by Algorithm 3. Let $s \in {\mathcal {X}}$ be such that $s\subset {\text {Fr}}{\mathcal {X}}$ and $\texttt{V}:=[s]_\texttt{mvf}$. Then:

• (i) If $s\in \texttt{Edges}({\mathcal {X}})$ then ${\text {ift}}_{\mathcal {X}}s = \left|\texttt{V}\right|_G$,

• (ii) If $s\in \texttt{Verts}({\mathcal {X}})$, $\mathtt e_1,e_2\in {\text {Cbd}}(s)\cap \texttt{Edges}({\mathcal {X}})$ and $\mathtt {\text {ift}}_{\mathcal {X}}e_1 ={\text {ift}}_{\mathcal {X}}e_2=\sigma \in {\mathcal {X}}_\textrm{top}$ then ${\text {ift}}_{\mathcal {X}}s=\sigma$,

• (iii) If $s \in \texttt{Verts}({\mathcal {X}})$ then ${\text {ift}}_{\mathcal {X}}s = \left|\texttt{V}\right|_G$.

Proof

(i) If $s\in \texttt{Edges}({\mathcal {X}})$ then also $s\in \texttt{Edges}(\texttt{T})$ and by Proposition 3.4 it follows that s is transversal. Thus, there exists a triangle $\mathtt t\in \texttt{Tops}(\texttt{T})$ such that ${\text {ift}}_\texttt{T}s=\texttt{t}$. In line 5 of Algorithm 3 we put s and $\texttt{t}$ into the same multivector. Hence, $\texttt{V}=[s]_\texttt{mvf}=[\texttt{t}]_\texttt{mvf}$ and consequently ${\text {ift}}_{\mathcal {X}}s = \left|\texttt{V}\right|_G$.

(ii) By Proposition 3.4 edges $\texttt{e}_1$ and $\texttt{e}_2$ are transversal. The rigorous computations guarantee that there exist vectors $n_1$ and $n_2$ normal to $\texttt{e}_1$ and $\texttt{e}_2$, respectively, such that for every $x\in \texttt{e}_1$ and $y\in \texttt{e}_2$ we have $n_1\cdot f(x)>0$ and $n_2\cdot f(y)>0$. It follows, that $n_1\cdot \texttt{f}(s)>0$ and $n_2\cdot \texttt{f}(s)>0$. Therefore, $f(s)\ne 0$ and points into the intersection of two half-planes defined by $\texttt{e}_1$ and $\texttt{e}_2$, i.e., $P:=\{x\in {\mathbb {R}}^2\mid (x-s)\cdot n_1> 0 \wedge (x-s)\cdot n_2 > 0\}$. There exists an $r>0$ such that ${\text {Ball}}(s,r)\cap P\subset \overset{\circ }{\sigma }$. Thus, the continuity of $\texttt{f}$ provides that we will find an $\varepsilon >0$ such that $\varphi (s,(0,\varepsilon ))\subset \overset{\circ }{\sigma }$.

(iii) Now, suppose that $s\in \texttt{Verts}({\mathcal {X}})$. Then, $s\in \texttt{Verts}(\texttt{T})$.

There exists a multivector $\mathtt V\in \texttt{mvf}$ such that $s\in \texttt{V}$. The fact that ${\text {bd}}_\texttt{T}\texttt{V}$ is a combinatorial circle provides that set ${\text {Cbd}}s\cap {\text {bd}}_\texttt{T}\texttt{V}$ consists of exactly two edges $\mathtt e_1$ and $\mathtt e_2$. The local closedness of $\texttt{V}$ imposes that $\mathtt e_1$ and $\mathtt e_2$ belongs to $\texttt{V}$ as well. It follows from (i) that ${\text {ift}}_{{\mathcal {V}}}\mathtt [e_1]_\texttt{mvf}={\text {ift}}_{{\mathcal {V}}}[e_2]_\texttt{mvf}=\sigma$, where $\sigma =\left|\texttt{V}\right|_G$. Hence, by (ii) we get ${\text {ift}}_{\mathcal {X}}(s)=\sigma = \left|[s]_\texttt{mvf}\right|_G$. $\square$

Recall that in Sect. 2.8 we defined a multivector field ${{\mathcal {V}}}$ induced by ${\mathcal {X}}$ by

$$\begin{aligned} {{\mathcal {V}}}:= \{V_\sigma \mid \sigma \in {\mathcal {X}}_{\text {top}}\}, \end{aligned}$$

(11)

where $V_\sigma := \{ \tau \in {\mathcal {X}}\mid {\text {ift}}_{\mathcal {X}}(\tau ) = \sigma \}$.

Note, that it follows from Proposition 3.5 that multivector field ${{\mathcal {V}}}$ is geometrically equivalent to the multivector field $\texttt{mvf}$ returned by Algorithm 3, i.e., for every $V\in {{\mathcal {V}}}$ there exists $\mathtt V\in \texttt{mvf}$ such that $\bigcup _{\sigma \in V} \overset{\circ }{\sigma }\ = \bigcup _{\texttt{s}\in \texttt{V}} \overset{\circ }{\texttt{s}}$. In practice, we can proceed without explicit construction of ${\mathcal {X}}$ and ${{\mathcal {V}}}$. It is enough to make computations using $\texttt{T}$ and $\texttt{mvf}$. Nevertheless, we need to verify that the related cellular decomposition ${\mathcal {X}}$ and multivector field ${{\mathcal {V}}}$ satisfies theoretical assumptions of the theory presented in Mrozek et al. (2022).

Proposition 3.6

Let ${\mathcal {X}}$ be a cellular decomposition of X induced by a multivector field $\texttt{mvf}$ returned by Algorithm 3. Let $s \in {\mathcal {X}}$ be such that $s\subset {\text {Fr}}{\mathcal {X}}$. Then:

• (i) If $s\in \texttt{Edges}({\mathcal {X}})$, then there exists a unique $\sigma \in {\mathcal {X}}_\textrm{top}$ such that $s\in {\text {mo}}[\sigma ]_{{\mathcal {V}}}$. Moreover, $\sigma$ is the immediate past of s, i.e., ${\text {ipt}}_{\mathcal {X}}(s)=\sigma$.

• (ii) If $s\in \texttt{Verts}({\mathcal {X}})$, $\mathtt e_1,e_2\in {\text {Cbd}}(s)\cap \texttt{Edges}({\mathcal {X}})$ and $\mathtt {\text {ipt}}_{\mathcal {X}}e_1 ={\text {ipt}}_{\mathcal {X}}e_2=\sigma$ then ${\text {ipt}}_{\mathcal {X}}s=\sigma$,

• (iii) If $s \in \texttt{Verts}({\mathcal {X}})$, then there exists a unique $\sigma \in {\mathcal {X}}_\textrm{top}$ such that $\#({\text {mo}}[\sigma ]_{{\mathcal {V}}}\cap {\text {Cbd}}_{\mathcal {X}}s)=2$ and $s\in {\text {mo}}[\sigma ]_{{\mathcal {V}}}$. Moreover, ${\text {ipt}}_{\mathcal {X}}(s)=\sigma$.

Proof

(i) By Proposition 3.4 we know that edge s is transversal and, therefore, there exists a unique $\texttt{t}\in \texttt{T}$ such that ${\text {ipt}}_\texttt{T}(s)=\texttt{t}$. Define $\texttt{V}:=[\texttt{t}]_\texttt{mvf}$ and $\sigma :=\left|\texttt{V}\right|_G\in {\mathcal {X}}_\textrm{top}$. Then, ${\text {ipt}}_{\mathcal {X}}(s)=\sigma$. We claim that $s\not \in [\sigma ]_{{\mathcal {V}}}$. Assume the contrary, then, by (11), we can find $\texttt{t}'\in \texttt{Tops}(\mathtt V)$ such that ${\text {ift}}_\texttt{T}(s)=\mathtt t'$. If $\mathtt t=t'$ then ${\text {ipt}}_\texttt{T}(s)={\text {ift}}_\texttt{T}(s)$ which contradicts the transversality assumption about s. Thus, $\mathtt t\ne t'$; but then we get ${\text {Cbd}}_\texttt{T}(s)=\{\texttt{t},\texttt{t}'\}\subset \texttt{V}$. Hence, $s\not \in {\text {bd}}_\texttt{T}\texttt{V}$ (s is an internal edge) and, consequently, $s\not \in {\mathcal {X}}$ (see (10)) which is a contradiction. We proved that $s\not \in [\sigma ]_{{\mathcal {V}}}$. Moreover, since $s\in {\text {cl}}_\texttt{T}\texttt{t}$ we get $s\in {\text {cl}}_{\mathcal {X}}\sigma$ which implies $s\in {\text {mo}}[\sigma _\texttt{V}]_{{\mathcal {V}}}$.

(ii) We prove this property using the same reasoning as in the proof of Proposition 3.5(ii).

(iii) Let $E_s:={\text {Cbd}}_{\mathcal {X}}s\cap \texttt{Edges}({\mathcal {X}})$, $C_s:={\text {Cbd}}_{\mathcal {X}}s\cap {\mathcal {X}}_\textrm{top}$ and $\xi (\sigma ):=\#({\text {mo}}[\sigma ]_{{\mathcal {V}}}\cap {\text {Cbd}}_{\mathcal {X}}s)$. By the construction of ${{\mathcal {V}}}$ there exists a unique $\tau \in C_s$ such that $s\in [\tau ]_{{\mathcal {V}}}$ and ${\text {ift}}_{\mathcal {X}}(s)=\tau$. The local closedness of $[\tau ]_{{\mathcal {V}}}$ and (9) imply that there are exactly two edges $e_0,e_1\in [\tau ]_{{\mathcal {V}}}\cap E_s$ and $\xi (\tau )=0$. In particular, ${\text {ift}}_{\mathcal {X}}(e_0)={\text {ift}}_{\mathcal {X}}(e_1)=\tau$. If there would exists another $\tau '\in C_s{\setminus }\{\tau \}$ such that $\xi (\tau ')=0$ then we have $\{e_0',e_1'\}=[\tau ']_{{\mathcal {V}}}\cap E_s$, ${\text {ift}}_{\mathcal {X}}(e_0')={\text {ift}}_{\mathcal {X}}(e_1')=\tau '$; but by Proposition 3.5 (ii) we get ${\text {ift}}_{\mathcal {X}}(s)=\tau '\ne \tau$ which is a contradiction. Thus, for every $\sigma \in C_s{\setminus }\{\tau \}$ we have $\xi (\sigma )>0$. Moreover, $\xi (\sigma )\le 2$ because ${\text {mo}}[\sigma ]_{{\mathcal {V}}}\subset {\text {bd}}_{\mathcal {X}}\sigma$ and (9).

Note that $N:=\#E_s=\# C_s$. Since $\sigma , e_0, e_1\in [\tau ]_{{\mathcal {V}}}$ we are left with $N-2$ edges to be assigned to $N-1$ 2-cells. If we try to assign at most 1 edge to each of the remaining 2-cells, we still end up with exactly one ($\text {N}-1 - (\text {N}-2) = 1$) 2-cell with 0 assigned edges. Thus, there exists a $\sigma _s\in C_s{\setminus }\{\tau \}$ such that $\xi (\sigma _s)=2$. The cell $\sigma _s$ is unique. Otherwise, then there would exists another $\tau '$ such that $\xi (\tau ')=0$, but we already excluded that case. By (i) if $e\in {\text {mo}}[\sigma _s]\cap {\text {Cbd}}_{\mathcal {X}}s$ then ${\text {ipt}}_{\mathcal {X}}(e)=\sigma _s$ and $s\in {\text {mo}}[\sigma ]_{{\mathcal {V}}}$ because ${\text {mo}}[\sigma ]_{{\mathcal {V}}}$ is closed. Finally, from (ii) it follows that ${\text {ipt}}_{\mathcal {X}}(s)=\sigma _s$. $\square$

Proposition 3.7

Let $x\in {\text {Fr}}{\mathcal {X}}$ then ${\text {ift}}_{\mathcal {X}}x\ne {\text {ipt}}_{\mathcal {X}}x$.

Proof

Let $s\in {\mathcal {X}}$ such that $x\in \overset{\circ }{s}$. Let assume by contradiction that there exists $\sigma \in {\mathcal {X}}_\textrm{top}$ such ${\text {ift}}_{\mathcal {X}}s= {\text {ipt}}_{\mathcal {X}}s=\sigma$. By the construction of ${{\mathcal {V}}}$, if ${\text {ift}}_{\mathcal {X}}s= \sigma$ then $[s]_{{\mathcal {V}}}=[\sigma ]_{{\mathcal {V}}}$. Moreover, by Proposition 3.6, if ${\text {ipt}}_{\mathcal {X}}s=\sigma$ then $s\in {\text {mo}}[\sigma ]_{{\mathcal {V}}}$ which contradicts $[\sigma ]_{{\mathcal {V}}}\cap {\text {mo}}[\sigma ]_{{\mathcal {V}}}=\emptyset$. Thus, we have ${\text {ift}}_{\mathcal {X}}s\ne {\text {ipt}}_{\mathcal {X}}s$ which implies ${\text {ift}}_{\mathcal {X}}x\ne {\text {ipt}}_{\mathcal {X}}x$. $\square$

Proposition 3.8

Let ${\mathcal {X}}$ be a cellular decomposition of X induced by a multivector field $\texttt{mvf}$ returned by Algorithm 3 from a continuous flow $\varphi$. Let $\sigma \in {\mathcal {X}}_\textrm{top}$ and $x\in \left|{\text {bd}}_{\mathcal {X}}\sigma \right|$. Then:

• (i) ${\text {ift}}_{\mathcal {X}}x= \sigma \implies x\not \in \sigma ^-$,

• (ii) ${\text {ift}}_{\mathcal {X}}x\ne \sigma \implies {x}\in \sigma ^-$,

• (iii) ${\text {ipt}}_{\mathcal {X}}x= \sigma \implies x\not \in \sigma ^+$,

• (iv) ${\text {ipt}}_{\mathcal {X}}x\ne \sigma \implies {x}\in \sigma ^+$.

Proof

(i) ${\text {ift}}_{\mathcal {X}}x=\sigma$ implies that there exists $\epsilon >0$ such that $\varphi (x,(0,\epsilon ))\subset \overset{\circ }{\sigma }$. Therefore, we get $\varphi (x,(0,t))\cap \sigma \ne \emptyset$ for every $t>0$. This implies that $x\not \in \sigma ^-$.

(ii) ${\text {ift}}_{\mathcal {X}}x\ne \sigma$ implies that there exists $\sigma _x\in {\mathcal {X}}$ such that ${\text {ift}}_{\mathcal {X}}x=\sigma _x$ and $\sigma _x\ne \sigma$. Since ${\text {ift}}_{\mathcal {X}}x=\sigma _x$ there exists $\epsilon >0$ such that $\varphi (x,(0,\epsilon ))\subset \overset{\circ }{\sigma _x}$. This implies that $\varphi (x,(0,\epsilon ))\cap \sigma =\emptyset$ and ${x}\in \sigma ^-$.

(iii) and (iv) are proven using the same reasoning as (i) and (ii) but with $(\epsilon ,0)$, $\epsilon <0$ instead of $(0,\epsilon )$, $\epsilon >0.$ $\square$

Proposition 3.9

Let ${\mathcal {X}}$ be a cellular decomposition of X induced by a multivector field $\texttt{mvf}$ returned by Algorithm 3. Then for every $\sigma \in {\mathcal {X}}_\text {top}$, $\sigma ^+$ and $\sigma ^-$ are closed.

Proof

Let $x\in \left|{\text {bd}}_{\mathcal {X}}\sigma {\setminus } {\text {mo}}[\sigma ]_{{\mathcal {V}}}\right|$. From definition of ${{\mathcal {V}}}$ and Proposition 3.8(i) we have ${\text {ift}}_{\mathcal {X}}x=\sigma$ and $x\not \in \sigma ^-$.

Therefore, since $\sigma ^-\subset \left|{\text {bd}}_{\mathcal {X}}\sigma \right|$ it follows that $\sigma ^-\subset \left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}\right|$. Now let $x\in \left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}\right|$. It follows that ${\text {ift}}_{\mathcal {X}}x\ne \sigma$ and by Proposition 3.8(ii) we get $x\in \sigma ^-$ which implies $\left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}\right|\subset \sigma ^-$. In conclusion, $\sigma ^-=\left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}\right|$. Since ${\text {mo}}[\sigma ]_{{\mathcal {V}}}$ is closed, $\sigma ^-$ is closed.

In a similar way, we will prove that $\sigma ^+$ is closed by showing that $\sigma ^+=\left|{\text {cl}}_{\mathcal {X}}({\text {bd}}_{\mathcal {X}}\sigma {\setminus } {\text {mo}}[\sigma ]_{{\mathcal {V}}})\right|$. Define $\eta (\sigma ):={\text {bd}}_{\mathcal {X}}\sigma {\setminus } {\text {mo}}[\sigma ]_{{\mathcal {V}}}$ and let $x\in \left|{\text {cl}}_{\mathcal {X}}(\eta (\sigma ))\right|$. If $x\in \left|\eta (\sigma )\right|$ then ${\text {ift}}_{\mathcal {X}}x=\sigma$. From Propositions 3.7 and 3.8(iv) we have ${\text {ipt}}_{\mathcal {X}}x\ne \sigma$ and $x\in \sigma ^+$. If $x\in \left|{\text {cl}}_{\mathcal {X}}(\eta (\sigma )){\setminus }\eta (\sigma )\right|$, then $x\in \left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}\cap \texttt{Verts}({\mathcal {X}})\right|$ and $\#({\text {mo}}[\sigma ]_{{\mathcal {V}}}\cap {\text {Cbd}}_{\mathcal {X}}x)=1$. From Propositions 3.6(iii) and 3.8(iv) we get ${\text {ipt}}_{\mathcal {X}}x\ne \sigma$ and $x\in \sigma ^+$. Therefore, $\left|{\text {cl}}_{\mathcal {X}}(\eta (\sigma ))\right|\subset \sigma ^+$. Now let $x\in \left|{\text {mo}}[\sigma ]_{{\mathcal {V}}}{\setminus } {\text {cl}}_{\mathcal {X}}(\eta (\sigma ))\right|$, then from Propositions 3.6 and 3.8(iii) we get ${\text {ipt}}_{\mathcal {X}}x=\sigma$ which implies that $x\not \in \sigma ^+$. Since $\sigma ^+\subset \left|{\text {bd}}_{\mathcal {X}}\sigma \right|$ we get $\sigma ^+\subset \left|{\text {cl}}_{\mathcal {X}}(\eta (\sigma ))\right|$ which finally implies $\sigma =\left|{\text {cl}}_{\mathcal {X}}(\eta (\sigma ))\right|$. $\square$

From Propositions 3.5, 3.6, 3.7 and 3.9 we can immediately show the following result.

Corollary 3.10

If a multivector field $\texttt{mvf}$ returned by Algorithm 3 induces a cellular decomposition ${\mathcal {X}}$ given by (10), then the flow $\varphi$, induced by the vector field $\texttt{f}$, is admissible with respect to ${\mathcal {X}}$.

3.3 Construction of a combinatorial Poincaré section

We recall that $\varphi$ is a flow related to the input vector field $\texttt{f}$. Let ${\mathcal {X}}$ be a $\varphi$-admissible cellular decomposition of X constructed as in (10). Moreover, by ${{\mathcal {V}}}$ we denote the $\varphi$-admissible multivector field induced by ${\mathcal {X}}$ (see (11)). Let ${\mathcal {A}}\subset {\mathcal {X}}$ be an isolated invariant set for ${{\mathcal {V}}}$ with the Conley index of a hyperbolic periodic orbit and let $\texttt{M}\subset {{\mathcal {V}}}$ be a multivector field restricted to ${\mathcal {A}}$. We additionally assume that $G_{\texttt{M}}^*$ is a strongly connected graph (which, by Proposition 2.5, is immediate if the ${\mathcal {A}}$ is a minimal Morse set). Here, we present how to find a combinatorial Poincaré section for ${\mathcal {A}}$.

Algorithm PoincaréSection describes the embraced strategy. We start by (randomly) choosing a multivector $\mathtt P:=[p]_\texttt{M}\in M$ that will serve as a seed for the Poincaré section construction. Then, we follow a greedy propagation extending $\mathtt P$ in the direction perpendicular to the flow (lines 6–8) while protecting its convexity (line 9). Note that $\texttt{M}$ is a partition of ${\mathcal {A}}\subset {\mathcal {X}}$; hence, the use of $\mathtt merge$ in line 7. The remaining part of the procedure verifies if the constructed set satisfies conditions for the combinatorial Poincaré section. The algorithm either returns a combinatorial Poincaré section $\texttt{P}$ of ${\mathcal {A}}$ or returns $\mathtt FAILURE$. In the latter case, we reinitialize the algorithm with another seed multivector until we succeed.

By $\mathtt {\text {mo}}_M$ we mean the mouth with respect to the finite topology induced by $\bigcup \texttt{M}$. Moreover, for $\mathtt P\in M$ we define:

$$\begin{aligned} \mathtt {\text {ft}}_{M}(P):= \{V \in M\mid V\cap {\text {mo}}_{M} P \ne \emptyset \}. \end{aligned}$$

Algorithm 4

PoincaréSection

Proposition 3.11

Algorithm 4 stops. It either returns FAILURE or computes a combinatorial Poincaré section.

Proof

A restricted multivector field $\texttt{M}$ contains a finite number of multivectors. We successively merge $\mathtt [p]_M$ with other multivectors in lines 7 and 9. Multivector $\mathtt [p]_M$ cannot fall into set $\mathtt N$ because of the definition of $\mathtt I$ (line 3). Thus, every multivector can be merged only once and the repeat-until loop stops. Consequently the entire algorithms terminates.

One can easily verify that $\mathtt H\cup {\text {mo}}_{\mathcal {X}}{\mathcal {A}}= {\text {mo}}_{\mathcal {X}}\texttt{P}\cup {\text {mo}}_{\mathcal {X}}{\mathcal {A}}$. Then, the check in line 15 verifies condition (iii) of Definition 2.8 via Proposition 2.6.

Set $\mathtt P$ is clearly ${{\mathcal {V}}}$-compatible as a union of multivectors. In the line 18 we check if P satisfies conditions (i), (ii), and (iv) of Definition 2.8.

If the conditions in lines 15 and 18 are satisfied, then Algorithm 4 returns a Combinatorial Poincaré section $\texttt{P}$ of ${\mathcal {A}}$. In other case, the algorithm returns FAILURE. $\square$

4 Construction of a transversal polytope around equilibrium points

Consider a smooth vector field $f:{\mathbb {R}^d}\rightarrow {\mathbb {R}^d}$ and the associated differential equation $x' = f(x)$ for $x \in {\mathbb {R}^d}$. Assume that $x_0$ is an equilibrium point of f, that is, $f(x_0)=0$. In this section, we present a method for the construction of a convex polytope containing point $x_{0}$ in its interior such that f is transversal to its boundary. We call it a transversal polytope (for f) around $x_0$.

A strong rotation around an equilibrium may cause a strong propagation, especially in the context of Algorithm 2. We can include the transversal polytopes in triangulations passed to algorithms in the previous section to weaken this effect.

Let $f_0(x) = A (x -x_0)$, where $A = D f(x_0)$, be the linearisation of f around a equilibrium point $x_0$. To achieve our goal, we first construct a transversal polytope around the origin of the linear system $f_A(x) = A x$ and then, if necessary, we shrink it (depending on the size of the linearisation errors) and translate it to $x_0$.

4.1 Transversal polytopes for linear vector fields

In this section, we assume that a vector field is linear, that is, $f_A(x)=A x$ where $A \in {\mathbb {R}}^{d \times d}$. Moreover, we assume that matrix A is diagonalizable over the complex field. Therefore, there exists a real eigenbasis (a real matrix $Q\in {\mathbb {R}}^{d\times d}$) such that the Jordan matrix $J=Q^{-1} A Q$ contains only simple Jordan blocks on the diagonal: $[ \lambda ]$ for the real eigenvalue $\lambda$ or $\begin{pmatrix} a &{} -b \\ b &{} a \end{pmatrix}$ for a pair of conjugate complex eigenvalues $\lambda = a \pm i b$.

We first construct a transversal polytope for a vector field in the "Jordan" coordinates. It is easier because the vector field is decomposed into independent 1- or 2-dimensional vector fields. Then, we transform it to the original coordinates. Since transversality does not depend on the coordinate frame, we have the following straightforward proposition.

Proposition 4.1

Let $f_A(x)=A x$ be a linear vector field, $Q\in {\mathbb {R}^{d \times d}}$ be an invertible matrix, and P be a polytope around $x_0=0$, which is transversal to $f_A$. Then, $Q\cdot P$, the image of P via Q, is a transversal polytope for the linear vector field ${\hat{f}}(y)=Q\cdot A \cdot Q^{-1} y$ at $y_0=0$.

Algorithm 5

Polytope—transversal polytope for $2\times 2$ matrix.

Theorem 4.2

If A is a $2\times 2$ matrix with complex eigenvalues $\lambda =a\pm ib$ with $a,b\ne 0$ and $r>0$ then the output of Algorithm 5 is a transversal polytope around origin for a vector field $f_A(x)=Ax$.

Proof

Since matrix A has eigenvalues $\lambda =a\pm ib$, there exists a transition matrix Q such that the Jordan matrix is $J=\begin{pmatrix} a &{} -b \\ b &{} a \end{pmatrix}$. The vector field $f_J(x,y) = J(x,y)^T$ is transversal to any circle with a center at the origin (see Theorem 22.3 in Arnold (1992)). We will approximate the circle of radius r with an inscribed polytope that is transversal to $f_J$.

First, for fixed $y_0$ we search for a point $(x_0,y_0)$ such that the vector field is parallel to the line $y=y_0$ (non transversal). We have $f_J(x_0, y_0)=(a x_0 - b y_0, b x_0 + a y_0)$. The vector field is non-transversal if $b x_0 + a y_0 =0$, which yields $x_0=-\dfrac{a}{b}y_0$. Therefore, the open segment from the point $(-x_0,y_0)$ to $(x_0,y_0)$ is transversal to $f_J$. This gives the maximal angle $\alpha _{max}$ of the arc that can be replaced by this segment as $\alpha _{max}=2\arctan \left| \dfrac{x_0}{y_0}\right| =2\arctan \left|\dfrac{a}{b}\right|$.

Since the vector field $f_J$ is invariant under rotation, if we rotate a transversal segment around the origin, we obtain another transversal segment. We need at least $N=\left\lfloor \dfrac{2\pi }{\alpha _{max}}\right\rfloor +1$ segments to cover the entire circle. Let $C = {\text {conv}}\{(r \cos (k\alpha ), r\sin (k\alpha )), k=0,..N{-}1\}$ where $\alpha = \dfrac{2 \pi }{N} < \alpha _{max}$, be regular N-gon inscribed in the circle of radius r. Then polytope C is transversal to $f_J$ and according to Proposition its image 4.1$Q\cdot C$ is a transversal polytope for the vector field $f_A$. $\square$

Algorithm 6

TransversalPolytope—a transversal polytope for the linear vector field in ${\mathbb {R}^d}$

Theorem 4.3

If the matrix $A\in {\mathbb {R}^{d \times d}}$ is diagonalizable and all the eigenvalues of A have a nonzero real part, and $r>0$, then the output of Algorithm 6, TransversalPolytope(A,r), is a transversal polytope enclosing the origin for the vector field $f_A(x) = A x$.

Proof

Diagonalizable matrix A can be decomposed (see Horn and Johnson 2012, Corollary 3.4.1.10) into $QJQ^{-1}$ where $Q\in {\mathbb {R}^{d \times d}}$ is an invertible transition matrix, J is the real Jordan form of A

$$\begin{aligned}J =\begin{pmatrix} J_1 &{} 0 &{} \dots &{} 0 \\ 0 &{} J_2 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} 0 \\ 0 &{} 0 &{} \dots &{} J_n \end{pmatrix} \end{aligned}$$

where real Jordan blocks $J_k$ are: $1{\times }1$ blocks consisting of a single real eigenvalue $(\lambda )$ or $2{\times }2$ blocks of the form $\begin{pmatrix} a &{} -b \\ b &{} a \end{pmatrix}$ that correspond to a eigenvalues $a \pm ib$.

The matrix J is the block diagonal; therefore, the vector field $f_J(x)=J x$ can be decomposed into the Cartesian product of independent linear vector fields $f_{J_k}$ generated by blocks $J_k$ and we can construct a transversal polytope $P_k$ for each block separately. For 2-dimensional blocks, we use Algorithm 5 and set $P_k=$Polytope(B,r). For 1-dimensional blocks $J_k=(\lambda _k)$ we set polytope $P_k = [-r,r]$. Since $f_{J_k}(\pm r) = \pm \lambda _r r \ne 0$, then the polytope $P_k$ is transversal to $f_{J_k}$.

The polytope P constructed in Algorithm 6, as the Cartesian product of transversal polytopes $P_k$, is transversal to $f_J$. Finally, we transform P using the transition matrix Q and obtain a transversal polytope for $f_A$ around the origin (see Corollary 4.1). $\square$

4.2 Transversal polytopes for general $C^2$ vector fields

Let us now consider a general $C^2$, possibly nonlinear, vector field $f:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}^{d}$ and the associated differential equation $x' = f(x)$ for $x \in {\mathbb {R}}^{d}$. Let $x_0$ be a equilibrium point of f and let A denote the matrix of the linearized system around $x_0$, that is, $f_0(x) = A(x-x_0)$. In general, a transversal polytope generated by Algorithm 6 for a linear system $f_A(y)=A y$ and translated to $x_0$ does not have to be transversal to f. We will show that if the size of a polytope is small enough (which means that we are close enough to $x_0$) then the polytope is also transversal to the nonlinear vector field f.

Theorem 4.4

Let the vector field $f:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}^{d}$ be a $C^2$ function with a equilibrium point $x_0$ and let A denote the Jacobian matrix $Df(x_0)$. If matrix A is diagonalisable, then there exists $r>0$ such that TransversalPolytope(A,r) returned by Algorithm 6 and translated to $x_0$ is a transversal polytope for f around $x_0$.

Proof

From Theorem 4.3, since matrix A is diagonalizable, it follows that for any size $r>0$ algorithm TransversalPolytope(A,r) returns a transversal polytope for the linearized vector field around the origin. Let denote it by $P^r$ and let $E_{P^r}$ denotes a set of edges of a polytope $P^r$. We define

$$\begin{aligned} \varepsilon _r = \inf _{\sigma \in E_{P_r}}\inf _{y\in \sigma }\left\| \langle A y,v_\sigma \rangle \right\| , \end{aligned}$$

where $v_\sigma$ is a normal vector to $\sigma$. Since $P^r$ is a transversal polytope, we have $\varepsilon _r>0.$

Observe that, by a construction, we can simply rescale one polytope to obtain another, that is, we have $P^{r} = \{ r x \mid x\in P^1\}$ and since corresponding edges of $P^r$ and $P^1$ are parallel we get

$$\begin{aligned} \varepsilon _r = \inf _{\sigma \in E_{P_1}}\inf _{y\in \sigma }\left\| \langle A r y,v_\sigma \rangle \right\| = r \inf _{\sigma \in E_{P_1}}\inf _{y\in \sigma }\left\| \langle A y,v_\sigma \rangle \right\| = r \varepsilon _1, \end{aligned}$$

Let $P^r_{x_0}$ denotes polytope $P^r$ translated to $x_0$, that is, $P^r_{x_0} = \{ x + x_0 \mid x \in P^r \}$. There exist $\delta >0$ such that $P^r_{x_0} \subset B(x_0,r \sigma )$, since sizes of polytopes scale linearly with r. We define

$$\begin{aligned} M = \sup \left\{ \left|\dfrac{\partial ^{2}f_i }{\partial x^k}(x)\right| \mid x\in B(x_0,\delta ), \left|k\right|=2, i=1,\dots ,d\right\} , \end{aligned}$$

Using the first-order Taylor expansion around equilibrium point $x_0$, we get

$$\begin{aligned} f(x)= Df(x_0) (x - x_0) + R(x), \end{aligned}$$

(12)

where $R(x)=(R_1(x), R_2(x),\dots ,R_d(x))$ and

$$\begin{aligned} R_{i}(x)=\sum _{\left|k\right|=2}\dfrac{\partial ^{2}f_i }{\partial y^k}(\mu _i)\dfrac{(y-x_0)^k}{k!} \text{ for } \text{ some } \mu _i \in [x_0, y]. \end{aligned}$$

If $r\le 1$ then for any $x\in P^r_{x_0} \subset B(x_0, r \sigma )$ we have

$$\begin{aligned} \left| R_{i}(x)\right|&\le M \left|\sum _{\left| k \right| =2}\dfrac{(y-x_0)^k}{k!}\right| \le M d^2 \sup _{\left| k \right| =2}\left|\dfrac{(y-x_0)^k}{k!} \right| \le M d^2 \left\| y-x_0\right\| ^2 \le M d^2 r^2 \sigma ^2 \end{aligned}$$

For any $x\in \sigma$, where $\sigma$ is an edge of the polytope $x_0 + P_r$, and $v_\sigma$ is a unit normal vector to $\sigma$, we have

$$\begin{aligned} \left| \langle f(x),v_\sigma \rangle \right|&= \left|\langle Df(x_0)(x-x_0),v_\sigma \rangle + \langle f(x) - Df(x_0)(x-x_0),v_\sigma \rangle \right|\\&\ge \left| \langle Df(x_0)(x-x_0),v_\sigma \rangle \right|-\left|\langle R(x),v_\sigma \rangle \right|\\&\ge \varepsilon _r - \left\| R(x)\right\| \cdot \left\| v_\sigma \right\| \\&\ge r \varepsilon _1 - M d ^2 r^2 \delta ^2 \end{aligned}$$

Finally, if we take

$$\begin{aligned} r<\min \left\{ \dfrac{\varepsilon _1}{M d^2 \delta ^2}, 1\right\} , \end{aligned}$$

(13)

then $\langle f(x),v_\sigma \rangle \ne 0$ for all point on the boundary of $P_{x_0}^{r}$. Therefore $P_{x_0}^{r}$ is a transversal polytope around $x_0$ for the vector field f. $\square$

Remark 4.5

Observe, that from the proof of Theorem  4.3 by the equation (13) we get explicit bounds for the size of the polytope constructed for linearization that remains transversal also for nonlinear flow.

Remark 4.6

For general nonlinear systems in higher dimensions applying algorithm TransversalPolytope(A,r) faces few problems:

• We are not able to get exact equilibrium points and hence we have only an approximated matrix of a linearization A,

• Available numerical algorithms provide only approximate Jordan form decomposition,

• Based on approximated data the bound for size r given by (13) do not guarantee transversality.

Therefore in practice we use Algorithm 6 to generate polytope around approximated equilibrium point and then using interval arithmetics we rigorously check if it contains single equilibrium point and if it is transversal to the flow. If it fails, we try to decrease size of the polytope or improve equilibrium point estimates.

4.3 Example

Consider Van der Pol system (see (van der Pol 1926) and (de Almeida Casaleiro et al. 2019) for more modern rendition):

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = -y\\ y'=(x^2-1)y+x \end{array}\right. } \end{aligned}$$

(14)

One can show that (0, 0) is the only equilibrium point of this system. The matrix of a linearized system is

$A=\begin{pmatrix} 0 &{} -1 \\ 1 &{} -1 \end{pmatrix}$

The eigenvalues of A are $\lambda _{1,2}=-\frac{1}{2}\pm \frac{\sqrt{3}}{2}i$. The real Jordan matrix J and the corresponding transition matrix Q are given by

$$\begin{aligned} J=\begin{pmatrix} -\frac{1}{2} &{} -\frac{\sqrt{3}}{2} \\ \frac{\sqrt{3}}{2} &{} -\frac{1}{2} \end{pmatrix} \ \ \ \quad \ \ \ Q = \begin{pmatrix} \frac{1}{2} &{} -\frac{\sqrt{3}}{2} \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

Algorithm 5 will compute $\alpha =2\arctan \left( -\dfrac{a}{b}\right) =\dfrac{\pi }{3}$ and $N =\left\lfloor \left|\dfrac{2\pi }{\alpha }\right|\right\rfloor +1$$= 7$ and therefore in the Jordan coordinates we obtain regular polytope with 7 faces that is inscribed in the circle with given radius r (see Fig. 6 (left)). The Algorithm 5 returns the image of that regular polytope through the transition matrix Q, shown in Fig. 6 (middle). This polytope is also transversal for the original Van der Pol system, see Fig. 6 (right), since at this scale it is very well approximated by its linearization.

Fig. 6

Transversal polytope with 7 faces and radius $r=0.2$ for Left: the linear system given by the Jordan matrix J. Center: the linearized Van der Pol system. Right: the Van der Pol system. It is very well approximated by linearization at this scale

Fig. 7

Polytopes returned by Algorithm 5 for the Van der Pol system for $r\in \{0.2, 0.5, 1\}$. Only the smallest one is a transversal polytope

The returned polytope is always transversal to a linearized vector field, but according to Theorem 4.4 it will be also transversal to the vector field of the Van der Pol system if radius r is small enough. In Fig. 7 we clearly see that for $r=1$ and $r=0.5$ some of the edges are not transversal to the flow but we get a transversal polytope for radius $r=0.2$.

5 Complete algorithm pipeline and applications

5.1 Compactification of a space

Algorithm 3 presented in Sect. 3 assumes that the input simplicial complex is a combinatorial model of a closed 2-manifold. In order to make the method useful also for planar bounded regions we endow the computations with a conceptual preprocessing.

Let f be a continuous planar flow and $X\subset {\mathbb {R}}^2$ be a region of interest homeomorphic to a 2-ball. Let $\texttt{T}$ be a triangulation of X. The phase space, that is ${\mathbb {R}}^2$, can be compactified into ${\mathbb {S}}^2$ by adding a point at infinity. We can modify f to a vector field ${\hat{f}}$ defined on ${\mathbb {S}}^2$ so that $\infty$ becomes an equilibrium point for ${\hat{f}}$ and $f={\hat{f}}$ on X. We can attach a cone on top of $\texttt{T}$ (see Fig. 8) which gives us a combinatorial model of ${\mathbb {S}}^2$. Denote the extended triangulation by ${\hat{\texttt{T}}}$. The tip of the cone represents the equilibrium point at infinity. Since f and ${\hat{f}}$ coincide on X, conclusions may be applied to the original vector field f as long as the results concern solutions located in the region X.

Edges being cofaces of point $\infty$ are non-transversal as they contain the equilibrium point. It follows that all simplices in the open star of $\infty$ will fall into a single multivector ${\hat{V}}$ of the original multivector field. All other simplices that the algorithm will adjoin to ${\hat{V}}$ will be excluded from the further analysis as ${\hat{V}}$ will be a multivector encapsulating the modified part of the flow.

Fig. 8

Extended simplicial model of space ${\hat{X}}$ obtained by the addition of the cone to the boundary of the complex in the left panel

5.2 Computer-assisted proof of the existence of a periodic orbit in a planar dynamical system

Let us briefly summarize constructions presented in this work by putting them together into a single pipeline that can be used to rigorously prove the existence of a periodic orbit in a planar dynamical system induced by a $C^2$ vector field $f:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$.

• (1) Choose a subset X of ${\mathbb {R}}^2$ homeomorphic to a 2-ball to be studied, e.g., a rectangle.

• (2) Find all equilibrium points of f located in X.

• (3) Using Algorithm 6 construct polytopes transversal to f around the found equilibrium points (see Sect. 4, Figs. 1 (right) and 7).

• (4) Triangulate X. In the process guarantee that the transversal polytopes around equilibria are included in the triangulation. Denote the triangulation (simplicial complex) by $\texttt{T}$.

• (5) Extend $\texttt{T}$ to an abstract complex ${\hat{\texttt{T}}}$ by adding an empty cone (see Fig. 8). In particular, ${\hat{\texttt{T}}}:=\texttt{T}\cup \{{\text {conv}}(\texttt{s}\cup p)\mid \texttt{s}\in \texttt{T}\text { such that } \texttt{s}\subset {\text {bd}}_{{\mathbb {R}}^2}X \}$, where p is an external point—a tip of the created cone. Note that ${\hat{\texttt{T}}}$ is now a simplicial model of ${\hat{X}}$, the compactified ${\mathbb {R}}^2$ (i.e., ${\mathbb {S}}^2$). We assume that ${\hat{f}}$ is a new vector field on ${\hat{X}}$ such that ${\hat{f}}_{\mid X}=f_{\mid X}$ and ${\hat{f}}(\infty )=0$.

• (6) Run Algorithm 3 for ${\hat{\texttt{T}}}$ and ${\hat{f}}$ to construct a multivector field $\texttt{mvf}$ on ${\hat{\texttt{T}}}$ (see Sect. 3.1). We can assume that edges added with the cone are non-transversal.

• (7) Verify that the computed multivector field $\texttt{mvf}$ induces an f-admissible cellular decomposition ${\mathcal {X}}$ of ${\hat{X}}$ (see Sect. 3.2). In the case of failure, go back to (4) starting with a finer triangulation of X.

• (8) Find the maximal combinatorial isolated invariant set $\texttt{S}$ with respect to $\texttt{mvf}$ such that $|S|\subset X$.

• (9) Compute minimal Morse decomposition of $\texttt{S}$ and choose a Morse set $\texttt{M}$ with the Conley index of a hyperbolic periodic orbit. Verify that $\texttt{M}$ does not contain any equilibrium points. Finish reporting failure if such a M does not exists.

• (10) Construct a combinatorial Poincaré section for $\texttt{M}$ using Algorithm 4 (see Sect. 3.3). Finish reporting failure if Algorithm 4 fails.

• (11) Apply Theorem 5.37 from (Mrozek et al. 2022) to conclude the existence of a non-trivial periodic orbit for vector field f in $|S|$.

To locate all equilibrium points we can try simply solve formulas for f. But in general we need only good approximations. We can use interval branch and bound algorithm to locate all possible equilibrium points and then validate them using for example interval Newton method (it gives also uniqueness in the given neighborhood).

In step (4) we recommend sampling region X with a density reflecting the local variation of vectors’ directions. We proceed with a two-step procedure. First, we divide X into larger boxes and we randomly sample points for each of them. For points in a box we compute corresponding vectors and use them to estimate the variation. If it exceeds a certain threshold, we draw an additional set of points for the box. In the second step, to smooth out the points distribution, we repeat the same procedure, but with a division of X into a smaller grid.

As explained in Lipiński et al. (2022), the maximal isolated invariant set in step (8) and its Morse decomposition in step (9) can be found with a simple algorithm detecting strongly connected components of a directed graph.

In step (7) we verify only admissibility, while the theorem used in step (11) assumes that the studied flow is strongly admissible with respect to the cellular decomposition ${\mathcal {X}}$. Let us recall that the strong admissibility (Sect. 2.8) implies that the invariant part of a regular multivector in $\texttt{M}$ is empty. However, at step (2) we detect all equilibrium points of f in the selected X. Thus, in the planar case the needed property follows by the Poincaré-Bendixon theorem (Teschl 2012, Theorem 8.8). Nevertheless, this condition can be rigorously verified also in higher dimensions by estimating the lower bound for the length of vectors within a cell.

Note that ${\hat{X}}$, ${\hat{f}}$ and ${\mathcal {X}}$ are just conceptual objects that help us to control the theoretical assumptions of the theory behind the Theorem 5.37 in Mrozek et al. (2022). However, they are not present in the actual computations. In fact, one could even avoid the construction of ${\hat{\texttt{T}}}$ and work just on $\texttt{T}$ by introducing a proper specialization of Algorithm 3.

5.3 Double periodic orbit system

Consider system

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = 1.4y-x(x^2+y^2-1)(x^2+y^2-4)\\ y'=-1.4x-y(x^2+y^2-1)(x^2+y^2-4) \end{array}\right. }, \end{aligned}$$

(15)

with an attracting equilibrium point at the origin, a repelling periodic orbit with radius one, and an attracting periodic orbit with radius two.

Fig. 9

Cellular decomposition computed for vector field (15)

We choose the square $[-3,3]\times [-3,3]$ to be the region of interest. We construct the regular 16-polygone around the equilibrium point using the Algorithm 5 and then sampled additional 6198 points outside of it to build the triangulation of the space.

The multivector field generated by Algorithm 3 is presented in Fig. 9. The found Morse sets are depicted in Fig. 10. Combinatorial Poincaré sections for both Morse sets representing periodic orbit are marked with blue color.

5.4 Van der Pol oscillator

As the second example we consider the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = -y\\ y'= (x^2-1)y+x \end{array}\right. } \end{aligned}$$

(16)

known as Van der Pol oscillator. This system has a repelling equilibrium point at the origin and an attracting periodic orbit. We use 24224 points in the square $[-10,10]\times [-10,10]$ and the transversal polytope around the equilibrium point to construct the triangulation.

The multivector field provided by Algorithm 3 is presented in Fig. 11. Note that the blue regions attached to the boundary of the regions are a part of the multivector which contains the cone. Thus, these elements are excluded from the search of the maximal isolated invariant set. The Morse decomposition of the remaining part is shown in Fig. 12. The yellow set corresponds to the equilibrium point and the red region is the Morse set with the Conley index of an attracting periodic orbit. The found combinatorial Poincaré section of for the orbit is marked with blue color.

Fig. 10

Morse decomposition for the multivector field presented in Fig. 9. The yellow set corresponds to the attracting equilibrium point, the green set—to the repelling periodic orbit, and the red set—to the attracting periodic orbit. The combinatorial Poincaré sections are highlighted with light blue color (colour figure online)

Fig. 11

Combinatorial multivector field computed for vector field (16)

Fig. 12

Morse decomposition for the multivector field presented in Fig. 11. The yellow set corresponds to the repelling equilibrium point and the red set—to the attracting periodic orbit. The combinatorial Poincaré section is highlighted with light blue color (colour figure online)

6 Final remarks

6.1 Computational considerations

In the C++ implementation of our algorithms we use several libraries and programs. The CAPD library (Kapela et al. 2021) was used for rigorous computations based on interval arithmetics especially to check transversality and to represent vector fields. Homology groups were computed with Gudhi library (Maria et al. 2014). To determine the Morse decomposition we use the graphs and graph algorithms provided by the Boost library (Boost Group 1999). To build Delaunay triangulation we use the delaunator-cpp library (Bilonenko et al. 2018).

6.2 Future work

The pipeline for the automatized proof for the existence of a periodic orbit presented in this paper is specialized for a planar case. However, none of the steps seems to admit any fundamental obstacle preventing its generalization from working in higher dimensions. Algorithm $\mathtt TransversalPolytope$ is already in a general form, and algorithm ${} \texttt{AdmissibleMVF}$ is suited for studying dynamics on 2-dimensional manifolds. Clearly, the generalized algorithm would be more complex. Nevertheless, it would be interesting to study the practical limits of our approach.

Another interesting extension for this project would be a study of other sets than periodic orbits. However, this would also require a modification of the theory presented by Mrozek et al. (2022). Moreover, revisiting our current approach to building the combinatorial Poincaré section would also be necessary.

Finally, the general idea of constructing a multivector field can be adapted to sampled vector fields where the equation governing the dynamics is unknown. The computations would no longer be rigorous, but we believe that still be helpful in the context of empirical data. The construction of a multivector field from data was already considered in Dey et al. (2019). However, the full potential of the multivector field theory was not exploited there, as the computations were based only on the early version of the theory.