Abstract
A standard problem in applied topology is how to discover topological invariants of data from a noisy point cloud that approximates it. We consider the case where a sample is drawn from a properly embedded  -submanifold without boundary in a Euclidean space. We show that we can deformation retract the union of ellipsoids, centered at sample points and stretching in the tangent directions, to the manifold. Hence the homotopy type, and therefore also the homology type, of the manifold is the same as that of the nerve complex of the cover by ellipsoids. By thickening sample points to ellipsoids rather than balls, our results require a smaller sample density than comparable results in the literature. They also advocate using elongated shapes in the construction of barcodes in persistent homology.
-submanifold without boundary in a Euclidean space. We show that we can deformation retract the union of ellipsoids, centered at sample points and stretching in the tangent directions, to the manifold. Hence the homotopy type, and therefore also the homology type, of the manifold is the same as that of the nerve complex of the cover by ellipsoids. By thickening sample points to ellipsoids rather than balls, our results require a smaller sample density than comparable results in the literature. They also advocate using elongated shapes in the construction of barcodes in persistent homology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Data is often unstructured and comes in the form of a non-empty finite metric space, called a point cloud. It is often very high dimensional even though data points are actually samples from a low-dimensional object (such as a manifold) that is embedded in a high-dimensional space. One reason may be that many features are all measurements of the same underlying cause and therefore closely related to each other. For example, if you take photos of a single object from multiple angles simultaneously there is a lot overlap in the information captured by all those cameras. One of the main tasks of ‘manifold learning’ is to design algorithms to estimate geometric and topological properties of the manifold from the sample points lying on this unknown manifold, in particular its homotopy type.
One successful framework for dealing with the problem of reconstructing shapes from point clouds is based on the notion of \(\epsilon \)-sample introduced by Amenta and Bern (1999). A sampling of a shape \(\mathcal {M}\) is an \(\epsilon \)-sampling if every point \(\texttt {P}\) in \(\mathcal {M}\) has a sample point at distance at most \(\epsilon \cdot \text {lfs}_\mathcal {M}(\texttt {P})\), where \(\text {lfs}_\mathcal {M}(\texttt {P})\) is the local feature size of \(\texttt {P}\), i.e. the distance from \(\texttt {P}\) to the medial axis of \(\mathcal {M}\). Surfaces smoothly embedded in \(\mathbb {R}^3\) can be reconstructed homeomorphically from any 0.06-sampling using the Cocone algorithm (Amenta et al. 2002).
One simple method for shape reconstructing is to output an offset of the sampling for a suitable value \(\alpha \) of the offset parameter (the \(\alpha \)-offset of the sampling is the union of balls with centers in sample points and radius \(\alpha \)). Topologically, this is equivalent to taking the Čech complex or the \(\alpha \)-complex (Edelsbrunner and Mücke 1994). This leads to the problem of finding theoretical guarantees as to when an offset of a sampling has the same homotopy type as the underlying set. In other words, we need to find conditions on a point cloud \(\mathcal {S}\) of a shape \(\mathcal {M}\) so that the thickening of \(\mathcal {S}\) is homotopy equivalent to \(\mathcal {M}\). This only works if the point cloud is sufficiently close to \(\mathcal {M}\), i.e. when there is a bound on the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\).
Niyogi et al. (2008) proved that this method indeed provides reconstructions having the correct homotopy type for densely enough sampled smooth submanifolds of \(\mathbb {R}^n\). More precisely, one can capture the homotopy type of a Riemannian submanifold \(\mathcal {M}\) without boundary of reach \(\tau \) in a Euclidean space from a finite \(\frac{\epsilon }{2}\)-dense sample \(\mathcal {S}\subseteq \mathcal {M}\) (meaning every point of the manifold has a sample point at most \(\frac{\epsilon }{2}\) away) whenever  by showing that the union of \(\epsilon \)-balls with centers in sample points deformation retracts to \(\mathcal {M}\).
by showing that the union of \(\epsilon \)-balls with centers in sample points deformation retracts to \(\mathcal {M}\).
Let us denote the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\) by \(\varkappa \)—that is, every point in \(\mathcal {M}\) has an at most \(\varkappa \)-distant point in \(\mathcal {S}\). We can rephrase the above result as follows: whenever  , the homotopy type of \(\mathcal {M}\) is captured by a union of \(\epsilon \)-balls with centers in \(\mathcal {S}\) for every
, the homotopy type of \(\mathcal {M}\) is captured by a union of \(\epsilon \)-balls with centers in \(\mathcal {S}\) for every  . Thus the bound of the ratio
. Thus the bound of the ratio

represents how dense we need the sample to be in order to be able to recover the homotopy type of \(\mathcal {M}\).
Other authors gave variants of Niyogi, Smale and Weinberger’s result. In Bürgisser et al. (2018, Theorem 2.8), the authors relax the conditions on the set we wish to approximate (it need not be a manifold, just any non-empty compact subset of a Euclidean space) and the sample (it need not be finite, just non-empty compact), but the price they pay for this is a lot lower upper bound on  , which in their case is \(\frac{1}{6} \approx 0.167\). One can potentially improve the result by using local quantities (\(\mu \)-reach etc.) (Chazal et al. 2009; Chazal and Lieutier 2005b, 2007; Turner 2013; Attali and Lieutier 2010; Attali et al. 2013) instead of the global reach \(\tau \), at least in situations when these are large compared to \(\tau \).
, which in their case is \(\frac{1}{6} \approx 0.167\). One can potentially improve the result by using local quantities (\(\mu \)-reach etc.) (Chazal et al. 2009; Chazal and Lieutier 2005b, 2007; Turner 2013; Attali and Lieutier 2010; Attali et al. 2013) instead of the global reach \(\tau \), at least in situations when these are large compared to \(\tau \).
In practice producing a sufficiently dense sample can be difficult and computationally expensive (Dufresne et al. 2019), so relaxing the upper bound of \(\frac{\varkappa }{\tau }\) is desirable. The purpose of this paper is to prove that we can indeed relax this bound when sampling manifolds (though we allow a more general class than Niyogi et al. 2008) if we thicken sample points to ellipsoids rather than balls. The idea is that since a differentiable manifold is locally well approximated by its tangent space, an ellipsoid with its major semi-axes in the tangent directions well approximates the manifold. This idea first appeared in Breiding et al. (2018), where the authors construct a filtration of “ellipsoid-driven complexes”, where the user can choose the ratio between the major (tangent) and the minor (normal) semi-axes. Their experiments showed that computing barcodes from ellipsoid-driven complexes strengthened the topological signal, in the sense that the bars corresponding to features of the data were longer. In our paper we make the ratio between semi-axes dependent on the ellipsoid size (the length of the minor semi-axis, to be exact), and give a proof that the union of ellipsoids around sample points (under suitable assumptions) deformation retracts onto the manifold. Hence our paper gives theoretical guarantees that the union of ellipsoids captures the manifold’s homotopy type, and thus further justifies the use of ellipsoid-inspired shapes to construct barcodes.
In this paper we assume that the information about the reach of the manifold and its tangent and normal spaces in the sample points are given. In practice, these quantities can be estimated from the sample, see e.g. Aamari et al. (2019), Berenfeld et al. (2020), Zhang and Zha (2004), Kaslovsky and Meyer (2011) and Zhang et al. (2011).
The central theorem of this paper (Theorem 6.1) is the following:
Theorem
Let \(n\in \mathbb {N}\) and let \(\mathcal {M}\) be a non-empty properly embedded \({\mathcal {C}}^1\)-submanifold of \(\mathbb {R}^n\) without boundary. Let \(\mathcal {S}\subseteq \mathcal {M}\) be a subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (the sample from the manifold \(\mathcal {M}\)). Let \(\tau \) be the reach of \(\mathcal {M}\) in \(\mathbb {R}^n\) and \(\varkappa \) the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\). Then for all  which satisfy
which satisfy

there exists a strong deformation retraction from  (the union of open ellipsoids around sample points with normal semi-axes of length \(p\) and tangent semi-axes of length
(the union of open ellipsoids around sample points with normal semi-axes of length \(p\) and tangent semi-axes of length  ) to \(\mathcal {M}\). In particular, \(\mathcal {M}\),
) to \(\mathcal {M}\). In particular, \(\mathcal {M}\),  and the nerve complex of the ellipsoid cover
and the nerve complex of the ellipsoid cover  are homotopy equivalent, and so have the same homology.
are homotopy equivalent, and so have the same homology.
By replacing the balls with ellipsoids, we manage to push the upper bound on  to approximately 0.913, an improvement by a factor of about 2.36 compared to Niyogi et al. (2008). In other words, our method allows samples with less than half the density.
to approximately 0.913, an improvement by a factor of about 2.36 compared to Niyogi et al. (2008). In other words, our method allows samples with less than half the density.
Due to the difficulty and length of our current work, we give the result in terms of the reach, i.e. a global feature. We leave the generalization to local features for future work.
The strategy of our proof is to define a deformation retraction from the union of ellipsoids around sample points to the manifold. On the intersection of ellipsoids, we show that the normal deformation retraction works. However, this appears too difficult to prove theoretically, so we provide a computer-assisted proof. We first reduce the general case to a set of cases which includes the “worst case scenarios”, i.e. the ones which come the closest to contradicting our desired results. At this step, we use a computer to show that these cases still satisfy our requirements. On the other hand, we define the deformation retraction outside of ellipsoid intersections by utilizing the flow of a particular vector field. We join the two parts with a suitable partition of unity.
The paper is organized as follows. Section 2 lays the groundwork for the paper, providing requisite definitions and deriving some results for general differentiable submanifolds of Euclidean spaces. In Sect. 3 we calculate theoretical bounds on the persistence parameter \(p\): the lower bound ensures that the union of ellipsoids covers the manifold and the upper bound ensures that the union does not intersect the medial axis. In Sect. 4 we explain the computer-assisted part of the proof used to show that the normal deformation retraction works on the intersections of ellipsoids. In Sect. 5 we construct the rest of the deformation retraction from the union of ellipsoids to the manifold. This section is divided into several subsections for easier reading. Section 6 collects the results from the paper to prove the main theorem. In Sect. 7 we discuss our results and future work.
1.1 Notation
Natural numbers  include zero. Unbounded real intervals are denoted by \(\mathbb {R}_{> a}\), \(\mathbb {R}_{\le a}\) etc. Bounded real intervals are denoted by \({\mathbb {R}}_{(a, b)}\) (open), \({\mathbb {R}}_{[a, b]}\) (closed) etc.
include zero. Unbounded real intervals are denoted by \(\mathbb {R}_{> a}\), \(\mathbb {R}_{\le a}\) etc. Bounded real intervals are denoted by \({\mathbb {R}}_{(a, b)}\) (open), \({\mathbb {R}}_{[a, b]}\) (closed) etc.
Glossary:
- \(d\):
-
Euclidean distance in \(\mathbb {R}^n\)
- \(\mathcal {N}\):
-
a submanifold of \(\mathbb {R}^n\)
- \(\mathcal {M}\):
-
\(m\)-dimensional
 -submanifold of \(\mathbb {R}^n\), embedded as a closed subset
-submanifold of \(\mathbb {R}^n\), embedded as a closed subset - \(\mathcal {M}_{r}\):
-
open r-thickening of \(\mathcal {M}\), i.e.

- \(\overline{\mathcal {M}}_{r}\):
-
closed r-thickening of \(\mathcal {M}\), i.e.

 :
:-
tangent space on \(\mathcal {M}\) at \(\texttt {X}\)
 :
:-
normal space on \(\mathcal {M}\) at \(\texttt {X}\)
- \(\mathcal {S}\):
-
manifold sample (a subset of \(\mathcal {M}\)), non-empty and locally finite
- \(\varkappa \):
-
the Hausdorff distance between \(\mathcal {M}\) and \(\mathcal {S}\)
- \({\mathcal {A}}\):
-
the medial axis of \(\mathcal {M}\)
- \({\mathcal {A}}^\complement \):
-
the complement of the medial axis in \(\mathcal {M}\), i.e. \(\mathcal {M}\setminus {\mathcal {A}}\)
- \(\tau \):
-
the reach of \(\mathcal {M}\)
- \(p\):
-
persistence parameter
 :
:-
open ellipsoid with the center in a sample point \(\texttt {S}\in \mathcal {S}\) with the major semi-axes tangent to \(\mathcal {M}\)
 :
:-
closed ellipsoid with the center in a sample point \(\texttt {S}\in \mathcal {S}\) with the major semi-axes tangent to \(\mathcal {M}\)
 :
:-
the boundary of
 , i.e.
, i.e. 
 :
:-
the union of open ellipsoids over the sample,

 :
:-
the union of closed ellipsoids over the sample,

- \(pr\):
-
the map \({\mathcal {A}}^\complement \rightarrow \mathcal {M}\) taking a point to the unique closest point on \(\mathcal {M}\)
- \(prv\):
-
the map taking a point \(\texttt {X}\) to the vector \(pr(\texttt {X}) - \texttt {X}\)
 :
:-
auxiliary vector field, defined on

- \(\widetilde{V}\):
-
auxiliary vector field, defined on

- \(V\):
-
the vector field of directions for the deformation retraction
- \(\Phi \):
-
the flow of the vector field \(V\)
- \(R\):
-
a deformation retraction from
 to a tubular neighbourhood of \(\mathcal {M}\)
to a tubular neighbourhood of \(\mathcal {M}\)
2 General definitions
All constructions in this paper are done in an ambient Euclidean space \(\mathbb {R}^n\), \(n\in \mathbb {N}\), equipped with the usual Euclidean metric \(d\). We will use the symbol \(\mathcal {N}\) for a general submanifold of \(\mathbb {R}^n\).
Given \(r \in \mathbb {R}_{> 0}\), we denote the open and closed r-thickening of \(\mathcal {N}\) by

By definition each point \(\texttt {X}\) of a manifold \(\mathcal {N}\) has a neighbourhood, homeomorphic to a Euclidean space or a closed Euclidean half-space. The dimension of this (half-)space is the dimension of \(\mathcal {N}\) at \(\texttt {X}\). Different points of a manifold can have different dimensions,Footnote 1 though the dimension is constant on each connected component. In this paper, when we say that \(\mathcal {N}\) is an \(m\)-dimensional manifold, we mean that it has dimension \(m\) at every point.
We quickly recall from general topology that it is equivalent for a subset of a Euclidean space to be closed and to be properly embedded.
Proposition 2.1
Let \((\mathcal {X}, d)\) be a metric space in which every closed ball is compact (every Euclidean space \(\mathbb {R}^n\) satisfies this property). The following statements are equivalent for any subset \(\mathcal {S} \subseteq \mathcal {X}\).
-
1.
\(\mathcal {S}\) is a closed subset of \(\mathcal {X}\).
-
2.
\(\mathcal {S}\) is properly embedded into \(\mathcal {X}\), i.e. the inclusion \(\mathcal {S} \hookrightarrow \mathcal {X}\) is a proper map.Footnote 2
-
3.
\(\mathcal {S}\) is empty or distances from points in the ambient space to \(\mathcal {S}\) are attained. That is, for every \(\texttt {X}\in \mathcal {X}\) there exists \(\texttt {Y}\in \mathcal {S}\) such that \(d(\texttt {X}, \mathcal {S}) = d(\texttt {X}, \texttt {Y})\).
Proof
-
\(\underline{(1 \Rightarrow 2)}\) If \(\mathcal {S}\) is closed in \(\mathcal {X}\), then its intersection with a compact subset of \(\mathcal {X}\) is compact, so \(\mathcal {S}\) is properly embedded into \(\mathcal {X}\).
-
\(\underline{(2 \Rightarrow 3)}\) If \(\mathcal {S}\) is non-empty, pick \(\texttt {S} \in \mathcal {S}\). For any \(\texttt {X}\in \mathcal {X}\) we have \(d(\texttt {X}, \mathcal {S}) \le d(\texttt {X}, \texttt {S})\), so \(d(\texttt {X}, \mathcal {S}) = d\big (\texttt {X}, \mathcal {S} \cap {d(\texttt {X}, \texttt {S})}\big )\). Since \(\mathcal {S}\) is properly embedded in \(\mathcal {X}\), its intersection with the compact closed ball \({d(\texttt {X}, \texttt {S})}\) is compact also. A continuous map from a non-empty compact space into reals attains its minimum, so there exists \(\texttt {Y}\in \mathcal {S}\) such that \(d(\texttt {X}, \texttt {Y}) = d\big (\texttt {X}, \mathcal {S} \cap {d(\texttt {X}, \texttt {S})}\big ) = d(\texttt {X}, \mathcal {S})\).
-
\(\underline{(3 \Rightarrow 1)}\) The empty set is closed. Assume that \(\mathcal {S}\) is non-empty. Then for every point in the closure \(\texttt {X}\in \overline{\mathcal {S}}\) we have \(d(\texttt {X}, \mathcal {S}) = 0\). By assumption this distance is attained, i.e. we have \(\texttt {Y}\in \mathcal {S}\) such that \(d(\texttt {X}, \texttt {Y}) = 0\), so \(\texttt {X}= \texttt {Y}\in \mathcal {S}\). Thus \(\overline{\mathcal {S}} \subseteq \mathcal {S}\), so \(\mathcal {S}\) is closed.
\(\square \)
In this paper we consider exclusively submanifolds of a Euclidean space which are properly embedded, so closed subsets. We mostly use the term ‘properly embedded’ instead of ‘closed’ to avoid confusion: the term ‘closed manifold’ is usually used in the sense ‘compact manifold with no boundary’ which is a stronger condition (a properly embedded submanifold need not be compact or without boundary, though every compact submanifold is properly embedded).
A manifold can have smooth structure up to any order  ; in that case it is called a
; in that case it is called a  -manifold. A
-manifold. A  -submanifold of \(\mathbb {R}^n\) is a
-submanifold of \(\mathbb {R}^n\) is a  -manifold which is a subset of \(\mathbb {R}^n\) and the inclusion map is
-manifold which is a subset of \(\mathbb {R}^n\) and the inclusion map is  .
.
If \(\mathcal {N}\) is at least a  -manifold, one may abstractly define the tangent space
-manifold, one may abstractly define the tangent space  and the normal space
and the normal space  at any point \(\texttt {X}\in \mathcal {N}\) (\(\texttt {X}\) is allowed to be a boundary point). As we restrict ourselves to submanifolds of \(\mathbb {R}^n\), we also treat the tangent and the normal space as affine subspaces of \(\mathbb {R}^n\), with the origins of
at any point \(\texttt {X}\in \mathcal {N}\) (\(\texttt {X}\) is allowed to be a boundary point). As we restrict ourselves to submanifolds of \(\mathbb {R}^n\), we also treat the tangent and the normal space as affine subspaces of \(\mathbb {R}^n\), with the origins of  and
and  placed at \(\texttt {X}\). The dimension of
placed at \(\texttt {X}\). The dimension of  (resp.
(resp.  ) is the same as the dimension (resp. codimension) of \(\mathcal {N}\) at \(\texttt {X}\). Because of this and because
) is the same as the dimension (resp. codimension) of \(\mathcal {N}\) at \(\texttt {X}\). Because of this and because  and
and  are orthogonal, they together generate \(\mathbb {R}^n\).
are orthogonal, they together generate \(\mathbb {R}^n\).
Definition 2.2
Let \(\mathcal {N}\) be a  -submanifold of \(\mathbb {R}^n\), \(\texttt {X}\in \mathcal {N}\) and \(m\) the dimension of \(\mathcal {N}\) at \(\texttt {X}\).
-submanifold of \(\mathbb {R}^n\), \(\texttt {X}\in \mathcal {N}\) and \(m\) the dimension of \(\mathcal {N}\) at \(\texttt {X}\).
-
A tangent-normal coordinate system at \(\texttt {X}\in \mathcal {N}\) is an \(n\)-dimensional orthonormal coordinate system with the origin in \(\texttt {X}\), the first \(m\) coordinate axes tangent to \(\mathcal {N}\) at \(\texttt {X}\) and the last \(n-m\) axes normal to \(\mathcal {N}\) at \(\texttt {X}\).
-
A planar tangent-normal coordinate system at \(\texttt {X}\in \mathcal {N}\) is a two-dimensional plane in \(\mathbb {R}^n\) containing \(\texttt {X}\), together with the choice of an orthonormal coordinate system lying on it, with the origin in \(\texttt {X}\), the first axis (the abscissa) tangent to \(\mathcal {N}\) at \(\texttt {X}\) and the second axis (the ordinate) normal to \(\mathcal {N}\) at \(\texttt {X}\).
Recall from Proposition 2.1 that distances from points to a non-empty properly embedded submanifold are attained. However, these distances need not be attained in just one point. We recall the familiar definitions of the medial axis and the reach.
Definition 2.3
The medial axis  of a submanifold \(\mathcal {N}\subseteq \mathbb {R}^n\) is the set of all points in the ambient space for which the distance to \(\mathcal {N}\) is attained in at least two points:
of a submanifold \(\mathcal {N}\subseteq \mathbb {R}^n\) is the set of all points in the ambient space for which the distance to \(\mathcal {N}\) is attained in at least two points:

The reach of \(\mathcal {N}\), denoted by  , is the distance between the manifold \(\mathcal {N}\) and its medial axis
, is the distance between the manifold \(\mathcal {N}\) and its medial axis  (if
(if  is empty,Footnote 3 the reach is defined to be \(\infty \)).
is empty,Footnote 3 the reach is defined to be \(\infty \)).
The manifold and its medial axis are always disjoint.
Definition 2.4
Let \(\mathcal {N}\) be a  -submanifold of \(\mathbb {R}^n\), \(\texttt {X}\in \mathcal {N}\) and \(\textbf{N}\) a non-zero normal vector to \(\mathcal {N}\) at \(\texttt {X}\). The
-submanifold of \(\mathbb {R}^n\), \(\texttt {X}\in \mathcal {N}\) and \(\textbf{N}\) a non-zero normal vector to \(\mathcal {N}\) at \(\texttt {X}\). The  -ball, associated to \(\texttt {X}\) and \(\textbf{N}\), is the closed ball (in \(\mathbb {R}^n\), so \(n\)-dimensional) with radius
-ball, associated to \(\texttt {X}\) and \(\textbf{N}\), is the closed ball (in \(\mathbb {R}^n\), so \(n\)-dimensional) with radius  and centered at
and centered at  , which therefore touches \(\mathcal {N}\) at \(\texttt {X}\).Footnote 4 A
, which therefore touches \(\mathcal {N}\) at \(\texttt {X}\).Footnote 4 A  -ball, associated to \(\texttt {X}\), is the
-ball, associated to \(\texttt {X}\), is the  -ball, associated to \(\texttt {X}\) and some non-zero normal vector to \(\mathcal {N}\) at \(\texttt {X}\).
-ball, associated to \(\texttt {X}\) and some non-zero normal vector to \(\mathcal {N}\) at \(\texttt {X}\).
The significance of associated  -balls is that they provide restrictions to where a manifold is situated. Specifically, a manifold is disjoint with the interior of its every associated
-balls is that they provide restrictions to where a manifold is situated. Specifically, a manifold is disjoint with the interior of its every associated  -ball.
-ball.
We will approximate manifolds with a union of ellipsoids (similar as to how one uses a union of balls to approximate a subspace in the case of a Čech complex). The idea is to use ellipsoids which are elongated in directions, tangent to the manifold, so that they “extend longer in the direction the manifold does”, so that we require a sample with lower density.
Let us define the kind of ellipsoids we use in this paper.
Definition 2.5
Let \(\mathcal {N}\) be a  -submanifold of \(\mathbb {R}^n\) and \(p\in \mathbb {R}_{> 0}\). The tangent-normal open (resp. closed) \(p\)-ellipsoid at \(\texttt {X}\in \mathcal {N}\) is the open (resp. closed) ellipsoid in \(\mathbb {R}^n\) with the center in \(\texttt {X}\), the tangent semi-axes of length
-submanifold of \(\mathbb {R}^n\) and \(p\in \mathbb {R}_{> 0}\). The tangent-normal open (resp. closed) \(p\)-ellipsoid at \(\texttt {X}\in \mathcal {N}\) is the open (resp. closed) ellipsoid in \(\mathbb {R}^n\) with the center in \(\texttt {X}\), the tangent semi-axes of length  and the normal semi-axes of length \(p\). Explicitly, in a tangent-normal coordinate system at \(\texttt {X}\) the tangent-normal open and closed \(p\)-ellipsoids are given by
and the normal semi-axes of length \(p\). Explicitly, in a tangent-normal coordinate system at \(\texttt {X}\) the tangent-normal open and closed \(p\)-ellipsoids are given by

where \(m\) denotes the dimension of \(\mathcal {N}\) at \(\texttt {X}\). If  , then these “ellipsoids” are simply thickenings of
, then these “ellipsoids” are simply thickenings of  :
:

Observe that the definitions of ellipsoids are independent of the choice of the tangent-normal coordinate system; they depend only on the submanifold itself.
The value \(p\) in the definition of ellipsoids serves as a “persistence parameter” (Ghrist 2008; Carlsson 2009; Carlsson and Zomorodian 2005; Edelsbrunner et al. 2002; Breiding et al. 2018). We purposefully do not take ellipsoids which are similar at all \(p\) (which would mean that the ratio between the tangent and the normal semi-axes was constant). Rather, we want ellipsoids which are more elongated (have higher eccentricity) for smaller \(p\). This is because on a smaller scale a smooth manifold more closely aligns with its tangent space, and then so should the ellipsoids. We want the length of the major semi-axes to be a function of \(p\) with the following properties: for each \(p\) its value is larger than \(p\), and when \(p\) goes to 0, the function value also goes to 0, but the eccentricity goes to 1. In addition, the function should allow the following argument. If we change the unit length of the coordinate system, but otherwise leave the manifold “the same”, we want the ellipsoids to remain “the same” as well, but the reach of the manifold changes by the same factor as the unit length, which the function should take into account. The simplest function satisfying all these properties is arguably  , which turns out to work for the results we want.
, which turns out to work for the results we want.
Figure 1 shows an example, how a manifold, associated balls and a tangent-normal ellipsoid look like in a tangent-normal coordinate system at some point on the manifold.
We now prove a few results that will be useful later.
Lemma 2.6
Let \(\mathcal {N}\) be a properly embedded  -submanifold of \(\mathbb {R}^n\). Let \(\texttt {X}\in \mathcal {N}\) and let \(m\) be the dimension of \(\mathcal {N}\) at \(\texttt {X}\). Assume \(0< m< n\).
-submanifold of \(\mathbb {R}^n\). Let \(\texttt {X}\in \mathcal {N}\) and let \(m\) be the dimension of \(\mathcal {N}\) at \(\texttt {X}\). Assume \(0< m< n\).
-
1.
For every \(\texttt {Y}\in \mathbb {R}^n\) a planar tangent-normal coordinate system at \(\texttt {X}\in \mathcal {N}\) exists which contains \(\texttt {Y}\). Without loss of generality we may require that the coordinates of \(\texttt {Y}\) in this coordinate system are non-negative (\(\texttt {Y}\) lies in the closed first quadrant).
-
2.
If
 and \(\textbf{N}\) is a vector, normal to
and \(\textbf{N}\) is a vector, normal to  at \(\texttt {Y}\), then we may additionally assume that the planar tangent-normal coordinate system from the previous item contains \(\textbf{N}\).
at \(\texttt {Y}\), then we may additionally assume that the planar tangent-normal coordinate system from the previous item contains \(\textbf{N}\). -
3.
Let \(\mathcal {O}\) be a closed \((n-m+1)\)-dimensional ball,
 -embedded in \(\mathbb {R}^n\) (in particular
-embedded in \(\mathbb {R}^n\) (in particular 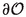 is a
is a  -submanifold of \(\mathbb {R}^n\), diffeomorphic to an \((n-m)\)-dimensional sphere). Assume that
-submanifold of \(\mathbb {R}^n\), diffeomorphic to an \((n-m)\)-dimensional sphere). Assume that  and that \(\mathcal {N}\) and
and that \(\mathcal {N}\) and  intersect transversely at \(\texttt {X}\) (i.e.
intersect transversely at \(\texttt {X}\) (i.e.  and
and  linearly generate the whole \(\mathbb {R}^n\), or equivalently, these two tangent spaces intersect at a single point). Then \(\texttt {X}\) is not the only intersection point, i.e. there exists
linearly generate the whole \(\mathbb {R}^n\), or equivalently, these two tangent spaces intersect at a single point). Then \(\texttt {X}\) is not the only intersection point, i.e. there exists  .
. -
4.
Assume
 . Let \(\texttt {Y}\in \mathbb {R}^n\) and let \((y_T, y_N)\) be the (non-negative) coordinates of \(\texttt {Y}\) in the planar tangent-normal coordinate system from the first item. Let \(\mathcal {D}\) be the set of centers of all
. Let \(\texttt {Y}\in \mathbb {R}^n\) and let \((y_T, y_N)\) be the (non-negative) coordinates of \(\texttt {Y}\) in the planar tangent-normal coordinate system from the first item. Let \(\mathcal {D}\) be the set of centers of all  -balls, associated to \(\texttt {X}\) (i.e. the \((n-m-1)\)-dimensional sphere within
-balls, associated to \(\texttt {X}\) (i.e. the \((n-m-1)\)-dimensional sphere within  with the center in \(\texttt {X}\) and the radius
with the center in \(\texttt {X}\) and the radius  ). Let \(\mathcal {C}\) be the cone which is the convex hull of
). Let \(\mathcal {C}\) be the cone which is the convex hull of  , and assume that
, and assume that  . Then
. Then 
Proof
-
1.
Fix an \(n\)-dimensional tangent-normal coordinate system at \(\texttt {X}\in \mathcal {N}\), and let \((y_1, \ldots , y_n)\) be the coordinates of \(\texttt {Y}\). Let \(\textbf{a} = (y_1, \ldots , y_m, 0, \ldots , 0)\), \(\textbf{b} = (0, \ldots , 0, y_{m+1}, \ldots , y_n)\). If both \(\textbf{a}\) and \(\textbf{b}\) are non-zero, they define a (unique) planar tangent-normal coordinate system at \(\texttt {X}\) which contains \(\texttt {Y}\). If \(\textbf{a}\) is zero (resp. \(\textbf{b}\) is zero), choose an arbitrary tangent (resp. normal) direction (we may do this since \(0< m< n\)).
-
2.
Assume that
 and \(\textbf{N}\) is a direction, normal to
and \(\textbf{N}\) is a direction, normal to  . In the \(n\)-dimensional tangent-normal coordinate system from the previous item, the boundary
. In the \(n\)-dimensional tangent-normal coordinate system from the previous item, the boundary  is given by the equation
is given by the equation 
The gradient of the left-hand side, up to a scalar factor, is

The vector \(\textbf{N}\) has to be parallel to it since
 has codimension 1, i.e. a non-zero \(\lambda \in \mathbb {R}\) exists such that
has codimension 1, i.e. a non-zero \(\lambda \in \mathbb {R}\) exists such that  . Hence \(\textbf{N}\) also lies in the plane, determined by \(\textbf{a}\) and \(\textbf{b}\). This proof works for
. Hence \(\textbf{N}\) also lies in the plane, determined by \(\textbf{a}\) and \(\textbf{b}\). This proof works for 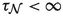 , but the required modification for
, but the required modification for  is trivial.
is trivial. -
3.
Since \(\mathcal {O}\) is a compact \((n-m+1)\)-dimensional disk and
 is closed, some thickening of \(\mathcal {O}\) exists—denote it by \(\mathcal {T}\)—which is diffeomorphic to an \(n\)-dimensional ball and is still disjoint with
is closed, some thickening of \(\mathcal {O}\) exists—denote it by \(\mathcal {T}\)—which is diffeomorphic to an \(n\)-dimensional ball and is still disjoint with  . With a small perturbation of \(\mathcal {N}\) around
. With a small perturbation of \(\mathcal {N}\) around  (but away from the intersection \(\mathcal {N}\cap \mathcal {O}\) which must remain unchanged) we can achieve that \(\mathcal {N}\) and
(but away from the intersection \(\mathcal {N}\cap \mathcal {O}\) which must remain unchanged) we can achieve that \(\mathcal {N}\) and  only have transversal intersections (Lee 2013). Imagine \(\mathbb {R}^n\) embedded into its one-point compactification \(S^n\) (denote the added point by \(\infty \)) in such a way that \(\mathcal {T}\) is a hemisphere. Replace the part of \(\mathcal {N}\) outside of \(\mathcal {T}\) with a copy of \(\mathcal {N}\cap \mathcal {T}\), reflected over
only have transversal intersections (Lee 2013). Imagine \(\mathbb {R}^n\) embedded into its one-point compactification \(S^n\) (denote the added point by \(\infty \)) in such a way that \(\mathcal {T}\) is a hemisphere. Replace the part of \(\mathcal {N}\) outside of \(\mathcal {T}\) with a copy of \(\mathcal {N}\cap \mathcal {T}\), reflected over  , and denote the obtained space by \(\mathcal {N}'\). This is an embedding of the so-called double of the manifold \(\mathcal {N}\cap \mathcal {T}\). Then \(\mathcal {N}'\) is a manifold without boundary, closed in the sphere, and therefore compact. If necessary, perturb it slightly around the point \(\infty \), so that \(\infty \notin \mathcal {N}'\). Hence \(\mathcal {N}'\) is a compact submanifold in \(\mathbb {R}^n\) without boundary and
, and denote the obtained space by \(\mathcal {N}'\). This is an embedding of the so-called double of the manifold \(\mathcal {N}\cap \mathcal {T}\). Then \(\mathcal {N}'\) is a manifold without boundary, closed in the sphere, and therefore compact. If necessary, perturb it slightly around the point \(\infty \), so that \(\infty \notin \mathcal {N}'\). Hence \(\mathcal {N}'\) is a compact submanifold in \(\mathbb {R}^n\) without boundary and  -smooth everywhere except possibly on
-smooth everywhere except possibly on  . The double of a
. The double of a  -manifold can be equipped with a
-manifold can be equipped with a  -structure. Therefore we can use Whitney’s approximation theorem (Lee 2013) to adjust the embedding of \(\mathcal {N}'\) on a neighbourhood of
-structure. Therefore we can use Whitney’s approximation theorem (Lee 2013) to adjust the embedding of \(\mathcal {N}'\) on a neighbourhood of  away from \(\mathcal {O}\), so that it is
away from \(\mathcal {O}\), so that it is  -smooth everywhere. The result is a compact manifold \(\mathcal {N}'\) without boundary satisfying all the properties we required of \(\mathcal {N}\), and we have \(\mathcal {N}' \cap \mathcal {O} = \mathcal {N}\cap \mathcal {O}\). This shows that we may without loss of generality assume that \(\mathcal {N}\) is compact without boundary. Any compact k-dimensional submanifold of \(S^n\) without boundary represents an element in the cohomology \(H^k(S^n; \mathbb {Z}_2)\) (we take the \(\mathbb {Z}_2\)-coeficients, so that we do not have to worry about orientation). For elements \([\mathcal {N}] \in H^m(S^n; \mathbb {Z}_2)\) and
-smooth everywhere. The result is a compact manifold \(\mathcal {N}'\) without boundary satisfying all the properties we required of \(\mathcal {N}\), and we have \(\mathcal {N}' \cap \mathcal {O} = \mathcal {N}\cap \mathcal {O}\). This shows that we may without loss of generality assume that \(\mathcal {N}\) is compact without boundary. Any compact k-dimensional submanifold of \(S^n\) without boundary represents an element in the cohomology \(H^k(S^n; \mathbb {Z}_2)\) (we take the \(\mathbb {Z}_2\)-coeficients, so that we do not have to worry about orientation). For elements \([\mathcal {N}] \in H^m(S^n; \mathbb {Z}_2)\) and 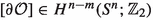 we know (see Bredon 2013, Chapter VI, Section 11 for the relevant definitions and results) that their cup-product
we know (see Bredon 2013, Chapter VI, Section 11 for the relevant definitions and results) that their cup-product  is the intersection number of \(\mathcal {N}\) and
is the intersection number of \(\mathcal {N}\) and  (times the generator). Since the cohomology of \(S^n\) is trivial except in dimensions 0 and \(n\), we have
(times the generator). Since the cohomology of \(S^n\) is trivial except in dimensions 0 and \(n\), we have  , and hence
, and hence 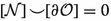 . But the local intersection number at the transversal intersection \(\texttt {X}\) is 1, and the intersection number is the sum of local ones, so \(\texttt {X}\) cannot be the only point in
. But the local intersection number at the transversal intersection \(\texttt {X}\) is 1, and the intersection number is the sum of local ones, so \(\texttt {X}\) cannot be the only point in  .
. -
4.
First consider the case when
 , i.e. \(y_T = 0\). Then
, i.e. \(y_T = 0\). Then 
Now suppose
 . Then the cone \(\mathcal {C}\) is homeomorphic to an \((n-m+1)\)-dimensional closed ball. This \(\mathcal {C}\) and its boundary are smooth everywhere except in \(\texttt {Y}\) and on \(\mathcal {D}\). Let \(\mathcal {E}\) be the \((n-m+1)\)-dimensional affine subspace which contains \(\texttt {Y}\) and
. Then the cone \(\mathcal {C}\) is homeomorphic to an \((n-m+1)\)-dimensional closed ball. This \(\mathcal {C}\) and its boundary are smooth everywhere except in \(\texttt {Y}\) and on \(\mathcal {D}\). Let \(\mathcal {E}\) be the \((n-m+1)\)-dimensional affine subspace which contains \(\texttt {Y}\) and  (thus the whole \(\mathcal {C}\)). We can smooth
(thus the whole \(\mathcal {C}\)). We can smooth  around the centers of the associated balls within \(\mathcal {E}\) without affecting the intersection with \(\mathcal {N}\) since \(\mathcal {N}\) is disjoint with the interiors of the associated
around the centers of the associated balls within \(\mathcal {E}\) without affecting the intersection with \(\mathcal {N}\) since \(\mathcal {N}\) is disjoint with the interiors of the associated  -balls. If \(\texttt {Y}\in \mathcal {N}\), then
-balls. If \(\texttt {Y}\in \mathcal {N}\), then  , and we are done. If \(\texttt {Y}\notin \mathcal {N}\), then \(d(\mathcal {N}, \texttt {Y}) > 0\) since \(\mathcal {N}\) is a closed subset. Then we can also smooth
, and we are done. If \(\texttt {Y}\notin \mathcal {N}\), then \(d(\mathcal {N}, \texttt {Y}) > 0\) since \(\mathcal {N}\) is a closed subset. Then we can also smooth  around \(\texttt {Y}\) within \(\mathcal {E}\) without affecting the intersection with \(\mathcal {N}\). The boundary smoothed in this way is diffeomorphic to an \((n-m)\)-dimensional sphere, and so by the generalized Schoenflies theorem splits \(\mathcal {E}\) into the inner part, diffeomorphic to an \((n-m+1)\)-dimensional ball, and the outer unbounded part. Since \(\mathcal {N}\) intersects
around \(\texttt {Y}\) within \(\mathcal {E}\) without affecting the intersection with \(\mathcal {N}\). The boundary smoothed in this way is diffeomorphic to an \((n-m)\)-dimensional sphere, and so by the generalized Schoenflies theorem splits \(\mathcal {E}\) into the inner part, diffeomorphic to an \((n-m+1)\)-dimensional ball, and the outer unbounded part. Since \(\mathcal {N}\) intersects 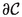 and therefore also its smoothed version orthogonally in \(\texttt {X}\) (because the smoothing was done at positive distance from \(\mathcal {N}\)), this intersection is transversal. By the previous item another intersection point
and therefore also its smoothed version orthogonally in \(\texttt {X}\) (because the smoothing was done at positive distance from \(\mathcal {N}\)), this intersection is transversal. By the previous item another intersection point  exists. It cannot lie in
exists. It cannot lie in  since we would then have a manifold point in the interior of some associated ball, so \(\texttt {X}'\) must lie on the lateral surface of the cone. That is, \(\texttt {X}'\) lies on the line segment between \(\texttt {Y}\) and some associated ball center, but it cannot lie in the interior of the associated ball, so \(d(\texttt {X}', \texttt {Y})\) is bounded by the distance between \(\texttt {Y}\) and the furthest associated ball center, decreased by
since we would then have a manifold point in the interior of some associated ball, so \(\texttt {X}'\) must lie on the lateral surface of the cone. That is, \(\texttt {X}'\) lies on the line segment between \(\texttt {Y}\) and some associated ball center, but it cannot lie in the interior of the associated ball, so \(d(\texttt {X}', \texttt {Y})\) is bounded by the distance between \(\texttt {Y}\) and the furthest associated ball center, decreased by  . The furthest center is the one within the starting planar tangent-normal coordinate system that has coordinates
. The furthest center is the one within the starting planar tangent-normal coordinate system that has coordinates  . Thus
. Thus 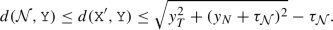
\(\square \)
Lemma 2.7
Let \(A, B \in \mathbb {R}_{\ge 0}\) which are not both 0 and let  . Then a unique \(q \in \mathbb {R}_{> 0}\) exists which solves the equation
. Then a unique \(q \in \mathbb {R}_{> 0}\) exists which solves the equation

Moreover, this q depends continuously on A and B, and if \((A, B) \rightarrow (0, 0)\) (with \(\tau \) fixed), then \(q \rightarrow 0\).
Proof
If \(A = 0\), then clearly \(q = \sqrt{B} > 0\) works. If \(B = 0\), then the unique positive solution to the quadratic equation  is
is  .
.
Assume that \(A, B > 0\). Multiply the equation from the lemma by  and take all terms to one side of the equation to get
and take all terms to one side of the equation to get

Define the function \(f:\mathbb {R}\rightarrow \mathbb {R}\) by  . The zeros of its derivative
. The zeros of its derivative  are
are

since \(A+B > 0\), both zeros are real and one is negative, the other positive. Let z denote the positive zero. We have  and \(f'\) is \(\le 0\) on \({\mathbb {R}}_{[0, z]}\), so f cannot have a zero here, and \(f(z) < 0\). Since f is strictly increasing on \(\mathbb {R}_{> z}\) and \(\lim _{x \rightarrow \infty } f(x) = \infty \), we conclude that f has a unique zero on \(\mathbb {R}_{> z}\) and therefore also on \(\mathbb {R}_{> 0}\).
and \(f'\) is \(\le 0\) on \({\mathbb {R}}_{[0, z]}\), so f cannot have a zero here, and \(f(z) < 0\). Since f is strictly increasing on \(\mathbb {R}_{> z}\) and \(\lim _{x \rightarrow \infty } f(x) = \infty \), we conclude that f has a unique zero on \(\mathbb {R}_{> z}\) and therefore also on \(\mathbb {R}_{> 0}\).
Since q is the root of the polynomial \(q^3 + \tau q^2 - (A+B) q - \tau B\) and polynomial roots depend continuously on the coefficients, q depends continuously on A and B as well. In particular, if A and B tend to 0, then q tends to one of the roots of \(q^3 + \tau q^2\). It cannot tend to \(-\tau \) since it is positive, so it tends to 0. \(\square \)
Given a properly embedded  -submanifold \(\mathcal {N}\subseteq \mathbb {R}^n\) without boundary and a point \(\texttt {Y}\in \mathcal {N}\), the dimension of \(\mathcal {N}\) at which we denote by \(m\), let us define the continuous function \(q_{\texttt {Y}}:\mathbb {R}^n\rightarrow \mathbb {R}_{\ge 0}\) in the following way.
-submanifold \(\mathcal {N}\subseteq \mathbb {R}^n\) without boundary and a point \(\texttt {Y}\in \mathcal {N}\), the dimension of \(\mathcal {N}\) at which we denote by \(m\), let us define the continuous function \(q_{\texttt {Y}}:\mathbb {R}^n\rightarrow \mathbb {R}_{\ge 0}\) in the following way.
Definition 2.8
If  , then \({q_{\texttt {Y}}(\texttt {X}) \mathrel {\mathop :}=d(\texttt {X}, \mathcal {N})}\) (this also covers the case \(m= n\) since then necessarily \(\mathcal {N}= \mathbb {R}^n\)). Otherwise, if \(\mathcal {N}\) has dimension 0, then \({q_{\texttt {Y}}(\texttt {X}) \mathrel {\mathop :}=d(\texttt {X}, \texttt {Y})}\). If both the dimension and codimension of \(\mathcal {N}\) are positive and
, then \({q_{\texttt {Y}}(\texttt {X}) \mathrel {\mathop :}=d(\texttt {X}, \mathcal {N})}\) (this also covers the case \(m= n\) since then necessarily \(\mathcal {N}= \mathbb {R}^n\)). Otherwise, if \(\mathcal {N}\) has dimension 0, then \({q_{\texttt {Y}}(\texttt {X}) \mathrel {\mathop :}=d(\texttt {X}, \texttt {Y})}\). If both the dimension and codimension of \(\mathcal {N}\) are positive and  , we split the definition of \(q_{\texttt {Y}}\) into two cases. Let \(q_{\texttt {Y}}(\texttt {Y}) \mathrel {\mathop :}=0\). For
, we split the definition of \(q_{\texttt {Y}}\) into two cases. Let \(q_{\texttt {Y}}(\texttt {Y}) \mathrel {\mathop :}=0\). For  introduce a tangent-normal coordinate system with the origin in \(\texttt {Y}\) (it exists by Lemma 2.6(1)). Let \(\texttt {X}= (x_1, \ldots , x_n)\) be the coordinates of \(\texttt {X}\) in this coordinate system. Define \(q_{\texttt {Y}}(\texttt {X})\) to be the unique element in \(\mathbb {R}_{> 0}\) which satisfies the equation
introduce a tangent-normal coordinate system with the origin in \(\texttt {Y}\) (it exists by Lemma 2.6(1)). Let \(\texttt {X}= (x_1, \ldots , x_n)\) be the coordinates of \(\texttt {X}\) in this coordinate system. Define \(q_{\texttt {Y}}(\texttt {X})\) to be the unique element in \(\mathbb {R}_{> 0}\) which satisfies the equation

Since the sum of squares of coordinates is independent of the choice of an orthonormal coordinate system, this equation depends only on \(\texttt {X}\) and \(\texttt {Y}\). Lemma 2.7 guarantees existence, uniqueness and continuity of \(q_{\texttt {Y}}(\texttt {X})\).
The point of this definition is that (except in the case \(m= n\), when all ellipsoids are the whole \(\mathbb {R}^n\)) the unique ellipsoid of the form  which has \(\texttt {X}\) in its boundary has \(r = q_{\texttt {Y}}(\texttt {X})\), i.e.
which has \(\texttt {X}\) in its boundary has \(r = q_{\texttt {Y}}(\texttt {X})\), i.e.  .
.
Lemma 2.9
Let \(\mathcal {N}\) be a properly embedded  -submanifold of \(\mathbb {R}^n\). Let \(\texttt {X}\in \mathbb {R}^n\) and \(\texttt {Y}\in \mathcal {N}\). Then \(d(\mathcal {N}, \texttt {X}) \le q_{\texttt {Y}}(\texttt {X})\).
-submanifold of \(\mathbb {R}^n\). Let \(\texttt {X}\in \mathbb {R}^n\) and \(\texttt {Y}\in \mathcal {N}\). Then \(d(\mathcal {N}, \texttt {X}) \le q_{\texttt {Y}}(\texttt {X})\).
Proof
If  , the statement is clear, so assume
, the statement is clear, so assume  .
.
Let \(m\) be the dimension of \(\mathcal {N}\) at \(\texttt {Y}\). If \(m= 0\), then \(d(\mathcal {N}, \texttt {X}) \le d(\texttt {Y}, \texttt {X}) = q_{\texttt {Y}}(\texttt {X})\).
For \(0< m< n\) we rely on Lemma 2.6. There is a planar tangent-normal coordinate system which has the origin in \(\texttt {Y}\) and contains \(\texttt {X}\). We can additionally assume that the axes are oriented so that \(\texttt {X}\) is in the closed first quadrant. Since  , there exists \(\varphi \in {\mathbb {R}}_{[0, \frac{\pi }{2}]}\) such that the coordinates of \(\texttt {X}\) in this coordinate system are
, there exists \(\varphi \in {\mathbb {R}}_{[0, \frac{\pi }{2}]}\) such that the coordinates of \(\texttt {X}\) in this coordinate system are

where we have shortened \(q \mathrel {\mathop :}=q_{\texttt {Y}}(\texttt {X})\). Hence

Clearly, the last expression is the largest where the function \({\mathbb {R}}_{[0, \frac{\pi }{2}]} \rightarrow \mathbb {R}\), \(\varphi \mapsto 2 - (1 - \sin (\varphi ))^2\) attains a maximum which is at \(\varphi = \tfrac{\pi }{2}\). Thus the distance \(d(\mathcal {N}, \texttt {X})\) is the largest in the normal space at \(\texttt {Y}\), where we get

\(\square \)
Let us also recall some facts about Lipschitz maps that we will need later. A map f between subsets of Euclidean spaces is Lipschitz when it has a Lipschitz coefficient \(C \in \mathbb {R}_{\ge 0}\), so that for all \(\texttt {X}, \texttt {Y}\) in the domain of f we have \(\big \Vert f(\texttt {X}) - f(\texttt {Y})\big \Vert \le C \cdot \Vert \texttt {X}- \texttt {Y}\Vert \). A function is locally Lipschitz when every point of its domain has a neighbourhood such that the restriction of the function to this neighbourhood is Lipschitz.
Let f and g be maps with Lipschitz coefficients C and D, respectively. Then clearly \(C+D\) is a Lipschitz coefficient for the functions \(f+g\) and \(f-g\), and \(C \cdot D\) is a Lipschitz coefficient for \(g \circ f\) (whenever these functions exist).
For bounded functions the Lipschitz property is preserved under further operations. A function being bounded is meant in the usual way, i.e. being bounded in norm.
Lemma 2.10
Let f and g be maps between subsets of Euclidean spaces with the same domain. Assume that f and g are bounded and Lipschitz.
-
1.
If b is bilinear with the property \(\big \Vert b(\texttt {X}, \texttt {Y})\big \Vert \le \Vert \texttt {X}\Vert \, \Vert \texttt {Y}\Vert \), then the map \(\texttt {X}\mapsto b\big (f(\texttt {X}), g(\texttt {X})\big )\) is bounded Lipschitz.Footnote 5
-
2.
Assume g takes values in \(\mathbb {R}\) and has a positive lower bound \(m \in \mathbb {R}_{> 0}\). Then the map \(x \mapsto \frac{f(\texttt {X})}{g(\texttt {X})}\) is bounded Lipschitz.
Proof
Let M be an upper bound for the norms of f and g and let C be a Lipschitz coefficient for f and g. Let \(\texttt {X}\), \(\texttt {X}'\) and \(\texttt {X}''\) be elements of the domain of f and g.
-
1.
Boundedness: \(\displaystyle {\big \Vert b\big (f(\texttt {X}), g(\texttt {X})\big )\big \Vert \le \big \Vert f(\texttt {X})\big \Vert \, \big \Vert g(\texttt {X})\big \Vert \le M^2}\). Lipschitz property:
$$\begin{aligned}&\big \Vert b\big (f(\texttt {X}'), g(\texttt {X}')\big ) - b\big (f(\texttt {X}''), g(\texttt {X}'')\big )\big \Vert \\&\quad = \big \Vert b\big (f(\texttt {X}'), g(\texttt {X}')\big ) - b\big (f(\texttt {X}''), g(\texttt {X}')\big ) + b\big (f(\texttt {X}''), g(\texttt {X}')\big ) - b\big (f(\texttt {X}''), g(\texttt {X}'')\big )\big \Vert \\&\quad \le \big \Vert f(\texttt {X}') - f(\texttt {X}'')\big \Vert \, \big \Vert g(\texttt {X}')\big \Vert + \big \Vert f(\texttt {X}'')\big \Vert \, \big \Vert g(\texttt {X}') - g(\texttt {X}'')\big \Vert \\&\quad \le 2 C M \big \Vert \texttt {X}' - \texttt {X}''\big \Vert . \end{aligned}$$ -
2.
Boundedness: \(\displaystyle {\Big \Vert \frac{f(\texttt {X})}{g(\texttt {X})}\Big \Vert = \frac{\Vert f(\texttt {X})\Vert }{|g(\texttt {X})|} \le \frac{M}{m}}\). Lipschitz property:
$$\begin{aligned} \Big \Vert \frac{f(\texttt {X}')}{g(\texttt {X}')} - \frac{f(\texttt {X}'')}{g(\texttt {X}'')}\Big \Vert&= \Big \Vert \frac{f(\texttt {X}') g(\texttt {X}'') - f(\texttt {X}'') g(\texttt {X}')}{g(\texttt {X}') g(\texttt {X}'')}\Big \Vert \\&= \frac{\Vert f(\texttt {X}') g(\texttt {X}'') - f(\texttt {X}'') g(\texttt {X}'') + f(\texttt {X}'') g(\texttt {X}'') - f(\texttt {X}'') g(\texttt {X}')\Vert }{|g(\texttt {X}') g(\texttt {X}'')|} \\&\le \frac{\Vert f(\texttt {X}') - f(\texttt {X}'')\Vert \, \Vert g(\texttt {X}'')\Vert + \Vert f(\texttt {X}'')\Vert \, \Vert g(\texttt {X}'') - g(\texttt {X}')\Vert }{|g(\texttt {X}')| \, |g(\texttt {X}'')|} \\&\le \frac{2 C M}{m^2} \big \Vert \texttt {X}' - \texttt {X}''\big \Vert . \end{aligned}$$
\(\square \)
Corollary 2.11
Let \((U_i)_{i \in I}\) be a locally finite open cover of a subset U of a Euclidean space, \((f_i)_{i \in I}\) a subordinate smooth partition of unity and \((g_i:U_i \rightarrow \mathbb {R}^n)_{i \in I}\) a family of maps. Let \(g:U \rightarrow \mathbb {R}^n\) be the map, obtained by gluing maps \(g_i\) with the partition of unity \(f_i\), i.e.
Then if all \(g_i\) are locally Lipschitz, so is g.
Proof
Every continuous map is locally bounded, including the derivative of a smooth map, the bound on which is then a local Lipschitz coefficient for the map. We can apply this for \(f_i\).
Given \(x \in U\), pick an open set \(V \subseteq U\), for which the following holds: \(x \in V\), there is a finite set of indices \(F \subseteq I\) such that V intersects only \(U_i\) with \(i \in F\) and \(V \subseteq \bigcap _{i \in F} U_i\), and the maps \(f_i\) and \(g_i\) are bounded and Lipschitz on V for every \(i \in F\). Then \(\left. {g}\right| _V = \sum _{i \in F} \left. {f_i}\right| _V \;\! \left. {g_i}\right| _V\) which is Lipschitz on V by Lemma 2.10. \(\square \)
3 Calculating bounds on persistence parameter
Having derived some results for more general manifolds, we now specify the manifolds for which our main theorem holds. We reserve the symbol \(\mathcal {M}\) for such a manifold.
Let \(\mathcal {M}\) be a non-empty \(m\)-dimensional properly embedded  -submanifold of \(\mathbb {R}^n\) without boundary, and let \({\mathcal {A}}\) be its medial axis. Let \(\tau \) denote the reach of \(\mathcal {M}\). In this section we assume \(\tau < \infty \) and in Sects. 4 and 5 we assume \(\tau = 1\). We will drop these assumptions on \(\tau \) for the main theorem in Sect. 6.
-submanifold of \(\mathbb {R}^n\) without boundary, and let \({\mathcal {A}}\) be its medial axis. Let \(\tau \) denote the reach of \(\mathcal {M}\). In this section we assume \(\tau < \infty \) and in Sects. 4 and 5 we assume \(\tau = 1\). We will drop these assumptions on \(\tau \) for the main theorem in Sect. 6.
By Proposition 2.1 and the definition of a medial axis the map \(pr:\mathbb {R}^n\setminus {\mathcal {A}} \rightarrow \mathcal {M}\), which takes a point to its closest point on the manifold \(\mathcal {M}\), is well defined. We also define  , \(prv(\texttt {X}) \mathrel {\mathop :}=pr(\texttt {X}) - \texttt {X}\). We view \(prv(\texttt {X})\) as the vector, starting at \(\texttt {X}\) and ending in \(pr(\texttt {X})\). This vector is necessarily normal to the manifold, i.e. it lies in
, \(prv(\texttt {X}) \mathrel {\mathop :}=pr(\texttt {X}) - \texttt {X}\). We view \(prv(\texttt {X})\) as the vector, starting at \(\texttt {X}\) and ending in \(pr(\texttt {X})\). This vector is necessarily normal to the manifold, i.e. it lies in  . By the definition of the reach, the maps \(pr\) and \(prv\) are defined on
. By the definition of the reach, the maps \(pr\) and \(prv\) are defined on  .
.
Lemma 3.1
For every  the maps \(pr\) and \(prv\) are Lipschitz when restricted to \(\overline{\mathcal {M}}_{r}\), with Lipschitz coefficients
the maps \(pr\) and \(prv\) are Lipschitz when restricted to \(\overline{\mathcal {M}}_{r}\), with Lipschitz coefficients  and
and  , respectively. Hence these two maps are continuous on
, respectively. Hence these two maps are continuous on  .
.
Proof
The map \(pr\) is Lipschitz on \(\overline{\mathcal {M}}_{r}\) by Chazal et al. (2017, Proposition 2) with a Lipschitz coefficient  (Federer 1959, Theorem 4.8(8)). As a difference of two Lipschitz maps, the map \(prv\) is Lipschitz as well, with a Lipschitz coefficient
(Federer 1959, Theorem 4.8(8)). As a difference of two Lipschitz maps, the map \(prv\) is Lipschitz as well, with a Lipschitz coefficient  . The maps \(pr\) and \(prv\) are therefore continuous on \(\mathcal {M}_{r}\) for all
. The maps \(pr\) and \(prv\) are therefore continuous on \(\mathcal {M}_{r}\) for all  , and hence also on the union . \(\square \)
, and hence also on the union . \(\square \)
We want to approximate the manifold \(\mathcal {M}\) with a sample. We assume that the sample set \(\mathcal {S}\) is a non-empty discrete subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (meaning, every point in \(\mathbb {R}^n\) has a neighbourhood which intersects only finitely many points of \(\mathcal {S}\)). It follows that \(\mathcal {S}\) is a closed subset of \(\mathbb {R}^n\).
Let \(\varkappa \) denote the Hausdorff distance between \(\mathcal {M}\) and \(\mathcal {S}\). We assume that \(\varkappa \) is finite. This value represents the density of our sample: it means that every point on the manifold \(\mathcal {M}\) has a point in the sample \(\mathcal {S}\) which is at most \(\varkappa \) away.
Since \(\mathcal {M}\) is properly embedded in \(\mathbb {R}^n\) and \(\varkappa < \infty \), the sample \(\mathcal {S}\) is finite if and only if \(\mathcal {M}\) is compact. A properly embedded non-compact submanifold without boundary needs to extend to infinity and so cannot be sampled with finitely many points (think for example about the hyperbola in the plane, \(x^2 - y^2 = 1\)). As it turns out, we do not need finiteness, only local finiteness, to prove our results.
If the sample is dense enough in the manifold, it should be a good approximation to it. Specifically, we want to recover at least the homotopy type of \(\mathcal {M}\) from the information, gathered from \(\mathcal {S}\). A common way to do this is to enlarge the sample points to balls, the union of which deformation retracts to the manifold, so has the same homotopy type (in other words, we consider a Čech complex of the sample).
As we already discussed in the introduction, in this paper we use ellipsoids instead of balls, since a tangent space at a point is a good approximation for the manifold at that point, so an ellipsoid with the major semi-axes in the tangent directions better approximates the manifold than a ball. Consequently we should require a less dense sample for the approximation. This idea indeed pans out (as demonstrated by Theorem 6), though it turns out that the standard methods, used to construct the deformation retraction from the union of balls to the manifold, do not work for the ellipsoids.
Given a persistence parameter \(p\in \mathbb {R}_{> 0}\), let us denote the unions of open and closed tangent-normal \(p\)-ellipsoids around sample points by

As a union of open sets,  is open in \(\mathbb {R}^n\). As a locally finite union of closed sets,
is open in \(\mathbb {R}^n\). As a locally finite union of closed sets,  is closed in \(\mathbb {R}^n\).
is closed in \(\mathbb {R}^n\).
We want a deformation retraction from  to \(\mathcal {M}\). Clearly this will not work for all \(p\in \mathbb {R}_{> 0}\). If \(p\) is too small,
to \(\mathcal {M}\). Clearly this will not work for all \(p\in \mathbb {R}_{> 0}\). If \(p\) is too small,  covers only some blobs around sample points, not the whole \(\mathcal {M}\). If \(p\) is too large,
covers only some blobs around sample points, not the whole \(\mathcal {M}\). If \(p\) is too large,  reaches over the medial axis \({\mathcal {A}}\), therefore creates connections which do not exist in the manifold, so differs from it in the homotopy type. This suggests that the lower bound on \(p\) will be expressed in terms of \(\varkappa \) (the denser the sample, the smaller the required \(p\) for
reaches over the medial axis \({\mathcal {A}}\), therefore creates connections which do not exist in the manifold, so differs from it in the homotopy type. This suggests that the lower bound on \(p\) will be expressed in terms of \(\varkappa \) (the denser the sample, the smaller the required \(p\) for  to cover \(\mathcal {M}\)), and the upper bound on \(p\) will be expressed in terms of \(\tau \) (the further away the medial axis, the larger we can make the ellipsoids so that they still do not intersect the medial axis).
to cover \(\mathcal {M}\)), and the upper bound on \(p\) will be expressed in terms of \(\tau \) (the further away the medial axis, the larger we can make the ellipsoids so that they still do not intersect the medial axis).
Lemma 3.2
-
1.
Assume \(p\in \mathbb {R}_{> 0}\) satisfies
 . Then
. Then  , i.e.
, i.e.  is an open cover of \(\mathcal {M}\).
is an open cover of \(\mathcal {M}\). -
2.
The map \(\mathbb {R}_{> 0} \rightarrow \mathbb {R}_{> 0}\),
 , is strictly increasing. Thus there exists a unique \(\lambda \in \mathbb {R}_{> 0}\) such that
, is strictly increasing. Thus there exists a unique \(\lambda \in \mathbb {R}_{> 0}\) such that 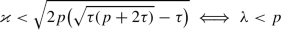
for all \(p\in \mathbb {R}_{> 0}\).
Proof
-
1.
Take any \(\texttt {X}\in \mathcal {M}\). By assumption there exists \(\texttt {S}\in \mathcal {S}\) such that \(d(\texttt {X}, \texttt {S}) \le \varkappa \). We claim that
 . If \(m= n\), then
. If \(m= n\), then  , and a quick calculation shows that
, and a quick calculation shows that 
so
 . If \(m= 0\), then
. If \(m= 0\), then  and the reach \(\tau \) is half of the distance between the two closest distinct points in \(\mathcal {M}\) (since we are assuming \(\tau < \infty \) and therefore \({\mathcal {A}} \ne \emptyset \), the manifold \(\mathcal {M}\) must have at least two points). If \(p\le 2\tau \), then
and the reach \(\tau \) is half of the distance between the two closest distinct points in \(\mathcal {M}\) (since we are assuming \(\tau < \infty \) and therefore \({\mathcal {A}} \ne \emptyset \), the manifold \(\mathcal {M}\) must have at least two points). If \(p\le 2\tau \), then 
so necessarily
 . If \(p> 2\tau \), then
. If \(p> 2\tau \), then 
so
 . Assume hereafter that \(0< m< n\). Choose a planar tangent-normal coordinate system with the origin in \(\texttt {S}\) which contains \(\texttt {X}\) (use Lemma 2.6(1)). In this coordinate system the boundary of
. Assume hereafter that \(0< m< n\). Choose a planar tangent-normal coordinate system with the origin in \(\texttt {S}\) which contains \(\texttt {X}\) (use Lemma 2.6(1)). In this coordinate system the boundary of  is given by the equation
is given by the equation  . A routine calculation shows that it intersects the boundaries of the \(\tau \)-balls, associated to \(\texttt {S}\) (with centers in \(\texttt {C}' = (0, \tau )\) and \(\texttt {C}'' = (0, -\tau )\)), given by the equations \(x^2 + (y \pm \tau )^2 = \tau ^2\), in the points
. A routine calculation shows that it intersects the boundaries of the \(\tau \)-balls, associated to \(\texttt {S}\) (with centers in \(\texttt {C}' = (0, \tau )\) and \(\texttt {C}'' = (0, -\tau )\)), given by the equations \(x^2 + (y \pm \tau )^2 = \tau ^2\), in the points 
the norm of which is
 . It follows that within the given two-dimensional coordinate system
. It follows that within the given two-dimensional coordinate system 
see Fig. 2. Since \(\texttt {S}\in \mathcal {M}\) and the reach of \(\mathcal {M}\) is \(\tau \), the manifold \(\mathcal {M}\) does not intersect the open \(\tau \)-balls, associated to \(\texttt {S}\), so
 .
. -
2.
The derivative of the given function is

which is positive for \(p, \tau > 0\) which assures the existence of the required \(\lambda \). Calculated with Mathematica, the actual value is
$$\begin{aligned}\lambda= & {} \frac{2 \tau \left( 3 \kappa ^2+\tau ^2\right) }{3 \root 3 \of {27 \kappa ^4 \tau ^2-36 \kappa ^2 \tau ^4+3 \sqrt{81 \kappa ^8 \tau ^4-408 \kappa ^6 \tau ^6-96 \kappa ^4 \tau ^8}-8 \tau ^6}}\\ {}{} & {} + \frac{\root 3 \of {27 \kappa ^4 \tau ^2-36 \kappa ^2 \tau ^4+3 \sqrt{81 \kappa ^8 \tau ^4-408 \kappa ^6 \tau ^6-96 \kappa ^4 \tau ^8}-8 \tau ^6}}{6 \tau }-\frac{\tau }{3}.\end{aligned}$$
\(\square \)
We can strengthen this result to thickenings of \(\mathcal {M}\) (recall the notation for open and closed thickenings,  ,
,  ).
).
Corollary 3.3
For every \(r \in \mathbb {R}_{\ge 0}\) and every \(p\in \mathbb {R}_{> \lambda + r}\) we have  .
.
Proof
Lemma 3.2 implies that  . Hence \(\overline{\mathcal {M}}_{r}\) is contained in the union of r-thickenings of open ellipsoids
. Hence \(\overline{\mathcal {M}}_{r}\) is contained in the union of r-thickenings of open ellipsoids  , and an r-thickening of
, and an r-thickening of  is contained in
is contained in  . \(\square \)
. \(\square \)
Let us now also get an upper bound on \(p\).
Lemma 3.4
Assume  . Then
. Then  ; in particular
; in particular  and
and  do not intersect the medial axis of \(\mathcal {M}\).
do not intersect the medial axis of \(\mathcal {M}\).
Proof
Take any \(\texttt {S}\in \mathcal {S}\) and  . By Lemma 2.9 we have
. By Lemma 2.9 we have  . \(\square \)
. \(\square \)
The results in this section give the theoretical bounds on the persistence parameter \(p\), within which we look for a deformation retraction from  to \(\mathcal {M}\), which we summarize in the following corollary (where \({\mathcal {A}}^\complement = \mathbb {R}^n \setminus {\mathcal {A}}\)).
to \(\mathcal {M}\), which we summarize in the following corollary (where \({\mathcal {A}}^\complement = \mathbb {R}^n \setminus {\mathcal {A}}\)).
Corollary 3.5
If  , then
, then  .
.
4 Program
In this section (as well as the next one) we assume that \(\tau = 1\) and \(0< m< n\).
Our goal is to prove that if we restrict the persistence parameter \(p\) to a suitable interval, the union of ellipsoids  deformation retracts to \(\mathcal {M}\). Recall that the normal deformation retraction is the map retracting a point to its closest point on the manifold, i.e. the convex combination of a point and its projection: \({(\texttt {X}, t) \mapsto (1-t) \;\! \texttt {X}+ t \;\! pr(\texttt {X}) = \texttt {X}+ t \;\! prv(\texttt {X})}\). For example, in Niyogi et al. (2008) this is how the union of balls around sample points is deformation retracted to the manifold.
deformation retracts to \(\mathcal {M}\). Recall that the normal deformation retraction is the map retracting a point to its closest point on the manifold, i.e. the convex combination of a point and its projection: \({(\texttt {X}, t) \mapsto (1-t) \;\! \texttt {X}+ t \;\! pr(\texttt {X}) = \texttt {X}+ t \;\! prv(\texttt {X})}\). For example, in Niyogi et al. (2008) this is how the union of balls around sample points is deformation retracted to the manifold.
The same idea does not in general work for the union of ellipsoids, or any other sufficiently elongated figures. Figure 3 shows what can go wrong.
However, it turns out that the only places where the normal deformation retraction does not work are the neighbourhoods of tips of some ellipsoids which avoid all other ellipsoids. This section is dedicated to proving the following form of this claim: for all points in at least two ellipsoids the normal deformation retraction works. This means that the line segment between a point \(\texttt {X}\) and \(pr(\texttt {X})\) is contained in the union of ellipsoids, but actually more holds: the line segment is contained already in one of the ellipsoids. More formally, the rest of the section is the proof of the following lemma.
Lemma 4.1
For every  , if there are \(\texttt {S}', \texttt {S}'' \in \mathcal {S}\), \(\texttt {S}' \ne \texttt {S}''\) such that
, if there are \(\texttt {S}', \texttt {S}'' \in \mathcal {S}\), \(\texttt {S}' \ne \texttt {S}''\) such that  , then there exists \(\texttt {S}\in \mathcal {S}\) such that
, then there exists \(\texttt {S}\in \mathcal {S}\) such that  . By convexity the entire line segment between \(\texttt {X}\) and \(pr(\texttt {X})\) is therefore in
. By convexity the entire line segment between \(\texttt {X}\) and \(pr(\texttt {X})\) is therefore in  .
.
To prove this, we would in principle need to examine all possible configurations of ellipsoids and a point. However, we can restrict ourselves to a set of cases, which include the “worst case scenarios”.
Let \(\texttt {S}', \texttt {S}'' \in \mathcal {S}\) be two different sample points, and let  (we purposefully take closed ellipsoids here). Denote \(\texttt {Y}\mathrel {\mathop :}=pr(\texttt {X})\). We claim that there is \(\texttt {S}\in \mathcal {S}\) (not necessarily distinct from \(\texttt {S}'\) and \(\texttt {S}''\)) such that
(we purposefully take closed ellipsoids here). Denote \(\texttt {Y}\mathrel {\mathop :}=pr(\texttt {X})\). We claim that there is \(\texttt {S}\in \mathcal {S}\) (not necessarily distinct from \(\texttt {S}'\) and \(\texttt {S}''\)) such that  and
and  . Due to convexity of ellipsoids, the line segment \(\texttt {X}\texttt {Y}\) is in
. Due to convexity of ellipsoids, the line segment \(\texttt {X}\texttt {Y}\) is in  ; with the possible exception of the point \(\texttt {X}\), this line segment is in
; with the possible exception of the point \(\texttt {X}\), this line segment is in  .
.
Assuming \(p\in {\mathbb {R}}_{(\lambda , 1)}\), the point \(\texttt {Y}\) is covered by at least one open ellipsoid. Suppose that none of the closed ellipsoids, containing \(\texttt {Y}\) in their interior, contains \(\texttt {X}\). Let us try to construct a situation where this is most likely to be the case. We will derive a contradiction by showing that even in these “worst case scenarios” we fail in satisfying this assumption.
To determine whether a point \(\texttt {X}\) is in the ellipsoid with the center \(\texttt {S}'\), the following two pieces of information are sufficient: the distance between \(\texttt {X}\) and \(\texttt {S}'\), and the angle between the line segment \(\texttt {X}\texttt {S}'\) and the normal space  . Moreover, membership of \(\texttt {X}\) in the ellipsoid is “monotone” with respect to these two conditions: if a point is in the ellipsoid, it will remain so if we decrease its distance to \(\texttt {S}'\) or increase the angle to the normal space.
. Moreover, membership of \(\texttt {X}\) in the ellipsoid is “monotone” with respect to these two conditions: if a point is in the ellipsoid, it will remain so if we decrease its distance to \(\texttt {S}'\) or increase the angle to the normal space.
We will produce a set of configurations which include the extremal points for these two criteria (maximal distance from the ellipsoid center, minimal angle to the normal space). If every such point is still in the ellipsoid, then all possible points are.
Consider a planar tangent-normal coordinate system with the origin in \(\texttt {S}'\) which contains \(\texttt {X}\) in the fourth quadrant (nonnegative tangent coordinate, nonpositive normal coordinate). In this coordinate system, the manifold passes horizontally through \(\texttt {S}'\). Consider the part of the manifold with positive tangent coordinate (i.e. the part of the manifold rightwards of \(\texttt {S}'\)). The fastest that this piece can turn away from \(\texttt {X}\) is in this plane along the boundary of the upper \(\tau \)-ball, associated to \(\texttt {S}'\).Footnote 6 Suppose the manifold continues along this path until some point \(\texttt {X}'\), and consider a plane containing the points \(\texttt {X}\), \(\texttt {X}'\) and \(\texttt {S}\) where the distance between \(\texttt {S}\in \mathcal {S}\) and \(\texttt {Y}\) is bounded by \(\varkappa \), so  . Going from \(\texttt {X}'\) to \(\texttt {S}\), the quickest way to turn the normal direction towards \(\texttt {X}\) is within this plane, and along a \(\tau \)-arc. While this second plane need not be the same as the first one, they intersect along the line containing \(\texttt {X}\) and \(\texttt {X}'\). We can turn the half-plane containing \(\texttt {S}'\) and the half-plane containing \(\texttt {S}\) along the line so that they form one plane, and that will be the configuration where it is equally (un)likely for
. Going from \(\texttt {X}'\) to \(\texttt {S}\), the quickest way to turn the normal direction towards \(\texttt {X}\) is within this plane, and along a \(\tau \)-arc. While this second plane need not be the same as the first one, they intersect along the line containing \(\texttt {X}\) and \(\texttt {X}'\). We can turn the half-plane containing \(\texttt {S}'\) and the half-plane containing \(\texttt {S}\) along the line so that they form one plane, and that will be the configuration where it is equally (un)likely for  to contain \(\texttt {X}\) (since we did not change any relative positions in the half-plane containing \(\texttt {X}\), \(\texttt {X}'\) and \(\texttt {S}\)), but where \(\texttt {S}'\), \(\texttt {X}\), \(\texttt {X}'\), \(\texttt {Y}\) and \(\texttt {S}\) all lie in the same plane.
to contain \(\texttt {X}\) (since we did not change any relative positions in the half-plane containing \(\texttt {X}\), \(\texttt {X}'\) and \(\texttt {S}\)), but where \(\texttt {S}'\), \(\texttt {X}\), \(\texttt {X}'\), \(\texttt {Y}\) and \(\texttt {S}\) all lie in the same plane.
We can make the same argument starting from \(\texttt {S}''\) instead of \(\texttt {S}'\), so we conclude the following: if our claim fails for some configuration of \(\texttt {X}\), \(\texttt {Y}\), \(\texttt {S}'\), \(\texttt {S}''\), \(\texttt {S}\), then it fails in a planar case where the part of the manifold connecting points \(\texttt {S}'\) and \(\texttt {S}''\) consists of (at most) three \(\tau \)-arcs, as in Fig. 4.
We started with the assumption  , but we may without loss of generality additionally assume
, but we may without loss of generality additionally assume  . If we had a counterexample \(\texttt {X}\) to our claim in the interior of all ellipsoids containing \(\texttt {X}\), we could project it in the opposite direction of \(pr(\texttt {X})\) to the first ellipsoid boundary we hit, and declare the center of that ellipsoid to be \(\texttt {S}'\).
. If we had a counterexample \(\texttt {X}\) to our claim in the interior of all ellipsoids containing \(\texttt {X}\), we could project it in the opposite direction of \(pr(\texttt {X})\) to the first ellipsoid boundary we hit, and declare the center of that ellipsoid to be \(\texttt {S}'\).
Although the reduction of cases we have made is already a vast simplification of the necessary calculations, we find that it is still not enough to make a theoretical derivation of the desired result feasible. Instead, we produce a proof with a computer.
We can reduce the possible configurations to four parameters (see Fig. 5):
-
\(\alpha \) denotes the angle measuring the length of the first \(\tau \)-arc,
-
\(\sigma \) denoted the angle for the second \(\tau \)-arc until \(\texttt {S}\),
-
\(p\) is, as usual, the persistence parameter,
-
\(\chi \) determines the position of \(\texttt {X}\) in the boundary
 .
.
Notice that Fig. 5 does not include both ellipsoids containing \(\texttt {X}\) but not \(\texttt {Y}\), like Fig. 4 does. In order to derive Lemma 4.1, we will prove with the help from the computer that as soon as \(\texttt {Y}\) is not in the first ellipsoid, both \(\texttt {X}\) and \(\texttt {Y}\) will be in an ellipsoid, the center of which is within \(\varkappa \) distance from \(\texttt {Y}\). This allows us to restrict ourselves to just the four aforementioned variables, which makes the program run in a reasonable time.
The space of the configurations we restricted ourselves to—let us denote it by \(\mathscr {C}\)—is compact (we give its precise definition below). We want to calculate for each configuration in \(\mathscr {C}\) that \(\texttt {X}\) is in some ellipsoid with the center within \(\varkappa \) distance from \(\texttt {Y}\) (it follows automatically that \(\texttt {Y}\) is in this ellipsoid). The boundary of the ellipsoid is a level set of a smooth function. We can compose it with a suitable linear function so that \(\texttt {X}\) is in the open ellipsoid if and only if the value of the adjusted function is positive. Let us denote this adjusted function by \(v:\mathscr {C}\rightarrow \mathbb {R}\); we have our claim if we show that \(v\) is positive for all configurations in \(\mathscr {C}\).
Of course, the program cannot calculate the function values for all infinitely many configurations in \(\mathscr {C}\). We note that the (continuous) partial derivatives of \(v\) are bounded on compact \(\mathscr {C}\), hence the function is Lipschitz. If we change the parameters by at most \(\delta \), the function value changes by at most \(C \cdot \delta \) where C is the Lipschitz coefficient. The program calculates the function values in a finite lattice of points, so that each point in \(\mathscr {C}\) is at most a suitable \(\delta \) away from the lattice, and verifies that all these values are larger than \(C \cdot \delta \). This shows that \(v\) is positive on the whole \(\mathscr {C}\).
Let us now define \(\mathscr {C}\) precisely and then calculate the Lipschitz coefficient of \(v\). We may orient the coordinate system so that the point \(\texttt {X}\) is in the closed fourth quadrant. Hence we have \(\texttt {X}= \big (\sqrt{p+ p^2} \cos (\chi ), -p\, \sin (\chi )\big )\), where \(\chi \) ranges over the interval \({\mathbb {R}}_{[0, \frac{\pi }{2}]}\).
Unfortunately due to our method we cannot allow \(p\) to range over the whole interval \({\mathbb {R}}_{(\lambda , 1)}\); if we did, the values of \(v\) would come arbitrarily close to zero, in particular below \(C \cdot \delta \), so the program would not prove anything. Let us set \(p\in {\mathbb {R}}_{[m_p, M_p]}\), where we have chosen in our program \(m_p\mathrel {\mathop :}=0.5\) and \(M_p\mathrel {\mathop :}=0.96\). The closer \(M_p\) is to 1, the smaller the density we prove is required. However, larger \(M_p\) necessitates smaller \(\delta \) which increases the computation time. Through experimentation, we have chosen bounds, so that the program ran for a few days. Ultimately, with better computers (and more patience) one can improve our result. We note that experimentally we never came across any counterexample to our claims even outside of \(\mathscr {C}\) (so long as the configuration satisfied the theoretical assumptions from Corollary 3.5). We discuss this further in Sect. 7.
We can now calculate the upper bound on \(\alpha \) (the lower bound is just 0). For fixed \(p\) and \(\chi \) we claim that the case \(\alpha \ge \arctan \big (\frac{\sqrt{p+ p^2} \cos (\chi )}{1 + p\, \sin (\chi )}\big )\) is impossible. In this case the point \((0, 1) + \frac{\texttt {X}- (0, 1)}{\Vert \texttt {X}- (0, 1)\Vert }\) lies on the manifold, and is the closest to \(\texttt {X}\) among points on \(\mathcal {M}\). This is because its distance to \(\texttt {X}\) is bounded by \(p\) (by Lemma 2.9) which is smaller than \(\tau = 1\), so its associated \(\tau \)-ball includes all points, closer to \(\texttt {X}\), and \(\mathcal {M}\) cannot intersect an open associated \(\tau \)-ball—see Fig. 6.
We claim that the point \(pr(\texttt {X}) = (0, 1) + \frac{\texttt {X}- (0, 1)}{\Vert \texttt {X}- (0, 1)\Vert }\) lies in  . This is a contradiction since then
. This is a contradiction since then  .
.
Clearly, it suffices to verify  for \(\chi = 0\) (for larger \(\chi \) the point \(pr(\texttt {X})\) lies on the \(\tau \)-arc further towards the ellipsoid center \(\texttt {S}'\)). If we put the coordinates of \(pr(\texttt {X})\) for \(\chi = 0\) into the equation for the ellipsoid, we see that we need \(\frac{2p^2 + p + 2 - 2 \sqrt{p^2+p+1}}{p^4 + p^3 + p^2} < 1\). This is equivalent to \(-p^8-2 p^7+p^6+4 p^5+5 p^4+2 p^3-p^2 > 0\), which is equivalent to \(-p^2 (p+1) \big (p^5+p^4-2 p^3-2 p^2-3 p+1\big ) > 0\) which is further equivalent to \(p^5+p^4-2 p^3-2 p^2-3 p+1 < 0\). The derivative of the polynomial on the left is
for \(\chi = 0\) (for larger \(\chi \) the point \(pr(\texttt {X})\) lies on the \(\tau \)-arc further towards the ellipsoid center \(\texttt {S}'\)). If we put the coordinates of \(pr(\texttt {X})\) for \(\chi = 0\) into the equation for the ellipsoid, we see that we need \(\frac{2p^2 + p + 2 - 2 \sqrt{p^2+p+1}}{p^4 + p^3 + p^2} < 1\). This is equivalent to \(-p^8-2 p^7+p^6+4 p^5+5 p^4+2 p^3-p^2 > 0\), which is equivalent to \(-p^2 (p+1) \big (p^5+p^4-2 p^3-2 p^2-3 p+1\big ) > 0\) which is further equivalent to \(p^5+p^4-2 p^3-2 p^2-3 p+1 < 0\). The derivative of the polynomial on the left is
so \(p^5+p^4-2 p^3-2 p^2-3 p+1\) is decreasing on \({\mathbb {R}}_{[m_p, M_p]} \subseteq {\mathbb {R}}_{(0, 1)}\). The value of this polynomial at \(m_p= 0.5\) is \(-1.15625 < 0\), so the polynomial is negative on \({\mathbb {R}}_{[m_p, M_p]}\), as required.Footnote 7
With this we have confirmed that it suffices to restrict ourselves to \(\alpha \le \arctan \big (\frac{\sqrt{p+ p^2} \cos (\chi )}{1 + p\, \sin (\chi )}\big )\). As mentioned, this bound will be the largest at \(\chi = 0\), so we will cover the relevant configurations for \(\alpha \le \arctan \big (\sqrt{p+ p^2}\big )\), or equivalently (for \(\alpha \in {\mathbb {R}}_{[0, \frac{\pi }{2})}\) and \(p\in {\mathbb {R}}_{(0, 1)}\)) \(\tan ^2(\alpha ) \le p+ p^2\), in particular \(\tan ^2(\alpha ) \le M_p+ M_p^2\).
Finally, we claim that we can restrict ourselves to \(\sigma \in {\mathbb {R}}_{[0, \pi ]}\). If the manifold were to trace a \(\tau \)-circle within a plane for longer than \(\pi \), it would necessarily be that \(\tau \)-circle. This is because if \(\pi< \sigma < 2\pi \), the center \(\texttt {C}\) of the circle would not be isolated in the medial axis; see Fig. 7 for an illustration.
Pick a point \(\texttt {P}\) on the medial axis at distance less than  from \(\texttt {C}\), but different from \(\texttt {C}\). If \(\texttt {P}\) is contained in the sector, spanned by \(\sigma \), then clearly
from \(\texttt {C}\), but different from \(\texttt {C}\). If \(\texttt {P}\) is contained in the sector, spanned by \(\sigma \), then clearly  , a contradiction. Otherwise, the same contradiction follows from the claim that \(\texttt {P}\) is contained in the union of the two open
, a contradiction. Otherwise, the same contradiction follows from the claim that \(\texttt {P}\) is contained in the union of the two open  -balls with centers where \(\mathcal {M}\) departs the circle. For this, set \(\varphi \mathrel {\mathop :}=\pi - \tfrac{\sigma }{2}\), see Fig. 8 and note that the solutions to the system of equations
-balls with centers where \(\mathcal {M}\) departs the circle. For this, set \(\varphi \mathrel {\mathop :}=\pi - \tfrac{\sigma }{2}\), see Fig. 8 and note that the solutions to the system of equations  , \(y = 0\) are \(x = 0\) (which we are not interested in) and
, \(y = 0\) are \(x = 0\) (which we are not interested in) and  .
.
If the manifold was indeed just a circle in a plane, then \(\texttt {Y}\) would be inside of  by the same argument we used when calculating the bound on \(\alpha \). Hence we may postulate \(\sigma \in {\mathbb {R}}_{[0, \pi ]}\).
by the same argument we used when calculating the bound on \(\alpha \). Hence we may postulate \(\sigma \in {\mathbb {R}}_{[0, \pi ]}\).
Having calculated the bounds on the variables, we may now define

For the sake of a later calculation we also define a slightly bigger area,

Both \(\mathscr {C}\) and \(\widetilde{\mathscr {C}}\) are 4-dimensional rectangular cuboids with a small piece removed; in the \(\alpha \)-\(p\)-plane they look as shown in Fig. 9.
Given \((\alpha , \sigma , p, \chi ) \in \mathscr {C}\), we have \(\texttt {X}= (\texttt {X}_T, \texttt {X}_N) = \big (\sqrt{p+ p^2} \cos (\chi ), -p\, \sin (\chi )\big )\). Let us denote the center of the \(\tau \)-ball, along the boundary of which lies the arc containing \(\texttt {S}\), by \(\texttt {C}\). Observe from Fig. 10 that \(\texttt {C}= (0, 1) + 2 \big (\sin (\alpha ), -\cos (\alpha )\big )\) and
(this works also if \(\alpha -\sigma \) is negative).
It will be convenient to define \(v\) on the larger area \(\widetilde{\mathscr {C}}\) (although we are still only interested in positivity of \(v\) on \(\mathscr {C}\)). Recall that we want \(v\) to be a function, so that its 0-level set is the boundary of  , and is positive on
, and is positive on  itself. Let x, y be coordinates in our current coordinate system, \(x', y'\) the coordinates in the coordinate system, translated by \(\texttt {S}\), and \(x'', y''\) the coordinates if we rotate the translated coordinate system by \(\alpha -\sigma \) in the positive direction. Hence
itself. Let x, y be coordinates in our current coordinate system, \(x', y'\) the coordinates in the coordinate system, translated by \(\texttt {S}\), and \(x'', y''\) the coordinates if we rotate the translated coordinate system by \(\alpha -\sigma \) in the positive direction. Hence
In the rotated translated coordinate system, the equation for the boundary of the ellipse is \(\frac{x''^2}{p+ p^2} + \frac{y''^2}{p^2} = 1\), or equivalently \(p^2 (p+1) - \big (x''^2 p+ y''^2 (p+1)\big ) = 0\). We therefore define \(f:\widetilde{\mathscr {C}}\rightarrow \mathbb {R}\) by
Recall that it follows from the multivariate Lagrange mean value theorem that for any \(a, b \in \widetilde{\mathscr {C}}\)
where the maximum of the norm of the gradient is taken over the line segment connecting the points a and b. In particular, the maximum over the entire \(\widetilde{\mathscr {C}}\) is a Lipschitz coefficient for \(v\).
This theorem holds for any pair of conjugate norms. We take the \(\infty \)-norm on \(\widetilde{\mathscr {C}}\), and the 1-norm for the gradient. The reason is that we cover the region \(\mathscr {C}\) by cuboids which are almost cubes (in the centers of which we calculate the function values). The smaller the distance between the center of a cube and any of its points, the better the estimate we obtain. Hence

Before we estimate the absolute values of partial derivatives, let us make several preliminary calculations.
First we put the function into a more convenient form.
Now we calculate the bound on \(\texttt {X}- \texttt {S}\) and its partial derivatives.
The norm will be the largest when either the components are largest (\(\chi = 0\), \(\alpha = 0\)) or smallest (\(\chi = \frac{\pi }{2}\), \(\alpha = \alpha _{\max } \mathrel {\mathop :}=\arctan (\sqrt{2p+ p^2})\)). In the first case we get \({\Vert \texttt {X}- \texttt {C}\Vert ^2 \le p^2 + p+ 1}\) and in the second (taking into account \(\cos (\alpha _{\max }) = \frac{1}{\sqrt{1 + \tan ^2(\alpha _{\max })}} = \frac{1}{\sqrt{1 + 2p+ p^2}} = \frac{1}{1 + p}\))
so either way \(\Vert \texttt {X}- \texttt {S}\Vert \le 2 + p\le 2 + M_p\).
Here the last equality holds because \((1 + 2p)^2 = 1 + 4p+ 4p^2 \ge 4p+ 4p^2 = (2 \sqrt{p+ p^2})^2\) and the last inequality holds because \(\frac{1 + 2p}{2 \sqrt{p+ p^2}}\) is a decreasing function: its derivative is \(-\frac{1}{4 (p+ p^2)^{\frac{3}{2}}}\).
Next we calculate a bound on the term \(\langle {(-\sin (\alpha -\sigma ), \cos (\alpha -\sigma ))}, {\texttt {X}- \texttt {S}}\rangle \) and its derivatives.
We can now estimate the partial derivatives of \(v\).
Hence a Lipschitz coefficient for \(v\) on \(\widetilde{\mathscr {C}}\) is
which is a little less than 125.
The idea behind the program is that it accepts a value \(\delta \in \mathbb {R}_{> 0}\), sets each of the variables \(\alpha \), \(\sigma \), \(p\), \(\chi \) at \(\delta \) away from the edge of \(\widetilde{\mathscr {C}}\) and calculates the values of \(v\) in a lattice of points, of which any two consecutive ones differ in the values of the variables by \(2\delta \). The idea is that \(\infty \)-balls (cubes) with the centers in the lattice points and radius \(\delta \) cover \(\mathscr {C}\), so if the values of \(v\) in these points is \(> L\, \delta \), then \(v\) is positive.
This requires two remarks, however. First, if one tries to evenly cover a cuboid by cubes with edge length \(2\delta \) and with centers within the cuboid, the cuboid will not be covered, if dividing any cuboid edge length by \(2\delta \) yields a remainder, greater than \(\delta \) (see Fig. 11 and its caption for further explanation). For this reason, in the program we decrease each cube edge length slightly (by reducing the step of each variable) so that the now slightly distorted cubes exactly cover the cuboid enclosing \(\mathscr {C}\) and \(\widetilde{\mathscr {C}}\) if we take their centers from the lattice spanning the cuboid (though since we are trying to only cover \(\mathscr {C}\), we do not need to take these centers from the entire cuboid).
The second problem is that \(\mathscr {C}\) is not actually a cuboid and might not get covered by the distorted cubes if we only took those with the centers in \(\mathscr {C}\). However, we claim that the distorted cubes cover \(\mathscr {C}\) if we take the centers from \(\widetilde{\mathscr {C}}\), as long as \(\delta \) is small enough.
Recall Fig. 9; since the dependence of the lower bound for \(p\) on \(\alpha \) is increasing for both \(\mathscr {C}\) and \(\widetilde{\mathscr {C}}\), it suffices to check that if \(\big (\alpha , \sigma , p, \chi \big ) \in \mathscr {C}\), then  .
.
We have
Hence \(\tan ^2(\alpha )\) has a Lipschitz coefficient of 9 on the relevant region. Similarly, \(p^2\) has a Lipschitz coefficient of 2.
Then
for \(\delta \in {\mathbb {R}}_{(0, \frac{m_p}{13}]}\). In particular, \(\delta \in {\mathbb {R}}_{(0, 0.01]}\) suffices, also in the cases where we hit the edges at \(\arctan (\sqrt{M_p+ M_p^2})\) and/or \(m_p\) (we did not have to be too picky about these particular estimates; the actual value of \(\delta \) we run the program with is far smaller, at 0.0004, as we explain below).
There is one more issue which prevents us from getting as nice of a result with a computer program as we would get with a theoretical derivation. Recall that we require  . The program verifies that if
. The program verifies that if  , then
, then  , where \(\texttt {S}\) is chosen within \(\varkappa \)-distance from \(\texttt {Y}\), hence the entire line segment from \(\texttt {X}\) to \(\texttt {Y}\) is in
, where \(\texttt {S}\) is chosen within \(\varkappa \)-distance from \(\texttt {Y}\), hence the entire line segment from \(\texttt {X}\) to \(\texttt {Y}\) is in  . However, if we allow \(\varkappa \) to get arbitrarily close to \(\sqrt{2p\big (\sqrt{p+ 2} - 1\big )}\), then the value of \(v\) gets arbitrarily close to zero, and we cannot use our method to prove that \(v\) is positive. To avoid this, we decrease the upper bound on the distance between \(\texttt {S}\) and \(\texttt {Y}\) to \(\sqrt{2p\big (\sqrt{p+ 2} - 1\big ) - \varkappa _\textrm{off}}\) for \(\varkappa _\textrm{off} = 0.55\) (we chose this value experimentally, so that the result of the program was sufficiently good).
. However, if we allow \(\varkappa \) to get arbitrarily close to \(\sqrt{2p\big (\sqrt{p+ 2} - 1\big )}\), then the value of \(v\) gets arbitrarily close to zero, and we cannot use our method to prove that \(v\) is positive. To avoid this, we decrease the upper bound on the distance between \(\texttt {S}\) and \(\texttt {Y}\) to \(\sqrt{2p\big (\sqrt{p+ 2} - 1\big ) - \varkappa _\textrm{off}}\) for \(\varkappa _\textrm{off} = 0.55\) (we chose this value experimentally, so that the result of the program was sufficiently good).
After some experimentation, we ran the program with \(\delta = 0.0004\). The resulting smallest value of \(v\) that the program returned, was 0.068546.
Recall that \(v\) has a Lipschitz coefficient of 125. Since any possible configuration is at most \({\delta = 0.0004}\) away from some point in the lattice where the program calculates \(v\), the values that \(v\) can take are at most \(125 \cdot 0.0004 = 0.05\) smaller than the values, calculated by the program. In particular, \(v\) is necessarily positive.
The possibility of numerical errors during the computation does not change this fact. The function \(v\) consists of polynomials of degree at most 3 and of sines and cosines, at most squared. All of these are output with at least 6 precise digits in the usual single floating-point precision (Overton 2001). Given the Lipschitz coefficient of 125, we are still easily within the margin of error \(0.068546 - 0.5 = 0.018546\).
The source code of our c++ program is available at https://people.math.ethz.ch/~skalisnik/ellipsoids.cpp and in the github repository https://github.com/kalisniks/Homology-of-Manifolds-using-Ellipsoids.
The price of this method is that we had to decrease the size of the theoretical interval for the persistence parameter  which in particular requires greater density sample for the proof than is strictly necessary. We discuss this in Sect. 7.
which in particular requires greater density sample for the proof than is strictly necessary. We discuss this in Sect. 7.
Let us summarize the results we have obtained in this section. We have seen that if a point  is in at least two of the closed ellipsoids, then there exists \(\texttt {S}\in \mathcal {S}\) such that
is in at least two of the closed ellipsoids, then there exists \(\texttt {S}\in \mathcal {S}\) such that  and
and  . This happened in one of two ways. The first closed ellipsoid we took \(\texttt {X}\) from could already satisfy this property, or we could find an ellipsoid with the center close to \(pr(\texttt {X})\) which contained both \(\texttt {X}\) and \(pr(\texttt {X})\) in its interior. If we start with
. This happened in one of two ways. The first closed ellipsoid we took \(\texttt {X}\) from could already satisfy this property, or we could find an ellipsoid with the center close to \(pr(\texttt {X})\) which contained both \(\texttt {X}\) and \(pr(\texttt {X})\) in its interior. If we start with  though, we can pick as the first ellipsoid one that has \(\texttt {X}\) in its interior, which means that we can always conclude the statement of Lemma 4.1.
though, we can pick as the first ellipsoid one that has \(\texttt {X}\) in its interior, which means that we can always conclude the statement of Lemma 4.1.
5 Construction of the deformation retraction
In this section we show that under the same assumptions on \(\tau \) and \(p\) as in the previous section, the union of the open ellipsoids around sample points deformation retracts onto the manifold \(\mathcal {M}\).
Informally, the idea of the deformation retraction is as follows. For a point \(\texttt {X}\) in an open ellipsoid  , consider the closed ellipsoid
, consider the closed ellipsoid  where \(q \mathrel {\mathop :}=q_{\texttt {S}}(\texttt {X})\) (Definition 2.8), the boundary of which contains \(\texttt {X}\). If the vector \(prv(\texttt {X})\) points into the interior of this closed ellipsoid, we move in the direction of \(prv(\texttt {X})\), i.e. we use the normal deformation retraction. Otherwise, we move in the direction of the projection of the vector \(prv(\texttt {X})\) onto the tangent space
where \(q \mathrel {\mathop :}=q_{\texttt {S}}(\texttt {X})\) (Definition 2.8), the boundary of which contains \(\texttt {X}\). If the vector \(prv(\texttt {X})\) points into the interior of this closed ellipsoid, we move in the direction of \(prv(\texttt {X})\), i.e. we use the normal deformation retraction. Otherwise, we move in the direction of the projection of the vector \(prv(\texttt {X})\) onto the tangent space  . This causes us to slide along the boundary
. This causes us to slide along the boundary  . Either way, we remain within
. Either way, we remain within  (and therefore within
(and therefore within  ) and eventually reach the manifold \(\mathcal {M}\). This procedure is problematic for points which are in more than one ellipsoid, but we can glue together the directions of the deformation retraction with a suitable partition of unity. Figure 12 illustrates this idea.
) and eventually reach the manifold \(\mathcal {M}\). This procedure is problematic for points which are in more than one ellipsoid, but we can glue together the directions of the deformation retraction with a suitable partition of unity. Figure 12 illustrates this idea.
To make this work, we will need precise control over the partition of unity, which is the topic of Sect. 5.1. Then in Sect. 5.2 we define the vector field which gives directions, in which we deformation retract. Sect. 5.3 proves that the flow of this vector field has desired properties. We then use this flow to explicitly give the definition of the requisite deformation retraction in Sect. 5.4.
5.1 The partition of unity
For each \(\texttt {S}\in \mathcal {S}\) define

The sets \(\mathcal {A}_{\texttt {S}}\) and \(\mathcal {B}_{\texttt {S}}\) are closed in  because they are complements within
because they are complements within  of open sets. Note that
of open sets. Note that  . In particular, \(\mathcal {A}_{\texttt {S}}\) and \(\mathcal {B}_{\texttt {S}}\) are disjoint.
. In particular, \(\mathcal {A}_{\texttt {S}}\) and \(\mathcal {B}_{\texttt {S}}\) are disjoint.
Proposition 5.1
If \(\texttt {S}', \texttt {S}'' \in \mathcal {S}\) and \(\texttt {S}' \ne \texttt {S}''\), then \(\mathcal {A}_{\texttt {S}'} \subseteq \mathcal {B}_{\texttt {S}''}\) and \(\mathcal {A}_{\texttt {S}'} \cap \mathcal {A}_{\texttt {S}''} = \emptyset \).
Proof
For any  , if \(\texttt {X}\in \mathcal {A}_{\texttt {S}'}\), then
, if \(\texttt {X}\in \mathcal {A}_{\texttt {S}'}\), then  , so \(\texttt {X}\in \mathcal {B}_{\texttt {S}''}\). Consequently \(\mathcal {A}_{\texttt {S}'} \cap \mathcal {A}_{\texttt {S}''} \subseteq \mathcal {B}_{\texttt {S}''} \cap \mathcal {A}_{\texttt {S}''} = \emptyset \). \(\square \)
, so \(\texttt {X}\in \mathcal {B}_{\texttt {S}''}\). Consequently \(\mathcal {A}_{\texttt {S}'} \cap \mathcal {A}_{\texttt {S}''} \subseteq \mathcal {B}_{\texttt {S}''} \cap \mathcal {A}_{\texttt {S}''} = \emptyset \). \(\square \)
The only way \(\mathcal {B}_{\texttt {S}}\) could be empty is if the sample \(\mathcal {S}\) is a singleton which can only happen when \(\mathcal {M}\) is a singleton, but this possibility is excluded by the assumption that the dimension of \(\mathcal {M}\) is positive. The distance to any non-empty set is a well-defined real-valued function, the zeroes of which form the closure of the set.
Define

The sets \(\mathcal {\widehat{A}}_{\texttt {S}}\) and \(\mathcal {\widehat{B}}_{\texttt {S}}\) are disjoint. If we had \(\texttt {X}\in \mathcal {\widehat{A}}_{\texttt {S}}\cap \mathcal {\widehat{B}}_{\texttt {S}}\), then \(d(\mathcal {A}_{\texttt {S}}, \texttt {X}) \le \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X}) \le \tfrac{3}{4} d(\mathcal {A}_{\texttt {S}}, \texttt {X})\), so \(d(\mathcal {A}_{\texttt {S}}, \texttt {X}) = d(\mathcal {B}_{\texttt {S}}, \texttt {X}) = 0\), meaning \(\texttt {X}\in \mathcal {A}_{\texttt {S}}\cap \mathcal {B}_{\texttt {S}}\), a contradiction. Note also that \(\mathcal {B}_{\texttt {S}}\subseteq \mathcal {\widehat{B}}_{\texttt {S}}\) and

The sets \(\mathcal {\widehat{A}}_{\texttt {S}}\) and \(\mathcal {\widehat{B}}_{\texttt {S}}\) are closed in  because they are (empty or) preimages of \(\mathbb {R}_{\ge 0}\) under continuous maps \({\texttt {X}\mapsto \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X}) - d(\mathcal {A}_{\texttt {S}}, \texttt {X})}\) and \({\texttt {X}\mapsto \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X}) - d(\mathcal {B}_{\texttt {S}}, \texttt {X})}\). Using the smooth version of Urysohn’s lemma (Lee 2013), choose a smooth function
because they are (empty or) preimages of \(\mathbb {R}_{\ge 0}\) under continuous maps \({\texttt {X}\mapsto \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X}) - d(\mathcal {A}_{\texttt {S}}, \texttt {X})}\) and \({\texttt {X}\mapsto \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X}) - d(\mathcal {B}_{\texttt {S}}, \texttt {X})}\). Using the smooth version of Urysohn’s lemma (Lee 2013), choose a smooth function  such that \({f_{\texttt {S}}}\) is constantly 1 on \(\mathcal {\widehat{A}}_{\texttt {S}}\) and constantly 0 on \(\mathcal {\widehat{B}}_{\texttt {S}}\).
such that \({f_{\texttt {S}}}\) is constantly 1 on \(\mathcal {\widehat{A}}_{\texttt {S}}\) and constantly 0 on \(\mathcal {\widehat{B}}_{\texttt {S}}\).
Recall that the support \(\textrm{supp}({f})\) of a continuous real-valued function f is defined as the closure of the complement of the zero set, where both the complementation and the closure are calculated in the domain of f.
Proposition 5.2
For every \(\texttt {S}\in \mathcal {S}\) and  , if \(\texttt {X}\in \textrm{supp}({{f_{\texttt {S}}}})\), then
, if \(\texttt {X}\in \textrm{supp}({{f_{\texttt {S}}}})\), then  , \(d(\mathcal {\widehat{B}}_{\texttt {S}}, \texttt {X}) \ge \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X})\) and
, \(d(\mathcal {\widehat{B}}_{\texttt {S}}, \texttt {X}) \ge \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X})\) and  .
.
Proof
Since \(\texttt {X}\in \textrm{supp}({{f_{\texttt {S}}}})\), the support of \({f_{\texttt {S}}}\) is non-empty, so  , therefore \(\mathcal {A}_{\texttt {S}}\ne \emptyset \). The set
, therefore \(\mathcal {A}_{\texttt {S}}\ne \emptyset \). The set  is closed in
is closed in  and contains \({f_{\texttt {S}}}^{-1}({\mathbb {R}}_{(0, 1]})\), so it contains \(\textrm{supp}({{f_{\texttt {S}}}})\).
and contains \({f_{\texttt {S}}}^{-1}({\mathbb {R}}_{(0, 1]})\), so it contains \(\textrm{supp}({{f_{\texttt {S}}}})\).
If \(\texttt {X}\in \mathcal {A}_{\texttt {S}}\), then  . If \(\texttt {X}\notin \mathcal {A}_{\texttt {S}}\), then \(d(\mathcal {B}_{\texttt {S}}, \texttt {X}) \ge d(\mathcal {\widehat{B}}_{\texttt {S}}, \texttt {X}) \ge \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X}) > 0\), so again
. If \(\texttt {X}\notin \mathcal {A}_{\texttt {S}}\), then \(d(\mathcal {B}_{\texttt {S}}, \texttt {X}) \ge d(\mathcal {\widehat{B}}_{\texttt {S}}, \texttt {X}) \ge \tfrac{3}{2} d(\mathcal {A}_{\texttt {S}}, \texttt {X}) > 0\), so again  . \(\square \)
. \(\square \)
Proposition 5.3
The supportsFootnote 8 of functions \({f_{\texttt {S}}}\) are pairwise disjoint. Hence every point in  has a neighbourhood which intersects the support of at most one \({f_{\texttt {S}}}\).
has a neighbourhood which intersects the support of at most one \({f_{\texttt {S}}}\).
Proof
Take \(\texttt {S}', \texttt {S}'' \in \mathcal {S}\), \(\texttt {S}' \ne \texttt {S}''\) and let \(\texttt {X}\in {f_{\texttt {S}'}} \cap {f_{\texttt {S}''}}\). Then \(d(\mathcal {A}_{\texttt {S}'}, \texttt {X}) \le \tfrac{2}{3} d(\mathcal {B}_{\texttt {S}'}, \texttt {X}) \le \tfrac{2}{3} d(\mathcal {A}_{\texttt {S}''}, \texttt {X})\) and likewise \(d(\mathcal {A}_{\texttt {S}''}, \texttt {X}) \le \tfrac{2}{3} d(\mathcal {A}_{\texttt {S}'}, \texttt {X})\), implying \(d(\mathcal {A}_{\texttt {S}'}, \texttt {X}) = d(\mathcal {A}_{\texttt {S}''}, \texttt {X}) = 0\), so \(\texttt {X}\in \mathcal {A}_{\texttt {S}'} \cap \mathcal {A}_{\texttt {S}''}\), a contradiction.
Since  for all \(\texttt {S}\in \mathcal {S}\), the family of supports of \({f_{\texttt {S}}}\) is also locally finite. Thus any
for all \(\texttt {S}\in \mathcal {S}\), the family of supports of \({f_{\texttt {S}}}\) is also locally finite. Thus any  has a neighbourhood
has a neighbourhood  which intersects only finitely many supports, at most one of which contains \(\texttt {X}\). The intersection of the complements of the rest with the set \(\mathcal {U}\) is a neighbourhood of \(\texttt {X}\) which intersects at most one support. \(\square \)
which intersects only finitely many supports, at most one of which contains \(\texttt {X}\). The intersection of the complements of the rest with the set \(\mathcal {U}\) is a neighbourhood of \(\texttt {X}\) which intersects at most one support. \(\square \)
From these results we can conclude that \(\texttt {X}\mapsto \sum _{\texttt {S}\in \mathcal {S}} {f_{\texttt {S}}}(\texttt {X})\) gives a well-defined smooth map  . We may therefore define a smooth map
. We may therefore define a smooth map  ,
,
Thus the family of maps \({f_{\texttt {S}}}\), \(\texttt {S}\in \mathcal {S}\), together with \(f_P\), forms a smooth partition of unity on  .
.
We will need two more subsets of  :
:

Lemma 5.4
The sets \(\mathcal {V}\) and \(\mathcal {W}\) are open in  and in \(\mathbb {R}^n\), and
and in \(\mathbb {R}^n\), and  .
.
Proof
The given sets are open in  since \(\mathcal {V}= \bigcup _{\texttt {S}\in \mathcal {S}, \mathcal {A}_{\texttt {S}}\ne \emptyset } \big (\texttt {X}\mapsto \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X}) - d(\mathcal {A}_{\texttt {S}}, \texttt {X})\big )^{-1}(\mathbb {R}_{> 0})\) and
since \(\mathcal {V}= \bigcup _{\texttt {S}\in \mathcal {S}, \mathcal {A}_{\texttt {S}}\ne \emptyset } \big (\texttt {X}\mapsto \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X}) - d(\mathcal {A}_{\texttt {S}}, \texttt {X})\big )^{-1}(\mathbb {R}_{> 0})\) and  . As
. As  is open in \(\mathbb {R}^n\), they are also open in \(\mathbb {R}^n\).
is open in \(\mathbb {R}^n\), they are also open in \(\mathbb {R}^n\).
Assume that  . If \(\texttt {X}\) was in any \(\mathcal {A}_{\texttt {S}}\), we would have \(0 = d(\mathcal {A}_{\texttt {S}}, \texttt {X}) \ge \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X})\), so \(\texttt {X}\in \mathcal {A}_{\texttt {S}}\cap \mathcal {B}_{\texttt {S}}\), a contradiction. Since \(\texttt {X}\) is in no \(\mathcal {A}_{\texttt {S}}\), it must be in at least two
. If \(\texttt {X}\) was in any \(\mathcal {A}_{\texttt {S}}\), we would have \(0 = d(\mathcal {A}_{\texttt {S}}, \texttt {X}) \ge \tfrac{1}{2} d(\mathcal {B}_{\texttt {S}}, \texttt {X})\), so \(\texttt {X}\in \mathcal {A}_{\texttt {S}}\cap \mathcal {B}_{\texttt {S}}\), a contradiction. Since \(\texttt {X}\) is in no \(\mathcal {A}_{\texttt {S}}\), it must be in at least two  , so \(\texttt {X}\in \mathcal {W}\) by Lemma 4.1. \(\square \)
, so \(\texttt {X}\in \mathcal {W}\) by Lemma 4.1. \(\square \)
5.2 The velocity vector field
Let us define for each \(\texttt {S}\in \mathcal {S}\) the vector field  as follows. Given
as follows. Given  , let \({\mathcal {H}_{\texttt {S}}{\texttt {X}}}\) denote the \(n\)-dimensional closed half-space which is bounded by the hyperplane
, let \({\mathcal {H}_{\texttt {S}}{\texttt {X}}}\) denote the \(n\)-dimensional closed half-space which is bounded by the hyperplane  and which contains
and which contains  . Define
. Define  to be the projection of the vector \(prv(\texttt {X})\) to the closest point in \({\mathcal {H}_{\texttt {S}}{\texttt {X}}}\). Explicitly, if we introduce any orthonormal coordinate system with the origin in \(\texttt {X}\) such that the last coordinate axis points orthogonally to
to be the projection of the vector \(prv(\texttt {X})\) to the closest point in \({\mathcal {H}_{\texttt {S}}{\texttt {X}}}\). Explicitly, if we introduce any orthonormal coordinate system with the origin in \(\texttt {X}\) such that the last coordinate axis points orthogonally to  into the interior of
into the interior of  , then the projection in these coordinates is given by
, then the projection in these coordinates is given by  .
.
Proposition 5.5
The vector field  is Lipschitz with a bound on a Lipschitz coefficient independent from \(\texttt {S}\).
is Lipschitz with a bound on a Lipschitz coefficient independent from \(\texttt {S}\).
Proof
The projection onto a half-space is 1-Lipschitz. By setting \(\tau = 1\) and \(r = p\) in Lemma 3.1, we see that the map \(prv\) is \((\frac{1}{1-p} + 1)\)-Lipschitz on  . As the composition of these two maps, the vector field
. As the composition of these two maps, the vector field  is Lipschitz with the product Lipschitz coefficient, i.e. also \(\frac{1}{1-p} + 1\). \(\square \)
is Lipschitz with the product Lipschitz coefficient, i.e. also \(\frac{1}{1-p} + 1\). \(\square \)
For any \(\texttt {S}\in \mathcal {S}\) and  let \(\alpha _{\texttt {S}}{\texttt {X}}\) denote the angle between the vectors \(prv(\texttt {X})\) and
let \(\alpha _{\texttt {S}}{\texttt {X}}\) denote the angle between the vectors \(prv(\texttt {X})\) and  , and let \(\textrm{hl}_{\texttt {S}}{\texttt {X}}\) denote the closed half-line which starts at \(\texttt {X}\), is orthogonal to
, and let \(\textrm{hl}_{\texttt {S}}{\texttt {X}}\) denote the closed half-line which starts at \(\texttt {X}\), is orthogonal to  and points into the exterior of
and points into the exterior of  .
.
Lemma 5.6
Let \(\texttt {S}\in \mathcal {S}\) and  . Then \(pr(\texttt {X}) \notin \textrm{hl}_{\texttt {S}}{\texttt {X}}\); in fact, the angle between \(prv(\texttt {X})\) and \(\textrm{hl}_{\texttt {S}}{\texttt {X}}\) is bounded from below by \(\textrm{arccot}(\tfrac{1}{\sqrt{2}})\). Hence \(0 \le \alpha _{\texttt {S}}{\texttt {X}}\le \arccos \big (\sqrt{\frac{2}{3}}\big )\); in particular \(\cos (\alpha _{\texttt {S}}{\texttt {X}}) \ge \sqrt{\frac{2}{3}}\).
. Then \(pr(\texttt {X}) \notin \textrm{hl}_{\texttt {S}}{\texttt {X}}\); in fact, the angle between \(prv(\texttt {X})\) and \(\textrm{hl}_{\texttt {S}}{\texttt {X}}\) is bounded from below by \(\textrm{arccot}(\tfrac{1}{\sqrt{2}})\). Hence \(0 \le \alpha _{\texttt {S}}{\texttt {X}}\le \arccos \big (\sqrt{\frac{2}{3}}\big )\); in particular \(\cos (\alpha _{\texttt {S}}{\texttt {X}}) \ge \sqrt{\frac{2}{3}}\).
Proof
Let \(q \mathrel {\mathop :}=q_{\texttt {S}}(\texttt {X})\). We have \(q \le p< 1\) and since \(\texttt {X}\notin \mathcal {M}\), in particular \(\texttt {X}\ne \texttt {S}\), we have \(q > 0\). Let \(\textbf{n}\) be the unit vector, orthogonal to the boundary of  and pointing into the exterior of
and pointing into the exterior of  , so that
, so that  . Let \(\ell \mathrel {\mathop :}=\Vert prv(\texttt {X})\Vert \); by assumption \(\texttt {X}\notin \mathcal {M}\), so \(\ell > 0\), and we may define \(\textbf{m} \mathrel {\mathop :}=\frac{prv(\texttt {X})}{\ell }\). Also, since
. Let \(\ell \mathrel {\mathop :}=\Vert prv(\texttt {X})\Vert \); by assumption \(\texttt {X}\notin \mathcal {M}\), so \(\ell > 0\), and we may define \(\textbf{m} \mathrel {\mathop :}=\frac{prv(\texttt {X})}{\ell }\). Also, since  , we have \(\ell < 1\).
, we have \(\ell < 1\).
Use Lemma 2.6 to introduce a planar tangent-normal coordinate system with the origin at \(\texttt {S}\) which contains \(\texttt {X}\) as well as \(\textbf{n}\), hence the whole \(\textrm{hl}_{\texttt {S}}{\texttt {X}}\). Without loss of generality assume that \(\texttt {X}\) lies in the closed first quadrant, so that we have \(\chi \in {\mathbb {R}}_{[0, \frac{\pi }{2}]}\) with \(\texttt {X}= \big (\sqrt{q+q^2} \sin (\chi ), q \cos (\chi )\big )\) (the angle is measured from  ).
).
Let us first prove that \(pr(\texttt {X}) \notin \textrm{hl}_{\texttt {S}}{\texttt {X}}\). Assume to the contrary that this were the case, so that \(\textbf{m} = \textbf{n}\). We will derive the contradiction by showing that the open \(\tau \)-ball with the center in \(\texttt {X}- (1-\ell ) \textbf{m}\), associated to \(\mathcal {M}\) at \(pr(\texttt {X})\), intersects all open \(\tau \)-balls, associated to \(\mathcal {M}\) at \(\texttt {S}\). Two of those have their centers in the tangent-normal plane we are considering, and necessarily one of those is the \(\tau \)-ball at \(\texttt {S}\) which is the furthest away from the \(\tau \)-ball with the center in \(\texttt {X}- (1-\ell ) \textbf{m}\). It thus suffices to check that the latter intersects the former two.
First we explicitly calculate \(\textbf{m}\).
We derive the contradiction by showing that \(d\big (\texttt {X}- (1-\ell ) \textbf{m}, (0, \pm {1})\big ) < 2\).
We verify that this expression is \(< 4\) for \(q, \ell \in {\mathbb {R}}_{(0, 1)}\) and \(\chi \in {\mathbb {R}}_{[0, \frac{\pi }{2}]}\) with the help from Mathematica, see file ProjectionNotOnHalfline.nb, available at https://people.math.ethz.ch/~skalisnik/ProjectionNotOnHalfline.nb and in the github repository https://github.com/kalisniks/Homology-of-Manifolds-using-Ellipsoids.
This has shown that \(\textbf{m}\) cannot be equal to \(\textbf{n}\) because in that case the open \(\tau \)-ball with the center in \(\texttt {X}- (1-\ell ) \textbf{m}\) would intersect all open \(\tau \)-balls, associated to \(\texttt {S}\). A lower bound on the angle between \(\textbf{m}\) and \(\textbf{n}\) is therefore the minimal angle, by which we must deviate from \(\textbf{n}\), so that we no longer have an intersection of the aforementioned balls.
Observe that if two balls intersect, the closer their centers are, the greater the angle we must turn one of them by around a point on its boundary, so that they stop intersecting—see Fig. 13 for a visualization of this.
Hence, if we try to turn the ball with the center in \(\texttt {X}- (1-\ell ) \textbf{n}\) around the point \(pr(\texttt {X})\) so that it no longer intersects all balls, associated to \(\texttt {S}\), we can get a lower bound on the angle by turning it by a minimal angle so that it no longer intersects the ball, associated to \(\texttt {S}\), which is furthest away. The center of this furthest ball lies in our planar tangent-normal coordinate system in which it has coordinates \((0, -1)\). Furthermore, the greater the \(\ell \) is, the further \(\texttt {X}- (1-\ell ) \textbf{n}\) is away from \((0, -1)\). The minimal angle by which we must turn the ball with this center continuously depends on \(\ell \) and can be continuously extended to \(\ell = 0\) (the case we excluded by the assumption \(\texttt {X}\notin \mathcal {M}\)). Once we set \(\ell = 0\), this minimal angle is still a function of q and \(\chi \), and its minimum is a lower bound for the angle for any \(\ell \).
Calculating this minimum is very complicated however, so we again resort to a computer proof with Mathematica, see file AngleBetweenProjectionAndHalfline.nb at https://people.math.ethz.ch/~skalisnik/AngleBetweenProjectionAndHalfline.nb and in the github repository https://github.com/kalisniks/Homology-of-Manifolds-using-Ellipsoids. \(\square \)
The desired deformation retraction should flow in the direction of  . However, the field
. However, the field  is defined only on a single ellipsoid
is defined only on a single ellipsoid  . Two such vector fields generally do not coincide on the intersection of two (or more) ellipsoids, so we use the partition of unity, constructed in Sect. 5.1, to merge the vector fields
. Two such vector fields generally do not coincide on the intersection of two (or more) ellipsoids, so we use the partition of unity, constructed in Sect. 5.1, to merge the vector fields  into one.
into one.
Define the vector field  as
as

We understand this definition in the usual sense: this sum has only finitely many non-zero terms at each \(\texttt {X}\) (in fact at most two by Proposition 5.3), and outside of the ellipsoid  , we take the value of
, we take the value of  to be 0.
to be 0.
Corollary 5.7
-
1.
If \(\texttt {S}\in \mathcal {S}\) and
 , then
, then 
-
2.
If
 , then \(\langle {\widetilde{V}(\texttt {X})}, {prv(\texttt {X})}\rangle \ge \tfrac{2}{3} \;\! \big \Vert prv(\texttt {X})\big \Vert ^2\).
, then \(\langle {\widetilde{V}(\texttt {X})}, {prv(\texttt {X})}\rangle \ge \tfrac{2}{3} \;\! \big \Vert prv(\texttt {X})\big \Vert ^2\).
In particular, these two scalar products are non-zero outside \(\mathcal {M}\). Hence the fields  and \(\widetilde{V}\) have no zeros outside \(\mathcal {M}\).
and \(\widetilde{V}\) have no zeros outside \(\mathcal {M}\).
Proof
-
1.
Assume first that \(prv(\texttt {X})\) points into the half-space bounded by
 which contains
which contains  . Then
. Then  and \(\alpha _{\texttt {S}}{\texttt {X}}= 0\), so the statement is clear. Otherwise,
and \(\alpha _{\texttt {S}}{\texttt {X}}= 0\), so the statement is clear. Otherwise,  is the orthogonal projection of \(prv(\texttt {X})\) onto
is the orthogonal projection of \(prv(\texttt {X})\) onto  , so
, so  and
and 
For the inequality, we use Lemma 5.6 to get \(\cos ^2(\alpha _{\texttt {S}}{\texttt {X}}) \ge \frac{2}{3}\).
-
2.
We have

\(\square \)
There is one more problem with taking \(\widetilde{V}\) as the direction vector field of the deformation retraction. The closer \(\texttt {X}\) is to the manifold, the shorter the vector \(prv(\texttt {X})\), and thus \(\widetilde{V}(\texttt {X})\), is. If we used \(\widetilde{V}\) as the velocity vector field for the flow, we would need infinite time to reach the manifold \(\mathcal {M}\). If we scale the vector field in the way that the distance to the manifold decreases with speed 1, we are sure to reach the manifold within time 1 which is how one usually gives a deformation retraction (or more generally any homotopy).
Since \(d(\texttt {X}, \mathcal {M}) = d(\texttt {X}, pr(\texttt {X}))\), we need to divide \(\widetilde{V}(\texttt {X})\) with the length of its projection onto the vector \(prv(\texttt {X})\). Hence the following definition of the vector field  :
:
Corollary 5.7 ensures that the vector field \(V\) is well defined and that it has the same direction as \(\widetilde{V}\).
Proposition 5.8
For every \(\texttt {S}\in \mathcal {S}\) the field  is bounded Lipschitz. The fields
is bounded Lipschitz. The fields  and
and  are bounded and locally Lipschitz.
are bounded and locally Lipschitz.
Proof
The projection onto a half-space is 1-Lipschitz; since the map \(prv\) is bounded in norm (by Lemma 2.9 we have \(\Vert prv(\texttt {X})\Vert = d(\texttt {X}, pr(\texttt {X})) = d(\texttt {X}, \mathcal {M}) \le q_{\texttt {S}}(\texttt {X}) < p\)), the field  is also bounded. Lemma 3.1 tells us that the map \(prv\) is \((\frac{1}{1-p} + 1)\)-Lipschitz on
is also bounded. Lemma 3.1 tells us that the map \(prv\) is \((\frac{1}{1-p} + 1)\)-Lipschitz on  . As the composition of two Lipschitz maps, the vector field
. As the composition of two Lipschitz maps, the vector field  is Lipschitz with the product Lipschitz coefficient, i.e. also \(\frac{1}{1-p} + 1\).
is Lipschitz with the product Lipschitz coefficient, i.e. also \(\frac{1}{1-p} + 1\).
Since the norm of the map \(prv\), as well as all  , has the same bound \(p\), this is also a bound on the norm of \(\widetilde{V}\):
, has the same bound \(p\), this is also a bound on the norm of \(\widetilde{V}\):

The field \(\widetilde{V}\) is locally Lipschitz by Corollary 2.11.
Assume now that  . Recall from Lemma 5.6 that \(\cos (\alpha _{\texttt {S}}{\texttt {X}}) \ge \sqrt{\frac{2}{3}}\). Thus
. Recall from Lemma 5.6 that \(\cos (\alpha _{\texttt {S}}{\texttt {X}}) \ge \sqrt{\frac{2}{3}}\). Thus

It follows that the norm of \(V\) is bounded by \(\sqrt{\frac{3}{2}}\).
Let \(\mathcal {U}\) be a neighbourhood of \(\texttt {X}\), where \(\widetilde{V}\) is Lipschitz. Let \(r \in \mathbb {R}_{> 0}\) be such that  and \(r < d(\mathcal {M}, \texttt {X}) = \Vert prv(\texttt {X})\Vert \) and \(r < 1 - d(\mathcal {M}, \texttt {X})\). We claim that \(V\) is Lipschitz on
and \(r < d(\mathcal {M}, \texttt {X}) = \Vert prv(\texttt {X})\Vert \) and \(r < 1 - d(\mathcal {M}, \texttt {X})\). We claim that \(V\) is Lipschitz on  and therefore locally Lipschitz.
and therefore locally Lipschitz.
By Lemma 3.1 the map \(prv\) is Lipschitz on  . The map\(\Vert prv(\text {---})\Vert \) is a composition of Lipschitz maps and therefore Lipschitz on
. The map\(\Vert prv(\text {---})\Vert \) is a composition of Lipschitz maps and therefore Lipschitz on  . Clearly, it is also bounded.
. Clearly, it is also bounded.
Since \(\widetilde{V}\) is also bounded and Lipschitz on  , so is the scalar product \({\texttt {Y}\mapsto \langle {\widetilde{V}(\texttt {Y})}, {prv(\texttt {Y})}\rangle }\) by Lemma 2.10. Recall from Corollary 5.7 that
, so is the scalar product \({\texttt {Y}\mapsto \langle {\widetilde{V}(\texttt {Y})}, {prv(\texttt {Y})}\rangle }\) by Lemma 2.10. Recall from Corollary 5.7 that
Hence Lemma 2.10 also tells us that the map \(\texttt {Y}\mapsto \frac{\Vert prv(\texttt {Y})\Vert }{\langle {\widetilde{V}(\texttt {Y})}, {prv(\texttt {Y})}\rangle }\) is bounded Lipschitz on  , and then so is its product with \(\widetilde{V}\), i.e. the field \(V\). \(\square \)
, and then so is its product with \(\widetilde{V}\), i.e. the field \(V\). \(\square \)
The reason we consider the local Lipschitz property is that it allow us to define the flow of the field \(V\).
5.3 The flow of the vector field
We will use the flow of the vector field \(V\) as part of the definition of the desired deformation retraction. Generally the flow of a vector field need not exist globally, and in our case the whole point is that the flow takes us to the manifold where the vector field is not defined. However, before we can establish what the exact domain of definition for the flow is, we will already need to refer to the flow to prove some of its properties. As such, it will be convenient to treat the flow as a partial function. Also, it is convenient to use Kleene equality \(\mathrel {\simeq }\) in the context of partial functions: \(a \mathrel {\simeq }b\) means that a is defined if and only if b is, and is they are defined, they are equal.
The flow of the vector field  can thus be given as a partial map
can thus be given as a partial map  which satisfies the following for all
which satisfies the following for all  and \(t, u \in \mathbb {R}_{\ge 0}\):
and \(t, u \in \mathbb {R}_{\ge 0}\):
-
1.
the domain of definition of \(\Phi \) is an open subset of
 ,
, -
2.
the flow \(\Phi \) is continuous everywhere on its domain of definition,
-
3.
if \(\Phi (\texttt {X}, u)\) is defined and \(t \le u\), then \(\Phi (\texttt {X}, t)\) is defined,
-
4.
\(\Phi (\texttt {X}, 0) \mathrel {\simeq }\texttt {X}\),
-
5.
\(\Phi \big (\Phi (\texttt {X}, t), u\big ) \mathrel {\simeq }\Phi (\texttt {X}, t + u)\),
-
6.
if \(\Phi (\texttt {X}, u)\) is defined, the derivative of the function \(\Phi (\texttt {X}, \text {---})\) exists at u, and is equal to \(V\big (\Phi (\texttt {X}, u)\big )\).
A standard result (Coleman 2012) tells us that if a vector field is locally Lipschitz, it has a local vector flow. That is, for every  there exists \(\epsilon \in \mathbb {R}_{> 0}\) such that \(\Phi (\texttt {X}, t)\) is defined for all \(t \in {\mathbb {R}}_{[0, \epsilon )}\).
there exists \(\epsilon \in \mathbb {R}_{> 0}\) such that \(\Phi (\texttt {X}, t)\) is defined for all \(t \in {\mathbb {R}}_{[0, \epsilon )}\).
We claim that if we move with the flow \(\Phi \) of the vector field \(V\), we approach the manifold \(\mathcal {M}\) with constant speed.
Lemma 5.9
If  is in the domain of definition of \(\Phi \), then
is in the domain of definition of \(\Phi \), then
Proof
Consider the functions \({\mathbb {R}}_{[0, u]} \rightarrow \mathbb {R}\), given by \(t \mapsto d\big (\mathcal {M}, \Phi (\texttt {X}, t)\big )\) and \(t \mapsto d(\mathcal {M}, \texttt {X}) - t\). To show that these two functions are the same (and thus in particular coincide for \(t = u\)), it suffices to show that they match in one point and have the same derivative.
For \(t = 0\), we have \(d\big (\mathcal {M}, \Phi (\texttt {X}, 0)\big ) = d(\mathcal {M}, \texttt {X})\). The derivative of the second function is constantly \(-1\). We calculate the derivative of the first function via the chain rule. Take \(t \in {\mathbb {R}}_{[0, u]}\) and introduce an orthonormal \(n\)-dimensional coordinate system with the origin in \(\texttt {Y}\mathrel {\mathop :}=\Phi (\texttt {X}, t)\), such that the first coordinate axis points in the direction of \(prv(\texttt {Y})\). In this coordinate system, the Jacobian matrix of the map \(d(\mathcal {M}, \text {---})\) at \(\texttt {Y}\) is a matrix row with the first entry \(-1\) and the rest 0. We need to multiply this matrix with the column, the first entry of which is \(\langle {\Phi '(\texttt {X}, t)}, {\tfrac{prv(\texttt {Y})}{\Vert prv(\texttt {Y})\Vert }}\rangle \), i.e. the scalar projection onto the direction \(\frac{prv(\texttt {Y})}{\Vert prv(\texttt {Y})\Vert }\) of the derivative of \(\Phi (\texttt {X}, \text {---})\) at \(\texttt {Y}\).
By the chain rule, the derivative of the function \(t \mapsto d\big (\mathcal {M}, \Phi (\texttt {X}, t)\big )\) is therefore
as required. \(\square \)
The next lemma is a tool which serves as a form of induction for real intervals.
Lemma 5.10
Let \(a \in \mathbb {R}_{\ge 0}\) and let I be either the interval \({\mathbb {R}}_{[0, a)}\) or the interval \({\mathbb {R}}_{[0, a]}\). Let \(L \subseteq I\) have the following properties:
-
L is a lower subset of I (i.e. \(\forall \hspace{0.2ex}{t, u \in I}\hspace{0.2ex}{.}\hspace{0.9ex}{u \in L \wedge t \le u \Rightarrow t \in L}\)),
-
\(0 \in L\),
-
for every \(t \in L_{< a}\) there exists \(u \in I_{> t}\) such that \(u \in L\),
-
for every \(t \in I\), if \({\mathbb {R}}_{[0, t)} \subseteq L\), then \(t \in L\).
Then \(L = I\).
Proof
To prove \(L = I\), it suffices to show that L is non-empty, open and closed in I since I is connected.
Because L contains 0, it is non-empty. Since L is a lower subset of I, the third assumption on L is equivalent to openness of L, and the fourth assumption is equivalent to closedness of L. \(\square \)
Lemma 5.11
An \(\epsilon \in {\mathbb {R}}_{(0, p)}\) exists so that for every  and every \(\texttt {S}\in \mathcal {S}\), such that
and every \(\texttt {S}\in \mathcal {S}\), such that  , the vector \(V(\texttt {X})\) has the same direction as \(prv(\texttt {X})\).
, the vector \(V(\texttt {X})\) has the same direction as \(prv(\texttt {X})\).
Proof
First we will require that \(\epsilon < \frac{p-\lambda }{2}\). In that case the inequality \(d(\texttt {X}, pr(\texttt {X})) < \frac{p-\lambda }{2}\) leads to contradiction  . Thus
. Thus  .
.
Consider the intersection of  with the closed half-space, bounded by the hyperplane, tangent to
with the closed half-space, bounded by the hyperplane, tangent to  , on the side not containing
, on the side not containing  . This intersection contains \(\texttt {X}\). If we take \(\texttt {X}\) arbitrarily close to
. This intersection contains \(\texttt {X}\). If we take \(\texttt {X}\) arbitrarily close to  (i.e. we consider \(q_{\texttt {S}}(\texttt {X})\) tending towards \(p\)), the intersection is contained in arbitrarily small balls around \(\texttt {X}\). For those interested, one can calculate that the intersection is contained in
(i.e. we consider \(q_{\texttt {S}}(\texttt {X})\) tending towards \(p\)), the intersection is contained in arbitrarily small balls around \(\texttt {X}\). For those interested, one can calculate that the intersection is contained in  , but we will not actually need the precise radius of the ball.
, but we will not actually need the precise radius of the ball.
If we choose \(\epsilon \) so that this intersection is contained in  , then this intersection cannot contain \(pr(\texttt {X})\), whence
, then this intersection cannot contain \(pr(\texttt {X})\), whence  . From \(0< \lambda< p< 1\) we get that
. From \(0< \lambda< p< 1\) we get that
If we pick any \(\epsilon \in {\mathbb {R}}_{(0, \frac{p-\lambda }{2})}\) satisfying \(\epsilon < p- \frac{1}{2} \sqrt{\frac{p(3p^2 - \lambda ^2 + 2 p(2+\lambda ))}{1+p}}\), then the aforementioned intersection is indeed contained in  .
.
By assumption \(\texttt {X}\in \mathcal {W}\), i.e. \(\texttt {X}\) and \(pr(\texttt {X})\) are in the same open ellipsoid. Recall from Proposition 5.3 that, aside from \(f_P\), at most one \({f_{\texttt {S}}}\) is non-zero. Thus the vector \(\widetilde{V}(\texttt {X})\) is a convex combination of  and \(prv(\texttt {X})\), so it is equal to \(prv(\texttt {X})\). Hence \(V(\texttt {X})\) has the same direction as \(prv(\texttt {X})\) for our choice of \(\epsilon \). \(\square \)
and \(prv(\texttt {X})\), so it is equal to \(prv(\texttt {X})\). Hence \(V(\texttt {X})\) has the same direction as \(prv(\texttt {X})\) for our choice of \(\epsilon \). \(\square \)
Lemma 5.12
An \(\epsilon \in {\mathbb {R}}_{(0, p)}\) exists so that for every  and every \(u \in \mathbb {R}_{\ge 0}\), for which \(\Phi (\texttt {X}, u)\) is defined, we have
and every \(u \in \mathbb {R}_{\ge 0}\), for which \(\Phi (\texttt {X}, u)\) is defined, we have  .
.
Proof
Take any positive \(\epsilon \), smaller than the one in Lemma 5.11. Let  and \(u \in \mathbb {R}_{\ge 0}\), so that \(\Phi (\texttt {X}, u)\) is defined. Let
and \(u \in \mathbb {R}_{\ge 0}\), so that \(\Phi (\texttt {X}, u)\) is defined. Let

We use Lemma 5.10 to show \(L = {\mathbb {R}}_{[0, u]}\); this finishes the proof.
Clearly \(0 \in L\) and L is a lower set. It is the preimage of  under the map \({\Phi (\texttt {X}, \text {---}):{\mathbb {R}}_{[0, u]} \rightarrow \mathbb {R}^n}\), so it is closed. We only still need to see that for every \(t \in L_{< u}\) there exists \(t' \in {\mathbb {R}}_{(t, u]}\) such that \(t' \in L\).
under the map \({\Phi (\texttt {X}, \text {---}):{\mathbb {R}}_{[0, u]} \rightarrow \mathbb {R}^n}\), so it is closed. We only still need to see that for every \(t \in L_{< u}\) there exists \(t' \in {\mathbb {R}}_{(t, u]}\) such that \(t' \in L\).
If  , the requisite \(t'\) clearly exists. Assume now that
, the requisite \(t'\) clearly exists. Assume now that  .
.
Recall from Lemma 5.4 that  . Suppose first that \(\Phi (\texttt {X}, t) \in \mathcal {V}\). Then \(V\) has the same direction as
. Suppose first that \(\Phi (\texttt {X}, t) \in \mathcal {V}\). Then \(V\) has the same direction as  on some neighbourhood of \(\Phi (\texttt {X}, t)\), meaning that it points into the interior of or is at worst tangent to
on some neighbourhood of \(\Phi (\texttt {X}, t)\), meaning that it points into the interior of or is at worst tangent to  on this neighbourhood, so the flow stays for awhile in
on this neighbourhood, so the flow stays for awhile in  which gives us the requisite \(t'\). On the other hand, if \(\Phi (\texttt {X}, t) \in \mathcal {W}\), then we have \(t'\) by Lemma 5.11. \(\square \)
which gives us the requisite \(t'\). On the other hand, if \(\Phi (\texttt {X}, t) \in \mathcal {W}\), then we have \(t'\) by Lemma 5.11. \(\square \)
We are now ready to prove that the domain of definition of \(\Phi \) is

Proposition 5.13
The flow \(\Phi \) is defined on \(\mathcal {D}\).
Proof
The flow is defined as long as it remains within the domain of \(V\), i.e.  . Take any
. Take any  and define
and define

We verify the properties for L from Lemma 5.10 to get \(L = {\mathbb {R}}_{[0, d(\mathcal {M}, \texttt {X}))}\). The basic properties of the flow tell us that \(0 \in L\) and that L is an open lower subset of \({\mathbb {R}}_{[0, d(\mathcal {M}, \texttt {X}))}\). Take \(t \in {\mathbb {R}}_{[0, d(\mathcal {M}, \texttt {X}))}\) such that \({\mathbb {R}}_{[0, t)} \subseteq L\). Because the vector field \(V\) is bounded (Proposition 5.8), the map  (of which the field is the derivative) is Lipschitz, in particular uniformly continuous. Hence it has a (uniformly) continuous extension
(of which the field is the derivative) is Lipschitz, in particular uniformly continuous. Hence it has a (uniformly) continuous extension  (since
(since  , as a closed subspace of \(\mathbb {R}^n\), is complete). Thus the limit \(\texttt {Y}\mathrel {\mathop :}=\lim _{t' \nearrow t} \Phi (\texttt {X}, t')\) exists and is in
, as a closed subspace of \(\mathbb {R}^n\), is complete). Thus the limit \(\texttt {Y}\mathrel {\mathop :}=\lim _{t' \nearrow t} \Phi (\texttt {X}, t')\) exists and is in  .
.
We need to show that  . Using Lemma 5.9, we get
. Using Lemma 5.9, we get
Hence \(\texttt {Y}\notin \mathcal {M}\).
We also have  . Before the flow could leave
. Before the flow could leave  , it would have to get arbitrarily close to
, it would have to get arbitrarily close to  which would contradict Lemma 5.12. \(\square \)
which would contradict Lemma 5.12. \(\square \)
5.4 The deformation retraction
We can now define a deformation retraction from  to \(\mathcal {M}\). The flow \(\Phi \) takes us arbitrarily close to the manifold without actually reaching it, so we will define the deformation retraction in two parts: first from
to \(\mathcal {M}\). The flow \(\Phi \) takes us arbitrarily close to the manifold without actually reaching it, so we will define the deformation retraction in two parts: first from  to a small neighbourhood of \(\mathcal {M}\), and then from this neighbourhood to \(\mathcal {M}\) itself.
to a small neighbourhood of \(\mathcal {M}\), and then from this neighbourhood to \(\mathcal {M}\) itself.
Recall that by assumption \(p> \lambda \), and we have

The distance of a point in  to the complement of
to the complement of  is the smallest in a co-vertex of
is the smallest in a co-vertex of  , where it is equal to \(p- \lambda \). Hence
, where it is equal to \(p- \lambda \). Hence  .
.
Denote \(w \mathrel {\mathop :}=\frac{p- \lambda }{2}\) and define the map  by
by

This map is well defined: if \(d(\mathcal {M}, \texttt {X}) = w\), the two function rules match. Each of them is continuous and defined on a domain, closed in  , so R is continuous on
, so R is continuous on  . Clearly \(R\) is a strong deformation retraction from
. Clearly \(R\) is a strong deformation retraction from  to \(\overline{\mathcal {M}}_{w}\): for
to \(\overline{\mathcal {M}}_{w}\): for  we have
we have

so \(d\big (\mathcal {M}, R(\texttt {X}, 1)\big ) = d(\mathcal {M}, \texttt {X}) - \big (d(\mathcal {M}, \texttt {X}) - w\big ) = w\) by Lemma 5.9.
Proposition 5.14
There exists a strong deformation retraction of  to \(\mathcal {M}\).
to \(\mathcal {M}\).
Proof
First use \(R\) to strongly deformation retract  to \(\overline{\mathcal {M}}_{w}\). From here, the usual normal deformation retraction works. Specifically, since w is less that the reach of \(\mathcal {M}\), the map \(pr\) is defined on \(\overline{\mathcal {M}}_{w}\). Hence the map \(\overline{\mathcal {M}}_{w} \times {\mathbb {R}}_{[0, 1]} \rightarrow \overline{\mathcal {M}}_{w}\), given by \((\texttt {X}, t) \mapsto (1-t) \cdot \texttt {X}+ t \cdot pr(\texttt {X})\), is well defined and a strong deformation retraction from \(\overline{\mathcal {M}}_{w}\) to \(\mathcal {M}\). \(\square \)
to \(\overline{\mathcal {M}}_{w}\). From here, the usual normal deformation retraction works. Specifically, since w is less that the reach of \(\mathcal {M}\), the map \(pr\) is defined on \(\overline{\mathcal {M}}_{w}\). Hence the map \(\overline{\mathcal {M}}_{w} \times {\mathbb {R}}_{[0, 1]} \rightarrow \overline{\mathcal {M}}_{w}\), given by \((\texttt {X}, t) \mapsto (1-t) \cdot \texttt {X}+ t \cdot pr(\texttt {X})\), is well defined and a strong deformation retraction from \(\overline{\mathcal {M}}_{w}\) to \(\mathcal {M}\). \(\square \)
6 Main theorem
Theorem 6.1
Let \(n\in \mathbb {N}\) and let \(\mathcal {M}\) be a non-empty properly embedded  -submanifold of \(\mathbb {R}^n\) without boundary. Let \(\mathcal {M}\) have the same dimension \(m\) around every point. Let \(\mathcal {S}\subseteq \mathcal {M}\) be a subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (the sample from the manifold \(\mathcal {M}\)). Let \(\tau \) be the reach of \(\mathcal {M}\) in \(\mathbb {R}^n\) and \(\varkappa \) the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\). Following the notation from Sect. 4, let \(m_p= 0.5\), \(M_p= 0.96\), \(\varkappa _\textrm{off} = 0.55\). Then for all
-submanifold of \(\mathbb {R}^n\) without boundary. Let \(\mathcal {M}\) have the same dimension \(m\) around every point. Let \(\mathcal {S}\subseteq \mathcal {M}\) be a subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (the sample from the manifold \(\mathcal {M}\)). Let \(\tau \) be the reach of \(\mathcal {M}\) in \(\mathbb {R}^n\) and \(\varkappa \) the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\). Following the notation from Sect. 4, let \(m_p= 0.5\), \(M_p= 0.96\), \(\varkappa _\textrm{off} = 0.55\). Then for all  which satisfy
which satisfy

there exists a strong deformation retraction from  (the union of open ellipsoids around sample points) to \(\mathcal {M}\). In particular, \(\mathcal {M}\),
(the union of open ellipsoids around sample points) to \(\mathcal {M}\). In particular, \(\mathcal {M}\),  and the nerve complex of the ellipsoid cover
and the nerve complex of the ellipsoid cover  are homotopy equivalent, and so have the same homology.
are homotopy equivalent, and so have the same homology.
Proof
First consider the case \(\tau = \infty \). Then \(\mathcal {M}\) is an \(m\)-dimensional affine subspace of \(\mathbb {R}^n\). In that case  is just \(\mathcal {M}_{p}\) (the tubular neighbourhood around \(\mathcal {M}\) of radius \(p\)) which clearly strongly deformation retracts to \(\mathcal {M}\) via the normal deformation retraction.
is just \(\mathcal {M}_{p}\) (the tubular neighbourhood around \(\mathcal {M}\) of radius \(p\)) which clearly strongly deformation retracts to \(\mathcal {M}\) via the normal deformation retraction.
A particular case of this is when \(m= n\) or when \(\mathcal {M}\) is a single point. If \(m= 0\), i.e. \(\mathcal {M}\) is a non-empty locally finite discrete set of points, and if \(\mathcal {M}\) has at least two points, then the reach is half the distance between two closest points. In this case we necessarily have \(\mathcal {S}= \mathcal {M}\) and the set  is a union of \(p\)-balls around points in \(\mathcal {M}\) which clearly deformation retracts to \(\mathcal {M}\).
is a union of \(p\)-balls around points in \(\mathcal {M}\) which clearly deformation retracts to \(\mathcal {M}\).
We now consider the case \(\tau < \infty \) and \(0< m< n\).
All our conditions and results are homogeneous in the sense that they are preserved under uniform scaling. In particular, we may rescale the whole space \(\mathbb {R}^n\) by the factor \(\frac{1}{\tau }\) and may thus without loss of generality assume \(\tau = 1\). The result now follows from Proposition 5.14. \(\square \)
Corollary 6.2
Let \(n\in \mathbb {N}\) and let \(\mathcal {M}\) be a non-empty properly embedded  -submanifold of \(\mathbb {R}^n\) without boundary. Let \(\mathcal {M}\) have the same dimension \(m\) around every point. Let \(\mathcal {S}\subseteq \mathcal {M}\) be a subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (the sample from the manifold \(\mathcal {M}\)). Let \(\tau \) be the reach of \(\mathcal {M}\) in \(\mathbb {R}^n\) and \(\varkappa \) the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\). Then whenever
-submanifold of \(\mathbb {R}^n\) without boundary. Let \(\mathcal {M}\) have the same dimension \(m\) around every point. Let \(\mathcal {S}\subseteq \mathcal {M}\) be a subset of \(\mathcal {M}\), locally finite in \(\mathbb {R}^n\) (the sample from the manifold \(\mathcal {M}\)). Let \(\tau \) be the reach of \(\mathcal {M}\) in \(\mathbb {R}^n\) and \(\varkappa \) the Hausdorff distance between \(\mathcal {S}\) and \(\mathcal {M}\). Then whenever

there exists \(p\in \mathbb {R}_{> 0}\) such that \(\mathcal {M}\) is homotopy equivalent to  .
.
Proof
The expression  is increasing in \(p\). Hence we get the required result from Theorem 6.1 by taking \(p= M_p\tau \). \(\square \)
is increasing in \(p\). Hence we get the required result from Theorem 6.1 by taking \(p= M_p\tau \). \(\square \)
7 Discussion
As already mentioned in the introduction, the ratio \(\frac{\varkappa }{\tau }\) is a measure of the density of the sample. We want the required sample density to be small, i.e. the ratio \(\frac{\varkappa }{\tau }\) should be as large as possible. Corollary 6.2 gave us the upper bound \(\frac{\varkappa }{\tau } < 0.913\). For comparison, recall that Niyogi et al. (2008) obtained the bound \(\frac{\varkappa }{\tau } < \frac{1}{2} \sqrt{\frac{3}{5}} \approx 0.387\). Hence our result allows approximately 2.36-times lower density of the sample.
There is clear room for improvement of our result. The bounds we obtained from the theoretical parts of the proof yield
which would be a further improvement of the above result \(\frac{\varkappa }{\tau } < 0.913\) by around a third (more than three times an improvement over the Niyogi, Smale and Weinberger’s result). The only reason we had to settle for the worse result was because to prove Lemma 4.1 in Sect. 4, we used a computer program. We can get closer to the theoretical bound by increasing \(M_p\) and decreasing \(m_p\) and \(\varkappa _\textrm{off}\), in which case the program yields a smaller lower bound on the values of the calculated function. Hence we would need to run the program with smaller \(\delta \), but since the loops in the program, the number of steps in which is inversely proportional to \(\delta \), are nested four levels deep, dividing \(\delta \) by some t makes the program run approximately \(t^4\)-times longer. The parameters, given in Sect. 4, are what we settled for in this paper in order for the program to complete the calculation in a reasonable amount of time—the program which computes in parallel ran for around 2.7 days on a 4-core Intel i7-7500 processor. Our bound on the sample density can thus be improved by anyone with more patience and better hardware.
One of the questions we do not answer in this paper concerns robustment of our results to noise. This is relevant because in practice, the reach and the tangent spaces are estimated from the sample, and are thus only approximately known. The sample points might also lie only in the vicinity of the manifold, not exactly on it. In this paper we wanted to establish the new methods, and we leave their refinement to take noise into account for future work.
Our result is expressed in terms of the reach of a manifold, which is a global feature. As the classical sampling theory advanced, researchers refined the notion of reach to local feature size, weak feature size, \(\mu \)-reach and related concepts (Amenta and Bern 1999; Chazal and Lieutier 2005a, 2008; Chazal et al. 2009; Turner 2013; Dey et al. 2017). A natural question arises whether we can apply these concepts to improve the bounds on a (local) density of a sample when using ellipsoids. In particular, it would be interesting to see whether we can improve our result by allowing differently sized ellipsoids around different sample points, with the upper bound on the size given in terms of the local feature size (local distance to the medial axis) or the distance to critical points.
Notes
A simple example is the submanifold of the plane, given by the equation \((x^2 + y^2)^2 = x^2 + y^2\) (a union of a point and a circle).
Recall that a map is proper when the preimage of every compact subspace of the codomain is compact.
If \(\mathcal {N}\) is empty, so is
 , though the medial axis can be empty even for non-empty manifolds (consider for example a line or a line segment in a plane).
, though the medial axis can be empty even for non-empty manifolds (consider for example a line or a line segment in a plane).If
 , this “ball” is the whole closed half-space which contains \(\textbf{N}\) and the boundary of which is the hyperplane, orthogonal to \(\textbf{N}\), which contains \(\texttt {X}\).
, this “ball” is the whole closed half-space which contains \(\textbf{N}\) and the boundary of which is the hyperplane, orthogonal to \(\textbf{N}\), which contains \(\texttt {X}\).In practice, b is the product of numbers or scalar product of vectors.
Imagine distinct points \(\texttt {A}\) and \(\texttt {B}\) in some higher-dimensional Euclidean space and a non-zero vector \(\textbf{a}\), starting at \(\texttt {A}\) and having a nonnegative scalar product with \(\textbf{AB}\). Consider paths, starting at \(\texttt {A}\) and going in the direction of \(\textbf{a}\), the curvature of which is bounded by some number. Then the fastest that we can get away from B along such a path is within the plane, determined by \(\texttt {A}\), \(\texttt {B}\) and \(\textbf{a}\)—specifically, along the arc with the maximum curvature.
We could reduce \(m_p\) to around 0.273, and the argument would still work. However, starting at 0.5 still leaves us with a decently sized length of the persistence interval, while (as we see later) reducing the Lipschitz constant for f and shortening the run-time of the program.
Recall that a function \({f_{\texttt {S}}}\) is defined on
 , so when calculating its support, we take the closure within
, so when calculating its support, we take the closure within  . This support is in general not closed in \(\mathbb {R}^n\).
. This support is in general not closed in \(\mathbb {R}^n\).
References
Aamari, E., Kim, J., Chazal, F., Michel, B., Rinaldo, A., Wasserman, L., et al.: Estimating the reach of a manifold. Electron. J. Stat. 13(1), 1359–1399 (2019)
Amenta, N., Bern, M.: Surface reconstruction by Voronoi filtering. Discrete Comput. Geom. 22(4), 481–504 (1999)
Amenta, N., Choi, S., Dey, T.K., Leekha, N.: A simple algorithm for homeomorphic surface reconstruction. Int. J. Comput. Geom. Appl. 12(01n02), 125–141 (2002)
Attali, D., Lieutier, A.: Reconstructing shapes with guarantees by unions of convex sets. In: Proceedings of the Twenty-Sixth Annual Symposium on Computational Geometry, pp. 344–353 (2010)
Attali, D., Lieutier, A., Salinas, D.: Vietoris-rips complexes also provide topologically correct reconstructions of sampled shapes. Comput. Geom. 46(4), 448–465 (2013)
Berenfeld, C., Harvey, J., Hoffmann, M., Shankar, K.: Estimating the reach of a manifold via its convexity defect function (2020). arXiv preprint arXiv:2001.08006
Bredon, G.E.: Topology and Geometry, vol. 139. Springer, Berlin (2013)
Breiding, P., Kalisnik, S., Sturmfels, B., Weinstein, M.: Learning algebraic varieties from samples. Rev. Mat. Complut. 31(3), 545–593 (2018)
Bürgisser, P., Cucker, F., Lairez, P.: Computing the homology of basic semialgebraic sets in weak exponential time. J. ACM 66(1), 1–30 (2018)
Carlsson, G.: Topology and data. Bull. Am. Math. Soc. 46, 255–308 (2009)
Carlsson, G., Zomorodian, A.J.: Computing persistent homology. Discrete Comput. Geom. 33, 249–274 (2005)
Chazal, F., Lieutier, A.: Weak feature size and persistent homology: computing homology of solids in \({\mathbb{R}}^n\) from noisy data samples. In: Proceedings of the Twenty-First Annual Symposium on Computational Geometry, pp. 255–262 (2005a)
Chazal, F., Lieutier, A.: The “\(\lambda \)-medial axis”. Graph. Models 67(4), 304–331 (2005b)
Chazal, F., Lieutier, A.: Stability and computation of topological invariants of solids in \(\mathbb{R} ^n\). Discrete Comput. Geom. 37(4), 601–617 (2007)
Chazal, F., Lieutier, A.: Smooth manifold reconstruction from noisy and non-uniform approximation with guarantees. Comput. Geom. 40(2), 156–170 (2008)
Chazal, F., Cohen-Steiner, D., Lieutier, A.: A sampling theory for compact sets in Euclidean space. Discrete Comput. Geom. 41(3), 461–479 (2009)
Chazal, F., Cohen-Steiner, D., Lieutier, A., Mérigot, Q., Thibert, B.: Inference of Curvature Using Tubular Neighborhoods, pp. 133–158. Springer, Cham (2017)
Coleman, R.: Calculus on Normed Vector Spaces. Springer, Berlin (2012)
Dey, T.K., Dong, Z., Wang, Y.: Parameter-free topology inference and sparsification for data on manifolds. In: Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms. SIAM, pp. 2733–2747 (2017)
Dufresne, E., Edwards, P., Harrington, H., Hauenstein, J.: Sampling real algebraic varieties for topological data analysis. In: 2019 18th IEEE International Conference on Machine Learning And Applications (ICMLA). IEEE, pp. 1531–1536 (2019)
Edelsbrunner, H., Mücke, E.P.: Three-dimensional alpha shapes. ACM Trans. Graph. 13(1), 43–72 (1994)
Edelsbrunner, H., Letscher, D., Zomorodian, A.J.: Topological persistence and simplification. Discrete Comput. Geom. 28, 511–533 (2002)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93(3), 418–491 (1959)
Ghrist, R.: Barcodes: the persistent topology of data. Bull. Am. Math. Soc. 45, 61–75 (2008)
Kaslovsky, D.N., Meyer, F.G.: Optimal tangent plane recovery from noisy manifold samples. arXiv eprints (2011)
Lee, J.: Smooth manifolds. In: Lee, J. (ed.) Introduction to Smooth Manifolds, pp. 1–31. Springer, Berlin (2013)
Niyogi, P., Smale, S., Weinberger, S.: Finding the homology of submanifolds with high confidence from random samples. Discrete Comput. Geom. 39(1–3), 419–441 (2008)
Overton, M.L.: Numerical Computing with IEEE Floating Point Arithmetic. SIAM, Philadelphia (2001)
Turner, K.: Cone fields and topological sampling in manifolds with bounded curvature. Found. Comput. Math. 13(6), 913–933 (2013)
Zhang, Z., Zha, H.: Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM J. Sci. Comput. 26(1), 313–338 (2004)
Zhang, P., Qiao, H., Zhang, B.: An improved local tangent space alignment method for manifold learning. Pattern Recognit. Lett. 32(2), 181–189 (2011)
Acknowledgements
We thank Paul Breiding, Peter Hintz and Jure Kališnik for helpful discussions.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kališnik, S., Lešnik, D. Finding the homology of manifolds using ellipsoids. J Appl. and Comput. Topology 8, 193–238 (2024). https://doi.org/10.1007/s41468-023-00145-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41468-023-00145-6





 -submanifold of
-submanifold of 

 :
: :
: :
: :
: :
: , i.e.
, i.e. 
 :
:
 :
:
 :
:

 to a tubular neighbourhood of
to a tubular neighbourhood of 
 and
and  at
at  -embedded in
-embedded in  is a
is a  -submanifold of
-submanifold of  and that
and that  intersect transversely at
intersect transversely at  and
and  linearly generate the whole
linearly generate the whole  .
. . Let
. Let  -balls, associated to
-balls, associated to  with the center in
with the center in  ). Let
). Let  , and assume that
, and assume that  . Then
. Then 
 and
and  . In the
. In the  is given by the equation
is given by the equation 

 has codimension 1, i.e. a non-zero
has codimension 1, i.e. a non-zero  . Hence
. Hence 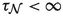 , but the required modification for
, but the required modification for  is trivial.
is trivial. is closed, some thickening of
is closed, some thickening of  . With a small perturbation of
. With a small perturbation of  (but away from the intersection
(but away from the intersection  only have transversal intersections (Lee
only have transversal intersections (Lee  , and denote the obtained space by
, and denote the obtained space by  -smooth everywhere except possibly on
-smooth everywhere except possibly on  . The double of a
. The double of a  -manifold can be equipped with a
-manifold can be equipped with a  -structure. Therefore we can use Whitney’s approximation theorem (Lee
-structure. Therefore we can use Whitney’s approximation theorem (Lee  away from
away from  -smooth everywhere. The result is a compact manifold
-smooth everywhere. The result is a compact manifold 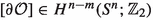 we know (see Bredon
we know (see Bredon  is the intersection number of
is the intersection number of  (times the generator). Since the cohomology of
(times the generator). Since the cohomology of  , and hence
, and hence 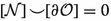 . But the local intersection number at the transversal intersection
. But the local intersection number at the transversal intersection  .
. , i.e.
, i.e. 
 . Then the cone
. Then the cone  (thus the whole
(thus the whole  around the centers of the associated balls within
around the centers of the associated balls within  -balls. If
-balls. If  , and we are done. If
, and we are done. If  around
around  and therefore also its smoothed version orthogonally in
and therefore also its smoothed version orthogonally in  exists. It cannot lie in
exists. It cannot lie in  since we would then have a manifold point in the interior of some associated ball, so
since we would then have a manifold point in the interior of some associated ball, so  . The furthest center is the one within the starting planar tangent-normal coordinate system that has coordinates
. The furthest center is the one within the starting planar tangent-normal coordinate system that has coordinates  . Thus
. Thus 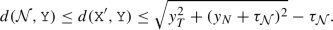
 . Then
. Then  , i.e.
, i.e.  is an open cover of
is an open cover of  , is strictly increasing. Thus there exists a unique
, is strictly increasing. Thus there exists a unique 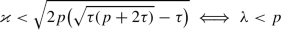
 . If
. If  , and a quick calculation shows that
, and a quick calculation shows that 
 . If
. If  and the reach
and the reach 
 . If
. If 
 . Assume hereafter that
. Assume hereafter that  is given by the equation
is given by the equation  . A routine calculation shows that it intersects the boundaries of the
. A routine calculation shows that it intersects the boundaries of the 
 . It follows that within the given two-dimensional coordinate system
. It follows that within the given two-dimensional coordinate system 
 .
.



 .
.








 , then
, then 
 , then
, then  which contains
which contains  . Then
. Then  and
and  is the orthogonal projection of
is the orthogonal projection of  , so
, so  and
and 

 ,
, , though the medial axis can be empty even for non-empty manifolds (consider for example a line or a line segment in a plane).
, though the medial axis can be empty even for non-empty manifolds (consider for example a line or a line segment in a plane). , this “ball” is the whole closed half-space which contains
, this “ball” is the whole closed half-space which contains  , so when calculating its support, we take the closure within
, so when calculating its support, we take the closure within  . This support is in general not closed in
. This support is in general not closed in