GIST: distributed training for large-scale graph convolutional networks

Abstract

The graph convolutional network (GCN) is a go-to solution for machine learning on graphs, but its training is notoriously difficult to scale both in terms of graph size and the number of model parameters. Although some work has explored training on large-scale graphs, we pioneer efficient training of large-scale GCN models with the proposal of a novel, distributed training framework, called GIST. GIST disjointly partitions the parameters of a GCN model into several, smaller sub-GCNs that are trained independently and in parallel. Compatible with all GCN architectures and existing sampling techniques, GIST (i) improves model performance, (ii) scales to training on arbitrarily large graphs, (iii) decreases wall-clock training time, and (iv) enables the training of markedly overparameterized GCN models. Remarkably, with GIST, we train an astonishgly-wide 32–768-dimensional GraphSAGE model, which exceeds the capacity of a single GPU by a factor of $8\times$, to SOTA performance on the Amazon2M dataset.

1 Introduction

Since not all data can be represented in Euclidean space (Bronstein et al. 2017), many applications rely on graph-structured data. For example, social networks can be modeled as graphs by regarding each user as a node and friendship relations as edges (Lusher et al. 2013; Newman et al. 2002). Alternatively, in chemistry, molecules can be modeled as graphs, with nodes representing atoms and edges encoding chemical bonds (Balaban et al. 1985; Benkö et al. 2003).

To better understand graph-structured data, several (deep) learning techniques have been extended to the graph domain (Defferrard et al. 2016; Gori et al. 2005; Masci et al. 2015). Currently, the most popular one is the graph convolutional network (GCN) (Kipf and Welling 2016), a multi-layer architecture that implements a generalization of the convolution operation to graphs. Although the GCN handles node- and graph-level classification, it is notoriously inefficient and unable to support large graphs (Chen et al. 2018a, b; Gao et al. 2018; Huang et al. 2018; You et al. 2020; Zeng et al. 2019), making practical, large-scale applications difficult to handle.

To deal with these issues, node partitioning methodologies have been developed. These schemes can be roughly categorized into neighborhood sampling (Chen et al. 2018b; Hamilton et al. 2017; Zou et al. 2019) and graph partitioning (Chiang et al. 2019; Zeng et al. 2019) approaches. The goal is to partition a large graph into multiple smaller graphs that can be used as mini-batches for training the GCN. In this way, GCNs can handle larger graphs during training, expanding their potential into the realm of big data. However, the size of the underlying model is still limited by available memory capacity, thus placing further constraints on the scale of GCN experimentation.

Although some papers perform large-scale experiments (Chiang et al. 2019; Zeng et al. 2019), the models (and data) used in GCN research remain small in the context of deep learning (Kipf and Welling 2016; Veličković et al. 2017), where the current trend is towards incredibly large models and datasets (Brown et al. 2020; Conneau et al. 2019). Despite the widespread moral questioning of this trend (Hao 2019; Peng and Sarazen 2019; Sharir et al. 2020), the deep learning community continues to push the limits of scale. Overparameterized models yield improvements in tasks like zero/few-shot learning (Brown et al. 2020; Radford et al. 2021), are capable of discovering generalizable solutions (Nakkiran et al. 2019), and even have desirable theoretical properties (Oymak and Soltanolkotabi 2020).

Although deeper GCNs may perform poorly due to oversmoothing (Kipf and Welling 2016; Li et al. 2018), GCNs should similarly benefit from overparameterization, meaning that larger hidden layers may be beneficial. Furthermore, recent work indicates that overparameterization is most impactful on larger datasets (Hoffmann et al. 2022), making overparameterized models essential as GCNs are applied to practical problems at scale. Moving in this direction, our work provides an efficient training framework for wide, overparameterized GCN models—beyond the memory capacity of a single GPU—of any architecture that is compatible with existing training techniques.

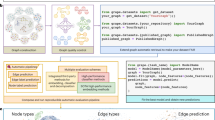
This paper. Inspired by independent subnetwork training (IST) (Yuan et al. 2019), our methodology randomly partitions the hidden feature space in each layer, decomposing the global GCN model into multiple, narrow sub-GCNs of equal depth. Sub-GCNs are trained independently for several iterations in parallel prior to having their updates synchronized; see Fig. 1. This process of randomly partitioning, independently training, and synchronizing sub-GCNs is repeated until convergence. We call this method Graph Independent Subnetwork Training (GIST), as it extends the IST framework to the training of GCNs.

Though IST was previously unexplored in this domain, we find that GIST pairs well with any GCN architecture, is compatible with node sampling techniques, can scale to arbitrarily large graphs, and significantly reduces wall-clock training time, allowing larger models and datasets to be explored. In particular, we focus on training “ultra-wide” GCNs (i.e., GCN models with very large hidden layers), as deeper GCNs are prone to oversmoothing (Li et al. 2018) and GISTs model partitioning strategy can mitigate the memory overhead of training these wider GCNs.

The contributions of this work are as follows:

• We develop a novel extension of IST for training GCNs, show that it works well for training GCNs with a variety of architectures, and demonstrate its compatibility with commonly-used GCN training techniques like neighborhood sampling and graph partitioning.

• We show that GIST can be used to reach state-of-the-art performance with reduced training time relative to standard training methodologies. GIST is a compatible addition to GCN training that improves efficiency.

• We propose a novel Graph Independent Subnetwork Training Kernel (GIST-K) that allows a convergence rate to be derived for two-layer GCNs trained with GIST in the infinite width regime. Based on GIST-K, we provide theory that GIST converges linearly –up to an error neighborhood– using distributed gradient descent with local iterations. We show that the radius of the error neighborhood is controlled by the overparameterization parameter, as well as the number of workers in the distributed setting. Such findings reflect practical observations that are made in the experimental section.

• We use GIST to enable the training of markedly overparameterized GCN models. In particular, GIST is used to train a two-layer GraphSAGE model with a hidden dimension of $32\,768$ on the Amazon2M dataset. Such a model exceeds the capacity of a single GPU by $8\times$.

Fig. 1

GIST pipeline: subGCNs divides the global GCN into sub-GCNs. Every sub-GCN is trained by subTrain using mini-batches (smaller sub-graphs) generated by Cluster. Sub-GCN parameters are intermittently aggregated through subAgg

Fig. 2

GCN partition into $m=2$ sub-GCNs. Orange and blue colors depict different feature partitions. Both hidden dimensions ($d_1$ and $d_2$) are partitioned. The output dimension ($d_3$) is not partitioned. Partitioning the input dimension ($d_0$) is optional, but we do not partition $d_0$ in GIST

2 What is the GIST of this work?

Algorithm 1

GIST Algorithm

GCN Architecture. The GCN (Kipf and Welling 2016) is arguably the most widely-used neural network architecture on graphs. Consider a graph $\mathcal {G}$ comprised of n nodes with d-dimensional features $\textbf{X} \in \mathbb {R}^{n \times d}$. The output $\textbf{Y} \in \mathbb {R}^{n \times d'}$ of a GCN can be expressed as $\textbf{Y} = \Psi _{\mathcal {G}}(\textbf{X}; \varvec{\Theta })$, where $\Psi _{\mathcal {G}}$ is an L-layered architecture with trainable parameters $\varvec{\Theta }$. If we define $\textbf{H}_0 = \textbf{X}$, we then have that $\textbf{Y} = \Psi _{\mathcal {G}}(\textbf{X}; \varvec{\Theta }) = \textbf{H}_L$, where an intermediate $\ell$-th layer of the GCN is given by

$$\begin{aligned} \textbf{H}_{\ell +1} = \sigma (\bar{\textbf{A}} \, \textbf{H}_\ell \, \varvec{\Theta }_\ell ). \end{aligned}$$

(1)

In (1), $\sigma (\cdot )$ is an elementwise activation function (e.g., ReLU), $\bar{\textbf{A}}$ is the degree-normalized adjacency matrix of $\mathcal {G}$ with added self-loops, and the trainable parameters $\varvec{\Theta } = \{\varvec{\Theta }_\ell \}_{\ell =0}^{L-1}$ have dimensions $\varvec{\Theta }_\ell \in \mathbb {R}^{d_{\ell } \times d_{\ell +1}}$ with $d_0 = d$ and $d_L = d'$. In Fig. 2 (top), we illustrate nested GCN layers for $L=3$, but our methodology extends to arbitrary L. The activation function of the last layer is typically the identity or softmax transformation – we omit this in Fig. 2 for simplicity.

GIST overview. We overview GIST in Algorithm 1 and present a schematic depiction in Fig. 1. We partition our (randomly initialized) global GCN into m smaller, disjoint sub-GCNs with the subGCNs function ($m=2$ in Figs. 1 and 2) by sampling the feature space at each layer of the GCN; see Sect. 2.1. Each sub-GCN is assigned to a different worker (i.e., a different GPU) for $\zeta$ rounds of distributed, independent training through subTrain. Then, newly-learned sub-GCN parameters are aggregated (subAgg) into the global GCN model. This process repeats for T iterations. Our graph domain is partitioned into c sub-graphs through the Cluster function ($c=2$ in Fig. 1). This operation is only relevant for large graphs ($n>50~000$), and we omit it ($c=1$) for smaller graphs that don’t require partitioning.¹

2.1 subGCNs: constructing sub-GCNs

GIST partitions a global GCN model into several narrower sub-GCNs of equal depth. Formally, consider an arbitrary layer $\ell$ and a random, disjoint partition of the feature set $[d_\ell ] = \{1, 2, \ldots , d_\ell \}$ into m equally-sized blocks $\{\mathcal {D}^{(i)}_\ell \}_{i=1}^m$.² Accordingly, we denote by $\varvec{\Theta }^{(i)}_{\ell } = [\varvec{\Theta }_{\ell }]_{\mathcal {D}^{(i)}_\ell \times \mathcal {D}^{(i)}_{\ell +1}}$ the matrix obtained by selecting from $\varvec{\Theta }_{\ell }$ the rows and columns given by the ith blocks in the partitions of $[d_\ell ]$ and $[d_{\ell +1}]$, respectively. With this notation in place, we can define m different sub-GCNs $\textbf{Y}^{(i)} = \Psi _{\mathcal {G}}(\textbf{X}^{(i)}; \varvec{\Theta }^{(i)}) = \textbf{H}^{(i)}_{L}$ where $\textbf{H}^{(i)}_{0} = \textbf{X}_{[n] \times \mathcal {D}^{(i)}_0}$ and each layer is given by:

$$\begin{aligned} \textbf{H}^{(i)}_{\ell +1} = \sigma (\bar{\textbf{A}} \, \textbf{H}^{(i)}_{\ell } \, \varvec{\Theta }^{(i)}_{\ell }). \end{aligned}$$

(2)

Notably, not all parameters within the global GCN model are partitioned to a sub-GCN. However, by randomly re-constructing new groups of sub-GCNs according to a uniform distribution throughout the training process, all parameters have a high likelihood of being updated. In Sect. 4, we provide theoretical guarantees that the partitioning of model parameters to sub-GCNs does not harm training performance.

Sub-GCN partitioning is illustrated in Fig. 2a, where $m=2$. Partitioning the input features is optional (i.e., (a) vs. (b) in Fig. 2). We do not partition the input features within GIST so that sub-GCNs have identical input information (i.e., $\textbf{X}^{(i)} = \textbf{X}$ for all i); see Sect. 5.1. Similarly, we do not partition the output feature space to ensure that the sub-GCN output dimension coincides with that of the global model, thus avoiding any need to modify the loss function. This decomposition procedure (subGCNs function in Algorithm 1) extends to arbitrary L.

2.2 subTrain: independently training sub-GCNs

Assume $c=1$ so that the Cluster operation in Algorithm 1 is moot and $\{\mathcal {G}_{(j)}\}_{j=1}^c = \mathcal {G}$. Because $\textbf{Y}^{(i)}$ and $\textbf{Y}$ share the same dimension, sub-GCNs can be trained to minimize the same global loss function. One application of subTrain in Algorithm 1 corresponds to a single step of stochastic gradient descent (SGD). Inspired by local SGD (Lin et al. 2018), multiple, independent applications of subTrain are performed in parallel (i.e., on separate GPUs) for each sub-GCN prior to aggregating weight updates. The number of independent training iterations between synchronization rounds, referred to as local iterations, is denoted by $\zeta$, and the total amount of training is split across sub-GCNs.³ Ideally, the number sub-GCNs and local iterations should be increased as much as possible to minimize communication and training costs. In practice, however, such benefits may come at the cost of statistical inefficiency; see Sect. 5.1.

If $c > 1$, subTrain first selects one of the c subgraphs in $\{\mathcal {G}_{(j)}\}_{j=1}^c$ to use as a mini-batch for SGD. Alternatively, the union of several sub-graphs in $\{\mathcal {G}_{(j)}\}_{j=1}^c$ can be used as a mini-batch for training. Aside from using mini-batches for each SGD update instead of the full graph, the use of graph partitioning does not modify the training approach outlined above. Some form of node sampling must be adopted to make training tractable when the full graph is too large to fit into memory. However, both graph partitioning and layer sampling are compatible with GIST (see Sects. 5.2 and 5.4). We adopt graph partitioning in the main experiments due to the ease of implementation. The novelty of our work lies in the feature partitioning strategy of GIST for distributed training, which is an orthogonal technique to node sampling; see Fig. 3 and Sect. 2.4.

2.3 subAgg: aggregating sub-GCN parameters

After each sub-GCN completes $\zeta$ training iterations, their updates are aggregated into the global model (subAgg function in Algorithm 1). Within subAgg, each worker replaces global parameter entries within $\varvec{\Theta }$ with its own, independently-trained sub-GCN parameters $\varvec{\Theta }^{(i)}$, where no collisions occur due to the disjointness of sub-GCN partitions. Thus, subAgg is a basic copy operation that transfers sub-GCN parameters into the global model.

Not every parameter in the global GCN model is updated by subAgg because, as previously mentioned, parameters exist that are not partitioned to any sub-GCN by the $\texttt {subGCNs}$ operation. For example, focusing on $\varvec{\Theta }_{1}$ in Fig. 2a, one worker will be assigned $\varvec{\Theta }^{(1)}_{1}$ (i.e., overlapping orange blocks), while the other worker will be assigned $\varvec{\Theta }^{(2)}_{1}$ (i.e., overlapping blue blocks). The rest of $\varvec{\Theta }_{1}$ is not considered within subAgg. Nonetheless, since sub-GCN partitions are randomly drawn in each cycle t, one expects all of $\varvec{\Theta }$ to be updated multiple times if T is sufficiently large.

2.4 What is the value of GIST?

Architecture-Agnostic Distributed Training. GIST is a generic, distributed training methodology that can be used for any GCN architecture. We implement GIST for vanilla GCN, GraphSAGE, and GAT architectures, but GIST is not limited to these models; see Sect. 5.

Fig. 3

Illustrates the difference between GIST and node sampling techniques within the forward pass of a single GCN layer (excluding non-linear activation). While graph partitioning and layer sampling remove nodes from the forward pass (i.e., either completely or on a per-layer basis), GIST partitions node feature representations (and, in turn, model parameters) instead of the nodes themselves

Compatibility with Sampling Methods. GIST is NOT a replacement for graph or layer sampling. Rather, it is an efficient, distributed training technique that can be used in tandem with node partitioning. As depicted in Fig. 3, GIST partitions node feature representations and model parameters between sub-GCNs, while graph partitioning and layer sampling sub-sample nodes within the graph.

Interestingly, we find that GIST’s feature and parameter partitioning strategy is compatible with node partitioning—the two approaches can be combined to yield further efficiency benefits. For example, GIST is combined with graph partitioning strategies in Sect. 5.2 and with layer sampling methodologies in Sect. 5.4. As such, we argue that GIST offers an easy add-on to GCN training that makes larger scale experiments more feasible.

Enabling Ultra-Wide GCN Training. GIST indirectly updates the global GCN through the training of smaller sub-GCNs, enabling models with hidden dimensions that exceed the capacity of a single GPU to be trained; in our experiments, we show results where GIST allows training of models beyond the capacity of a single GPU by a factor of $8\times$. In this way, GIST allows markedly overparametrized (“ultra-wide") GCN models to be trained on existing hardware. In Sect. 5.2, we leverage this capability to train a two-layer GCN model with a hidden dimension of 32 768 on Amazon2M.

Overparameterization through width is especially relevant to GCNs because deeper models suffer from oversmoothing (Li et al. 2018). Additionally, the theoretical results provided within Sect. 4 reveal that the performance of GIST is best as the number of neurons within each hidden layer is increased, which further reveals the benefit of wide, overparameterized layers. We do not explore depth-wise partitions of different GCN layers to each worker, but rather focus solely upon partitioning the hidden neurons within each layer.

Improved Model Complexity. Consider a single GCN layer, trained over M machines with input and output dimension of $d_{i-1}$ and $d_{i}$, respectively. For one synchronization round, the communication complexity of GIST and standard distributed training is $\mathcal {O}(\frac{1}{M}d_i d_{i-1})$ and $\mathcal {O}(M d_{i} d_{i-1})$, respectively. GIST reduces communication by only communicating sub-GCN parameters. Existing node partitioning techniques cannot similarly reduce communication complexity because model parameters are never partitioned. Furthermore, the computational complexity of the forward pass for a GCN model trained with GIST and using standard methodology is $\mathcal {O}(\frac{1}{M} N^2 d_i + \frac{1}{M^2} N d_i d_{i-1})$ and $\mathcal {O}(N^2 d_i + N d_i d_{i-1})$, respectively, where N is the number of nodes in the partition being processed.⁴ Node partitioning can reduce N by a constant factor but is compatible with GIST.

Relation to IST. Our work extends the IST distributed training framework—originally proposed for fully-connected network architectures (Yuan et al. 2019)—to GCNs. Due to the unique aspects of GCN training (e.g., non-euclidean data and aggregation of node features), it was previously unclear whether IST would work well in this domain. Though IST is applicable to a variety of architectures, we find that it is especially useful for efficiently training GCNs to high accuracy. GIST i) provides speedups and performance benefits, ii) is compatible with other efficient GCN training methods, and iii) enables training of uncharacteristically-wide GCN models, allowing overparameterized GCNs to be explored via greater width. The practical utility of GIST and interplay of the approach with unique aspects of GCN training differentiate our work from the original IST proposal.

3 Related work

GCN training. In spite of their widespread success in several graph related tasks, GCNs often suffer from training inefficiencies (Gao et al. 2018; Huang et al. 2018). Consequently, the research community has focused on developing efficient and scalable algorithms for training GCNs (Chen et al. 2018a, b; Chiang et al. 2019; Hamilton et al. 2017; Zeng et al. 2019; Zou et al. 2019). The resulting approaches can be divided roughly into two areas: neighborhood sampling and graph partitioning. However, it is important to note that these two broad classes of solutions are not mutually exclusive, and reasonable combinations of the two approaches may be beneficial.

Neighborhood sampling methodologies aim to sub-select neighboring nodes at each layer of the GCN, thus limiting the number of node representations in the forward pass and mitigating the exponential expansion of the GCNs receptive field. VRGCN (Chen et al. 2018a) implements a variance reduction technique to reduce the sample size in each layer, which achieves good performance with smaller graphs. However, it requires to store all the intermediate node embeddings during training, leading to a memory complexity close to full-batch training. GraphSAGE (Hamilton et al. 2017) learns a set of aggregator functions to gather information from a node’s local neighborhood. It then concatenates the outputs of these aggregation functions with each node’s own representation at each step of the forward pass. FastGCN (Chen et al. 2018b) adopts a Monte Carlo approach to evaluate the GCN’s forward pass in practice, which computes each node’s hidden representation using a fixed-size, randomly-sampled set of nodes. LADIES (Zou et al. 2019) introduces a layer-conditional approach for node sampling, which encourages node connectivity between layers in contrast to FastGCN (Chen et al. 2018b).

Graph partitioning schemes aim to select densely-connected sub-graphs within the training graph, which can be used to form mini-batches during GCN training. Such sub-graph sampling reduces the memory footprint of GCN training, thus allowing larger models to be trained over graphs with many nodes. ClusterGCN (Chiang et al. 2019) produces a very large number of clusters from the global graph, then randomly samples a subset of these clusters and computes their union to form each sub-graph or mini-batch. Similarly, GraphSAINT (Zeng et al. 2019) randomly samples a sub-graph during each GCN forward pass. However, GraphSAINT also considers the bias created by unequal node sampling probabilities during sub-graph construction, and proposes normalization techniques to eliminate this bias.

As explained in Sect. 2, GIST also relies on graph partitioning techniques (Cluster) to handle large graphs. However, the feature sampling scheme at each layer (subGCNs) that leads to parallel and narrower sub-GCNs is a hitherto unexplored framework for efficient GCN training.

Distributed training. Distributed training is a heavily studied topic (Shi et al. 2020; Zhang et al. 2018). Our work focuses on synchronous and distributed training techniques (Lian et al. 2017; Yu et al. 2019; Zhang et al. 2015). Some examples of synchronous, distributed training approaches include data parallel training, parallel SGD (Agarwal and Duchi 2011; Zinkevich et al. 2020), and local SGD (Lin et al. 2018; Stich 2019). Our methodology holds similarities to model parallel training techniques, which have been heavily explored (Ben-Nun and Hoefler 2019; Gholami et al. 2017; Günther et al. 2018; Kirby et al. 2020; Pauloski et al. 2020; Tavarageri et al. 2019; Zhu et al. 2020). More closely, our approach is inspired by IST, explored for feed-forward networks in Yuan et al. (2019). Later work analyzed IST theoretically (Liao and Kyrillidis 2021) and extended its use to more complex ResNet architectures (Dun et al. 2022). We explore the extension of IST to the GCN architecture both theoretically and empirically, finding that IST-based methods are suited well for GCN training. However, the IST framework is applicable to network architectures beyond the GCN.

4 Theoretical results

We draw upon analysis related to neural tangent kernels (NTK) Jacot et al. (2018) to derive a convergence rate for two-layer GCNs using gradient descent—as formulated in (1) and further outlined in “Appendix C.1”—trained with GIST. Given the scaled Gram matrix of an infinite-dimensional NTK $\textbf{H}^\infty$, we define the Graph Independent Subnetwork Training Kernel (GIST-K) as follows:

$$\begin{aligned} \textbf{G}^{\infty } = \bar{\textbf{A}}\textbf{H}^\infty \bar{\textbf{A}}. \end{aligned}$$

Given the GIST-K, we adopt the following set of assumptions related to the underlying graph; see “Appendix C.3” for more details.

Notations. Let n denote the number of nodes (training samples) in graph of interest, $d = d_0$ be dimension of the feature vector of each node, and m be the number of sub-GCNs in procedure 4. Let $\lambda _0 = \lambda _{\min }\left( \textbf{G}^\infty \right)$ and $\lambda ^* = \lambda _{\max }\left( \textbf{G}^\infty \right)$ be the minimum and maximum eigenvalue of $\textbf{G}^\infty$, respectively. Lastly, we denote $\mathbb {E}_{[\mathcal {M}_t]}[\cdot ] = \mathbb {E}_{\mathcal {M}_0,\dots ,\mathcal {M}_{t}}[\cdot ]$ to denote the total expectation with respect to $\mathcal {M}_0,\dots ,\mathcal {M}_t$.

Assumption 1

Assume $\lambda _{\min }(\bar{\textbf{A}}) \ne 0$ and there exists $\epsilon \in (0,1)$ and $p\in \mathbb {Z}_+$ such that $(1-\epsilon )^2p\le \textbf{D}_{ii}\le (1+\epsilon )^2p$ for all $i \in [n] = \{1, 2, \dots , n\}$, where $\textbf{D}$ is the degree matrix. Additionally, assume that i) input node representations are bounded in norm and not parallel to any other node representation, ii) output node representations are upper bounded, iii) sub-GCN feature partitions are generated at each iteration from a categorical distribution with uniform mean $\frac{1}{m}$.

Given this set of assumptions, we can guarantee that $\lambda _0 > 0$ (a detailed discussion is deferred to Sect. C.5). Under such conditions, we derive the following result for GCN models trained with GIST.

Theorem 1

Suppose assumptions 2–4 hold. Moreover, suppose in each global iteration the masks are generated from a categorical distribution with uniform mean . Fix the number of global iterations to T and local iterations to $\zeta$. Consider a two-layer GCN with parameters $\varvec{\Theta }$. If each entry of $\varvec{\Theta }$ is initialized I.I.D. from $\mathcal {N}(0,\kappa ^2\textbf{I})$, and the number of hidden neurons satisfies $d_1\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2}\max \left\{ \frac{n^3}{\delta ^2\kappa ^2}, \frac{n^2d}{\delta ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}, T^2\lambda ^{*2}d\right\} \right)$, then procedure (4) with constant step size $\eta = \mathcal {O}\left( \tfrac{\lambda _0}{n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}\right)$ converges according to

$$\begin{aligned} \mathbb {E}_{[\mathcal {M}_{t-1}]}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right]&\le \left( \gamma + (1-\gamma )\left( 1 - \frac{\eta \lambda _0}{2}\right) ^\zeta \right) ^t\left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2 +\\&\quad \quad \quad \mathcal {O}\left( \frac{\gamma ^2d\kappa ^2\lambda ^{*2}}{m^2(1-\gamma )\lambda _0^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

with probability at least $1 - \delta$, where $\gamma = \left( 1 - m^{-1}\right) ^{\frac{1}{3}}$.

A full proof of this result is deferred to “Appendix C”, but a sketch of the techniques used is as follows:

• 1. We define the GIST-K and show that it remains positive definite throughout training given our assumptions and sufficient overparameterization.

• 2. We show that local sub-GCN training converges linearly, given a positive definite GIST-K.

• 3. We analyze the change in training error when sub-GCNs are sampled (subGCNs), locally trained (subTrain), and aggregated (subAgg).

• 4. We establish a connection between local and aggregated weight perturbation, showing that network parameters are bounded by a small region centered around the initialization given sufficient overparameterization.

Discussion. Stated intuitively, the result in Theorem 1 shows that, given sufficient width, two-layer GCNs trained using $\texttt {GIST}$ converge to approximately zero training error. The convergence rate is linear and on par with training the full, two-layer GCN model (i.e., without the feature partition utilized in GIST), up to an error neighborhood. Notice choosing a smaller initialization scale $\kappa$ will result in a smaller size of the error neighborhood but at the same time a larger overparameterization requirement. Such theory shows that the feature partitioning strategy of GIST does not cause the model to diverge in training. Additionally, the theory suggests that wider GCN models should be used to maximize the convergence rate of GIST and minimize the impact of the additive term within Theorem 1. Such findings reflect practical observations that are made within Sect. 5 and reveal that GIST is particularly-suited towards training extremely wide models that cannot be trained using a traditional, centralized approach on a single GPU due to limited memory capacity.

5 Experiments

Table 1 Test accuracy of GCN models trained on small-scale datasets with GIST

We use GIST to train different GCN architectures on six public, multi-node classification datasets; see “Appendix A” for details. In most cases, we compare the performance of models trained with GIST to that of models trained with standard methods (i.e., single GPU with node partitioning). Comparisons to models trained with other distributed methodologies are also provided in “Appendix B”. Experiments are divided into small and large scale regimes based upon graph size. The goal of GIST is to (i) train GCN models to state-of-the-art performance, (ii) minimize wall-clock training time, and (iii) enable training of very wide GCN models.

5.1 Small-scale experiments

In this section, we perform experiments over Cora, Citeseer, Pubmed, and OGBN-Arxiv datasets (Sen et al. 2008; Hu et al. 2020). For these small-scale datasets, we train a three-layer, 256-dimensional GCN model (Kipf and Welling 2016) with GIST; see “Appendix A.3” for further experimental settings. All reported metrics are averaged across five separate trials. Because these experiments run quickly, we use them to analyze the impact of different design and hyperparameter choices rather than attempting to improve runtime (i.e., speeding up such short experiments is futile).

Which layers should be partitioned? We investigate whether models trained with GIST are sensitive to the partitioning of features within certain layers. Although the output dimension $d_3$ is never partitioned, we selectively partition dimensions $d_0$, $d_1$, and $d_2$ to observe the impact on model performance; see Table 1. Partitioning input features ($d_0$) significantly degrades test accuracy because sub-GCNs observe only a portion of each node’s input features (i.e., this becomes more noticeable with larger m). However, other feature dimensions cause no performance deterioration when partitioned between sub-GCNs, leading us to partition all feature dimensions other than $d_0$ and $d_L$ within the final GIST methodology; see Fig. 2b.

Table 2 Performance of models trained with GIST on Reddit and Amazon2M

How many Sub-GCNs to use? Using more sub-GCNs during GIST training typically improves runtime because sub-GCNs (i) become smaller, (ii) are each trained for fewer epochs, and (iii) are trained in parallel. We find that all models trained with GIST perform similarly for practical settings of m; see Table 1. One may continue increasing the number sub-GCNs used within GIST until all GPUs are occupied or model performance begins to decrease.

GIST Performance. Models trained with GIST often exceed the performance of models trained with standard, single-GPU methodology; see Table 1. Intuitively, we hypothesize that the random feature partitioning within GIST, which loosely resembles dropout (Srivastava et al. 2014), provides regularization benefits during training, but some insight into the favorable performance of GIST is also provided by the theoretical guarantees outlined in Sect. 4.

5.2 Large-scale experiments

For large-scale experiments on Reddit and Amazon2M, the baseline model is trained on a single GPU and compared to models trained with GIST in terms of F1 score and training time. All large-scale graphs are partitioned into 15 000 sub-graphs during training.⁵ Graph partitioning is mandatory because the training graphs are too large to fit into memory. One could instead use layer sampling to make training tractable (see Sect. 5.4), but we adopt graph partitioning in most experiments because the implementation is simple and performs well.

Reddit Dataset. We perform tests with 256-dimensional GraphSAGE (Hamilton et al. 2017) and GAT (Veličković et al. 2017) models with two to four layers on Reddit; see “Appendix A.4” for more details. As shown in Table 2, utilizing GIST significantly accelerates GCN training (i.e., a $1.32\times$ to $7.90\times$ speedup). GIST performs best in terms of F1 score with $m=2$ sub-GCNs (i.e., $m=4$ yields further speedups but F1 score decreases). Interestingly, the speedup provided by GIST is more significant for models and datasets with larger compute requirements. For example, experiments with the GAT architecture, which is more computationally expensive than GraphSAGE, achieve a near-linear speedup with respect to m.

Amazon2M Dataset. Experiments are performed with two, three, and four-layer GraphSAGE models (Hamilton et al. 2017) with hidden dimensions of 400 and 4 096 (we refer to these models as “narrow” and “wide”, respectively). We compare the performance (i.e., F1 score and wall-clock training time) of GCN models trained with standard, single-GPU methodology to that of models trained with GIST; see Table 2. Narrow models trained with GIST have a lower F1 score in comparison to the baseline, but training time is significantly reduced. For wider models, GIST provides a more significant speedup (i.e., up to $7.12\times$) and tends to achieve comparable F1 score in comparison to the baseline, revealing that GIST works best with wider models.

Within Table 2, models trained with GIST tend to achieve a wall-clock speedup at the cost of a lower F1 score (i.e., observe the speedups marked with parenthesis in Table 2). When training time is analyzed with respect to a fixed F1 score, we observe that the baseline takes significantly longer than GIST to achieve a fixed F1 score. For example, when $L=2$, a wide GCN trained with GIST ($m=8$) reaches an F1 score of 88.86 in $\sim 4~000$ seconds, while models trained with standard methodology take $\sim 10~000$ seconds to achieve a comparable F1 score. As such, GIST significantly accelerates training relative to model performance.

Table 3 Performance of GraphSAGE models of different widths trained with GIST on Amazon2M

5.3 Training ultra-wide GCNs

We use GIST to train GraphSAGE models with widths as high as 32 000 (i.e., $\varvec{8\times }$ beyond the capacity of a single GPU); see Table 3 for results and “Appendix A.5” for more details. Considering $L=2$, the best-performing, single-GPU GraphSAGE model ($d_i=4~096$) achieves an F1 score of 90.58 in 5.2 hours. With GIST ($m=2$), we achieve a higher F1 score of 90.87 in 2.8 hours (i.e., a $1.86\times$ speedup) using $d_i=8~192$, which is beyond single GPU capacity. Similar patterns are observed for deeper models. Furthermore, we find that utilizing larger hidden dimensions yields further performance improvements, revealing the utility of wide, overparameterized GCN models. GIST, due to its feature partitioning strategy, is unique in its ability to train models of such scale to state-of-the-art performance.

5.4 GIST with layer sampling

As previously mentioned, some node partitioning approach must be adopted to avoid memory overflow when the underlying training graph is large. Although graph partitioning is used within most experiments (see Sect. 5.2), GIST is also compatible with other node partitioning strategies. To demonstrate this, we perform training on Reddit using GIST combined with a recent layer sampling approach (Zou et al. 2019) (i.e., instead of graph partitioning); see “Appendix A.6” for more details.

As shown in Table 4, combining GIST with layer sampling enables training on large-scale graphs, and the observed speedup actually exceeds that of GIST with graph partitioning. For example, GIST with layer sampling yields a $1.83\times$ speedup when $L=2$ and $m=2$, in comparison to a $1.50\times$ speedup when graph partitioning is used within GIST (see Table 2). As the number of sub-GCNs is increased beyond $m=2$, GIST with layer sampling continues to achieve improvements in wall-clock training time (e.g., speedup increases from $1.83\times$ to $2.90\times$ from $m=2$ to $m=4$ for $L=2$) without significant deterioration to model performance. Thus, although node partitioning is needed to enable training on large-scale graphs, the feature partitioning strategy of GIST is compatible with numerous sampling strategies (i.e., not just graph sampling).

Table 4 Performance of GCN models trained with a combination of GIST and LADIES Zou et al. (2019) on Reddit

6 Future work

There are a few notable extensions of GIST that may be especially useful to the research community. We leave these extensions as future work, as they go beyond the core focus of our proposal: formulating an easy-to-use, efficient training framework for large-scale experiments with GCNs.

GCNs with Edge Features. Recent work has explored using edge features within the GCN architecture (Gong and Cheng 2019; Jiang et al. 2020; Bergen et al. 2021). Given that GIST can be applied to any GCN architecture, we argue that (i) GIST is similarly compatible with architectural variants that exploit edge features and (ii) using edge features within the graph could yield further performance benefits.

To understand why such techniques would be compatible, we emphasize that—similar to node partitioning—edge features operate orthogonally to the model partitioning performed by GIST. For example, the EGNN model (Gong and Cheng 2019) injects edge information into the GCN model via the adjacency matrix at each layer, which modifies node representations and their relationships within the graph. As shown in Fig. 3, GIST simply partitions the feature space of each individual node within the hidden layers of the GCN, which has no impact or dependence on node or edge information within the underlying graph.

Deeper GCNs. Our analysis focuses upon the exploration of wide, but not deep, GCNs due to presence of oversmoothing in deep GCNs (Li et al. 2018). However, GIST is applicable to GCN architectures of any depth—the feature partitioning strategy is just applied separately to each layer. To further reduce the memory overhead of deeper GCN models, one could explore extensions of GIST that combine layer and feature partitioning strategies. Such a variant would independently train narrow sub-GCNs that contain only a small fraction of the global model’s total layers. Layer partitioning strategies—without feature partitioning—have already been shown to be effective for IST-based training of convolutional neural networks with residual connections (Dun et al. 2022).

More Settings. The analysis of GIST could be extended to alternative tasks (e.g., link prediction) and larger-scale datasets. However, performing experiments over datasets larger than Amazon2M is difficult due to the lack of moderately-large-scale graphs that are available publicly. For example, the only graph larger than Amazon2M provided via the Open Graph Benchmark (Hu et al. 2020) is Papers100M, which requires 256 Gb of CPU RAM to load.

7 Conclusions

We present GIST, a distributed training approach for GCNs that enables the exploration of larger models and datasets. GIST is compatible with existing sampling approaches and leverages a feature-wise partition of model parameters to construct smaller sub-GCNs that are trained independently and in parallel. We have shown that GIST achieves remarkable speed-ups over large graph datasets and even enables the training of GCN models of unprecedented size. We hope GIST can empower the exploration of larger, more powerful GCN architectures within the graph community.

Supplementary information

All code for this project is publicly-available via github at the following link: https://github.com/wolfecameron/GIST.

Appendices

Experimental details

1.1 Datasets

The details of the datasets utilized within GIST experiments in Sect. 5 are provided in Table 5. Cora, Citeseer, PubMed and OGBN-Arxiv are considered “small-scale” datasets and are utilized within experiments in Sect. 5.1. Reddit and Amazon2M are considered “large-scale” datasets and are utilized within experiments in Sect. 5.2.

Table 5 Details of relevant datasets

1.2 Implementation details

We provide an implementation of GIST in PyTorch (Paszke et al. 2019) using the NCCL distributed communication package for training GCN (Kipf and Welling 2016), GraphSAGE (Hamilton et al. 2017) and GAT (Veličković et al. 2017) architectures. Our implementation is centralized, meaning that a single process serves as a central parameter server. From this central process, the weights of the global model are maintained and partitioned to different worker processes (including itself) for independent training. Experiments are conducted with 8 NVIDIA Tesla V100-PCIE-32 G GPUs, a 56-core Intel(R) Xeon(R) CPU E5-2680 v4 @ 2.40GHz, and 256 GB of RAM.

1.3 Small-scale experiments

Small-scale experiments in Sect. 5.1 are performed using Cora, Citeseer, Pubmed, and OGBN-Arxiv datasets (Sen et al. 2008; Hu et al. 2020). GIST experiments are performed with two, four, and eight sub-GCNs in all cases. We find that the performance of models trained with GIST is relatively robust to the number of local iterations $\zeta$, but test accuracy decreases slightly as $\zeta$ increases; see Fig. 5. Based on the results in Fig. 5, we adopt $\zeta =20$ for Cora, Citeseer, and Pubmed, as well as $\zeta =100$ for OGBN-Arxiv.

Experiments are run for 400 epochs with a step learning rate schedule (i.e., $10\times$ decay at 50% and 75% of total epochs). A vanilla GCN model, as described in Kipf and Welling (2016), is used. The model is trained in a full-batch manner using the Adam optimizer (Kingma and Ba 2014). No node sampling techniques are employed because the graph is small enough to fit into memory. All reported results are averaged across five trials with different random seeds. For all models, $d_0$ and $d_L$ are respectively given by the number of features and output classes in the dataset. The size of all hidden layers is the same, but may vary across experiments.

We first train baseline GCN models of different depths and hidden dimensions using a single GPU to determine the best model depth and hidden dimension to be used in small-scale experiments. The results are shown in Fig. 4. Deeper models do not yield performance improvements for small-scale datasets, but test accuracy improves as the model becomes wider. Based upon the results in Fig. 4, we adopt a three-layer GCN with a hidden dimension of $d_1 \!= \!d_2 \!= \!256$ as the underlying model used in small-scale experiments. Though two-layer models seem to perform best, we use a three-layer model within Sect. 5.1 to enable more flexibility in examining the partitioning strategy of GIST.

Fig. 4

Test accuracy for different sizes (i.e., varying depth and width) of GCN models trained with standard, single-GPU methodology on small-scale datasets. We adopt three-layer, 256-dimensional GCN models as our baseline architecture

Fig. 5

Test accuracy of GCN models trained on small-scale datasets with GIST using different numbers of local iterations and sub-GCNs. Models trained with GIST are surprisingly robust to the number of local iterations used during training, no matter the number of sub-GCNs

1.4 Large-scale experiments

Reddit Dataset. For experiments on Reddit, we train 256-dimensional GraphSAGE and GAT models using both GIST and standard, single-GPU methodology. During training, the graph is partitioned into 15 000 sub-graphs. Training would be impossible without such partitioning because the graph is too large to fit into memory. The setting for the number of sub-graphs is the optimal setting proposed in previous work (Chiang et al. 2019). Models trained using GIST and standard, single-GPU methodologies are compared in terms of F1 score and training time.

All tests are run for 80 epochs with no weight decay, using the Adam optimizer (Kingma and Ba 2014). We find that $\zeta =500$ achieves consistently high performance for models trained with GIST on Reddit. We adopt a batch size of 10 sub-graphs throughout the training process, which is the optimal setting proposed in previous work (Chiang et al. 2019).

Amazon2M Dataset. For experiments on Amazon2M, we train two to four layer GraphSAGE models with hidden dimensions of 400 and 4 096 using both GIST and standard, single-GPU methodology. We follow the experimental settings of Chiang et al. (2019). The training graph is partitioned into 15000 sub-graphs and a batch size of 10 sub-graphs is used. We find that using $\zeta = 5000$ performs consistently well. Models are trained for 400 total epochs with the Adam optimizer (Kingma and Ba 2014) and no weight decay.

1.5 Training ultra-wide GCNs

All settings for ultra-wide GCN experiments in Sect. 5.3 are adopted from the experimental settings of Sect. 5.2; see “Appendix A.4” for further details. For $d_i > 4096$ evaluation must be performed on graph partitions (not the full graph) to avoid memory overflow. As such, the graph is partitioned into 5000 sub-graphs during testing and F1 score is measured over each partition and averaged. All experiments are performed using a GraphSAGE model, and the hidden dimension of the underlying model is changed between different experiments.

1.6 GIST with layer sampling

Experiments in Sect. 5.4 adopt the same experimental settings as Sect. 5.2 for the Reddit dataset; see “Appendix A.4” for further details. Within these experiments, we combine GIST with LADIES (Zou et al. 2019), a recent layer sampling approach for efficient GCN training. LADIES is used instead of graph partitioning. Any node sampling approach can be adopted—some sampling approach is just needed to avoid memory overflow.

We train 256-dimensional GCN models with either two or three layers. We utilize a vanilla GCN model within this section (as opposed to GraphSAGE or GAT) to simplify the implementation of GIST with LADIES, which creates a disparity in F1 score between the results in Sects. 5.2 and 5.4. Experiments in Sect. 5.4 compare the performance of the same models trained either with GIST or using standard, single-GPU methodology. In this case, the single-GPU model is just a GCN trained with LADIES.

GIST vs. other distributed training methods

Although GIST has been shown to provide benefits in terms of GCN performance and training efficiency in comparison to standard, single-GPU training, other choices for the distributed training of GCNs exist. Within this section, we compare GIST to other natural choices for distributed training, revealing that GCN models trained with GIST achieve favorable performance in comparison to those trained with other common distributed training techniques.

Table 6 Performance of GraphSAGE models trained using local SGD and GIST on Reddit

1.1 Local SGD

A simple version of local SGD (Lin et al. 2018) can be implemented for distributed training of GCNs by training the full model on each separate worker for a certain number of local iterations and intermittently averaging local updates. In comparison to such a methodology, GIST has better computational and communication efficiency because i) it communicates only a small fraction of model parameters to each machine and ii) locally training narrow sub-GCNs is faster than locally training the full model. We perform a direct comparison between local SGD and GIST on the Reddit dataset using a two-layer, 256-dimensional GraphSAGE model; see Table 6. As can be seen, GCN models trained with GIST have lower wall-clock training time and achieve better performance than those trained with local SGD in all cases.

Table 7 Performance of GraphSAGE models trained both with GIST and as ensembles of shallow sub-GCNs on Reddit

1.2 Sub-GCN ensembles

As previously mentioned, increasing the number of local iterations (i.e., $\zeta$ in Algorithm 1) decreases communication requirements given a fixed amount of training. When taken to the extreme (i.e., $\zeta \rightarrow \infty$), one could minimize communication requirements by never aggregating sub-GCN parameters, thus forming an ensemble of independently-trained sub-GCNs. We compare GIST to such a methodology⁶ in Table 7 using a two-layer, 256-dimensional GraphSAGE model on the Reddit dataset. Though training ensembles of sub-GCNs minimizes communication, Table 7 reveals that (i) models trained with GIST achieve better performance and (ii) inference time for sub-GCN ensembles becomes burdensome as the number of sub-GCNs is increased.

Theoretical results

1.1 Formulation of GIST for one-hidden-layer GCNs

In our analysis, we consider a GCN with one hidden-layer and a ReLU activation. Given training data $\{(\textbf{x}_i, y_i)\}_{i=1}^n$ with input features $\textbf{x}_i\in \mathbb {R}^d$ and labels $y_i\in \mathbb {R}$, we assume that the GCN outputs a scalar value $\tilde{y}_i$ for each node in the graph. Denoting $\tilde{\textbf{y}} = [\tilde{y}_1,\dots ,\tilde{y}_n]$, we can write the output of the GCN as

$$\begin{aligned} \tilde{\textbf{y}} = \frac{1}{\sqrt{d_1}}\bar{\textbf{A}}\sigma \left( \bar{\textbf{A}}\textbf{X}\varvec{\Theta }\right) \textbf{a} \end{aligned}$$

where $\varvec{\Theta } = [\varvec{\theta }_1,\dots ,\varvec{\theta }_{d_1}]\in \mathbb {R}^{n\times d_1}$ is the weights within the GCN’s first layer and $\textbf{a} = [a_1,\dots , a_{d_1}]\in \mathbb {R}^{d_1}$ is the weights within the GCN’s second layer. To simplify the analysis, we denote $\hat{\textbf{X}} = \bar{\textbf{A}}\textbf{X} = [\hat{\textbf{x}}_1,\dots \hat{\textbf{x}}_n]$. Then, we have $\hat{\textbf{x}}_i = \sum _{i'=1}^n\bar{\textbf{A}}_{ii'}\textbf{x}_{i'}$ and the output of each node within the graph can be written as

$$\begin{aligned} \tilde{y}_i = \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}a_r\sigma \left( \left\langle \hat{\textbf{x}}_{i'}, \varvec{\theta }_r\right\rangle \right) \end{aligned}$$

As in previous convergence analysis for training neural networks, we assume that second-layer weights $\textbf{a}$ are fixed and only the first layer weights $\varvec{\Theta }$ are trainable. Following the GIST feature partitioning strategy, we only partition the hidden layer. Specifically, in global iteration t, sub-GCNs are constructed by sampling a set of masks $\mathcal {M}_t \in \mathbb {R}^{m\times d_1}$. We denote the jth column of $\mathcal {M}_t$ as $\mathcal {M}^{(j)}_t\in \mathbb {R}^{m}$, the rth row of $\mathcal {M}_t$ as $\mathcal {M}_{t,r}\in \mathbb {R}^{d_1}$, and the entry in the rth row and jth column as $\mathcal {M}_{t,r}^{(j)}$. Each $\mathcal {M}^{(j)}_{t,r}$ is a binary values: $\mathcal {M}^{(j)}_{t,r} = 1$ if neuron r is active in sub-GCN j, and $\mathcal {M}^{(j)}_{t,r} = 0$ otherwise. Using this mask notation, the output for node i within sub-GCN j can be written as

$$\begin{aligned} \hat{y}_i^{(j)}(t,k) = f_{\mathcal {M}_{t}^{(j)}}\left( \varvec{\Theta }_{t,k}^{(j)},\textbf{x}\right) _i= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\sigma \left( \left\langle \hat{\textbf{x}_{i'}}, \varvec{\theta }_{t,k,r}^{(j)}\right\rangle \right) \end{aligned}$$

(3)

t and k denote the current global and local iterations, respectively. We assume that each $\mathcal {M}_{t,r}$ is sampled from a one-hot categorical distribution. We formally define the random variables $\mathcal {M}_{t,r}^{(j)}$ as follows: for each t, let $\{\hat{m}_{t,r}\}_{r=1}^{d_1}$ be a set of I.I.D. uniform random variables taking values on the index set $[m] = \{1,\dots ,m\}$, i.e., $\mathcal {P}\left( \hat{m}_{t,r} = j\right) = \frac{1}{m}$ for $j\in [m]$. Then, we define each mask entry as $\mathcal {M}_{t,r}^{(j)} = \mathbb {I}\left\{ \hat{m}_{k,r} = j\right\}$. Masks sampled in such a fashion have the following properties

• $\mathcal {P}\left( \mathcal {M}_{t,r}^{(j)} = 1\right) = \frac{1}{m}$

• $\mathcal {P}\left( \mathcal {M}_{t,r}^{(j)} = 0\right) = 1 - \frac{1}{m}$

• $\sum _{j=1}^m\mathcal {M}_{t,r}^{(j)} = 1$

• $\mathcal {M}_{t,r}^{(j)}\mathcal {M}_{t,r}^{(j')} = 0$ if $j'\ne j$.

Here, the first and second properties guarantee that the expected number of neurons active in each sub-GCN is equal. The third and fourth properties guarantee that each neuron is active in one and only one sub-GCN. Within this setup, we consider the GIST training procedure, described as

$$\begin{aligned} \begin{aligned} \varvec{\theta }_{t, 0, r}^{(j)}&= \varvec{\theta }_{t, r}\\ \varvec{\theta }_{t, k+1, r}^{(j)}&= \varvec{\theta }_{t, k, r}^{(j)} - \eta \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\\ \varvec{\theta }_{t+1, r}&= \varvec{\theta }_{t,r} + \sum _{j=1}^m\left( \varvec{\theta }_{t,\zeta ,r}^{(j)} - \varvec{\theta }_{t,0,r}^{(j)}\right) \end{aligned} \end{aligned}$$

(4)

Within this formulation, $\zeta$ represents the total number of local iterations performed for each sub-GCN, while $L\left( \varvec{\Theta }_{t,k}^{(j)}\right)$ is the loss on the jth sub-GCN during the t-th global and kth local iteration. We can express $L\left( \varvec{\Theta }_{t,k}^{(j)}\right)$ as

$$\begin{aligned} L\left( \varvec{\Theta }_{t,k}^{(j)}\right) = \left\| \textbf{y} - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 = \left\| \textbf{y} - f_{\mathcal {M}_{t}^{(j)}}\left( \varvec{\Theta }_{t,k}^{(j)},\textbf{x}\right) \right\| _2^2 \end{aligned}$$

and the gradient has the form

$$\begin{aligned} \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r} = \frac{1}{\sqrt{d_1}}\sum _{i=1}^n\sum _{i'=1}^n\left( \hat{y}_i^{(j)}(t,k) - y_i\right) \bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\hat{\textbf{x}}_{i'}\mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \end{aligned}$$

1.2 Preliminary and notations

We use bold lower-case letters (e.g. $\textbf{a}$) to denote vectors, bold upper-case letters (e.g. $\textbf{A}$) to denote matrices, and standard letters (e.g. a) for scalars. For a vector $\textbf{a}$, $\left\| \textbf{a}\right\| _1$ and $\left\| \textbf{a}\right\| _1$ denote its $\ell _1$ and $\ell _2$ norm, respectively. We also use $\texttt {abs}(\textbf{a}) = [|a_1|,\dots ,|a_n|]$ to denote the vector with entry-wise absolute value of $\textbf{a}$. For a matrix $\textbf{A}$, we use $\left\| \textbf{A}\right\| _2, \left\| \textbf{A}\right\| _F, \left\| \textbf{A}\right\| _{1,1}$ to denote its operator norm, Frobenius norm, and $L_{1,1}$ norm, respectively. We denote $\mathbb {E}_{[\mathcal {M}_t]}[\cdot ] = \mathbb {E}_{\mathcal {M}_0,\dots ,\mathcal {M}_{t}}[\cdot ]$ to denote the total expectation with respect to $\mathcal {M}_0,\dots ,\mathcal {M}_t$. For a full description of the symbols used in the proof, please refer to Table 8.

In the proof, we will also utilize the following probability tools

Property 1

(Markov’s Inequality) For a non-negative random variable X, we have

$$\begin{aligned} \mathcal {P}\left( X\ge a\right) \le \frac{1}{a}\mathbb {E}[X] \end{aligned}$$

Property 2

(Jensen’s Inequality for Expectation) For a non-negative random variable X, we have

$$\begin{aligned} \mathbb {E}[X^{\frac{1}{2}}]\le \mathbb {E}[X]^\frac{1}{2} \end{aligned}$$

Table 8 Table of Notations

1.3 Properties of the transformed input

The GCN (Kipf and Welling 2016) uses a first-degree Chebyshev polynomial to approximate a spectral convolution on the graph, which results in an aggregation matrix of the form

$$\begin{aligned} \begin{aligned} \bar{\textbf{A}} = \textbf{I} + \textbf{D}^{-\frac{1}{2}}\textbf{A}\textbf{D}^{-\frac{1}{2}} \end{aligned} \end{aligned}$$

(5)

where $\textbf{A}$ is the adjacency matrix and $\textbf{D}$ is the degree matrix with $\textbf{D}_{ii} = \sum _{j=1}^n\textbf{A}_{ij}$. This is the same form of the aggregation matrix in Eq. (7) of Kipf and Welling (2016). In practice, the re-normalization trick is applied to control the magnitude of the largest eigenvalue of $\bar{\textbf{A}}$ (see Eq. (8) of Kipf and Welling (2016)). Here, however, we keep the original formulation of (5) to facilitate our analysis, and our assumption on the depth of the GCN does not lead to numerical instability even if $\lambda _{\max }(\bar{\textbf{A}}) > 1$. Moreover, the definition of $\bar{\textbf{A}}$ connects with the degree-normalized Laplacian $\mathcal {L}$ in the sense that $\bar{\textbf{A}} = 2\textbf{I}- \mathcal {L}$. It is a well-known result that $2 = \lambda _{\max }(\bar{\textbf{A})} \ge \lambda _{\min }(\bar{\textbf{A}}) \ge 0$. In particular, the lower bound on the minimum eigenvalue is obtained by considering

$$\begin{aligned} \textbf{v}^\top \bar{\textbf{A}}\textbf{v} = \sum _{i=1}^nv_i^2 + \sum _{(i,j)\in E}\frac{v_iv_j}{\sqrt{\textbf{D}_{ii}\textbf{D}_{jj}}} = \sum _{(i,j)\in E}\left( \frac{v_i}{\sqrt{\textbf{D}_{ii}}} + \frac{v_j}{\sqrt{\textbf{D}_{jj}}}\right) ^2 \end{aligned}$$

In our analysis, we require the aggregation matrix $\bar{\textbf{A}}$ to be positive definite. Thus, the following assumption can be made about $\lambda _{\min }(\bar{\textbf{A}})$.

Assumption 2

$\lambda _{\min }(\bar{\textbf{A}}) \ne 0$.

Going further, we must make a few more assumptions about the aggregation matrix and the graph itself to satisfy certain properties relevant to the analysis.

Assumption 3

There exists $\epsilon \in (0,1)$ and $p\in \mathbb {Z}_+$ such that for all $i\in [n]$

$$\begin{aligned} (1-\epsilon )^2p\le \textbf{D}_{ii}\le (1+\epsilon )^2p \end{aligned}$$

Assumption 3 implies the following property

Property 3

For all $i\in [n]$, we have $\left\| \hat{\textbf{x}}_i\right\| _2\le 1$.

Proof of Property 3

Under assumption 3, we have that for all $i,i'\in [n]$

$$\begin{aligned} \left( \frac{1-\epsilon }{1+\epsilon }\right) ^2\le \frac{\textbf{D}_{ii}}{\textbf{D}_{i'i'}}\le \left( \frac{1 + \epsilon }{1 - \epsilon }\right) ^2 \end{aligned}$$

Therefore, we can write

$$\begin{aligned} \left\| \hat{\textbf{x}}_i\right\| _2&= \left\| \sum _{i'=1}^n\bar{\textbf{A}}_{ii'}\textbf{x}_i\right\| _2\\&= \left\| \sum _{i'=1}^n\left( \textbf{I} + \textbf{D}^{-\frac{1}{2}}\textbf{A}\textbf{D}^{-\frac{1}{2}}\right) _{ii'}\textbf{x}_i\right\| _2\\&= \left\| \textbf{x}_i + \textbf{D}_{ii}^{-\frac{1}{2}}\sum _{i'\ne i}\textbf{A}_{ii'}\textbf{D}^{-\frac{1}{2}}_{i'i'}\textbf{x}_i\right\| _2\\&\le \frac{1-\epsilon }{2} + \textbf{D}_{ii}^{-\frac{1}{2}}\sum _{i'\ne i}\textbf{A}_{ii'}\textbf{D}^{-\frac{1}{2}}_{i'i'}\left( \frac{1-\epsilon }{2}\right) \\&\le \frac{1-\epsilon }{2} + \textbf{D}_{ii}^{-\frac{1}{2}}\sum _{i'\ne i}\textbf{A}_{ii'}\textbf{D}^{-\frac{1}{2}}_{ii}\left( \frac{1+\epsilon }{1-\epsilon }\right) \left( \frac{1-\epsilon }{2}\right) \\&= 1 \end{aligned}$$

where the first inequality follows from Assumption 4 and the triangle inequality.

Additionally, we make the following assumption regarding the graph itself

Assumption 4

For all $i\in [n]$, we have $\left\| \textbf{x}_i\right\| _2\le \frac{1-\epsilon }{2}$, and $|y_i|\le C$ for some constant C. Moreover, for all $j\in [n]$ and $j\ne i$, we have $[\bar{\textbf{A}}\textbf{X}]_i\not \parallel [\bar{\textbf{A}}\textbf{X}]_j$.

1.4 Full statement theorem 1

We now state the full version of Theorem 1 from Sect. 4, which characterizes the convergence properties of one-hidden-layer GCN models trained with GIST.

Theorem 2

Suppose assumptions 2–4 hold. Moreover, suppose in each global iteration the masks are generated from a categorical distribution with uniform mean . Fix the number of global iterations to T and local iterations to $\zeta$. Consider a two-layer GCN with parameters $\varvec{\Theta }$. If each entry of $\varvec{\Theta }$ is initialized I.I.D. from $\mathcal {N}(0,\kappa ^2\textbf{I})$, and the number of hidden neurons satisfies $d_1\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2}\max \left\{ \frac{n^3}{\delta ^2\kappa ^2}, \frac{n^2d}{\delta ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}, T^2\lambda ^{*2}d\right\} \right)$, then procedure (4) with constant step size $\eta = \mathcal {O}\left( \tfrac{\lambda _0}{n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}\right)$ converges according to

$$\begin{aligned} \mathbb {E}_{[\mathcal {M}_{t-1}]}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right]&\le \left( \gamma + (1-\gamma )\left( 1 - \frac{\eta \lambda _0}{2}\right) ^\zeta \right) ^t\left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2 +\\&\quad \quad \quad \mathcal {O}\left( \frac{\gamma ^2d\kappa ^2\lambda ^{*2}}{m^2(1-\gamma )\lambda _0^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

with probability at least $1 - \delta$, where $\gamma = \left( 1 - m^{-1}\right) ^{\frac{1}{3}}$.

In the following subsections, we will provide a proof for Theorem 2 In Sect. C.5, we first show that the local training of each sub-GCN enjoys linear convergence (Theorem 3). In Sect. C.6, we use this result to show Theorem 2. In Sect. C.7, we provide proof for the auxiliary lemmas.

1.5 GIST and local training progress

In this section, our goal is to show the following theorem

Theorem 3

Suppose the number of hidden nodes satisfies . If for all $r\in [d_1]$ it holds that

$$\begin{aligned} \begin{aligned} \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 + \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\textbf{W}_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^\frac{1}{2} + (T - t)B\le R \end{aligned} \end{aligned}$$

(6)

with

$$\begin{aligned} B = 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} + \frac{20T\zeta \gamma \kappa \lambda ^*}{m\delta \alpha }\sqrt{\frac{\eta ^3nd}{\lambda _0d_1}}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}};\quad R\le \frac{\lambda _0}{192n} \end{aligned}$$

then we have

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k+1)\right\| _2^2\le \left( 1 - \frac{\eta \lambda _0}{2}\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

and for all $r\in [d_1], j\in [m]$ it holds that

$$\begin{aligned} \left\| \varvec{\theta }_{t,\zeta ,r}^{(j)} - \varvec{\theta }_{0,r}^{(j)}\right\| _2&\le \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\textbf{W}_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} +\\&\quad \quad \quad 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

with probability at least $1- \frac{\delta }{T}$

For a one-hidden-layer MLP, the analysis often depends on the (scaled) Gram Matrix of the infinite-dimensional NTK

$$\begin{aligned} \textbf{H}^\infty _{ij} = \frac{1}{d_1m}\left\langle \hat{\textbf{x}}_i, \hat{\textbf{x}}_j\right\rangle \mathbb {E}_{\varvec{\theta }\sim \mathcal {N}(0,\textbf{I})}\left[ \mathbb {I}\{\left\langle \hat{\textbf{x}}_i, \varvec{\theta }\right\rangle \ge 0, \left\langle \hat{\textbf{x}}_j, \varvec{\theta }\right\rangle \ge 0\}\right] \end{aligned}$$

(7)

We can extend this definition of the Gram Matrix to an infinite-width, one-hidden-layer GCN as follows

$$\begin{aligned} \textbf{G}^{\infty } = \bar{\textbf{A}}\textbf{H}^\infty \bar{\textbf{A}} \end{aligned}$$

With Assumption 4, prior work (Du et al. 2019) shows that $\lambda _{\min }(\textbf{H}) > 0$. Since $\bar{\textbf{A}}$ is also positive definite, we must have that $\textbf{G}^\infty$ is at least positive semidefinite. Moreover, for any $\textbf{v}\in \mathbb {R}^n$ such that $\textbf{v}\ne 0$, we must have that $\bar{\textbf{A}}\textbf{v}\ne 0$, and thus $\textbf{H}^\infty \bar{\textbf{A}}\textbf{v}\ne 0$, which implies that $\bar{\textbf{A}}\textbf{H}^\infty \bar{\textbf{A}}\textbf{v}\ne 0$. Thus, for any $\textbf{v}\ne 0$, $\textbf{G}^\infty \textbf{v}\ne 0$. Therefore, we must have that $\lambda _{\min }\left( \textbf{G}^\infty \right) > 0$. In our analysis, we define the Graph Independent Subnetwork Tangent Kernel (GIST-K)

$$\begin{aligned} \textbf{G}^{(j)}(t, t', k) = \bar{\textbf{A}}\textbf{H}(t, t', k)\bar{\textbf{A}} \end{aligned}$$

where $\textbf{H}(t, t', k)$ is defined as

$$\begin{aligned} \textbf{H}(t, t', k) = \frac{1}{d_1}\left\langle \hat{\textbf{x}}_i, \hat{\textbf{x}}_j\right\rangle \sum _{r=1}^{d_1}\mathcal {M}_{t,r}^{(j)}\mathbb {I}\left\{ \left\langle \hat{\textbf{x}}_i, \varvec{\theta }_{t',k,r}^{(j)}\right\rangle \ge 0, \left\langle \hat{\textbf{x}}_j, \varvec{\theta }_{t',k,r}^{(j)}\right\rangle \ge 0\right\} \end{aligned}$$

for masks $\mathcal {M}_t$ and weights $\varvec{\Theta }_{t',k}^{(j)}$. Following previous work (Liao and Kyrillidis 2021) on subnetwork theory, we obtained Lemma 3, which shows that, if , and for all t, k it holds that $\left\| \varvec{\theta }_{t,k,r} - \varvec{\theta }_{0,r}\right\| _2\le R:= \frac{\kappa \lambda _0}{192n}$, then with probability at least $1-\delta$, for all $t,t'\in [T]$ we have:

$$\begin{aligned} \lambda _{\min }(\textbf{G}^{(j)}(t, t', k))\ge \tfrac{\lambda _0}{2} \end{aligned}$$

The lemma above shows that every GIST-K is positive definite. To proceed, the proof for the linear convergence relies on the following quadratic expansion of the loss

$$\begin{aligned} \begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k+1)\right\| _2^2&= \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 + \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\\&\quad \quad \quad - 2\left\langle \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k), \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}(t,k)\right\rangle \end{aligned} \end{aligned}$$

(8)

Thus, it is natural to focus on the change of the output of the sub-GCN in each local iterations $\hat{y}^{(j)}_i(t,k+1) - \hat{y}^{(j)}_i(t,k)$. The following lemma shows that this term is bounded

Analyzing the inner-product term on the right-hand side of Eq. (8) involves a detailed study of the change of activation pattern $\mathbb {I}\left\{ \left\langle \varvec{\theta }, \hat{\textbf{x}}_i\right\rangle \ge 0\right\}$ Then, following Song and Yang (2020), we first fix $R = \frac{\kappa \lambda _0}{192n}$, and denote

$$\begin{aligned} A_{ir}&= \exists \varvec{\theta }:\left\| \varvec{\theta } - \varvec{\theta }_{0,r}\right\| _2\le R,\mathbb {I}\{\left\langle \varvec{\theta }, \hat{\textbf{x}}_i\right\rangle \ge 0\}\ne \mathbb {I}\{\left\langle \varvec{\theta }_{0,r}, \hat{\textbf{x}}_i\right\rangle \ge 0\}\\ S_i&= \{r\in [m]: \lnot A_{ir}\};\quad S_i^\perp = [m]\setminus S_i \end{aligned}$$

Based on the definition of $\hat{\textbf{y}}(t,\cdot )$, we can write

$$\begin{aligned}&\hat{y}^{(j)}_i(t,k+1) - \hat{y}^{(j)}_i(t,k) \\&\quad \quad = \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\left( \sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) \right) \end{aligned}$$

Thus, we can decompose $\hat{y}^{(j)}_i(t,k+1) - \hat{y}^{(j)}_i(t,k) = I_{i,1}^{(j)}(t,k) + I_{i,2}^{(j)}(t,k)$ with

$$\begin{aligned} I_{i,1}^{(j)}(t,k)&= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\cdot \\&\quad \quad \quad \left( \sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) \right) \\ I_{i,2}^{(j)}(t,k)&= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}^{\perp }}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\cdot \\&\quad \quad \quad \left( \sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) \right) \end{aligned}$$

Let $\textbf{I}_1^{(j)}(t,k) = \left[ I_{1,1}^{(j)}(t,k),\dots ,I_{n,1}^{(j)}(t,k)\right]$ and similarly $\textbf{I}_2^{(j)}(t,k) = \left[ I_{1,2}^{(j)}(t,k),\dots ,I_{n,2}^{(j)}(t,k)\right]$ be the vectorized notation. For $\textbf{I}_1^{(j)}(t,k)$, we need a more detailed analysis. To start, we define

$$\begin{aligned} \textbf{H}^\perp (t,t',k) = \frac{1}{d}\left\langle \hat{\textbf{x}}_i, \hat{\textbf{x}}_{i'}\right\rangle \sum _{r\in S_i^\perp }\mathcal {M}_{t,r}^{(j)}\mathbb {I}\{\left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_i\right\rangle \ge 0; \left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\} \end{aligned}$$

and let $\textbf{G}^\perp (t,t',k) = \bar{\textbf{A}}\textbf{H}^\perp (t,t',k)\bar{\textbf{A}}$. Notice that

$$\begin{aligned} I_{i,1}^{(j)}(t,k)&= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\left\langle \varvec{\theta }_{t,k+1,r}^{(j)} - \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \cdot \\&\quad \quad \quad \mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \\&= -\frac{\eta }{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\left\langle \frac{\partial L\left( \varvec{\Theta }^{(j)}_{t,k}\right) }{\partial \varvec{\theta }_r}, \hat{\textbf{x}}_{i'}\right\rangle \cdot \\&\quad \quad \quad \mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \\&= \frac{\eta }{d_1}\sum _{i'=1}^n\sum _{i_1=1}^n\sum _{i_1'=1}^n\sum _{r\in S_i}\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{i_1i_1'}\mathcal {M}^{(j)}_{t,r}\left( y_{i_1} - \hat{y}^{(j)}_{i_1}(t,k)\right) \cdot \\&\quad \quad \quad \left\langle \hat{\textbf{x}}_{i_1'}, \hat{\textbf{x}}_{i'}\right\rangle \mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0;\left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i_1'}\right\rangle \ge 0\right\} \\&= \eta \sum _{i'=1}^n\sum _{i_1=1}^n\sum _{i_1'=1}^n\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{i_1i_1'}\left( y_{i_1} - \hat{y}^{(j)}_{i_1}(t,k)\right) \cdot \\&\quad \quad \quad \left( \textbf{H}^{(j)}(t,t,k)_{i'i_1'} - \textbf{H}^{(j)\perp }(t,t,k)_{i'i_1'}\right) \end{aligned}$$

Thus for $\textbf{I}_{i,1}^{(j)}(t,k) = [I_{1,1}^{(j)}(t,k),\dots ,I_{n,1}^{(j)}(t,k)]$ we have

$$\begin{aligned} \begin{aligned} \textbf{I}_{i,1}^{(j)}(t,k)&= \eta \bar{\textbf{A}}\left( \textbf{H}^{(j)}(t,t,k) - \textbf{H}^{(j)\perp }(t,t,k)\right) \bar{\textbf{A}}\left( \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right) \\&= \eta \left( \textbf{G}^{(j)}(t,t,k) - \textbf{G}^{(j)\perp }(t,t,k)\right) \left( \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right) \end{aligned} \end{aligned}$$

(9)

which implies that

$$\begin{aligned}&\left\langle \hat{\textbf{y}}^{(j)}(t,k) - \textbf{y}, \textbf{I}_1^{(j)}(t,k)\right\rangle \\&\quad \quad \quad = \eta \left\langle \hat{\textbf{y}}^{(j)}(t,k) - \textbf{y}, \left( \textbf{G}^{(j)}(t,t,k) - \textbf{G}^{(j)\perp }(t,t,k)\right) \left( \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right) \right\rangle \\&\quad \quad \quad \le -\eta \left( \lambda _{\min }\left( \textbf{G}^{(j)}(t,t,k)\right) - \left\| \textbf{G}^{(j)\perp }(t,t,k)\right\| _2\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

Thus, Eq. (8) can be written as

$$\begin{aligned} \begin{aligned}&\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k + 1)\right\| _2^2 \\&\quad \quad \quad \le \left( 1 - 2\eta \left( \lambda _{\min }\left( \textbf{G}^{(j)}(t,t,k)\right) - \left\| \textbf{G}^{(j)\perp }(t,t,k)\right\| _2\right) \right) \cdot \\&\quad \quad \quad \quad \quad \quad \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 + 2\left|\left\langle \hat{\textbf{y}}^{(j)}(t,k) - \textbf{y}, \textbf{I}_2^{(j)}(t,k)\right\rangle \right|+ \\&\quad \quad \quad \quad \quad \quad \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned} \end{aligned}$$

(10)

Now, we are ready to prove Theorem 3.

Proof of Theorem 3

We use induction on the following three conditions to prove the theorem.

$$\begin{aligned}{} & {} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k+1)\right\| _2^2 \le \left( 1 - \frac{\eta \lambda _0}{2}\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \left\| \varvec{\theta }_{t,k,r}^{(j)} - \varvec{\theta }_{0,r}^{(j)}\right\| _{2} \le \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\textbf{W}_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} +\nonumber \\{} & {} \quad \quad \quad \eta \zeta n\sqrt{\frac{8(m-1)T}{md_1\delta }} \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \left\| \varvec{\theta }_{t,k,r}^{(j)} - \varvec{\theta }_{0,r}^{(j)}\right\| _2 \le R \end{aligned}$$

(13)

Part 1. To start, we show that (13) $\rightarrow$ (11) for all k. As illustrated in Eq. (10), we have

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k + 1)\right\| _2^2&\le \left( 1 - 2\eta \left( \lambda _{\min }\left( \textbf{G}^{(j)}(t,t,k)\right) - \left\| \textbf{G}^{(j)\perp }(t,t,k)\right\| _2\right) \right) \cdot \\&\quad \quad \quad \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 + 2\left|\left\langle \hat{\textbf{y}}^{(j)}(t,k) - \textbf{y}, \textbf{I}_2^{(j)}(t,k)\right\rangle \right|+\\&\quad \quad \quad \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

Using Lemmas 3 and 6, we have that

$$\begin{aligned} \lambda _{\min }\left( \textbf{G}^{(j)}(t,t,k)\right) \ge \frac{\lambda _0}{2};\quad \left\| \textbf{G}^{(j)\perp }\right\| _2 \le \frac{\lambda _0}{12} \end{aligned}$$

which implies that

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k + 1)\right\| _2^2&\le \left( 1 - \frac{5}{6}\eta \lambda _0\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 +\\&\quad \quad \quad 2\left|\left\langle \hat{\textbf{y}}^{(j)}(t,k) - \textbf{y}, \textbf{I}_2^{(j)}(t,k)\right\rangle \right|+\\&\quad \quad \quad \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

Choosing $\eta =\frac{\lambda _0}{24n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}$, we further use Lemma 5 with $\textbf{v}= \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)$, and Lemma 7 to simplify the second and third term, respective. This gives that

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k+1)\right\| _2^2&\le \left( 1 - \frac{5}{6}\eta \lambda _0\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 + \frac{\eta \lambda _0}{6}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 + \\&\quad \quad \quad \frac{\eta \lambda _0}{6}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\\&= \left( 1 - \frac{\eta \lambda _0}{2}\right) \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

This shows that (13) $\rightarrow$ (11).

Part 2. Next, we show that if Eq. (11) hold for all $k=0,1,\dots ,k'-1$, then Eq. (12) holds for $k=k'$. Thus, for all $k = 0,1,\dots ,k'-1$, we have

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}(t,k)\right\| _2^2 \le \left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 \end{aligned}$$

(14)

Lemma 4 gives that

$$\begin{aligned} \left\| \frac{\partial L(\varvec{\Theta }_{t,k}^{(j)})}{\partial \varvec{\theta }_r}\right\| _2 \le \sqrt{\frac{n}{d_1}}\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2 \end{aligned}$$

Using Markov’s inequality, we have that with probability at least $1 - \frac{\delta }{2T}$

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 \le \frac{2T}{\delta }\mathbb {E}_{[\mathcal {M}_{t-1}]}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] \end{aligned}$$

Thus, with probability at least $1 - \frac{\delta }{2T}$, we have

$$\begin{aligned} \left\| \varvec{\theta }_{t,k,r}^{(j)} - \varvec{\theta }_{t,0,r}^{(j)}\right\| _2&\le \sum _{k'=0}^{k-1}\left\| \varvec{\theta }_{t,k'+1,r} - \varvec{\theta }_{t,k',r}\right\| _2\\&\le \eta \sum _{k'=0}^{k-1}\left\| \frac{\partial L\left( \varvec{\Theta }_{t,k'}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2\\&\le \eta \sqrt{\frac{n}{d_1}}\sum _{k'=0}^{k-1}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k')\right\| _2\\&\le \eta \sqrt{\frac{n}{d_1}}\sum _{k'=0}^{k - 1}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\\&\le \eta \zeta \sqrt{\frac{n}{d_1}}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\\&\le \eta \zeta \sqrt{\frac{n}{d_1}}\left( \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2 +\left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\right) \\&\le \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}]}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} +\\&\quad \quad \quad 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

where in the fourth inequality we use Eq. (14), and in the sixth inequality we use the triangle inequality. This shows that if Eq. (11) hold for all $k=0,1,\dots ,k'-1$, then Eq. (12) holds for $k=k'$.

Part 3. Now, we use induction to show that (13) holds for all k. At $k = 0$, we have that $\varvec{\theta }_{t,k,r} = \varvec{\theta }_{t,r}$. Thus, Eq. (6) implies (13) naturally. Assume (13) holds for all $k=0,1,\dots , k'-1$. Then we that Eq. (11) holds for all $k=0,1,\dots ,k'$. As we have shown in the previous part, Eq. (12) holds for $k = k'$. Since $\alpha< 1 < 2$, we have that

$$\begin{aligned} \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}} \le \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}} \end{aligned}$$

Also we have

$$\begin{aligned} 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \le B \end{aligned}$$

Therefore, by Eq. (6), and using $\varvec{\theta }_{t,k,r} = \varvec{\theta }_{t,r}$, we have that

$$\begin{aligned} \left\| \varvec{\theta }_{t,k',r}^{(j)} - \varvec{\theta }_{0,r}^{(j)}\right\| _2\le \left\| \varvec{\theta }_{t,r}^{(j)} - \varvec{\theta }_{0,r}^{(j)}\right\| _2 + \left\| \varvec{\theta }_{t,k',r}^{(j)} - \varvec{\theta }_{t,0,r}^{(j)}\right\| _2\le R \end{aligned}$$

Now that Eq. (13) holds for all k, we have Eq. (11) holds and thus Eq. (12) holds for all k.

1.6 Convergence of GIST

We now prove the convergence result for GIST outlined in “Appendix C.4”. In showing the convergence of GIST, we care about the regression loss $\left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2$ with

$$\begin{aligned} \hat{\textbf{y}}(t) = f(\varvec{\Theta }_t,\textbf{x}) = \frac{1}{m\sqrt{d_1}}\bar{\textbf{A}}\sigma \left( \bar{\textbf{A}}\textbf{x}\varvec{\Theta }_t\right) \textbf{A}\end{aligned}$$

(15)

As in previous work (Liao and Kyrillidis 2021), we add the scaling factor $\frac{1}{m}$ to make sure that $\mathbb {E}_{\mathcal {M}_t}[\hat{\textbf{y}}^{(j)}(t,0)] = \hat{\textbf{y}}(t)$. Moreover, by properties of the masks $\mathcal {M}_t^{(j)}$, we have

$$\begin{aligned} f(\varvec{\Theta },\textbf{x}) = \sum _{j=1}^mf_{\mathcal {M}}^{(j)}(\varvec{\Theta },\textbf{x}) \end{aligned}$$

Thus, we can invoke lemmas 13 and 14 from Liao and Kyrillidis (2021). We state the two key lemmas here in accordance with our own notation.

Lemma 1

The t-th global step produces squared error satisfying

$$\begin{aligned}&\left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\\&\quad \quad \quad = \frac{1}{m}\sum _{j=1}^m\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2 - \frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\left\| \hat{\textbf{y}}^{(j)}(t,\zeta ) - \hat{\textbf{y}}^{(j')}(t,\zeta )\right\| _2^2 \end{aligned}$$

Lemma 2

In the t-th global iteration, the sampled subnetwork’s deviation from the whole network is given by

$$\begin{aligned} \sum _{j=1}^m\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2 = \frac{1}{m}\sum _{j=1}^m\sum _{j'=1}^{j-1}\left\| \hat{\textbf{y}}^{(j)}(t,\zeta ) - \hat{\textbf{y}}^{(j')}(t,\zeta )\right\| _2^2 \end{aligned}$$

Moreover, Lemma 22 from Liao and Kyrillidis (2021) show that with probability at least $1 - 2n\exp (-\frac{m}{32})$, for all $R\le \frac{\kappa }{2}$, it holds that

$$\begin{aligned} \left\| \varvec{\Theta }_0\right\| _F\le \kappa \sqrt{2d_1d} - \sqrt{d_1}R \end{aligned}$$

For convenience, we assume that such an initialization property holds. Given that for all $r\in [d_1]$, we have $\left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2\le R$, we must have that $\left\| \varvec{\Theta }_t - \varvec{\Theta }_0\right\| _F\le \kappa \sqrt{d_1}R$. Thus, $\left\| \varvec{\Theta }_t\right\| _F\le \kappa \sqrt{2d_1d}$ for all t. We point out that, within the proof, we use $R = \frac{\kappa \lambda _0}{192n}$, which satisfies the condition above. Using Lemma 1 to expand the loss at the $(t+1)$th iteration and invoking Theorem 3 gives

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2&= \frac{1}{m}\sum _{j=1}^m\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2 -\\&\quad \quad \quad \frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\left\| \hat{\textbf{y}}^{(j)}(t,\zeta ) - \hat{\textbf{y}}^{(j')}(t,\zeta )\right\| _2^2\\&\le \frac{1}{m}\sum _{j=1}^m\left( 1 - \frac{\eta \lambda _0}{2}\right) ^\zeta \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 - \\ {}&\quad \quad \quad \frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\left\| \hat{\textbf{y}}^{(j)}(t,\zeta ) - \hat{\textbf{y}}^{(j')}(t,\zeta )\right\| _2^2\\&= \frac{1}{m}\sum _{j=1}^m\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 -\\&\quad \quad \quad \frac{\eta \lambda _0}{2m}\sum _{k=0}^{\zeta -1}\sum _{j=1}^m\left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 \\&\quad \quad -\frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\left\| \hat{\textbf{y}}^{(j)}(t,\zeta ) - \hat{\textbf{y}}^{(j')}(t,\zeta )\right\| _2^2\\ \end{aligned}$$

Using the fact that $\mathbb {E}_{\mathcal {M}_t}[\hat{\textbf{y}}^{(j)}(t,0)] = \hat{\textbf{y}}(t)$ we have

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] = \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 + \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \end{aligned}$$

Then, using Lemma 2 to rewrite the last term in the equation above and plugging in gives

$$\begin{aligned}&\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] \\ {}&\quad \quad \le \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 - \frac{\eta \lambda _0}{2m}\sum _{k=0}^{\zeta -1}\sum _{j=1}^m\left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \\&\quad \quad \quad + \frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2-\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\right] \end{aligned}$$

We denote the last term within the equation above as $\iota _t$

$$\begin{aligned} \iota _t = \frac{1}{m^2}\sum _{j=1}^m\sum _{j'=1}^{j-1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2-\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\right] \end{aligned}$$

Lemma 8 shows the bound on $\iota _t$

$$\begin{aligned} \iota _t&\le \frac{\eta \gamma \lambda _0}{2m}\sum _{j=1}^m\sum _{k=0}^{\zeta - 1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2^2\right] + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

for $\gamma = \left( 1 - m^{-1}\right) ^{\frac{1}{3}}$ Therefore, we can derive the following

$$\begin{aligned}&\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] \\&\quad \quad \le \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 - \frac{\eta \lambda _0}{2m}\sum _{k=0}^{\zeta -1}\sum _{j=1}^m\left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \\&\quad \quad \quad \quad \quad + \frac{\eta \gamma \lambda _0}{2m}\sum _{j=1}^n\sum _{k=0}^{\zeta -1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\right] + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\\&\quad \quad \le \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 - \\&\quad \quad \quad \quad \quad \frac{(1-\gamma )\eta \lambda _0}{2m}\sum _{k=0}^{\zeta -1}\sum _{j=1}^m\left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \\&\quad \quad \quad \quad \quad + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\\&\quad \quad \le \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 - \frac{(1-\gamma )\eta \lambda _0}{2}\sum _{k=0}^{\zeta -1}\left( 1 - \frac{\eta \lambda _0}{2}\right) ^k\left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\\&\quad \quad \quad \quad \quad + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\\&\quad \quad = \left( \gamma + (1-\gamma )\left( 1 - \frac{\eta \lambda _0}{2}\right) ^\zeta \right) \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

Starting from here, we use $\alpha$ to denote the global convergence rate

$$\begin{aligned} \alpha = (1-\gamma )\left( 1 - \left( 1 - \frac{\eta \lambda _0}{2}\right) ^\zeta \right) \end{aligned}$$

Since $\zeta \ge 1$, we have that $\alpha \ge \frac{\eta \lambda _0}{2}(1-\gamma )$. Then, the convergence rate above yields the following

$$\begin{aligned} \mathbb {E}_{[\mathcal {M}_{t-1}]}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right]&\le (1-\alpha )^t\left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2 + \end{aligned}$$

(16)

$$\begin{aligned}&\quad \quad \quad \mathcal {O}\left( \frac{\gamma ^2d\lambda ^{*2}}{m^2(1-\gamma )\lambda _0^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

(17)

Lastly, we provide a bound on weight perturbation using overparameterization. In particular, we can show that Eq. (6) holds for iteration $t+1$

$$\begin{aligned} \left\| \varvec{\theta }_{t+1,r} - \varvec{\theta }_{0,r}\right\| _2&+ \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] ^\frac{1}{2} + \\&\quad \quad \quad (T-t - 1)B\le R \end{aligned}$$

under the assumption that it holds in iteration t

$$\begin{aligned} \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 + \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^\frac{1}{2} + (T - t)B\le R \end{aligned}$$

and given the global convergence result

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right]&\le \left( 1 - \alpha \right) \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2 + \frac{18\eta \gamma ^2d\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

Thus, it suffices to show that

$$\begin{aligned}&\left\| \varvec{\theta }_{t+1,r} - \varvec{\theta }_{0,r}\right\| _2 - \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 \\&\quad \quad \le \left( \mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^\frac{1}{2} - \mathbb {E}_{[\mathcal {M}_{t}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] ^\frac{1}{2}\right) \\&\quad \quad \quad \cdot \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}} + B \end{aligned}$$

Using the sub-additivity of the square root function, we derive the following

$$\begin{aligned}&\mathbb {E}_{[\mathcal {M}_{t}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] ^\frac{1}{2} \\&\quad \quad \le \left( \left( 1-\alpha \right) \mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] + \frac{18\eta \gamma ^2d\kappa ^2\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) ^{\frac{1}{2}} \\&\quad \quad \le \left( 1 - \frac{\alpha }{2}\right) \mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} + \frac{5\gamma \kappa \lambda ^*}{m}\sqrt{\frac{\eta d}{\lambda _0}}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}} \end{aligned}$$

It then suffices to show that

$$\begin{aligned} \left\| \varvec{\theta }_{t+1,r} - \varvec{\theta }_{0,r}\right\| _2 - \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2&\le \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}} \mathbb {E}_{[\mathcal {M}_{t}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] ^\frac{1}{2} \\&\quad \quad + B - \frac{20T\zeta \gamma \kappa \lambda ^*}{m\delta \alpha }\sqrt{\frac{\eta ^3nd}{\lambda _0d_1}}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}}\\&= \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}} \mathbb {E}_{[\mathcal {M}_{t}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t+1)\right\| _2^2\right] ^\frac{1}{2} \\&\quad \quad + 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

By Lemma 4, we have

$$\begin{aligned} \left\| \frac{\partial L(\varvec{\Theta }_{t,k}^{(j)})}{\partial \varvec{\theta }_r}\right\| _2&\le \sqrt{\frac{n}{d_1}}\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\\&\le 2\sqrt{\frac{n}{d_1}}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\\&\le 2\sqrt{\frac{n}{d_1}}\left( \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2 + \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| \right) \\ \end{aligned}$$

Lemma 10 gives that

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \le \frac{2d\kappa ^2(m-1)}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

Apply Markov’s inequality gives that with probability at least $1- \frac{\delta }{2T}$, it holds that

$$\begin{aligned} \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2 \le \frac{2T}{\delta }\mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}}\\ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2 \le 2\kappa \sqrt{\frac{Td(m-1)}{m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

Thus, with probability at least $1- \frac{\delta }{2T}$, it holds for all k and j that

$$\begin{aligned} \left\| \frac{\partial L(\varvec{\Theta }_{t,k}^{(j)})}{\partial \varvec{\theta }_r}\right\| _2&\le \frac{2T}{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} + \\&\quad \quad \quad 4\kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

Fix $r\in [d_1]$ and let $\hat{j}$ be the index of the sub-GCN in which r is active. Then with probability at least $1 - \frac{\delta }{2T}$, we have that

$$\begin{aligned} \left\| \varvec{\theta }_{t,\zeta ,r}^{(\hat{j})}-\varvec{\theta }_{t,r}\right\| _2&= \left\| \sum _{k=0}^{\zeta -1}\left( \varvec{\theta }_{t,k+1,r} -\varvec{\theta }_{t,k,r}\right) \right\| _2\\&\le \sum _{k=0}^{\zeta -1}\left\| \varvec{\theta }_{t,k+1,r} -\varvec{\theta }_{t,k,r}\right\| _2\\&= \eta \sum _{k=0}^{\zeta -1}\left\| \frac{\partial L(\varvec{\Theta }_{t,k}^{(j)})}{\partial \varvec{\theta }_r}\right\| _2\\&\le \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} +\\&\quad \quad \quad 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

Then, it is easy to see that we indeed have

$$\begin{aligned} \left\| \varvec{\theta }_{t+1,r} - \varvec{\theta }_{0,r}\right\| _2&\le \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 + \left\| \varvec{\theta }_{t+1,r}-\varvec{\theta }_{0,r}\right\| _2\\&=\left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 + \left\| \varvec{\theta }_{t,\zeta ,r}^{(\hat{j})}-\varvec{\theta }_{t,r}\right\| _2\\&\le \left\| \varvec{\theta }_{t,r} - \varvec{\theta }_{0,r}\right\| _2 + \frac{2T\eta \zeta }{\delta }\sqrt{\frac{n}{d_1}}\mathbb {E}_{[\mathcal {M}_{t-1}],\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(t)\right\| _2^2\right] ^{\frac{1}{2}} \\&\quad \quad + 4\eta \zeta \kappa \sqrt{\frac{Tdn(m-1)}{d_1m\delta }}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2} \end{aligned}$$

What remains is to prove Eq. (6) in Theorem 3 for $t = 0$. In that case, we need

$$\begin{aligned} \begin{aligned} R&\ge \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right] ^\frac{1}{2} + \\&\quad \quad \quad 4T\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\left( \eta \zeta \sqrt{\frac{Tdn(m-1)}{d_1m\delta }} + \frac{5T\zeta \gamma \lambda ^*}{m\delta \alpha }\sqrt{\frac{\eta ^3nd}{\lambda _0d_1}}\right) \end{aligned} \end{aligned}$$

(18)

Using Lemma 11 and using $\alpha \ge \frac{\eta \lambda _0}{2}(1-\gamma )$ to solve for $d_1$ gives

$$\begin{aligned} d_1\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2}\max \left\{ \frac{n^3}{\delta ^2\kappa ^2}, \frac{n^2d}{\delta ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}, T^2\lambda ^{*2}d\right\} \right) \end{aligned}$$

A detailed computation of the form of $d_1$ is provided in Sect. C.8.

1.7 Auxiliary lemmas

We now provide all proofs for the major properties and lemmas utilized in deriving the convergence results for GIST.

Lemma 3

Suppose the number of hidden nodes satisfies . If for all t, k it holds that $\left\| \varvec{\theta }_{t,k,r} - \varvec{\theta }_{0,r}\right\| _2\le R:= \frac{\kappa \lambda _0}{192n}$, then with probability at least $1-\delta$, for all $t,t'\in [T]$ we have:

$$\begin{aligned} \lambda _{\min }\left( \textbf{G}^{(j)}(t, t', k)\right) \ge \tfrac{\lambda _0}{2} \end{aligned}$$

Proof of Lemma 3

Fix some $R > 0$. Following Theorem 2 by Liao and Kyrillidis (2021), we have that with probability at least $1 - 2n^2e^{-2d_1t^2}$ it holds that

$$\begin{aligned} \left\| \textbf{H}^{(j)}(t,0,0) - \textbf{H}^\infty \right\| _2 \le nt \end{aligned}$$

and with probability at least $1 - n^2e^{-\frac{d_1R}{10m}}$ it holds that

$$\begin{aligned} \left\| \textbf{H}^{(j)}(t,t',k) - \textbf{H}^{(j)}(k,0,0)\right\| _2 \le \frac{3nR}{m} \end{aligned}$$

Choosing $t = \frac{\lambda _0}{16n}$ and $R = \frac{\kappa \lambda _0}{192n}$ gives

$$\begin{aligned} \left\| \textbf{G}^{(j)}(t,t',k) - \textbf{G}^\infty \right\| _2 \le \left\| \bar{\textbf{A}}\right\| _2^2\left\| \textbf{H}^{(j)}(t,t',k) - \textbf{H}^\infty \right\| _2 \le \left\| \bar{\textbf{A}}\right\| ^2\cdot \frac{\lambda _0}{8}\le \frac{\lambda _0}{2} \end{aligned}$$

with probability at least $1 - n^2\left( 2\exp \left( -\frac{d_1\lambda _0^2}{128n^2}\right) + \exp \left( -\frac{d_1\lambda _0}{480mn}\right) \right)$. Taking a union bound over all values of $t'$ and j, then plugging in the requirement gives the desired result. $\square$

Lemma 4

For all $j\in [m], r\in [d_1]$, and t, k, the norm of the sub-GCN gradient is bounded by

$$\begin{aligned} \left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2\le \sqrt{\frac{n}{d_1}}\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2 \end{aligned}$$

Proof

Recall that

$$\begin{aligned} \frac{\partial L(\varvec{\Theta }_{t,k}^{(j)})}{\partial \varvec{\theta }_r} = \frac{1}{\sqrt{d_1}}\sum _{i=1}^n\sum _{i'=1}^n\left( \hat{y}_i^{(j)}(t,k) - y_i\right) \bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\hat{\textbf{x}}_{i'}\mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \end{aligned}$$

Since $\left|\mathcal {M}_{t,r}^{(j)}\right|\le 1, \left|a_r\right|\le 1, \left\| \hat{\textbf{x}}_{i'}\right\| \le 1$, and $\mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \le 1$, we must have that

$$\begin{aligned} \left\| \mathcal {M}_{t,r}^{(j)}a_r\hat{\textbf{x}}_{i'}\mathbb {I}\left\{ \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \right\| _2 \le 1 \end{aligned}$$

Thus, applying triangle inequality for the double-summation gives

$$\begin{aligned} \left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2&\le \frac{1}{\sqrt{d_1}} \sum _{i=1}^n \sum _{i'=1}^n\bar{\textbf{A}}_{ii'} \left|\hat{\textbf{y}}_i^{(j)}(t,k) - \textbf{y}_i \right|\\&= \frac{1}{\sqrt{d_1}}\left\| \bar{\textbf{A}}{} \texttt {abs}\left( \hat{\textbf{y}}_i^{(j)}(t,k) - \textbf{y}_i\right) \right\| _1\\&\le \sqrt{\frac{n}{d_1}}\left\| \bar{\textbf{A}}{} \texttt {abs}\left( \hat{\textbf{y}}_i^{(j)}(t,k) - \textbf{y}_i\right) \right\| _2\\&\le \sqrt{\frac{n}{d_1}}\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2 \end{aligned}$$

where in the last inequality we use $\left\| \texttt {abs}(\textbf{v})\right\| _2 = \left\| \textbf{v}\right\| _2$. $\square$

Lemma 5

Suppose $\left\| \varvec{\theta }_{t,k,r} - \varvec{\theta }_{0,r}\right\| \le R:=\frac{\kappa \lambda _0}{192n}$. Then we have that with probability at least $1 - n\exp \left( d_1\kappa ^{-1}R\right)$, for all $\textbf{v}\in \mathbb {R}^n$

$$\begin{aligned} \left|\left\langle \textbf{v}, \textbf{I}_2^{(j)}(t,k)\right\rangle \right|\le \frac{\eta \lambda _0}{12}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\left\| \textbf{v}\right\| _2 \end{aligned}$$

Proof of Lemma 5

Using 1-Lipschitzness of $\sigma (\cdot )$, and that $\left\| \hat{\textbf{x}}_{i}\right\| _2=1$, we have that for all i, t, k, r

$$\begin{aligned} \left|\sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) \right|&\le \left|\left\langle \varvec{\theta }_{t,k+1,r}^{(j)} -\varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right|\\&\le \left\| \varvec{\theta }_{t,k+1,r}^{(j)} -\varvec{\theta }_{t,k,r}^{(j)}\right\| _2\\&= \eta \left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2 \end{aligned}$$

Lemma 16 from Liao and Kyrillidis (2021) shows that

$$\begin{aligned} \mathcal {P}\left( \left|S_i^\perp \right|\le 4d_1R\right) \ge \exp (-d_1R) \end{aligned}$$

Thus, with probability at least $1 - n\exp \left( d_1\kappa ^{-1}R\right)$, it holds that

$$\begin{aligned} \max _{i\in [n]}\left|S_i^\perp \right|\le 4d_1\kappa ^{-1}R \end{aligned}$$

Thus, for $I_{i,2}^{(j)}(t,k)$, we use Lemma 4 to have

$$\begin{aligned} \left|I_{i,2}^{(j)}(t,k)\right|&\le \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}^\perp }\bar{\textbf{A}}_{ii'}\left|\sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \right) \right|\\&\le \frac{\eta }{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r\in S_{i'}^\perp }\bar{\textbf{A}}_{ii'}\left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2\\&\le 4\eta \sqrt{n}\kappa ^{-1}R\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\sum _{i'=1}^n\bar{\textbf{A}}_{ii'} \end{aligned}$$

which yields the following

$$\begin{aligned} \left|\left\langle \textbf{v}, \textbf{I}_{i,2}^{(j)}(t,k)\right\rangle \right|&\le \sum _{i=1}^n\left|v_i\right|\cdot \left|I_{i,2}^{(j)}(t,k)\right|\\&\le 4\eta \sqrt{n}\kappa ^{-1}R\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\sum _{i,i'=1}^n\bar{\textbf{A}}_{ii'}\left|v_i\right|\\&= 4\eta \sqrt{n}\kappa ^{-1}R\left\| \bar{\textbf{A}}\right\| _2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\left\| \bar{\textbf{A}}{} \texttt {abs}(\textbf{v})\right\| _1\\&\le 4\eta n\kappa ^{-1}R\left\| \bar{\textbf{A}}\right\| _2^2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\left\| \textbf{v}\right\| _2\\&\le 16\eta n\kappa ^{-1}R\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2\left\| \textbf{v}\right\| _2 \end{aligned}$$

Plugging in $R = \frac{\kappa \lambda _0}{192n}$ gives the desired result. $\square$

Lemma 6

Under the same condition as Lemma 5, with probability at least $1 - n\exp \left( -d_1\kappa ^{-1}R\right)$, we have

$$\begin{aligned} \left\| \textbf{G}(t,t',k)^\perp \right\| _2 \le \frac{\lambda _0}{12} \end{aligned}$$

Proof of Lemma 6

Lemma 16 from Liao and Kyrillidis (2021) shows that

$$\begin{aligned} \mathcal {P}\left( \left|S_i^\perp \right|\le 4d_1\kappa ^{-1}R\right) \ge \exp (-d_1\kappa ^{-1}R) \end{aligned}$$

Thus, with probability at least $1 - n\exp \left( -d_1R\right)$, it holds that

$$\begin{aligned} \max _{i\in [n]}\left|S_i^\perp \right|\le 4d_1\kappa ^{-1}R \end{aligned}$$

Recall the definition of $\textbf{H}^\perp$

$$\begin{aligned} \textbf{H}^\perp (t,t',k) = \frac{1}{d}\left\langle \hat{\textbf{x}}_i, \hat{\textbf{x}}_{i'}\right\rangle \sum _{r\in S_i^\perp }\mathcal {M}_{t,r}^{(j)}\mathbb {I}\{\left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_i\right\rangle \ge 0; \left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\} \end{aligned}$$

Since $\left|\left\langle \hat{\textbf{x}}_i, \hat{\textbf{x}}_{i'}\right\rangle \right|\le \left\| \hat{\textbf{x}}_i\right\| _2\left\| \hat{\textbf{x}}_{i'}\right\| _2 \le 1$, we have that

$$\begin{aligned} \left\| \textbf{H}^\perp (t,t',k)\right\| _2^2&\le \left\| \textbf{H}^\perp (t,t',k)\right\| _F^2\\&= \sum _{i,i'=1}^n\left( \textbf{H}^\perp (t,t',k)_{ij}\right) ^2\\&\le \frac{1}{d_1^2}\sum _{i,i'=1}^n\sum _{r,r'\in S_i^\perp }\mathbb {I}\left\{ \left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_i\right\rangle \ge 0; \left\langle \varvec{\theta }_{t',k,r}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \cdot \\&\quad \quad \quad \mathbb {I}\left\{ \left\langle \varvec{\theta }_{t',k,r'}^{(j)}, \hat{\textbf{x}}_i\right\rangle \ge 0; \left\langle \varvec{\theta }_{t',k,r'}^{(j)}, \hat{\textbf{x}}_{i'}\right\rangle \ge 0\right\} \\&\le \frac{n^2}{d_1^2}\left( \max _{i\in [n]}\left|S_i^\perp \right|\right) ^2 = 16n^2\kappa ^{-2}R^2 \end{aligned}$$

which yields the following

$$\begin{aligned} \left\| \textbf{G}^{(j)\perp }(t,t',k)\right\| \le \left\| \bar{\textbf{A}}\right\| _2^2\left\| \textbf{H}^{(j)\perp }(t,t',k)\right\| _2 = 16n\kappa ^{-1}R \end{aligned}$$

Plugging in $R = \frac{\kappa \lambda _0}{192n}$ gives the desired result.

Lemma 7

Choosing $\eta = \frac{\lambda _0}{24n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}$, we have that

$$\begin{aligned} \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \le \frac{\eta \lambda _0}{6}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

Proof of Lemma 7

Using 1-Lipschitzness of $\sigma (\cdot )$, and that $\left\| \hat{\textbf{x}}_{i}\right\| _2=1$, we have that for all i, t, k, r

$$\begin{aligned} \left|\sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) \right|&\le \left|\left\langle \varvec{\theta }_{t,k+1,r}^{(j)} -\varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right|\\&\le \left\| \varvec{\theta }_{t,k+1,r}^{(j)} -\varvec{\theta }_{t,k,r}^{(j)}\right\| _2\\&= \eta \left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2 \end{aligned}$$

Using the fact that $\left|\mathcal {M}_{t,r}^{(j)}\right|\le 1$, and $\left|a_r\right|\le 1$, we have

$$\begin{aligned}&\left( \hat{y}_i^{(j)}(t,k+1) - \hat{y}_i^{(j)}(t,k)\right) ^2 \\&\quad \quad \le \frac{1}{d_1}\left( \sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\left|\sigma \left( \left\langle \varvec{\theta }_{t,k+1,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) - \sigma \left( \left\langle \varvec{\theta }_{t,k,r}^{(j)}, \hat{\textbf{x}}_{i}\right\rangle \right) \right|\right) ^2\\&\quad \quad \le \frac{\eta ^2}{d_1}\left( \sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2\right) ^2\\&\quad \quad \le \frac{\eta ^2}{d_1}\sum _{i'=1}^n\sum _{i''=1}^n\sum _{r=1}^{d_1}\sum _{r'=1}^{d_1}\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{ii''}\left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_r}\right\| _2\cdot \left\| \frac{\partial L\left( \varvec{\Theta }_{t,k}^{(j)}\right) }{\partial \varvec{\theta }_{r'}}\right\| _2 \end{aligned}$$

Applying Lemma 4 to bound the norm of the gradient gives

$$\begin{aligned}&\left( \hat{y}_i^{(j)}(t,k+1) - \hat{y}_i^{(j)}(t,k)\right) ^2\\&\quad \quad \le \frac{\eta ^2n}{d_1^2}\left\| \bar{\textbf{A}}\right\| _2^2\sum _{i'=1}^n\sum _{i''=1}^n\sum _{r=1}^{d_1}\sum _{r'=1}^{d_1}\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{ii''}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\\&\quad \quad \le \eta ^2n\left\| \bar{\textbf{A}}\right\| _2^2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\sum _{i'=1}^n\sum _{i''=1}^n\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{ii''} \end{aligned}$$

Therefore

$$\begin{aligned} \left\| \hat{\textbf{y}}^{(j)}(t,k+1) - \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2&= \sum _{i=1}^n\left( \hat{y}_i^{(j)}(t,k+1) - \hat{y}_i^{(j)}(t,k)\right) ^2\\&= \eta ^2n\left\| \bar{\textbf{A}}\right\| _2^2\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2\sum _{i=1}^n\sum _{i'=1}^n\sum _{i''=1}^n\bar{\textbf{A}}_{ii'}\bar{\textbf{A}}_{ii''}\\&= 4\eta ^2n\left\| \bar{\textbf{A}}^2\right\| _{1,1}\left\| \textbf{y}- \hat{\textbf{y}}^{(j)}(t,k)\right\| _2^2 \end{aligned}$$

Choosing $\eta = \frac{\lambda _0}{24n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}$ gives the desired result. $\square$

Lemma 8

As long as $\left\| \varvec{\theta }_{t,k,r}^{(j)} - \varvec{\theta }_{0,r}\right\| _2\le R$ for all t, k, j, and the initialization satisfies $\left\| \varvec{\Theta }_0\right\| _F\le \kappa \sqrt{2d_1d} - \sqrt{d_1}R$, then we have

$$\begin{aligned} \iota _t \le \frac{\eta \gamma \lambda _0}{2m}\sum _{j=1}^m\sum _{k=0}^{\zeta - 1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2^2\right] + \frac{18\eta \gamma ^2d\kappa ^2\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

for $\gamma = \left( 1 - m^{-1}\right) ^{\frac{1}{3}}$

Proof of Lemma (8)

Recall the definition of $\iota _k$

$$\begin{aligned} \iota _t = \frac{1}{m}\sum _{j=1}^m\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2-\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\right] \end{aligned}$$

Notice that

$$\begin{aligned}&\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\\&\quad \quad = \left\| \left( \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right) + \left( \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}(t+1) + \hat{\textbf{y}}^{(j)}(t,\zeta )\right) \right\| _2^2\\&\quad \quad = \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 + \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}(t+1) + \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2 - \\&\quad \quad \quad \quad \quad 2\left\langle \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}(t+1) + \hat{\textbf{y}}^{(j)}(t,\zeta ), \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}(t)\right\rangle \\&\quad \quad \ge \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2 - 2\left\langle \hat{\textbf{y}}(t) - \hat{\textbf{y}}(t+1), \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}(t)\right\rangle - \\&\quad \quad \quad \quad \quad 2\left\langle \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}^{(j)}(t,\zeta ), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \\ \end{aligned}$$

Thus,

$$\begin{aligned}&\left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2-\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\\&\quad \quad \le 2\left\langle \hat{\textbf{y}}(t) - \hat{\textbf{y}}(t+1), \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}(t)}\right\rangle + \\&\quad \quad \quad \quad \quad 2\left\langle \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}^{(j)}(t,\zeta ), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \\ \end{aligned}$$

Also notice that

$$\begin{aligned} \sum _{j=1}^m\left\langle \hat{\textbf{y}}(t) - \hat{\textbf{y}}(t+1), \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}(t)}\right\rangle&= \left\langle \hat{\textbf{y}}(t) - \hat{\textbf{y}}(t+1), \sum _{j=1}^m\hat{\textbf{y}}^{(j)}(t,0) - m\hat{\textbf{y}(t)}\right\rangle \\&= 0 \end{aligned}$$

Therefore

$$\begin{aligned} \sum _{j=1}^m&\left( \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2-\left\| \hat{\textbf{y}}(t+1) - \hat{\textbf{y}}^{(j)}(t,\zeta )\right\| _2^2\right) \\&\quad \quad \quad \le 2\sum _{j=1}^m\left\langle \hat{\textbf{y}}^{(j)}(t,0) - \hat{\textbf{y}}^{(j)}(t,\zeta ), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \\&\quad \quad \quad =2\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\left\langle \hat{\textbf{y}}^{(j)}(t,k) - \hat{\textbf{y}}^{(j)}(t,k+1), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \\&\quad \quad \quad =2\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\left\langle \textbf{I}_1^{(j)}(t,k) + \textbf{I}_2^{(j)}(t,k), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \end{aligned}$$

if we recall the definition of $\textbf{I}_1^{(j)}(t,k)$ and $\textbf{I}_2^{(j)}(t,k)$. Thus, we can bound $\iota _t$ as

$$\begin{aligned} \iota _t&\le \frac{2}{m}\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\langle \textbf{I}_1^{(j)}(t,k) + \textbf{I}_2^{(j)}(t,k), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \right] \\&\le \frac{2}{m}\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{I}_1^{(j)}(t,k)\right\| \cdot \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| \right] +\\&\quad \quad \quad \mathbb {E}_{\mathcal {M}_t}\left[ \left|\left\langle \textbf{I}_2^{(j)}(t,k), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \right|\right] \end{aligned}$$

Using Lemma (5) with $\textbf{v}= \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)$, we have that for all $j\in [m]$

$$\begin{aligned} \left|\left\langle \textbf{I}_2^{(j)}(t,k), \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\rangle \right|&\le \frac{\eta \lambda _0}{12}\left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2\left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\\&\le \eta \lambda ^*\left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2\left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2 \end{aligned}$$

Furthermore, Lemma 9 gives a bound on $\left\| \textbf{I}_1^{(j)}(t,k)\right\| _2$

$$\begin{aligned} \left\| \textbf{I}_1^{(j)}(t,k)\right\| _2 \le 2\eta \lambda ^*\left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2 \end{aligned}$$

Therefore,

$$\begin{aligned} \iota _t\le & {} \frac{6\eta \lambda ^*}{m}\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2\cdot \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2\right] \nonumber \\\le & {} \frac{3\eta \lambda ^*}{m}\sum _{j=1}^m\sum _{k=0}^{\zeta -1}\mathbb {E}_{\mathcal {M}_t}\left[ \frac{\lambda _0\left( 1 - m^{-1}\right) ^{\frac{1}{3}}}{6\lambda _*}\left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2^2\right] \nonumber \\{} & {} +\mathbb {E}_{\mathcal {M}_t}\left[ \frac{6\lambda _*}{\lambda _0\left( 1 - m^{-1}\right) ^{\frac{1}{3}}}\left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \nonumber \\= & {} \frac{\eta \lambda _0}{2m}\left( 1 - m^{-1}\right) ^{\frac{1}{3}}\sum _{j=1}^m\sum _{k=0}^{\zeta - 1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2^2\right] + \nonumber \\{} & {} \frac{18\eta \lambda ^{*2}}{m\lambda _0\left( 1 - m^{-1}\right) ^{\frac{1}{3}}}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \end{aligned}$$

(19)

Substituting Lemma (10) to the last step of Eq. (19) gives the desired result

$$\begin{aligned} \iota _t&\le \frac{\eta \lambda _0}{2m}\left( 1 - m^{-1}\right) ^{\frac{1}{3}}\sum _{j=1}^m\sum _{k=0}^{\zeta - 1}\mathbb {E}_{\mathcal {M}_t}\left[ \left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2^2\right] +\\&\quad \quad \quad \frac{18\eta \left( 1-m^{-1}\right) ^{\frac{2}{3}}d\kappa ^2\lambda ^{*2}}{m^2\lambda _0}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

$\square$

Lemma 9

Suppose, then we have

$$\begin{aligned} \left\| \textbf{I}_1^{(j)}(t,k)\right\| \le 2\eta \lambda ^*\left\| \textbf{y}-\hat{\textbf{y}}(t,k)\right\| _2 \end{aligned}$$

Lemma 10

Suppose $\left\| \varvec{\Theta }_t\right\| _F\le 2\kappa \sqrt{d_1d}$. Then we have that for all $j\in [m]$

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right] \le \frac{2d\kappa ^2(m-1)}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

Proof

Recall that

$$\begin{aligned} \hat{y}_i^{(j)}(t,0)&= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\sigma \left( \left\langle \hat{\textbf{x}_{i'}}, \varvec{\theta }_{t,r}\right\rangle \right) \\ \hat{y}_i(t)&= \frac{1}{m\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\mathcal {M}_{t,r}^{(j)}a_r\sigma \left( \left\langle \hat{\textbf{x}_{i'}}, \varvec{\theta }_{t,r}\right\rangle \right) \end{aligned}$$

Thus

$$\begin{aligned} \hat{y}_i^{(j)}(t,0) - \hat{y}_i(t)&= \frac{1}{\sqrt{d_1}}\sum _{i'=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'}\left( \mathcal {M}_{t,r}^{(j)} - m^{-1}\right) a_r\sigma \left( \left\langle \hat{\textbf{x}}_{i'}, \varvec{\theta }_{t,r}\right\rangle \right) \end{aligned}$$

Notice that, by independence of $\mathcal {M}_{t,r}^{(j)}$ and $\mathcal {M}_{t,r'}^{(j)}$ for $r\ne r'$, we have

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_{t}}\left[ \left( \mathcal {M}_{t,r}^{(j)} - m^{-1}\right) \left( \mathcal {M}_{t,r'}^{(j)} - m^{-1}\right) \right] = {\left\{ \begin{array}{ll} \frac{m-1}{m^2} &{} \text {if }r= r'\\ 0 &{} \text {if } r\ne r' \end{array}\right. } \end{aligned}$$

Therefore

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left( \hat{y}_i^{(j)}(t,0) - \hat{y}_i(t)\right) ^2\right]&= \frac{m-1}{d_1m^2}\sum _{i'_1,i'_2=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'_1}\bar{\textbf{A}}_{ii'_2}\cdot \\&\quad \quad \quad \sigma \left( \left\langle \hat{\textbf{x}}_{i'_1}, \varvec{\theta }_{t,r}\right\rangle \right) \sigma \left( \left\langle \hat{\textbf{x}}_{i'_2}, \varvec{\theta }_{t,r}\right\rangle \right) \\&\le \frac{m-1}{d_1m^2}\sum _{i'_1,i'_2=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii'_1}\bar{\textbf{A}}_{ii'_2}\left\| \varvec{\theta }_{t,r}\right\| _2^2\\&= \frac{m-1}{d_1m^2}\left\| \varvec{\Theta }_{t}\right\| _F^2\sum _{i'_1,i'_2=1}^n\bar{\textbf{A}}_{ii'_1}\bar{\textbf{A}}_{ii'_2}\\&\le \frac{2d\kappa ^2(m-1)}{m^2}\sum _{i'_1,i'_2=1}^n\bar{\textbf{A}}_{ii'_1}\bar{\textbf{A}}_{ii'_2} \end{aligned}$$

Thus,

$$\begin{aligned} \mathbb {E}_{\mathcal {M}_t}\left[ \left\| \hat{\textbf{y}}(t) - \hat{\textbf{y}}^{(j)}(t,0)\right\| _2^2\right]&= \sum _{i=1}^n\mathbb {E}_{\mathcal {M}_t}\left[ \left( \hat{y}_i^{(j)}(t,0) - \hat{y}_i(t)\right) ^2\right] \\&\le \frac{2d\kappa ^2(m-1)}{m^2}\sum _{i=1}^n\sum _{i'_1,i'_2=1}^n\bar{\textbf{A}}_{ii'_1}\bar{\textbf{A}}_{ii'_2}\\&= \frac{2d\kappa ^2(m-1)}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

Lemma 11

It holds that $\square$

$$\begin{aligned} \mathbb {E}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right] \le C^2n + \frac{d}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

where C is defined in Assumption 4.

Proof of Lemma 11

Note that

$$\begin{aligned} \mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right]&= \sum _{i=1}^n\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ (y_i - \hat{y}_i(0))^2\right] \\&=y_i^2 -2y_i\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)\right] + \mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)^2\right] \\&\le C^2 + \mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)^2\right] \end{aligned}$$

where the last inequality follows from the bound on $|y_i|$ and the fact that $\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)\right] = 0$. Moreover, we have

$$\begin{aligned}&\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)^2\right] \\&\quad \quad = \frac{1}{m^2 d_1}\sum _{i_1=1}^n\sum _{i_2=1}^n\sum _{r_1=1}^{d_1}\sum _{r_2=1}^{d_1}\bar{\textbf{A}}_{ii_1}\bar{\textbf{A}}_{ii_2}\mathbb {E}_{\textbf{A}}[a_{r_1}a_{r_2}]\cdot \\&\quad \quad \quad \quad \quad \mathbb {E}_{\varvec{\Theta }_0}\left[ \sigma \left( \left\langle \varvec{\theta }_{0,r_1}, \hat{\textbf{x}}_{i_1}\right\rangle \right) \sigma \left( \left\langle \varvec{\theta }_{0,r_2}, \hat{\textbf{x}}_{i_2}\right\rangle \right) \right] \\&\quad \quad = \frac{1}{m^2d_1}\sum _{i_1=1}^n\sum _{i_2=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii_1}\bar{\textbf{A}}_{ii_2}\mathbb {E}_{\varvec{\Theta }_0}\left[ \sigma \left( \left\langle \varvec{\theta }_{0,r}, \hat{\textbf{x}}_{i_1}\right\rangle \right) \sigma \left( \left\langle \varvec{\theta }_{0,r}, \hat{\textbf{x}}_{i_2}\right\rangle \right) \right] \\&\quad \quad \le \frac{1}{m^2d_1}\sum _{i_1=1}^n\sum _{i_2=1}^n\sum _{r=1}^{d_1}\bar{\textbf{A}}_{ii_1}\bar{\textbf{A}}_{ii_2}\mathbb {E}_{\varvec{\Theta }_0}\left[ \left\| \varvec{\theta }_{0,r}\right\| _2^2\right] \\&\quad \quad = \frac{d}{m^2}\sum _{i_1=1}^n\sum _{i_2=1}^n\bar{\textbf{A}}_{ii_1}\bar{\textbf{A}}_{ii_2} \end{aligned}$$

Thus

$$\begin{aligned} \mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right] \le \sum _{i=1}^n\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \hat{y}_i(0)^2\right] \le C^2n + \frac{d}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1} \end{aligned}$$

$\square$

1.8 Computation of overparameterization

In this section, we provide the computation of the exact overparameterization requirement such that Theorem 2 holds. Recall from the end of Sect. C.6, Eq. (18) that we need to satisfy the following requirement

$$\begin{aligned} R&\ge \frac{4T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right] ^\frac{1}{2} + \\&\quad \quad \quad 4T\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\left( \eta \zeta \sqrt{\frac{Tdn(m-1)}{d_1m\delta }} + \frac{5T\zeta \gamma \lambda ^*}{m\delta \alpha }\sqrt{\frac{\eta ^3nd}{\lambda _0d_1}}\right) \end{aligned}$$

To start, Lemma 11 gives that

$$\begin{aligned} \mathbb {E}_{\varvec{\Theta }_0,\textbf{A}}\left[ \left\| \textbf{y}- \hat{\textbf{y}}(0)\right\| _2^2\right] ^\frac{1}{2} \le \left( C^2n + \frac{d}{m^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \le C\sqrt{n} + \frac{\sqrt{d}}{m}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}} \end{aligned}$$

Plugging this into Eq. (18) and using $O(\cdot )$ to hide constants, we have

$$\begin{aligned} \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right)&\ge \frac{T\eta \zeta }{\delta \alpha }\sqrt{\frac{n}{d_1}}\left( \sqrt{n} + \frac{\sqrt{d}}{m}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}}\right) + \end{aligned}$$

(20)

$$\begin{aligned}&\quad \quad \quad T\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\left( \eta \zeta \sqrt{\frac{Tdn(m-1)}{d_1m\delta }} + \frac{T\zeta \gamma \lambda ^*}{m\delta \alpha }\sqrt{\frac{\eta ^3nd}{\lambda _0d_1}}\right) \end{aligned}$$

(21)

Opening the parenthesis and plugging in $\alpha \ge \frac{\eta \lambda _0}{2}(1-\gamma )$ gives

$$\begin{aligned} \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right)&\ge \frac{T\zeta n}{\delta \lambda _0(1-\gamma )\sqrt{d_1}} + \frac{T\zeta }{\delta \lambda _0(1-\gamma )m}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}}\sqrt{\frac{nd}{d_1}} +\\&\quad \quad \quad T\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\eta \zeta \sqrt{\frac{Tdn(m-1)}{d_1m\delta }} +\\&\quad \quad \quad T^2\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\frac{\zeta \gamma \lambda ^*}{m(1-\gamma )}\sqrt{\frac{\eta d}{\lambda _0^3d_1}} \end{aligned}$$

Further plugging in $\eta = \frac{\lambda _0}{24n\left\| \bar{\textbf{A}}^2\right\| _{1,1}}$ gives

$$\begin{aligned} \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right)&\ge \frac{T\zeta n}{\delta \lambda _0(1-\gamma )\sqrt{d_1}} + \frac{T\zeta }{\delta \lambda _0(1-\gamma )m}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}}\sqrt{\frac{nd}{d_1}} +\\&\quad \quad \quad T\lambda _0\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^{-\frac{1}{2}}\zeta \sqrt{\frac{Td(m-1)}{d_1nm\delta }} + T^2\kappa \frac{\zeta \gamma \lambda ^*}{\lambda _0m(1-\gamma )}\sqrt{\frac{d}{nd_1}} \end{aligned}$$

Equation (20) is satisfied if each term on the left-hand side is bounded by the right-hand side when hiding constants. Thus, it holds as long as the following holds

$$\begin{aligned} \frac{T\zeta n}{\delta \lambda _0(1-\gamma )\sqrt{d_1}} \le \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right) \end{aligned}$$

(22)

$$\begin{aligned} \frac{T\zeta }{\delta \lambda _0(1-\gamma )m}\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{\frac{1}{2}}\sqrt{\frac{nd}{d_1}}\le \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right) \end{aligned}$$

(23)

$$\begin{aligned} T\lambda _0\kappa \left\| \bar{\textbf{A}}^2\right\| _{1,1}^{-\frac{1}{2}}\zeta \sqrt{\frac{Td(m-1)}{d_1nm\delta }}\le \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right) \end{aligned}$$

(24)

$$\begin{aligned} T^2\kappa \frac{\zeta \gamma \lambda ^*}{\lambda _0m(1-\gamma )}\sqrt{\frac{d}{nd_1}}\le \mathcal {O}\left( \frac{\kappa \lambda _0}{n}\right) \end{aligned}$$

(25)

where in requirement of Eq. (22) we use the simplification $\alpha \ge \frac{\eta \lambda _0}{2}(1-\gamma )$. Notice that $d_1$ appears in the denominator on the left-hand side for Eqs. (22)–(25). Thus, as long as $d_1$ is large enough, the above requirements can be satisfied. Next, we solve each of these requirements individually. We move $\sqrt{d_1}$ to the right-hand side of Eqs. (22)–(25) and $\frac{\kappa \lambda _0}{n}$ to the left-hand side to get that

$$\begin{aligned} \sqrt{d_1}&\ge \Omega \left( \frac{T\zeta n^2}{\delta \lambda _0^2(1-\gamma )\kappa }\right) \\ \sqrt{d_1}&\ge \Omega \left( \frac{T\zeta \sqrt{n^3d}}{\delta \lambda _0^2(1-\gamma )m\kappa }\left\| \bar{\textbf{A}}^2\right\| _{1,1}^\frac{1}{2}\right) \\ \sqrt{d_1}&\ge \Omega \left( T\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{-\frac{1}{2}}\zeta \sqrt{\frac{Td(m-1)n}{m\delta }}\right) \\ \sqrt{d_1}&\ge \Omega \left( \frac{T^2\zeta \gamma \lambda ^*}{\lambda _0^2m(1-\gamma )}\sqrt{nd}\right) \end{aligned}$$

Squaring both sides gives

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^2\zeta ^2n^4}{\delta ^2\lambda _0^4(1-\gamma )^2\kappa ^2}\right) \end{aligned}$$

(26)

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^2\zeta n^3d}{\delta ^2\lambda _0^4(1-\gamma )^2m^2\kappa ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

(27)

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^3\zeta ^2nd(m-1)}{m\delta }\left\| \bar{\textbf{A}}^2\right\| _{1,1}^{-1}\right) \end{aligned}$$

(28)

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^4\zeta ^2\gamma ^2\lambda ^{*2}nd}{\lambda _0^4m^2(1-\gamma )^2}\right) \end{aligned}$$

(29)

First, notice that

$$\begin{aligned} \left\| \bar{\textbf{A}}^2\right\| _{1,1} \ge n\left\| \bar{\textbf{A}}^2\right\| _F\ge n \end{aligned}$$

Substituting this and $\frac{m-1}{m} = \gamma ^3$ into Eq. 28 to get

$$\begin{aligned} d_1\ge & {} \Omega \left( \frac{T^2\zeta ^2n^4}{\delta ^2\lambda _0^4(1-\gamma )^2\kappa ^2}\right) \end{aligned}$$

(30)

$$\begin{aligned} d_1\ge & {} \Omega \left( \frac{T^2\zeta n^3d}{\delta ^2\lambda _0^4(1-\gamma )^2m^2\kappa ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

(31)

$$\begin{aligned} d_1\ge & {} \Omega \left( \frac{T^3\zeta ^2\gamma ^3d}{\delta }\right) \end{aligned}$$

(32)

$$\begin{aligned} d_1\ge & {} \Omega \left( \frac{T^4\zeta ^2\gamma ^2\lambda ^{*2}nd}{\lambda _0^4m^2(1-\gamma )^2}\right) \end{aligned}$$

(33)

Notice that $\gamma \le 0$ and $\lambda _0\le 0$, and treat $\delta$ as some constants. Thus Eq. (33) implies Eq. (32). Noticing that $m\ge 1, \zeta \ge 1$ and $\gamma \le 1$. Factoring out $\frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2}$ for Eq. (30), (31), and (33), the requirements boils down to

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2} \cdot \frac{n^3}{\delta ^2\kappa ^2}\right) \end{aligned}$$

(34)

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2} \cdot \frac{n^2d}{\delta ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}\right) \end{aligned}$$

(35)

$$\begin{aligned} d_1&\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2} \cdot T^2\lambda ^{*2}d\right) \end{aligned}$$

(36)

Taking a maximum over Eqs. (34)–(36) gives the final requirement

$$\begin{aligned} d_1\ge \Omega \left( \frac{T^2\zeta ^2 n}{\lambda _0^4(1-\gamma )^2}\max \left\{ \frac{n^3}{\delta ^2\kappa ^2}, \frac{n^2d}{\delta ^2}\left\| \bar{\textbf{A}}^2\right\| _{1,1}, T^2\lambda ^{*2}d\right\} \right) \end{aligned}$$