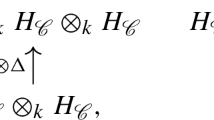Cosheaf representations of relations and Dowker complexes

Abstract

The Dowker complex is an abstract simplicial complex that is constructed from a binary relation in a straightforward way. Although there are two ways to perform this construction—vertices for the complex are either the rows or the columns of the matrix representing the relation—the two constructions are homotopy equivalent. This article shows that the construction of a Dowker complex from a relation is a non-faithful covariant functor. Furthermore, we show that this functor can be made faithful by enriching the construction into a cosheaf on the Dowker complex. The cosheaf can be summarized by an integer weight function on the Dowker complex that is a complete isomorphism invariant for the relation. The cosheaf representation of a relation actually embodies both Dowker complexes, and we construct a duality functor that exchanges the two complexes.

1 Introduction

This article studies the structure of an abstract simplicial complex that is built according to a binary relation between two sets, as originally described by Dowker (1952). Dowker complexes, as these simplicial complexes are now known, are simple to construct and apply, finding use in many areas of mathematics and data science (Ghrist 2014). Dowker’s classic result is that there are two ways to build such an abstract simplicial complex, and that both of these complexes have the same homology. This fact is a kind of duality, because it arises from the transpose of the underlying relation’s defining matrix. It was later shown by Björner (1995) that the two dual Dowker complexes have homotopy equivalent geometric realizations.

This article explains how the Dowker complex can be augmented with an integer weight function, and develops this idea into several functorial representations of the underlying relation. Although the integer weight is not functorial, we show how it is the decategorification of a functorial, faithful cosheaf representation, and explore some of the implications of that fact. In particular, Dowker’s famous duality result arises as a functor that exchanges the base space and the space of global cosections of the cosheaf. Considering only the Dowker complex without the weight function yields a non-faithful functor, since many different relations can have the same Dowker complex.

Probably because of the topological nature of the duality result in Dowker (1952), most of the literature discussing Dowker complexes focuses on their topological properties. For instance, Minian (2010) links the construction of the Dowker complex from a relation to the order complex of a partial order, and proves a number of homotopy equivalences. Because Dowker complexes respect filtrations (Chowdhury and Mémoli 2016), they seem ripe for use in topological data analysis, which typically focuses on the persistent homology of a filtered topological space. This line of reasoning recently culminated in a functoriality result (Chowdhury and Mémoli 2018, Thm. 3), which establishes that Dowker duality applies to the geometric realizations of sub-relations. Specifically, consider a pair of nested subsets $R_1 \subseteq R_2 \subseteq (X \times Y)$ of the product of two sets X and Y. The Dowker complexes $D(X,Y,R_1)$ and $D(X,Y,R_2)$ for $R_1$ and $R_2$ and their duals $D(Y,X,R_1^T)$ and $D(Y,X,R_2^T)$ are related through a commutative diagram

of continuous maps on their respective geometric realizations, in which the vertical maps are homotopy equivalences.

The paper (Chowdhury and Mémoli 2018) appears to have set off a flurry of interest in Dowker complexes. For instance, Brun and Blaser (2019) showed how to use Dowker complexes instead of Čech complexes for studying finite metric spaces. Since topological data analysis often takes a finite metric space as an input, constructing a Vietoris-Rips complex is frequently an intermediate step; Virk (2019) shows how Dowker complexes and Vietoris-Rips complexes are related. Finally, Salbu (2019) extended Dowker duality to simplicial sets, pointing the way to much greater generality.

The present paper is also inspired by the functoriality result (Chowdhury and Mémoli 2018, Thm. 3), but in a somewhat different way. Instead of focusing on sub-relations, we show that the Dowker complex construction is a functor from a category whose objects are relations and whose morphisms are relation-preserving transformations (Definition 6). Furthermore, we show that the isomorphism classes of this category are completely characterized by two different weight functions on the Dowker complex, and that these are derived from a faithful cosheaf representation of the category.

Given a relation between two sets, the main results of this article are as follows:

• (1) The existence of two integer weighting functions, differential and total weights, on the Dowker complex for the relation that are complete isomorphism invariants (Theorems 1 and 2),

• (2) The Dowker complex is a functor from an appropriately constructed category of relations (Theorem 3),

• (3) The existence of faithful functors that render the relation into a cosheaf (Theorem 4 and Corollary 4) or sheaf (Theorem 5), whose (co)stalks determine the total weight function,

• (4) The space of global cosections of the cosheaf is the dual Dowker complex for the relation (Theorem 6), and

• (5) There is a duality functor that exchanges the cosheaf’s base space and space of global cosections (Theorem 7).

2 Motivation

This article grew out of the need to classify the behavior of various computer programs that read data files written according to an informal standard. Since there is considerable variability in the interpretation of the file format, the behavior of the programs can vary as well. Worryingly, files can sometimes be crafted to exploit these differences in behavior in malicious ways. It is therefore generally unwise to run the programs on one’s computer as they read a set of these files. That brings an interesting and somewhat vexing problem to mind: how can one proceed safely?

The solution is to run the programs within a controlled environment, wherein their inputs consist only of the files to be read, and the only permitted output is to merely report whether a file has been successfully (and safely) read or not. Mathematically, this means that the only data one gets from running a set of programs X against a set of files Y is a binary relation: a subset $R \subseteq X \times Y$. We interpret an element (x, y) of R as witnessing the fact that file y was successfully read by program x. The absence of an element (x, y) of the product $X \times Y$ from R means that the program x did not successfully read the corresponding file y (or that something untoward happened in the process of reading file y).

Given a particular relation R created in this way, one encounters two problems: (1) how to find structure within R that identifies problematic files and (2) how to curate the data when new files or programs are added or changed.

The treatment of the first problem is aided by the realization that a relation R can be interpreted topologically via the Dowker complex. This article proves that the Dowker complex is functorial, which means that it preserves a particular kind of structure present in the relation. In short, the topology of the Dowker complex is a reliable proxy for the somewhat more statistical information present in R. Moreover, using the two weighting functions presented in this article, that statistical information is paired with the topology to tell a rather complete story. Indeed, in a separate paper (Ambrose et al. 2020) we expain how the weighting functions can be exploited algorithmically to detect problematic files.

This article additionally shows that the topological structure present in the file-program relation R goes quite a bit deeper. This structure sheds insight into the second problem, that of curation. Although the weighting functions are not functorial, which means that a systematic change to the list of files or programs may change the weighting functions in a complicated way, there is a richer faithful cosheaf representation that is functorial. The cosheaf representation we present in this article promises to become a useful tool for organizing the file-program results, although that is not the focus of this article.

One may wonder if the problem is symmetric: instead of trying to find problematic files, can we instead use the same relation to find problematic programs? The famous Dowker duality theorem indicates that the topology ought to be unchanged in that case. This article shows that the Dowker duality extends to the cosheaf representations, which means that the problem is completely symmetric: one can build the cosheaf representation for $R^T$ directly from the representation for R, without having to go back to R itself.

It should be emphasized that the results of this paper are in no way dependent upon the particular application mentioned above. Relational data abounds, and the results are written with generality in mind.

3 Recovery of a relation from a weight function on the Dowker complex

Definition 1

An abstract simplicial complex X on a set $V_X$ consists of a set X of subsets of $V_X$ such that if $\sigma \in X$ and $\tau \subseteq \sigma$, then $\tau \in X$. Each $\sigma \in X$ is called a simplex of X, and each element of $V_X$ is a vertex of X. Every subset $\tau$ of a simplex $\sigma$ is called face of $\sigma$.

It is usually tiresome to specify all of the simplices in a simplicial complex. Instead, it is much more convenient to supply a generating set S of subsets of the vertex set. The unique smallest simplicial complex containing the generating set is called the abstract simplicial complex generated by S.

Let $R \subseteq X \times Y$ be a relation between finite sets X and Y, which can be represented as a Boolean matrix $(r_{x,y})$.

Definition 2

The Dowker complex D(X, Y, R) is the abstract simplicial complex given by

$$\begin{aligned} D(X,Y,R)&= \{ [x_{i_0}, \dotsc , x_{i_k}] : \text {there exists a }y\in Y\text { such that }(x_{i_j},y)\\&\quad \in R\text { for all }j=0, \dotsc , k \}. \end{aligned}$$

The total weight is a function $t: D(X,Y,R)\rightarrow {\mathbb {N}}$ given by

$$\begin{aligned} t(\sigma ) = \# \{y \in Y : (x,y) \in R\text { for all }x \in \sigma \}. \end{aligned}$$

The differential weight (Ambrose et al. 2020) is a function $d : D(X,Y,R) \rightarrow {\mathbb {N}}$ given by

$$\begin{aligned} d(\sigma ) = \# \{y \in Y: \left( (x,y)\in R\text { if } x\in \sigma \right) \text { and } \left( (x,y)\notin R\text { if } x\notin \sigma \right) \}. \end{aligned}$$

It is immediate by the definition that the Dowker complex is an abstract simplicial complex.

Example 1

Consider the sets $X_1 = \{a,b,c,d\}$, and $Y_1=\{1,2, \dotsc , 20\}$ and the relation $R_1$ given by the matrix

$$\begin{aligned} r_1 = \left( \begin{array}{llllllllllllllllllll} 1&{}0&{}0&{}0&{}0&{}0&{}1&{}1&{}\mathbf{1}&{}1&{}1 &{}1&{}\mathbf{0}&{}0&{}0&{}0&{}1&{}1&{}1&{}\mathbf{1}\\ 0&{}1&{}1&{}0&{}0&{}0&{}1&{}1&{}\mathbf{1}&{}0&{}0&{}0&{}\mathbf{1}&{}0&{}0&{}0&{}0&{}0&{}0&{}\mathbf{0}\\ 0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}\mathbf{0}&{}1&{}0&{}0&{}\mathbf{1}&{}1&{}1&{}1&{}1&{}1&{}1&{}\mathbf{1}\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}\mathbf{0}&{}0&{}1&{}1&{}\mathbf{0}&{}1&{}1&{}1&{}1&{}1&{}1&{}\mathbf{1}\\ \end{array}\right) \end{aligned}$$

whose rows correspond to elements of $X_1$ and columns correspond to elements of $Y_1$. The Dowker complex for this relation is generated by the simplices [a, c, d], [a, b], and [b, c], a fact witnessed by the columns marked with bold type. The Dowker complex $D(X_1,Y_1,R_1)$ and its weighting functions are shown in Fig. 1. Notice in particular that the differential weighting function counts the number of columns of $r_1$ of each simplex. The total weighting accumulates all of the counts of columns for its faces as well.

Fig. 1

The Dowker complex for Example 1 (left), its total weight (center), and its differential weight (right)

Example 2

If we keep the same set $X_2=X_1$ as in Example 1, but change the $Y_2$ set, with a different relation $R_2$ given by the matrix

$$\begin{aligned} r_2 = \begin{pmatrix} 1&{}0&{}1&{}0&{}0&{}1\\ 1&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}0&{}1&{}0\\ \end{pmatrix} \end{aligned}$$

we obtain the same Dowker complex, $D(X_2,Y_2,R_2) = D(X_1,Y_1,R_1)$. However, as Fig. 2 shows, the weight functions are different.

Fig. 2

The Dowker complex for Example 2 (left), its total weight (center), and its differential weight (right)

Proposition 1

The sum of the differential weight d on the Dowker complex D(X, Y, R) is the number of elements of Y.

(Do not forget to count the differential weight of the empty simplex!)

Proof

Observe that sets of the form $\{y \in Y: \left( (x,y)\in R\text { if } x\in \sigma \right)$ and $\big ((x,y)\notin R\text { if } x\notin \sigma \big ) \}$ are disjoint for different $\sigma$ in D(X, Y, R). The sum of the differential weight is therefore the cardinality of

$$\begin{aligned} \sum _{\sigma \in D(X,Y,R)} d(\sigma )&= \# \bigcup _{\sigma \in D(X,Y,R)} \{y \in Y: \left( (x,y)\right. \left. \quad \in R\text { if } x\in \sigma \right) \text { and } \left( (x,y)\notin R\text { if } x\notin \sigma \right) \}, \end{aligned}$$

which completes the argument. $\square$

Proposition 2

The total weight t defines a filtration by super-level sets on the Dowker complex D(X, Y, R).

In other words, the total weight on a simplex is not more than the total weight on any of its faces.

Proof

This follows from showing that t is order-reversing in the following way: if $\sigma \subseteq \tau$, then $t(\sigma ) \ge t(\tau )$.

Suppose $\sigma \subseteq \tau$, and that $y \in Y$ satisfies $(x,y) \in R$ for all $x \in \tau$. Since $\sigma \subseteq \tau$, then $(x,y) \in R$ for all $x \in \sigma$ also. Thus

$$\begin{aligned} \{y \in Y : (x,y) \in R\text { for all }x \in \tau \}\subseteq & {} \{y \in Y : (x,y) \in R\text { for all }x \in \sigma \} \\ \# \{y \in Y : (x,y) \in R\text { for all }x \in \tau \}\le & {} \# \{y \in Y : (x,y) \in R\text { for all }x \in \sigma \} \\ t(\tau )\le & {} t(\sigma ). \end{aligned}$$

$\square$

Theorem 1

Given the Dowker complex D(X, Y, R) and differential weight d, one can reconstruct R up to a bijection on Y.

Proof

The differential weight $d(\sigma )$ simply specifies the number of columns of the matrix r for R that can be realized as an indicator function for each $\sigma \in D(X,Y,R)$. Thus, we can construct r up to a column permutation. $\square$

Theorem 2

Given the Dowker complex D(X, Y, R) and the total weight t, one can reconstruct R up to a bijection on Y.

Proof

We construct the relation matrix r of R iteratively. Let $t_0 = t$.

• (1) Set $r_0$ to the zero matrix with no columns and as many rows as vertices of D(X, Y, R). That is, each row of $r_0$ corresponds to an element of X, so let us index rows of $r_0$ by elements of X.

• (2) If $t_n(\sigma ) = 0$ for all simplices $\sigma \in D(X,Y,R)$, declare $r= r_n$ and exit.

• (3) Select a simplex $\sigma$ with $t_n(\sigma ) \not = 0$ such that either there is no simplex $\tau$ containing $\sigma$ as a face, or if such a $\tau$ exists, then $t_n(\tau ) = 0$.

• (4) Define $r_{n+1}$ to be the horizontal concatenation of $r_n$ with $t_n(\sigma )$ columns, each an indicator function for $\sigma$. That is, each new column is a Boolean vector v given by

  $$\begin{aligned} v_x = {\left\{ \begin{array}{ll} 0 &{} \text {if }x\notin \sigma \\ 1 &{} \text {if }x\in \sigma . \end{array}\right. } \end{aligned}$$

• (5) Define a new function $t_{n+1}:D(X,Y,R) \rightarrow {\mathbb {N}}$ by

  $$\begin{aligned} t_{n+1}(\gamma )= {\left\{ \begin{array}{ll} t_n(\gamma ) - t_n(\sigma )&{}\text {if }\gamma \subseteq \sigma \\ t_n(\gamma )&{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

• (6) Increment n

• (7) Go to step (3).

Since $t_{n+1} < t_n$ on at least one simplex, and the relation R is finite, the algorithm will always terminate.

Secondly, the update step for $r_{n+1}$ by adding columns, establishes that r relates the elements of X contained in a given simplex by the appended $\sigma$ columns.

Thirdly, notice that the apparent ambiguity in step (3) about selecting a simplex $\sigma$ merely results in a column permutation, since two maximal simplices do not interact with the update to $t_{n+1}$ in step (5), since another maximal simplex is not a face of $\sigma$.

$\square$

Example 3

Starting with the relation from Example 2 and its total weight function, the algorithm described in the proof of Theorem 2 produces the relation matrix

$$\begin{aligned} r= \begin{pmatrix} 1&{}0&{}1&{}1&{}0&{}0\\ 1&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}1&{}1&{}0\\ 0&{}0&{}1&{}0&{}0&{}1\\ \end{pmatrix} \end{aligned}$$

which differs from the original matrix $r_2$ by a cyclic permutation of the last three columns. Figure 3 shows the progression of the steps of the algorithm.

Fig. 3

Recovering the relation from the total weight function as described in Example 3

Example 4

Not every nonnegative integer filtration of an abstract simplicial complex corresponds to the total weighting of a Dowker complex of a relation. Although the algorithm in Theorem 2 may appear to run, it can produce negative values for the intermediate $t_\bullet$ weights, which cannot correspond to a number of columns in a relation! For instance, the constant function on the simplicial complex generated by [a, b] and [b, c], as shown in Fig. 4 is a filtration. However, running the algorithm on this filtration produces a negative value at [b], so we conclude that no relation can have this as a total weight function.

Fig. 4

Attempting to recover the relation from a filtration that is not a total weight function can result in negative values, as described in Example 4

4 Functoriality of the Dowker complex

The Dowker complex D(X, Y, R) is a functor between an appropriately constructed category of relations and the category of abstract simplicial complexes. We prove this fact in Theorem 3 along with a few other observations.

Definition 3

Consider an arbitrary set P and a partial order $\le$ on P. A partial order is a relation between elements in P such that the following hold:

• (1) (Reflexivity) $x \le x$ for all $x \in P$,

• (2) (Transitivity) if $x \le y$ and $y \le z$, then $x \le z$, and

• (3) (Antisymmetry) if $x \le y$ and $y \le x$, then $x = y$.

The category of partial orders $\mathbf{Pos}$ has every partially ordered set $(P,\le )$ as an object. Each morphism $g: (P,\le _P) \rightarrow (Q,\le _Q)$ consists of an order preserving function $g: P \rightarrow Q$ such that if x and y are two elements of P satisfying $x \le _P y$, then $g(x) \le _Q g(y)$ in Q. Morphisms compose as functions on their respective sets.

To see that $\mathbf{Pos}$ is a category, notice that the identity function is always order preserving and that the composition of two order preserving functions is another order preserving function. Associativity follows from the associativity of function composition.

Definition 4

The face partial order for an abstract simplicial complex X has the simplices of X as its elements, and $\sigma \le \tau$ whenever $\sigma \subseteq \tau$.

Example 5

The face partial order for the Dowker complex shown in Fig. 1 is given by its Hasse diagram

Definition 5

Suppose X and Y are abstract simplicial complexes with vertex sets $V_X$ and $V_Y$, respectively. A function $f: V_X \rightarrow V_Y$ on vertices is called a simplicial map $f:X \rightarrow Y$ if it transforms each simplex $[v_0,\cdots , v_k]$ of X into a simplex $[f(v_0), \cdots , f(v_k)]$ of Y, after removing duplicate vertices. The category $\mathbf{Asc}$ has abstract simplicial complexes as its objects and simplicial maps as its morphisms.

Lemma 1

Let $f:X \rightarrow Y$ be a simplicial map. For every pair of simplices $\sigma$, $\tau$ of X satisfying $\sigma \subseteq \tau$, their images in Y satisfy $f(\sigma ) \subseteq f(\tau )$.

Proof

Since f is a simplicial map, then $f(\sigma )$ is a simplex of Y and so is $f(\tau )$. If $\sigma \subseteq \tau$, then every vertex v of $\sigma$ is also a vertex of $\tau$. By the definition of simplicial maps, f(v) is a vertex of both $f(\sigma )$ and $f(\tau )$. Conversely, every vertex of $f(\sigma )$ is the image of some vertex w of $\sigma$. $\square$

Proposition 3

The face partial order is a covariant functor $Face: \mathbf{Asc}\rightarrow \mathbf{Pos}$.

Proof

The construction of the face partial order from a simplicial complex establishes how the functor transforms objects. Let us denote the face partial order for X by Face(X). Lemma 1 establishes that every simplicial map $f:X \rightarrow Y$ induces an order preserving function $Face(f) : Face(X) \rightarrow Face(Y)$ on the face partial orders for X and Y.

To verify that the functor is covariant, suppose that we have another simplicial map $g: Y \rightarrow Z$. The composition of these is a simplicial map $g \circ f : X \rightarrow Z$ that induces an order preserving map $Face(g\circ f) : Face(X) \rightarrow Face(Z)$ on the face partial orders for X and Z. On the other hand, $Face(g) \circ Face(f) : Face(X) \rightarrow Face(Z)$ is also an order preserving map. Any simplex $\sigma$ in X can be reinterpreted as an element of Face(X), which means that the simplex $(g \circ f)(\sigma )$ of Z corresponds to the same element of Face(Z) as does $g( f(\sigma ))$, thought of as the image of an element of Face(Y). $\square$

Definition 6

(which has (Adámek et al. 2004, Sect. 3.3) or (Rydeheard and Burstall 1988, pg. 54) as a special case, and is manifestly the same as what appears in Brun and Blaser (2019)) The category of relations $\mathbf{Rel}$ has triples (X, Y, R) for objects, in which X, Y are sets and $R \subseteq X \times Y$ is a relation. A morphism $(X,Y,R) \rightarrow (X',Y',R')$ in $\mathbf{Rel}$ is defined by a pair of functions $f:X\rightarrow X'$, $g:Y\rightarrow Y'$ such that $(f(x),g(y))\in R'$ whenever $(x,y)\in R$. Composition of morphisms is simply the composition of the corresponding pairs of functions, which means that $\mathbf{Rel}$ satisfies the axioms for a category. It will be useful to consider the full subcategory $\mathbf{Rel_+}$ of $\mathbf{Rel}$ in which each object (X, Y, R) has the property that for each $x \in X$, there is a $y \in Y$ such that $(x,y) \in R$, and conversely for each $y \in Y$, there is an $x \in X$ such that $(x,y) \in R$.

Example 6

Consider the relation $R_1$ between the sets $X_1=\{a,b,c,d,e\}$ and $Y_1=\{1,2,3,4,5\}$, given by the matrix

$$\begin{aligned} r_1 = \begin{pmatrix} 1&{}1&{}0&{}0&{}0\\ 1&{}0&{}1&{}0&{}0\\ 0&{}1&{}1&{}1&{}1\\ 0&{}0&{}1&{}1&{}0\\ 0&{}0&{}0&{}1&{}1\\ \end{pmatrix}. \end{aligned}$$

Suppose that $X_2=\{A,B,C\}$ and $Y_2=\{1,2,3,4,5\}$, that $f:X_1 \rightarrow X_2$ is given by

$$\begin{aligned} f(a) = A,\; f(b) = B,\; f(c) = C,\; f(d) = C,\; f(e) = C, \end{aligned}$$

and that $g: Y_1 \rightarrow Y_2$ is given by the identity function, namely

$$\begin{aligned} g(1) = 1,\; g(2) = 2,\; g(3) = 3,\; g(4) = 4,\; g(5) = 5. \end{aligned}$$

Then (f, g) is a $\mathbf{Rel}$ morphism $(X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_2)$ if $R_2$ is given by the matrix

$$\begin{aligned} r_2 =\begin{pmatrix} 1&{}1&{}0&{}0&{}0\\ 1&{}0&{}1&{}0&{}0\\ 0&{}1&{}1&{}1&{}1\\ \end{pmatrix}. \end{aligned}$$

Additionally if $g': Y_1 \rightarrow Y_2$ is given by

$$\begin{aligned} g'(1) = 1,\; g'(2) = 2,\; g'(3) = 3,\; g'(4) = 3,\; g'(5) = 3, \end{aligned}$$

then $(f,g')$ is a $\mathbf{Rel}$ morphism $(X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_3)$ if $R_3$ is given by the matrix

$$\begin{aligned} r_3 =\begin{pmatrix} 1&{}1&{}0&{}0&{}0\\ 1&{}0&{}1&{}0&{}0\\ 0&{}1&{}1&{}0&{}0\\ \end{pmatrix}. \end{aligned}$$

However, (f, g) is not a $\mathbf{Rel}$ morphism $(X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_3)$, since $(f(e),g(5))=(C,5)$ is not in the relation $R_3$ even though (e, 5) is in $R_1$.

Theorem 3

The Dowker complex defined in Definition 2 is a covariant functor $D: \mathbf{Rel} \rightarrow \mathbf{Asc}$.

Proof

Given the construction of the Dowker complex D(X, Y, R) from $R \subseteq X \times Y$, we must show that

• (1) Each morphism in $\mathbf{Rel}$ translates into a simplicial map, and

• (2) Composition of morphisms in $\mathbf{Rel}$ translates into composition of simplicial maps.

To that end, suppose that $(X_1,Y_1,R_1)$, $(X_2,Y_2,R_2)$, and $(X_3,Y_3,R_3)$ are three objects in $\mathbf{Rel}$ with $f_1 : X_1 \rightarrow X_2$, $g_1 : Y_1 \rightarrow Y_2$ defining a morphism $(X_1,Y_1,R_1) \rightarrow (X_2, Y_2, R_2)$, and with $f_2 : X_2 \rightarrow X_3$, $g_2 : Y_2 \rightarrow Y_3$ defining a morphism $(X_2,Y_2,R_2) \rightarrow (X_3, Y_3, R_3)$. The first claim to be proven is that $f_1$ is the vertex function for a simplicial map $D(X_1,Y_1,R_1) \rightarrow D(X_2,Y_2,R_2)$. Suppose that $\sigma$ is a simplex of $D(X_1,Y_1,R_1)$. Under the vertex map $f_1$, the set of vertices of $\sigma$ get transformed into the set

$$\begin{aligned} f_1(\sigma ) = \{f_1(x) : x \in \sigma \}. \end{aligned}$$

But the defining characteristic of $\sigma$ is that there is a $y \in Y$ such that $(x,y) \in R_1$ for each $x \in \sigma$. Using the function $g_1$ and the fact that the pair $(f_1,g_1)$ is a $\mathbf{Rel}$ morphism, we have that $(f_1(x),g_1(y)) \in R_2$ for every $x \in \sigma$. This means that the set $f_1(\sigma )$ is actually a simplex of $D(X_2,Y_2,R_2)$. Since $\sigma$ was arbitrary, this establishes that $f_1$ is a simplicial map.

Since the composition of the $\mathbf{Rel}$ morphisms $(f_2,g_2) \circ (f_1,g_1)$ is defined to be $(f_2 \circ f_1, g_2 \circ g_1)$, this means that D is a covariant functor, since this composition of $\mathbf{Rel}$ morphisms becomes a composition of simplicial maps. $\square$

Example 7

Continuing Example 6, the Dowker complex $D(X_1,Y_1,R_1)$ is shown at left in Fig. 5. The Dowker complexes $D(X_2,Y_2,R_2)$ and $D(X_2,Y_2,R_3)$ are identical, and are shown at right in Fig. 5. The $\mathbf{Rel}$ morphism (f, g) from Example 6 induces a simplicial map according Theorem 3. The vertex function for this simplicial map is shown in Fig. 5 as well. The simplicial map collapses the simplex [c, d, e] to the vertex [C], while it collapses the simplex [b, c, d] to the edge [B, C].

Fig. 5

The simplicial map induced on the Dowker complexes by the $\mathbf{Rel}$ morphism (f, g), which is used in Examples 6, 7, 10, and 16

Observe that $\mathbf{Pos}$ can be realized as a (non-full) subcategory of $\mathbf{Rel}$: each object in this subcategory is a partially ordered set $(X,\le _X)$ realized as $(X,X,\le _X)$, and each order preserving function $f: (X,\le _X) \rightarrow (Y,\le _Y)$ corresponds to a $\mathbf{Rel}$ morphism $(f,f) : (X,X,\le _X) \rightarrow (Y,Y,\le _Y)$ since the axioms coincide. Beyond this relationship between $\mathbf{Pos}$ and $\mathbf{Rel}$, there is a different, functorial relationship.

Proposition 4

There is a covariant functor $PosRep : \mathbf{Rel} \rightarrow \mathbf{Pos}$, called the poset representation of a relation, that takes each (X, Y, R) to a collection PosRep(X, Y, R) of subsets of $2^X$, for which $A \in PosRep(X,Y,R)$ if there is a $y\in Y$ such that $(x,y)\in R$ for every $x\in A$. The elements of PosRep(X, Y, R) are ordered by subset inclusion.

Proof

PosRep translates morphisms in $\mathbf{Rel}$ into order preserving maps among partially ordered sets. Specifically, the morphism $(X,Y,R) \rightarrow (X',Y',R')$ implemented by $f:X\rightarrow X'$ and $g:Y \rightarrow Y'$ is transformed into the function that takes $A\in PosRep(X,Y,R)$ to f(A). By definition there is a $y\in Y$ such that $(x,y)\in R$ for every $x\in A$. Therefore, $(f(x),g(y))\in R'$ by construction. Since each $x' \in f(A)$ is given by $x'=f(x)$ for some x, this means that $(x',g(y))\in R'$ for all $x \in f(A)$. Thus, $f(A) \in PosRep(X',Y',R')$. Furthermore, the order relation among subsets is evidently preserved.

The same argument from the proof of Theorem 3 can be used mutatis mutandis to show that PosRep is a covariant functor, namely that composition of morphisms is preserved in order. $\square$

Proposition 5

The composition of the Dowker functor $D : \mathbf{Rel} \rightarrow \mathbf{Asc}$ with the face partial order functor $Face : \mathbf{Asc} \rightarrow \mathbf{Pos}$ yields the PosRep functor.

In brief, the diagram

of functors commutes.

Proof

To establish this result, we merely need to observe that the set of elements of $(Face \circ D)(X,Y,R)$ is the same set as PosRep(X, Y, R), with the same order relation (subset inclusion). Under that identification, the morphisms are the same, too. $\square$

Fig. 6

The order preserving map induced by the $\mathbf{Rel}$ morphism (f, g) in Example 6 via the PosRep functor. See Example 8

Example 8

Continuing Examples 6 and 7, the order preserving map induced by the $\mathbf{Rel}$ morphism (f, g) is a bit tedious to construct from the data in Example 6, as shown in Fig. 6. It is much more convenient to work from the simplicial map shown in Fig. 5. Simply note that the only two nontrivial actions to be captured are related to the collapse of the simplices [b, c, d] and [c, d, e]. All of the faces of [c, d, e] are mapped to [C], while the remaining two edges of [b, c, d] (those that are not also faces of [c, d, e]) are mapped to [B, C].

5 Functoriality of (co)sheaves on Dowker complexes

The Dowker functor $D: \mathbf{Rel} \rightarrow \mathbf{Asc}$ is not faithful: non-isomorphic relations can have the same Dowker complex. The weighting functions distinguish between $\mathbf{Rel}$ isomorphism classes. $\mathbf{Rel}$ morphisms sometimes induce transformations between weighting functions, for instance if the morphism transforms only the rows, or if the morphism permutes columns. However, this does not always occur. For instance, if the columns of one relation are included into another while simultaneously the rows are combined, the resulting transformation on the weighting functions is not described in a convenient way. We really need a richer category for weighted Dowker complexes; this is found in the categories of cosheaves or of sheaves. Specifically, each relation can be rendered as a cosheaf of sets, whose costalk cardinality is the total weight function on the Dowker complex. Alternatively, a relation can be transformed into a sheaf of vector spaces, whose stalk dimensions specify a total weight function on the Dowker complex.

For convenience, let us begin by defining

$$\begin{aligned} Y_\sigma = \{y\in Y : (x,y) \in R\text { for all }x\in \sigma \} \end{aligned}$$

for a simplex $\sigma$ of D(X, Y, R). The total weight function is simply the cardinality of this set: $t(\sigma ) = \# Y_\sigma$.

Lemma 2

If $\sigma \subseteq \tau$ are two simplices of D(X, Y, R), then $Y_\tau \subseteq Y_\sigma$.

Proof

Suppose $y \in Y_\tau$, so that $(x,y) \in R$ for all $x\in \tau$. Since $\sigma \subseteq \tau$, it follows that $(x,y) \in R$ for all $x\in \sigma$. Thus $y\in Y_\sigma$. $\square$

Lemma 3

For each simplex $\sigma$ of $D(X_1,Y_1,R_1)$, and each $\mathbf{Rel}$ morphism $(f,g) : (X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_2)$,

$$\begin{aligned} g\left( \left( Y_1\right) _\sigma \right) \subseteq \left( Y_2\right) _{f(\sigma )}. \end{aligned}$$

Proof

Suppose $z \in g\left( \left( Y_1\right) _\sigma \right)$, which means that $z = g(y)$ for some $y \in Y_1$ that satisfies $(x,y) \in R_1$ for all $x \in \sigma$. Since (f, g) is a $\mathbf{Rel}$ morphism, this means that $(f(x),g(y))=(f(x),z) \in R_2$ for all $x \in \sigma$ as well. Therefore, $z \in \left( Y_2\right) _{f(\sigma )}$. $\square$

Corollary 1

As a result of Lemmas 2 and 3, the diagram

commutes when (f, g) is a $\mathbf{Rel}$ morphism.

Although the total and differential weight functions are complete isomorphism invariants for $\mathbf{Rel}$, they are not functorial. To remedy this deficiency, these weights can be thought of as summaries of a somewhat more sophisticated object: a cosheaf or a sheaf.

Definition 7

Bacławski (1975) A cosheaf of sets $\mathfrak {C}$ on a partial order $(X,\le )$ consists of the following specification:

• For each $x \in X$, a set $\mathfrak {C}(x)$, called the costalk at x, and

• For each $x \le y \in X$, a function $\left( \mathfrak {C}(x \le y)\right) : \mathfrak {C}(y) \rightarrow \mathfrak {C}(x)$, called the extension along $x \le y$, such that

• Whenever $x \le y \le z \in X$, $\mathfrak {C}(x \le z) = \left( \mathfrak {C}(x \le y)\right) \circ \left( \mathfrak {C}(y \le z)\right)$.

Briefly, a cosheaf is a contravariant functor to the category $\mathbf{Set}$ from the category generated by $(X,\le )$, whose objects are elements of X and whose morphisms $x \rightarrow y$ correspond to ordered pairs $x \le y$.

Dually, a sheaf of sets $\mathcal {S}$ on a partial order $(X,\le )$ consists of the following specification:

• For each $x \in X$, a set $\mathcal {S}(x)$, called the stalk at x, and

• For each $x \le y \in X$, a function $\left( \mathcal {S}(x \le y)\right) : \mathcal {S}(x) \rightarrow \mathcal {S}(y)$, called the restriction along $x \le y$, such that

• Whenever $x \le y \le z \in X$, $\mathcal {S}(x \le z) = \left( \mathcal {S}(y \le z)\right) \circ \left( \mathcal {S}(x \le y)\right)$.

In this way, a sheaf is covariant functor to $\mathbf{Set}$ from the category generated by the partially ordered set $(X,\le )$.

Given that every abstract simplicial complex X corresponds to a partially ordered set $(X,\subseteq )$ via the face partial order $Face : \mathbf{Asc} \rightarrow \mathbf{Pos}$, we will often use (co)sheaves on an abstract simplicial complex as a shorthand for (co)sheaves on the face partial order of an abstract simplicial complex.

This definition of a (co)sheaf is traditionally that of a pre(co)sheaf on a topological space. The connection is that a (co)sheaf of sets of a partially ordered set is a minimal specification for a (co)sheaf on the partial order with the Alexandrov topology, via the process of (co)sheafification (Curry 2013, 2019). Definition 7 is unambiguous in the context of this article, since we only consider (co)sheaves on partially ordered sets.

Definition 8

We can use the information in a relation (X, Y, R) to define a cosheaf $\mathfrak {R}^0$ on the face partial order¹ of D(X, Y, R) by

Costalks:

Each costalk is given by $\mathfrak {R}^0(\sigma ) = Y_\sigma$, and

Extensions:

If $\sigma \subseteq \tau$ in D(X, Y, R), then the extension $\mathfrak {R}^0(\sigma \subseteq \tau ): \mathfrak {R}^0(\tau ) \rightarrow \mathfrak {R}^0(\sigma )$ is the inclusion $Y_\tau \subseteq Y_\sigma$.

In a dual way, we can also define a sheaf $\mathcal {R}^0$ by:

Stalks:

Each stalk is given by $\mathcal {R}^0(\sigma ) = {{\,\mathrm{span}\,}}Y_\sigma$, and

Restrictions:

If $\sigma \subseteq \tau$ in D(X, Y, R), then the restriction $\mathcal {R}^0(\sigma \subseteq \tau ): \mathcal {R}^0(\sigma ) \rightarrow \mathcal {R}^0(\tau )$ is defined to be the projection induced by the inclusion $Y_\tau \subseteq Y_\sigma$.

Notice that the basis for each stalk of $\mathcal {R}^0$ is the corresponding costalk of $\mathfrak {R}^0$.

Corollary 2

For the cosheaf $\mathfrak {R}^0$ or sheaf $\mathcal {R}^0$ constructed from a relation R as above,

$$\begin{aligned} t(\sigma ) = \# \mathfrak {R}^0(\sigma ) = \dim \mathcal {R}^0(\sigma ), \end{aligned}$$

and

$$\begin{aligned} d(\sigma ) = \# \mathfrak {R}^0(\sigma ) - \# \bigcup _{\sigma \subsetneqq \tau } \mathfrak {R}^0(\tau ) = \dim \mathcal {R}^0(\sigma ) - \dim {{\,\mathrm{span}\,}}_{\sigma \subsetneqq \tau } \mathcal {R}^0(\tau ). \end{aligned}$$

The interpretation is that the total weight t computes how many columns of r start at $\sigma$, while the differential weight d counts columns of r that are related to the elements of $\sigma$ and no others.

The main use of (co)sheaf theory is to formalize the notion of local and global consistency over some space, by way of identifying the data that are consistent with respect to the (co)sheaf. These data are captured within global (co)sections.

Definition 9

For a cosheaf $\mathfrak {C}$ on a partially ordered set $(X,\le )$, consider the disjoint union of all costalks

$$\begin{aligned} \bigsqcup _{x\in X} \mathfrak {C}(x). \end{aligned}$$

Let $\sim$ be the equivalence relation on this disjoint union generated by $c_x \sim c_y$ whenever there exists an $x \le y$ in X that satisfies

• (1) $c_x \in \mathfrak {C}(x)$ and

• (2) $c_y \in \mathfrak {C}(y)$, such that

• (3) $c_x = \left( \mathfrak {C}(x \le y)\right) (c_y)$.

The set of global cosections $\mathfrak {C}(X)$ of the cosheaf $\mathfrak {C}$ is given by the set of equivalence classes

$$\begin{aligned} \mathfrak {C}(X) = \left( \bigsqcup _{x\in X} \mathfrak {C}(x)\right) / \sim . \end{aligned}$$

Each element of $\mathfrak {C}(X)$ is called a (global) cosection of $\mathfrak {C}$.

Dually, the set of global sections of a sheaf $\mathcal {S}$ a on partially ordered set $(X,\le )$ is denoted by $\mathcal {S}(X)$ and is given by the subset

$$\begin{aligned} \mathcal {S}(X) = \left\{ s \in \prod _{x\in X} \mathcal {S}(x) : s_y = \left( \mathcal {S}(x \le y)\right) (s_x) \right\} . \end{aligned}$$

Each element of $\mathcal {S}(X)$ is called a (global) section of $\mathcal {S}$.

Example 9

Recall the relation $R_2$ between $X=\{a,b,c,d\}$ and $Y=\{1,2,3,4,5,6\}$ from Example 2, which was given by the matrix

$$\begin{aligned} r_2 = \begin{pmatrix} 1&{}0&{}1&{}0&{}0&{}1\\ 1&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}0&{}1&{}0\\ \end{pmatrix}. \end{aligned}$$

Using the partial order constructed for this relation in Example 5, the cosheaf $\mathfrak {R}^0$ for the relation has the diagram

where the numbers specify elements of Y (also column indices of $r_2$). According to Definition 9, the set of global cosections of this cosheaf is precisely

$$\begin{aligned} \mathfrak {R}^0(X)= & {} \left( \bigsqcup _{\sigma \in D(X,Y,R_2)} \mathfrak {R}^0(\sigma ) \right) / \sim \\= & {} \left( \mathfrak {R}^0([a,c,d]) \sqcup \right. \\&\mathfrak {R}^0([a,b]) \sqcup \mathfrak {R}^0([b,c]) \sqcup \mathfrak {R}^0([a,c]) \sqcup \mathfrak {R}^0([a,d]) \sqcup \mathfrak {R}^0([c,d]) \sqcup \\&\left. \mathfrak {R}^0([b]) \sqcup \mathfrak {R}^0([a]) \sqcup \mathfrak {R}^0([c]) \sqcup \mathfrak {R}^0([d]) \right) / \sim \\= & {} \left( \{3\} \sqcup \right. \\&\{1\} \sqcup \{2\} \sqcup \{3,6\} \sqcup \{3\} \sqcup \{3\}\sqcup \\&\left. \{1,2\} \sqcup \{1,3,6\} \sqcup \{2,3,4,6\} \sqcup \{3,5\}\right) / \sim \\= & {} \left( \{3,1,2,3,6,3,3,1,2,1,3,6,2,3,4,6,3,5\} \right) / \sim \\= & {} \{1,2,3,4,5,6\}, \end{aligned}$$

where the last step follows since the extension maps are all inclusions. The equivalence classes involved merely identify equal elements of Y (column indices) in the the disjoint union. Each global cosection of $\mathfrak {R}^0$ therefore corresponds to an element of Y (equivalently, a column of $r_2$).

The costalk cardinalities in the above diagram agree exactly with the total weight t shown in Fig. 2. Furthermore, the nonzero differential weights are

$$\begin{aligned} d([a,c,d])= & {} \# \mathfrak {R}^0([a,c,d]) = 1,\\ d([a,b])= & {} \# \mathfrak {R}^0([a,b]) = 1,\\ d([a,c])= & {} \#\mathfrak {R}^0([a,c]) - \#\mathfrak {R}^0([a,c,d]) = 2 - 1 = 1,\\ d([c])= & {} \#\mathfrak {R}^0([c]) - \# \left( \mathfrak {R}^0([a,c,d]) \cup \mathfrak {R}^0([a,c]) \cup \mathfrak {R}^0([b,c]) \cup \mathfrak {R}^0([c,d]) \right) \\= & {} 4 - \#\{2, 3,6\} = 4 - 3 = 1, \text { and } \\ d([d])= & {} \#\mathfrak {R}^0([c]) - \# \left( \mathfrak {R}^0([a,c,d]) \cup \mathfrak {R}^0([a,d]) \cup \mathfrak {R}^0([c,d]) \right) \\= & {} 2 - \#\{ 3 \} = 2 - 1 = 1. \end{aligned}$$

By contrast, the sheaf is given by the diagram

We can interpret each global section of this sheaf as a formal linear combination of elements of Y, or a formal linear combination of columns of $r_2$.

To render cosheaves and sheaves into their own categories $\mathbf{CoShv}$ and $\mathbf{Shv}$, respectively, we need to define morphisms. Typical definitions (for instance, (Curry 2013, Def. 4.1.10)) require the construction of morphisms between cosheaves or sheaves on the same partial order, but it is important to be a bit more general in our situation.

Definition 10

(Robinson (2014) or (Bredon 1997, Sect. I.4)) Suppose that $\mathfrak {R}$ is a cosheaf on a partially ordered set $(X,\le _X)$ and that $\mathfrak {S}$ is a cosheaf on a partially ordered set $(Y,\le _Y)$. A cosheaf morphism $m: \mathfrak {R} \rightarrow \mathfrak {S}$ along an order preserving base map

$$\begin{aligned} f: (X,\le _X) \rightarrow (Y,\le _Y) \end{aligned}$$

consists of a set of component functions $m_x: \mathfrak {R}(x) \rightarrow \mathfrak {S}(f(x))$ for each $x \in X$ such that the following diagram commutes

Dually, suppose that $\mathcal {R}$ is a sheaf on a partially ordered set $(X,\le _X)$ and that $\mathcal {S}$ is a sheaf on a partially ordered set $(Y,\le _Y)$. A sheaf morphism $m: \mathcal {S}\rightarrow \mathcal {R}$ along an order preserving base map $f: (X,\le _X) \rightarrow (Y,\le _Y)$ (careful: m and f go in opposite directions!) consists of a set of component functions $m_x: \mathcal {S}(f(x)) \rightarrow \mathcal {R}(x)$ for each $x \in X$ such that the following diagram commutes

for each $x \le _X y$.

The category of cosheaves $\mathbf{CoShv}$ (or category of sheaves $\mathbf{Shv}$) consists of all cosheaves (or sheaves) on partially ordered sets as the class of objects, with cosheaf morphisms (or sheaf morphisms) as the class of morphisms. Composition of morphisms in both cases is accomplished by simply composing the base map and component functions.

Lemma 4

The transformation of a cosheaf to its underlying partial order is a covariant functor $Base : \mathbf{CoShv} \rightarrow \mathbf{Pos}$. Likewise, the transformation of a sheaf to its underlying partial order is a contravariant functor $Base'$.

Proof

Both of these statements follow immediately from the definition. $\square$

Lemma 5

The transformation of cosheaves to global cosections is a covariant functor $\Gamma : \mathbf{CoShv} \rightarrow \mathbf{Set}$. Specifically, every cosheaf morphism $p: \mathfrak {R} \rightarrow \mathfrak {S}$ induces a function on global cosections.

Proof

Suppose that $p: \mathfrak {R} \rightarrow \mathfrak {S}$ and $q: \mathfrak {S} \rightarrow \mathfrak {T}$ are cosheaf morphisms along order preserving base maps $f: (X,\le _X) \rightarrow (Y,\le _Y)$ and $g:(Y,\le _Y) \rightarrow (Z,\le _Z)$. Let us use these data to define a function $p_* : \mathfrak {R}(X) \rightarrow \mathfrak {S}(Y)$ (and a function $q_* : \mathfrak {S}(Y) \rightarrow \mathfrak {T}(Z)$ by the same construction) such that $(q_* \circ p_*) = (q \circ p)_*$. To that end, consider a cosection c of $\mathfrak {R}$. This is an element of

$$\begin{aligned} \left( \bigsqcup _{x\in X} \mathfrak {R}(x)\right) / \sim . \end{aligned}$$

Because of this, $c_x \in \mathfrak {R}(x)$ for some $x\in X$. Define

$$\begin{aligned} p_*(c) = p_x(c_x). \end{aligned}$$

To verify that this is well-defined, suppose that $c_{x'} \in \mathfrak {R}(x')$ for some other $x' \in X$. Under the equivalence relation $\sim$, the only way $c_{x'} \sim c_x$ can happen is if $x \le x'$ or $x' \le x$. But since c is a cosection, it happens that if $x' \le x$,

$$\begin{aligned} \left( \mathfrak {R}(x' \le x)\right) (c_x) = c_{x'}. \end{aligned}$$

Since p is a cosheaf morphism, this means that

$$\begin{aligned} p_{x'}(c_{x'})= & {} \left( p_{x'} \circ \left( \mathfrak {R}(x' \le x)\right) \right) (c_x))\\= & {} \left( \mathfrak {S}(f(x') \le f(x)) \circ p_x \right) (c_x),\\= & {} \left( \mathfrak {S}(f(x') \le f(x))\right) \left( p_x (c_x) \right) , \end{aligned}$$

which implies that $p_{x'}(c_{x'}) \sim p_x(c_x)$ in $\mathfrak {S}(X)$. On the other hand, if $x \le x'$

$$\begin{aligned} \left( \mathfrak {R}(x \le x')\right) (c_{x'}) = c_x. \end{aligned}$$

Since p is a cosheaf morphism, this means that

$$\begin{aligned} p_x(c_x)= & {} \left( p_x \circ \left( \mathfrak {R}(x \le x')\right) \right) (c_{x'})\\= & {} \left( \left( \mathfrak {S}(f(x) \le f(x'))\right) \circ p_{x'} \right) (c_{x'}), \end{aligned}$$

which also implies that $p_{x'}(c_{x'}) \sim p_x(c_x)$ in $\mathfrak {S}(X)$. Thus, $p_*(c)$ is a well-defined global cosection of $\mathfrak {S}$.

Repeating this construction with q, notice that

$$\begin{aligned} (q \circ p)_*(c)= & {} (q \circ p)_x (c) \\= & {} (q_x \circ p_x)(c)\\= & {} (q_* \circ p_*)(c), \end{aligned}$$

which establishes covariance. $\square$

Theorem 4

The transformation $(X,Y,R) \mapsto \mathfrak {R}^0$ given in Definition 8 is a covariant functor $CoShvRep^0: \mathbf{Rel} \rightarrow \mathbf{CoShv}$. In particular, each $\mathbf{Rel}$ morphism induces a cosheaf morphism. Furthermore, if the domain is restricted to $\mathbf{Rel_+}$, the functor becomes faithful. (Recall Definition 6: $\mathbf{Rel_+}$ is the full subcategory of $\mathbf{Rel}$ in which every relation has a matrix in which there are no zero rows nor zero columns.)

Proof

Suppose that $(f_1,g_1) : (X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_2)$ and $(f_2,g_2) : (X_2,Y_2,R_2) \rightarrow (X_3,Y_3,R_3)$ are two $\mathbf{Rel}$ morphisms. Suppose that $\mathfrak {R}_1^0$ is the cosheaf associated to $(X_1,Y_1,R_1)$ according to the recipe given in Definition 8, and likewise $\mathfrak {R}_2^0$ and $\mathfrak {R}_3^0$ are the cosheaves associated to $(X_2,Y_2,R_2)$ and $(X_3,Y_3,R_3)$, respectively. We first show how to construct a cosheaf morphism $m_1: \mathfrak {R}_1^0 \rightarrow \mathfrak {R}_2^0$.

Recognizing that the cosheaves $\mathfrak {R}_1^0$ and $\mathfrak {R}_2^0$ are defined on the simplices of $D(X_1,Y_1,R_1)$ and $D(X_2,Y_2,R_2)$, recall that Theorem 3 implies that $D(f_1)$ is a simplicial map $D(X_1,Y_1,R_1)\rightarrow D(X_2,Y_2,R_2)$, and that Propositions 4 and 5 imply that this can be interpreted as an order preserving function. This is the order preserving base map along which $m_1$ is defined.

Suppose that $\sigma \subseteq \tau$ in $D(X_1,Y_1,R_1)$. As far as vertices are concerned, the diagram

commutes. Corollary 1 therefore states that

commutes. We therefore merely need to realize that according to Definition 8, this is equal to the diagram

which establishes that $m_1$ is a cosheaf morphism, with $m_\sigma = g|_{(Y_1)_\sigma }$ as components. Given that $m_2 : \mathfrak {R}_2^0 \rightarrow \mathfrak {R}_3^0$ can be constructed in the same way, the composition $(f_2,g_2)\circ (f_1,g_1)$ of $\mathbf{Rel}$ morphisms induces the composition of component functions, which is precisely the composition $m_2 \circ m_1$ of cosheaf morphisms.

To show that this functor is faithful when restricted to objects in $\mathbf{Rel_+}$, a rather direct argument suffices. Suppose that (f, g) and $(f',g')$ are two $\mathbf{Rel}$ morphisms $(X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_2)$ in which $(X_1,Y_1,R_1)$ is an object of $\mathbf{Rel_+}$. Recall that the latter constraint means that for every $x \in X_1$, there is a $y \in Y_1$ such that $(x,y) \in R_1$, and conversely for every $y \in Y_1$, there is an $x \in X_1$ such that $(x,y) \in R_1$. To establish faithfulness, let us suppose additionally that (f, g) and $(f',g')$ induce the same cosheaf morphism $m:\mathfrak {R}_1^0 \rightarrow \mathfrak {R}_2^0$.

Let $y \in Y_1$ be given. By assumption, there is an $x \in X_1$ such that $(x,y) \in R_1$, so there is also a simplex $\sigma$ (usually several simplices, actually) for which $y \in Y_\sigma$. But, since both (f, g) and $(f',g')$ both induce the same cosheaf morphism m, this means that

$$\begin{aligned} g(y) = g|_{(Y_1)_\sigma }(y) = m_\sigma (y) = g'|_{(Y_1)_\sigma }(y) = g'(y). \end{aligned}$$

Hence $g=g'$.

Now let $x \in X_1$ be given. By assumption, there is a $y \in Y_1$ such that $(x,y) \in R_1$, so this means that [x] is a simplex of $D(X_1,Y_1,R_1)$. Since both (f, g) and $(f',g')$ induce the same cosheaf morphism m, this means that both (f, g) and $(f',g')$ induce the same order preserving map on simplices of $D(X_1,Y_1,R_1) \rightarrow D(X_2,Y_2,R_2)$. When restricted to vertices, this map is simply f or $f'$, respectively, so they must also be equal. $\square$

Example 10

Consider again the relation $R_1$ between the sets $X_1=\{a,b,c,d,e\}$ and $Y_1=\{1,2,3,4,5\}$, given by the matrix

$$\begin{aligned} r_1 = \begin{pmatrix} 1&{}1&{}0&{}0&{}0\\ 1&{}0&{}1&{}0&{}0\\ 0&{}1&{}1&{}1&{}1\\ 0&{}0&{}1&{}1&{}0\\ 0&{}0&{}0&{}1&{}1\\ \end{pmatrix}, \end{aligned}$$

from Example 6. However, this time let us consider a different morphism. Define the relation $R_4$ between $X_4=\{A,B,C\}$ and $Y_4 =\{1,2,3\}$ given by

$$\begin{aligned} r_4 = \begin{pmatrix} 1&{}1&{}0\\ 1&{}0&{}1\\ 0&{}1&{}1\\ \end{pmatrix}. \end{aligned}$$

The function $f: X_1 \rightarrow X_4$ given by

$$\begin{aligned} f(a) = A,\; f(b) = B,\; f(c) = C,\; f(d) = C,\; f(e) = C, \end{aligned}$$

and the function $g: Y_1 \rightarrow Y_2$ given by

$$\begin{aligned} g(1) = 1,\; g(2) = 2,\; g(3) = 3,\; g(4) = 3,\; g(5) = 3 \end{aligned}$$

together define a $\mathbf{Rel}$ morphism $(X_1,Y_1,R_1) \rightarrow (X_4,Y_4,R_4)$.

This relation morphism clearly maps each column of $r_1$ to a column of $r_4$, so it also acts on the costalks of the cosheaf representations. If we define $\mathfrak {A} = CoShvRep^0(X_1,Y_1,R_1)$ and $\mathfrak {B} = CoShvRep^0(X_4,Y_4,R_4)$, the resulting cosheaf morphism $\mathfrak {A} \rightarrow \mathfrak {B}$ is given by the diagram shown in Fig. 7. Notice that each dashed arrow represents a component map of the cosheaf morphism, and is given by restricting the domain of g to each costalk, since this is how the columns are transformed.

Fig. 7

The cosheaf morphism induced by the $\mathbf{Rel}$ morphism (f, g) in Example 10 via the $CoShvRep^0$ functor

Theorem 5

The transformation $R \mapsto \mathcal {R}^0$ given in Definition 8 is a contravariant functor $ShvRep^0:\mathbf{Rel} \rightarrow \mathbf{Shv}$. When restricted to $\mathbf{Rel_+} \rightarrow \mathbf{Shv}$, the functor becomes faithful.

The proof of this Theorem starts out exactly dual to that of the proof of Theorem 4, but then diverges due to differences in the algebraic structure of the stalks. The argument from that point looks different, but is actually the same (modulo a transpose, which is the duality) when restricted to basis elements of the stalk.

Proof

Suppose that $(f_1,g_1) : (X_1,Y_1,R_1) \rightarrow (X_2,Y_2,R_2)$ and $(f_2,g_2) : (X_2,Y_2,R_2) \rightarrow (X_3,Y_3,R_3)$ are two $\mathbf{Rel}$ morphisms. Suppose that $\mathcal {R}_1^0$ is the sheaf associated to $(X_1,Y_1,R_1)$ according to the recipe from Definition 8, and likewise $\mathcal {R}_2^0$ and $\mathcal {R}_3^0$ are the sheaves associated to $(X_2,Y_2,R_2)$ and $(X_3,Y_3,R_3)$, respectively. We first show how to construct a sheaf morphism $m_1: \mathcal {R}_2^0 \rightarrow \mathcal {R}_1^0$. Given that $m_2 : \mathcal {R}_3^0 \rightarrow \mathcal {R}_2^0$ can be constructed in the same way, we show that the composition $(f_2,g_2)\circ (f_1,g_1)$ of $\mathbf{Rel}$ morphisms induces the composition $m_1 \circ m_2$ of sheaf morphisms.

Recognizing that the sheaves $\mathcal {R}_1^0$ and $\mathcal {R}_2^0$ are defined on the simplices of $D(X_1,Y_1,R_1)$ and $D(X_2,Y_2,R_2)$, recall that Theorem 3 implies that $D(f_1)$ is a simplicial map $D(X_1,Y_1,R_1)\rightarrow D(X_2,Y_2,R_2)$, and that Propositions 4 and 5 imply that this can be interpreted as an order preserving function. This is the order preserving map along which $m_1$ is defined.

The component maps go the other way, and are expansions of the preimage of g. For a simplex $\sigma$ of $D(X_1,Y_1,R_1)$, the $m_{1,\sigma } : \mathcal {R}_2^0(f(\sigma )) \rightarrow \mathcal {R}_1^0(\sigma )$ is given by the formula

$$\begin{aligned} m_{1,\sigma }\left( \sum _{z \in (Y_2)_{f(\sigma )}} a_z z\right) = \sum _{z \in (Y_2)_{f(\sigma )},} \sum _{y \in g^{-1}(z)} a_z y. \end{aligned}$$

To show that this is indeed a sheaf morphism requires showing that it commutes with the restriction maps. This follows from the diagram of Corollary 1, since that diagram explains how the basis vectors transform; the sheaf uses the dual of each map. To show this explicitly, it suffices to show this for a pair of simplices $\sigma \subseteq \tau$ in $D(X_1,Y_1,R_1)$ and for a basis element $z \in (Y_2)_{f(\sigma )}$, because we can extend by linearity,

$$\begin{aligned} \left( \mathcal {R}_1^0(\sigma \subseteq \tau ) \circ m_{1,\sigma }\right) (z)= & {} \left( \mathcal {R}_1^0(\sigma \subseteq \tau )\right) \left( \sum _{y \in g^{-1}(z)} y \right) \\= & {} \sum _{y \in g^{-1}(z)} \left( \mathcal {R}_1^0(\sigma \subseteq \tau )\right) \left( y \right) \\= & {} \sum _{y \in g^{-1}(z)\text { and }y\in (Y_1)_\tau } y. \end{aligned}$$

According to Lemma 3, $y\in (Y_1)_\tau$ implies that $z \in (Y_2)_{f(\tau )}$. Thus we may continue the calculation along the other path

$$\begin{aligned} \left( m_{1,\tau } \circ \mathcal {R}_2^0(f(\sigma ) \subseteq f(\tau ))\right) (z)= & {} m_{1,\tau }(z)\\= & {} \sum _{y \in g^{-1}(z)\text { and }y\in (Y_1)_\tau } y, \end{aligned}$$

establishing commutativity of the diagram

As for composition $(f_2,g_2)\circ (f_1,g_1)$ of $\mathbf{Rel}$ morphisms, suppose that $\sigma$ is a simplex of $D(X_1,Y_1,R_1)$. We compute for $z \in (Y_3)_{f_2(f_1(\sigma ))}$:

$$\begin{aligned} \left( m_{1,\sigma } \circ m_{2,f_1(\sigma )}\right) (z)= & {} m_{1,\sigma } \left( \sum _{y \in g_2^{-1}(z)} y\right) \\= & {} \sum _{w \in g_1^{-1}(y),} \sum _{y \in g_2^{-1}(z)} w\\= & {} \sum _{w \in (g_2\circ g_1)^{-1}(z)} w, \end{aligned}$$

which is precisely what is induced by $(f_2 \circ f_1,g_2 \circ g_1)$.

To show that this a faithful functor when restricted to $\mathbf{Rel_+}$, it suffices to recount the same argument for the cosheaf given in the proof of Theorem 4, making the observation that the components of the cosheaf morphism are simply the functions on the basis elements of the stalks of the sheaf, after a transpose. $\square$

By comparing the proofs of Theorems 4 and 5, one could conclude that the cosheaf $\mathfrak {R}^0$ seems a bit more natural than the sheaf $\mathcal {R}^0$! At least, $\mathfrak {R}^0$ doesn’t entrain any linear algebraic machinery, which may be ancillary to the main point. On the other hand, the sheaf has cohomology, which may be worth exploring. However, at present it is unclear what the cohomology of $\mathcal {R}^0$ might contain.

Example 11

Notice that if we tried to define $\mathfrak {R}^0$ as a sheaf of sets on the opposite face partial order for D(X, Y, R), then sheaf morphisms do not induce maps on global sections correctly. This is not an accident, since any functor $\mathbf{Rel} \rightarrow \mathbf{Shv}$ should compose with the global sections functor $\Gamma :\mathbf{Shv} \rightarrow \mathbf{Set}$ to ensure that $\mathbf{Rel}$ morphisms induce functions on the space of global sections. The reader is reminded that the directions of morphisms in $\mathbf{Shv}$ given in Definition 10 makes $\Gamma$ work properly.

This fails outright for a small example in which $X_1=\{A,B,C\}$, $X_2=\{A\}$, $Y_1=Y_2=\{a,b,c\}$, where $R_1$ and $R_2$ are given by the matrices

$$\begin{aligned} r_1 = \begin{pmatrix}1&{}0&{}0\\ 0&{}1&{}1 \\ 0&{}0&{}1 \end{pmatrix}\text { and }r_2 = \begin{pmatrix}1&1&1\end{pmatrix}. \end{aligned}$$

Noting that there is only one option to define $f: X_1 \rightarrow X_2$, we define $g = \text {id }_{Y_1}$. This is clearly a relation morphism as every pair $(x,y) \in R_1 \subseteq X_1 \times Y_1$ maps to a pair that are related by $R_2$.

Using the reverse partial order, the sheaf diagram of basis elements for $(X_1,Y_1,R_1)$ is

while the sheaf diagram for basis elements of $(X_2,Y_2,R_2)$ has only one element $\{a,b,c\}$. (Both of these are identical to the cosheaf diagrams, since the unions in the Alexandrov topology are not shown). There is only one global section of the first sheaf, which consists of choosing a for the leftmost simplex, and c for the three elements on the right. However, this cannot obviously be mapped to a global section of the second sheaf, since that needs to be a single element of $\{a,b,c\}$. Conversely, if we consider a global section of the second sheaf as being any one of its elements, this cannot correspond to a global section of the first sheaf.

Corollary 3

The composition of $CoShvRep^0: \mathbf{Rel} \rightarrow \mathbf{CoShv}$ with the functor $Base: \mathbf{CoShv} \rightarrow \mathbf{Pos}$ that forgets the structure of the costalks is $PosRep : \mathbf{Rel} \rightarrow \mathbf{Pos}$. This also works for the composition $(Base' \circ ShvRep^0): \mathbf{Rel} \rightarrow \mathbf{Shv} \rightarrow \mathbf{Pos}$. Briefly,

$$\begin{aligned} PosRep = Base \circ CoShvRep^0 = Base' \circ ShvRep^0. \end{aligned}$$

Notice that in the case of sheaves on partial orders, both functors – $Base'$ (Lemma 4) and $ShvRep^0$ (Theorem 5)—are contravariant. Therefore, their composition is a covariant functor, which aligns with the covariance of PosRep (Proposition 4).

6 Duality of cosheaf representations of relations

The most striking fact proven in Dowker’s original paper (Dowker 1952) is that the homology of the Dowker complex is the same whether it is produced by the relation or by its transpose. Dowker provides a direct, if elaborate, construction of a map inducing isomorphisms on homology. This construction was later enhanced to a homotopy equivalence by Björner (1995). More recently, Chowdhury and Mémoli (2018) showed that the homotopy equivalence between these two complexes is functorial in a particular way. This section shows that the duality is also visible in a somewhat different way: one Dowker complex is the base space of a particular cosheaf, while the other is its space of global cosections.

Let us begin by connecting the relation to its transpose.

Definition 11

If (X, Y, R) is a relation, then its transpose is a relation $(Y,X,R^T)$ given by $(y,x) \in R^T$ if and only if $(x,y) \in R$.

Evidently, the matrix for the transpose of a relation is simply the transpose of the original matrix.

Lemma 6

The transformation $(X,Y,R) \mapsto (Y,X,R^T)$ defines a fully faithful covariant functor $Transp:\mathbf{Rel} \rightarrow \mathbf{Rel}$.

Proof

Every $\mathbf{Rel}$ morphism $(f,g) : (X,Y,R) \rightarrow (X',Y',R')$ is transformed to $(g,f) : (Y,X,R^T) \rightarrow (Y',X',(R')^T)$. Composition is still composition of functions and is preserved in order. $\square$

Example 12

Recall the relation $R_2$ between $X_2=\{a,b,c,d\}$ and $Y_2=\{1,2,3,4,5,6\}$ from Example 2, which was given by the matrix

$$\begin{aligned} r_2 = \begin{pmatrix} 1&{}0&{}1&{}0&{}0&{}1\\ 1&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}0&{}1&{}0\\ \end{pmatrix}. \end{aligned}$$

The transpose of this relation has the matrix

$$\begin{aligned} r_2^T = \begin{pmatrix} 1&{}1&{}0&{}0\\ 0&{}1&{}1&{}0\\ 1&{}0&{}1&{}1\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\\ 1&{}0&{}1&{}0\\ \end{pmatrix}. \end{aligned}$$

Their Dowker complexes are shown in Fig. 8. Clearly these complexes have the same homotopy type!

Fig. 8

The Dowker complex for a relation $R_2$ and its transpose given in Example 12

Definition 12

The category $\mathbf{CoShvAsc}$ consists of the full subcategory of $\mathbf{CoShv}$ whose objects are cosheaves on abstract simplicial complexes of abstract simplicial complexes, and whose extensions are simplicial inclusions. Briefly, an object of $\mathbf{CoShvAsc}$ is a contravariant functor $\mathfrak {C}$ from the face partial order of an abstract simplicial complex to $\mathbf{Asc}$, with the additional condition that each extension $\mathfrak {C}(\sigma \subseteq \tau ) : \mathfrak {C}(\tau ) \rightarrow \mathfrak {C}(\sigma )$ is a simplicial map whose vertex function is an inclusion.

The reader is reminded that contravariant functors from the face partial order are covariant with respect to the Alexandrov topology; this is sometimes helpful in remembering why objects in $\mathbf{CoShvAsc}$ are cosheaves.

Definition 13

The cosheaf representation of a relation (X, Y, R) is a cosheaf $\mathfrak {R}=CoShvRep(X,Y,R)$ of abstract simplicial complexes, defined by the following recipe:

Costalks:

If $\sigma$ is a simplex of D(X, Y, R), then $\mathfrak {R}(\sigma ) = D\left( Y_\sigma ,\sigma ,(R|_{\sigma ,Y_\sigma })^T\right)$,

Extensions:

If $\sigma \subseteq \tau$ are two simplices of D(X, Y, R), then the extension $\mathfrak {R}(\sigma \subseteq \tau ) : \mathfrak {R}(\tau ) \rightarrow \mathfrak {R}(\sigma )$ is the simplicial map along the inclusion $Y_\tau \hookrightarrow Y_\sigma$.

The cosheaf $\mathfrak {R}^0 = CoShvRep^0(X,Y,R)$ for a relation (X, Y, R) defined in Sect. 5 is a sub-cosheaf of $\mathfrak {R}=CoShvRep(X,Y,R)$. Evidently, $\mathfrak {R}$ is an object of $\mathbf{CoShvAsc}$.

Lemma 7

For any simplex $\tau$ of D(X, Y, R), the costalk $\mathfrak {R}(\tau ) = D\left( Y_\tau ,\tau ,(R|_{\tau ,Y_\tau })^T\right)$ is always a complete simplex on the vertex set $Y_\tau$.

Proof

Every subset $\{y_0,y_1, \dotsc , y_n\}$ consisting of elements $y_i$ of $Y_\tau$ is a simplex of $D\left( Y_\tau ,\tau ,(R|_{\tau ,Y_\tau })^T\right)$, since that merely requires there to be at least one $x \in \tau$ to exist such that $(x,y_i) \in R$ for all i. $\square$

Lemma 8

The extensions defined for the cosheaf $\mathfrak {R}$ for a relation (X, Y, R) in Definition 13 are well-defined simplicial maps.

Proof

Suppose that $\sigma \subseteq \tau$ are two simplices of D(X, Y, R). Lemma 7 establishes that both $\mathfrak {R}(\sigma )$ and $\mathfrak {R}(\tau )$ are complete simplices. Accordingly, consider the subset $\{y_0,y_1, \dotsc , y_n\}$ consisting of elements $y_i$ of $Y_\tau$. Notice that by the definition of $Y_\tau$, for every $x \in \tau$ and every i, it follows that $(x,y_i) \in R$. Therefore, since $\sigma \subseteq \tau$, this condition also holds for every $x \in \sigma$. Thus, every simplex of $D\left( Y_\tau ,\tau ,(R|_{\tau ,Y_\tau })^T\right)$ is also a simplex of $D\left( Y_\sigma ,\sigma ,(R|_{\sigma ,Y_\sigma })^T\right)$ whenever $\sigma \subseteq \tau$. $\square$

Lemmas 7 and 8 together imply that Theorem 4 extends immediately to a functoriality result for $\mathfrak {R}$.

Corollary 4

The transformation $(X,Y,R) \mapsto \mathfrak {R}$ is a covariant functor $CoShvRep: \mathbf{Rel} \rightarrow \mathbf{CoShvAsc}$. If we restrict to $\mathbf{Rel_+} \rightarrow \mathbf{CoShvAsc}$, this becomes a faithful covariant functor.

The structure of the space of global cosections for cosheaves constructed by the CoShvRep functor is rather special, as the next result shows.

Proposition 6

Consider the cosheaf $\mathfrak {R} = CoShvRep(X,Y,R)$ for some relation (X, Y, R). Suppose that $\sigma$ and $\tau$ are both simplices of D(X, Y, R). There is a simplex $\mu$ (which may be empty) of D(X, Y, R) such that the following equation holds:

$$\begin{aligned} \mathfrak {R}(\mu ) = \mathfrak {R} (\sigma ) \cap \mathfrak {R}(\tau ). \end{aligned}$$

(1)

Consequently, the space of global cosections of $\mathfrak {R}$ can be computed by taking the (non-disjoint) union of all costalks.

Proof

According to Lemma 7, we have that $\mathfrak {R}(\sigma )$ is the complete simplex on the vertex set

$$\begin{aligned} Y_\sigma = \{y \in Y : (x,y) \in R \text { for all }x \in \sigma \} \end{aligned}$$

and $\mathfrak {R}(\tau )$ is the complete simplex on the vertex set

$$\begin{aligned} Y_\tau = \{y \in Y : (x,y) \in R \text { for all }x \in \tau \}. \end{aligned}$$

If $Y_\sigma \cap Y_\tau$ is the empty set, then consequently $\mathfrak {R} (\sigma ) \cap \mathfrak {R}(\tau ) = \mathfrak {R}(\emptyset ) = \emptyset$. Therefore, let us assume that $Y_\sigma \cap Y_\tau$ is nonempty. Evidently

$$\begin{aligned} Y_\sigma \cap Y_\tau= & {} \{y \in Y : (x,y) \in R \text { for all }x \in \sigma \} \cap \{y \in Y : (x,y) \in R \text { for all }x \in \tau \} \\= & {} \{y \in Y : (x,y) \in R\text { for all }x \in \sigma \text { and for all }x' \in \tau \}\\= & {} \{y \in Y : (x,y) \in R\text { for all }x \in \sigma \cup \tau \}. \end{aligned}$$

However, since we assumed that $Y_\sigma \cap Y_\tau$ is nonempty, this means that there is a $y \in Y$ such that $(x,y) \in R$ for all $x \in \sigma \cup \tau$. This implies that $\sigma \cup \tau$ is a simplex of D(X, Y, R). If we let $\mu = \sigma \cup \tau$, it’s immediate that $\mathfrak {R}(\mu )$ is the complete simplex on the vertex set $Y_\mu = Y_\sigma \cap Y_\tau$. Therefore the claimed Eq. (1) holds. $\square$

Example 13

Recall the relation $R_2$ between $X_2=\{a,b,c,d\}$ and $Y_2=\{1,2,3,4,5,6\}$ from Example 2, which was given by the matrix

$$\begin{aligned} r_2 = \begin{pmatrix} 1&{}0&{}1&{}0&{}0&{}1\\ 1&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}0&{}1&{}0\\ \end{pmatrix}. \end{aligned}$$

The cosheaf $\mathfrak {R}^0 = CoShvRep^0(X_2,Y_2,R_2)$ was described in Example 9. The diagram for $\mathfrak {R} = CoShvRep(X_2,Y_2,R_2)$ is shown in Fig. 9, which incorporates all of the data from the previous examples into a single figure. Notice that each costalk shown in the diagram is a complete simplex as required by Lemma 7. Let us consider the set $U_1$ formed from the union of the open stars on the vertices b and c. Explicitly, this set is given by

$$\begin{aligned} U_1 = \{[b],[c],[a,b], [a,c], [b,c], [c,d], [a,c,d]\}. \end{aligned}$$

The space of cosections over the set $U_1$ can be computed using Definition 9. Specifically, since $U_1$ is formed from the open stars on b and c, the space of cosections on $U_1$ is a quotient of the disjoint union of $\mathfrak {R}([b])$ and $\mathfrak {R}([b])$ in which vertices are identified whenever they appear in a costalk over a coface of b or c in $D(X_2,Y_2,R_2)$. Using primes to mark the vertices of $\mathfrak {R}([c])$, we can compute this quotient directly

$$\begin{aligned} \left( \mathfrak {R}([b]) \sqcup \mathfrak {R}([c])\right) / \sim= & {} \left( \{[1,2]\} \sqcup \{[2,3,4,6]\}\right) / \sim \\= & {} \{[1,2],[2',3',4',6']\} / \sim \\= & {} \{[1,2],[2,3',4',6']\}, \end{aligned}$$

which is an abstract simplicial complex that is not a complete simplex. It is shown at left in Fig. 10.

Fig. 9

The diagram of the cosheaf $\mathfrak {R}$ defined in Example 13 for the relation $(X_2,Y_2,R_2)$ defined in Example 2

Fig. 10

Some spaces of cosections of the cosheaf $\mathfrak {R}$ defined in Example 13: (left) cosections on the set $U_1$, (right) cosections on the set $U_2$

However, because of Proposition 6, the space of cosections over $U_1$ can be computed as a union, which may be dramatically easier than using Definition 9 directly. Specifically, the space of cosections on $U_1$ is the union

$$\begin{aligned} \mathfrak {R}([b]) \cup \mathfrak {R}([c]) = \{[1,2]\}\cup \{[2,3,4,6]\} = \{[1,2],[2,3,4,6]\}, \end{aligned}$$

which is evidently isomorphic (as simplicial complexes) to what we computed from Definition 9.

Likewise, consider the set $U_2$ formed of the union of the open stars on a and c, namely

$$\begin{aligned} U_2 = \{[a],[c],[a,b],[b,c],[a,c],[a,d],[c,d],[a,c,d]\}. \end{aligned}$$

The space of cosections over the set is shown at right in Fig. 10, which may again be computed easily by Proposition 6.

To obtain the space of global cosections, Definition 9 asks us to consider an open cover of $D(X_2,Y_2,R_2)$, but again Proposition 6 simplifies this task to simply being the union of all costalks. The result is that the space of global cosections is indeed $D(Y_2,X_2,R_2^T)$, as shown in Fig. 8.

Proposition 6 allows us to be rather cavalier when computing the space of global cosections for cosheaves in the image of CoShvRep. Indeed, the reader is cautioned that Proposition 6 does not hold for typical objects in $\mathbf{CoShvAsc}$. One must use Definition 9 to compute the global cosections as usual.

Example 14

As an example of what can go wrong outside the image of CoShvRep in $\mathbf{CoShvAsc}$, consider the cosheaf $\mathfrak {F}$ on the abstract simplicial complex generated by the 1-simplex [a, b], whose costalks are the abstract simplicial complexes

$$\begin{aligned} \mathfrak {F}([a])= & {} \{[1,2],[3],[1],[2],\emptyset \}, \\ \mathfrak {F}([a,b])= & {} \{[2],\emptyset \}, \end{aligned}$$

and

$$\begin{aligned} \mathfrak {F}([b]) = \{[1],[2,3],[2],[3],\emptyset \}, \end{aligned}$$

and whose extensions are given by the obvious inclusions. The space of global cosections is not the union of the simplices involved (namely $\{[1,2],[2,3],[1],[2],[3],\emptyset \}$), as would be suggested by an incautious application of Proposition 6. Notice that the Eq. (1) also does not hold, because there is no simplex with costalk

$$\begin{aligned} \mathfrak {F}([a]) \cap \mathfrak {F}([b]) = \{[1],[2],[3],\emptyset \}. \end{aligned}$$

The correct space of global sections must instead be computed via Definition 9, by forming a disjoint union and then identifying common extensions. Specifically in this case,

$$\begin{aligned} \left( \mathfrak {F}([a]) \sqcup \mathfrak {F}([b])\right) /\sim= & {} \left( \{[1,2],[3],[1],[2],\emptyset ,[1'],[2',3'],[2'],[3'],\emptyset '\}\right) /\sim \\= & {} \{[1,2],[2,3'],[3],[1],[2],[1'],[3'],\emptyset \}. \end{aligned}$$

We are now in a position to characterize the space of global cosections of any cosheaf in the image of CoShvRep.

Theorem 6

The space of global cosections of $\mathfrak {R}=CoShvRep(X,Y,R)$ is simplicially isomorphic to $D(Y,X,R^T)$, the Dowker complex for the transpose.

Proof

Before we begin, notice that the vertices of $D(Y,X,R^T)$ are elements of Y that are related to at least one element of X. These are also elements of the costalks of $\mathfrak {R}$, and since the extensions of $\mathfrak {R}$ are inclusions, we need not worry about conflicting names for elements of Y. Therefore, to establish this result, we simply need to show that every simplex $\sigma \in D(Y,X,R^T)$ appears in at least one costalk of $\mathfrak {R}$, and conversely that every simplex in every costalk of $\mathfrak {R}$ is also a simplex of $D(Y,X,R^T)$.

Suppose that $\sigma =[y_0,y_1,\dotsc ,y_n]$ is a simplex of $D(Y,X,R^T)$. This means that there is an $x \in X$ such that $(x,y_i) \in R$ for all $i=0,\dotsc ,n$. Put another way, every $y_i \in \sigma$ is also an element of $Y_{[x]}$. Therefore, the costalk $\mathfrak {R}([x])$ contains $\sigma$.

Suppose that $\sigma =[y_0,y_1,\dotsc ,y_n]$ is a simplex of $\mathfrak {R}(\tau )$ for some simplex $\tau$ of D(X, Y, R). This means that $\sigma$ is a simplex of $D\left( Y_\tau ,\tau ,(R|_{\tau ,Y_\tau })^T\right)$, by definition. That means that if we select any $x \in \tau$, it follows that $(y_i,x) \in (R|_{\tau ,Y_\tau })^T \subseteq R^T$. Therefore, $\sigma$ is a simplex of $D(Y,X,R^T)$. $\square$

What Corollary 4 and Theorem 6 imply is that we have the following functorial diagram

where $\mathbf{CW}$ is the category of CW complexes and homotopy classes of continuous maps, G is the geometric realization of an abstract simplicial complex, Base is the functor that forgets the costalks of a cosheaf (Corollary 4), and $\Gamma$ is the functor that constructs the space of global cosections from a cosheaf (Lemma 5). The traditional statement of Dowker duality asserts that the top and bottom paths in this diagram, namely

$$\begin{aligned} G \circ D \text { and } G \circ D \circ Transp \end{aligned}$$

are equivalent up to homotopy. What we have shown is that Dowker duality can also be expressed as the statement that

$$\begin{aligned} G \circ Base \circ CoShvRep \text { and } G \circ \Gamma \circ CoShvRep \end{aligned}$$

are equivalent up to homotopy.

For a cosheaf $\mathfrak {C}$ on an abstract simplicial complex X of abstract simplicial complexes whose extensions are inclusions, let us define a new cosheaf $Dual(\mathfrak {C})$ on the space of global cosections of $\mathfrak {C}$. Noting that the space of global cosections $\mathfrak {C}(X)$ is also an abstract simplicial complex, suppose $\sigma$ is a simplex of $\mathfrak {C}(X)$. Define the costalk $\left( Dual(\mathfrak {C})\right) (\sigma )$ to be the simplicial complex formed by the union of every simplex $\alpha$ in X whose costalk $\mathfrak {C}(\alpha )$ contains $\sigma$. Abstractly, this is equivalent to a union

$$\begin{aligned} \left( Dual(\mathfrak {C})\right) (\sigma ) = \bigcup \{ \alpha \in X : \sigma \in \mathfrak {C}(\alpha )\}, \end{aligned}$$

which implies that $Dual(\mathfrak {C})$ is a well-defined cosheaf when the extensions are all chosen to be inclusions.

Example 15

Figure 11 shows a cosheaf $\mathfrak {B}$ of abstract simplicial complexes on an abstract simplicial complex. Since each extension map is an inclusion, this cosheaf is an object in $\mathbf{CoShvAsc}$. The space of global cosections of this cosheaf is an abstract simplicial complex, which is shown at right in Fig. 11. The cosheaf $Dual(\mathfrak {B})$ can therefore be constructed on this new abstract simplicial complex using the definition above. The resulting cosheaf is shown in Fig. 12, where it is clear that each extension of this new cosheaf is an inclusion. It is also easily seen that the space of global cosections of $Dual(\mathfrak {B})$ is the base space of $\mathfrak {B}$. Notice that the space of global cosections cannot be computed using Proposition 6 because this cosheaf is evidently not in the image of CoShvRep – simply notice that $\mathfrak {B}([c])$ is not a complete simplex.

Fig. 11

A cosheaf $\mathfrak {B}$ of abstract simplicial complexes described in Example 15: (left) the base space of $\mathfrak {B}$, (center) the diagram of $\mathfrak {B}$, (right) the space of global cosections of $\mathfrak {B}$

Fig. 12

The cosheaf $Dual(\mathfrak {B})$ that is dual to the cosheaf $\mathfrak {B}$ shown in Fig. 11 and described in Example 15

Lemma 9

Dual is a covariant functor $\mathbf{CoShvAsc} \rightarrow \mathbf{CoShvAsc}$.

Proof

The Dual functor exchanges the base space with the space of global cosections. For a cosheaf $\mathfrak {R}$ on X that is an object of $\mathbf{CoShvAsc}$,

$$\begin{aligned} Base(Dual(\mathfrak {R})) =\mathfrak {R}(X), \end{aligned}$$

by definition and

$$\begin{aligned} \Gamma (Dual(\mathfrak {R}))= & {} \left( \bigsqcup _{\sigma \in Base(Dual(\mathfrak {R}))} (Dual(\mathfrak {R}))(\sigma ) \right) /\sim \\= & {} \left( \bigsqcup _{\sigma \in \mathfrak {R}(X)} (Dual(\mathfrak {R}))(\sigma ) \right) /\sim \\= & {} \bigcup _{\sigma \in \mathfrak {R}(X)} (Dual(\mathfrak {R}))(\sigma ) \\= & {} \bigcup _{\sigma \in \mathfrak {R}(X)} \bigcup \{\alpha \in X : \sigma \in \mathfrak {R}(\alpha ) \} \\= & {} \left\{ \alpha \in X : \text {there is a }\sigma \in \mathfrak {R}(X) \text { such that }\sigma \in \mathfrak {R}(\alpha ) \right\} \\= & {} \left\{ \alpha \in X : \text {there is a }\sigma \in \bigcup _{\tau \in X} \mathfrak {R}(\tau ) \text { such that }\sigma \in \mathfrak {R}(\alpha ) \right\} \\= & {} X. \end{aligned}$$

A cosheaf morphism $m: \mathfrak {R} \rightarrow \mathfrak {S}$ along a simplicial map $f: X \rightarrow Y$ induces a map $m_*: \mathfrak {R}(X) \rightarrow \mathfrak {S}(Y)$ on each space of cosections (Lemma 5). We use these data to define a morphism $w : Dual(\mathfrak {R}) \rightarrow Dual(\mathfrak {S})$. As such, the induced map $m_*$ on the space of global cosections becomes the new base space map, along which the new cosheaf morphism w is written. The individual simplices map by way of restricting to the components of the old morphism, since $m_*$ is a simplicial map. Conversely, the old base space map f defines the new component maps $w_\sigma$ by restriction.

Explicitly, if $\sigma$ is a simplex of $Base(Dual(\mathfrak {R})) = \mathfrak {R}(X)$, we have that

$$\begin{aligned} (Dual(\mathfrak {R}))(\sigma ) = \bigcup \{\alpha \in X : \sigma \in \mathfrak {R}(\alpha )\}. \end{aligned}$$

The component $w_\sigma$ must be a function $(Dual(\mathfrak {R}))(\sigma ) \rightarrow Dual(\mathfrak {S})(m_*(\sigma ))$. Since every element of $(Dual(\mathfrak {R}))(\sigma )$ is an $\alpha \in X$, and the domain of f is X, we may define

$$\begin{aligned} w_\sigma = f|_{(Dual(\mathfrak {R}))(\sigma )}. \end{aligned}$$

This is well-defined because if $\sigma \in \mathfrak {R}(\alpha )$ then $m_*(\sigma ) \in \mathfrak {S}(f(\alpha ))$, and

$$\begin{aligned} (Dual(\mathfrak {S}))(m_*(\sigma )) = \bigcup \{\beta \in Y : m_*(\sigma ) \in \mathfrak {S}(\beta )\}. \end{aligned}$$

To establish that these component maps form a cosheaf morphism, we need to establish that the diagram below commutes for all simplices $\alpha \subseteq \beta$ in $\mathfrak {R}(X)$:

This follows because the vertical maps are inclusions and the horizontal maps are both restrictions of f to nested subsets.

Finally, composition of morphisms is preserved because that is simply composition of the base and global cosection functions. $\square$

Theorem 7

(Cosheaf version of Dowker duality) Dual is a functor that makes the diagram of functors commute:

Proof

The way that $Dual(\mathfrak {R})$ has been defined, we might end up with a simplicial complex as a costalk that is not a complete simplex—which is a problem according to Lemma 7—but this does not happen in the image of CoShvRep because of Proposition 6. Suppose that $\mathfrak {R} = CoShvRep(X,Y,R)$. We claim that for every simplex $\sigma$ in $\mathfrak {R}(X) = D(Y,X,R^T)$, the set of simplices

$$\begin{aligned} \{ \alpha \in X : \sigma \in \mathfrak {R}(\alpha )\} \end{aligned}$$

has a unique maximal simplex in the inclusion order, so that the union in the definition of $\left( Dual(\mathfrak {R})\right) (\sigma )$ really is just that one simplex. To see that, suppose that $\alpha$ and $\beta$ are simplices of X for which $\sigma \in \mathfrak {R}(\alpha )$ and $\sigma \in \mathfrak {R}(\beta )$. Suppose that any other simplex $\gamma$ that contains $\alpha$ has $\sigma \notin \mathfrak {R}(\gamma )$, so $\alpha$ is maximal in the sense of inclusion. We want to show that $\beta \subseteq \alpha$. Going back to the definition of $\mathfrak {R}$, we have that

$$\begin{aligned} \mathfrak {R}(\alpha ) = D\left( Y_\alpha ,\alpha ,(R|_{\alpha ,Y_\alpha })^T\right) \end{aligned}$$

and

$$\begin{aligned} \mathfrak {R}(\beta ) = D\left( Y_\beta ,\beta ,(R|_{\beta ,Y_\beta })^T\right) . \end{aligned}$$

Both contain $\sigma$. What about the simplex $\delta$ whose vertices are the union of the vertices of $\alpha$ and $\beta$? Suppose that $y\in Y$ is a vertex of $\sigma$. This means that $y \in Y_\alpha \cap Y_\beta$, which means that $(x,y) \in R$ for every $x \in \alpha \cup \beta = \delta$. Thus $\sigma \subseteq Y_\delta$, or in other words $\sigma \in \mathfrak {R}(\delta )$ according to Lemma 7. On the other hand, if $\alpha \subsetneqq \delta$, we assumed that $\sigma \notin \mathfrak {R}(\delta )$. So the only way this can happen is if $\alpha = \delta$, which implies $\beta \subseteq \alpha$.

With this fact in hand, we can observe that

$$\begin{aligned}&\left( (Dual \circ CoShvRep)(X,Y,R)\right) (\sigma ) \\&\quad = \left( Dual(\mathfrak {R})\right) (\sigma ) \\&\quad = \bigcup \{ \alpha \in X : \sigma \in \mathfrak {R}(\alpha )\} \\&\quad = \bigcup \{\alpha \in X : \sigma \subseteq Y_\alpha \} \\&\quad = \bigcup \{\alpha \in X : \text {for all }y \in \sigma \text { and all }x \in \alpha , \; (x,y) \in R\}\\&\quad = \{x \in X : (x,y)\text { for all }y \in \sigma \} \\&\quad = D\left( X_\sigma ,\sigma ,R|_{X_\sigma ,\sigma }\right) \\&\quad = \left( CoShvRep(Y,X,R^T)\right) (\sigma )\\&\quad = \left( (CoShvRep \circ Transp)(X,Y,R)\right) (\sigma ). \end{aligned}$$

$\square$

Example 16

Consider the relation morphism $\mathbf{Rel}$ morphism $(f,g) : (X_1,Y_1,R_1) \rightarrow (X_4,Y_4,R_4)$ defined in Example 10. Recall that the relation $R_1$ between the sets $X_1=\{a,b,c,d,e\}$ and $Y_1=\{1,2,3,4,5\}$, was given by the matrix

$$\begin{aligned} r_1 = \begin{pmatrix} 1&{}1&{}0&{}0&{}0\\ 1&{}0&{}1&{}0&{}0\\ 0&{}1&{}1&{}1&{}1\\ 0&{}0&{}1&{}1&{}0\\ 0&{}0&{}0&{}1&{}1\\ \end{pmatrix}, \end{aligned}$$

and the relation $R_4$ between $X_4=\{A,B,C\}$ and $Y_4 =\{1,2,3\}$ was given by

$$\begin{aligned} r_4 = \begin{pmatrix} 1&{}1&{}0\\ 1&{}0&{}1\\ 0&{}1&{}1\\ \end{pmatrix}. \end{aligned}$$

The function $f: X_1 \rightarrow X_4$ was given by

$$\begin{aligned} f(a) = A,\; f(b) = B,\; f(c) = C,\; f(d) = C,\; f(e) = C, \end{aligned}$$

and the function $g: Y_1 \rightarrow Y_2$ was given by

$$\begin{aligned} g(1) = 1,\; g(2) = 2,\; g(3) = 3,\; g(4) = 3,\; g(5) = 3. \end{aligned}$$

Let is define $\mathfrak {A}=CoShvRep(X_1,Y_1,R_1)$ and $\mathfrak {B}=CoShvRep(X_4,Y_4,R_4)$. The cosheaf morphism induced by $CoShvRep^0$ was shown in Fig. 7, but what interests us now is the cosheaf morphism $\mathfrak {A} \rightarrow \mathfrak {B}$ induced by CoShvRep and $Dual(\mathfrak {A}) \rightarrow Dual(\mathfrak {B})$ induced by $Dual \circ CoShvRep$ (or equally well, induced by $CoShvRep \circ Transp$). These two morphisms are shown in Figs. 13 and 14 , respectively. Notice in particular that each component map (in both morphisms) is a simplicial map, so that whenever two vertices are collapsed (for instance $g(3)=g(4)=g(5)$) the associated simplices are collapsed as well.

Fig. 13

The cosheaf morphism induced by CoShvRep described in Example 16

Fig. 14

The cosheaf morphism induced by $Dual \circ CoShvRep$ described in Example 16