Abstract
We study a remarkable simplicial complex X on countably many vertexes. X is universal in the sense that any countable simplicial complex is an induced subcomplex of X. Additionally, X is homogeneous, i.e. any two isomorphic finite induced subcomplexes are related by an automorphism of X. We prove that X is the unique simplicial complex which is both universal and homogeneous. The 1-skeleton of X is the well-known Rado graph. We show that a random simplicial complex on countably many vertexes is isomorphic to X with probability 1. We prove that the geometric realisation of X is homeomorphic to an infinite dimensional simplex. We observe several curious properties of X, for example we show that X is robust, i.e. removing any finite set of simplexes leaves a simplicial complex isomorphic to X. The robustness of X leads to the hope that suitable finite approximations of X can serve as models for very resilient networks in real life applications. In a forthcoming paper (Even-Zohar et al. Ample simplicial complexes, arXiv:2012.01483, 2020) we study finite approximations to the Rado complex, they can potentially be useful in real life applications due to their structural stability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the 1920’s, P. S. Urysohn constructed a remarkable complete, separable metric space \({{\mathcal {U}}}\), which is known as the Urysohn space. The space \({{\mathcal {U}}}\) is universal in the sense that it contains an isometric copy of any complete, separable metric space. Additionally, the Urysohn space \({{\mathcal {U}}}\) is homogeneous in the sense that any partial isometry between its finite subsets can be extended to a global isometry. The properties of universality and homogeneity determine \({{\mathcal {U}}}\) uniquely up to isometry, see Vershik (2004) for a detailed exposition.
The Rado graph \(\Gamma \) is another notable mathematical object, which can also be characterised by its universality and homogeneity. The graph \(\Gamma \) has countably many vertexes, and it is universal in the sense that any graph with countably many vertexes is isomorphic to an induced subgraph of \(\Gamma \). Moreover, any isomorphism between finite induced subgraphs of \(\Gamma \) can be extended to the whole of \(\Gamma \) (homogeneity). The properties of universality and homogeneity determine \(\Gamma \) uniquely up to isomorphism. One may mention the surprising robustness of \(\Gamma \): removing any finite set of its vertexes and edges produces a graph isomorphic to \(\Gamma \). We refer to Cameron (1997) for a comprehensive survey.
Erdős and Rényi (1963) showed that a random graph on countably many vertexes has the following characteristic property with probability one: given finitely many distinct vertexes \(u_1, \dots , u_m, v_1, \dots , v_n\) there exists a vertex which is adjacent to \(u_1, \dots , u_m\) and nonadjacent to \(v_1, \dots , v_m\). It is not difficult to see that the Rado graph \(\Gamma \) is the unique countable graph possessing the characteristic property, and hence a random countable graph is isomorphic to \(\Gamma \) with probability 1; this result explains why \(\Gamma \) is sometimes called “the random graph”. Rado (1964) suggested a deterministic construction of \(\Gamma \) in which the vertexes \(V(\Gamma )\) are labelled by integers \({{\mathbb {N}}}\) and a pair of vertexes labelled by \(m<n\) are connected by an edge iff the mth digit in the binary expansion of n is 1. This same graph construction implicitly appeared in an earlier paper by Ackermann (1937), who studied the consistence of the axioms of set theory.
The Rado graph \(\Gamma \) and the Urysohn space \({{\mathcal {U}}}\) are related. Any graph determines a metric on the set of its vertexes, where the distance between a pair of distinct vertexes is either 1 (if they are connected by an edge) or 2 (otherwise). Thus, the Rado graph \(\Gamma \) admits an isometric embedding into \({{\mathcal {U}}}\); it can be viewed as a restricted version of the Urysohn space limited to metric spaces with the metric taking values in the set \(\{0, 1, 2\}\).
In this paper we study a high-dimensional generalisation of the Rado graph which we call the Rado simplicial complex X. The complex X has countably many vertexes and is universal in the sense that any countable simplicial complex is an induced subcomplex of X. Additionally, X is homogeneous, i.e. any two isomorphic finite induced subcomplexes are related by an automorphism of X. Moreover, X is the unique (up to isomorphism) countable simplicial complex which is both universal and homogeneous. The 1-skeleton of X is the Rado graph \(\Gamma \). We introduce a characteristic property of the Rado complex called ampleness, which generalises the characteristic property of the Rado graph. We show that a random simplicial complex on countably many vertexes (in a certain regime) is isomorphic to X with probability 1. We also give explicit deterministic constructions of the Rado complex. The geometric realisation of the Rado complex X is homeomorphic to an infinite dimensional simplex.
We observe several curious properties of X, for example we show that if the set of vertexes of X is partitioned into finitely many parts, the simplicial complex induced on at least one of these parts is isomorphic to X. The link of any simplex of X is isomorphic to X. One of the key properties of X is its robustness: removing any finite set of simplexes leaves a simplicial complex isomorphic to X.
Modern network science uses high-dimensional simplicial complexes for modelling complex networks of many objects whose interactions can occur in groups of two or more objects; the pairwise interactions can be recorded by representating the system by a graph, while higher order interactions require exploiting simplicial complexes of dimension \(\ge 2\) (see Battiston et al. (2020) for a recent survey with a vast list of references, including applications to social systems, neuroscience, ecology, and others). The robustness of X leads to the hope that suitable finite approximations of X can serve as models for very resilient networks in real life applications. We also expect that, like expanders and other combinatorial objects that can be constructed probabilistically, the Rado complex X developed in this paper can also be relevant for proving lower bound and impossibility results for certain (algorithmic) tasks. In a forthcoming paper Even-Zohar et al. (2020) we study finite simplicial complexes with “limited” robustness and topological properties of their geometric realisations.
The Rado complex X can be viewed as the limit of a finite random simplicial complex in the medial regime, studied in Farber and Mead (2020). Informally, finite random simplicial complexes in the medial regime are subcomplexes of the Rado complex X induced on a random subset of n vertexes. It was proven in Farber and Mead (2020) that, with probability tending to 1, such simplicial complexes are quite special; for example, they have dimension \(\sim \log _2\ln n +\log _2 \log _2 \ln n\) and have vanishing Betti numbers in dimensions \(\le \log _2\ln n +c\), where c is a constant. Note however that by universality any finite simplicial complex arises as an induced subcomplex of X.
Next we comment on relations with previously known results. Theorem 3 of Rado (1964) suggests a construction of a universal uniform hypergraph of a fixed dimension \(\ell \). Equivalently, uniform hypergraphs can be understood as simplicial complexes of a fixed dimension \(\ell \) having complete \((\ell -1)\)-dimensional skeleta.
Blass and Harary (1979) study the 0–1 law for the first order language of simplicial complexes of fixed dimension \(\ell \) with respect to the counting probability measure. They show that a typical \(\ell \)-dimensional simplicial complex has a full \((\ell -1)\)-skeleton. In Blass and Harary (1979), the authors introduce “Axiom n”, which generalises the characteristic property of the Rado graph; it is a special case of our notion of ampleness.
When this paper was nearly completed we became aware of the 2013 preprint (Brooke-Taylor and Testa 2013), revised in 2018; as far as we know, it has not been published yet. Paper Brooke-Taylor and Testa (2013) applies the methods of mathematical logic and model theory to study the geometry of simplicial complexes; it uses language very different from ours. A well-known general construction of model theory is the Fraïssé limit for a class of relational structures possessing certain amalgamation properties, see Hodges (1993). The Fraïssé limit construction, when applied to the class of all finite simplicial complexes, produces a simplicial complex F on countably many vertexes which is universal and homogeneous, i.e. it is a Rado complex in the terminology of this paper. The universality of the Fraïssé limit F is stated with respect to finite simplicial complexes, but this is equivalent to the countable version of universality as appears in Definition 1, see Remark 11.
In Brooke-Taylor and Testa (2013) the authors study the group automorphisms of F and state that any direct limit of finite groups and any metrisable profinite group embeds into the group of automorphisms of F. Besides, Brooke-Taylor and Testa (2013) contains a proof that the geometric realisation of F is homeomorphic to an infinite-dimensional simplex, a result which we independently establish below in Sect. 5. The authors of Brooke-Taylor and Testa (2013) also consider a probabilistic approach and claim the 0–1 law for first order theories. We were unable to fully understand the construction of their probability measure and the related proofs.
Although the current paper and Brooke-Taylor and Testa (2013) study the same object, the motivation, language, and methods of this paper are totally different compared to Brooke-Taylor and Testa (2013), and the current paper and Brooke-Taylor and Testa (2013) perfectly complement each other. For us the Rado complex is a model of an astonishingly stable network, and our notion of ampleness (which does not appear in Brooke-Taylor and Testa 2013) is crucial in illustrating its resilience.
The authors thank the anonymous referees for their helpful comments.
2 The definition of the rado complex
2.1 Basic terminology
A simplicial complex X is a set of vertexes V(X) and a set of non-empty finite subsets of V(X), called simplexes, such that any vertex \(v\in V(X)\) is a simplex \(\{v\}\) and any subset of a simplex is a simplex. A simplicial complex X is said to be countable (finite) if its vertex set V(X) is countable (finite). The symbol F(X) stands for the set of all simplexes of X. For a simplex \(\sigma \in F(X)\) we shall also write \(\sigma \subset X\).
Two simplicial complexes are isomorphic if there is a bijection between their vertex sets which induces a bijection between the sets of simplexes.
The standard simplex \(\Delta _n\) has the set of vertexes \(\{1, 2, \dots , n\}\) with all non-empty subsets as simplexes. Another standard simplex is \(\Delta _{{\mathbb {N}}}\); its vertex set is \({{\mathbb {N}}}=\{1, 2, \dots \}\) and all non-empty finite subsets of \({{\mathbb {N}}}\) are simplexes.
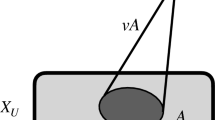
A simplicial subcomplex \(Y\subset X\) is said to be induced if every simplex \(\sigma \in F(X)\) with all its faces in V(Y) belongs to F(Y). The induced subcomplex \(Y\subset X\) is completely determined by the set of its vertexes, \(V(Y)\subset V(X)\). We shall use the notation \(Y=X_U\) where \(U=V(Y)\).
For a vertex \(v\in V(X)\) the symbol \(\mathrm{{Lk}}_X(v)\) stands for the link of v; the latter is the union of simplexes \(\sigma \) of X with \(v\notin \sigma \) and \(v\sigma \subset X\).
Definition 1
(1) A countable simplicial complex X is said to be universal if every countable simplicial complex is isomorphic to an induced subcomplex of X. (2) We say that X is homogeneous if for every two finite induced subcomplexes \(X_U, X_{U'}\subset X\) and for every isomorphism \(f:X_U\rightarrow X_{U'}\) there exists an isomorphism \(F:X\rightarrow X\) with \(F|X_U=f\). (3) A countable simplicial complex X is a Rado complex if it is universal and homogeneous.
It is clear that the 1-skeleton of a Rado complex is a Rado graph; the latter can be defined as a universal and homogeneous graph having countably many vertexes, see Cameron (1997).
Theorem 2
Rado simplicial complexes exist and any two Rado complexes are isomorphic.
The following property is a useful criterion of being a Rado complex:
Definition 3
We shall say that a countable simplicial complex X is ample if for every finite subset \(U\subset V(X)\) and for every simplicial subcomplex \(A\subset X_U\) there exists a vertex \(v\in V(X)-U\) such that
Remark 4
Condition (1) can equivalently be expressed as
where \(U'=U\cup \{v\}\) and vA denotes the cone with apex v and base A. In the literature the cone vA is sometimes denoted by \(v*A\), understood as the simplicial join of the vertex v and the complex A.
Remark 5
Suppose that X is a simplicial complex with countable set of vertexes V(X). One may naturally consider exhaustions \(U_0\subset U_1\subset U_2\subset \dots \subset V(X)\) consisting of finite subsets \(U_n\) satisfying \(\cup U_n = V(X)\). In order to check that X is ample as defined in Definition 3 it is sufficient to verify that for every \(n\ge 0\) and for every subcomplex \(A\subset X_{U_n}\) there exists a vertex \(v\in V(X)-U_n\) satisfying \(\mathrm{{Lk}}_X(v)\cap X_{U_n}= A\).
Remark 6
Suppose that X is an ample simplicial complex. Given finitely many distinct vertexes \(u_1, \dots , u_m, v_1, \dots , v_n\in V(X)\), there exists a vertex \(z\in V(X)\) which is adjacent to \(u_1, \dots , u_m\) and nonadjacent to \(v_1, \dots , v_n\). To see this we apply Definition 3 with \(U= \{u_1, \dots , u_m, v_1, \dots , v_n\}\) and \(A=\{u_1, \dots , u_m\}\). This shows that the 1-skeleton of a Rado complex satisfies the characteristic property of the Rado graph (Cameron 1997). This also shows that ampleness is a high dimensional generalizaton of this graph property.
The following property of ample complexes will be useful in the sequel.
Lemma 7
Let X be an ample complex and let \(L'\subset L\) be a pair consisting of a finite simplical complex L and an induced subcomplex \(L'\). Let \(f': L' \rightarrow X_{U'}\) be an isomorphism of simplicial complexes, where \(U'\subset V(X)\) is a finite subset. Then there exists a finite subset \(U\subset V(X)\) containing \(U'\) and an isomorphism \(f: L \rightarrow X_{U}\) with \(f|L' =f'\).
Proof
It is enough to prove this statement under an additional assumption that L has a single extra vertex, i.e. \(|V(L)| - |V(L')| =1\). In this case L is obtained from \(L'\) by attaching a cone wA where \(w\in V(L) - V(L')\) denotes the new vertex and \(A\subset L'\) is a subcomplex (the base of the cone). Applying the defining property of the ample complex to the subset \(U'\subset V(X)\) and the subcomplex \(f'(A)\subset X_{U'}\) we find a vertex \(v\in V(X)-U'\) such that \(\mathrm{{Lk}}_X(v)\cap X_{U'} =f(A)\). We can set \(U=U'\cup \{v\}\) and extend \(f'\) to the isomorphism \(f: L\rightarrow X_{U}\) by setting \(f(w)=v\). \(\square \)
Theorem 8
A simplicial complex is Rado if and only if it is ample.
Proof
Suppose X is a Rado complex, i.e. X is universal and homogeneous. Let \(U\subset V(X)\) be a finite subset and let \(A\subset X_U\) be a subcomplex of the induced complex. Consider an abstract simplicial complex \(L=X_U\cup wA\) which obtained from \(X_U\) by adding a cone wA with vertex w and base A where \(X_U\cap wA= A\). Clearly, \(V(L) = U\cup \{w\}\). By universality, we may find a subset \(U'\subset V(X)\) and an isomorphism \(g:L \rightarrow X_{U'}\). Denoting \(w_1=g(w)\), \(A_1=g(A)\) and \(U_1=g(U)\) we have \(X_{U'} = X_{U_1} \cup w_1 A_1.\) Obviously, g restricts to an isomorphism \(g| X_U\, :\, X_U \rightarrow X_{U_1}\). By the homogeneity property we can find an isomorphism \(F:X\rightarrow X\) with \(F|X_U =g|X_U\). Denoting \(v=F^{-1}(w_1)\) we shall have \(X_{U\cup \{v\}} = X_U \cup vA\) as required, see Remark 4.
Now suppose that X is ample. To show that it is universal consider a simplicial complex L with at most countable set of vertexes V(L). We may find a chain of induced subcomplexes \(L_1\subset L_2\subset \cdots \) with \(\cup L_n=L\) and each complex \(L_{n}\) has exactly n vertexes. Then \(L_{n+1}\) obtained from \(L_n\) by adding a cone \(v_{n+1}A_n\) where \(v_{n+1}\) is the new vertex and \(A_n\subset L_n\) is a simplicial subcomplex. We argue by induction that we can find a chain of subsets \(U_1\subset U_2\subset \dots \subset V(X)\) and isomorphisms \(f_n: L_n \rightarrow X_{U_n}\) satisfying \(f_{n+1}|L_n = f_n\). If \(U_n\) and \(f_n\) are already found then the next set \(U_{n+1}\) and the isomorphism \(f_{n+1}\) exist because X is ample: we apply Definition 3 with \(U=U_n\) and \(A=f_n(A_n)\) and we set \(U_{n+1} = U_n \cup \{v\}\) where v is the vertex given by Definition 3. The sequence of maps \(f_n\) defines an injective map \(f: V(L)\rightarrow V(X)\) and produces an isomorphism between L and the induced subcomplex \(X_{f(V(L))}\).
The fact that any ample complex is homogeneous follows from Lemma 9 below. We state it in a slightly more general form so that it also implies the uniqueness of Rado complexes. \(\square \)
Lemma 9
Let X and \(X'\) be two ample complexes and let \(L\subset X\) and \(L'\subset X'\) be two induced finite subcomplexes. Then any isomorphism \(f: L\rightarrow L'\) can be extended to an isomorphism \(F: X\rightarrow X'\).
Proof
We shall construct chains of subsets of the sets of vertexes \(U_0\subset U_1\subset \dots \subset V(X)\) and \(U'_0\subset U'_1\subset \dots \subset V(X')\) such that \(\cup U_n=V(X)\), \(\cup U'_n=V(X')\), \(X_{U_0}=L\), \(X_{U'_0}=L'\), and \(|U_{n+1}-U_n|=1\), \(|U'_{n+1}-U'_n|=1\). We shall also construct isomorphisms \(f_n: X_{U_n} \rightarrow X_{U'_n}\) satisfying \(f_0=f\) and \(f_{n+1}|X_{U_n} =f_n\). The whole collection \(\{f_n\}\) will then define a required isomorphism \(F: X\rightarrow X'\) with \(F|L=f\).
To constructs these objects we shall use the well known back-and-forth procedure. Enumerate vertexes \(V(X)-V(L) =\{v_1, v_2, \dots \}\) and \(V(X')-V(L') =\{v'_1, v'_2, \dots \}\) and start by setting \(U_0=V(L)\), \(U'_0=L'\) and \(f_0=f\). We act by induction and describe \(U_n\), \(U'_n\) and \(f_n\) assuming that the objects \(U_i\), \(U'_i\) and \(f_i:U_i\rightarrow U'_i\) have been already defined for all \(i<n\).
The procedure will depend on the parity of n. For n odd we find the smallest j with \(v_j\notin U_{n-1}\) and set \(U_n=U_{n-1}\cup \{v_j\}\). Applying Lemma 7 to the simplicial complexes \(L=X_{U_n}\), \(L'=X_{U_{n-1}}\) and the isomorphism \(f_{n-1}: X_{U_{n-1}}\rightarrow X'_{U'_{n-1}}\) we obtain a subset \(U'_n\subset V(X')\) containing \(U'_{n-1}\) and an isomorphism \(f_n: X_{U_n}\rightarrow X'_{U'_n}\) extending \(f_{n-1}.\)
For n even we proceed in the reverse direction. We find the smallest j with \(v'_j\notin U'_{n-1}\) and set \(U'_n=U'_{n-1}\cup \{v'_j\}\). Next we applying Lemma 7 to the simplicial complexes \(L=X'_{U'_n}\), \(L'=X'_{U'_{n-1}}\) and the isomorphism \(f_{n-1}^{-1}: X'_{U'_{n-1}}\rightarrow X_{U_{n-1}}\). We obtain a subset \(U_n\subset V(X)\) containing \(U_{n-1}\) and an isomorphism \(f_n^{-1}: X'_{U'_n}\rightarrow X_{U_n}\) extending \(f_{n-1}^{-1}.\) \(\square \)
Corollary 10
Any two Rado complexes are isomorphic.
Proof
This follows from Theorem 8 with subsequent applying Lemma 9 with \(L=L'=\emptyset \). \(\square \)
Remark 11
In Definition 1 we defined universality with respect to arbitrary countable simplicial subcomplexes. A potentially more restrictive definition dealing only with finite subcomplexes together with homogeneity is in fact equivalent to Definition 1; this follows from the arguments used in the proof of Theorem 8.
3 Deterministic constructions of Rado complexes
3.1 An inductive construction
One may construct a Rado simplicial complex X inductively as the union of a chain of finite induced simplicial subcomplexes
Here \(X_0\) is a single point and each complex \(X_{n+1}\) is obtained from \(X_n\) by first adding a finite set of vertexes v(A), labeled by subcomplexes \(A\subset X_n\) (including the case when \(A=\emptyset \)); secondly, we construct the cone \(v(A) *A\) with apex v(A) and base A, and thirdly we attach each such cone \(v(A)*A\) to \(X_n\) along the base \(A\subset X_n\). Thus,
To show that the complex \(X=\cup _{n\ge 0} X_n\) is ample, i.e. a Rado complex, we refer to Remark 5 and observe that any subcomplex \(A\subset X_n\) the vertex \(v=v(A)\in V(X_{n+1})\) satisfies \(\mathrm{{Lk}}_X(v)\cap X_n =A.\)
3.2 An explicit construction
Here we shall give an explicit construction of a Rado complex X. To describe it we shall use the sequence \(\{p_1, p_2, \dots , \}\) of all primes in increasing order, where \(p_1=2\), \(p_2=3\), etc.
The set of vertexes V(X) is the set of all positive integers \({{\mathbb {N}}}\). Each simplex of X is uniquely represented by an increasing sequence \(a_0<a_1< \dots <a_k\) with certain properties. Subsequences of \(a_0<a_1< \dots <a_k\) are obtained by erasing one or more elements in the sequence.
Definition 12
(1) A sequence \(a_0<a_1\) is a 1-dimensional simplex of X if and only if \(p_{a_0}\)-th binary digit of \(a_1\) is 1. (2) We shall say that an increasing sequence of positive integers \(0<a_0<a_1< \dots < a_k\) represents a simplex of X if all its proper subsequences are in X and additionally the \(p_{a_0}p_{a_1} \dots p_{a_{k-1}}\)-th binary digit of \(a_k\) is 1.
Proposition 13
The obtained simplicial complex X is Rado.
Proof
With any increasing sequence \(\sigma \) of positive integers \(0<a_0<a_1< \dots < a_k\) we associate the product
which is an integer without multiple prime factors. Note that for two such increasing sequences \(\sigma \) and \(\sigma '\) one has \(N_\sigma =N_{\sigma '}\) if and only if \(\sigma \) is identical to \(\sigma '\).
Given a finite subset \(U\subset V(X)\) and a simplicial subcomplex \(A\subset X_U\), consider the vertex
where
The binary expansion of v has ones exactly on positions \(N_\sigma \) where \(\sigma \in F(A)\) and it has zeros on all other positions except an additional 1 at position \(K_U\). Note that \(K_U>N_\sigma \) for any simplex \(\sigma \subset X_U\). In particular, we see that vertex v defined by (4) satisfies \(v> w\) for any \(w\in U\).
Consider a simplex \(\sigma \subset X_U\). By definition, the simplex \(v\sigma \) with apex v and base \(\sigma \) lies in X if and only if the \(N_\sigma \)-th binary digit of v is 1. We see from (4) that it happens if and only if \(\sigma \subset A\). This means that \(\mathrm{{Lk}}_X(v)\cap X_U=A\) and hence the complex X is a Rado complex. \(\square \)
4 Some properties of the Rado complex
Lemma 14
Let X be a Rado complex, let \(U\subset V(X)\) be a finite set and let \(A\subset X_U\) be a subcomplex. Let \(Z_{U,A}\subset V(X)\) denote the set of vertexes \(v\in V(X)-U\) satisfying (1). Then \(Z_{U,A}\) is infinite and the induced complex on \(Z_{U,A}\) is also a Rado complex.
Proof
Consider a finite set \(\{v_1, \dots , v_N\}\subset Z_{U, A}\) of such vertexes. One may apply Definition 3 to the set \(U_1=U\cup \{v_1, \dots , v_N\}\) and to the subcomplex \(A\subset X_{U_1}\) to find another vertex \(v_{N+1}\) satisfying the condition of Definition 3. This shows that \(Z_{U,A}\) must be infinite.
Let \(Y\subset X\) denote the subcomplex induced by \(Z_{U, A}\). Consider a finite subset \(U'\subset Z_{U,A}=V(Y)\) and a subcomplex \(A'\subset X_{U'}=Y_{U'}\). Applying the condition of Definition 3 to the set \(W= U\cup U'\subset V(X)\) and to the subcomplex \(A\sqcup A'\) we find a vertex \(z\in V(X)-W\) such that
Since \(X_{W} \supset X_U\cup X_{U'}\), the equation (5) implies \(\mathrm{{Lk}}_X(z)\cap X_U=A\), i.e. \(z\in Z_{U, A}\). Intersection both sides of (5) with \(X_{U'}=Y_{U'}\) and using \(\mathrm{{Lk}}_Y(z) =\mathrm{{Lk}}_X(z)\cap Y\) (since Y is an induced subcomplex) we obtain
implying that Y is Rado. \(\square \)
Corollary 15
Let X be a Rado complex and let Y be obtained from from X by selecting a finite number of simplexes \(F\subset F(X)\) and deleting all simplexes \(\sigma \in F(X)\) which contain simplexes from F as their faces. Then Y is also a Rado complex.
Proof
Let \(U\subset V(Y)\) be a finite subset and let \(A\subset Y_U\) be a subcomplex. We may also view U as a subset of V(X) and then A becomes a subcomplex of \(X_U\) since \( Y_U\subset X_U\). The set of vertexes \(v\in V(X)\) satisfying \(\mathrm{{Lk}}_X(v)\cap X_U=A\) is infinite (by Lemma 14) and thus we may find a vertex \(v\in V(X)\) which is not incident to simplexes from the family F. Then \(\mathrm{{Lk}}_Y(v)=\mathrm{{Lk}}_X(v)\cap Y\) and we obtain \(\mathrm{{Lk}}_Y(v)\cap Y_U=A\). \(\square \)
Corollary 16
Let X be a Rado complex. If the vertex set V(X) is partitioned into a finite number of parts then the induced subcomplex on at least one of these parts is a Rado complex.
Proof
It is enough to prove the statement for partitions into two parts. Let \(V(X)= V_1\sqcup V_2\) be a partition; denote by \(X^1\) and \(X^2\) the subcomplexes induced by X on \(V_1\) and \(V_2\) correspondingly. Suppose that none of the subcomplexes \(X^{1}\) and \(X^{2}\) is Rado. Then for each \(i=1, 2\) there exists a finite subset \(U_i\subset V_i\) and a subcomplex \(A_i\subset X^i_{U_i}\) such that no vertex \(v\in V_i\) satisfies \(\mathrm{{Lk}}_{X^i}(v) \cap X^i_{U_i}= A_i\). Consider the subset \(U= U_1\sqcup U_2\subset V(X)\) and a subcomplex \(A=A_1\sqcup A_2\subset X_{U}\). Since X is Rado we may find a vertex \(v\in V(X)\) with \(\mathrm{{Lk}}_X\cap X_U = A. \) Then v lies in \(V_1\) or \(V_2\) and we obtain a contradiction, since \(\mathrm{{Lk}}_{X^i}(v) \cap X^i_{U_i} =A_i.\) \(\square \)
Lemma 17
In a Rado complex X, the the link of every simplex is a Rado complex.
Proof
Let \(Y=\mathrm{{Lk}}_X(\sigma )\) be the link of a simplex \(\sigma \in X\). To show that Y is Rado, let \(U\subset V(Y)\) be a subset and let \(A\subset Y_U\) be a subcomplex. We may apply the defining property of the Rado complex (i.e. ampleness) to the subset \(U'=U\cup V(\sigma )\subset V(X)\) and to the subcomplex \(A\sqcup {{\bar{\sigma }}}\subset X_{U'}\); here \({{\bar{\sigma }}}\) denotes the subcomplex containing the simplex \(\sigma \) and all its faces. We obtain a vertex \(w\in V(X)-U'\) with \(\mathrm{{Lk}}_X(w)\cap X_{U'} = A\sqcup \bar{\sigma }\) or equivalently, \(X_{U'\cup w} = X_{U'} \cup wA\), see Remark 4. Note that \(w\in Y=\mathrm{{Lk}}_X(\sigma )\) since the simplex \(w\sigma \) is in X. Besides, \(Y_{U\cup w} =Y_U \cup wA\). Hence we see that the link Y is also a Rado complex. \(\square \)
5 Geometric realisation of the Rado complex
Recall that for a simplicial complex X the geometric realisation |X| is the set of all functions \(\alpha : V(X)\rightarrow [0,1]\) such that the support \(\mathrm{{supp}}(\alpha )=\{v; \alpha (v)\not =0\}\) is a simplex of X (and hence finite) and \(\sum _{v\in X} \alpha (v)=1\), see Spanier (1971). For a simplex \(\sigma \in F(X)\) the symbol \(|\sigma |\) denotes the set of all \(\alpha \in |X|\) with \(\mathrm{{supp}}(\alpha )\subset \sigma \). The set \(|\sigma |\) has natural topology and is homeomorphic to the affine simplex lying in an Euclidean space. The weak topology on the geometric realisation |X| has as open sets the subsets \(U\subset |X|\) such that \(U\cap |\sigma |\) is open in \( |\sigma |\) for any simplex \(\sigma \).
Theorem 18
The Rado complex is isomorphic to a triangulation of the simplex \(\Delta _{{\mathbb {N}}}\). In particular, the geometric realisation |X| of the Rado complex is homeomorphic to the geometric realisation of the infinite dimensional simplex \(|\Delta _{{\mathbb {N}}}|\).
The result of Theorem 18 is also stated in preprint (Brooke-Taylor and Testa 2013).
Note that the geometric realisation |X| of a Rado complex X (equipped with the weak topology) does not satisfy the first axiom of countability and hence is not metrizable. This follows from the fact that X is not locally finite. See Spanier (1971), Theorem 3.2.8.
The geometric realisation of a simplicial complex carries yet another natural topology, the metric topology, see Spanier (1971). The geometric realisation of X with the metric topology is denoted \(|X|_d\). While for finite simplicial complexes the spaces |X| and \(|X|_d\) are homeomorphic, it is not true for infinite complexes in general. For the Rado complex X the spaces |X| and \(|X|_d\) are not homeomorphic. Moreover, in general, the metric topology is not invariant under subdivisions, see Mine and Sakai (2012), where this issue is discussed in detail. We do not know if for the Rado complex X the spaces \(|X|_d\) and \(|\Delta _{{\mathbb {N}}}|_d\) are homeomorphic.
The following general statement about subdivisions of simplicial complexes will be used in the proof of Theorem 18.
Lemma 19
Let (K, L) be a pair consisting of a finite simplicial complex K and its subcomplex L. Then there is a subdivision \(K'\) of K with the following properties: (1) \(K'\) contains L as a subcomplex, i.e. no simplex of L is subdivided; (2) L is an induced subcomplex of \(K'\) and (3) The number of new vertexes \(|V(K')-V(K)|\) equals the number of external simplexes of L in K of positive dimension.
Proof
Recall that a simplex \(\sigma \subset K\) is said to be an external simplex of L if \(\sigma \not \subset L\) but all proper faces of \(\sigma \) lie in L. A characteristic property of an induced subcomplex is that all its external simplexes are zero-dimensional. Based on this remark one can prove Lemma 19 by induction as follows.
Suppose the number of external simplexes of L in K of positive dimension is \(N>0\) and let \(\sigma \) be one of such simplexes, i.e. \(\sigma \subset K\), \(\sigma \not \subset L\), \(\partial \sigma \subset L\) and finally \(\dim \sigma >0\). We introduce a new vertex \(v_\sigma \) in the centre of \(\sigma \) and replace the closed star \(\mathrm{St}(\sigma )\) by the simplicial cone \(v_\sigma *(\mathrm{{Lk}}(\sigma )*\partial \sigma );\) this is similar to the star subdivision as described in Rourke and Sanderson (1972), chapter 2. We obtain a subdivision \(K_1\) of K having one extra vertex (lying outside L) such that the number of external simplexes of positive dimension of L in \(K_1\) is \(N-1\). Repeating this process N times, we arrive at the desired subdivision. At each step the number of external simplexes of positive dimension is reduced by one. \(\square \)
The construction of the proof of Lemma 19 is illustrated on Fig. 1. On the left we see a 2-simplex K with its subcomplex \(L=[A, B]\cup \{C\}\) consisting of the interval [A, B] and the vertex C. This subcomplex L is not induced, it has two external simplexes of dimension one. On the right picture we see two extra vertexes D and E lying on each of the external simplexes and a subdivision in which L is an induced subcomplex.
Lemma 20
Let X be a Rado complex. Then there exists a sequence of finite subsets \(U_0\subset U_1\subset U_2\subset \dots \subset V(X)\) such that \(\cup U_n = V(X)\) and for any \(n=0, 1, 2, \dots \) the induced simplicial complex \(X_{U_n}\) is isomorphic to a triangulation \(L_n\) of the standard simplex \(\Delta _{n+1}\) of dimension n. Moreover, for any n the complex \(L_n\) is naturally an induced subcomplex of \(L_{n+1}\) and the isomorphisms \(f_n: X_{U_n} \rightarrow L_n\) satisfy \(f_{n+1}|X_{U_n} = f_n\).
Proof
Let \(V(X)=\{v_0, v_1, \dots \}\) be a labelling of the vertexes of X. One constructs the subsets \(U_n\) and complexes \(L_n\) by induction stating from \(U_0=\{v_0\}\) and \(L_0=\{v_0\}\). Suppose that the sets \(U_i\) and complexes \(L_i\) with \(i\le n\) have been constructed. Consider the subset \(U'_{n+1} = U_n\cup \{v_i\}\subset V(X)\) where \(i\ge 0\) is the smallest integer satisfying \(v_i\notin U_n\). The induced simplicial complex \(X_{U'_{n+1}}\) has dimension \(\le n+1\). Clearly, the complex \(X_{U'_{n+1}}\) has the form \(X_{U_n}\cup (v_i*A_n)\) for some subcomplex \(A_n\subset X_{U_n}\). Applying Lemma 19 to the simplicial pair
we obtain a subdivision \(L_{n+1}\) of the cone \(v_i*X_{U_n}\) which contains
as an induced subcomplex. The map
is a simplcial isomorphism. By induction, \(L_n\) is a subdivison of a simplex of dimension n, and hence the simplicial complex \(L_{n+1}\) is a subdivision of a simplex of dimension \(n+1\) containing \(L_n\) as a codimension one face.
Next we apply Lemma 7 to the abstract simplicial complexes \(L_{n+1}\) and \(X_{U'_{n+1}}\subset L_{n+1}\); it gives a subset \(U_{n+1}\subset V(X)\) containing \(U'_{n+1}\) and an isomorphism \(f_{n+1}: X_{U_{n+1}} \rightarrow L_{n+1}\) satisfying \(f_{n+1}|{X_{U_n}} =f_n\).
Obviously, we have \(\cup U_n = V(X)\). This completes the proof. \(\square \)
Proof of Theorem 18
It follows from Lemma 20. Indeed, the isomorphisms \(f_n: X_{U_n} \rightarrow L_n\) of Lemma 20 determine an isomorphism of simplicial complexes \(f: X\rightarrow L\) where \(L= \cup L_n\) is a subdivision of the simplex \(\Delta _{{\mathbb {N}}}\). Here f is defined by \(f|_{L_n} =f_n\). \(\square \)
Corollary 21
The geometric realisation |X| of the Rado complex is contractible.
Proof
The Corollary follows from Theorem 18. We also give a short independent proof below. Let X be a Rado complex. By the Whitehead theorem we need to show that any continuous map \(f: S^n\rightarrow X\) is homotopic to the constant map. By the Simplicial Approximation theorem f is homotopic to a simplicial map \(g: S^n\rightarrow X\). The image \(g(S^n)\subset X\) is a finite subcomplex. Applying the property of Definition 3 to the set of vertexes U of \(g(S^n)\) and to the subcomplex \(A=X_U\) we find a vertex \(v\in V(X)-U\) such that the cone vA is a subset of X. Since the cone is contractible, we obtain that g, which is equal the composition \(S^n \rightarrow A\rightarrow vA \rightarrow X\), is null-homotopic. \(\square \)
6 Infinite random simplicial complexes
We show in the following Sect. 7 that a random infinite simplicial complex is a Rado complex with probability 1, in a certain regime. In this section we prepare the grounds and describe the probability measure on the set of infinite simplicial complexes.
6.1 Let L be a finite simplicial complex. We denote by F(L) the set of simplexes of L; besides, V(L) will denote the set of vertexes of L. Suppose that with each simplex \(\sigma \subset L\) one has associated a probability parameter \(p_\sigma \in [0,1]\). We shall use the notation \(q_\sigma =1- p_\sigma \). Given a subcomplex \(A\subset L\) we may consider the set E(A|L) consisting of all simplexes of L which are not in A but such that all their proper faces are in A. Simplexes of E(A|L) are called external for A in L. As an example we mention that any vertex \(v\in L-A\) is an external simplex, \(v\in E(A|L)\).
With a subcomplex \(A\subset L\) one may associate the following real number
For example, taking \(A=\emptyset \) we obtain \(p(\emptyset )=\prod _{v\in V(L)} q_v\), the product is taken with respect to all vertexes v of L.
Lemma 22
One has \(\sum _{A\subset L} p(A) =1,\) where A runs over all subcomplexes of L, including the empty subcomplex.
The proof can be found in Sect. 9.
6.2 Let \(\Delta =\Delta _{{\mathbb {N}}}\) denote the simplex spanned by the set \({{\mathbb {N}}}=\{ 1, 2, \dots \}\) of positive integers. We shall denote by \(\Omega \) the set of all simplicial subcomplexes \(X\subset \Delta \). Each simplicial complex \(X\in \Omega \) has finite or countable set of vertexes \(V(X)\subset {{\mathbb {N}}}\) and any finite or countable simplicial complex is isomorphic to one of the complexes \(X\in \Omega \).
6.3 Let \(\Delta _n\) denote the simplex spanned by the vertexes \([n]=\{1, 2, \dots , n\}\subset {{\mathbb {N}}}\). Let \(\Omega _n\) denote the set of all subcomplexes \(Y\subset \Delta _n\). One has the projection
In other words, for \(X\in \Omega \) the complex \(\pi _n(X)\subset \Delta _n\) is the subcomplex of X induced on the vertex set \([n]\subset {{\mathbb {N}}}\).
For a subcomplex \(Y\subset \Delta _n\) we shall consider the set
Note that for \(n=n'\) the sets Z(Y, n) and \(Z(Y', n')\) are either identical (if and only if \(Y=Y'\)) of disjoint; for \(n>n'\) the intersection \(Z(Y, n)\cap Z(Y', n')\) is nonempty if and only if \(Y\cap \Delta _{n'} = Y'\) and in this case \(Z(Y, n) \subset Z(Y', n')\). Note also that for \(n>n'\) and \(Y\cap \Delta _{n'} = Y'\) one has
where \(Y_j\subset \Delta _n\) are all subcomplexes with \(Y_j\cap \Delta _{n'} =Y'\); one of these subcomplexes \(Y_j\) coincides with Y.
Let \({\mathcal {A}}\) denote the set of all subsets \(Z(Y, n)\subset \Omega \) (as Y and n vary) and \(\emptyset \). The set \({\mathcal {A}}\) is a semi-ring, see Klenke (2013), i.e. \({\mathcal {A}}\) is \(\cap \)-closed and for any \(A, B\in {\mathcal {A}}\) the difference \(B-A\) is a finite union of mutually disjoint sets from \({\mathcal {A}}\). We shall denote by \({\mathcal {A}}'\) the \(\sigma \)-algebra generated by \({\mathcal {A}}\).
Example 23
Let \(U\subset {{\mathbb {N}}}\) be a finite subset and let L be a simplicial complex with vertex set \(V(L)\subset U\). Then the set \(\{X\in \Omega ; X_U=L\}\) is the union of finitely many elements of the semi-ring \({\mathcal {A}}\) and in particular, \(\{X\in \Omega ; X_U=L\}\in {\mathcal {A}}'.\) Indeed, let n be an integer such that \(U\subset [n]\) and let \(Y_j\subset \Delta _n\), for \(j\in I\), be the list of all subcomplexes of \(\Delta _n\) satisfying \((Y_j)_U=L\); in other words, \(Y_j\) induces L on U. Then the set \(\{X\in \Omega ; X_U=L\}\) is the union \(\sqcup _{j\in I} Z(Y_j, n).\)
6.4 Next we define a function \(\mu : {\mathcal {A}} \rightarrow {\mathbb {R}}\) as follows. Fix for every simplex \(\sigma \subset \Delta _{{\mathbb {N}}}\) a probability parameter \(p_\sigma \in [0,1]\). The function
will be called the system of probability parameters. Here \(\sigma \) runs over all simplexes \(\sigma \in F(\Delta _{{\mathbb {N}}})\). We shall use the notation \(q_\sigma =1-p_\sigma \).
For an integer \(n\ge 0\) and a subcomplex \(Y\subset \Delta _n\) define
Let us show that \(\mu \) is additive. We know that the set Z(Y, n) equals the disjoint union
where \(Y_j\) are all subcomplexes of \(\Delta _{n+1}\) satisfying \(Y_j \cap \Delta _n =Y\). One of these subcomplexes \(Y_{j_0}\) equals Y and the others contain the vertex \((n+1)\) and have the form
where \(A_j\subset Y\) is a subcomplex. In other words, all complexes \(Y_j\) with \(j\not =j_0\) are obtained from Y by adding a cone with apex \(n+1\) over a subcomplex \(A_j\subset Y\). Clearly, any subcomplex \(A_j\subset Y\) may occur, including the empty subcomplex \(A_j=\emptyset \).
Applying the definition (10) we have
and for \(j\not =j_0\),
where \(n+1\) denotes the new added vertex and \(p'_\sigma \) denotes the probability parameter \(p_{(n+1)\sigma }\) associated to the simplex \((n+1)*\sigma \) (the cone over \(\sigma \) with apex \(n+1\)); besides, \(q'_\sigma = 1- p'_\sigma \). Hence we obtain, using Lemma 22:
Thus we see that \(\mu \) is additive with respect to relations of type (11). But obviously, by (8), these relations generate all additive relations in \({\mathcal {A}}\). This implies that \(\mu \) is additive.
Note that \(\Omega \) can be naturally viewed as the inverse limit of the finite sets \(\Omega _n\), i.e. \(\Omega = \underset{\leftarrow }{\lim }\Omega _n.\) Introducing the discrete topology on each \(\Omega _n\) we obtain the inverse limit topology on \(\Omega \) and with this topology \(\Omega \) is compact and totally disconnected; it is homeomorphic to the Cantor set. The sets \(Z(Y, n)\subset \Omega \) are open and closed in this topology, hence they are compact.
Next we apply Theorem 1.53 from Klenke (2013) to show that \(\mu \) extends to a probability measure on the \(\sigma \)-algebra \(\mathcal A'\) generated by \({\mathcal {A}}\). This theorem requires for \(\mu \) to be additive, \(\sigma \)-subadditive and \(\sigma \)-finite. By Theorem 1.36 from Klenke (2013), \(\sigma \)-subadditivity is equivalent to \(\sigma \)-additivity. Recall that \(\sigma \)-additivity means that for \(A=\sqcup _i A_i\) (disjoint union of countably many elements of \({\mathcal {A}}\)) one has \(\mu (A) =\sum _i \mu (A_i)\). In our case, since the sets \(A_i\subset \Omega \) are open and closed and since \(\Omega \) is compact, any representation \(A=\sqcup _i A_i\) must be finite and hence \(\sigma \)-additivity of \(\mu \) follows from additivity.
For fixed n we have \(\Omega =\sqcup Z(Y, n)\) where Y runs over all subcomplexes of \(\Delta _n\) (including \(\emptyset \)). Using additivity of \(\mu \) and applying Lemma 22, we have \(\mu (\Omega ) = \sum _{Y\subset \Delta _n} \mu (Z(Y, n)) =1.\) This shows that \(\mu \) is \(\sigma \)-finite and hence by Theorem 1.53 from Klenke (2013) \(\mu \) extends to a probability measure on \({\mathcal {A}}'\). The extended measure on \({\mathcal {A}}'\) will be denoted by the same symbol \(\mu \).
Example 24
As in Example 23, let \(U\subset {{\mathbb {N}}}\) be a finite subset and let L be a simplicial complex with vertex set \(V(L)\subset U\). Then
Here \(\Delta _U\) denotes the simplex spanned by U. The proof is left to the reader as an exercise.
7 Random simplicial complex in the medial regime is Rado
In this section we prove that an infinite random simplicial complex in the medial regime is a Rado complex with probability one.Footnote 1
Definition 25
We shall say that a system of probability parameters \(p_\sigma \), see (9), is in the medial regime if there exist \(0<p_-<p_+<1\) such that the probability parameter \(p_\sigma \) satisfies \(p_\sigma \in [p_-, p_+]\) for any simplex \(\sigma \in F(\Delta _{{\mathbb {N}}})\).
In other words, in the medial regime the probability parameters \(p_\sigma \) are uniformly bounded away from zero and one.
Theorem 26
A random simplicial complex with countably many vertexes in the medial regime is a Rado complex, with probability one.
Proof
For a finite subset \(U\subset {{\mathbb {N}}}\) and for a simplicial subcomplex \(A\subset \Delta _U\) of the simplex \(\Delta _U\) consider the set
This set belongs to the \(\sigma \)-algebra \({\mathcal {A}}'\) and has positive measure, see Example 24.
Consider also the subset \(\Omega ^{U, L, A, v}\subset \Omega ^{U, L}\) consisting of all subcomplexes \(X\in \Omega \) satisfying \(X_{U\cup v}=L\cup vA\). Here \(A\subset L\) is a subcomplex and \(v\in {{\mathbb {N}}}-U\).
The conditional probability equals
see (13). Note that the events \(\Omega ^{U, L, A, v}\), conditioned on \(\Omega ^{U, L}\) for various v, are independent and the sum of their probabilities is \(\infty \). Hence we may apply the Borel-Cantelli Lemma (see Klenke 2013, page 51) to conclude that the set of complexes \(X\in \Omega ^{U, L}\) such that \(X_{U\cup v}=L\cup vA\) for infinitely many vertexes v has full measure in \(\Omega ^{U, L}\).
By taking a finite intersection with respect to all possible subcomplexes \(A\subset L\) this implies that the set \(\Omega _*^{U, L}\subset \Omega ^{U, L}\) of simplicial complexes \(X\in \Omega ^{U, L}\) such that for any subcomplex \(A\subset L\) there exists infinitely many vertexes v with \(X_{U\cup v}=L\cup vA\) has full measure in \(\Omega ^{U, L}\).
Since \(\Omega = \cap _U \cup _{L\subset \Delta _U} \Omega ^{U, L}\) (where \(U\subset {{\mathbb {N}}}\) runs over all finites subsets) we obtain that the set \(\cap _U \cup _{L\subset \Delta _U} \Omega ^{U, L}_*\) has measure 1 in \(\Omega \). But the latter set \(\cap _U \cup _{L\subset \Delta _U} \Omega ^{U, L}_*\) is exactly the set of all Rado simplicial complexes, see Lemma 14. \(\square \)
8 Random induced subcomplexes of a Rado complex
In this section we consider a different situation. Let X be a fixed Rado complex with vertex set \(V(X)={{\mathbb {N}}}\). Suppose that each of the vertexes \(n\in {{\mathbb {N}}}\) is selected at random with probability \(p_n\in [0, 1]\) independently of the selection of all other vertexes. Denote by \(X_\omega \) the subcomplex of X induced on the selected set of vertexes. Here \(\omega \) stands for the selection sequence, one may think that \(\omega \in \{0, 1\}^{{\mathbb {N}}}\). Under which condition on the sequence \(\{p_n\}\) the complex \(X_\omega \) is Rado with probability 1?
Applying Borel-Cantelli Lemma we get:
-
(1)
If \(\sum p_n <\infty \) then complex \(X_\omega \) has finitely many vertexes, with probability 1.
-
(2)
If \(\sum p_n =\infty \) then complex \(X_\omega \) has infinitely many vertexes, with probability 1.
-
(3)
If \(\sum q_n <\infty \) (where \(q_n=1-p_n\)) then the set of vertexes of \(X_\omega \) has a finite complement in \({{\mathbb {N}}}\) and hence \(X_\omega \) is a Rado complex with probability 1. In (3) we use Corollary 15.
The following result strengthens point (3) above:
Lemma 27
Suppose that for some \(p>0\) one has \(p_n\ge p>0\) for any \(n\in {{\mathbb {N}}}\). Then \(X_\omega \) is a Rado complex with probability 1.
Proof
Denote by \(X_n\) the subcomplex of X induced on the set \([n]= \{1, 2, \dots , n\}\subset {{\mathbb {N}}}\). For a subcomplex \(A\subset X_n\) consider the set of vertexes
We know that this set is infinite (see Lemma 14) and since each of the elements of this set is a vertex of \(X_\omega \) with probability at least \(p>0\) we obtain (using Borel–Cantelli) that with probability 1 the intersection \(V(X_\omega ) \cap W(A, n)\) is infinite. Hence the set
has measure 1 (as intersection of countably many sets of measure one). Here we use \(\sigma \)-additivity of the Bernoulli measure. It is obvious that for any \(\omega \) lying in the intersection (15) the induced complex \(X_\omega \) is ample and hence Rado. \(\square \)
9 Proof of Lemma 22
We obviously have
In the above sum, J can be also the empty set. Denote by \(A(J)\subset J\) the set of all simplexes \(\sigma \in J\) such that for any face \(\tau \subset \sigma \) one has \(\tau \in J\). Note that \(A= A(J)\) is a simplicial complex, it is the largest simplicial subcomplex of L with \(F(A)\subset J\). We also note that the set of external simplexes E(A|L) is disjoint from J.
Fix a subcomplex \(A\subset L\) and consider all subsets \(J\subset F(L)\) with \(A(J)=A\). Any such subset \(J\subset F(L)\) contains F(A) and is disjoint from E(A|L). Conversely, any subset \(J\subset F(L)\) containing F(A) and disjoint from E(A|L) satisfies \(A(J)=A\).
Denoting \(S(A) = F(L) - F(A) -E(A|L)\) and \(I=J\cap S(A)\) we see that any term of (16) corresponding to a subset J with \(A(J)=A\) can be written in the form
and the first factor above is p(A), see (6). Hence the sum of all terms in the sum (16) corresponding to the subsets J with \(A(J)=A\) equals
We therefore see that the statement of Lemma 22 follows from (16).
Notes
Finite simplicial complexes in the medial regime were studied in Farber and Mead (2020).
References
Ackermann, W.: Die Widerspruchsfreiheit der allgemeinen Mengenlehre. Math. Ann. 114, 305–315 (1937)
Battiston, F., et al.: Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. (2020). https://doi.org/10.1016/j.physrep.2020.05.004
Blass, A., Harary, F.: Properties of almost all graphs and complexes. J. Graph Theory 3(3), 225–240 (1979)
Brooke-Taylor, A., Testa, D.: The infinite random simplicial complex (2013). arXiv: 1308.5517v1
Cameron, P.: The Random graph. The mathematics of Paul Erdős, II, Algorithms Combin., vol. 14, pp 333–351. Springer, Berlin (1997)
Cameron, P.: The random graph revisited. European Congress of Mathematics, Vol. I (Barcelona, 2000), Progr. Math., vol. 201, pp. 267–274. Birkhäuser, Basel (2001)
Erdős, P., Rényi, A.: Asymmetric graphs. Acta Math. Acad. Sci. Hungar. 14, 295–315 (1963)
Even-Zohar, C., Farber, M., Mead, L.: Ample simplicial complexes (2020). arXiv:2012.01483
Farber, M., Mead, L.: Random simplicial complexes in the medial regime. Topol. Appl. 272, 107065 (2020)
Hodges, W.: Model Theory. Cambridge University Press, Cambridge (1993)
Klenke, A.: Probability Theory. Springer, Berlin (2013)
Mine, K., Sakai, K.: Subdivisions of simplicial complexes preserving the metric topology. Canad. Math. Bull. 55(1), 157–163 (2012)
Rado, R.: Universal graphs and universal functions. Acta Arith. 9, 393–407 (1964)
Rotman, B.: Remarks on some theorems of Rado on universal graphs. J. Lond. Math. Soc. (2) 4, 123–126 (1971)
Rourke, C., Sanderson, B.: Introduction to Piecewise-Linear Topology. Springer, Berlin (1972)
Spanier, E.: Algebraic Topology (1971)
Vershik, A. M.: Random metric spaces and universality. (Russian) Uspekhi Mat. Nauk 59 (2004), no. 2(356), 65–104; translation in Russian Math. Surveys, vol. 59, no. 2, pp. 259–295 (2004)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Michael Farber was partially supported by a grant from the Leverhulme Trust.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Farber, M., Mead, L. & Strauss, L. The Rado simplicial complex. J Appl. and Comput. Topology 5, 339–356 (2021). https://doi.org/10.1007/s41468-021-00069-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41468-021-00069-z
Keywords
- Rado graph
- Rado simplicial complex
- Random simplicial complex
- Ample simplicial complex
- Universal simplicial complex