1 Introduction

Mirrlees (1971) addresses the optimal taxation of a government that values an additional dollar net income higher for low income earners, assuming: (a) a fixed revenue requirement (as Ramsey (1927)) and (b) that the agents have private information about their earning abilities. This analysis turned out to be important not only for the theory of taxation but even more important for the theory of mechanism design (earning Mirrlees the Nobel prize). In spite of a government’s egalitarian concern, the framework of Mirrlees (1971) including the many follow ups (Casamatta (2021) is a recent variant allowing for efforts in order to avoid taxes) cannot justify progressive taxation and in fact implies zero marginal tax for the most able agent (due to the property of ‘no distortion at the top’ characterizing optimal mechanisms, see e.g., Fudenberg and Tirole (1992)).

Brennan and Buchanan (1977, 1980) argue that tax revenues are not exogenously fixed. Instead, they are endogenously determined and depend also on how efficient the tax scheme is. More precisely, a tax scheme that minimizes the deadweight loss allows a government to raise more revenues. Hence, an inefficient tax code can limit the tax burdenFootnote 1. Indeed, the 20th century has seen a dramatic rise in tax revenues in particular but not only in the industrialized countries from below 10% to around 50% of GDP for many industrialized (mostly European) countries (see Piketty (2014)). Although the expansion can be attributed to the introduction of a welfare state and the elimination of some social ills, this cannot be the entire story, because of the large differences in tax revenues (in absolute terms, $ per capita, but even in relative terms, shares of GDP) across countries that have comparable social indicators. Tanzi and Schuknecht (1997, 2005) show that a share of government revenues beyond a threshold (of around 30%) does not improve social indicators (in industrialized countries) anymore. While the governments of France, Sweden, Germany and a few others collect around 50% of GDP, countries like South Korea, Japan, Australia and Switzerland top all social indicators yet have total tax revenues (from social contributions, direct and indirect taxes given as a share of GDP) of around and even below 30% in 2017 (according to https://ourworldindata.org/taxation). Therefore, the assumption - the amount of tax revenues is exogenously given - seems implausible.

Brennan and Buchanan (1980) find the assumption of a welfare maximizing and deadweight loss minimizing government unrealistic and turn it upside-down by assuming a government that maximizes tax revenues. They call it a “Leviathan” government (of course, with reference to Thomas Hobbes’ Leviathan). Even if one disagrees with this pessimistic view, it makes sense according to Sandmo (1990): “Suppose that you are entering into a contract with a carpenter about repairs on your house. You may already have a theory of the behavior of carpenters as being on average highly skilled, punctual, and honest. Would you write the contract on the assumption that the theory applied also in this particular case? Probably not; the careful homeowner would like to have a contract that protected him against the possibility of the carpenter having the opposite characteristics. Buchanan argues that the same principle applies to the relationship between the individual and the public sector in a democracy.” The debate between (Buchanan & Musgrave, 1999) about the proper role of governments is very interesting in this context too.

Many papers address different issues related to the Leviathan hypothesis, in reviews, e.g., in the so called Mirrlees review on tax design, Mirrlees et al. (2010), and in the review of Boettke and Palagashvili (2015) but, surprisingly, not in many other and quite prominent reviews, e.g., in Mankiw et al. (2009) and Diamond and Saez (2011). Many papers paying more than lip service to the Leviathan hypothesis focus on capital taxation and tax competition: e.g., Rauscher (2005) and Keen and Kotsogiannis (2003); Brülhart and Jametti (2019) show for the Swiss cantons that tax competition tames the Leviathan; Keisuke, Ogawa and Taiki (2019), Itaya et al. (2014), followed up by Eichner and Pethig (2015), study the sustainability and stability of capital tax coordination in a repeated game model with tax-revenue maximizing governments. However and to my surprise no paper applies, as Mirrlees (1971), the insights of mechanism design to a Leviathan government that taxes agents who have private information about their earning ability (productivity, work ethic, talents, etc.). Only Homburg (2001) indicates how a Leviathan objective would change the tax system and mentions the formal similarity with the welfare maximization problem. The differences to this paper are: he does not include a participation constraint so that the Leviathan can tax all the income of the least efficient agent, on a formal aspect, he carries out the calculations in a different (discrete type) framework, and last but not least, his paper has a different objective (an axiomatic restatement of the standard approach to nonlinear income taxation).

Given this lack of treatment in the literature, I address how a Leviathan government designs a tax scheme in which the people earning’s capabilities are their private information. Of course, agents with a high earning potential seem a prime target from a Leviathan’s perspective (and also for an egalitarian government). However, if those agents are taxed, they will lower their efforts, e.g., by substituting leisure activities, ranging from more time spent with the family or for hobbies like sports, playing piano or another instrument, painting, acting, etc. A Leviathan government will account for this effect as well as that high taxes on agents with a high earning potential can induce them to mimic a less efficient type. Hence, the Leviathan’s tax regime must be incentive compatible and this is one reason why it shares some features with a government collecting the necessary and ex ante fixed tax revenues in a deadweight loss minimizing way. A second explanation is that both kinds of governments with their different objectives and with revenues either fixed or unconstrained behave in way like a monopolist facing similar ‘demands’, i.e., how the agents respond to taxation.

The model of the Leviathan government is introduced in Section 2 and analyzed in Section 3. The sensitivity of the results is analyzed with respect to some assumptions (about the distribution and different measures of efficiency, convex instead of linear) in Section 4.

2 The Model

2.1 Government

The objective of a Leviathan government is to tax the earning of each individual such that the total tax revenues are maximized,

$$\begin{aligned} \underset{\tau }{\max }\underset{\underline{t}}{\overset{\bar{t}}{\int }} \tau \left( t\right) dF\left( t\right) . \end{aligned}$$
(1)

The instrument, \(\tau \left( t\right)\), denotes the tax collected from individuals with characteristic \(t\in \left[ \underline{t},\bar{t}\right]\), which describes their capability to earn money. The total tax revenues are obtained by aggregating over the set of all agents. Although the individual characteristic of any agent is unknown to the government, it knows (or assumes a corresponding prior of) the cumulative distribution function \(F\left( t\right)\) with full support, i.e., \(f:=dF/dt>0\) for all \(t\in \left[ \underline{t},\bar{t}\right]\).

The characteristics are taken as given although education and the development of one’s talent are endogenous, which depend on an agent’s intertemporal investments that depend in turn on the (expected) future taxes. An individual’s investment into human capital is affected by the tax system, which can lead to thresholds whether to pursue a career, say in sports or arts, or not, compare Yegorov and Wirl (2020). However, the intertemporal interplay between the development of one’s abilities and thus one’s earning capabilities and the tax code is left for future research; Golosov et al. (2003) consider an intertemporal set up but have to assume that (i) the government commits to its tax policy and (ii) that the abilities are private information but independent draws from a probability distribution (i.e., not acquired by the agent).

2.2 Agents

For concreteness, I assume that the agents differ with respect to their individual type \(\left( t\right)\), which is their private information. Depending on their type, they can earn the observable gross income \(\left( x\left( t\right) \right)\) that delivers the subjective gross (i.e., prior to paying taxes) payoff \(\left( W\right)\) accounting for the cost of effort \(\left( C\right)\),

$$\begin{aligned} W\left( x,t\right)= & {} x-C\left( x,t\right) , \nonumber \\ C_{x}> & {} 0,\;C_{xx}>0,\;C_{t}<0. \end{aligned}$$
(2)

Therefore, a larger value of t characterizes a more efficient type, because of the lower costs of earning the income x due to the assumption \(C_{t}<0\). Furthermore,

$$\begin{aligned} W_{xt}=-C_{xt}>0, \end{aligned}$$
(3)

in order to satisfy the single crossing property (Fudenberg & Tirole, 1992). The assumption in (3) is not only a technical necessity but is also plausible, because a more efficient type has lower costs of earning an additional dollar, i.e., \(C_{xt}<0\).

In the absence of taxes, the earning of each agent type, denoted \(x^{0}\left( t\right)\), satisfies the first order condition of maximizing W ,

$$\begin{aligned} x^{0}\left( t\right) :W_{x}=1-C_{x}=0. \end{aligned}$$
(4)

Therefore, the larger and thus more efficient types t (as explained above) earn more, \(\dot{x}^{0}>0\), due to the implicit function theorem; throughout the paper, dots above variables denote their total derivative with respect to the type t.

2.3 Example

I use the following reference example,

$$\begin{aligned} C\left( x,t\right) =\frac{c\left( x\right) }{t},\;c\left( x\right) =\frac{ \gamma }{2}x^{2}, \end{aligned}$$
(5)

to sketch the Leviathan’s tax system and to derive further, in particular, comparative static results. If untaxed, agents will earn,

$$\begin{aligned} x^{0}\left( t\right) =\frac{t}{\gamma }, \end{aligned}$$
(6)

i.e., their gross earnings would be linear in t, their measure of ability (or efficiency).

The economics underlying the specification in (5) is the following: agents exercise effort e in order to earn x. All have the same convex (and in (5) quadratic) cost of effort \(c\left( e\right)\) but differ in their productivity \(\left( \varphi \right)\): \(x=\varphi \left( t\right) e\). Using

$$\begin{aligned} c\left( e\right) =\frac{\gamma }{2}e^{2}\text { and }\varphi \left( t\right) = \sqrt{t} \end{aligned}$$
(7)

yields (5). Alternatively, one can assume that all types are equally productive but differ in their work ethic. If more efficient types have lower effort costs, \(\left( c/t\right)\), then the same cost function (5) results. Therefore, both characterizations of the types - either by their productivity or work ethic - are equivalent; this equivalence does not extend to multitasking, see Helm and Wirl (2021).

Assuming a linear instead of a concave (square root) relation for individual productivity, i.e., \(\varphi \left( t\right) =t\), then

$$\begin{aligned} C\left( x,t\right)= & {} \frac{c\left( x\right) }{t^{2}}, \end{aligned}$$
(8)
$$\begin{aligned} C_{xt}= & {} -2\frac{\gamma x}{t^{3}}<0,C_{xtt}=6\frac{\gamma x}{t^{4}}>0. \end{aligned}$$
(9)

Or even more general,

$$\begin{aligned} C\left( x,t\right) =\frac{c\left( x\right) }{\eta \left( t\right) },\;\eta ^{\prime }>0,\;2\frac{\eta ^{\prime }t}{\eta }>\frac{\eta ^{\prime \prime }t }{\eta ^{\prime }}, \end{aligned}$$

in which \(\eta\) is a measure of an agent’s efficiency and \(\eta\) is linear in the reference example (5) and quadratic in (8); the last condition, twice the elasticity of the efficiency measure \(\left( \eta \right)\) exceeds the elasticity of the marginal efficiency \(\left( \eta ^{\prime }\right)\), ensures \(C_{xtt}>0\). The positive sign of this third order derivative ensures the monotonicity of the solution, which is necessary for an implementable tax scheme (see Fudenberg and Tirole (1991)).

The inclusion of a cost parameter \(\left( \gamma \right)\) allows to normalize the expected value of the measure of individual efficiency, \(Et=1\) . The uniform distribution with the density \(\left( f\right)\), the distribution function \(\left( F\right)\),

$$\begin{aligned} f\left( t\right) =\frac{1}{2\Delta }\text { and }F\left( t\right) =\frac{ t+\Delta -1}{2\Delta },\text { }t\in \left[ \underline{t},\bar{t}\right] = \left[ 1-\Delta ,1+\Delta \right] , \end{aligned}$$
(10)

and the implied hazard rate

$$\begin{aligned} h:=\frac{f}{1-F}=\frac{1}{1+\Delta -t} \end{aligned}$$
(11)

serves as example.

The reference parameter values are,

$$\begin{aligned} \gamma =1/2,\;\underline{t}=0.25,\;\bar{t}=1.75\Longrightarrow \Delta =0.75, \end{aligned}$$
(12)

so that the types \(\left( \bar{t}/\underline{t}\right)\) as well their earnings in the absence of taxation differ up to a factor of \(7=x^{0}\left( \bar{t}\right) /x^{0}\left( \underline{t}\right)\).

The sensitivity of the results is tested by considering different measures of efficiency \(\left( \eta \right)\) and different distributions (but assuming an increasing hazard rate, \(\dot{h}>0\), in line with the agency literature, see Fudenberg and Tirole (1992)).

3 A Leviathan’s Optimal Tax Schedule

The government’s optimization (1) faces two constraints if taxing observable gross incomes. The first is the incentive compatibility constraint: An agent of type t facing the tax schedule \(\tau \left( .\right)\) will pretend that type \(\hat{t}\), which maximizes his type t -payoff, denoted \(U\left( \hat{t},t\right)\) and defined below in (13 ), after paying the taxes corresponding to the pretended type. The revelation principle allows to restrict the analysis to mechanisms that incentivize the agent to tell the truth, i.e.,

$$\begin{aligned} t=\arg \underset{\hat{t}}{\max }\;U\left( \hat{t},t\right) :=x\left( \hat{t} \right) -C\left( x\left( \hat{t}\right) ,t\right) -\tau \left( \hat{t} \right) . \end{aligned}$$
(13)

Therefore, the revelation principle allows to define \(U\left( t\right) :=U\left( t,t\right)\) with the derivative,

$$\begin{aligned} \dot{U}:=\frac{dU}{dt}=\frac{\partial U}{\partial t}=-C_{t}>0, \end{aligned}$$
(14)

due to the envelope theorem. All governments face in addition the participation constraint, because a worker can either walk away (in a Tiebout model, but, e.g., not in the Communist countries before 1989 and even today in North Korea) or can refuse to work (this option might be restricted in some countries). Therefore, the second constraint is

$$\begin{aligned} U\left( t\right) \ge R\left( t\right) \quad \forall t\in \left[ \underline{t}, \bar{t}\right] , \end{aligned}$$
(15)

in which R denotes an agent’s utility from exercising the outside option (often called reservation price in IO-settings), e.g., either refusing to work or working in the shadow economy. Although R could depend on an agent’s type, a constant is assumed. This assumption has no effect as long as \(\dot{R}<\dot{U}\), so that the constraint (15) binds only at \(t= \underline{t}\). If the utility from the outside option exceeds an (inefficient) agent’s earning potential, then subsidies, i.e., welfare payments, are due. The participation constraint (15) is ignored in the classical set up of Mirrlees (1971) and the follow ups, which impose an exogenously fixed revenue requirement.

Since,

$$\begin{aligned} U\left( t\right) =W\left( t\right) -\tau \left( t\right) \ge R\Longrightarrow \tau \left( t\right) =W\left( t\right) -U\left( t\right) \end{aligned}$$

the government’s optimization problem, (1) subject to the constraints (14) and (15), can be turned into an optimal control problem. The constraints are the differential equation (17) implied by incentive compatibility constraint (14) and the inequality in (18) accounts for the individual rationality constraint (15 ),

$$\begin{aligned}&\underset{\left\{ x\left( t\right) ,\;t\in \left[ \underline{t},\bar{t} \right] \right\} }{\max }\;\underset{\underline{t}}{\overset{\overline{t}}{ \int }}\left[ W\left( x\left( t\right) ,t\right) -U\left( t\right) \right] dF\left( t\right) =\underset{\underline{t}}{\overset{\overline{t}}{\int }} \frac{x\left( t\right) -\frac{\gamma }{2t}x^{2}\left( t\right) -U\left( t\right) }{\overline{t}-\underline{t}}dt, \end{aligned}$$
(16)
$$\begin{aligned}&\dot{U}\left( t\right) =W_{t}=-C_{t}=\frac{\gamma x^{2}\left( t\right) }{ 2t^{2}}, \end{aligned}$$
(17)
$$\begin{aligned}&U\left( t\right) =x-C\left( x\left( t\right) ,t\right) -\tau \left( t\right) =x\left( t\right) -\frac{\gamma x^{2}\left( t\right) }{2t}-\tau \left( t\right) \ge R\text { }\forall t\in \left[ \underline{t},\overline{t}\right] . \end{aligned}$$
(18)

The reference example is substituted on the right hand sides.

According to Fudenberg and Tirole (1992), an implementable mechanism requires monotonicity,

$$\begin{aligned} \dot{x}\left( t\right) \ge 0\text { }\forall t\in \left[ \underline{t}, \overline{t}\right] . \end{aligned}$$
(19)

This property can be ensured by additional assumptions about the costs (such as \(C_{xtt}>0\) above) or must be checked after solving the optimization problem (16) - (18). The reason is that the above optimal control problem, more precisely, the differential equation (17) is based only on a necessary optimality condition implied by the revelation principle, i.e., (13). It turns out that monotonicity is guaranteed by the assumption \(C_{xtt}>0\) but can be violated for the extension that a government includes the agents’ welfare in its objective (see online Appendix and how to render the mechanism implementable if the control problem yields a non-monotonic solution \(x\left( t\right)\)).

A crucial question is how to account for the participation constraint (18)? The Leviathan could allow for the untaxed outcome, \(x=x^{0}\) from (4) along a binding state constraint (18), \(U=R\), and could complement that by subsidies, \(\tau \le 0\), if they were necessary to satisfy (18). This would require a drop in gross earnings x at the type at which the boundary solution is joined with the interior solution (derived below). This violates the requirement of monotonicity in (19 ). Another possibility is to apply the interior solution (called the relaxed program, i.e., ignoring the state constraint (18)) for all types and to back it up by subsidies, \(\tau \le 0\), if necessary such that \(U=W-\tau \ge R\). This solution is continuous, monotonic as we will see, and is thus incentive compatible. Therefore, assuming a constant R, the state constraint (18) can be turned into an initial condition for the state differential equation (17),

$$\begin{aligned} U\left( \underline{t}\right) =R. \end{aligned}$$
(20)

The reason is that \(\dot{U}\ge 0\) from the incentive compatibility constraint (17) ensures that the participation constraint (18 ) is then met for all types.

Defining the Hamiltonian

$$\begin{aligned} H:=\left( W-U\right) f+\lambda , \end{aligned}$$

with \(\lambda\) denoting the shadow price (or costate variable) of the state U, the first order optimality conditions are:

$$\begin{aligned} H_{x}= & {} W_{x} \quad f+\lambda W_{xt}=0, \end{aligned}$$
(21)
$$\begin{aligned} \dot{\lambda }= & {} f,\;\lambda \left( \overline{t}\right) =0\Longrightarrow \lambda \left( t\right) =F\left( t\right) -1. \end{aligned}$$
(22)

Therefore, the Leviathan’s optimal mechanism is to ‘demand’ from an agent of the (unknown) type t the gross earning \(x^{L}\left( t\right)\) that is characterized by the following condition,

$$\begin{aligned} x^{L}\left( t\right) :W_{x}=\frac{W_{xt}}{h},\;h:=\frac{f}{1-F}. \end{aligned}$$
(23)

The left hand side is the agent’s marginal benefit from earning one dollar more \(\left( W_{x}\right)\). The right hand side accounts for the agency costs that the government faces due to the private information held by each agent (about his type t). It consists of the hazard rate \(\left( h\right)\) and of the mixed derivative \(W_{xt}>0\). As a consequence, taxation lowers each agent’s output relative to the untaxed case, \(x^{L}<x^{0}\) for all \(t< \overline{t}\), because \(x^{0}\) results from equating the left hand side in ( 23) to zero according to (4). Only at the top, \(t= \overline{t}\), both solutions coincide, \(x^{L}\left( \overline{t}\right) =x^{0}\left( \overline{t}\right)\), which is known as no distortion at the top, because of (23) and \(h\rightarrow \infty\) for \(t\rightarrow \overline{t}\).

An agent of type t will earn the type-specific gross income \(x^{L}\left( t\right)\) determined in (23) and will pay the tax

$$\begin{aligned} \tau \left( t\right) =W\left( x^{L}\left( t\right) ,t\right) -U\left( t\right) . \end{aligned}$$
(24)

The agent’s net payoff \(\left( U\right)\) follows from integrating the incentive compatibility constraint (17) after substituting the optimal program \(x^{L}\) and using the initial condition (20),

$$\begin{aligned} U\left( t\right) =R+\underset{\underline{t}}{\overset{t}{\int }}C_{v}\left( x^{L}\left( v\right) ,v\right) dv. \end{aligned}$$
(25)

Solving the equation (23) for the type, \(t=t\left( x\right)\), and substituting this relation into the tax schedule (24) allows to express the tax payment as a function of the agent’s gross earning, \(\tau \left( x\right) =\tau \left( t\left( x\right) \right)\).

Proposition 1

(i) The agents’ (gross) earnings are lowered by taxation, i.e., \(x^{L}\left( t\right) \le x^{0}\left( t\right)\), increase with respect to the type, \(\dot{x}^{L}>0\) if \(W_{xtt}=-C_{xtt}<0\), and approach the untaxed outcome for the most efficient type, \(x^{L}\left( \bar{t}\right) =x^{0}\left( \bar{t} \right)\), i.e., no distortion at the top.

(ii) The tax is increasing, \(\dot{\tau }\ge 0\). This growth peters out for the efficient types, \(\dot{\tau }\rightarrow 0\) for \(t\rightarrow \bar{t}\). Therefore, the marginal tax is reduced to zero at the top, \(\tau ^{\prime }\left( x^{L}\left( \bar{t}\right) \right) =0\), as in Mirrlees (1971), and the average tax payment, \(\tau \left( x\right) /x\), declines at least for high types.

(iii) Taxation increases inequality, more precisely, the spread of gross incomes, \(x^{L}\left( \overline{t}\right) /x^{L}\left( \underline{t}\right) >x^{0}\left( \overline{t}\right) /x^{0}\left( \underline{t}\right)\).

(iv) A higher utility from exercising the outside option (i.e., a larger value of R) lowers tax levels as well as average taxes.

The monotonicity property, \(\dot{x}>0\), follows from the assumptions about W (concavity and the single crossing property), the hazard rate (increasing) and the additional assumption about the third derivative (sufficient, so that weaker assumptions still allow for monotonicity) due to the implicit function theorem,

$$\begin{aligned} \dot{x}^{L}=W_{xt}-\frac{hW_{xtt}-W_{xt}\dot{h}}{h^{2}}>0. \end{aligned}$$
(26)

By construction and the revelation principle, an agent of type t will exercise the effort that earns him \(x^{L}\left( t\right)\) and will pay the tax \(\tau \left( t\right) =W\left( x^{L}\left( t\right) ,t\right) -U\left( t\right)\) that increases since

$$\begin{aligned} \dot{\tau }=\dot{W}-\dot{U}=W_{x}\dot{x}\ge 0. \end{aligned}$$
(27)

Hence, \(\dot{\tau }\rightarrow 0\) for \(t\rightarrow \bar{t}\) due to \(W_{x}\rightarrow 0\) and \(\dot{x}>0\) with the consequences addressed in Proposition 1.

The tax need not be positive for all types, because even a Leviathan has to subsidize highly inefficient types who cannot make a living from their work, \(\tau <0\) if \(W\left( x^{L}\left( t\right) ,t\right) <R\) for a type t. A higher value of R lowers the tax levels as well as the average taxes because the net payoff \(\left( U\right)\) of all agents is increased so that also their net incomes, \(x-\tau\), must increase. Taxation increases the spread of gross incomes, \(x^{L}\left( \overline{t}\right) /x^{L}\left( \underline{t}\right) >x^{0}\left( \overline{t}\right) /x^{0}\left( \underline{t}\right)\), because \(x^{L}\left( \underline{t}\right) <x^{0}\left( \underline{t}\right)\) yet, \(x^{L}\left( \overline{t}\right) =x^{0}\left( \overline{t}\right)\).

4 Example

Since further properties of the Leviathan’s optimal programme, \(\left\{ x\left( t\right) ,\tau \left( t\right) ,\;t\in \left[ \underline{t}, \overline{t}\right] \right\}\), depend on third and even higher order derivatives of W, I turn to the example (5) and the uniform distribution (20). The government ‘asks’ each agent to earn,

$$\begin{aligned} x^{L}\left( t\right) =\frac{t^{2}}{\gamma \overline{t}}, \end{aligned}$$
(28)

I.e., the taxed gross earning \(x^{L}\left( t\right)\) is a convex (quadratic) function of individual efficiency type \(\left( t\right)\). Therefore, taxation increases the spread of gross earnings from a linear to a quadratic relation. Output is flattened for low but steepened for high types (and even for types below the average type, \(t=1\)),

$$\begin{aligned} \dot{x}^{L}=\frac{2t}{\gamma \overline{t}}>\dot{x}^{0}=\frac{1}{\gamma } \Longleftrightarrow t>\frac{\overline{t}}{2}=1. \end{aligned}$$

An agent’s payoff after paying his tax follows from substituting the derived solution (28) into (25),

$$\begin{aligned} U\left( t\right) =R+\frac{1}{2\gamma \overline{t}^{2}}\underset{\underline{t} }{\overset{t}{\int }}v^{2}dv=R+\frac{t^{3}-\underline{t}^{3}}{6\gamma \overline{t}^{2}}. \end{aligned}$$
(29)

This expression allows to compute the tax,

$$\begin{aligned} \tau \left( t\right) =x^{L}\left( t\right) -\frac{\gamma }{2}\left( x^{L}\left( t\right) \right) ^{2}-U\left( t\right) =\frac{\left( 6\overline{t }t^{2}+\underline{t}^{3}-4t^{3}\right) }{6\gamma \overline{t}^{2}}-R. \end{aligned}$$
(30)

The tax increases with the agent’s type,

$$\begin{aligned} \dot{\tau }=\frac{2t\left( \overline{t}-t\right) }{\gamma \overline{t}^{2}}>0, \end{aligned}$$

at an increasing rate for low, more precisely, \(t<\frac{\overline{t}}{2}\), but at a diminishing rate for large types and stopping at the most efficient type, \(\dot{\tau }\left( \overline{t}\right) =0\), which holds generally according to Proposition 1.

Solving the relaxed program, (23) or (28), for t instead of x,

$$\begin{aligned} t=\sqrt{\gamma \overline{t}x}, \end{aligned}$$
(31)

and substituting this relation into the type dependent tax schedule (30) determines the tax with respect to gross incomes (instead of depending on the unobservable type),

$$\begin{aligned} \tau \left( x\right) =x-R+\frac{\underline{t}^{3}}{6\gamma \overline{t}^{2}}- \frac{2\sqrt{\gamma }x^{3/2}}{3\sqrt{\overline{t}}}. \end{aligned}$$
(32)

Therefore, the tax increases with income,

$$\begin{aligned} \tau ^{\prime }\left( x\right) =1-\frac{\sqrt{\gamma x}}{\sqrt{\overline{t}}} \ge 0, \end{aligned}$$

because \(x\le \overline{t}/\gamma\). However, the marginal tax rate must decline given the concave function \(\tau \left( x\right)\) in (32) and turns zero at the top, i.e., \(\tau ^{\prime }\left( x^{L}\left( \bar{t} \right) \right) =0\). Therefore, the average tax,

$$\begin{aligned} \frac{\tau \left( x\right) }{x}=1-\frac{R}{x}+\frac{\underline{t}^{3}}{ 6\gamma \overline{t}^{2}x}-\frac{2\sqrt{\gamma }\sqrt{x}}{3\sqrt{\overline{t} }}, \end{aligned}$$
(33)

need not increase either, since

$$\begin{aligned} \left( \frac{\tau \left( x\right) }{x}\right) ^{\prime }=\frac{R}{x^{2}}- \frac{\underline{t}^{3}}{6\gamma \overline{t}^{2}x^{2}}-\frac{\sqrt{\gamma } }{3\sqrt{\overline{t}}\sqrt{x}}. \end{aligned}$$
(34)

Indeed, \(\left( \tau /x\right) ^{\prime }<0\) at and thus close to \(\overline{ t}\) (due to \(\dot{\tau }\rightarrow 0\) yet \(\dot{x}>0\) for \(t\rightarrow \overline{t}\)) and even globally for \(R=0\). If \(R>0\), then the average tax increases at low but declines at high levels of earnings. However, the average tax is declining in the agent’s cost parameter \(\gamma\) for all levels of income, i.e., \(\left( \tau /x\right) _{\gamma }<0\).

The explicit solution, (28) - (32), allows not only for the computations shown in Fig. 1 but also for characterizations in addition to those in Proposition 1.

Proposition 2

Assuming the specification (5) and the uniform distribution (10), then:

(i) Taxes increase with respect to gross earning \(\left( x\right)\) and type \(\left( t\right)\) at an increasing rate for low types, more precisely, \(t< \frac{\overline{t}}{2}=Et=1\) and thus below the average type, but at a diminishing rate for the larger types.

(ii) A higher cost parameter \(\gamma\), i.e., a less efficient population due to a lower work ethic (or productivity), lowers the tax level, \(\tau _{\gamma }<0\) for all types, and the average tax for all levels of income, \(\left( \tau \left( x\right) /x\right) _{\gamma }<0\).

Fig. 1 shows the results for the reference example. The chart at the top left hand side compares the gross earnings with \(\left( x^{L}\right)\) and without taxation \(\left( x^{0}\right)\) with respect to an agent’s type t . It highlights how private information, incentives and taxes widen the spread of gross earnings from a factor of 7 for \(x^{0}\) to \(49=x^{L}\left( \overline{t}\right) /x^{L}\left( \underline{t}\right)\). Taxation combined with subsidies reduces this ratio for the net earnings to around 23, which is still much less egalitarian than in the absence of taxation. The chart on the top and right hand side shows the tax that the Leviathan charges. Accounting for a positive valuations of the outside options leads to subsidies for low types (for less than 10% of the population for \(R=0.10\)). However, for \(R=0\), even the inefficient types would have to pay taxes with the consequence of a very large spread of net incomes (at 457!) due to the then very low net income of the inefficient types. The tax levels are convex for low but concave for high types (as addressed above) so that the marginal tax increases at low types (and at low levels of income) but declines for high types and so does the average tax per dollar earning (the chart at the bottom below the tax schedule); \(R=0\) implies that the average tax declines across all levels of income, which follows from derivative in (34 ). The chart at the bottom left hand side compares the agents’ payoffs without taxes \(\left( W\right)\) and with taxes \(\left( U\right)\) and for both assumptions about R (which affect U but not W).

Fig. 1
figure 1

Leviathan Government: Earning, tax and welfare, \(\Delta =3/4\), \(\gamma =1/2\), \(R=1/10\)

Full size image

5 Sensitivity

5.1 Different Distributions

An interesting question is how different distributions of efficiencies, in particular those different from the uniform one, affect a Leviathan’s tax regime. From (23) follows that only the implied hazard rate matters. For a start, assume a larger spread \(\Delta\) of the uniform distribution (10). Since, \(\left( 1/h\right) =1+\Delta -t\), any increase to \(\tilde{\Delta }>\Delta\) reduces the hazard rate in the original interval and thus increases the right hand side of the relaxed program condition (23). Therefore, less output will be demanded, i.e., \(\tilde{x}^{L}<x^{L}\) for all \(t\in \left[ 1-\Delta ,1+\Delta \right]\), if the width of the uniform distribution is increased from \(\Delta\) to \(\tilde{\Delta }\). A corresponding example is, when technological changes (or globalization) increase the productivity at the top but lower it at the bottom.

Because of the importance of the hazard rate, it is useful to introduce the definition of hazard rate dominance: Given two densities, \(f_{1}\) dominates \(\left( \succ \right)\) \(f_{2}\) in terms of the hazard rate,

$$\begin{aligned} f_{1}\succ f_{2}\Longleftrightarrow h\left( f_{1}\left( t\right) \right) \le h\left( f_{2}\left( t\right) \right) \text { for all }t\in \left[ \underline{t},\bar{t}\right] . \end{aligned}$$

This means that the probability of observing an outcome within a neighborhood of t, conditional on the outcome being not less than t, is smaller under \(f_{1}\) than under \(f_{2}\) for all ts. Hazard rate dominance implies first order stochastic dominance of \(f_{1}\) over \(f_{2}\) and thus a higher expected value of t. Hence, hazard rate dominance of f over the uniform distribution characterizes a government with an optimistic prior with a higher average type (here normalized to 1 for the uniform distribution). This property is crucial, because the reciprocal of the hazard rate affects the agency costs on the right hand side of the relaxed program condition (23), while the left hand side, declining in x, remains unchanged from the condition that determines the agent’s and the first best choice.

Proposition 3

Assume two different distributions \(f_{1}\) and \(f_{2}\) with the same support \(t\in \left[ \underline{t},\bar{t}\right]\) about an agent’s efficiency, which can be ordered along the criterion of hazard rate dominance, say \(f_{1}\succ f_{2}\) so that \(h\left( f_{1}\left( t\right) \right) \le h\left( f_{2}\left( t\right) \right)\) for all \(t\in \left[ \underline{t},\bar{t} \right]\). Then the government will ask for less earnings (i.e., a lower level of \(x^{L}\)) for the dominant one (i.e., \(f_{1}\)).

This is a direct consequence of the relaxed program condition: the left hand side of (23) remains unchanged and the right hand side is lowered for a larger hazard rateFootnote 2.

What are the consequences on taxes,

$$\begin{aligned} \tau =W-U? \end{aligned}$$

A higher output for the hazard rate dominated distribution will raise W since \(W_{x}>0\) along the optimal program but also U since \(\dot{U}=W_{t}\) is increased too to due to the assumption \(W_{xt}>0\). Which of the two countervailing effects dominates is unclear. To address the question whether the tax collected from each type can be ordered with respect to hazard rate dominance in a way similar to the gross earnings, I use the reference example amended for linear increasing (i.e., optimistic) and decreasing (i.e., pessimistic) densities instead of the constant one for the uniform distribution. More precisely,

$$\begin{aligned} f\left( t\right) =1-\frac{\delta }{\Delta }\left( 1-t\right) ,\;f\left( \underline{t}\right) =f\left( 1-\Delta \right) =1-\delta ,\;f\left( \overline{t}\right) =f\left( 1+\Delta \right) =1+\delta ,\;-\Delta \le \delta \le \Delta , \end{aligned}$$
(35)

where \(\delta >0\) refers to an optimistic prior distribution since \(f\left( \underline{t}\right) <f\left( \overline{t}\right)\) so that efficient types are more likely, and \(\delta <0\) to a pessimistic one; Fig. 2 (top, left) shows optimistic and pessimistic examples of (35). The average type,

$$\begin{aligned} Et=1+\frac{2\Delta ^{2}}{3}\delta , \end{aligned}$$

is now different from 1 (and larger for the optimistic, \(\delta >0\), and smaller for the pessimistic, \(\delta <0\), prior). The implied hazard rate,

$$\begin{aligned} h\left( t\right) =\frac{2\left( \Delta -\left( 1-t\right) \delta \right) }{ \Delta \left( 2\left( 2-t\right) -\Delta \left( 2-\delta \right) \right) -\delta \left( 1-t\right) ^{2}}, \end{aligned}$$

is increasing in the types, \(\dot{h}>0\), but declining with respect to \(\delta\) so that the parameter \(\delta\) introduces an order into the set of hazard rates associated with the family defined in (35). More precisely, a larger value of \(\delta\) implies hazard rate dominanceFootnote 3 and thus for an optimistic probability distribution, \(\delta >0\) (thus \(\dot{f}>0\), a higher share of efficient types and a higher expected value, \(Et>1\)). The hazard rate is below the uniform one since

$$\begin{aligned} h<\frac{1}{\overline{t}-t}=\frac{1}{2\Delta }\Longleftrightarrow \delta >0. \end{aligned}$$

The relaxed program (23) implies the gross earnings,

$$\begin{aligned} x^{L}\left( t;\delta \right) =\frac{1+2\delta \left( t-1\right) t^{2}}{ \gamma \left( 1+\Delta +\Delta ^{2}\delta +\delta \left( t^{2}-1\right) \right) }, \end{aligned}$$

for the quadratic cost function (5). The outcome \(x^{L}\left( t;\delta \right)\) is monotonically increasing due to (9) and is below the one from (28) for any \(\delta >0\) (i.e., for an optimistic prior) but above for any \(\delta <0\). That is, a Leviathan government with a pessimistic prior about the efficiency of its people will ask them to earn more than if the government assumed a uniform distribution a priori. An optimistic assumption, with less inefficient but more efficient agents around \(\left( \delta >0\right)\) lowers a fortiori the government’s demand for their earnings.

The computations of the agents’ payoffs and their taxes follows the procedure outlined in Sect. 3 but the calculations are suppressed due to the cumbersome (but by and large still analytical) expressions. Therefore, the further analysis follows the computations shown in Fig. 2. The top left hand side shows the assumed density functions. The top right hand side shows the earnings of each agent type confirming the theoretical findings: a pessimistic (optimistic) prior increases (decreases) the earnings demanded from each type compared with the uniform distribution. Therefore, the on average less efficient types due to \(\delta <0\) in the linear density functions (35)) must earn (and thus work) more. However, this result, which counters common sense, is turned upside-down for the aggregate gross earnings, i.e., a larger ‘GDP’ results the larger \(\delta\) is. Although, the optimistic prior lowers each agent’s earning, the higher share of efficient types compensates for that. Therefore and as expected, a higher GDP is associated with a population with a higher share of efficient types.

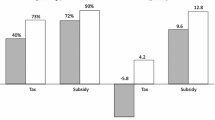
The charts at the bottom of Fig. 2 compare the taxes. Inefficient types have to be subsidized in the reference case and if an optimistic prior is assumed, which enlarges the set of agents who have to be subsidized. In contrast, no subsidies are necessary if a pessimistic prior is assumed. The reason is that the Leviathan cannot be generous with so many inefficient types around and does not only pay no subsidies but charges higher taxes to all types with a low efficiency compared with the uniform distribution; this comparison holds a fortiori for a comparison with an optimistic distribution. These relations are reversed for relatively efficient types: the Leviathan with the optimistic prior collects higher taxes than a government with the pessimistic prior and this although the gross earnings are lower for each type (according to the chart on the top and right hand side and the analytical result for all types). The comparison of the average taxes (not shown) confirms intuition: an optimistic prior allows the government to raise (average) taxes (and also the total tax revenues) and this explains the at first sight counterintuitive relation between the pre-tax earnings by type: an optimistic prior allows the Leviathan to impose high taxes that depress efforts and hence reduce the gross earnings \(\left( x^{L}\right)\). Therefore, all agents are better of with a government having a pessimistic prior, see the chart at the bottom right hand side of Fig. 2.

Fig. 2
figure 2

Impact of different distributions (large dashing = optimistic, small = pessimistic), \(\Delta =3/4\), \(\gamma =1/2\), \(R=1/10\)

Full size image

5.2 Convex Efficiency

The idea that the return to individual talent (in our case t) increases disproportionately dates back at least to Merton (1968) who coined his observation (in science) the Matthew effect; see also Merton (1988) and Yegorov et al. (2022) for a recent theoretical analysis of the Matthew effect on an agent’s intertemporal investment. One of the side effects of globalization is that the returns to (exceptional) talent have indeed increased by enlarging the market at the cost of local champions. In order to address this point, I modify in the reference example only the measure of efficiency: \(\eta \left( t\right)\) is convex instead of linear in the type, i.e., \(\eta ^{\prime \prime }>0\) and for concreteness quadratic (e.g., due to a linear instead of the concave square root productivity function as outlined in Sect. 2.3),

$$\begin{aligned} C\left( x,t\right) =\frac{\gamma }{2}\frac{x^{2}}{t^{2}}. \end{aligned}$$
(36)

Therefore, the earning is also convex (and quadratic) in the absence of taxation,

$$\begin{aligned} x^{0}\left( t\right) =\frac{t^{2}}{\gamma }, \end{aligned}$$
(37)

and thus less for below average types, \(t<1\) but larger for all \(t>1\) compared with the reference example. The corresponding aggregate (i.e., the hypothetical ‘GDP’ in the absence of taxation),

$$\begin{aligned} \underset{1-\Delta }{\overset{1+\Delta }{\int }}x^{0}\left( t\right) dt= \frac{2\Delta ^{3}+3\Delta ^{2}+12\Delta -1}{6\gamma }>\frac{2\Delta }{ \gamma }\Longleftrightarrow \Delta >\frac{1}{2}, \end{aligned}$$
(38)

exceeds its counterpart of the reference example (6), if and only if \(\Delta >1/2\), i.e., for a sufficiently large range of types.

Computing the corresponding relaxed program,

$$\begin{aligned} W_{x}=1-\frac{\gamma x}{t^{2}}=\frac{W_{xt}}{h}=\left( \overline{t}-t\right) \frac{2\gamma x}{t^{3}}, \end{aligned}$$

implies that the gross earnings are cubic in the agent’s type (and thus of course monotonically increasing),

$$\begin{aligned} x^{L}\left( t\right) =\frac{t^{3}}{\gamma \left( 2\overline{t}-t\right) }. \end{aligned}$$
(39)

Therefore, taxing the same set of uniformly distributed agents, \(t\in \left[ 1-\Delta ,1+\Delta \right]\), with a convex efficiency characteristic according to (36) instead of (5) lowers the output of the types,

$$\begin{aligned} t<\tilde{t}:=\frac{1+\Delta }{1+\frac{\Delta }{2}}>1, \end{aligned}$$
(40)

and thus also for a subset of above average types, \(1<t<\tilde{t}\), who would earn (and work) more in the absence of taxes than assuming the linear counterpart (5).

The computation of the agents’ payoffs and taxes is suppressed for the same reason as in the previous subsection: the analytical results are too cumbersome to allow for meaningful insights.

Proposition 4

Assuming a convex (quadratic) instead of a linear measure of efficiency \(\left( \eta \right)\) implies:

(i) The aggregate earnings potential (i.e., in the absence of taxation, \(x^{0}\)) increases only for a sufficiently large spread (\(\Delta >1/2\) for the quadratic measure of efficiency).

(ii) Taxation increases this effect: the majority of types, more precisely, \(t<\tilde{t}\) from (40) and \(\tilde{t}>1\), produces less and only the very high types, \(t>\tilde{t}>1\), may but need not compensate for that shortfall.

(iii) Indeed, unless the range of efficiency types \(\left( \Delta \right)\) is very large, agents characterized by convex instead of linear efficiency lead to less aggregate earnings (i.e. GDP). That is, a society taxed by a Leviathan benefits from the Matthew effect only if the range of talents is sufficiently large.

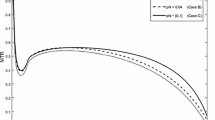
Figure 3 shows how the alternative assumption about efficiency, convex in the type, affects a Leviathan’s policy. The chart at the top and left hand side shows the above already addressed implications on the gross earnings. In spite of the very large differences of untaxed earnings (i.e., of \(x^{0}\)) for all \(t>1\) (by a factor \(>2\) for for \(t\rightarrow \bar{t}\) between the quadratic and the linear efficiency measure), the pre-tax earnings of a taxed population \(\left( x^{L}\right)\) characterized by a convex measure of efficiency exceed those of the linear efficiency measure only for types much larger than the average (\(t>\tilde{t}\approx 1.25\) compared with \(t>1\) if untaxed). The assumption of a convex measure of efficiency lowers the taxes of the low types and enlarges the set of subsidized agents (Fig. 3, top right hand side). Furthermore, it increases the convexity of the tax schedule at low and the concavity at high types. Again, \(\dot{\tau } \rightarrow 0\), and the marginal tax, \(\tau ^{\prime }\left( x\left( t\right) \right) \rightarrow 0\), for \(t\rightarrow \bar{t}\). The tax surpasses its counterpart of the reference case (the linear measure of efficiency in (5)) before the equality of gross earnings is reached. The taxes for the high types are substantially higher than for (5). The impact on the average tax \(\left( \tau /x\right)\) is negligible for low types, but more efficient types allow the government to charge higher average taxes if efficiency is convex (quadratic) in the type. Therefore, a kind of Matthew effect following the globalization during the recent decades should have induced a Leviathan government to increase the average tax on its high earners. This conclusion seems counterfactual, presumably not so much due to governments’ social concerns but due to international tax competition. The last chart (bottom and right hand side) highlights that the impact of a convex efficiency relationship on the agents’ net payoffs \(\left( U\right)\) is negligible (but substantial in the absence of taxes) except for the very high types (\(t>1.4\) in the example).

Fig. 3
figure 3

Impact of a convex (quadratic) efficiency measure (dashed), \(\Delta =3/4\), \(\gamma =1/2\), \(R=1/10\)

Full size image

Figure 4 addresses how the range of types, i.e., the parameter value \(\Delta\) , affects the GDP for the linear and the convex (quadratic) measures of efficiency. The GDP of a population with a linear measure of efficiency is,

$$\begin{aligned} \frac{1}{2\Delta }\overset{1+\Delta }{\underset{1-\Delta }{\int }}x^{L}(t)dt= \frac{3+\Delta ^{2}}{3\gamma \left( 1+\Delta \right) }\text { and }x^{L}(t) \text { from }(28). \end{aligned}$$

Hence, it is monotonically declining with respect to \(0<\Delta <1\). Therefore, a more diverse population subject to a Leviathan’s tax lowers the GDP. In contrast, the GDP based on the convex efficiency measure (36), i.e., \(x^{L}\) from (39), is non-monotonic in \(\Delta\). Although an analytical solution can be given, the further discussion is confined to the reference cost parameter \(\gamma =1/2\), see Fig. 4. The convex efficiency leads to a higher GDP in this example but only if \(\Delta >0.54\), which is slightly above the threshold in the untaxed case according to (38).

Fig. 4
figure 4

Comparing the GDP for increasing the range of types (\(\Delta\)) if efficiency is linear (line) or convex (dashed), \(\gamma =1/2\)

Full size image

5.3 Adding Welfare

An obvious extension is to account for social concerns of a government. However, including the agents’ true welfare in the Leviathan’s objective does not change the basic message, except that it leads to higher earnings for all agents due to a lower tax burden. Therefore and because its analysis leads to some mathematical complications (the relaxed program need not be monotonic anymore), this analysis is not part of the paper but is available online using the reference example and a logarithmic evaluation of the agents’ net incomes by a government thereby accounting for egalitarian concerns.

6 Final Remarks

The analysis departed from the Leviathan hypothesis of Brennan and Buchanan (1981) in order to determine income taxes if the earning abilities are the people’s private information. Given the stark difference in objectives, maximizing the tax revenues instead of a welfare function (often constrained by an exogenously fixed revenue requirement), it is surprising that the implied tax schemes have similar features. There are two reasons. First, the welfare concerned government behavior is not free from monopolistic considerations (of the Ramsey-type, Ramsey (1927)). Second, both governments are bound by the incentive compatibility constraint. The realistic assumption of private information about one’s earning ability imposes this constraint to all kinds of income taxing governments. It is this constraint that increases the spread of real incomes after taxation substantially over and above the untaxed case.

An interesting and in this paper ignored feature is the intertemporal interplay between the development of one’s abilities and thus earning capabilities and the tax code and how destructive a Leviathan can be. This could then provide for additional insights about the harm that the Leviathan causes in an intertemporal context. Golosov et al. (2003) show a way how to do this but their analysis is restricted by the assumptions that the government can commit and that the abilities are exogenous (albeit a stochastic process, similarly also in Kocherlakota (2005)); Sannikov (2008) and Cvitanic and Zhang (2012) sketch a general approach about how to solve dynamic principal-agent problems.