Introduction

Untethered manipulation of helical magnetic micro/nanomachines has received a lot of attention in the recent times, mostly due to their promising applications in targeted drug delivery, imaging and nanomanipulation (Erkoc et al. 2019; Ghosh and Fischer 2009; Fischer and Ghosh 2011; Qiu et al. 2015; Ghosh et al. 2020; Yan et al. 2015, 2017; Zhang et al. 2009; Bozuyuk et al. 2018). They are particularly attractive compared to their counterparts such as chemically active motors, whose operation is dependent on the media composition or the optically active motors which are limited by the low depth of penetration of optical fields (Sitti and Wiersma 2020). Controlled navigation of these micro/nanomachines in biologically relevant environments is however challenging, due to the inherent media complexity and heterogeneity present at these small length scales (Schamel et al. 2014; Venugopalan et al. 2014). For example, recent research with helical nanopropellers has shown a strong effect of pore size, surface charge as well as steric interactions in intracellular or tissue-like environments (Dasgupta et al. 2020; Pal et al. 2018; Schamel et al. 2014; Wu et al. 2018). Theoretical predictions and experiments also point towards an unprecedented effect of adjoining walls or confinements as well as the viscoelasticity of the surrounding fluid on the speed and aggregation of helical swimmers (Leshansky 2009; Lee 2013; Liu et al. 2011, 2014; Nelson and Peyer 2014; Spagnolie et al. 2013; Martinez et al. 2014; Gomez et al. 2016; Chen et al. 2020; Zöttl and Yeomans 2019). For instance, experiments revealed both decrease as well as increase of the speed of helical propulsion in elastic media, which is a complicated function of the helical geometry, as well as the ratio of the actuation to the relaxation time scales of the elastic medium. Thus, understanding the motion of helical nanomachines in complex fluidic environments is important for technological applications in biomedicine and also to gain insight about the physics of swimming in heterogeneous or time varying fluids.

Recently, we demonstrated the sensitivity of the dynamics of magnetic nanopropellers to the local viscosity in both Newtonian and shear-thinning fluids (Ghosh et al. 2018). Our experiments showed that helical nanomachines can probe the local viscosities of fluids with unprecedented spatial and temporal resolutions. In this paper, we extend our study to linear viscoelastic systems, for which we used dilute methyl cellulose (MC) gel as a model fluid and looked at the effect of increasing MC concentrations on both the instantaneous dynamical configuration and the speed of the helical nanopropeller. Our study enables the nanopropeller to simultaneously probe both the local viscosity and elasticity of the surrounding media with very high precision. The paper is organized as follows: first, we describe the fabrication of the magnetic nanopropellers and the experimental method to look into the effect of fluid rheology on the motion of propellers. We then characterize the swimming dynamics of the nanopropellers in both viscous and linear viscoelastic media. The second part of the paper relates the speed of helical nanopropellers with the degree of elasticity of a medium. This was obtained by driving the nanopropellers across a region with varying degrees of concentration of MC gel. We used the methodology described in the first part to estimate the viscosity and thereby concentrations of the MC gel locally and subsequently relate the speed of the nanopropeller to the local elastic relaxation time. Our experiments open up possibilities to simultaneously measure the local viscosity and elasticity of a complex fluid.

Experimental Procedure

The magnetic nanopropellers used for the experiments were fabricated using a physical vapor deposition technique called GLancing Angle Deposition (Hawkeye and Brett 2007; Ghosh et al. 2012). At first, we fabricate a monolayer of polystyrene beads (700 nm to 1 µm diameter) using Langmuir Blodgett deposition technique. This was followed by the evaporation of silicon dioxide by electron beam evaporation on the top of the beads, while the substrate was manipulated in a controlled manner. As a result, helical structures of controlled shape and size could be fabricated. The individual nanostructures, each of length 3 µm, were released using sonication in water and laid down on silicon wafers (Fig. 1a). They were rendered magnetic by depositing a thin layer of cobalt (thickness ≈ 50 nm) on one side of the propellers, with a 10 nm layer of chromium to improve the adhesion. They were then put into microfluidic cells containing the desired fluid and placed inside a triaxial Helmholtz coil, which was capable of generating rotating magnetic fields and the motion imaged under an Olympus IX71 microscope with 40× objective, using high-speed CMOS camera (Thorlabs) (Fig. 1b). As reported in previous publications (Peyer et al. 2010; Ghosh et al. 2012, 2013, 2018), the nanopropellers showed a range of different dynamical configurations under the action of a rotating magnetic field, and the dynamics can be tuned by changing the magnitude or frequency of the rotating magnetic field. For example, a nanopropeller can be taken from a precessing configuration to a helical propulsion configuration, by increasing the magnetic field frequency or by reducing the magnetic field magnitude and vice versa.

Fig. 1
figure 1

a SEM image of a magnetic nanohelix (scale bar equals 200 nm). b Schematic of the experimental setup

Full size image

The experiments were conducted at room temperature (27 °C) in microfluidic cells which were constructed using thin (100 µm) double-sided tapes, glass slides and coverslips, to create a two-fluid boundary in the cell. The lateral dimensions of the microfluidic chamber were around 2 cm by 2 cm and the height of chamber was around 100 µm, which was controlled using the thickness of the tape. For easier visualization of the boundary, one of the fluids was colored using methylene blue dye for few experiments. The nanopropellers were first dispersed in the fluid of known viscosity (generally water). One of the nanopropellers at the extreme end of the water side was then chosen for measurement. During the viscosity measurements, at first, a passive rheological measurement was performed, in which the translational diffusion coefficients of the nanopropeller were measured in water (Ghosh et al. 2014). The nanopropeller was then moved across the two-fluid boundaries and switched between the states of precession and propulsion. While precessing, the angle of precession was measured (Ghosh et al. 2012), which provided an estimate of the local viscosity of the surrounding. The measurements were carried out with an averaging time of 10–15 s while the nanopropellers were moving at a speed of around 1 µm/s, implying the spatial resolution of the measurement was around 13–18 µm, considering a 3 µm length of the nanopropeller used in the present studies. We add more details on the spatial resolution of the measurement method in the “Results and Discussion”. Once the measurement was done, the nanopropeller was propelled to a new location, having different rheological properties to carry out the viscosity measurement. The experiment continued until the nanopropeller reaches deep inside the boundary. The magnetic field was then turned off and the diffusion coefficients of the nanopropeller were again measured. The ratio of the diffusion coefficients in water and at the end point provided an accurate estimate of the local viscosity at the final point of measurement.

The rheological experiments in MC gel were also conducted similarly as above. The preparation of MC gel followed standard procedures (MC Ether Technical Handbook 1997). First, one third of the required volume of deionized water was heated to 90 °C. Then, the desired amount of MC powder (%w/w) (Methocel 90 HG, Sigma Aldrich), was mixed thoroughly in the hot water using a magnetic stirrer till all the particles were wetted properly and the solution looked turbid. Then, the heating was removed and icy cold water in the remaining proportion (two-third of the required amount) was added to the solution, as the stirring was continued. The solution lost its turbidity and became transparent. The stirring was continued for 1 or 2 h more and the solution was then refrigerated at 4 °C overnight as the viscosity increased to the desired value. The viscoelastic properties of MC solutions having different gel concentrations were first investigated using particle-tracking experiments, where 1 µm diameter polystyrene beads (Spherotec Inc.) were dispersed in the gel and placed in a microfluidic chamber. The trajectories of the beads were observed under a microscope and captured using a high-speed camera at a frame rate of 60–80 fps. We then used the passive microrheology methods developed by Mason and Weitz (1995), Mason et al. (1997) and Gittes et al. (1997) to extract the elastic moduli of the medium from the trajectories.

For probing the viscoelastic properties of MC gel using the nanopropellers, the nanopropellers were dispersed in the water end of the microfluidic chamber. One of the nanopropellers was then moved across the boundary at a rotation speed of 25 Hz, while the propulsion speed was measured continuously, averaged over a length of around 100 µm. As the propeller was moving, it was brought to precessional motion using a magnetic field frequency of 5 Hz while keeping the magnetic field constant. We increased the strength of the magnetic field, to keep the precession angle measurable, as the propellers reached a location with higher concentration of MC gel.

Results and Discussion

When an elongated structure like a ferromagnetic nanopropeller used in the present paper is subjected to a rotating magnetic field, the dynamics of the nanopropeller is governed by the tendency of the magnetic moment to be pointed along the direction of the externally applied field. In the calculations and experiments presented here, we assume the magnetic moment of the nanopropellers to be permanent and have neglected any possible effects arising out of induced moments (superparamagnetism) or demagnetization (coercivity assumed to be higher than the applied fields). As shown in Fig. 2a, the magnetization was assumed to be of strength M at an arbitrary angle (θm) to the short axis of the nanopropeller. The strength and frequency of the rotating magnetic field was B0 and ΩB, respectively. This problem was considered theoretically in one of our earlier papers (Ghosh et al. 2013), where the dynamical equations were solved for an elongated nanorod in an unbound Newtonian fluid at low Reynolds number. The dynamical equations (Eq. 1) provided a scheme of viscosity (η) measurement which was used in Ghosh et al. (2018), to measure the local viscosities using the instantaneous values of the precession angle (αp) of a nanopropeller having rotational drag coefficient γs:

$$\alpha_{{\text{p}}} = \sin^{ - 1} \left[ {\frac{{{\text{MB}}_{0} \sin (\theta_{{\text{m}}} )}}{{\gamma_{{\text{s}}} \Omega_{{\text{B}}} }}} \right] = \sin^{ - 1} \left[ {\frac{{{\text{MB}}_{0} \sin (\theta_{{\text{m}}} )}}{{\eta f_{{\text{g}}} \Omega_{{\text{B}}} }}} \right].$$
(1)
Fig. 2
figure 2

a Schematic representation of a helical nanoscale probe with permanent magnetic moment at an angle θm to the short axis. Under the action of a magnetic field of magnitude B0 and frequency ΩB the helix precesses about the perpendicular (z direction) to the plane of the rotating magnetic field (x–y plane) with angle αp. b Plot of the angle of precession as a function of Ω1/ΩB in purely viscous medium water (square symbols) and the viscoelastic gel 0.3% MC (diamond symbols). While the open symbols correspond to a measurement at lower magnetic fields, the solid symbols correspond to measurements at double the field magnitudes. The green solid line corresponds to a plot of sin−1(Ω1/ΩB)

Full size image

Here, fg is the geometrical contribution of the nanopropeller to γs. It may be noted that Eq. (1) was originally derived for elongated objects in which the rotational and the translational degrees of freedom are not coupled. Thus, it is only approximately correct for a helical geometry, in which the mobility tensor contains extra terms originating from the coupling. Because of this coupling, the axis of a finite sized helix can deviate from the principal axes of rotation, and the rotational drag coefficients have to be modified with contributions from the coupling terms of the mobility tensor. This problem was first considered with approximate calculations by Morozov and Leshansky (2014), who estimated the misalignment of the axis directions to be negligible for typical experimental geometries. A more detailed theoretical formulae and analysis was published by Fu et al. (2015). To summarize these theoretical analyses, it is indeed justified to split the dynamics of a nanopropeller into two problems: (1) precessional motion of a rod governed by Eq. (1) with an effective \(\gamma_{{\text{s}}}\) that differs from that of a rod by less than 10% (Fu et al. 2015), and (2) translation motion of a helix due to rotation about its long axis, that depends on the angle of precession and an effective hydrodynamic pitch. To check it experimentally, we have collected data with various magnetic field parameters. The results are shown in Fig. 2b, where αp is plotted as a function of \(\Omega_{1} /\Omega_{{\text{B}}}\) in water at magnetic field magnitudes 10 G and 20 G and in 0.3% MC gel at 30G and 60G. Here, \(\Omega_{1}\) stands for the characteristic cut off frequency, at which the nanopropeller stops tumbling about the short axis and starts precessional motion around the long axis (Ghosh et al. 2012, 2013). The measurements indicate clearly that the precession angle of the nanopropellers both in viscous and viscoelastic media at different field magnitudes can be well described with the form shown in Eq. (1), \(\alpha_{{\text{p}}} = \sin^{ - 1} (\Omega_{1} /\Omega_{{\text{B}}} )\). It is important to note that the viscosity of the MC gel at such low concentrations remains unaltered at the low shear rates used in these experiments, and therefore, it is not surprising that the equation derived for a purely viscous medium was applicable here.

First, we demonstrate that the local viscosity of a purely viscous media can be accurately measured using the nanopropellers. The propellers were maneuvered from the reference medium (viscosity = ηref) to the fluid of unknown viscosity (ηmeas) (Fig. 3a), and analyzing their images provided a measurement of the precession angles (αp,ref and αp,meas) in the two media and across the gradient. The viscosities could be estimated from the values of the magnetic field strengths Bref and Bmeas, and frequencies Ωref and Ωmeas used for the reference and the test media, respectively. The viscosity of the test medium was obtained using \(\frac{{\eta_{{{\text{meas}}}} }}{{\eta_{{{\text{ref}}}} }} = \frac{{B_{{{\text{meas}}}} }}{{B_{{{\text{ref}}}} }}\frac{{\Omega_{{{\text{ref}}}} }}{{\Omega_{{{\text{meas}}}} }}\frac{{\sin \alpha_{{\text{p,ref}}} }}{{\sin \alpha_{{\text{p,meas}}} }}\). Although the measurement of αp was most sensitive when it was slightly less than 90°, the speed of the propellers in the tumbling state was too low. Accordingly, we carried out the experiments keeping αp ~ 30°–50°, while adjusting Bmeas and Ωmeas as the propellers were moved from one end of the chamber to another within a reasonable time. A key point to note is that the experimental procedure is self-referenced, and therefore, does not require prior measurements of the magnetic moments or the friction coefficients.

Fig. 3
figure 3

a Schematic of the microfluidic device. The chamber has two inlets and two outlets, with deionized (DI) water and some test fluid (blue) flowing through. The propeller is driven from the water side towards the test fluid along the concentration gradient. Measurements of the precession angle at the reference point (green solid circle) and the measurement point (red solid circle), gives a measure of the relative viscosity at that particular point. Relative viscosity measured across the two-fluid boundaries of b glycerol–water and c dextrose–water mixtures plotted as a function of the distance across the boundary. The estimates of the viscosity obtained from passive measurements have been shown as dark and light colored stars, which correspond to the ratio of translational diffusion coefficients along the long axis and short axis of the propeller, respectively

Full size image

In Fig. 3b, c, we show results of the viscosity measurements as the nanopropellers were taken from deionized water across the concentration gradient to a different fluid. We present data for the other fluid being 55% glycerol solution (Fig. 3b) as well as 30% w/w aqueous dextrose solution (Fig. 3c). Typically, the nanopropellers were propelled over a few millimeters from the starting point, and the local viscosity was measured as a function of position. Note, the final positions of the propellers for the cases shown in Fig. 3 were somewhere deep in between the two pure phases of the liquids, and therefore, it is not surprising that the estimated viscosity of 5 cP and 2.33 cP were smaller than the bulk viscosity of the test samples, 8.7 cP and 10 cP, respectively.

In addition, it is important to note that the width of the boundary of the two fluids changes during the course of measurement due to mixing in the microfluidic chamber and the applicability of the experiments is ensured by the significantly high Péclet number (~ 100) of the system (Ghosh et al. 2018). The Péclet number in this case is given by the ratio of the time scales of mixing of the two fluids across the boundary to the time scale of propulsion of the propeller. Interestingly, the spatial resolution of this measurement technique is intrinsically limited by viscosity of the surrounding environment either through time of mixing at the interface, and/or the thermal fluctuations of the suspended nanopropellers. To verify the measured values of viscosity using the nanopropellers, we observed the position fluctuations of the propeller in the absence of the magnetic field at the start and end locations. The passive fluctuations of the propellers are inversely related to the local viscosity of a location, and therefore measuring the diffusivities of the propellers along their long and short axes provided alternate estimates of the local viscosity. These measurements were also self-referenced since we measured the ratio of the diffusivities at the start and end locations, giving a ratio of the viscosities at the two end points. The results of the passive measurements of the ratio of the diffusion constants matched very well with the estimates obtained from the precession angle measurements at the end point, as marked clearly in Fig. 3b, c by star symbols, which validates the quantitative accuracy of this technique. It may be noted that the accuracy of measurement of viscosity using the nanopropellers is dependent only on the rotational thermal fluctuations of the propeller (Ghosh et al. 2014, 2018). We found that the accuracy is significantly better (3–20 times) than passive rheological techniques for the same time of measurement (Ghosh et al. 2018). Although the variation of the precession angle can be used for microrheological measurements for purely viscous and also shear-thinning fluids (Ghosh et al. 2018), many fluidic media encountered in practice, especially those of biological relevance are non-Newtonian/complex in nature. To characterize their mechanical properties completely, one needs to measure both the viscosity and elasticity of the medium. We chose MC gel to carry out our elastic fluids’ experiments with the nanopropellers. Although MC is known to be shear thinning, it can be considered to follow a Maxwell model for linear viscoelasticity at shear rates typical (30–160/s) of our experiments (Fig. 4a, b), considering the typical magnetic field frequencies ranging between 5 and 25 Hz. The results for the storage and loss moduli are shown for MC solutions of two different concentrations. Both the moduli increased monotonically with angular frequency. The complex viscosity of the gel, as shown in Fig. 4b, was estimated using the empirical Cox–Merz rule (Cox and Merz 1958): \(\hat{\eta } = \sqrt {(G^{\prime}(\omega )/\omega )^{2} + (G^{\prime\prime}(\omega )/\omega )^{2} }\). We also characterized the elastic relaxation times of the linear MC gel using passive rheology experiments and plotted them as a function of the concentration and viscosities of the MC gel (Fig. 4c, d). Note, the representative length scales of heterogeneity (~ 10 nm) (Baumgartner et al. 2002) for these samples such as the mean spacing between the polymer fibers were significantly less than the size of the propellers (~ 1 µm), and therefore, the elastic response of the system was indeed probed as a whole (Fig. 5a). This is unlike the navigation of magnetic nanopropellers in heterogeneous media of larger mesh sizes like human blood (Venugopalan et al. 2014) or vitreous humor (Wu et al. 2018), where the sizes of the helices were comparable to the length scales of heterogeneity in the medium. Perhaps a closer analogy would be the motion of similarly sized swimmers in the intracellular environments (Pal et al. 2018, 2020; Venugopalan et al. 2020).

Fig. 4
figure 4

a Storage and loss moduli for 0.3% (dotted line) and 0.5% (solid line) MC, obtained from particle-tracking microrheology experiments; b complex viscosity of 0.3% and 0.5% MC gel extracted from the dynamic moduli data. c Stress modulus of the different concentrations of the methyl cellulose gel measured using particle-tracking microrheology. The solid line shows a sample of the fit used to estimate the relaxation time of the gel. d Viscosity (right axis) and relaxation time (left axis) of the MC gel at different concentrations as measured by passive rheology experiments. The horizontal line shows the viscosity of water. The black straight line corresponds to a linear fit of relaxation time to log of the concentration

Full size image
Fig. 5
figure 5

a Schematic of the measurement chamber containing DI water at one end and methyl cellulose gel (0.5 wt %) on the other side. The inset schematics show a helix driven from water towards the gel. The two different configurations of the same helix (propulsion (top) and precession (bottom)) were used to measure the pitch and viscosity, respectively, in a single experiment as a function of position. b Result of the simultaneous measurement of the local viscosity (black, left axis) and the local pitch (blue, right axis) as a function of position. The starting position (distance = 0 µm) corresponded to initial position in pure DI water, and subsequently the helices were moved towards the gel. The end position of the helix (distance = 2200 µm) corresponded to MC gel concentration of about 0.4%

Full size image

As shown in the schematic of Fig. 5a, the procedure of the experiments was similar to what has been described above, where the nanopropeller was maneuvered from water to the other side of the microfluidic device containing a solution of 0.5% methyl cellulose. As the propeller was moved across the boundary it was alternately driven in the helical propulsion mode (ΩB = 25 Hz) and the precessional mode (ΩB = 5 Hz). The strength of the magnetic field was varied such that the precession angles were around 30°–50°, and the driving torque during the propulsion was greater than the frictional torque. The idea was to measure the pitch and the viscosity (from precession angle) at approximately the same location, where the hydrodynamic pitch is the distance moved by the nanopropeller for one complete rotation about its long axis. In Fig. 5b, a representative plot of the hydrodynamic pitch has been shown as a function of the distance across the boundary along with the corresponding viscosity measurements obtained from precession angle measurements. Each point here denotes the effective hydrodynamic pitch of the helical nanopropeller, averaged over a measurement distance of 100 µm. Very interestingly, within a small distance (< 900 µm) from the starting point (within DI water), a large (~ 30%) reduction in pitch was observed. In this small region, the change in the viscosity was negligibly small, from where we could estimate (see Fig. 4d) the concentration of the MC gel to be less than 0.005% at a distance of 900 µm from the starting position. While it is interesting to note that the pitch of the nanopropeller was very sensitive to such a small amount of gel concentration, the corresponding variations in gel viscosity were too small to be accurately measured using the precession angle measurements. We observed similar strong dependencies of the pitch of the nanopropeller on the MC gel concentration in all the experiments with different nanopropellers and microfluidic cells (Data not shown in this paper).

As the nanopropeller was moved further into the gel, the pitch increased to values almost similar to that in water. The measured values of viscosity, on the other hand, increased monotonically as the propellers moved from water towards methyl cellulose, similar to what we obtained in our spatial viscosity mapping experiments discussed in Fig. 3. The viscosity measurements provided a quantitative estimate of the gel concentration as a function of position. The variation was linear, as would be expected in a slow microfluidic mixing scenario. The viscosity of the region around the final measurement position of the nanopropeller was found to be 14.1 cP, which corresponded to 0.4% gel concentration. This was slightly lower than the initial concentration of gel (0.5%) at the beginning of the experiment, which was due to the mixing between water and the gel during the course of the experiment. As shown in Fig. 5b, once the nanopropeller moved more than 900 µm away from the starting point, the viscosity increased considerably. It may be noted that we observed two points of extremums in the Newtonian pitch of the nanopropeller as the propeller navigates deep into the MC gel. As pointed out earlier, the literature shows both an increase and decrease in the pitch of a helix in viscoelastic media, but the exact reason of the behavior reported here needs to be further investigated.

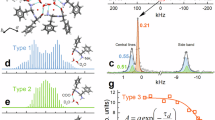
A crucial step was to estimate the local concentration of the gel from the measurement of the local viscosity, and then to relate the pitch measured at that position to the gel concentration. We used passive rheological measurements to create this “look-up table” for the viscosities at various concentrations of the MC gel (Fig. 4d). In Fig. 6, we show the variation of the pitch of the helices as a function of gel concentrations, where the concentration was obtained from local viscosity estimates, which in turn was obtained from precession angle measurements. We show data for different helices, including the one shown in Fig. 5b. These data were collected in different microfluidic chambers, of which the data shown in circles had 0.3% gel at the beginning of the experiment, while the other two datasets (shown as squares and triangles) contained 0.5% gel. Irrespective of the concentration of the gel used in one end of the chamber, the pitch could be measured at a concentration as low as 0.01%, which corresponds to a viscosity of 1.4 cp, below which the method of relying concentration from local viscosity measurement is not accurate. All the different datasets clearly show a common general trend, where the hydrodynamic pitch increases by around 30% as the gel concentration increases from 0.01% (relaxation time 0.31 s) to 0.45% (relaxation time 0.5 s). The exact absolute values of the pitch varied between the helices, which arose due to their structural differences, and would also happen in a Newtonian fluid. However, the strong and similar sensitivity of the pitch on the relaxation time of the elastic medium is in agreement with the analysis of helical propulsion of biological swimmers in viscoelastic media (Spagnolie et al. 2013), and qualitatively similar to the measurement (Nelson and Peyer 2014) of artificial helical flagella in gels. We must stress that our measurements were inherently self-referenced, in which the same propeller could be used to do the measurements of viscosity and relaxation time at the different concentrations of the gel, and as far as we know, there is no other technique that can achieve the same.

Fig. 6
figure 6

Results of multiple experiments on the dependence of the pitch of the helices on concentration of the MC gel. Different propellers and initial concentration of the MC gel were used in the different experiments. The variation of the pitch as a function of position was converted to the dependence of the pitch on the concentration of the gel (bottom axis) and the corresponding relaxation time (top axis) of the elastic medium. See text for detailed description of the experimental procedure

Full size image

The measurement accuracy of the local relaxation time using the nanopropellers is inherently tied to the velocity fluctuations in a fluid of certain viscosity. We found that the error in estimation of the relaxation time using this technique was within 1% for 0.4% MC gel to within 10% in water. In addition, it may be noted that the significantly larger thicknesses of the microfluidic chamber used (compared to the length of the nanopropeller), helped to reduce the wall effects on the velocity fluctuations and in turn improves the estimation accuracies of the rheological parameters (Ghosh and Ghosh 2014).

We could achieve measurement of local elastic relaxation times up to 0.5 s and viscosities up to 60 cP (Ghosh et al. 2018) using the current system, which can be further improved by enhancing the magnetic moment of the nanopropellers or using larger magnetic fields to drive them. For the experiments reported in this paper, the nanopropellers were driven at magnetic field frequencies between 5 Hz (precession, for viscosity measurement) and 25 Hz (for speed/elasticity measurement) and the field magnitude was varied between 10 and 60 G to keep the motion of the nanopropeller phase locked to the magnetic field (Ghosh et al. 2013).

Conclusion

In conclusion, magnetic nanopropellers, which were previously proved to be biocompatible (Kadiri et al. 2020), and can be precisely driven in intra- or extracellular environments (Pal et al. 2018, 2020), have been used as active probes for microrheological mapping of complex heterogeneous environments. The nanopropellers provide several advantages over existing microrheological techniques, such as high spatial accuracy and speed of measurement. As the technique only requires imaging the propellers, it may be combined with other applications demonstrated with helical magnetic nanomachines, such as on demand gene transfection (Kadiri et al. 2020), local heating (Venugopalan et al. 2018) or cargo transport (Ghosh and Ghosh 2018). Although the present experiments were performed with a single nanopropeller under observation, it may be possible to extend these experiments with two or more propellers independently positioned (Mandal et al. 2015) at different locations of the microfluidic chamber, or in applications requiring autonomous sampling of the local environment (Mandal and Ghosh 2013; Mandal et al. 2018). We envision this technique to be useful in scenarios that require controlled temperature changes locally induced (e.g., through plasmonic nanotweezers (Ghosh and Ghosh 2018)), fast mechanical changes such as gelation studies (Celli et al. 2007), or materials with complex mechanical heterogeneities, such as a biological cell (Berret 2016). Also, the very large sensitivity (30% reduction for the presence of 50 ppm of MC gel) of the pitch to the lower concentrations of the gel shows the possible use of the nanopropellers for detecting elastic impurities. In view of the current interest and advances in the development of intelligent nanomotors (Venugopalan et al. 2020) and adaptive swimming strategies (Huang et al. 2019) as well as for biological (Soto et al. 2020; Wan et al. 2020) applications, this technique may be extended to other (Wang et al. 2012) nanomotor designs as well.