1 Introduction

Since its advent in the 1950 s, nuclear energy has been crucial for meeting the world’s energy needs and is an important component of clean energy. Nuclear energy is primarily generated through nuclear reactors, which are generally designed to operate for 30–40 years and can last even longer with license renewals. Data from the Power Reactor Information System indicates that among the total of 437 reactors, 289 reactors have been in operation for more than 30 years [1]. Thus, more than 60% of the current nuclear reactors face aging issues, which implies an increase in operational problems or anomalies in reactors. The aging of operational reactors also leads to increased mechanical vibrations of reactor internals, such as core barrels, control rods, in-core instruments, and fuel assemblies, or other vibrations such as flow blockage and coolant inlet perturbations [2,3,4,5,6].

Various reactor core monitoring techniques aim to address these challenges, and they are primarily based on observations of the neutron flux acquired by in-core and ex-core instrumentation combined with numerical simulations. These techniques and systems include CORTEX [7], BEACON [8], and RAINBOW [9]. A detailed overview of reactor core monitoring techniques is available in [10]. Field reconstruction combines observed data in the core and simulation data [11, 12] and aims to determine the neutronic field in the core. Subsequently, safety-related parameters are calculated, such as enthalpy rise hot channel factor, peak heat flux hot channel factor, linear power density of fuel rods, and deviation from nucleate boiling ratio.

Data assimilation is a key algorithm for field reconstruction, which originated from earth sciences, including meteorology and oceanography [13]. The data assimilation framework allows the combination of observations and models in an optimal and consistent manner, including information about their uncertainties [14,15,16]. It has been applied in several studies in nuclear engineering [9, 17,18,19,20,21] for field reconstruction in a unified formalism. Data assimilation with a reduced basis is another framework, which has been extensively researched in recent years [22,23,24,25,26,27,28,29,30,31,32]. In summary, studies on data assimilation have aimed to improve the accuracy, efficiency, and robustness of physical field reconstructions. Further details are available in Ref. [33].

However, as the location of the sensors affects the accuracy and robustness of the reconstructed field, optimization of sensor placement is an important aspect of the study. In [22], the authors proposed a generalized empirical interpolation method (GEIM) [34] to select quasi-optimal sensor locations in the framework of data assimilation and reduced basis, which was validated on three types of operational reactors at Électricité de France (EDF). In [35], simulated annealing was applied to optimize the placement of fixed in-core detectors using variance-based and information entropy-based methods to define the objective function. Recently, clustering methods, such as the K-means algorithm, have been used to optimize in-core detector locations for flux mapping in Advanced Heavy Water Reactor [36, 37]. In a recent study for building nuclear digital twins based on the Transient Reactor Test facility at the Idaho National Laboratory, a greedy algorithm was used to optimize sensor locations on a grid, adhering to user-defined constraints [38]. All these methods attempted to optimize the placement of the in-core detectors in a heuristic manner and were limited to a fixed sensor arrangement similar to that used during the training process. However, research on algorithms for handling detector vibrations is scanty.

The vibration of the in-core sensors near their nominal locations is a new problem that may arise from the aging of operational reactors. A typical limitation is attributed to the inability of all the aforementioned methods to handle spatially moving sensors. Recently, the work of [39] facilitated the practical use of neural networks for global field estimation, considering that sensors could move and become online or offline over time. The Voronoi tessellation [40] was used to obtain a structured-grid representation from sensor locations; subsequently, convolutional neural networks (CNNs) were used to build a map from movable sensors to the physical field. Inspired by this work, we adapted the framework to perform field reconstruction in nuclear reactors, such that the vibration of sensors was considered during the reconstruction of neutronic fields.

The remainder of this paper is organized as follows. In Sect. 2, we provide a detailed description of the methodology for field reconstruction with movable sensors by using Voronoi tessellation along with convolutional neural networks (V-CNN). In Sect. 3, we present the physical model and the detailed process for neutronic field reconstructing. Section 4 illustrates the numerical results, in which various error metrics have been presented to evaluate the performance of the method. Finally, we provide a brief conclusion and discuss future work in Sect. 5.

2 Methodology for field reconstruction with movable sensors

We aim to reconstruct a two-dimensional (2D) neutronic field \(\varvec{\phi }\in {\mathbb {R}}^{n_x \times n_y}\) in the reactor core domain \(\Omega \in {\mathbb {R}}^2\) from sparse and limited in-core sensor observations \(\varvec{y} \in {\mathbb {R}}^{n_\text {obs}}\) at location \(\varvec{r}_{\varvec{y}_i},~i=1,...,n_\text {obs}\). Here, \(n_\text {obs}\) indicates the number of in-core sensor observations, while \(n_x\) and \(n_y\) denote the number of grid points in the horizontal (x) and vertical (y) directions in a high-resolution field, respectively. Handling movable sensors at their nominal locations in the field are a challenging task. Field reconstruction should be performed using only a single machine learning model to avoid retraining when the sensors move from their nominal locations. This was achieved through two key processes, as described below:

  1. (i)

    A partition method using Voronoi tessellation which tolerated the local perturbations of sensor locations;

  2. (ii)

    A machine learning framework that mapped the observations to the global physical field in the same structure.

We note that, considering that the sensors in the core of a reactor were fixed, such as self-powered neutron detectors (SPND), we only considered cases of sensor vibration near their fixed positions, rather than significant movement in the entire domain over time. The latter corresponds to the cases referred to in [39].

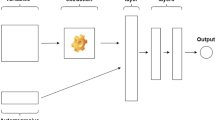
In Fig. 1, we present V-CNNs for neutronic field reconstruction and provide a detailed description of each component in the following sections.

Fig. 1
figure 1

(Color online) V-CNNs for neutronic field reconstruction from discrete sensor locations in a 2D reactor core. The input Voronoi field is constructed from 81 sensors from each center of fuel assembly. The Voronoi field is then fed into a CNN with the Voronoi mask field \(\varvec{\phi }_\text {m}\), and the output of the CNN is the reconstructed field \(\varvec{\phi }_\text {r}\). In the mask field, a grid with a sensor i (black circle) has a value of \(\varvec{\phi }_{\text {m},i}\), which reflects the detected value of the underlying field at site

Full size image

2.1 Voronoi tessellation for spatial domain partitions

For reconstruction using movable sensors, Voronoi tessellation is an essential step that maps the observations to the entire spatial domain. For a given space \(\Omega\), which is generally in 2D, a set of points \(\{ \varvec{r}_{i},~i=1,...,n_\text {obs} \} \in \Omega\). The tessellation approach optimally partitions the given space \(\Omega\) into \(n_\text {obs}\) regions \(G=\{g_1,g_2,...,g_{n_\text {obs}} \}\) using the boundaries determined by the measure d among the given points. Using the measure d, Voronoi tessellation can be expressed as

$$\begin{aligned} g_i = \{ \varvec{r} \in \Omega ~|~ d(\varvec{r},\varvec{r}_i) < d(\varvec{r}, \varvec{r}_j), ~j \ne i \}. \end{aligned}$$
(1)

In this study, the Euclidean measure was used, and the Voronoi boundaries between the points were their bisectors. Figure 2 shows an example of 81 points and the related Voronoi partitions in the Euclidean measure. The Voronoi tessellation conveniently projects sparse sensor observations to the global physical field. Thus, learning the map from sparse observations to the global field via CNNs is possible. More importantly, this partitioning process can tolerate local perturbations in the sensor locations. For more details on the mathematical theory of the Voronoi tessellation, we refer readers to [40,41,42,43].

Fig. 2
figure 2

(Color online) Example of 81 points and the related Voronoi tessellation using Euclidean measure

Full size image

2.2 Input and output of the machine learning model

To reconstruct the physical field using machine learning, we prepared the input data for the model using the following process:

  1. (i)

    Determine the sensor locations \(\varvec{r}_{\varvec{y}_i},~i=1,...,n_\text {obs}\) in the reactor core. \(\varvec{r}_{\varvec{y}_i}\) may vibrate from its nominal location \(\varvec{r}_{\varvec{y}_i}^\text {nominal}\).\(\varvec{r}_{\varvec{y}_i} = \varvec{r}_{\varvec{y}_i}^\text {nominal} + \delta \varvec{r}_{\varvec{y}_i}\), where \(\delta \varvec{r}_{\varvec{y}_i}\) presents the amplitude of the vibration. In the following, for reasons of convenience, we denote \(\delta r_{y_i}\) as \(\delta\).

  2. (ii)

    Calculate the Voronoi tessellation \(\varvec{s}_i \in {\mathbb {R}}^{n_x \times n_y}\) using \(\varvec{r}_{\varvec{y}_i},~i=1,...,n_\text {obs}\). The Voronoi tessellation first partitions the reactor domain \(\Omega\) into \(n_\text {obs}\) regions \(G=\{ g_1,...,g_{n_\text {obs}} \}\) with \(\Omega = \cup _{i=1}^{n_\text {obs}} g_i\), such that each region \(g_i\) contains one sensor located at \(\varvec{r}_{\varvec{y}_i}\). \(\varvec{s}_i\) is defined as follows:

    $$\begin{aligned} \varvec{s}_i (\varvec{r}) = \left\{ \begin{array}{ll} 1 &{} \text {if} ~ \varvec{r} \in g_i \\ 0 &{} \text {otherwise} \end{array} \right. . \end{aligned}$$
    (2)
  3. (iii)

    Prepare the Voronoi mask field \(\varvec{\phi }_\text {m} \in {\mathbb {R}}^{n_x \times n_y}\) using Voronoi tessellation \(\varvec{s}_i,~~i=1,...,n_\text {obs}\). The element \(\varvec{\phi }_\text {m}(\varvec{r})\) satisfies

    $$\begin{aligned} \varvec{\phi }_\text {m} (\varvec{r}) = \varvec{y}_{\varvec{r}_i} ~, ~~\text {if} ~ \varvec{r} \in g_i. \end{aligned}$$
    (3)

The Voronoi mask field \(\varvec{\phi }_\text {m}\) and related target neutronic field \(\varvec{\phi }_\text {n}\) are provided to a machine learning model \(\mathcal {F}_{\delta }\) such that \(\mathcal {F}_{\delta }: \varvec{\phi }_\text {m} \longmapsto \varvec{\phi }_\text {n}\), where \(\delta\) indicates that the model is trained for a given \(\delta\). The final output of the model is then denoted by \(\varvec{\phi }_\text {r} = \mathcal {F}_{\delta }(\varvec{\phi }_\text {m})\), where the subscript ‘\(\text {r}\)’ denotes the reconstructed neutronic field. As the specified input vector contains the observed values and position information of the sensors, the proposed model can handle arbitrary sensor locations and an arbitrary number of sensors.

The perturbations of sensor locations and its impact on the effectiveness of the network were also investigated in this study. The typical amplitude \(\delta\) of the vibration of sensors in a reactor core is less than 1 cm [6], and we investigated the cases of \(\delta =\) 1 cm, 3 cm, and 5 cm. The effects of the number and locations of sensors in these scenarios are described in the numerical results section.

To construct the training \(\{\phi _\text {m}^{\text {(train)}},\phi _\text {n}^{\text {(train)}} \}\) and test \(\{ \phi _\text {m}^{\text {(test)}},\phi _\text {n}^{\text {(test)}} \}\) sets for the learning process, a physical model of the underlying problem

$$\begin{aligned} \mathcal {M}(\phi (\mu ),\mu )=0, \end{aligned}$$
(4)

was solved numerically. Here, \(\mu \in \mathcal {D}\subset {\mathbb {R}}^p\) denotes the p-dimensional parameter of the model, while \(\mathcal {D}\) denotes the feasible parameter domain. The training and test sets were accumulated by solving Eq. (4) over a discrete set \(\mathcal {D}^{\text {(discrete)}}\) which is representative of \(\mathcal {D}\).

2.3 Learning the map using convolutional neural networks

After preparing the input data for the model, a CNN model can be used to learn the map from observations to the field, in the same manner as handling images [44,45,46]. In this study, the channel of the CNN was set to one, and for each layer, the extraction of t key features of the input data through filtering operations was expressed as

$$\begin{aligned} q^{(l)}_{ijm} = \sigma \left( \sum _{p=0}^{H-1} \sum _{c=0}^{H-1} q^{(l-1)}_{i+p-C,j+c-C,m} h_{pcm} + b_m \right) . \end{aligned}$$
(5)

Here, \(C=\text {floor}(H/2)\), \(q^{(l-1)}\) and \(q^{(l)}\) are the input and output data at layer l, respectively; \(h_{pcm}\) represents a filter of size \(H \times H\) and \(b_m\) is the bias. \(l_\text {max}\), H, and m denote the number of layers, filter size, and number of filters, respectively. The output of each filter operation is fed to the activation function \(\sigma (\cdot )\) as the output of the neurons. In this study, we selected a rectified linear unit (ReLU) \(\sigma (z) = \text {max}(0,z)\) as the activation function [47]. We used the ADAM optimizer with an early stopping criterion for training and threefold cross-validation [48,49,50]. Furthermore, the \(L_2\) norm was used to measure the errors in the learning process. The detailed parameters of the CNN used in this study are summarized in Table 1.

The Voronoi mask field \(\varvec{\phi }_\text {m} \in {\mathbb {R}}^{n_x \times n_y}\) was used to model \(\mathcal {F}\); that is, \(q^{(0)} = \varvec{\phi }_\text {m}\), and the output of the model was a high-resolution neutronic field \(q^{(l_\text {max})}\). The learning process is formulated as follows.

$$\begin{aligned} \varvec{w} = \arg \min _{\varvec{w}} \Vert \varvec{q} - \mathcal {F}(\varvec{\phi }_\text {m},\varvec{w}) \Vert _2, \end{aligned}$$
(6)

where \(\varvec{w}\) denotes the model parameters, specifically the filters of the CNN in this study. After completing the training process, the field was reconstructed by feeding the observations \(\varvec{y}\) to the model \(\mathcal {F}\), i.e., \(\varvec{\phi }(\varvec{y}) = \mathcal {F}(\varvec{\phi }_\text {m}(\varvec{y}),\varvec{w})\).

Table 1 Parameter settings of the CNN
Full size table

3 Application to neutronic field reconstructions

3.1 Physical model

In this section, the reconstruction method for nuclear reactor cores is tested. We considered a typical benchmark in nuclear reactor physics, namely the 3D IAEA benchmark problem [51] prepared by the Computational Benchmark Problems Committee of the Mathematics and Computation Division of the American Nuclear Society. This benchmark was selected because it is adapted from realistic reactors, and its geometry and composition are much more complex than those of single-region or two-region problems. After completing this test, the method was directly tested based on real reactor calculations.

To test the algorithm, we used the 2D IAEA case, which represents the midplane \(z=190\) cm of the 3D IAEA benchmark see [51, page 437] for a detailed description. The 2D geometry of the reactor is shown in Fig. 3, where only one-quarter is shown because the rest can be inferred from the symmetry along the x and y axes. This quarter is denoted by \(\Omega\) and comprises four subregions with different physical properties: the first three subregions form the core domain \(\Omega _{1,2,3}\), while the fourth subregion is the reflector domain \(\Omega _{4}\). Certain Newman boundary conditions are satisfied on the x and y axes considering symmetry, and the zero-boundary condition is satisfied on the external border, see Fig. 3.

Fig. 3
figure 3

(Color online) Geometry of the 2D IAEA nuclear core, upper octant: region assignments, lower octant: fuel assembly identification (from [51])

Full size image

The neutron fields consist of fast and thermal fluxes, that is, \(\varvec{\phi }=\left( \phi _1,\phi _2 \right)\) are modeled using a two-group neutron diffusion equation with suitable boundary conditions. The fluxes are the solutions to the following eigenvalue problem (see [52, 53]): Specifically, the flux \(\phi\) satisfies the following eigenvalue problem: Find \(\left( \lambda ,\phi \right) \in {\mathbb {C}}\times L^\infty (\Omega )\times L^\infty (\Omega )\), such that

$$\begin{aligned} \begin{array}{r@{}l} \left\{ \begin{aligned} &{} -\nabla \left( D_1\nabla \phi _1\right) +\left( \Sigma _{\textrm{a}, 1} + \Sigma _{ 1\rightarrow 2} + D_1 B_{z1}^2 \right) \phi _1 = \frac{1}{\lambda } \nu \Sigma _{\textrm{f}, 2}\phi _2 \\ &{} -\nabla \left( D_2\nabla \phi _2\right) + (\Sigma _{\textrm{a}, 2} + D_2 B_{z2}^2 ) \phi _2 = \Sigma _{ 1\rightarrow 2} \phi _1 \end{aligned} \right. , \end{array} \end{aligned}$$
(7)

with the zero-boundary condition \(\phi _i = 0, ~i=1,2\) on the external border \(\partial \Omega\) and the Newman boundary conditions \(\partial (\phi _i)/\partial (\varvec{n}) = 0, ~i=1,2\) on axes. The generated nuclear reactor rate \(P=\nu \Sigma _{\textrm{f}, 1}\phi _1\) reflects the power distribution over the core. The following parameters were used in the above equation:

  • \(D_i\): diffusion coefficient of group i with \(i\in \{1,2\}\);

  • \(\Sigma _{\textrm{a}, i}\): macroscopic absorption cross section of group i;

  • \(\Sigma _{1\rightarrow 2}\): macroscopic scattering cross section from group 1 to 2;

  • \(\Sigma _{\textrm{f}, i}\): macroscopic fission cross section of group i;

  • \(\nu\): average number of neutrons emitted per fission.

The axial buckling \(B_{zi}^2=0.8 \times 10^{-4}\) for all the regions and energy groups (Table 2). The nominal values of the coefficients in diffusion model (7) are listed in Sect. 3.1.

Table 2 Parameters of the 2D IAEA benchmark problem
Full size table

Under certain mild conditions of the parameters, the maximum eigenvalue \(\lambda _{\text {max}}\) is real and strictly positive (see [54, Chapter XXI]). The associated eigenfunction \(\phi\), which is also real and positive at each point \({\textbf{x}}\in \Omega\), and is the flux of interest. In neutronics, the inverse of \(\lambda _{\text {max}}\) is conventionally used and is called the multiplication factor

$$\begin{aligned} k_{\text {eff}}:= \frac{1}{\lambda _{\text {max}}}. \end{aligned}$$
(8)

For each parameter setting, \(k_{\text {eff}}\) is determined by the solution to the eigenvalue problem (7). The maximum eigenvalue \(\lambda _{\textrm{max}}\) is computed using the well-known power method (see [52]). In this study, Freefem++ [55] was used to solve the 2D IAEA benchmark problem. The spatial approximation used \({\mathbb {P}}_1\) finite elements with a grid size of \(h = 1\) cm; thus, the resolution of the field was \(n_x \times n_y = 171 \times 171\).

3.2 Field reconstruction

To simulate the variation in the neutronic fields with respect to the parameter variations, we considered the parameters in Sect. 2 as uncertain parameters. Specifically, we assumed the following:

$$\begin{aligned} \mu = (\mu _1,\mu _2,...,\mu _n) \in \mathcal {D} = [\mu _{i,\text {nominal}}\cdot 0.8, \mu _{i,\text {nominal}}\cdot 1.2]^{n} \end{aligned}$$
(9)

where \({\mathcal {D}}\) is the parameter domain. We randomly generated 10000 samplings of \(\mu\) in \(\mathcal {D}\) and solved Eq. (7) to obtain a collection of 10000 samples of neutronic fields \(\mathcal {M} = \{ \varvec{\phi }_1(\mu ), \varvec{\phi }_2(\mu ),\) \(\varvec{P}(\mu ) ~ | ~ \mu \in \mathcal {D} \}\). Among them, 8000, 1000, and 1000 samples were used for training, validation, and testing, respectively. We trained three CNN models with the same input data, that is, the thermal flux \(\varvec{\phi }_2\) which is measurable with in-core detectors, and the output fields, which are the fast flux \(\varvec{\phi }_1\), thermal flux \(\varvec{\phi }_2\), and reaction rate \(\varvec{P}\) (see Fig. 4 for a schematic).

Fig. 4
figure 4

(Color online) Schematic for the reconstruction of neutronic fields

Full size image

To synthesize the observations, we assumed that an in-core sensor was located at the center of each assembly to acquire the thermal flux. We further assumed that these sensors could move in a local square with a width \(\delta\) cm, centered at the center of each assembly. We performed numerical tests for the cases \(\delta = 1, 3,\) and 5 cm to investigate the effect of different levels of vibration of the sensors. Thus, observations were generated randomly from windows of width \(\delta\) centered at their nominal locations (see Fig. 5). Then, the model \(\mathcal {F}\) was trained based on set \(\mathcal {M}\), and schematics of the training process are shown in Figs. 1 and 4.

Fig. 5
figure 5

Different amplitudes of vibrations of a sensor near the nominal location in an assembly

Full size image

3.3 Error metrics

Before presenting the numerical results, we define several metrics to evaluate the quality of the field reconstructions. The normalized root-mean-square residual of the difference between the reconstruction \(\varvec{\phi }_\text {r}\) and test field \(\varvec{\phi }_\text {t}\) is

$$\begin{aligned} e_2(\varvec{\phi }):=\frac{\Vert \varvec{\phi }_\text {r} - \varvec{\phi }_\text {t} \Vert _2}{\Vert \varvec{\phi }_\text {t} \Vert _2}. \end{aligned}$$
(10)

In nuclear engineering, the error in the reconstructed field in \(L_{\infty }\) is another import metric that reflects the worst case scenario for each reconstruction.

$$\begin{aligned} e_{\infty }(\varvec{\phi }):=\frac{\Vert \varvec{\phi }_\text {r} - \varvec{\phi }_\text {t} \Vert _{L_{\infty }}}{\Vert \varvec{\phi }_\text {t} \Vert _{L_{\infty }}}. \end{aligned}$$
(11)

The total average root-mean-square residual and standard deviation over the given test set \(\mathcal {M}\) are defined as

$$\begin{aligned} \begin{array}{ll} E(e_{\chi }(\varvec{\phi })) &{}:=\text {average}_{\varvec{\phi }\in \mathcal {M}} (e_{\chi }(\varvec{\phi })) \\ \textrm{STD}(e_{\chi }(\varvec{\phi })) &{}:=\text {standard deviation}_{\varvec{\phi }\in \mathcal {M}} (e_{\chi }(\varvec{\phi })) \end{array}, \end{aligned}$$
(12)

where \(\chi\) denotes the \(L_{2}\) or \(L_{\infty }\) norm.

Furthermore, the average assembly field (fluxes and power rate) and related errors were investigated. The average assembly power is defined as

$$\begin{aligned} \phi _{\text {ass},k}= \frac{1}{v_k} \int _{v_k} \phi \textrm{d}v, \end{aligned}$$
(13)

where \(\phi\) denotes \(\varvec{\phi }_1, \varvec{\phi }_2\) or \(\varvec{P}\), \(v_k\) denotes the volume of the k-th subassembly, and k denotes the fuel assemblies, as shown in the lower octant of Fig. 3. The average error \(e_2(\phi _\text {ass})\), maximum relative error \(e_{\infty }(\phi _\text {ass})\), related average \(E(e_{\chi }(\varvec{\phi }_\text {ass}))\), and standard deviation STD\((e_{\chi }(\varvec{\phi }_\text {ass}))\) of the errors over the given test set \(\mathcal {M}\) can also be similarly defined.

Therefore, we introduce the structural similarity (SSIM) [56] index to measure the field reconstruction. In contrast to the general \(L_2\) error, the SSIM index measures similarity by comparing two images based on luminance, contrast, and structural similarity information.

4 Numerical results

We have described the methodology for field reconstruction with movable sensors using a CNN in Sect. 2 and presented a detailed process for neutronic field reconstruction based on a typical benchmark nuclear engineering domain in Sect. 3. In this section, we describe the numerical performance of the proposed method.

4.1 Performance for the benchmark problem

In Fig. 6, we present the error distributions of the reconstructed fields for different vibration amplitudes, namely \(\delta = 1,3,\) and 5 cm, for the 2D IAEA benchmark problem. The reconstruction of \(\varvec{\phi }_1\) using observations from \(\varvec{\phi }_2\) performs better than those of \(\varvec{\phi }_2\) and \(\varvec{P}\). Furthermore, the reconstruction error increases with the amplitude of the vibration, that is, when \(\delta\) varies from 1 cm to 5 cm. The largest error appears around the interface of the fuel and reflector because of discontinuities in the materials, particularly for the fields of the thermal flux \(\varvec{\phi }_2\) and the power rate \(\varvec{P}\).

The average assembly values of the reconstructed fluxes and power rate are shown in Fig. 7, and the same conclusions can be drawn. Because of the averaging process, the assembly exhibits considerably smaller relative errors than the pin-wise case.

Three main conclusions can be drawn from analysis of the numerical results.

  1. (i)

    The proposed V-CNN can reconstruct the multi-field using observations only from thermal flux;

  2. (ii)

    The reconstruction errors for the assembly are significantly lower than 5%, which is acceptable for engineering applications, i.e., less than 10%, which is an acceptable criterion in reactor physics (more information is available in [57]);

  3. (iii)

    Even with a movement of amplitude \(\delta = 5\) cm for the sensors, the proposed V-CNN reconstructs the field with an error less than 10%.

4.2 Average performance over a test set

To investigate the generalizability of the field reconstruction method, we analyzed the error performance for 1000 test samples. The error metrics were the average relative \(L_2\) error \(E(e_{2}(\varvec{\phi }))\), average relative \(L_{\infty }\) error \(E(e_{\infty }(\varvec{\phi }))\), average relative assembly \(L_2\) error \(E(e_{2}(\varvec{\phi }_\text {ass}))\), average relative assembly \(L_{\infty }\) error \(E(e_{\infty }(\varvec{\phi }_\text {ass}))\), average SSIM, \(E(\textrm{SSIM}(\varvec{\phi }))\), and the standard deviation of the aforementioned errors.

Table 3 illustrates the numerical results of the errors for the reconstruction of \(\varvec{\phi }_1\) over the 1000 test samples. All error metrics exhibit good agreement between the reconstructed and original fields. The maximum errors, that is, the \(L_{\infty }\) errors in both the pin-wise and assembly wise cases, are below 2%. The good performance is attributed to the smoothness of the fast flux owing to its relatively longer diffusion length than the thermal flux. Thus, the fast flux is less affected by the heterogeneity of the materials in this benchmark (Fig. 6a for example).

Tables 4 and 5 illustrate the numerical results of the errors for the reconstruction of \(\varvec{\phi }_2\) and \(\varvec{P}\) over the 1000 test samples. The average \(L_{\infty }\) errors in the pin-wise of the thermal flux and power rate were below 10% when the vibration amplitude was less than 3 cm. When the amplitude of the vibration increases, the average \(L_{\infty }\) error exceeds 10%, which unsuitable for practical engineering applications. However, the \(L_{\infty }\) errors are much smaller for the assembly. The worst case occurs for \(\delta = 5\) cm when reconstructing \(\phi _{2}\), which leads to an error of \(E(e_{\infty }(\varvec{\phi }_\text {ass})) = 0.0288\) and standard deviation \(\textrm{STD}(e_{\infty }(\varvec{\phi }_\text {ass})) = 0.0109\). These results further confirm its acceptability for engineering applications. Although the relative \(L_{\infty }\) errors are 10%, most of the points appear around the interface between the fuel and reflector. A relatively large error in this domain is not crucial for safety analysis. Thus, the SSIM indices in all the three tables exceeded 0.99, which further demonstrates the excellent performance for all the field reconstructions.

Fig. 6
figure 6

(Color online) Reconstructed fields for different vibration amplitudes, \(\delta = 1,3,5\) cm for the 2D IAEA benchmark problem

Full size image
Fig. 7
figure 7

(Color online) Reconstructed fields in assembly wise for different vibration amplitudes, and \(\delta = 1,3,\) and 5 cm for the 2D IAEA benchmark problem

Full size image
Table 3 Errors in the different metrics for the reconstruction of \(\varvec{\phi }_1\) using thermal flux observations from movable sensors
Full size table
Table 4 Errors in the different metrics for the reconstruction of \(\varvec{\phi }_2\) using thermal flux observations from movable sensors
Full size table
Table 5 Errors in the different metrics for the reconstruction of \(\varvec{P}\) using thermal flux observations from movable sensors
Full size table

4.3 Robustness analysis

The robustness of the reconstruction with respect to the number of observations \(n_{\text {obs}}\) and amount of training data \(n_{\text {snapshot}}\) was examined. In Fig. 8, we show the dependence of the relative reconstruction errors in \(L_2\) norm and \(L_{\infty }\) norm on \(n_{\text {snapshot}} = 128, 1280, 4096, 8192, 15743\) and on \(n_{\text {obs}}=25, 45, 81\) to recover the thermal flux \(\phi _2\) over the test set. The number of observations \(n_{\text {obs}}=25, 45\), and 81 correspond to sparsities of 0.0855%, 0.154%, and 0.277%, respectively, against the number of grid points in the field. The two figures demonstrate the robustness of the proposed method with respect to the sparsity of the sensors and training data. Few observations and training data lead to low-level reconstruction errors. Furthermore, the addition of training data improves the reconstruction accuracy more significantly than the addition of sensors. This result demonstrates that the proposed field-reconstruction framework is robust against sensor failures and confirms its potential for practical applications.

To investigate the robustness of the recovery with respect to the observation noise, a noise \(\epsilon _{\sigma }\) that was randomly sampled in the range \((-\sigma ,\sigma )\) was added to each clean observation y, thereby generating a noisy observation \(y^o=y(1+\epsilon _{\sigma })\) for each sensor. The dependence of the relative reconstruction errors in the \(L_2\) and \(L_{\infty }\) norms of different noise levels, that is, \(\sigma =0.01,0.02,0.03,0.04,0.05\) for recovering the thermal flux \(\phi _2\) are shown in Table 6. The test was performed using 81 sensors with a vibration amplitude \(\delta = 5\) cm. The errors were first averaged over 100 repeated random observation samplings for each field reconstruction, and then averaged over the test set. On average, the reconstruction error changes significantly for noisy observations. The reconstruction error exhibits a slow linear growth trend with respect to the noise level. Although the \(L_2\) error is below 10%, which is satisfactory for nuclear engineering applications, the \(L_{\infty }\) error remains at approximately 30%, which is unsatisfactory. This provides a direction for further research on reducing the \(L_{\infty }\) error.

Fig. 8
figure 8

Dependence of the relative reconstruction errors in the \(L_2\) and \(L_{\infty }\) norms on the number of training snapshots \(n_{\text {snapshot}} = 128, 1280, 4096, 8192, 15743\) and the number of observations \(n_{\text {obs}}=25, 45, 81\) for recovering the thermal flux \(\phi _2\)

Full size image
Table 6 Dependence of the relative reconstruction errors in the \(L_2\) and \(L_{\infty }\) norms of the noise level \(\sigma\) for recovering the thermal flux \(\phi _2\)
Full size table

5 Conclusion

In this study, a V-CNN was proposed for neutronic field reconstruction to resolve the vibrations of in-core sensors, which may arise from the aging of operational reactors. Observations from movable in-core sensors were projected onto the same global field structure using Voronoi tessellation, holding the magnitude and location information of the sensors. General convolutional neural networks were used to learn maps from observations to the global field. Furthermore, the proposed method reconstructed multi-physics fields, including the fast flux, thermal flux, and power rate distributions, using observations from a single field, such as the thermal flux.

Numerical tests based on the IAEA benchmark demonstrated the efficiency of the proposed method. Three main conclusions can be drawn from the analysis of the numerical results.

  1. (i)

    V-CNN can reconstruct the multi-field using observations only from thermal flux;

  2. (ii)

    All the reconstruction errors in average are below 5%, which is satisfactory for engineering applications;

  3. (iii)

    Even with a vibration amplitude of \(\delta = 5\) cm for sensors, V-CNN exhibits satisfactory performance.

In this study, the original CNN framework was used for image processing and was adapted for field reconstruction with rectangular mesh division. Field reconstruction with an irregular mesh requires additional mesh mapping to map the irregular mesh to a rectangular mesh. The adaptability of the proposed method to various reactor configurations is a continuation of this study.

This study provides a novel approach for field reconstruction using vibration sensors. Future work could highlight the uncertainty quantification of V-CNN considering observation noise systematically and proceed to practical engineering applications based on real nuclear reactors such as the HPR1000 reactor developed in China [58]. In this aspect, data uncertainty could be evaluated using a probabilistic neural network [59] or Bayesian neural network [60]in combination with V-CNN, while the epistemic uncertainty of the model could be examined using the Gaussian stochastic weight averaging technique [61] or other techniques.

To investigate the adaptability of the proposed method to an HPR1000 reactor, a pin-wise field calculation is necessary to consider the fuel and sensor vibrations, which is now being performed by our group. However, in practical engineering cases, the vibrations of reactor components, such as fuel and in-core sensors, lead to complex phenomena in the core. Many studies [2,3,4,5,6] have analyzed the induced variation of neutronic fields (also called neutron noise), considering the induced variation in the cross section parameters of the neutron diffusion equations. Inspired by the neutron noise analysis process, a synthetic modeling approach is necessary for considering the effects of component vibrations. This approach is useful for clarifying the interplay or distinguish between field reconstructions using in-core sensor vibrations and general reactor noise analyses.

In addition, the combination of V-CNN and fault diagnosis [62] is a possible future research topic. With the development of machine learning in the field of nuclear physics [63, 64], the adoption of V-CNNs in nuclear physics, where CNNs are used [65,66,67], is also worth investigating.