1 Introduction

Clothes are an indispensable aspect of people’s social lives. Therefore, cloth products are manufactured in large quantities in factories daily. One of the main steps in the manufacturing process involves grasping cloth parts and transporting them to the required workspaces. This process is executed multiple times during the sequence of cloth assembly and plays a crucial role in the manufacturing of clothing products.

Sportswear and polo shirts are a major category in cloth production. Because of the strong flexibility and susceptibility to deformation of the materials used, achieving automated singular picking and neat stacking of cloth parts remains challenging, primarily relying on manual labor. Conversely, if this task could be automated and integrated with the automation of the feeding section of the sewing machine, the overall automation efficiency of the sewing process could be significantly improved. It is anticipated that this will have a significant impact on addressing the issue of labor shortages.

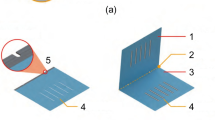
Furthermore, for some small factories, the primary focus is on the production of various clothes in smaller quantities. Therefore, they require the ability to classify and package multiple types of clothes simultaneously within a limited workspace. If it is possible to automate processes while reducing the space required for arranging cloth parts, it would enable the handling of a greater variety of clothes simultaneously, as shown in Fig. 1, significantly improving overall work efficiency. The focus of this paper is on the automation of the task of gripping, sorting and stacking of cloth parts.

Fig. 1
figure 1

Flow of fabrication process for small-lot, multivariety production facilities

Full size image

The purpose of this study is to automate the picking and placing of cloth parts, particularly thin and large fabric materials commonly used in clothes, such as sportswear and polo shirts. Specifically, our task involves picking up and stacking cloth parts that are cut by a cutting machine. The authors previously devised a method (Kawasaki et al. 2021) that involved pressing a cylindrical brush against the edge of the fabric and then rotating the cylindrical brush to wrap the cotton fabric, demonstrating its effectiveness through practical experiments. In addition, the authors developed an end-effector that not only retains the original functionality but can also carry fabric rubber by squeezing and gripping (Yamazaki and Abe 2021). To achieve this goal, the authors improved the previous end-effector to successfully fold and grasp long strips of fabric (Zhu et al. 2023), a task previously unattainable. This study extends upon this work and provides a more detailed design for handling various cloth parts.

This study serves as a sequel to previous research endeavors. While previous studies have focused solely on small fabrics, the actual cloth production process involves not only small fabrics but also numerous large fabrics that cannot be easily lifted or stacked through simple winding. In this study, we developed a new end-effector that retains its compact structure while combining the functionality of winding and scooping up thin fabrics. Furthermore, considering the characteristics of the end-effector and the motion of the robotic arm, we proposed a method called “zigzag folding” for folding the fabric back and forth. Small fabrics such as collars that require only one zigzag fold or no folding can be easily transported and stacked. However, for large fabrics such as long sleeves and the front and back of clothes that require multiple folds, it is possible to combining the longitudinal folding strategy of this zigzag folding method with a transverse folding strategy, large sections of fabric were folded into smaller sections, scooping up the entire folded piece, and then transporting and stacking them. This enables the simultaneous handling and stacking of various types of clothes, even in situations where the vertical motion range of the robot is limited and the space for placement is confined.

The contributions of this study are as follows:

  • We developed a compact end-effector that can roll up large fabrics and scoop them up for transportation after folding them into smaller ones.

  • We proposed zigzag and transverse folding methods for folding large fabrics into smaller ones and designed the motion trajectories of these folding strategies. Additionally, we developed a method for autonomously determining the folding strategy based on the diverse dimensions of the fabric.

  • We successfully used the manufactured end-effector and proposed a folding method to handle long and wide fabrics. Furthermore, we simulated a factory environment and conducted experiments on various cloth parts, affirming the practical feasibility of the proposed end-effector in factory production.

The structure of this paper is as follows: We present related work in the next section. Section 3 explains related issues and our approach. Section 4 introduces the proposed end-effector in detail. Section 5 introduces the trajectory design of zigzag folding and the folding strategy. Section 6 presents the experimental results of zigzag folding and the folding strategy applied to various fabric sizes. Section 7 presents the experimental results of the pick-and-place experiments conducted in a simulated factory environment using the proposed end-effector. Finally, we summarize the study in Sect. 8.

2 Related work

Cloth manipulation is common task in both housework and manufacturing. However, robotic manipulation of cloth is challenging due to the high dimensionality of the configuration space and the complexity of the dynamics affected by different material properties. Ganapathi et al. (2020) learn a visual representation of deformable fabrics by training a dense object descriptor that facilitates the task of folding multi-step fabrics on a real physical system. Hietala et al. (2022) proposed a scheme that uses reinforcement learning to learn strategies in simulation and transfer learned strategies directly to the real world, and evaluated the contribution of visual feedback and material randomization in real-world experiences. Petrík et al. (2016) designed a folding path algorithm based on a balance of forces that takes into account the properties of the cloth material while preventing slippage.

Thus far, the manipulation of cloth products has been realized using automated machines. Borràs et al. (2019) summarized several methods for grasping fabrics and provided examples of various end-effectors for each method. Petrik et al. (2015) demonstrated a prototype gripper designed for handling soft materials. The end-effector was designed according to the considerations of grasping force, mechanical flexibility, and sufficient dexterity for tactile exploration. Le et al. (2013a) developed an end-effector that can grasp fabric by inserting a finger between the gaps in the fabric. Contact sensors and a stereo camera with varying light intensities were embedded at the tip of the end-effector. The purpose of these end-effectors is to manipulate fabric products, such as towels and thin fabric parts. However, it seems difficult to accomplish the task of grasping and sorting various cloth parts during the cloth production process.

One method used to pick cloth parts at sewing factory premises involves specialized end-effectors. Therefore, various studies and developments have been ongoing (Le et al. 2013, 2015; Koustoumpardis, et al. 2017; von Drigalski et al. 2017; Donaire et al. 2020). Schulz (1991) introduced several gripping devices for cloth picking. One is the “Needle” claw gripper, which is designed to wrap around the fabric by snagging the clothes. Others include the “Bonding” gripper, which grasps a piece of fabric by sticking out adhesive tape, and the “Freezing” gripper, which adheres to the target piece by freezing and bonding after giving water. Ku et al. (2020) referenced the attachment mechanism of the lamprey, achieving a mechanism that uses small pointed hooks to grasp and clamp the fabric. However, these methods may damage or temporarily stain fabric. A method for transporting large fabric parts using electroadhesion has also been proposed. He et al. (He et al. 2022) recently developed an electroadhesion gripper specifically designed for adhering to large fabric parts. Sun and Zhang (2019) combined the characteristics of a crank–slider mechanism with four electrostatic pads to create an electroadhesion gripper capable of gripping fabric panels of various sizes and flattening folded/wrinkled fabrics. However, because of their high-voltage power consumption and large dimensions, these grippers face difficulties lifting the intended fabric part within densely woven fabric environments. Digumarti et al. (2021) proposed a fingertip-sized electroadhesion gripper capable of successfully picking up fabric pieces 100 times larger than its size. Although it avoids larger dimensions, it still fails to address the issue of high-voltage power consumption. Ono et al. (1990) proposed a robotic hand for picking up a piece of fabric. The sensor at the tip of the end-effector measured the number of stacked items.

An effective method for handling fabrics is to pull up a part of the fabric using a rolling mechanism. Kabaya and Kakikura (1998) developed a mechanism that tightens a piece of fabric by rotating two rollers facing each other. Its performance was validated through experiments with thicker fabric, such as towels and felt. Shibata and Miyasaka (2018) proposed a roller-end actuator equipped with a piezoelectric sensor. It was used to flip through a small booklet and to assess whether a page had been turned. Manabe et al. (2021) focused on the fabric of Y-shaped shirts and demonstrated a fabric retrieval device that rolls up the fabric using two rollers with rubber-coated surfaces. Zhang et al. (2023) designed a three-finger gripper with a roller on one finger and rubber tips on the other fingers. They used a roller to roll up the fabric and the edge of the T-shirts before completing the grasp by combining the other fingers and the center point. Yamazaki and Abe (2021) proposed a versatile end-effector for pick-and-place fabric parts. A roller wrapped in remover fabric was used to pick up cotton sheets. Two opposing rollers were used to pick up the fabric rubber.

As previously mentioned, various end-effectors have been developed. Although mechanisms for grasping and placing fabrics have been assessed, there seems to be a lack of research on the transportation of fabric parts with diverse shapes and dimensions. In sewing factories, it is necessary to transport fabric parts of diverse shapes and dimensions, and in some cases, each fabric piece must be compact and neatly stacked in a confined space, irrespective of its dimensions. Therefore, the end-effector must possess the capability to fold, transport, and neatly stack fabric. In this study, we propose a method that uses existing mechanisms to handle such situations.

3 Issues and approach

A. Issues

The focus of this study is a fabric primarily made of materials such as cotton and polyester, which are commonly used in the production of polo shirts, sportswear, and similar clothes, and are known for their thin and lightweight characteristics. The target audience is small-scale clothing manufacturing factories that typically specialize in producing clothes to meet different customer needs to reduce costs and increase revenue. Consequently, they frequently need to produce multiple types of clothes in a batch.

To prevent mismatches between parts during the production of various clothes and to enable the simultaneous production of a wider variety of clothes, the primary task is to classify and stack these cloth parts according to the specific products after cutting and striving to minimize the space required for stacking each product. The sorted parts were then bundled and transported to the sewing area for stitching. Because of the necessity of stacking cloth parts of various sizes and shapes in one location, different motions are required for each part during the automated handling process.

Based on the above assumptions, the issues in this study can be summarized as follows:

  1. 1.

    Ability to pick up cloth parts of various sizes even if their edges are in close contact with the remaining fabric on the cutting machine.

  2. 2.

    While picking up the parts, the structure should endeavor to minimize the risk of failure during transportation, even for long or large cloth parts.

  3. 3.

    The ability to transport various long or large cloth parts by folding them into smaller parts without requiring the robot arm to have a large range of motion in the vertical direction.

In addition, every effort should be made to make the end-effector lightweight and as small as possible and to minimize the initial introduction and operating costs.

B. Our Approach

The following is a response to the issues presented in the previous subsection. Numbers 1–3 below correspond to the issues in the previous subsection:

  1. 1.

    Adopt a winding mechanism, as described in Yamazaki and Abe (2021), to grasp the cloth parts by winding the edges of the target cloth parts. This ensured that only the target cloth parts were grasped, even when they were closely situated among surrounding fabrics.

  2. 2.

    Install a horizontally movable board on the end-effector. While the edges of the cloth parts are lifted by winding, the board can smoothly slide underneath the cloth parts, thereby increasing the contact area with the cloth parts to prevent them from falling off during rapid motion.

  3. 3.

    Devise a proposal to fold the cloth parts back and forth into a zigzag pattern and design a method for determining the folding strategy based on the dimensions of the cloth parts. Combine the characteristics of the end-effector to fold the cloth parts, and then use the flat board to scoop the folded cloth parts for transportation.

In a previous study (Zhu et al. 2023), we demonstrated the capabilities of the end-effector in folding and handling long fabric sheets. Building on this groundwork, the present study further investigates the functionalities of the end-effector in handling long and wide fabric pieces and provides a more detailed design regarding the folding strategy for cloth parts. Finally, an experiment was conducted in a simulated factory environment to verify the feasibility of this end-effector and folding strategy for use in the factory.

4 Proposed end-effecttor

A. Structural Overview

A schematic of the proposed end-effector is shown in Fig. 2. This mechanism consists of three parts. The first part is the connecting part that links the robot to the remaining two parts of the end-effector. The second part is a cylindrical brush on the left side, which is used to grip the fabric. Finally, the third part is a flat board on the right side, which is responsible for supporting and scooping fabric up.

Fig. 2
figure 2

Proposed end-effector

Full size image

To stably pick up a piece of fabric, it is necessary to consistently apply the same force when contacting the target fabric. Therefore, a method is employed that uses the weight of the end-effector to apply the contact force. As shown in Fig. 2, the connecting part primarily consists of three shafts and a bracket with three linear bearings, which are used to connect the robot to the other two parts of the end-effector and allow the structure to move passively up and down. Thus, when the cylindrical brush comes into contact with the fabric portion, the contact force of the end-effector is 0.257 g [N] (g: standard gravity). The passive move range is set to 15 mm. Because of the compact design and lightweight nature of the proposed end-effector, this contact force can be fully achieved through its weight.

In the following sections, we explain each important part in order. In Sect. 5, we provide a detailed explanation of the zigzag folding strategy of the proposed end-effector.

B. Winding with a cylindrical brush (Kawasaki et al. 2021).

The left side of the proposed end-effector is equipped with a motor-driven cylindrical roller with a radius of 7 mm. The surface of the roller is attached to a fabric used for removing dust from clothes and winding a piece of fabric. The dust removal fabric consists of polyolefin fibers with a diameter of less than 0.1 mm, a length of 1–3 mm, and an inclination angle of 1°–5°, densely occupying the fabric area.

The remover fabric was chosen as the surface material because it possesses the following characteristics: short fibers on the surface of the remover fabric are captured by cotton fabric, resulting in weaker adhesion. By adhering to a large area on the cylindrical surface, the cotton fabric can be lifted without slipping. A method for gradually adhering fabric pieces to the surface of a cylindrical brush by rolling the brush on the fabric has been proposed in Kawasaki et al. (2021), as shown in Fig. 3, and its effectiveness is described through experiments conducted on cotton fabric. This end-effector uses the cylindrical brush with a length of 185 mm, and by grabbing fabric experiments it has been proved that it can successfully grab fabrics with gripping edge length six times longer than its own length, even when the fabrics are tightly fitted to each other.

Fig. 3
figure 3

Motion to wind up the edge of the cloth fabric: (1) contact with the top of the fabric sheet, (2) gently rotate the brush in place while lightly gripping the fabric, and (3) rotate and move horizontally (wind up while rolling) (Kawasaki et al. 2021)

Full size image

C. Scooping with a Flat Board

The end-effector on the right side is equipped with a horizontal movable flat board with 105 mm in working length \({L}_{Board}\) and 94 mm in width \({W}_{Board}\) as shown in Fig. 4, which can be easily inserted beneath the fabric. The main functions of this board are twofold: (1) providing support underneath the fabric to prevent it from falling during the fabric handling process; (2) scooping up the entire fabric after folding back and forth the fabric which is too large to be fully grasped into a smaller size. The next section will delve further into the latter function.

Fig. 4
figure 4

Motion of expanding the flat board. a Shows the contracted state of the flat board, b Shows the movement states of each component, c shows the flat board extended to its maximum state

Full size image

The functions of the proposed flat board primarily rely on the rotational motion of the rotate rod. As shown in Fig. 4, the rotate rod connects with the flat board through a small slider, which allows the rotational motion of the rotate rod to be transformed into the horizontal motion of the flat board. The radius of the rotate rod is 60 mm, and the relationship between the rotational angle θ and the horizontal motion distance is calculated using 60(1 − cos θ). The range of motion of the flat board is 0–120 mm, which enables it to grasp fabrics of different materials and sizes while maintaining a lightweight mechanism.

To smoothly insert and remove the flat board from the fabric, it is necessary to polish the contact surface between the flat board and the fabric, which reduces the friction between the flat board and the fabric to less than that between the fabrics. In addition, the front edge of the flat board is inclined at 5° to facilitate insertion below the fabric.

Finally, to scoop up the fabric and feed it to the end-effector, a certain height difference between the cylindrical brush and the flat board should be established. However, when winding the fabric, it is necessary to keep the cylindrical brush and the flat board in contact with the ground on the same horizontal line. To address this issue, a method similar to the connecting part is employed to passively move the flat board up and down, with a set range of motion of 18 mm.

5 Folding strategy

A. Principle of Zigzag Folding

The end-effector introduced in the previous section can stably handle the fabric from winding to lifting because of its large contact area with the fabric. However, if the fabric part is too large to lift, it will have to be transported by dragging one end which is undesirable.

Therefore, considering the characteristics of the end-effector and the motion of the manipulator, we propose a method for folding the fabric in a zigzag pattern and then scooping up the entire fabric, as shown in Fig. 5. Consequently, it is expected that after zigzag folding \(n\) times, the length of the fabric decreases to \(1/(2n+ 1)\) times the original length.

Fig. 5
figure 5

Motion of the zigzag folding \(n\) times. a, b Do zigzag folding \(n-1\) times, c retract the flat board, d, e do the final zigzag folding, finally f insert the board into the fabric underneath to scoop up the fabric

Full size image

B. Calculation of Zigzag Folding Trajectory

When folding the fabric under ideal conditions, each layer of fabric adheres closely together, as shown in Fig. 6a; however, under actual conditions, the cross-section of the folded fabric exhibits a droplet-like shape, as shown in Fig. 6b (Plaut 2015). This study proposes a method that combines linear motion to achieve multiple equidistant folds in the fabric. To achieve this, it is necessary to calculate the difference between the ideal and actual lengths produced by the droplet-like gaps at each curved part of the fabric.

Fig. 6
figure 6

Folded fabric shape. a, b Represent the ideal and actual under the same folding length, respectively. The red part in (b) is the difference length caused by the gap of each curved part \(\epsilon /2\)

Full size image

Assuming that the length of the overlapping part of the fabric is \({d}_{Fold}\), the actual length of fabric required for zigzag fold \(n\) times is \({L}_{Fold}\), and the height of each curved part is \({h}_{Fold}\). Therefore, we can calculate the difference \(\epsilon\) between the ideal and actual lengths of fabric required for a single zigzag fold as \(({L}_{Fold}-(2n+1){d}_{Fold})/n\). Therefore, the difference in length caused by the gaps in each curved part can be obtained as \(\epsilon /2\). The next step is to compute the coordinates of each motion point in the trajectory of the end-effector motion.

In Fig. 7, the blue line represents the trajectory of the twice zigzag folding motion. The points \({O}_{0}-{O}_{4}\) are connected in sequence with straight lines, starting from \({O}_{0}\), which coincides with the rightmost point O of the cylindrical brush. Here, \(r\) represents the radius of the cylindrical brush, \({d}_{Board}\) denotes the horizontal distance from the forward edge of the flat board to point O, \({h}_{Board}\) denotes the vertical distance from the surface of the flat board to point O, \({d}_{Fold}\) denotes the length of the overlapping part of the fabric, and \({d}_{Remain}\) denotes the length of the remaining part. The total length of the fabric \(L\) can be obtained by \({L}_{Fold}+{d}_{Remain}\). With these variables, we can determine the Y and Z coordinates of the starting point \({O}_{0}\) for the zigzag folding (X coordinate remains constant while zigzag folding):

$$\begin{array}{*{20}c} {O_{0} : \left( {L - \pi r - d_{Fold} - d_{Remain} - d_{Board} , L - d_{Fold} - d_{Remain} - \frac{\epsilon}{2} - d_{Board} + h_{Board} } \right)} \\ \end{array}$$
(1)
Fig. 7
figure 7

The motion trajectory of using twice zigzag folding

Full size image

When performing the zigzag folding n times, the end-effector moves 2 \(n\) times. The target coordinates for the \(i\)-th motion can be calculated using the following equation, where \(i\) ranges from 0 to 2 \(n\)-2:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {O_{iy} = L - \pi r - d_{Remain} - d_{Board} - \left| {\cos \left( {\frac{i\pi }{2}} \right)d_{Fold} } \right| + \left| {\sin \left( {\frac{i\pi }{2}} \right)\frac{\epsilon}{2}} \right|} \\ {O_{iz} = L - d_{Remain} - d_{Board} + h_{Board} - \left( {i + 1} \right)\left( {d_{Fold} + \frac{\epsilon}{2}} \right)} \\ \end{array} } \\ \end{array}$$
(2)

Regarding the final two motion coordinates for the trajectory (the (2 \(n\)-1)-th and 2 \(n\)-th in ascending order), the originally extended flat board must be retracted before the motion and inserted below the fabric after the motion is complete. The coordinates can be calculated using the following equation:

$$\begin{array}{*{20}c} {O_{{2n - 1}} :~\left( {L - \pi r - d_{{Remain}} + \frac{\epsilon}{2},~~d_{{Fold}} + \frac{\epsilon}{2} + r + nh_{{Fold}} } \right)} \\ {O_{{2n}} :~\left( {L - \pi r - d_{{Remain}} - d_{{Fold}} ,~r + nh_{{Fold}} } \right)} \\ \end{array}$$
(3)

C. Strategy of Folding the Clothes Parts

Cloth parts of different shapes and dimensions, the corresponding folding strategies may vary. Therefore, a method for automatically generating folding strategies based on the shape and dimensions of the parts has been proposed.

First, the length and width of the cloth parts are measured using a camera. Subsequently, the longitudinal and transverse folding strategies are determined on the basis of the length and width of the part. Finally, the end-effector is controlled to fold the cloth parts according to the defined strategy.

To achieve the best results in picking and placing cloth parts, we designed longitudinal and transverse folding strategies and attempted to optimize them. For the longitudinal folding strategy, it is advisable to keep the overlapping length \({d}_{Fold}\) as close to the working length \({L}_{Board}\) of the flat board as possible, and then develop Eq. (4) to optimize this folding strategy. The length of cloth part \(L\) is then measured in advance, and if it is less than two times the working length of the flat board, folding is deemed unnecessary. Conversely, input the predetermined range of overlapping length \({d}_{Fold}\) and remaining length \({d}_{Remain}\) into Eq. (4) to derive the optimal longitudinal folding strategy \({P}^{*}\):

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {P^{*} = \arg \max P\left( {L, n, d_{Fold} , d_{Remain} } \right)} \\ {P = - w_{1} \frac{{\left| {d_{Fold} - L_{Board} } \right|}}{{\max_{{d_{{Fold \in \left[ {\min_{Fold} ,\max_{Fold} } \right]}} }} \left| {d_{Fold} - L_{Board} } \right|}} + w_{2} \left( {1 - \frac{{d_{Remain} }}{{\max d_{Remain} }}} \right) } \\ {L = \left( {2n + 1} \right)d_{Fold} + d_{Remain} + n\epsilon} \\ \end{array} } \\ \end{array}$$
(4)

The zigzag folding times \(n\) is predetermined by the individual. By conducting prior experiments to measure the length difference \(\epsilon\) caused by the gaps of the curved part, multiple strategies can be derived on the basis of the cloth part length and a predefined range of overlapping and remaining lengths. To evaluate each strategy and obtain the evaluation parameter \(P\), the one with the highest score is determined as the optimal strategy, where \({w}_{1}\) and \({w}_{2}\) are predetermined by the individual (In this study \({w}_{1}\) = 0.7, \({w}_{2}\) = 1-\({w}_{1}\) = 0.3).

For long and wide cloth parts, only considering the longitudinal folding strategy is insufficient. Therefore, we devised a transverse folding strategy. After the longitudinal folding of the cloth parts in the YZ plane, transverse folding is performed toward the X-axis. If the measured width of the cloth part \({W}_{cloth}\) is less than three times the working width of the flat board \({W}_{Board}\), folding is deemed unnecessary. Conversely, transverse folding is required. The overall folding operation is shown in Fig. 8.

Fig. 8
figure 8

Motion of folding the long and wide fabric. The original shape of the fabric (a) is folded into shape (b) using the zigzag folding method; the flat board is then inserted underneath the fabric. c The fabric is raised to height of \({h}_{raise}=({W}_{cloth}-{W}_{Board})/2\) so that its edge touches the surface and is then moved diagonally downward to the left. d The flat board is retracted and inserted underneath the fabric again, and e steps (c, d) are repeated in the opposite direction to complete the folding process

Full size image

6 Verification experiments

A. Experimental Settings

To verify the feasibility of the proposed end-effector and folding strategy for cloth parts, validation experiments were conducted using fabric with the same materials as real clothes. The end effector was attached to a Dobot M1 manufactured by Dobot Inc. with a height working range of 5–250 mm. A large board was placed as the experimental platform, and an Azure Kinect camera manufactured by Microsoft was installed at one end of the board to capture information about the fabric.

In Sect. 6-B, we investigated the feasibility of the longitudinal folding strategy and zigzag folding using a long fabric sheet as the subject. We placed the experimental fabric on the experimental platform and used the dimensions obtained through Azure Kinect to input the previously designed folding strategy and motion generation system. Subsequently, the coordinates of each moving point were input into the Dobot M1 to control its folding, gripping, and placement operations.

In Sect. 6-C, we used long and wide fabrics to assess the entire strategy and the capability of the end-effector in handling large fabrics. In addition, we added a defined placement area to the existing experimental setup, as shown in Fig. 9. To account for potential errors arising from changes in fabric thickness post-folding, the dimension of this area was determined according to the results of the folding strategy with 10-mm tolerance as fault tolerance, aimed at validating its ability to stack fabrics.

Fig. 9
figure 9

Experimental environment settings

Full size image

B. Long Fabric Folding Experiment

To validate the feasibility of the zigzag folding strategy for large fabric folding by the end-effector, the longitudinal folding strategy obtained through Sect. 5-C based on the fabric length captured by the camera was introduced into the equations of Sect. 5-B to generate the motion trajectory for experimentation, and the overlap rate \({\delta }_{1}\) was defined to evaluate the experimental results of long fabric. The overlap rate as shown in Eq. (5), reflects the effectiveness of the zigzag folding. Here, \({l}_{i}\) denotes the length of the overlapping part of the \(i\)-th layer of fabric, and \({l^{\prime}}\) denotes the expected overlapping length.

$$\delta _{1} = \frac{{\mathop \sum \nolimits_{i}^{{2n + 1}} l_{i} }}{{\left( {2n + 1} \right)l^{\prime}}} \times 100\%$$
(5)

The fabrics used in the experiment were divided into three categories: sportswear, innerwear, and polo shirts, with three sizes (400 × 100 mm, 450 × 100 mm, and 500 × 100 mm, respectively) prepared for each, the properties were shown in Table 1, the smoothness and stiffness are rated on a scale of 1–5. A higher smoothness rating indicates a smoother fabric, while a higher stiffness rating indicates a stiffer fabric, and the GSM is the weight of the fabric per square meter. The difference in length caused by the gaps in each curved part of the various materials \(\epsilon /2\) can be roughly determined in advance through experiments as 6, 4, and 10 mm, as shown in Fig. 10. Finally, we set the length range of the overlapping part to 80–160 mm and the length range of the remaining part to 0–40 mm. Subsequently, we performed zigzag folding experiments once and twice on these nine objects individually, with each experiment conducted 50 times. The final experimental results are presented in Fig. 11a.

Table 1 The Properties of Experimental Fabrics
Full size table
Fig. 10
figure 10

Example of determining difference length \(\epsilon /2\) for sportswear, total length is 450 mm

Full size image
Fig. 11
figure 11

Overlap rates of different fabrics in various folding scenarios. The left diagram (a) only considers the longitudinal zigzag folding strategy, whereas the right diagram (b) considers the transverse folding strategy. The horizontal axis represents the different experimental subjects and their respective zigzag folding times, and the overlap rate range is distinguished by color

Full size image

Figure 11a shows that the proposed zigzag folding method achieves an overlap rate of over 90% when folding long fabric strips, with most cases showing an overlap rate exceeding 95%. This validates the feasibility of employing a longitudinal folding strategy and motion generation system based on the proposed end-effector.

C. Long and Wide Fabric Folding Experiments

The goal of this study is to fold multiple large fabrics into smaller pieces and then stack them. However, for long and wide fabrics, simply relying on the zigzag folding strategy still results in a large dimension in terms of width. Therefore, considering using the transverse folding strategy to fold fabrics into smaller widths, we experimented to evaluate the feasibility of stacking the folded long and wide fabric.

The experimental setup was previously described in Sect. 6-A. In contrast to experiment Sect. 6-B, the various fabric dimensions were set at 400 × 400 mm, 450 × 400 mm, and 500 × 400 mm. We then evaluated the results of the folding strategy using Eq. (6).

$$\begin{array}{*{20}c} {\delta_{2} = \left( {1 - \frac{{\left| {S_{T} - S_{F} } \right|}}{{S_{T} }}} \right) \times 100\% } \\ \end{array}$$
(6)

Here, the overlap rate \({\delta }_{2}\) is the experimental result of long and wide fabric, which reflects the quality of folding, \({S}_{T}\) denotes the folding area obtained using the folding strategy, and \({S}_{F}\) denotes the folding area obtained by projecting the point cloud data of folded fabric captured through the camera onto the experimental platform. The results are presented in Fig. 11b. Regarding the results, as this study mainly focuses on the stacking of fabrics, any potential impact on the results due to factors such as measurement errors from the camera can be temporarily disregarded within the scope of this study.

Holding success was defined as the end-effector successfully folding and grasping the fabric, and placing success was defined as the folded fabric being placed within the placement area after transportation. If both conditions were met simultaneously, the process was considered successful. The experimental process of performing twice zigzag folding is depicted in Fig. 12. Figure 12a–c show the longitudinal folding method. Figure 12d–g show the transverse folding method. Figure 12h, i show the process of transferring and placing the fabric.

Fig. 12
figure 12

Folding of long and wide fabric sheet with twice zigzag folding. a–c Fold the length of the fabric by zigzag folding twice, d–g fold the width of the fabric by transverse folding, h transfer the folded fabric and i place it in the placement area

Full size image

The holding success rate is the ratio of the number of holding successes to the total number of experiments. The placing success rate is the ratio of the number of placing successes to the number of holding successes. The success rate is the ratio of the number of placing successes to the total number of experiments. Each object underwent zigzag folding experiments once and twice, with each experiment conducted 50 times. Then three sizes of each material were aggregated for analysis, which means that 150 experiments were conducted for each combination of material and folding times, and the experimental results shown in Table 2, combined with the experiments in Sect. 6-B, indicate that the end-effector and folding strategy demonstrate a certain level of handling capability for various types of fabrics.

Table 2 Evaluation results for long and wide fabric
Full size table

In addition, we completed the task of stacking several folded long and wide fabrics, as shown in Fig. 13. After folding and scooping up the fabric (Fig. 13a), the fabric was moved to be stacked (Fig. 13b) and then descended until the bottom of the flat board contacted the fabric below; the flat board was retracted, and the cylindrical brush was rotated to complete the placement of the fabric (Fig. 13c, d). The stacking results are shown in Fig. 13e, f. These results indicate that the end-effector has good capability for stacking folded fabrics.

Fig. 13
figure 13

Stacking the folded long and wide fabric. a, b Transfer the folded fabric onto the stacked fabric and descend until the bottom of the flat board contact the fabric, c, d rotate the cylindrical brush and retract the flat board. e, f Show the result of the stacking

Full size image

7 Experiments in factory environments

A. Experimental Settings

The goal of the proposed end-effector was to fold the various cloth parts cut using a cutting machine into smaller pieces and stack them at a designated location within the factory. To validate the applicability of the end-effector in actual production processes, we simulated a factory environment and conducted a series of experiments. Each part of the T-shirt cut using a cutting machine was picked up and stacked on the table to the right.

The end-effector was attached to an IX-NNN10040 manufactured by IAI Inc. The positions of each part of the T-shirt and the experimental environment are depicted in Fig. 14(I). Three types of fabric parts (sportswear, innerwear, and polo shirts) were selected as test pieces, and 10 experiments were conducted on each piece.

Fig. 14
figure 14

Pick-and-place experiment in factory. I Shows the experimental settings. II(a–d) fold the T-shirt parts, II(e–h) transfer the folded parts from the cutting machine to the table, and II(i) shows the final result of picking and placing the T-shirt parts

Full size image

B. Experimental Results

In this experiment, the pick-and-place process was performed in ascending order of the label of each part. Part 1 was folded twice using the zigzag folding method, as depicted in Fig. 14(II)a–d, and then scooped up and placed on the table at the right, as depicted in Fig. 14(II)e–h. Next, Part 2 was placed on top of Part 1 using the same folding method, and the following parts were placed on top without the need to use zigzag folding. The final experimental results are shown in Fig. 14(II)i.

The results are summarized in Table 3, which shows the definitions for each success rate: the holding success rate is the ratio of the number of successful holds to the total number of trials; the removal success rate is the ratio of the number of successful removals to the number of successful holds; the placement success rate is the ratio of the number of successful placements to the number of successful holds; the total success rate is the ratio of the number of successful placements to the total number of trials.

Table 3 Evaluation results of each part of T-shirt
Full size table

In this experiment, we conducted 10 experiments on each part of T-shirts made of three different materials. The results are shown in Table 3. For the holding success rate, the end effector failed to grip the large fabric (Parts 1 and 2) because the gripping position was changed and the moving speed was too fast. However, it exhibited good holding ability for small fabrics (other parts). The 100% removal success rate demonstrates the stability of this end-effector in removing the fabric. Regarding the release success rate, the main reason for failure was that the contact surface between the board and the fabric was not sufficiently smooth, and there were many possibilities for improvement. In summary, the overall success rate was over 90%, indicating that the proposed end-effector has the potential for practical application in a factory setting. In addition, this end-effector still has room to improve the success rate.

8 Conclusions

In this study, we proposed a novel end-effector for grasping fabric parts, folding them into smaller sizes, and stacking them for packaging before delivering them to the sewer for sewing operations. In the proposed end-effector, we used cylindrical brushes to grasp the fabric edge and designed a flat board to scoop the entire fabric. Furthermore, we proposed a zigzag folding method for folding large fabric pieces into smaller pieces and scooping them, thereby enabling the handling of sizable fabric while maintaining the compactness of the end-effector. In addition, we determined the zigzag folding trajectory and a method for determining the folding strategy based on the fabric size. Ultimately, the feasibility of the folding method and the ability of the end-effector to stack fabrics were confirmed through experimentation. We also conducted retrieval and placement experiments on various sections of T-shirts made from three different materials within a simulated factory environment. With an overall success rate exceeding 90%, the performance was commendable; however, there remains room for improvement.

In the future, we intend to increase the success rate of end-effector in factory settings and expand experiments to include a wider variety of materials and types of cloth parts to enhance their applicability. At the same time, we intend to introduce a visual feedback mechanism to correct the trajectory and discuss whether there are better methods for trajectory design to achieve better folding results. Finally, we will explore various packaging methods, such as packaging after rolling the cloth parts into a round tube shape, and corresponding handling techniques to adapt to different factory environments.