A rule-based robotic assistance system providing physical relief for nurses during repositioning tasks at the care bed

Abstract

In nursing care, physical overload is an important issue that plays a main role in adding to the number of sick days or even causing staff to withdrawal from the profession. In addition to existing physical aids, robotics in particular has the potential to provide general physical relief during extremely stressful care activities provided at the bedside by performing assistance activities. To shed more light on the relief potential offered, we conducted a study involving 12 caregivers who used a lightweight robot attached to a nursing care bed to assist in the repositioning process. We relied on a robot system architecture that enables rule-based movement adjustments in real time using the Robot Operating System and Unity. The study focused on the repositioning of a patient simulator from the supine to the lateral position. The comparison of the measured ground reaction forces and muscle activity data suggests that robotic assistance during the performance of the activity reduces load peaks and generally leads to more attenuated ground reaction force curves, which results overall in a healthier way of working. With robotic assistance, the average back extensor muscle activations were 25.7% lower compared to conventional repositioning. In addition, the measured maximum occurring muscle activations were reduced by 61.2% when the robotic assistance system was deployed.

1 Introduction

The shortage of nurses is becoming apparent in many countries (Haddad et al. 2018; Oulton 2006; Marć et al. 2019; Maier and Afentakis 2013). While the reason for the shortage is often explained by demographic change, other factors also play an important role in the decline. For example, there is an increased number of sick days among nurses and also an early withdrawal from the profession, since the profession involves performing physically demanding tasks. Mobilizing patients, if done conventionally (i.e. not ergonomically or with no additional aids) or incorrectly, can cause tremendous strain on the spine, leading to an increased incidence of musculoskeletal disorders among caregivers (Trinkoff et al. 2003; Kennedy 2005; Jones-Berry and Munn 2017).

Fig. 1

Example of the robotic assistance system in our care lab during the repositioning of the patient simulator from the supine to the lateral position

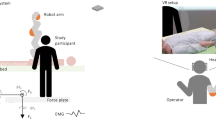
In addition, the shortage of nursing staff exacerbates this problem. In the past, a second employee would help with the strenuous task of mobilizing a patient, but nowadays labor resources are scarce and these activities usually have to be performed alone, resulting in an overall increase in stress. The premature departure of caregivers ultimately leads to fewer nurses being available, causing a vicious circle, because a smaller number of staff increases the level of physical stress among those nurses who remain active. This is the point where it becomes necessary to provide support by means of technical aids, which is possible nowadays. While capacities on the human side are exhausted, even simple technical aids such as a bed height adjustment or an anti-slip mat can provide physical relief. One possible future aid could be provided by robotic assistance systems that can work collaboratively with the caregiver on site at the care bed (see Fig. 1). Many aids provide isolated solutions and support for certain problems, but a robotic assistance system would be able to solve a variety of tasks, offering greater enrichment for care. On the path to achieving a general assistance system, ensuring that it provides assistance in the everyday life of the caregiver and the person in need of care, the following three criteria must be met:

• 1. Development of force transmission concepts for a potentially vulnerable patient, serving a multitude of manipulations and body anatomies.

• 2. Identification of appropriate points to interact with the patient.

• 3. Operation of the robot in orchestration with the caregiver for optimal interaction during task execution.

In this paper, we focus on providing initial insights for the first of the three aforementioned points. To investigate this physical human–robot interaction (pHRI), we conducted a case study comparing physical workload of caregivers with and without robotic assistance. We address the question whether robotic assistance during the frequently performed activity of repositioning a patient simulator from a supine to a lateral position in a care bed can reduce the maximum load peaks that occur, and whether there is a reduction in muscle activity in the lower back of the person performing the task. We hypothesize that there will be a measurable physical relief due to the robot’s assistance, which can be determined by our measurement techniques (Brinkmann 2020). For the analysis, ground reaction forces, surface electromyography (sEMG) data of the back extensor, and visual sensor data were used.

2 Related work

Physical human–robot interaction is addressed in many different research papers for different application areas  (De Santis et al. 2008; Haddadin and Croft 2016). So far, there are only a few application areas in which interaction is designed in such a way that a force is intentionally applied to a human by the robot. We looked for examples where assistive robot systems were intentionally in physical contact with a caregiver or patient in order to provide any kind of support, ranging from mobility assistance to stabilization.

The prime example for the category of physically assistive robots in the healthcare sector is the so-called ROBEAR, whose predecessor models were called RIBA and RIBA-II. Due to its design, this assistance robot has the ability to lift and carry patients out of bed or out of a wheelchair with its two high degrees of freedom (DOF) arms (Ding 2012). The robot can approach the patient, who may be lying on their back in bed, for instance, and put its arms underneath the back of the knees with one arm and the back with the other arm to perform the lifting motion. It has to be mentioned that the patient must lift their upper body—either themselves or with the aid of a caregiver—so that the robot can get into position accordingly. Moreover, it is worth mentioning that the patient’s weight in the study was around 63 kg, which seems to be the robot’s approximate limit. However, a patient’s weight may vary greatly, limiting the general use of this robot. It’s support does not appear to be designed to move the patient within the bed or to assist during repositioning, and the robot largely performs the movement independently without help from the nurse. A similar but more recent concept of a dual-arm mobile nursing robot was proposed by Zhang et al. (2020). This concept involves a 15 DOF robot on an omni-directional mobile platform. Although there is mention of the goal to transport patients, there is no description of a maximum load capacity nor any further elaboration of a concept of support. Nevertheless, a prototype was developed and built so that the capacity specification could be provided in future work.

Another study involved developing a pneumatically driven growing sling to assist in the patient transfer process, reducing the caregiver’s burden (Choi 2020). For this type of transfer, the sling must be placed beneath the patient, which may prove difficult, depending on the physical condition of the patient and the caregiver. The pneumatically driven growing sling starts to grow underneath the patient from the footboard towards the headboard of the bed, making it unnecessary for them to be transferred manually onto the lifter system. Once the sling has finished its movement, the transfer process is similar to that of a regular patient lift. However, the system also has the same mobilization limitations as regular patient lifts, i.e. only transport is possible, and additional partial movements such as turning the patient onto their side are not physically supported.

Another solution to provide physical support at the nursing bed in an effort to relieve the spine can be found in exoskeletons such as the hybrid assisted limb (HAL) (Miura 2018). However, exoskeletons generally have the disadvantage of having to be equipped before strenuous activities; also, they are unable to act as a supportive “third arm”, and only augment the user’s physical abilities, eliminating a variety of potential support scenarios that would be possible with an additional robotic manipulator at the bedside.

Another category of robotic support options includes actuated bed systems that can move patients into different positions. For example, early mobilization in intensive care units can be supported by performing guided movements in bed as therapy (Klamt 2020).

Apart from bed support systems, there are also systems such as the iARM, an assistive robotic manipulator for wheelchairs, and the Lean Empowering Assistant LEA, which can perform autonomous functions acting as a rollator walker (Christoforou et al. 2019).

To assess the efficiency of physical support, it is important to be able to quantify the actual burden, especially in the context of nursing. Considerable research has been undertaken by Jäger et al. for this particular purpose. In this case, the measurement setup in the lab consisted of infrared cameras, a force-sensory bed, and force measuring plates placed in front of the bed (Jäger 2013). This setup was then used to analyze lumbar strain in caregivers while they performed various nursing activities at the bedside. The posture of the nurse and patient, and the measured forces all play an important role in this analysis. Using a biomechanical model, the collected data were used to estimate the load on the spine. In addition to the forces and torques for lumbar loading, action forces on the hands were also considered over the time course of performing the activity. This study also revealed that the use of assistive devices can lead to a reduction in the forces that occur. While all the systems presented in advance aim to provide assistance with nursing activities, each system has different advantages and disadvantages. The assistance system we used for the study, consisting of at least one lightweight robot arm mounted onto a care bed, has the advantage that it does not have to be worn on the body. Furthermore, the robot arm can act as an additional arm, so to speak, and thus does not restrict the movement of the caregiver. This is not the case, for example, with intelligent mattresses, exoskeletons or regular patient lifts. The greatest benefit, however, lies in the versatility of the possible uses. This makes it possible to stabilize the patient, support patient movement or even hold individual body parts during bandaging or similar tasks. In the following section, we describe our experimental setup, resembling the work just described, designed to measure the strain on nurses during the performance of a nursing activity. This setup was used to quantify the differences in workload of caregivers with and without robotic assistance at the nursing bed within a study. In the process, we rely in part on the approach of Jäger et al. for our evaluation (Jäger 2013). To the best of our knowledge, there have been no studies to date regarding the physical relief achieved by a robotic assistance system that applies a supporting force during task performance at the bedside.

3 Materials and methods

In the following part, the study setup is presented together with the associated requirements.

3.1 Study setup

The aim of the study conducted was to compare the physical stress of caregivers during the repositioning of a patient simulator in its lateral position with and without robotic assistance. The hardware setup used for the study, shown in Fig. 2 (Kowalski et al. 2020), and its general functionality were tested in a previous exploratory trial (Brinkmann 2020). A height-adjustable care bed was equipped with a lightweight robot KUKA LBR iiwa 7 R800, which in turn was also equipped with a custom-made end effector (EE) featuring a silicone cover for pushing tasks. Using the robot, it is possible to read the external torque in Nm of each joint and the end effector’s Cartesian forces in N to provide a force-controlled support movement. In addition, a 183 cm high mannequin weighing approximately 83 kg is used as a patient simulator for the scenario. A force measuring plate (FMP) of the model AccuPower from the company AMTI is positioned in front of the bed. The FMP, which has a minimum sampling rate of 100 Hz, is used to measure the ground reaction force components in N and torque components in Nm in all three axes. The forces applied by the subject during the repositioning of the patient simulator can be measured from this data as well as the known weight of the subject and the patient simulator. A vision system is necessary to evaluate the participants’ poses and location. While attaching a camera to the robot is a common method, we need to have a good overview of the entire scene and the subject at all times during robotic movement to avoid occlusions. During the near-body movements between the robot and the human, occlusions can often occur, making it difficult to evaluate the scene. For this case we use a multi-depth camera system, which is originally based on the work of Fifelski et al. (2018), consists of a maximum of four Microsoft Azure Kinect RGB-D cameras. The camera’s RGB and depth data (point cloud) streams are used to precisely record the movements of the subjects during the study. This enables the individual phases of the nursing activity to be precisely annotated in terms of time. In addition, it is possible to investigate any inconsistencies in the results in more detail by visual inspection, if needed.

Fig. 2

The hardware setup used for the study consisting of: (a) a regular nursing bed with a patient simulator weighing 80 kg, (b) a KUKA LBR iiwa 7 R800 robot manipulator, (c) an AMTI AccuPower force measuring plate and (d) Microsoft Azure Kinect RGB-D Depth Cameras

Finally, each subject was equipped with sensors to obtain sEMG measurements in V so that conclusions could be drawn about muscle activity during the performance of the nursing task. For this purpose, an sEMG device from the company Biovision was used to record muscle activity during the study execution. In this study, we concentrate on the activity of the lower back (erector spinae left and right) due to the predominant role it plays during heavy pull movements. The sEMG was recorded using bipolar surface electrodes attached to the appropriate locations parallel to the general muscle fiber direction using adhesive rings. The signals are amplified during the recording process, filtered with a bandpass (10–700 Hz), and then transmitted to the input box via an analog-to-digital conversion unit by National Instruments. Dasy-Lab 4.010 software was used for the actual data acquisition.

Fig. 3

Visualization of the motion phases of the robotic support to be compared. The study participant prepares the patient simulator for the docking of the robot, whereby this movement has a stressful effect on the study participant. After the robot has made contact in a supportive manner, full rotation to the side of the body is performed. The unloading potential of the robot will be investigated by comparing these two phases

The overall study for each subject included a conventional repositioning of a patient simulator from the supine to the lateral position, a kinesthetic repositioning of a patient simulator, a kinesthetic repositioning of a human and rule-based robotic assistance with a predefined trajectory (see Fig. 3). In the present work, we compare both the support potential of robotic-assisted repositioning with conventional execution and the relief potential between two phases of robotic-assisted execution. The hypothesis put forward in the study is as follows: Compared to repositioning without robot assistance, an individual reduction in the ground reaction forces in the x- and z-direction as well as a dissipation of the reduced forces via the robot arm are expected. At the same time, an individual reduction in the sEMG muscle potentials at the back extensor muscle of the subject is expected. There are significant differences with regard to the forces measured on the study participant in the case of rule-based robotic assistance, in which the robot assistance system follows a predefined trajectory and is controlled by its Cartesian force sensor measurements. The measurements as well as the quantitative analysis and evaluation of the nursing activities are carried out in a laboratory environment which is modeled after a standard nursing home room. The procedure was explained to all subjects in advance. After initial reference measurements for calibration, a test run for handling the patient simulator was performed. For each measurement, the subjects stepped onto the FMP, performed a jump, completed an activity, and performed another jump at the end so that the individual phases of the different sensor readings could be calibrated to each other. Then, the repositioning activity is done. The subjects were also told in advance which activity was to be performed and along which trajectory the robot would travel during the assisted execution, so that they could adjust to this type of collaborative work. In our study, each subject performed each action once (see Fig. 5). After all activities had been carried out, the ground reaction forces were related and compared so as to be able to draw conclusions about the actual physical relief. The study design was approved by the Commission for Research Impact Assessment and Ethics of Carl von Ossietzky University, Oldenburg (Drs.EK/2019/078). The study was carried out in accordance with the Declaration of Helsinki. A total of 12 subjects with a caregiving background were analyzed during the study; the data sets of two subjects had to be removed due to corrupted robot sensor signals. The age of the ten remaining subjects was between 24 and 58 years, with an average of 32.83 years. Eight of them were women, and two were men. The weight of the subjects ranged from a minimum of 41 kg to a maximum of 101 kg, with an average of 72.5 kg. The datasets generated and analyzed during the study are available from the corresponding author on reasonable request.

4 Robot assistant system

In this section, we focus on describing our approach for robot-assisted nursing. After providing an overview of the overall system architecture setup for handling the robot during assistance, we take a closer look at exactly how the robot moves based on different rules and how it performs the force transmission in our study scenario under consideration of safety limits.

4.1 System architecture

The following section focuses on the system architecture of the hardware setup. In our case, the robot controller of the KUKA LBR iiwa 7 R800, namely the KUKA Sunrise Cabinet, uses the Fast Robot Interface (FRI) to communicate with the main control computer featuring the Robot Operating System (ROS) for its message passing (see Fig. 4). We made use of the FRI for a faster signal control loop, which proved to be beneficial when dealing with force control systems. For our task, we chose the position command mode with a joint impedance control where a joint stiffness of 1000 Nm/rad is set, which is a default parameter value and may need to be optimized for enhanced force transmission. In this command mode, the response rate is less than or equal to 10 ms, and the robot’s behavior is compliant to a certain degree. The impedance control scheme is used because it enhances safety when humans have to share a workspace with robots (Siciliano and Khatib 2007). The safety and convenience of using the system should also be briefly mentioned. Since this is a research prototype, the primary concern was safety during the conduct of the study. In addition to the actual use of the emergency stop switch, the lightweight robot arm has an internal safety shutdown when external force-torque limits are exceeded. The force control and thus the behavior of the robot can be individually defined. The extent to which the final user control concept should be designed is still the subject of research and must be evaluated with the target group. Initially, however, the prototype should primarily demonstrate the effectiveness of the physical support. Furthermore, Azure Kinect depth cameras were connected to the ROS Master as needed, so that visual sensor data could be recorded for analysis. In addition, the robot’s inverse kinematics was based on memetic evolution (Starke et al. 2018). Force data from the FMP was recorded on a separate computer with the associated proprietary software and used for later analysis. For the synchronization of the data, a jump was performed before the actual task execution.

Fig. 4

Overview of the system architecture for the study to measure physical relief during the execution of a specific nursing task with robotic assistance. The components with an orange outline record sensor data while the ones with a blue outline are used for the robot’s message handling and movement

4.2 Comparison of physical robot support

In our study, repositioning with rule-based robotic assistance was considered in essence and analyzed regarding the physical relief potential of the caregiver acting as a study participant (Fig. 5).

Fig. 5

Example point clouds (depth data of the RGB-D cameras) to visualize each individual phase during the study’s nursing task. (a) Start of the pull movement to position the patient simulator from the supine into the lateral position. (b) The caregiver holds the simulator for a brief moment after reaching the lateral position. (c) The caregiver initiates the recline phase to bring the patient simulator to its original position. (d) The patient simulator reaches the original position

Depth camera data, force measuring plate data, an electromyogram, and robot data (position, velocity and external joint forces) were also recorded during the study. Since the FRI is used for a fast control loop frequency, not all of the information from the KUKA Sunrise Cabinet Controller can be accessed. This is why necessary information regarding the external forces have to be computed and are not available from the start. In general, the robot’s purpose is to apply a certain force vector ${\textbf {f}}_{ext}$ in the end effector frame while maintaining or moving along pre-defined positions ${\textbf {x}}$ in Cartesian space, which we declare as rule-based behavior. This means that we make use of a sequence of rules when moving the robot, which thus define the control behavior, for example by setting force thresholds, velocities or fixed poses. It’s possible to make use of the external joint torques to calculate the external force vector ${\textbf {f}}_{ext}$ of a n-DOF mounted-base robot using the joint space dynamic model:

$$\begin{aligned} {\textbf {M}}({\textbf {q}})\,\ddot{{\textbf {q}}} + {\textbf {C}}({\textbf {q}},\dot{{\textbf {q}}})\,\dot{{\textbf {q}}} + {\textbf {G}}({\textbf {q}}) = \varvec{\tau } - {\textbf {J}}^{\top }({\textbf {q}}) \,{\textbf {f}}_{ext}, \end{aligned}$$

(1)

with the inertia matrix ${\textbf {M}}({\textbf {q}}) \in \mathbb {R}^{n \times n}$, the robot’s joint angular position vector ${\textbf {q}} \in \mathbb {R}^{n}$, the angular velocity $\dot{{\textbf {q}}} \in \mathbb {R}^{n}$, the angular acceleration $\ddot{{\textbf {q}}} \in \mathbb {R}^{n}$, the joint torques $\varvec{\tau } \in \mathbb {R}^{n}$, the Coriolis force and centripetal force matrix ${\textbf {C}}({\textbf {q}},\dot{{\textbf {q}}}) \in \mathbb {R}^{n \times n}$, the gravity component ${\textbf {G}}({\textbf {q}}) \in \mathbb {R}^{n}$ and the Jacobian matrix ${\textbf {J}}({\textbf {q}}) \in \mathbb {R}^{m \times n}$. It is necessary to compute the Cartesian forces at the end effector separately to monitor the forces applied to the patient simulator during the supporting movement. To determine these forces, the aforementioned joint space model can be reduced to the quasi-static relation using the relationship between the end effector wrenches applied and the forces and torques applied to the joints as in Siciliano and Khatib (2007)

$$\begin{aligned} \varvec{\tau } = {\textbf {J }}\,({\textbf {q}})^\top \varvec{f}_{ext}, \end{aligned}$$

(2)

where ${\textbf {J}}^\top$ is the transposed Jacobian matrix, ${\textbf {f}}$ is the end effector force vector. To obtain the actual Cartesian end effector forces, it is possible to make use of the Moore-Penrose inverse to finally obtain

$$\begin{aligned} {\textbf {f}}_{ext} = ({\textbf {J}}({\textbf {q}})^\top )^{-1}\varvec{\tau }. \end{aligned}$$

(3)

However, the coordinate system of these forces still lies at the base of the robot manipulator. Using the transformation matrix $R_{e}^{b}$ from the end effector to the base frame, the Cartesian end effector forces in the 7th joint become available as

$$\begin{aligned} {\textbf {f}}_{ext}^{b} = R_{b}^{e} ({\textbf {q}})\, {\textbf { f}}_{ext}^{e}. \end{aligned}$$

(4)

This has the advantage that the forces along the local axes of the end effector can be used for control when performing a force transmission. One must bear in mind that this kind of Cartesian end effector force computation is only an approximation that is prone to varying values; the use of an additional force-torque sensor attached to the end effector would be beneficial in terms of accuracy. While the caregiver repositioned the patient simulator with the assistance of the robot at the bedside, we relied on a controlled environment for the assistance scenario within the study, and specified the start position ${\textbf {q}}_{start}(t)$ and the target position ${\textbf {q}}_{goal}(t+n)$ in joint space beforehand. For the generation of trajectories, so-called objectives and constraints were specified for the individual joints based on the work of Starke et al. (2018); solutions were then sought simultaneously using different weights, allowing the robot to react to environmental changes in real time. This approach by Starke et al. (2018) is briefly explained below, focusing on the key aspects. For optimization, the following objective function plays the most important role:

$$\begin{aligned} \phi = \Omega ({\textbf {x}}) = \sqrt{\frac{1}{k}\sum _{j=1}^{k}w_{j}\mathcal {L}_{j}^{2}({\textbf {x}})}, \end{aligned}$$

(5)

where $\phi$ is the fitness of an individual to be minimized under the objective function $\Omega$ with the root-mean-square-error over all objectives with the general loss term $\mathcal {L}$. These can be weighted by w, depending on the objective to be prioritized. x represents the gene of each single joint for the evolutionary optimization. To define a full pose, it is necessary to provide a position and orientation function. For the position, the goal is to minimize the translational error between a robot segment and the position goal to be reached. To solve the problem of excessive position errors, normalization is performed in the following position objective function. For the trajectory generation of the physical support movement, the following loss term needs to be minimized for the position:

$$\begin{aligned} \mathcal {L} = \frac{\pi d}{\sqrt{(L+d)(\lambda +d)}}, \end{aligned}$$

(6)

where L represents the constant length of the kinematic chain from the robot’s root to the robot segment, $d = || \mathcal {Y}^{pos} - \mathcal {X}^{pos}||$ is the Euclidean distance between the resulting transformation of a particular robot segment $\mathcal {X}$ and the segment’s Cartesian target $\mathcal {Y}$, and $\lambda$ is the variable distance between $\mathcal {X}$ and the chain’s root. The Euclidean distance is multiplied by the mathematical constant $\pi$, so that it is clamped between $[0, \pi ]$ for use in position optimization. In addition, Starke et al. (2018) derive the orientation objective function by calculating the quaternion (quat) dot product between a chosen robot segment $\mathcal {X}$ and the Cartesian target $\mathcal {Y}$, which results in an error between $[0, \pi ]$ that becomes zero if the robot segments are aligned correctly in terms of their orientation. Thus, for orientation, the following term needs to be minimized:

$$\begin{aligned} \mathcal {L} = 2cos^{-1}(\mathcal {X}^{quat} \cdot \mathcal {Y}^{quat}). \end{aligned}$$

(7)

In this way, the position and orientation of the end effector can be specified as desired and, at the same time, the position of the fourth joint can be adjusted to the working space for better force transmission and to avoid collisions. During the support movement, of which the individual steps are shown in Fig. 6, the impedance controller ensures a certain adaptation to the normal of the surface to be pushed. For the maximum acceptable pushing forces of the robot’s end effector, we used limits based on safety standards. These safety values (DIN ISO/TS 15066) determine that in the body region near the shoulder, a maximum force of 210 N is allowed during a quasi-static contact, which should never be exceeded. For the robotic support movement performed during the study, we did not come close to this limit with a measured maximum of approximately 65 N in the x-direction, as the robot required much lower forces to move the patient simulator to the desired position. Initially, the robot’s support movement trajectory was based on the caregiver’s actual hand trajectory, which served as a reference for the final trajectory used within the study. However, the stiffness of the patient simulator does not allow for an exact replication of the process as it would be performed in real life. Nevertheless, this trajectory was then taken as a motion model and the robot travels along it to assist the subject. An operator triggered the start of the robot’s support movement during the study. Due to the preset environment and the fixed start and end position, the subject was able to hand over the movement almost completely to the robot as soon as the padded end effector came into contact with the patient simulator. The patient simulator required only minor stabilization provided by the subject during the movement. If the counterforce had been above the predefined safety limit, the robot would have moved back along its trajectory to reduce the force. Thus, a combined force and pose controller was used, which additionally ensures variability in the movement due to the upstream impedance controller. Due to the compliance of the impedance controller, the robot adapts to slight deviations in motion by applying force, which is sufficient for the context of the issue investigated in this study.

Fig. 6

Sequence of the robot’s support movement. It can be seen that the patient simulator must already be lifted before the actual contact with the robot happens in order to ensure a suitable positioning of the end effector. This circumstance was considered in the annotation of the resulting data and was also used to compare the caregiver’s burden without (a–c) and with robot support (d, e)

5 Results and discussion

Fig. 7

Example plots of the FMP, sEMG and robot end effector force data for one subject. A conventional (left) and a robot-assisted (right) trial are shown. The weight of the subjects was subtracted from the FMP force along the z-axis to obtain only the deviations. The vertical red lines indicate the start or end of each phase which has been annotated by using the point cloud data as a reference. The first phase during the robot-assisted task execution (green) shows the caregiver’s activity to hold up the patient simulator until the robot is positioned correctly at the shoulder region to apply its force along the predetermined trajectory. The patient simulator is pulled to the goal position either with or without robot-assistance in the second phase (blue). During the third phase (red) the patient simulator is kept on its side for a short resting period before moving back to the initial position with or without the robot’s support during the last phase (yellow). In addition, the top plot shows the FMP forces of each axis, the middle figure shows the overall muscle activity of the back extensor muscle (erector spinae left and erector spinae right) while the bottom plot shows the overall measured Cartesian robot end effector forces during robot assistance

After the activities were performed by all study subjects, the ground reaction forces recorded in the process, measured by the FMP, served as the basis for the load comparison between handling the patient simulator with and without robot assistance. Due to the large time difference between execution with and without a robot, where the execution without a robot took only about a quarter of the time on average, the final comparison was adjusted for better comparability. For that, we took a closer look at the first phase of the robotic support scenario where the patient simulator had to be lifted a few centimeters at the shoulder before the robot’s end effector could make contact for support purposes. In this time window, the subject is heavily loaded due to the acting leverage forces and is not yet supported. We take advantage of this circumstance and compare this unsupported phase with the subsequent phase where the robot is in contact with the patient simulator. The comparison between these two phases acts as the main comparison within the study to differentiate the level of support with and without robotic assistance. This unsupported handling of the patient simulator is indicated by the green color in Fig.  7, followed by the robot-assisted repositioning phases. The phase annotation is based on the depth camera data. Table 1 shows the final results based on the aforementioned recorded data. The table shows the mean and maximum values of the force in the x-, y and z-direction of all phases averaged over all subjects. It also presents the data of the sEMG measurement and the robot force of the end effector. In addition to these measured values, the results for the paired t-test are shown. This test was performed exclusively between the first and second phase. This was because there was no assistance by the robot in the first phase, while the robot actively pushes the simulator along in the second phase. It must therefore be examined whether there is a significant difference between the recorded data in the first and second phase.

Table 1 Summary of the results of the robot-assisted and conventional repositioning

Let us take a closer look at the individual results in Table 1. First, we take a look at the robot-assisted repositioning results. The average value of $F_{x}$ at the FMP increases in the negative direction from phase 1 with − 7.8 N to − 89.46 N in phase 2. This value then moves to − 49.03 N in the holding phase in phase 3, and finally goes back up to − 27.97 N during the phase of moving the patient simulator back to its original position. This shift of forces is significant in both directions, indicated by the P value of 0.02 of the two-tailed paired t-test between phases 1 and 2. For the average values of $F_{y}$, a reduction in the force occurs from phase 1 (3.15 N) to phase 2 (− 0.87 N); this increases again in phase 3 to 0.12 N and decreases again in phase 4 to − 1.2 N. The differences between phases 1 and 2 are too small and thus insignificant, as shown by the t-test with a P-value of 0.25. $F_{z}$ starts with an average value of − 1.52 N in phase 1, decreases to − 17.28 N in phase 2, increases to − 5.72 N in phase 3, and decreases slightly to − 6.54 N when reclining in phase 4. It should be mentioned again at this point that the weight of the subjects was subtracted in the z-direction beforehand, so that the values are zeroed. The lower value in phase 2 may be due to the caregiver propping on the patient simulator or leaning against the bed. According to the P-value, the change between phases 1 and 2 is also significant, with a P value of 0.03. Looking at the average maximum values of the individual phases, a reduction from phase 1 (65.52 N) to phase 2 (11.38 N) is achieved in $F_{x}$. Phase 3, in turn, shows a maximum value of − 31.48 on average, and phase 4 a value of 23.89 N. The reduction between the first two phases is significant with a difference of 54.14 N. For $F_{y}$, the differences in maximum values are not quite as drastic, with a value of 32.56 N in phase 1, 37.91 N in phase 2, 15.17 N in phase 3, and 36.46 N in phase 4. The motion sequence of the activity itself shows that force application in the y-axis is uncommon and does not appear to be relevant in our case. The situation is somewhat different for $F_{z}$, as a maximum value of 42.45 N was measured on average for the subjects in Phase 1, which fell to 39.22 N in phase 2 with robotic assistance. Holding on to the side of the patient simulator in phase 3 further reduced the measured force to 16.48 N, which increased again to 40.78 N in phase 4 when the simulator was laid back. The results of the muscle activity measurement on the back extensor during the execution of the movement are promising. On average, an increased muscle activity potential of 0.43 V was measured in phase 1, which fell to 0.29 V in phase 2, increased very slightly to 0.31 V during the hold activity in phase 3, and then increased even further to 0.37 V in phase 4. The changes between phases 1 and 2 are significant on both sides, with a P-value of 0.01. A similar pattern emerged for the maximum values. Here, in phase 1, the average value for the sEMG was 0.81 V, which decreased in phase 2 to 0.42 V with robotic assistance, then increased again slightly to 0.43 V in phase 3 and 0.76 V in phase 4. Thus, overall, it appears that the maximum values of the muscle activity measured in the first phase, when the patient simulator is lifted slightly, were almost twice as high compared to the second phase, when the robot performed its assistance; it increased by about a third on average in general. The robot forces at the end effector were very low on average in phase 1 (3.75 N), because here the movement was performed for contact purposes, and no force was applied at that point. In phase 2, the force increased on average to 14.91 N, and increased to 19.32 N in phase 3, then decreases to 15.3 N in phase 4. Again, the results between phases 1 and 2 are statistically significant. Maximum force was 10.04 N for phase 1, increasing to 34.55 N in phase 2, and then decreasing to 23.58 N in phase 3 and 23.2 N in phase 4. Overall, the results show that there is a relationship between the increased force effect of the robot and a reduction in the measured forces on the FMP, with a simultaneous reduction in muscle activity. Verification by means of significance tests between phases 1 and 2 confirmed this assumption—except for the case at $F_{y}$—which was key to the consideration of the physical relief potential in our scenario. It must additionally be noted that $F_{y}$ can be neglected due to its insignificance in the performance of the movement, owing to the minor contribution of lateral movements. This also shows that the movements were not performed asymmetrically, which, based on Jäger (2013), may be an indication of correct task execution. While the force of the robot never exceeded the force limit of 210 N from the literature, nor did it need to in order to perform its task, the average maximum value was 34.55 N in total, which was still sufficient to achieve a reduction of 0.39 V in the measured maximum muscle activity. While the difference in forces occurring in the z-direction was not too large for the FMP, with an average difference of − 3.23 N, the difference in the x-direction was extremely large. This suggests that robotic assistance causes the activity to be performed differently in terms of the caregiver’s motion sequence, resulting in a force shift in the ground reaction forces. In the next step, the results of the conventional repositioning are listed and discussed. Phase 1 is omitted here, as no robot is used. Thus, the process is limited to pulling, holding and reclining. For $F_{x}$, an average value of 50.74 N is achieved in phase 1. This decreases to − 22.22 N during holding and then increases again in phase 3 to 13.39 N. There is statistical significance in comparison to the robot-assisted pulling phase with a P-value of 0.06 $\cdot 10^{-2}$. For $F_{y}$, the value in phase 2 is − 21.87 N, becomes slightly smaller in phase 3 to − 24.42 N and then increases again in phase 4 to − 19.16 N. This value is also significantly different compared to the robot-assisted variant with a P-value of 0.08. The value for $F_{z}$ is on average 21.02 N in phase 2, decreases to − 0.53 N for phase 3 and increases minimally in phase 4 to 0.99 N. Again, statistical significance is found in the comparison with a P-value of 0.06. The average maximum value for $F_{x}$ is 194.77 N in phase 2, decreases to 3.87 N in the holding phase and then increases again to 66.57 N. The average maximum value for $F_{y}$ is similar, but lower with 8.35 N in phase 2, 19.34 N in phase 3 and 1.65 in phase 4. For $F_{z}$, the average maximum value in phase 2 is 97.51 N, decreases to 19.34 N and then increases to 34.06 N in phase 4. The average muscle activity is 0.39 V in phase 2 and settles at 0.16 V in phase 3 and 0.15 V in phase 4. There is statistical significance compared to the muscle activity of the robotic-assisted variant. The maximum occurring muscle activity of the back extensor is 1.08 V at phase 2, is more than halved to 0.50 V at phase 3 and further decreases to 0.35 V for the recline. It must be kept in mind that despite filtering, artifacts can also make the maximum values appear somewhat higher than they really are.

The large standard deviations in some cases (e.g. for the average values for $F_{x}$ or the maximum force values) also show that the fluctuations vary greatly within the phases but also between the subject runs. Especially in the x-direction of the measured ground reaction forces the high standard deviations become obvious. This is due to the sum of different factors such as the subject’s weight, foot position and movement during support execution.

Based on the work of Jäger (2013), reducing force peaks can prevent the negative impact on the lumbosacral disc and long-term effects such as injuries. Moreover, if the execution process is slowed down, this has a direct effect on the load peaks occurring, because fast and sudden movements introduce the risk to damage the skeletal-muscular system. Due to time pressures, caregivers tend to use sudden movements; however, such movements should be avoided, and decelerating the process may be beneficial in this case. Fig. 7 shows an a plot of the FMP, sEMG, and robot force data with a short phase of uncoordinated cooperation with the robot, becoming apparent in the robot force data. Abrupt end effector force changes, as seen in the blue phase of the right bottom plot, indicate that the force transmission was not ideal for a brief moment, which could be a result of the caregiver pulling too quickly and not collaborating correctly. In order to ensure continuous contact, the robot must be fast enough during force application so that even a faster pulling of the patient simulator does not lead to a break in contact. However, high speeds again lead to a problem with safety, as too much force could be applied briefly on contact. A compromise between speed and responsiveness must be found, which could be derived from real data from several nursing activities. Further adjustment of the end effector could also be an advantage in providing safe support. In the case of vulnerable patients, on the other hand, it would have to be clarified in advance which body regions cannot be used for contact by the robot, so that the trajectories can be adapted or the target group of the assistance system must be deliberately limited. Thus, the most critical technologies for ensuring safe support in this physical human–robot interaction scenario is the appropriate design of force control and the generation of suitable trajectories, either based on visual sensing or through tactile feedback. A number of problems and discoveries noted during the analysis must also be mentioned. Despite instructing each subject on how to perform the task, it was unavoidable that, for some subjects, force was derived through the bed and not through the FMP. This happens, for example, when the caregiver leans their knees against the bed or props themselves on the patient simulator during activity execution. This problem can be solved by additional sensors attached to the bed to measure the derived forces. What is more, collaborative work between the subjects and the robot was not always ideal. For example, abrupt pulling or uneven movement of the patient simulator, which can also be seen on the right side in phase 2 of the robot force values in Fig. 7, led to a deterioration of the force transfer. Thus, there is still room for improvement in the alignment of the collaborative operation of the robot. Moreover, the patient simulator’s stiffness is not comparable to the kinematics of a normal human being due to differences in the number of joints, which has an effect on how the support movement creation is approached. The last factor to be mentioned is the time factor in the execution. A deceleration of the process is beneficial to health overall, but at the same time not necessarily practical for everyday work. Optimization of the speed of execution is therefore desirable.

Overall, physical relief was achieved using the back extensor during the robot-assisted execution of the study scenario based on the measurement results of the muscle activity. The slight but overall decrease in FMP forces indicates that robot support does have an actual impact on the ground reaction forces, and thus on the resulting forces in the caregiver’s body.

6 Conclusion and outlook

We conducted a study with ten caregivers to measure physical relief during the task of repositioning a patient simulator from the supine to the lateral position. It must be mentioned again that the patient simulator does not move like a real human being, and thus the data might not necessarily be directly comparable to a real human patient. The few joints, the general stiffness, and the lack of cooperation on the part of the patient simulator lead to slightly different movements during the repositioning process compared to a real patient. The results, representing an important step in our further research projects in the field of pHRI, show that it was possible to achieve an overall relief of forces and a reduction in the occurring load peaks based on sEMG muscle activity and FMP data in both scenarios that were compared. In the comparison between conventional and robotic-assisted activity performance, muscle activity of the back extensor was reduced by the robot by an average of 25.7%. At the same time, the maximum sEMG load peaks occurring in the pulling phase were reduced by an average of 61.2%. The FMP data showed that in the pulling phase, the robotic assistance reduced the forces in the x-direction by 140.21 N compared to the conventional execution. In the y-direction, a reduction of 20.98 N was achieved, and again 38.30 N in the z-direction. Comparing the first and second phase of the robot-assisted task execution, the average back extensor muscle activations were 32.6% lower during the assisted phase. Furthermore, the maximum occurring sEMG values were 48.2% lower on average, a strong indication that robot support provided physical relief. The mean ground reaction forces were significantly reduced by 81.66 N in the x-direction and 15.56 N in the z-direction. As assumed at the beginning, the reduction of the forces in y-direction turned out to be very small, since these do not have a large influence in the task execution and only increase in case of a strongly asynchronous activity execution. These observations are also supported by the forces recorded at the end effector of the robot. Overall, both comparisons show that a reduction of the applied forces could be achieved by using the robot, which led to a physical relief. In the comparison between conventional and robot-assisted execution, the differences are even greater than in the comparison between phase 1 and phase 2 of the robot-assisted scenario.In the future, for even better comparability, the execution time of the robot is to be reduced, the support process itself is to be improved by an adapted end effector, and additional sensors will ensure that the forces dissipated through the bed can also be recorded and interpreted. Another point which can be investigated is the impact of the patient simulator. The behavior of the acting forces likely differs significantly depending on the weight of the patient. A patient simulator with variable weight could be used in future studies so that the different effects could be exposed. The robot’s movement is also to be made more adaptive so that different patients can be optimally supported. This can be implemented, for example, through extended interaction methods in which the nurse dictates the support movement. In addition, we want to consider further improving the force transmission support movements executed by the robot, adding the possibility of supporting more nursing care activities. We want to investigate the case of using a depth camera attached to the robot or test control approaches that only use the robot’s force sensor technology, which would simplify the utilization in the real work environment.