1 Introduction

The maritime industry has shown increased attention to autonomy over the past decade. By promising reduced costs and improved safety, autonomous vessels may revolutionize industries such as shipping, public transportation, and remote surveillance (Kretschmann et al. 2017). However, several challenges remain before autonomous vessels are ready to enter the commercial market. In particular, autonomous vessels must provide highly robust navigation solutions for safety-critical operations to be widely accepted by authorities, classification societies, and the general public (Bolbot et al. 2020).

Global Navigation Satellite Systems (GNSS) are used as the main positioning system onboard most ships today. The technology is well-established, and GNSS onboard ships often hold a high standard. However, satellite-based navigation systems are vulnerable to a number of cyber-physical attacks such as spoofing, meaconing, and jamming (Carroll 2003). Hence, the satellite signals can easily be manipulated by such attacks (Grant et al. 2009), thereby posing significant security threats for autonomous vessels. For example, the vessel can be hijacked, potentially causing a collision with other vehicles or the harbor itself. Such an attack is devastating for the industry and the trust among the general public. Because of this, vendors and the class societies require an independent navigation system that is less vulnerable to cyber-physical attacks (Androjna et al. 2020).

Among maritime operations, the docking of a vessel is considered to be one of the most critical. This is because the vessel operates in a constrained area where highly accurate positioning measurements are required. Unfortunately, commercial GNSS estimates position with errors in the orders of meters (Aqel et al. 2016), and Differential GNSS typically provides 1 m global accuracy (Monteiro et al. 2005). These errors are considered too significant for critical applications that require centimeter accuracy, such as autonomous docking. Real-time kinematic (RTK) GNSS can be used to determine position in centimeters. However, RTK GNSS is an expensive solution and has a large number of dropouts (Gryte et al. 2017). It is therefore of interest to supplement the traditional navigation system with alternative sensors. If such sensors can increase positioning accuracy and redundancy, autonomous vessels have the potential to operate reliably under safety-critical docking operations.

Many researchers have shown increased interest in visual-based localization systems because they are more robust and reliable than other sensor-based localization systems (Aqel et al. 2016). The car industry has already adopted vision-based sensors, e.g., cameras, for autonomous navigation for many years (Badue et al. 2021), and we believe that the maritime sector will follow. Compared to proximity navigation sensors, optical cameras are low-cost sensors that provide a large amount of information. In terms of docking, they show another advantage over the GNSS: Since GNSS is an absolute positioning system, it usually requires exact global coordinates for the target position, e.g., a floating dock, which is impractical. In contrast, cameras can provide relative positioning directly as long as easily recognizable features from the docking station are available. For this reason, relative positioning is preferred over absolute positioning under docking operations, especially since the docking control system regulates the relative position to zero.

The two main approaches to estimate the camera pose are based on natural features (Engel et al. 2014; Mur-Artal et al. 2015; Zhong et al. 2015), e.g., keypoints and textures, and artificial landmarks (Ababsa and Mallem 2004; Olson 2011; Garrido-Jurado et al. 2014), respectively. The first approach requires no intervention in the environment, thus proving to be a flexible choice. It is, however, computationally expensive and typically fails in textureless areas. It also tends to fail in case of blurring due to camera movements. For these reasons, the second approach with artificial landmarks is the most common method if accuracy, robustness, and speed are essential (Mondjar-Guerra et al. 2018). In robotic applications, fiducial markers such as ARTags (Fiala 2005), ARToolkit (Kato and Billinghurst 1999), ArUco (Garrido-Jurado et al. 2014), AprilTag (Olson 2011) and AprilTag2 (Wang and Olson 2016) have been of crucial importance for obtaining an accurate pose estimate of the marker. However, detecting and locating fiducial markers in complex backgrounds is a challenging step. This is because electro-optical (EO) cameras are highly sensitive to environmental conditions such as light conditions, illumination changes, shadows, motion blur, and textures (Aqel et al. 2016). Zhang et al. (2006) propose a method to detect non-uniformly illuminated and perspectively distorted 1D barcode based on textual and shape features, while Xu and McCloskey (2011) developed an approach for detecting blur 2D barcodes based on coded exposure algorithms. These methods show high detection rates on certain barcodes, but their performance may be affected by environmental conditions, i.e., they are based on handcrafted features using prior knowledge of specific conditions. On the other hand, Convolutional Neural Networks (CNNs) have shown outstanding robustness in terms of detecting objects in arbitrary orientations, scales, blur, and different light conditions with complex backgrounds as long as such examples are widely represented in the data set, e.g., as demonstrated by Chou et al. (2015). In the context of a complex harbor environment, this paper aims to show how a learning-based method, i.e., a CNN, can be used for robust detections of fiducial markers. We also aim to demonstrate how traditional computer vision methods produce robust and accurate positioning of an unmanned surface vehicle (USV) when the harbor complexity is reduced.

1.1 Related work

In relation to model-based methods, Jin et al. (2017), Kallwies et al. (2020), and Zakiev et al. (2020) benchmark and improve fiducial marker systems, e.g., ArUco and AprilTag, influenced by elements such as gaussian noise, lighting, rotation, and occlusion. However, the experimental data is limited to synthetic data or indoor environments. dos Santos Cesar et al. (2015) evaluate ArUco, ARToolkit, and AprilTag in underwater environments, but do not propose any methods to improve performance compared to existing fiducial marker systems.

Of learning-based methods, Hu, Detone and Malisiewicz present Deep ChArUco (Hu et al. 2019), a deep CNN system trained to be accurate and robust for ChArUco marker detection and pose estimation under low-light, high-motion scenarios. Instead of a regular deep CNN for object detection, e.g., Yolo (Redmon et al. 2016) or Single Shot Detector (Liu et al. 2016), they use a deep learning-based technique for feature point detection. Although they show very promising detection results on image data influenced by extreme lighting and motion, it is limited to synthetic data or indoor environments. Mondjar-Guerra et al. (2018) benchmark different types of classifiers, i.e., Multilayer Perceptron, CNN, and Support Vector Machine, against the state-of-the-art fiducial marker systems, i.e., ArUco and AprilTag, to detect fiducial markers in both outdoor and indoor scenarios. Hence, they cover challenging elements such as motion blur, defocus, overexposure, and non-uniform lighting. Still, the indoor environment is overrepresented, and the outdoor environment is limited to one single scenario. At last, Li et al. (2020) compare the detection rate between the traditional ArUco detector and the deep learning model Yolov3 (Redmon and Farhadi 2018) in an unmanned aerial vehicle landing environment. They show that Yolov3 slightly outperforms the ArUco detector at distances up to 8 m, under no occlusion. They also demonstrate that Yolov3 performs well under various occlusion conditions, even under 30\(\%\) occlusion coverage.

In terms of relevant outdoor environments, Mateos (2020) benchmarks his proposed AprilTag3D framework, a redundant system of two coupled Apriltags, against the traditional AprilTag detector. His experiments showed that the AprilTag detector had an 85% detection rate in the indoor swimming pool and a 60% detection rate under outdoor tests in the river, while his proposed framework achieved a 99% and 95% score in the same settings, respectively. At last, Dhall et al. (2019) investigate landmark-based navigation, where naturally occurring cones on the track are used as reference objects for local navigation of a racing car under varying lighting and weather conditions. They use learning-based methods to estimate the points of a cone and Perspective n-Point (PnP) to estimate the camera pose relative to the cone.

The work described above examined different approaches for vision-based detection and pose estimation of reference objects, e.g., fiducial markers and natural landmarks. While much of the work is limited to indoor experiments or synthetic data, some work tests their proposed methods in relevant outdoor scenarios. In particular, Mateos demonstrates the closest application-specific work where a vision-based USV and fiducial markers are used in open water influenced by environmental elements similar to the harbor environment. However, he only tests his model-based framework in close-range scenarios, i.e., up to 2 m, and it is unknown how an increasingly complex environment is handled. Dhall, Dai, and Gool, however, demonstrate the closest method-specific work. This is because they employ a similar hybrid data-driven and model-based scheme where a learning-based object detector is used to reduce detection complexity. In contrast to our work, they also design a CNN for keypoint detection on the cone. However, we believe the ArUco detector for corner detection in a much smaller and less complex image to provide sufficient accuracy and robustness. We also prefer to rely on model-based methods wherever possible to increase the interpretability of the method.

1.2 Main contributions

This paper demonstrates how low-cost cameras mounted on a USV (see Fig. 1) can be used for auto-docking and relative positioning in the harbor environment. The main objective is to develop an independent vision-based positioning system to increase the redundancy and accuracy of autonomous vehicles’ navigation systems under the terminal docking phase. None of the related works deal with vision-based auto-docking of small USVs in comparable docking environments.

Fig. 1
figure 1

The Otter USV from Maritime Robotics is armed with two (EO) cameras and a LiDAR for vision-based navigation. The guidance, navigation, and control (GNC) computer to control the vehicle is located in the grey box. The image is reproduced with kind permission of Maritime Robotics, https://www.maritimerobotics.com

Full size image

We present two novel contributions in this paper. First, we describe and examine a hybrid model-based and data-driven scheme, based on existing frameworks and tools, i.e., ROS, OpenCV, and Yolov3, to perform vision-based positioning of a USV under various docking operations. More specifically, we use a learning-based method, e.g., Yolov3, for robust detection of fiducial markers and model-based computer vision methods, i.e., ArUco, point triangulation, and PnP, for accurate corner detections and subsequent 3D reconstruction when the harbor complexity is reduced. Both monocular and stereo vision methods are investigated for comparison. The developed methods are characterized by incremental improvements and adjustments that require extensive testing in the field to work reliably, especially since we combine model-based and data-driven methods. The final design choices in Sect. 2 are reflected by this. Secondly, we use a LiDAR sensor for experimental verification of the proposed methods. A subsequent evaluation of the accuracy and reliability of the methods is highly relevant for the maritime industry. In particular, small high-tech companies that manufacture low-cost unmanned vehicles and even large-scale companies developing navigation solutions for ferries are interested in vision-based docking.

Source code and instructions have been made available in a public Github repository (Volden 2020), thus providing a recipe to develop low-cost vision-based positioning systems. The work is based on the master thesis ”Vision-Based Positioning System for Auto-Docking of Unmanned Surface Vehicles (USVs)” (Volden 2020) submitted January 20, 2020, under the direction of Professor Thor I. Fossen. However, it is further extended with more experimental data and field experiments followed up by an analysis of the experimental results and how they relate to existing work in the field.

1.3 Outline

This paper is organized as follows. Section 2 describes a step-by-step methodology in which design choices and algorithms for robust vision-based detection and positioning are introduced. Section 3 describes the hardware used in the experiments and experiment-specific details. It also includes results and discussions regarding the experiments. Finally, we summarize the most important findings in Sect. 4.

Fig. 2
figure 2

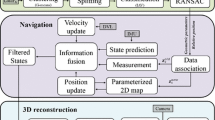
The figure gives an overview of the proposed vision-based positioning system with stereo vision. The main idea is to input the relative position of the USV during the docking operation. A slightly different design with monocular vision is discussed in Sect. 2.4

Full size image

2 Design, algorithms and implementation

The final working system employs a complementary modular approach that uses a combination of data-driven deep learning methods, utilizing data wherever required, and at the same time uses traditional computer vision methods when the scope and complexity of the environment are reduced. Two implementations are proposed, referred to as Design 1 and Design 2, respectively. Implementation details and differences are discussed in Sect. 2.4. However, the functionality of the methods shares many commonalities. Following is a brief introduction to the high-level design with a focus on stereo vision, as seen in Fig. 2.

2.1 Pipeline overview

Initially, the object detector receives image data from the cameras through the camera driver. Once a marker is visible, we use the object detector twice to output detections, i.e., one per camera view. Furthermore, we concatenate the detections into a bounding box pair representing the same marker seen from a stereoscopic view. Then, the bounding box pair is fed into a corner detector. Since the corner detector outputs the corner positions in the same clockwise order, we match corresponding marker corners directly. Furthermore, we utilize image rectification to simplify the correspondence problem, i.e., we search for corresponding points along horizontal scanlines. Once the stereo pairs are matched, we use a triangulation algorithm to compute the disparity map. Finally, we use the disparity map to obtain the relative position between the left camera and the marker corners.

2.2 Camera integration

We use a ROS compatible camera driver (Shah 2020) to simplify the communication and data transmission between the cameras and the object detection model. The camera driver let us specify which cameras to connect and which camera to be master for triggering the other camera, e.g., for a stereo setup. In particular, the camera driver supports hardware triggering to enable reliable, low-latency synchronization between the cameras. This is particularly important for accurate 3D reconstruction with stereo vision in a rapidly changing environment.

2.3 Object detection pipeline

This section discusses the steps necessary to obtain a fine-tuned object recognition model using data-driven methods. An overview of the process can be seen in Fig. 3

Fig. 3
figure 3

The figure shows the necessary steps to obtain a fined-tuned object recognition model. First, images are prepared and labeled to obtain ground truth for the supervised CNN to learn. Labeled data are then fed into the data-driven detection model, together with pre-trained model weights, to fine-tune the model. A validation set is used for model selection to decide when the model should stop training. Finally, the fine-tuned model is tested on unseen data to evaluate its accuracy, e.g., by using the mean average precision (MaP) metric. If results are satisfying, the final model weights are used for object recognition tasks in the prediction phase

Full size image

.

2.3.1 Step 1—data preparation and marker configurations

In the field of supervised learning, data is essential for training CNNs. Data is used to give ground truth examples relevant to the predefined learning task. The first step includes the construction of custom datasets representing examples of the features that the model should learn. Hence, data collection was conducted to gather image data of different markers in the harbor environment. Two custom datasets, i.e., custom dataset 1 and custom dataset 2, were constructed to test the proposed solution in realistic docking environments. The first dataset includes colored image data recorded with a GoPro camera, while the second dataset includes monochrome image data recorded with a Blackfly S GiGE camera, as seen in Fig. 10. Only relevant examples, i.e., images that show at least one marker, from the records were included in the custom datasets. The relevant records were downsampled to a rate of 2 Hz. The custom datasets was randomly shuffled before 80% was assigned to training, while 10% was assigned to validation and testing, respectively. Table 1 shows the amount of images for each data set. This separation ensures that the training, test, and validation set are independent, which is essential when evaluating the accuracy of the trained model on unseen data.

Table 1 Split between training, validation, and test images for the custom datasets
Full size table

Two types of marker configurations are used in this work. Marker configuration 1 relates to custom dataset 1, while marker configuration 2 relates to custom dataset 2. Both configurations use low dictionary size, i.e., 4 \(\times\) 4, such that feature extraction of the inner codification is possible for low-resolution images. For object detection, we assign one marker type per class during the training scheme. In that sense, object tracking is simplified as we assume the predicted objects to represent distinct markers for a well-trained CNN. We refer to Table 2 for more marker-specific details.

Table 2 The marker configurations consist of two and three ArUco markers, respectively, each associated with their class names during the training scheme
Full size table

2.3.2 Step 2—labeling process

Ground truth labels are used to guide the supervised model towards the correct answer. We use the annotation program, Yolo Mark, to create ground truth labels. That is, rectangle-shaped bounding boxes are dragged around the markers in the scene. Consequently, the features to fine-tune the model are those to recognize ArUco markers, i.e., combinations of black and white pixels representing the inner codification of the marker. Notice that precise labeling is essential for the learning process. Unexpected learning is often a result of inaccurate labels, e.g., only label parts of the object can be dangerous as the model then interprets this is as the complete object.

2.3.3 Step 3—training and validation procedure

For this work, we apply transfer learning. It is a popular approach where a pre-trained model is used as a starting point to fine-tune the model for the final detection task. The pre-trained model parameters are trained on the ImageNet dataset (Deng et al. 2009), a dataset with more than 14 million hand-annotated, labeled images. As seen in Fig. 3, the pre-trained weights, and the training data are used as input to the model during the training scheme. The original YOLOv3 network architecture with spatial pyramid pooling (SPP) is chosen as it achieves the highest Mean average Precision (MaP) value (60.6%) on the COCO dataset (Lin et al. 2014) when a 0.5 Intersection over Union (IOU) threshold was used. To balance the detection accuracy vs. inference time tradeoff, we resize the training images to 416 \(\times\) 416 resolution. The remaining hyperparameters, i.e., those to control the learning process, are shown in Table 3, thus summarizing the final choice of training parameters used for the experiments.

Table 3 The table shows the final choice of hyperparameters used for the Yolov3-spp architecture
Full size table

The validation set is a sub-part of the custom dataset, usually left away from training and used for model selection, thus picking the model that performs the most accurately on unseen data. We mainly use MaP to validate the training data. Hence, we compute the MaP on the validation set for every thousand iterations and identifies a peak across iterations per model. By this, we ensure that model parameters are not overfitted. For the model parameters trained on custom dataset 1 and custom dataset 2, we found such a peak in the MaP value after 7000 iterations and 6000 iterations, respectively. As a result, we choose the model parameters corresponding to 7000 iterations and 6000 iterations for the first and second model, respectively. We emphasize that we use one custom dataset per model during the training and validation scheme.

2.3.4 Step 4—test procedure

Finally, the chosen models are tested on new unseen data, i.e., the test set, to verify how the models work in reality. Again we use MaP as the quantitative metric. In general, the model is accepted if the MaP achieves an acceptable high score. Intuitively, we expect the CNN to produce high MaP values on the test sets as the datasets contain easily identifiable markers. The final models was tested on the test sets, i.e., 84 and 85 unseen randomized images from custom dataset 1 and custom dataset 2, respectively. As a result, the first model, trained on custom dataset 1, achieved a 99.05% score. The second model, trained on custom dataset 2, achieved a 99.40% MaP score. These model parameters will be used for the final experiments.

2.3.5 Step 5—prediction phase

If results from the test sets are satisfying, the final model weights are used for object recognition tasks in the prediction phase, e.g., for commercial use. We use a GoPro camera and BlackFly S GiGE cameras to input image data during the prediction phase, as seen in the rightmost part of Fig. 3. These cameras provide on-camera pre-processing to deliver crisp, high-quality images with low image noise.

2.4 3D reconstruction pipeline

Following a hybrid data-driven and model-based scheme, corner detection and 3D reconstruction are performed on a sub-part of the whole image, thus reducing the number of potential outliers. In particular, we assume the ArUco detector to be less vulnerable to environmental elements in the harbor when accurate bounding box predictions are handled rather than the whole image. In the following, we introduce some common design choices for both techniques, i.e., monocular and stereo vision, before specific characteristics for each design are discussed.

2.4.1 Some common design choices

As a design choice, the predicted bounding boxes were sent along with their coordinates relative to the whole image from one ROS node to the other using the publish&subscribe scheme in ROS. This way, we can compare both 3D reconstruction techniques at once. As both methods are implemented in OpenCV’s C++ interface for high-performance computing, we assume them to be performed approximately at the same time. This makes them attractive for direct comparison. Both designs are also strongly dependent on the corners to be visible inside the bounding box. Therefore, we extend the bounding box slightly to ensure that the ArUco detector can recognize the markers in case of inaccurate bounding box predictions, as seen in Fig. 4. To be robust to scale, e.g., different ranges, the bounding boxes are resized as a function of their size.

Fig. 4
figure 4

The figure shows an illustration of how the bounding box is extended. Initially, the CNN predicts the inner bounding box, which may not include all the marker corners. As a consequence, the red, original corner point (x, y), and the height (h) and the width (w) of the bounding box are resized as a function of the bounding box size to include all the marker corners (color figure online)

Full size image

2.4.2 Camera calibration

In order to determine the camera location in the scene, we need to perform camera calibration. 3D world points and their corresponding 2D image projections were obtained using 48 images of a 7 × 10 checkerboard taken from different views and orientations, i.e., 24 images per view. Then, the length of the checkerboard square was measured and used as input to the Stereo camera calibrator app (2019). A regular camera model was chosen, and the distortion parameters were estimated with three radial distortion coefficients and two tangential distortion coefficients. The final calibration resulted in a 0.13 reprojection error, measured in pixels. We consider this as acceptable results with 1280 \(\times\) 1024 image resolution.

2.4.3 Stereo vision design

As seen in Fig. 5a, we use the ArUco detector twice to locate the four marker corners inside the bounding boxes relative to the left and the right camera view, respectively. To identify the marker type, it searches for marker ids within the specified dictionary. If correctly identified with four marker corners available, the next step concerns corner matching. Since the ArUco detector always return the marker corners in the same clockwise order for both cameras, we match them directly. We also express the coordinates of the stereo pairs relative to the whole image. For 3D reconstruction, a fixed rectification transforms for each head of a calibrated stereo camera is computed, given the calibration parameters. Such transforms allow us to search for corresponding points along horizontal scanlines in the new rectified coordinate system for each camera. Finally, we triangulate the corresponding points to obtain the relative position between the left camera and the marker corners. We transform the four triangulated points from their corner positions into the center of the marker to compare directly with monocular vision. We also compute the median of the four shifted 3D points to produce a robust positioning estimate.

Fig. 5
figure 5

a Design 1 represents 3D reconstruction with stereo vision. b Design 2 represents 3D reconstruction with monocular vision. A flowchart of the corresponding OpenCV functions is shown in Fig. 11

Full size image

2.4.4 Monocular vision design

In the same manner, we apply the ArUco detector to detect where the marker corners are located in the bounding box. However, the monocular vision design relies on single-view geometry to reconstruct 3D points. That is, we use PnP to solve the pose of a square planar object defined by its four corners. As seen in Fig. 5b, we pass the detected corners and the calibration parameters to the monocular pose estimation algorithm, which then output the marker pose relative to each camera individually. To overcome scale ambiguity, we also input the actual size of the marker. As before, we include an offset such that the detected corners are expressed relative to the whole image. Note that the monocular pose estimation algorithm returns translation and rotation vectors relative to the marker frame, i.e., centered in the middle of the marker with the z-axis perpendicular to the marker plane. In contrast, the triangulation algorithm returns 3D points relative to the camera frame, i.e., centered in the left camera.

3 Experimental setup and testing

Following the description of the proposed vision-based positioning system, we move over to the experiments. The experiments are divided into two parts, where each focuses on different aspects related to the proposed solution. The first experiment investigates the performance of the proposed detection model, as described in Sect. 2.3. The second experiment benchmarks the proposed positioning system against a LiDAR-based positioning system, as described in Sect. 2.4. For each experiment, we describe how it was conducted and the obtained results. Finally, we make some remarks regarding the obtained results.

3.1 Experiment 1: detection accuracy

The first experiment investigates how well the proposed detector, i.e., Yolov3-spp, detects ArUco markers in the harbor environment compared to the traditional ArUco detector. It covers two docking scenarios in the harbor environment, where both include marker configuration 1. The learning-based method, Yolov3-spp, uses custom dataset 1 to train for the detection task. To ensure independence, the image data from the two scenarios are not included in custom dataset 1. We refer to Table 4 for the image specifications. For evaluation of the detectors, we use the statistical metrics precision and recall. Given the four possible outcomes of a binary classifier, i.e., true positive (TP), false positive (FP), false negative (FN), and true negative (TN), we define precision and recall as

$$\begin{aligned} p&= \frac{TP}{TP + FP} \end{aligned}$$
(1a)
$$\begin{aligned} r&= \frac{TP}{TP + FN} \end{aligned}$$
(1b)

where p denotes the precision and r denotes the recall. If a detection exceeds a 0.25 IOU threshold, we consider it as a TP.

Table 4 Camera specifications for Experiment 1
Full size table

3.1.1 Experimental description

To test the detectors in a realistic setting, we include two docking scenarios in the first experiment where environmental elements such as non-uniform lights and water reflections are presented. The first scenario shows a USV docking with marker configuration 1 located at the dockside, as seen in Fig. 6a, b. The video sequence, sampled at a rate of 5 Hz, is divided into two parts. They present image data of the initial and the terminal part of the docking phase, respectively. The second scenario covers a USV undocking from another dockside in the same harbor using the same marker configuration, as seen in Fig. 6c, d. Again, the video sequence is sampled at a rate of 5 Hz, and divided into two parts. In that sense, they present image data of the docking phase in reverse order. Table 5 shows the largest and smallest bounding box size of the relevant markers in the two scenarios.

Fig. 6
figure 6

a–d show the different docking scenarios in the harbor environment with markers detected by Yolov3-spp

Full size image
Table 5 The table shows the upper and lower pixel resolution of the ground truth bounding boxes in the first experiment. The markers, i.e., m1, m2, and m3, correspond to those defined in the first marker configuration in Table 2
Full size table

3.1.2 Results

Table 6 summarizes the detection accuracy, i.e., represented by precision and recall, for Yolov3-spp and ArUco on image data from the first experiment. Since all images include the three markers from marker configuration 1, the True Negative (TN) outcome is not of relevance. As shown in Table 6, Yolov3-spp achieve the highest precision and recall score in both scenarios. In particular, Yolov3-spp significantly outperforms the ArUco detector in terms of the recall score. However, Yolov3-spp only achieve a marginally higher precision score except for the second part of scenario 2.

Table 6 The table compares the relevant detection metrics between Yolov3-spp and ArUco in the first experiment
Full size table

3.2 Experiment 2: Positioning accuracy

In the second experiment, we benchmark the positioning accuracy of the proposed solution. We use custom dataset 2 to train Yolov3-spp for marker detection. For simplicity, we only consider the first marker, i.e., m1, from the second marker configuration. As described in Sects. 2.4.3 and 2.4.4, we use ArUco and OpenCV for corner detection and relative positioning, respectively. Regarding the image data, we use the monochrome pixel format as it provides high sensitivity suitable for light-critical conditions. It also requires less bandwidth and processing. For a visual representation of the scene, some images can be seen in Fig. 10b. Furthermore, we use a LiDAR-based positioning system for experimental verification. In the following, we highlight some necessary assumptions to consider such that the second experiment can be conducted with meaningful results.

  • Sensor locations and transformations: We assume both the LiDAR and the cameras to produce measurements located at their centers. Furthermore, since the cameras and the LiDAR are fixed to each other and point in the same direction, we assume a static position offset between the sensors. Based on these assumptions, the LiDAR positioning measurements are mapped into the left camera coordinate system for verification.

  • Reference system: The reference system is fixed to the left camera with its origin at the center-of-projection of the camera, its z-axis aligned with the camera optical axis, x-axis and y-axis aligned with the horizontal and vertical axes of the image plane, respectively. Rather than treating the distance along the x-axis and z-axis separately, we merge them into a 2D Euclidean distance between the middle point of the marker and the center of the left camera, as seen in Fig. 7.

  • Ground truth: The relative position between the LiDAR sensor and the middle point of the marker can be obtained accurately in the point cloud by using the 3D visualization tool Rviz. With a static position offset, we express the relative position with respect to the left camera frame. At last, we compute the resulting Euclidean distance. The LiDAR measurements are recorded with ROSbags. The ROSbag includes the global start time such that we can compare the camera and LiDAR measurements directly.

Fig. 7
figure 7

From a top-down view, the two cameras are shown with the LiDAR in between. The left camera is used as the reference system. The static offset to transform between the LiDAR frame and the left camera frame is shown with green arrows, while the red line shows the Euclidean distance between the marker and the left camera (color figure online)

Full size image

3.2.1 Hardware setup

Figure 8 shows an overview of the hardware components used for the second experiment. As seen, the Guidance, navigation, and control (GNC) computer supply the payload system with power and an ethernet connection for communication. We perform the experiments on an Nvidia Jetson Xavier (Developer Kit), an efficient edge-computing unit with a small form factor applicable for USVs. Of sensors, we use two cameras/lenses for monocular and stereo vision and a mid-range LiDAR for verification of the camera measurements. We refer to Table 7 for the details. We also use a general-purpose input/output cable for the hardware synchronization of the cameras and Power over Ethernet (PoE) for fast and reliable data and power transmission in one cable per camera. At last, we use DC/DC converters for power interfacing between the onboard battery system and the hardware components.

Fig. 8
figure 8

The figure gives an overview of the hardware components used to design the vision-based positioning system. It also shows the power and ethernet interface between the hardware components and the GNC computer

Full size image
Table 7 Sensor specifications for the second experiment
Full size table

3.2.2 Experimental description

The second experiment includes four distinct scenarios for USV docking in the harbor environment. A visual representation of the paths, generated through monocular vision and stereo vision, can be seen in Figs. 12, 13, 14, 15. While USV path 1 shows a straight-line docking maneuver, USV paths 2–4 represent various undocking maneuvers. The main objective is to evaluate the positioning accuracy as a function of the range under different docking scenarios. The paths show the position of the left camera relative to marker m1. Hence, we only use the first marker m1 as a reference throughout the second experiment. The LiDAR and the camera measurements are originally sampled at 10 Hz and 7.5 Hz, respectively. However, we use a rate of 1 Hz for experimental verification.

3.2.3 Results

Figure 9 shows the error in Euclidean distance between the ground truth LiDAR and the camera measurements as a function of the ground truth Euclidean distance for each USV path. The camera measurements concern the Euclidean distance of the left camera relative to marker m1. Both methods, i.e., stereo vision and monocular vision, are compared to the ground truth LiDAR at the same timestamps. As seen, monocular vision produces lower error than stereo vision across any range. The error also tends to increase linearly with the Euclidean distance from the dockside for both methods. At last, Figs. 12, 13, 14, 15 confirms the high detection ratio of the ArUco detector when bounding box predictions are processed rather than the whole image.

Fig. 9
figure 9

a–d show the error between the ground truth LiDAR and the camera measurements as a function of the ground truth Euclidean distance for USV paths 1, 2, 3, and 4, respectively. A visual representation of the corresponding USV paths can be seen in Figs. 12, 13, 14, 15

Full size image

3.3 Discussion of results

In the first experiment, we found Yolov3-spp to significantly outperform the ArUco detector. The ArUco detector demonstrates poor performance for robust detection in the harbor environment, especially since it rarely detects the markers at large distances. This is likely because the ArUco detector typically fails under non-uniform light and when the markers are seen at low resolutions, as pointed out by Mondjar-Guerra et al. (2018). In contrast, Yolov3-spp achieves much higher detection rates at longer distances, thus proving to be considerably more robust to environmental elements in the harbor. We believe this is because the markers are widely represented in the training data in other but similar contexts. However, Yolov3-spp also produces a certain amount of FPs, mainly at large distances. As seen in Table 5 and Fig. 6, the pixel resolution is rather low at such distances. Hence, the features to distinguish between the markers are rather low, even for small dictionary sizes. Therefore, it is likely that the decision boundaries to classify the markers are blurred, potentially leading to more FPs.

Regarding the detection results, Mateos (2020) shows that his proposed “AprilTag3D” framework achieves a 95% detection rate under outdoor tests in the river. His marker configuration consists of two AprilTags that are not lying in the same plane. In that sense, at least one tag can be detected in highly reflective environments, e.g., outdoor in open water. The marker size length is 0.13 m, i.e., half the size compared to ours, and they also use a larger dictionary size (8 \(\times\) 8). However, he does only test the framework for close-range applications, i.e., it is limited to a 2-m range. Our most comparable scenario, i.e., the second part of scenario 1, shows slightly better performance in terms of precision and recall, as seen in Table 6.

In the second experiment, we found monocular vision to outperform stereo vision across any range. We believe high-demanding processing and subsequent failures in system architecture caused lower accuracy for the stereo vision method. In particular, we experienced that the use of two full-speed CNNs for object detection induced heat issues. Subsequently, we used sleep functions to reduce computational effort, resulting in 5 Hz positioning measurements. The cameras provide a slightly higher acquisition rate, approximately 7.5 Hz per camera. In that sense, the stereo pairs to reconstruct 3D points may not represent the same timestamp since the algorithm runs on two individual ROS nodes. Consequently, the position accuracy may be affected slightly if the scene is changing rapidly. We also experienced that the cameras were slightly moved out of their fixed, original orientation under physical perturbations, e.g. if the USV hit the dockside. The transformation matrix to relate the cameras may therefore be negatively affected. We also emphasize that the chosen lens provides a limited field of view (82.4\(^\circ\)). Hence, the stereoscopic view is even lower for close-range applications since it requires the target marker to be visible in both camera views for matching and triangulation. In contrast, monocular vision provides a less complex design based on single-view geometry and is not limited by this requirement. It can even combine the cameras to extend the total field of view, thus proving to be a flexible choice for both close and long-range applications. It also takes advantage of the actual marker size to overcome scale ambiguity.

For comparison of monocular positioning accuracy, Dhall et al. (2019) achieve a 5% error relative to the ground truth Euclidean distance at a 5 m distance. We produce a 1.31% mean error among USV paths 1–4 at the same distance. Note that they use a 2-megapixel camera, while we use a 1.3-megapixel camera. Although our proposed monocular vision method induces a relative error closer to 5% when the USV is at a 7 m range or more, we believe the accuracy is sufficient in the terminal docking phase of a small USV, i.e., within a 10 m range. However, for large-scale vessels operating in larger areas, it might be necessary to increase image resolution and marker size. We also assume corner refinement methods to provide more precise 2D corner detections, thus improving the positioning accuracy for both methods at the cost of a more computational step.

4 Conclusions

This paper demonstrates how a complete vision-based positioning system can be used for auto-docking and relative positioning of USVs in the field, thus providing an independent positioning system to complement the traditional navigation system under safety-critical operations. In terms of detection accuracy, we found Yolov3-spp to significantly outperform the ArUco detector. As a result, we believe the learning-based detector, i.e., Yolov3-spp, to be a suitable choice if the day-to-day variation and complexity of the harbor environment are entirely covered in the training data. In terms of positioning accuracy, we found monocular vision to outperform the stereo vision method. We learned throughout the experiments that several elements related to the hardware and the physical design influenced the stereo vision design. In contrast, the monocular vision method proved to be less complicated and vulnerable to these elements. Through experiments conducted using the proposed methods, we have shown that a hybrid data-driven and model-based scheme outperforms work proposed by other authors in relevant outdoor scenarios. The proposed solution shows promising results under certain outdoor conditions, i.e., sunny and cloudy weather incluenced by non-uniform light and water reflections in the harbor. However, system performance under other adverse conditions is not tested yet. In future work, we plan to overcome some of these limitations by collecting more adverse weather data. We also plan to provide all necessary motion states to implement the proposed methods in feedback control.