Bayesian mediation analysis methods to explore racial/ethnic disparities in anxiety among cancer survivors

Abstract

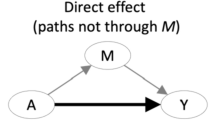
Third-variables refer to the middle variables that are positioned in the pathway between an exposure and an outcome variable. Mediation analysis is a statistical approach to identify third variables, and to estimate and test third-variable effects that explain the exposure – outcome association. In this paper, we propose three methods for mediation analysis in Bayesian settings: (1) the function of coefficients method, (2) the product of partial differences method, and (3) the resampling method. The explicit benefit of the Bayesian mediation analysis is that the hierarchical relationships between the exposure variable and third variables, and between third variables and the outcome are naturally built into the Bayesian models. We performed sensitivity analysis to assess the impact of the choice of prior distributions in the three Bayesian inference methods. We found that the proposed methods are robust across a range of priors. Finally, we illustrate the proposed methods using real data from the MY-Health Study to explore racial/ethnic disparities in anxiety among cancer survivors. The results are comparable to those from the Frequentist’s general mediation analysis but request shorter computing time.

Appendix

1.1 Bayesian mediation analysis approach for general predictive models

Denote $\varvec{\beta }$ as the parameters to build f and $\varvec{\alpha }_k$ the parameters to build $f_k$. We first fit the posterior predictive models.

• 1. Given the prior distribution for $\varvec{\beta },~\pi _0(\varvec{\beta })$, fit the predictive model for Y, $E(Y)=f(\varvec{M,X}|\varvec{\beta })$.

• 2. For $k=1, \ldots , P$, given the prior distribution for $\varvec{\alpha }_k,~\pi _k(\varvec{\alpha }_k)$, fit the predictive model for $M_k$, $E(M_k)=f_k(\varvec{X}|\varvec{\alpha }_k)$.

Algorithm 1

Method 2: The product of differences method Let $\varvec{z}_i=\{\varvec{X}_i,\varvec{M}_i,Y_i\}$ denote the observed data, where $i=1,\ldots , n$, $\varvec{X}_i=(X_{i1},\ldots ,X_{iJ})$ is the vector of J predictors, $\varvec{M}_i$ is the vector of K third-variables, and $Y_i$ is the outcome variable.

For $l=1, \ldots , N$, where N is the posterior sample size,

• 1. Draw lth sample, $\varvec{\beta }_l$, from the posterior distribution $\pi _0(\varvec{\beta }|\varvec{z})$.

• 2. For $k=1, \ldots , P$, draw lth sample, $\varvec{\alpha }_{kl}$, from the posterior distribution $\pi _k(\varvec{\alpha }_{kl}|\varvec{z})$.

• 3. For the jth predictor $X_j,~j=1, \ldots , J$,

• (a) The lth sample from the posterior distribution of the direct effect of $X_j\rightarrow Y$ given $X_j=x_{ij}, i=1, \ldots , n$, is

• $\frac{f(\varvec{x}_{i,-j}, x_{ij}+\Delta x_j,\varvec{m}_i|\varvec{\beta }_l)-f(\varvec{x}_{i,-j}, x_{ij},\varvec{m}_i|\varvec{\beta }_l)}{\Delta x_j},$ if $X_j$ is a continuous variable; $\varvec{x}_{i,-j}$ denotes the vector $\varvec{x}_{i}$ with the jth item removed, and $\Delta x_j$ is the pre-specified changing value in $X_j$. By default, we set $\Delta x_j=0.001$.

• $f(\varvec{x}_{i,-j}, x_{ij}=1, \varvec{m}_i|\varvec{\beta }_l)-f(\varvec{x}_{i,-j}, x_{ij}=0,\varvec{m}_i|\varvec{\beta }_l),$ if $X_j$ is binary. $x_{ij}=0$ refers to the reference group of $X_j$.

• (b) For $k=1, \ldots , P$, the lth sample from the posterior distribution of the indirect effect of $X_j-M_k\rightarrow Y$ given $X_j=x_{ij}, i=1, \ldots , n$, is

• $\frac{f_k(x_{ij}+\Delta x_j|\varvec{\alpha }_{kl})-f_k(x_{ij}|\varvec{\alpha }_{kl})}{\Delta x_j}\times \frac{f(\varvec{x}_i,\varvec{m}_{i, -k}, m_{ik}+\Delta _m|\varvec{\beta }_l)-f(\varvec{x}_i,\varvec{m}_{i, -k}, m_{ik}|\varvec{\beta }_l)}{\Delta m_k},$ if $M_k$ is continuous. $\Delta x_j$ is 1 if $X_j$ is binary and $\Delta m_j$ is set at a small value, e.g., $\Delta m_j=0.001$.

• $\frac{f_k(x_{ij}+\Delta x_j|\varvec{\alpha }_{kl})-f_k(x_{ij}|\varvec{\alpha }_{kl})}{\Delta x_j}\times [f(\varvec{x}_i,\varvec{m}_{i, -k}, m_{ik}=1|\varvec{\beta }_l)-f(\varvec{x}_i,\varvec{m}_{i, -k}, m_{ik}=0|\varvec{\beta }_l)],$ if $M_k$ is binary. $\Delta m_j$ is set at a small value, e.g., $\Delta m_j=0.001$.

• (c) The lth sample from the posterior distribution of the total effect of $X_j - Y$ given $X_j=x_{ij}, i=1, \ldots , n$, is the summation of the above direct effect and P indirect effects.

Algorithm 2

Method 3: The resampling method For the jth predictor $X_j,~j=1, \ldots , J$, at $X_j=x_{ij}, i=1,\ldots ,n$ and $l=1, \ldots , N$, where N is the posterior sample size,

• 1. Draw lth sample, $\varvec{m}_{l1}$, from the joint posterior distribution of $\varvec{M}$ given $\varvec{X}=\varvec{x}_i$.

• 2. Draw lth sample, $\varvec{m}_{l2}$, from the joint posterior distribution of $\varvec{M}$ given $\varvec{X}=(\varvec{X}_{-j}=\varvec{x}_{i,-j},X_{j}=x_{i,j}+\Delta x_j)$.

• 3. The lth sample from the posterior distribution for the total effect given $X_j=x_{ij}$ is

  $$\begin{aligned} te_{ijl}=\frac{f(\varvec{x}_{i,-j},x_{ij}+\Delta x_j,\varvec{m}_{l2})-f(\varvec{x}_{i},\varvec{m}_{l1})}{\Delta x_j}. \end{aligned}$$

• 4. Draw lth sample, $\varvec{m}_{l0}$, from the posterior marginal distribution of $\varvec{M}$.

• 5. The lth sample from the posterior distribution for the direct effect given $X_j=x_{ij}$ is

  $$\begin{aligned} de_{ijl}=\frac{f(\varvec{x}_{i,-j},x_{ij}+\Delta x_j,\varvec{m}_{l0})-f(\varvec{x}_{i},\varvec{m}_{l0})}{\Delta x_j}. \end{aligned}$$

• 6. For $k=1,\ldots ,P$, the direct effect not from $M_k$ is

  $$\begin{aligned} de_{ijl,-k}=\frac{f(\varvec{x}_{i,-j},x_{ij}+\Delta x_j,\varvec{m}_{l2,-k},\varvec{m}_{l0,k})-f(\varvec{x}_{i},\varvec{m}_{l1,-k},\varvec{m}_{l0,k})}{\Delta x_j}. \end{aligned}$$

  Therefore, the lth sample from the posterior distribution for the indirect effect of $X_j-M_k\rightarrow Y$ given $X_j=x_{ij}$ is

  $$\begin{aligned} ie_{ijl,k}=te_{ijl}-de_{ijl,-k}. \end{aligned}$$

Note that when $X_j$ is binary, we set all $x_{ij}$ as 0 (at the reference level) and $\Delta x_j$ as 1.

1.2 The BUGS model