Abstract
Forensic science often involves the comparison of crime-scene evidence to a known-source sample to determine if the evidence and the reference sample came from the same source. Even as forensic analysis tools become increasingly objective and automated, final source identifications are often left to individual examiners’ interpretation of the evidence. Each source identification relies on judgements about the features and quality of the crime-scene evidence that may vary from one examiner to the next. The current approach to characterizing uncertainty in examiners’ decision-making has largely centered around the calculation of error rates aggregated across examiners and identification tasks, without taking into account these variations in behavior. We propose a new approach using IRT and IRT-like models to account for differences among examiners and additionally account for the varying difficulty among source identification tasks. In particular, we survey some recent advances (Luby 2019a) in the application of Bayesian psychometric models, including simple Rasch models as well as more elaborate decision tree models, to fingerprint examiner behavior.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Validity and reliability of the evaluation of forensic science evidence are powerful and crucial to the fact-finding mission of the courts and criminal justice system (President’s Council of Advisors on Science and Technology 2016). Common types of evidence include DNA taken from blood or tissue samples, glass fragments, shoe impressions, firearm bullets or casings, fingerprints, handwriting, and traces of online/digital behavior. Evaluating these types of evidence often involves comparing a crime scene sample, referred to in this field as a latent sample,Footnote 1 with a sample from one or more persons of interest, referred to as reference samples; forensic scientists refer to this as an identification task. Ideally, the result of an identification task is what is referred to as an individualization, i.e. an assessment by the examiner that the latent and reference samples come from the same source, or an exclusion, i.e. an assessment that the sources for the two samples are different. For a variety of reasons, the assessments in identification tasks for some kinds of evidence can be much more accurate and precise than for others.
The evaluation and interpretation of forensic evidence often involve at least two steps: (a) comparing a latent sample to a reference sample and (b) assessing the meaning of that reported match or non-match (Saks and Koehler 2008). There are often additional steps taken, for example, to assess whether the latent sample is of sufficient quality for comparison. Many kinds of identification tasks, e.g. those involving fingerprint, firearms and handwriting data, require human examiners to subjectively select features to compare in the latent and reference samples. The response provided by a forensic examiner is thus more nuanced than a dichotomous match or no-match decision. Further, each of these steps introduces potential for variability and uncertainty by the forensic science examiner. Finally, the latent samples can be of varying quality, contributing further to variability and uncertainty in completing identification tasks. Forensic examination is thus ripe for the application of item response theory (IRT) and related psychometric models, in which examiners play the role of respondents or participants, and identification tasks play the role of items (Kerkhoff et al. 2015; Luby and Kadane 2018).
In this paper, we survey recent advances in the psychometric analysis of forensic examiner behavior (Luby 2019a). In particular, we will apply IRT and related models, including Rasch models (Rasch 1960; Fischer and Molenaar 2012), models for collateral or covarying responses (similar to Thissen 1983), item response trees (IRTrees, De Boeck and Partchev 2012) and cultural consensus theory models (CCT, Batchelder and Romney 1988), to better understand the operating characteristics of identification tasks performed by human forensic examiners. We will focus on fingerprint analysis, but the same techniques can be used to understand identification tasks for other types of forensic evidence. Understanding examiners’ performance is obviously of interest to legal decision-makers, for whom the frequency and types of errors in forensic testimony is important (Garrett and Mitchell 2017; Max et al. 2019), but it can also lead to better pre-service and in-service training for examiners, to reduce erroneous or misleading testimony.
1.1 Fingerprint analysis
Fingerprint identification tasks in which an examiner compares a latent print to one or more reference prints involve many sources of variation and uncertainty. The latent print may be smudged or otherwise degraded to varying degrees, making comparison with the reference print difficult or impossible. The areas of the print available in the latent image may be difficult to locate in the reference print of interest. Even if the latent print is clear and complete, the degree of similarity between the latent and reference prints varies considerably across identification tasks. See, e.g. Bécue et al. (2019) for a comprehensive review of fingerprint comparison.
Examiners also contribute variability and uncertainty to the process. Different examiners may be differentially inclined in their determinations of whether print quality is sufficient to make a comparison. They may choose different features, or minutiae, on which to base a comparison, and they may have different personal thresholds for similarity of individual minutiae, or for the number of minutiae that must match (respectively, fail to match) to declare an individualization (respectively, exclusion); see for example Ulery et al. (2014).
1.2 Empirical work to date
Proficiency tests do exist for examiners (President’s Council of Advisors on Science and Technology 2016), but they are typically scored with number-right or percent-correct scoring (Gardner et al. 2019). This approach does not account for differing difficulty of identification tasks across different editions of the same proficiency test, nor across tasks within a single proficiency test. Thus, the same score may indicate very different levels of examiner proficiency, depending on the difficulty of the tasks on a particular edition of the test, or even on the difficulty of the particular items answered correctly and incorrectly by different examiners with the same number-correct score on the same edition of the test.
Error rate studies, that aggregate true-positive, true-negative, false-positive and false-negative rates across many examiners and identification tasks, contain unmeasured biases due to the above variations in task difficulty and examiner practice and proficiency; see for example Luby and Kadane (2018). Furthermore, if a latent variable model in which monotonicity and local independence hold (such as an IRT model) applies, responses from the same participant will be positively associated in the resulting marginal model (Holland and Rosenbaum 1986). Consequently, standard errors for error rates and other quantities of interest, which are a function of the marginal model, will be understated unless this positive association is taken into account.
1.3 Preview
In this paper, we review some recent advances (Luby 2019a) in the application of Bayesian IRT and IRT-like models to fingerprint examiner proficiency testing and error rate data. We show the additional information that can be obtained from application of even a simple IRT model (e.g., Rasch 1960; Fischer and Molenaar 2012) to proficiency data, and compare that information with examiners’ perceived difficulty of identification tasks. We also explore models for staged decision-making and polytomous responses when there is no ground truth (answer key). In this latter situation, even though there is no answer key, we are able to extract useful diagnostic information about examiners’ decision processes, relative to a widely recommended decision process (known as ACE-V: Analysis, Comparison, Evaluation, Verification, Taylor et al. 2012), using the IRTrees framework of De Boeck and Partchev (2012). Interestingly, the latent traits or person parameters in these models no longer represent proficiencies in performing identification tasks but rather tendencies of examiners toward one decision or another. This leads to a better understanding of variation among examiners at different points in the analysis process. Finally we compare the characteristics of IRT-like models for generating answer keys with the characteristics of social consensus models (Batchelder and Romney 1988; Anders and Batchelder 2015) applied to the same problem.
2 Available forensic data
The vast majority of forensic decision-making occurs in casework, which is not often made available to researchers due to privacy concerns or active investigation policies. Besides real-world casework, data on forensic decision-making are collected through proficiency testing and error rate studies. Proficiency tests are periodic competency exams that must be completed for forensic laboratories to maintain their accreditation, while error rate studies are research studies designed to measure casework error rates.
2.1 Proficiency tests
Proficiency tests usually involve a large number of participants (often \(>400\)), across multiple laboratories, responding to a small set of identification task items (often \(<20\)). Since every participant responds to every item, we can assess participant proficiency and item difficulty largely using the observed scores. Since proficiency exams are designed to assess basic competency, most items are relatively easy and the vast majority of participants score 100% on each test.
In the US, forensic proficiency testing companies include Collaborative Testing Services (CTS), Ron Smith and Associates (RSA), Forensic Testing Services (FTS), and Forensic Assurance (FA). Both CTS and RSA provide two tests per year in fingerprint examination, consisting of 10–12 items, and make reports of the results available. FA also provides two tests per year, but does not provide reports of results. FTS does not offer proficiency tests for fingerprint examiners but instead focuses on other forensic domains.
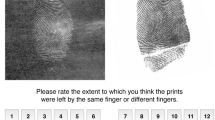
In a typical CTS exam, for example, 300–500 participants respond to eleven or twelve items. In a typical item, a latent print is presented (e.g. Fig. 1a), and participants are asked to determine the source of the print from a pool of four known donors (e.g. Fig. 1b), if any.
Proficiency tests may be used for training, known or blind proficiency testing, research and development of new techniques, etc. Even non-forensic examiners can participate in CTS exams (Max et al. 2019) and distinguishing between experts and non-experts from the response data alone is generally not feasible since most participants correctly answer every question (Luby and Kadane 2018). Moreover, since the test environment is not controlled, it is impossible to determine whether responses correspond to an individual examiner’s decision, to the consensus answer of a group of examiners working together on the exam, or some other response process.
2.2 Error rate studies
Error rate studies typically consist of a smaller number of participants (fewer than \(200\)), but use a larger pool of items (often 100 or more). In general, the items are designed to be difficult, and every participant does not respond to every item.
A recent report published by the American Association for the Advancement of Science (AAAS 2017) identified twelve existing error rate studies in the fingerprint domain, and a summary of those studies is provided here. The number of participants (N), number of items (J), false-positive rate, false-negative rate, and reporting strategy vary widely across the studies and are summarized in Table 1 below. For example, Evett and Williams (1996) did not report the number of inconclusive responses, making results difficult to evaluate relative to the other studies. And Tangen et al. (2011) and Kellman et al. (2014) required examiners to make a determination about the source of a latent print in only 3 min, likely leading to larger error rates. Ulery et al. (2011) is generally regarded as the most well-designed error rate study for fingerprint examiners (AAAS 2017; President’s Council of Advisors on Science and Technology 2016). Ulery et al. (2012) tested the same examiners on 25 of the same items they were shown 7 months earlier, and found that 90% of decisions for same-source pairs were repeated, and 85.9% of decisions for different-source pairs were repeated. For additional information on all twelve studies, see Luby (2019a) or AAAS (2017).
2.3 FBI Black Box Study
All analyses in this paper use results from the FBI Black Box Study and are based on practices and procedures of fingerprint examiners in the United States. The FBI Black Box study (Ulery et al. 2011, dataset available freely from the FBIFootnote 2), was the first large-scale study performed to assess the accuracy and reliability of fingerprint examiners’ decisions. 169 fingerprint examiners were recruited for the study, and each participant was assigned roughly 100 items from a pool of 744. The items (fingerprint images) were designed to include ranges of features (e.g. minutiae, smudges, and patterns) and quality similar to those seen in casework, and to be representative of searches from an automated fingerprint identification system. The overall false-positive rate in the study was 0.1% and the overall false-negative rate was 7.5%. These computed quantities, however, excluded all “inconclusive” responses (i.e. neither individualizations nor exclusions).
Each row in the data file corresponds to an examiner \(\times\) task response. In addition to the Examiner ID and item Pair ID (corresponding to the latent-reference pair), additional information is provided for each examinee \(\times\) task interaction, as shown in Table 2.
Examiners thus made three distinct decisions when they were evaluating the latent and reference prints in each item: (1) whether or not the latent print has value for a further decision, (2) whether the latent print was determined to come from the same source as the reference print, different sources, or inconclusive, and (3) their reasoning for making an inconclusive or exclusion decision. While the main purpose of the study was to calculate casework error rates (and thus focused on the Compare_Value decision), important trends in examiner behavior are also present in the other decisions, to which we return in Sect. 3.3.
3 Proficiency and process modelling for fingerprint examiners
3.1 Applying the Rasch model
The Rasch model (Rasch 1960; Fischer and Molenaar 2012) is a relatively simple, yet powerful, item response model, that allows us to separate examiner proficiency from task difficulty. The probability of a correct response is modeled as a logistic function of the difference between the participant proficiency, \(\theta _i\) (\(i=1, \ldots , N\)), and the item difficulty, \(b_j\) (\(j=1, \ldots , J\)),
To fit an IRT model to the Black Box Study, we will score responses as correct if they are true identifications or exclusions and as incorrect if they are false identifications or exclusions.
For the purpose of illustration, we will consider “inconclusive” responses as missing completely at random (MCAR), following the scoring method in the original study (Ulery et al. 2011), who treated inconclusive responses as missing instead of scoring them as false positives or false negatives. However, there are a large number of inconclusive answers (4907 of 17,121 responses), which can be scored in a variety of ways (see Luby 2019b, for examples), and we will return to the inconclusives in Sect. 3.4.
The Rasch model was fitted in a Bayesian framework, with \(\theta _i \sim N(0, \sigma _\theta ^2)\), \(b_j \sim N(\mu _\mathrm{b}, \sigma _\mathrm{b}^2)\), \(\mu _b \sim N(0,10)\), \(\sigma _\theta \sim \text {Half-Cauchy}(0, 2.5)\) and \(\sigma _\mathrm{b} \sim \text {Half-Cauchy}(0, 2.5)\), using Stan (Stan Development Team 2018a, b). Item difficulties and examiner proficiencies were estimated together from a single fitting of the Rasch model to the Black Box data. Posterior predictive checks indicated that the overall fit of the Rasch model was adequate, though some tendency to over-predict examiners’ total scores suggested room for improvement with more detailed models. Figure 2 shows estimated proficiencies of examiners when responses are scored as described above, with 95% posterior intervals, plotted against the raw false-positive rate (left panel) and against the raw false-negative rate (right panel). Those examiners who made at least one false-positive error are colored in purple in the right panel of Fig. 2. One of the examiners who made a false-positive error still received a relatively high proficiency estimate due to having a small false-negative rate.
In the left panel of Fig. 3, we see as expected a positive correlation between proficiency estimates and observed score (% correct); variation in proficiency at each observed score is due to the fact that different examiners saw subsets of items of differing difficulty. The highlighted examiners in the left panel in Fig. 3 all had raw percent-correct (observed scores) between 94 and 96%, and are re-plotted in the right panel showing average question difficulty, and percent of items with conclusive responses, illustrating substantial variation in both Rasch proficiency and relative frequency of conclusive responses, for these examiners with similar, high observed scores.
The left panel shows proficiency by observed score under the “inconclusive MCAR” scoring scheme, with those examiners with scores between 94 and 96% highlighted. The right panel shows proficiency by average item difficulty, colored by percent conclusive, for the highlighted subset from the left panel. Estimated proficiency is related to observed score, item difficulty, and conclusive decision rates
Luby (2019b) explores other scoring schemes as well as partial credit models for these data. Treating the inconclusives as MCAR leads to both a small range of observed scores and a relatively large range of estimated proficiencies; harsher scoring methods, such as treating inconclusives as incorrect, generally also lead to a higher distribution of estimated proficiencies, since more items are estimated to be difficult. For example, it is easy to construct examples in which a higher number-correct score on five easy Rasch items produces a lower proficiency estimate than a lower number-correct score on five harder items.
Results from an IRT analysis are largely consistent with conclusions from an error rate analysis (Luby 2019b). However, IRT provides substantially more information than a more traditional analysis, specifically through accounting for the difficulty of items seen. Additionally, IRT implicitly accounts for the inconclusive rates of different examiners in its estimates of uncertainty for both examiner proficiency and item difficulty.
3.2 Covarying responses: self-reported difficulty
As shown in Table 2, the FBI Black Box study also asked examiners to report the difficulty of each item they evaluated on a five-point scale. These reported difficulties are not the purpose of the test, but are secondary responses for each item collected at the same time as the responses and can, therefore, be thought of as ‘collateral information’.
When the additional variables are covariates describing either the items or the examiners—for instance, image quality, number of minutiae, examiner’s experience, type of training—it would be natural to incorporate them as predictors for proficiency or difficulty in the IRT model (de Boeck and Wilson 2004). However, since reported difficulty is, in effect, a secondary response in the Black Box study, we take an approach analogous to response time modeling in IRT: in our case, we have a scored task response, and a difficulty rating rather than a response time, for each person \(\times\) item pair. Thissen (1983) provides an early example of this type of modeling, where the logarithm of response time is modeled as a linear function of the log-odds \(\theta _i - b_j\) of a correct response, and additional latent variables for both items and participants. Ferrando and Lorenzo-Seva (2007) and van der Linden (2006) each propose various other models for modeling response time jointly with the traditional correct/incorrect IRT response. Modeling collateral information alongside responses in this way has been shown generally to improve estimates of IRT parameters through the sharing of information (van der Linden et al. 2010).
3.2.1 Model
Recall from Sect. 2.3 (Table 2) that examiners rate the difficulty of each item on a five-point scale: ‘A-Obvious’, ‘B-Easy’, ‘C-Medium’, ‘D-Difficult’, ‘E-Very Difficult’. Let \(Y_{ij}\) be the scored response of participant i to item j, and let \(X_{ij}\) be the difficulty reported by participant i to item j. \(Y_{ij}\) thus takes the values 0 (incorrect) or 1 (correct), and \(X_{ij}\) is an ordered categorical variable with five levels (A-Obvious to E-Very Difficult). Following Thissen (1983), we combine a Rasch model,
with a cumulative-logits ordered logistic model for the reported difficulties
where
The additional variables \(h_i\) and \(f_j\) in Eq. (3) allow for the possibilities that examiners over-report (\(h_i>0\)) or under-report (\(h_i<0\)) item difficulty, and that item difficulty tends to be over-reported (\(f_j>0\)) or under-reported (\(f_j<0\)), relative to the Rasch logit \((\theta _i - \beta _j)\) and the reporting tendencies of other examiners. These parameters will be discussed further in Sect. 3.2.2.
We assume that each participant’s responses are independent of other participants’ responses, \(Y_{i\cdot } \perp Y_{i'\cdot }\); that within-participant responses and reports are conditionally independent of one another given the latent trait(s), \(Y_{ij} \perp Y_{ij'} | \theta _i\) and \(X_{ij} \perp X_{ij'} | \theta _i, h_i\); and that responses are conditionally independent of reported difficulty given all latent variables, \(X_{ij} \perp Y_{ij} | \theta _i, b_j, g, h_i, f_j\). Then the likelihood is
and
where \(\gamma _0 = -\infty\) and \(\gamma _5 = \infty\).
We chose a cumulative-logits approach because it is directly implemented in Stan and, therefore, runs slightly faster than adjacent-category logits and other approaches. We have no reason to believe this choice has a practical effect on modeling outcomes, but if desired other formulations could certainly be used. Luby (2019a) compares the predictive performance and prediction error of the above model with fits of other models for \(X_{ij}\) and finds the above model to best fit the Black Box data.
3.2.2 Results
For each examiner in the dataset, their observed score, \(\frac{1}{n_i} \sum _{j \in J_i} y_{ij}\), and their predicted score under the model, \(\frac{1}{n_i} \sum _{j \in J_i} {\hat{y}}_{ij}\), were calculated. Similarly, predicted and observed average reported difficulty were calculated, where the observed average reported difficulty is \(\frac{1}{n_i} \sum _{j \in J_i} x_{ij}\) and the predicted average reported difficulty is \(\frac{1}{n_i} \sum _{j \in J_i} {\hat{x}}_{ij}\). If the model is performing well, the predicted scores should be very similar to the observed scores.
Figure 4 shows the predicted scores compared to the observed scores (left panel), and the predicted average difficulty compared to the observed average reported difficulty (right panel). Reported difficulties for inconclusive responses were also treated as MCAR under this scoring scheme. While the joint model tends to over-predict percent correct, it predicts average reported difficulty quite well.
Figure 5 (left panel) plots the proficiency estimates from the joint model against the Rasch proficiency estimates (i.e. the model for correctness from Sect. 3.1without modeling reported difficulty). The proficiency estimates from the joint model do not differ substantially from the Rasch proficiency estimates, although there is a slight shrinkage towards zero of the joint model proficiency estimates. Figure 5 (right panel) plots the item difficulty estimates from the joint model against the item difficulty estimates from the Rasch model. Like proficiency estimates, the difficulties under the joint model do not differ substantially from the Rasch difficulties. This is due to the inclusion of the \(h_i\) and \(f_j\) parameters for the reported difficulty part of the model, which sufficiently explains the variation in reported difficulty without impacting the IRT parameters.
Recall that the joint model predicts reported difficulty as \(g \times (\theta _i - b_j) + h_i + f_j\). In addition to proficiency and difficulty, “reporting bias” parameters for examiners (\(h_i\)) and items (\(f_j\)) are also included. Positive \(h_i\) and \(f_j\) thus increase the expected reported difficulty while negative \(h_i\) and \(f_j\) decrease the expected reported difficulty.
Thus, \(h_i\) can be interpreted as examiner i’s tendency to over or under-report difficulty, after accounting for the other parameters. The left panel of Fig. 6 shows the \(h_i\) estimates and 95% posterior intervals compared to the proficiency (point) estimates. Since there are many examiners whose 95% posterior intervals do not overlap with zero, Fig. 6 provides evidence that there exist differences among examiners in the way they report difficulty. This reporting bias does not appear to have any relationship with the model-based proficiency estimates. That is, examiners who report items to be more difficult (positive \(h_i\)) do not perform worse than examiners who report items to be easier (negative \(h_i\)).
Person reporting bias (\(h_i\), left) and item reporting bias (\(f_j\), right) with 95% posterior intervals from the joint model compared to proficiency estimate (\(\theta _i\)) and difficulty estimate (\(b_j\)), respectively. Points with intervals that overlap with zero are colored in gray. There is substantial variation in \(h_i\) not explained by \(\theta _i\). Items with estimated difficulties near zero are most likely to have over-reported difficulty
Similarly, \(f_j\) can be interpreted as item j’s tendency to be over or under-reported, after accounting for other parameters. The right panel of Fig. 6 shows the \(f_j\) estimates and 95% posterior intervals compared to the point estimates for difficulty (\(b_j\)). There are a substantial number of items whose posterior intervals do not overlap with zero; these are items that are consistently reported as more or less difficult than the number of incorrect responses for that item suggests. Additionally, there is a mild arc-shaped relationship between \(f_j\) and \(b_j\): items with estimated difficulties near zero are most likely to have over-reported difficulty, and items with very negative or very positive estimated difficulties (corresponding to items that examiners did very poorly or very well on, respectively) tend to have under-reported difficulty.
Reported difficulty may provide additional information about the items beyond standard IRT estimates. For example, consider two items with identical response patterns (i.e. the same examiners answered each question correctly and incorrectly) but one item was reported to be more difficult than the other by all examiners. It is plausible that at least some examiners struggled with that item, but eventually came to the correct conclusion. Standard IRT will not detect the additional effort required for that item, compared to the less effortful item with the same response pattern.
3.3 Sequential responses
Although the purpose of the Black Box study was to estimate false-positive and false-negative error rates, the recorded data also contains additional information about examiners’ decision-making process. Recall from Sect. 2.3 that each recorded response to an item consists of three decisions:
-
1.
Value assessment for the latent print only (No Value, Value for Exclusion Only, or Value for Individualization).
-
2.
Source evaluation of the latent/reference print pair (i.e. Individualization [match], Exclusion [non-match], or Inconclusive).
-
3.
(If Inconclusive) Reason for inconclusive.
For our analysis, we do not distinguish between ‘value for individualization’ and ‘value for exclusion only’, and instead treat the value assessment as a binary response (‘Has value’ vs ‘No value’). As Haber and Haber (2014) note, only 17% of examiners reported that they used ‘value for exclusion only’ in their normal casework on a post-experiment questionnaire, and examiners in the Black Box study may have interpreted this decision in different ways. For example, there were 32 examiners (of 169) who reported that a latent print had ‘value for exclusion only’ and then proceeded to make an individualization for the second decision. These discrepancies led us to treat the value evaluation as a binary response—either ‘has value’ or ‘no value’.
The Item Response Trees (IRTrees, De Boeck and Partchev 2012) framework provides a solution for modeling the sequential decisions above explicitly. IRTrees represent responses with decision trees where branch splits represent hypothesized internal decisions, conditional on the previous decisions in the tree structure, and leaves are observed outcomes. Sequential decisions can be represented explicitly in the IRTree framework, and node splits need not represent scored decisions.
Fingerprint examiners have been found to vary in their tendencies to make ‘no-value’ and ‘inconclusive’ decisions (Ulery et al. 2011). Figure 7 shows the distribution of the number of inconclusive and no value decisions reported by each examiner. Although most examiners report 20–40 inconclusives and 15–35 ‘no value’ responses, some examiners report as much as 60 or as few as 5. By modeling these responses explicitly within the IRTree framework, individual differences in proficiency among examiners be assessed alongside differences in tendency towards value assessments (vs no-value assessments) and inconclusive responses (vs conclusive responses).
3.3.1 Model
Figure 8 depicts an IRTree based on one possible internal decision process, motivated by the ACE-V decision process (Taylor et al. 2012). Each internal node \(Y^*_1, \ldots , Y^*_5\) represents a possible binary (0/1) decision that each examiner could makes on each item; these decisions will be modeled with IRT models. The first node, \(Y_{1}^*\), represents the examiner’s assessment of whether the latent print is “of value” or “no value”. The second node, \(Y_{2}^*\), represents whether the examiner found sufficient information in the (reference, latent) print pair to make a further decision. \(Y_{3}^*\) represents whether the pair of prints is more likely to be a match or a non-match, and \(Y_{4}^*\) and \(Y_{5}^*\) represent whether this determination is conclusive (individualization and exclusion, respectively) or inconclusive (close and no overlap, respectively). This binary decision process tree thus separates examiners’ decisions into both (a) distinguishing between matches and non-matches (\(Y_{3}^*\)) and (b) examiner “willingness to respond with certainty” (\(Y_{1}^*, Y_2^*, Y_4^*, Y_5^*\)).
Since each internal node in the IRTree in Fig. 8 is a binary split, we use a Rasch model to parameterize each branch in the tree. That is,
where i indexes examiners, j indexes items, and k indexes internal nodes (sequential binary decisions). Thus, we account for examiner tendencies to choose one branch vs. the other at decision k with \(\theta _{ki}\), and features of the task that encourage choice of one branch vs. the other at decision k with \(b_{kj}\). Clearly other IRT models could be chosen as well; see Luby (2019a) for further discussion. The full IRTree model is
Furthermore, an item-explanatory variable (\(X_j\)) for each item was included at all k nodes, where \(X_j = 1\) if the latent and reference print came from the same source (i.e. a true match) and \(X_j = 0\) if the latent and reference print came from different sources (i.e. a true non-match). Then
where \(b_{kj}\) are the item parameters and \(\beta _{0k}, \beta _{1k}\) are linear regression coefficients at node k. This is an instance of the Linear Logistic Test Model (Fischer 1973) with random item effects (Janssen et al. 2004); see also de Boeck and Wilson (2004) for more elaborate models along these lines. This allows for the means of item parameters to differ depending on whether the pair of prints is a true match or not. The random effects \(\epsilon _{kj} \sim N(0,\sigma ^2_{kb})\), as specified in the second line of (15) below, allow for the possibility that print pairs in an identification task may have other characteristics that impact task difficulty (e.g. image quality, number of features present), beyond whether the pair of prints is a same-source or different-source pair.
We fit this model under the Bayesian framework with Stan in R (Stan Development Team 2018a; Core Team 2013), using the following prior distributions,
Here \({{\mathcal {X}}}_j\) is the column vector \((1, X_j)'\), \(\varvec{\beta } = (\varvec{\beta _1}, \ldots , \varvec{\beta _5})\) is the \(5\times 2\) matrix whose \(k^{th}\) row is \((\beta _{0k}, \beta _{1k})\), and \(\varvec{\sigma _b}\) is a \(5\times 5\) diagonal matrix with \(\sigma _{1b}, \ldots , \sigma _{5b}\) as the diagonal entries; \(\varvec{\sigma _\theta }\) in the previous line is defined similarly. Multivariate normal distributions for \(\varvec{\theta }_i\) and \({\varvec{b}}_j\) were chosen to estimate covariance between sequential decisions explicitly. The Stan modeling language does not rely on conjugacy, so the Cholesky factorizations (\(L_\theta\) and \(L_b\)) are modeled instead of the covariance matrices for computational efficiency. The recommended priors (Stan Development Team 2018b) for L and \(\sigma\) were used: an LKJ prior (Lewandowski et al. 2009, LKJ = last initials of authors) with shape parameter 4, which results in correlation matrices that mildly concentrate around the identity matrix (LKJ(1) results in uniformly sampled correlation matrices), and half-Cauchy priors on \(\sigma _{kb}\) and \(\sigma _{k\theta }\) to weakly inform the correlations. N(0, 5) priors were assigned to the linear regression coefficients (\(\beta _k\)).
There are, of course, alternative prior structures, and indeed alternate tree formulations, that could reasonably model these data. For example Luby (2019a) constructs a novel bipolar scale, shown in Fig. 9, from the possible responses, and a corresponding IRTree model. This not only provides an ordering for the responses within each sub-decision (i.e. source decision and reason for inconclusive), but allows the sub-decisions to be combined in a logical way. This scale is also consistent with other hypothetical models for forensic decision-making (Dror and Langenburg 2019). Based on the description of each option for an inconclusive response, the ‘Close’ inconclusives are more similar to an individualization than the other inconclusive reasons. The ‘No overlap’ inconclusives are more similar to exclusions than the other inconclusive reasons, under the assumption that the reference prints are relatively complete. That is, if there are no overlapping areas between a latent print and a complete reference print, the two prints likely came from different sources. The ‘insufficient’ inconclusives are treated as the center of the constructed match/no-match scale. For more details, and comparisons among multiple tree structures, see Luby (2019a).
3.3.2 Results
Our discussion of results will focus on estimated parameters from the fitted IRTree model. For brevity, we will write \(\theta _k = (\theta _{k1}, \ldots , \theta _{kN})\) and \(b_k = (b_{k1}, \ldots , b_{kJ})\), \(k=1, \ldots , 5\), in Eq. (7) and Fig. 8.
The posterior medians for each examiner and item were calculated, and the distribution of examiner parameters (Fig. 10) and item parameters (Fig. 11) are displayed as a whole. The item parameters are generally more extreme than the person parameters corresponding to the same decision (e.g. \(\theta _1\) ranges from \(\approx -6\) to 6, while \(b_1\) ranges from \(\approx -10\) to 20). This suggests that many of the responses are governed by item effects, rather than examiner tendencies.
The greatest variation in person parameters occurs in \(\theta _1\) (‘no value’ tendency), \(\theta _4\) (conclusive tendency in matches) and \(\theta _5\) (conclusive tendency in non-matches). Item parameters are most extreme in \(b_1\) (tendency towards has value) and \(b_4\) (inconclusive tendency in matches). For example, \(b_{1,368}=-8.99\) and indeed all examiners agreed that item 368 has no value; similarly \(b_{4,166}=10.01\) and all examiners indeed agree that no individualization determination can be made for item 166.
Using probabilities calculated from the IRTree model estimates provides a way to assess the observed decisions in each examiner \(\times\) item pair in light of other decisions that examiner made, and how other examiners evaluated that item. Inconclusives that are ‘expected’ under the model can then be determined, along with which examiners often come to conclusions that are consistent with the model-based predictions. For example, an examiner whose responses often match the model-based predictions may be more proficient in recognizing when there is sufficient evidence to make a conclusive decision than an examiner whose responses do not match the model-based predictions.
As one example, Examiner 55 decided Item 556 was a ‘Close’ inconclusive, but Item 556 is a true non-match. Using posterior median estimates for \(\theta _{k,55}\) and \(b_{k,556}\) under the binary decision process model (where \(k = 1, \ldots , 5\) and indexes each split in the tree), the probability of observing each response for this observation can be calculated: P(No Value) \(< 0.005\), P(Individualization) \(< 0.005\), P(Close) \(= 0.20\), P(Insufficient) \(< 0.005\), P(No Overlap) \(= 0.01\) and P(Exclusion) \(=0.78\). According to the model, the most likely outcome for this response is an exclusion. Since an inconclusive was observed instead, this response might be flagged as being due to examiner indecision. This process suggests a method for determining “expected answers” for each item using an IRTree approach, which we further discuss in Sect. 3.4.
The estimated \(\beta _{0k}\) and \(\beta _{1k}\), with 90% posterior intervals, are displayed in Table 3. Since the estimated \(\beta _{1k}\)s all have posterior intervals that are entirely negative (\(k=1, 2, 3\)) or overlap zero (\(k=4, 5\)), we can infer that the identification tasks for true matches (e.g. \(X_j = 1\) in Eq. 14) tend to have lower \(b_{jk}\) parameters than the true non-matches (\(X_j=0\)), leading to matching pairs being more likely fall along the left branches of the tree in Fig. 8.
We also note that the IRTrees approach is compatible with the joint models for correctness and reported difficulty introduced in Sect. 3.2.1. By replacing the Rasch model for correctness with an IRTree model, Luby (2019a) demonstrates that reported difficulty is related to IRTree branch propensities (\(\theta _{ik} - b_{jk}\)), with items tending to be rated as more difficult when the IRTree branch propensities are near zero.
Moreover, examiners are likely to use different thresholds for reporting difficulty, just as they do for coming to source evaluations (AAAS 2017; Ulery et al. 2017); the IRTrees analysis above has been helpful in making these differing thresholds more explicit. In the same way, the IRTrees analysis of reported difficulty may lead to insights into how examiners decide how difficult an identification task is.
3.4 Generating answer keys from unscored responses
Generating evidence to construct test questions is both time-consuming and difficult. The methods introduced in this section provide a way to use evidence collected in non-controlled settings, for which ground truth is unknown, for testing purposes. Furthermore, examiners should receive feedback not only when they make false identifications or exclusions, but also if they make ‘no value’ or ‘inconclusive’ decisions when most examiners are able to come to a conclusive determination (or vice versa). It is, therefore, important to distinguish when no value, inconclusive, individualization, and exclusion responses are expected in a forensic analysis.
There are also existing methods for ‘IRT without an answer key’, for example the cultural consensus theory (CCT) approach (Batchelder and Romney 1988; Oravecz et al. 2014). CCT was designed for situations in which a group of respondents shares some knowledge or beliefs in a domain area which is unknown to the researcher or administrator (similar approaches have been applied to ratings of extended response test items, e.g. Casabianca et al. 2016). CCT then estimates the expected answers to the items provided to the group. We primarily focus on comparing the Latent Truth Rater Model (LTRM), a CCT model for ordinal categorical responses (Anders and Batchelder 2015), to an IRTree-based approach.
Although the individualization/exclusion scale in Fig. 9 could be used to generate an answer key for the source evaluations (i.e. individualization, exclusion, or inconclusive), it would not be possible to determine an answer key for the latent print value assessments (i.e. no value vs has value). Instead, a ‘conclusiveness’ scale, Fig. 12, can be used. This scale does not distinguish between same source and different source prints, but does allow for the inclusion of no value responses on the scale. Using an answer key from this scale, alongside the same-source/different-source information provided by the FBI, provides a complete picture of what the expected answers are: an answer key generated for items placed on the scale of Fig. 12 identifies which items are expected to generate conclusive, vs. inconclusive answers; for the conclusive items, same-source pairs should be individualizations and different-source pairs should be exclusions.
3.4.1 Models
We fit four models to the Black Box data: (1) the LTRM (Anders and Batchelder 2015), (2) an adapted LTRM using a cumulative logits model (C-LTRM), (3) an adapted LTRM based using an adjacent logits model (A-LTRM), and (4) an IRTree model. The LTRM was fitted using the R package CCTpack (Anders 2017), while all other models were fitted using Stan (Stan Development Team 2018b, a). Each of the four models is detailed below, and information on prior specification may be found in Table 7.
3.4.2 Latent truth rater model
Let \(Y_{ij}=c\) denote examiner i’s categorical response to item j, where \(c=1\) is the response “No Value”, \(c=2\) is the response “Inconclusive”, and \(c=3\) is the response “Conclusive”. Key features of the LTRM in our context are \(T_j\), the latent “answer key” for item j, and \(\gamma _c\) (\(c=1,2\)), the category boundaries between ‘No Value’ vs. ‘Inconclusive’, and for ‘Inconclusive’ vs. ‘Conclusive’, respectively. Each examiner draws a latent appraisal of each item (\(Z_{ij}\)), which is assumed to follow a normal distribution with mean \(T_j\) (the ‘true’ location of item j) and precision \(\tau _{ij}\), which depends on both examiner competency (\(E_i\)) and item difficulty (\(\lambda _j\)) (that is, \(\tau _{ij} = \frac{E_i}{\lambda _j}\)). If every examiner uses the ‘true’ category boundaries, then if \(Z_{ij} \le \gamma _1\) then \(Y_{ij} =\) ‘No Value’, if \(\gamma _1 \le Z_{ij} \le \gamma _2\) then \(Y_{ij} =\) ‘Inconclusive’, and if \(Z_{ij} \ge \gamma _2\) then \(Y_{ij} =\)‘Conclusive’. Individuals, however, might use a biased form of the category thresholds, and so individual category thresholds, \(\delta _{i,c} = a_i \gamma _c + b_i\), are defined, where \(a_i\) and \(b_i\) are examiner scale and shift biasing parameters, respectively. That is, \(a_i\) shrinks or expands the category thresholds for examiner i, and \(b_i\) shifts the category thresholds to the left or right. The model is thus
where F(u) is the CDF of a normal variable with mean \(T_j\) and precision \(\tau _{ij}\) (Anders and Batchelder 2015). The likelihood of the data under the LTRM is then
where \(\delta _{i, 0} = - \infty\), \(\delta _{i,3} = \infty\), and \(\delta _{i,c} = a_i \gamma _c + b_i\). In addition to the LTRM model (Anders and Batchelder 2015), we also consider adaptations of the LTRM to a logistic modeling framework, with some simplifying assumptions on the LTRM parameters.
3.4.3 Adapted LTRM as a Cumulative Logits Model (C-LTRM)
The original LTRM [Eq. 20, Anders and Batchelder (2015)] is a cumulative-probits model, and is, therefore, more closely related to more standard IRT models than it might seem at first glance. Specifically, if (1) the latent appraisals (\(Z_{ij}\)) are modeled with a logistic instead of a normal distribution, (2) it is assumed that \(\tau _{ij} =\frac{E_i}{\lambda _j} = 1\) for all i, j, and (3) it is assumed \(a_i = 1\) for all i, then the model collapses into a more familiar cumulative logits IRT model,
This transformed model has the same form as the Graded Response Model, which is identifiable under standard conditions (Samejima 1969; Muraki 1990). Relaxing the assumption that \(a_i = 1\), a cumulative logits model with a scaling effect for each person on the item categories is obtained, which we call the cumulative-logits LTRM (C-LTRM),
The likelihood for the data under Eq. 22 is
where \(\gamma _0 = -\infty\) and \(\gamma _C = \infty\).
3.4.4 Adapted LTRM as an adjacent category logits model (A-LTRM)
Making the same assumptions as above, \(P(Y_{ij} = c)\) could instead be expressed using an adjacent-categories logit model,
which takes the same form as the Rating Scale Model (Andrich 1978). The RSM has nice theoretical properties due to the separability of \(T_j\) and \(b_i\) in the likelihood, and is identifiable under standard conditions (Fischer 1995). Re-casting the LTRM as an adjacent-category model opens the possibility of more direct theoretical comparisons between models. Relaxing the assumption that \(a_i = 1\), a generalized adjacent-category logit model with a scaling effect for each person on the item categories is obtained, which we call the adjacent-logits LTRM (A-LTRM),
The likelihood is then
3.4.5 IRTree for answer key generation
For comparison, we also consider a simplified IRTree model for answer key generation, which does not include the reason provided for inconclusive responses (as the model in Sect. 3.3 did). This simplification was made for two reasons: first, this simplified IRTree model allows us to make inferences on the ‘conclusiveness’ scale in Fig. 12, facilitating comparison with the CCT model; second, the reasons provided for inconclusive responses are relatively inconsistent. Indeed, in a follow-up study done by the FBI (Ulery et al. 2012), 72 Black Box study participants were asked to re-assess 25 items. 85% of no value assessments, 90% of exclusion evaluations, 68% of inconclusive responses, and 89% of individualization evaluations were repeated; while only 44% of ‘Close’, 21% of ‘Insufficient’, and 51% of ‘No Overlap’ responses were repeated. Inconclusive reasoning thus varies more within examiners than the source evaluations, and a generated answer key containing reasons for inconclusives may not be reliable or consistent across time.
The tree structure for the simplified IRTree model is shown in Fig. 13. The first internal node (\(Y_{1}^*\)) represents the value assessment, the second internal node (\(Y_{2}^*\)) represents the conclusive decision, and the third internal node represents the individualization/exclusion decision. Note that \(Y_3^*\) is not a part of the conclusiveness scale in Fig. 12, and thus provides additional information beyond the ‘conclusiveness’ answer key.
3.4.6 Results
We focus on comparing the answer keys generated by each of the models. As a simple baseline answer key, we also calculate the modal response for each item using the observed responses. Unlike the IRTree and LTRM approaches, this baseline answer key does not account for different tendencies of examiners who answered each item; nor does it account for items being answered by different numbers of examiners. The LTRM, A-LTRM, and C-LTRM all estimate the answer key, a combination of \(T_j\)s and \(\gamma _c\)s, directly. The answer for item j is ‘No Value’ if \(T_j < \gamma _1\), ‘Inconclusive’ if \(\gamma _1< T_j < \gamma _2\) and ‘Conclusive’ if \(T_j > \gamma _2\). For the IRTree model, an answer key was calculated based on what one would expect an ‘unbiased examiner’ to respond. The response of a hypothetical unbiased examiner (i.e. \(\theta _{ki}= 0\) for all k) to each question was predicted, using the estimated item parameters in each split.
There are thus five answer keys: (1) Modal answer key, (2) LTRM answer key, (3) C-LTRM answer key, (4) A-LTRM answer key, and (5) IRTree answer key. Each of the answer keys has three possible answers: no value, inconclusive, or conclusive. Table 4 shows the number of items (out of 744) that the answer keys disagreed upon. The most similar answer keys were the A-LTRM and C-LTRM, which only disagreed on six items: three that disagreed between inconclusive/conclusive and three that disagreed between no value and inconclusive. The original LTRM model most closely matched the modal answer, with the A-LTRM model disagreeing with the modal answer most often.
Recall that the three possible answers were (1) ‘no value’, (2) ‘inconclusive’, or (3) ‘conclusive’. There were 48 items for which at least one of the models disagreed with the others. The vast majority of these disagreements were between ‘no value’ and ‘inconclusive’ or ‘inconclusive’ and ‘conclusive’. Of the 48 items in which models disagreed, only five items were rated to be conclusive by some models and no value by others. All of these five items were predicted to be ‘no value’ by the LTRM, ‘inconclusive’ by the A-LTRM and C-LTRM, and ‘exclusion’ by the IRTree. Table 5 shows the number of observed responses in each category for these five items and illuminates two problems with the LTRM approaches. First, the original LTRM strictly follows the modal response, even when a substantial number of examiners came to a different conclusion. In Question 665, for example, eight examiners were able to make a correct exclusion, while the LTRM still chose ‘no value’ as the correct response. Second, the A-LTRM and C-LTRM models may rely too much on the ordering of outcomes. Both adapted LTRM models predicted these items to be inconclusives, yet most examiners who saw the items rated it as either a ‘no value’ or ‘exclusion’.
Using a model-based framework to generate expected answers provides more robust answer keys than relying on the observed responses alone. Both IRTrees and a CCT-based approach allow for the estimation of person and item effects alongside an answer key. Furthermore, although the two approaches are formulated quite differently, they lead to similar generated answer keys in the Black Box data. This similarity is due to the fact that the conditional sufficient statistics for the item location parameters in the two models both rely on the marginal category totals for each item. In fact, the conditional sufficient statistic for the item parameter in the A-LTRM is a function of the conditional sufficient statistics for the item parameters in the IRTree model (see Luby 2019a, for further details).
For this setting, we prefer using the IRTree framework to analyze responses because it does not require the responses to be ordered and because each decision may be modeled explicitly. In addition, model fit comparisons using the Widely Applicable AIC index (WAIC, Vehtari et al. 2017; Watanabe 2010), as well as in-sample prediction error, prefer the IRTree model for these data; see Table 6.
4 Discussion and future work
In this survey of recent advances in the psychometric analysis of forensic examiner decision-making process data, we have applied a wide variety of models, including the Rasch model, Item Response Trees, and Cultural Consensus Models, to identification tasks in the FBI Black Box study of error rates in fingerprint examination. Careful analysis of forensic decision-making processes unearths a series of sequential responses that to date have often been ignored, while the final decision is simply scored as either correct or incorrect. Standard IRT models applied to scored data, such as the Rasch model of Sect. 3.1, provide substantial improvements over current examiner error rate studies: examiner proficiencies can be justifiably compared even if the examiners did not do the same identification tasks, and the influence of the varying difficulty of identification tasks can be seen in examiner proficiency estimates. Additional modeling techniques are needed to account for the co-varying responses present in the form of reported difficulty (Sect. 3.2), the sequential nature of examiner decision-making (Sect. 3.3), and the lack of an answer key for scoring ‘no value’ and ‘inconclusive’ responses (Sect. 3.4). See Luby (2019a) for further developments of all methods presented here.
In our analyses, we found a number of interesting results with important implications for subjective forensic science domains. Taken together, the results presented here demonstrate the rich possibilities in accurately modeling the complex decision-making in fingerprint identification tasks.
For instance, results from Sect. 3.2.2 show that there are differences among fingerprint examiners in how they report the difficulty of identification tasks, and that this behavior is not directly related to examiners’ estimated proficiency. Instead, examiners tended to over-rate task difficulty when the task was of middling difficulty, and under-rate the difficulty of tasks that were either extremely easy or extremely hard. A similar effect also holds for the intermediate decisions in an IRTree analysis (Luby 2019a).
Furthermore, we have shown that there is substantial variability among examiners in their tendency to make no value and inconclusive decisions, even after accounting for the variation in items they were shown (Sect. 3.3.2). The variation in these tendencies could lead to additional false identifications (in the case of “no value” evidence being further analyzed), or to guilty perpetrators going free (in the case of “valuable” evidence not being further analyzed). To minimize the variation in examiner decisions, examiners should receive feedback not only when they make false identifications or exclusions, but also when they make mistaken ‘no value’ or ‘inconclusive’ decisions. Finally, in Sect. 3.4, we show how to use the data to infer which ’no value’ or ’inconclusive’ responses are likely to be mistaken.
Our analyses were somewhat limited by available data; the Black Box study was designed to measure examiner performance without ascertaining how those decisions were made. Privacy and confidentiality considerations on behalf of the persons providing fingerprints for the study make it impossible for the FBI to share the latent and reference prints for each identification task; if they were available we expect meaningful item covariates could be generated, perhaps through image analysis. Similar considerations on behalf of examiners preclude the possibility of demographic or background variables (e.g. nature of training, number of years in service, etc.) linked to individual examiners; auxiliary information such as examiners’ annotations of selected features, or their clarity and correspondence determinations, is also not available. Each of these, if available, might help elucidate individual differences in examiner behavior and proficiency.
We anticipate future collaboration with experts in human decision making to improve the models and with fingerprint domain experts to determine the type and amount of data that would be needed to make precise and accurate assessments of examiner proficiency and task difficulty. Finally, we expect a future line of work will be to consider what would be needed to connect error rates, statistical measures of uncertainty, and examiner behavior collected from standardized/idealized testing situations such as those discussed in this paper, with task performance by examiners in authentic forensic investigations.
Notes
This usage should not be confused with the usage of “latent” in psychometrics, meaning a variable related to individual differences that is unobservable. We will use the word in both senses in this paper, the meaning being clear from context.
References
AAAS (2017) Forensic science assessments: a quality and gap analysis—latent fingerprint examination. Technical report, (prepared by William Thompson, John Black, Anil Jain, and Joseph Kadane)
Anders R (2017) CCTpack: Cultural Consensus Theory applications to data. R package version 1.5.2
Anders R, Batchelder WH (2015) Cultural consensus theory for the ordinal data case. Psychometrika 80(1):151–181
Andrich D (1978) Application of a psychometric rating model to ordered categories which are scored with successive integers. Appl Psychol Measur 2(4):581–594
Batchelder WH, Romney AK (1988) Test theory without an answer key. Psychometrika 53(1):71–92
Bécue A, Eldridge H, Champod C (2019) Fingermarks and other body impressions—a review (august 2016 – june 2019)
Casabianca JM, Junker BW, Patz RJ (2016) Hierarchical rater models. In: van der Linden W (ed) Handbook of item response theory, vol 1. Chapman and Hall/CRC, New York, pp 477–494
de Boeck P, Wilson M (2004) Explanatory item response models: a generalized linear and nonlinear approach. Springer, New York
De Boeck P, Partchev I (2012) IRTrees: tree-based item response models of the glmm family. J Stat Softw Code Snippets 48(1):1–28
Dror IE, Langenburg G (2019) ‘Cannot Decide’: the fine line between appropriate inconclusive determinations versus unjustifiably deciding not to decide. J Forensic Sci 64(1):10–15
Evett I, Williams R (1996) A review of the sixteen point fingerprint standard in England and Wales. J Forensic Identif 46:49–73
Ferrando PJ, Lorenzo-Seva U (2007) An item response theory model for incorporating response time data in binary personality items. Appl Psychol Meas 31(6):525–543
Fischer GH (1973) The linear logistic test model as an instrument in educational research. Acta Psychol 37(6):359–374
Fischer GH (1995) The derivation of polytomous rasch models. In: Fischer GH, Molenaar IW (eds) Rasch models. Springer, New York, pp 293–305
Fischer GH, Molenaar IW (2012) Rasch models: foundations, recent developments, and applications. Springer Science & Business Media, New York
Gardner BO, Kelley S, Pan KD (2019) Latent print proficiency testing: an examination of test respondents, test-taking procedures, and test characteristics. J Forensic Sci 65(2):450–457
Garrett BL, Mitchell G (2017) The proficiency of experts. Univ Pa Law Rev 166:901
Haber RN, Haber L (2014) Experimental results of fingerprint comparison validity and reliability: a review and critical analysis. Sci Justice 54(5):375–389
Holland PW, Rosenbaum PR (1986) Conditional association and unidimensionality in monotone latent variable models. Ann Stat 14(4):1523–1543
Janssen R, Schepers J, Peres D (2004) Models with item and item group predictors. In: De Boeck P, Wilson M (eds) Explanatory item response models. Statistics for social science and public policy, Springer, New York, NY, pp 189–212
Kellman PJ, Mnookin JL, Erlikhman G, Garrigan P, Ghose T, Mettler E, Charlton D, Dror IE (2014) Forensic comparison and matching of fingerprints: using quantitative image measures for estimating error rates through understanding and predicting difficulty. PLoS One 9(5):e94617
Kerkhoff W, Stoel R, Berger C, Mattijssen E, Hermsen R, Smits N, Hardy H (2015) Design and results of an exploratory double blind testing program in firearms examination. Sci Justice 55(6):514–519
Langenberg G (2009) A performance study of the ACE-V process: a pilot study to measure the accuracy, precision, reproducibility, repeatability, and biasability of conclusions resulting from the ACE-V process. J Forensic Identif 59(2):219
Langenburg G, Champod C, Genessay T (2012) Informing the judgments of fingerprint analysts using quality metric and statistical assessment tools. Forensic Sci Int 219(1–3):183–198
Langenburg G, Champod C, Wertheim P (2009) Testing for potential contextual bias effects during the verification stage of the ace-v methodology when conducting fingerprint comparisons. J Forensic Sci 54(3):571–582
Lewandowski D, Kurowicka D, Joe H (2009) Generating random correlation matrices based on vines and extended onion method. J Multivar Anal 100(9):1989–2001
Liu S, Champod C, Wu J, Luo Y et al (2015) Study on accuracy of judgments by chinese fingerprint examiners. J Forensic Sci Med 1(1):33
Luby A (2019a) Accounting for Individual Differences among Decision-Makers with Applications in Forensic Evidence Evaluation. PhD thesis, Carnegie Mellon University. http://www.swarthmore.edu/NatSci/aluby1/files/luby-dissertation.pdf. Accessed 15 Oct 2019
Luby A (2019b) Decision-making in forensic identification tasks. In: Tyner S, Hofmann H (eds), Open Forensic Science in R, chapter 8. rOpenSci Foundation, US, https://sctyner.github.io/OpenForSciR. Accessed 15 Oct 2019
Luby AS, Kadane JB (2018) Proficiency testing of fingerprint examiners with Bayesian Item Response Theory. Law Probab Risk 17(2):111–121
Max B, Cavise J, Gutierrez RE (2019) Assessing latent print proficiency tests: lofty aims, straightforward samples, and the implications of nonexpert performance. J Forensic Identif 69(3):281–298
Muraki E (1990) Fitting a polytomous item response model to likert-type data. Appl Psychol Meas 14(1):59–71
Oravecz Z, Vandekerckhove J, Batchelder WH (2014) Bayesian cultural consensus theory. Field Methods 26(3):207–222
Pacheco I, Cerchiai B, Stoiloff S (2014) Miami-dade research study for the reliability of the ace-v process: Accuracy & precision in latent fingerprint examinations. Unpublished report, pp 2–5
President’s Council of Advisors on Science and Technology (2016) Forensic science in criminal courts: Ensuring scientific validity of feature-comparison methods. Technical report, Executive Office of The President’s Council of Advisors on Science and Technology, Washington DC
R Core Team (2013) R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria
Rasch G (1960) Probabilistic models for some intelligence and attainment tests. University of Chicago Press, Chicago
Saks MJ, Koehler JJ (2008) The individualization fallacy in forensic science evidence. Vand L Rev 61:199
Samejima F (1969) Estimation of latent ability using a response pattern of graded scores. p 97
Stan Development Team (2018a) RStan: the R interface to Stan. R package version 2(18):2
Stan Development Team (2018b) Stan modeling language users guide and reference manual
Tangen JM, Thompson MB, McCarthy DJ (2011) Identifying fingerprint expertise. Psychol Sci 22(8):995–997
Taylor MK, Kaye DH, Busey T, Gische M, LaPorte G, Aitken C, Ballou SM, Butt L, Champod C, Charlton D et al. (2012) Latent print examination and human factors: Improving the practice through a systems approach. report of the expert working group on human factors in latent print analysis. Technical report, U.S. Department of Commerce, National Institute of Standards and Technology (NIST)
Thissen D (1983) Timed testing: an approach using item response theory. In: Weiss DJ (ed) New Horizons in Testing, chapter 9. Academic Press, San Diego, pp 179–203
Ulery BT, Hicklin RA, Buscaglia J, Roberts MA (2011) Accuracy and reliability of forensic latent fingerprint decisions. Proc Natl Acad Sci 108(19):7733–7738
Ulery BT, Hicklin RA, Buscaglia J, Roberts MA (2012) Repeatability and reproducibility of decisions by latent fingerprint examiners. PLoS One 7(3):e32800
Ulery BT, Hicklin RA, Roberts MA, Buscaglia J (2014) Measuring what latent fingerprint examiners consider sufficient information for individualization determinations. PLoS One 9(11):e110179
Ulery BT, Hicklin RA, Roberts MA, Buscaglia J (2017) Factors associated with latent fingerprint exclusion determinations. Forensic Sci Int 275:65–75
van der Linden WJ (2006) A lognormal model for response times on test items. J Educ Behav Stat 31(2):181–204
van der Linden WJ, Klein Entink RH, Fox J-P (2010) IRT parameter estimation with response times as collateral information. Appl Psychol Meas 34(5):327–347
Vehtari A, Gelman A, Gabry J (2017) Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat Comput 27(5):1413–1432
Watanabe S (2010) Asymptotic equivalence of bayes cross validation and widely applicable information criterion in singular learning theory. J Mach Learn Res 11(Dec):3571–3594
Wertheim K, Langenburg G, Moenssens A (2006) A report of latent print examiner accuracy during comparison training exercises. J Forensic Identif 56(1):55
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Kazuo Shigemasu.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The material presented here is based upon work supported in part under Award No. 70NANB15H176 from the U.S. Department of Commerce, National Institute of Science and Technology. Any opinions, findings, or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Institute of Science and Technology, nor the Center for Statistics and Applications in Forensic Evidence.
Appendix: LTRM prior distribution specifications
Appendix: LTRM prior distribution specifications
The IRTree model was fit using the same priors as the efficient implementation discussed in Sect. 3.3. The prior distributions for the LTRM, A-LTRM, and C-LTRM are given below (see Table 7).
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Luby, A., Mazumder, A. & Junker, B. Psychometric analysis of forensic examiner behavior. Behaviormetrika 47, 355–384 (2020). https://doi.org/10.1007/s41237-020-00116-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41237-020-00116-6