Abstract
Due to biased assumptions on the underlying ordinal rating scale in subjective Quality of Experience (QoE) studies, Mean Opinion Score (MOS)-based evaluations provide results, which are hard to interpret and can be misleading. This paper proposes to consider the full QoE distribution for evaluating, reporting, and modeling QoE results instead of relying on MOS-based metrics derived from results based on ordinal rating scales. The QoE distribution can be represented in a concise way by using the parameters of a multinomial distribution without losing any information about the underlying QoE ratings, and even keeps backward compatibility with previous, biased MOS-based results. Considering QoE results as a realization of a multinomial distribution allows to rely on a well-established theoretical background, which enables meaningful evaluations also for ordinal rating scales. Moreover, QoE models based on QoE distributions keep detailed information from the results of a QoE study of a technical system, and thus, give an unprecedented richness of insights into the end users’ experience with the technical system. In this work, existing and novel statistical methods for QoE distributions are summarized and exemplary evaluations are outlined. Furthermore, using the novel concept of quality steps, simulative and analytical QoE models based on QoE distributions are presented and showcased. The goal is to demonstrate the fundamental advantages of considering QoE distributions over MOS-based evaluations if the underlying rating data is ordinal in nature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The concept of Quality of Experience (QoE) constitutes a major research field, which aims to understand and improve the subjective perception of the quality of a technical system as a whole by the end user. It is widely recognized that the QoE is influenced by different QoE factors, which are characteristics of the user, system, service, application, or context [1]. In order to identify these factors and quantify their influence on the QoE of a system, extensive subjective studies have to be conducted. In these studies, users assess their experience with a given stimulus on a rating scale, such as the Absolute Category Rating (ACR) scale [2,3,4,5,6,7], which is widely used. The ACR scale allows to quantify the user experience as one of five values ranging from 1 (bad) to 5 (excellent). Then, the numerical values of the ratings are typically aggregated by using the arithmetic mean to obtain the Mean Opinion Score (MOS) [8], which has attracted a very high popularity and is widely used as the de facto QoE metric in both industry and academia.
However, the major pitfall of QoE evaluations based on the ACR scale is the underlying assumption about the mapping of QoE to the rating scale, which can be traced back to a long dispute on measurement scales and appropriate statistics, e.g., [9,10,11,12]. When conducting a subjective user study, user ratings are actually collected on a categorical scale, hence the name “Absolute Category Rating”, which allows to indicate the subjective QoE as one of five categories, namely, “bad”, “poor”, “fair”, “good”, or “excellent”. As the different categories can be sorted according to the QoE, i.e., “bad” < “poor” < “fair” < “good” < “excellent”, this rating scale also represents an ordinal scale. Although the numerical values associated to the categories might suggest so, however, the rating scale is not an interval scale as the elements of the scale cannot be included into arithmetic operations. The reason is that, while some differences might look numerically equidistant, the corresponding differences between categories might not be actually equal [13,14,15]. In particular for QoE ratings, it is unclear and highly questionable if, e.g., the difference in user experience between “bad” (1) and “poor” (2) is the same as between “fair” (3) and “good” (4). Moreover, the differences between the rating categories might be different for each participant of a QoE study [16]. See Fig. 1 for a visualization of this pitfall, showing the differences between the categories as colored boxes.
Note that this pitfall applies not only to the 5-point ACR scale, but to all rating scales with discrete options. One alternative could be to use continuous rating scales in QoE studies, where users rate a continuous score, typically within a given range, e.g., [17]. Also most standards typically allow both discrete and continuous rating scales, e.g., [3,4,5,6,7]. These continuous scales should not be considered ordinal scales, thus, the described pitfall might not apply. Nevertheless, ordinal rating scales are indeed frequently used in QoE studies. Apart from the 5-point ACR scale, this includes other discrete rating scales with a different number of options, ranging from binary acceptance scales, with as low as two options [18], to scales with a high number of options, such as 9- or 11-point rating scales as defined in [4]. The increase in the number of options of an ordinal scale is considered to be a compromise towards purely continuous scales, but, as it is still an ordinal scale, the pitfall remains. Moreover, rating scales might have different labels, such as the Degradation Category Rating (DCR) scale [4], or show a different visual appearance, such as horizontally or vertically oriented scales, as well as color-coded, numerical, or purely linguistic scales. Still, these scales are conceptually similar to the classical 5-point ACR scale, and might not even lead to significantly different QoE results [19]. Thus, this paper will focus on the widely used 5-point ACR scale as a showcase, although the paper generalizes to all discrete rating scales.
The pitfall of ordinal scales continues to severely affect the evaluation and presentation of the results of QoE studies. Given that a discrete rating scale of a subjective user study is not an interval scale, averaging ratings by using the arithmetic mean is not an interpretable quantity. As a measure of central tendency, ordinal scales only allow to compute the mode, i.e., the category with the highest number of ratings, as well as the median, which is the 50-percentile of the ratings, i.e., the category, for which 50% of the ratings are less or equal. If the ratings of a subjective study are nevertheless aggregated in terms of arithmetic mean to a MOS, the implicit assumption is introduced that the differences between numerical values represent the actual differences in QoE. This would imply that all the differences in experience between adjacent QoE rating categories are equal, which is a substantial bias and can lead to systematic errors, e.g., [20].
When quantifying QoE differences or QoE improvements of different stimuli, often differences of MOS values are reported, e.g., the MOS value of stimulus B is by x larger than the MOS value of stimulus A. However, these differences between MOS values face the same issues as differences between the rating categories, and are not a meaningful metric. Other works continue to quantify QoE improvements also in terms of percentages of MOS, e.g., stimulus B has a MOS improvement of \(x\%\) over stimulus A. However, such operation would - in contrast to interval scales - be only interpretable on a ratio scale, which requires an absolute zero, and thereby, allows to compute multiplications and ratios of quantities. Still, an absolute zero for experience is hard to find, and the definition of ratios between categories has strange effects, such that, for example, a MOS increase of 100% is an increase of one category when having “bad” (1) as baseline, but an increase of two categories when considering “poor” (2) as baseline. Consequently, this would allow for highly questionable interpretations that, for example, a “good” (4) experience is two times better than “poor” (2) experience, or four times better than “bad” (1) experience. Therefore, the expression of QoE differences in terms of MOS ratios is also not a meaningful quantity.
This paper proposes to consider the full QoE distribution over the ordinal rating categories for evaluating, reporting, and modeling QoE results instead of relying on MOS-based metrics. The QoE distribution can be represented in a concise way by using the parameters of a multinomial distribution without losing any information about the underlying QoE ratings, and even keeps backward compatibility with previous, biased MOS-based results. Considering QoE results as a realization of a multinomial distribution takes a more holistic perspective of the subjective user study and allows to rely on a well-established theoretical background, which has various options for more meaningful evaluations. Existing and novel statistical methods that can be applied to QoE distributions in the context of a QoE study are summarized in this work, and their advantages over MOS-based evaluations are outlined in this work with the help of examples.
Moreover, using the novel concept of quality steps, this paper proposes simulative and analytical QoE models based on QoE distributions, which keep detailed information from the results of a QoE study of a technical system. They allow to inspect the rating behavior for observed values of the parameters of a technical system, and allow to predict the experience at unobserved values. For each parameter value, the full QoE distribution can be extracted and evaluated with the methods presented in this paper, which gives an unprecedented richness of insights into the end users’ experience with the technical system.
Note that this paper is an extension of [21]. Compared to the earlier work, this paper presents background information about the dispute on proper statistical analysis of ordinal data, which has been ongoing in many related research fields. Moreover, it adds more statistical methods for QoE distributions to provide a comprehensive summary, and it is the first to tackle QoE models based on multinomial QoE distributions.
The remainder of this paper is organized as follows. Section 2 describes related works on the dispute on scales and statistics, as well as on QoE and MOS fundamentals. Section 3 introduces the theoretical background on multinomial distributions, from which QoE distributions form a small subset. Statistical methods for QoE evaluations based on QoE distributions are described in Sect. 4, showing their advantages over MOS-based evaluations. Section 5 discusses the design and applications of simulative and analytical QoE models based on QoE distributions, and finally, Sect. 6 concludes this paper.
Related work
This section first presents the dispute on scales and statistics, which has been going on for a long time in many research disciplines. Afterwards, related works on QoE assessment and modeling methodology are outlined.
Dispute on scales and statistics
During an extensive survey of related works, it was found that the dispute on scales and statistics is mostly centered around two aspects, which are both relevant to the QoE community:
-
1.
Should single rating scales with a set of ordered, verbally labeled alternatives be considered ordinal or interval scales?
-
2.
What kind of statistics can be used to analyze the data of such rating scales?
To answer these questions, first, the terminology and historical context of these questions is outlined. Afterwards, concrete answers to these questions are given, pointing the interested reader to further literature on this dispute.
The dispute on rating scales and the appropriate statistical methods to evaluate the resulting data has been around since the mid of the last century, especially since the increased popularity of Likert scales in psychometric assessment of attitudes [22]. This methodology requires individual Likert items, which are statements that can be rated with one of five ordered alternatives, originally, “strongly approve”, “approve”, “undecided”, “disapprove”, and “strongly disapprove”, which were assigned consecutive numerical values, i.e., 1 to 5. The Likert scale is the average or sum of the answers to several individual items, based on the assumption that attitudes are distributed fairly normally [22].
Nowadays, such questionnaires exist in many variations [23], e.g., containing single or multiple Likert-type items or Likert response formats with a number of ordered, verbally labeled alternatives. In contrast to the original design, these items can be unipolar, unsymmetric, or have a different number of alternatives. As there is a lot of confusion around the terminology, in the following, the term “scale” will exclusively refer to the measurement scale of a single experiment, such as the measurement of a physical quantity, or the rating of a single item or stimulus. In that sense, the 5-point ACR scale [2, 4] typically used in QoE studies to rate the experience with a stimulus, which is an unipolar Likert-type item, is also considered a measurement scale.
Stevens [24] distinguishes four levels of measurement scales (nominal, ordinal, interval, and ratio) depending on the rules for the assignment of numbers to the measured objects or events, the mathematical properties of the scales, and the statistical operations applicable to data measured on each scale. He provided a set of permissible statistics, which could be applied to each data depending on the level of measurement scale. For ordinal scales, for example, which require the determination of equality (nominal) and the determination of greater or less (ordinal), all statistics of nominal scales (number of cases, mode, contingency correlation), as well as median and percentiles (without interpolation) are permissible. Moreover, the ordinal scale is considered invariant under monotone transformations, i.e., order-preserving transformations. This concept was extended in [25], which suggests the usage of non-parametric statistics for ordinal data. In contrast, for interval scales, which additionally require the determination of equality of intervals or differences, further statistics are permissible, such as the mean, standard deviation, and product-moment correlation coefficients, as well as parametric methods.
Having defined the basic terminology, the reader is encouraged to follow the dispute in chronological order. From the huge amount of available works in many disciplines, such as psychology, psychometrics, medicine, statistics, education, and social sciences, the review in [9], the purely statistical perspective in [26], the corresponding reply from a measurement perspective in [27], and the reviews in [10,11,12] are highly recommended. They cover most of the arguments regarding the level of rating scales and the appropriate statistical methods.
Level of rating scales
The first aspect of the dispute is the level of the rating scale. Here, most works agree that a single rating scale with a set of ordered, labeled alternatives has to be considered ordinal, e.g., [28,29,30]. The most confusion arises from the different terminology of each work, especially regarding the often misleading usage of the term “(Likert) scale” for a multi-item questionnaire. In contrast to single items, which are considered ordinal, multiple items are often considered to produce interval or ratio data, e.g., [31, 32]. Please recall the above definition that, in this work, the term “scale” refers to the measurement/rating scale of a single experiment/item/stimulus. This is in line with the typical usage in QoE studies as the rating scale, on which the experience with a single stimulus is rated.
Only [33] found in direct comparison to a visual analog scale (VAS) that interval data could be generated from a single rating scale, however, they noted that this effect could be due to the particular format of their experiment. Also [34] confirmed a high correlation to VAS, but points to works that even VAS could be considered an ordinal scale, e.g., [35]. [12] noted that adjectival scales were ordinal, but it was concluded from related experiments on the mental representation of numbers in [36, 37] that numerical scales with five or more categories could be considered interval. However, no results from dedicated studies were given to support this statement.
Considering the normality of obtained ratings, which is often a requirement for certain parametric statistics, the argument of [26] was that if the obtained data followed a normal distribution, then the data would be of interval scale nature because the intervals between any data points were known in terms of probability, i.e,. areas under the curve. However, as [38] replied, the issue here was that without knowing the exact nature of distances between scale points, the concept of normality of distribution became meaningless.
Focusing on the distance between rating categories, there are many works that emphasize the ordinal character of rating scales. The review in [39] stated that ordinal scores have unequal intervals, and [40] noted that, even in presence of numbers, which are an equidistant sequence, the subjective interpretations of the rating scale labels were nonlinear. [16] reviewed related works and concluded that the differences between the rating categories might be different for each participant. More detailed descriptions and visualizations of the biases in quantifying judgments are given in [13].
These statements are supported by dedicated studies. [41] found that the distances between the points of one single 7-point rating scale were not equal. Participants reported bigger differences between the extreme as compared to the moderate categories. The presented study was a repetition of a previous study [42], which also found that categories are not equidistant. Also two other studies found from direct comparison to a VAS that the categories of a 7-point [43] and a 5-point rating scale [35], respectively, were not equidistant. [14, 15] presented similar findings for audio quality studies.
To sum up the presented arguments, there is clear evidence that single rating scales cannot be considered interval scales, and the manner or extent to which given data deviate from an interval scale cannot be known. Thus, treating ordinal data as interval data in statistical analyses involves possible errors, and researchers typically cannot determine the extent to which such errors are being made [44]. In the next subsection, this aspect is investigated in more detail.
Meaningful statistics
As stated in [45], measurement theory is important to the interpretation of statistical analyses. It was argued that the use of inappropriate statistics lead to the formulation of statements which are either semantically meaningless or empirically non-significant [46]. However, there is a huge dispute about the applicability of the level of measurements to statistics as recommended by Stevens [24]. This especially includes parametric statistics, i.e., statistics which assume that the data stem from a family of probability distributions with a fixed set of parameters. An example is Student’s t-test, which assumes that the mean follows a normal distribution. As the distribution parameter, e.g., mean, has to be estimated from the data, at least interval data would be required for parametric statistics according to Stevens.
Some gave counterarguments noting that statistics applied only to numbers [47], and that there was a difference between measurement theory, i.e., meaning of numbers, and statistical theory, i.e., relation of numbers [26, 48]. It was argued that, as numbers were naturally on a ratio scale, all statistics were permissible. In that sense, many works experimentally confirmed the applicability and robustness of parametric statistics to monotone transformations of ordinal data, e.g., with respect to t-test [49], F-test/ANOVA [26, 48, 50], or correlations [30, 38, 51, 52]. Nevertheless, there was an early warning in [53] that while the violation of one assumption did not appreciably alter the test, the violation of two or more assumptions frequently did have a marked effect.
However, it was also found that in functional analysis where partial regression coefficients were calculated, ordinal statistical tests cannot be interchanged with interval ones [54]. Moreover, it was suggested that the early studies underestimated the magnitude of violations in data [55], and errors and dangers in practical applications were pointed out [56]. [57] found that also ANOVA was not invariant to monotone transformations leading to inconsistent results. In a simulation study, [58] found that correlations between continuous ratings and discrete ratings were high when the underlying distribution was symmetric, but low when it was skewed. Also [20] showed false alarms, misses, and inversions when applying metric models to ordinal data. [59] summarized robustness studies with respect to t- and F-test. It was noted that previous robustness studies mostly focused on ordinality, discreteness, nonlinearity, and skewness, but often neglected ceiling and floor effects, which could be a co-occurrence of the former concepts. Ceiling and floor effects were shown to increase bias and uncertainty, which caused inferior performance of t- and F-test. To overcome the problems caused by ceiling and floor effects, rank-based tests and generalized linear models were recommended [59], which already were applied in a QoE study [60]. Here, probability distributions were estimated per QoE category as a function of independent variables, e.g., link capacity, which, thus, can serve as a QoE model for a technical system.
Many works found that the data obtained from rating scales in fact cannot be considered normal and also often violated other typical assumptions for parametric statistics. [61] found a bias towards the left side of scale and pointed to more works which studies this effect. [40, 62] described three “form-related errors” resulting from subjects’ psychological reactions to different item formats in questionnaires: leniency (the tendency to rate either too high or too low); central tendency (reluctance to rate at the extremes); and proximity (the tendency to rate similarly for questions occurring close to one another in the survey). Also [11] noted that rating data was often skewed or had floor or ceiling effects, and that normality checks necessitated post hoc selection of inference procedures. Moreover, they highlighted the low statistical power of normality tests with small sample sizes. [63] noted that ordinal data were not continuous and normally distributed, which created problems for many statistical procedures, especially since ratings just used a small number of choices but standard statistical tools assumed a continuous variable [40].
Noticing these problems, which [39] traces back to classical test theory, some works suggest to rely on other theories, such as item-response theory, which allows to construct interval data from ordinal rating scores, e.g., using the Rasch model, as input to parametric statistics [39, 63,64,65].
Another approach to avoid the issues of applying parametric statistics to ordinal data is using non-parametric statistics [12, 25, 66, 67]. In contrast to parametric statistics, non-parametric statistics are not based on assumptions about the family of probability distributions of the data. For example, the Mann-Whitney U test is a non-parametric test to investigate whether two independent samples were selected from populations having the same distribution.
The application of non-parametric statistics preserves the ordinal nature of the rating data, and was thus favored by followers of Stevens’ arguments. [68] even called the usage of parametric statistics for ordinal data a sin. More constructively, [9] noted that the transition from meaningful assertions about numbers to meaningful assertion of concepts required to consider the scale, and [54] emphasized that assumptions regarding the measurement level of the data and the corresponding analysis to be used affected the conclusions. [27] stated that the measurement scale gave meaning to numbers and showed examples of scale transformations that changed statistical properties. Also [35] endorsed that numerical statements of rating scales should not be generalized to interpretations of the ordinal variable.
The early concern that non-parametric statistics were less powerful [57, 63] was countered by several works, e.g., [57, 69]. Instead, many works highly recommended the application of non-parametric statistics for ordinal data, such that several appropriate methods can be found in [11, 70,71,72,73].
To sum up, some works suggested that parametric statistics could be applied to ordinal data as they were robust to mild violations of their assumptions [30], however, the analysis might only investigate the relation of the numbers, but not the meaning of the numbers [26]. In contrast, some works emphasized that ordinality, discreteness, nonlinearity, skewness, as well as ceiling and floor effects in rating data [59] would create problems for many parametric statistical procedures [40]. The clean way out of this dilemma – without having to switch to other study designs or other rating scales, without having to separate measurement theory (meaning of numbers) and statistical theory (relation of numbers), and without having to hope for robustness when violating assumptions of parametric statistics – is to rely on statistical methods that can handle ordinal data. Thus, in this article, existing and novel methods for ordinal data will presented, which are well suited for the domain of QoE research.
QoE assessment and modeling
A comprehensive definition of QoE was given in [1] including influence factors of QoE, such as human, system, and context influence factors. However, it was not specified how QoE assessment should be conducted. After a variety of practical implementations in a multitude of studies, cf., e.g., [74,75,76,77], an overview document was provided in [78], which links to several recommendations for QoE assessment for particular services, such as speech [2], web browsing [79], or multimedia applications [4]. Here, [78] names MOS as a QoE metric, although it recognizes that test methods can be classified according the applied scaling method and scale level, i.e., nominal, ordinal, interval, and ratio. However, the linked documents might lack this awareness, such as [2, 4], which recommend the usage of the 5-point ACR scale, from which MOS, confidence intervals, and standard deviations shall be computed. However, as the ACR scale is an ordinal scale, but not an interval scale, these metrics are not interpretable without introducing substantial bias. As an alternative method for QoE assessment, [18] compared the classical assessment of user satisfaction based on MOS with the notion of acceptability of service quality. Evaluation methods are reviewed and differences between both perspectives on QoE assessment are discussed.
Substantial contributions towards improving QoE assessment beyond the MOS were started in [80], which emphasizes that MOS values lose considerable amount of information about the QoE ratings. To overcome this issue, the authors suggested to additionally consider the standard deviation of opinion scores (SOS). However, SOS values face the same substantial bias as MOS, as it is implicitly assumed that the rating scale of user experience is an interval scale. The work in [80] was extended in [81], in which quantiles, entropy, and probability distribution were added to a recommended set of QoE descriptors. In contrast to MOS and SOS, the newly added descriptors do not face the issues that were previously discussed. Additionally, [81] postulated the idea that individual ratings for a single test condition can be described as realizations of a binomial distribution. [82] continued the previous works and elaborated more on the value of quantiles and acceptance thresholds, such as percentage of Poor-or-Worse (%PoW) and Good-or-Better (%GoB). [83] modeled an individual user rating with a truncated normal distribution. Most recently, the concept of QoE was extended to QoE fairness [84], i.e., the notion that users in a shared system should experience a fair QoE distribution. The proposed fairness metric is based on the standard deviation of individual QoE ratings, which is again the SOS. Thus, the fairness metric also inherits the problems of SOS, which were described above.
Finally, there has not been much work towards QoE modeling beyond the MOS. [85] reaches out to the QoE of entire technical systems, which includes the formulation of analytical relationships between QoE distributions to derive system-wide QoE metrics of interest. However, full knowledge of the QoE distributions at any value of the parameter of the technical system is required or needs to be approximated by a model to obtain the system QoE distribution, which describes an aggregated experience over the whole domain of the technical parameters. A first approach was presented in [60], which applied generalized linear models in a QoE study to obtain probability functions for each rating category, but did not consider a multinomial QoE distribution.
Both meaningful QoE assessment and the modeling of QoE based on multinomial QoE distributions, which are missing in related works, will be addressed in the remainder of this article.
Theoretical background on QoE distributions
This section introduces QoE distributions as a subset of multinomial distributions and shortly recaps the theoretical background. Afterwards, it is outlined how previously used MOS-based evaluations could be obtained from QoE distributions. However, except for some backward compatibility, this would not be recommended due to the inherent bias when applied to QoE ratings on ordinal scales.
Multinomial distributions
In this article, the typical pitfall of QoE assessment is avoided by considering that all ratings of a test condition follow a multinomial distribution on the ordinal rating categories, which also takes a more holistic perspective of the subjective user study. Multinomial distributions describe probabilities in an experiment where n balls are drawn with replacement from a bag with balls of k different colors. The probability that a ball of color i is drawn is \(p_i\) with \(\sum _{i=1}^k p_i = 1\). The random variables \(X_i\) count how often a ball of color i is drawn. Then, the probability mass function of the multinomial distribution is given as:
Thus, Eq. 1 describes the joint probability for all \(i=1,\ldots ,k\) that in an experiment, in which n balls are drawn with replacement, \(X_i=x_i\) balls are drawn with color i.
QoE Distributions
This experiment, which constitutes multinomial distributions, can be easily mapped to QoE studies, in which n participants rate the QoE of a stimulus. There are k categories on the rating scale, and the numbers \(X_i\) count the participants, which rate category i. The parameters \(p_i\) describe the underlying and hidden probability that the presented stimulus gives an experience in category i. In case of the 5-point ACR scale [2, 4], which is the most widely used rating scale in QoE studies, \(k=5\) and i represents the numerical value assigned to the rating categories, namely, “bad” (\(i=1\)), “poor” (\(i=2\)), “fair” (\(i=3\)), “good” (\(i=4\)), and “excellent” (\(i=5\)). However, QoE distributions can be constructed from any number of ratings categories, such as \(k=2\) (binary satisfaction/acceptance [18]) or \(k=9\) (nine-grade numerical quality scale [4]). In the remainder of this work, only \(k=5\) will be considered, such that all methods are directly applicable to QoE studies based on the 5-point ACR scale. Note that some formulae, which are presented in this article, have to be modified accordingly if another number of categories k is used.
Thus, the result of a QoE study is a rating distribution \({\varvec{x}} = (x_1, x_2, x_3, x_4, x_5),\ x_i \ge 0,\ i=1,\ldots ,5,\) based on \(n=\sum _{i=1}^5x_i\) participants. It is important to note that the rating distribution \({\varvec{x}}\) is a realization of an underlying QoE distribution \({\varvec{p}} = (p_1, p_2, p_3, p_4, p_5)\) with \(p_i\ge 0, i=1,\ldots ,5\) and \(\sum _{i=1}^5p_i=1\), which comprise a subset of multinomial distributions. As each and every rating, which was collected in the QoE study, is included in \({\varvec{x}}\), this representation does not lead to any information loss.
The vector notation \({\varvec{x}}\) of the rating distribution is a very compact and concise way to report the results of a QoE study. From this representation, also the underlying parameters of the QoE distribution \(p_i\) can be estimated using a maximum likelihood approach, which allows to fully make use of the advantages of considering QoE distributions. For this, the estimated parameters \({\hat{p}}_i\) can be obtained as:
Following Eq. 2, the outcome of a QoE study can also be reported with another compact representation \(\varvec{{\hat{p}}} = ({\hat{p}}_1, {\hat{p}}_2, {\hat{p}}_3, {\hat{p}}_4, {\hat{p}}_5, n)\), from which one of the \({\hat{p}}_i\) could be omitted as \(\sum _{i=1}^5 {\hat{p}}_i = 1\). Obviously both representations \({\varvec{x}}\) and \(\varvec{{\hat{p}}}\) can be easily converted into the other representation. This also means that, given the study size n, the results of a QoE study can be identified by a multinomial distribution \({\hat{p}}_i\), as there is a trivial mapping via Eq. 2.
Note that the maximum likelihood approach in Eq. 2 results in a point estimate for the underlying unknown QoE distribution, and thus, the estimated multinomial distribution with parameters \({\hat{p}}_i\) might be different from the actual underlying multinomial distribution with parameters \(p_i\). Nevertheless, the estimated multinomial distribution \({\hat{p}}_i\) is the most probable multinomial distribution given the observed results of the QoE study, and the discrepancy between \({\hat{p}}_i\) and \(p_i\) can be diminished by increasing the sample size n.
The presented aspects of multinomial distributions so far apply to any categorical scale. However, QoE distributions additionally consider the ordinal nature of the rating scale, which means that the order of all categories i is fixed and monotonically increasing in terms of QoE. Without loss of generality, it is assumed that the index i follows the natural numbers from 1 to \(k=5\), and it is assigned to each rating category, such that categories with a better experience have a higher index value. For example, see the mapping of the categories of the 5-point ACR scale from bad QoE (\(i=1\)) to excellent QoE (\(i=5\)) above. Consequently, the order of the corresponding \(x_i\) in \({\varvec{x}}\), or \({\hat{p}}_i\) in \(\varvec{{\hat{p}}}\), is fixed, as already indicated by the tuple notation. This allows to relate each \({\hat{p}}_i\) with the probabilities of preceding categories as follows: Let \(\varvec{{\hat{c}}} = ({\hat{c}}_1, {\hat{c}}_2, {\hat{c}}_3, {\hat{c}}_4, {\hat{c}}_5, n)\) be the vector containing cumulative probabilities computed from \(\varvec{{\hat{p}}}\), i.e., \({\hat{c}}_i = \sum _{j=1}^i {\hat{p}}_j\). Then, \({\hat{c}}_i\) gives the probability of obtaining a rating of at most category i, which is intuitively based on the ordinal nature of the categories, but does not consider any differences between the categories. Note that \(\varvec{{\hat{c}}}\) is also a representation equivalent to \({\varvec{x}}\) and \(\varvec{{\hat{p}}}\).
This compact representations allows to compute quantiles easily, which are a meaningful metric for ordinal scales. Thus, the q-quantile \(Q_q\) is the category i given by:
Moreover, it is possible to directly compute a more intuitive percentage of Poor-or-Worse (%PoW) and Good-or-Better (%GoB), which is different from the previous definition based on the E-model [82]. This means, it is possible to literally obtain the %PoW as the percentage of users who rated the category “poor” (2) or worse, i.e., “bad” (1), and also the %GoB as the percentage of users who rated the category “good” (4) or better, i.e., “excellent” (5):
Note that, based on the parameter estimation in Eq. 2, if the context is unambiguous, the term QoE distribution might also be used for a rating distribution \({\varvec{x}}\), \(\varvec{{\hat{p}}}\), or \(\varvec{{\hat{c}}}\), which is a realization of a QoE distribution \({\varvec{p}}\) or \({\varvec{c}}\).
Backward compatibility towards MOS-based evaluations
Although MOS-based evaluations face the issues described above, for the sake of backward compatibility, MOS-based QoE metrics can be computed from QoE results expressed as rating distributions. In the following, these computations are outlined briefly.
First, the sample mean of ratings, or MOS value, can be obtained from \({\varvec{x}}\) or \(\varvec{{\hat{p}}}\) as follows:
The sample standard deviation of ratings, or SOS value [80], is given by:
The confidence interval (CI) of the MOS for a confidence level of \(1-\alpha\) can be computed for large enough n (cf. central limit theorem) using the \((1-\frac{\alpha }{2})\)-quantile of the standard normal distribution \(z_{(1-\frac{\alpha }{2})}\):
Note that for small sample sizes, the standard normal distribution should be replaced by Student’s t-distribu-tion. However, [86] generally considers a sample size greater than 25 or 30 as sufficient for using the standard normal distribution. By substituting a desired CI width d in the error margin \(\frac{d}{2} = z_{(1-\frac{\alpha }{2})}\frac{SOS}{\sqrt{n}}\) of Eq. 7 and solving for n, also required sample sizes \(n_S\) can be easily obtained:
Finally, also the QoE fairness index F [84], which was proposed to quantify the fairness of the QoE among multiple users in a shared system in terms of the dispersion of the QoE distribution, can be obtained as:
Given the inherent bias of these MOS-based evaluations, in the following, improved QoE evaluations will be presented, which leverage the advantages of QoE distributions.
Statistical methods for QoE distributions
This section summarizes existing and novel statistical methods of QoE distributions, which give more meaningful QoE evaluations based on the ordinal rating scales of QoE studies. These methods solely require categorical or ordinal data, but do not assume interval or even ratio data. To demonstrate the improved evaluations, the ratings for three stimuli \(S_1\), \(S_2\), and \(S_3\) are considered, which have been collected in a past crowdsourcing QoE study and have been filtered to exclude unreliable ratings [87]. In this study, the participants watched short video clips of 30s, which included a number of stalling events from 0 to 6 with different lengths. Note that more details to this study were reported in [88]. Three exemplary rating distributions are taken from this study and described in Table 1. The number of stalling events for these stimuli differ, however, the length of a stalling event was always 4s, and the stalling events were regularly spaced within the video. Table 1 shows that \(S_1\) (condition: more than four stalling events) has a significantly lower MOS than the other stimuli, but the highest fairness score. \(S_3\) (condition: one stalling event) has a higher MOS than \(S_2\) (condition: two stalling events), but the 95% CIs overlap, and the fairness score is lower for \(S_2\). The rating distributions of \(S_1\) (black), \(S_2\) (dark brown) and \(S_3\) (light brown) are also visualized in Fig. 2 as PDFs (\(\varvec{{\hat{p}}}\), bars) and CDFs (\(\varvec{{\hat{c}}}\), dashed lines).
Confidence intervals and sample size
After a QoE study has been conducted, the parameters of the multinomial QoE distribution can be estimated from the collected ratings in a maximum likelihood fashion using Eq. 2. In the following, different methods are presented, which allow to compute confidence intervals (CIs) for these parameter estimations. If the width of a CI is fixed before a QoE study, the methods also allow to compute the minimal amount of ratings needed for the desired CI width, i.e., the sample size. This can be helpful to plan in advance how many participants should be recruited for a QoE study.
Binomial confidence intervals for the parameters \(p_i\) of the QoE distribution
Equation 2 described the maximum likelihood estimation of each of the parameters \(p_i\) of the QoE distribution. To obtain confidence intervals, a binomial confidence interval can be computed for each parameter \(p_i\) individually for large enough n based on an approximation with the normal distribution (cf. central limit theorem):
This and further methods for binomial CIs were compared in [89]. Note again that, if the sample size is small, the standard normal distribution should be replaced by the Student’s t-distribution. According to [86], a typical rule of thumb is that n is sufficiently large to use the standard normal distribution if \(n\cdot {\hat{p}}_i\ge 5\) and \(n\cdot (1-{\hat{p}}_i)\ge 5\). Eq. 10 results in five confidence intervals for each parameter \(p_i\) of the QoE distribution. In Table 2, the 95% CIs are computed for each stimulus \(S_1\), \(S_2\), and \(S_3\). Some CIs for the same parameter do not overlap, which indicates that there is significant difference for this parameter on a significance level of 5%, e.g., for \(p_1\) between \(S_1\) and the other two QoE distributions, or for \(p_4\) between \(S_2\) and \(S_3\). Note that computing five CIs from the same data faces the multiple comparisons problem. This means that the global coverage probability for all CIs will be lower than the desired \(1-\alpha\) of each individual CI (cf. Bonferroni inequalities), however, this problem can be compensated, e.g., by using Bonferroni correction. For this, the five individual CIs have to be computed with a confidence level
to reach a global coverage probability of \(1-\alpha\). For the considered example, Table 2 also shows the larger \(CI^{0.99}_{p_i}\), which reach a global confidence level of 95%.
Equation 10 also allows to compute sample sizes \(n_{S_i}\) for a desired width \(d_i\) of \(CI^{1-\alpha }_{p_i}\) with confidence level of \(1-\alpha\), which gives \(CI^{1-\alpha }_{p_i} = \left[ {\hat{p}}_i-\frac{d_i}{2};{\hat{p}}_i+\frac{d_i}{2}\right]\) with half-length \(\frac{d_i}{2}\):
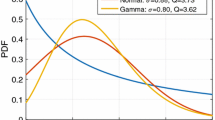
After the sample sizes \(n_{S_i}\) have been computed with a desired width \(d_i\) for all parameters \(p_i\), the maximum sample size \(n_S=\max _i{n_{S_i}}\) should be used as the sample size of the entire QoE study. For the considered stimuli, a desired CI width of \(d=0.1\) would result in \(n_S=355\) for \(S_1\), \(n_S=370\) for \(S_2\), and \(n_S=328\) for \(S_3\) using \(CI^{0.95}_{p_i}\) considering an individual confidence level of 95% for each CI, and \(n_S=612\) for \(S_1\), \(n_S=639\) for \(S_2\), and \(n_S=567\) for \(S_3\) using \(CI^{0.99}_{p_i}\) for a global confidence level of 95% based on the Bonferroni correction, see Table 2.
Simultaneous confidence intervals for the parameters \(p_i\) of the QoE distribution
Instead of computing binomial CIs for each parameter \(p_i\) of the QoE distribution one-at-a-time, i.e., pointwise, there exist also methods to compute simultaneous CIs. The advantage of simultaneous CIs is that they allow to control the coverage probability for the entire set of parameters [90], which is typically less conservative than the Bonferroni correction. The approach presented by Goodman [91] constructs simultaneous CIs for a multinomial distribution with k categories using the \((1-\frac{\alpha }{k})\)-quantile of the chi-square distribution with one degree of freedom. Thus, for QoE distributions with five categories, the \((1-\frac{\alpha }{5})\)-quantile of the chi-square distribution with one degree of freedom \(\chi ^2_{(1-\frac{\alpha }{5}), 1}\) has to be used:
Goodman intervals are recommended when the the expected counts are at least 10 per category and the number of categories is small [90], which is the case for QoE distributions. The results of the simultaneous CIs for the exemplary QoE distributions \(S_1\), \(S_2\), and \(S_3\) can be found in Table 2. It can be observed that simultaneous CIs are generally larger as the binomial 95%-CIs, which is an expected finding. The reason is that with simultaneous CIs, the probability \(1-\alpha\) must hold for all individual CIs to contain their respective parameter at the same time, which leads to larger CIs. Moreover, it has to be noted that Goodman CIs are not symmetric around the observed \({\hat{p}}_i\), which accounts for the skewness of the multinomial distribution, and they tend to extend towards parameter regions with high variance, i.e., towards 0.5. This can also be seen in Table 2. Except for \({\hat{p}}_i\) of \(S_1\), which is above 0.5, for all three stimuli and all parameters, the Goodman CIs are quite close to the binomial 95%-CIs at the lower bound of the CI, but they are particularly relaxed at the upper bound of the CI. If the estimated parameter is above 0.5, such as for \({\hat{p}}_1\) of \(S_1\), the opposite trend can be observed.
Again, Goodman CIs can be used to determine the required minimal sample size \(n_S\) necessary to achieve a specified coverage probability \(1-\alpha\) for a given volume D of the confidence region. In a simple algorithmic approach, CIs can be calculated for increasing n using the Goodman formula in Eq. 13. Note that when n increases in Eq. 13, also the \(x_i\) have to be updated: \(x_i = {\hat{p}}_i\cdot n\). At each step the current volume is computed from the current widths \(d_{i, (G)}(n)\) of \(CI^{1-\alpha }_{p_i, sim.(G)}\), which obviously depend on n. This gives the sample size
For the considered stimuli, a desired volume of \(D=(0.1)^5=10^{-5}\) would result in \(n_{S(G)}=167\) for \(S_1\), \(n_{S(G)}=286\) for \(S_2\), and \(n_{S(G)}=358\) for \(S_3\), see Table 2. These sample sizes behave different than the numbers obtained with binomial confidence intervals. The reason is that, in the binomial approach, the sample size was determined by the number of samples required to confine the width of the CI of the parameter with the highest variance, e.g., \(p_1\) for \(S_1\). In contrast, as the volume of simultaneous CIs is a product of all CI widths, it will become small when more parameters have more extreme values, and thus, a low variance and a small CI width, e.g., \(p_3, p_4, p_5\) in \(S_1\). Thus, the required sample size will be smaller for simultaneous CIs in this case.
If all simultaneous CIs shall be constrained to a maximum width of d, Eq. 14 changes to:
As can be seen in Table 2, for a desired maximum width \(d=0.1\), the trend of the results is again in line with the sample sizes computed from binomial CIs. However, slightly lower numbers can be observed compared to the binomial 99%-CIs, namely, \(n_{S(G)}=606\) for \(S_1\), \(n_{S(G)}=633\) for \(S_2\), and \(n_{S(G)}=561\) for \(S_3\).
Another approach to simultaneous CIs was presented by Sison and Glatz in [92] following a parametric bootstrap approach. If the expected counts are small and nearly equal across categories, [90] recommended this method over Goodman CIs, however, the intervals are harder to construct. The presented approach iteratively increases the CIs with respect to an integer c until the desired coverage probability \(v(c) = P(x_i-c\le X_i\le x_i+c, i=1,\ldots ,5)\approx 1-\alpha\) for the multinomial distribution \(X_i\) is reached. The method is based on Poisson distributions \(V_i\) with mean \(x_i\), and their truncations \(Y_i\) to the interval \([b_i; a_i]\) with mean \(E[Y_i]=\mu _i\), variance \(Var[Y_i] = \mu _{2,i} = \sigma _i^2\), and rth central moments \(\mu _{r,i}\). Then, for the computation of v(c), the following approximation is used:
where
using \(\gamma _1=\frac{1}{\sqrt{5}}\frac{\frac{1}{5}\sum _{i=1}^5\mu _{3,i}}{(\frac{1}{5}\sum _{i=1}^5\sigma ^2_i)^{3/2}}\) and \(\gamma _2=\frac{1}{\sqrt{5}}\frac{\frac{1}{5}\sum _{i=1}^5\mu _{4,i}-3\sigma _i^4}{(\frac{1}{5}\sum _{i=1}^5\sigma ^2_i)^{2}}\), and the required central moments \(\mu _{r,i}\) can be derived according to [93] as:
Equation 18 requires the Stirling number of the second kind [94]
and a formula for the factorial moments given in [92]:
The approximation in Eq. 16 can evaluate v(c) by setting \(b_i=x_i-c\) and \(a_i=x_i+c\). Then, the integer c is iteratively increased until a value is found, such that \(v(c)< 1-\alpha < v(c+1)\), and the simultaneous confidence intervals are given by:
Sison/Glatz CIs are almost symmetric around the observed \({\hat{p}}_i\), except for a skewness correction at the upper bound. The resulting CIs for \(S_1\), \(S_2\), and \(S_3\) are reported in Table 2. It can be seen that in this exemplary study, the CIs are wider than Goodman CIs, which is a worse performance. However, according to [95], the advantage of the Sison/Glatz CI is especially evident in the sample size determination problem.
For this, Sison/Glatz follow a different approach by decomposing the given volume D as \(D=(2\frac{d}{2})^5\), which gives \(d=\frac{\root 5 \of {D}}{2}\) as the maximum width of each CI. At each iteration of their algorithm, Eq. 16 is used to compute
until the desired confidence level is reached. The resulting sample size \(n_{S(SG)}\) is given by:
As this algorithm forces all CIs to have at most width d at the same time, it requires a higher number of samples as in the binomial approach presented first, however, the resulting sample sizes are typically much smaller than those using Goodman CIs. This can also be observed for the exemplary rating distributions, for which the Sison/Glatz sample sizes are \(n_{S(SG)}=597\) for \(S_1\), \(n_{S(SG)}=526\) for \(S_2\), and \(n_{S(SG)}=477\) for \(S_3\).
Confidence intervals for the parameters \(c_i\) of the cumulative QoE distribution
With respect to cumulative QoE distributions \({\varvec{c}}\), there are again the options to compute either pointwise or simultaneous CIs. In the pointwise case, each CI for \(c_i\) can be based on the binomial distribution considering the probability that users rated at most category i. This allows to reuse Eq. 10. The only required modification is to replace \({\hat{p}}_i\) with \({\hat{c}}_i\):
Note that when computing CIs for cumulative QoE distributions, it is not useful to compute a CI for \(c_5\), because \(P(c_5=1)=1\) by definition of the QoE distribution. Table 3 shows the \(CI^{0.95}_{c_i}\) for the three exemplary rating distributions. It can be seen that the CIs for \(c_1\) are obviously identical to the CIs for \(p_1\) in Table 2 as \(p_1=c_1\). Moreover, it can be seen that the cumulative CIs can overlap, e.g., for \(c_2\) and \(c_3\) in \(S_1\). When constructing multiple CIs from the same data, again the Bonferroni correction has to be applied to control the global confidence level. Table 3, thus, also shows the larger \(CI^{0.9875}_{c_i}\), which reach a global coverage probability of 95% for the four CIs. However, it has again to be noted that the CIs only guarantee this coverage probability pointwise, i.e., for each cumulative probability individually.
The required sample sizes \(n_S\) can be likewise computed using Eq. 12, again replacing \({\hat{p}}_i\) with \({\hat{c}}_i\), and taking the maximum of the sample sizes for each \(c_i\). For the exemplary stimuli and a desired CI width \(d=0.1\), this results in \(n_S=351\) for \(S_1\), \(n_S=375\) for \(S_2\), and \(n_S=373\) for \(S_3\) using \(CI^{0.95}_{c_i}\) considering an individual confidence level of 95% for each CI, and \(n_S=575\) for \(S_1\), \(n_S=608\) for \(S_2\), and \(n_S=605\) for \(S_3\) using \(CI^{0.9875}_{c_i}\) for a global confidence level of 95% based on the Bonferroni correction, see Table 3.
When it comes to simultaneous confidence intervals, the Dvoretzky–Kiefer–Wolfowitz inequality [96, 97] can be leveraged to compute a confidence band from the empirical distribution function \(\varvec{{\hat{c}}}\), which gives simultaneous bounds for the cumulative probabilities. The confidence band is symmetric around \(\varvec{{\hat{c}}}\) and can be computed as follows:
Note again that the simultaneous CIs are typically wider than the pointwise CIs, and that the above comment on the CI for \(c_5\) applies here as well. Table 3 shows the \(CI^{0.95}_{c_i, sim.(DKW)}\) for \(S_1\), \(S_2\), and \(S_3\). It can be seen that the resulting CIs are larger than \(CI^{1-\alpha }_{c_i}\), which is as expected. The half-length of the \(CI^{0.95}_{c_i, sim.(DKW)}\) is only depending on the number of ratings n and the significance level \(\alpha\), and thus, allows to easily compute the required sample size \(n_{S(DKW)}\) for a desired maximum width d of each CI:
Consequently, the sample size is independent of the actual QoE distribution, which can be seen in Table 3, where the required sample size to reach a CI width of \(d=0.1\) is \(n_{S(DKW)}=738\) for all three exemplary QoE distributions.
This section presented methods for the computation of confidence intervals and sample sizes. In contrast to MOS-based evaluations, multinomial QoE distributions have five parameters \({\hat{p}}_i\) or four parameters \({\hat{c}}_i\), which have to be estimated from the rating data. Different methods for pointwise (i.e., one by one) and simultaneous (i.e., all at the same time) confidence intervals have been presented. These methods further allow to compute sample size for the desired width of a confidence intervals. This means, given a desired width of the confidence interval, the presented methods can be used to compute the minimum number of ratings that need to be collected. Thus, these methods are especially useful in the design phase before conducting a QoE study.
Testing for significant QoE differences
QoE studies are often conducted when researchers are interested whether two or more stimuli give different experience to users. Thus, they present the stimuli to the participants, which return ratings according to their experience. After the rating distribution of each stimulus has been obtained, it has to be tested if there is a significant difference between them. The null hypothesis is that all realizations, i.e., all observed rating distributions, were drawn from the same QoE distribution. The p-value is the probability of facing the observed or more extreme realizations assuming that the null hypothesis was true. If the p-value is below the significance level \(\alpha\), which is the maximum acceptable probability of a type I error that was selected by the researchers, the null hypothesis is rejected, and thus, the QoE distributions are considered as being significantly different.
Independent groups of ratings
While many non-parametric statistical tests exist, which compare two probability distributions, the Wilcoxon-Mann-Whitney U test [98, 99] should be considered for ordinal data [25] if the groups of ratings are independent, e.g., if they were collected in different QoE studies or from different participants. It computes the U statistic from the ranks of the ratings in both QoE distributions A and B, considering the number of tied ranks \(t_i = x^A_i + x^B_i\). In the following, the formulae are given for computing the U statistic of distribution A only, however, they equally apply for distribution B. First, the sum of ranks \(R_A\) has to be computed:
Then, the \(U^A\) statistic of a QoE distribution A can be easily computed from the sum of ranks \(R^A\) and the number of samples \(n^A\) as follows:
The smaller value of \(U^A\) and \(U^B\) is used and its significance can be looked up in dedicated tables. For large samples, the standardized value \(z_U=\frac{U-\mu _U}{\sigma _U}\) with mean \(\mu _U=\frac{n^A\cdot n^B}{2}\) and tie-corrected standard deviation
approximately follows a standard normal distribution, and thus, can be compared to the critical values \(\pm z_{(1-\frac{\alpha }{2})}\). In the considered QoE study, the p-value for the Wilcoxon-Mann-Whitney U test between \(S_2\) and \(S_3\) is 0.04 (two-tailed), i.e., the null hypothesis that both QoE distributions are equal has to be rejected on a significance level of \(\alpha = 5\%\). The p-values between \(S_1\) and \(S_2\) and between \(S_1\) and \(S_3\) are much smaller (\(<10^{-7}\)), thereby, also indicating significant differences.
Note that, similar to the construction of multiple confidence intervals, conducting multiple hypothesis tests on the same data also faces the multiple comparisons problem. Thus, in this case, also a correction method has to be applied in order to avoid the inflation of the probability of a type I error (\(\alpha\)), such as the Bonferroni correction (cf. Sect. 4.1.1) or the Holm-Bonferroni method [100]. For the latter, consider that all m tested hypotheses are sorted according to their p-values from lowest to highest: \(p_{(1)},\ldots ,p_{(m)}\). For the given global significance level \(\alpha\), let j be the minimal index, such that
Then reject all \(j-1\) hypotheses with p-value lower than \(p_{(j)}\), and do not reject all hypotheses with p-value greater or equal to \(p_{(j)}\). If \(j=1\), do not reject any hypothesis, and if no j exists, reject all hypotheses. This procedure ensures that the global significance level, i.e., probability of a type I error, is less or equal than \(\alpha\). Thereby, the Holm-Bonferroni method shows a lower increase of the probability of a type II error compared to the classical Bonferroni correction.
When comparing a set \({\mathcal {A}}\) of multiple QoE distributions with \(|{\mathcal {A}}| > 2\), the Kruskal-Wallis test [101], which is the one-way analysis of variance (ANOVA) on ranks, can be used if the groups of ratings are independent. It is a non-parametric test for ordinal data, which is similar to the Wilcoxon-Mann-Whitney U test. Again, the sum of ranks for each QoE distribution \(A\in {\mathcal {A}}\) have to be computed considering the the number of tied ranks \(t_i = \sum _{A\in {\mathcal {A}}}x^A_i\) among all QoE distributions in \({\mathcal {A}}\), cf. Eq. 27. Then, the test statistic H can be computed as follows:
where \(N = \sum _{A\in {\mathcal {A}}}n^A\) is the sum of all ratings in all compared QoE distributions. The significance of the test statistic H can then be looked up in dedicated tables. For large samples, H approximately follows a chi-square distribution with \(|{\mathcal {A}}|-1\) degrees of freedom. When comparing the three exemplary QoE distributions \({\mathcal {A}} = \{S_1,S_2,S_3\}\), the Kruskal-Wallis test rejects the null hypothesis that all three QoE distributions are equal with a p-value \(<10^{-11}\). This was expected as already the Wilcoxon-Mann-Whitney U test rejected all hypotheses that any two QoE distributions in \(\{S_1,S_2,S_3\}\) were equal.
Dependent groups of ratings
If the groups of ratings are dependent, e.g., if the same participants rated different stimuli in a single QoE study, the Friedman test [102, 103] can be used to compare a set \({\mathcal {A}}\) of QoE distributions with \(|{\mathcal {A}}| \ge 2\). However, the individual ratings have to be identified and matched in this scenario. Let x(A, a) be the rating of participant \(a,\ a\in \{1,\ldots ,n\},\) on QoE stimulus \(A\in {\mathcal {A}}\). Based on these ratings, each QoE stimulus A obtains an individual rank \(r^a(A)\) considering again the number of ties \(t^a_i = \sum _{A\in {\mathcal {A}}}\mathbb {1}_{\{x(A,a)=i\}}\) among a’s ratings for all QoE stimuli. Then, the sum of ranks \(R^A\) can computed for each QoE stimulus A:
The test statistic \(T_1\) of the Friedman test can be computed as:
The significance of the test statistic \(T_1\) can be looked up in dedicated tables. For large samples, \(T_1\) approximately follows a chi-square distribution with \(|{\mathcal {A}}|-1\) degrees of freedom. Note that this approximation is sometimes poor, so it is recommended to use the statistic
which follows an F-distribution with parameters \(|{\mathcal {A}}|-1\) and \((n-1)(|{\mathcal {A}}|-1)\) [104]. For the QoE stimuli in the considered example, the Friedman test is not applicable, as the stimuli were rated independently.
To sum up, this section presented methods for testing differences between rating distributions. Such hypothesis tests can be conducted to investigate if one stimulus from a group of two or more stimuli gives a significantly different rating distribution. Thus, the presented methods allow to distinguish (groups of) stimuli based on their underlying QoE distributions.
Comparison of QoE distributions
Next, researchers typically want to select the stimulus, which gives the best experience. So, instead of just testing for significant differences between the observed rating distributions of the stimuli, the QoE distributions should be compared in terms of the resulting experience. For comparing different QoE distributions, the concept of stochastic dominance [105] from decision theory can be utilized and transferred. Stochastic dominance describes a partial ordering between random variables. It can indicate if a gamble, i.e., a probability distribution over possible outcomes, is dominant and should be preferred. For QoE distributions, this means, that, if ratings (outcomes) are obtained from a superior QoE distribution, the corresponding stimulus (gamble) should be preferred. Different orders of dominance exist, but as it is a partial ordering, there might not always be a dominant distribution in comparisons of QoE results.
A QoE distribution B with cumulative representation \({\varvec{c}}^B\) has a first-order stochastic dominance (FSD) over a QoE distribution A with \({\varvec{c}}^A\), if:
Intuitively, this FSD of B indicates that the probability of having a rating of at least category i, i.e., \(1-c^B_{i-1}\) is higher than the corresponding probability for A, i.e., \(1-c^A_{i-1}\), for all categories. A weaker form of dominance is second-order stochastic dominance. QoE distribution B has a second-order stochastic dominance (SSD) over a QoE distribution A, if:
The intuitive explanation of SSD is that overall differences in probability mass between B and A are shifted more towards categories with higher QoE, i.e., \(\sum _{i=1}^j c^A_i-c^B_i \ge 0\) for all j. Obviously, FSD implies SSD. Note that the definition of SSD in this work avoids the typical definition via integrals, cf. [105], as integrals are not meaningful for ordinal scales. For the exemplary QoE distributions, \(S_2\) and \(S_3\) show FSD over \(S_1\), while for \(S_2\) and \(S_3\), neither FSD nor SSD can be observed in any direction.
To put it in a nutshell, this section transferred the concept of stochastic dominance in order to compare QoE distributions. This general concept allows to find stimuli that give superior ratings. Consequently, those stimuli can be considered to provide a better experience.
Quantification of QoE differences
Researchers are often interested in the QoE difference between two stimuli, e.g., if one stimulus represents the baseline configuration and other stimuli represent alternative configurations of the system under test. In this case, the difference between the resulting experience with the different stimuli has to be evaluated.
Statistical distances between QoE distributions
To quantify differences between two QoE distributions, there exist a plethora of statistical distances, e.g., [106]. Simple examples include the total variation distance
which is the largest difference between the probabilities that both distributions assign to the same category [106], or the Kolmogorov-Smirnov test statistic
which is the maximum vertical distance between the corresponding cumulative probability distributions [107, 108]. The widely used Kullback-Leibler divergence \(D_{KL}\) [109], however, is not recommended as it is not a metric. Moreover, if one of the categories was never rated by any users, i.e., its probability is zero, \(D_{KL}\) and its derived symmetric versions become \(\infty\), e.g., in \(S_1\) for “excellent” (5).
A more robust and intuitive distance metric is given by the Wasserstein metric [110], which is also called earth mover’s distance \(D_{EM}\) [111, 112]. It indicates the minimal amount of probability mass that has to be moved to change the shape and make one probability distribution look exactly the same as the other probability distribution. Obviously, the more different the distributions are, the more probability mass has to be moved, hence, \(D_{EM}\) will be larger. A simple formula exists to compute \(D_{EM}\) between QoE distributions A and B:
Note that \(D_{EM}\) indicates the absolute value of probability mass, which has to be shifted. However, the probability mass is counted for each of the intermediate categories, if it flows between categories that are not adjacent. Thus, it can only be interpreted as the shifted probability mass weighted by the number of categories that it has to be shifted. For example, considering \(A=(0,0,0.1,0,0.9)\), \(B=(0,0,0,0.2,0.8)\), and \(I_5=(0,0,0,0,1)\), both \(D_{EM}(A,I_5) = D_{EM}(B,I_5) = 0.2\). However, in the case of A, it means that a probability mass of 0.1 has to be shifted by two categories, while, in case of B, a probability mass of 0.2 has to be shifted by one category. Note once again that it has to be carefully avoided to interpret these numbers in terms of numerical differences or ratios between QoE rating categories, which is not possible for ordinal rating scales and would again introduce the inherent bias discussed above. This means, for example, that although the above discussed shifts from A to \(I_5\) (0.1 for two categories) and from B to \(I_5\) (0.2 for one category) are numerically equal, they cannot be considered equal in terms of QoE improvement, which is also indicated by the fact that \(D_{EM}(A,B) = 0.2 \ne 0\).
For two arbitrary QoE distributions A and B, the maximum distance \(\max _{A,B}D_{EM}(A,B) = 4\), which is reached for the distance between \(I_1=(1,0,0,0,0)\) and \(I_5=(0,0,0,0,1)\), i.e., a probability mass of 1 has to be shifted by four categories. Thus, it is possible to normalize the \(D_{EM}\) to the unit interval [0, 1] by computing
For the considered QoE study, it can again be seen from \(D_{EM,norm}(S_1,S_2) = 0.22\) and from \(D_{EM,norm}(S_1,S_3) = 0.33\) that \(S_1\) is not very close to \(S_2\) and \(S_3\). In contrast, \(D_{EM,norm}(S_2,S_3) = 0.11\), which confirms that \(S_2\) and \(S_3\) are rather similar.
Novel metrics derived from \(D_{EM}\)
Since the Wasserstein metric or earth mover’s distance \(D_{EM}\) nicely captures the intuition that users and their experience transition from one rating category to another, in the following, novel metrics are defined, which allow to evaluate QoE differences in a purely ordinal way, without any assumption on the distances between rating categories.
First, a novel QoE deficit index QDI of a QoE distribution A can be constructed based on \(D_{EM,norm}\). For this, QDI is defined as the normalized distance to the ideal QoE distribution \(I_5 = (0,0,0,0,1)\), for which all participants rated an “excellent” (5) experience:
QDI is in the unit interval, i.e., a QoE deficit index of 0 indicates an ideal QoE distribution (\(A=I_5\)), and a QDI of 1 means that A has the worst possible QoE distribution \(I_1 = (1,0,0,0,0)\). Also, a novel corresponding QoE level index QLI of a QoE distribution A can be derived as
As QDI and QLI are based on \(D_{EM}\), the same limitations apply in terms of interpretation. Here again, consider the example discussed for \(D_{EM}\) above, which equally applies to QDI. Note that there is also a mathematical relation to MOS via
It allows to define MOS based on a distance metric between QoE distributions over ordinal categories, rather than relying on a biased cast of ordinal rating data to an interval scale. Thus, it allows for an unbiased interpretation of MOS in terms of QoE probability masses, which are shifted and weighted by the number of shifted rating categories. Consequently, the ranking of the stimuli \(S_1\), \(S_2\), and \(S_3\) in terms of QLI with \(QLI(S_1) = 0.12< QLI(S_2) = 0.35 < QLI(S_3) = 0.45\) is equivalent to the ranking based on MOS. The ranking and the QLI scores indicate that the highest QoE deficit is in \(S_1\), in terms of the number of ratings and/or number of categories that would have to be shifted to reach an ideal QoE.
Next, the net flow of probability mass \(NF_i(A\rightarrow B)_i\) from each category i of A towards category \(i+1\) of B is introduced, which can be obtained from the terms of the sum in Eq. 39:
Here, a positive \(NF_i(A\rightarrow B)\) means that probability mass of A flows from category i towards \(i+1\) in B, i.e., towards higher QoE. In contrast, if \(NF_i(A\rightarrow B)\) is negative, A’s probability mass flows from category \(i+1\) to i in B, i.e., towards lower QoE. Note that, in contrast to \(D_{EM}\), \(NF_i\) is signed and directed, such that \(NF_i(A\rightarrow B) = -NF_i(B\rightarrow A)\). This concept also allows to count the number of categories with a positive or negative net flow from A to B and vice versa. At the same time, \(NF_i(A\rightarrow B)\) also quantifies the net probability mass, which flows between the categories. Confer with Eq. 35, which indicates FSD when all \(NF_i(A\rightarrow B)\) are positive.
When all signed net flows are added, the resulting number indicates the net balance, which is a novel metric for the overall directed net probability flow from A to B:
Note the relation to SSD in Eq. 36, which follows if all partial sums of \(NB(A\rightarrow B)\) are positive. Also note the relationship to QDI, i.e., \(NB(A\rightarrow B) = 4\cdot (QDI(A)-QDI(B))\), which follows directly from the definitions. Generally speaking, \(NB(A\rightarrow B)\) is a signed number that for positive values indicates a shift of probability mass towards higher QoE categories, such as in the considered example, in which \(NB(S_1\rightarrow S_2) = 0.89\) and \(NB(S_2\rightarrow S_3) = 0.41 > 0\). Again, it is weighted by the number of categories and, as differently signed shifts of probability mass have been canceled out, it should not be interpreted in terms of quantitative differences or ratios between QoE rating categories, which cannot be obtained from ordinal scales.
To sum up, several methods for quantifying the difference between two QoE distributions were outlined. All methods purely rely on ordinal data, and thus, do not need to implicitly consider experience differences between rating categories, which allows for a meaningful interpretation of the QoE difference. For this, the Wasserstein metric or earth mover’s distance proves to be a versatile metric, which is well suited to illustrate the rating process. This means, the movement of probability mass, on which the metric is based, nicely resembles the concept that users move to a different rating category if the underlying experience changes. Novel metrics have been proposed, which allow to inspect the net flow and net balance between two QoE distributions in detail, at the same time quantifying the net movement of users between rating categories in a single metric.
Metrics for QoE fairness
There is a recent development to consider the QoE fairness among users of a shared system, such that a system is considered QoE-fair if all users obtain the same QoE. The metric proposed in [84] quantified the fairness in terms of the dispersion of the QoE distribution, however, it relies on the standard deviation, which interprets the rating scales as an interval scale and considers equidistant differences between the categories. To overcome this issue, also a novel concept for assessing the QoE fairness of a QoE distribution is presented. This novel concept is based on the ordinal scale of ratings, and thus, allows to derive meaningful metrics.
The novel QoE fairness concept is based on the intuition that for any given QoE distribution A, the closest, perfectly fair QoE distribution \(I_{m_A}\) is the monolithic distribution, for which all participants have rated the modal QoE category of A, i.e., the category of A with the highest number of participants. This intuition of the closest, perfectly fair QoE distribution \(I_{m_A}\) is supported by the fact that, in order to reach \(I_{m_A}\) from A, the experience of the fewest number of users would have to be changed. The fair QoE distribution \(I_m\), which has category \(m \in \{1,\ldots ,5\}\) as mode, can be described by \(p_{m} = 1\) and \(p_i = 0,\ \forall i\ne m\). Consequently, a simple QoE fairness metric \(F_a\) can be described by the level of agreement on the modal category normalized to the unit interval:
The normalization takes into account that, due to the five rating categories, the minimum mode of any QoE distribution is \(\frac{1}{5}\). A fairness score of 1 indicates that all participants have rated the same category, while a fairness score of 0 indicates a uniform rating distribution. In the considered example, the QoE distributions reach the following fairness scores: \(F_a(S_1) = 0.55\), \(F_a(S_2) = 0.25\), and \(F_a(S_3) = 0.14\).
This concept of fairness towards a monolithic distribution also allows to define a more advanced QoE fairness score \(F_d\), which is based on the \(D_{EM}\) distance between A and its corresponding \(I_{m_A}\). Considering the maximum distance between any QoE distribution A and its closest, perfectly fair QoE distribution \(I_{m_A}\), which is \(\max _A{D_{EM}(A,I_{m_A})}=\frac{7}{3}\), the QoE fairness score can be normalized to the unit interval:
Here again, a fairness score of 1 indicates perfect fairness of the QoE ratings, i.e., all participants have rated the same category, which is the mode of A. In contrast, a fairness score of 0 indicates the highest unfairness in the QoE ratings in terms of \(D_{EM}\). This is achieved, e.g., for \(A=(\frac{1}{3}, \frac{1}{3}-\varepsilon , 0, 0, \frac{1}{3}+\varepsilon )\) with a small \(\varepsilon >0\), which has mode \(m=5\). The distance to the corresponding \(I_5 = (0,0,0,0,1)\) is \(D_{EM}(A,I_5) = \frac{7}{3}-3\varepsilon\), which approaches the maximum value. In the considered QoE study, \(F_d(S_1) = 0.79\), \(F_d(S_2) = 0.68\), and \(F_d(S_3) = 0.45\), i.e., the fairness decreases from \(S_1\) to \(S_3\), with \(S_1\) being closest to a monolithic QoE distribution.
In short, this section presented two novel QoE fairness metrics for QoE distribution. They rely on the difference to the respectively closest monolithic QoE distribution, which is a perfectly fair QoE distribution, for which all users rate the same experience. Thus, there is a change of the fairness concept from a dispersion measure, which required interval data, to the difference between ordinal QoE distributions.
All in all, throughout Sect. 4, existing and novel statistical methods were presented that can handle ordinal data and that are well suited for the domain of QoE research. Table 4 lists the presented methods according to their typical use case and provides a link to the corresponding equations. Note that most of the methods up to line “Differences between QoE distributions” are existing and well established methods, which can be found in standard statistical software, so there is no need to implement all the equations in this article. However, the presented equations help to fully understand the methods, which is beneficial for the interpretation of results. The novel methods for QoE distributions from line “Absolute experience level of QoE distribution” can be easily implemented from the provided equations.
QoE models based on QoE distributions
When considering QoE distributions, the question arises how to formulate QoE models for technical systems. Here, the assumption is made that the system under test can be configured by one or more parameters, which influences the resulting QoE distribution. For a start, technical systems with a single, continuous parameter will be considered, which has a monotonic relationship with QoE. Without loss of generality, it will be assumed that the experience increases monotonically when the technical parameter increases.
Quality steps
In the following, the range of the technical parameter will be discretized into quality steps, which is a novel concept introduced in this article. Thereby, a quality step is defined as an interval of the technical parameter range, in which the corresponding QoE distribution is fixed. Note that quality steps are a simple, yet universal metric, which can be applied to any technical system. In the following, their properties are elaborated.
Let n be a population of users of a fixed size. Then, there are a total of \(4\cdot n\) quality steps from the worst possible rating distribution \(I_1\) to the best possible rating distribution \(I_5\), and the technical system moves one quality step forward if and only if one user rates one category higher. At each quality step \(t\in \{0,\ldots ,4\cdot n\}\), there might be numerous possible rating distributions. In fact, at quality step t, all rating distributions A are possible, which fulfill
having \(x_1 = n - \sum _{i=2}^5 x_{i}\) and all \(x_i \ge 0\ \forall i\in \{1,\ldots ,5\}\). Normalizing this equation by the number of users n, this also gives a relation between the normalized quality steps \(\frac{t}{n}\in [0;4]\) and the quality level index QLI as defined above:
Following Eq. 49, when n tends towards infinity, there will be infinitely many quality steps, and moving one quality step becomes equivalent to shifting an infinitesimally small probability mass one category higher. Thus, the concept of quality steps can be transferred to QoE distributions even without the need for a realization, i.e., a rating distribution:
Assuming a finite population n, the concept of quality steps discretizes the range of the technical parameter and is general, such that it covers the situations when multiple users rate a category higher at the same time or one user rates more than one category higher by simply moving forward more steps at a time. Still, the technical system itself characterizes where the quality steps are located and which QoE distribution can be found at each quality step.
To get a better understanding of the quality steps and their different characteristics, Fig. 3 shows the quality steps for three different technical systems. Three simulation studies were conducted with 1000 simulation runs each considering a population of \(n=100\) users. The three plots show the means of the cumulative probabilities \({\hat{c}}_i\) over all runs at each quality step.
System A is designed such that a user is randomly selected from category 1, and in the next four quality steps, he always rates one category higher. Thus, System A shows a highly imbalanced progress of the users’ experience. The resulting QoE distributions have the probability mass in category 1 linearly decreasing and in category 5 linearly increasing, while only a negligibly small amount of probability mass, if any, resides at categories 2 to 4, as can be seen in Fig. 3a.
In System B, on the other hand, at each quality step, a user is randomly selected from the lowest rated category \(\min _i{x_i > 0}\) and simulated to rate one category higher to reach the next quality step. Thus, System B shows a very slow and balanced progress of the users’ experience and it visits all monolithic QoE distributions \(I_i\) at quality step \(t=(i-1)\cdot 100\) as can be seen from Fig. 3b. Note that for System A and B all simulation runs result in the same QoE distribution at each quality step, so confidence intervals were omitted.
System C is designed to follow a stochastic process, such that at each simulation step, a random user is selected (excluding users which have already rated category 5) to rate one category higher. The users are randomly selected according to a uniform distribution. This design follows the rationale that it is not known in advance, which user will switch next to a higher category, so all users are equally likely (principle of indifference). As can be seen in Fig. 3c, this results in a highly concave decrease of the mean of \({\hat{c}}_1\), sigmoidal decreases of the means of \({\hat{c}}_2\) and \({\hat{c}}_3\), and a convex decrease of the mean of \({\hat{c}}_4\). Note that although the QoE distributions at each quality step differ at each simulation run, the 95% confidence intervals were negligibly small \(<0.005\), so CIs were also omitted in Fig. 3c for better readability.
Since System C does not take any underlying assumptions – remember that all quality steps are taken uniformly random – it can be considered an average system in that sense, and will be studied in more detail. As no analytical solution could be derived for the curves of the probability functions \(p_i(t)\) and \(c_i(t)\), which describe the mean probabilities \({\hat{p}}_i\) and \({\hat{c}}_i\) at each quality step t, the observed probabilities from 100,000 simulation runs will be fitted using a non-linear method of least squares. Table 5 shows the resulting curve fits and their goodness of fit in terms of the coefficient of determination \(R^2\). Note that all \(R^2\) values are close to 1, which indicates that almost all of the variance in the simulation data could be explained by the model. It can be seen that the probability functions consist of three building blocks, namely, a power of \(\frac{t}{400}\), a power of the mirrored function \(1-\frac{t}{400}\), and an exponential function of \(\frac{t}{400}\). The polynomial functions were chosen based on the shape of the curves, and models relying only on them already reach quite decent fits. However, the fits could be improved by extending the models with exponential factors, which increased \(R^2\) by around 0.02 for p(t), and between 0.02 and 0.08 for c(t). Note that an analytical confirmation of the presented results is still open. However, also the numerically fitted functions already allow to obtain – in the above described sense – average probabilities and cumulative probabilites at each quality step.
To sum up, quality steps are a very general approach, which map the full range of a technical parameter to a bounded range of its corresponding experience. At any quality step, a plethora of QoE distributions can exist. However, each investigated technical system will only show a specific QoE distribution at each step. Thus, it is the ultimate goal of each QoE model of a technical system to fully describe its QoE distribution at each quality step.
Identifying quality steps in QoE studies
Figure 3 visualized how the QoE distributions at each quality step fully characterize the users’ experience of a technical system. However, in practice, not all QoE distributions at each quality step will be known for a given technical system, as a QoE study typically allows to only obtain the rating distributions for some values of the technical parameter. Nevertheless, the rating distributions resulting from a QoE study allow to determine the quality steps where each investigated parameter value is located using Eq. 48 or 49. Here, the normalized quality steps of Eq. 49 can also be applied to locate distributions with different numbers of ratings.
QoE studies further allow to find implausible rating distributions at other quality steps with respect to the observed rating distributions. Thereby, a rating distribution A at quality step u is plausible with respect to an observed rating distribution B at quality step \(v,\ v>u\), if B is reachable from A in \(v-u\) valid quality steps, i.e., B’s user ratings can only be shifted towards a higher category to reach QoE distribution A. This means, for two rating distributions A and B with the same population size n, that B is reachable from A if
Given that A and B have the same population size n, \(\sum _{j=1}^4(\sum _{i=1}^j x^A_i - \sum _{i=1}^j x^B_i) = v-u\). Similarly, following Eq. 49, B is reachable from A if
and it follows that \(NB(A\rightarrow B) = v-u\) for normalized quality steps u and v.
As each observed rating distribution is a realization of the underlying QoE distribution, the simultaneous confidence regions of the parameters are of interest, cf. Eq. 13 for the probabilities \({\varvec{p}}\) or Eq. 25 for the cumulative probabilities \({\varvec{c}}\). Consider that \(p_i\) is the probability of interest for now. The symmetric confidence interval with width \(d_i>0\) indicates that the true \(p_i\) is within \(l_{p_i}=\max ({\hat{p}}_i-\frac{d_i}{2},0)\) and \(u_{p_i}=\min ({\hat{p}}_i+\frac{d_i}{2},1)\). Now, it becomes clear that, at the lower bound of the confidence interval, probability mass was removed from category i, while at the upper end of the confidence interval, probability mass was added. However, since probability mass was moved to other categories, the quality steps at \(l_{p_i}\) and \(u_{p_i}\) are different from the observed rating distribution. This suggests to consider confidence areas instead of confidence intervals.
A confidence area for \(p_i\) can be constructed between four “bounding” QoE distributions, namely, the smallest and greatest QoE distributions, which reach \(l_{p_i}\) and \(u_{p_i}\), respectively. Here, “smallest” and “greatest” are meant in terms of quality steps. The smallest bounding QoE distributions will be called \(p_{i,l,s}\) and \(p_{i,u,s}\), while the greatest bounding QoE distributions will be called \(p_{i,l,g}\) and \(p_{i,u,g}\). They can be computed as described in Algorithm 1:

First, \(p_{i,l,s} = p_{i,l,g}\) and \(p_{i,u,s} = p_{i,u,g}\) are initialized with the lower and upper CI bounds, respectively (Lines 1-2). Note that \(p_{i,l,s}, p_{i,l,g}, p_{i,u,s}\), and \(p_{i,u,g}\) are no valid QoE distributions yet as \(\sum _{k=1}^5{l_{p_k}}\) is typically less than 1 and \(\sum _{k=1}^5{u_{p_k}}\) is typically greater than 1, and the missing or excess probability mass still has to be redistributed (Lines 3-4). For \(p_{i,l,s}\), fix \(l_{p_i}\) and distribute the missing probability mass leftmost. This means, starting from category 1 to 5, fill the missing probability mass into category \(j\ (j\ne i)\), until – in order to stay within the CI bounds of category j – at most \(u_{p_j}\) probability mass resides (Lines 5-9). If all other categories \(j\ (j\ne i)\) have been filled until \(u_{p_j}\), and still some probability mass is missing, add it to category i (Line 14). Following this simple algorithm will result in \(p_{i,l,s}\), which is the smallest valid QoE distribution, which approaches the lower bound of the CI for \(p_i\), such that no CI bound of any other category is violated. Similarly, \(p_{i,l,g}\) can be computed by redistributing the missing probability mass rightmost, i.e., starting from category 5 down to 1, but following the same procedure (Lines 16–20,25). The same procedure also applies to \(p_{i,u,s}\) and \(p_{i,u,g}\), where the excess probability mass is subtracted rightmost (Lines 16–17,21–23,26) or leftmost (Lines 5–6,10–13,15), respectively. The resulting confidence area for \(p_i\) is then given by the quality steps of the bounding QoE distribution and their respective probability masses at category i.
The concept of confidence areas will be visualized for an exemplary QoE study. Again, the filtered ratings of the crowdsourcing QoE study in [87, 88] are used. Remember that the participants watched short video clips of 30s, which included a number of stalling events from 0 to 6. Each stalling lasted for 4s, and the stalling events were regularly spaced within the video. Thus, the technical parameter of this system is number of stalling events. Table 6 shows the corresponding rating distributions \(\varvec{{\hat{p}}}\) obtained during the QoE study and the number of reliable ratings for each condition. Note that for illustrating the confidence areas, an overall population of \(n=100\) users is assumed, and the rating distributions of Table 6 are scaled accordingly. Moreover, the convention will be kept that an increase in quality steps increases the experience, although for this system, the experience increases when the parameter (i.e., number of stalling events) decreases. This means, for now, the axis of the technical parameter will be “reversed”, such that the worst experience still resides at quality step 0, and the best experience resides at quality step 400. The corresponding quality step of each rating distribution is given in the last column of Table 6.
Figure 4a shows the cumulative QoE distributions at their corresponding quality step. Thereby, the colors indicate the rating categories in a traffic light style from “bad” (red), “poor” (dusky pink), “fair” (yellow), “good” (green) to “excellent” (dark green). For each cumulative probability, the four bounding QoE distributions were computed according to Algorithm 1 with respect to the simultaneous confidence intervals from Eq. 25. The bounding QoE distributions indicate the smallest and largest quality step at which the lower and upper bound of the CI of a cumulative probability can be reached without violating any other of the simultaneous CIs. Thus, there are four bounding distributions and they span the confidence area along the horizontal axis, i.e., the quality step axis (smallest to largest quality step) and along the vertical axis (lower bound to upper bound of CI). Given the restriction to not violate any other of the simultaneous CIs, the confidence areas are not completely trapezoid as can be seen in Fig. 4a, but they can be irregular quadrilateral polygons. The advantage of the confidence areas is that they not only show the range of the parameters of a QoE distribution, but also the range of quality steps at which the QoE distribution can be located.
Simulative QoE models
The purpose of a QoE model is to describe the relationship between a technical parameter \(z\in {\mathbb {R}}\) of a system and the corresponding Quality of Experience. It allows to investigate the QoE response when a technical parameter is varied, and it also allows to interpolate the QoE of technical parameters, which were not explicitly studied. As a QoE distribution \({\varvec{p}}\) consists of five parameters, it is thus required to find a QoE model as a mapping \(m:{\mathbb {R}}\rightarrow [0;1]^5, m(z)\mapsto (p_1, p_2, p_3, p_4, p_5)\) with \(\sum _{i=1}^5p_i = 1\). Similarly, a QoE model can also map from the same domain to \((c_1, c_2, c_3, c_4, c_5)\) with \(c_1\le c_2\le c_3\le c_4 \le c_5 = 1\), as the representations \({\varvec{p}}\) and \({\varvec{c}}\) are equivalent.
As a technical system is fully characterized by the QoE distributions at each quality step, a straightforward approach is to compute or simulate the most likely path through QoE distributions at any quality step based on the observed rating distributions. Figure 4b shows this path for the exemplary QoE study. For this, the range of quality steps was split at each observed rating distribution into segments, and a Viterbi-like algorithm was employed to compute the path with the highest probability for each segment. Here, the QoE distributions at each quality step are the hidden states. Again, a uniform distribution was assumed for \(\sum _{i=1}^4x_i\) active participants, i.e., those participants that could still increase their rating category. this means that all active participants were equally likely to trigger a transition to another state, namely, a QoE distribution at the next quality step.
As it can be seen in Fig. 4b, the resulting Viterbi paths show the characteristics of System B, cf. above, such that there is a slow and balanced increase of rating categories, starting from the lowest category. The reason is that this behavior first bundles the probability mass in the lowest rating category, which will lead to higher transition probabilities, and thus, a higher path probability. To fully understand this behavior, consider an example with a Viterbi path between (1, 99, 0, 0, 0) and (0, 99, 1, 0, 0) for a population of \(n=100\). The path \((1,99,0,0,0)\rightarrow (0,100,0,0,0)\rightarrow (0,99,1,0,0)\) has a probability of \(\frac{1}{100}\cdot \frac{100}{100} = \frac{100}{10000}\), which is clearly superior to the alternative path \((1,99,0,0,0)\rightarrow (1,98,1,0,0)\rightarrow (0,99,1,0,0)\) with probability \(\frac{99}{100}\cdot \frac{1}{100} = \frac{99}{10000}\). As a side note, it shall also be mentioned that the behavior of System A reflects the path with the smallest probability.
Nevertheless, the Viterbi path is only one of a multitude of possible paths through the quality steps, and in particular, it does not consider that QoE distributions can reside on multiple paths. For instance, see the example above where the two paths split at (1, 99, 0, 0, 0) but reunite at (0, 99, 1, 0, 0). Thus, it is better suited to simulate many paths through the quality steps and take the average QoE distributions at each step. Again, for each segment, a uniform approach is employed for all active participants, which resembles the behavior of System C. Afterwards, the mean paths for each segment are computed. Figure 4c shows the resulting mean paths for the exemplary QoE study with solid lines. The mean paths are compared to the mean probabilities of System C, i.e., a technical system without any observed rating distributions, which are shown with dotted lines. It can be seen that the mean probabilities of System C approximate the mean probabilities of the observed technical system well, and reach a high goodness of fit of \(R^2=0.9927\).
However, when taking a closer look, it becomes evident that the fit is especially good at low quality steps below 100, but shows some divergence between 100 and 200. Starting from the observed rating distribution at quality step 139 (two stalling events), it can be seen that the observed \({\hat{c}}_3\) and its yellow confidence area are slightly above the dashed yellow line (mean \(c_3\), category “fair”), and that \({\hat{c}}_1\) and its red confidence area are below the dashed red curve (mean \(c_1\), category “bad”). The divergence becomes especially pronounced at the rating distribution for one stalling event (quality step 179). Here, the \({\hat{c}}_3\) and the yellow area are below the dashed yellow curve, and \({\hat{c}}_4\) and the tiny green area are above the dashed green curve (mean \(c_4\), category “good”). This shows a substantial difference from the average behavior of System C.
In particular, in this QoE study, it can be seen that the technical system exhibits a substantial QoE distortion between quality steps 100 and 200. This means that the observed rating distributions have many ratings in a lower category than would be on average. For example, compare the difference between the solid and dashed green and yellow curves at quality step 179 (one stalling event), which indicate the difference between the average and the observed probability for the category “good”. In the considered QoE study, this results from the fact that the first stalling event of a video is a substantial degradation of the experience. This locates the observed rating distribution at a relatively low quality step, where the QoE distortions with respect to the average QoE distribution at this quality steps become evident. To get more detailed insights in the deviation from an average technical system, distortion curves could be computed showing the differences between the average \(c_i(t)\) and the observed \({\hat{c}}_i\), or the average \({\hat{c}}_i\), which were simulated based on the observed rating distributions.
To sum up, simulative QoE models not only allow to interpolate the QoE distributions at intermediate quality steps, which were not observed during the QoE study, but they also allow to compare the behavior of the technical system to an average rating behavior over the progression of quality steps. With this, it is possible to detect substantial QoE distortions caused by the investigated technical parameters when the corresponding rating distribution is located at a quality step, where other rating distributions would be expected assuming an average rating behavior.
Analytical QoE models
After the simulative QoE models were presented, analytical QoE models are discussed next. The goal of analytical models is to provide a functional relationship between the technical parameter z and the resulting QoE. Figure 5a presents a QoE model for the exemplary QoE study, which maps z to the normalized quality steps of the corresponding rating distribution. As the normalized quality steps have a linear relationship to the quality level index QLI (cf. Eq. 50), which in turn has a (numerical) linear relationship to MOS (cf. Eq. 43), this model is equivalent to the QoE models in [87, 88], which mapped the technical parameter to MOS for different lengths of the stalling events. Thus, here again an exponential function can be fitted, cf. [113], which is shown as a dotted line in Fig. 5a.
The fitted exponential model \(m(z) = 3.36\cdot \exp (-0.82\cdot z)+0.57\) shows a high goodness of fit of \(R^2=0.9782\) and is almost identical to the model for MOS reported in [88] (\(m_{MOS}(z) = 3.35\cdot \exp (-0.89\cdot z)+1.62,\ R^2=0.978\)). The slight differences, i.e., most notably the vertical shift of around 1, can be attributed to the different codomains (quality steps: [0; 4], MOS: [1; 5]) and to minor numerical issues during the fitting. Nevertheless, an even better fit could be achieved by considering an additional linear term in the model, namely, \(m(z) = 2.21\cdot \exp (-2.17\cdot z)-0.24\cdot z+1.79\), which gives an almost perfect fit with \(R^2=0.9991\). This fit is shown as a dashed line in Fig. 5a.
Two insights can be derived from the QoE models for quality steps. First, it becomes clear that any such QoE model represents a transformation of the quality step axis into the axis of the technical parameter, see x-axes in Figs. 4 and 5a. For this, different segments of the quality step axis are scaled differently, e.g., in the exemplary QoE study, quality steps 400-179 are contracted to [0; 1], whereas quality steps 179-139 are contracted to [1; 2] on the axis of the technical parameter (number of stalling events), and so on. Second, the problem remains that the quality step only gives an indication of how much probability mass has been shifted from the worst experience at 0 towards the best experience at 4, weighted by the number of shifted rating categories, cf. the relationship to QLI (Eq. 50). However, it does not indicate how the probability mass has been shifted. In fact, at each quality step, numerous QoE distributions are plausible as indicated in Eqs. 48–50. Thus, the descriptive power of such QoE models for quality steps, or equivalent QoE models for MOS, is very limited, which again advocates against the usage of MOS-based evaluations.
In contrast, QoE models should fully leverage all information that can be obtained from a QoE study. Thus, they should consider the entire QoE distribution for the mapping of the technical parameter z. Figure 5b shows such a QoE model for the exemplary QoE study. It models the rating probabilities \(p_i, i=1,\ldots ,5,\) for each value z of the technical parameter, which results in five mapping functions \(m_{p_i}(z)\). The five mapping functions are shown by solid lines whose color matches the rating category from \(i=1\) (“bad”) in red to \(i=5\) (“excellent”) in green. They were fitted based on the observed rating distributions only, this means, e.g., \(m_{p_1}(z)\) (red) was fitted based on the seven \({\hat{p}}_1\) values for \(z=0,\ldots ,6\). The resulting model functions are given in the first column of Table 7. However, during the selection of the functions also the simulated mean probabilites from Fig. 4c (dotted lines) were considered such that the mapping functions also approximate them well. This is why two goodness of fit values are presented in Table 7. \(R_p\) describes the goodness of fit only at \(z=0,\ldots ,6\), whereas \(R_{p,sim}\) describes the goodness of fit with respect to the simulated mean probabilities for all \(z\in [0;6]\). Note that in addition to \(R^2\), also the compatibility of the mapping functions with the CIs of \({\hat{p}}_i\) has to be checked, and that mapping functions always have to be bounded to the domain [0; 1] as they model a probability.
It can be seen that the same building blocks can be reused that were already used above for fitting the mean probabilities of System C, but with two exceptions. \(m_{p_1}(z)\) shows a clearly linear behavior and \(m_{p_5}(z)\) shows an exponential relationship. These different relationships also point to the obvious QoE distortion of the observed technical system compared to the average System C. Moreover, \(\frac{1}{7}\) was used as a scaling factor for the parameter z due to the different domain of the model. All five fittings show decent \(R^2_p\) values at the seven investigated parameter values. Also with respect to the simulated mean probabilities, the \(R^2_{p,sim}\) values are high, except for \(m_{p_4}(z)\). Although it is expected that \(R^2_{p,sim}\) might be lower than \(R^2_p\), because the fittings are not optimized on the whole parameter range \(z\in [0;6]\), \(R^2_{p,sim}\) is only moderate for \(m_{p_4}(z)\). Thus, in this case, the fitted model cannot extrapolate well with respect to the simulated mean probabilities at other quality steps, especially for z between 0 and 1. However, as the number of stalling events can never actually be in between 0 and 1, this issue can be neglected here. For the exemplary QoE study, the most important property of a QoE model is that the mappings are accurate for all realistic values of z, i.e., for all \(z=0,\ldots ,6\).
The presented model achieves this goal, and is thus well suited for the considered use case. If the purpose of the QoE model was to inter- or extrapolate for realistic, but unobserved values of the technical parameter, more attention would have to be given to the design of the QoE model, as the selection of the fitted mapping functions will influence the goodness of the prediction of the QoE model for the unobserved values. Note also that for practical applications, i.e., to obtain the QoE distribution for a certain value of z, the outcomes of the five mapping functions might have to be normalized. This means, due to the fitting, the obtained probabilities might not perfectly sum to 1, so some minor scaling might be required.
Finally, Fig. 5c shows a fitted QoE model for the cumulative probabilities observed in the exemplary QoE study. Here, the model consists of four individual mappings \(m_c\) from the technical parameter z to \(c_i, i=1,\ldots 4\). Note that \(m_{c_5}(z)=c_5(z)=1\) by definition, and thus, does not need to be fitted. Moreover, it also implies that all probabilities obtained from this model perfectly sum to 1. During fitting, the same procedure was followed as described above, and the resulting mapping functions are shown in the fourth column of Table 7. It can be seen that all mapping functions are composed of a power of \(\frac{z}{7}\) and an exponential function of \(\frac{z}{7}\), except for \(m_{c_1}\), which is identical to \(m_{p_1}\), and thus, also linear. Here, all coefficients of determination \(R^2_c\) are very high, which indicates a good fit for the observed cumulative probabilities \({\hat{c}}_i\). With respect to the simulated mean probabilities, the mappings show a good fit for category 1 and 2. However, \(R_{c, sim}^2\) is lower for \(i=3\) and especially for \(i=4\), again because of bad approximations for z in between 0 and 1. Nevertheless, as discussed above, the fitted QoE model shows an overall very good performance for all realistic values of \(z=0,\ldots ,6\), which is the most important aspect for the considered use case.
Also generalized linear models can be used to fit similar QoE models, as was demonstrated in [60]. They can include multiple technical parameters directly in the underlying linear model, and share a subset of the estimated model parameters for all rating categories. In contrast, the approach presented in this work is a more easily applicably approach, which is not restricted to any model assumptions, e.g., a certain family of functions. Instead, the proposed QoE models show a high flexibility as distributions for each category can be fitted with arbitrary functions. Moreover, the proposed QoE models purely rely on the observed ratings, and abstract any technical parameters into the notion of quality steps.
To sum up, the most striking advantage of this kind of QoE models is that they allow to deduce the full QoE distribution at each observed value of the technical parameter. The proposed QoE models come with the additional effort of fitting five mapping functions (or four for \(\varvec{{\hat{c}}}\)) instead of one function, which is required for MOS-based QoE models. However, this additional effort is justified, as the models keep detailed information from the results of a QoE study. At any value of the technical parameter, the corresponding QoE distribution can be extracted to inspect the rating behavior. Then, the obtained QoE distributions can be further analyzed with the statistical methods summarized in Sect. 4, e.g., in terms of QoE differences, or in terms of QoE fairness. Finally, the QoE models can be used to predict the rating behavior also at unobserved values of the technical parameter. This gives an unprecedented richness of insights into the end users’ experience with the technical system.
Conclusion
This work described the inherent bias in many MOS-based evaluations of QoE studies, which is caused by too simplistic assumptions about the mapping of QoE to the rating scale. Very often, QoE studies use only ordinal rating scales, such as the 5-point ACR scale, for which means, differences, and ratios between categorical values are not meaningful. The dispute on scales and appropriate statistics was outlined based on works from many research domains. Given the partially contradicting arguments and counterexamples, the clean way out of this dilemma – without having to switch to other study designs or other rating scales, without having to separate measurement theory (meaning of numbers) and statistical theory (relation of numbers), and without hoping for robustness when violating assumptions of parametric statistics – is to rely on statistical methods that can handle ordinal data.
For this, this work considered QoE distributions, which can be based on the well-established theoretical framework of multinomial distributions. Existing and novel statistical methods for QoE distributions were summarized and exemplary evaluations were described. All methods purely rely on ordinal data, and thus, do not need to implicitly consider experience differences between rating categories. This gives meaningful results also for ordinal rating scales, and thus, shows fundamental advantages over biased MOS-based evaluations. All presented methods are applicable to the typical use cases when planning a QoE study and analyzing the obtained ratings, and thus, should be helpful for QoE researchers to come up with meaningful results.
Moreover, this work proposed to also design QoE models for a technical system based on QoE distributions. For this, the novel concept of quality steps was introduced, which allows to discretize the range of the technical parameters using a simple, yet universal metric. Methods to obtain simulative and analytical QoE models were presented, and exemplary models were demonstrated. The resulting QoE models keep detailed information from the results of a QoE study, and allow to extract the full QoE distribution at each value of the technical parameter. This provides rich insights into the end users’ experience with the technical system along the whole investigated parameter range.
As future work, several arguments and possible solutions to the dispute on scales and statistics should be revisited. For example, it should be investigated if item-response theory can be used in the QoE domain to obtain interval data from ordinal QoE ratings [63, 64]. Another option would be to present other rating scales in QoE studies, such that parametric statistics can be meaningfully applied. This especially includes continuous rating scales, which should provide interval data, such that the described issues do not apply. Nevertheless, this property of continuous scales to provide interval data has been questioned for a visual analogue scale (VAS) in [34, 35], and thus, still has to be confirmed for QoE studies. Moreover, when relying on ordinal rating scales, the modeling of QoE results using generalized linear models [60] could serve as an alternative to the QoE models presented in this article, and thus, also deserves another close look from the research community.
Finally, the presented concept of QoE distributions is still in its infancy, and the provided statistical methods and models in this paper can rather be considered as a first step and a motivation to the problem, than as a final solution. Thus, any additional contributions to the tool box of statistical methods for QoE distributions based on ordinal data and the presented approach to QoE models, which were initialized in this article, will only further advance the methodology in the QoE domain, and therefore, would be highly appreciated.
References
Le Callet P, Möller S, Perkis A (eds) (2013) Qualinet White Paper on Definitions of Quality of Experience. European Network on Quality of Experience in Multimedia Systems and Services (COST Action IC 1003), Lausanne, Switzerland, Tech. Rep., version 1.2
International Telecommunication Union. ITU-T Recommendation P.800: Methods for Subjective Determination of Transmission Quality (1996)
International Telecommunication Union. ITU-T Recommendation P.809: Subjective Evaluation Methods for Gaming Quality (2018)
International Telecommunication Union. ITU-T Recommendation P.910: Subjective Video Quality Assessment Methods for Multimedia Applications (2008)
International Telecommunication Union. ITU-T Recommendation P.913: Methods for the Subjective Assessment of Video Quality, Audio Quality and Audiovisual Quality of Internet Video and Distribution Quality Television in any Environment (2016)
International Telecommunication Union. ITU-T Recommendation P.1301: Subjective Quality Evaluation of Audio and Audiovisual Multiparty Telemeetings (2017)
International Telecommunication Union. ITU-R Recommendation BT.500: Methodology for the Subjective Assessment of the Quality of Television Pictures (2019)
International Telecommunication Union. ITU-T Recommendation P.800.1: Mean Opinion Score (MOS) Terminology (2016)
Gardner PL (1975) Scales and statistics. Rev Educ Res 45(1):43–57
Knapp TR (1990) Treating ordinal scales as interval scales: an attempt to resolve the controversy. Nursing Res 39(2):121–123
Clason DL, Dormody TJ (1994) Analyzing data measured by individual Likert-type items. J Agric Educ 35(4):4
Harpe SE (2015) How to analyze Likert and other rating scale data. Curr Pharm Teach Learn 7(6):836–850
Poulton EC, Poulton S (1989) Bias in quantifying judgements. Taylor & Francis, Abingdon
Zielinski S, Rumsey F, Bech S (2008) On some biases encountered in modern audio quality listening tests - a review. J Audio Eng Soc 56(6):427–451
Zielinski S (2016) On some biases encountered in modern audio quality listening tests (Part 2): selected graphical examples and discussion. J Audio Eng Soc 64(1/2):55–74
Zeithaml VA (1988) Consumer perceptions of price, quality, and value: a means-end model and synthesis of evidence. J Mark 52(3):2–22
Köster F, Guse D, Wältermann M, Möller S (2015) Comparison between the discrete ACR scale and an extended continuous scale for the quality assessment of transmitted speech. In: Proceedings of the 41st annual German conference on acoustics (DAGA). Nuremberg, Germany
Schatz R, Egger S, Platzer A (2011) Poor, good enough or even better? bridging the gap between acceptability and QoE of mobile broadband data services. In: Proceedings of the IEEE international conference on communications (ICC). Kyoto, Japan
Gardlo B, Egger S, Hoßfeld T (2015) Do scale-design and training matter for video QoE assessments through crowdsourcing?. In: Proceedings of the 4th international workshop on crowdsourcing for multimedia (CrowdMM). Australia, Brisbane, pp 15–20
Liddell TM, Kruschke JK (2018) Analyzing ordinal data with metric models: what could possibly go wrong? J Exp Soc Psychol 79:328–348
Seufert M (2019) Fundamental advantages of considering quality of experience distributions over mean opinion scores. In: Proceedings of the 11th international conference on quality of multimedia experience (QoMEX), Berlin, Germany
Likert R (1932) A technique for the measurement of attitudes. Arch Psychol 22(140):55
Willits FK, Theodori GL, Luloff A (2016) Another look at Likert scales. J Rural Soc Sci 31(3):6
Stevens SS (1946) On the Theory of Scales of Measurement. In: Neil JS (ed) Encyclopedia of Research Design. https://doi.org/10.4135/9781412961288.n292
Siegel S (1956) Nonparametric Statistics for the Behavioral Sciences
Gaito J (1980) Measurement Scales and Statistics: Resurgence of an Old Misconception. Psychol Bull 87(3):564–567. https://doi.org/10.1037/0033-2909.87.3.564
Townsend JT, Ashby FG (1984) Measurement scales and statistics: the misconception misconceived. Psychol Bull 96(2):394–401. https://doi.org/10.1037/0033-2909.96.2.394
Jöreskog KG (1994) On the estimation of polychoric correlations and their asymptotic covariance matrix. Psychometrika 59(3):381–389
Jamieson S (2004) Likert scales: how to (Ab)Use them. Med Educ 38(12):1217–1218
Norman G (2010) Likert scales, levels of measurement and the “Laws” of statistics. Adv Health Sci Educ 15(5):625–632
Carifio J, Perla RJ (2007) Ten common misunderstandings, misconceptions, persistent myths and urban legends about Likert scales and Likert response formats and their antidotes. J Soc Sci 3(3):106–116
Carifio J, Perla R (2008) Resolving the 50-year debate around using and misusing Likert scales. Med Educ 42(12):1150–1152
Parker PL, McDaniel HS, Crumpton-Young LL (2002) Do research participants give interval or ordinal answers in response to Likert scales?. In: Proceedings of the IIE annual conference. Citeseer, p. 1
Hasson D, Arnetz BB (2005) Validation and findings comparing VAS versus Likert scales for psychosocial measurements. Int Electron J Health Educ 8:178–192
Svensson E (2000) Comparison of the quality of assessments using continuous and discrete ordinal rating scales. Biom J J Math Methods Biosci 42(4):417–434
Deheane S, Dupoux E, Mehler J (1990) Is numerical comparison digital? analogical and symbolic effects in two-digit comparison. J Exp Psychol Human Percept Perform 16:626–641
Dehaene S, Bossini S, Giraux P (1993) The mental representation of parity and number magnitude. J Exp Psychol General 122(3):371
Baggaley AR, Hull AL (1983) The effect of nonlinear transformations on a Likert scale. Eval Health Prof 6(4):483–491
Hobart JC, Cano SJ, Zajicek JP, Thompson AJ (2007) Rating scales as outcome measures for clinical trials in neurology: problems, solutions, and recommendations. Lancet Neurol 6(12):1094–1105
Gardner HJ, Martin MA (2007) Analyzing ordinal scales in studies of virtual environments: Likert or Lump it!. Presence Teleoperators Virtual Environ 16(4):439–446
Hart M (1996) Improving the dissemination of SERVQUAL by using magnitude scaling. In: Kanji GK (ed) Total Quality Management in Action. Springer, pp. 267–270
Lodge M (1981) Magnitude scaling: quantitative measurement of opinions. SAGE Publications, Incorporated, Thousand Oaks, p 25
Vickers AJ (1999) Comparison of an ordinal and a continuous outcome measure of muscle soreness. Int J Technol Assess Health Care 15(4):709–716
Henkel RE (1975) Part-whole correlations and the treatment of ordinal and quasi-interval data as interval data. Pac Sociol Rev 18(1):3–26
Velleman PF, Wilkinson L (1993) Nominal, ordinal, interval, and ratio typologies are misleading. Am Stat 47(1):65–72
Adams EW, Fagot RF, Robinson RE (1965) A theory of appropriate statistics. Psychometrika 30(2):99–127
Lord FM (1953) On the statistical treatment of football numbers. American Psychol 8(12):750–751. https://doi.org/10.1037/h0063675
Anderson NH (1961) Scales and statistics: parametric and nonparametric. Psychol Bull 58(4):305
Baker BO, Hardyck CD, Petrinovich LF (1966) Weak measurements versus strong statistics: an empirical critique of S. S. stevens proscriptions on statistics. Educ Psychol Meas 26(2):291–309
Glass GV, Peckham PD, Sanders JR (1972) Consequences of failure to meet assumptions underlying the fixed effects analyses of variance and covariance. Rev Educ Res 42(3):237–288
Labovitz S (1970) The assignment of numbers to rank order categories. Am Sociol Rev 35(3):515–524
Murray J (2013) Likert Data: What to Use, Parametric or Non-parametric?. Int J Bus Soc Sci 4(11):258–264
Labovitz S (1967) Some observations on measurement and statistics. Soc Forces 46(2):151–160
Vigderhous G (1977) The level of measurement and “Permissible” statistical analysis in social research. Pac Sociol Rev 20(1):61–72
Micceri T (1989) The unicorn, the normal curve, and other improbable creatures. Psychol Bull 105(1):156
Merbitz C, Morris J, Grip JC (1989) Ordinal scales and foundations of misinference. Arch Phys Med Rehabil 70(4):308–312
Kaptein MC, Nass C, Markopoulos P (2010) Powerful and consistent analysis of Likert-type rating scales. In: Proceedings of the SIGCHI conference on human factors in computing systems, pp. 2391–2394
Wu H, Leung S-O (2017) Can Likert scales be treated as interval scales? - a simulation study. J Soc Serv Res 43(4):527–532
Šimkovic M, Träuble B (2019) Robustness of statistical methods when measure is affected by ceiling and/or floor effect. PloS one 14(8):e0220889
Janowski L, Papir Z (2009) Modeling subjective tests of quality of experience with a generalized linear model. In: Proceedings of the 1st international workshop on quality of multimedia experience (QoMEX). San Diego, CA, USA
Friedman HH, Herskovitz PJ, Pollack S (1994) The biasing effects of scale-checking styles on response to a Likert scale. In: Proceedings of the American statistical association annual conference: survey research methods, vol. 792
Albaum G (1997) The Likert scale revisited. J Mark Res Soc 39(2):1–21
Harwell MR, Gatti GG (2001) Rescaling ordinal data to interval data in educational research. Rev Educ Res 71(1):105–131
Andrich D (1978) A rating formulation for ordered response categories. Psychometrika 43(4):561–573
Grimby G, Tennant A, Tesio L (2012) The use of raw scores from ordinal scales: time to end malpractice? J Rehabil Med 44:97–98
Forrest M, Andersen B (1986) Ordinal scale and statistics in medical research. British Med J 292(6519):537–538
Boone HN, Boone DA (2012) Analyzing Likert data. J Ext 50(2):1–5
Kuzon W, Urbanchek M, McCabe S (1996) The seven deadly sins of statistical analysis. Ann Plast Surg 37:265–272
Brunner E, Puri ML (2001) Nonparametric methods in factorial designs. Stat Papers 42(1):1–52
Agresti A (1999) Modelling ordered categorical data: recent advances and future challenges. Stat Med 18(17–18):2191–2207
Svensson E (2001) Guidelines to statistical evaluation of data from rating scales and questionnaires. J Rehabil Med 33(1):47–48
Göb R, McCollin C, Ramalhoto MF (2007) Ordinal methodology in the analysis of Likert scales. Qual Quant 41(5):601–626
Choi J, Peters M, Mueller RO (2010) Correlational analysis of ordinal data: from Pearson’s r to Bayesian polychoric correlation. Asia Pac Educ Rev 11(4):459–466
Raake A (2006) Speech quality of VoIP: assessment and prediction. Wiley Online Library, Hoboken
Alreshoodi M, Woods J (2013) Survey on QoE QoS Correlation Models for Multimedia Services. International Journal of Distributed and Parallel Systems, 4(3)
Garcia M-N, De Simone F, Tavakoli S, Staelens N, Egger S, Brunnström K, Raake A (2014) Quality of experience and HTTP adaptive streaming: a review of subjective studies. In: Proceedings of the 6th international workshop on quality of multimedia experience (QoMEX), Singapore
Seufert M, Egger S, Slanina M, Zinner T, Hoßfeld T, Tran-Gia P (2015) A survey on quality of experience of HTTP adaptive streaming. IEEE Commun Surv Tutor 17(1):469–492
International Telecommunication Union. ITU-T Recommendation G.1011: Reference Guide to Quality of Experience Assessment Methodologies (2015)
International Telecommunication Union. ITU-T Recommendation P.1501: Subjective Testing Methodology for Web Browsing (2013)
Hoßfeld T, Schatz R, Egger S (2011) SOS: The MOS is not Enough!. In: Proceedings of the 3rd international workshop on quality of multimedia experience (QoMEX). Mechelen, Belgium
Hoßfeld T, Heegaard PE, Varela M (2015) QoE beyond the MOS: added value using quantiles and distributions. In: Proceedings of the 7th international workshop on quality of multimedia experience (QoMEX). Costa Navarino, Greece
Hoßfeld T, Heegaard PE, Varela M, Möller S (2016) QoE beyond the MOS: An In-depth Look at QoE via Better Metrics and their Relation to MOS. Qual User Exp 1(1):2
Hoßfeld T, Heegaard PE, Skorin-Kapov L, Varela M (2017) No silver bullet: QoE metrics, QoE fairness, and user diversity in the context of QoE management. In: Proceedings of the 9th international workshop on quality of multimedia experience (QoMEX). Erfurt, Germany
Hoßfeld T, Skorin-Kapov L, Heegaard PE, Varela M (2017) Definition of QoE fairness in shared systems. IEEE Commun Lett 21(1):184–187
Hoßfeld T, Heegaard PE, Skorin-Kapov L, Varela M (2019) Fundamental relationships for deriving QoE in systems. In: Proceedings of the 11th international conference on quality of multimedia experience (QoMEX), Berlin, Germany
Hogg RV, Tanis EA, Zimmerman DL (2010) Probability and statistical inference. Pearson, London
Hoßfeld T, Schatz R, Seufert M, Hirth M, Zinner T, Tran-Gia P (2011) Quantification of YouTube QoE via Crowdsourcing. In: Proceedings of the international workshop on multimedia quality of experience - modeling, evaluation, and directions (MQoE). Dana Point, CA, USA
Hoßfeld T, Schatz R, Zinner T, Seufert M, Tran-Gia P (2011) Transport Protocol Influences on YouTube QoE. University of Würzburg. Tech. Rep. 482
Brown LD, Cai TT, DasGupta A (2001) Interval estimation for a binomial proportion. Stat Sci 16(2):101–117
May WL, Johnson WD (1997) Properties of simultaneous confidence intervals for multinomial proportions. Commun Stat Simul Comput 26(2):495–518
Goodman LA (1965) On simultaneous confidence intervals for multinomial proportions. Technometrics 7(2):247–254
Sison CP, Glaz J (1995) Simultaneous confidence intervals and sample size determination for multinomial proportions. J Am Stat Assoc 90(429):366–369
Ewis KM (2012) Central moments via factorial moments for some discrete distributions. Am Acad Sch Res J 4(1):64–67
Gould HW (1960) Stirling number representation problems. Proc Am Math Soc 11(3):447–451
Glaz J, Sison CP (1999) Simultaneous confidence intervals for multinomial proportions. J Stat Plann Inference 82(1–2):251–262
Dvoretzky A, Kiefer J, Wolfowitz J (1956) Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. Ann Math Stat 27(3):642–669
Massart P (1990) The Tight Constant in the Dvoretzky-Kiefer-Wolfowitz Inequality. Ann Probab, pp. 1269–1283
Wilcoxon F (1945) Individual comparisons by ranking methods. Biom Bull 1(6):80–83
Mann HB, Whitney DR (1947) On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat 18(1):50–60
Holm S (1979) A simple sequentially rejective multiple test procedure. Scand J Stat 6(2):65–70
Kruskal WH, Wallis WA (1952) Use of ranks in one-criterion variance analysis. J Am Stat Assoc 47(260):583–621
Friedman M (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 32(200):675–701
Friedman M (1939) A correction: the use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 34(205):109–109
Conover WJ, Conover WJ (1999) Practical nonparametric statistics. Wiley, New York
Hadar J, Russell WR (1969) Rules for ordering uncertain prospects. Am Econ Rev 59(1):25–34
Gibbs AL, Su FE (2002) On choosing and bounding probability metrics. Int Stat Rev 70(3):419–435
Kolmogorov A (1933) Sulla Determinazione Empirica di una Legge di Distribuzione. Giornale dell’ Istituto Italiano degli Attuari 4:83–91
Smirnov N (1948) Table for estimating the goodness of fit of empirical distributions. Ann Math Stat 19(2):279–281, 06
Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22(1):79–86, 03
Rüschendorf L (1985) The Wasserstein distance and approximation theorems. Probab Theory Relat Fields 70(1):117–129
Rubner Y, Tomasi C, Guibas LJ (1998) A metric for distributions with applications to image databases. In: Proceedings of the sixth international conference on computer vision (ICCV). Bombay, India
Villani C (2003) Topics in optimal transportation. American Mathematical Soc, Providence
Fiedler M, Hoßfeld T, Tran-Gia P (2010) A generic quantitative relationship between quality of experience and quality of service. IEEE Netw 24(2):36–41
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest Statement
The author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seufert, M. Statistical methods and models based on quality of experience distributions. Qual User Exp 6, 3 (2021). https://doi.org/10.1007/s41233-020-00044-z
Received:
Published:
DOI: https://doi.org/10.1007/s41233-020-00044-z