Abstract
Solar meridional circulation is an axisymmetric flow system, extending from the equator to the poles (\(\sim \)20 m/s at the surface, \(\approx \)1% of the mean solar rotation rate), plunging inwards and subsequently completing the circuit in the interior through an equatorward return flow and a radially outward flow back up to the surface. This article reviews the profound role that meridional circulation plays in maintaining global dynamics and regulating large-scale solar magnetism. Because it is relatively weak in comparison to differential rotation (\(\sim \)300 m/s, \(\approx \)7% of the mean solar rotation rate) and owing to numerous systematical errors, accurate surface measurements were only first made in 1978 and initial inferences of interior meridional circulation were obtained using helioseismology two decades later. However, systematical biases have made it very challenging to reliably recover flow in the deep interior. Despite numerous advances that have served to improve the accuracy of inferences, the location of the return flow and the full extent of the circulation are still open problems. This article follows the historical developments and summarises contemporary advances that have led to modern inferences of surface and interior meridional flow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As is the case with many solar phenomena, the story of meridional circulation (MC) begins with sunspots. Sunspots appear at low latitudes and the frequency of their emergence is cyclical, in that the number of spots is modulated over a timescale of roughly 11 years. In other words, \(\sim \)11 years marks the temporal separation between successive solar maxima, when the number of sunspots reaches a local peak. Each cycle is statistically of the opposite polarity as compared to the temporally adjacent cycles. The question of why this particular timescale is one of most important open questions in solar and stellar physics (Charbonneau 2020). In recent decades, the timescale associated with the transport of magnetic flux by MC has been identified as crucial to the solar-cycle period. In particular, the flow speed and direction in the deep-interior layers is extremely important to the overall behaviour of solar magnetism. Thus, observational efforts to map MC at the surface and interior have gained prominence in recent times.
The first type of MC to be predicted was the Eddington–Sweet circulation, theoretically anticipated a century ago (1925). Rotation causes the equatorial layers to bulge slightly outwards and the poles to flatten, leading to a large-scale meridional flow straddling the poles and equator deep in the radiative zone. The Eddington–Sweet circulation has a timescale comparable to the age of the star or longer, and is not relevant for the discussion at hand. The prevalence however of an MC in the convection zone (Kippenhahn 1959), on the other hand, is a topic of contemporary interest, relevant to solar cycle prediction, angular momentum transport and the physics of convection. Despite its relatively small magnitude, MC is centrally connected to the overall angular momentum budget of the Sun.
The Sun rotates differentially, in that the rotation rate varies as a function latitude and radius (for a review, see Howe 2009). Predating the first modern measurements of MC by nearly 15 years, Kippenhahn (1963) made a striking and elegant theoretical prediction, linking differential rotation and MC. The premise of the analysis (Kippenhahn 1959) was that convection in the stratified solar interior broke the isotropy of fluid motion. Radial motion is significantly more constrained than in the lateral direction, which Kippenhahn (1963) modelled using an effective anisotropic kinematic viscosity. He further showed that this would lead to both differential rotation and MC, closely tying these features to convective turbulence. This was in line with the work of Lebedinsky (1941), who had already anticipated the connection between turbulent motions and differential rotation two decades prior. Although these ideas have been refined since, the foundation of convection as a driver of large-scale circulations had thus been established.
MC is an axisymmetric flow system, with fluid moving from the equator towards the poles at the surface. Because the circulation is mass conserving, the loop has to be closed; thus, the fluid submerges into the interior at high latitudes, switches direction and drifts towards the equator at some depth. The loop is completed at the equator when the flow turns radially outward and reconnects with the poleward flow at the surface. This picture may possibly be more complicated, with multiple cells in latitude and radius. Measuring the depth at which the direction of MC reverses, the flow speed and direction at the base of the convection zone and whether it penetrates into the radiative interior are questions of outstanding contemporary importance.
Mean-field theory has significantly advanced our understanding of MC and elucidated the profound role that MC plays in regulating global solar dynamics. The application of these techniques to characterise the delicate angular momentum balance struck between rotation and MC is at a mature stage. Mean-field theory cannot by itself predict details of the turbulent flows that persist in the convection zone, but rather, relies on closure models that need to be independently provided. Modern numerical simulations, however, appear to make notably different predictions of rotation and MC. Observational constraints can help resolve these differences, i.e., between mean-field predictions and simulations, by providing detailed images of flows prevalent in the solar interior. Unfortunately, this too has proven to be challenging owing to observational systematics and realization noise, and although several advances have been made, much still remains to be accomplished.
2 Surface observations of MC
Even at the surface, MC has proven difficult to measure accurately, primarily because of its small amplitude and systematical biases of comparable magnitudes. Unfortunately, a silver-bullet technique does not exist; we describe various approaches, the benefits and attendant drawbacks.
2.1 Sunspot tracking
The first measurements of MC, obtained by analyzing the latitudinal motion of sunspots (Dyson and Maunder 1913; Tuominen 1942), suggested that it was equatorward at low latitudes and poleward at high latitudes. The proper motions of sufficiently long-lived sunspots (\(\sim \) 2 weeks) have the added benefit of being easily identifiable at the photosphere. Using a more substantial dataset of sunspot motion, Ward (1973) constrained MC at low latitudes to be less than 1 m/s. Other studies have arrived at very different conclusions, e.g., Ribes et al. (1985) found large alternating flows on the order of 100 m/s, Howard and Gilman (1986) also estimated pole- and equatorward alternating flows, and Kambry et al. (1991) measured 20 m/s equatorward MC below \(20^\circ \) in latitude and poleward at high latitudes. Using sunspots to measure MC turns out to be problematic because they do not move at the speed of the plasma, and additionally, there are very few sunspots at high latitudes and cycle minima (e.g., Jiang et al. 2014). In Figs. 1 and 2, we show measurements of differential rotation and MC respectively using sunspot tracking (both taken from Jiang et al. 2014).
2.2 Magnetic-element tracking
Tracking small magnetic elements is one of the most powerful and reliable methods with which to measure surface MC (Schroeter and Woehl 1975; Topka et al. 1982; Komm et al. 1993; Latushko 1994; Meunier 1999, 2005; Hathaway and Rightmire 2010, 2011; Rightmire-Upton et al. 2012). In fact, Hathaway and Rightmire (2010) demonstrated that it is possible to measure MC at high latitudes (\(75^\circ \)) using this technique. The idea is to track the axisymmetric drift of small magnetic elements, allowing for constraining both differential rotation and MC. These elements tend to evolve over relatively short timescales, making them difficult to identify over multiple disparate temporal windows. The other issue is that they move at velocities different than that of the plasma at various latitudes (although not quite as dramatically different as sunspots), attributed by Dikpati et al. (2010) to differing rates of magnetic diffusion. Magnetic elements are likely rooted at different depths, thereby influencing their estimation of surface flows. In Figs. 1 and 2, we show measurements of differential rotation and MC respectively using motions of magnetic elements (both taken from Jiang et al. 2014).

Image reproduced with permission from Jiang et al. (2014), copyright by Springer
Comparison of surface differential rotation estimates obtained using different techniques; a mean background rotation rate has been subtracted. The magnetic-element tracking estimate is reproduced from Komm et al. (1993), global helioseismology inference at \(r=0.995\,R_\odot \) from Schou et al. (1998), individual-sunspot tracking data from Howard et al. (1984) and direct-Doppler measurement from Ulrich et al. (1988). Differential rotation, which is thought to be extremely well known, registers differently in amplitude between different techniques. Note that sunspot inferences extend only to latitudes of \(\pm 30^\circ \). Each technique is evidently differently sensitive to plasma motions, i.e., magnetic elements may be shallow and susceptible to drag, Doppler inferences rely on measurements of lines formed at the photosphere, sunspots are rooted at different depths, rotating therefore at a different rate and helioseismology uses modes that sample the near-surface layers in a specific manner, all thus providing different inferences.

Image reproduced with permission from Jiang et al. (2014), copyright by Springer
Comparison of surface MC obtained using different techniques; the magnetic-element tracking estimate is from Komm et al. (1993), local helioseismology inference at \(r=0.998\,R_\odot \) from Basu and Antia (2010), sunspot-group tracking data from Tuominen and Kyrolainen (1982) and direct Doppler measurement from Hathaway (1996). While sunspots are poor estimators of MC, the other techniques are in fair agreement. This is somewhat surprising given the sizeable differences seen in Fig. 1.
2.3 Doppler estimation
Modern estimates of MC began with Duvall (1978), who analyzed one year’s worth of daily averages of Doppler images, measuring an equatorial rotation rate of 447 nHz and MC of around 20 m/s between 10\(^\circ \) and 50\(^\circ \) in latitude. These estimates have more or less held steady since, although the matter, in equal parts, has become simultaneously clearer and more complicated. The benefit of using Doppler data is that it can provide insight into surface flows at latitudes as high as \(\sim 80^\circ \), provided that appropriate centre-to-limb corrections are applied (Hathaway 1996; Ulrich 2010).
Doppler measurements of MC are primarily complicated by the convective blueshift, an effect that can significantly affect inferences. This shift, loosely related to the centre-to-limb effect in helioseismology, occurs due the correlation between velocity and intensity in unresolved granulation (Beckers and Nelson 1978; Baldner and Schou 2012). It presents as a strong blue shift at the disk centre, decreasing towards the limb, and can even turn into a red shift depending on the absorption line used to perform the analysis (e.g., Hathaway 1996). Removing this shift is critical to retrieving the correct sign and amplitude of MC, as evidenced by inconclusive early results on the topic (Duvall 1978; Beckers and Nelson 1978; Duvall 1979; Perez Garde et al. 1981; Labonte and Howard 1982; Snodgrass 1984; Cavallini et al. 1985, 1986), which span large ranges in amplitude, from 5 to 100 m/s, ambivalent estimates of the flow direction—equatorward and poleward by different studies, and a varying number of cells in latitude. Of these many results, Duvall (1979) stands out, not just due to its accuracy, but because it was the first to subtract the blueshift estimated along the East-West direction from the North-South Doppler velocity. This method allowed Duvall (1979) to correctly estimate the flow amplitude (\(\sim \)20 m/s) and the direction. Hathaway (1996) also obtained similar results, although finding temporal swings in the amplitude, possibly indicating why earlier studies arrived at such different conclusions. Ulrich et al. (1988) and Ulrich (2010) found evidence of a high latitude (\(>60^\circ \)) equatorward MC, although this has not been corroborated by other lines of evidence (Hathaway and Rightmire 2010, 2011).
2.4 Supergranular waves and tracking
Supergranules are convective features of spatial scales \(\sim \)35 Mm, time scales \(\sim \)36 h (Rincon and Rieutord 2018). They dot the surface of the Sun and are advected by solar rotation and MC. The benefits of using supergranules as tracers or diagnostic agents are that they are stable, easily identified at the photosphere and Doppler data are able to capture their motions at high latitudes with fidelity.
Gizon et al. (2003) analysed the spatio-temporal evolution of flow-divergence spectra of supergranules, obtained using time-distance helioseismology applied on the surface-gravity (f) mode (Duvall and Gizon 2000), a measurement dominantly sensitive to the uppermost 2 Mm below the photosphere. They showed that supergranules are actually wave-like phenomena, with a clearly observed dispersion relation. This result has since been confirmed using different techniques, both seismic (Hanson et al. 2021) and non-seismic (Langfellner et al. 2018). These waves are observed to propagate in all directions, providing a powerful means by which to measure underlying flows. Much as rotation is inferred by measuring the induced seismic mode-frequency splitting, flows locally Doppler shift the supergranular waves. For instance, consider the high-latitude branch of MC. Northward propagating supergranular waves would be sped up and their frequencies would therefore reduce by the amount kV, where k is the wavenumber in the north-south direction and V the local meridional-flow speed. Similarly, southward waves would show an increase in frequency by kV. Thus, the difference the two frequencies from each other can be used to infer local meridional flow, a principle exploited first by Gizon et al. (2003). Schou (2003) showed that the wave-like behaviour of supergranules could also be retrieved from Doppler measurements. Applying the dispersion analysis described above, Schou (2003) extended inferences of MC up to high latitudes (\(\sim 80^\circ \)), finding no signs of an additional latitudinal cell.
Supergranules show a power spatial power spectrum spread over a broad range of scales and are known to exhibit super-rotation at all latitudes (Beck 2000; Rincon and Rieutord 2018). Hathaway (2012) measured the rotation rates of supergranules as a function of their scale. Keeping in mind that the Sun exhibits radial differential rotation, i.e., the rate changes as a function of depth, Hathaway (2012) attributed the supergranular rotation rate variations to the depths at which the supergranules are rooted, thus obtaining a calibration between supergranular scale and its depth. Hathaway (2012) then tracked the supergranules as features, measured their north-south motions as a function of spatial scale. Using the calibration between the supergranular scale and its depth, Hathaway (2012) inferred an equatorward meridional flow at a depth of 70 Mm, an unusually shallow determination of the reversal. However, Hathaway (2012) did not explicitly account for the time evolution of the supergranulation pattern, i.e., did not account for the propagation of the supergranulation pattern in the prograde direction and towards the equator, thereby calling into question this interpretation. Additionally, the depths to which supergranules penetrate have not been independently determined (e.g., Hanasoge and Sreenivasan 2014).
Local-correlation tracking, a widely adopted method (November and Simon 1988) uses the proper motions of granules or supergranules to measure large-scale flows. Using supergranular tracers, Švanda et al. (2008) have demonstrated the ability to measure MC using this method, obtaining consistently poleward flows up to latitudes of about \(40^\circ \), beyond which they see equatorward flows for some datasets.
2.5 Granulation tracking
Roudier et al. (2018) tracked the proper motions of granules to obtain MC estimates that are in general agreement with the results of Švanda et al. (2008); they too observe an equatorward flow at latitudes beyond \(45^\circ \). Because the centre-to-limb effect arises due to flows associated with granules (Baldner and Schou 2012), MC measurements are particularly challenging when using granules. The fidelity and ease of granulation tracking has greatly improved since the advent of HMI, since the observations are of high enough resolution (\(4096\times 4096\) pixels) and images are taken at sufficient temporal cadence as to spatially capture granules and trace their temporal evolution.
2.6 Ring diagram analysis
Ring diagram analysis (RDA Hill 1988) uses shifts in the frequencies of high-degree normal modes over finite spatial patches on the surface to infer the underlying average flow. High-degree modes are typically associated with large linewidths, i.e., short lifetimes, and therefore decay before creating global resonances. As a consequence, they sample local parts of the Sun, and can be used to measure the mean drifts in that region. The solar surface is covered with patches of a given size and the mean flow associated with each patch is thus inferred. The mean flows over these patches taken together provide a low-resolution image of the circulation at the surface. The resolution that RDA affords is sufficient to capture the spatially smooth MC—inferences thus obtained have proved to be trustworthy (Schou and Bogart 1998; Basu and Antia 2000; González Hernández et al. 2008; Komm et al. 2015, 2020; Lekshmi et al. 2019). These are particularly useful in studying the variation of MC with the solar cycle, as shown in Fig. 11, and measuring the extent of cross-equatorial flow (i.e., only in the near-surface layers). The centre-to-limb systematical error, for instance, can be somewhat alleviated by applying RDA to regions in the vicinity of the central meridian (e.g., Gough and Hindman 2010). In general, because RDA uses mode frequencies to make inferences, its robustness and reliability is comparable to that of global-mode helioseismology (the gold standard in a manner of speaking).
3 Role of MC in global angular momentum transport and balance
The theoretical importance of a circulation straddling the equator and poles was recognized early on (e.g., Lebedinsky 1941; Kippenhahn 1959, 1963). Detailed expositions on the critical role played by MC in angular momentum balance in the context of mean-field theory date back many decades (e.g., Durney 1974; Ruediger 1989; Kichatinov and Rudiger 1993; Durney 1999, 2000, 2003; Miesch 2005; Rempel 2005; Dikpati 2014; Choudhuri 2021).
To illustrate the delicate balance that is struck in solar convection zone, we first study the zonal component of the angular momentum equation, which is derived from the governing non-linear magnetohydrodynamic equation (e.g., Miesch 2005). This equation is further simplified by computing longitudinal and temporal averages, denoted by angular brackets \(\langle \rangle \) around each term,
We adopt spherical coordinates \((r,\theta ,\phi )\), which are radius, co-latitude and longitude respectively, \(\varvec{\nabla }\) is the covariant spatial derivative, \(\rho \) density, \(u_\phi \) and \(B_\phi \) are longitudinal velocity and magnetic field, \(\mathbf{u}_m\) and \(\mathbf{B}_m\) are the mean meridional velocity and magnetic field, \(\varOmega (r,\theta )\) is differential rotation and \(\nu \) is viscosity. Primed variables denote spatio-temporal fluctuations around the background terms, which are denoted as unprimed quantities. The meridional term comprises radial and co-latitudinal components.
Angular rotation rate \(\varOmega (r,\theta )/(2\pi )\) as a function of radius and latitude (upper-left panel), the rotation rates at specific latitudes as a function of radius (right panel) and contours of constant angular momentum per unit mass (bottom-left panel) \(\varOmega \,r^2\sin ^2\theta \), from internal rotation deduced using global-mode helioseismology (Larson and Schou 2018)
Typically, the Lorentz-stress terms and viscous dissipation are ignored or prove to be small (e.g., as predicted in numerical simulations Miesch 2005; Karak et al. 2014), although they may indeed be significant in reality (see more recent work by Hotta and Kusano 2021, who identify magnetism as a significant driver, especially in the near-surface layers). This simplifying assumption reduces the balance to between meridional transport of angular momentum (per unit mass) \({{\mathcal {L}}} = r^2\sin ^2\theta \,\varOmega \) and the Reynolds stresses, \(\langle u'_\phi \mathbf{u}'_m\rangle \). In the formalism of the anelastic approximation (e.g., Gough 1969), \({\varvec{\nabla }}\cdot (\rho \mathbf{u}_m) = 0\), allowing us to write,
The structure of the term on the right hand side of Eq. (2), \(-\rho \mathbf{u}_m\cdot {\varvec{\nabla }}{{\mathcal {L}}}\) has important consequences:
-
Streamlines of the meridional flow (\(\mathbf{u}_m\)) are, by definition, locally parallel to the flow velocity at every point. Also useful to recognize is that \(\varvec{\nabla }{{\mathcal {L}}}\) is perpendicular to surfaces of constant \({{\mathcal {L}}}\). Thus, only meridional flows perpendicular to surfaces of constant \({{\mathcal {L}}}\) contribute to angular momentum transport.
-
If the Reynolds stress term were zero in Eq. (2), then the meridional transport of angular momentum would also have to be zero, implying \(\varvec{\nabla }{{\mathcal {L}}}\) is perpendicular to the flow streamlines. Thus, a poleward MC, as we observe in the Sun, would indicate \({{\mathcal {L}}}\) is constant along MC streamlines, i.e., not changing as a function latitude. However, since the the lever arm reduces at high latitudes, this would require the poles to spin up in relation to the equator, contrary to what we see in the Sun, as seen on upper-left panel of Fig. 3. Indeed, we observe that the surfaces of constant angular momentum are approximately cylindrical (bottom-left panel of Fig. 3), and \(\varvec{\nabla }{{\mathcal {L}}}\) points away from the rotation axis. Thus, Reynolds stresses play an important role in maintaining this balance.
-
The direction of MC is decided by the sign of the divergence of the Reynolds stress. In other words, when \({\varvec{\nabla }} \cdot (\rho r \sin \theta \,\langle u_\phi ^\prime \mathbf{u}_m^\prime \rangle )<0\), MC points away from the rotation axis and vice versa, since the angular momentum gradient points away from the rotation axis (see Fig. 3. lower-left panel). This principle is known as gyroscopic pumping (e.g., Miesch and Hindman 2011, and references therein). An analysis of MC and convection in numerical simulations confirms this simple and elegant idea (see Fig. 4).
-
The uppermost layers of the convection zone are dominated by vigorous turbulent flows and strong photospheric cooling. Descending convective plumes, produced in the relatively cool intergranular lanes transport angular momentum radially into the interior, resulting in \({\varvec{\nabla }} \cdot (\rho r \sin \theta \,\langle u_\phi ^\prime \mathbf{u}_m^\prime \rangle )>0\), as seen in the left panel of Fig. 4. This in turn induces an MC pointing towards the rotation axis, i.e., a poleward directed flow at the surface. At some depth, these plumes are slowed down and the inward transport of angular momentum ceases. This induces an equatorward circulation and closes the loop.
-
There are three terms in Eq. (2), of which we know the rotation rate from helioseismology (Schou et al. 1998). Thus, substituting different models of MC or Reynolds stresses allows for determining the other term (e.g., Durney 2000), a means by which mean-field perdictions are made.

Image reproduced with permission from Karak et al. (2014), copyright by Springer
Illustration of the principle of gyroscopic pumping from numerical simulations; the Anelastic Spherical Harmonic (ASH) code was used to obtain this result (Featherstone and Miesch 2015). The sign of the divergence of the Reynolds stresses determines the direction of MC. Negative \({{\mathcal {F}}}_c\), indicated by red, implies meridional flow directed away from the rotation axis and vice versa (indicated by blue). At low latitudes, \({{\mathcal {F}}}_c\) is negative in the upper convection zone and positive in the deeper layers, and as a consequence, we anticipate counter-clockwise MC in the shallower layers and clockwise in the deeper region. A cell is also seen at higher latitudes, associated with the sign of the Reynolds stresses there. These expectations are confirmed by panel c, which shows the temporally averaged stream function; red indicates counter-clockwise cells and blue denotes clockwise circulation. The differences in the simulated convective flows in the low latitudes (dominated by banana cells) and high latitudes (ballistically descending convective plumes) are thought to result in different Reynolds stress distributions, in turn inducing MC.
The second independent and important relationship that is relevant to the discussion at hand is the zonal component of the curl of the momentum equation. The temporally stationary longitudinal-vorticity equation captures the balance between the deviation of rotation from constancy on cylinders and two driving terms: baroclinicity and fluid and magnetohydrodynamic stresses. A barotropic fluid is one where the pressure \(p = p(\rho )\) is solely a function of density, resulting in the pressure term in the momentum equation, \((\varvec{\nabla } p)/\rho = \varvec{\nabla } F\), where F is some function of \(\rho \). Thus, the curl of this term is zero, and would vanish from the subsequent vorticity equation (which is derived by taking the curl of the momentum equation). A baroclinic fluid is one where pressure is a function of not just density, leading to \({\varvec{\nabla }}{\varvec{\times }} [({\varvec{\nabla }}p)/\rho ] \ne \mathbf{0}\). In an exactly stationary state, the baroclinic driving, Reynolds stresses and the term arising from the deviation from cylindrically aligned rotation should balance,
where \(\varOmega _0\) is the background solid-body rotation, \(\varOmega \) denotes differential rotation, g(r) is gravity, \(C_p\) is the specific heat at constant pressure, \(z = r\cos \theta \) is the coordinate along the axis of rotation, \(\langle S\rangle (r,\theta )\) is the mean entropy averaged over longitude and time and the forcing term \({{\mathcal {F}}}\) is given by
where \(\hat{\varvec{\phi }}\) is the unit vector in the longitudinal direction. Magnetic fields and convective flows are relatively weak in the deep interior (e.g., Miesch and Hindman 2011; Karak et al. 2014), and the balance is therefore likely given by \(\varOmega _0\partial _z\varOmega \approx {g/(2C_p r)}{\partial _\theta \langle S\rangle }\), a state termed thermal wind balance. Thus, baroclinic driving must solely sustain deviations from cylindrically aligned rotation contours in the deep interior. This equation governs the ‘thermal-wind component’ of rotation, i.e., the part of rotation that deviates from constancy on cylinders. If the latitudinal entropy gradient were zero, \(\varOmega \) would be constant on cylinders, i.e., independent of z (the celebrated Taylor–Proudman state.)
Latitudinal entropy gradients are typically attributed to rotation, which causes the equatorial layers to spread outward due to centrifugal forces, with the poles slightly flattened in relation. Being slightly closer to the core, the poles are expected to be warmer as compared to the equator (entropy gradients can also set up latitudinal thermal fluxes.) Additional reasons include the efficiency of convection, which may change as a function of the angle between the local direction of thermal transport (radially outwards) and the rotation axis. For instance, at the poles, the axis of rotation and thermal transport direction are co-aligned, whereas they differ by \(90^\circ \) at the equator. This anisotropy of convective efficiency may serve to thus create a latitudinal entropy gradient. Indeed, an equator-to-pole latitudinal temperature gradient (poles being hotter), on the order of 1.5 K (Kuhn et al. 1998) and less than 2.5 K (Rast et al. 2008), is observed using intensity measurements.
Solar thermal convection is a statistically stationary process, although the magnetic cycle is capable of modulating it, especially in the surface layers. The non-detection of vigorous convective motions in the bulk of the convection zone (Hanasoge et al. 2012) and the observed depletion of power on large scales (van Ballegooijen 1986; Lord et al. 2014; Hanasoge et al. 2016) likely suggests that the bulk of the convection zone is largely adiabatically stratified and therefore persists in a rough state of thermal-wind balance (Kitchatinov 2016).
Thermal-wind balance is only approximately valid: small deviations from the state establish MC that transports thermal flux and angular momentum to re-engineer a balance. For instance, differential rotation is observed to undergo systematic changes—on the order of 10 m/s—as a function of latitude and phase of the solar cycle (first detected and termed ‘torsional oscillations’ by Kosovichev and Schou 1997; see also Howe et al. 2000 and Howe 2008]). In contrast, surface measurements of MC suggest correlated variations on the order of 2–4 m/s, as reported by Gizon and Rempel (2008). Numerical calculations are able to explain the observed flow variations—both the torsional oscillations and MC variations in the surface layers (Rempel 2006a, b; Gizon and Rempel 2008). However, Hazra and Choudhuri (2017) and Choudhuri (2021) argue that detailed calculations and simple scaling relations would imply much larger variations in MC than the torsional oscillations, a matter that remains unresolved.
Significant turbulent motions are observed only at the surface layers of the Sun, driven by radiative cooling at the upper boundary, a region where thermal-wind balance is possibly inapplicable (although fluid motions on large scales at the surface are measured to be weak, e.g., Hathaway et al. 2015; Roudier et al. 2018; Kashyap and Hanasoge 2021). As Miesch and Hindman (2011) and Karak et al. (2014) note, the Reynolds stress forcing term in the near-surface shear layer, which is spatially coincident with vigorous convection (Stein and Nordlund 2000), will likely dominate, suggesting that \(\varOmega _0\partial _z\varOmega \approx {{\mathcal {F}}}\) in these layers.
While MC does not explicitly appear in these equations, the forcing \({{\mathcal {F}}}\) has been modelled as the eddy viscous resistance to meridional driving (Kitchatinov 2012; Dikpati 2014). This formulation has been used widely invoked over the past several decades in a series of papers on the topic by Ruediger (1989); Kichatinov and Rudiger (1993) etc. Reproducing Eq. (2.2) of Kichatinov and Rudiger (1993), the diffusivity \({{\mathcal {F}}}\) is connected through a fourth-rank viscosity tensor to the gradients of MC, i.e., \({{\mathcal {F}}} = -\varepsilon _{\phi j k}\partial _j[\rho ^{-1}\partial _l({{\mathcal {N}}}_{klpq}\partial _q V^m_p)]\), where \({{\mathcal {N}}}\) is the viscosity tensor, \(\rho \) density, \(\partial _j\) the derivative along the j direction, \(V^m_p\) the mean MC, with subscript p referring to the component and \(\varepsilon _{\phi jk}\) is the Levi-Civita symbol with the first index set to the longitudinal direction. Models of \({{\mathcal {N}}}\) must either be introduced by hand or obtained from numerical simulations.
In summary, the longitudinal momentum and thermal-wind balance equations serve as the foundations from which to generate models of differential rotation and MC. Although the broad principles are relatively simple, the eventual formulation is non-linear and a variety of different approaches with differing extents of complexity have been applied to solve the mean-field equations.
4 Role of MC in the flux-transport dynamo model
The solar cycle is one of the most important aspects of the Sun—from both physics and practical perspectives. Despite substantial observational constraints on solar interior, surface, atmospheric and heliospheric physics, a comprehensive understanding of what drives solar magnetism continues to elude us. There are many compelling theories of solar dynamo action, and it is beyond the scope of the present article to describe them at any length, although there are many thorough reviews of the topic (e.g., Charbonneau 2020). These models have attempted to explain the following prominent aspects of solar magnetism:
-
1.
Sunspots, which have lifetimes of around 2–3 weeks, appear in plenty during periods termed as “solar maxima”. Their appearance gradually wanes and and they nearly disappear, marking the period known as “solar minima”. Two consecutive maxima are observed to be spaced roughly 11 years apart.
-
2.
Observations show that during minima, poloidal field has the largest magnitude (on the order of 1–2 Gauss; e.g., Hathaway 2015) and during maxima, toroidal field of magnitude 1–2 Gauss dominates (e.g., Cameron et al. 2018). These correspond to fluxes of \(\sim 2\times 10^{23}\) Mx in the toroidal and \(\sim 10^{22}\) Mx in the poloidal directions. The sign of the poloidal field reverses every 11 years.
-
3.
Sunspots typically appear in pairs (“bipolar active regions”) that are of opposite magnetic signs, i.e., the “leading” sunspot may show positively signed field and the “following” sunspot a negative sign. In a given hemisphere, the leading sunspot generally shows the same polarity over the duration of the cycle.
-
4.
The cycle has a very well defined progression, with sunspots erupting at latitudes of around \(30^\circ \) at the start of the cycle (immediately following the preceding minimum), and emerging at lower latitudes with the evolution of the cycle. By the end the cycle, new field appears very close to the equator.
-
5.
Bipolar active regions show a statistical tilt (“Joy’s law”), with the line joining the centres of the two poles inclined at a small angle such that the leading spot is statistically slightly closer to the equator than its following counterpart. The tilt angle increases with latitude although a large amount of scatter is observed.
-
6.
The spot cycle is known to have entered into an extremely quiet period from 1645–1715, known as the “Maunder minimum”. Some evidence suggests that there have been other epochs in time where the Sun has passed through such extended or “grand” minima.
Early models of the cycle did not incorporate MC (for details, see, e.g., Hathaway 2015; Charbonneau 2020) but measurements of surface and interior differential rotation, MC and a theoretical appreciation for their role in establishing the dynamo brought forth the contemporary era solar cycle modelling (although Babcock 1961 had speculated about the existence of a poleward MC). In the current flux-transport model (Wang et al. 1991; Choudhuri et al. 1995; Durney 1995), the interchange between poloidal and toroidal magnetic field is mediated by a combination of differential rotation and MC. Poloidal flux (of the current cycle) from the equator is transported by MC to the poles at the surface, cancelling the poloidal field from the previous cycle and creating new field, of the opposite sign as that of the preceding cycle. This field is dragged down to the deep interior by the inward traversing component of the MC loop, where it is stably held against magnetic buoyancy by the sub-adiabatic layers. The poloidal field strength would not need to be very strong at all; indeed, differential rotation winds up the poloidal field, converting it into toroidal field in this process and gradually strengthening it over several rotation periods. Magnetic buoyancy associated with sufficiently strong toroidal field would cause it to rise into the convection zone, where, acted on by Coriolis force, it would gain a twist, manifesting as the inclination of bipolar active regions at the surface in opposite senses in the two hemispheres. The time taken to complete a full meridional circuit by a fluid element being advected by the MC would then set the timescale of the dynamo cycle (Hathaway et al. 2003; Gizon et al. 2020). Thus MC plays a profound role in regulating the cycle period—faster MC implies shorter cycles and rapid reversal of poloidal fields, thereby influencing cycle amplitude. During relatively long magnetic cycles, two major processes involved in regulating the dynamo, diffusion and amplification of toroidal field (by differential rotation), compete. If diffusion were to be the stronger of the two, weaker cycles would result and vice versa (e.g, Karak et al. 2014). Weak MC can disrupt the cycle by lengthening it enough to even set off a grand minimum. Multiple cells in latitude and/or radius can ostensibly reverse the direction of drift of sunspots. Hazra et al. (2014) however demonstrated that the observed cycle can still be reproduced in simulations provided MC at the base of the convection zone is directed equatorward. Indeed, Cameron and Schüssler (2017) have shown that what controls this process is the average MC in the region where toroidal flux is stored, because the term \(\mathbf{v}{\varvec{\times }}{} \mathbf{B}\) governs the induction equation. The flux-transport dynamo model has been widely accepted in the community (Charbonneau 2020). Additional evidence such as cycle-correlated temporal variations in the surface measurements of MC and interior inferences (see Sect. 8) have given weight to the theory and guided recent interpretations of the lengths and amplitudes of cycles.
5 MC in numerical simulations
Ever since the seminal calculations by Gilman and Glatzmaier (1981), global simulations of solar convection have been seen as an important tool with which understand the Sun. The advent of modern computing and more accurate numerical methods have led to an explosion of sophisticated 3D models of the solar convection zone, and millions of core hours are dedicated today to simulating the dynamics of solar and stellar convection zones (see, e.g., Kupka and Muthsam 2017, for a review). Owing to the vastly disparate spatial and temporal scales in the problem, these are very challenging calculations to perform, and, without sufficiently robust theoretical guidance, they are generally unable to access the correct convective regime (e.g., Rast 2020). In addition to the enormous dynamical range, flows such as MC, which are weak but critically important to large-scale dynamics, emerge as a consequence of a delicate balance between plausibly large terms—differential rotation and convective Reynolds stresses, not easily achieved in dynamical simulations.

Image reproduced with permission from Featherstone and Miesch (2015), copyright by AAS
Differential rotation (upper panels) and corresponding MC profiles (lower panels) from numerical simulations of spherical convection in a shell spinning at rotation rates ranging from \(2\varOmega _0\) down to \(0.75\varOmega _0\), where \(\varOmega _0 \approx 420\,\mathrm{nHz}\) is the nominal solid-body solar rotation rate. The colourbar limits associated with each of the upper plots are indicated in units of nHz, e.g., \(-20\) nHz and 200 nHz as the lower and upper limits on panel e. The red and blue colours in the lower panels indicate counter-clockwise and clockwise motions respectively. As the fluid spins faster, the rotation is more solar-like in that the equator rotates faster than the poles. The corresponding MC profile acquires multiple cells in latitude and radius. At lower rotation rates, the poles are seen to spin up relative to the equator and the MC profile becomes unicellular.
A major question relates to the conditions that lead to equatorial spin up relative to the poles, i.e., solar-like latitudinal differential rotation in stars, and how to transition the system to anti-solar behaviour (where the poles rotate faster than the equator). Numerical simulations appear to indicate that weakly rotating systems, i.e., where the Rossby number \(Ro = \omega _c/\varOmega \gtrsim 1\), where \(\varOmega \) is the rotation rate and \(\omega _c = 2\pi /\tau _c\) is the inverse convective turnover timescale, generate anti-solar differential rotation. These are typically associated with a single-cell MC directed poleward in the upper convection zone and surface layers. In rapidly rotating systems, where \(Ro \ll 1\), solar-like latitudinal differential rotation is recovered, along with a multi-cellular (in both latitude and radius) MC. These flows are directed poleward in the upper convection zone as well. A variety of different numerical calculations agree with this broad view (e.g., Gastine et al. 2013; Guerrero et al. 2013; Käpylä et al. 2014; Gastine et al. 2014; Featherstone and Miesch 2015) and an illustration of this is shown in Fig. 5. These experiments do not allow us to conclude that the Sun is a fast rotator—they merely suggest that the best calculations available to us all appear to computationally access similar convective regimes and therefore see comparable behaviour. In any case, MC in simulations is quite different in shape and structure from that of the Sun.
5.1 Mean-field description of MC
The mean-field approach involves taking temporal and longitudinal averages of the governing equation, writing prescriptions for the convective flux, Reynolds stresses and latitudinal thermal gradients (e.g., Kichatinov and Rudiger 1993; Kitchatinov and Ruediger 1995). An instance of the results that are typically obtained from these calculations is shown in Fig. 6, where differential rotation and MC are obtained upon prescribing anisotropic thermal flux and Reynolds stress distributions.

Image reproduced with permission from Kitchatinov and Olemskoy (2011), copyright by the authors
Mean-field predictions of MC and differential rotation. A comparison with Fig. 3 reveals that the differential rotation profile is very similar to the Sun and the corresponding MC obtained appears reasonable: consistent with surface observations, at any rate. In this approach, Kitchatinov and Olemskoy (2011) prescribe convective flux and Reynolds stresses as functions of radius and latitude to obtain the differential rotation and MC.
In sharp contrast to 3D numerical simulations, mean-field theoretic approaches overwhelmingly predict solar-like differential rotation, with anti-solar rotation achievable only under very specific conditions (e.g., Featherstone and Miesch 2015). Indeed, Kitchatinov and Rüdiger (2004) note that only significant baroclinicity, created possibly by large magnetic spots or tidal forcing by a binary companion, would result in MC on the order 200 m/s, which in turn is capable of inducing anti-solar rotation.
This is, to some extent, in line with observations of stellar latitudinal differential rotation of Sun-like and other conventional stars, which generally appear to show solar-like contrasts (i.e., fast rotating equators; e.g., Benomar et al. 2018).
6 Interior structure of MC
Inferring MC as a function of depth is a topic of contemporary concern in helioseismology and the return flow depth of MC is among the most important questions in solar physics. Van Ballegooijen and Choudhuri (1988) have argued for a more deeply penetrating MC as a means of suppressing magnetic buoyancy and storing field at the base of the convection zone. Nandy and Choudhuri (2002) suggest that the flux transport model works best if the field were allowed to penetrate down to \(0.6\,R_\odot \). However, this has been strongly contested by Gilman and Miesch (2004), who, based on boundary-layer analyses, estimates of the expected kinetic energy of MC (velocity \(\sim \)2 m/s at \(r=0.7\,R_\odot \)), and the observed abundances of Lithium and Beryllium, argue that the maximum allowed depth of penetration of MC is \(0.7\,R_\odot \).
6.1 Helioseismology
The solar interior is optically thick and direct imaging of flows in the interior layers is therefore impossible. Helioseismology (Christensen-Dalsgaard 2002; Gizon and Birch 2005) is the only means by which to study the solar interior. Acoustic oscillations, excited by vigorous turbulent convection in the near-surface layers, propagate within the solar interior, setting up resonances at discrete frequencies and wavenumbers. These normal modes of oscillation were observed first by Leighton et al. (1962), whose speculation that they could one day be used build complex images of the solar interior was remarkable and prescient. While the full promise of the method is yet to be realised, e.g., building 3D images of the convection zone, results from helioseismology such as the inferences of structure, composition and rotation have had resounding impact, both in solar physics and astrophysics at large. Efforts are underway to build increasingly sophisticated models of solar interior dynamics while simultaneously taking into account systematical instrumental errors (for a review, see, e.g. Gizon et al. 2010).
At its heart, helioseismology is a perturbation theory. A seismic measurement, which will be defined in due course, is related through a linear equation to the perturbation of interest. A ‘perturbation’ is defined as a departure from the reference or background model of the Sun. Thus, the basic assumption is that we have a good guess for a background solar model (e.g., model S; Christensen-Dalsgaard et al. 1996), i.e., the properties of the Sun are a small deviation away from the reference model. This background is typically only a function of radius, prescribing sound speed, density, composition, gravity etc. as a function of radius r. Although more complex reference models are permitted, the general approach of choosing a temporally static, non-rotating, non-magnetic 1D background has generally sufficed. That this approach works at all is surprising, considering the broad range of spatio-temporal dynamics that the Sun displays. Indeed, it is a non-trivial consequence of the scale separation we see in the Sun: the normal-mode periods (\(\sim \)5 min) are widely separated from the temporal scales associated with supergranules (\(\sim \)36 h), large-scale magnetic field evolution (months to years), change in rotation (months to years), evolution of meridional circulation (months to years), Rossby waves (\(\sim 26\) days) etc. Additionally, most of these features possess small amplitudes, i.e., in comparison to the local sound speed, and are therefore well described in the limit of first-order perturbation theory. A prominent exception is that of sunspots (Gizon et al. 2009), which represent locally large deviations from the background state and are not well suited to description using simple perturbation theory.
Global-mode oscillation frequencies, which have been very successful at constraining solar structure and rotation, are unfortunately not very sensitive to MC. This is because, at leading order, mode frequencies are sensitive to axisymmetric (which MC is) and north-south symmetric (MC is anti-symmetric across the equator) flows. Thus MC can only cause frequency shifts at higher orders (Gough and Hindman 2010), where magnetic fields and convective flows are comparably important (Roth and Stix 2008; Swisdak and Zweibel 1999; Dziembowski and Goode 2004, 2005). For instance, Roth and Stix (2008) attempted to use quasi-degenerate perturbation theory (Lavely and Ritzwoller 1992), which models the effect of non-axisymmetric perturbations on global-mode frequencies, but encountered significant interpretational challenges. One approach is to thus turn to other, more local seismic measurements, i.e., where averages over the full disk are not taken. Time-distance helioseismology (Duvall et al. 1993), ring-diagram analysis (Hill 1988) and the Fourier-Legendre technique (Braun and Fan 1998) have been applied vigorously to this problem, and some attempts have been made at using normal-mode coupling (Woodard 1989; Woodard et al. 2013; Schad et al. 2011b).
Waves in the Sun are stochastically excited all over the surface, which implies that the observed velocity field is a zero-mean random process. Thus, without knowledge of the exact distribution of sources, the raw wavefield itself contains no information. The higher moments of the wavefield, primarily the variance and covariance, are useful. Because we observe over a finite temporal window, the associated realization noise is non-trivial and can significantly decrease the inferential quality of the measurement, especially when attempting to constrain MC in deep layers. The measurement of cross correlations of the surface wavefield velocities between pairs of points forms the basis of time-distance helioseismology (TD; Duvall et al. 1993). Waves propagating from one point to the other would cause the two-point correlation of the surface velocity field to be finite. Additionally, suppose a flow were pointed along the line joining the point pair; the travel times of waves propagating along the direction of the flow would decrease since the waves would be advected and therefore sped up. Conversely, waves propagating in the direction opposing the flow are slowed down and their travel times correspondingly increase. Waves travelling perpendicular to the ray path joining the two points would not register a time shift. This schematic picture, although complicated by so-called ‘finite-frequency’ effects, i.e., when wavelengths are comparable to the length scale of the perturbation, applies well to MC (e.g., Birch et al. 2001), whose associated length scale is likely very large in comparison to the acoustic wavelength all through the interior.
TD can, in principle, use the entirety of the available seismic information and as a consequence, capable of probing deep into the solar interior. A major challenge with TD is one of organizing the enormous amount of seismic information available in the spatio-temporal domain. Given N observational pixels, \(N^2\) cross correlations may be computed at a variety time lags \(N_\tau \), resulting in a total of \(N^2\,N_\tau \) data points. With each successive observing instrument, the quality and quantity of data has grown. For instance, HMI has a 16 Mpixel camera, of which 10 Mpixels contain potentially useful information, resulting in an astronomically large number of correlations. Of course, most of these correlations will have redundant or possess too little information to be of significance in the eventual analysis. Although seismologists have developed various rules of thumb to organize these data, much useful information is likely discarded in the analysis. The main goal thus is to maintain a sufficiently high signal-to-noise ratio to be able to infer MC in the deep interior. For instance, Braun and Birch (2008) noted that an entire solar cycle’s worth of data may be required to image flows on the order 1–2 m/s at the base of the convection zone using TD.
Ring-diagram analysis (RDA), an important seismology technique, has been described in Sect. 2.6. The horizontal patch size in RDA is typically \(15^\circ \times 15^\circ \) on the surface, and one flow velocity is output for each tile of this size, thereby providing coarse-resolution images (in comparison to other helioseismic methods, at any rate). However, because mode frequencies are the primary measurement, and because they are obtained from reasonably sized patches, the inferences are robust. Additionally, since only high-degree modes are used in the analysis, RDA can probe down to about 20 Mm in depth.
The axisymmetric non-rotating reference Sun hosts a set of modes with associated eigenfrequencies and eigenfunctions. Perturbations cause both the resonant frequencies and eigenfunctions to be altered. RDA uses changes in eigenfrequencies to infer structure whereas TD relies on eigenfunctions (at least the case for MC, e.g., Birch and Kosovichev 2001). Normal-mode coupling (Woodard 1989; Dahlen and Tromp 1998) also extracts information present in eigenfunction deviations. Nominally, the eigenfunctions of the wave operator in spherical geometry for modes in a solely radially stratified medium are spherical harmonics multiplied by radial functions. Thus, each mode is identified by three quantum numbers, \((\ell , m, n)\), the harmonic degree, azimuthal order and radial order, respectively. However, flows and rotation alter the operator so that spherical harmonics are no longer the correct eigenfunctions, and the radial dependence of these flows also changes the radial form of the eigenfunction. Keeping in mind that we are only able to observe the wavefield at the surface, we can, at best, measure the departure of the lateral part of the eigenfunction from spherical harmonics. This is obtained by measuring correlations of the global-mode series across harmonic degree; a robust theory links these measurements to flows in the interior (Woodard 2014; Hanasoge et al. 2017). Two important benefits of mode coupling are that it allows for modelling the range of systematical biases introduced by line-of-sight observations, and because the correlations are taken in the spectral domain, the entirety of seismic mode information can be used. Since global modes are used in these analyses, the method has, in principle, access to all depths.
6.2 Data sources
Helioseismology can only be performed on sufficiently high-cadence (\(\sim \)60 seconds between consecutive images or more frequently) observations of the Sun. Some of the most significant results over 1980s and 1990s have been obtained through analysis of (relatively) short-sequence continuous observations taken in Antarctica (see Gizon and Birch 2005, for a brief review on this). However, long-term continuous and steady observations, which are required to investigate circulations and other phenomena in the Sun in detail, have only been possible since 1995, with the establishment of the ground-based Taiwanese Oscillation Network (TON; Chou et al. 1995, observing since 1995) and the Global Oscillation Network Group (GONG; Leibacher 1999, ongoing observational programme, from 1995–present), and the launch of space-based Michelson Doppler Imager (MDI; Scherrer et al. 1995, observations taken during 1996–2011) onboard the Solar and Heliospheric Observatory and Helioseismic and Magnetic Imager (HMI; Schou et al. 2012, ongoing observational programme, from 2010–present), onboard the Solar Dynamics Observatory.
7 Systematical errors
Accurate estimates of MC require that all known systematical errors be corrected for. To the best of our knowledge, each of the biases described below affect all methods of helioseismology, although to varying degrees (depending on the type of measurement, modes that are used etc.), and reliable inferences can only be made if these are removed from seismic measurements.
7.1 Centre-to-limb bias
The single most important problem in inferring MC is the infamous centre-to-limb systematic, far more critical than optimising the signal-to-noise ratio of the seismic measurements. The effect is comparable to or dominates the expected MC signal by many times, depending on the measurement (see Fig. 7). While the origins of the systematic are a matter of some debate, it is reflected in seismic measurements as arising due to a fixed flow originating from disk centre to the limb, and does not rotate along with the Sun, which is one way in which it was recognized as a systematic. In TD analyses, the bias is most pronounced for waves travelling large distances, especially if one of the correlation points were to be close to the limb and the other proximal to disk centre. Although already known informally to some in the community, Duvall and Hanasoge (2009) were the first to formally discuss the effect in the context helioseismology. Duvall and Hanasoge (2009) noted that light emerging from the disk edge would be delayed by roughly \(R_\odot /c \approx 2.3\, \mathrm{s}\), where c is the speed of light, in comparison to the centre, with the phase lag linearly decreasing from the limb to the centre. Thus, seismic measurements at the disk edge would have an intrinsic 2.3 s time lag in comparison to the disk centre. Measurements of correlations between a point at the centre and another at the limb would indicate a fixed and non-rotating inflow to disk centre. However, we actually observe an outflow from disk centre, indicating that additional systematical biases are present. It is now speculated that this arises due to a combination of radiative-transfer processes resulting in a changing height of observation from the centre to the limb and the asymmetry of rising and descending radial granulation flows (due to the steep stratification of the near-surface layers; Baldner and Schou 2012). Bhattacharya et al. (2015) theoretically calculated the effect of a field of temporally evolving granules with spatial scales much smaller than the wavelengths of acoustic waves propagating through, finding that this would introduce tensor terms to the wave equation. But this was never implemented in the context of modelling the centre-to-limb bias, although its effect could be important to include. Unfortunately, the centre-to-limb effect is still remains to be fully explained and a derivation from first principles is lacking.
Centre-to-limb effect (panel A), as measured by Liang et al. (2017); Chen and Zhao (2017) and Rajaguru and Antia (2015), three disparate efforts. The close agreement between the results, despite many differences such as the use of high-resolution data by Chen and Zhao (2017) and Rajaguru and Antia (2015) whereas Liang et al. (2017) analyzed a lower-resolution version of the observations (corresponding to ‘medium-\(\ell \)’), suggests a robustness to the estimates. The systematic is also a function of instrument, as seen in the difference between the MDI and HMI curves. Panel B shows the final MC travel-time signal (Gizon et al. 2020), obtained after removing all the systematical errors. Strikingly, the MC signal is directly comparable to the centre-to-limb bias, which is why it is critical to account for
The systematic varies with choice of measurement, e.g., seismic travel times retrieved from line-core and Doppler observations show opposite trends with different latitudes (Zhao et al. 2012). They are also sensitive to the instrument and period of observation (see Figs. 7 and 8). In particular, instrumental effects are likely play a very important effect. As seen in Fig. 8, the bias is very weak at the start of the MDI campaign and secularly grows with time, implicating changes in the instrument. An unexpected coincidence is the comparable extents of biases of HMI (launched in 2010) from MDI (14 years old by that point) over the period 2010–2011.

Image reproduced with permission from Liang et al. (2018), copyright by ESO
The temporal evolution of the anti-symmetrized (about the equator) north-south travel-time shifts is shown in the upper panel and anti-symmetrized (about the central-meridian) east-west shift (lower panel). Each circle or cross represents a measurement obtained from one month’s worth of data, where travel times have been averaged over the distance range \(\varDelta = 6^\circ \)–\(42^\circ \) and latitude range \(20^\circ \)–\(35^\circ \) and the solid lines represent linear fits. The secular change in the biases is likely instrumental in origin. These temporal shifts in north-south travel times have a profound impact on the eventual inference of MC whereas the east-west shifts affect inferences of differential rotation. The systematic error appears to be smallest at the start of MDI’s observational campaign, gradually increasing with time.
Based on prior evidence (such as the light travel-time effect discussed by Duvall and Hanasoge 2009), this bias was initially assumed to vary only as a function of heliocentric angle. This was studied in detail by Zhao et al. (2012), who demonstrated that, by subtracting the East-West systematic bias from the desired North-South measurements (which are sensitive to MC), they were able to remove the different trends in the observations. A strong piece of evidence was that travel times computed using different raw observables all converged to the same vales after subtracting the centre-to-limb bias. Greer et al. (2013), using RDA, measured and removed the bias for each individual normal mode used in the analysis, which is perhaps the most effective means so far. They found that the the bias is a strong function of mode frequency and radial order, which was later also shown for TD by Chen and Zhao (2018) and Rajaguru and Antia (2020). Not all studies have explicitly taken into account the frequency variation, potentially pointing to the source of discrepancies between the consequent inferences (see Fig. 16).
Chen and Zhao (2017) performed a more thorough analysis, measuring the systematic bias all across the disk, and showed that it varied only as a function of heliocentric angle. Chen and Zhao (2017) also concluded that subtracting the East-West systematic from the North-South measurements was about as effective as performing the elaborate analysis all across the disk.
The simplified scheme proposed by Zhao et al. (2013) to subtract the East-West outflow signal from the North-South measurements has proven to be successful and has been used since, in all TD-based inferences of MC. Without a comprehensive theory of the centre-to-limb effect, pre-processing to remove it from the raw seismic data is (currently) not possible and the systematic bias will likely be present in all helioseismic techniques applied to measure MC. Although the empirical correction procedure described by Zhao et al. (2013) cannot be directly translated to inferences using, e.g., mode coupling, the basic concept applies. While some prior efforts have focused on inferring MC using mode coupling, they have not accounted for the centre-to-limb effect (Woodard et al. 2013; Schad et al. 2011a, b, 2012, 2013). It is critical to either formally demonstrate that the centre-to-limb effect does not extend to mode coupling and, failing that, fully account for it.
7.2 B0 angle
Earth’s orbit is inclined to the ecliptic plane at \(7.25^\circ \) (although this estimate is slightly uncertain; see, e.g., Giles 2000; Beck and Giles 2005), which implies that the angle with which we view the Sun undergoes an annual variation, and depending on the phase of the orbit, allows us to directly observe the poles and the high-latitude far side. This viewing angle, termed B0, is important to take into account when inferring MC, especially at high latitudes. For instance, Haber et al. (2002) observed an equatorward flow at latitudes beyond \(60^\circ \), which Zaatri et al. (2006) concluded was strongly driven by the B0-angle. Accounting for it significantly reduced the amplitude of the equatorward flow, although not eliminating it entirely. Other analyses, e.g., Schou (2003); González Hernández et al. (2008); Hathaway and Rightmire (2010) and Rightmire-Upton et al. (2012) have found no evidence for equatorward flow at high latitudes. A useful way to test if the B0 angle correction is well implemented is to verify that MC, when measured over different 3-month epochs in a year, remains largely constant (since MC changes over longer timescales; e.g., see the analysis by Gizon et al. 2020).
7.3 P angle and ‘upside-down’ systematics
Because rotation is of a much higher magnitude than MC, errors in the determination the solar rotation axis (Beck and Giles 2005) can cause rotation to add to the weak MC signals. Thus, it is important that the observed image is not rotated in the plane of the camera with respect to the rotation axis. This offset, known as the P angle, was obtained for MDI by eliminating an annual variation in MC amplitude (Hathaway and Rightmire 2010) and independently, by comparing MDI and HMI images taken concurrently during the months of overlap in 2010 (Liang et al. 2017). It was found that MDI images were rotated clockwise with respect to the rotation axis by about \(0.2^\circ \), leading to systematic errors in seismic measurements, shown for instance in Fig. 9. These errors thus affect inferences of MC obtained from MDI data at all depths, from the surface to the interior. Correcting for this systematic error is important, since matching MC profiles from different instruments (in which systematical errors are known to vary) improves confidence in the inferences. Because of the slight remaining uncertainty in determining the axis of solar rotation, the P angle correction likely does not completely fix the issue.
Due to a failure of one of its antennae in 2003, the MDI camera has since had to be flipped upside down every few months. Using data taken during this upside-down period leads to additional systematical errors, as noted by Liang et al. (2017), and shown in Fig. 10.
P-angle correction to travel times obtained from MDI by Liang et al. (2017). These systematic shifts, although small, are due to a slight rotation of the observed image with respect to the true rotation axis of the Sun (\(0.2^\circ \) in the case of MDI), thereby causing solar rotation to contribute to MC signals. This can lead to notable errors in inferring MC because of the large magnitudes of rotation speeds. The ray-theory curve, which shows the theoretical estimate of the travel-time shift associated with this effect, is in good agreement with the observations
North-south travel-time measurements (\(\delta \tau \)) as measured in the upright (top panel) and upside-down (bottom) positions of MDI (Liang et al. 2017). Ever since 2003, the MDI instrument was flipped approximately every three months, taking observations in its ‘upright’ and ‘upside down’ positions, respectively. This has led to unresolved systematics; plotted in blue and red are north-south travel-time shifts averaged over the travel-distance range \(20.4^\circ \)–\(34.2^\circ \), as measured by MDI and HMI respectively. The two instruments show similar signals in the upper panel but are quite different in the lower panel, an indication of systematical errors associated with this observational mode
7.4 Methodological systematics and error bars
One of the challenges in constructing MC models (or any seismic model, really) is in placing appropriate errors bars. Validating a seismic technique requires retrieving a flow profile and comparing with the corresponding ground truth. Owing to the robustness of the inference, differential rotation is possibly the most definitive benchmark. We focus here on time-distance-derived profiles, the preferred helioseismic method this past decade, at least in the context of imaging MC. Giles (2000) performed a careful comparison between TD and global-mode-frequency estimates of differential rotation, finding differences that were many times the standard deviations of the inferences. The biases were on the order of 10–20 m/s at various depths in the interior, and were surprisingly most pronounced in the upper 10%, i.e., the near-surface layers. Jackiewicz et al. (2015) also performed a comparative analysis, measuring much larger differences between TD and global-mode inferences of rotation than error bars suggested. Particularly problematic is that these systematic deviations appear to persist at low latitudes and near-surface layers in both prior efforts. Zhao et al. (2012) have also measured differential rotation but did not make detailed comparisons with mode-frequency estimates. Methodological biases on the order of 10 m/s are therefore a cause for worry, especially when attempting to infer MC. TD thus needs to be validated more thoroughly in order to allow for greater faith in the MC inversions.
Another source of concern is the extremely small error assigned to the flow in deep layers, i.e., \(r/R_\odot < 0.8\). For instance, Gizon et al. (2020) suggest errors on the order 3–4 m/s at \(r/R_\odot = 0.713\); in comparison, rotation inferences using global mode frequencies (associated with the lowest uncertainties in helioseismology) from a 6-year analysis of HMI (Larson and Schou 2018) shows similar error bars (see also the analysis by Braun and Birch 2008). However, these inversions are performed with constraints, such as placing the lower boundary of MC at the base of the convection zone and relying on mass conservation to build the flow model at depths where direct imaging using helioseismology is not possible. For instance, placing these constraints on their inversions, Gizon et al. (2020) recover flows down to the base of the convection zone although they are unable to directly image layers below \(r/R_\odot = 0.86\) due to a poor signal-to-noise ratio associated the seismic measurements, thus complicating the interpretation of the uncertainties, which in this case are obtained by solely propagating a realization-noise model through the inversion. Better uncertainty quantification may be achieved by determining the sensitivity of the inferred flows to assumptions such as a fixed lower boundary of the inversion.
To establish confidence in these inferences and the associated error bars, it is critical to carefully apply time-distance to determine differential rotation at all depths at which MC is constrained. Error bars obtained from a test that successfully retrieves the rotation profile obtained from time-distance (or a relevant seismic method) would be much more meaningful.
8 Active region inflows and solar-cycle evolution of MC
Local flows are known to persist around active regions, directed inwards (Gizon et al. 2001; Zhao and Kosovichev 2004; Gizon 2004; González Hernández et al. 2008; Hathaway and Rightmire 2010; Jiang et al. 2014). These have been attributed to the pressure drop within active regions or possibly to large-scale convective cells that collect and concentrate magnetic regions (Yoshimura 1971). In fact, early helioseismic analyses (Chou and Dai 2001; Basu and Antia 2003; Zhao and Kosovichev 2004) suggested that MC at low latitudes showed additional rolls on either side of the corresponding active latitude. Gizon (2004) and González Hernández et al. (2008) however refuted this analysis by masking large active regions (and therefore their associated inflows) and showing that the low-latitude structure at solar maximum did not appear in their inferences (see Fig. 11). Lin and Chou (2018) argue that magnetism in and around the active latitudes changes MC at a variety of depths. Some of these systematic differences relate to the definition of MC, i.e., it is not clear whether the circulation is indeed locally influenced by active-region-induced flows (with multiple local cells in radius at low latitudes etc.) or if we are imaging a combination of MC (decoupled from the local inflows) and the active-region inflows.

Image reproduced with permission from Jiang et al. (2014), copyright by Springer
Near-surface temporal variation of MC as inferred using local helioseismology. Curves at different years are shifted by multiples of 10 ms−1 in order to contrast them. In blue are shown the north-south advection rates of supergranular flows as measured using time-distance applied to MDI observations (Gizon and Rempel 2008). The red lines mark ring-diagram analyses of GONG data (González Hernández et al. 2008); these were multiplied by 0.8 to the blue curves in the overlap period 2001–2002. These measurements have been anti-symmetrized across the equator.
Analyzing the motions of small magnetic elements from observations over the period 1978–1990, Komm et al. (1993) concluded that MC is relatively fast during solar minima in comparison to the maxima. Indeed, subsequent analyses also agree that MC shows higher speeds at the start of cycle than at the end (see Fig. 12). Analysing data from GONG, MDI and HMI using RDA, Komm et al. (2018) measured the temporal variation of MC over an 18-year span in Fig. 13. Further, González Hernández et al. (2008) found that changes to MC with evolving magnetism were most significant in the uppermost layers of the convection zone, and appeared to be broadly fixed at depths \(r \lesssim 0.98\,R_\odot \).

Image reproduced with permission from Hathaway and Rightmire (2010), copyright by AAAS
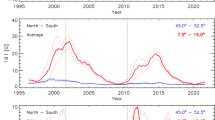
Surface MC amplitude obtained using magnetic-element tracking. The amplitude was estimated by fitting the retrieved MC to the Legendre polynomial \(P^2_1(\cos \theta ) = 2\cos \theta \,\sin \theta \), which tends to dominate the flow profile. The solid red line marks the sunspot number (scaled down by a factor of 20) and the fluctuating line with symbols above it shows the variation in MC amplitude with time. It is seen that surface MC amplitude increases with a drop in sunspot number and vice versa.

Image reproduced with permission from Komm et al. (2018), copyright by Springer
Time variability of ring-diagram-based seismic inference of MC at a depth of 7.1 Mm. At each latitude, the mean MC has been subtracted. GONG, MDI and HMI have all been used to create this plot; offsets have been removed and the MC inferences from the three datasets have been calibrated and averaged. The two vertical dotted lines mark the start of high-resolution GONG (circa 2001) and HMI datasets (2010). The horizontal dashes at \(\pm 75^\circ \) mark periods when the absolute \(B_0\) angle \(> 3^\circ \). Changes to MC are strongly correlated with the magnetic cycle.
9 Inversions for interior MC
Seismic inverse problems relate to obtaining best-fit models of the interior that satisfy surface seismic and other constraints (such as surface-Doppler observations of the velocity profile, mass conservation etc.). If the seismic measurements were to contain the centre-to-limb effect, i.e., if the correction were not applied, the inversions would show km/s meridional flows at the base of the convection zone (Duvall and Hanasoge 2009). The first attempt at inferring MC as a function of depth was by Giles et al. (1997), who applied time-distance helioseismology to two years of seismic observations taken by the Michelson Doppler Imager (MDI; Scherrer et al. 1995) onboard the Solar and Heliospheric Observatory (SOHO). Interestingly, although Giles (2000) obtained a very reasonable MC profile throughout the convection zone, there was no mention of the centre-to-limb bias, which was not known to affect helioseismic measurements at the time. One reason that Giles (2000) obtained a reasonable flow profile is that the magnitude of the centre-to-limb effect was very small at the start of MDI’s observational campaign, however appearing to increase in magnitude with time, as shown in Fig. 8. This suggests that, in addition to physical mechanisms such as radiative transfer and convective blue-shifting, changes in the instrument with time are likely important to account for.
Inversions are carried out in specified domains, i.e., over a range of depths and latitude. Seismic measurements, however, are not necessarily sensitive to all the regions in the domain, which is why the inverse problem is generally ill conditioned. Helioseismic inverse problems are typically posed as
where \(d_i\) is a travel-time or other seismic measurement, \(\epsilon _i\) is realization noise on the measurement, \(\mathbf{x}\) is the 3D spatial coordinate in spherical geometry, \(K_i\) is a sensitivity kernel that connects the seismic measurement to the flow, and \(\psi (\mathbf{x})\) is the stream-function describing MC, i.e., \(\mathbf{v} = \varvec{\nabla }\varvec{\times }(\psi \mathbf{e}_\phi )\), where \(\mathbf{v}\) is the flow vector. Note that this inverse problem could also be rewritten so as to obtain a direct relationship with vector velocity \(\mathbf{v}\); however, this suffers from the drawback that it does not allow for enforcing mass conservation (e.g., the approach followed by Zhao et al. 2013; Chen and Zhao 2017).
Equation (5) may be rewritten as a matrix equation, and because \(K_i\) is only dominant along and in the vicinity of the ray path, the condition number of the kernel matrix can be very large. This poses challenges to obtaining accurate models of \(\psi \). Regularization terms and constraints are typically added to improve the condition number of the system. Giles (2000), for instance, explicitly enforced the base of the convection zone as the lower boundary of the meridional flow, and even though there was insufficient signal to infer the flow configuration in those deep layers, Giles (2000) obtained a one-cell circulation cell.
Controlling the uncertainty of the solution is another major challenge. A standard approach is to place restrictions on the smoothness class of the solutions by projecting it on to a basis such as B-splines or Chebyshev polynomials. This prevents the solution from being overly sensitive to seismic noise, i.e., it improves the overall condition number of the inverse problem.
Properly propagating uncertainties is critical to ensuring the quality of the inferences. One way to test whether the error bars are appropriate is to perform ensemble forward calculations of different models, i.e., compute the observed travel times using a variety of MC models. This Bayesian approach (e.g., Jackiewicz 2020; Gizon et al. 2020) provides a means to build more robust uncertainties. Figure 14 is shown specifically to highlight the substantial differences in uncertainties in various inferences. Some of the inferences are in broad agreement with each (e.g., Rajaguru & Antia and Gizon et al.), despite the differences in temporal periods of coverage and the instruments used in the analysis. Additionally, Gizon et al. (2020) require that the radial component of MC go to zero at the base of the convection zone (\(r=0.7\,R_\odot \)), whereas the other approaches shown in Fig. 15 do not explicitly enforce this.
Comparison of inversions with error bars of MC profiles obtained by Chen and Zhao (2017); Rajaguru and Antia (2015), and Jackiewicz et al. (2015); positive velocities indicate northward flow and vice versa. The estimates of error bars with depth are very different for the four inversions shown here. The Rajaguru & Antia and Gizon et al. inversions are in good agreement with each other
Comparison between inversions of MC profiles obtained by Chen and Zhao (2017); Rajaguru and Antia (2015); Gizon et al. (2020) and Jackiewicz et al. (2015); positive velocities indicate northward flow and vice versa. The choice of instrument and temporal ranges of data are stated below each of the plots. The colourbar below applies to all panels. There are numerous differences in the details—the data, the analysis methods and inversion methodology, contributing to the variations among the results. Ensuring consistency in the centre-to-limb correction is also critical to the eventual inference, as seen in Fig. 7
Rajaguru and Antia (2015), using travel times obtained from HMI, and applying ray-theoretic kernels to perform inversions, also arrived at a one-cell profile (see Fig. 15). Mandal et al. (2017), using the same set of travel-time measurements, but with kernels computed in the limit of the first-Born approximation, found a similar one-cell profile. Rajaguru and Antia (2015); Mandal et al. (2017) and Gizon et al. (2020) all used a stream-function formalism to invoke mass conservation, and thereby reducing the dimensionality of the problem to one unknown scalar function. Zhao et al. (2013) and Chen and Zhao (2017) for instance do not explicitly invoke mass conservation, possibly leading to some systematic differences. Among these set of interior inferences, Chen and Zhao (2017) indicates the possibility of two cells in radius, also supported by Jackiewicz et al. (2015) and Lin and Chou (2018).
Chen and Zhao (2018) performed an extensive analysis and showed that the centre-to-limb effect is strongly dependent on mode frequency, switching sign at 4 mHz. Figure 16 shows a result from Rajaguru and Antia (2020), who found that when modes with frequencies >4 mHz were used in the analysis, a two-cell structure in radius appeared, whereas when only lower frequencies were retained, the inversion produced a one-cell flow. The centre-to-limb bias, which in addition to all its other dependencies, is also sensitive to the mode frequencies used, thus creating significant discrepancies between inferred models.
Gizon et al. (2020) applied time-distance helioseismology to the full available sets of HMI, MDI and GONG observations, masking strong-field regions, correcting for the centre-to-limb systematic, accounting for the instrumental B angle and MDI’s P-angle and upside-down errors, and found a good match between GONG and MDI inferences of MC. HMI shows unexplained disagreement, well above the error bars. Braun et al. (2021) also point to an anomaly in the HMI data not present in MDI and GONG observations. Gizon et al. (2020) find evidence for a single-cell MC, with a possibility of a weak secondary cell in radius at low latitudes in the southern hemisphere from 2005–2011. Rajaguru and Antia (2015) also see a weak secondary cell in radius in the southern hemisphere from their analysis of HMI observations over the period 2010–2014.

Image reproduced with permission from Rajaguru and Antia (2020), copyright by the authors
Inversions for MC showing differing numbers of cells in radius as a function of mode frequencies used in the analysis. When higher-frequency modes are included, a two-cell structure is seen (third and fourth panels), whereas lower frequencies produce a one-cell flow (first and second panels). This is problematic, since the inversion ought to be robust to these differences; it also implies that the centre-to-limb effect changes as a function of mode frequency (first discussed by Chen and Zhao 2018). Rajaguru and Antia (2020) attribute the two-cell flow model inferred by Chen and Zhao (2017) to this effect.
Braun et al. (2021) applied the Fourier–Legendre method (Braun and Fan 1998; Roth et al. 2016) to HMI data and obtained different flows for the northern and southern hemispheres, which they attributed to their inability to remove systematical errors.
9.1 MC extending across the equator
Systematical errors also play a major role in accurately retrieving the MC signal near the equator, and thereby controlling the N-S asymmetry to some extent. For instance, correcting the P angle (see Sect. 7.3) can make a substantial difference to removing the cross-equator flow (González Hernández et al. 2008; Komm et al. 2015; Liang et al. 2017). Constraints obtained using RDA (e.g., see Figs. 12 and 16 of Komm et al. 2015) suggest that only the uppermost surface layers contain notable cross-equator MC whereas it appears to vanish in deeper layers. González Hernández et al. (2008) have performed careful analyses using RDA to infer the variation of the shallow MC with the phase of the magnetic cycle; the cross-equator flow indeed appears to change with time although no obvious correlation with the magnetic index was measured. Indeed, this is a delicate analysis, requiring masking strong magnetic regions and addressing the flows that active regions induce in their vicinity. However, whether signals of cross-equatorial MC that are seen in inversions for cycle 23 by Gizon et al. (2020) are real or due to an inadequate removal of systematics, remains to be seen. Despite not enforcing the North-South symmetries that “ideal” MC is expected to obey, Gizon et al. (2020) inferred very weak cross-equatorial flow. Hathaway and Rightmire (2010), for instance, do not see signs of an equatorial crossover.
10 Discussion and conclusions
The aim of this review was to summarise some of the major developments in our theoretical and computational understanding of meridional circulation, aided by significant advances in observational constraints. A general understanding of MC has been prevalent for more than half a century, entirely due to the substantial contributions of mean-field theory. It is only in the last two decades that numerical simulations have had sufficient computing power to attempt this problem seriously. Disagreement still persists between these two approaches although why that is the case is still a matter of debate.
Observations have been slow to catch up, owing to the relatively small magnitude of MC (in comparison to differential rotation) and systematical biases comparable to the expected signal from MC. Measuring the surface manifestation of MC has itself been a very challenging problem because of the substantially different responses of various observational methods, such as feature tracking and Doppler imaging. Additional instrumental systematical errors and the centre-to-limb shift have served to complicate the measurement process. It has only been in the most recent two decades that enough of an appreciation has been developed—for the range of issues that afflict MC inferences—to be able to explain the differences between techniques.
Interior inferences are even more difficult because of the manifold challenges associated with seismic techniques, methodological and other systematics and realization noise. Two decades of persistent effort have however paid off and we have a good understanding of how to deal with many of the issues. As a consequence, we have constraints on the flows in the upper convection zone, with the preponderance of observational efforts appearing to indicate a single-cell poleward flow down to about \(0.9\,R_\odot \). Below this depth, seismic observations are increasingly noisy and also dominated by systematical errors. The artificial limit on the bottom boundary of the return MC strongly influences deep-interior inferences and the true uncertainty is therefore likely larger than those suggested in current literature.
To enhance these inferences, it may be productive in the future to look to normal-mode coupling, a very powerful technique potentially capable of extracting higher signal-to-noise measurements and performing mode-by-mode accounting for systematical biases (both line-of-sight projection and centre-to-limb shift). Whether this will allow for better constraining MC in the deeper layers remains to be determined.
References
Babcock HW (1961) The topology of the Sun’s magnetic field and the 22-year cycle. Astrophys J 133:572. https://doi.org/10.1086/147060
Baldner CS, Schou J (2012) Effects of asymmetric flows in solar convection on oscillation modes. Astrophys J Lett 760:L1. https://doi.org/10.1088/2041-8205/760/1/L1. arXiv:1210.1583 [astro-ph.SR]
Basu S, Antia HM (2000) Solar cycle variations of large-scale flows in the Sun. Sol Phys 192:469–480. https://doi.org/10.1023/A:1005256817534. arXiv:astro-ph/0001294 [astro-ph]
Basu S, Antia HM (2003) Changes in solar dynamics from 1995 to 2002. Astrophys J 585(1):553–565. https://doi.org/10.1086/346020
Basu S, Antia HM (2010) Characteristics of Solar Meridional Flows during Solar Cycle 23. Astrophys J 717(1):488–495. https://doi.org/10.1088/0004-637X/717/1/488. arXiv:1005.3031 [astro-ph.SR]
Beck JG (2000) A comparison of differential rotation measurements - (Invited Review). Sol Phys 191(1):47–70. https://doi.org/10.1023/A:1005226402796
Beck JG, Giles P (2005) Helioseismic determination of the solar rotation axis. Astrophys J 621(2):L153–L156. https://doi.org/10.1086/429224
Beckers JM, Nelson GD (1978) Some comments on the limb shift of solar lines. II: The effect of granular motions. Sol Phys 58(2):243–261. https://doi.org/10.1007/BF00157270
Benomar O, Bazot M, Nielsen MB, Gizon L, Sekii T, Takata M, Hotta H, Hanasoge S, Sreenivasan KR, Christensen-Dalsgaard J (2018) Asteroseismic detection of latitudinal differential rotation in 13 Sun-like stars. Science 361(6408):1231–1234. https://doi.org/10.1126/science.aao6571. arXiv:1809.07938 [astro-ph.SR]
Bhattacharya J, Hanasoge S, Antia HM (2015) Frequency Shifts of Resonant Modes of the Sun due to Near-Surface Convective Scattering. Astrophys J 806:246. https://doi.org/10.1088/0004-637X/806/2/246. arXiv:1505.04048 [astro-ph.SR]
Birch AC, Kosovichev AG (2001) The Born approximation in time-distance helioseismology. In: Wilson A, Pallé PL (eds) SOHO 10/GONG 2000 Workshop: Helio- and Asteroseismology at the Dawn of the Millennium. ESA Special Publication, vol 464. pp 187–190
Birch AC, Kosovichev AG, Price GH, Schlottmann RB (2001) The Accuracy of the Born and Ray Approximations in Time-Distance Helioseismology. Astrophys J Lett 561:L229–L232. https://doi.org/10.1086/324766
Braun DC, Birch AC (2008) Prospects for the Detection of the Deep Solar Meridional Circulation. Astrophys J Lett 689:L161–L165. https://doi.org/10.1086/595884. arXiv:0810.0284
Braun DC, Fan Y (1998) Helioseismic measurements of the subsurface meridional flow. Astrophys J 508(1):L105–L108. https://doi.org/10.1086/311727
Braun DC, Birch AC, Fan Y (2021) Probing the solar meridional circulation using fourier legendre decomposition. Astrophys J 911(1):54. https://doi.org/10.3847/1538-4357/abe7e4
Cameron, R H, Schüssler, M (2017) An update of Leighton’s solar dynamo model. Astron Astrophys 599:A52. https://doi.org/10.1051/0004-6361/201629746
Cameron, R H, Duvall, T L, Schüssler, M, Schunker, H (2018) Observing and modeling the poloidal and toroidal fields of the solar dynamo. Astron Astrophys 609:A56. https://doi.org/10.1051/0004-6361/201731481
Cavallini F, Ceppatelli G, Righini A (1985) Meridional and equatorial center-to-limb variation of the asymmetry and shift of three Fe I solar photospheric lines around 6300 Å. Astron Astrophys 150(2):256–265
Cavallini F, Ceppatelli G, Righini A (1986) Solar limb effect and meridional flow - Results on the Fe I lines at 5569.6 A and 5576.1 A. Astron Astrophys 163(1-2):219–228
Charbonneau P (2020) Dynamo Models of the Solar Cycle. Living Rev Sol Phys 17:4. https://doi.org/10.1007/s41116-020-00025-6
Chen R, Zhao J (2017) A Comprehensive Method to Measure Solar Meridional Circulation and the Center-to-limb Effect Using Time-Distance Helioseismology. Astrophys J 849(2):144. https://doi.org/10.3847/1538-4357/aa8eec. arXiv:1709.07905 [astro-ph.SR]
Chen R, Zhao J (2018) Frequency Dependence of Helioseismic Measurements of the Center-to-Limb Effect and Flow-induced Travel-time Shifts. Astrophys J 853(2):161. https://doi.org/10.3847/1538-4357/aaa3e3
Chou DY, Dai DC (2001) Solar Cycle Variations of Subsurface Meridional Flows in the Sun. Astrophys J Lett 559:L175–L178. https://doi.org/10.1086/323724
Chou DY, Sun MT, Huang TY, Lai SP, Chi PJ, Ou KT, Wang CC, Lu JY, Chu AL, Niu CS, Mu TM, Chen KR, Chou YP, Jimenez A, Rabello-Soares MC, Chao H, Ai G, Wang GP, Zirin H, Marquette W, Nenow J (1995) Taiwan Oscillation Network. Sol Phys 160(2):237–243. https://doi.org/10.1007/BF00732806
Choudhuri AR (2021) The meridional circulation of the Sun: Observations, theory and connections with the solar dynamo. Sci China Phys Mech Astron 64(3):239601. https://doi.org/10.1007/s11433-020-1628-1. arXiv:2008.09347 [astro-ph.SR]
Choudhuri AR, Schussler M, Dikpati M (1995) The solar dynamo with meridional circulation. Astron Astrophys 303:L29
Christensen-Dalsgaard J (2002) Helioseismology. Rev Mod Phys 74:1073–1129. https://doi.org/10.1103/RevModPhys.74.1073. arXiv:astro-ph/0207403
Christensen-Dalsgaard J, Dappen W, Ajukov SV, Anderson ER, Antia HM, Basu S, Baturin VA, Berthomieu G, Chaboyer B, Chitre SM, Cox AN, Demarque P, Donatowicz J, Dziembowski WA, Gabriel M, Gough DO, Guenther DB, Guzik JA, Harvey JW, Hill F, Houdek G, Iglesias CA, Kosovichev AG, Leibacher JW, Morel P, Proffitt CR, Provost J, Reiter J, Rhodes EJ Jr, Rogers FJ, Roxburgh IW, Thompson MJ, Ulrich RK (1996) The Current State of Solar Modeling. Science 272:1286
Dahlen FA, Tromp J (1998) Theoretical global seismology. Princeton University Press
Dikpati M (2014) Generating the Sun’s global meridional circulation from differential rotation and turbulent Reynolds stresses. Mon Not R Astron Soc 438(3):2380–2394. https://doi.org/10.1093/mnras/stt2353
Dikpati M, Gilman PA, Ulrich RK (2010) Physical origin of differences among various measures of solar meridional circulation. Astrophys J 722(1):774–778. https://doi.org/10.1088/0004-637X/722/1/774. arXiv:1008.2772 [astro-ph.SR]
Durney BR (1974) On the Sun’s Differential Rotation: its Maintenance by Large-Scale Meridional Motions in the Convection Zone. Astrophys J 190:211–222. https://doi.org/10.1086/152865
Durney BR (1995) On a Babcock-Leighton dynamo model with a deep-seated generating layer for the toroidal magnetic field. Sol Phys 160(2):213–235. https://doi.org/10.1007/BF00732805
Durney BR (1999) The Taylor-Proudman Balance and the Solar Rotational Data. Astrophys J 511(2):945–957. https://doi.org/10.1086/306696
Durney BR (2000) Meridional motions and the angular momentum balance in the solar convection zone. Astrophys J 528(1):486–492. https://doi.org/10.1086/308166
Durney BR (2003) The energy equation in the lower solar convection zone. Sol Phys 217(1):1–37. https://doi.org/10.1023/A:1027324825877
Duvall JTL (1978) A study of large-scale solar magnetic and velocity fields. PhD thesis, Stanford Univ, CA
Duvall TL Jr (1979) Large-scale solar velocity fields. Sol Phys 63:3–15. https://doi.org/10.1007/BF00155690
Duvall TL Jr, Gizon L (2000) Time-Distance Helioseismology with f Modes as a Method for Measurement of Near-Surface Flows. Sol Phys 192:177–191. https://doi.org/10.1023/A:1005239503637
Duvall TL Jr, Jefferies SM, Harvey JW, Pomerantz MA (1993) Time-distance helioseismology. Nature 362:430–432. https://doi.org/10.1038/362430a0
Duvall TLJ, Hanasoge SM (2009) Measuring Meridional Circulation in the Sun. ArXiv e-prints arXiv:0905.3132
Dyson FW, Maunder EW (1913) Sun, Axis, the position of, from photographs, 1874–1912. Mon Not R Astron Soc 73:673. https://doi.org/10.1093/mnras/73.9.673
Dziembowski WA, Goode PR (2004) Helioseismic Probing of Solar Variability: The Formalism and Simple Assessments. Astrophys J 600:464–479. https://doi.org/10.1086/379708
Dziembowski WA, Goode PR (2005) Sources of Oscillation Frequency Increase with Rising Solar Activity. Astrophys J 625:548–555. https://doi.org/10.1086/429712
Featherstone NA, Miesch MS (2015) Meridional Circulation in Solar and Stellar Convection Zones. Astrophys J 804(1):67. https://doi.org/10.1088/0004-637X/804/1/67. arXiv:1501.06501 [astro-ph.SR]
Gastine T, Wicht J, Aurnou JM (2013) Zonal flow regimes in rotating anelastic spherical shells: An application to giant planets. Icarus 225(1):156–172. https://doi.org/10.1016/j.icarus.2013.02.031. arXiv:1211.3246 [astro-ph.EP]
Gastine T, Yadav RK, Morin J, Reiners A, Wicht J (2014) From solar-like to antisolar differential rotation in cool stars. Mon Not R Astron Soc 438(1):L76–L80. https://doi.org/10.1093/mnrasl/slt162. arXiv:1311.3047 [astro-ph.SR]
Giles PM (2000) Time-distance measurements of large-scale flows in the solar convection zone. PhD thesis, Stanford University
Giles PM, Duvall TL Jr, Scherrer PH, Bogart RS (1997) A Flow of Material from the Suns Equator to its Poles. Nature 390:52
Gilman PA, Glatzmaier GA (1981) Compressible convection in a rotating spherical shell. I. Anelastic equations. II. A linear anelastic model. III. Analytic model for compressible vorticity waves. Astrophys J Suppl Ser 45:335–388. https://doi.org/10.1086/190714
Gilman PA, Miesch MS (2004) Limits to Penetration of Meridional Circulation below the Solar Convection Zone. Astrophys J 611:568–574. https://doi.org/10.1086/421899
Gizon L (2004) Helioseismology of Time-Varying Flows Through The Solar Cycle. Sol Phys 224:217–228. https://doi.org/10.1007/s11207-005-4983-9
Gizon L, Birch AC (2005) Local Helioseismology. Living Rev Sol Phys 2:6. https://doi.org/10.12942/lrsp-2005-6
Gizon L, Rempel M (2008) Observation and Modeling of the Solar-Cycle Variation of the Meridional Flow. Sol Phys 251:241–250. https://doi.org/10.1007/s11207-008-9162-3. arXiv:0803.0950
Gizon L, Duvall JTL, Larsen RM (2001) Probing surface flows and magnetic activity with time-distance helioseismology. In: Brekke P, Fleck B, Gurman JB (eds) Recent insights into the physics of the sun and heliosphere: highlights from SOHO and other space missions. vol 203. p 189
Gizon L, Duvall TL, Schou J (2003) Wave-like properties of solar supergranulation. Nature 421:43–44. arXiv:astro-ph/0208343
Gizon L, Schunker H, Baldner CS, Basu S, Birch AC, Bogart RS, Braun DC, Cameron R, Duvall TL, Hanasoge SM, Jackiewicz J, Roth M, Stahn T, Thompson MJ, Zharkov S (2009) Helioseismology of Sunspots: A Case Study of NOAA Region 9787. Space Sci Rev 144:249–273. https://doi.org/10.1007/s11214-008-9466-5
Gizon L, Birch AC, Spruit HC (2010) Local Helioseismology: Three-Dimensional Imaging of the Solar Interior. Annu Rev Astron Astrophys 48:289–338. https://doi.org/10.1146/annurev-astro-082708-101722. arXiv:1001.0930 [astro-ph.SR]
Gizon L, Cameron RH, Pourabdian M, Liang ZC, Fournier D, Birch AC, Hanson CS (2020) Meridional flow in the Sun’s convection zone is a single cell in each hemisphere. Science 368(6498):1469–1472. https://doi.org/10.1126/science.aaz7119
González Hernández I, Kholikov S, Hill F, Howe R, Komm R (2008) Subsurface Meridional Circulation in the Active Belts. Sol Phys 252(2):235–245. https://doi.org/10.1007/s11207-008-9264-y. arXiv:0808.3606 [astro-ph]
Gough D, Hindman BW (2010) Helioseismic Detection of Deep Meridional Flow. Astrophys J 714(1):960–970. https://doi.org/10.1088/0004-637X/714/1/960. arXiv:0911.2013 [astro-ph.SR]
Gough DO (1969) The Anelastic Approximation for Thermal Convection. Journal of Atmospheric Sciences 26:448–456. https://doi.org/10.1175/1520-0469(1969)026
Greer B, Hindman B, Toomre J (2013) Center-to-limb velocity systematic in ring-diagram analysis. Fifty Years of Seismology of the Sun and Stars 478:199
Guerrero G, Smolarkiewicz PK, Kosovichev AG, Mansour NN (2013) Differential Rotation in Solar-like Stars from Global Simulations. Astrophys J 779(2):176. https://doi.org/10.1088/0004-637X/779/2/176. arXiv:1310.8178 [astro-ph.SR]
Haber DA, Hindman BW, Toomre J, Bogart RS, Larsen RM, Hill F (2002) Evolving Submerged Meridional Circulation Cells within the Upper Convection Zone Revealed by Ring-Diagram Analysis. Astrophys J 570(2):855–864. https://doi.org/10.1086/339631
Hanasoge S, Gizon L, Sreenivasan KR (2016) Seismic Sounding of Convection in the Sun. Annu Rev Fluid Mech 48:191–217. https://doi.org/10.1146/annurev-fluid-122414-034534. arXiv:1503.07961 [astro-ph.SR]
Hanasoge SM, Sreenivasan KR (2014) The Quest to Understand Supergranulation and Large-Scale Convection in the Sun. Sol Phys 289:3403–3419. https://doi.org/10.1007/s11207-014-0471-4. arXiv:1401.0110 [astro-ph.SR]
Hanasoge SM, Duvall TL Jr, Sreenivasan KR (2012) Anomalously Weak Solar Convection. Proc Natl Acad Sci USA 109(30):11928–11932
Hanasoge SM, Woodard M, Antia HM, Gizon L, Sreenivasan KR (2017) Sensitivity of helioseismic measurements of normal-mode coupling to flows and sound-speed perturbations. Mon Not R Astron Soc 470:1404–1420. https://doi.org/10.1093/mnras/stx1298. arXiv:1705.08204 [astro-ph.SR]
Hanson CS, Hanasoge S, Sreenivasan KR (2021) Analyzing supergranular power spectra using helioseismic normal-mode coupling. Astrophys J 910(2):156. https://doi.org/10.3847/1538-4357/abe770
Hathaway DH (1996) Doppler Measurements of the Sun’s Meridional Flow. Astrophys J 460:1027. https://doi.org/10.1086/177029
Hathaway DH (2012) Supergranules as Probes of the Sun’s Meridional Circulation. Astrophys J 760(1):84. https://doi.org/10.1088/0004-637X/760/1/84. arXiv:1210.3343 [astro-ph.SR]
Hathaway DH (2015) The solar cycle. Living Rev Sol Phys 12:4. https://doi.org/10.1007/lrsp-2015-4
Hathaway DH, Rightmire L (2010) Variations in the Sun’s Meridional Flow over a Solar Cycle. Science 327(5971):1350. https://doi.org/10.1126/science.1181990
Hathaway DH, Rightmire L (2011) Variations in the Axisymmetric Transport of Magnetic Elements on the Sun: 1996–2010. Astrophys J 729(2):80. https://doi.org/10.1088/0004-637X/729/2/80. arXiv:1010.1242 [astro-ph.SR]
Hathaway DH, Nandy D, Wilson RM, Reichmann EJ (2003) Evidence that a deep meridional flow sets the sunspot cycle period. Astrophys J 589(1), 665–670. https://doi.org/10.1086/374393
Hathaway DH, Teil T, Norton AA, Kitiashvili I (2015) The Sun’s Photospheric Convection Spectrum. Astrophys J 811(2):105. https://doi.org/10.1088/0004-637X/811/2/105. arXiv:1508.03022 [astro-ph.SR]
Hazra G, Choudhuri AR (2017) A theoretical model of the variation of the meridional circulation with the solar cycle. Mon Not R Astron Soc 472(3):2728–2741. https://doi.org/10.1093/mnras/stx2152. arXiv:1708.05204 [astro-ph.SR]
Hazra G, Karak BB, Choudhuri AR (2014) Is a deep one-cell meridional circulation essential for the flux transport solar dynamo? Astrophys J 782(2):93. https://doi.org/10.1088/0004-637x/782/2/93
Hill F (1988) Rings and trumpets - three-dimensional power spectra of solar oscillations. Astrophys J 333:996–1013. https://doi.org/10.1086/166807
Hotta H, Kusano K (2021) Solar differential rotation reproduced with high-resolution simulation. Nature Astron 5:1100–1102. https://doi.org/10.1038/s41550-021-01459-0. arXiv:2109.06280 [astro-ph.SR]
Howard R, Gilman PA (1986) Meridional Motions of Sunspots and Sunspot Groups. Astrophys J 307:389. https://doi.org/10.1086/164425
Howard R, Gilman PI, Gilman PA (1984) Rotation of the sun measured from Mount Wilson white-light images. Astrophys J 283:373–384. https://doi.org/10.1086/162315
Howe R (2008) Helioseismology and the solar cycle. Adv Space Res 41:846–854. https://doi.org/10.1016/j.asr.2006.12.033
Howe R (2009) Solar interior rotation and its variation. Living Rev Sol Phys 6:1. https://doi.org/10.12942/lrsp-2009-1. arXiv:0902.2406
Howe R, Christensen-Dalsgaard J, Hill F, Komm RW, Larsen RM, Schou J, Thompson MJ, Toomre J (2000) Dynamic variations at the base of the solar convection zone. Science 287:2456–2460. https://doi.org/10.1126/science.287.5462.2456
Jackiewicz J (2020) Probabilistic Inversions for Time-Distance Helioseismology. Sol Phys 295(10):137. https://doi.org/10.1007/s11207-020-01667-3. arXiv:2007.01432 [astro-ph.SR]
Jackiewicz J, Serebryanskiy A, Kholikov S (2015) Meridional flow in the solar convection zone. II. Helioseismic inversions of GONG data. Astrophys J 805(2):133. https://doi.org/10.1088/0004-637x/805/2/133
Jiang J, Hathaway DH, Cameron RH, Solanki SK, Gizon L, Upton L (2014) Magnetic Flux Transport at the Solar Surface. Space Sci Rev 186(1–4):491–523. https://doi.org/10.1007/s11214-014-0083-1. arXiv:1408.3186 [astro-ph.SR]
Kambry MA, Nishikawa J, Sakurai T, Ichimoto K, Hiei E (1991) Solar Meriodional Motions Derived from Sunspot Observations. Sol Phys 132(1):41–48. https://doi.org/10.1007/BF00159128
Käpylä PJ, Käpylä MJ, Brandenburg A (2014) Confirmation of bistable stellar differential rotation profiles. Astron Astrophys 570:A43. https://doi.org/10.1051/0004-6361/201423412. arXiv:1401.2981 [astro-ph.SR]
Karak BB, Jiang J, Miesch MS, Charbonneau P, Choudhuri AR (2014) Flux Transport Dynamos: From Kinematics to Dynamics. Space Sci Rev 186(1–4):561–602. https://doi.org/10.1007/s11214-014-0099-6
Kashyap SG, Hanasoge SM (2021) Characterizing Solar Surface Convection Using Doppler Measurements. Astrophys J 916(2):87. https://doi.org/10.3847/1538-4357/ac05bc. arXiv:2105.12055 [astro-ph.SR]
Kichatinov LL, Rudiger G (1993) A-effect and differential rotation in stellar convection zones. Astron Astrophys 276:96
Kippenhahn R (1959) 23. Meridional circulations in the hydrogen convective layer of the Sun. In: Modeles d'Etoiles et Evolution Stellaire. Liege international astrophysical colloquia, vol 9. pp 249–255
Kippenhahn R (1963) Differential Rotation in Stars with Convective Envelopes. Astrophys J 137:664. https://doi.org/10.1086/147539
Kitchatinov LL (2012) Theory of differential rotation and meridional circulation. Proceedings of the International Astronomical Union 8(S294), 399–410
Kitchatinov LL (2016) Meridional circulation in the sun and stars. Geomagn Aeron 56(8):945–951. https://doi.org/10.1134/S0016793216080107. arXiv:1603.07852 [astro-ph.SR]
Kitchatinov LL, Olemskoy SV (2011) Differential rotation of main-sequence dwarfs and its dynamo efficiency. Mon Not R Astron Soc 411(2):1059–1066. https://doi.org/10.1111/j.1365-2966.2010.17737.x. arXiv:1009.3734 [astro-ph.SR]
Kitchatinov LL, Rüdiger G (2004) Anti-solar differential rotation. Astron Nachr 325(6):496–500. https://doi.org/10.1002/asna.200410297. arXiv:astro-ph/0504173 [astro-ph]
Kitchatinov LL, Ruediger G (1995) Differential rotation in solar-type stars: revisiting the Taylor-number puzzle. Astron Astrophys 299:446
Komm R, González Hernández I, Howe R, Hill F (2015) Subsurface zonal and meridional flow derived from GONG and sdo/hmi: A comparison of systematics. Sol Phys 290(4):1081–1104. https://doi.org/10.1007/s11207-015-0663-6
Komm R, Howe R, Hill F (2018) Subsurface zonal and meridional flow during cycles 23 and 24. Sol Phys 293(10):145. https://doi.org/10.1007/s11207-018-1365-7
Komm R, Howe R, Hill F (2020) Solar-Cycle Variation of the Subsurface Flows of Active- and Quiet-Region Subsets. Sol Phys 295(3):47. https://doi.org/10.1007/s11207-020-01611-5
Komm RW, Howard RF, Harvey JW (1993) Meridional flow of small photospheric magnetic features. Sol Phys 147(2), 207–223. https://doi.org/10.1007/BF00690713
Kosovichev AG, Schou J (1997) Detection of zonal shear flows beneath the Sun’s surface from f-mode frequency splitting. Astrophys J Lett 482(2), L207–L210. https://doi.org/10.1086/310708
Kuhn JR, Bush RI, Scherrer P, Scheick X (1998) The Sun’s shape and brightness. Nature 392:155. https://doi.org/10.1038/32361
Kupka F, Muthsam HJ (2017) Modelling of stellar convection. Living Rev Comput Astrophys 3:1. https://doi.org/10.1007/s41115-017-0001-9
Labonte BJ, Howard R (1982) Solar rotation measurements at Mount Wilson. III. Meridional flow and limbshift. Sol Phys 80(2):361–372. https://doi.org/10.1007/BF00147982
Langfellner, J, Birch, A C, Gizon, L (2018) Evolution and wave-like properties of the average solar supergranule. Astron Astrophys 617:A97. https://doi.org/10.1051/0004-6361/201732471
Larson TP, Schou J (2018) Global-Mode Analysis of Full-Disk Data from the Michelson Doppler Imager and the Helioseismic and Magnetic Imager. Sol Phys 293(2):29. https://doi.org/10.1007/s11207-017-1201-5
Latushko S (1994) Meridional drift in the large-scale solar magnetic field pattern. Sol Phys 149(2):231–241. https://doi.org/10.1007/BF00690611
Lavely EM, Ritzwoller MH (1992) The effect of global-scale, steady-state convection and elastic-gravitational asphericities on helioseismic oscillations. Philos Trans R Soc London Ser A 339:431–496. https://doi.org/10.1098/rsta.1992.0048
Lebedinsky AI (1941) Rotation of the Sun. Astron Zh 18(10). In Russian
Leibacher JW (1999) The global oscillation network group (GONG) project. Adv Space Res 24(2):173–176. https://doi.org/10.1016/S0273-1177(99)00497-4
Leighton RB, Noyes RW, Simon GW (1962) Velocity Fields in the Solar Atmosphere. I. Preliminary Report. Astrophys J 135:474. https://doi.org/10.1086/147285
Lekshmi B, Nandy D, Antia HM (2019) Hemispheric asymmetry in meridional flow and the sunspot cycle. Mon Not R Astron Soc 489(1):714–722. https://doi.org/10.1093/mnras/stz2168
Liang ZC, Birch AC, Duvall J Thomas L, Gizon L, Schou J (2017) Comparison of acoustic travel-time measurements of solar meridional circulation from SDO/HMI and SOHO/MDI. Astron Astrophys 601:A46. https://doi.org/10.1051/0004-6361/201730416. arXiv:1704.00475 [astro-ph.SR]
Liang ZC, Gizon L, Birch AC, Duvall TL, Rajaguru SP (2018) Solar meridional circulation from twenty-one years of SOHO/MDI and SDO/HMI observations. Helioseismic travel times and forward modeling in the ray approximation. Astron Astrophys 619:A99. https://doi.org/10.1051/0004-6361/201833673. arXiv:1808.08874 [astro-ph.SR]
Lin CH, Chou DY (2018) Solar-cycle Variations of Meridional Flows in the Solar Convection Zone Using Helioseismic Methods. Astrophys J 860(1):48. https://doi.org/10.3847/1538-4357/aac026
Lord JW, Cameron RH, Rast MP, Rempel M, Roudier T (2014) The Role of Subsurface Flows in Solar Surface Convection: Modeling the Spectrum of Supergranular and Larger Scale Flows. Astrophys J 793:24. https://doi.org/10.1088/0004-637X/793/1/24. arXiv:1407.2209 [astro-ph.SR]
Mandal K, Bhattacharya J, Halder S, Hanasoge S (2017) Finite-frequency sensitivity kernels in spherical geometry for time-distance helioseismology. ArXiv e-prints arXiv:1705.04020 [astro-ph.SR]
Meunier N (1999) Large-Scale Dynamics of Active Regions and Small Photospheric Magnetic Features. Astrophys J 527(2):967–976. https://doi.org/10.1086/308111
Meunier N (2005) Large-scale dynamics and polarities of magnetic structures. Astron Astrophys 437(1), 303–310. https://doi.org/10.1051/0004-6361:20042415
Miesch MS (2005) Large-scale dynamics of the convection zone and Tachocline. Living Rev Sol Phys 2:1. https://doi.org/10.12942/lrsp-2005-1
Miesch MS, Hindman BW (2011) Gyroscopic Pumping in the Solar Near-surface Shear Layer. Astrophys J 743:79. https://doi.org/10.1088/0004-637X/743/1/79. arXiv:1106.4107 [astro-ph.SR]
Nandy D, Choudhuri AR (2002) Explaining the latitudinal distribution of sunspots with deep meridional flow. Science 296:1671–1673. https://doi.org/10.1126/science.1070955
November LJ, Simon GW (1988) Precise proper-motion measurement of solar granulation. Astrophys J 333:427. https://doi.org/10.1086/166758
Perez Garde M, Vazquez M, Schwan H, Woehl H (1981) Large-Scale Solar Motions as Determined by Doppler Shift Measurements Using a Linear Photodiode Array. Astron Astrophys 93(1–2):67–70
Rajaguru SP, Antia HM (2015) Meridional circulation in the solar convection zone: time-distance helioseismic inferences from four years of HMI/SDO observations. Astrophys J 813(2):114. https://doi.org/10.1088/0004-637X/813/2/114. arXiv:1510.01843 [astro-ph.SR]
Rajaguru SP, Antia HM (2020) Time-distance helioseismology of deep meridional circulation. In: Monteiro MJPFG, García RA, Christensen-Dalsgaard J, McIntosh SW (eds) Dynamics of the Sun and Stars. Astrophysics and Space Science Proceedings, vol 57. Springer, Cham, pp 107–113. https://doi.org/10.1007/978-3-030-55336-4_11. arXiv:2004.12708 [astro-ph.SR]
Rast MP (2020) Deciphering solar convection. In: Monteiro MJPFG, García RA, Christensen-Dalsgaard J, McIntosh SW (eds) Dynamics of the Sun and Stars. vol 57. Springer, Cham, pp 149–161. https://doi.org/10.1007/978-3-030-55336-4_23
Rast MP, Ortiz A, Meisner RW (2008) Latitudinal variation of the solar photospheric intensity. Astrophys J 673:1209–1217. https://doi.org/10.1086/524655. arXiv:0710.3121
Rempel M (2005) Solar Differential Rotation and Meridional Flow: The Role of a Subadiabatic Tachocline for the Taylor-Proudman Balance. Astrophys J 622:1320–1332. https://doi.org/10.1086/428282. arXiv:astro-ph/0604451
Rempel M (2006) Flux-transport dynamos with Lorentz force feedback on differential rotation and meridional flow: Saturation mechanism and torsional oscillations. Astrophys J 647(1):662–675. https://doi.org/10.1086/505170
Rempel M (2006b) Transport of toroidal magnetic field by the meridional flow at the base of the solar convection zone. Astrophys J 637(2):1135–1142. https://doi.org/10.1086/498440
Ribes E, Mein P, Mangeney A (1985) A large-scale meridional circulation in the convective zone. Nature 318(6042):170–171. https://doi.org/10.1038/318170a0
Rightmire-Upton L, Hathaway DH, Kosak K (2012) Measurements of the Sun’s High-latitude Meridional Circulation. Astrophys J Lett 761(1):L14. https://doi.org/10.1088/2041-8205/761/1/L14. arXiv:1211.0944 [astro-ph.SR]
Rincon F, Rieutord M (2018) The Sun’s supergranulation. Living Rev Sol Phys 15:6. https://doi.org/10.1007/s41116-018-0013-5
Roth M, Stix M (2008) Meridional circulation and global solar oscillations. Sol Phys 251(1):77–89. https://doi.org/10.1007/s11207-008-9232-6
Roth, M, Doerr, H-P, Hartlep, T (2016) Verification of the helioseismic fourier-legendre analysis for meridional flow measurements. Astron Astrophys 592:A106. https://doi.org/10.1051/0004-6361/201526971
Roudier T, Švanda M, Ballot J, Malherbe JM, Rieutord M (2018) Large-scale photospheric motions determined from granule tracking and helioseismology from SDO/HMI data. Astron Astrophys 611:A92. https://doi.org/10.1051/0004-6361/201732014. arXiv:1712.05255 [astro-ph.SR]
Ruediger G (1989) Differential rotation and stellar convection. Sun and the solar stars. Berlin: Akademie Verlag
Schad A, Roth M, Timmer J (2011a) Observation of oscillation coupling ratios and the meridional flow. J Phys Conf Ser 271:012079. https://doi.org/10.1088/1742-6596/271/1/012079
Schad A, Timmer J, Roth M (2011) A Unified Approach to the Helioseismic Inversion Problem of the Solar Meridional Flow from Global Oscillations. Astrophys J 734:97. https://doi.org/10.1088/0004-637X/734/2/97
Schad A, Timmer J, Roth M (2012) Measuring the solar meridional flow from perturbations of eigenfunctions of global oscillations. Astron Nachr 333(10):991. https://doi.org/10.1002/asna.201211815
Schad A, Timmer J, Roth M (2013) Global Helioseismic Evidence for a Deeply Penetrating Solar Meridional Flow Consisting of Multiple Flow Cells. Astrophys J Lett 778(2):L38. https://doi.org/10.1088/2041-8205/778/2/L38. arXiv:1311.7623 [astro-ph.SR]
Scherrer PH, Bogart RS, Bush RI, Hoeksema JT, Kosovichev AG, Schou J, Rosenberg W, Springer L, Tarbell TD, Title A, Wolfson CJ, Zayer I, MDI Engineering Team (1995) The Solar Oscillations Investigation - Michelson Doppler Imager. Sol Phys 162:129–188. https://doi.org/10.1007/BF00733429
Schou J (2003) Wavelike Properties of Solar Supergranulation Detected in Doppler Shift Data. Astrophys J Lett 596(2):L259–L262. https://doi.org/10.1086/379529
Schou J, Bogart RS (1998) Flow and horizontal displacements from ring diagrams. Astrophys J Lett 504:L131+. https://doi.org/10.1086/311575
Schou J, Antia HM, Basu S, Bogart RS, Bush RI, Chitre SM, Christensen-Dalsgaard J, di Mauro MP, Dziembowski WA, Eff-Darwich A, Gough DO, Haber DA, Hoeksema JT, Howe R, Korzennik SG, Kosovichev AG, Larsen RM, Pijpers FP, Scherrer PH, Sekii T, Tarbell TD, Title AM, Thompson MJ, Toomre J (1998) Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager. Astrophys J 505:390–417. https://doi.org/10.1086/306146
Schou J, Scherrer PH, Bush RI, Wachter R, Couvidat S, Rabello-Soares MC, Bogart RS, Hoeksema JT, Liu Y, Duvall TL, Akin DJ, Allard BA, Miles JW, Rairden R, Shine RA, Tarbell TD, Title AM, Wolfson CJ, Elmore DF, Norton AA, Tomczyk S (2012) Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO). Sol Phys 275:229–259. https://doi.org/10.1007/s11207-011-9842-2
Schroeter EH, Woehl H (1975) Differential rotation, meridional and random motions of the solar Ca\(^{+}\) network. Sol Phys 42(1):3–16. https://doi.org/10.1007/BF00153278
Snodgrass HB (1984) Separation of large-scale photospheric Doppler patterns. Sol Phys 94(1):13–31. https://doi.org/10.1007/BF00154804
Stein RF, Nordlund Å (2000) Realistic Solar Convection Simulations. Sol Phys 192:91–108. https://doi.org/10.1023/A:1005260918443
Swisdak M, Zweibel E (1999) Effects of Large-Scale Convection on p-Mode Frequencies. Astrophys J 512:442–453. https://doi.org/10.1086/306764. arXiv:astro-ph/9809135
Topka K, Moore R, Labonte BJ, Howard R (1982) Evidence for a Poleward Meridional Flow on the Sun. Sol Phys 79(2):231–245. https://doi.org/10.1007/BF00146242
Tuominen J (1942) Die systematische Strombewegung der Sonnenflecke in heliographischer Breite. Z Astrophys 21:96
Tuominen J, Kyrolainen J (1982) On the Latitude Drift of Sunspot Groups and Solar Radiation. Sol Phys 79(1):161–172. https://doi.org/10.1007/BF00146980
Ulrich RK (2010) Solar meridional circulation from doppler shifts of the Fe I line at 5250 Å as measured by the 150-foot solar tower telescope at the Mt. Wilson observatory. Astrophys J 725(1):658–669. https://doi.org/10.1088/0004-637X/725/1/658. arXiv:1010.0487 [astro-ph.SR]
Ulrich RK, Boyden JE, Webster L, Snodgrass HB, Padilla SP, Gilman P, Shieber T (1988) Solar rotation measurements at Mt. Wilson. V. Reanalysis of 21 years of data. Sol Phys 117(2):291–328. https://doi.org/10.1007/BF00147250
Van Ballegooijen A, Choudhuri AR (1988) The possible role of meridional flows in suppressing magnetic buoyancy. Astrophys J 333:965–977
van Ballegooijen AA (1986) On the surface response of solar giant cells. Astrophys J 304:828–837. https://doi.org/10.1086/164219
Švanda M, Klvaňa M, Sobotka M, Bumba V (2008) Large-scale horizontal flows in the solar photosphere. II. Long-term behaviour and magnetic activity response. Astron Astrophys 477(1):285–292. https://doi.org/10.1051/0004-6361:20077718. arXiv:0710.2693 [astro-ph]
Wang YM, Sheeley JNR, Nash AG (1991) A new solar cycle model including meridional circulation. Astrophys J 383:431. https://doi.org/10.1086/170800
Ward F (1973) The latitudinal motion of sunspots and solar meridional circulations. Sol Phys 30(2):527–537. https://doi.org/10.1007/BF00152681
Woodard M (2014) Detectability of Large-Scale Solar Subsurface Flows. Sol Phys 289:1085–1100. https://doi.org/10.1007/s11207-013-0386-5
Woodard M, Schou J, Birch AC, Larson TP (2013) Global-Oscillation Eigenfunction Measurements of Solar Meridional Flow. Sol Phys 287:129–147. https://doi.org/10.1007/s11207-012-0075-9
Woodard MF (1989) Distortion of high-degree solar p-mode eigenfunctions by latitudinal differential rotation. Astrophys J 347:1176–1182. https://doi.org/10.1086/168206
Yoshimura H (1971) Complexes of Activity of the Solar Cycle and Very Large Scale Convection. Sol Phys 18(3):417–433. https://doi.org/10.1007/BF00149064
Zaatri A, Komm R, González Hernández I, Howe R, Corbard T (2006) North South Asymmetry of Zonal and Meridional Flows Determined From Ring Diagram Analysis of Gong++ Data. Sol Phys 236:227–244. https://doi.org/10.1007/s11207-006-0106-5
Zhao J, Kosovichev AG (2004) Torsional Oscillation, Meridional Flows, and Vorticity Inferred in the Upper Convection Zone of the Sun by Time-Distance Helioseismology. Astrophys J 603(2):776–784. https://doi.org/10.1086/381489
Zhao J, Couvidat S, Bogart RS, Parchevsky KV, Birch AC, Duvall TL, Beck JG, Kosovichev AG, Scherrer PH (2012) Time-distance helioseismology data-analysis pipeline for Helioseismic and Magnetic Imager onboard Solar Dynamics Observatory (SDO/HMI) and its initial results. Sol Phys 275(1):375–390. https://doi.org/10.1007/s11207-011-9757-y
Zhao J, Nagashima K, Bogart RS, Kosovichev AG, T L Duvall J (2012b) Systematic center-to-limb variation in measured helioseismic travel times and its effect on inferences of solar interior meridional flows. Astrophys J 749(1):L5. https://doi.org/10.1088/2041-8205/749/1/L5
Zhao J, Bogart RS, Kosovichev AG, Duvall TL Jr, Hartlep T (2013) Detection of equatorward meridional flow and evidence of double-cell meridional circulation inside the Sun. Astrophys J Lett 774:L29. https://doi.org/10.1088/2041-8205/774/2/L29. arXiv:1307.8422 [astro-ph.SR]
Acknowledgements
I thank several colleagues for their assistance in reading and helping improve the manuscript: Mark Miesch, Aaron Birch, Jesper Schou, Junwei Zhao and Robert Cameron. I acknowledge support from the Department of Atomic Energy, India.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hanasoge, S.M. Surface and interior meridional circulation in the Sun. Living Rev Sol Phys 19, 3 (2022). https://doi.org/10.1007/s41116-022-00034-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41116-022-00034-7