Abstract
This paper provides new tools for analyzing spatio-temporal event networks. We build time series of directed event networks for a set of spatial distances, and based on scan-statistics, the spatial distance that generates the strongest change of event network connections is chosen. In addition, we propose an empirical random network event generator to detect significant motifs throughout time. This generator preserves the spatial configuration but randomizes the order of the occurrence of events. To prevent the large number of links from masking the count of motifs, we propose using standardized counts of motifs at each time slot. Our methodology is able to detect interaction radius in space, build time series of networks, and describe changes in its topology over time, by means of identification of different types of motifs that allows for the understanding of the spatio-temporal dynamics of the phenomena. We illustrate our methodology by analyzing thefts occurred in Medellín (Colombia) between the years 2003 and 2015.
Similar content being viewed by others
Introduction
The analysis of spatio-temporal point patterns appears in many areas of research related to crime, earthquakes, ecology, epidemiology, among many others. In this context, the identification of any connection between events and their evolution throughout space and time is of particular interest. Spatio-temporal event interactions, clustering or regularity, and distances that inform about any of these interactions are important to understand the underlying phenomenon under study. For example, Hegemann et al. (2011) reconstruct gang rivalries in Hollenbeck with an agent-based model that employs geographical information to understand the hidden underlying network. Another example can be found in an ecological community level, where interactions of competition and facilitation among the trees are the main goal of the analysis. Thus, the combination of network and statistical analysis is needed to describe and summarize key features and dynamics of a particular phenomenon (Barthelemy 2018; Ferreira et al. 2020). The study of network dynamics faces many challenges. For instance, Jaros et al. (2013) discuss the difficulties of modeling them with time-variant properties, and they propose to model time series of nodes and edges based on time-aggregated graphs. Likewise, Coscia et al. (2014) analyze the influence of spatial and temporal dimensions in mobility data. They analyze a data set of human trajectories, building complex networks at each time, and then studying the evolution of these dynamic networks varying the spatial resolution to find the optimal grid (Friedman et al. 2016).
For spatio-temporal point patterns, it is crucial to establish spatial and/or temporal distances for which the characteristics of the phenomenon under study change. In this line, Salje et al. (2016) analyze distances between sequential cases in a transmission chain and characterize transmission distances. Trifonova et al. (2019) use the juxtaposition of seismogenic features based on geological, geophysical and seismological data, and outline the areas with the highest earthquake capacity. Elliott and Wartenberg (2004) considered that spatially organized socio-economic effects can have important influence on the disease rates observed in small areas and on areas where some people are exposed to the effects of pollution. To study disease propagation in spatial networks (Lang et al. 2018) apply a distance-based kernel to generate a range of spatial structures. Crime Prevention Through Environmental Design (CPTED), a specific theory built for crime, is based on geographical juxtaposition and Cozens et al. (2019) show its importance given the impact of crime in public health, surveillance, sustainability, and quality of life.
Crime has also been analyzed through networks for many reasons. Indeed, network analysis handles crime organization (Scott and Carrington 2011), a key aspect studying illegal acts. Actually, the network approach has been useful in scrutinizing terrorist groups in order to capture prominent delinquents (Borgatti et al. 2009). da Cunha and Gonçalves (2018) present a unique criminal intelligence network for different classes of federal crimes all over Brazil, and analyse its topological structure, robustness, and response to different attack strategies, among others. da Cunha et al. (2020) explore the networked nature of criminal behavior. They build a topic-view network on dark web and compare network disruption strategies with real police work.
Davies and Marchione (2015) propose a way to handle street thefts with event networks. Following the Knox-test idea (Grubesic and Mack 2008), they build networks by varying spatial and temporal radius, obtaining location similarities ties (Borgatti et al. 2009). Their procedure allows to observe the spatio-temporal closeness and the form of crimes, namely motifs, and find patterns with a fixed approach. Boers et al. (2013) uses the development of a network of events to discover the patterns of spatio-temporal co-occurrences, and build an approximation to the synchronization of rains in different areas in the South American Monsoon System; the concentration of places with the highest incidence in the rapid spread of heavy rains, coincide with the nodes that present the highest cluster coefficient. Co-occurrence patterns are related to the emergence of spatial clusters highly enriched with the structural information of the network, Nadini et al. (2020a). We can also find techniques to detect spatio-temporal patterns from discovering subgraphs that occur with a particular frequency in the network, contributing to understanding the emergence of clusters or spatial buffers in particular time windows that are crucial to predict the new events’ probability of occurrence [24,43]. These subgraphs are motifs. For example, Davies and Marchione (2015), Atluri et al. (2018), Pasquaretta et al. (2021), Oberoi and Del Mondo (2021), Dang et al. (2018) are an excellent selection of papers related with methods for detecting patterns using subgraphs and its properties. Jazayeri and Yang (2020) present a complete and updated review of motif discovery algorithms. In addition, motifs have allowed for the generation of important applications for decision-making in population dynamics, among which epidemiology, mobility and criminology stand out. Especially in criminology, motifs facilitate the emergence of related embedded spatio-temporal patterns to establish mechanisms related to CPTED, allowing prioritization of geographic juxtaposition (GJ) in proximal, meso and criminogenic phenomena. Cozens et al. (2019) establish the impacts that distance has for the CPTED category, and define that the types of space-time events that can be captured by motifs are: Micro GJ (GJ factors acting at the crime location), Proximal GJ (GJ factors acting from locations close to the crime location), Meso GJ (GJ crime factors originating in areas more distant from the crime location), and Macro GJ (GJ factors acting as remote influences on crime regardless of the location of their origin in terms of physical distance from crime location.)
Our main interest here is to use networks for analyzing patterns of events embedded in space-time. From its metrics and topological properties, it is possible to build approximations of the co-occurrence, shift, and dependence between events (Wang and Zhang 2020). Although, this research is motivated by the analysis of the space-time interactions and the evolutionary behavior of certein types of crimes in the city of Medellin (Colombia), having reported the exact coordinates in space and time of each crime for a number of years, It can be extended to any spatio-temporal point pattern. The intrinsic richness of this type of data providing the exact locations is crucial for our approach and makes a difference with respect other alternative approaches which are more based on the analysis of aggregated data. We, following Landau and Fridman (1993), consider that it is important to analyze the dynamics of the networks, and choose one distance to relate events in the network so that it is suitable in practical resolutions and helpful for decision-makers (Cozens et al. 2019). In this context, all the literature above commented do consider networks that neither preserve the topology nor vary with time. To solve this problem, we construct a new random generator of networks that preserves the topology of data and varies across time. Consequently, we extend the idea of Davies and Marchione (2015) by building a time series of event networks based on a division of the whole period into several time slots and spatial distances. Our new mechanism for generating randomized networks (ERGEN) maintains spatial locations fixed, varies the order of the occurrence of events, standardizes the results to prevent the count of motifs being masked by the number of links, and allows for the comparison of networks across time. Note the importance of ERGEN to establish if the observed network meets some characteristics or if it is only a random arrangement. Specifically, we use this method here to find motifs. Furthermore, we adapt statistical tools such as change point, scan-statistics (SS), Runadi and Widyaningsih (2017) and Costa and Kulldorff (2009) and matrix standardization, to decide at which distance the amount of connectivities notoriously changes, and to control the bias caused by the network size (Nadini et al. 2020a). Finally, we explore the association between motifs.
The plan of the paper is the following. The methodological approach, including some background concepts, is presented in “Methods” section. The analysis of real data related to crime in Medellin is shown in “Real data analysis” section, and the paper ends with some concluding remarks in “Discussion and conclusions” section.
Methods
In this section, we outline our methodological proposal. First, we consider a number of concepts that will appear in the rest of the paper for clarification and general setup. Then, we build time series of event networks using time slots and a set of spatial radii. We also describe some statistical tools for choosing the spatial distance that generates more connectivities. We finally present the ERGEN, that represents our novel contribution to analyze numerous motifs throughout space and time. See Fig. 1 for a graphical summary that will be further detailed.
Background concepts
A spatio-temporal point process is a random collection of points, where each point, called event in this context, is associated with the time and location of such an event. We call a network a collection of interconnected things, or a configuration of relationships among a group of things or events (Kolaczyk 2009). A graph G is a mathematical structure composed by two sets: a set of nodes, V, and a set of links or edges E, such that each edge element \(e_k=(v_i,v_j)\in E\) represents a connection between two elements \(v_i,v_j\in V\) (Rahman 2017). In other words, a graph is the mathematical abstraction of a network represented by \(G=(V,E)\) such that \(E\subseteq V \times V\). A graph is directed if each edge \(e_k\) is associated with a direction, that is, \((v_i,v_j)\) is different from \((v_j,v_i)\) (Rahman 2017). A directed graph without a path that starts and finishes in the same node is named Direct Acyclic Graph (DAG). If a weight is assigned to each node or edge in a graph, it is call a weighted graph (Rahman 2017). Finally, for \(V'\subset V\) and \(E'\subset E\), an induced graph is a subgraph \(G'=(V',E')\subset G\) that, on its restricted node set \(V'\), contains exactly the links that G has (Kolaczyk and Csárdi 2014).
A crucial concept we will be using throughout the paper is the idea of motifs. A network motif is a subgraph occurring far more frequently in a given network in comparison to general random graphs (Kolaczyk 2009). An event network is a graph in which its nodes are events and some links are placed between close pairs, i.e. nearby events in space (Davies and Marchione 2015). Some properties related to an event network are the following: (a) The number of events is a random variable, and so the number of nodes; (b) The links depend on event locations, and so the event network does not support links between far events. In other words, the links are fixed and conditioned on the events locations. Now, a sequence of random elements Z over time is called a time series and it is usually denoted as \(\{Z_t, t \in T\subset {\mathbb {R}}\}\). So, \(\{G_t, t\in T\}\) is a time series of event networks where each \(G_t\) is an event network itself.
The structure of a graph G is said to be analyzed in a macroscopic way if there is an interest on global characteristics about the whole graph G. Instead, the microscopic approach studies properties of the elements of graphs, for example of nodes, subgraphs, etc. (Trøjelsgaard and Olesen 2016).
Time series of event networks
We assume that the ocurrence of the events of interest is recorded in a study region \(R\subset {{\mathbb {R}}}^2\) during a certain interval of time \([0,T]\subset {{\mathbb {R}}}\). Let \(t\in [0,T]\subset {{\mathbb {R}}}\) be the time point, and let \({\varvec{s}}_i=(x_i,y_i)\in R\subset {{\mathbb {R}}}^2\), be the spatial location, so that \(({\varvec{s}}_i,t)\) stands for the spatio-temporal locations with \(t=1,\ldots ,T\) and \(i=1,\ldots ,n\). Clearly, nT events have been recorded in total. Note that \(x_i\) and \(y_i\) are eastern and northern coordinates in a Cartesian Coordinates System. We emphasize here that these locations cannot be fixed or predetermined by any sampling design leading to a spatio-temporal point pattern. As we used here coordinates on a plane, the metric \(d(\cdot ,\cdot )\) that quantifies the spatial distance between any two events is the Euclidean distance. We follow the idea of Davies and Marchione (2015) to construct the time series of event network. Define the set \({\mathcal {A}}\) of all spatio-temporal locations where events have occured as
We now define a set \({\mathcal {D}}=\{D_1,D_2,\ldots ,D_{z-1},D_z\}\) of spatial distances, and we split the temporal interval T into N time slots, obtaining
so that the first time slot is \(\left\{ t=1,\ldots ,T_{1}\right\}\) and so on (see the first two columns of Fig. 1). We denote the time slots as \(t'\), so that \(t'=1,\ldots ,N\). Then, for example, events in the first time slot are given by \(\left\{ ({\varvec{s}}_i,t);\quad i=1,\ldots ,n_{t};\quad t=1,\ldots ,T_{1}\right\}\).
Considering all events appearing at each time slot \({t'}\), we define the set of nodes \(V_{t'}\) as those events that occurred in time slot \({t'}\). See dots representing the nodes in the third column of Fig. 1. With all the point pattern data, we obtain N sets of nodes \(V_{t'}\) given by
where \(n_{t'}\) stands for the number of events in that particular time slot.
Let D be a generic spatial distance that connects events of \(V_{t'}\) (this D could be any of the spatial distances \(D_i\) before considered). In other words, we connect events of \(V_{t'}\) if the spatial distance \(d(\cdot ,\cdot )\) between them is less than D while respecting their occurrence in time. For each time slot \(t'\) let
be the set of links. See an example of linked pairs of dots in the third column of Fig. 1. Consequently, we define the collection of graphs \(\{G_{t'}=(V_{t'},E_{t'})\}\) with \({t'}=1,\ldots ,N\) as the time series of event networks. These graphs are examples of geometric graphs (Davies and Marchione 2015) and also of Directed Acyclic Graphs (Barber 2012).
Note that we do not consider a set of temporal radii, to keep things simple but our method has room for this. Additionally, to avoid subjectivity in the selection of D, we propose to studying a number of networks with different spatial radii contained in \({\mathcal {D}}=\{D_1,D_2,\ldots ,D_{z-1},D_z\}\). So, we will have a time series of event networks for each \(D_q\in {\mathcal {D}}\), namely \(\{G_{t'}\}_{D_q}\). Each element of \(\{G_{t'}\}_{D_q}\) will be denoted as \(G_{{t'}D_q}\in \{G_{t'}\}_{D_q}\), \(q=1,\ldots ,z\). We illustrate these time series in columns 3, 6 and 9 of Fig. 1, sorting the columns according to \(D_q\). In addition, an illustrative example of each element involved at each step of the methodology is depicted in Fig. 2.
A change point analysis to relate events in an optimal way
We now aim to choose the ideal \(D_q\in {\mathcal {D}}\) to set up the time series of event networks. Therefore, it is of interest to detect where the structure of the whole graph changes qualitatively in space (Csárdi and Nepusz 2006). Thus we propose a macroscopic analysis that studies change points. First, we present an approach based on scan statistics (SS) which assumes that networks are nested. Then, we use the idea of Edge Difference Distance, making unsupervised classification to classify \(D_q\in {\mathcal {D}}\). We associate nestedness with a hierarchical organization, given that the network built with the smaller distance is contained in the network with the second smaller distance, and so on.
The SS method (Wang et al. 2014) was developed to detect change points in a time series of graphs with the same order. It detects changes based on dense communities. Thus, within each time slot \(t'\), the index will be the radius \(D_q\in {\mathcal {D}}\) instead of time, leading to compare nested networks: if \(D_q\le D_w\) then \(G_{t'D_q} \subseteq G_{t'D_w}\) for each \(G_{t'D_q}\in \{G_{t'}\}_{D_q}\) and \(G_{t'D_w}\in \{G_{t'}\}_{D_w}\). We will have a total of z SS for each \(t'=1,\ldots ,N\). We indeed use here a spatial SS. For a fixed time slot \({t'}\), as an statistic for the SS method, we consider the total count of edges between any pair of events, that is, the amount of interactions between the spatial events. Figure 1 shows an illustration of such edges counts, that is, SS, for each \(D_q\) at each time slot \(t'\). See also Fig. 2 for an illustration of the methodology for two time slots and two radii. We indeed are looking for such distances at which the total number of interactions shows an excessive increase of connections.
For formalities about SS, we adapt here the proposal in Wang et al. (2014). Let \(\varPsi _{{t'};{D_q}}({\varvec{s}}_i)\) and \(\varPhi _{{t'},t^*;{D_q}}({\varvec{s}}_i)\) be two quantities that capture a local shift based on \({\varvec{s}}_i\in V_{t'}\), and are defined as follows.
For a given \(t'\), \(\varPsi _{t';{D_q}}({\varvec{s}}_i)\) is defined for all \({D_q}\ge {D_1}\) and \({\varvec{s}}_i\in V_{t'}\) as
where \(V_{t'D_q}({\varvec{s}}_i;G_{t'})=\{{\varvec{s}}_j\in V_{t'}:d({\varvec{s}}_j,{\varvec{s}}_i)\le {D_q}\}\) is the set of vertexes with a distance at most \({D_q}\), and so \(\varOmega (V_{t'D_q}({\varvec{s}}_i;G_{t'});G_{t'})\) is the subgraph induced by \(V_{t'D_q}({\varvec{s}}_i;G_t')\). \(E_{t'}(\cdot )\) is the edge set and \(|\cdot |\) denotes the cardinality of the set.
If we have two time slots \(t^*\le {t'}\), then for all \({D_q}\ge {D_1}\) and \({\varvec{s}}_i\in V_{t'}\) we can also define
Finally, given \(G_1\) and \(G_2\) two graphs with the same order, with \(A_1\) and \(A_2\) their respective adjacency matrices, the Edge Difference Distance \(d(\cdot ,\cdot )\) is defined as the Frobenius norm of the matrix \(D=A_1-A_2\) (Hammond et al. 2013). We then consider the Edge Difference Distance to quantify the similarity between two graphs based on their adjacency matrices. With this, we construct a time slot similarity matrix to compare graphs under different spatial radii \(D_q\).
For the detection and counts of motifs used in the analysis of spatio-temporal patterns, there are some computationally efficient algorithms with highly significant subgraphs (see Kashani et al. 2009; Kobayashi et al. 2019. However, in our case, the motif detection algorithm must recognize the subgraphs formed inside the radius \(D_q\), with the directionality of their edges depending on t. Thus we use the concept of temporal motifs defining them as “ \(\ldots\) a class of valid isomorphic subgraphs, where the isomorphism is taken by including the similarity of the temporal order of the events”. In other words, according to this criterion, two subgraphs are isomorphic if they are topologically equivalent, and the order of their events is identical. We refer to Kobayashi and Génois (2021), Kobayashi et al. (2019), Nadini et al. (2020a) and Nadini et al. (2020b) for insights on the algorithms and their validation. The algorithm that we propose prioritizes some subgraphs related to the spatio-temporal patterns of events, providing information on co-occurrence and shift. Co-occurrence and close co-occurrence is based on the proximity of events in space-time, based on two behaviors that Wang and Zhang (2020) called boost (which indicates that the event is related to memories of past events) and flag (which is related to the opportunism of the event due to the conditions of space-time). Finally, the shift has to do with the movement of the event from places where it has previously occurred. In this line, the motifs that we look for in the detection of these patterns are In-2-Star, Out-2-Star and 2-Path, that we describe in “Empirical random network event generator (ERGEN) and motifs” section.
Empirical random network event generator (ERGEN) and motifs
In the microscopic approach, we explain the reasons behind the selection of several motifs. We then present the empirical random network event generator, an original contribution to handle problems with random order of networks over time. Finally, we study the correlation between the number of motifs. We study spatial motifs as building blocks to understand the underlying spatio-temporal process. In short:

Out-2-Star are subgraphs that impose an spatial order of events: from inside to outside. Basically, successive events are farther from each other comparing to their distance from past events.

In-2-Star are subgraphs that represent another spatial order: from outside to inside. In other words, those are successive and far events.

2-Path are subgraphs that display an interesting behavior of cases: Successive events move away from past events.
Column t contains all times of the registered events, and \(t'\) column shows the N time slots in which the whole period is divided. Columns \(G_{t'D_q}\) illustrate the construction of networks and multivariate time series of motifs counts, \(Y_{t'D_q}\), at each time \(t'\) and each distance \(D_q, q=1,\ldots ,z\). These motifs counts, \(Y_{t'D_q}\), have to be standardized as mentioned in “Empirical random network event generator (ERGEN) and motifs” section. The numbers with each network are the amount of edges for that case; that is, SS
Toy example. For illustrative purposes, we assume the spatio-temporal pattern occurs at 5 spatio-temporal locations. In the first time slot, the events occur three times (\(t_1,t_2,t_3\) depicted in black) and in the second time slot they occur two times (\(t_4,t_5\) depicted in red). The arrows are oriented according to the time-order of events inside each time slot. For each time slot and each distance, spatial motifs are counted. Links generated with the first distance, \(D_1\), are in black and links generated with the second distance, \(D_2\), are in blue. On the right side, we show the vector time series of motif counts for each case. Note that for each distance there is a time series of these vectors. Also, for each time point there is a sequence of vectors that depends on the set of distances. Finally, we show by extension the set of links for each spatial motif for the case \(t'=2,D_2\)
In this context, based on the observed events, we need to know whether the counts of each type of motifs are unusually high or unusually low, and thus establish patterns in the spatio-temporal configuration of events. We have one realization of the spatiotemporal pattern. Using ERGEN we generate B random networks and hence an empirical distribution of any measure of them. ERGEN carry out permutation of events time-order. In particular, we are interested in counts of each type of motifs that we are analyzing here. So, we find the empirical distributions of these motifs counts. Hence, we have to generate many random configurations of spatio-temporal point patterns and count each type of motifs at each of these random realizations. For this purpose, we consider a random sample generator of complex networks embedded in space and time, which we name here as ERGEN. Due to the fact that the order of \(G_{t'}\) is a random process, so is the size of \(G_{t'}\), because it is a function of the graph’s order and \(D_q\). Therefore, the number of any motifs will change as the amount of links changes, and this would mask the dynamic relationship between Out-2-Star, In-2-Star and 2-Path. As a solution, we standardized the corresponding counts of motifs. This procedure is summarized as follows:
-
1.
For each radius \(D_q\in {\mathcal {D}}\) and time slot \(t'=1,\ldots ,N\), we consider the time order of the set \(V_{t'D_q}\).
-
2.
The time series of event networks represent how points appear successively in a spatial neighborhood \(D_q\) at time slot \(t'\). So, we consider all possible ways that events could happen, that is, a different arrangement of \(V_{t'D_q}\). Exchanging the order of points and keeping their spatial distance would maintain the map of hazard locations but would simulate different movements in time slot \(t'\).
-
3.
Take B permutation samples of \(V_{t'D_q}\) (taking all possible permutations would be intractable in practice).
-
4.
Build B networks for each radius \(D_q\) and time slot \(t'\). Then, \(\left\{ G_{t'D_q}\right\} _{b=1}^B\) represents a sample of size B that shows different possible movements of points at the time slot \(t'\). This approach maintains exogenous features, hazard locations and time slot \(t'\). In fact, it is a sample generator of complex networks embedded in space and time.
As a result, we arrange the number of motifs of each \(\left\{ G_{t'D_q}\right\} _b\) in form of a matrix \({Y_{t'D_q}}\) which also contains the original number of motifs given by \(G_{t'D_q}\). Our interest is in the subgraphs described above, so \({Y_{t'D_q}}\) will have three columns and \(B+1\) rows. Then, to solve the masking problem, we scale the original counts as \({S}_{t'D_q}^{-\frac{1}{2}}({Y_{t'D_q}}-{{\bar{Y}}_{t'D_q}})\) where \({S}_{t'D_q}\) is the sample covariance matrix for \({Y_{t'D_q}}\), and \({{\bar{Y}}_{t'D_q}}\) the associated mean. The multivariate time series of motif counts obtained is
Consequently, this approach makes it possible to analyze dynamic relationships of motifs regardless of the size associated with the network, and also to perform a multivariate time-series analysis using the standardized counts. The detection of patterns such as spatial and/or temporal concentration of events allow to propose intervention strategies according to the application field. This methodology can be applied for zoning and gaining comprehension of the dynamic behavior of any type of spatio-temporal pattern. For example, in earthquakes it could provide additional parameters to assess the seismic threat, in epidemiology it can show ways a disease can spread and general patterns of incidence and mortality rates. In addition, this proposal presents essential solutions to the typical problems of other validation techniques. Through the building networks algorithm and the Empirical Random Network Generator (ERGEN), this approach allows decision-making about the statistical significance of motif using empirical distributions of standardized values of time series of motif counts. In fact, the ERGEN can be used to build empirical distributions of others networks measures. Note that this methodology does not require models or additional assumptions.
Real data analysis
Medellín is the second most populated city in Colombia (DANE 2019) that has suffered with crime for many years, being known as home of dangerous criminals. In 2018 Secretaría de Seguridad de Medellín showed that 40% of the citizens felt unsecure, and about 20607 theft complaints were received (Restrepo 2019). Furthermore, the police department recognizes the need of hiring almost 2.000 more policeman to fight against homicide, theft and micro-traffic (Monsalve 2019). In this paper, we analyze street thefts occurred in Medellín from years 2003 to 2015. The urban territory encloses an area of roughly 105 \(\mathrm{km}^2\).
To analyze the spatio-temporal patterns of crime events in Medellín, we consider two aspects. First, the global behavior of these events is analyzed by considering the spatial units based on the geographical juxtaposition Micro GJ, Proximal GJ, and Meso GJ; therefore, we consider radii of 500, 1000, 1500, and 2500 m. Second, and regarding the temporal component, the study unit will be slots of hours within weeks per months, to accommodate the time slots established by the Colombian national police following the historical reports of crimes reported in databases. The hourly time slots are 00:00 - 05:59, 06:00-11:59, 12:00-17:59, 18:00-23:59, for every week in every month during the years 2003–2015. We present an alternative analysis using time bands in “A tool for exploratory analysis: identification of spatio-temporal patterns by time bands” section.
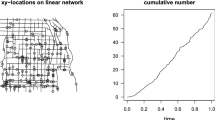
For each event, we have the hour, day and spatial location. We note that 18528 crimes were recorded in the considered period, with the following facts: 61% of the victims were men, the most dangerous neighborhood was La Candelaria, the most common type of theft was holdup (51% of all events) and the victims tended to be young, between 20 and 40 years of age. These events define a spatio-temporal point pattern. We use here monthly time slots, so we consider these events as a time series of spatial point patterns (see Baddeley et al. 2015). Figure 10 shows the spatial point pattern occurred on the first time window, January 2003, and the accumulated events until the last month of December 2015. We now proceed to analyze the dynamics of these thefts. First, we show construction and description of monthly time series of crime networks, then present the change point analysis to define the spatial distance at which networks change and finally we present ERGEN results.
Descriptive analysis of time series event networks
We built the time series of event networks with empirical spatial radii. We found that the network in Medellín is quite sparse with many isolated events: thefts tended to repel each other for distances less than 500 m within the same month. This is compatible with a regular or inhibitory point pattern (Baddeley et al. 2015). Therefore, we decided to use the following bins (meters): \({\mathcal {D}}=\{D_1,D_2,D_3,D_4,D_5\}=\{500,1000,1500,2000,2500\}\), and constructed five time series of graphs \(\{G_{t'}\}_{D_q}\), \({D_q}\in {\mathcal {D}}\), having an arrangement of data as shown in Table 1.
Given the importance of extracting all the information embedded in space and time through the linking of crime events, we analyzed all data from January 2003 to December 2015. By December 2015, a network contains all the motifs configured in space-time at a specific geographical distance (in this case, 500, 1000, 1500, 2000, 2500 m) (Fig. 3).
An attractive characteristic of this network is that they have a modular structure because most of them have one large component and two isolated components. Hence, the importance of analyzing some topological measures of these networks to understand the spatio-temporal patterns that underline the events’ interactions. For this particular case, some results of the topological metrics of the event networks obtained in January 2005 in a radius of 1500 m are in Table 2. the spatiotemporal patterns of crime events in Medellin at radial distances of 1500 m have a mixture. Thus, within these network’s components we can identify vital information that helps to understand the dynamics of the phenomenon.
Change point analysis
We now compare the several spatial radii \(D_q\) of the event networks to choose one in terms of practical and pragmatic decisions. We first calculated the SS monthly using the R package (Csárdi and Nepusz 2006) (see an example in Fig. 4). Following the statistical treatment to detect the change point in each month, we obtained the estimated point changes shown in Table 3. As a result, the change in the networks comes above 1500 m. Thus, we suggest building networks with a radius around 1000 m because the structure changes qualitatively for 1500 ms or more.
We then calculated the monthly similarities of \(G_{t'D_q}\) using the Edge Difference Distances across \(D_q\) to classify event networks. Table 4 shows the results of spatial scan statistics that allow to identify the behavior of clusters at each distance. The goal of this table is to detect the distance at which there are homogeneous networks. That is, the distance at which most of event networks are clustered; using unsupervised clustering, we found that graphs built with \(D_q\le\) 1500 ms are always together in the same homogeneous cluster. This leads to the same remark of the SS analysis. Consequently, we relate events for \(D_q\le\) 1500 m distances since gangs change their acting zones by a little margin given the fact that they typically have greater city areas where they act most of the time (Hegemann et al. 2011).
Motifs analysis with the ERGEN
We used ERGEN with 10000 permutation to generate a random sample of complex networks at each \(t'\) and \(D_q\). ERGEN randomizes the time-order of events. This allows to analyze the dynamics of observed subgraphs presented in “Empirical random network event generator (ERGEN) and motifs” section, without the bias of the network size. First, We consider counts for each time window (Table 5). Clearly these counts depend on the size of each network and on \(D_q\). For each \(D_q\in {\mathcal {D}}\), we built a multivariate time series in the form \(\left\{ {Y}_{t'}=(\#{In-2-Star},\#{Out-2-Star},\#{2-Path} )_{t'} \right\} _{D_q}\) presented in Table 5.
Note that from the results of Table 5, it is not possible to compare motifs given the difference in network size. To solve this issue, we standardized all time series, see “Empirical random network event generator (ERGEN) and motifs” section. Table 6 shows results for standardized time series \({S}_{t'D_q}^{-\frac{1}{2}}({Y_{t'D_q}}-{{\bar{Y}}_{t'D_q}})\). Now, it is possible to compare counts of different type of motifs and to detect those that are significant. These results are illustrated in Fig. 5.
Time series of the scaled counts of motifs for \(D=1500\) m obtained with the ERGEN. See Eq (1)
The scaled counts seem to be compatible with a stationary uncorrelated process. Indeed, for each \(D_q\) we calculated the multivariate Ljung-Box Statistics (Tsay 2013) and we did not reject the hypothesis of no cross-correlation (see Fig. 6). The number of past motifs does not have a linear association with the number of present motifs. Thus, we perform a Principal Component Analysis (see Fig. 7).
In other words, for each \(D_q\), \(q=1,\ldots ,z\), the components are:
-
1.
D=500
-
(a)
\(Out-2-Star\) Vs \(In-2-Star\)+\(2-Path\)
-
(b)
\(In-2-Star\) Vs \(2-Path\)
-
(a)
-
2.
D=1000
-
(a)
\(In-2-star\) Vs \(2-Path\)
-
(b)
\(Out-2-star\) Vs \(In-2-star\)+\(2-Path\)
-
(a)
-
3.
D=1500
-
(a)
\(2-Path\) Vs \(Out-2-star\)+\(In-2-Star\)
-
(b)
\(In-2-Star\) Vs \(Out-2-star\)
-
(a)
-
4.
D=2000
-
(a)
\(In-2-Star\) Vs \(2-Path\) + \(Out-2-star\)
-
(b)
\(Out-2-star\) Vs \(2-Path\)
-
(a)
-
5.
D=2500
-
(a)
\(Out-2-star\) Vs \(In-2-Star\)+\(Two-Path\)
-
(b)
\(In-2-Star\) Vs \(2-Path\)
-
(a)
It is important to remark that the number of past subgraphs does not have a correlation with their future number in this case. However, we performed a Principal Component Analysis (PCA) to explore association regardless of the time effect. The principal components under \(D_q\le 1000\) m build the same subgraphs, and for \(D_q>\) 1000 m components tend to disorganize. Again, there is a qualitative difference between the networks built under 1000 m and the rest of them. We thus reinforce our recommendation of constructing networks with a radius of roughly \(D=1000\) m. Therefore, the principal components of the number of motifs in networks built with radius 500 and 1000 m are similar, but different from the rest. Again, as in the macroscopic analysis, there is a qualitative difference between the networks built under 500 and 1000 m and the others. The recommendation is to construct networks with radius of roughly \(D=1000\) m. Furthermore, there is a negative linear association between subgraphs for each time window \(t'\). Despite the absence of linear association across time, for each \(t'\), the excessive occurrence of one shape implies less quantities of others (Table 7).
The results in Table 7 have direct consequences on decision-making. Police should move according to the dominant subgraph. For example, if 2-path is the dominant, after a theft occurs, police should make dynamic contours of 1000 m around the event till another crime appears, considering the likelihood that crime would not return. In fact, for \(D=1000\) m the classification of the dominating shape along time is possible using the individual coordinates in the principal components analysis, since the first component separates graphs with many 2-paths (positive x axis), and graphs with many In-2-stars (negative x axis); and the second component distinguishes graphs with many Out-2-stars (positive y axis). In fact, Fig. 8 represents the time series of the individuals projected on the first two components, with \(D=1000\) m.
Thus, positive values of the first time series (Fig. 8-top row represents the first component) indicate that crime movements are dominated by 2-Path, meanwhile negative values represent an inward succession of crimes. For the second time series (Fig. 8-bottom row represents the second component), positive values indicate an outward sequence of thefts. Since these subgraphs are occurring more frequently in comparison to a random graph, we conclude that they are motifs.
Discussion and conclusions
We have proposed a general methodology for analyzing events embedded in space and time. We follow the network construction of Davies and Marchione (2015), but we have gone beyond and constructed a time series of event networks. This is a general methodology for any type of interacting events that evolve in space and time. The application of event networks for the detection of spatio-temporal patterns demonstrates the ability of capturing different types of configurations that generate these patterns. Although here we have focused on crime data, the method can be equally adapted to locations of infected people in a particular region to analyze the spread of the disease, social networks, or other types of health and environmental studies.
The case of study in Medellín revealed numerous features. First, thefts tend to occur 500 m further from past crimes within the same season when we constructed the time series of event networks. In other words, we recommend that police should patrol in big areas surrounding robberies (more than 500 m). Besides, our first approach to divide seasons was ad-hoc using months and another technique based on data would be valuable, see additional material in “Discussion and conclusions” section.
We defined a technique to recommend one particular distance radius to build the theft network. Macroscopic analysis indeed suggests that it is suitable to build the networks with roughly 1000 m, because graphs changed qualitatively from 1500 onwards; so it is better to keep shorter distances to relate events. We suggest repeating the analysis with a range of radii between 1000 and 1500 m to increase the accuracy of the network.
Since the number of subgraphs was masked by the size of network, we have proposed the empirical random network event generator to analyze them. With this approach, we found that quantities of past subgraphs are not correlated with future configurations but each month tends to be dominated by one shape between In-2-Star, Out-2-Star or 2-Path guiding decision making in real time. The subgraphs presented in “Empirical random network event generator (ERGEN) and motifs” section were motifs because they occurred more frequently in comparison to a random graph. It would be valuable to study the exogenous factors deeper and improve the ERGEN because it currently takes lots of computational time.
Based on crime theory, the results obtained with the application of event networks in the identification of patterns in the city of Medellín have two components that suggest the combination of several theories. The first component is that the types of motifs that frequently occur in networks, refer to crime patterns exercised by territorial controls. The empirical evidence that supports this statement is the interaction between criminal actors in their mission of being invisible to the authorities, developing a series of territorial pacts in space-time, thereby increasing control in favor of the benefit obtained once the theft has been perpetrated. For example, there is a high similarity between crimes that occur late at night, especially at times where public force in the city is limited. According to crime theory, crimes committed late at night often tend to be controlled by actors with a high interference of territorial control. An emerging pattern of territorial control by illegal actors is observed by means of the sequential appearance of thefts in small areas for constant time slots.
The second component refers to aspects related to the CPTED (Crime Prevention Through Environmental Design), that can explain the significance and unexpected occurrences of motifs in this type of events. These results are in the macroscopic analysis (SS) since the changes in the properties of networks are due to the interaction of crimes with space-time. Thus, the configuration of neighborhoods becomes a determinant of the vulnerability of the victims. Therefore, the modification of the physical state of the neighborhoods increases the diversity of crimes, and territorial controls are lost. Another element that reflected the connection with the CPTED theory is the topological number of changes of networks when increasing the radial distance, especially if the radius is larger than 1000 m. This dynamic is repeated in different geographical locations.
In case of applying this methodology to analyze motifs of order 4, which are a total of 24, it would be necessary to apply dimensionality reduction methods, such as principal component analysis to study the structure of correlation and determine the most relevant characteristics. Also it is necessary to incorporate the attributes of events in the analysis.
Availability of data and materials
Data and R-code that support the findings of this study are available on Martha Bohorquez GitHub repository.
Abbreviations
- ERGEN:
-
Empirical random network event generator
- CPTED:
-
Crime Prevention Through Environmental Design
- GJ:
-
Geographic juxtaposition
- SS:
-
Scan-statistics
- PCA:
-
Principal component analysis
References
Atluri G, Karpatne A, Kumar V (2018) Spatio-temporal data mining: a survey of problems and methods. ACM Comput Surv 51(4):1–41
Baddeley A, Rubak E, Turner R (2015) Spatial point patterns: methodology and applications with R. Chapman and Hall/CRC
Barber D (2012) Bayesian reasoning and machine learning. Cambridge University Press
Barthelemy M (2018) Morphogenesis of spatial networks. Springer
Boers N, Bookhagen B, Marwan N, Kurths J, Marengo J (2013) Complex networks identify spatial patterns of extreme rainfall events of the south American monsoon system. Geophys Res Lett 40(16):4386–4392
Borgatti SP, Mehra A, Brass DJ, Labianca G (2009) Network analysis in the social sciences. Science 323(5916):892–895
Coscia M, Rinzivillo S, Giannotti F, Pedreschi D (2014) Spatial and temporal evaluation of network-based analysis of human mobility. In: State of the art applications of social network analysis. Springer, pp 269–293
Costa MA, Kulldorff M (2009) Applications of spatial scan statistics: a review. In: Scan statistics. Springer, pp 129–152
Cozens P, Love T, Davern B (2019) Geographical juxtaposition: a new direction in cpted. Soc Sci 8(9):252
Csárdi G, Nepusz T (2006) The igraph software package for complex network research. InterJournal Complex Syst 1695 http://igraph.org
da Cunha BR, Gonçalves S (2018) Topology, robustness, and structural controllability of the Brazilian federal police criminal intelligence network. Appl Netw Sci 3(1):1–20. https://doi.org/10.1007/s41109-018-0092-1
da Cunha BR, MacCarron P, Passold JF, dos Santos LW, Oliveira KA, Gleeson JP (2020) Assessing police topological efficiency in a major sting operation on the dark web. Sci Rep 10(1):1–10. https://doi.org/10.1038/s41598-019-56704-4
DANE (2019) Proyecciones de población departamentales y municipales por área 2005–2020. www.dane.gov.co. Accessed 25 Feb 2019
Dang TA, Chiam J, Li Y (2018) A comparative study of urban mobility patterns using large-scale spatio-temporal data. In: 2018 IEEE international conference on data mining workshops (ICDMW). IEEE, pp 572–579
Davies T, Marchione E (2015) Event networks and the identification of crime pattern motifs. PLoS ONE 10(11), e0143638 . https://doi.org/10.1371/journal.pone.0143638
Elliott P, Wartenberg D (2004) Spatial epidemiology: current approaches and future challenges. Environ Health Perspect 112(9):998–1006
Ferreira LN, Vega-Oliveros DA, Cotacallapa M, Cardoso MF, Quiles MG, Zhao L, Macau EE (2020) Spatiotemporal data analysis with chronological networks. Nat Commun 11(1):1–11
Friedman EJ, Landsberg AS, Owen J, Hsieh W, Kam L, Mukherjee P (2016) Edge correlations in spatial networks. J Complex Netw 4(1):1–14
Grubesic TH, Mack EA (2008) Spatio-temporal interaction of urban crime. J Quant Criminol 24(3):285–306
Hammond DK, Gur Y, Johnson CR (2013) Graph diffusion distance: a difference measure for weighted graphs based on the graph Laplacian exponential kernel. In: 2013 IEEE global conference on signal and information processing (GlobalSIP). IEEE, pp 419–422
Hegemann R, Smith L, Barbaro A, Bertozzi A, Reid S, Tita G (2011) Geographical influences of an emerging network of gang rivalries. Phys A 390:3894–3914
Jaros RG, Edwards JL, George D, Hawkins JC (2013) Spatio-temporal learning algorithms in hierarchical temporal networks. US Patent 8,504,494
Jazayeri A, Yang CC (2020) Motif discovery algorithms in static and temporal networks: a survey. arXiv preprint arXiv:2005.09721
Kashani ZRM, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A (2009) Kavosh: a new algorithm for finding network motifs. BMC Bioinform 10(1):1–12
Kobayashi T, Génois M (2021) The switching mechanisms of social network densification. Sci Rep 11(1):1–11
Kobayashi T, Takaguchi T, Barrat A (2019) The structured backbone of temporal social ties. Nat Commun 10(1):1–11
Kolaczyk E (2009) Statistical analysis of network data: methods and models. Springer
Kolaczyk E, Csárdi G (2014) Statistical analysis of network data with R. Springer
Landau SF, Fridman D (1993) The seasonality of violent crime: the case of robbery and homicide in Israel. J Research Crime Delinq 30(2):163–191
Lang JC, De Sterck H, Kaiser JL, Miller JC (2018) Analytic models for sir disease spread on random spatial networks. J Complex Netw 6(6):948–970
Monsalve C (2019) Medellín necesita 2000 uniformados más para reforzar seguridad. Blu Radio . www.bluradio.com/medellin/medellin-necesita-2000-uniformados-mas-para-reforzar-seguridad-policia-205513-ie1994153
Nadini M, Bongiorno C, Rizzo A, Porfiri M (2020a) Detecting network backbones against time variations in node properties. Nonlinear Dyn 99(1):855–878
Nadini M, Rizzo A, Porfiri M (2020b) Reconstructing irreducible links in temporal networks: which tool to choose depends on the network size. J Phys Complex 1(1):015001
Oberoi KS, Del Mondo G (2021) Graph-based pattern detection in spatio-temporal phenomena. In: 16th Spatial analysis and geomatics conference (SAGEO 2021)
Pasquaretta C, Dubois T, Gomez-Moracho T, Delepoulle VP, Le Loc’h G, Heeb P, Lihoreau M (2021) Analysis of temporal patterns in animal movement networks. Methods Ecol Evol 12(1):101–113
Rahman S(2017) Basic graph theory. Springer
Restrepo V (2019) ¿qué tan segura se siente la gente en medellín? El Colombiano. https://www.elcolombiano.com/antioquia/seguridad/percepcion-de-seguridad-en-medellin-encuesta-de-victimizacion-PC10033581
Runadi T, Widyaningsih Y (2017) Application of hotspot detection using spatial scan statistic: study of criminality in indonesia. In: AIP conference proceedings, vol 1827. AIP Publishing LLC, p 020011
Salje H, Cummings DA, Lessler J (2016) Estimating infectious disease transmission distances using the overall distribution of cases. Epidemics 17:10–18
Scott J, Carrington PJ(2011) The SAGE handbook of social network analysis. SAGE
Trifonova P, Metodiev M, Stavrev P, Simeonova S, Solakov D (2019) Integration of geological, geophysical and seismological data for seismic hazard assessment using spatial matching index. J Geograph Inf Syst 11(2):185–195
Trøjelsgaard K, Olesen JM (2016) Ecological networks in motion: micro-and macroscopic variability across scales. Funct Ecol 30(12):1926–1935
Tsay RS (2013) Multivariate time series analysis: with R and financial applications. Wiley
Wang Z, Zhang H (2020) Construction, detection, and interpretation of crime patterns over space and time. ISPRS Int J Geo-Inf 9(6):339
Wang H, Tang M, Park Y, Priebe CE (2014) Locality statistics for anomaly detection in time series of graphs. IEEE Trans Signal Process 62(3):703–717
Acknowledgements
We are thankful with the Policía Metropolitana de Medellín for providing access to data used in this paper.
Authors' information
Alan Miguel Forero Sanabria Bachelor in Statistics with in multivariate data analysis, time series, spatial statistics, statistical learning, network data analysis. I have experience in statistical consultancy, risk management, portfolio division, operational warnings, researching and teaching. My research involves the analysis of social problems through dynamic networks, functional data analysis, among others.Alan Miguel Forero Sanabria web page https://www.linkedin.com/in/alan-forero-4181a2188/?originalSubdomain=co.
Martha Patricia Bohorquez Castañeda Bachelor degree in Mathematics, M.Sc. and PhD in Statistics. Her research involves designs of sampling, analysis and modeling spatio-temporal data and functional data and their applications in various areas such as agriculture, environment, meteorology, epidemiology, among others. She has developed works on spatio-temporal covariance models, dynamic spatial sampling designs, univariate and multivariate prediction and optimal sampling for spatial functional data. Martha Patricia Bohorquez Castañeda web page https://sites.google.com/unal.edu.co/marthapatriciabohorquezcastaed/home.
Rafael Ricardo Renteria Ramos Postdoctoral in network analysis and statistical methods applied to health determinants, Doctor in Economic Sciences with a specialty in modeling and simulation of population dynamics, demography, and Industrial Engineer. As a researcher, he has experience in constructing statistical, mathematical, and computational models related to the internal armed conflict (especially in victims and shift), crime, violence, epidemiology, public health, biostatistics, and bioinformatics. Rafael Ricardo Rentería Ramos web page https://www.linkedin.com/in/rafael-ricardo-renteria-ramos-3b6aa7a3/?originalSubdomain=co.
Jorge Mateu Undergraduate Studies in Mathematics and Statistics, M.Sc. and Ph.D.in Mathematics. His research involves many topics of spatio-temporal modelling such as point processes, linear networks, Markov processes, Nonparametric statistics, spectral methods, positive definite functions, generalized additive models, data mining, geostatistics, Gaussian random fields and their applications to crime, public health, environmental pollution among others. He is editor-in-chief and associate editor of several Journals. Jorge Mateu web page http://www3.uji.es/~mateu/.
Funding
Work supported by Red de Violencia y Criminalidad - Universidad Nacional Abierta y a Distancia UNAD, Bogotá Colombia and Universidad Nacional de Colombia sede Bogotá.
Author information
Authors and Affiliations
Contributions
AM.F.S.: Conceptualization, methodology, investigation, data curation, writing-original Draft, writing-review, editing and project administration. M.P.B.C.: Methodology, validation, formal analysis, writing-review, editing, visualization and project administration. R.R.R.R.: Methodology, software, formal analysis, writing-review, editing, visualization and project administration. J.M.: Methodology, formal analysis, writing-review, editing, visualization and project administration. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
No potential competing interest is reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Identification of the time slot
We here consider a note about a simple tool that can help to identify the time slot in case this is not clear based on the specific phenomena. Multiple correspondence analysis (MCA) helps to choose the appropriate way to split times such that there is a clear correlation between hours and days, for example. This was not necessary in the case of hourly time slots of the police department because they have been stablished. Thus, we considered a correspondence analysis between days and hours (see Fig. 9), showing that light hours (between 6 and 18) on weekdays (Monday-Friday) report more thefts. Based on the distance between categories, the crimes on weekends are associated with early morning. So, this suggests the creation of a new variable named time slots Hour, a factor with two levels: Light hours (6–18), and Dark hours (19–5). The number of monthly thefts between the years 2003 and 2015 reveals a jump in 2013 and clearly suggests a non-stationary process. So, each month between the years 2013 and 2015 has a distinct behavior, supporting the idea of splitting the theft season.
The temporal and spatial ranges should come from informed decisions. Ripley’s K or pair correlation functions can also be used.
Table 8 shows the dynamics of event networks defined with police intervention action time slots. In studying the spatio-temporal dynamics of crime events in Medellín, it is necessary to analyze bands or areas of higher intensity and incidence defined by the control organisms. Table 9 shows how the algorithm works finding networks and interactions of these spatio-temporal events at the same distances used in the monthly analysis and defined by the concepts of the geographical juxtaposition of the CPTED. One of the most important results obtained with this approach (see Table 10) is the change in the radio of 1000 m, in comparison with the monthly analysis. The same behavior extends to a radius of 1500 m. The dynamics of crime events by time slots have a more significant geographical juxtaposition that dynamizes the configuration of a basic pattern for prioritizing risk management and crime prevention. To validate this result, Table 11 contains clusters based on the different geographical distances studied, and important and significant changes can be observed in the motifs structure at distances less than 1500 m.
A tool for exploratory analysis: identification of spatio-temporal patterns by time bands
To identify the spatio-temporal patterns by weekly time bands, for 2015, the typology and the number of reported crime events are key elements in the constructed data set. However, this analysis can be applied indifferently between 2003 - 2015 because the analysis is standardized.
For the first week of January, crimes do not present a defined spatio-temporal pattern since none of the defined motifs have a significant presence during each of the weekly time bands. That is, the crimes found in a radial distance of 500m are dispersed for this month. However, from the second week to the end of the month, the \(\text {2-Path}\) motifs are predominant until week 4, followed by the \(\text {Out-2-Star}\) with two essential behaviors. The first one is in week three, where the \(\text {Out-2-Star}\) and \(\text {2-Path}\) motifs are inversely related and in the same time slot. However, when carrying out an analysis between consecutive time slots, a spatial extension is observed that conditions sequencing of the events in the following time slot. Regarding the second behavior located in week four, the counts of the \(\text {Out-2-Star}\) and \(\text {2-path}\) motifs are synchronous. This particular convergence of graphs configures the creation of zones with a high clustering coefficient (by triads) of crimes in the time bands where there is greater mobility of the population.
In February, the crime activity behavior is much more active because from the first week, the \(\text {2-Path}\) motifs are repeated the most in each week of this month. Even as the weeks go by, it becomes more intense until it becomes concentrated in the early morning and afternoon time slots. In March, the first weeks are more intense between 06:00 - 17:59 with the \(\text {2-path}\) motifs, but then it reduces until disappearing in the last weeks of the month. This situation may be due to an accumulated effect from the previous month, which favors these motifs in the first part of March.
An important difference with the first quarter is in the number of motifs that were configured in this period; however, there is an important similarity with the previous quarter, and it is the predominance of the \(\text {2-Path}\) motifs over the others. This result is important because it allows us to infer that the conservation of this form speaks of a marked pattern in the first semester of the year and with greater intensity in the time bands of 06:00 - 17:59 between the second and fourth week. This result is an important planning opportunity for the allocation of police resources to mitigate criminogenic events in a radius of 500 m.
In recent quarters, the importance of the \(\text {2-Path}\) motif is preserved, as the most predominant pattern of the crime event in the city of Medellín in space-time. With a higher intensity since the second week (except September and November), something that is striking is that in every month in between, the last week is the most precise time to generate crime events throughout the city. This result is very interesting, because it seems to reinforce the hypothesis of the cost-benefit of criminal activity, since they are the dates on which most of the population receive pay for their work activities. Therefore, it is frequent that the mobility of the population is mainly concentrated in the commercial areas of the city during the hours of 06:00 - 17:59.
The month of January continues the prevailing behavior of the \(\text {2-path}\) motifs continues, followed by \(\text {Out--2--Star}\) and at the end of the month they promote the creation of clusters within the city, therefore it concentrates on some areas of the city, those coordinates becoming the priority points for police management (Fig. 10).
Locations of thefts denounced in Medellín city (Colombia)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sanabria, A.M.F., Castañeda, M.P.B., Ramos, R.R.R. et al. Identification of patterns for space-time event networks. Appl Netw Sci 7, 3 (2022). https://doi.org/10.1007/s41109-021-00442-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41109-021-00442-y