Dynamic failure and crash simulation of carbon fiber sheet moulding compound (CF-SMC)

Abstract

Carbon fiber sheet moulding compounds (CF-SMC) are a promising class of materials with the potential to replace aluminium and steel in many structural automotive applications. In this paper, we investigate the use of CF-SMC materials for the realization of a lightweight battery case for electric cars. A limiting factor for a wider structural adoption of CF-SMC has been a difficulty in modelling its mechanical behaviour with a computational effective methodology. In this paper, a novel simulation methodology has been developed, with the aim of enabling the use of FE methods based on shell elements. This is practical for the car industry since they can retain a good fidelity and can also represent damage phenomena. A hybrid material modelling approach has been implemented using phenomenological and simulation-based principles. Data from computer tomography scans were used for micro mechanical simulations to determine stiffness and failure behaviour of the material. Data from static three-point bending tests were then used to determine crack energy values needed for the application of hashing damage criteria. The whole simulation methodology was then evaluated against data coming from both static and dynamic (crash) tests. The simulation results were in good accordance with the experimental data.

Graphic abstract

1 Introduction

This paper focuses on the use of lightweight material for the construction of a battery cases for electric vehicles (Fig. 1). Battery cases can be large components, up to 1.5 $\times$ 2.5 m, and are usually placed low in the car between the front and rear axles. A good battery case has to provide a secure positioning of all the components inside. At the same time, it has to protect the electrical components in case of an external accident and a battery malfunction or run-off [1,2,3]. Generally traction battery systems comprise a multitude of cells or cell modules that are housed inside a battery case together with the auxiliaries for power distribution, cooling and control. The overall weight for the whole battery system can easily overcome 400 kg in case of a medium sized 50 kW/h system, given a typical ratio of 6,7 kg/kWh, with the battery case alone weighting over 80 kg [4]. The most widely adopted construction materials for battery cases are steel and aluminium, held together with welds and bolted connections [4]. These materials present a lower stiffness to weight ratio compared to unidirectional carbon fiber but at the advantage of being price competitive and easier to manufacture.

Fig. 1

Battery case concept showing the outer shell made of CF-SMC and the inner components such as the battery cells and auxiliaries

Carbon fiber sheet molding compounds (CF-SMC) are a class of materials composed of pre-preg chips or bundles of chopped carbon fibers dispersed in a matrix material. The most common matrix materials are epoxy and vinyl-ester resins [5, 6]. CF-SMC material possess a unique combination of properties being lightweight, having high strength values, crack resistance and a competitive price. Using this material to replace the aluminium for a battery case, can lead up to 30% weight reduction, while maintaining excellent mechanical properties [6]. The CF-SMC raw material possesses a certain viscosity level, thus allowing complex geometry to be moulded by using a pressing and curing process. In order for the resin to polymerize and solidify, the pressed parts need to be exposed to heat. The heat is generally provided within the press tool. Curing time is in the order of minutes, [6] allowing for high-output industrial applications. In comparison with traditional carbon fiber products, CF-SMC allows for the decoupling of the product quality from the operator ability. This is due to the quasi-isotropic nature of the material, as well as the adoption of pressing techniques [5,6,7,8,9].

In addition, old components can be recycled to new raw material with similar mechanical properties [10].

Currently, the material is applied, for example, to the window frames of the Boeing 787 Dreamliner [11], for structural parts of the Lamborghini Sesto Elemento [12], for Audi R-8 components [6, 13], for Dodge Viper Convertible [14] and bicycle drive train components of Campagnolo [15].

Common industrial simulation practise is to represent the properties of this material class with an elastic modulus and a static Yield strength only [6]. However experimental and numerical studies have shown that the mechanical characteristics are also determined by the chip dimensions and their mutual interactions [16,17,18]. Several studies have been performed to characterise the failure mechanism of such materials [5, 19,20,21]. Results indicate that the damage mechanism depends both on the nature of fibers and matrix as well as on the loading conditions. Compared to unidirectional ply based composites, CF-SMC exhibits similar stiffness values but with reduced strength [22, 23]. The material is tolerant to manufacturing defects and notches [8, 22,23,24]. Failure is a matrix-dominated phenomena based on intralaminar chip fracture and interlaminar chip delamination, with little to none fiber breakage [17, 22, 22]. The stress transfer and interaction between the chips makes the failure modelling for this material class difficult. Further influence factors are the energy of the loading event, the strain rate and the impactor geometry [21, 25]. Some phenomena, as for instance the strain rate dependency, might disappear if a particular fiber is used, with carbon fiber exhibiting almost no dependency [21]. Since many automotive components have to be designed to absorb energy in the event of a crash, it is of great importance to have a good understanding of the dynamical mechanical properties and failure mechanisms.

This paper aims to develop a modelling procedure for industrial simulation practices. In detail, the material model and damage model should be able to capture the complex dynamic mechanical properties [19, 20, 26], while at the same time being applicable to shell elements with a dimension greater than 1 mm.

2 Experimental work

2.1 Material and specimen manufacture

The material used is HexMC®-i [6] manufactured by Hexcel®. It comes from the producer as a rolled pre-preg mat of 460 mm width and 4 mm thickness, that is composed of randomly oriented 50 $\times$ 8 mm pre-preg chips. These mats can be cut, transferred into a mould and then compression moulded and cured.

Fiber	Matrix	Nominal fiber volume
HS Carbon	M77 Hexel Epoxy	57%

Cure time	Material density	Curing temperature
3 min	1.55 g/cm$^3$	$150 \, ^{\circ }{\text {C}}$

Yield strength	Elastic modulus
300 Mpa	38 Gpa

The specimens tested in this work were hat-profiles produced by SGL CARBON GmbH [27] (Fig. 2).

Fig. 2

Production process the mats of randomly oriented chips are loaded into the press dies. The pressure allows the material to flow and the imposed temperature cures the specimen within the press tool

In detail, the mould was filled with a preformed charge with a coverage of 82 percent of the die surface. The mould temperature was $150\,^{\circ }{\text {C}}$ with curing times of 3 min and a pressure of 690 kN/m$^2$. The specimen geometry (Fig. 3) was chosen due to the complex local stress and failure modes of a 3-point bending test. Ease of production allowed for a large number of samples. The radii and inclined surfaces create general tension and compression states of the specimen while complex stress configurations are locally generated under the impactor. The hat profile test was preferred upon a classic cut-out rectangular “coupon test” because the latter would have not allowed for a complex loading scenario.

Fig. 3

CF-SMC test specimen dimensions of the profile

2.2 Quasi-static testing

Quasi-static monotonic three-point bending tests (Fig. 4) of the hat profiles were performed on a servo-hydraulic MTS 852 test system. The steel fixture had a length of 360 mm with half cylinder supports and a striker with a diameter of 20 mm. Displacement signals were recorded from the position of the actuator piston. Force signals were recoded from a MTS load cell mounted on the striker. This was secured underneath the non-movable crosshead. All tests were performed at room temperature ($23 \pm 1\, ^{\circ }{\text {C}}$) and at a constant actuator speed of 2 mm/min until complete failure of a specimen.

Fig. 4

Static test rig the hat profile specimen (a), is supported by two half cylinders (b). The lateral movement of the hat profile is restricted by two lateral lobes (c) positioned on both sides of the supports (b). Four hand-tighten screws placed on the lobes (d) allow for a secure positioning. The impactor (e) applies force in the middle of the specimen

2.3 Sled impact tests

The test velocities were between 6.9 and 9.38 m/s. These velocities are determined by the Euro NCAP side pole test 8.88 m/s ($32.0\pm 0.5 \, {\text {km/h}}$) [28] and 8.94 m/s ($32.20 \pm 0.80 \, {\text {km/h}}$) for the American counterpart [29].

To obtain dynamic loading and failure data, a horizontal sled rig was used (Fig. 5). This consists of an instrumented support, a rail structure and an impactor element.

Fig. 5

Dynamic test rig two aluminium rails support the cart structure. Over it lays the striker (d). The striker can move horizontally on the cart structure. The specimen (c) is supported by a steel structure identical to the static test, and that is anchored to the wall through the force sensor (b). A position sensor is present as well (a). The Hat specimen is held into position by four screws present on the lobes of the supports. The impact is recorded by high-speed cameras

The rail structure is 6 m long, and its function is to support and guide a cart structure. The cart consists of a base, mounted on the rail via bearings, and an instrumented striker Fig. 5a, that is free to move longitudinally. The whole cart assembly is accelerated via a steel cable passing through a pulley system. At the beginning the striker element is located on the farthest end of the cart. The movement of the cable is provided by a falling mass situated on a remote location, behind the rigid crash wall. Once the cart approaches the end of the rail system, a hydraulic shock absorber paired with a coil spring, decelerate suddenly the cart. The striker is free to continue its longitudinal trajectory until impact with the specimen (Fig. 5c). Teflon and a thin layer of grease ensure minimal friction between the cart surface and the striker bottom. The specimen is supported by an U shaped steel support, that is anchored to the steel wall via a three component quartz force link (Kistler Type 9367C) (Fig. 5b). To have an accurate trigger for the data acquisition system, a physical copper switch is located on the top of the specimen. The switch is composed of two thin strips of copper divided by a small air gap. As the striker makes contact with the specimen, the two copper elements touch together, closing the trigger circuit. This trigger is used to start the flash lightning as well as for selecting the correct start time for the data acquisition procedure. On top of the structure a high speed and high accuracy laser displacement sensor (Keyence LK-H152) is placed, that records the position of the striker via a target on top of the striker structure. In addition, the striker is also instrumented with an accelerometer that is placed on the non-striker side.

2.4 Experimental conditions

Testing conditions are described in Table 1.

Table 1 Test conditions for all the dynamic experiment conducted on the HexMC hat profile

3 Model development

For the development of CF-SMC applications an advanced industrially usable modelling and simulation method has to be devised. For vehicle development purposes, it is common practice to limit the size and number of the elements in a simulation. Specifically for explicit simulations, element size has a direct impact on computational time. The maximum time increment is related to the element size and speed of sound in the material with the following relation [30]:

$$\begin{aligned} \Delta t \leqslant {\text {min}}\left( L_e \sqrt{\frac{\rho }{{\hat{\lambda }} + 2 {\hat{\mu }}}}\right) \end{aligned}$$

(1)

$L_{e}$ is a characteristic length associated with an element, $\rho$ is the density of the material in the element, and ${\hat{\lambda }}$ and ${\hat{\mu }}$ are the effective Lamé’s constants for the material in the element. Lamé constant are defined in terms of Young’s modulus E and Poisson’s ratio $\nu$ with the following equations:

$$\begin{aligned} {\hat{\lambda }}= & {} \frac{E\nu }{(1+\nu )(1-2\nu )} \end{aligned}$$

(2)

$$\begin{aligned} {\hat{\mu }}= & {} \frac{E}{2(1+\nu )} \end{aligned}$$

(3)

For this reason, we target on element and material formulation that enables the use of shell elements between approximately 1 and 5 mm.

At any given location in the test specimen, an average of 12 layers of carbon fibres are present. These layers consist of carbon chips that are randomly oriented during the manufacture process (Fig. 11). For this reason, the fiber lay up differs from place to place in the specimen. From a macroscopic perspective, it has been measured that the properties of CF-SMC materials are quasi-isotropic [6, 16, 22, 31]. The level of fiber randomness guarantees a homogeneous plane response. The elastic response of straight-sided rectangular specimens (305 $\times$ 38 $\times$ 3 mm) during bending tests is well captured using a simplified quasi-isotropic approach [32]. Quasi isotropic material properties are commonly used in industry [6, 31].

However, failure initiation and damage progression depend on local fiber orientation. The very nature of the fibers creates a modelling challenge for dynamic events [33]. The yield strength of the fiber is almost an order of magnitude higher compared to the matrix. During crash events, the crack propagation exhibits a preferred direction along the fiber chips as can bee seen in Fig. 12. Generally the crack front travels along the path of least resistance even if this means an increase of the crack length.

4 Material modelling

To simulate the damage behaviour two aspects have to be considered: damage initiation and damage evolution. The Hashin criterion was adopted as a criterion for damage initiation [34]. Damage evolution was modelled with a continuum mechanics linear-damage model [30].

4.1 Hashin damage initiation criterion

Lets consider a generic laminar shell element. The element is referred to a fixed coordinate system $x_1$ $x_2$ and a material coordinate system $x'_1$ $x'_2$ rotated by an angle $\theta$. Fibers are oriented along the axle $x'_1$ and the transverse direction is the one on $x'_2$ (Fig. 6).

Fig. 6

Generic element $x_1$ $x_2$ are the fixed reference system, $x'_1$ $x'_2$ are the material reference system

A generic plane state of stress $\sigma _{11} \ \sigma _{22} \ \sigma _{12}$ is transformed into $\sigma '_{11} \ \sigma '_{22} \ \sigma '_{12}$ with respect to the material system.

The following notation is adopted, where f stands for fiber mode and m for matrix mode failure.

$$\begin{aligned} \sigma '_{11}= & {} \sigma _{\text {f}} \end{aligned}$$

(4)

$$\begin{aligned} \sigma '_{22}= & {} \sigma _{\text {m}} \end{aligned}$$

(5)

$$\begin{aligned} \sigma '_{12}= & {} \tau _{\text {f}} \end{aligned}$$

(6)

The simplest loading scenario consist in an uniform uniaxial stress applied in the $x_1$ direction. Expressing the stress state in the material system results in:

$$\begin{aligned} \sigma _{\text {f}}= & {} \sigma _{11} \cos ^2 \theta \end{aligned}$$

(7)

$$\begin{aligned} \sigma _{\text {m}}= & {} \sigma _{11} \sin ^2 \theta \end{aligned}$$

(8)

$$\begin{aligned} \tau _{\text {f}}= & {} \sigma _{11} \sin \theta \cos \theta \end{aligned}$$

(9)

The failure indicator is expressed by the function F.

For F = 1 the material has failed. f stands for fiber, m stands for matrix, + indicates tensile, − indicates compressive.

For each mode (fiber and matrix) two possible scenario are possible: compressive and tensile. The choice of a particular failure mode, depends from the sign of the diagonal components of the stress tensor. The two-dimensional failure criteria are:

Tensile fiber mode $( \sigma _{11} \geqslant 0 )$

$$\begin{aligned} F^{+}_{f}=\left( \frac{\sigma _{11}}{\sigma ^+_{\text {f}}}\right) ^{2} + \left( \frac{\sigma _{12}}{\tau _{\text {f}}}\right) ^{2} \end{aligned}$$

(10)

Fiber compressive mode $( \sigma _{11} < 0 )$

$$\begin{aligned} F^{-}_{f}=\left( \frac{\sigma _{11}}{\sigma ^-_{\text {f}}}\right) ^{2} \end{aligned}$$

(11)

Tensile matrix mode $( \sigma _{22} \geqslant 0 )$

$$\begin{aligned} F^{+}_{m}=\left( \frac{\sigma _{22}}{\sigma ^+_{\text {m}}}\right) ^{2} + \left( \frac{\sigma _{12}}{\tau _{\text {m}}}\right) ^{2} \end{aligned}$$

(12)

Compressive matrix mode $( \sigma _{22} < 0 )$

$$\begin{aligned} F^{-}_{m}=\left( \frac{\sigma _{22}}{2\tau _{\text {m}}}\right) ^{2} + \left[ \left( \frac{\sigma ^-_{\text {m}}}{2\tau _{\text {m}}}\right) ^2-1\right] \left( \frac{\sigma _{22}}{\sigma ^-_{\text {m}}}\right) +\left( \frac{\sigma _{12}}{\tau _{\text {f}}}\right) ^2 \end{aligned}$$

(13)

where

$\sigma ^+_{\text {f}}$	Tensile failure stress in fiber mode
$\sigma ^-_{\text {f}}$	Compressing failure stress in fiber mode
$\sigma ^+_{\text {m}}$	Tensile failure stress in matrix mode
$\sigma ^-_{\text {m}}$	Compressing failure stress in matrix mode
$\tau _{\text {f}}$	Failure shear stress in fiber mode
$\tau _{\text {m}}$	Failure shear stress in matrix mode
$\delta$	Strain
$\alpha$	Shear component contribution
$\nu _{12}$	Poisson ratio in direction 1 2
$\nu _{13}$	Poisson ratio in direction 1 3
$L_{\text {c}}$	Characteristic length

$G^+_{\text {f}}$	Tensile failure energy in fiber mode
$G^-_{\text {f}}$	Compressing failure energy in fiber mode
$G^+_{\text {m}}$	Tensile failure energy in matrix mode
$G^-_{\text {m}}$	Compressing failure energy in matrix mode
$\eta$	Viscous damping
$E_{\text {f}}$	Young’s modulus fiber
$E_{\text {m}}$	Young’s modulus matrix

4.2 Continuum damage mechanics

4.2.1 Equivalent formulation of constitutive equation

A quantity called characteristic length $L_{\text {c}}$ is introduced into the formulation of the stress–displacement constitutive equation. This number is based on the element geometry and element formulation. In the case of a first-order element such as the shell elements used, it is the typical lengths of a line across the element itself [30, 35].

This allows for the material constitutive equation to be expressed as equivalent_stress ($\sigma _{\_{\text {eq}}}$) vs equivalent_ displacement ($\delta _{\_{\text {eq}}}$) instead of stress ($\sigma$) vs strain ($\delta$).

Both equivalent_stresses and equivalent_displacement can be expressed as function of the characteristic length L^c as follows.

$\delta _{xy}$ is the xy component of the strain tensor. The $\langle \rangle$ represents the Maculay bracket operator, which is defined as $\langle \sigma _{11} \rangle = \left( \sigma _{11} + |\sigma _{11} |\right) / 2$.

Fiber tension $( \sigma _{11} \geqslant 0 )$

$$\begin{aligned} \delta _{f \_ eq}^{+}&={L}^{\text {c}} \sqrt{\langle \epsilon _{11} \rangle ^2 + \alpha \epsilon ^2_{12}} \end{aligned}$$

(14)

$$\begin{aligned} \sigma _{f \_ eq}^{+}&=\frac{\langle \sigma _{11} \rangle \langle \epsilon _{11} \rangle +\alpha \tau _{12}\epsilon _{12}}{\delta _{{\text {f}}\_{\text {eq}}}^{+} / {L}^{\text {c}}}, \end{aligned}$$

(15)

Fiber compression $( \sigma _{11} < 0 )$

$$\begin{aligned} \delta _{f\_ eq}^{-}&={L}^{\text {c}} \langle -\epsilon _{11} \rangle \end{aligned}$$

(16)

$$\begin{aligned} \sigma _{f \_ eq}^{-}&=\frac{\langle \sigma _{11} \rangle \langle \epsilon _{11} \rangle }{\delta _{{\text {f}}\_{\text {eq}}}^{-} /{L}^{\text {c}}}, \end{aligned}$$

(17)

Matrix tension $( \sigma _{22} \geqslant 0 )$

$$\begin{aligned} \delta _{m\_ eq}^{+}&={L}^{\text {c}} \sqrt{\langle \epsilon _{22} \rangle ^2 + \epsilon ^2_{12}} \end{aligned}$$

(18)

$$\begin{aligned} \sigma _{m\_ eq}^{+}&=\frac{\langle \sigma _{22} \rangle \langle \epsilon _{22} \rangle +\alpha \tau _{12}\epsilon _{12}}{\delta _{{\text {m}}\_{\text {eq}}}^{+} / {L}^{\text {c}}}, \end{aligned}$$

(19)

Matrix compression $( \sigma _{22} < 0 )$

$$\begin{aligned} \delta _{m\_ eq}^{-}&={L}^{\text {c}} \sqrt{\langle -\epsilon _{22} \rangle ^2 + \epsilon ^2_{12}} \end{aligned}$$

(20)

$$\begin{aligned} \sigma _{m\_ eq}^{-}&=\frac{\langle -\sigma _{22} \rangle \langle -\epsilon _{22} \rangle +\alpha \tau _{12}\epsilon _{12}}{\delta _{{\text {m}}\_{\text {eq}}}^{-} / {L}^{\text {c}}}, \end{aligned}$$

(21)

4.2.2 Damage evolution

As the damage starts, a damage variable d is assigned to the element material.

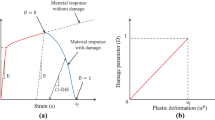
The damage variable will evolve such that the stress–displacement behaves as shown in Fig.  7 in each of the four failure modes (fiber and matrix in compression and tension). The positive slope of the stress–displacement curve prior to damage initiation (point (1), corresponding to $\delta ^0_{\text {eq}}$ in Fig. 7) corresponds to linear elastic material behaviour. At this point, the failure value F has reached value 1. The negative slope after damage initiation is achieved by evolution of the respective damage variables according to the Eq. 22 until point (2) in Fig. 7 denoted by $\delta ^{\text {failure}}_{\text {eq}}$.

Fig. 7

Source [30]

Equivalent stress vs equivalent displacement $\delta ^0_{\text {eq}}$ corresponds to the damage initiation, F = 1. $\delta ^{\text {failure}}_{\text {eq}}$ corresponds to the displacement after which the element does not offer any more mechanical resistance

The damage index d for a particular failure mode is given by the expression

$$\begin{aligned} d=\frac{\delta _{\text {eq}}^{\text {failure}} \left( \delta _{\text {eq}}-\delta _{\text {eq}}^0\right) }{\delta _{\text {eq}} \left( \delta ^{\text {failure}}_{\text {eq}}-\delta _{\text {eq}}^0\right) } \end{aligned}$$

(22)

where $\delta _{\text {eq}}^0$ represents the initial equivalent displacement at which the initial criterion for that failure mode was met and $\delta _{\text {eq}}^{\text {failure}}$ is the displacement at which the material is completely damaged. Graphical representation of damage evolution is shown in Fig. 8. The damage value d is zero until reaching the damage criterion. After the critical equivalent displacement, the d value increases up to 1.

Fig. 8

Damage variable until the failure initiation is reached (point (1) in Fig. 7), the damage variable value remains zero. As the equivalent displacement increases, the damage values rises up to 1 (point (2) in Fig. 7), when the element does not offer any resistance to deformation

The damage coefficient D is defined as

$$\begin{aligned} D=1-(1-d_{\text {f}})(1-d_{\text {m}})\nu _{12}\nu _{21} \end{aligned}$$

(23)

with $\nu _{12}$ and $\nu _{21}$ Poisson ratios.

To chose the proper damage index for a specific load case, the first and second diagonal stress components are observed. Based on these values, the damage indexes defined in 22 are chosen such that:

$$\begin{aligned} d_{\text {f}}= & {} \left\{ \begin{array}{ll} d^+_{\text {f}}\ {\text {if}} \ \sigma _{11} \geqslant 0\\ d^-_{\text {f}}\ {\text {if}} \ \sigma _{11} < 0 \end{array} \right. \end{aligned}$$

(24)

$$\begin{aligned} d_{\text {m}}= & {} \left\{ \begin{array}{ll} d^+_{\text {m}}\ {\text {if}} \ \sigma _{22} \geqslant 0\\ d^-_{\text {m}}\ {\text {if}} \ \sigma _{22} < 0 \end{array} \right. \end{aligned}$$

(25)

$$\begin{aligned} d_s= & {} 1-(1-d^+_{\text {f}})(1-d^-_{\text {f}})(1-d^+_{\text {m}})(1-d^-_{\text {m}}) \end{aligned}$$

(26)

After the damage initiation (point (1) in Fig. 7), the material response is computed by the following equation:

$$\begin{aligned} {\varvec{\sigma }}={\mathbf {C}}_{\text {d}}{\varvec{\epsilon }} \end{aligned}$$

(27)

where ${\varvec{\epsilon }}$ is the strain tensor and the term ${\mathbf {C}}_{\text {d}}$ is the damaged elasticity matrix, having the form :

$$\begin{aligned} \begin{array}{c} {\mathbf {C}}_{\text {d}} = \\ {\frac{1}{D} \left[ \begin{matrix}(1-d_{\text {f}})E_{\text {f}}&{}(1-d_{\text {f}})(1-d_{\text {m}})\nu _{21}E_{\text {f}}&{}0\\ (1-d_{\text {f}})(1-d_{\text {m}})\nu _{12}E_{\text {m}}&{}(1-d_{\text {m}})E_{\text {m}}&{}0\\ 0&{}0&{}(1-d_s)G D\end{matrix}\right] }\\ \end{array} \end{aligned}$$

(28)

4.2.3 Dissipated energy

For each failure mode a specific dissipated energy G due to failure must be defined. This consists of the area of the triangle OAC in Fig. 9. The $\delta _{\text {eq}}^f$ for the various modes thus depend on the respective energy parameter G.

Fig. 9

Loading–unloading path a loading cycle with complete damage follows the 0-A-C path. In case of unloading at a partially damage state (point B) the elastic modulus will be represented by the steepness of the line 0-B. In case of further loading, the line 0-B, instead of the line 0-A, will be followed

4.3 Viscous regularization

In Explicit simulations, the viscous regularization is a parameter used for taking into account possible material behaviour that is strain rate dependent. No need to change the viscous damping during the simulations has been observed. The viscous damping value is kept constant at 0.00001 throughout the whole simulation series. The absence of strain rate dependency for the various dynamics of our tests is in accordance with existing literature [21].

5 FEM calculation

5.1 Finite element model description

The model is represented in Fig. 10. It consists of three main parts: a roughly meshed steel support, the CF-SMC finely meshed part and the rigid impactor. The test specimen consists of S4 elements with 4 integration points, with orthotropic material. Average element size is 5 $\times$ 5 mm. The boundary conditions consist in a rigid support of the steel base, created by a multi-point constraint (COUPLING KINEMATIC) in the same location and size of the actual force sensor. The CF-SMC piece is in contact with the steel base with a friction coefficient of 0.1. The rigid impactor is commanded a specific initial velocity with direction towards the CF-SMC piece. The solver used is ABAQUS v2019

Fig. 10

FEM modell total number of elements is ca 19,000

5.2 Random element orientation approach

The CF-SMC material is composed of a high number of carbon fiber chips, held together by resin (Fig. 11). In the uncured mats, the chips are horizontally laid. During the pressing process, the chips can move relative to one other and flow into the tool’s form.

Fig. 11

X-ray tomography images of a CF-SMC tensile test specimen. Top image is taken from above the press-plane. Bottom image is a slice in the thickness of the specime. Resolution is respectively $(30 \, \upmu {\text {m}})^3$ voxel size (top) and $(5 \, \upmu {\text {m}})^3$ voxel size (bottom). A voxel corresponds to a pixel for a given slice thickness in the magnetic resonance imaging

The complex spatial disposition of the chips and their high number pose a great modelling challenge. It is theoretically possible to map all the chip positions in every specimen and to model every individual one with solid elements. Nevertheless, this would require an enormous amount of elements. Also with simple mechanical simulations of such models, the calculation time would become enormous.

Shell elements are the workhorse of the car industry for thin walled structures. Thus we developed a model based on them. In order to predict the complex failure behaviour during crack propagation (as seen in Figs. 12, 13) a randomized direction approach was used. In this approach each shell element is assigned an in-plane random material orientation with a value from $0^{\circ }$ to $180^{\circ }$ respective to the local element coordinate system (Fig. 14).

This allows for the damage to travel along a complex path along the hat profile, thus recreating a stochastic crack propagation dynamics that was observed during the tests.

Fig. 12

Crack through CF-SMC close up of a typical failed specimen. The crack has run along with the chips where the resin has failed. The fiber are almost undamaged

Fig. 13

Damage process of the specimen the three stages of the dynamic test: contact (1), crack initiation (2) and crack propagation (3). Note the material fails along the edges of the fiber chips. The nature of the crack is quite complex due to the local anisotropy of the material

Fig. 14

FEM model close up of hat profile FEM model. The green lines represent the normal to the principal direction of each element

To cope with the high number of elements, we used a script to modify the FEM input file and to assign to every element a random orientation angle.

5.2.1 Material fitting

The parameters for the material fitting were determined in two stages. Initially, the rough values were calculated based on data from with CT-scans (computerized tomography scan) and the material modelling software Digimat [36]. In the second step, force displacement data coming from a three-point bending static test were used to validate the initially estimated material values.

5.2.2 Simulation: equivalent volume method

The elastic, yield and shear moduli are derived from a technique called representative volume element. Material data for the individual fibers and resin came from the producer (elastic modulus and strengths of fiber and resin). Ct-scans (as in Fig. 11) were used to determine the fiber location, orientation and stacking in a CF-SMC sample.

A material modelling software (digimat) [36] combined all this informations and computed the equivalent properties for a certain volume. The volume considered corresponds to the size of the element used in the simulation of the hat profile. In this way, we determined the equivalent material parameter for a representative element.

5.2.3 Validation: 3 point bending static test

A three-point bending test was performed (Fig. 4) to validate the material parameters derived from the simulation in Sect. 5.2.2. This test was also used to empirically determine the breaking energies (specific dissipated energies G) of the material (Table 2, Fig. 15).

Fig. 15

Force displacement for 3 point bending static test

Table 2 Material data values

6 Results for dynamic simulations

FEM simulations of the 3 point bending dynamic loading were performed matching all the test conditions of Table 1. The tests were grouped in test sets based on the common impactor velocity and mass (Table 3).

Table 3 Results analysis data from the test-set-up

6.1 Damage distribution in FEM model

The simulated damage evolution and distribution (Fig. 16) is in accordance with the observed damage in the hat-profiles during dynamic testing (Fig. 13).

Fig. 16

Hashin fiber damage top view of the simulated dynamic impact for test-set $\#$4. Bottom figures represent the early interaction phase. Second figure is taken at half contact time. Third figure represents the maximum penetration. In red the elements that have failed under the Hashin criteria

6.2 Force displacement results

The following images compare the force–displacement curve from explicit FEM simulations to measured ones. The force is measured on the back of the support structure, where the force sensor is placed. The displacement refers to the movement of the impactor. By the simulations the viscous damping parameter was adjusted. A constant value of $10^{-6}$ led to satisfactory forces vs displacement prediction. This is a very small number, thus excluding a strain-rate material response (Figs. 17, 18, 19, 20, 21, 22, 23).

Fig. 17

Test-FEM test-set # N1. Around 8 mm the impactor has rebounced away from the hat profile

Fig. 18

Test-FEM test-set # N2

Fig. 19

Test-FEM test-set # N3

Fig. 20

Test-FEM test-set # N4

Fig. 21

Test-FEM test-set # N5

Fig. 22

Test-FEM test-set # N6

Fig. 23

Test-FEM test-set # N7

6.2.1 Maximum predicted force

The maximum deviation of the maximum computed force was between 0.2 and 15% depending on the crash series. The spread in some of the measurements is attributed to manufacturing process and the random chip distribution of the hat profile (Table 4).

Table 4 Results analysis data from the test-sets ordered from the interaction with the highest energy

6.2.2 Correlation of force curves

To estimate the difference between the measured and simulated values, the correlation and $R^2$ were calculated. The values refer to the correlation between force and displacement. Both values are calculated on an interval starting at 0 mm and going until data from measurement are present or at the first zero crossing of the computed force. The correlation, averaged on all the data is 0.78 and $R^2$ is 0.62 (Table 5).

Table 5 Correlation and $R^2$ values of force data vs displacement

6.3 Influence of initial element orientation

To exclude a possible influence on the initial orientation of the elements principal direction, a series of the simulation were performed with different initial element orientation (Fig. 24). We observed little variation related to the initial element orientation.

Fig. 24

Data comparison result comparison of the FEM and measured forces for dynamic 3 point bending for test serie $\#$4. Different FEM lines correspond to different initial random orientation of the element material direction

6.4 Mesh size sensitivity

Mesh-size sensitivity was analysed running simulations where the model’s element size was varied. Elements of 0.5, 1 and 5 mm were considered. From the analysis, a scatter band of the force–displacement results can be observed. The smoothed response curves show a small element size sensitivity (Fig. 25).

Fig. 25

Mesh dependency analysis FEM simulated forces for different element size: 0.5, 1 and 5 mm. Performed for test-set $\#2$ conditions

6.5 Fluctuation the force–displacement curves

An Eigenfrequency analysis was performed on the support and we found a strong component at ca 3000 Hz, corresponding to the outward-inward movement of the supports lobes (Fig. 27). This frequency is responsible for the crests present in the computed force displacement curves (Fig. 26). The surface interaction between the steel support and the carbon hat profile limits the lateral swings of the steel support lobes (Fig. 27). To recreate this effect in the simulation, it is possible to constraint the inward-outward movement of the lobes of the steel support. This has the effect of smoothing the force vs displacement curve (Fig. 28).

The analysis of the frequency content of the simulated and measured force in time, reveals a reasonable frequency matching of the basic peaks.

Fig. 26

FFT analysis frequency content of the force vs time for the measured and simulated signal. The force was measured under crash_test_n10 conditions

Fig. 27

3280 Hz mode shape the movement of the lobes that follow the red lines around the black dashed lines are responsible for the amplification of the signal around 3000 Hz. A constraint of the lateral movement of the lobes along the red lines, subdues the spikes in the force vs displacement curve

Fig. 28

Force curve smoothing comparison of the same test conditions with different supports. In yellow a support structure with artificially stiffer support lobes. The force was measured under crash_test_n10 conditions

7 Complete battery simulation

The battery is modelled with shell elements, whose minimum size is 1 mm. The simulation is performed with 35 g acceleration in z direction. The vertical acceleration is a demanding requirement for a battery case, given the high weight of the modules inside. In our particular case, the side crushing is of less importance, given the presence of protective structures coming from the car body. The battery case geometry derives from an ongoing industrial project representing therefore a real case.

The simulation methods developed during this work are currently used to simulate the mechanical behaviour of the aforementioned battery case. Mechanical crash tests are going to be used to extend the validity of the simulation methodology to big components (Fig. 29).

Fig. 29

35 g z acceleration complete battery FEM simulation. Hashin damage

8 Conclusion

The material modelling was successfully verified by static and dynamic experiments. The value for viscous regularization throughout all simulations is small (0.000001) and constant. This means, that a strain rate dependency is not present for this material within testing conditions typical for automotive engineering. Specifically this means that a static test is sufficient to capture the mechanical behaviour needed to simulate automotive test impact speeds. This work demonstrates an efficient and accurate simulation method for CF-SMC materials based on shell elements. The simulation procedure adopts a random orientation of the elements principal direction and an orthotropic continuum-based material definition.

This modelling procedure leads to a satisfactory representation of damage and crack behaviour, including stochastic effects.

Prediction of maximal force, force displacement curves and energy absorption are found to be sufficiently accurate, and within the scatter of experimental testing.

This approach is suitable for simulating large components such as battery cases for electric vehicles. Considering the material damage in the design phase, allows for a reduction of weight. This is an important step for evaluating further introduction of CF-SMC components in the automotive industry. We observed a highly damage tolerant material behaviour, with a large amount of energy absorbed before complete material failure. Crack growth was also hampered by the presence of randomly oriented carbon chips, that resulted in segmented cracks. All of these properties make the CF-SMC an advantageous material for safety critical car components.

Some potential improvement that could be implemented in future are: a stiffer support structure and a better positioning of the force sensor for the dynamic test of hat profiles. The first would result in the reduction of spurious frequencies in the force signal. The second, by placing the sensor directly on the sled, would generate a force signal with a stronger emphasis from the carbon hat-profile and reduced effect from the steel support.