1 Introduction

For moderate water heights up to 3 mm between pure wet-grip and hydroplaning, the friction level is influenced, among other parameters, significantly by pattern layout, vehicle speed and water height. The water between tire and road has to be squeezed out in order to establish contact between road and track. Although no full hydroplaning occurs, which means the water film completely separates the tire from the road, the grip level can already be significantly reduced [3, 5]. According to the three-zone model [7], this is caused by a longer squeeze film zone. On the one hand, the pattern layout determines the geometric stiffness, which influences wet braking behaviour. In addition, number and design of edges have a direct impact on the wet braking performance. On the other hand, pattern design and profile depth determine how fast water on the road is squeezed out under single tread blocks and transported outside the contact patch to allow the transmission of braking forces [10]. Driving speed and water height have a direct impact on the squeeze out process. Wet friction is influenced by the slip velocity in the contact patch [4]. Additionally, both driving speed and water height influence the temperature of rubber and road, which has an impact on rubber properties [6, p. 18–20]. To further improve tires, it is essential to know and understand in detail the mechanisms that determine the braking forces that can be transmitted under different operating conditions. To determine the contribution of inertia driven squeeze in the complex wet braking process, the pressure inside the fluid film is directly measured by a piezoelectric sensor mounted inside the track for various free rolling tires. The friction level is measured by braking these tires on the same track. Especially for high vehicle speeds, inertia effects are expected to have a significant impact on the squeeze out process as shown by [1, p. 31]. In [8] hydroplaning is identified for a water height of 8 mm by comparing the signal obtained from acceleration sensors mounted on the inner liner of the tire carcass with data from a high-speed camera which observes the footprint through a glass plate. The acceleration signal, however, allows no direct inference to the fluid pressure and the water height of 8 mm is already in the region of full hydroplaning. As far as known to the authors, the fluid pressure has never been directly measured under wet braking conditions with a water height below 3 mm on a realistic asphalt track before.

2 Test setup

2.1 Inner drum test bench

The inner drum test bench at KIT has a diameter of 3.8 m and is equipped with a realistic asphalt track. The drum rotates with an orbital speed corresponding to the driving speed of the tire. The tested tire is driven or braked by a hydraulic motor. A built-in measuring hub captures the resulting braking forces. A detailed description of the test bench is given in [2]. A water supply system allows the adjustment of a steady water film of up to 3 mm of height. The water height is measured capacitively, which means 1 mm corresponds to 1 lm−2.

2.2 Pressure measurements

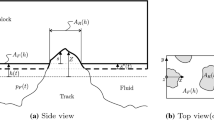
The piezoelectric pressure sensor is mounted horizontally in a sledge, which is held by a bracket integrated into the roadway as shown in Fig. 1. The bracket has a width of 20 mm. Together with the joints, the asphalt surface is interrupted for a distance of  25 mm in the direction of travel. A telemetry unit transfers the data out of the rotating drum, as the sensor moves with the drum. The sledge allows a lateral displacement of the sensor. The fluid is in contact with the integrated pressure sensor through an opening in the steel cover. As the tire rolls over the steel cover above the sensor, the fluid pressure in front of the sensor increases. The piezoelectric sensor S112A22 from PCB SynotechTM operates in a range of ±3.5 bar and a measuring frequency of 50 kHz. The rotating transmitter side of the datatelTM telemetry system consists of a power supply for the sensor, a voltage frequency converter and a high- frequency modulator. The stationary receiver side consists of a high- frequency demodulator, a frequency-voltage converter and an output amplifier.

Fig. 1
figure 1

Setup with sensor, bracket integrated in track and telemetry unit (left). Steel cover removed (right)

Full size image

2.2.1 Measuring procedure

Each parameter combination of speed, water height and pattern layout is recorded for at least 30 s with a free rolling tire. The position of the drum is recorded parallel to the pressure signal. Water height, speed, tire load and tire inflation pressure are kept constant during each measurement.

2.2.2 Signal processing

Fig. 2
figure 2

Filtered pressure signal for big block pattern measured at 2 mm water height and 100 km h−1

Full size image

The measured pressure values are assigned to the corresponding drum position and the resulting signal of pressure over drum position is filtered. Figure 2 shows an exemplary filtered pressure signal measured at 2 mm water height and 100 km h−1 with pattern layout BB (see Fig. 4). A steep increase in the pressure is observed once the sensor enters the footprint. After the maximum, the pressure decreases towards zero and reaches an area of underpressure when the tread is lifted off the road at the rear end of the footprint. The absolute values of the single pressure signals are rather difficult to interpret and compare for different parameters. To compare test results for different water heights, speeds and patterns we derive a quantity which characterizes the pressure signal and allows a comparison with the results of braking tests. This new quantity \(\varLambda \) is determined by the hatched area in Fig. 2. A detailed derivation of \(\varLambda \) and its relation to a friction force is given in the following paragraph.

We assume the tire load is carried by the track asperities penetrating the fluid film on the track and the fluid film itself. Since the viscous friction between fluid and rubber is much smaller than the hysteretic friction between track asperities and rubber, we neglect viscous friction and write

$$\begin{aligned} \mu&= \mu _{{\text {wet}}} \frac{F_{{\text {C}}}}{F_{Z}} = \mu _{{\text {wet}}} \frac{F_{Z}-F_{\text {F}}}{F_{Z}} = \mu _{{\text {wet}}} \left( 1 - \frac{F_{F}}{F_{Z}}, \right) . \end{aligned}$$
(1)

where \(\mu _{{\text {wet}}}\) describes the reference friction coefficient for a damp track without inertia effects of the fluid. \(F_{\text {Z}}\) is the tire load and \(F_{{\text {C}}}\) is the part of the tire load which is carried by the asperities. Since fluid and track asperities together carry the tire we can write \(F_C=F_{\text {Z}} - F_{\text {F}}\), where \(F_{\text {F}}\) is the load support of the fluid. For an infinite small pressure measuring device which does not disturb the conditions in the fluid film we can write

$$\begin{aligned} F_{\text {F}}&= \int p_{\text {F}}(x,y) {\text {d}}A_{{\text {cp}}} = \bar{p}_{\text {F}} \cdot A_{{\text {cp}}} \end{aligned}$$
(2)

with the mean fluid pressure \(\bar{p}_{\text {F}}\) and the size of the contact patch \(A_{{\text {cp}}}\). \(p_{\text {F}}(x,y)\) describes the local fluid pressure inside the contact patch. Where contact is established, we assume \(p_{\text {F}}(x,y)=0\); therefore, we integrate over the whole contact patch \(A_{{\text {cp}}}\) and not only the part which is covered by water. The tire load can approximately be written as

$$\begin{aligned} F_{\text {Z}}&= \int p_i(x,y) {\text {d}}A_{{\text {cp}}} = \bar{p}_i \cdot A_{{\text {cp}}}, \end{aligned}$$
(3)

with the mean tire inflation pressure \(\bar{p}_i\). This leads to

$$\begin{aligned} \frac{F_{\text {F}}}{F_{\text {Z}}}&= \frac{\bar{p}_{\text {F}}}{\bar{p}_i}. \end{aligned}$$
(4)

The mean tire inflation pressure \(\bar{p}_i\) is kept constant during our tests. The mean fluid pressure is calculated from the measured pressure signal (see Fig. 2) according to

$$\begin{aligned} \bar{p}_{\text {F}} = \frac{1}{l_{{\text {cp}}}}\int p_{\text {F}} {\text {d}}l_{{\text {cp}}}, \end{aligned}$$
(5)

where \(l_{{\text {cp}}}\) is the length of the contact patch. The underlying assumption is that the fluid pressure measured in the center line of the contact patch is representative for the whole contact patch. We only consider positive values of the fluid pressure for the evaluation. The underpressure observed at the rear end of the contact patch (see Fig. 2) is not considered. For the small water heights tested here, the wet grip reduction is mainly caused by fluid inertia effects in the front part of the footprint. At the end of the footprint, the tread blocks are lifted off the steel cover and the resulting underpressure is not expected to be the same as on an undisturbed track without sensor. Therefore, we set \(p_{\text {F}} = 0\) if the measured pressure is negative. Under these assumptions (Eqs. 1, 4), the friction coefficient is

$$\begin{aligned} \mu&= \mu _{{\text {wet}}} \left( 1 - \overbrace{\frac{\bar{p}_{\text {F}}}{\bar{p}_i}}^{\varLambda } \right) \end{aligned}$$
(6)

with the loss term

$$\begin{aligned} \varLambda&=\frac{\bar{p}_{\text {F}}}{\bar{p}_i}, \end{aligned}$$
(7)

which we introduced earlier. It describes the hatched area in Fig. 2 normalized by the area expected for full hydroplaning conditions. In this study we are especially interested in how fluid pressure and friction coefficients change with water height and speed. The absolute value of \(\varLambda \) is strongly influenced by the specific design of sledge, bracket and cover shown in Fig. 1. The absolute value of \(\mu \) is determined by track roughness on different length scales [9], rubber properties and temperature. Based on Eq. 6, we calculate the change of \(\mu \) normalized by \(\mu _{{\text {wet}}}\), which is described by the gradients

$$\begin{aligned} \overbrace{\frac{\partial \varLambda }{\partial v}}^{\partial \varLambda _v}&= - \overbrace{\frac{1}{\mu _{{\text {wet}}}}\frac{\partial \mu }{\partial v}}^{\partial \mu _v}, \end{aligned}$$
(8)
$$\begin{aligned} \overbrace{\frac{\partial \varLambda }{\partial h}}^{\partial \varLambda _h}&= - \overbrace{\frac{1}{\mu _{{\text {wet}}}}\frac{\partial \mu }{\partial h}}^{\partial \mu _h}. \end{aligned}$$
(9)

They describe how much the tested conditions influence the pressure signal and allow a comparison with friction forces measured during braking. This is of course only valid if the friction level is completely determined by the fluid pressure. Temperature, wet friction effects and many more effects will influence the maximum friction force, but are not expected to be directly correlated to the fluid pressure. Equations 8 and 9 represent a working hypothesis to be checked with the results from our tests. Even if a correlation between \(\mu \) and \(\varLambda \) is not given, \(\partial \varLambda _v\) and \(\partial \varLambda _h\) describe physically meaningful scalar quantities to compare pressure signals measured at different parameters independently from the consideration of braking forces.

2.3 Braking tests

With the parameters shown in Table 1 braking tests were done at the inner drum test bench. The \(\mu -\)slip curves are recorded during braking and the maximum friction coefficients are determined. The quantities \(\partial \mu _v\) and \(\partial \mu _h\) are calculated according to Eqs. 8 and 9. For each pattern layout \(\mu _{{\text {wet}}}\) is set to the maximum friction coefficient measured with 80 km h−1 and 1 mm water height.

Table 1 Speeds and water heights for braking tests
Full size table

3 Results and discussion

First we discuss the pressure signals measured with different pattern layouts. Afterwards we compare the values of \(\partial \mu _v, \partial \mu _h\), \(\partial \varLambda _v\) and \(\partial \varLambda _h\) to examine the influence of fluid pressure on braking performance.

3.1 Fluid pressure

We measured the pressure signal as described in paragraph 2.2 for tires with the dimension 245/45 R18 and the pattern layouts shown in Fig. 4. Except for the small blocks with high void, all patterns have a relative surface void and a relative void volume of 20 %. For the arrow shaped patterns, forward means that for a rolling tire the arrowhead enters the footprint first. Water heights h and speeds v tested are shown in Table 3. Tire load is set to 4875 N with an inflation pressure of 2.1 bar. The loss term \(\varLambda \) is calculated for each parameter combination according to Eq. 7. During each measurement the sensor is rolled over several times. Table 2 shows the mean standard deviation of \(\varLambda \) during the successive rollovers for all patterns dependent on speed v and water height h. The relative standard deviation is particularly large for small speeds and water heights, where the measured fluid pressure is small. For each drum rotation the sensor can be either positioned under a tread block or under a groove of the tire. Under the center of a tread block the fluid pressure is larger than at the edge of a tread block or even under a groove, which explains the rather large deviations between the successive rollovers. Dependent on driving speed, we measured at least 40 rollovers for each parameter combination and calculated the mean fluid pressure of all rollovers. Therefore, the influence of the sensor position is averaged out in the results discussed in the following and we can expect that \(\varLambda \) is a valid parameter for the description of the fluid pressure despite the relatively large deviations between the individual rollovers.

Table 2 Mean standard deviation of loss term \(\varLambda \) in % for all water heights h and vehicle speeds v for multiple rollovers
Full size table

For each water height a linear regression is calculated for the values of \(\varLambda \) and \(\partial \varLambda _v\) is calculated from the regression with Eq. 8. This procedure is shown in Fig. 3. The calculation of \(\partial \varLambda _h\) is carried out analogously. The calculation of the gradients is obviously more sensitive to outliers if fewer data points are available. Still, since \(\varLambda \) is calculated from various rollovers, even the gradients calculated with only two speeds or water heights will be evaluated and discussed in the following.

Fig. 3
figure 3

Loss term \(\varLambda \) with linearization over speed v and exemplary gradient \(\partial \varLambda _v\) for 1 mm water height for pattern layout BB

Full size image
Fig. 4
figure 4

Pattern layouts

Full size image
Table 3 Test conditions: Speeds and water heights
Full size table
Fig. 5
figure 5

\(\partial \varLambda _v\) for big (BB) and small (SB) blocks

Full size image

The comparison between big and small blocks in Fig. 5 shows a slightly lower value of \(\partial \varLambda _v\) for 1–2 mm for small blocks. The squeeze out distance to the next groove is shorter for the smaller blocks and the groove capacity is sufficient to take the fluid from the surrounding blocks. At 3 mm the grooves start to fill. The grooves between the big blocks are much wider than between the small blocks. The better drainage of the footprint through the larger circumferential grooves overcompensates the larger squeeze out distance for the big blocks. Therefore, \(\partial \varLambda _v\) increases much faster for the small blocks.

Fig. 6
figure 6

\(\partial \varLambda _v\) for small blocks with void variation (SB and SBv)

Full size image

In Fig. 6 we compare small blocks at two different void levels. The block size changes slightly as well, but this can be neglected. For all water heights the higher void leads to a smaller value of \(\partial \varLambda _v\). Also, at the higher void level, the grooves seem to be filled at 3 mm water height, since the difference between 2 and 3 mm is much larger than between 1 and 2mm.

Fig. 7
figure 7

\(\partial \varLambda _v\) for arrow pattern (AF and AB)

Full size image

Figure 7 shows an arrow pattern driven forward and backward. As expected the forward orientation performs better, because the water gets transported from the center of the contact patch to the outside, which leads to a smaller pressure build up. The difference is especially high at 2 mm. This is the water height where the grooves start to fill.

Fig. 8
figure 8

\(\partial \varLambda _v\) for big blocks (BB) and central rib (CR)

Full size image

If we replace the big blocks in the center with a solid rib, we get the results shown in Fig. 8. At 2–3 mm the results are very similar. Only for 1 mm the missing lateral grooves seem to have a significant effect on the pressure build up.

Fig. 9
figure 9

\(\partial \varLambda _v\) for sipe variations (BB, BBs1, BBs2)

Full size image

Figure 9 shows the results for the big blocks with no, one and two lateral sipes. The outer dimensions of the blocks remain the same; therefore, the void level slightly increases with the additional sipes. For 1–2 mm the influence of the sipes is very small. The sipes seem to be too narrow to provide a significant benefit due to the additional void volume. At 3mm the additional sipes even cause a higher value of \(\partial \varLambda _h\). A possible explanation would be that the sipes disturb the fluid squeeze out by causing a more turbulent flow and hence a higher pressure build up at higher speeds.

Fig. 10
figure 10

\(\partial \varLambda _h\) for small blocks with void variation (SB and SBv)

Full size image

\(\partial \varLambda _h\) was examined, too. In Table 3 it can be seen that there are fewer measurement points available to calculate the gradient \(\partial \varLambda _h\); therefore, it is more sensitive to outliers. In Fig. 10 we compare small blocks on different void levels. The influence of the water height is rather small at 30 km h−1. At higher velocities the influence of water height on the low void pattern increases. This can be explained by filling grooves. In general the high void pattern layout is less sensitive to water height at higher speeds. At 80–100 km h−1\(\partial \varLambda _h\) is calculated with values from 1 and 2 mm. At low void this is the point where the grooves start to fill, and hence we have a strong influence of the water height at this point. At the high void the grooves do not start to fill yet; therefore, the influence of the water height is much smaller. Still for both patterns the grooves are filled at 3 mm, which causes the strong increase of \(\partial \varLambda _v\) shown in Fig. 6.

3.2 Fluid pressure vs. friction forces

Figures 11 and 12 compare the gradients of \(\mu \) and \(\varLambda \) over the velocity v at a water height of 1 and 2 mm for five pattern layouts, respectively. The negative algebraic sign for \(\partial \varLambda _v\) is motivated in Eq. 8 and for \(\partial \varLambda _h\) in Eq. 9. The influence of the driving speed is much higher for \(\partial \mu _v\) compared to \(\partial \varLambda _v\) for both cases. This means the decrease of \(\mu \) cannot be fully explained with an increasing fluid pressure build up in the footprint. At rather low water heights of 1-2 mm effects like higher absolute slip speed or higher tire temperatures can be more relevant for the decrease of \(\mu \) at higher velocities than the water height. On the other hand, the fluid pressure is measured through the steel cover which acts like an orifice. With increasing velocities, the losses caused by the orifice will be larger. We cannot exclude that \(\partial \varLambda _v\) is reduced by the losses caused by our test setup and is, therefore, underestimated. The values measured with an infinite small sensor in an undisturbed track could be much higher.

Figures 13 and 14 show the gradients of \(\mu \) and \(\varLambda \) over the water height h at speeds of 50 km h−1, respectively, 80 km h−1 for five pattern layouts. For 50 km h−1 the influence of h on \(\mu \) is very small and for some patterns an increasing water height even leads to a higher grip level. This could be explained by the cooling effect of the water, because a lower rubber temperature can lead to a higher grip. Still we measure a small influence of h on \(\varLambda \). The fluid squeeze out between track and tire does not have a significant effect at such low speeds and, therefore, the friction coefficient is not reduced with increasing water heights. The small pressure build up which is captured with our test setup is located in the front part of the footprint (see Fig. 2), where no friction forces are transmitted yet due to the small local slip values [7, p. 45].

For 80 km h−1 the values of \(\partial \varLambda _h\) and \(\partial \mu _h\) are much larger. The fluid squeeze out has to happen in a shorter time span and the pressure build up is large enough to significantly reduce the transmittable braking forces with higher water heights. Losses caused by the orifice are not relevant here, because \(\partial \varLambda _h\) is measured at a constant speed and the losses are expected to be rather independent of the water height. Since the values of \(\partial \varLambda _h\) are even higher than the values of \(\partial \mu _h\), inertia effects seem to explain the majority of the differences between the different water heights. For constant driving speeds temperature, slip speed and other effects are rather constant and, therefore, at least partly neutralized by the normalization of \(\mu \) with \(\mu _{\text {wet}}\) introduced in Eq. 6. \(\partial \varLambda _h\) is larger than \(\partial \mu _h\), which makes sense since the major part of the pressure build up takes place in the front part of the contact patch, whereas the majority of the braking forces is transmitted in the rear end of the footprint. The influence of \(\varLambda \) on \(\mu \) should, therefore, always be smaller than introduced in Eq. 6. The differences between the single pattern layouts are not discussed here, because too many additional effects influence the results of the braking tests for the different patterns.

Fig. 11
figure 11

\(\partial \varLambda _v\) and \(\partial \mu _v\) at 1 mm water height

Full size image
Fig. 12
figure 12

\(\partial \varLambda _v\) and \(\partial \mu _v\) at 2 mm water height

Full size image
Fig. 13
figure 13

\(\partial \varLambda _h\) and \(\partial \mu _h\) at 50 km h−1

Full size image
Fig. 14
figure 14

\(\partial \varLambda _h\) and \(\partial \mu _h\) at 80 km h−1

Full size image

4 Conclusions

We examined the influence of pattern, water height and vehicle speed on the pressure build up in the fluid film between tire and an asphalt track. The results are conclusive in themselves if the fluid pressure is compared between different parameters, water heights and speeds. Where an impact of the fluid pressure on the braking performance can be expected, the gradients of friction coefficient \(\mu \) and loss term \(\varLambda \) have the same order of magnitude. Where wet braking effects like slip speed or temperature effects are dominant, the gradients of \(\varLambda \) are much smaller than the gradients of \(\mu \). The test setup allows a direct access to the effects in the fluid film between tire and road. It is possible to separate effects determining the transmittable braking forces such as fluid inertia and wet friction and learn from the results for a better understanding of the wet braking mechanisms. We showed a significant influence of inertia effects already for low water heights of 1–3 mm, especially at high vehicle speeds. The test method could be used in tire development to further improve pattern design by minimizing the fluid pressure build up during braking and, therefore, improving wet grip and hydroplaning performance.

Tests at higher water heights up to full hydroplaning conditions would be of interest for further studies. A smaller bracket and steel cover for the pressure sensor would reduce the impact of the test setup on the results. It could also help to answer the question, if the steel cover acts as an orifice and corrupts the measured influence of driving speed. To further examine the influence of fluid pressure on transmittable braking forces, a local evaluation of the fluid pressure in the contact patch would be necessary. For the presented model conception even the influence of a correctly measured fluid pressure on friction forces is overestimated due to the uneven transmission of friction forces inside the contact patch.