1 The Univariate Half-Logistic Distribution

The half-logistic distribution is a random distribution over the positive real half line obtained by folding the logistic distribution, which is defined over the whole real line (Balakrishnan 1985), about the origin. Thus, if Y is a random variable (rv) that follows the logistic distribution, the rv \(X=|Y|\) is said to follow the half-logistic distribution. Its probability density functions is

$$\begin{aligned} f(x)=\frac{2\theta e^{-\theta x}}{(1+e^{-\theta x})^2},\quad x\in {\mathbb{R}}^+,\theta \in {\mathbb{R}}^+, \end{aligned}$$
(1)

its cumulative distribution function (cdf) is

$$\begin{aligned} F^{(c)}(x)=P(X\le x)=\frac{2}{1+e^{-\theta x}}-1=\frac{2e^{\theta x}}{1+e^{\theta x}}-1 =\frac{e^{\theta x}-1}{e^{\theta x}+1},\quad x\in {\mathbb{R}}^+, \end{aligned}$$
(2)

and its survival function

$$\begin{aligned} S(x)=P(X\ge x)=\frac{2}{1+e^{\theta x}},\quad x\in {\mathbb{R}}^+. \end{aligned}$$

The expressions for the expected value and variance are

$$\begin{aligned} \mu ={\mathbb{E}}(X)=\log 4/\theta ,\quad \sigma ^2=\left( \pi ^2/3 - \log ^2 4\right) /\theta ^2. \end{aligned}$$

Since the ratio between variance and expected value is \(\frac{1}{\theta }\frac{\pi ^2/3 - \log ^2 4}{\log (4)}\), we have that the half-logistic distribution is overdispersed if \(\theta <\theta _0=\frac{\pi ^2/3-\log ^2 4}{\log 4}\approx 0.9868439\); it is underdispersed if \(\theta >\theta _0\).

Fisher’s measure of skewness, i.e., the third standardized central moment \(\beta _1 = {\mathbb{E}}\left( \frac{X-\mu }{\sigma }\right) ^3\) is approximately 1.540, indicating that the distribution is highly positively skewed; whereas Fisher’s measure of kurtosis, i.e., the fourth standardized central moment \(\beta _2 = {\mathbb{E}}\left( \frac{X-\mu }{\sigma }\right) ^4\), is approximately 6.584, indicating that the half-logistic distribution is leptokurtic.

The ’naïve’ hazard rate function, defined as \(r(x)=f(x)/S(x)\) has the following expression:

$$\begin{aligned} r(x)=\frac{\theta }{1+e^{-\theta x}}=\frac{\theta e^{\theta x}}{1+e^{\theta x}}, \end{aligned}$$

which is an increasing function in x with minimum value \(\theta /2\), attained at zero, and supremum value \(\theta\), attained asymptotically for \(x\rightarrow +\infty\). This means that the half-logistic distribution belongs to the increasing failure rate (IFR) class (Barlow and Proschan 1981). This represents one of the main attractions of this distribution in the context of reliability theory, a property shared by relatively few distributions that have support on the positive real half line.

A standard version of the half-logistic distribution, obtained by setting \(\theta\) equal to 1 in (1), was investigated in Balakrishnan (1985), who established some recurrence relations for the moments and product moments of order statistics, as well as modes and quantiles.

As occurs for the exponential distribution, an alternative parametrization of the half-logistic distribution, instead of considering the rate parameter \(\theta\), uses the scale parameter \(\sigma =1/\theta\): the pdf becomes

$$\begin{aligned} f(x)=\frac{2 e^{- x/\sigma }}{\sigma (1+e^{-x/\sigma })^2},\quad x\in {\mathbb{R}}^+,\sigma \in {\mathbb{R}}^+. \end{aligned}$$

When modeling lifetimes, such as the curing time of a particular disease, or the survival time of cancer patients, continuous random distributions are usually employed. However, one often comes across situations where lifetimes are actually measured on a discrete scale: for example, the curing time is measured in days, the survival time in months, etc. In these cases, using a discrete random variable would be much more appropriate. Developing a discrete version of continuous distributions has thus drawn attention of researchers in recent decades, and a large number of contributions dealing with discrete distributions derived by discretizing continuous random variables have appeared in the statistics literature (Chakraborty 2015). Barbiero and Hitaj (2020, 2024) introduced and discussed a discrete counterpart of the half-logistic distribution, based on the matching of the survival function at the integer values of its support.

In the next section, we will introduce and discuss an alternative discrete analogue of the continuous half-logistic distribution, which is defined by letting the probability mass function (PMF) “mimick” the pdf, i.e., by retaining the expression of the pdf of the parent distribution. Its main properties, with particular regard to moments and reliability concepts, are described. Section 3 deals with parameter estimation: different estimators are proposed, which are assessed and compared also through a Monte Carlo simulation study. In Sect. 4 the distribution is fitted to two real datasets taken from the literature. Section 5 introduces a two-parameter generalization allowing for a greater degree of flexibility. Final remarks are provided in the last section.

2 A Discrete Half-Logistic Distribution

A discrete counterpart of a continuous random distribution with pdf f(x), which we assume to be supported over \({\mathbb{R}}^+\), can be constructed letting its PMF be equal to

$$\begin{aligned} p(x)=\frac{f(x)}{\sum _{k\in {\mathbb{N}}_0}f(k)}, x\in {\mathbb{N}}_0 \end{aligned}$$
(3)

with \({\mathbb{N}}_0=\left\{ 0,1,2,\dots \right\}\) being the set of non-negative integers. If one considers an exponential rv with rate parameter \(\lambda\), it is well-known that its counterpart is the geometric distribution with parameter \(1-e^{-\lambda }\). If one considers a rv supported over the whole real line, then its discrete counterpart is supported on \({\mathbb{Z}}\) and its PMF is given by (3) for \(x\in {\mathbb{Z}}\), where the sum at the denominator is now extended over \({\mathbb{Z}}\). The discrete normal distribution (Kemp 1997) and the discrete Laplace distribution (Inusah and Kozubowski 2006) are examples of discrete distributions constructed according to this rationale.

A discrete counterpart of the continuous model of Eq. (1) can be therefore introduced by defining its PMF as

$$\begin{aligned} p(x)=\frac{2\theta e^{-\theta x}/\left( 1+e^{-\theta x}\right) ^2}{\sum _{k\in {\mathbb{N}}_0}2\theta e^{-\theta k}/\left( 1+e^{-\theta k}\right) ^2}=\frac{e^{-\theta x}/\left( 1+e^{-\theta x}\right) ^2}{\sum _{k\in {\mathbb{N}}_0} e^{-\theta k}/\left( 1+e^{-\theta k}\right) ^2},\quad x=0,1,2,\dots \end{aligned}$$
(4)

The denominator acting as a normalizing constant in the last member of the equation above, \(C(\theta )={\sum _{k\in {\mathbb{N}}} e^{-\theta k}/(1+e^{-\theta k})^2}\), does not possess in general a closed analytic form, except for some very special cases; however, it can be expressed in terms of theta functions and their derivatives (see the “Appendix”).

In general, note that since f(x) in (1) is a strictly decreasing function with x, the following inequalities hold (see also Fig. 1):

$$\begin{aligned} \sum _{i=1}^\infty f(i)< 1=\int _0^{\infty } f(x)\text {d}x < \sum _{i=0}^\infty f(i), \end{aligned}$$

which becomes

$$\begin{aligned} 2\theta C(\theta ) - \theta /2< 1 < 2\theta C(\theta ), \end{aligned}$$

which can be rewritten as an inequality chain for \(C(\theta )\):

$$\begin{aligned} \frac{1}{2\theta }< C(\theta ) < \frac{1}{2\theta } +\frac{1}{4}, \end{aligned}$$

or for \(2\theta C(\theta )\):

$$\begin{aligned} 1< 2\theta C(\theta ) < 1+\theta /2. \end{aligned}$$
Fig. 1
figure 1

Genesis of the discrete half-logistic distribution. The solid line represents the pdf of the continuous half-logistic distribution with parameter \(\theta\) (\(=1/2\)), whose area subtended with the x-axis equals 1. The values of the pdf at each integer point, after being normalized, correspond to the values of the PMF of the discrete distribution. The area subtended by the red broken line equals \(2\theta C(\theta )\), the area subtended by the green-line histogram equals \(2\theta C(\theta )-\theta /2\)

Full size image
Fig. 2
figure 2

Plot of \(2\theta C(\theta )\); the dashed lines represent the theoretical lower and upper bounds for \(2\theta C(\theta )\), obtained by mathematical considerations

Full size image

A plot of the function \(2\theta C(\theta )\) versus \(\theta\) is reported in Fig. 2. We note that for high values of \(\theta\), \(2\theta C(\theta )\) can be approximated by \(\theta /2\), or equivalently, \(\lim _{\theta \rightarrow \infty }C(\theta )=1/4\). For small values of \(\theta\), \(C(\theta )\) can be approximated by \(1/(2\theta )\) or, equivalently, \(\lim _{\theta \rightarrow \infty }2\theta C(\theta )=1\). For values of \(\theta\) equal to 1/n, n integer, we have \(C(\theta )=1/8+n/2\). Then, for example, if \(\theta =1\), since \(C(1)={\sum _{k\in {\mathbb{N}}}e^{-k}/(1+e^{-k})^2}=1/4+3/8=5/8\), the PMF (4) becomes

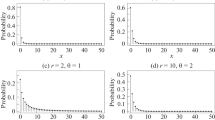
$$\begin{aligned} p(x) = \frac{8}{5}\frac{e^{- x}}{(1+e^{- x})^2},\quad x=0,1,2,\dots \end{aligned}$$

The PMF (4) is obviously strictly decreasing with x, and thus the mode is always 0. Figure 3 displays its graph for four different values of \(\theta\); decreasing the value of \(\theta\) makes the distribution spread towards higher support values.

Fig. 3
figure 3

PMF of the discrete half-logistic distribution for different values of \(\theta\)

Full size image

2.1 Cumulative Distribution Function

The cdf \(F(x)=P(X\le x)\) of the discrete half-logistic distribution can be written as

$$\begin{aligned} F(x)={\left\{ \begin{array}{ll} 0 &{}\quad x<0\\ \dfrac{\sum _{y=0}^{\lfloor x\rfloor } e^{-\theta y}/\left( 1+e^{-\theta y}\right) ^2}{C(\theta )} &{}\quad x\ge 0 \end{array}\right. } \end{aligned}$$

and thus is not available in a manageable closed form. However, if \(\theta<<1\), for what we said in the previous section, we have that \(F(x;\theta )\approx F^{(c)}(x;\theta )\) for \(x=0,1,2,\dots\), and then the discrete half-logistic distribution can be seen as a discrete approximation to the continuous half-logistic distribution with the same parameter.

2.2 Ratio Between Successive Probabilities

The ratio between successive probabilities is given by

$$\begin{aligned} \frac{p(x+1)}{p(x)} = \frac{2\theta e^{-\theta (x+1)}}{\left( 1+e^{-\theta (x+1)}\right) ^2} \frac{\left( 1+e^{-\theta x}\right) ^2}{2\theta e^{-\theta x}} = e^{-\theta }\left( \frac{1+e^{-\theta x}}{1+e^{-\theta (x+1)}}\right) ^2, \end{aligned}$$

which is a strictly decreasing function with x, for any \(\theta >0\), and satisfies the following limit:

$$\begin{aligned} \lim _{x\rightarrow \infty } \frac{p(x+1)}{p(x)}=e^{-\theta }. \end{aligned}$$

2.3 Log-Concavity

A discrete distribution is said to be log-concave if

$$\begin{aligned} p(x)^2\ge p(x-1)\cdot p(x+1) \end{aligned}$$

for each \(x\ge 1\) (Keilson and Gerber 1971). For the discrete half-logistic distribution

$$\begin{aligned} p^2(x) = \frac{4\theta ^2e^{-2\theta x}}{(1+e^{-\theta x})^4}\bigg /C^2(\theta ) \end{aligned}$$

and

$$\begin{aligned} p(x-1)\cdot p(x+1)=\frac{4\theta ^2e^{-\theta (x-1)}e^{-\theta (x+1)}}{(1+e^{-\theta (x-1)})^2(1+e^{-\theta (x+1)})^2}\bigg /C^2(\theta )=\frac{4\theta ^2e^{-2\theta x}}{(1+e^{-\theta (x-1)})^2(1+e^{-\theta (x+1)})^2}\bigg /C^2(\theta ); \end{aligned}$$

then one has to check whether

$$\begin{aligned} \left[ 1+e^{-\theta (x-1)}\right] ^2\left[ 1+e^{-\theta (x+1)}\right] ^2\ge (1+e^{-\theta x})^4, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \left( 1+w^{x-1}\right) ^2\left( 1+w^{x+1}\right) ^2 \ge (1+w^x)^4, \end{aligned}$$

with \(0<w=e^{-\theta }<1\); this inequality is easily proved for any \(x\in {\mathbb{N}}\), and one can therefore state that the discrete half-logistic distribution is log-concave for any \(\theta >0\).

2.4 Failure Rate

The naïve failure rate function for a discrete rv can be defined as

$$\begin{aligned} r(x)=p(x)/\sum _{y\ge x} p(y); \end{aligned}$$

thus for the discrete half-logistic distribution we have

$$\begin{aligned} r(x;\theta ) = \frac{f(x)}{\sum _{y\ge x} f(y)} = \frac{e^{-\theta x}/(1+e^{-\theta x})^2}{\sum _{y\ge x} e^{-\theta y}/(1+e^{-\theta y})^2}; \end{aligned}$$

since we know p(x) is log-concave, we can deduce that r(x) is strictly increasing for any value of \(\theta\) (see An 1997, Proposition 10).

2.5 Quantile Function and Pseudo-random Simulation

As we have seen, the cdf of the discrete half-logistic distribution cannot be expressed in a closed-form, and this prevents from calculating the quantile function in a simple form either. Analogously, pseudo-random generation is not straightforward since the usual inverse transform sampling cannot be directly carried out. One can adopt the following naïve algorithm for determining the u-quantile of the discrete half-logistic distribution with parameter \(\theta\):

  1. 1.

    Set \(x=0\)

  2. 2.

    While \(F(x; \theta )<u\), set \(x=x+1\)

  3. 3.

    Return x, which is a pseudo-random value from the discrete half-logistic distribution with parameter \(\theta\)

A much less time-demanding algorithm can be conceived, which uses as a proxy for the u-quantile of the discrete distribution the (rounded) u-quantile of the parent continuous distribution, obtained as the mathematical inverse of the cdf in (2):

$$\begin{aligned} q^{(c)}_u(\theta ) = \frac{1}{\theta }\ln \frac{1+u}{1-u}; \end{aligned}$$

in this way, instead of starting the search for the u-quantile from 0, one can start from the possibly closer value \(q^{(c)}_u(\theta )\), hence reducing the computational time:

  1. 1.

    Set \(x=\lfloor q^{(c)}_u(\theta )\rfloor\)

  2. 2.

    If \(F(x)<u\)

    1. 1.

      While \(F(x; \theta )<u\), set \(x=x+1\)

    2. 2.

      Return x

    else

    1. 1.

      While \(F(x; \theta )\ge u\), set \(x=x-1\)

    2. 2.

      Return \(x+1\)

As one can see from Table 1, which reports the quantiles for the continuous and the discrete half-logistic distributions for several combinations of \(\theta\) and u, the values for the discrete version always correspond to one of the two integers closer to the homologous quantile of the parent continuous distribution; we have that \(F^{(c)}(h;\theta )<F(h;\theta )<F^{(c)}(h+1;\theta )\) for any \(h\in {\mathbb{N}}_0\). The algorithm above can be then further simplified:

  1. 1.

    Set \(x=\lfloor q^{(c)}_u(\theta )\rfloor\)

  2. 2.

    If \(F(x)<u\) set \(x=x+1\) and return x else if \(F(x)\ge u\) return x

Once we are able to compute the u-quantile of a discrete half-logistic distribution with parameter \(\theta\), its pseudo-random simulation is simple:

  1. 1.

    Simulate a pseudo-random value u from a standard uniform rv \(U\sim \text {Unif}(0,1)\)

  2. 2.

    Calculate \(x=q_u(\theta )\)

Table 1 Quantiles of the continuous half-logistic and its discrete counterpart, for several combinations of the parameter \(\theta\) and of the probability level u
Full size table

2.6 Moments of the Distribution

The first moment of the distribution is computed as

$$\begin{aligned} {\mathbb{E}}(X)=\sum _{x=0}^{\infty } xp(x)=\sum _{x=0}^{\infty } \frac{xe^{-\theta x}}{(1+e^{-\theta x})^2}/C(\theta ); \end{aligned}$$

it appears that the expression cannot be simplified significantly, even when resorting to the special functions mentioned in the Appendix. Numerical evidence suggests that it is a decreasing function with \(\theta\), mirroring the behavior of the first moment of the continuous parent distribution, which equals \(\log 4/\theta\).

Similarly to the expectation, the variance of the distribution can be computed numerically. Computations show that the variance is greater than the expectation, and thus the distribution is overdispersed, for \(\theta <\theta ^*=1.818\); for \(\theta >\theta ^*\) the distribution is underdispersed. Then, in this sense, the discrete half-logistic distribution exhibits a behavior similar to that of its parent distribution.

Also higher moments can be calculated numerically. It is of interest to evaluate the usual measures of skewness and kurtosis, \(\beta _1\) and \(\beta _2\). We notice that differently from the parent distribution, the values of \(\beta _1\) and \(\beta _2\) are no longer constant with \(\theta\): this occurs because \(\theta\) is no longer the reciprocal of a scale parameter for the discrete distribution. The plots of \(\beta _1\) and \(\beta _2\) as functions of the parameter \(\theta\) are displayed in Fig. 4; from it, we can state that the discrete half-logistic distribution is always positively skewed (\(\beta _1>0\)) and is always leptokurtic (\(\beta _2>3\)), properties that it has therefore inherited from its continuous parent.

Table 2 displays the values of expectation, variance, skewness, and kurtosis for several values of \(\theta\). When \(\theta \,{<}{<}\,1\), the moments of the continuous and discrete half-logistic distributions with parameter \(\theta\) tend to coincide, as a consequence of the fact that the discrete analogue can be seen as an approximation to the continuous parent distribution, as underlined in Sect. 2.1.

Fig. 4
figure 4

Graphs of the customary measures of skewness (left) and kurtosis (right) for the discrete half-logistic distribution. Note that the scales on the y-axes are not the same across the two graphs

Full size image
Table 2 Moments of the discrete half-logistic distribution for several values of \(\theta\)
Full size table

2.7 Zero-Modification Index

An important index that can be calculated for a count distribution is the zero-modification index (ZMI), given by \(\text {ZMI}=1+\ln p(0)/{\mathbb{E}}(X)\), which is defined based on the Poisson distribution (see, e.g., Bertoli et al. 2019). This measure can be easily interpreted since \(\text {ZMI} > 0\) indicates zero-inflation, \(\text {ZMI} < 0\) indicates zero-deflation, and \(\text {ZMI} = 0\) indicates no zero-modification. For the distribution in question, the graph of this index as a function of the parameter \(\theta\) is displayed in Fig. 5, which shows that it is positive and decreasing down to zero for \(\theta\) between 0 and \(\theta ^*\approx 1.708\); it is negative and decreasing between \(\theta ^*\) and \(\theta ^{**}\approx 2.540\); it is negative and increasing, asymptotically tending to zero, after \(\theta ^{**}\).

Fig. 5
figure 5

Graph of the ZMI as a function of \(\theta\)

Full size image

2.8 Infinite Divisibility

We show that the discrete half-logistic distribution is in general non-divisible. In fact, we know that a necessary condition for infinite divisibility of a discrete distribution is that \(p(1)^2\le 2p(0)p(2)\) (see Steutel and Van Harn 2003, Eq. (4.11)), but if we set \(\theta =2\), we obtain that \(p(1)^2=0.07817741\) and \(2p(0)p(2)=2\cdot 0.6657603\cdot 0.04703651=0.06263008\), and the above inequality is not satisfied, so we conclude that the discrete half-logistic distribution is not a family of infinite divisible distributions.

2.9 Shannon Entropy

Shannon entropy is a measure of uncertainty of a rv. For a discrete rv X with support \({\mathcal {S}}\), it is defined as \(H(X)=-\sum _{x\in {\mathcal {S}}} p(x)\log p(x)\) (Shannon 1951) and for the proposed distribution we can then write

$$\begin{aligned} H(X;\theta )&= -\sum _{x=0}^\infty p(x;\theta )\cdot \big [-\theta x -2\log \big (1+e^{-\theta x}\big )-\log C(\theta )\big ]\\&=\theta {\mathbb{E}}(X;\theta )+2{\mathbb{E}}\big (\log \big (1+e^{-\theta x}\big );\theta \big )+\log C(\theta ). \end{aligned}$$

The graph of Shannon entropy as a function of the parameter \(\theta\) is displayed in Fig. 6; we notice that it is strictly decreasing with \(\theta\), and that \(\lim _{\theta \rightarrow +\infty }H(X;\theta )=0\) and \(\lim _{\theta \rightarrow 0^+}H(X;\theta )=+\infty\).

Fig. 6
figure 6

Graph of Shannon entropy as a function of \(\theta\)

Full size image

3 Estimation

We now focus on the problem of estimating the unknown parameter \(\theta\), given an i.i.d. sample \(x_1,x_2,\dots ,x_n\), which we assume to come from the discrete half-logistic distribution (4).

3.1 Method of Proportion

Since \(p(0)=1/(4C(\theta ))\) is the largest probability among the p(x)’s, one can equate it to the sample proportion of zeros \({\hat{p}}_0\) and solve (numerically) the non-linear equation \(C(\theta )-1/(4{\hat{p}}_0)=0\) with respect to \(\theta\); we denote its unique root as \(\hat{\theta }_P\). The non-linear equation can be easily solved in the R environment (R Core Team 2023) by using the standard uniroot function. This technique always provides a feasible estimate of \(\theta\), as long as \({\hat{p}}_0>0\).

Alternatively, exploiting the fact that the ratio of successive probabilities does not depend upon \(C(\theta )\), one can compute the ratio \(p(0)/p(1)=\frac{1}{4}\frac{(1+e^{-\theta })^2}{e^{-\theta }}\) and equate it to the corresponding sample quantity \({\hat{r}}={\hat{p}}_0/{\hat{p}}_1\). The resulting equation is a second-degree equation in \(q=e^{-\theta }\): \(q^2+q(2-4{\hat{r}})+1=0\); its unique feasible solution is \({\hat{q}}=2{\hat{r}}-1 - 2\sqrt{{\hat{r}}({\hat{r}}-1)}\) from which we derive \(\hat{\theta }_P^*=-\log {\hat{q}}\). This technique works if and only if the value of \({\hat{r}}\) is greater than 1, i.e., if the sample proportion of zeros is greater than the sample proportion of ones.

Both techniques are expected to provide not very efficient estimates of \(\theta\) (if compared to those provided by the methods we will discuss later), since they rely on only a piece of information contained in the sample, i.e., the sample proportion of zeros (and ones). However, these estimates may turn out to be useful if used as starting values for other estimation techniques based on some optimization routine as the maximum likelihood method.

3.2 Method of Moments

The unknown value of \(\theta\) can be estimated resorting to the method of moments, i.e., finding the value \(\hat{\theta }_M\) that satisfies \({\mathbb{E}}(X;\hat{\theta }_M)={\bar{x}}\). Since the relationship between the expectation and the parameter is one-to-one, the solution always exists and is unique. Due to the lack of a closed-form expression for \({\mathbb{E}}(X;\theta )\), the estimate \(\hat{\theta }_M\) can be obtained only numerically, yet quite easily. The following algorithm can be implemented, which relies on the fact that the expectation is a decreasing function of \(\theta\):

  1. 1.

    Choose an arbitrary small positive value \(\epsilon\) (say, \(\epsilon =0.0001\)) to be used for ensuring convergence

  2. 2.

    Set \(t=0\) and \(\hat{\theta }_M^{(t)} = \log 4/{\bar{x}}\)

  3. 3.

    While \(|{\mathbb{E}}(X;\hat{\theta }_M^{(t)})-{\bar{x}}|/{\bar{x}}>\epsilon\),

    1. 1.

      Set \(\hat{\theta }_M^{(t+1)}=\hat{\theta }_M^{(t)}\cdot {\mathbb{E}}(X;\hat{\theta }_M^{(t)})/{\bar{x}}\)

    2. 2.

      Update the iteration index t: \(t\leftarrow t+1\)

  4. 3.

    Return \(\hat{\theta }_M^{(t)}\)

The algorithm can be easily implemented; alternatively, one can use existing root-finding algorithms such as the one implemented by uniroot in the R environment.

Table 3 reports, in the second column, the method of moments’ estimate of \(\theta\) for a single observation x (\(x=1,2,\dots ,10\)).

3.3 Maximum Likelihood Method

The log-likelihood function for the distribution in question is equal to

$$\begin{aligned} \ell (\theta ;x_1,\dots ,x_n)&= \log \prod _{i=1}^n p(x_i;\theta )= \log \prod _{i=1}^n \left[ \frac{e^{-\theta x_i}}{(1+e^{-\theta x_i})^2}\big/C(\theta )\right] \nonumber \\&= - \theta \sum _{i=1}^n x_i - 2\sum _{i=1}^n \log (1+e^{-\theta x_i}) -n\log C(\theta ). \end{aligned}$$
(5)

Taking its first order derivative with respect to \(\theta\) and equating it to zero, we obtain the equation

$$\begin{aligned} \ell '(\theta ;x_1,\dots ,x_n)=-n{\bar{x}}+ 2\sum _{i=1}^n \frac{x_i e^{-\theta x_i}}{1+e^{-\theta x_i}} - n C'(\theta )=0, \end{aligned}$$
(6)

with \(C'(\theta )=\sum _{i=0}^\infty \frac{i\cdot e^{-\theta i}(e^{-\theta i}-1)}{(1+e^{-\theta i})^3} \big / \sum _{i=0}^\infty \frac{e^{-\theta i}}{(1+e^{-\theta i})^2}\). In order to find the maximum likelihood estimate (MLE) of \(\theta\), one can solve the normal equation (6) above. Clearly, this equation cannot be solved analytically, but can only be solved numerically quite easily, by using some numerical searching algorithm (in R, the function uniroot can be employed).

Obviously, an approximation needs to be introduced for handling the infinite sums in \(C'(\theta )\); once one truncates them, the normal equation becomes a polynomial function in the variable \(q=e^{-\theta }\). For determining an appropriate upper bound \(x_{\max }\) at which truncating the sum, one can consider the maximum observed value for the sample at hand, \(x_{(n)}\), and set \(x_{\max }\) equal to a properly high value, say \(Kx_{(n)}\), with \(K>10\); alternatively, a more refined value for \(x_{\max }\) can be obtained by considering a first rough estimate of \(\theta\), \({\tilde{\theta }}\), and recalling the expressions for expected value and variance for the continuous half-logistic distribution: after defining \({\tilde{\mu }}=\log 4/{\tilde{\theta }}\) and \({\tilde{\sigma }}=\sqrt{\pi ^2/3-(\log 4/{\tilde{\theta }})^2}\), a reasonable choice for the upper bound is \({\tilde{\mu }}+K{\tilde{\sigma }}\).

Instead of solving the normal equation (6), one can directly find the maximum of (5) numerically, for example by using the R functions optim or mle2, the latter contained in the package bbmle (Bolker 2022); an appropriate truncation of the infinite series sum appearing in the expression of the log-likelihood function is however still required.

Table 3 reports, in the last column, the MLEs of \(\theta\) for a single observation x (\(x=1,2,\dots ,10\)), obtained by using mle2. Note that the MLE does not exist if \(n=1\) and \(x=0\) (actually, the log-likelihood would tend to its supremum as \(\theta \rightarrow \infty\)).

Table 3 Method of moments’ and maximum likelihood estimates of \(\theta\), rounded to the third decimal digit, for different sample values x
Full size table

Along with the point estimate \(\hat{\theta }_{ML}\), one can construct also (approximate) 95% likelihood-based confidence intervals (see, e.g., Venzon and Moolgavkar 1988) for \(\theta\): this can be carried out numerically, for example by inverting a spline fit to the likelihood profile, which is the default option when using the confint function provided by the R package bbmle.

3.4 A Comparison Through Monte Carlo Simulation

Since the statistical properties (e.g., unbiasedness and relative efficiency) of the estimation methods described so far cannot be derived analytically, we resort to a Monte Carlo simulation study in order to assess such properties numerically. We considered a sufficiently wide array of parameter values (\(\theta \in \left\{ 0.01,0.02,0.05,0.1,0.2,0.5,1,1.5,2\right\}\)) and sample sizes (\(n\in \left\{ 20,50,100 \right\}\)); we simulated for each combination of \(\theta\) and n a huge number, \(N=10,000\), of samples of size n from a discrete half-logistic distribution with parameter \(\theta\); we estimated the expected value and the root-mean-squared error of the estimators \(\hat{\theta }_{P}\), \(\hat{\theta }_{P*}\), \(\hat{\theta }_{M}\), \(\hat{\theta }_{ML}\), by computing the following two quantities

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{\bar{\theta }} = \dfrac{1}{N} \sum _{h=1}^N \hat{\theta }^{(h)}\\ \widehat{\text {rmse}}(\hat{\theta }) = \sqrt{\dfrac{1}{N} \sum _{h=1}^N (\hat{\theta }^{(h)} -\theta )^2} \end{array}\right. } \end{aligned}$$

where \(\hat{\theta }^{(h)}\) is the generic estimate computed on the h-th sample. Along with the point estimate, based on each pseudo-random sample we constructed also a 95% likelihood-based confidence interval for \(\theta\), and over all the N samples we computed their actual coverage (i.e., the proportion of samples containing the true value of \(\theta\)) and their average length. We recall that the estimated variance of any estimator can be calculated as

$$\begin{aligned} \widehat{\text {Var}}(\hat{\theta }) = \widehat{\text {rmse}}^2(\hat{\theta }) - [\hat{\bar{\theta }}-\theta ]^2, \end{aligned}$$

where \(\hat{\bar{\theta }}-\theta\) represents its estimated bias.

Table 4 reports the values of the Monte Carlo average \(\hat{\bar{\theta }}\) and the estimated root-mean-squared-error \(\widehat{\text {rmse}}(\hat{\theta })\) for all the combinations of \(\theta\) and n considered. Note that the results related to the estimator \(\hat{\theta }_{P^*}\) are not displayed in Table 4, since under each scenario, for a non-negligible proportion of samples, it cannot be applied, and when applicable, it provides results much worse than the other estimators. Furthermore, for some of the combinations \((\theta ,n)\) considered in this simulation study, the results related to the estimator \(\hat{\theta }_P\) are not shown, because in those cases the percentage of samples that do not return a valid estimate was non-negligible—larger than 25% (if \(\theta\) is small, the probability of not getting any zero in the sample becomes considerable, especially if n is small too)—thus making comparisons not sound.

Table 4 Monte Carlo summary results: average value and root-mean-squared error for the three estimators derived through the method of proportion (P), method of moments (M), and maximum likelihood method (ML); coverage probability and average length of 95% log-likelihood-based confidence intervals (CI)
Full size table

From Table 4, it is quite evident that the estimators obtained through the method of moments and the maximum likelihood method show a similar performance in terms of bias and root-mean-squared error under any setting; to be more precise, under each scenario, the method of moments shows a smaller bias in absolute value, but a larger rmse than the maximum likelihood method. Such differences almost disappear when \(n=100\). We notice that the bias of both estimators is always positive, though negligible, especially when increasing the sample size. The method of proportion, although its bias in absolute value is often negligible, is characterized, as expected, by comparatively (much) larger values of root-mean-squared error, especially when \(\theta\) gets smaller; so its use is discouraged.

As for the performance of interval estimators, their actual coverage is always very close to the nominal 95% level and, at least when \(\theta\) is smaller than 1, we observe that overall the coverage tends to get very close to 95% when n increases; some discrepancies and irregularities are noted when \(\theta \ge 1\), i.e., when the probability mass tends to be concentrated over the first non-negative integers. As for the average length of confidence intervals, it is an increasing function of θ for any sample size n examined; it is a decreasing function of n, for any value of \(\theta\) examined—roughly, it is of the order of \(1/\sqrt{n}\).

Figure 7 displays the Monte Carlo joint and marginal distributions of the estimators \(\hat{\theta }_M\) and \(\hat{\theta }_{ML}\) calculated on the N samples of size \(n=100\) drawn from the discrete half-logistic rv with \(\theta =0.5\). Not only the marginal distributions of the two sample estimators are very similar, as one can note looking at the boxplots, but they also return, on each sample, two values very close to each other, since all the N points in the scatterplot lie very near to the first and third orthants’ bisector. Similar considerations can be made for the other settings examined.

Fig. 7
figure 7

Scatter plot (left) and boxplots (right) of the Monte Carlo joint and marginal distributions of \(\hat{\theta }_M\) and \(\hat{\theta }_{ML}\) when \(\theta =0.5\) and \(n=100\)

Full size image

4 Real Data Analysis

This section is devoted to illustrating the modeling capabilities of the proposed distribution. To show how it works in practice, we used two real datasets.

4.1 Count Data

We considered the dataset in Table 5, which reports the counts of number of claims of automobile liability policies and appeared in Gómez-Déniz et al. (2008) and Gómez-Déniz et al. (2011, Table 4), among others. We fitted the discrete half-logistic distribution on this data set, by first considering the methods of proportion, which provide \(\hat{\theta }_P=0.7968\) and \(\hat{\theta }_P^*=1.343\). The method of moments yields \(\hat{\theta }_M=0.6833\). The MLE of \(\theta\) is equal to 0.6734; the maximum value of the log-likelihood function is \(\ell _{\max }=-529.7721\), the \(\text {AIC}=2p-2\ell _{\max }\) is 1061.544, being \(p=1\) the number of unknown parameters. The corresponding theoretical frequencies of the discrete half-logistic model, with the parameter \(\theta\) set equal to \(\hat{\theta }_{ML}\), are reported in the third column in Table 5, next to the observed ones. It is apparent that there is some discrepancy regarding the frequencies of the counts 0 and 1, which has been also suggested by the value \(\hat{\theta }_P^*\) which is quite different from the other estimates. We computed the value of the chi-squared statistic, defined as \(X^2=\sum _{i=1}^K (O_i-E_i)^2/E_i\), where \(O_i\) and \(E_i\) are the observed and expected frequencies of the i-th category, respectively. Here, i ranges from 1 to \(K=8\), after pooling the last five categories (in order to have all the \(E_i\) greater than 5); \(X^2\) is equal to 5.045 and the corresponding p-value under the null hypothesis that the data follow the discrete half-logistic distribution with parameter \(\hat{\theta }_{ML}\) is 0.538, indicating a more than satisfactory goodness-of-fit. Figure 8 displays the graphs of the empirical and the fitted cdf for the dataset, which seems to confirm that the proposed distribution is able to model the data adequately.

Table 5 Distribution of a number of claims of automobile liability policies (Gómez-Déniz et al. 2011, Table 4)
Full size table

The proposed distribution shows a performance slightly inferior (in terms of AIC) than the two-parameter distributions analysed in Gómez-Déniz et al. (2011): the negative binomial, the Poisson inverse Gaussian, and the distribution introduced by the same authors, which is unimodal with a zero vertex as ours; but it shows the best fit in terms of p -alue associated to the chi-squared goodness-of-fit test.

Fig. 8
figure 8

Probability–Probability plot for the insurance claims dataset, showing the empirical and the fitted cumulative distributions

Full size image

4.2 Discrete Failure Time Data

In order to check the fitting capability of the proposed distribution for discrete failure time data, we used the second dataset of Bakouch et al. (2014). This dataset consists of remission times in weeks for 20 leukemia patients randomly assigned to a certain treatment and is summarized as

$$\begin{aligned} 1\, 3\, 3\, 6\, 7\, 7\, 10\, 12\, 14\, 15\, 18\, 19\, 22\, 26\, 28\, 29\, 34\, 40\, 48\, 49 \end{aligned}$$

Since there are no zeros in the sample, the method of proportion cannot be applied. If we estimate the unknown \(\theta\) through the method of moments, we obtain \(\hat{\theta }_M=0.06969\). Using the maximum likelihood method, we obtain \(\hat{\theta }_{ML}=0.070341\) (a value very close to the previous one) and the 95% confidence interval (0.047571, 0.098868). The maximum value of the log-likelihood function is \(-\,79.00915\) and hence the value of the AIC is 160.0183 and that of the BIC is 161.014. According to these two latter indicators, the discrete half-logistic distribution shows a better fit than the discrete Pareto, the discrete Weibull, the generalized Poisson, the discrete logistic, the discrete Lomax, and the discrete Burr distribution, which were all examined in Tyagi et al. (2020). In Fig. 9, the empirical and the theoretical cdf’s, the latter obtained by setting \(\theta\) equal to its MLE, are plotted superimposed.

Fig. 9
figure 9

Probability–Probability plot for the remission times dataset, showing the empirical and the fitted cumulative distributions

Full size image

5 Generalization

The discrete analogue introduced here exhibits a unique mode at zero, making it particularly useful for fitting sample data where the most frequent value is zero, and can be regarded as a valid alternative to well-established count distributions, as demonstrated in Sect. 4. For the same reason, however, it turns out unsuitable for modeling count data with a mode other than zero. This limitation can be addressed by constructing a possible generalization, starting with the generalized half-logistic distribution mentioned in Liu et al. (2018), which accepts an additional shape parameter \(\alpha >0\) and whose pdf is

$$\begin{aligned} f(x)=\frac{\alpha \theta (2e^{-\theta x})^\alpha }{(1+e^{-\theta x})^{\alpha +1}} \end{aligned}$$

and survival function

$$\begin{aligned} S(x)=\left( \frac{2}{1+e^{\theta x}}\right) ^\alpha ; \end{aligned}$$

if \(\alpha =1\), then the one-parameter half-logistic distribution of Eq. (1) is obtained. The PMF of the discrete generalized half-logistic can be then defined as \(p(x)=f(x;\theta ,\alpha )/\sum _{k\in {\mathbb{N}}_0} f(k;\theta ,\alpha )\) for any non-negative integer x. In this way, for any value of \(\theta\), it is possible to calibrate the parameter \(\alpha\) to ensure that the PMF is no longer decreasing with x, exhibiting a unique mode at 0, but rather follows an increasing-decreasing trend with a mode at some positive integer value.

6 Conclusion

We introduced a discrete analogue of the one-parameter half-logistic distribution by setting the probability of each non-negative integer value proportional to the corresponding value of the probability density function of the continuous model. Such a construction calls for the numerical computation of an infinite series sum, acting as a normalizing constant in the definition of the probabilities. Despite manifest complication, the widespread availability of statistical and mathematical software and the increased computational power facilitate its use.

The discrete distribution is log-concave, has a decreasing PMF with a unique mode at zero, and allows for both under- and over-dispersion, although under-dispersion is achievable only when the probability mass is mostly concentrated on 0 and 1. It is positively skewed and leptokurtic; its failure rate function is shown to be always a strictly increasing function. These features make it suitable for modelling purposes in many fields (e.g., insurance and ecology). Simulation and inferential issues were discussed; despite the non-analytic expression of probabilities, the practical supplementary effort to be implemented for simulating or estimating the model is affordable under any statistical environment. The comparison among different parameter estimators pointed out that the method of moments and the maximum likelihood method have an almost equal performance. The application to two real data sets (one concerning pure counts, the other discrete failure times), where the proposed model was compared to other popular count distributions, shows that it provides an at least satisfactory fit in both cases, and therefore it can be deemed a valid candidate for the modeling of count data and can profitably join the class of existing discrete random distributions; a two-parameter extension might however deserve attention in future research.