Fuzzy information granulation towards interpretable sentiment analysis

Abstract

Sentiment analysis, which is also referred to as opinion mining, is aimed at recognising the attitude or emotion of people through natural language processing, text analysis, and computational linguistics. In the past years, many studies have been focused on sentiment classification in the context of machine learning, e.g., to identify that an instance of sentiments is positive or negative. In particular, the bag-of-words method has been popularly used for transforming textual data into structural data, to enable machine learning algorithms to be used directly for tasks of sentiment classification. Through the use of the bag-of-words method, each single word in a set of textual instances is turned into a single attribute in a structural data set transformed from the textual data set. This form of transformation usually results in massively high dimensionality and thus impacts negatively on the interpretation of sentiment analysis models. In this paper, we propose an approach based on fuzzy information granulation towards interpretable sentiment analysis models. We review the concepts and techniques of granular computing in general, and focus on the characteristics of fuzzy information granulation in particular. Based on this review and on previous experimental results on movie data, we position the research of sentiment analysis in the context of fuzzy information granulation.

1 Introduction

Sentiment analysis is also referred to as opinion mining and its aim is at identifying the emotion or attitude of people through natural language processing, text analysis, and computational linguistics. In the past years, sentiment analysis has been mainly considered as a classification problem in the setting of machine learning, e.g., polarity classification of sentiments to one of two categories, namely, positive and negative. This has led to broad applications in other areas, e.g., cyberbullying detection (Reynolds et al. 2011; Cocea 2016), emotions recognition (Teng et al. 2007), and movie reviews (Tripathy et al. 2015).

In the machine learning context, textual data need to be transformed into structural data to enable traditional learning approaches to be used directly for sentiment classification. In particular, the bag-of-words method, which considers each single term (word) in a training set of documents to be an attribute in a structural data set, has been used as a popular approach for the above required form of data transformation (Sivic 2009). Based on the above case, two popular machine learning algorithms, namely, support vector machine (Cristianini 2000) and Naive Bayes (Rish 2001), have been used typically towards accurate prediction of sentiment instances in terms of their labels (e.g., positive and negative). However, it is generally not easy to interpret computational models learned through using the above two algorithms, due to the nature of the learning strategies of the two algorithms. In particular, the support vector machine algorithm generally happens to build models that have limitations in transparency and depth of learning, and the Naive Bayes algorithm also happens to build models that are not sufficiently interpretable, due to the constraint that Bayesian learning approaches work based on the assumption that all input attributes are totally independent of each other. More detailed arguments in the above context can be found in Liu et al. (2016a).

Sentiment analysis is typically aimed at discovering opinions from texts, which means to be an exploratory task in which the results of analysis need to be interpretable to people; however, sentiment analysis has been typically undertaken as a machine learning task, with the focus on classification performance and virtually no attention paid to the interpretation of the results. Building interpretable sentiment analysis models would enable the understanding of which aspects of a product could result in a positive or a negative review, and thus provides the possibility of addressing these aspects.

Following the use of the bag-of-words method, textual data are transformed to structural data, which generally result in massively high dimensionality that needs to be dealt with by adopting machine learning methods. This high dimensionality, which is coupled with the incomprehensibility (i.e., “black box” approach) of predictive models, makes models not only poorly interpretable, but also highly complex, leading to the requirement of considerable computational resources for using these models practically.

We argued in Liu and Cocea (2017a) that fuzzy rule learning approaches can address limitations in terms of both the interpretability and the computational complexity, while a classification performance is preserved by the fuzzy approaches in line with the most popular algorithms used for sentiment analysis (e.g., support vector machine and Naive Bayes). However, the experimental results reported in Liu and Cocea (2017a) show that the dimensionality of training data is still very high, even if a great number of irrelevant words (attributes) have been filtered following the use of natural language processing techniques. Therefore, the interpretation of fuzzy rule-based sentiment models is still constrained due to the massively high dimensionality of training data. To deal with the dimensionality issue that impacts on interpretability, we position in this paper the research of sentiment analysis in the setting of information granulation. In particular, fuzzy information granulation is recommended as an effective approach for text processing.

The rest of the paper is organized as follows. Section 2 introduces theoretical preliminaries related to sentiment analysis, granular computing, and machine learning. In particular, concepts on fuzzy logic, rule-based systems, sentiment classification, and information granulation are described. Section 3 presents how the use of fuzzy rule-based systems may lead to advances in interpretability of computational models for sentiment classification. In Sect. 4, we position the above interpretability issue in the setting of information granulation. In particular, we propose a multi-granularity approach of text processing towards reduction of the dimensionality of training data for advancing the interpretation of fuzzy rule-based sentiment models. Section 5 summarises the contributions of this paper and outlines research directions towards achieving further advances in this research area.

2 Theoretical preliminaries

Fuzzy rule learning approaches are considered to be effective for advancing the interpretation of computational models for sentiment analysis (Liu and Cocea 2017a). We also argue that granular computing can be an effective approach for reducing the dimensionality of sentiment data towards advancing the interpretation of sentiment models. To highlight the characteristics of fuzzy logic, rule-based systems, and granular computing that can contribute to increasing the level of interpretability of sentiment analysis models; in contrast to the typical sentiment analysis approach through the use of bag-of-words, this section describes theoretical preliminaries related to fuzzy logic, rule-based systems, sentiment analysis, and granular computing.

2.1 Fuzzy logic

Fuzzy logic is generally viewed as an extension of deterministic logic, i.e., it employs continuous truth values ranging from 0 to 1, rather than binary truth values (0 or 1). The purpose of using fuzzy logic is mainly to turn a black and white problem into a grey problem (Zadeh 2015). In the setting of set theory, crisp sets employ deterministic logic, which means that all elements in a crisp set have full memberships to the set, i.e., all the elements fully belong to the set. In contrast, fuzzy sets employ fuzzy logic, which means that all elements in a fuzzy set only have partial memberships to the set, i.e., each of the elements belongs to the set to a certain degree. Each fuzzy set is defined with a particular function of fuzzy membership, such as trapezoidal, triangular, or Gaussian membership functions (Ross 2010).

Fuzzy logic has been applied broadly in many different areas. For example, fuzzy logic can be used in machine learning tasks, such as fuzzy classification, regression, or clustering, towards reduction of bias in both learning and prediction (Hllermeier 2015). In operational research, fuzzy logic can be used for fuzzy decision making  (Chen and Lee 2010) to support people towards reduction of judgement bias. In engineering, fuzzy logic can be used to build fuzzy models (Gegov et al. 2011). In rule-based systems (RBSs), fuzzy logic can be used to learn and represent fuzzy rules towards more accurate and interpretable predictions being made (Wang and Mendel 1992). A more detailed description of fuzzy rule-based systems (FRBSs) is provided in Sect. 2.2.

2.2 Rule-based systems

A rule-based system (RBS) typically consists of a set of rules and is viewed as a special type of expert systems. Each rule is also made up of rule terms which are also referred to as conditions or antecedents. In general, RBSs can be designed using expert knowledge or through learning from real data. The former way of design is typically referred to as expert-based approaches, whereas the latter way of design is generally referred to as machine learning approaches. In the big data era, machine learning approaches have been considered increasingly popular for the design of RBSs and learning approaches for the above design purpose are referred to as rule learning. In this context, there are two main approaches of rule learning, namely, divide and conquer (DAC) (Quinlan 1993) and separate and conquer (SAC) (Furnkranz 1999).

The DAC approach is also referred to as Top–Down Induction of Decision Trees (TDIDT). This is due to the fact that this approach is aimed at learning rules represented in the form of a decision tree. Some examples for learning decision trees include ID3 (Quinlan 1986) and C4.5 (Quinlan 1993). The DAC approach has a serious limitation, which is known as the replicated sub-tree problem (Cendrowska 1987), i.e., a decision tree learned through using this approach may contain redundant terms that result in the presence of several identical sub-trees in the decision tree, as illustrated in Fig. 1.

Fig. 1

Replicated sub-tree problem Liu et al. (2016a)

Because of the presence of the replicated sub-tree problem, the SAC approach, which is aimed at generating if-then rules directly through learning from training instances, has been increasingly getting popular. This approach is also referred to as the covering approach because of the fact that the SAC approach generally involves learning one rule that covers some training instances and then learning the next rule based on the remaining instances, i.e., the instances, which are covered by the rules generated previously, are deleted from the training set prior to the learning of the next rule. Some typical examples of the SAC approach include Prism (Cendrowska 1987) and Ripper (Cohen 1995).

Both the above two approaches are aimed at the learning of deterministic rules, which means that the rules are assumed to be consistent without uncertainty. However, in reality, it is not appropriate to assume that the training data are complete towards the learning of deterministic rules. From this viewpoint, deterministic rules are considered to be biased and less reliable when these rules are used for predicting on unseen instances in practice (Liu and Cocea 2017b). Therefore, the learning of fuzzy rules, which leads to the production of a fuzzy rule-based system (FRBS), has been adopted towards addressing the above problem.

There are three popular types of FRBSs, namely, Mamdani, Sugeno, and Tsukamoto (Ross 2010). The first two types of FRBSs apply to regression problems, since the output from such fuzzy systems is a real (numerical) value, and the third type of FRBSs generally applies to classification problems, since the output is a discrete (categorical) value. As we focus on classification tasks in this paper, an illustrative example of a Tsukamoto system is thus provided below to show how fuzzy rules work for classification.

The Tsukamoto system has two input variables $x_1$ and $x_2$ and one output variable y. The variable $x_1$ has two linguistic terms, ‘Tall’ and ‘Short’, and $x_2$ has two linguistic terms, ‘Large’ and ‘Small’. The output variable y has two linguistic terms, ‘Positive’ and ‘Negative’. The fuzzy sets corresponding to the above linguistic terms are expressed as follows:

Tall = $0/1.3 + 0.25/1.4 + 0.5/1.6 + 0.75/1.7 + 0.85/1.8 + 0.95/1.9 + 1/2.0$

Short = $1/1.3 + 0.75/1.4 + 0.5/1.6 + 0.25/1.7 + 0.15/1.8 + 0.05/1.9 + 0/2.0$

Large = $0/0 + 0.3/1 + 0.4/2 + 0.6/3 + 0.7/4 + 0.9/5 + 1/6$

Small = $1/0 + 0.7/1 + 0.6/2 + 0.4/3 + 0.3/4 + 0.1/5 + 0/6$.

Positive: each value of y has a membership degree to the fuzzy set, which is equal to the rule firing strength, if the fuzzy set is provided as the linguistic output of the fuzzy rule.

Negative: each value of y has a membership degree to the fuzzy set, which is equal to the rule firing strength, if the fuzzy set is provided as the linguistic output of the fuzzy rule.

There are four rules as follows:

• Rule 1: If $x_1$ is ‘Tall’ and $x_2$ is ‘Large’, then y = ‘Positive’;

• Rule 2: If $x_1$ is ‘Tall’ and $x_2$ is ‘Small’, then y = ‘Positive’;

• Rule 3: If $x_1$ is ‘Short’ and $x_2$ is ‘Large’, then y = ‘Negative’;

• Rule 4: If $x_1$ is ‘Short’ and $x_2$ is ‘Small’, then y = ‘Negative’.

For each rule, the firing strength is derived based on the given input values, e.g., if $x_1$ and $x_2$ are assigned the numerical values of 1.7 and 3, respectively, then the firing strength of Rule 2 will be 0.4, as the fuzzy truth values for ‘Tall’ and ‘Small’ are 0.75 and 0.4, respectively. Rule 2 provides the linguistic term ‘Positive’ as the output with the fuzzy membership degree of 0.4 towards predicting a test instance.

Each of the four rules listed above works in the same way and the value of the final output is determined by taking the output value derived from the rule that has the highest firing strength. The advantages of FRBSs are discussed in more detail in Sect. 3.1.

2.3 Sentiment analysis

Sentiment analysis generally involves five stages, namely, enrichment, transformation, preprocessing, vectoring, and mining (Thiel and Berthold 2012).

The enrichment stage is aimed at adding semantic information through recognition and tagging of named entities, such that the filtering of terms (words) can be executed in the later stages. Popular taggers include POS Tagger, Abner Tagger, and Dictionary Tagger. More details on text enrichment can be found in Thiel and Berthold (2012).

Transformation is aimed at transforming textual data into structural data, so that traditional machine learning methods can be used directly for learning sentiment prediction models towards classifying any unseen instances of sentiments. In particular, the bag-of-words approach is seen as one of the most popular ways to achieve such a transformation (Reynolds et al. 2011; Zhao et al. 2016) by turning each single term (word) in a training set of documents into a single attribute in the transformed (structural) data set. Following the use of the bag-of-words method, it is also necessary to count the frequency of each word, so that those less frequently occurring words can be filtered as expected. In this approach, the dimensionality of the structural data can be reduced significantly, which leads to more efficient processing of data in the later stages.

Preprocessing is aimed at filtering those irrelevant words, e.g., stop words, punctuation, numbers, and words that contain no more than n characters (Thiel and Berthold 2012).

In addition, it is necessary to covert upper cases to lower cases for single words and remove endings using stemming (Thiel and Berthold 2012). Usually, the words, which are extracted through creating a bag of words but are less frequently occurring, are filtered in the preprocessing stage, i.e., only those highly relevant words need to be used in the next stage (vectoring) (Thiel and Berthold 2012) towards creating a vector of words.

In the vectoring stage, each word is turned into a binary or numerical attribute. If the attribute is of the binary type, the binary value reflects the presence/absence of the word in a particular document(textual instance). Otherwise, the numerical value reflects the relative frequency of the word appearing in a textual instance or the absolute frequency of the word appearing in the training set, i.e., the total number of times the word appears in any of the documents that contain this word.

Mining, which is the last stage of a sentiment analysis task, is aimed at adopting machine learning methods towards dealing with the structural data set transformed following the previous four stages, i.e., building sentiment prediction models and classifying unseen instances of sentiments.

2.4 Granular computing

Granular computing is a powerful approach for processing of information. Yao (2005b) stressed that granular computing could be applied with two main aims. The first one is aimed at adopting structured thinking in a philosophical manner, and the second one is aimed at conducting structured problem solving in a practical manner. As introduced in Yao (2005a); Hu and Shi (2009), Zadeh indicated three basic concepts, namely, granulation, organization, and causation. Granulation generally involves decomposing whole into parts. In practical applications, this indicates that a complex problem is divided into several simpler sub-problems. Organization involves integrating several parts into a whole. In practice, this means to merge several modular problems into a systematic problem. Causation involves identifying the relationships between causes and effects. Based on the above definition, granular computing involves two operations (Yao 2005a), namely, granulation and organization.

As described in Yao (2005a), granulation can be done in the ways of partitions or coverings. In the machine learning context, partitions and coverings are involved in DAC rule learning and SAC rule learning, respectively. In fact, the DAC approach is aimed at partitioning a training set into several disjoint subsets and repeating the same procedure on each of the subsets on a recursive basis, unless a subset contains the instances that belong to only one class. In other words, the DAC approach ends up with a decision tree learned from a training set and each of the branches starting from a non-leaf node in the tree is corresponding to a training subset resulting from a partition. The SAC is aimed at learning a rule that covers a subset of training instances and then learning the next rule on the basis of the remaining training instances. In other words, the SAC approach ends up with a set of if-then rules learned from a training set as mentioned in Sect. 2.2 and these rules may cover overlapping instances.

Partitions are also involved in the context of set theory, i.e., different types of sets, such as probabilistic sets, fuzzy sets, and rough sets. All the three above types of sets can be viewed as extensions of deterministic sets. In particular, a probabilistic set can be viewed as a deterministic set when all elements certainly belong to the set, the chance is 100%. Moreover, a fuzzy set can be viewed as a deterministic set when all elements fully belong to the set, i.e., the degree of fuzzy membership is 100%. Similarly, a rough set can be viewed as a deterministic set when all elements unconditionally belong to the set, i.e., the possibility is 100%. The above description indicates that deterministic sets employ deterministic logic for dealing with the relationships between sets and elements, whereas the other three types of sets employ non-deterministic logic for dealing with such relationships.

In the probabilistic sets context, each set is viewed as a granule and is provided with a chance space that could be divided into subspaces. Each of these subspaces would be considered as a particle that is selected randomly towards activating the occurrence of an event. From this perspective, all these particles are integrated into a whole chance space. As introduced in Liu et al. (2016b), an element in a probabilistic set is provided with a probability towards being offered a full membership to the set. In the granular computing setting, the probability is treated as a percentage of the particles that compose the chance space. For instance, if an element is granted a probability of 90% towards being offered a full membership to a set, it means that the element is provided with 90% of the particles that result in the full membership being granted.

In the fuzzy sets context, each set is viewed as a granule and each of its elements is assigned a certain degree of membership to the set. In other words, an element belongs to a fuzzy set to a certain degree. In the granular computing setting, a membership could be divided into different parts. Every part of the membership is treated as a particle. For instance, if an element is granted the membership degree of 90% to a set, it means that the element is provided with 90% of the particles for relating it to the set. The above example is very similar to the case that a digital library supplies different membership types and different types of members are provided with different levels of electronic access to the resources.

In the rough set context, each set is viewed as a granule. A rough set employs a boundary region to allow an element conditionally belonging to the set due to insufficient information, i.e., all elements inside the boundary region can just have conditional memberships to the set, due to the case that these elements only partially fulfil the conditions for getting into the non-boundary region of the set. While the conditions have been fully satisfied, these elements would be given unconditional memberships to the set. In the granular computing setting, the condition for an element to get into the non-boundary region of the set can be divided into different sub-conditions. Each of these sub-conditions is treated as a particle. As described in Liu et al. (2016b), possibility is treated as a measure of the degree to which a condition is satisfied. For instance, if an element is granted the possibility of 90% for belonging to a set, it means that the element is provided with 90% of the particles, each of which provides the partial fulfilment towards having the unconditional membership offered.

In real applications, the granular computing theory has been popularly used for advancing other research areas, such as computational intelligence (Dubois and Prade 2016; Kreinovich 2016; Yao 2005b; Livi and Sadeghian 2016), artificial intelligence (Wilke and Portmann 2016; Yao 2005b; Skowron et al. 2016), and machine learning (Min and Xu 2016; Peters and Weber 2016; Liu and Cocea 2017b; Antonelli et al. 2016). In addition, ensemble learning is an area that has a strong link with granular computing. This can be supported by the fact that ensemble learning approaches, such as Bagging, involve decomposing a training set into a number of overlapping samples and a combination of predictions made from different classifiers towards classifying a test instance. Such a similar perspective was also stressed and discussed in Hu and Shi (2009). Section 3 will present how fuzzy set theory can be used to deal with linguistic uncertainty. More details on how granular computing can be used effectively for text processing are discussed in Sect. 4.

3 Fuzzy rule-based classification of sentiments

We proposed in Liu and Cocea (2017a) the use of FRBSs for sentiment analysis towards more accurate and interpretable classifications being made. To show how a FRBS works, this section presents the key features of this approach and justifies the significance of this approach in both theoretical and practical contexts. In addition, constraints on the interpretation of fuzzy rules, due to the dimensionality issue mentioned in Sect. 1, are also identified and discussed.

3.1 Key features

The fuzzy approach proposed in Liu and Cocea (2017a) involves using the Tsukamoto system, because of the fact that this type of fuzzy systems is typically used for classification problems, as mentioned in Sect. 2.1. For each input attribute, the trapezoid fuzzy membership function is employed for converting continuous (numerical) values into fuzzy linguistic terms, since the above fuzzy membership function is popularly used in practice (Chen 1996).

When the trapezoid fuzzy membership function is used, each linguistic term T involves four key points a, b, c, d regarding the change pattern of a membership degree. An example is illustrated below and in Fig. 2:

$$\begin{aligned} f_T(x) = \left\{ \begin{array}{ll} 0, &{} \text { when } x\le a \text { or } x\ge d;\\ (x-a)/(b-a), &{} \text { when } a<x<b;\\ 1, &{} \text { when } b\le x \le c;\\ (d-x)/(d-c), &{} \text { when } c<x<d;\\ \end{array} \right. \end{aligned}$$

Fig. 2

Trapezoid fuzzy membership function (Liu and Cocea 2017a)

In the training stage, the values of the above four parameters a, b, c, d are derived for each single attribute so that fuzzy rules are generated. In the testing stage, fuzzy classification involves the following steps: fuzzification, application, implication, aggregation and defuzzification (Ross 2010). The example given in Sect. 2.1 includes the following rules:

• Rule 1: If $x_1$ is ‘Tall’ and $x_2$ is ‘Large’ then y = ‘Positive’;

• Rule 2: If $x_1$ is ‘Tall’ and $x_2$ is ‘Small’ then y = ‘Positive’;

• Rule 3: If $x_1$ is ‘Short’ and $x_2$ is ‘Large’ then y = ‘Negative’;

• Rule 4: If $x_1$ is ‘Short’ and $x_2$ is ‘Small’ then y = ‘Negative’;

when $a = 1.3$, $b = 1.8$, $c=1.8$, and $d=1.8$ for the linguistic term ‘Tall’, $a = 2$, $b = 8$, $c=8$, and $d=8$ for the linguistic term ‘Large’, and if $x_1=1.425$ and $x_2=6.5$, then the following steps are executed.

Fuzzification:

• Rule 1: $f_Tall(1.425)=0.25$, $f_Large(6.5)=0.75$;

• Rule 2: $f_Tall(1.425)=0.25$, $f_Small(6.5)=0.25$;

• Rule 3: $f_Short(1.425)=0.75$, $f_Large(6.5)=0.75$;

• Rule 4: $f_Short(1.425)=0.75$, $f_Small(6.5)=0.25$.

In the fuzzification stage, the notation $f_Tall(1.425)$ represents the fuzzy membership degree of the numerical value ‘1.425’ to the fuzzy linguistic term ‘Tall’. Similarly, the notation $f_Large(6.5)$ represents the fuzzy membership degree of the numerical value ‘6.5’ to the fuzzy linguistic term ‘Large’. The fuzzification stage is aimed at mapping the numerical value of a variable to a membership degree to a particular fuzzy set.

Application:

• Rule 1: $f_Tall(1.425) \wedge f_Large(6.5)= Min(0.25, 0.75)= 0.25$;

• Rule 2: $f_Tall(1.425) \wedge f_Small(6.5)= Min(0.25, 0.25)= 0.25$;

• Rule 3: $f_Short(1.425) \wedge f_Large(6.5)= Min(0.75, 0.75)= 0.75$;

• Rule 4: $f_Short(1.425) \wedge f_Small(6.5)= Min(0.75, 0.25)= 0.25$.

In the application stage, the conjunction of the two fuzzy membership degrees, respectively, for the two variables ‘$x_1$ and ‘$x_2$’ is aimed at deriving the firing strength of a fuzzy rule.

Implication:

• Rule 1: $f_1(Positive)= Min(0.25, 1)= 0.25$;

• Rule 2: $f_2(Positive)= Min(0.25, 1)= 0.25$;

• Rule 3: $f_3(Negative)= Min(0.75, 1)= 0.75$;

• Rule 4: $f_4(Negative)= Min(0.25, 1)= 0.25$.

In the implication stage, the firing strength of a fuzzy rule derived in the application stage can be used further to identify the membership degree of the value of the output variable ‘y’ to the fuzzy linguistic term ‘Positive’ or ‘Negative’, depending on the consequent of the fuzzy rule. For example, $f_1(Positive)= 0.25$ indicates that the consequent of Rule 1 is the fuzzy linguistic term ‘Positive’ and the value of the output variable ‘y’ has the membership degree of 0.25 to the fuzzy linguistic term ‘Positive’. Similarly, $f_3(Negative)= 0.75$ indicates that the consequent of Rule 3 is the fuzzy linguistic term ‘Negative’ and the value of the output variable ‘y’ has the membership degree of 0.75 to the fuzzy linguistic term ‘Negative’.

Aggregation:

$$\begin{aligned} f(Positive)= f_1(Positive) \vee f_2(Positive)\\ = max(0.25, 0.25)=0.25;\\ f(Negative)= f_1(Negative) \vee f_2(Negative)\\ = max(0.75, 0.25)=0.75.\\ \end{aligned}$$

In the aggregation stage, the value of the output variable ‘y’ derived from each rule needs to have its membership degree to the corresponding fuzzy linguistic term (‘Positive’ or ‘Negative’) taken towards finding the maximum among all the membership degrees. For example, Rule 3 and Rule 4 both provide ‘Negative’ as the linguistic output and the values of the output variable ‘y’ derived through the two rules have the membership degrees of 0.75 and 0.25, respectively, to the fuzzy linguistic term ‘Negative’. As the maximum of the fuzzy membership degrees is 0.75, the output value is considered to have the membership degree of 0.75 to the fuzzy linguistic term ‘Negative’. Similarly, the maximum of the fuzzy membership degrees derived through Rule 1 and Rule 2 is 0.25, so the output value is considered to have the membership degree of 0.25 to the fuzzy linguistic term ‘Positive’.

Defuzzification: $f(Negative)>f(Positive) \rightarrow y= Negative$.

In the defuzzification stage, the aim is to identify the fuzzy linguistic term to which the output value has the highest membership degree. In this example, as the membership degree of the output value to the term ‘Negative’ is 0.75, which is higher than the the membership degree (0.25) to the term ‘Positive’, the final output is ‘Negative’ towards classifying an unseen instance.

3.2 Discussion

We proposed in Liu and Cocea (2017a) the use of FRBS for sentiment classification based on the advantages of fuzzy logic and RBSs, as well as their suitability for this type of classification problems, as outlined below (Liu and Cocea 2017a).

Firstly, fuzzy logic is well capable of dealing with linguistic uncertainty. In particular, the theory of fuzzy logic is aimed at considering a classification problem to be a ‘degree of grey’ one rather than a ‘black and white’ one (currently used in sentiment analysis). In the above way of defining a classification problem, bias in sentiment classification can be reduced on both positive and negative sides. For example, popular machine learning algorithms for sentiment classification, such as C4.5 and Naive Bayes, deal with continuous (numerical) attributes by getting their numerical values into different intervals. Each of the intervals is used as a condition judgement towards classifying test instances to a particular category. This way of dealing with numerical attributes has been criticised in fuzzy logic literature and is generally considered to be judgement bias. The above problem in dealing with numerical attributes can be resolved using fuzzy linguistic terms instead of intervals. In addition, the use of fuzzy logic theory can result in a classification outcome being provided with a certainty factor (degree of truth) rather than an absolute truth.

Second, as argued in Liu et al. (2016a), RBSs are generally considered to be more interpretable than predictive models learned using other popular learning algorithms in tasks of sentiment classification, e.g., the support vector machines and Naive Bayes algorithms. This can be explained by the fact that rule-based models work in a white box manner and, thus, are fully transparent in terms of how to map an input to an output.

Third, the combination of fuzzy logic and RBSs can lead to rules being represented in the form of natural languages and can thus advance the interpretation of the information extracted from rules. The above way of representing rules would result in higher confidence (i.e., a higher degree of trust) in the results of sentiment classification, in order for people to see the reasoning process of sentiment analysis when machine learning techniques are used. In particular, to demonstrate a high level of interpretability, fuzzy rules can be represented in the following form (taking the example given in Sect. 3):

When $x_1= 1.425$ and $x_2=6.5$:

• Rule 1: If $x_1$ is ‘Tall’ (membership degree: 0.25) and $x_2$ is ‘Large’ (membership degree: 0.75), then y = ‘Positive’ (firing strength: 0.25);

• Rule 2: If $x_1$ is ‘Tall’ (membership degree: 0.25) and $x_2$ is ‘Small’ (membership degree: 0.25), then y = ‘Positive’ (firing strength: 0.25);

• Rule 3: If $x_1$ is ‘Short’ (membership degree: 0.75) and $x_2$ is ‘Large’ (membership degree: 0.75), then y = ‘Negative’ (firing strength: 0.75);

• Rule 4: If $x_1$ is ‘Short’ (membership degree: 0.75) and $x_2$ is ‘Small’ (membership degree: 0.25), then y = ‘Negative’ (firing strength: 0.25).

Through the representation of fuzzy rules, when a test instance is given, people can clearly see the degree to which each of the conditions as part of the antecedent of a rule is satisfied, i.e., the fuzzy membership degree of a numerical value of a variable for a particular fuzzy set (linguistic term), and the degree of certainty of a rule, i.e., the firing strength of a rule, towards classifying the test instance.

In tasks of sentiment analysis, it is not appropriate to consider all types of classification problems to be ‘black and white’. For instance, in the context of multi-class classification, it is possible that different classes are actually not mutually exclusive. In movie categorization, it can really occurs that the same movie can be put into two or more categories without conflicts. In addition, in emotion recognition, it is quite sensible that the same person can be identified having two or more different emotions at the same time. From this viewpoint, FRBSs can be helpful to support the judgement that an item belongs to two or more categories, since this item has a very high degree of fuzzy membership to each of the two or more categories.

On the other hand, it is also necessary to consider sentiment classification problems to be grey to various degrees. This is due to the case that different people usually have different criteria when they judge that a review is positive or negative, which involves a high degree of subjectivity. In fact, it is generally not appropriate to consider things to be perfect, i.e., everything in general may have both positive and negative aspects. For people who seek for things to be perfect, it is more likely that the judgement made by these people on a review is negative.

In contrast, a review may even be judged as positive, while people can only find a few positive aspects on the review, due to the reason that they think that those aspects are of the highest importance and lead to outweighing the negative ones. It is also fairly possible that a sentence does not contain any negative words but is actually aimed at pointing out negative aspects in a positive/constructive way.

In the big data era, the judgement bias on both positive and negative sides can be reduced effectively through the use of fuzzy rules, due to the fact that fuzzy rule-based models involve classifying sentiments though weighted voting at the defuzzification stage, as described in Sect. 3. As argued in Liu et al. (2016c), the presence of big data can generally result in the reduction of the overfitting of predictive models, especially when the models are in the form fuzzy rules, as each of these rules is provided with a certainty factor (degree of certainty) for avoiding any judgement bias.

In addition, the use of fuzzy rules would enable the interpretation of the judgement process, which allows people to understand how the final classification was derived and provided from a classifier. Moreover, the representation of fuzzy rules would allow people to understand in more detail the positive and negative aspects, which, in turn, would make people able to act to make improvements, such as, achieving advances for the travel industry (hotels or restaurants).

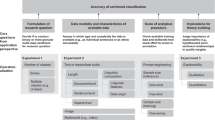
We also conducted an experimental study in Liu and Cocea (2017a) using four polarity data sets on movie reviews (Pang and Lee 2016). The data sets with the number of instances in the positive and negative categories are listed in Table 1 and more details can be found in Pang et al. (2002); Pang and Lee (2004, 2005).

Table 1 Data sets on movie review with number of positive and negative instances (Liu and Cocea 2017a)

All the experiments were conducted in Liu and Cocea (2017a) through the following procedure:

Step 1: The textual data are enriched using POS Tagger and Abner Tagger (Thiel and Berthold 2012).

Step 2: The enriched data are transformed through using the Bag-of-Words method (Reynolds et al. 2011).

Step 3: For each word, its relative frequency, absolute frequency, inverse category frequency, and inverse document frequency are calculated towards filtering out words with low frequency.

Step 4: The words, which are not filtered following Step 3, are preprocessed by filtering stop words, words with no more than N characters, numbers, stemming porter, and erasing punctuation.

Step 5: Each instance (document) is turned into a vector that consists of all the words appearing in the textual data set, each of which is turned into a numerical attribute that reflects the frequency of the word through the value of the attribute.

Step 6: All the test instances (document vectors) are classified to be either positive or negative through using machine learning algorithms.

The bag-of-words method mentioned in Step 2 generally means extracting terms (defined as different numbers of words, e.g., 1-word terms, 2-word terms, etc) from the text and counting the frequency of each term. The most frequent approach is for a term to correspond to a single word. The following example is given for illustration:

Here are two text instances:

• 1. Alice encrypts a message and sends it to Bob.

• 2. Bob receives the message from Alice and decrypts it.

Based on the two instances above, a list of distinct words is created: [Alice, Bob, encrypts, decrypts, sends, receives, sage, a, the, and, it, from, to]

Two feature vectors for the two instances are created:

• 1. [1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1]

• 2. [1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0].

In the above two feature vectors, each numerical value represents the frequency of a corresponding word.

In the stage of text mining, the structural data set is partitioned into a training set and a test set in the ratio of 7:3.

The classification accuracy performed using a fuzzy rule learning approach is compared with the ones performed using Naive Bayes and C4.5, respectively. This is to test the performance of the fuzzy rule learning approach in terms of the accuracy of sentiment classification in comparison with popular learning algorithms that are known to be capable of performing well in sentiment prediction tasks. The results reported in Liu and Cocea (2017a) show that the fuzzy rule learning approach performs slightly better than the two well-known algorithms (Naive Bayes and C4.5), and thus indicate the suitability of fuzzy rule learning approaches for sentiment analysis tasks.

In addition, the experimental study also involved the investigation of the number of rules and the number of terms produced by C4.5 and the fuzzy rule learning approach, respectively, on the basis of the chosen textual data of massively high dimensionality. This is to investigate the level of the complexity of the produced fuzzy and non-fuzzy rule-based models, which is closely related to the interpretability issue. The results reported in Liu and Cocea (2017a) indicate that the fuzzy rule learning approach produces fewer rules than C4.5 in all the four cases and fewer terms than C4.5 in three out of the four cases.

As analysed in Liu et al. (2016a), the model interpretability can be impacted by four main factors, namely, model transparency, model complexity, model redundancy, and human characteristics. The first three impact factors indicate, respectively, the degree to which the model is transparent to people (transparency), the degree to which the model is easy for people to read and understand (complexity) and the degree to which different parts of the model are redundant (redundancy).

Model transparency highly depends on the nature of learning algorithms. As reported in Liu et al. (2016a), all the three chosen learning algorithms, Naives Bayes, C4.5 and fuzzy rule learning, are capable of generating transparent models, due to the nature of their learning strategies.

Model complexity depends on both the nature of learning algorithms and the characteristics of data. An example is given in Liu and Cocea (2017a), which gives three attributes a, b, and c. The three attributes have the number of values of 3, 4, and 5, respectively. In this example, Naive Bayes would lead to the production of a model that consists of 60 ($3\times 4 \times 5$) probabilistic correlations, and fuzzy rule learning would lead to the production of a model that consists of 60 ($3\times 4 \times 5$) fuzzy rules. However, C4.5 would lead to the production of a more complex model that consists of 12 ($3+4+5$) first-order rules (each rule has only one rule term), 47 ($3\times 4+3\times 5+4\times 5)$ second-order rules (each rule has two rule terms), and 60 ($3\times 4\times 5$) third-order rules (each rule has three rule terms). In addition, as discussed in Liu and Cocea (2017a), fuzzy rule learning is also capable of reducing the complexity of continuous attributes by replacing numerical values with fuzzy linguistic terms, which also leads to the reduction of model complexity.

Model redundancy depends on the nature of learning algorithms. As discussed in Liu and Cocea (2017a), decision tree learning algorithms, such as C4.5, are likely to result in the replicated subtree problem illustrated in Fig. 1, which leads to the production of a model that contains a large number of redundant rule terms and is thus considered as a disadvantage comparing with Naive Bayes and fuzzy rule learning.

The last factor (human characteristics) that impacts on model interpretability typically depends on people’s preference and cognitive capacity, i.e. the extent to which people like to look at computational models in detail and the degree to which they are able to understand the information extracted from the models. In fact, people in different fields usually have different preferences of reading information and different cognitive capacity of understanding information. For example, mathematical formulas are generally not interpretable for people without background in mathematics, so this kind of people would prefer to be provided with a more accessible form of representation of the information extracted from models. From this viewpoint, the interpretation of fuzzy rules would be generally easier due to the fact that fuzzy rules are represented in the form of natural languages, as illustrated earlier in this section. In addition, since natural languages are used as one of the most common ways of communication between people, the use of fuzzy rules would be considered as a preferred way of information representation over other ways.

Table 2 Number of words extracted through using bag-of-words and number of words left after filtering low frequent words (Liu and Cocea 2017a)

Although fuzzy rule learning approaches have the above advantages, through the experimentation on the extraction of sentiment features from data on movie reviews, the results presented in Table 2 show empirically that sentiment data are generally of massively high dimensionality following the transformation of textual data into structural data using the bag-of-words method. Even after any irrelevant words have been filtered, the data dimensionality is still very high (over thousands). The experimental results provide the general indication that the interpretation of fuzzy rules is still much constrained and interpretability is thus still an issue that is needed to be dealt with through more in-depth research. This indicates the need to address the data dimensionality issue, for which we propose the use of fuzzy information granulation. In Sect. 4, we propose to adopt fuzzy information granulation for text processing, towards significant reduction of data dimensionality.

4 Text processing through fuzzy information granulation

As described in Yao (2005a), a granule is defined as “a small particle; especially, one of numerous particles forming a larger unit”. The definition can be found in the Merriam–Webster’s Dictionary (Merriam-Webster 2016). In the setting of granular computing, a granule can be in the form of a subset, class, object, or cluster (Yao 2005a). According to different formalisms of information granulation, the corresponding granules are of different types, such as crisp granules, probabilistic granules, fuzzy granules, and rough granules. In practice, a program module can be viewed as a granule, since it is a part of a software program. In addition, a taught unit can be viewed as a granule, since it is a part of a course. More details on information granules can be found in Pedrycz and Chen (2011, 2015b, 2015a); Pedrycz (2011).

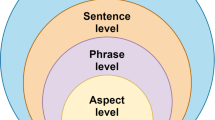
In the context of text processing, information granules are typically of fuzzy type, such as sections, subsections, paragraphs, passages, sentences, phrases, and words. The above examples of fuzzy information granules are actually in different levels of granularity so we propose a multi-granularity approach of text processing in this section. In particular, textual data are decomposed into several parts and each of these parts may be divided again depending on its complexity, through fuzzy information granulation.

As reported in Sect. 3.2, processing of textual data usually results in massively high dimensionality, which leads to difficulty in the interpretation of fuzzy rules or other types of models. This is mainly because the bag-of-words method is used too early for transforming textual data into structural data. In other words, traditional approaches of text processing only involve single granularity learning, and all features extracted through using the bag-of-words method are global ones. In fact, an instance of textual data can be decomposed into sub-instances in the setting of granular computing. In this context, text processing can involve multi-granularity learning and there could be more local features extracted from those subinstances of the original textual instances. For example, text can be divided into phrases, and a document can be decomposed into several sections, each of which can be again divided into subsections. Therefore, information granules in different levels of granularity would involve different local features to be extracted. The above way of text processing is also in line with the main requirements of big data processing, namely, decomposition, parallelism, modularity, and recurrence (Wang and Alexander 2016), which can lead to the reduction of instance complexity, so that each instance of textual data (as an information granule) can have its dimensionality and fuzziness reduced.

Overall, the above approach of text processing involves multi-granularity learning, which decomposes a textual data set into several modules/sub-modules, so that each module/sub-module can be much less complex (of much lower dimensionality and fuzziness), and enables the extraction of local features from each module/sub-module of original textual data. In addition, the above approach also leads to the reduction of computational complexity, since parallelism can be involved in processing the modules/sub-modules of textual data following the decomposition of the data.

To adopt the above multi-granularity approach of text processing, there are four questions that need to be considered as follows:

• 1. How many levels of granularity are required?

• 2. Is text clustering required towards the reduction of data size through modularizing a textual data set?

• 3. In each level of granularity, how many information granules are involved?

• 4. At which level of granularity should the bag-of-words be used for transforming textual data into structural data?

With regard to question 1, the number of granularity levels partially depends on the type of text. In other words, text can be of different scalability, such as documents, comments, and messages. Documents usually do not have any word limits, and thus can be very long and complex resulting in massive dimensionality, if information granulation is not adopted. However, documents are generally well structured leading to a more straightforward way of information granulation based on different levels of headings, e.g., sections and subsections. In addition, paragraphs in each section/subsection generally still need to be divided further into passages/sentences towards reaching the bottom level of granularity for words, which indicates that the number of granularity levels is generally greater than the number of heading levels in a text document.

Comments are typically involved on any web platforms, such as social media, forums, and e-learning environments. In this context, comments are usually limited to a small number of words, e.g., 200 words. Therefore, the dimensionality issue mentioned above is less likely to arise comparing with documents processing. However, comments are typically not structured, which results in the difficulty in information granulation. In this case, the number of granularity levels depends highly on the complexity of text, i.e., the top level of granularity may be paragraphs or passages, while the bottom level is typically words.

Messages are also typically involved on web platforms, but the number of words is generally limited to a few words/sentences, unlike comments. Therefore, the issue on massive dimensionality is much less likely to arise, but messages, similar to comments, are not well structured, which also results in the difficulty in information granulation. In this case, the number of granularity levels also depends highly on the complexity of text, i.e., the top level of granularity may be sentences or phrases with the bottom level consisting typically of words.

With regard to question 2, text clustering is needed typically in two cases. First, when the training data is large, it is very likely to involve a large total number of words resulting in the massive dimensionality problem. In addition, large training data are also likely to contain instances in different contexts, which make a learning task less focused and thus shallow. Second, when the textual data are in the form of documents, each document would usually contain much more words than a comment or a message, which is still more likely to result in the massive dimensionality problem. Therefore, in the above two cases, text clustering is highly required towards the reduction of data dimensionality and having more focused learning in depth.

With regard to question 3, the number of information granules involved in each level of granularity depends on the consistency of structure among instances of textual data. For example, a training set of documents can be of the exactly same structure or different structures. In the former case, information granulation for each of the documents in a particular level of granularity is simply undertaken based on the document headings in the corresponding level, e.g., information granulation in level one is simply done by having each heading 1 with its text contents as an information granule in this level of granularity. In the latter case, the number of information granules needs to be determined based upon the structure complexity of the documents on average. This is very similar to the problem of determining the number of clusters on the basis of the given training instances. In this context, each information granule can be interpreted as a deterministic/fuzzy cluster of training instances of high similarity. For textual data, each information granule would represent a cluster of sub-instances of textual training instances.

With regard to question 4, it is highly expected that the bag-of-words approach is not adopted until each information granule in a particular level of granularity is small and simple enough. In this case, the dimensionality of training data from each information granule (cluster) is much reduced comparing with traditional approaches of text processing, which involve direct use of bag-of-words on the basis of original textual data. For example, a section may have a number of sub-sections. In this context, the first paragraph is generally aimed at outlining the whole section, which is typically short and simple, so bag-of-words can be used immediately at this point for transforming the text of this paragraph or it is used shortly following a simple decomposition of this paragraph. However, for all the other paragraphs in this section that directly belong to its subsections, it is not expected to adopt bag-of-words immediately at this point, since these paragraphs still need to be moved into other granules located in the next deeper level of granularity.

The multi-granularity approach of text processing is illustrated in Fig. 3 This illustration is based on the following scenario: each document is a research paper, which consists of four main sections, i.e., Sects. 1, 2, 3 and 4. Also, Sect. 3 contains two subsections, i.e., Sects. 3.1 and 3.2. In addition, an abstract is included as an independent part of text in each research paper.

Fig. 3

Fuzzy information granulation for text processing

Figure 3 indicates that the parent of an information granule may not necessarily be located in a direct upper level of granularity. For example, an abstract is an information granule that belong to the granularity of paragraphs but the parent of the information granule (abstract) is located in the top level of granularity (paper). In addition, a section may consist of several subsections, but the first paragraph in this section typically directly belongs to this section rather than any subsections.

On the other hand, it is a normal phenomenon that the number of paragraphs involved in each section, especially for different documents (papers), is not deterministic. Therefore, information granulation in the level of granularity for paragraphs would be considered as a fuzzy granulation problem, since it is not deterministic to decide the number of information granules (paragraphs) provided from each section/subsection. In practice, it is even very likely to have different documents with different structures. From this point of view, the decision on the number of information granules in the level of granularity for sections/subsections is not deterministic either, and thus, it is also considered as a fuzzy granulation problem. On the basis of the above descriptions, in the last two levels of granularity for sentences and words (see Fig. 3), respectively, the information granulation also needs to be undertaken through fuzzy approaches, in terms of deciding the number of bags of sentences/words (BOS/BOW).

As mentioned in Sect. 2.4, granular computing involves both granulation and organization. In general, the former is a top–down process and the latter is a bottom–up process. Decomposition of a text document into smaller granules belongs to granulation. Following this granulation, organization is required to get the final classification for test instances, i.e., documents. In this context, as shown in Fig. 3, there are a number of granules in each level of granularity, and each of the information granules is typically interpreted as a fuzzy cluster. In the testing stage, each test instance (document) is divided recursively into sub-instances which are located in different levels of granularity. In each level of granularity, each sub-instance is related to several particular information granules, depending if the parents of the particular information granules relate to the parent of the sub-instance, and each sub-instance is also assigned a certain degree of fuzzy membership to each of the related information granules (fuzzy clusters), following the fuzzification step illustrated in Sect. 2.1.

Furthermore, each sub-instance is inferred by these related fuzzy information granules towards finalising the fuzzy membership degree of the sub-instance to each of the given classes (e.g., positive and negative), following the inference step (that consists of application, implication, and aggregation), as illustrated in Sect. 2.1. Finally, the fuzzy membership degrees of these sub-instances (to all of the given classes) need to be aggregated through disjunction towards providing an overall degree of fuzzy membership (to each of the classes) for the parent of these sub-instances. For example, a sentence S has two sub-instances $W_1$ and $W_2$ located in a lower level of granularity and S belongs to one of the two classes: positive and negative. In this case, if the fuzzy membership degrees of $W_1$ to the positive and negative classes are 0.7 and 0.3, respectively, and the degrees of $W_2$ to the two classes are 0.5 and 0.5, respectively, then the fuzzy membership degrees of S to the two classes are 0.7 and 0.5, respectively.

On the basis of the above paragraph, except for the top and bottom levels of granularity, each of sub-instances in a particular level would be given two sets of fuzzy membership degrees. In particular, one of the set of fuzzy membership degrees is provided from disjunction of the fuzzy membership degrees of the sub-subinstances of a particular sub-instance and the other set of the membership degrees is provided from the inference by the related granules (fuzzy clusters) in this level of granularity. However, the appearance of the two sets of fuzzy membership degrees raises the question: how are the two sets of fuzzy membership degrees combined towards having an overall set of fuzzy membership degrees for each sub-instance in each level of granularity (except for the top and bottom levels)? This research direction is further discussed in the following section.

In terms of the interpretation of prediction results, from each level of information granularity, the fuzzy membership degrees of each sub-instance to all of the given classes are shown explicitly. In addition, the hierarchical relationships between a sub-instance and each of its sub-subinstances can be shown clearly. Therefore, the final result of classifying a test instance can be derived implicitly through the bottom up process as described in the above two paragraphs. This derivation can also be described in natural language to facilitate interpretability; for examples, an output at paragraph level could be expressed as “this paragraph contains 3 positive sentences and 2 negative sentences”. In addition, the fuzzy membership degrees can also be given as an output for each of the sentences in the paragraphs based on which the above output was created.

5 Conclusions

In this paper, we positioned the research in sentiment analysis in the context of granular computing, based on the experimental results on interpretability reported in Liu and Cocea (2017a) and presented in Sect. 3.2. In particular, we stressed the role of fuzzy information granules in dealing with the issue on interpretability of computational models for sentiment analysis, and proposed a multi-granularity approach of text processing through fuzzy information granulation. In other words, traditional approaches of text processing are typically in the form of single-granularity learning, since feature extraction just involves extracting each single word from text through the use of the Bag-of-Words method. In this paper, we have turned single-granularity learning to multi-granularity learning towards more effective and efficient processing of textual data.

This paper also explored why and how the nature of fuzzy rule-based approaches makes it suitable to deal with linguistic uncertainty and interpret the results of sentiment predictions. In addition, this paper also provided an overview of granular computing concepts and techniques in the setting of set theory and the practical importance for advancing artificial intelligence, computational intelligence, and machine learning.

In the future, it is recommended to focus on approaches for multi-granularity processing of sentiment data and other types of textual data in the setting of granular computing. In particular, the four questions raised in Sect. 4 are worth to be considered towards effective granulation of fuzzy information and effective determination of the number of granularity levels and the number of information granules involved in each level of granularity. The number of granularity levels and the number of information granules involved in each level of granularity do not only impact on the depth of learning for sentiment prediction but also on the interpretation of prediction results. In other words, increasing the above two numbers can increase the depth of learning, but may make it more difficult to interpret the derivation of prediction results through a bottom up process (from the bottom level of granularity to the top level), which indicates the importance of effective determination of the two numbers.

In addition, computing with words, which is proposed in Zadeh (2002) and a principle motivation of fuzzy logic, will be explored towards advancing the proposed multi-granularity approach of text processing. In fact, it is much easier to classify words or small phrases than to classify sentences, paragraphs or even documents, especially in the context of polarity classification. In particular, each single word or small phrase can be classified depending on its role and position in a sentence, i.e., some words are more important than other words in a sentence. Following the classification of words/phrases, sentences can be classified through weighted voting of the word classifications, i.e., a sentence can be given a degree of fuzzy membership to the positive/negative class. On this basis, classifying a higher level of instance can be undertaken through the bottom up aggregation described above.

Furthermore, as mentioned in Sect. 3, clustering may be required towards the reduction of data size through modularizing a textual data set. This would be another direction on investigating different clustering techniques towards effective decomposition of a training set of textual instances into a number of modules, to achieve parallel processing of different modules of the training set for speeding up the process of learning. In the case that new data instances are added into a module of the training set, it is also necessary to consider how to involve incremental learning to avoid starting the learning process from the beginning.

In addition, regarding the question raised in Sect. 3: how are the two sets of fuzzy membership degrees combined towards having an overall set of fuzzy membership degrees for each sub-instance in each level of granularity (except for the top and bottom levels)? It is necessary to consider which one of the two operations (conjunction and disjunction) should be taken between the two sets of fuzzy membership degrees, towards having an overall set of fuzzy membership degrees for each sub-instance in a particular level of granularity, i.e., the minimum or the maximum of the two fuzzy membership degrees (from the two sets, respectively) for each class should be chosen as the overall degree of fuzzy membership to the class.

In summary, in this paper, we positioned the research in the area of sentiment analysis in the context of granular computing and fuzzy logic by proposing a fuzzy information granulation approach. The proposed approach not only facilitates interpretability, but is also in line with the requirements of big data processing. We highlighted several research directions that present challenges and opportunities in this research area.