1 Introduction

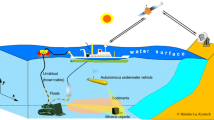
More than half of Earth’s surface is situated in the deep ocean, covered by several hundred or several thousand meters of water above it. However, only very little of this largest surface portion of Earth has been explored, because accessing the deep sea is challenging. Among the different sensing and exploration technologies, optical images are attractive because of their resolution, and because they are well-suited for human interpretation and do not require physical contact for data collection. On land and in space, the rapid growth of optical imaging techniques enables excellent quality photogrammetric surveys. Nowadays hundreds of satellites and airborne imaging platforms are frequently updating high resolution imagery which is playing a fundamental role in the modern society. Image-based mapping of the surface even is an important step in planetary explorations and even the Moon and Mars surface have been visually charted. Unfortunately, all these matured solutions cannot be directly transferred to deep ocean mapping. Optical imaging in the deep ocean not only requires the camera to deal with the extremely high water pressure as well as navigation in a satellite-denied environment, but also adequate artificial lighting to illuminate the scene in the permanent darkness (see Fig. 1). Besides special technical necessities, deep sea mosaicing needs effective image restoration algorithms to remove strong water attenuation, scattering and lighting patterns for producing high-quality data products.

Fig. 1
figure 1

GEOMAR AUV ANTON (Girona 500) performing subsea visual mapping tasks in the darkness with its own lighting offshore Norway. The co-moving light source creates a light cone in water, illuminates the seafloor non-homogeneously and forms up an artificial pattern in image

Full size image

1.1 Deep Sea Exploration Platforms

To carry out imaging in the deep ocean, imaging systems have to be brought to location and navigated to scan a survey area. In this article we focus on dynamic platforms and omit stationary observatories. Dynamic platforms for deep sea operations can roughly be categorized into four basic types of vehicles: Remotely Operated Vehicles (ROVs), Autonomous Underwater Vehicles (AUVs), Human Occupied Vehicles (HOVs), and towsleds (see Fig. 2). They can be classified into two major groups according to their power supply: Cabeled and uncabeled platforms. Cabeled platforms are connected to operating ships or surface stations, such as ROVs (Drap et al. 2015; Johnson-Roberson et al. 2010). They are tethered underwater platforms electrically connected to the ship, all control commands and signals are transmitted between platforms and the operators via these cables. Additionally, more passive, towsleds are also often used for deep ocean imaging: they can either be remotely powered and transmit signals directly to the support vessel via cables (Barker et al. 1999; Lembke et al. 2017; Purser et al. 2018), or operate independently of the ship (Fornari and Group 2003; Jones et al. 2009). Uncabeled platforms refer to untethered underwater vehicles (UVs), including AUVs (Iscar et al. 2018; Kunz et al. 2008; Singh et al. 2004; Yoerger et al. 2007) and HOVs. AUVs are unoccupied underwater robots which are fully controlled by their onboard computers. HOVs are crewed craft that bring a few passengers directly underwater for limited periods of time. Uncabeled platforms survey the ocean depths without any attached cables thus they are battery powered. They have limited deployment endurance that mainly depends on the platforms’ energy budget (or living supplies for HOVs).

Because of the poor underwater visibility conditions, all these platforms have to be operated close to the seafloor, leading to small footprints and mapping speeds in the order of a hectare per hour or less (Kwasnitschka et al. 2016). Also diving up and down to great depths takes several hours and so large scale benthic visual maps require very long missions. ROVs, HOVs and towsleds all demand labor intensive operation, and, whenever cables are in the water, very careful coordination is mandatory to avoid the surface vessel’s propellers. Often, safety guidelines forbid using more than one cabled device in the water at the same time, making parallelization difficult. In contrast, in the case of AUVs, multiple fully automatic vehicles can work together or in parallel for vast deep ocean mapping tasks.

Fig. 2
figure 2

Examples of four different types of platforms which been employed for deep sea mapping. From left to right: ROV (GEOMAR KIEL 6000), AUV (GEOMAR ABYSS Tiffy), HOV (GEOMAR JAGO) and towsled (OFOS frame)

Full size image

1.2 Overview of Deep Sea Visual Mapping

Deep sea imaging has a long history since the second world war. Pioneering work in deep sea photography was performed by Harvey (1939), using a pressure chamber enduring two miles of water depth. At that time, the basic composition of a deep sea imaging system was already defined: camera, pressure housing and artificial illumination. Early examples implemented deep sea photo mosaicing for visualizing the sunken submarine Thresher (Ballard 1975) and the famous sunken ship Titanic (Ballard et al. 1987). At that time, digital image processing was not available, researchers manually pieced photos together to create larger mosaics. Nowadays, quantitative underwater visual mapping has been deployed for wide applications in the deep sea scenario: (1) geological mapping; (Escartín et al. 2008; Yoerger et al. 2000) created mosaics for hydrothermal vents and spreading ridges, assessments of ferromanganese-nodule distribution (Peukert et al. 2018) (2) biological surveys; (Corrigan et al. 2018; Lirman et al. 2007; Ludvigsen et al. 2007; Simon-Lledó et al. 2019; Singh et al. 2004) used them to map benthic ecosystems and species. (3) in archaeology; (Ballard et al. 2002; Bingham et al. 2010; Foley et al. 2009; Johnson-Roberson et al. 2017) documented ancient shipwrecks via mosiacs. (Gracias and Santos-Victor 2000; Gracias et al. 2003) applied charted mosaics for later (4) navigation purposes. (5) underwater structure inspection; (Shukla and Karki 2016) produced mosaics to inspect underwater industry infrastructure.

Early works mainly demonstrate 2D subsea mosaicing in relatively small areas, directly compiled from image stitching (Eustice et al. 2002; Marks et al. 1995; Pizarro and Singh 2003; Vincent et al. 2003). At that time, lighting issues have already been considered, compensation methods have also been demonstrated later in some large area mapping tasks (Prados et al. 2012; Singh et al. 2004). Moreover, recently 3D photogrammetric reconstruction (Drap et al. 2015; Johnson-Roberson et al. 2010, 2017; Jordt et al. 2016) by using structure from motion (SfM) (Hartley and Zisserman 2004; Maybank and Faugeras 1992) or simultaneous localization and mapping (SLAM) (Durrant-Whyte and Bailey 2006) are providing more advanced 3D mosaics.

Traditionally, vision systems are designed for inspection or exploration purposes. A visual mapping system requires the camera not only to “see” the subsea, but also to capture images according to a well understood photogrammetry model that allows measuring with high accuracy. For early systems, and even for some systems of today, photogrammetric mapping was however not a key design goal, leading to the problem that cameras often suffer from refractive distortions at the housings. In case the overall system cannot be considered central anymore (pinhole model), calibration is additionally complicated by the bulky hardware. Desirable geometric properties and hardware design considerations for a deep sea imaging system for accurate mapping, will be discussed in Sect. 2. On top of the refraction issues, captured images usually suffer from several water and lighting effects: (1) loss of contrast and sharpness due to scattering, (2) distorted color by attenuation and (3) uneven illumination generated by co-moving artificial light sources, all of which are unsuitable for creating mosaics directly. In the subsequent Sect. 3, image restoration methods are surveyed which can be utilized to generate a high quality subsea mosaics with uniform and correct color texture. At the end, in Sect. 4, missing pieces for deep sea mapping are identified and open issues are discussed.

2 Deep Sea Imaging System Design

A deep sea imaging system usually consists of a camera, a water proof housing with a window and an artificial illumination system. Many commercial cameras on the market are able to acquire high definition images, but they might still be difficult to use for visual mapping, as is discussed in this section.

2.1 Camera Housings and Optical Interfaces

As water pressure increases by about 1 atmosphere for every 10 meters of depth, deep sea camera systems are typically protected by a housing with a thick transparent window (e.g. glass or sapphire) against the salt water and high pressures. The two most common interfaces for underwater imaging systems are flat ports and dome ports. However, also other constructions, including upcoming pressure-proof deep ocean lenses employed directly in the water or cylindrical windows exist, but have not been used extensively for deep seafloor mapping so far. Flat ports are being widely employed in underwater photography due to a relatively cheap and easy manufacturing process. Flat refractive geometry has been intensively studied in both photogrammetry (Kotowski 1988; Maas 1995; Telem and Filin 2010) and computer vision (Agrawal et al. 2012; Treibitz et al. 2011), many methods have been proposed to calibrate the flat port underwater camera systems (Jordt-Sedlazeck and Koch 2012; Lavest et al. 2000; Shortis 2015) and to consider refraction correction during the visual 3D reconstruction pipeline (Jordt et al. 2016; Chadebecq et al. 2017; Song et al. 2019). However, underwater reconstructions solutions for flat port images are either closed source or do not consider refraction correction in all parts of the reconstruction steps. The community still does not have a complete and mature solution that considers refractive geometry in each step during the entire dense 3D reconstruction pipeline. Several scholars (Kunz and Singh 2008; Menna et al. 2016; Nocerino et al. 2016; She et al. 2019, 2022) point out that dome ports have several advantages over flat ports, they are better suited for visual mapping. She et al. (2022) gives an in-depth overview on refractive geometry with domes and camera decentering calibration.

Fig. 3
figure 3

Left: when the entrance pupil of the camera is precisely positioned at the center of the dome, the principal rays are not refracted because they all pass through the air-glass-water interface orthogonally (She et al. 2019). The complete system can be considered as a normal pinhole camera. Right: An ROV equipped with a deep sea camera rig with multiple dome ports

Full size image

In underwater photography, light rays change direction when they pass interfaces between media with different optical densities according to Snell’s law. For flat ports only the ray perpendicular to the interface is not refracted, and the refraction drastically reduces the field of view of the camera underwater. In dome ports, the situation is different: incoming principal rays will not be refracted if the camera’s optical center is positioned exactly in the center of the dome (see Fig. 3). The remaining intrinsic characteristics, such as lens distortions, can be obtained from standard camera calibration procedures. Therefore dome ports are able to preserve the FOV and focal length of the camera, which is particularly vital for subsea mapping. Compared to a flat port system, a camera behind a dome port produces a larger footprint on the seafloor and requires less photos to cover the same area on the same flying attitude. Additionally, images taken by a large FOV lens tend to perform better in pose estimation than narrow ones (Streckel and Koch 2005), which is even more important in the satellite-denied deep sea environment with challenging external localization. Moreover, dome ports bear less chromatic aberration and can achieve a sharper image (Menna et al. 2017).

Besides optical properties, deep sea devices need to be mechanically stable for operating in high water pressure environments. The thickness requirements of flat port glass for deep sea imaging do not scale well with its diameter and the water depth, allowing only tiny flat ports in the deep ocean, or extremely thick glass. Spherical ports (dome ports) are geometrically more stable as the spherical shape withstands water pressure from different directions symmetrically and equally. Therefore it requires much thinner glass as compared to the flat port for the same pressure. During the mechanical design of the system, one more critical issue is that the camera has to be fixed directly to the port in order to achieve stable optical properties (Harvey and Shortis 1998).

We sample some of the currently available high definition (HD) subsea cameras on the market and list their technical features relevant to deep sea mapping in Table 1. Many of the systems use a dome port nowadays that can avoid refraction when properly centered. Here, e.g. (She et al. 2019) introduced a practical solution to precisely center the camera inside a dome port housing, which enables us to simply assemble a refraction free dome port imaging system (She et al. 2021). Avoiding refraction largely simplifies subsequent processing steps, as existing software can be used that cannot consider refraction. Upcoming lens systems as announced by (ZEISS 2022) even use a lens directly computed for use in water that does not suffer from refraction.

Table 1 A non-exhaustive selection of popular subsea HD camera systems on the market
Full size table

2.2 Lighting System

Light is absorbed when it travels through the water body, and sunlight from the water surface only penetrates the first few hundred meters into the ocean. To illuminate the scene in the absolute darkness of the deep sea, UVs need to bring additional artificial light sources to provide adequate illumination. The co-moving light sources project illumination patterns onto the seafloor and the light cones generate scattering effects that are much less homogeneous than in sunlight: the appearance of deep sea images strongly depends on the geometric relationships between the camera, light source and the object (see Fig. 4).

Fig. 4
figure 4

The appearance of the captured deep sea images is significantly influenced by its particular lighting configuration. Left: two spotlights are on the left and right sides from the camera in the South Pacific Ocean. Right: a light rig with 24 LED arrays are placed 1.9 m on top of the camera in the South Pacific Ocean (Kwasnitschka et al. 2016)

Full size image

These geometric relationships also strongly influence the captured image quality. Close object distances and large separation of lights and camera are beneficial to limit the water effects, especially the backscatter in images (Jaffe et al. 2001; Patterson 1975; Sheinin and Schechner 2016; Singh et al. 2004). However, image footprints become very small with low altitudes, so efficient subsea mapping requires underwater vehicles to fly at higher altitudes in order to cover larger areas. This brings more water volume in front of the camera and leads to stronger light attenuation in the images, as the signal is attenuated exponentially with distance. Flying higher therefore demands more powerful light sources to compensate for this. On the other hand, deep sea robotic platforms have to have a very compact design for being deployable and operable, and the illumination layout usually is strictly limited by the vehicle size and payload. Therefore, at higher altitudes, the limited distance of camera and light forms smaller angles with the seafloor, which introduces heavier backscatter into the image. Recent advances in light emitting diode (LED) technology allow more lightweight and flexible illumination configurations with many small light sources (see Fig. 5), but this creates the question of how to choose a good lighting setup. Multi-LED illumination optimization approaches were suggested (Jaffe 1990; Song et al. 2021b) to tackle this question.

Fig. 5
figure 5

LED has the advantage of lightweight, flexible installation and less energy consumption over traditional Xenon strobes. It is being increasingly employed in modern underwater system design. Left: GEOMAR manned submersible JAGO with multiple LEDs. Right: A newly designed AUV underwater imaging camera system equips with 8 LEDs on a ring shaped frame

Full size image

In traditional underwater photography, scuba divers often use thin color filters (mostly warm colors in ocean water) in front of the lens or flashes to capture aesthetic images (Edge 2012). By suppressing green and blue light such filters relatively amplify the warm parts of the signal, but typically at the expense of requiring much longer exposure times or ISO settings, effectively loosing a lot of the available energy. However, large scale robotic visual mapping must consider energy limitations for scene illumination, in particular uncabled vehicles. (Jordt 2014) illustrates that only 10% of the red light intensity is left after 6.6 m in pure water, so the amount of warm light one is willing to invest into a mission has to be carefully weighed. Details and discussions about using LEDs of different light spectra underwater can be found in Sticklus et al. (2018a, 2018b).

2.3 Localization Systems

Georeferencing of deep-sea data is a difficult challenge, as water blocks electromagnetic signals from navigation satellites, such that UVs cannot be localized using global navigation satellite systems (GNSS) underwater. The deep sea is also inaccessible to divers and it is very challenging and time-consuming to setup external instruments in several kilometers water depth, making good localization a major challenge in the deep sea even nowadays. UVs in shallow water can frequently surface to receive GNSS signal for a position fix, but this is not applicable in deep diving missions. The live GPS reference can be transferred from the support vessels to deep UVs via cables (Salgado-Jimenez et al. 2010; Vincent et al. 2003). The most frequently applied way to achieve absolute positioning is based on runtime differences of acoustic signals through beacons, such as ultra-short-baseline localization (USBL) and long baseline localization (LBL). However, acoustic sensors have a local range underwater and can not be installed like a worldwide GNSS. Rather they are temporarily deployed (LBL) or operated from vessels (USBL). Due to refraction at water layers, multi-path propagation, background noise and other effects, absolute localization errors of tens of meters are not uncommon in practice, which is an order of magnitude higher than robotic visibility in the deep sea. Deep diving UVs usually integrate multiple sensors, such as Doppler velocity loggers (DVL) and inertial navigation systems (INS), and combine them with surface absolute position information to georeference the underwater vehicles (Zhang et al. 2020). Visual SLAM techniques, which have been widely utilized on land, are also being gradually adapted to ocean applications, but are still facing many challenges (Köser and Frese 2020). These dead reckoning (DR) sensors provide differential measurements such that the error accumulates without bound as the vehicle stays underwater. The other sensors which provide partly absolute positioning information, such as pressure sensors (altimeter), compass, inclinometer, and attitude-heading reference systems (AHRS). Their measurements are often integrated and fused (e.g. by Kalman filters) to improve the localization. More details about UV localization techniques are summarized in (Leonard and Bahr 2016; Paull et al. 2013).

Ultimately, all sensors including camera-lighting systems need to be synchronized within a unique time reference and each image must be georeferenced (position and orientation) by fusing global positioning data with measurements of the DR sensors. Since image matching can provide accurate relative pose estimation, utilizing image matching techniques for post-processing can refine the coarse UV localization information (Elibol et al. 2011; Eustice et al. 2008; Negahdaripour and Xu 2002; Woock and Frey 2010). Furthermore, additional constraints such as loop detection and geophysical maps-based correction (Gracias et al. 2013) can also be applied during post processing to further improve the localization data. Examples of deep sea mapping deployments with their imaging and navigation configurations are summarized in Table 2.

Table 2 Selected deep sea visual mapping deployments with their imaging system design details, part of the data migrate from (Kwasnitschka et al. 2016). For cabled platforms, they also get positioning corrections from the surface vessels
Full size table

3 Underwater Image Restoration

Captured subsea images suffer from water and artificial lighting effects that require complex post-processing before creating mosaics (see Fig. 6). Such underwater image processing either utilizes a physical based image formation model or targets at qualitative criteria. The corresponding approaches are named restoration or enhancement, respectively. According to a strict definition, restoration should refer to real world distances and optical properties in order to recover the “true” color as it is seen in air. Dozens of literature surveys and reviews were published with regard to underwater image enhancement or restoration over the past decade (Anwar and Li 2020; Vlachos and Skarlatos 2021; Yang et al. 2019). Ideally, subsea mapping should deliver correct spectral information of the seafloor that enables later scientific usage (e.g. inferring material properties, identification of fauna etc.), which demands a “real” restoration during the image processing and not only an image that looks plausible. Unfortunately, the extra information that is required to achieve this is often not available, in particular in single image restoration methods. These methods thus often utilize prior knowledge or assumptions (e.g. gray world) to infer depth variations and combine the depth proxy with a physical model to restore images. While image enhancement is a very useful technique for many applications, it is very difficult to quantitatively evaluate, and often the suggested way for qualitative evaluation is how much humans like the enhanced image (Mangeruga et al. 2018), i.e. human visual inspection. Therefore, this section does not focus on image enhancement but primarily surveys image restoration techniques.

Fig. 6
figure 6

Around 20m\(\times\)20m area of orthomosaic constructed from 106 images taken by an AUV with artificial illumination in Kiel Fjord, Germany. Left: directly generated from raw images (During capturing, the camera red channel gain was set to a higher number in order to acquire more contrast). Right: generated from restored images (Köser et al. 2021). Image processing is vital for producing high quality subsea mosaics as it restores the correct spectrum information, improves the contrast and removes the uneven lighting, which will benefit the later biological, geochemical, geological and mapping applications

Full size image

3.1 Underwater Image Formation and Approximations

The low level physics of light transport in water are well understood (Mobley 1994; Preisendorfer 1964) when looking at infinitesimally small volumes. Essentially, when light travels through such a small volume, a fraction of the light is absorbed. Another fraction changes direction due to interaction with the water, i.e. by scattering. The direction of the scattering is encoded in a physically- or empirically-motivated phase function, which is a water parameter. Using statistical or physical models, the amount of light leaving a small volume into a particular direction can be predicted from the water parameters and the distribution of the incoming light over all directions. Considering the interactions of all the (infinitesimally) small volumes of an underwater scene at the same time in order to obtain a closed-form solution for image restoration is a challenging, if not impossible, endeavour. Consequently, several approximations to the low-level physical model have been proposed in the literature, including assuming a macroscopic atmosphere-like fog model for shallow water, a single scatter-model for artificial light sources and numerical/discretized simulation of the full problem using Monte-Carlo-based methods. In the following we outline approaches based on these assumptions.

Early works modeled underwater effects (mainly scattering) using a point spread function (PSF) (Mertens and Replogle 1977). Based on the PSF, a group of methods (Barros et al. 2018; Chen et al. 2019; Han et al. 2017; Hou et al. 2007; Liu et al. 2001) synthesize underwater images by generating in-air images of scenes, convolving them by the imaging system’s response at the particular distance and applying the water effects of attenuation and backscatter. The underwater light transmission can then be simplified as a linear system and the restoration is basically a denoised deconvolution on images.

The most commonly adopted underwater image formation approximation for shallow water is derived from the atmospheric scattering model (Cozman and Krotkov 1997), which describes the underwater image I(x) as a linear combination of the attenuated signal and the backscatter:

$$\begin{aligned} I(x) = J(x) \cdot T(x) + B_{\infty } \cdot (1 - T(x)) \end{aligned}$$
(1)

where J(x) represents the object color without any perturbation at pixel location x and \(B_{\infty }\) denotes the “pure” water color. The transmission map T is often expressed by \(T(x) = e^{-\eta d(x)}\), which comprises the water attenuation effect. Here \(\eta\) is the attenuation coefficient and d is the scene distance. Many variations have been developed starting from this formulation for underwater applications. The atmospheric model was initially designed for in-air dehazing applications and it assumes that the scene is seen under the homogenous illumination, ignoring particular water properties. For non-homogeneous illumination cases, T(x) often multiplies with an extra illumination term which approximates the light propagation by Koschmieder’s model (Koschmieder 1924). The basic atmospheric model applies the same coefficient in the transmission and the backscatter term which does not represent the underwater conditions well (Akkaynak and Treibitz 2018; Song et al. 2021a). According to the definition from (Mobley 1994), the attenuation in the transmission is composed of absorption and total scattering. (Blasinski et al. 2014) simplified the backscatter term and extended the total attenuation by the summation of pure water and three other particle absorption coefficients. (Akkaynak and Treibitz 2018) revised the model by applying different attenuation coefficients associated with the direct signal and the backscatter.

Another well known underwater image formation approximation, mostly used for settings with artificial light (e.g. deep ocean) is the Jaffe–McGlamery (J–M) model (Jaffe 1990; McGlamery 1980). It composes the underwater image by direct signal, forward scattering and backscatter components. It describes the entire underwater light transportation from light sources to the object and finally to the camera. Therefore it better suits the settings in which the scene is illuminated by artificial light sources and utilizes the knowledge of relative geometry between the camera, the underwater scene and the light sources. Several modifications have been proposed to improve the model to adapt to multiple and non-isotropic spotlights (Bryson et al. 2016; Sedlazeck and Koch 2011; Song et al. 2021a).

In the J–M model, the scattering components are complicated as scattered light does not only cumulate along the distance, but also varies with respect to the direction into which the ray is scattered. Most work considers only single scattering that is assumed symmetric around the incident light ray, which is formulated by a scattered angle dependent volume scattering function (VSF) or its corresponding phase function. In early oceanography optics, (Petzold 1972) built an instrument and carefully measured the VSFs for three types of oceanic water (very clear, productive coastal and turbid water) over almost the whole range of scattering angles. Later, several approaches (Lee and Lewis 2003; Narasimhan et al. 2006; Sullivan and Twardowski 2009; Tan et al. 2013) have been developed to measure the VSFs for different types of water. Besides the direct oceanographic measurement of VSF, many analytic formulas of phase functions have been proposed to describe the angular scattering distribution of the photons interacting with different sizes and properties of particles. The Mie phase function (Mie 1976) and the Rayleigh phase function (Lord 1871) formulate the scattering of light when interacting with small spherical particles, which have been intensively utilized in atmospheric research. However, (Mobley 1994) stresses the issue that a sphere might not be a good representative for the shape of aquatic particles. (Chandrasekhar 2013) introduced a low-order polynomial phase function relating to planetary illumination, due to its simplicity, it has been used in several photometric stereo methods for estimating the water scattering phase function. Another popular analytic model is the Henyey-Greenstein (HG) phase function which was initially proposed for simulating the scattering by interstellar dust clouds and has later been widely adopted in many fields, one reason being its simplicity and tractability. (Mobley 1994) pointed out that obvious discrepancies exist between the HG phase functions and real oceanic measurements. One property of HG is that depending on the value of its free “g”-parameter it can only represent forward or backward scattering. A linear combination of two HG phase functions, which is also called two-term HG (TTHG) phase function, was proposed to address this drawback (Haltrin 1999, 2002). Alternatively, a more realistic Fournier-Forand (FF) phase function (Fournier and Forand 1994) and its later form (Fournier and Jonasz 1999) have been proposed which yield increasing attention in oceanography.

After this short overview of different concepts, we start looking in depth into the “fog model” based methods, before we come to the other approaches.

3.2 Atmospheric Fog Approximation based Methods

These methods assume the scene is illuminated by sunlight. But rather than explicitly modeling the sun, it is assumed that the object is illuminated uniformly and that the intensity received at the camera is a blend of attenuated object color and backscatter. The backscatter is often represented by a uniform background color and the attenuation between object and camera is induced by a transmittance map that depends on the distance to each scene point. Most of these methods are proposed for single image restoration which is ill-posed: They require additional distance measurements (e.g. a depth map) or have to guess a proxy depth map derived from priors for the restoration. Generally, these methods can be concluded to three basic steps: scene distance (or equivalent representations) estimation, backscatter removal and transmission map estimation.

3.2.1 Scene Distance Estimation

Scene distance (depth maps) is essential in physical model based restoration approaches. It is the prerequisite to estimate the transmission image, to correct the attenuation and leverage the backscatter removal according to the image formation model. Depth information can be directly acquired using external devices e.g. a Lidar (He and Seet 2004) or acoustic sensors (Kaeli et al. 2011), estimated from images pairs via stereo matching (Akkaynak and Treibitz 2019; Geiger et al. 2010; Shortis et al. 2009) or images with structured light (Bodenmann et al. 2017; Narasimhan and Nayar 2005; Narasimhan et al. 2005; Sarafraz and Haus 2016) or images captured by light-field cameras (Tao et al. 2013; Wang et al. 2015). Depth information can also be estimated from multiple measurements: A group of methods (Hu et al. 2018; Schechner et al. 2001; Schechner and Karpel 2004; Treibitz and Schechner 2008) use polarization filters and acquire multiple images with varying polarizer orientations to infer depth information from estimated backscatter. Nayar and Narasimhan (1999) estimates the structure of a static scene from multiple images with different illumination conditions. Structure-from-motion (SfM) has also been applied to estimate the depth map (Sedlazeck et al. 2009) but it requires scale information, e.g. from a stereo system, from reference targets in the scene with known sizes or from navigation data. Deducing depth from multiple images requires the images to have sufficient overlap and baseline, which is not applicable for single image settings. However, it is suitable for visual mapping as this is also the prerequisite to stitch images.

In case depth information is not available directly, it can be inferred or approximated as often done in single underwater image restoration approaches. A popular idea is related to using the dark channel prior (DCP) (He et al. 2010), which was applied succesfully for single image dehazing in white or bright grey fog or smoke. It assumes that in a haze-free image most of the local patches should contain at least one color channel with a very low intensity, but in a real image in fog, the more fog is in between the observer and the scene, the more the “dark” channels appear brighter. DCP inspired the development of single image dehazing methods and later this scene-depth derivation method has also been intensively applied in single underwater image enhancement (Chao and Wang 2010; Chiang and Chen 2011; Li et al. 2016a, b; Mathias and Samiappan 2019; Yang et al. 2011; Zhao et al. 2015). Nevertheless, due to the severe attenuation of red light in underwater images, the standard DCP result does not fit for underwater scenarios and requires some modifications: (Carlevaris-Bianco et al. 2010) computes the intensity difference between the red channel and the maximum of the green and blue channels per-patch which terms maximum intensity prior (MIP). (Drews et al. 2013) proposes Underwater DCP (UDCP) which omits the red channel and apply DCP only in the green and blue channels. Later (Galdran et al. 2015) extends the UDCP with the inverted red channel, namely the Red Channel Prior (RCP). Lu et al. (2015) discovered that ω in a turbid underwater images is not always the red channel but is occasionally the blue channel, it uses these two channels through a median operator to define the underwater median DCP (UMDCP). (Łuczyński and Birk 2017) inverts red and green channel to calculate the DCP by shifting the RGB coordinate system of underwater images from blue to white. Peng et al. (2018) suggests a generalized DCP (GDCP) based on the depth-dependent color change, via calculating the difference between the ambient light and the raw intensity.

Besides DCP and its derivatives, some other priors are also proposed as a proxy to indicate depth variation in the image. (Peng et al. 2015) leverages the image blurriness which is increasing with distance and suggests the blurriness prior, later (Peng and Cosman 2017) combines it with the MIP and proposes the image blurring and light absorption (IBLA) prior. (Fattal 2014) discovers that pixels in a small image patch distribute along a straight line in RGB color space, known as the Color-Lines Prior (CLP). The Color Attenuation Prior (CAP) (Zhu et al. 2015) creates a linear model for depth estimation according to the brightness and the saturation of the image. (Berman et al. 2016) introduces a non-local prior, the Haze-Lines Prior (HLP), which suggests that pixels in a image can be clustered into few clusters. Pixels which belong to the same cluster in a hazy image are distributing along a line in RGB color space and all these lines pass through the background light. Bui and Kim (2017) proposes the Color Ellipsoid Prior (CEP) based on the observation that the vectors in the RGB color space of a small patch from hazy images are clustering in a ellipsoid. In the underwater scenario, image degradation is influenced not only by the object distance but also by the wavelength dependent attenuation, which the standard HLP does not consider. Wang et al. (2017b) claims that the pixels in the same color cluster will no longer form a straight line but a power function curve in RGB space, which is named Attenuation-Curve Prior (ACP). Afterwards, (Wang et al. 2017a) improves the ACP to the adaptive ACP (AACP), which is more general for different kinds of imaging environments.

Finally, learning based depth estimation approaches also been intensively studied on land (Eigen et al. 2014; Godard et al. 2019; Li and Snavely 2018; Pillai et al. 2019) and have later been transferred to the underwater field (Gupta and Mitra 2019; Zhou et al. 2021). However, similar to other prior based methods, learning based approaches are able to provide plausible relative object relations, but the derived depth information is not in physical units and depends on the training data.

3.2.2 Backscatter Removal

As an additive effect, backscatter introduces a loss of contrast or a foggy appearance that increases with distance. The total backscatter that the camera sees is a cumulative effect which sums up all the scattered light along a viewing direction through the medium between the camera and the object. Since it is superimposed onto the image, subtracting the backscatter component (if known) can effectively improve the image contrast. This backscatter removal issue has been studied in image de-hazing for a long time and current underwater methods mostly are based on them. Physical model based de-hazing mechanisms require the knowledge of the scene depth, therefore de-hazing is highly correlated to the depth estimation and, vice versa, scene depth can be achieved as a by-product once de-hazing is solved.

This paper classifies image de-hazing solutions into four main categories: Hardware-based, multiple-image based, prior-based approaches and learning-based.

  1. 1.

    Hardware-based approaches use additional devices for image acquisition, for instance, directly blocking the backscattered signal through range gated imaging (Li et al. 2009; Tan et al. 2005, 2006), taking at least two static scene images with different orientations of a polarization filter in front of the camera (Schechner et al. 2001, 2003; Schechner and Karpel 2004, 2005; Schechner and Averbuch 2007; Shwartz and Schechner 2006) or the light source (Dubreuil et al. 2013; Hu et al. 2018; Huang et al. 2016; Treibitz and Schechner 2006, 2008), capture images by a light field camera system (Skinner and Johnson-Roberson 2017) or a stereo imaging system (Roser et al. 2014).

  2. 2.

    Multiple-image approaches have first been proposed for in-air applications which take multiple images under varying visibility conditions and scene depth, and backscatter is estimated simultaneously during the optimization (Liu et al. 2018; Narasimhan and Nayar 2002, 2003a; Tarel and Hautiere 2009), similar underwater approaches have been introduced in Sect. 3.4. These methods are developed for webcam like stationary settings. They not only require a static camera, but also demand significant changes between different conditions. When illumination configurations are relatively fixed, the non object image contains the complete backscatter information. (Fujimura et al. 2018; Tsiotsios et al. 2014) assume that images share the same backscatter component and subtract the non-object image from the underwater images to remove the backscatter. In shallow water, this solution is difficult to apply since the amount of scatter observed depends on the camera orientation relative to the sun as well as the water depth through which the sunlight has passed. However, in deep sea mapping scenarios most of UVs carry a fixed artificial lighting system and often fly on a fixed, relative high altitude, therefore the backscatter pattern is stable over images. Additionally, it takes hours for UVs to dive down to the seafloor, during this period of time, large amount of pure water images with only backscatterred lighting patterns are acquired, which is ideal for backscatter removal (Bodenmann et al. 2017; Köser et al. 2021).

  3. 3.

    Prior-based approaches are mostly single image approaches in shallow water with sunlight. When the scene geometry and distance is exactly known (Hautière et al. 2007; Kopf et al. 2008; Narasimhan and Nayar 2003b), backscatter can be directly fitted by an analytical model, or separated from a raw image by Independent Component Analysis (ICA) (Fattal 2008). If the scene geometry is not measured, prior knowledge can be used to obtain an approximate depth map. According to the most commonly used atmospheric model in Eqt. 1, the backscatter component of the image is expressed as \(B_{\infty } \cdot (1 - T(x))\). Consequently, the background light (BL) \(B_{\infty }\), which is also named background color, veiling light, ambient light or water color in the literature, is needed for computing the backscatter component. Usually, pixel that do not see an object (with maximum depth) will be picked as the BL (Kratz and Nishino 2009). Most of the priors were initially proposed for in-air de-hazing, such as DCP, CLP and HLP (see Sect. 3.2.1), they often take the uniform BL assumption over the entire field of view. DCP based in-air de-hazing approaches select the brightest pixel (in the image or dark channel) from a far scene as the BL (He et al. 2010; Tan 2008). Here, bright objects in the scene can lead to erroneous results. Several adaptations were developed for more accurate BL selection, such as using hierarchical quadtree ranking (Emberton et al. 2015; Kim et al. 2013; Park et al. 2014a; Peng and Cosman 2017; Wu et al. 2017), patch-based selection (Chiang and Chen 2011; Serikawa and Lu 2014), estimated from different priors or using extended models (Akkaynak and Treibitz 2019; Carlevaris-Bianco et al. 2010; Henke et al. 2013) and additional selection according to some other rules (Ancuti et al. 2010; Li et al. 2017; Wang et al. 2014; Zhao et al. 2015). Besides that, the BL can also be detected from the smoothest spot on the background for in-air de-hazing (Berman et al. 2016; Fattal 2014) and underwater backscatter removal (Berman et al. 2017, 2020; Li and Cavallaro 2018; Lu et al. 2015; Peng et al. 2015; Peng and Cosman 2017; Wang et al. 2017a). Moreover, using an unique value to represent backscatter assumes that the illumination is uniform, which is an approximation from outdoor hazy scenes. For the deep sea scenario the backscatter depends on the lighting configurations (Song et al. 2021a) and significantly varies with image position. Using a local estimator to provide a more accurate backscatter map is desired for precise artificial lighting backscatter removal (Ancuti et al. 2016; Li and Cavallaro 2018; Tarel and Hautiere 2009; Treibitz and Schechner 2008; Yang et al. 2019).

  4. 4.

    Learning-based image dehazing has become very popular in recent years (Cai et al. 2016; Fu et al. 2017; Liu et al. 2018, 2019; Ren et al. 2018; Zhang et al. 2017a). But these methods generally have the problem that the processing quality strongly depends on the training data, it is difficult to predict how well it generalizes to other scenes.

Backscatter is actually a macroscopic effect that results from the volume scattering function, or the phase function, of the medium (Mobley 1994). These functions characterize in which directions an incoming photon is scattered when it interacts with the medium. In ocean water, this function has a peak in backwards direction, therefore backscatter is an important effect. But photons are also redirected into other directions. In particular also small optical density variations (due to temperature, pressure or salinity fluctuations) of the medium lead to tiny direction changes of photons. On a macroscopic level, all these effects are summarized as forward scattering, leading to distance-dependent unsharpness of the image, since photons silghtly deviate slightly from the direct line of sight. In simulation, forward scattering is often modeled by analytical filtering (Fujimura et al. 2018; Negahdaripour et al. 2002; Murez et al. 2015), that incorporates the underwater optical properties and convolves the image with the appropriate blur kernel. When removing forward scattering, PSF (or its frequency domain form MTF) is often estimated (Barros et al. 2018; Chen et al. 2015, 2019; Han et al. 2017; Hou et al. 2007; Liu et al. 2001), and one tries to reverse the effects by deconvolution. Other filters such as joint trilateral filter (JTF) (Serikawa and Lu 2014; Xiao and Gan 2012), self-tuning filter (Trucco and Olmos-Antillon 2006), trigonometric bilateral filter (Lu et al. 2013) and Wiener filter (Wang et al. 2011) also been used to describe the forward scattering effect. However, these methods are essentially spatially varying image sharpening operators that can introduce artifacts. Hence, many image restoration methods simply ignore forward scattering.

3.2.3 Transmission Estimation

From Eq. 1, after removing the additive backscatter in the image, the transmission map is estimated to restore the scene radiance from the direct signal. Similar to the Retinex model for artificial lighting compensation introduced in Sect. 3.3, the direct signal in underwater image formation is represented by the multiplication of the transmission and the object reflectance. Transmission is reciprocal to the attenuation (Mobley 1994; Preisendorfer 1964), which has to be integrated along the line of sight, leading to an exponential expression based on the Beer-Lambert law and depends to the scene depth and water attenuation coefficient. Therefore, transmission is also strongly correlated to scene distance. Once the attenuation coefficient is obtained, the transmission can be computed for recovering the scene radiance (Akkaynak and Treibitz 2019; Schechner and Karpel 2004).

The attenuation coefficients can either be directly measured by optical instruments like transmissiometers (Bongiorno et al. 2013), or be estimated from the image (Akkaynak and Treibitz 2019; Schechner and Karpel 2004). Jerlov classified global ocean waters into eight types (Jerlov 1968) and measured their attenuation, following his work, the attenuation parameters then can be directly obtained according to the water types (Akkaynak et al. 2017; Solonenko and Mobley 2015). However, once taken transmissiometer or spectrometer measurements might not perfectly apply to all captured images, even the same type of water may have varying attenuation in different season and depth, and coefficients vary with wavelength. Additionally, the image color depends on the spectral sensitivity of the camera, which is usually not known. In this case, attenuation coefficients can be derived from in-situ images by photographing a reference target with known spectrum at different known distances (Blasinski et al. 2014; Winters et al. 2009).

If neither scene distances, nor the reference target are available, an approximate scene layout can be derived from priors to estimate the transmission. For example transmission estimation make use of DCP (Chao and Wang 2010; Chiang and Chen 2011; Serikawa and Lu 2014; Yang et al. 2011; Zhao et al. 2015), MIP (Carlevaris-Bianco et al. 2010; Li et al. 2016b), UDCP (Drews et al. 2013; Emberton et al. 2015; Lu et al. 2015), RCP (Wen et al. 2013), CLP (Zhou et al. 2018), HLP (Berman et al. 2017, 2020) and ACP (Wang et al. 2017a, b). The Red channel is the most degraded channel in an underwater image, thus it is also used to estimate the transmission map (Li et al. 2016b).

Per-pixel transmittance estimation is sensitive to the image noise. In order to achieve a dense and accurate transmittance map, post refinement is often needed to improve the transmittance estimation quality. A popular refinement technique is guided image filtering (He et al. 2012), this edge-preserving smoothing operator has been widely applied in transmission map refinement (Berman et al. 2020; Drews et al. 2015; Li et al. 2016b; Wen et al. 2013; Zhou et al. 2021). Other refinement techniques are e.g. median filter (Tarel and Hautiere 2009), fuzzy segmentation (Bui and Kim 2017), Markov random field (Fattal 2008, 2014; Tan 2008), weighted least squares (WLS) filter (Emberton et al. 2015) and image matting (Drews et al. 2013; Chiang and Chen 2011).

3.2.4 Exemplary Systems

This section gives a detailed survey on the representative underwater image restoration pipelines. Their corresponding approaches for estimating depth, backscatter (including BL) and transmission (with refinement) are introduced and summarized in Table 3.

Schechner and Karpel (2004) images the scene through a polarizer at different orientations, the backscatter component is derived from the extreme intensity measurements. Global parameter BL is estimated by measuring pixels corresponding to non object regions, which is later used to derive the transmission map. It is the pioneer work which utilizes the atmospheric model for underwater image restoration.

Trucco and Olmos-Antillon (2006) assumes uniform illumination and low-backscatter conditions, and considers only the forward scattering component. They present a self-tuning restoration filter based on a simplified J–M model. The Tenengrad criterion (average squared gradient magnitude) is measured as the optimization target to determine the filter parameters by a Nelder-Mead simplex search. Image restoration is performed by inverting the filter in frequency domain on the raw image.

Hou et al. (2007) models image formation as the original signal convolved by the imaging system’s response and extends the PSF by incorporating underwater effects. The actual image restoration is then implemented by a denoised deconvolution.

Sedlazeck et al. (2009) first utilizes SfM and dense image matching to generate depth maps for color correction. The BL is defined from the background patch in the image. Based on the atmospheric model, the backscatter and transmission (one attenuation coefficient) are estimated from a set of known white objects seen from different distances.

Chao and Wang (2010) first introduces DCP from He et al. (2010) to underwater image de-scattering. The pixels with highest intensity among the the brightest pixels in the dark channel is picked as the BL. The dark channel of the normalized image is used to estimate the transmission. It removes the scattering effect in the image but the absorption issue still remains unsolved.

Inspired by DCP, (Drews et al. 2013) proposed UDCP which considers the blue and green channels are underwater informative and ignores red channel. It provides a rough initial estimate of the medium transmission which later been refined by image matting. Similar to DCP, the BL is estimated by finding the brightest pixel in the underwater dark channel.

Galdran et al. (2015) inverts the red channel and proposes the RCP for BL and transmission estimation. The BL is picked from the brightest 10% of pixels the one that has lowest red intensity. The transmission map is later refined by using the guided filter.

Emberton et al. (2015) adopts a hierarchical rank-based estimator for backscatter removal. The method exams over three features in the image, UDCP, the standard deviation of each color channel and magnitude of the gradient, to estimate the BL. The transmission map is generated from the UDCP and refined with the WLS filter (Farbman et al. 2008).

Ancuti et al. (2016) uses the DCP over both small and large patches to locally estimate the backscatter, later fuse them together with the Laplacian of the original image to improve the underwater image visibility. These three derived inputs are seamlessly blended via a multi-scale fusion approach, using saliency, contrast, and saturation metrics to weight each input.

Peng and Cosman (2017) computes the blurriness prior according to their previous work (Peng et al. 2015). The BL is also determined from the candidates estimated from blurry regions. Afterwards, the scene depth is estimated based on light absorption and image blurriness and refined by image matting or guided filter. The transmission map then is calculated for scene radiance recovery.

Wang et al. (2017a) omits the depth estimation and acquires relative transmission based on ACP. It first filters the smooth patches with the low total variation (TV), then the homogeneous BL is located where the pixel has considerable differences in R-G and R-B channel; Pixels are classified into attenuation-curves in RGB space and turned into the lines using logarithm, transmission of the red channel is estimated from each line, and refined by WLS filter similar to Berman et al. (2016). The attenuation factor is then estimated to compute B,G transmissions.

Inspired by the illumination estimation method from Rahman et al. (2004), Yang et al. (2019) decomposed the dark channel and extracted the transmission based on the Retinex model. The backscatter light is obtained locally by using Gaussian lowpass filtering of the observed image. Afterwards, a statistical colorless slant correction and contrast stretch is adopted to correct the color.

Akkaynak and Treibitz (2019) applies a revised image formation model (Akkaynak and Treibitz 2018) which formalizes the direct signal and the backscatter components with distinct attenuation coefficients. It first generates the scene depth using SfM. Estimation of the backscatter (BL and backscatter attenuation coefficient) is inspired by DCP, but is based on the darkest RGB triplet and utilizes a known range map. The transmission (direct signal attenuation coefficient) is estimated using an illumination map obtained using local space average color as input.

Bekerman et al. (2020) provides a method for robustly estimating attenuation ratios and BL directly from the image. The initial BL is searched in a textureless background area and is later fine-tuned through an iterative curve fitting minimization. In each iteration the attenuation ratios are calculated accordingly. In the end, the transmission is estimated based on the HLP from Berman et al. (2016) and regularized by a constrained WLS for scene radiance restoration.

Table 3 Underwater image restoration methods with their processing details
Full size table

3.3 Artificial Lighting Pattern Compensation

Artificial light patterns have a strong effect on the global homogeneity of the mosaic, therefore their compensation is of high importance for the performance and result of subsequent mosaicing processing. Small brightness differences (for very narrow field of view cameras with almost uniform illumination) can be treated similar to image vignetting in air, simply by multi-band-blending strategies (e.g. Brown and Lowe (2007)) during image stitching that make the patterns less obvious. For wide-angle lenses, as often used for deep sea mapping, uniform illumination becomes more difficult or impossible. Unfortunately, above mentioned restoration methods barely consider the artificial lighting effects. Since the exact illumination conditions are often unknown, in the previous literature, this problem is mostly addressed by subjective approaches according to qualitative criteria. We individually survey this issue here, as we want to raise awareness of considering lighting compensation in deep sea visual mapping.

A group of methods that tackle the lighting dispersion depends on histogram information, another group is based on the Retinex theory (Land and McCann 1971; Land 1977) which assumes the image to be a product of an illumination and a reflectance signal, the illumination signal is modeled and exploited to recover the reflectance image. It has been widely adopted to estimate the local illuminant (Beigpour et al. 2013; Bleier et al. 2011; Finlayson et al. 1995; Kimmel et al. 2003) in image processing and later also been utilized in underwater cases (Fu et al. 2014; Zhang et al. 2017b). Garcia et al. (2002) gives a nice overview on this issue and categorizes the solutions by four strategies. Here, we adopt their definitions and summarize the related work into following three categories: (1) Exploitation of the illumination-reflectance model, it considers the image as a product of the illumination and reflectance, the illumination-reflectance model is estimated by a smooth function. The uneven lighting effect is then eliminated by removing the illumination pattern. Several methods have been proposed: (Pizarro and Singh 2003) averages frames to estimate an illumination image in log space. Arnaubec et al. (2015) employs a mean or median filter to extract the illumination pattern and describes this spot pattern as a third order polynomial. Köser et al. (2021) robustly estimates all multiplicative effects including the light pattern, also using a sliding window median. Bodenmann et al. (2017) also approximates the lighting and water effects as an multiplicative factor. It is estimated empirically from a series of images taken at different distances on known seafloor objects. Borgetto et al. (2003) uses natural halo images to model the lighting pattern. Johnson-Roberson et al. (2010) assumes a single unimodal Gaussian distribution to correct illumination variations and later (Johnson-Roberson et al. 2017) proposes a two-level clustering process to improve the performance. Rzhanov et al. (2000) de-trends the illumination field through a polynomial spline adjustment. (2) Histogram equalization adjusts the image intensity histogram to a desired shape. This technique increases the image contrast by flattening its histogram, but does not perform well in non-uniformly illuminated cases such as deep sea images. Adaptive histogram equalization (AHE) (Pizer et al. 1987) is applied in (Eustice et al. 2000), to enhance the mosaicing images by equalizing the histogram in the local window through the entire image. Eustice et al. (2002) utilizes a variant of AHE, called contrast limited adaptive histogram equalization (CLAHE) (Zuiderveld 1994), which executes histogram equalization in each block of the image and interpolates the neighboring blocks to eliminate the boundary artifacts. (Lu et al. 2013, 2015) expand the histogram in different color spaces based on pixel intensity redistribution. (3) Homomorphic filtering: since illumination effects are multiplicative, they become additive in log-space. Here, the illumination component can be modelled through low-pass filtering or parametric surface fitting, since the illumination-reflectance model is linear (Bazeille et al. 2006; Guillemaud 1998; Singh et al. 1998, 2007).

Besides above mentioned approaches particularly deal with artificial lighting compensation, this issue is also considered in several underwater image enhancement approaches (Chiang and Chen 2011; Peng and Cosman 2017) during the depth or transmission estimation, or fused with several processing steps (e.g. Gamma correction (Cao et al. 2014), white balancing) to enhance the image contrast (Ancuti et al. 2012, 2016, 2017a, b; Bazeille et al. 2006).

Early researches in this section only deal with monochromatic images, where underwater image processing methods at that time were still aimed to improve and image contrast (remove scattering) and to compensate light pattern for mosaicing. The loss of attenuation variations in different channels make the early lighting pattern compensation approaches non-physically based, they are mostly utilized in the image enhancement applications. Overall, the quantitative properties ignore the differences in image position and are strongly correlated with the image content, such that any relative geometry changes between camera, light sources and scene can create abrupt patterns in the mosaic.

3.4 J–M Approximation Based Methods

The J–M model considers light propagation of artificial light sources, therefore it better suits deep sea scenarios. It assumes single scattering and approximates the forward scattering and backscatter using PSF and VSF respectively. Based on the J–M model, if any of the properties of scene depth, water parameters and lighting configuration is known, the remaining unknown properties can be derived from the appearance variations between image correspondences of multiple images. In most of the cases, the water properties are part of the unknown parameters to be estimated. The water properties in the complete J–M model consist of two groups of parameters: attenuation and VSF parameters, and the number of the VSF parameters depend on the phase function model used. Some researchers assume the proportion of scattered light has a uniform directional distribution, such that the corresponding VSF becomes constant (Bryson et al. 2016) and might be negligible during the restoration. Only some works actually attempt to estimate the VSF parameters from images: (Narasimhan and Nayar 2005; Narasimhan et al. 2005; Tsiotsios et al. 2014) use the phase function from Chandrasekhar (2013), (Murez et al. 2015; Nakath et al. 2021; Narasimhan et al. 2006; Spier et al. 2017; Tian et al. 2017) utilize the HG phase function and (Pegoraro et al. 2010) models a general phase function model by using Legendre polynomial basis or Taylor series.

Similar to the depth cue estimation in haze images, this group of methods requires multiple correspondences with variations to solve the final optimization. When capturing multiple images under different known lighting configurations, this becomes a typical underwater photometric stereo problem (Fujimura et al. 2018; Murez et al. 2015; Narasimhan and Nayar 2005; Negahdaripour et al. 2002; Queiroz-Neto et al. 2004; Tian et al. 2017; Tsiotsios et al. 2014). (Spier et al. 2017) shows that the water properties can be derived even from empty scene backscatter images with a controlled light source movement. If the scene depth information is given, it becomes a light source calibration problem using a known lambertian surface (Park et al. 2014b; Weber and Cipolla 2001) where, however, additional water effects have to be considered.

Estimation of the unknown parameters requires the observations to be in a good configuration (e.g. significant differences). As directly solving the equations can be very complex or intractable, often iterative methods are employed that minimize some error function in a gradient descent manner. Those schemes need to start from good initial values, otherwise parameter estimation can be trapped in local minima or degenerate cases. Additional constraints with respect to the lighting configurations together with scene depth information can further strengthen the robustness of water parameters estimation (Bryson et al. 2016).

3.5 Monte Carlo Based Methods

The J–M approximation only considers single scattering in the model, which is still a simplification of underwater radiative transfer. Mobley (1994) introduced Monte Carlo techniques for solving the underwater Radiative Transfer Equation (RTE) and discussed ray-tracing techniques for simulating light ray propagation underwater. Powered by advances in GPU technology and physics-based simulation, nowadays graphic engines are able to synthesize complex underwater effects using ray-tracing efficiently (Zwilgmeyer et al. 2021). Latest approaches even employ Monte Carlo-based differentiable ray-tracing to replace an explicit image formation model for image restoration, by simply characterizing the water by differential properties and then optimizing (Nakath et al. 2021). Such an approach can implicitly handle multi-scattering, shadows as well as different phase functions.

3.6 Learning Based Methods

Many learning based underwater image restoration methods emerged over the last decade, e.g. (Fabbri et al. 2018; Lu et al. 2021; Torres-Méndez and Dudek 2005; Yu et al. 2018). However, Akkaynak and Treibitz (2019); Bekerman et al. (2020) have addressed the shortcomings of these methods, such as strong dependence on the training data, and there is still large uncertainty in what scenarios they can reliably be applied e.g. when a robot is diving to a previously unseen ocean region and for other open applications. Simply, there is a massive shortage of underwater image datasets with ground truth (in terms of in air appearance) available for training. In particular, it is very difficult to know how a particular seafloor spot in the deep sea would really look without water, which is however what would be naturally needed for training. Current learning based methods either use synthetic images or restoration results from other methods as the training data, which make their training problematic. Meanwhile, deep sea images’ appearances strongly depend on the camera-lighting-scene configurations and water properties, which is even more challenging for learning methods to restore such images with general training sets. Therefore, we did not list this group of methods in this survey as they currently are not applicable for deep ocean mapping.

4 Discussion

Hardware for Deep Sea Imaging  Three key issues of deep sea imaging systems for mapping are discussed in Sect. 2: (1) Several technical barriers for building a refraction-free deep sea imaging system have been overcome. Dome port housing with wide angle cameras are gradually replacing the traditional flat port camera systems on the market. Latest system design even drops the camera housing window and embeds the front lens of the camera in direct contact with water. The development of subsea cameras is transferring from simple inspection to professional measuring and mapping purposes. (2) Advances in LED technology allow deep sea imaging systems to carry more flexible illumination configurations with multiple light sources. Optimization of multi-LED illumination for different configurations and tasks, is increasingly considered in UV designs, the development can be supported by simulation techniques. (3) Deep sea localization still remains challenging nowadays, fused localization data are much less precise than on land and can only be used to initialize the georeferencing process for each image: visual geo-localization, place recognition and loop detection could be future tools to improve the situation.

Image Restoration  In Sect. 3, we surveyed the image restoration techniques for deep sea mapping. It requires the algorithms to recover the degradation from scattering, attenuation effects and artificial light cones. We notice that there were few missing pieces and gaps between the real ocean visual mapping and current image processing approaches: (1) Most of the underwater image restorations apply the atmospheric scattering model or its derivatives, but these are only suitable in shallow water cases where the scene is illuminated by sunlight. Single image restoration is the most popular researched topic, but it is an ill-posed problem and requires extra observations and does not consider consistency for mapping: practical applications need more reliable approaches. Assumptions like the DCP allow to restore single images without additional measurements which has been widely adopted. Similar to the enhancement approaches, most of these single view restoration approaches do not use true distance, may have consistency problem when processing over the image sequences. Moreover, the presence of artificial lighting could easily influence the prior estimation. (2) Removing artificial illumination patterns (light cones) has the most significant impact on underwater mosaicing, but so far it did not draw much attention within the underwater image restoration community. Current lighting compensation methods either analyze quantitative properties in single images, which may perform inconsistently over image sequences, especially when the scene contents change significantly, and are not able to handle complex lighting conditions; or subtract some sort of “mean” pattern of an image sequence, which has strict assumptions on flatness and uniformity of the scene and the relative poses between the camera, the light sources and the scene have to be stable. (3) The J–M approximation based approaches consider point light source propagation which is desirable for dealing with the deep sea image restoration problem with artificial illumination. Since the scene depth estimation and image restoration is a chicken-egg dilemma, current methods all require multiple observations of the same 3D point to estimate the water properties and the scene depth. Most of these work are only demonstrated in turbid media in a well controlled lab environment. At the same time, the J–M methods model each light source individually, which becomes tricky for complex lighting conditions. Recent imaging platforms tend to utilize many LEDs in complex configurations, such that it becomes more difficult and impractical to execute calibration for each light source separately. (4) The J–M approximation only considers single scattering, which is a simplification for the complex underwater radiative transfer. The upcoming GPU-enabled Monte Carlo based ray tracing simulates the light propagation in the micro scale physics, and is able to solve more challenging restoration problems with multi-scattering and shadows. However, it still has a similar problem as the J–M based approaches that restoration and reconstruction depend on one another, and multi light sources increase the computational complexity. (5) Learning based approaches have the consistency problem. The difficulties of acquiring ground truth for underwater (and more so: deep sea) images becomes the bottle neck of developing training based restoration approaches. (6) In situ calibration in the deep sea is still a missing part. To our best knowledge, there is no real implementation yet for calibrating radiometric, light pattern and water properties in the deep ocean.

Besides the aforementioned issues, underwater images could also be degraded because of several other additional real-world effects such as smoke from the black smokers, plankton or marine snow (see Fig. 7) which makes restoration an even more challenging task. Such images require additional procedures to filter the effects and more robust solutions for depth estimation and restoration.

Fig. 7
figure 7

Underwater images can also be heavily degraded by floating particles which requires additional efforts during the image restoration. Left: Dense “smoke” blown from hydrothermal vents in SE Pacific Ocean. Right: Heavy floating particles (e.g. marine snow) in the Baltic Sea

Full size image

5 Conclusions

In this paper we have first discussed the key components of imaging systems for deep ocean visual mapping. We discussed the advantages of using non-refractive systems, pointed out the tendency of using optimized multi-LED lighting system and addressed the current status of deep sea vehicle localization. Afterwards, we comprehensively surveyed the image processing techniques for underwater image restoration, particularly the images under artificial illumination in the deep sea scenario. Methods were grouped according to the image formation approximations they are based on, and only a small fraction applies to deep sea data. After the survey, we discussed several missing pieces and gaps between the real ocean visual mapping applications and current approaches, and outlined the open problems in the last section.