1 Introduction

Living in a technically advanced society like ours, the impression of an increasing segregation of human life and natural environment is not far to seek. On the other hand, our everyday life, even as the inhabitant of a megacity, cannot be imagined without a living, natural environment to some degree. In urbanised areas, this is often visible by large parks and single dominant trees along roads and in gardens. These trees have a considerable significance in a populated city (Nowak et al. 2006; Armson et al. 2013). Yet besides their noticeable positive effects on micro-climate and their soothing aura, we also have to consider problems and trade-offs caused by the density of urban areas. People—afoot or by bike—cars, trucks, buildings, infrastructural installations, and the mentioned natural elements have to find a good way of coexistence. This means that trees, as the possibly tallest plants in a city, must not endanger persons or other objects in case branches break down or the whole tree falls. Additionally, deciduous trees cause a considerable amount of biomass that has to be taken care of in autumn. To keep track of all possible dangers and to take preventive measures, all trees should be identified and added to a tree cadastre (Tanhuanpää et al. 2014). The actual benefit then results from regular updates of the information associated with each tree: Health, size in height and diameter, measures taken on the object like pruning or replacement. At that point, clear definitions and regulations are available. On the other hand, the irregular shape of plants is a challenge to any automated processing.

Introducing cadastres (sometimes also referred to as registers or inventories) always requires a transition from the real world to a certain model structure. To transfer the essential information from the actual environment to the proposed model, we need precise measurements. For capturing the filigree structure of branches and skinny twigs, mobile laser scanning (MLS) is a fitting choice due to the active acquisition by light detection and ranging (LiDAR). Important model parameters are the position of the stem and its diameter. The use of an unmanned aerial vehicle (UAV) does not seem applicable at the moment due to legal restrictions regarding flight permits over populated areas; airborne laser scanning (ALS) is not suited because of its low point density on tree stems (Lin et al. 2012). Hence, considering the significance of trees at the roadside where most traffic and thus the potential of endangering people and objects is to be expected, MLS is the best choice for this application. It guarantees coverage of large areas in a reasonable time, operates at a very high level of detail, and is optimised for capturing the street canyon to acquire the street trees. Figure 1 shows an exemplary area scanned by MLS. The zoomed-in panel emphasises the highly detailed structure captured and also the decreasing point density farther away from the vehicle trajectory.

Fig. 1
figure 1

Bird’s eye view on a MLS data set (grey-scale values denote the measured LiDAR intensities). The zoomed-in panel shows a nadir view of street trees (the ground level has been removed for better visualisation). The yellow line indicates the trajectory of the MLS vehicle

Full size image

Generally, when change detection is considered, and especially when dealing with vegetation, different questions arise:

  • How do we define a change?

  • How can we detect such changes from measurements?

  • How will we interpret this information based on the measurements?

To define a change, one has to consider that change detection per se is the comparison of two states of something—ideally, this would be two time epochs of an object in the real world. However, to quantitatively evaluate such changes, we clearly have to define the elements that should be compared. Moreover, the elements to compare—i.e. measured points in this case—suffer from the inherent property of laser scanning: The measurements typically do not exactly lie at the same positions when repeated. Due to this fact, a certain volume has to be defined, considering the uncertainty of the point. Instead of examining the point cloud of a tree, a model description of tree objects can be compared, too.

Once an element is found to detect changes, the interpretation must be defined. The types of changes involve the simple question of existence: Has a new object appeared or did a previously existing object disappear? Characteristics can be compared, too: Besides the attributes of existence mentioned above, tree parameters like the diameter at breast height (DBH) or the height can be analysed (Herrero-Huerta et al. 2018).

In this paper, a method for change detection of urban vegetation is introduced. The main contributions are the segmentation of individual trees, automated build-up and comparison of 3D occupancy grids, and their analysis. This covers the complete processing from raw measurement data to specific tree changes including object parameters and geometric extent. We examine the performance of change detection and the influence of data acquisition, in our case with the additional requirement of comparing leaf-on and leaf-off data. For the processing, we propose a pipeline consisting of three major steps:

  • Extracting individual tree instances from a merged MLS point cloud, which is briefly described in Sect. 3.1.

  • Building an occupancy grid of the area of interest by traversing the path of a laser ray, thereby deriving basic status information for each volume element (empty, occupied, unknown) (Sect. 3.2.1).

  • Deriving the change status (confirmed, new, disappeared) within the grid from the occupancy comparison of both epochs. This is used in the comparison of object geometry (Sect. 3.2.2) and on semantic object level (Sect. 3.2.3).

Having presented the methods in Sect. 3, the test data set from TUM City Campus is introduced in Sect. 4. We then present the results in Sect. 5 followed by their discussion (Sect. 6).

2 Related Work

For achieving the object-level 3D change detection of trees, the segmentation of single trees and the change detection on the individual tree are two essential tasks in the entire processing workflow. In the following subsections, we give a brief review of the related studies.

2.1 Segmentation of Individual Trees

The segmentation of individual trees from MLS point clouds involves two stages. The first stage is semantic segmentation, which distinguishes points of trees from non-tree ones and extracts them from the entire point cloud. This stage can be achieved via semantic labelling methods like (Weinmann et al. 2015; Qi et al. 2017; Thomas et al. 2019) using either conventional or deep learning-based approaches. For example, in Sirmacek and Lindenbergh (2015), a probability matrix computation-based method is proposed to classify MLS point clouds into “tree” and “non-tree” classes.

Then, the second stage is an over-segmentation for separating tree instances from the tree points. Here, both geometric characteristics (e.g. point density, Zhong et al. 2013, and tree height, Yue et al. 2015) and local structures (e.g. spherical crown shapes, Yadav et al. 2018, and eigenvalue based features, Xu et al. 2018) of tree trunks and crowns are utilised to achieve this task. Similar to general over-segmentation methods, the point cloud segmentation approaches for tree extraction can be classified into three categories: region growing-based, clustering-based, and model-fitting methods.

For region growing-based methods, due to the concept of region growing, the correctness and completeness of segments (i.e. trees) highly rely on the selection of seeds, which are generally set on the axes of trunks or the vertex of crowns. Afterwards, starting from the seeds, the entire tree structure can be found by conventional growing procedure or its variants. For example, in Wu et al. (2013), a novel competing growing strategy is used based on the seeds selected by identifying the geometric centers of tree crowns projecting on a horizontal plane. In Li et al. (2016), a dual growing strategy is implemented based on the seeds selected from tree trunks according to their cylindrical shapes and relatively smaller radius comparing the crowns. In Zhong et al. (2013), the growing uses seeds that were selected by the local maxima in the horizontal histogram of the voxelised point cloud by octree decomposition. Using the improved supervoxel structure, in Wu et al. (2016), a breadth-first search-based growing is employed, in which the seeds are selected by the gravity center of the supervoxel, which contains concentrated points. However, due to the scanning pattern of MLS, the identification of optimised seeds for growth is always a challenging task since either tree trunks or crowns suffer from occlusions, with merely partially scanned points acquired.

Clustering-based methods, on the other hand, require no seeds. Euclidean distance-based clustering that measures the spatial distances between points is the most commonly used method. For example, in Guan et al. (2015), it is utilised to cluster points of individual trees. Apart from Euclidean distance clustering, meanshift (Weinmann et al. 2017) and normalised cut (Yu et al. 2014) are also commonly used clustering approaches for single tree extraction. It is also noteworthy that the clustering can not only be implemented based on points but also on voxels (Yu et al. 2014; Li et al. 2021). In Gorte et al. (2015), tree point clouds are voxelised into 3D voxels and then clustered by considering the connected components. Those points of connected voxels will be aggregated into individual single trees. Parameters of trees are then estimated. The use of voxel structures can overcome the shortcomings of unstructured point clouds and significantly down-sample the original data. However, due to the complexity of the urban tree scenario, a simple clustering procedure may not reach satisfying performance. So, hierarchical clustering methods are also explored for tree segmentation. For instance, in Xu et al. (2018), a bottom-up hierarchical clustering is presented to derive various tree components in sequence according to their geometric characteristics. However, for any clustering-based method, the identification of tree numbers still plays a crucial role in the segmentation procedure. With inaccurate or not defined tree numbers, over-segmentation or under-segmentation may frequently occur.

Regarding the model fitting-based methods, there is only a limited number of studies that have been reported. This is mainly because for a model fitting-based method, a rational and mathematical model representation must be given. For example, in Lindenbergh et al. (2015), MLS point clouds are first consecutively downsampled, retiled, and segmented into separated point sets. Then, point clouds of tree instances are parameterised to achieve tree locations, tree heights, canopy diameters, and trunk diameters by the use of a DBH model. Similarly, in Li et al. (2020), ground and low objects are filtered from measured MLS point clouds. Then, based on a geometric tree model and semantic information, points of each tree are segmented, with parameters such as locations and trunk radius obtained simultaneously. However, for trees with irregularly shaped crowns consisting of branches and leaves, it is truly a challenge. Thus, a common way of using model fitting is to only fit the tree trunks with cylindrical models (Li et al. 2016; Polewski et al. 2017) or crowns with ellipsoid models (Schmitt et al. 2015). By doing so, an approximate geometric representation of trees can be achieved. Then, to get the complete tree structure, subsequent steps like growing or clustering are usually required. A combination of segmentation and modeling is presented by Raumonen et al. (2015). They connect point cloud patches beginning from the base of the stems. From growing rules, modeling in stems and branches of various order is derived. The role of mere model-fitting is closer to the process of finding growing seeds or localisation of trees with shape centers. The use of a shape descriptor to recognise and separate points of trees (Monnier et al. 2012) can also be regarded as a model-based method; but in such methods, a supervised learning-based classifier should always be applied, which requires annotated training samples.

2.2 Change Detection on Urban Trees

While change detection on point clouds in urban environments has been examined thoroughly through the past years, the focus on trees is still not often mentioned. Most existing works use data from airborne laser scanning (ALS). For example, Tran et al. (2018) define a change class for trees while performing a general urban change detection. Hebel et al. (2013) introduce occupancy grids to derive object status changes from ALS point clouds. Xiao et al. (2016) investigate tree object and crown changes based on ALS data. The aim is similar to ours, yet due to the differences in data characteristics, not all previously mentioned methods can be successfully transferred to mobile laser scanning.

Voelsen et al. (2021) entirely rely on MLS data while detecting changes in the built environment by separating them into static and non-static objects. They identify the effects and interpretation of vegetation changes as problematic, primarily due to the semi-static behaviour of vegetation—the objects are not as rigid over time as, for example, buildings. A deep analysis of the field of MLS-based change detection is done in Xiao et al. (2015), adapting some of the concepts from Hebel et al. (2013).

To investigate combined acquisition methods, Wu et al. (2018) compare the characteristics of MLS and ALS and propose a combination of the scanning methods and also imagery. In terms of tree detection and completeness, ALS performs better, but as soon as the focus sets on details and point density, MLS is gaining importance. Although Wu et al. (2018) only map and classify one epoch of trees, change detection from multi-sensor combinations seems promising and should be further investigated. For the sake of efficiency and feasibility for smaller municipalities, we, on the other hand, only focus on one acquisition method, MLS. Especially, the distinct features of vegetation in comparison to artificial structures promise interesting new challenges.

In conclusion, detecting changes of urban trees has been addressed in several studies and identified as an important topic. However, most of the methods that explicitly deal with trees use data from airborne acquisition or even optical remote sensing. To our knowledge, a method and investigations for utilising MLS data for automated change detection of urban trees has not been presented yet.

3 Methodology

Change detection is the last step in a long pipeline of point cloud processing. At the scope of this work, especially the instance identification of single tree objects is a crucial step to enable comparisons on object level. Thus, we introduce an approach of single tree extraction in Sect. 3.1 before continuing with the actual change detection on geometry and object level (Sect. 3.2). Here, we assume that the semantic labelling that separates points of trees from those of other objects in the scene has been implemented. In previous work (Zhu et al. 2020; Xu et al. 2020), we have achieved promising results using the same data set. In this case, the focus is on the change detection of trees. We directly use manually labelled results as the input for instance segmentation and change detection to avoid negative influences by semantic segmentation errors. Hence, except for occupancy computation, the processed point clouds we utilise contain only points of trees.

3.1 Instance Segmentation

The objective of the presented instance segmentation is to extract individual trees from MLS point clouds. To achieve this, we have developed a tree segmentation method consisting of three major steps: trunk extraction, tree separation, and crown expansion. The objective of trunk extraction is to extract tree trunks from the entire point cloud, aiming at facilitating the following tree separation. The tree separation is meant to identify individual trees from extracted trunks, while the crown expansion focuses on obtaining the complete tree structure based on the individual tree trunks.

In trunk extraction, height-based filtering is applied. Points having a height between a lower bound and upper bound are kept, corresponding to only tree trunks. Afterwards, for the tree separation, we applied an improved voxel- and graph-based segmentation (VGS, Xu et al. 2018) using a global graphical model. Here, regarding the feature used to describe the voxel, we only consider the centroid of points within the voxel and use proximity as the primary indicator when weighting the edges in the graphical model. After the segmentation, each segment corresponds to the trunk of a tree. An axis aligned bounding box of a fixed size will be selected, centering the trunk axis. The top of the corresponding tree crown is identified by finding the highest point within this bounding box. Finally, in the crown expansion, we utilised a local k-means clustering strategy, which is inspired by the VCCS KNN mentioned by Lin et al. (2018). In this clustering step, a point will be assigned to one of its k nearest trunks by calculating its weighted distance to the tree trunks and the crown tops. Here, the spatial distance and the local point density are the two factors that we considered in the calculation of the weighted distance. To be specific, for each point, its perpendicular distance d to the axis of the trunk and its local point density \(\rho\) are calculated. To estimate the local density, a spherical neighbourhood centered at this point is selected and then density is estimated by the number of points covered by this spherical neighbourhood. The distance allows measuring the proximity between the point and the possible tree trunk that it belongs to. The point density is used to avoid the incorrect assignment of points when two adjacent trees have a significant difference in size. Here, we have a strong assumption that the tree should have a conically shaped crown. Under such an assumption, if we link the point of a tree to its crown top, there should be no “gap”. The “gap” denotes the area with sparse point density (see Fig. 2). To detect such sparse area and give a penalty weight in the clustering of a point P between two trees, the weighted distance \(d_w\) from a point P to its kth nearest trunk is formulated as follows:

$$\begin{aligned} d_w = d_k \cdot \left( 1 - \sigma \cdot \exp \left( \frac{-({\rho }_k- {\overline{\rho }})^2 }{2 \delta {\rho }^*}\right) \right) , \end{aligned}$$
(1)

where \(d_k\) is the distance to the axis of the kth trunk. \({\rho }_k\) is the local point density of the middle point \({P^\text {m}}_k\). \({\overline{\rho }}\) and \({\rho }^*\) are the mean and standard deviation of the local point densities in the point cloud. \(\sigma\) and \(\delta\) are the balance factor of density and the bandwidth factor of the Gaussian kernel, respectively. These two factors are set empirically. To be specific, \(\sigma\) is used to judge the contribution of the factor “density”, ranging from 0 to 1. In case the points have a higher density around the tree area, then \(\sigma\) should be set to a relatively larger value, ensuring the points are assigned to their nearest trees. \(\delta\) is the scale factor that compensates the scale difference between the density and the distance measurements, which is set purely empirically depending on the real scale difference between the estimated density and distances. Assuming a point P is between two trees i and j, as shown in Fig. 2, the middle points \({P^\text {m}}_i\) and \({P^\text {m}}_j\) between P and two crown tops \(T_i\) and \(T_j\) are selected. The local point densities \({\rho }_i\) and \({\rho }_j\) are estimated as well. They will be used to balance the weight of spatial distances. After the clustering, the point P will be assigned to the tree trunk having the smallest weighted distance \(d_w\).

Fig. 2
figure 2

Point clustering in the crown expansion. The weighted distance for a point P between two trunks is computed from the distances \(d_k\) to these trunks and the point densities at the middle points \({P^\text {m}}_k\) between P and the crown tops \(T_k\)

Full size image

3.2 Change Detection Based on Occupancy Grids

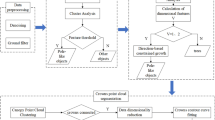
As discussed in the introduction, a change detection on point clouds needs to be defined so that discrete elements can be compared. We propose an occupancy grid of the 3D space containing all the available information on occupation and ray traversal for each voxel (Sect. 3.2.1). With such a grid—one for each area and epoch—the individual cells can be compared as described in Sect. 3.2.2. Besides staying with the geometric changes only, one can profit from the instance segmentation and analyse certain tree features or simply the existence of objects (Sect. 3.2.3). All these steps are summarised schematically by Fig. 3.

Fig. 3
figure 3

Workflow for change detection from occupancy grids and point cloud comparison

Full size image

3.2.1 Marking Occluded Areas: Occupancy Grid

The points of MLS point clouds are irregular and distributed with varying densities. One approach to compare unambiguous, clearly defined elements is a regular partition of 3D space, a voxel grid. Each voxel contains variables, which are initialised by zero: “empty”, “occupied”, and “sensor position” (Hebel et al. 2013). As long as the values of all of these variables remain zero, a voxel’s state is “unknown”. Then, all the raw scan files are processed in the same order as the points were captured. With the prerequisite of knowing the position of the sensor for each measurement, we can follow the line of sight between sensor and point using an adapted Bresenham line algorithm (Bresenham 1965). This algorithm is usually defined and implemented in most libraries for 2D images. Hence, we apply the standard process on the X and Y coordinates of the line of sight. Having regular positions in the plane, a height value is added by using linear interpolation between sensor height \(O_\text {Z}\) and the point’s Z coordinate \(P_\text {Z}\):

$$\begin{aligned} z_i = z_{i-1} + \frac{P_\text {Z} - O_\text {Z}}{n_\text {pix}} \end{aligned}$$
(2)

with i iterating over all \(n_\text {pix}\) pixels marked by Bresenham’s algorithm.

Traversing through the voxels defined by the planar line coordinates and the computed height values, we can increase the “empty” counter of each of these voxels by one. The voxel containing the measured point is incremented at the “occupied” counter, the sensor’s voxel at “sensor position”. If the values of the variables “empty” and “occupied” of a voxel are both zero, we cannot deduce its state. It is not in sight of the sensor, be it because of occlusions or because of its position, and hence “unknown”. The allocation of these values for one single ray is displayed in Fig. 4.

Fig. 4
figure 4

One measurement ray traversing through the voxel grids. Each voxel’s values are increased based on the voxel’s state in that case: Grey is the “sensor position”, all green voxels are identified as “empty” and the blue voxel contains the measured point and is, thus, “occupied”. All other voxels, especially the ones occluded by the tree, are “unknown” at that moment

Full size image

The occupancy grids are stored and will be referred to by the following methods. We choose a voxel size of 10 cm. It can be expected that the absolute point accuracy will not be much better than that considering the accumulated errors of measurement, irregular object properties and movement, positioning, and inter-epoch registration.

3.2.2 Finding Changes by Comparison of Occupancy States

This approach derives a comparison of two point cloud epochs by direct cell-by-cell comparison of the occupancy grids. It shows how every single voxel has changed. This is important to detect possible decision conflicts. To reliably decide whether a voxel is occupied or not, we, in general, take into account its direct 26 neighbours. By doing so, we gain two advantages: First, we consider the accumulated errors from positioning, ranging, registration, and hence object stability. Especially while dealing with trees, one must be aware that due to wind or long-term deformations, some branches can move between epochs without having actually changed. Second, we guarantee that—in case an object exists at this position—it is hit by a sufficient number of measurements so that it can be assumed that not some noise or outlier was generated.


Dynamic neighbourhood adaption Mobile laser scanning suffers from strongly varying point densities. In connection with the respective sensor mounting on the acquisition system, some areas of a point cloud might only be sparsely covered by points, although there are massive objects. To overcome that issue, we propose a simple heuristic extension of the area of interest for change detection: The angular resolution of scanners can be interpreted as the number of points along a specific axis. If scanners with multiple beams are used, values for horizontal and vertical resolution can be found. At a distance d from the sensor with vertical angular resolution \(\delta _\text {V}\), there can be a maximum number of

$$\begin{aligned} {n_{\text {P}}}_{\text {V}} = \frac{l}{\Delta p_\text {V}} = \frac{l}{\delta _\text {V} \cdot d} \end{aligned}$$
(3)

single points along a vertical line of length l. \(\Delta p_\text {V}\) denotes the space in between two neighbouring points. The number \({n_{\text {P}}}_{\text{H}}\) of points along a horizontal axis can be derived analogously. Thus, a voxel with a side (face) of area \(l^2\), can be reached by a maximum of

$$\begin{aligned} n_\text {hits} = \frac{l^2}{d^2 \delta _\text {V} \delta _\text {H}} \end{aligned}$$
(4)

points per laser swath. This can be reversed to derive the maximum distance from the sensor for a voxel to be potentially hit by at least \(n_\text {hits}\) points:

$$\begin{aligned} d_\text {max} = \sqrt{ \frac{l^2}{\delta _\text {V} \delta _\text {H} \cdot n_\text {hits} }}\,. \end{aligned}$$
(5)

When comparing two epochs, we increase the neighbourhood around a voxel if it is farther than \(d_\text {max}\) away from the sensor. It is considered empty only if all the neighbourhood voxels are empty as well. By doing so, we try to compensate for the decreasing point density and put emphasis on the correctness of the resulting change point cloud.


Cell-by-cell occupancy comparison Both occupancy grids are needed to indicate conflicts in the change detection. Iterating over the 3D voxel space, we examine each voxel and its neighbourhood as defined beforehand. The occupancy state variables are added up for all voxels in the neighbourhood and the values of “empty” and “occupied” are analysed. Based on the states of these counters, five comparison types are possible:

  1. 1.

    “Appeared”: In the base epoch, the voxel is empty (“empty” \(> 0\)) and not occupied (“occupied” \(=0\)). In the change epoch, the voxel is occupied (“occupied” \(>0\)).

  2. 2.

    “Disappeared”: In the base epoch, the voxel is occupied (“occupied” \(>0\)). In the change epoch, it is empty (“empty” \(> 0\)) and not occupied (“occupied” \(=0\)).

  3. 3.

    “Confirmed”: The voxels in both epochs are occupied (“occupied” \(>0\)).

  4. 4.

    “No information in base epoch”: The voxel in the base epoch is neither “occupied” nor “empty” (both values \(=0\)). Thus, no information is available and a definitive statement on changes is not possible.

  5. 5.

    “No information in change epoch”: The same as case 4, but for the new epoch without occupancy information.

This change detection by comparison of occupancy states is applied to the whole point cloud, since the occupancy grids were generated from all points. Yet, for the specific analysis of tree changes, we only consider tree points. Using the results from semantic segmentation, the voxels containing tree points are identified and extracted.

3.2.3 Finding Changes in Tree Parameters

Trees can be described by several parameters. Whereas classical forestry is mainly interested in the volume and thus the value of trees (Hackenberg et al. 2015), in the urban environment geometric extent and health or stability are the most interesting properties. In terms of occupied space, the diameter at breast height and the height are most characteristic and often referred to in official documents. Moreover, considering rather regularly formed trees, the diameter of the tree crown and the height from the ground to the crown’s base could be used (Herrero-Huerta et al. 2018).

In this work, we focus on DBH and tree height as the most common parameters. For each epoch and each tree, both values are determined. Furthermore, we have to identify a tree as the same object in both epochs.

DBH computation Breast height is defined as 1.30 m above ground. To have enough points to derive the diameter, we define a horizontal slice of a certain extent in height from the point cloud of a single tree. Due to the dense MLS point cloud, an area of \({1.30}\,{\text{m}}\pm {10} \,{\text {cm}}\) is considered sufficient, but could still be adapted to the distance to the sensor. We have to assume that at this height, only the stem is visible and branching has not started yet. Due to the chosen acquisition method, most of the time, stems are only captured from one side, leading to points on half the stem’s circumference. Classical least-squares fitting is not robust enough in that case. Thus, we split the point cloud slice into n height bins (3 in this case) and project each sub-slice on the XY-plane. For each, we use random sample consensus (RANSAC) to fit a circle. Projected points and fitted circles are stored as an image for validation purposes (Sect. 5.3). From the n derived DBHs, we compute the mean and standard deviation. If one of the values is outside the 1.5-sigma interval, it is considered an outlier and removed recursively. Figure 5 illustrates the steps of slice extraction and circle fitting. Finally, we derive the DBH, its standard deviation and an indicator on how certain we are based on the number of removed outliers and the differences in DBH circle centers. The centers of the fitted circles are later used to match tree objects between epochs.

Fig. 5
figure 5

Extraction of a point cloud slice from a single tree for DBH computation: a Individual tree colour coded by height. b Slice taken from the stem with three circles fitted at three sample heights. c Top view with resulting DBH (red)

Full size image

Height determination Assuming a point cloud free of outliers due to pre-processing, correct terrain removal, and segmentation, the height of a tree can be seen as the difference in Z-coordinates of the lowest and highest point. This naive approach is chosen to evaluate the necessity of more complex modeling and the influence of data quality. If a terrain model is available or could be derived from the measurements, this should be used as the correct reference.


Multi-epoch tree identification For finding the same tree in both epochs, the centre point of the circle from DBH determination is used. This value is preferred over a comparison of the trees’ base position where the stem meets the ground since in many cases MLS does not capture such low areas due to occlusions by cars or other low objects. Two trees from different epochs are considered to be the same object if their DBH centres have a horizontal distance not greater than 50 cm. To be sure that a tree has not been replaced at the exact same position—which could happen in urban areas—we also define thresholds for the difference in DBH. This is considered more robust than comparing the height because the top of a tree can more easily be obstructed by other objects.


Building the tree database To structure the multi-temporal objects, a tree database is constructed. If a tree was matched to its equivalent in the other epoch, each epoch contains a tree object with the exact same label. Each object, on the other hand, includes information on DBH and height and can be extended to hold further values like species, crown extent, or volumes. If the difference in DBH between both epochs exceeds a certain threshold (10 cm in our case), the matching is considered as an anomaly and flagged for further investigation. While the database is generated, the reference data is used to identify detected trees with their respective in-situ measurement. If a match to reference is possible, the tree object is named by the reference label. If no reference can be found, the tree’s label is set negative to indicate missing reference.

4 Multi-temporal Data Set

One prerequisite for change detection is data with comparable properties, ideally from the same sensor system, captured at several points in time. This section shall present the two campaigns used in this article and will shortly introduce the processing steps applied to derive a point cloud scene from raw data.

4.1 TUM-MLS-2016/2018

For this study, we examine mobile laser scanning data sets from 2016 and 2018, both acquired by the same platform. We concentrate on the Arcisstraße at the city campus of the Technical University of Munich. The whole system and details on the 2016 data set are described by Gehrung et al. (2017) and Zhu et al. (2020). The two Velodyne HDL-64E scanners are mounted at the front roof corners of the measurement vehicle. They are tilted 25\({^{\circ }}\) to the front and rotated 45\({^{\circ }}\) outwards from the direction of travel. By that configuration, occlusion by elements of the vehicle itself is prevented, and a considerably large area of overlap between the two scanners is guaranteed. The data contains information on reflected intensities and the position of the laser’s origin for each point. Hence, the complete ray can be reconstructed.

Table 1 summarises some essential specifications of the LiDAR sensor and the positioning system, especially concerning the factors influencing point accuracy. As for change detection, the absolute position is of interest. We must note that by combining geo-reference and measurement uncertainties, a point in this data set is only reliable to the accuracy of several centimeters. Of course, on a global scale, this can be improved by point cloud registration methods. However, the setup allows an object to be captured by both scanning heads at slightly different times. Short-term uncertainties in positioning and attitude determination can, thus, increase the noise on a certain object’s surface.

For this application, it is important to note that the 2016 campaign took place in April, with vegetation already in full growth and trees having leaves. The 2018 measurements, on the other hand, were taken in December at leaf-off state. The initially shown Fig. 1 contains the measurements from the December 2018 campaign, with the zoom-in revealing some branching structures of the here leafless trees.

Table 1 Specifications and setup parameters for the MLS system according to the sensor data sheet (Velodyne HDL-64E) and measurement setup (Borgmann et al. 2018; Zhu et al. 2020)
Full size table

4.2 Initial Processing of the Point Cloud Scene

The raw data are stored in scan files containing one rotation of the scanner head. We define the area of interest and merge all included scans from one drive-by. The derived point cloud has to be optimised. We filter the lowest intensity values with almost no return—most likely imprecise range measurements because the object was hit only by a part of the beam, or the majority of the beam was reflected away by an artificial, polished surface (e.g. a car chassis). The highest reflectance means an incidence angle of almost 0\({^{\circ }}\). Whereas this does not seem bad, it has been observed to cause strong noise effects on tree stems. To reduce the number of points, we then eliminate duplicates. A point is considered a duplicate if it is closer than 5 mm to another point. The last step is a statistical outlier removal. The mean distance from a point to its 10 closest neighbours is compared to the global mean distance. If it lies outside an interval of 3 times the standard deviation, it is considered an outlier point and removed.

For change detection, it is crucial to keep the viewpoint information for every point. This is the position of the sensor from which that point has been captured. It is also important to note that both data epochs have already been registered in terms of loop closure and to each other. The corresponding offsets were directly applied to the 2018 point data. In preparation of the experiments, manually derived semantic labels were applied to the point clouds to extract all tree points, which are then used as input for the instance segmentation.

4.3 Testing Areas

For the evaluation of the presented approaches, two testing areas in the data set are defined. From their relative position, they are named North and South. Figure 7 shows both areas. They are of approximately rectangular shape and contain trees along a street in the vicinity of the “Alte Pinakothek” in Munich. Area North contains 37 trees in an area of approximately 80 × 25 m. In the area South, 24 trees are included at an extent of 125 × 15 m. For all trees except the southernmost three, the position and the tree parameters have been derived manually in March 2021. DBH was computed from the circumference, which was measured by tape, and the height was derived trigonometrically from total station observations.

5 Results in Change Detection and Object Parametrisation

The primary results of the change detection workflow are voxel change indicators derived from the occupancy grids. Table 2 summarises for each epoch how many voxels are mainly empty, occupied, or unknown. The large number of unknown voxels results from the grid being aligned to the North and East directions, while the scanner trajectory runs diagonally through that raster. For visualisation, point cloud extractions based on change/no change will also be used in detailed analysis and to show interesting properties of changing elements. In that context, only tree points are evaluated. The initially needed segmentation results are shown in Fig. 6. From the object-based change detection, we derive a tree database, visualised by 2D maps of the detected tree objects. Section 5.3 additionally presents exemplary results of the RANSAC circle fitting together with a quantitative evaluation with respect to reference measurements.

Table 2 Resulting occupancy grids: classification of all voxels in the grid. A voxel is only empty if it has never been marked as occupied before to avoid conflicts. Voxels in the grid structure that could not be seen by the sensor and hence not be evaluated are unknown
Full size table
Fig. 6
figure 6

Exemplary results of the instance segmentation, seen from a above (area South, 2016) and b–e from the East. Each random colour corresponds to the label of one tree instance. b Area South in 2016. c Area North in 2016. d, e respectively for epoch 2018

Full size image

5.1 Detected Changes by Occupancy Evaluation

For a quick analysis of change types, we use the direct occupancy grid comparison. Figure 7 shows the two testing areas with coloured change point clouds. Each point represents a voxel of the occupancy grid. Red colours indicate voxels that disappeared from the reference epoch 2016. Blue stands for new appearances in 2018. The black colour marks areas that were observed in only one epoch. There, a reliable statement on changes is not possible. All tree voxels in light grey have been confirmed; they are occupied in both epochs. A numerical evaluation of the change types for tree voxels is given in Table 3. Furthermore, Fig. 8 shows a zoom-in on the southern area from another perspective.

Fig. 7
figure 7

Nadir view on the areas of interest with the tree voxel change point clouds from occupancy grid comparison. For the changes, red colour means voxel occupation in 2016 only, blue colour new occupation in 2018. a Top view. The grey-scaled street and building scene is for orientation only. b Northern part. c Southern part

Full size image
Table 3 Resulting change types of voxels containing tree points in both testing areas
Full size table
Fig. 8
figure 8

Both change sets seen from the Northwest. The tree change cloud of area South is shown in side-view for more detail

Full size image
Fig. 9
figure 9

Mapping (WGS84/UTM 32U) of the detected and matched tree objects in area North on the positions and IDs from in situ reference measurements from 2021

Full size image
Fig. 10
figure 10

Mapping of the detected and matched tree objects in area South on the positions and IDs from in situ reference measurements from 2021. Objects with negative IDs are in areas with no reference

Full size image

5.2 Detected Changes on Object Level

For the object-based change detection, we derived a database containing tree objects. As a visualisation of these object catalogs, we plotted change maps for each area (Fig. 9 for area North, Fig. 10 for South). Inter-epoch matches are indicated with green dots. Suspected anomalies with a difference in DBH between both epochs greater than 10 cm are marked yellow. Additionally, we included the reference measurements taken by hand in 2021. Trees matched to these reference positions are displayed by other symbols than trees that could not be assigned to a reference. As the absolute measurement may differ from the point cloud based position because of different acquisition techniques, a match to reference is defined within 50 cm radius.

The tree detection is evaluated with the reference measurements as ground truth. Comparing the tree objects extracted from the point cloud to the reference trees, we derive the statistics shown in Table 4. A match to reference is a true positive (TP), a detected tree without corresponding reference is false positive (FP), and reference trees without corresponding measured objects are false negative (FN). We derive the quality metrics \(\mathrm{precision} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}\), \(\mathrm{recall} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}\), and \(F1=\frac{\mathrm{TP}}{TP+0.5\cdot (\mathrm{FP}+\mathrm{FN})}\). The three southernmost trees of area South were not considered in the evaluation because they are not included in the reference data. Their labels (\(-1000, -1001\), and \(-1002\)) are, hence, negative.

Analogously, the matches between epochs are evaluated. From the 59 trees existing in both epochs, 50 inter-epoch matches were detected correctly (85%). The other tree objects without a partner in the respective other epoch remain in the database, too. In 2016, there are 7 tree objects without a matching partner in the other epoch; in 2018, the number is 8.

Table 4 Quality evaluation of the tree detection regarding the matching to reference data. These values are strongly influenced by the matching threshold
Full size table

5.3 DBH Circle Fitting

Correct DBH fitting strongly relies on accurate segmentation and a free stem at 1.30 m height. In many cases, the points of a tree object fulfill these requirements and the approach works well (Fig. 11a). Even if some overlapping branches occur at the outer edges of a DBH slice like in Fig. 11b, the method stays robust as long as a stem can clearly be identified. If a completely different object is put in due to complete misclassification or an occluded stem, the matched circle does not fit at all and most of the time gets unrealistically large (Fig. 11d). For very thin stems as Fig. 11c shows, the outline cannot clearly be identified as a circle, but the fitting matches the data as well as possible.

The available reference data has been acquired in 2021, so it will be used for validation of the 2018 data only. As most of the trees are fully grown, the increase in diameter over 3 years is expected to be below measurement accuracy. Comparing the diameters derived from the 2018 point clouds to the reference values, 37 out of 45 DBHs are inside an ±15 cm interval of the reference with an RMSE of 6.1 cm.

Fig. 11
figure 11

Results of the DBH fitting approach. Projected points are displayed in red, the fitted circle in blue. Each panel has a side length of 2 m

Full size image

6 Evaluating the Influence of Data Quality on Change Detection

In the results presented previously, especially the change grid, we can clearly see qualitative changes at first glance. Their interpretation, however, is not always straightforward. This section shall investigate the eye-catching changes and their reasons, combined with a look at how measurement setup and quality influence the results. We start with a discussion of the results at the object level (Sect. 6.1), before analysing the results of voxel-based change detection (Sect. 6.2).

6.1 Changes on Object Level

For pure inventory purposes, location and tree parameters are sufficient. The inter-epoch matching can be encoded in maps like Figs. 9 and 10 but might need further analysis. If a tree could only be found in one epoch, this can be an indicator that it has been removed or newly planted. However, measurement and segmentation accuracy have a strong influence on the correctness of these interpretations.

Regarding the northern part (Fig. 9), the trees #2, #32 and #33 were only found in 2018. However, all of them already existed in 2016. Tree #2 was so small back then that some leaf-weighted branches were hanging down to breast height. Thus, the slices for DBH computation could not be fitted correctly, resulting in an unrealistically large diameter and hence the removal of that potential tree object. For trees #32 and #33, also the time of measurement is the key: Both trees being placed far from the street, their upper and middle parts were occluded by the leaves of the trees in the front. Moreover, their trunks were not classified as tree, maybe because they are surrounded by low hedges. Both point clouds can be seen in Fig. 12 with the points from other classes displayed in grey, showing a considerable amount of points beneath the segmented trees. Unsurprisingly, the height of 1.30 m was counted from the lowest tree point, and thus the slices were extracted from the middle of dense branchwood or just void. Also, the tree height estimation is falsified accordingly. Like in the case of tree #2, the diameters were larger than 3 m and the objects deleted. As these effects occur in the third row of trees and not directly at the street, erroneous estimations will not lead to severe safety issues. A correct height estimation could only be achieved if a terrain model was known or could be derived from incomplete data. We described ideas on such an approach in Hirt et al. (2021), which might be of use in these cases. Another phenomenon is a large difference in estimated DBH, indicating that the tree would have grown more than 10 cm in diameter over 2 years. This can be systematically observed at the most northern row of trees in Fig. 9. It is related to their relative position to the vehicle which turned left at that point. Thus, the stems are less completely captured compared to other locations and DBH computation is not reliable. Figure 13 compares both epochs for the marked trees. In most cases, only the DBH varies while height does not change considerably, which means it must be the same tree. For trees #26 and #35, we again observe the phenomenon of a not entirely acquired stem in 2016, reducing the height significantly. Four tree objects like the one around reference tree #14 or #20 did not exactly match their reference as well as in between epochs because of a slightly too large variation in their centre points. However, from their respective parameter data, it can be deduced that it is the same tree. Most of the 15 isolated objects are very close to their respective equivalent and could be drawn together by a bigger matching radius or more sophisticated matching method. In three cases (#2, #32, #33), a match was not possible because the tree was deleted in one epoch due to an erroneous segmentation and thus unrealistic derived tree parameters.

Fig. 12
figure 12

The segmented point clouds with trees #32 and #33 in 2016 (coloured in blue and light blue). A part of the other segmented trees and points from non-tree classes are given for orientation (grey)

Full size image
Fig. 13
figure 13

Inter-epoch comparison of computed height and DBH for trees with large DBH difference. Indicators state a computation was marked as unreliable in the (first\(\mid\)second) epoch, * for DBH, # for tree position (and thus matching)

Full size image

In the southern area (Fig. 10), most of the trees were confirmed. We concentrate on three interesting findings: First, near reference tree #66, an object has only been found in 2016, not in 2018, and did not fit the reference measurements from 2021. This would indicate that it had been cut before 2018, and indeed the second epoch does not contain a tree at this position. This is also clearly visible in the change grid from Figs. 7 and 8. Back on the map, the red circle at tree #69 indicates a duplication conflict. This means that in one epoch, two potential tree objects are found at almost the same position. Again, we observe an error in segmentation, because a part of this tree’s stem was identified as an own instance, possibly influenced by a very small tree near to it. Nonetheless, the RANSAC circle fitting proved to be robust towards this fragmentation effect caused by segmentation.

6.2 Changes on Geometry Level

With the information that a certain change has happened from object analysis, we can focus on these indicated trees in order to find out what exactly has happened or changed. In the case of tree #66, which was removed indeed, the behaviour in the change grid is obvious: In the zoom in Fig. 8, it can be seen in the second row of trees as a red stump a bit to the left of the centre. The only time it was captured was 2016—hence, only its lower part is visible due to obstruction from leaves of the first row of trees.

Similarly, tree #59 only seems to exist in 2016 and also Figs. 7 and 8 indicate something missing by red colour, although it seems to be only the crown. And indeed, here, we encounter a special case that becomes obvious when inspecting the original point clouds. Figure 14a shows the trees #59, #60 and #61. The point cloud is from the 2016 campaign, the colours indicate whether the points are in areas that are also occupied in 2018 (blue) or which are then empty (red). Judging from this only, the leftmost tree (which is #59) seems to have lost its crown. However, a glance at the same constellation using the 2018 data (Fig. 14b) reveals the true circumstances: tree #59 has been replaced by a new tree which is still protected by two stakes around it. Unfortunately, these two stakes are included in the tree segment, meaning they also influence DBH computation. The slice in the heights 1.20–1.40 m contains these three dense point clusters. RANSAC seems to interpret all of them as lying on one big circle, leading to a vast overestimation of DBH, and thus the rejection of the tree object in 2018. Besides that blunder, the comparison Fig. 14 clearly depicts the growing of the rightmost tree.

Fig. 14
figure 14

The trees #59, #60 and #61 as captured in a 2016 and b 2018. Blue colour indicates areas with occupancy at both times, red coloured points exist only in that specific epoch

Full size image

Whereas one could argue that the identification of the tree replacement could also have been interpreted from the change grid in Fig. 8, another crucial effect will be observed in the point clouds only. If we zoom into the change grid for the northern area and remove the first row of trees, Fig. 15 shows more change colours than usual on tree #15. However, it seems that the tree has not been completely replaced. The point clouds from each epoch lead to the answer: We isolate the tree by its segmentation label and compare the different point clouds. This time, we superimpose the points that only exist in one epoch (Fig. 16); green for 2016, purple for 2018. Both point clouds contain more or less the same structures, but at different positions. As this is only a local effect, we can exclude registration errors. The tree itself must have tilted. And indeed, in the reference measurements in 2021, this tree has been replaced by a new one. Its structure must have weakened so badly that it began to lean to one side, causing it to be a danger to the public.

Fig. 15
figure 15

Change grid of area North with the first row of trees removed. Annotated with reference TreeIDs for orientation

Full size image
Fig. 16
figure 16

Tree points that only exist in 2016 (green) or 2018 (purple). The tree has tilted

Full size image

Besides those locally significant changes, we observe in both Figs. 7 and 8 a band of red elements at the lowest crown edges, facing the street. That would mean that something had been there in 2016 and the same space was empty in 2018. Whilst a first intuition would point in the direction of tree pruning, this is contradicted as the phenomenon can be observed at every tree, not only those near streets or walkways. Hence, another effect has to be considered: In April 2016, freshly grown leaves added considerable weight to all branches. Especially, the almost horizontal branches at the lower crown edges must have been torn down by this weight, causing them to occupy space that would usually be empty in leaf-off season. This effect will be apparent at every part of the tree and thus makes a direct, detailed change detection on branch level impossible when leaf-on and leaf-off season are mixed.

Another factor in precision is the distance from the sensor to the object. This influences beam divergence and thus the precision of the return signal. With a broader beam, mixed signals from an uneven surface are more likely. As Fig. 17 shows, due to the specific sensor setup the main part of the crowns is measured from rather short distance, whereas stems and of course trees in the second and third row are farther away from the sensor at the time of their acquisition. It is important to note that because of the tilted sensors, one scanner rotation covers not only the areas 90\({^{\circ }}\) to the left or right of the vehicle, but rather an inclined plane. For the stems, this especially means that different sides of them are captured from severely varying distances and angles. The influence on DBH computation due to inaccurate point positions has been observed in Sect. 6.1. This might also influence model fitting at later stages.

Fig. 17
figure 17

Point cloud of the occupancy cells in area South coloured by the lowest distance from an included point to the sensor at the time of acquisition. Some exemplary measurements are indicated by red lines

Full size image

7 Conclusion and Outlook

We introduced a pipeline for the comparison of urban trees extracted from MLS point clouds. With the instance segmentation as the foundation for object-based multi-epoch analysis, the transition to the point cloud geometry is realised by occupancy grids. Comparing these in between epochs, we can deduce areas of interest where possible changes or anomalies are observed. This is supported by the 2D map of object changes. Finally, detailed analysis is possible by deriving differences between the measured point clouds. There, we can concentrate on one epoch and directly compare it to the occupancy states of the respective other epoch.

Our analyses have shown great potential in updating or creating tree inventories. Essential parameters like the diameter at breast height and tree height can be derived and compared for each tree. However, the results cannot yet convince in terms of robustness. Major error influences are accuracy of the instance segmentation, tree parameter computation, and inter-epoch object matching. The latter both are strongly influenced by the segmentation quality as well. In all these areas, we see the potential for more sophisticated and robust approaches. Completely model-based methods would facilitate the comparability of objects. Nonetheless, it has to be stated that trees are natural objects and a universal approach for detection and modeling is hard to achieve, especially considering the large variability of potential disturbances and obstructions met in an urban environment. This leads to another crucial factor: the data quality of the mobile laser scanning has to be sufficient and especially the completeness is of great importance. Street-based acquisition always leads to decreasing point density at trees farther from the trajectory. Considering this and possible obstructions, it is highly recommended to perform the measurement at leaf-off season. The effects of acquisition under foliated conditions were shown in the 2016 data set, resulting in errors in localisation, mapping and matching.

Tackling these challenges needs progress in data quality as well as in the processing approaches. However, already at this state, the application of change detection can be imagined in practice, most likely in combination with human analysis at areas of interest. It is also possible to compare the automatically detected changes with those already known to the inventory, since planned pruning and cutting is documented. In that context, intended changes can be separated from unintended ones and follow-on measures can be taken accordingly. The whole process can also be transferred from an urban street canyon to a clearance analysis of railroad tracks, covering another important sector of infrastructure.