Introduction

The beam and the beam-like structures resting on elastic foundations have wide applications in engineering practices, such as railway tracks, highway pavements, and pipelines lying on soil. In this case, numerous studies have been performed to analyze the static deflections, dynamic responses, and dynamic stability of beams on elastic or viscoelastic foundations. So, the computational models of a beam on elastic foundation or classical supports have large applications in various domains of engineering: transportation, marine, pavement, aerospace, mechanical, petroleum, geotechnical and civil engineering [1].

One of the principal problems in structural and geotechnical engineering aims to compute response of structures together with the surrounding soils. Certainly, the analysis of dynamic behavior of SSI is a very complicate task due to the complexities of soil behaviors and dynamic approach. Therefore, numerical models should consider SSI effects in the analysis and design of structures founded on soil medium. The modeling of the interfacial continuum between a beam and a soil is a main factor in the analysis of such problem [2]. This modeling becomes more complicated task for structures whose responses are influenced by the surrounding media.

The dynamic analysis of SSI is convoluted by the soil behavior, interface medium, structure, and dynamic procedure. For this concern, Far [3] has illustrated a comprehensive review on accurate and realist modeling technique and computational methods treating the SSI effects on structures resting on soft soils. The elaborated investigations aimed to study the effect of SSI and the seismic impact on structural response [4,5,6,7].

With the advances in computational field, the numerical finite element method (FEM) has been intensively used to predict the dynamic responses of engineering structures. Really, it is an important tool used to analyze the behavior of structures under static or dynamic loadings. To obtain significant responses using this method, the entire system must be discretized to a large number of finite and infinite elements which complicate the computational task [8]. The FEM is employed as a device to describe the behavior both of the beam and soil medium having various profiles [9, 10].

Besides the FEM, the boundary element method (BEM) is also one of the most powerful alternative numerical methods and among the most appropriate technique for seismic wave propagation in a complex geological media [11,12,13]. Both methods can be formulated either in time or in frequency domains and each one has own advantages and drawbacks. The choice of the numerical method in modeling depends on the properties of the system such as geometry, material properties, type of loading and boundary conditions. Therefore offered technologies, combined models of FEM and BEM are advantageously employed in numerical modeling of the infinite or semi-infinite domains.

On the other side, Doyle [14,15,16], Leung [17], Lee et al. [18: 1–2], Lee [19], Bashir and Ahmad [20] and Penava et al. [21] have contributed to the development of SEM. This numerical method has been extended to study dynamic responses of structures, which provides accurate results compared to the FEM and BEM. Firstly, the concept of SEM was introduced by Narayanan and Beskos [22] in which the dynamic stiffness matrix of the beam element is derived and corresponding solution is obtained by using the fast Fourier transform (FFT). Later, Rizzi and Doyle [23] used the terminology “Spectral Element Method” for the first time combined with FFT based spectral element analysis approach. Adding, the spectral element method finds its wide application in engineering domains. Due to their universal nature, the spectral methods are most commonly used to model the detection and identification of structural damage [24]. Fourier et al. [25] presented an application of the spectral element method to model axisymmetric flows in rapidity domain. Also, to simulate room acoustics, a wave-based numerical scheme is elaborated based on the spectral element method [26].

The formulation of SEM is similar to the conventional FEM but in spectral element formulation, the governing partial differential equation of motion is transferred from the time domain to the frequency domain by using discrete Fourier transform (DFT). In this case, the time variable disappears and the frequency variable appears as the mathematical variable of the problem. Based on obtained results [27,28,29], only one spectral finite element can be used to obtain satisfactory dynamic results. This numerical method reduces considerably the number of conventional finite elements and of the degrees of freedom [14], the time consuming, and the area of storage on the computer memory. Among the objectives of this work, the spectral element method is used to quantify the effects of the soil–structure interaction on free vibrations of beams.

Modeling of the soil–structure interaction

Recently the fixed-base of the structure assumption is rarely used studying the dynamic response of the structure. The compliance of soil foundation induces two distinct effects on the dynamic response of the structure (1) the modification of the free field motion at the base of the structure (kinematic interaction) and (2) the introduction of deformation from dynamic response of the structure into the supporting soil (inertial interaction) that is used in this work. Initial forces induced by the motion of foundation during the earthquake engender the compliant soil to deform affecting the super-structure inertial forces. This deformation propagates away from the structure which causes a decrease of the dynamic attenuation of the super-structure [30]. Adding, the compliance of the soil can be interpreted by a stiffness value that can be combined with damping propriety of the foundation forming a complex impedance function [31].

Mathematical formulation

The dynamic soil–structure interaction problems can be analyzed in time domain or in frequency domain. If the frequency domain is chosen then the structure can be modeled by using the spectral element method while the dynamic stiffness of the soil can be substituted by impedance functions. The discrete equation of the soil–structure system can be formulated in the displacement field with

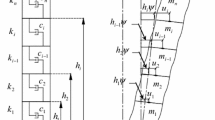
$$\left[ {\begin{array}{*{20}c} {K_{\text{BB}}^{\text{B}} } &\quad {K_{\text{BI}}^{\text{B}} } &\quad 0 \\ {K_{\text{IB}}^{\text{B}} } &\quad {K_{\text{BB}}^{\text{B}} + K_{\text{II}}^{\text{S}} } &\quad {K_{\text{IS}}^{\text{S}} } \\ 0 &\quad {K_{\text{SI}}^{\text{S}} } &\quad {K_{\text{SS}}^{\text{S}} } \\ \end{array} } \right]\left\{ \begin{aligned} u_{\text{B}}^{{}} \hfill \\ u_{\text{I}}^{{}} \hfill \\ u_{\text{S}}^{{}} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} F_{\text{B}}^{{}} \hfill \\ F_{\text{I}}^{{}} \hfill \\ F_{\text{S}}^{{}} \hfill \\ \end{aligned} \right\}$$
(1)

where KB and KS are the dynamic stiffness submatrices of beam and soil (exponents B, I and S stand for beam, interaction, and soil, respectively). \(u_{\text{B}}^{{}}\), \(u_{\text{I}}^{{}}\) and \(u_{\text{S}}^{{}}\) constitute kinematic degrees of freedom of the system and \(F_{\text{B}}^{{}}\), \(F_{\text{I}}^{{}}\) and \(F_{\text{S}}^{{}}\) are the dynamic forces for various components as indicated on Fig. 1.

Fig. 1
figure 1

Modeling of the subsuper-structure

Full size image

If no external forces are assumed to act on the structure, the displacement vectors \(u_{\text{B}}^{{}}\), \(u_{\text{I}}^{{}}\) can be computed using the first two equations of the relationship (1) that becomes as

$$\left[ {\begin{array}{*{20}l} {K_{\text{BB}}^{\text{B}} } &\quad {K_{\text{BI}}^{\text{B}} } \\ {K_{\text{IB}}^{\text{B}} } &\quad {K_{\text{II}}^{\text{B}} + K_{\text{II}}^{\text{S}} } \\ \end{array} } \right]\left\{ \begin{aligned} u_{\text{B}}^{{}} \hfill \\ u_{\text{I}}^{{}} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} 0 \hfill \\ - K_{\text{IS}}^{{}} u_{\text{S}}^{{}} \hfill \\ \end{aligned} \right\}$$
(2)

For free vibration of the beam, the determinant of the equation should be null.

$$\left| {\left[ {\begin{array}{*{20}c} {K_{\text{BB}}^{\text{B}} } &\quad {K_{\text{BI}}^{\text{B}} } \\ {K_{\text{IB}}^{\text{B}} } &\quad {K_{\text{II}}^{\text{B}} + K_{\text{II}}^{\text{S}} } \\ \end{array} } \right]} \right| = 0$$
(3)

The eigenvalues of the expression (3) using the spectral element method are described as bellow.

In the general case, a beam elastically restrained at ends and subjected to external load q(x, t), having a length L, cross-section \(\varOmega\), flexural rigidity EI and mass density \(\rho\) (Fig. 2).

Fig. 2
figure 2

Mechanical model of the beam

Full size image

K and \(R\) are the translational and rotational stiffness of the soil under foundation.

The partial differential equation for transverse vibrations of the Euler–Bernoulli beam can be written as follows:

$$c^{2} \frac{{\partial_{{}}^{4} v(x,t)}}{{\partial x_{{}}^{4} }} + \frac{{\partial_{{}}^{2} v(x,t)}}{{\partial t_{{}}^{2} }} = \frac{q(x,t)}{\rho \varOmega }$$
(4)

where \(c^{2} = \frac{\text{EI}}{\rho \varOmega }\) and \(v(x,t)\) is the vertical deflection of point of the beam at the spatial abscissa x and the temporal time t.

For free vibration of the system, the external load should be null and Eq. (4) becomes

$$c^{2} \frac{{\partial_{{}}^{4} v(x,t)}}{{\partial x_{{}}^{4} }} + \frac{{\partial_{{}}^{2} v(x,t)}}{{\partial t_{{}}^{2} }} = 0$$
(5)

The solution of Eq. (5) can be written as follows:

$$v(x,t) = X(x){\kern 1pt} \,T(t)$$
(6)

Introducing Eq. (6) into Eq. (4), this leads to:

$$c^{2} \frac{{\frac{{{\text{d}}_{{}}^{4} X(x)}}{{{\text{d}}x_{{}}^{4} }}}}{X(x)} = - \frac{{\frac{{{\text{d}}_{{}}^{2} T(t)}}{{{\text{d}}t_{{}}^{2} }}}}{T(t)} = \omega_{{}}^{2}$$
(7)

\(\omega\) is the natural frequency.

Thus, the spatial part of Eq. (7) can be deduced as

$$\frac{{{\text{d}}_{{}}^{4} X(x)}}{{{\text{d}}x_{{}}^{4} }} - \left( {\frac{\omega }{c}} \right)_{{}}^{2} X(x) = 0$$
(8)

The quantity \(\alpha\) that \(\alpha_{{}}^{4} = \left( {\frac{\omega }{c}} \right)_{{}}^{2} = \frac{\rho \varOmega }{EI}\omega_{{}}^{2}\), is denoted the dimensionless natural frequency and \(X(x)\) is the mode shape of the beam. The general solution of Eq. (8) is then

$$X(x,\omega ) = \left\langle {\cos \alpha x\;\,\sin \alpha x\;\cosh \alpha x\;\sinh \alpha x} \right\rangle \left\{ {c_{i}^{{}} } \right\}\quad \left( {i = 1 - 4} \right)$$
(9)

ci are coefficients of the general solution.

The nodal displacement vector \(\left\{ {q_{e}^{{}} } \right\}\) can be deduced by using kinematic conditions.

$$\left\{ {q_{e}^{{}} } \right\} = \left\{ \begin{aligned} v_{1}^{{}} \hfill \\ \theta_{1}^{{}} \hfill \\ v_{2}^{{}} \hfill \\ \theta_{2}^{{}} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad \alpha &\quad 0 &\quad \alpha \\ {\cos \alpha L} &\quad {\sin \alpha L} &\quad {\cosh \alpha L} &\quad {\sinh \alpha L} \\ { - \alpha \sin \alpha L} &\quad {\alpha \cos \alpha L} &\quad {\alpha \sinh \alpha L} &\quad {\alpha \cosh \alpha L} \\ \end{array} } \right]\left\{ \begin{aligned} c_{1}^{{}} \hfill \\ c_{2}^{{}} \hfill \\ c_{3}^{{}} \hfill \\ c_{4}^{{}} \hfill \\ \end{aligned} \right\}$$
(10)

With the rotation is \(\theta (x) = \frac{\partial X(x,\omega )}{\partial x}\)

Thus, the vector of generalized coefficients can be computed by

$$\left\{ c \right\} = \left[ {B(w)} \right]_{{}}^{ - 1} \left\{ {q_{e}^{{}} } \right\}$$
(11)
$${\text{With}}\,\left[ {B(\omega )} \right] = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad \alpha &\quad 0 &\quad \alpha \\ {\cos \alpha L} &\quad {\sin \alpha L} &\quad {\cosh \alpha L} &\quad {\sinh \alpha L} \\ { - \alpha \sin \alpha L} &\quad {\alpha \cos \alpha L} &\quad {\alpha \sinh \alpha L} &\quad {\alpha \cosh \alpha L} \\ \end{array} } \right]$$

Thus to resolve this problem, it is necessary to offer four independently boundary conditions. Based on the general problem (Fig. 2), the vector of forces at the ends of the beam can be established by using boundary conditions of the beam.

at x = 0

$$T_{1}^{{}} = {\text{EI}}\frac{{{\text{d}}_{{}}^{3} X(0)}}{{{\text{d}}x_{{}}^{3} }} + K_{0}^{{}} X(0)$$
(12a)
$$M_{1}^{{}} = {\text{EI}}\frac{{{\text{d}}_{{}}^{2} X(0)}}{{{\text{d}}x_{{}}^{2} }} - R_{0}^{{}} \frac{{{\text{d}}X(0)}}{{{\text{d}}x}}$$
(12b)

at x = L

$$T_{2}^{{}} = {\text{EI}}\frac{{{\text{d}}_{{}}^{3} X(L)}}{{{\text{d}}x_{{}}^{3} }} - K_{1}^{{}} X(L)$$
(12c)
$$M_{2}^{{}} = {\text{EI}}\frac{{{\text{d}}_{{}}^{2} X(L)}}{{{\text{d}}x_{{}}^{2} }} + R_{1}^{{}} \frac{{{\text{d}}X(L)}}{{{\text{d}}x}}$$
(12d)

In matrix form, the forces at the ends of beam (Fig. 1) using Eq. (12) are

$$\left\{ {F_{e}^{{}} } \right\} = \left\{ \begin{aligned} T_{1}^{{}} \hfill \\ M_{1}^{{}} \hfill \\ T_{2}^{{}} \hfill \\ M_{2}^{{}} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {K_{0}^{{}} } &\quad { - {\text{EI}}\alpha_{{}}^{3} } &\quad {K_{0}^{{}} } &\quad {{\text{EI}}\alpha_{{}}^{3} } \\ { - {\text{EI}}\alpha_{{}}^{2} } &\quad {R_{0}^{{}} \alpha } &\quad {{\text{EI}}\alpha_{{}}^{2} } &\quad { - R_{0}^{{}} \alpha } \\ {{\text{EI}}\alpha_{{}}^{3} \sin \alpha L - K_{1}^{{}} \cos \alpha L} &\quad { - {\text{EI}}\alpha_{{}}^{3} \cos \alpha L - K_{1}^{{}} \sin \alpha L} &\quad {{\text{EI}}\alpha_{{}}^{3} \sinh \alpha L - K_{1}^{{}} \cosh \alpha L} &\quad {{\text{EI}}\alpha_{{}}^{3} \cosh \alpha L - K_{1}^{{}} \sinh \alpha L} \\ { - {\text{EI}}\alpha_{{}}^{2} \cos \alpha L - R_{1}^{{}} \alpha \sin \alpha L} &\quad { - {\text{EI}}\alpha_{{}}^{2} \sin \alpha L + R_{1}^{{}} \alpha \cos \alpha L} &\quad {{\text{EI}}\alpha_{{}}^{2} \cosh \alpha L + R_{1}^{{}} \alpha \sin \alpha L} &\quad {{\text{EI}}\alpha_{{}}^{2} \sinh \alpha L + R_{1}^{{}} \alpha \cosh \alpha L} \\ \end{array} } \right]$$
(13)

In compact form, Eq. (13) becomes

$$\left\{ {F_{e}^{{}} } \right\} = \left[ {F(\omega )} \right]\left\{ c \right\}$$
(14)

Substituting Eq. (11) into Eq. (14), we obtain

$$\left\{ {F_{e}^{{}} } \right\} = \left[ {F(\omega )} \right]\left[ {B(\omega )} \right]_{{}}^{ - 1} \left\{ {q_{e}^{{}} } \right\}$$
(15)

The spectral stiffness matrix for a spectral finite element of classical boundary conditions can be evaluated by

$$\left[ {K_{e}^{{}} (\omega )} \right] = \left[ {F(\omega )} \right]\left[ {B(\omega )} \right]_{{}}^{ - 1}$$
(16)

The parameters of the spectral stiffness matrix can be easily deduced by applying the product \(\left[ {F(\omega )} \right]\) by \(\left[ {B(\omega )} \right]_{{}}^{ - 1}\).

Numerical examples

Validation of the approach

Beam without soil foundation

In order to show the accuracy of this procedure, free vibration of cantilever beam without foundation is used [31] in which the solution is obtained by the differential transform method (DTM) (Table 1).

Table 1 Comparison of \(\alpha\) values with DTM and exact solutions
Full size table

As it has seen from Table 1, this approach provides exact results compared to DTM method and exact solution, respectively.

Cantilever beam on translational spring

In this case, the characteristics of the cantilever beam are of a stainless steel one (Fig. 3). So the mechanical properties and geometrical dimensions are regrouped in Table 2.

Fig. 3
figure 3

Stainless steel beam on translational spring

Full size image
Table 2 Mechanical and geometrical properties of the stainless steel beam
Full size table

Again the performance of SEM instead the conventional FEM is shown in Table 3.

Table 3 First three frequencies of vibration by FEM and SEM
Full size table

To obtain accurate results using FEM, it is necessary meshing the beam into about 200 finite elements leading to the formulation of stiffness and masses matrices of size (400*400). Thus, computing time and space memory of the machine must be necessary in this phase.

Cantilever beam on rotational spring

The same stainless beam on a rotational spring \(K = 10_{{}}^{4} \,{\text{N}}/{\text{m}}/{\text{rad}}\) is used (Fig. 4)

Fig. 4
figure 4

Stainless steel beam on rotational spring

Full size image

Table 4 shows the first three modes of vibrations using FEM and SEM. Also, about 200 finite elements are required to obtain correct results and therefore one spectral element suffuses to obtain suitable resultants.

Table 4 First three frequencies of vibration by FEM and SEM
Full size table

The convergence of numerical results is validated using many numerical programs of SEM and FEM developed for this concern. The first category is focused on the use of the finite element program to calculate natural frequencies, mode shapes, and the second one is devoted to SEM to compute dimensionless frequency coefficient and to deduce natural frequencies.

Analysis using this approach

Concrete beam on elastic foundation

Then, a concrete cantilever beam is used; the concrete is of the class C30. The beam is characterized by geometrical and mechanical properties (Table 5). The beam is assumed on an equivalent Winkler spring substituting the soil stiffness (Fig. 5).

Table 5 Mechanical and geometrical properties of the concrete beam
Full size table
Fig. 5
figure 5

Beam on elastic springs

Full size image

To prove the robustness of SEM, only one spectral finite element is suffused to obtain the first three frequencies while the finite element analysis requires about 150 finite elements. Translational and rotational of the first three modes of vibration are depicted in Fig. 6 (Table 6).

Fig. 6
figure 6

First three modes of vibrations

Full size image
Table 6 First three frequencies of vibration by FEM and SEM
Full size table

It can be noted that major deflections are obtained by the first mode of vibration; therefore, major slope is resulted due to the third mode of vibration. More, the third mode of vibration engenders maximum deflections and slopes at the establishment of equivalent stiffness.

Effect of the beam length

Three lengths of the beam are selected to study their influence on the free vibration of Euler–Bernoulli beam (Fig. 7).

Fig. 7
figure 7

Beam studied with variable length

Full size image

Table 7 illustrates the first three modes of vibration obtained using SEM and FEM. Based on above results, the beam is always meshing with 150 finite elements. The length of the beam has an effect on the dynamic response of the beam that’s when the length is important, frequencies of vibration decrease with a considerable way. In this case, varying of the length of three times the frequency decreases with seven time. More, the natural frequencies of the beam decrease with increasing length.

Table 7 First three frequencies of vibration by FEM and SEM
Full size table

More from the beam theory, beams having short length vibrate with different manner than those of moderate and long lengths. Short lengths engender maximum deflections and slopes along beams due to neglecting of shear deformations (Figs. 8, 9). Both in translational and rotational vibrations, the length of the beam influences on the amplitude of the vibrations; beams with short length vibrate with great amplitudes (Figs. 8, 9).

Fig. 8
figure 8

Effect of beam length on translational vibrations

Full size image
Fig. 9
figure 9

Effect of beam length on rotational vibrations

Full size image

Effect of the properties of soil

The effect of mechanical properties of the soil is among objective of this study. For this reason, three types of soil are selected based on Winkler springs, which vary from loose, moderate to firm soil, which their stiffness values change as \(k_{0}^{{}} = (0.5,\,5,\,50)\,{\kern 1pt} 10_{{}}^{4} \,{\text{kN}}/{\text{m}}_{{}}^{3}\), respectively. Thus, the results of the first three natural frequencies of this system with varied soil parameters are listed in Table 8. This table shows eventually that frequencies increase with the soil property increases.

Table 8 First three frequencies of vibration for different soil parameters
Full size table

It is seen from Fig. 10 that when feeble properties of soil are used, rotational vibrations of the beam are opposite to those with better properties. Figure 10 shows the first three mode shapes of the cantilever beam considering into account the properties of the soil. It is remarkable that the vibration shape is affected by the properties of the soil on translational and rotational vibrations of the beam. For better characteristics of the soil, the beam vibrates with the same shape in the rotational case.

Fig. 10
figure 10

Effect of soil properties on the beam vibration

Full size image

Conclusion

In this paper, the spectral element method is used to analyze the vibration of beams on non-classical supported boundary conditions. The conclusions that can be tired from this analysis are:

  • The validation of this approach compared to the differential transform method and analytical method is verified using cantilever beam with and without Winkler springs.

  • The convergence of SEM is quite fast compared to FEM; one spectral finite element is suffused to reach accurate results.

  • Maximum deflections are observed with the 1st mode while similar slopes are obtained with the third mode of vibration.

  • Natural frequencies of the beam decrease with the increasing of the length and the short beams that vibrate with high amplitudes.

  • The properties of the soil influence considerably on mode shape of vibrations, on the deflections and slopes of beams.