Introduction

The present overlay design guidelines [1] in India considers the deterministic values of input parameters, such as, 15th percentile backcalculated layer moduli from falling weight deflectometer (FWD), average existing pavement layer thicknesses, Poisson’s ratios, commercial vehicle per day (CVPD), tire pressure, lane distribution factor (LDF), vehicle growth rate (r) and vehicle damage factor (VDF). Similarly, the pavement design guideline by American Association of State Highway and Transportation Officials (AASHTO) and the Mechanistic-Empirical Design Guide (MEPDG) considers deterministic values of existing pavement layer thicknesses and moduli in the overlay design process [2, 3]. Therefore, these design processes are essentially deterministic in nature. Analysis of data obtained by in situ cores and ground penetration radar indicates spatial variations in pavement layer thicknesses [4]. Likewise, the variations of layer moduli, tire pressure and VDF are well noted in the literature [5–8]. The available overlay design processes have limited capability in effectively considering the possible variations of design input parameters.

The variations of design input parameters can be accommodated in the probabilistic design approach. It has the capability of providing an accurate and reliable design process. Hence, the primary objective of this paper is to consider variability of various design input parameters and develop a probabilistic overlay design process. Some design input parameters (such as Poisson’s ratios, wheel spacing and tire pressure) do not have significant influence on pavement performance [5, 9, 10]. These parameters can be considered as deterministic. Whereas the design input parameters (such as layer thicknesses, resilient moduli, CVPD, LDF, VDF and r) with significant influence on pavement performance can be considered as probabilistic. The proposed design approach adopts both deterministic and probabilistic design input parameters.

The FWD data of a 30 km long stretch of highway is collected, and asphaltic overlay is designed based on deterministic [1] design approach and the proposed probabilistic design approach. The obtained results from both approaches are compared. Further, a systematic design example is presented. It can be used by the highway agencies as a reference calculation process in implementing the proposed approach. In addition, the effect of resilient moduli of different pavement layers on overlay thickness is studied using sensitivity analysis. Overall, it is expected that the outcome of this paper would be helpful to the practitioners and researchers to effectively incorporate variability of design input parameters in the asphaltic overlay design process.

Background

Variation in pavement layer thicknesses follows normal distribution with coefficient of variance (COV) ranging from 3 to 25% and 5–35% for asphaltic concrete (AC) layer and granular layer (GL), respectively [11–13]. Other parameters, such as, resilient moduli, cumulative traffic loading and regression coefficients of transfer functions also exhibit variations [5]. The resilient moduli follow either lognormal [6–8] or normal distribution [6, 11]. Similarly, the variation in Poisson’s ratios of pavement layers is well documented [9, 14, 15]. However, the influence of Poisson’s ratio variations on pavement performance is negligible [5, 9, 10]. Maji and Das [5] argued that the transfer functions calibrated from field performance studies can inherit variabilities and it can be accommodated by considering variations in the regression coefficients of these transfer functions. Overall, these variations in pavement layer related parameters would lead to variation in the remaining life of pavement (N). Similarly, the variations in commercial vehicle count (CVPD), lane distribution factor (LDF), vehicle damage factor (VDF) and vehicle growth rate (r) affect pavement design significantly [5]. However, variation in other traffic related pavement design input parameters, such as wheel spacing and tire pressure have negligible influence on pavement performance compared to layer thicknesses, layer moduli, CVPD, LDF and VDF [5]. Accommodating the variations in traffic related parameters would lead to variation in cumulative traffic loading (CTL).

The concept of probabilistic pavement design can be found as early as 1970s [11, 16, 17]. In the recent past, various concepts related to probabilistic pavement design method are widely researched [5, 18–26]. Most of these research works are related to design of new flexible pavement [5, 23, 27, 28]. Some available research works on uncertainties in asphaltic overlay are limited to reliability estimation of pavement service life or pavement performance [4, 19]. So far, none of these methods demonstrates probabilistic approach for designing asphaltic overlay thickness.

The probabilistic design approach requires numerical simulation method, such as Monte Carlo simulation [5, 12] or analytical tools, such as first order second moment (FOSM), point estimation method (PEM) and first order reliability method (FORM) [5, 21, 29] for the solution process. The numerical simulation yields accurate results; however, requires extensive computing power. On the other hand, analytical tools are less computer-dependent; however, requires the knowledge of probability distribution properties of input parameters. The results from analytical methods are found to be comparable with simulation results [4]. Further, FOSM requires comparatively less sampling for three or more probabilistic design input parameters and can easily be implemented. Hence, the FOSM method is adopted in the proposed probabilistic approach of asphaltic overlay design.

First order second moment (FOSM) method

In this method, the variability of design input parameters is represented by its probability distribution properties, such as, mean and variance or standard deviation. These properties are used in the design process to obtain the probability distribution properties of output parameters. The mean and variance of output parameters are obtained by first and second moment of truncated Taylor series expansion of the design function, respectively. Suppose, there are ‘m’ design input parameters, x 1, x 2,…, x i ,…, and x m , with the corresponding mean values of \(\mu_{1} ,\mu_{2} , \ldots ,\mu_{i} , \ldots {\text{ and }}\mu_{m}\). The expected mean value of output parameter can be obtained from the first moment of Taylor series expansion of the representative design function, f(.), as given in Eq. 1. Similarly, the variance of output parameter can be obtained from the second moment of Taylor series expansion. For computational efficiency, it can be approximated until the first order terms. The obtained variance is given in Eq. 2. These basic equations in FOSM method would be used in deriving reliability of asphaltic overlay design.

$$E\left[ {f\left( {x_{1} ,x_{2} , \ldots ,x_{i} , \ldots ,x_{m} } \right)} \right] = f\left( {\mu_{1} ,\mu_{2} , \ldots ,\mu_{i} , \ldots ,\mu_{m} } \right)\quad \left[ {{\text{5}}} \right]$$
(1)
$$V\left[ {f\left( {x_{1} ,x_{2} , \ldots ,x_{i} , \ldots x_{m} } \right)} \right] = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {\left( {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x_{i} }}} \right. \kern-0pt} {\partial x_{i} }}} \right)\left( {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x_{j} }}} \right. \kern-0pt} {\partial x_{j} }}} \right) \times\, {\text{COV}}\left[ {x_{i} ,x_{j} } \right]} } \quad \left[ {{\text{5}}} \right]$$
(2)

Concept of reliability in pavement design

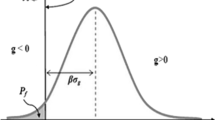
A pavement section is considered failed when cumulative traffic loading exceeds remaining life of pavement. As explained before, these are probabilistic parameters and are derived from other basic probabilistic design input parameters, such as, layer thicknesses, resilient moduli, CVPD, LDF, VDF and r. The probability distribution of these two parameters are compared to estimate the failure probability, P(f) [5, 23]. It is represented as the overlapped area of the two probability distribution functions in Fig. 1. This overlapped area depends on (1) the difference between the mean values (i.e., \(\mu_{\text{CTL}}\) and \(\mu_{N}\)), and (2) the probability distribution of cumulative traffic loading and remaining life of pavement. Now, these two factors finally depends on the variability of asphaltic overlay design input parameters. Hence, the overlapped area is not deterministic. Studies indicate that remaining life of a new pavement and cumulative traffic loading follows lognormal distribution [5, 16, 30, 31]. Pavement materials do deteriorate over time. The material deteriorations are nonlinear and unequal. Overall, this deterioration would instigate a time dependent variability in material properties. This would finally induce variation in remaining life of in-service pavement. In the absence of detailed information, this variation can be assumed to follow lognormal distribution. Hence, the natural logarithm of remaining life of in-service pavement, i.e., \({\text{ln(}}N )\), and cumulative traffic loading data, i.e., \({ \ln }({\text{CTL}})\), would follow normal distribution. The mean value and standard deviation of normally distributed \({\text{ln(}}N )\) and \({\text{ln(CTL)}}\) can be estimated using Eqs. 3 and 4, respectively. This conversion would simplify the standardized normal variate estimation (needed for reliability assessment). Generally, the appropriate guidance for estimating remaining life of in-service pavement and cumulative traffic loading data can be found in the asphaltic overlay design guidelines. Proper care should be taken to incorporate the effect of time dependent variability in material properties.

$$\mu _{{\ln (.)}} = \ln \left( {\mu _{{(.)}} / \sqrt {1 + \left( {\sigma _{{(.)}}^{2} /\mu _{{(.)}}^{2} } \right)} } \right)$$
(3)
$$\sigma_{\ln (.)} = \sqrt {\ln \left( {1 + \left( {{{\sigma_{(.)}^{2} } \mathord{\left/ {\vphantom {{\sigma_{(.)}^{2} } {\mu_{(.)}^{2} }}} \right. \kern-0pt} {\mu_{(.)}^{2} }}} \right)} \right)} ,$$
(4)

where \(\mu_{{{ \ln }(.)}}\) = mean value of normally distributed \({ \ln }(N)\) or \({ \ln }({\text{CTL}})\), \(\sigma_{{{ \ln }(.)}}\) = standard deviation of normally distributed \({ \ln }(N)\) or \({ \ln }({\text{CTL}})\), \(\mu_{(.)}\) = mean value of N or CTL in lognormal distribution, \(\sigma_{(.)}\) = standard deviation of N or CTL in lognormal distribution.

Fig. 1
figure 1

Schematic plot of cumulative traffic loading and remaining life of pavement

Full size image

Another way of representing the probability of failure is by safety margin (S) [5, 32]. It is represented as \(S = { \ln }(N) - { \ln }({\text{CTL}})\). In this definition, a pavement overlay design is considered failed when safety margin is less or equal to zero [32]. This concept is illustrated in Fig. 2 and mathematically represented by Eq. 5. By definition, reliability is the measure of design adequacy and considered as complimentary to the probability of failure. Mathematically, reliability can be represented by Eq. 6.

$$P\left( f \right) = P\left( {S \le 0} \right) = P\left\lfloor {\left\{ {\ln \left( N \right) - \ln \left( {\text{CTL}} \right)} \right\} \le 0} \right\rfloor ,$$
(5)

where P(f) = probability of failure, S = safety margin, CTL = cumulative traffic loading, N = remaining life of pavement

$${\text{Reliability}}(R) = 1 \, {-}{\text{ Probability of failure or }}P(f).$$
(6)
Fig. 2
figure 2

Schematic plot of safety margin

Full size image

Assuming remaining life of pavement and cumulative traffic loading are uncorrelated, the mean \(\mu_{S}\) and standard deviation \(\sigma_{S}\) of safety margin can be derived from Eqs. 1 and 2. These derivations are shown in Eqs. 7 and 8. Since, \({ \ln }(N)\) and \({ \ln }({\text{CTL}})\) are normally distributed, the safety margin, S, is also normally distributed with mean \(\mu_{S}\) and standard deviation \(\sigma_{S}\) [32]. The standardized normal variate (z) of normally distributed S can be obtained from Eq. 9. However, pavement overlay design is considered as failed when S is less or equal to zero. Hence, the standardized normal variate of failed overlay design can be obtained from Eq. 10. Hence, Eq. 6 can be rewritten as Eq. 11.

$$\mu_{S} = \mu_{\ln \left( N \right)} - \mu_{{\ln \left( {\text{CTL}} \right)}}$$
(7)
$$\sigma_{S} = \sqrt {\sigma_{\ln \left( N \right)}^{2} + \sigma_{{\ln \left( {\text{CTL}} \right)}}^{2} }$$
(8)
$$Z = {{\left( {\mu_{S} - S} \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{S} - S} \right)} {\sigma_{S} }}} \right. \kern-0pt} {\sigma_{S} }}$$
(9)
$$Z = {{\mu_{S} } \mathord{\left/ {\vphantom {{\mu_{S} } {\sigma_{S} }}} \right. \kern-0pt} {\sigma_{S} }}$$
(10)
$$R = 1 - \left\{ {0.5 - \psi \left( Z \right)} \right\} = 0.5 + \psi \left( {{{\left( {\mu_{\ln (N)} - \mu_{{\ln ({\text{CTL}})}} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{\ln (N)} - \mu_{{\ln ({\text{CTL}})}} } \right)} {\sqrt {\sigma_{\ln (N)}^{2} + \sigma_{{\ln ({\text{CTL}})}}^{2} } }}} \right. \kern-0pt} {\sqrt {\sigma_{\ln (N)}^{2} + \sigma_{{\ln ({\text{CTL}})}}^{2} } }}} \right)$$
(11)

Methodology

The proposed reliability based asphaltic overlay design methodology is similar to the current deterministic design process (see Fig. 3 for details). Instead of deterministic input parameters, it considers probabilistic input parameters. The probability distribution properties of input parameters are represented by their mean and standard deviation values. Incorporation of the probability distribution properties (i.e., mean and standard deviation) of each individual design input parameter and development of the proposed probabilistic overlay design process is explained through the following steps.

Fig. 3
figure 3

Deterministic process of asphaltic overlay design

Full size image

Step 1

The expected cumulative traffic loading (CTL) for the asphaltic overlay design is estimated from the basic probabilistic design input parameters, such as, CVPD, LDF, VDF and r. The basic formulation to estimate this parameter is adopted from IRC: 37 [33] and is represented by Eq. 12. The mean value and variance of CTL (i.e., \(\mu_{\text{CTL}}\) and \(\sigma_{\text{CTL}}^{2}\)) are derived from first and second moment of Taylor series expansion (see Eqs. 1 and 2) of Eq. 12, respectively. These derivations are shown in Eqs. 13a and 13b. Now, these values (\(\mu_{\text{CTL}}\) and \(\sigma_{\text{CTL}}^{2}\)) are for log-normally distributed CTL. Hence, the mean value and variance of normally distributed \(\ln ({\text{CTL}})\) (i.e., \(\mu_{{\ln \left( {\text{CTL}} \right)}}\) and \(\sigma_{{\ln \left( {\text{CTL}} \right)}}^{2}\)) are recalculated using Eqs. 3 and 4.

$${\text{CTL}} = {{365 \times {\text{VDF}} \times {\text{LDF}} \times {\text{CVPD}} \times \left\{ {\left( {1 + r} \right)^{n} - 1} \right\}} \mathord{\left/ {\vphantom {{365 \times {\text{VDF}} \times {\text{LDF}} \times {\text{CVPD}} \times \left\{ {\left( {1 + r} \right)^{n} - 1} \right\}} r}} \right. \kern-0pt} r},$$
(12)

where CTL = cumulative traffic loading, VDF = vehicle damage factor, LDF = lane distribution factor, CVPD = commercial vehicles per day, r = vehicle growth rate, n = design period.

$$\mu_{\text{CTL}} = 365 \times \mu_{\text{LDF}} \times \mu_{\text{CVPD}} \times \left\{ {n + n\left( {n - 1} \right){{\mu_{r} } \mathord{\left/ {\vphantom {{\mu_{r} } 2}} \right. \kern-0pt} 2}} \right\}$$
(13a)
$$\begin{aligned} \sigma_{\text{CTL}}^{2} &= \left\{ {{{\partial {\text{TCV}}} \mathord{\left/ {\vphantom {{\partial {\text{TCV}}} {\partial {\text{VDF}}}}} \right. \kern-0pt} {\partial {\text{VDF}}}}|_{{(\mu_{\text{VDF}} ,\mu_{\text{LDF}} ,\mu_{\text{CVPD}} ,\mu_{r} )}} } \right\}^{2} \sigma_{\text{VDF}}^{2} + \left\{ {{{\partial {\text{TCV}}} \mathord{\left/ {\vphantom {{\partial {\text{TCV}}} {\partial {\text{LDF}}}}} \right. \kern-0pt} {\partial {\text{LDF}}}}|_{{(\mu_{\text{VDF}} ,\mu_{\text{LDF}} ,\mu_{\text{CVPD}} ,\mu_{r} )}} } \right\}^{2} \sigma_{\text{LDF}}^{2} \hfill \\ &\quad + \left\{ {{{\partial {\text{TCV}}} \mathord{\left/ {\vphantom {{\partial {\text{TCV}}} {\partial {\text{CVPD}}}}} \right. \kern-0pt} {\partial {\text{CVPD}}}}|_{{(\mu_{\text{VDF}} ,\mu_{\text{LDF}} ,\mu_{\text{CVPD}} ,\mu_{r} )}} } \right\}^{2} \sigma_{\text{CVPD}}^{2} + \left\{ {{{\partial {\text{TCV}}} \mathord{\left/ {\vphantom {{\partial {\text{TCV}}} {\partial r}}} \right. \kern-0pt} {\partial r}}|_{{(\mu_{\text{VDF}} ,\mu_{\text{LDF}} ,\mu_{\text{CVPD}} ,\mu_{r} )}} } \right\}^{2} \sigma_{r}^{2} \hfill \\ \end{aligned}$$
(13b)

Step 2

The existing pavement layer thicknesses are obtained from the field. It can be obtained from construction history, core cut samples or ground penetration radar data. This is followed by FWD deflection data collection and processing. From the backcalculation process, the resilient moduli of pavement layers are estimated using the normalized deflection data, obtained layer thicknesses and assumed Poisson’s ratios. Pavement temperature affects resilient modulus of asphaltic layer. Similarly, the resilient modulus of base layer and subgrade are influenced by moisture content. The pavement design codes of a region stipulate these critical pavement temperature and moisture content. Hence, relevant temperature and moisture corrections are applied to these estimated resilient moduli for the critical values. Generally, based on the obtained information, the study area is divided into representative homogeneous pavement sections. Now, the variability in resilient moduli of all layers in each homogeneous section is examined. The variability is represented by the mean and standard deviation of corrected resilient moduli values for each homogeneous pavement section. The distribution type is identified and reported as well.

Step 3

The variability in layer thicknesses of each homogeneous pavement section is either derived from the collected field data or adopted from the literature review. It is recommended to use the field data to estimate the probability distribution properties of pavement layer thicknesses. However, acquisition of field data is expensive. In the absence of field data, information from other reliable source might be acceptable. Past studies indicate that pavement reliability is less sensitive to Poisson’s ratios, wheel spacing and tire contact pressure [5]. Hence, the variations of these parameters may not be considered in the design process. Using Eqs. 14a and 14b, the mean and standard deviation of fatigue and rutting strain are calculated from the probability distribution properties of resilient moduli and layer thickness, and deterministic values of Poisson’s ratios, wheel spacing and tire pressure.

$$\mu_{{\varepsilon_{t} }} \,or\,\mu_{{\varepsilon_{z} }} = f\left( {\mu_{{{\text{MR}}_{1} }} ,\mu_{{{\text{MR}}_{2} }} ,\mu_{{{\text{MR}}_{3} }} ,\rho_{1} ,\rho_{2} ,\rho_{3} ,\mu_{{H_{1} }} ,\mu_{{H_{2} }} ,{\text{ws}},{\text{tp}}} \right)$$
(14a)
$$\begin{aligned} \sigma_{{\varepsilon_{t} \,{\text{or}}\,\varepsilon_{z} }}^{2} &= \left\{ {\partial \varepsilon_{t} \,\,{\text{or}}\,\,{{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial {\text{MR}}_{1} |}}} \right. \kern-0pt} {\partial {\text{MR}}_{1} |}}_{{\left( {\mu_{{{\text{MR}}_{1} }} ,\mu_{{{\text{MR}}_{2} }} ,\mu_{{{\text{MR}}3}} ,\rho_{1} ,\rho_{2} ,\rho_{3} ,\mu_{{H_{1} }} ,\mu_{{H_{2} }} ,{\text{ws}},{\text{tp}}} \right)}} } \right\}^{2} \sigma_{{{\text{MR}}_{1} }}^{2} \hfill \\ &\quad + \left\{ {\partial \varepsilon_{t} \,\,{\text{or}}\,\,{{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial H_{2} |}}} \right. \kern-0pt} {\partial H_{2} |}}_{{\left( {\mu_{{{\text{MR}}_{1} }} ,\mu_{{{\text{MR}}_{2} }} ,\mu_{{{\text{MR}}3}} ,\rho_{1} ,\rho_{2} ,\rho_{3} ,\mu_{{H_{1} }} ,\mu_{{H_{2} }} ,{\text{ws}},{\text{tp}}} \right)}} } \right\}^{2} \sigma_{{H_{2} }}^{2} , \hfill \\ \end{aligned}$$
(14b)

where \(\varepsilon_{t}\) = maximum tensile strain at the bottom of asphaltic layer, \(\varepsilon_{z}\) = maximum compressive strain at the top of subgrade, \({\text{MR}}_{1}\) = resilient modulus of asphaltic layer, \({\text{MR}}_{2}\) = resilient modulus of base layer, \({\text{MR}}_{3}\) = resilient modulus of subgrade, \(\rho_{1}\) = Poisson’s ratio of asphaltic layer, \(\rho_{2}\) = Poisson’s ratio of base layer, \(\rho_{3}\) = Poisson’s ratio of subgrade, \(H_{1}\) = thickness of asphaltic layer, \(H_{2}\) = thickness of base layer, \({\text{ws}}\) = wheel spacing, \({\text{tp}}\) = tire pressure.

The mean fatigue and rutting strain in Eq. 14a can be obtained using the mean values of the design input parameters in pavement analysis software. A software that can analyze pavements as multi-layered elastic system with rough interface can be used for the purpose. In this study, IITPave is considered to estimate the strain values (refer [1, 33] for detail information about the software). However, estimating the variance using Eq. 14b requires partial derivation. This can be achieved by numerical analysis and the centered finite difference method as given in Eq. 15.

$$f^{\prime}\left( {x_{i} } \right) = {{\left\{ { - f\left( {x_{i + 2} } \right) + 8f\left( {x_{i + 1} } \right) - 8f\left( {x_{i - 1} } \right) + f\left( {x_{i - 2} } \right)} \right\}} \mathord{\left/ {\vphantom {{\left\{ { - f\left( {x_{i + 2} } \right) + 8f\left( {x_{i + 1} } \right) - 8f\left( {x_{i - 1} } \right) + f\left( {x_{i - 2} } \right)} \right\}} {12\delta }}} \right. \kern-0pt} {12\delta }},$$
(15)

where \(f^{\prime}\left( {x_{i} } \right)\) = first order derivative of \(x_{i}\), \(x_{i + 1}\) = \(x_{i} + \delta\), \(x_{i + 2}\) = \(x_{i} + 2\delta\), \(x_{i - 1}\) = \(x_{i} - \delta\), \(x_{i + 2}\) = \(x_{i} - 2\delta\), \(\delta\) = step size.

Step 4

The probability distribution properties (i.e., mean value and variance) of fatigue and rutting strain, obtained in the previous step, are used in appropriate transfer functions to estimate the probability distribution properties of fatigue and rutting remaining life of pavement (i.e., \(N_{\text{f}}\) and \(N_{\text{r}}\)), respectively. In this study, these transfer functions are adopted from IRC: 115 [1] and are represented in Eqs. 16a and 16b, respectively. Please note that these transfer functions were initially calibrated from field performance study of newly constructed asphaltic pavement. Though recommended by IRC: 115 [1], appropriate study is recommended for its application in estimating the remaining life of in-service pavement and thin asphaltic overlay. The mathematical derivations to estimate the mean value and variance of \(N_{\text{f}}\) and \(N_{\text{r}}\) are shown in Eqs. 17a, 17b, 17c and 17d. Since \(N_{\text{f}}\) and \(N_{\text{r}}\) follows lognormal distribution, the mean value and standard deviation of normally distributed \(\ln (N_{\text{f}} )\) and \(\ln (N_{\text{r}} )\) (i.e., \(\mu_{{\ln \left( {N_{\text{f}} } \right)}}\), \(\sigma_{{\ln \left( {N_{\text{f}} } \right)}}\), \(\mu_{{\ln \left( {N_{\text{r}} } \right)}}\) and \(\sigma_{{\ln \left( {N_{\text{r}} } \right)}}\)) are recalculated using Eqs. 3 and 4. Now, the recalculated probability distribution properties of \(\ln (N_{\text{f}} )\), \(\ln (N_{\text{r}} )\) and \(\ln \left( {\text{CTL}} \right)\) are used in Eq. 11 to estimate the fatigue and rutting reliability of existing pavement. The smaller of the two reliability values is considered as the critical reliability of existing pavement. A pavement requires asphaltic overlay when the critical reliability of existing pavement is lesser than a predefined threshold reliability value. Highway agencies can define the threshold reliability values based on roadway category, traffic volume, etc. Once the requirements of asphaltic overlay are established, the design process moves on to next steps for the estimation of suitable overlay thickness.

$$N_{\text{f}} = 0.711 \times 10^{ - 4} \times \left( {{1 \mathord{\left/ {\vphantom {1 {\varepsilon_{t} }}} \right. \kern-0pt} {\varepsilon_{t} }}} \right)^{3.89} \times \left( {{1 \mathord{\left/ {\vphantom {1 {{\text{MR}}_{1} }}} \right. \kern-0pt} {{\text{MR}}_{1} }}} \right)^{0.854} \quad \left( {{\text{IRC}}:{ 115 2}0 1 4} \right)$$
(16a)
$$N_{\text{r}} = 1.41 \times 10^{ - 8} \times \left( {{1 \mathord{\left/ {\vphantom {1 {\varepsilon_{z} }}} \right. \kern-0pt} {\varepsilon_{z} }}} \right)^{4.5337} \quad \left( {{\text{IRC}}:{ 115 2}0 1 4} \right)$$
(16b)
$$\mu_{{N_{\text{f}} }} = 0.711 \times 10^{ - 4} \times \left( {{1 \mathord{\left/ {\vphantom {1 {\mu_{{\varepsilon_{t} }} }}} \right. \kern-0pt} {\mu_{{\varepsilon_{t} }} }}} \right)^{3.89} \left( {{1 \mathord{\left/ {\vphantom {1 {\mu_{{{\text{MR}}_{1} }} }}} \right. \kern-0pt} {\mu_{{{\text{MR}}_{1} }} }}} \right)^{0.854}$$
(17a)
$$\sigma_{{N_{\text{f}} }}^{2} = \left\{ {\left. {{{\partial N_{\text{f}} } \mathord{\left/ {\vphantom {{\partial N_{\text{f}} } {\partial \varepsilon_{t} }}} \right. \kern-0pt} {\partial \varepsilon_{t} }}} \right|_{{(\mu_{{\varepsilon_{t} }} ,\mu_{{{\text{MR}}_{1} }} )}} } \right\}^{2} \sigma_{{\varepsilon_{t} }}^{2} + \left\{ {\left. {{{\partial N_{\text{f}} } \mathord{\left/ {\vphantom {{\partial N_{\text{f}} } {\partial \varepsilon_{t} }}} \right. \kern-0pt} {\partial \varepsilon_{t} }}} \right|_{{(\mu_{{\varepsilon_{t} }} ,\mu_{{{\text{MR}}_{1} }} )}} } \right\}^{2} \sigma_{{{\text{MR}}_{1} }}^{2}$$
(17b)
$$\mu_{{N_{\text{r}} }} = 1.41 \times 10^{ - 8} \times \left( {{1 \mathord{\left/ {\vphantom {1 {\mu_{{\varepsilon_{z} }} }}} \right. \kern-0pt} {\mu_{{\varepsilon_{z} }} }}} \right)^{4.5337}$$
(17c)
$$\sigma_{{N_{\text{r}} }}^{2} = \left\{ {{{\partial N_{r} } \mathord{\left/ {\vphantom {{\partial N_{r} } {\partial \varepsilon_{z} |_{{(\mu_{{\varepsilon_{z} }} )}} }}} \right. \kern-0pt} {\partial \varepsilon_{z} |_{{(\mu_{{\varepsilon_{z} }} )}} }}} \right\}^{2} \sigma_{{\varepsilon_{z} }}^{2}$$
(17d)

Step 5

In this step, the probability distribution properties of the target fatigue and rutting remaining life of pavement, \(N_{\text{f}}^{\text{T}}\) and \(N_{\text{r}}^{\text{T}}\), are estimated. First, the mean values of normally distributed \({ \ln }(N_{\text{f}}^{\text{T}} )\) and \({ \ln }(N_{\text{r}}^{\text{T}} )\) for the overlaid pavement (i.e., \(\mu_{{{ \ln }(N_{\text{f}}^{\text{T}} )}}\) and \(\mu_{{{ \ln }(N_{\text{r}}^{\text{T}} )}}\)) are estimated from Eq. 11. It is an iterative process where the target mean value of overlaid pavement remaining life is adjusted to match the given threshold reliability. In this process, the target standard deviation values of overlaid pavement remaining life, \(\sigma_{{{ \ln }(N_{\text{f}}^{\text{T}} )}}\) and \(\sigma_{{{ \ln }(N_{\text{r}}^{\text{T}} )}}\), are assumed to be equal to \(\sigma_{{{ \ln }\left( {N_{\text{f}} } \right)}}\) and \(\sigma_{{{ \ln }\left( {N_{\text{r}} } \right)}}\), respectively. In addition, the mean, \(\mu_{{{ \ln }({\text{CTL}})}}\), and standard deviation, \(\sigma_{{{ \ln }\left( {\text{CTL}} \right)}}\), of normally distributed \({ \ln }({\text{CTL}})\) remains unchanged. Then, using Eq. 3, the target mean value of overlaid pavement remaining life is recalculated for log-normally distributed \(N_{\text{f}}^{\text{T}}\) and \(N_{\text{r}}^{\text{T}}\) (i.e., \(\mu_{{N_{\text{f}}^{\text{T}} }}\) and \(\mu_{{N_{\text{r}}^{\text{T}} }}\)). It is to be noted that the target standard deviation of overlaid pavement remaining life (i.e., \(\sigma_{{N_{\text{f}}^{\text{T}} }}\) and \(\sigma_{{N_{\text{r}}^{\text{T}} }}\)) are same as \(\sigma_{{N_{\text{f}} }}\) and \(\sigma_{{N_{\text{r}} }}\).

Step 6

The target mean strain (\(\mu_{{\varepsilon_{t}^{\text{T}} }}\) and \(\mu_{{\varepsilon_{z}^{\text{T}} }}\)) of overlaid pavement is estimated using the adopted transfer functions (see Eq. 16a and 16b). Equations 18a and 18b are used for critical fatigue and rutting life, respectively. It is to be noted that equivalent resilient modulus of asphaltic layer (\(\mu_{{{\text{MR}}_{\text{eqv}} }}\)) should be adopted for critical fatigue life.

$$\mu_{{\varepsilon_{t}^{\text{T}} }} = \left( 0.711 \times 10^{ - 4} / \mu_{{N_{\text{f}}^{\text{T}} }} \times \mu _{{{\text{MR}}_{{{\text{eqv}}}} }}^{{0.854}} \right)^{1/3.89}$$
(18a)
$$\mu_{{\varepsilon_{z}^{\text{T}} }} = \left( 1.41 \times 10^{ - 8} / \mu_{{N_{\text{r}}^{\text{T}} }} \right)^{1/4.5337}$$
(18b)

Step 7

This is the final step of the design process where the mean overlay thickness is decided iteratively. In this step, the asphaltic overlay is considered as the top layer of a four-layer pavement system. The overlay thickness is iteratively adjusted till the target mean strain obtained in the previous step matches with the corresponding strain from pavement analysis. Again, a software that can analyze the pavements as multi-layered elastic system with rough interface can be used for the purpose. As indicated in Step 3, this study uses IITPave. Now, Eq. 19 is the modified Eq. 14a for a four-layer pavement system.

$$\mu_{{\varepsilon_{t}^{\text{T}} }} \,\,{\text{or}}\,\,\mu_{{\varepsilon_{z}^{\text{T}} }} = f\left( {\mu_{{{\text{MR}}_{\text{OL}} }} ,\mu_{{{\text{MR}}_{1} }} ,\mu_{{{\text{MR}}_{2} }} ,\mu_{{{\text{MR}}_{3} }} ,\rho_{\text{OL}} ,\rho_{1} ,\rho_{2} ,\rho_{3} ,\mu_{{H_{\text{OL}} }} ,\mu_{{H_{1} }} ,\mu_{{H_{2} }} ,{\text{ws}},{\text{tp}}} \right),$$
(19)

where \({\text{MR}}_{\text{OL}}\) = resilient modulus of asphaltic overlay, \(\rho_{\text{OL}}\) = Poisson’s ratio of asphaltic overlay, \(H_{\text{OL}}\) = asphaltic overlay thickness.

Illustration of probabilistic overlay design process

An example based on real world data is discussed here to explain the proposed design steps. The data is obtained from a 30 km long roadway stretch, connecting Nadiad and Modasa in the state of Gujarat, India. In this study, the FWD data is collected at every kilometer, pavement layer thickness information is obtained from the construction records and the commercial vehicles are counted at the site. However, the COV values of layer thicknesses and commercial vehicle count are assumed from the literature [5] and Poisson’s ratios, wheel spacing and tire pressure are taken from IRC: 115 [1]. Similarly, the mean values of VDF, LDF and r are taken from IRC: 37 [33] and its COV values from the literature [5]. The values of all input parameters are shown in Table 1. A step-by-step illustration of the proposed design procedure is discussed in the subsequent paragraphs.

Table 1 Properties of design input parameters
Full size table

Step 1: Using relevant values from Table 1, the mean value and standard deviation of cumulative traffic loading \((\mu_{\text{CTL}} )\) is calculated from Eqs. 13a and 13b, respectively. These calculated values are 9.2 million standard axles (MSA) and 2.46 MSA, respectively. Further, the mean value and standard deviation of normally distributed \({ \ln }({\text{CTL}})\) (i.e., \(\mu_{{{ \ln }\left( {\text{CTL}} \right)}}\) and \(\sigma_{{{ \ln }\left( {\text{CTL}} \right)}}^{2}\)) are estimated as 2.18 MSA and 0.26 MSA, respectively.

Step 2: The mean critical value, standard deviation and distribution type of backcalculated resilient moduli obtained from post-processed FWD data of the homogeneous pavement section are given in Table 2. As per Indian design standards, i.e., IRC: 37 [33] and IRC: 115 [1], the annual average pavement temperature (AAPT) is considered as standard pavement temperature for resilient modulus of asphaltic layer, and moisture content during recession of monsoon for resilient modulus of granular layer and subgrade. Hence, the mean critical values are obtained after applying appropriate corrections for standard pavement temperature of 35 °C and maximum subgrade moisture during the recession of monsoon.

Table 2 Backcalculated resilient moduli
Full size table

Step 3: The mean value and variance of fatigue and rutting strains are calculated from Eqs. 14a and 14b, respectively. The mean rutting and fatigue strains are obtained by considering the mean value of all parameters in the pavement analysis software, IITPAVE. In this process, the estimated mean fatigue and rutting strains (i.e., \(\mu_{{\varepsilon_{t} }}\) and \(\mu_{{\varepsilon_{z} }}\)) are \(2.882 \times 10^{ - 4}\) and \(5.867 \times 10^{ - 4}\), respectively. However, estimating variance requires partial derivations using Eq. 15. This partial derivation is done with respect to probabilistic parameters that follow either lognormal distribution (such as resilient moduli of the pavement layers) or normal distribution (such as pavement layer thicknesses). Estimating \(x_{i \pm 1}\) and \(x_{i \pm 2}\) for normally distributed parameters are straightforward. However, parameters that follow lognormal distribution requires additional steps to estimate \(x_{i \pm 1}\) and \(x_{i \pm 2}\). These steps are given below.

  1. (a)

    Calculate the mean value and standard deviation of normally distributed parameter, \(\ln \left( . \right)\) from Eqs. 3 and 4, respectively. For example, the calculated mean value and standard deviation of normally distributed \({ \ln }({\text{MR}}_{1} )\) is 7.28 and 0.1685 MPa, respectively.

  2. (b)

    Appropriate step size, \((\delta )\) less than the obtained standard deviation, is selected. For \({ \ln }({\text{MR}}_{1} )\) it can be 0.1 MPa (0.1 < 0.1685).

  3. (c)

    Calculate \(x_{i \pm 1}\) and \(x_{i \pm 2}\) for the normally distributed parameter, \(\ln \left( . \right)\). For \({ \ln }({\text{MR}}_{1} )\), the calculated \(x_{i \pm 2}\), \(x_{i \pm 1}\), \(x_{i - 1}\) and \(x_{i - 2}\) values are 7.48, 7.38, 7.18 and 7.08 MPa, respectively.

  4. (d)

    Now, \(x_{i \pm 1}\) and \(x_{i \pm 2}\) of the normally distributed parameters are recalculated for their lognormal distribution. It is done by taking the exponential of \(x_{i \pm 1}\) and \(x_{i \pm 2}\) (i.e., \({\text{e}}^{{x_{i} }}\)). For MR1, these values are 1772.24, 1603.59, 1312.91 and 1187.97 MPa, respectively. These values are used in pavement analysis software to estimate \(f(x_{i \pm 2} )\), \(f(x_{i \pm 1} )\), \(f(x_{i - 1} )\) and \(f(x_{i - 2} )\).

  5. (e)

    The equivalent step size \((\delta )\) is estimated as \(({\text{e}}^{\delta } - 1)\mu_{\left( . \right)}\). For MR1 it is 154.917 MPa.

Following the above steps, the partial derivatives of rutting strain with respect to MR1 (i.e., \({{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial {\text{MR}}_{1} }}} \right. \kern-0pt} {\partial {\text{MR}}_{1} }}\)) is estimated as \(- 8.095 \times 10^{ - 8}\). Similarly, the other derivatives are estimated as \({{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial {\text{MR}}_{2} }}} \right. \kern-0pt} {\partial {\text{MR}}_{2} }} = 4.8136 \times 10^{ - 7}\) and \({{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial {\text{MR}}_{3} }}} \right. \kern-0pt} {\partial {\text{MR}}_{3} }} = 3.788 \times 10^{ - 6}\).

The values of \(x_{i \pm 1}\) and \(x_{i \pm 2}\) for normally distributed parameters are calculated by selecting step size \((\delta )\) that is less than the standard deviation \((\sigma_{\left( . \right)} )\). These values are used in pavement analysis software to estimate \(f(x_{i + 2} )\), \(f(x_{i + 1} )\), \(f(x_{i - 1} )\) and \(f(x_{i - 2} )\). Thereafter, the partial derivatives are obtained using Eq. 15. Following this process, the partial derivatives with respect to asphaltic and base layer thicknesses are estimated as \({{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial H_{1} }}} \right. \kern-0pt} {\partial H_{1} }} = - 3.35 \times 10^{ - 6}\) and \({{\partial \varepsilon_{z} } \mathord{\left/ {\vphantom {{\partial \varepsilon_{z} } {\partial H_{2} }}} \right. \kern-0pt} {\partial H_{2} }} = - 1.81 \times 10^{ - 6}\), respectively. Using these estimated partial derivatives and appropriate standard deviations from Tables 1 and 2 in Eq. 14b, the standard deviation of rutting strain \((\sigma_{{\varepsilon_{z} }} )\), is obtained as \(11.34 \times 10^{ - 5}\). In a similar process, the standard deviation of fatigue strain \((\sigma_{{\varepsilon_{t} }} )\) is obtained as \(5.19 \times 10^{ - 5}\).

Step 4: Using Eqs. 17a and 17b, the calculated mean value \((\mu_{{N_{\text{f}} }} )\) and standard deviation \((\sigma_{{N_{\text{f}} }} )\) of fatigue remaining life are \(8.279\) MSA and \(5.922\) MSA, respectively. Similarly, Eqs. 17c and 17d yielded mean value \((\mu_{{N_{\text{r}} }} )\) of \(6.31\) MSA and standard deviation \((\sigma_{{N_{\text{r}} }} )\) of \(5.532\) MSA for rutting remaining life, respectively. It is evident that rutting remaining life is critical for this pavement section. Since the critical mean remaining life of pavement is lesser than the mean cumulative traffic loading obtained in Step 1, asphaltic overlay is necessary. Now, the mean value and standard deviation of normally distributed \(\ln (N_{\text{r}} )\) (i.e., \(\mu_{{\ln (N_{\text{r}} )}}\) and \(\sigma^{2}_{{\ln \left( {N_{r} } \right)}}\)) are estimated as 1.56 MSA and 0.76 MSA, respectively.

Step 5: In this example, the asphaltic overlay is designed for 90% reliability. Using Eq. 11, the target mean rutting remaining life for 90% reliability is calculated. It is an iterative process and the statistical properties of normally distributed \({ \ln }({\text{CTL}})\) and \({ \ln }(N_{\text{r}} )\) are used in the process. The obtained target mean rutting remaining life, \(\mu_{{\ln (N_{\text{r}}^{\text{T}} )}}\), for normally distributed \({ \ln }({\text{CTL}})\) is 3.21 MSA and hence, the recalculated mean rutting remaining life for log-normally distributed \(N_{\text{r}}^{\text{T}}\) (i.e., \(\mu_{{N_{\text{r}}^{\text{T}} }}\)) is 25.33 MSA. The corresponding distributions of CTL, N r and \(N_{\text{r}}^{\text{T}}\) with 90% reliability are shown in Fig. 4.

Fig. 4
figure 4

Distribution of cumulative traffic loading and remaining life of pavement

Full size image

Step 6: Corresponding to the target rutting remaining life of 25.33 MSA, the target mean rutting strain, \(\mu_{{\varepsilon_{z}^{\text{T}} }}\), for the overlaid pavement is 4.32 × 10−4. Equation 18b is used for the estimation.

Step 7: The asphaltic overlay with resilient modulus of 1700 MPa and Poisson’s ratio of 0.35 is considered as the top layer of a four-layer pavement system. Existing pavement layers represents the other three layers of the pavement system. The asphaltic layer thickness is iteratively adjusted till the rutting strain meets the target value of 4.32 × 10−4. In this process, the overlay thickness of 53 mm meets the criteria. The corresponding fatigue remaining life of the overlaid pavement is compared with the cumulative traffic loading and found to be safe. Hence, overlay thickness of 53 mm (rounded-up to 55 mm) is recommended for 90% reliable pavement overlay.

Results and discussion

The design example is extended for other reliability values. Table 3 summarizes the results obtained for reliability level of 75–100% with an increment of 5%. For this pavement section, the estimated overlay thickness by deterministic method of IRC: 115 [1] is 58 mm. It can be rounded-up to 60 mm. Further, comparing the deterministic overlay thickness (i.e., [1] process) with the probabilistic overlay thickness (given in Table 3), it is noted that the reliability of deterministic overlay thickness is little less than 95%. This might be good for roadways at the top of hierarchical roadway classification (e.g., national highway, freeway and expressway) with conservative design standards and stringent construction practice. However, overlay thickness of 46 mm (rounded-up to 50 mm), yielding reliability of more than 85%, could be sufficient for roadways in the mid-tier of hierarchical roadway classification (e.g., major district road and other district road). Figure 5 represents the variation of reliability with mean value of overlay thicknesses. The figure also represents the expected fatigue and rutting remaining life as given in Table 3. It is noted that the overlay thickness and pavement life increases almost linearly till 95% reliability, and thereafter it increases exponentially. The huge leap in the expected pavement remaining life, and thus overlay thickness beyond 95% reliability may be attributed to the high coefficient of variance (i.e., standard deviation to mean value ratio) of fatigue and rutting remaining life. A high coefficient of variance indicates wide or flatter distribution of fatigue and rutting remaining life. Therefore, to achieve 100% reliability, the expected safety margin, and thus the expected remaining life of pavement would be very high (refer Fig. 1 and Eq. 11).

Table 3 Overlay thickness for various reliability levels
Full size table
Fig. 5
figure 5

Overlay thickness and pavement life at varying reliability

Full size image

Obtaining resilient moduli by backcalculation is an iterative process, where the finally obtained resilient moduli greatly depend on the initial seeding values. Therefore, it would be interesting to observe the effect of change in asphaltic overlay thickness for any possible variation in resilient moduli of pavement layers. Hence, sensitivity analysis of pavement layer’s resilient moduli has been carried out. Here, the mean value of a selected pavement layer’s resilient modulus is varied while the mean values of all other design input parameters are considered as fixed. In addition, the standard deviation of all the parameters remains unaltered. The process is repeated separately for fatigue and rutting remaining life. Changes in asphaltic overlay thickness are noted for the variation of each pavement layer’s resilient modulus. This information is plotted in the graph as shown in Figs. 5 and 6 for fatigue and rutting remaining life, respectively. In these figures, the slope of each line indicates its level of sensitivity. For critical fatigue remaining life, asphaltic overlay thickness is highly sensitive to resilient modulus of base layer (see Fig. 6). This is in conformation with similar studies related to asphaltic pavement design [5]. Similarly, for critical rutting life, the asphaltic overlay thickness is highly sensitive to resilient modulus of subgrade (see Fig. 7). This supports the conclusion made by Maji and Das [5] and Deshpande et al. [19]. Further, it is observed that the asphaltic overlay thickness is least sensitive to resilient moduli of overlaid layer. Sensitivity analysis by Deshpande et al. [19] for fatigue and rutting reliability of overlaid pavement revealed similar findings.

Fig. 6
figure 6

Sensitivity of resilient moduli for fatigue remaining life

Full size image
Fig. 7
figure 7

Sensitivity of resilient moduli for rutting remaining life

Full size image

Conclusions

This study proposed reliability based probabilistic approach for design of asphaltic overlay that can consider variability in various design input parameters. A less computer dependent analytical method (FOSM based) is adopted for the purpose. The FWD data of a 30 km long stretch of highway are collected and overlay design is performed based on deterministic and proposed probabilistic design approach. A systematic design example is presented which can be used by highway agencies as a reference solution to easily implement the proposed approach. The proposed probabilistic method can accommodate variations in various design input parameters (such as layer thicknesses, resilient moduli, CVPD, LDF, VDF and r) in the design of overlay thickness. This makes the proposed approach different from the existing overlay design procedures found in IRC: 115 [1], AASHTO [2] and MEPDG [3]. Considerably thicker overlay is obtained by the present deterministic method and it corresponds to approximately 95% reliability. The asphaltic overlay thickness is found to be sensitive to resilient modulus of base and subgrade layers; thus, these two parameters should be estimated carefully in the backcalculation process. It is recommended that proposed reliability based method be verified from field performance of the overlaid pavement. Studies conducted by Deshpande et al. [19] and Hong [4] may be helpful for this purpose. In addition, effects of reliability on maintenance cost should be analyzed. It is expected that the proposed probabilistic overlay design approach would be helpful to highway agencies in adopting reliability based overlay design. Overall, it can accommodate variability of field material properties and construction practices in the asphaltic overlay design process.