Introduction

It is essential to understand the basic causes and mechanisms of slope failures which are often associated with the progressive mechanism of failure involving decreased shear strength and increased pore water pressure. The progressive mechanism of shear strength decrease may be simply described as follows. Initially, a soil element within a slope may be at its ‘peak’ shear strength. During the process of deformation, shear strength decreases till it reaches the lower limit called the ‘residual’ shear strength. This process is denoted as ‘strain-softening’. The extent of strain-softening along a potential slip surface in a slope may vary from 0 to 100 % depending on how much of the slip surface length is at residual shear strength. The term ‘residual factor’ was proposed by Skempton [11, 12] to denote the extent of decrease from peak to residual strength. The factor of safety is highest if the entire slip surface is at peak shear strength and at the lowest if the entire slip surface is at the residual strength. In general, however, the factor of safety would be at a value between peak and residual depending on the extent of strain-softening which is often unknown. Historical factors which would influence the extent of strain-softening within a slope include the process of slope formation, fluctuations in pore water pressure over time, seismic activity and other processes. Consequently, it is necessary for slope stability and reliability assessments to consider the role of strain-softening in a more comprehensive manner.

Results of conventional assessments of stability based on traditional deterministic models of slope stability are subject to significant uncertainty. The sources of uncertainty include natural variability of geotechnical parameters, systematic errors and imperfect geotechnical models. Both spatial and temporal uncertainties play an important part in the assessments of long-term performance of slopes. Reliability analysis within a probabilistic framework offers a very powerful tool for taking into consideration the variability of key geotechnical parameters as well as other uncertainties.

In this paper, the progressive decrease in shear strength along potential slip surfaces is considered in terms of the Skempton’s residual factor. The residual factor may be considered as one among several random variables in the slope reliability formulation for finite slope, which has been developed on the basis of a limit equilibrium model, specifically, the Bishop’s simplified method. The first order reliability method (FORM) [7] has been used for the purpose of reliability analysis. An assumption of suitable probability distribution (out of the generalized beta distribution) for residual factor has been made. Parametric analyses will prove to be very useful for understanding the change in reliability considering uncertainty, spatial and temporal, in the residual factor. A sensitivity analysis based on the FORM method shows the relative importance of residual factor as a random variable.

Methodology

Deterministic slope stability analysis

Limit equilibrium based slope stability analyses have conventionally been performed in a deterministic manner and the entire process consists of two joint tasks, namely, computation of factor of safety of a trial slip surface using a method of slices, and then search for the critical slip surface having the minimum factor of safety FSmin (commonly called as the deterministic critical slip surface) using an optimization technique. Among the methods of slices, the Bishop simplified method is known to yield values of factor of safety comparable to those from the rigorous methods. Furthermore, assumption of circular slip surfaces greatly simplifies the determination of critical slip surfaces. In this study, therefore, the Bishop simplified method has been adopted. However, keeping the basic principles unchanged, the present analysis can be extended in future in terms of use of a rigorous method of slices. Therefore, the optimization problem involved in the deterministic slope stability analysis has been solved using the sequential quadratic programming (SQP) [10] technique which has been rated as a powerful optimization technique [5] and can be easily implemented in the MATLAB platform with its optimization toolbox.

Residual factor for a potential slip surface

In strain-softening soils, the processes of progressive failure are often associated with a decrease in the values of shear strength. The extent to which shear strength has decreased from its peak value to its residual value at a point in a soil mass can be expressed in terms of a ‘residual factor’ introduced by Skempton [11, 12]. If no decrease has occurred, the residual factor is equal to 0; if the strength has decreased to the residual value, the residual factor is 1; and in all other cases this factor lies between 0 and 1. It is useful to consider an alternative definition of the residual factor which represents the whole of a potential slip surface. For a perfectly brittle soil, strain-softening will lead to one part of slip surface being at residual shear strength and the remaining part at peak shear strength. Skempton [11] proposed that the average residual factor R F over a slip surface could be represented as the proportion of slip surface length along which the shear strength has decreased to the residual, i.e., R F = L r/L in which L is the total length of a slip surface of which the length L r is at the residual shear strength, the remaining length (L − L r) being still at the peak shear strength. The magnitude of the average residual factor represents the state of nature for a slope at a given point in time, being a consequence of the decrease in material strength parameters associated with processes of progressive failure.

Estimation of residual factor using an LEM based progressive failure model [2]

Chowdhury et al. [2] proposed a simple model for progressive failure of slopes in strain-softening soils under the framework of the conventional limit equilibrium methods of slices (LEM). Assuming that the soil is perfectly brittle strain-softening, the shear strength parameters of overstressed slices will reduce to residual values \(c^{\prime}_{\text{r}}\) and \(\tan \phi^{\prime}_{\text{r}}\), whereas the remaining segments of the slip surface will still be at the peak shear strength \(c^{\prime}_{\text{p}}\) and \(\tan \phi^{\prime}_{\text{p}}\). An iterative process is required to identify the failed segments of slip surface and redistribute excess shear stress until no more segments are overstressed. Once the overstressed or failed slices have been identified, the residual factor R F, representing the entire slip surface can be estimated by the ratio of the summation of lengths of the failed slices to the overall length of the slip surface.

Performance function for a curved slip surface—Bishop simplified method

The commonly used expression for factor of safety (FS) based on the Bishop simplified method (no strain-softening) is given by:

$${\text{FS}} = \frac{{\sum {\left[ {\left\{ {c^{\prime}b + W(1 - r_{\text{u}} ) \times \tan \phi^{\prime}} \right\}/m_{\upalpha} } \right]} }}{{\sum {W\sin \alpha } }}$$
(1)

where, b is the slice width, W is the slice weight, r u is the non-dimensional pore water pressure ratio at slice base, and α is the inclination of slice base. The factor m α is given by:

$$m_{\alpha } = \left( {1 + \frac{{\tan \alpha \tan \phi^{\prime}}}{\text{FS}}} \right)\cos \alpha$$
(2)

To analyze the slope in strain-softening soil, the shear strength parameters would need to be redefined so that strain-softening process can be incorporated in the Bishop method, by including the residual factor R F. The modified shear strength parameters, \(c^{\prime}_{rf}\) and \(\phi^{\prime}_{\text{rf}}\) are as follows:

$$c^{\prime}_{\text{rf}} = R_{\text{F}} c^{\prime}_{\text{r}} + (1 - R_{\text{F}} )c^{\prime}_{\text{p}}$$
(3)
$$\tan \phi^{\prime}_{\text{rf}} = R_{\text{F}} \tan \phi^{\prime}_{\text{r}} + (1 - R_{\text{F}} )\tan \phi^{\prime}_{\text{p}}$$
(4)

where, R F is the overall or average residual factor for the entire length of the curved slip surface of circular shape. These modified shear strength parameters follow directly from Skempton’s definition of residual factor as shown by Chowdhury and Bhattacharya [1].

Now, the expression for the factor of safety, FS, associated with a curved slip surface of circular shape for a simple slope (Eqs. 1, 2), based on the Bishop simplified method has been modified for a strain-softening soil, by including modified shear strength parameters from Eqs. (3) and (4). The modified expression is as follows:

$${\text{FS}} = \frac{{\sum {\left[ {\left\{ {c^{\prime}_{\text{rf}} b + W(1 - r_{\text{u}} ) \times \tan \phi^{\prime}_{\text{rf}} } \right\}/m_{{\alpha {\text{rf}}}} } \right]} }}{{\sum {W\sin \alpha } }}$$
(5)

Where,

$$m_{{\alpha {\text{rf}}}} = \left( {1 + \frac{{\tan \alpha \tan \phi^{\prime}_{\text{rf}} }}{\text{FS}}} \right)\cos \alpha$$
(6)

It may be noted that Eq. (5) is analogous to Eq. (1) except that c′ is replaced by \(c^{\prime}_{\text{rf}}\) given by Eq. (3), tanϕ′ is replaced by \(\tan \phi^{\prime}_{\text{rf}}\) given by Eq. (4), and m α is replaced by m αrf given by Eq. (2).

Residual factor R F as a random variable

Nature of probability distribution for the residual factor

Due to the absence of published studies as well as limited availability of information on the probability distribution of the residual factor R F, a choice may be made between the assumption of a normal distribution and that of a generalized beta distribution. The choice of a normal distribution allows wide flexibility in accommodating the mean of R F and standard deviation of R F. However, errors will arise as the mean values approach the end points 0 and 1. Moreover, use of normal distribution excludes consideration of skewed distributions. A generalized beta distribution with the end points of 0 and 1 seems more appropriate. Both symmetrical and skewed distributions can be included with the assumption of a beta system. For given values of mean and standard deviation of R F, a corresponding beta distribution can be obtained. Therefore, it is feasible to vary independently the mean of R F and the standard deviation of R F.

Probability density function for the generalized beta distribution

The probability density function (PDF) for the generalized beta distribution representing a variable between given bounding values a and b is represented by the following equation [8].

$$f(x) = \frac{1}{C}(x - a)^{q - 1} (b - x)^{r - 1}$$
(7)

Where,

$$C = \frac{{(q - 1)!(r - 1)!(b - a)^{q + r - 1} }}{(q + r - 1)!}$$
(8)

and, q and r are called the beta distribution parameters.

Expected value and variance for the generalized beta distribution

The expected value and variance of the beta distribution [a, b] are given by:

$$E[x] = a + \frac{q}{q + r}(b - a)$$
(9)

and

$$V[x] = \frac{{qr(b - a)^{2} }}{{(q + r)^{2} (q + r - 1)}}$$
(10)

Correlation between random variables

It is important to note that significant data are not available concerning correlations between shear strength parameters. Consequently, it is not surprising that slope reliability assessments are often based on the assumption of uncorrelated random variables (e.g., [3, 5, 14]). In particular, in regard to slope reliability analysis in strain-softening soils, there are no data available concerning correlation between R F and any other geotechnical parameter.

In view of the above, two categories of analyses have been carried out in respect of taking correlation into account. One category of analysis has been conducted considering all random variables as uncorrelated. In the other category of analysis, the residual factor as well as the pore pressure ratio has been regarded as statistically independent (uncorrelated) while the peak and the residual components of each of the two shear strength parameters have been considered as correlated. In the absence of published data, the effect of correlation between the corresponding peak and residual shear strength parameters on the results of reliability analysis has been examined based on a range of assumed values of the correlation coefficient ρ, specifically, taking ρ = 0.25, 0.5, 0.75, and 1.0. The cross correlation coefficient between the cohesion and the friction parameters are, however, assumed as zero. No negative value for ρ has been considered, because results of preliminary studies have revealed that such consideration leads to anomalous variation of the reliability index with the residual factor.

Adopted method of reliability analysis

For reliability analysis of earth slopes, the first order reliability method (FORM) is widely accepted as the most versatile among the approximate methods of reliability analysis [7] including the mean-value first-order second-moment method (MVFOSM). A potential problem with the MVFOSM method is its lack of invariance for nonlinear performance functions. A further shortcoming with the MVFOSM method is that the statistical moments of the performance function are evaluated at the mean values of the basic variables and not on the limit state surface. The use of MVFOSM method, therefore, introduces error of an unknown magnitude; the degree of error depends on the degree of nonlinearity of the performance function and the coefficients of variation (COV) of the random variables. The FORM method is, on the other hand, free from the above-mentioned shortcomings [7], and therefore, has been adopted in this study. In this method, the reliability index β is defined as the minimum distance from the origin to the failure surface in the standard normal space, using a linearization of the performance function around the design point as originally proposed by Hasofer and Lind [4]. The limit state function for the slope stability is usually defined as

$$g({\mathbf{X}}) = {\text{FS}} - 1$$
(11)

Where, X is the vector representing the set of basic state (or design) variables of the system consisting of the uncertain geotechnical parameters; and FS is the conventional factor of safety, which is computed by deterministic slope stability analysis using limit equilibrium method of slices (Eq. 5). The most commonly used matrix formulation of β for correlated non-normal random variables [6, 9] is as given by Eq. (12).

$$\beta = \mathop {\hbox{min} }\limits_{{g({\mathbf{X}}) = 0}} \sqrt {\left\{ {\frac{{X_{i} - \mu_{i}^{N} }}{{\sigma_{i}^{N} }}} \right\}^{T} [R]^{ - 1} \left\{ {\frac{{X_{i} - \mu_{i}^{N} }}{{\sigma_{i}^{N} }}} \right\}}$$
(12)

where \(\mu_{i}^{N}\) and \(\sigma_{i}^{N}\) are the equivalent normal mean and standard deviation of the ith random variable X i and [R] is the matrix of correlations coefficients ρ between the standard normal variables.

The determination of the reliability index β is, thus, a problem of optimization, and as indicated by Wang et al. [13], the successful application of FORM relies on the selection of a robust optimization algorithm for multi-dimensional minimization. The sequential quadratic programming (SQP) in the MATLAB platform, as described above for the determination of deterministic critical slip surface, can also be employed here. The solution yields the design point on the failure surface and the corresponding reliability index β.

Illustrative example and results

Example description

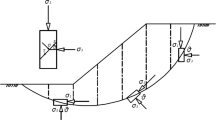
To elucidate the methodology presented in the preceding section, an example of a simple slope in a strain-softening soil has been selected from the literature [2]. Figure 1 presents a section of the slope with height 25 m, inclination 22°, and unit weight of soil 20.8 kN/m3. The statistical properties of the peak and the residual strength parameters are as given in Table 1.

Fig. 1
figure 1

Cross section of a homogenous c–ϕ slope

Full size image
Table 1 Statistical properties of strength parameters
Full size table

Deterministic analysis and estimation of residual factor

Initially, considering the shear strength parameters as deterministic with values equal to their respective mean values as given in Table 1, critical slip surfaces were determined based on the Bishop simplified method of slices coupled with the sequential quadratic programming (SQP) [10] technique of optimization. Specifically, two such deterministic critical slip surfaces were obtained for the two extreme cases, namely, Case A, when the entire slip surface is at peak strength, and Case B, when the entire slip surface is at residual strength. For the sake of convenience these surfaces are marked B p and B r and values of the associated minimum factor of safety (FSmin) are obtained as 1.652 and 0.819, respectively, using a total of 48 slices. In addition to the above, a third critical slip surface considering strain-softening (Case C) was also determined using the progressive failure model as proposed by Chowdhury et al. [2]. This surface is marked B prc for which the associated minimum reduced factor of safety was obtained as 1.331. After identifying the failed slices (out of 48 slices) in the surface B prc, the residual factor R F, being the ratio of the summation of lengths of the failed slices to the overall length of the slip surface, is estimated as 0.392.

The critical slip surfaces determined above are shown in Fig. 2 in which the strain-softened portions (failed slices) of the slip surfaces are highlighted by bullet points. It is observed that the critical slip surfaces for Case A and Case C are very close to one another but substantially different from the critical slip surface for Case B.

Fig. 2
figure 2

Deterministic critical slip surfaces for Case A, Case B and Case C

Full size image

Reliability analyses on the deterministic critical slip surfaces considering residual factor as a deterministic parameter

Using FORM, reliability analyses have been carried out on all the three critical slip surfaces determined in the preceding section. For these analyses, the peak and residual shear strength parameters (Table 1) are treated as random variables and are assumed to be normally distributed and uncorrelated. The residual factor R F is considered as a deterministic parameter which is estimated from the progressive failure model proposed by Chowdhury et al. [2] as described in the preceding section. The performance function is based on the expression for the Bishop simplified method modified for strain-softening soils (Eqs. 1, 2). Table 2 presents a summary of the values of reliability index β of these slip surfaces along with the values of their factor of safety (FSmin) as detailed in the preceding section.

Table 2 Summary of results of deterministic analyses and reliability analyses on deterministic critical slip surfaces assuming random variables as uncorrelated
Full size table

From Table 2 it is observed that F min values for the strain-softening case (Case C) are in between the two extreme cases, i.e., F min value for all peak case (Case A) and all residual case (Case B), which is expected. From the results of the reliability analysis on all the critical slip surfaces for each of above cases, it is observed that nature of variation of β values are same as that of F min values.

Influence of residual factor R F as a random variable

In view of the uncertainties associated with the residual factor R F, it would be of real interest to study the influence of the residual factor as a random variable on the results of reliability analysis. Thus, in this case, reliability analysis will involve five random variables as against four random variables in the earlier analysis. As stated before, the residual factor is assumed to follow a beta distribution while the remaining four random variables are assumed to follow normal distribution, as before. The mean of R F for a slip surface is determined based on the progressive failure model proposed by Chowdhury et al. [2], while the COV of R F is assumed here as 0.3 (The impact of this COV on the reliability results is separately studied in a later sub-section). The parameters q and r defining the specific shape of beta distribution are then calculated using Eqs. (9) and (10). The values of the reliability indices are calculated for the critical slip surface for the strain-softening case B prc. Results are presented in Table 3. The values of the reliability indices when R F is deterministic as obtained from the proposed procedure based on the limit equilibrium method are also tabulated for the sake of comparison.

Table 3 Summary of reliability results to show the influence of R F as a random variable for a specific slip surface (slip surface marked B prc in Fig. 2)
Full size table

Effect of correlation

It would be of interest to study the effect of correlation among the random variables on the results of reliability analysis whichi is presented in Table 2. In the absence of published data on correlation coefficients, a parametric study has been carried out with assumed values of the correlation coefficients between \(c^{\prime}_{\text{p}}\) and \(c^{\prime}_{\text{r}}\) and between \({ \tan }\phi^{\prime}_{\text{p}}\) and \({ \tan }\phi^{\prime}_{\text{r}}\). For simplicity, these two correlation coefficients are assumed to be of equal value and denoted by ρ. A parametric study has been conducted considering the values of ρ as 0.25, 0.5, 0.75 and 1.0. The cross correlation coefficients between the different strength parameters are, however, assumed to be zero. These results are also presented in Table 3. From Table 3, it is seen that there is a significant reduction in the β values obtained when R F is deterministic and when R F is random (largest reduction is 25.59 %). It is also observed that when R F is random, as the value of ρ increases from 0.0 to 1.0, the reliability index decreases by nearly 16 %.

Sensitivity analysis

Figure 3 presents the values of sensitivity index for various random variables based on the FORM method (values of direction cosines) for the slip surface marked B prc for the particular case of ρ = 0.0. The figure clearly shows that the residual factor R F has the largest influence among the five random variables considered in this study. For other values of ρ, the observations are similar.

Fig. 3
figure 3

Results of sensitivity analysis based on the FORM method

Full size image

Effect of variation of COV of R F on the reliability index β

In the above reliability analyses considering the residual factor R F as a random variable, the coefficient of variation of R F has been assumed arbitrarily as 0.3. It is, therefore, important to study the effect of variation of this parameter on the reliability index. Such a study is undertaken here by varying the COV within a reasonable range from 0.1 to 0.5, for different values of ρ. The results are presented in Fig. 4.

Fig. 4
figure 4

Variation of reliability index with increasing variability of R F

Full size image

From this figure the following can be observed.

  1. 1.

    The COV of R F has a significant influence on the value of β, as expected.

  2. 2.

    This influence becomes more and more significant as the value of the correlation coefficient ρ decreases.

Concluding remarks

This paper presents a systematic approach for reliability analysis of a simple slope in a strain-softening cohesive soil by considering the average residual factor R F over a potential slip surface as both a deterministic parameter and a random variable. The value of R F was estimated based on a progressive failure model under the framework of LEM. When considered as random, R F was assumed to follow the generalized beta distribution, while the peak and residual shear strength parameters were assumed to follow normal distribution. The latter variables were recognized as correlated, but, in the absence of published data, the values of the correlation coefficients were varied within a range of 0–1. The performance function was based on the Bishop simplified method modified for strain-softening soils. The reliability analysis for each case, based on the FORM, was carried out on the deterministic critical slip surface for that case as located using a rigorous optimization technique, namely, the sequential quadratic programming method (SQP) in the MATLAB environment. To investigate the relative influence on the reliability index, sensitivity indices of the random variables were obtained as a part of the detailed output of the reliability computations based on the FORM. Based on the numerical results obtained for the illustrative example, the following concluding remarks can be made:

  1. 1.

    The effect of including the average or overall residual factor over a potential slip surface (R F) as one of the random variables in a slope reliability analysis in a strain-softening slope is substantial; the value of reliability index reduces by a margin of 26 %, compared to when R F is considered deterministic.

  2. 2.

    The effect of consideration of positive correlation among the peak and residual shear strength parameters is relatively less. It is observed that when R F is random, as the value of ρ increases from 0.0 to 1.0, the reliability index decreases by nearly 16 %.

  3. 3.

    Sensitivity studies confirm that, amongst the five random variables, residual factor has the most dominant influence on the estimated reliability index.

  4. 4.

    The COV of the residual factor R F has a significant influence on the value of reliability index β, and this influence becomes more and more significant as the value of the correlation coefficient ρ between the peak and the residual components of each shear strength parameter decreases.