Introduction

The piled–raft foundation concept, in which raft shares piles in transferring the total load to the supporting soil, is widely used in many countries as an economical solution for the foundations of high rise buildings. Many cases of successful application of this concept are reported in the literature (e.g. Poulos [1], Yamashita et al. [2], Khoury et al. [3], El-Mossallamy et al. [4], and Katzenbach and Shmitt [5]). Randolph [6] classified the design philosophies of piled–raft foundation into three types as follows:

  • The conventional approach, in which the piles are designed as a group to carry the major part of the load, while making some allowance for the contribution of the raft, primarily to ultimate load capacity.

  • Creep piling in which the piles are designed to operate at a working load at which significant creep starts to occur, typically 70–80 % of the ultimate load capacity. Sufficient piles are included to reduce the net contact pressure between the raft and the soil to below the pre-consolidation pressure of the soil.

  • Differential settlement control, in which the piles are located strategically to reduce the differential settlements, rather than to substantially reduce the overall average settlement.

Poulos [7] presented a more extreme version of creep piling, in which the full load capacity of the piles is utilized, i.e., some or all of the piles operate at 100 % of their ultimate load capacity. This gives rise to the concept of using piles primarily as settlement reducers, while recognizing that they also contribute to increasing the ultimate load capacity of the entire foundation system. Both the creep piling and differential settlement control philosophies are suitable for design of foundations of new buildings, and they provide the most economical foundation alternative. It requires less number of piles at relatively wide spacing between piles (e.g., Abdel-Fattah and Hemada [8]). However, some building codes, including the Egyptian geotechnical code 202/4-2001 [9], require a minimum factor of safety for individual piles, and consequently, these approaches cannot be directly applied. Russo and Viggiani [10] clarified that the conventional design philosophy is the case where the bearing capacity of the unpiled raft is insufficient, and in this case, the spacing between piles is typically from 3 to 4 times the pile diameter. Thus, the primary reason to add the piles is to achieve a suitable safety factor. Based on the experimental evidence, Mandolini et al. [11] reported that for pile groups with piles at small spacing (3–4 times the pile diameter) and covering the entire raft area, the percentage of load carried by the raft is not less than 20 % approximately. An example of this approach is the well-monitored foundations of the Stonebridge park building reported by Cooke et al. [12]; this building is found on London clay. Although the foundation of this building was originally designed as a standalone pile group without contribution of the raft, the measurements show that about 25 % of the building load was transferred to supporting soil directly through the raft. This concept may be applied when evaluating existing unsatisfactorily designed and/or constructed piled foundations to avoid relatively high cost of unnecessary underpinning; examples for the unsatisfactorily designed and/or constructed piled foundations include the cases of unsuccessful pile load test, increase in total load due to additional floors, etc. Abdel-Fattah et al. [13] employed the creep piling concept when assessing the safety of a piled–raft compressing considerable number of defective piles.

ISSMGE [14] recommends that the computational model used for the design of a combined-pile–raft foundation (CPRF) shall contain: (1) a realistic geometric modelling of the foundation elements and the soil, (2) a realistic description of the material behaviour of both structure and subsoil, and (3) a rational description of the contact behaviour between the soil and the foundation elements.

These requirements may be satisfied only using a 3D non-linear numerical modelling program (Poulos et al. [15] and Reul and Randolph [16]). Modern European building codes, such as the Italian construction code 2008 (cited by Allievi et al. [17]) and the Deutsche norm DIN1054:2005-01 [18], give provisions for using piled–raft foundation. DIN 1054:2005-1 classified the piled–raft construction into the category of structures that require highest technical category for the geotechnical investigation works.

This paper presents an application of the conventional piled–raft design philosophy to evaluate the adequacy of existing piled foundations (piles and raft) for two identical residential towers located in Cairo, Egypt. 3D finite-element analyses that fulfil the above-mentioned requirements of the ISSMGE for combined pile–raft foundation [14] are employed in this study. This type of advanced analysis is capable of predicting the part of the load that is directly transferred by the raft as well as the settlement of the foundation.

Case studies of existing piled foundations

The investigated cases are two identical residential towers located in Cairo, Egypt. Each tower consists of 47 stories; the height of the tower above ground surface is 162 m. The structural system is a reinforced concrete skeleton consisting of a central core and perimeter columns. The foundation of each tower consists of piles originally designed as a standalone group capped with raft in direct contact with the supporting soil. The estimated total load of each tower, including own weight of the raft, is about 550 MN.

Only the foundations of both towers were constructed more than 25 years ago. At present, the owner has decided to complete the construction of the two towers, and entrusted the authors of this paper to evaluate the adequacy of the existing foundations to support the expected loads from super-structure, and to propose the method of underpinning of these foundations if required. The plan of both towers is square and symmetric with an area of 800.0 m2. It was decided to evaluate the adequacy of these existing foundations based on the conventional piled–raft philosophy defined in the previous section.

Description of the existing foundations

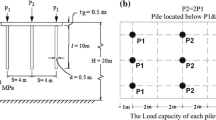
Although both towers have identical super-structure and a 3.25-m-thick raft, they have different bored pile diameters and arrangements. The foundation of the first tower (denoted as tower A) consists of 96 18-m-long bored piles of 1.50-m-diameter spaced at 3.75 m, as shown in Fig. 1a. The foundation of the second tower (denoted as tower B) consists of 140 18-m-long bored piles of 1.20-m-diameter spaced at 3.00 m, as shown in Fig. 1b. The bored piles were constructed by drilling holes with aid of bentonite slurry and using temporary casing of 4.0–5.0-m depth to support the upper part of the hole. The concrete of the piles was placed using tremie pipe. The raft area is almost the same for both towers; the two rafts are in direct contact with the ground.

Fig. 1
figure 1

Pile layout for both towers

Full size image

Soil conditions

To explore the soil stratification and soil properties at the site, an extensive geotechnical investigation program, including 12 boreholes of depths ranging from 20.0 to 60.0 m, was carried out. These boreholes were mechanically drilled with standard penetration test performed every 1.0 m of borehole depth in granular soil. In the case of cohesive layers, undisturbed samples were obtained using Shelby tube sampler. In addition, compression and shear-wave refraction tests were carried out near the existing raft edges. The average shear-wave velocity at small shear strains (less than 10−3 percent strain) in top 30 m measured from these tests ranged from 370 to 630 m/s.

The main soil formation is sand with different gradations. Amounts of silt are encountered at the top 3.0 m. This layer is underlain by a layer of medium dense sand of about 5.0 m-thick followed by a layer of very dense gravelly sand with density increasing with depth down to depth of about 35.0 m. A layer of hard clay was then encountered down to the maximum boring depth of 60.0 m below ground surface. The ground-water table appears at about 2.50 m below the ground surface.

The soil type below the bottom level of the raft, which is granular soil with relative density increasing with depth, can provide considerable bearing resistance, and consequently, soil conditions are suitable for the raft to transfer part of the total load directly to soil. The piles are expected to transfer loads to soil via both friction an end bearing.

The soil material parameters are estimated based on the results of both laboratory and in situ tests. Figure 2 shows a schematic cross section of tower A with soil profile at site.

Fig. 2
figure 2

Schematic section of tower A with soil profile

Full size image

Material properties

The concrete parameters for both raft and piles used in the finite-element analyses are listed in Table 1.

Table 1 Reinforced concrete material parameters
Full size table

The soil parameters used in the finite-element analyses have been estimated as shown in Table 2. Elasto-plastic Mohr–Coulomb model has been used as a constitutive model for soil layers beneath the foundation level down to the end of the granular layers, whereas the over consolidated hard clay layer of 20.0-m thickness encountered below this level is modelled as an elastic sub-grade to minimize the size of the used mesh (Hemada et al. [19]). The values of the sub-grade moduli are back calculated from the unloading/reloading deformation modulus (E ur) of the clay layer calculated from the odometer test carried out on representative clay specimens as follows:

$$K_{n} = \frac{{E_{\text{ur}} }}{{H_{\text{clay}} }} = \frac{{3(1 + e_{o} )(p_{0} {\prime } + p_{t} )(1 - 2\nu_{\text{ur}} )}}{{\kappa \times H_{\text{clay}} }}$$
(1)
$$K_{t} = \frac{{K_{n} }}{{2(1 + \nu_{\text{ur}} )}},$$
(2)

where K n normal sub-grade, K h shear sub-grade, E ur unloading/reloading deformation modulus, e 0 initial void ratio, p 0′ insitu mean stress, p t ′ tensile strength, ν ur unloading/reloading Poisson’s ratio = 0.25, H clay thickness of the clay layer, κ rebound modulus = \(\frac{{C_{r} }}{\ln 10}\), C r elastic reloading modulus resulted from the Odometer test.

Table 2 Soil material parameters
Full size table

Estimation of single pile capacity

Tower A

The design working load for single pile (W L) of tower A is 6.66 MN according to design documents. The analysis of the test results of the available pile load test for tower A shows that the predicted ultimate static load according to the Egyptian Geotechnical Code of Practice No. 202/4-2001 [9] is about 17.5 MN which corresponds to the average value obtained from modified Chin’s and Brinch Hansen’s methods presented in Fig. 3a and b, respectively. Hence, the allowable pile load for this pile is governed by the concrete strength. For working stress of 4.5 MPa, the allowable pile load will be equal to 7.9 MN.

Fig. 3
figure 3

Prediction of ultimate pile load from pile load test of tower A

Full size image

A 2D finite-element back analysis was carried out using the general purpose finite-element program DIANA® (TNO DIANA BV. [20]) to predict the single pile behaviour beyond the test load (1.5W L) and to define the pile–soil interface parameters to be used in the 3D model of the foundation system. The finite-element simulation of the analysed pile load test is shown in Fig. 4. The results of the analysis prove that the data of the test beyond the maximum test load (10 MN) could be extrapolated to the level of the ultimate pile capacity.

Fig. 4
figure 4

Comparison between pile load test and FE back analysis results

Full size image

Tower B

Similar to the procedure carried out for tower A, the ultimate load obtained from the analysis of pile load test data for tower B was about 7.2 MN. However, tower B test results showed that plastic settlement begins to occur very early, i.e., at low load level and the allowable pile, load is governed by the geotechnical capacity. Hence, the maximum allowable working load for the single pile (W L), taking a safety factor of 2, is 3.60 MN which is less than the design value (4.2 MN). This means that a reduction in the pile group capacity of about 15 % is expected.

Finite-element model

Description of the model

A 3D non-linear finite-element analysis is used to model the behaviour of the piled–raft system. The analysis is carried out as a phased analysis to simulate the sequence of the construction. Due to symmetry, the model of tower A represents only a quarter of the real building. Furthermore, for tower B and for simplicity, a slight difference between loads of mid edge columns was neglected; consequently, three-fold symmetry was assumed. Hence, a model representing one-eighth of the real building is considered to be accurate enough. The results of the quarter model of tower A verify that the assumption of three-fold symmetry used for tower B is practically accurate.

The purpose of this model is to predict settlement and the straining actions of the raft, and the load distribution between the raft and piles.

The finite-element analyses are carried out using the general purpose finite-element program DIANA® (TNO DIANA BV. [20]).

The 3D finite-element mesh for the piled–raft model is shown in Fig. 5. The raft is modelled using both 8-noded and 6-noded shell elements. The piles are modelled using both 16-noded wedge elements and 20-noded brick elements. Figure 6 shows the meshing for the raft and the piles. The soil layers denoted by SSand, MSand, GSand1, and GSand2 (refer to Table 2) are modelled using 16-noded wedge elements and 20-noded brick elements. The interaction between the soil and both raft and piles is modelled using 12-noded and 16-noded interface elements, respectively. The interface elements between the different components of the model are shown in Fig. 7. The effect of presence of the clay layer is presented as an elastic base modelled using interface with normal stiffness and tangential stiffness calculated as described before. For tower B, no interface elements between raft and supporting soil are provided, and raft is assumed to be rigidly connected to soil.

Fig. 5
figure 5

Finite-element mesh

Full size image
Fig. 6
figure 6

Finite-element mesh of the raft and piles

Full size image
Fig. 7
figure 7

Finite-element mesh of interface elements

Full size image

Analysis procedure and loadings

The analysis is performed in three phases to simulate the construction sequence as follows:

Phase 1: only soil layers are modelled to calculate the in situ stresses. The effect of the soil layer above foundation level is taken as a uniform surcharge of 65 kPa. This phase is done under drained condition.

Phase 2: this phase represents the case after executing the piles and the raft. The excavation is implicitly modelled by removing the uniform surcharge from the area of the raft. This case represents the current construction stage. In this phase, drained condition has been selected to represent the current situation, since the piled–raft system was constructed about 25 years ago.

Phase 3: in this phase, the rigid beams representing the super-structure are added to the model, and the loads of the columns are increased in steps up to the full load. This phase is carried out under both undrained and drained conditions.

Results of analyses and discussion

Detailed outputs for tower B are presented in this section, and a comparison with their counterparts for tower A is provided where necessary. Figure 8 shows the raft layout with key-node numbers.

Fig. 8
figure 8

Raft layout; key-node numbers

Full size image

Contours of vertical displacement

Figure 9 plots the contours of the short-term vertical displacement of the raft due to total vertical loading. The maximum values of vertical displacements are 24 and 19 mm at the raft centre for towers A and B, respectively, whereas the minimum values are 19 and 10 mm at the corner of the raft for towers A and B, respectively. Figure 10 plots the contours of the long-term vertical displacement of the raft due to total vertical loading. The maximum values of vertical displacements are 36 and 42 mm for towers A and B, respectively, whereas the minimum values are 29 and 31 mm for towers A and B, respectively. These settlement values prove that serviceability requirements are satisfied for both towers.

Fig. 9
figure 9

Contours of vertical displacement at full load—undrained condition (units: m)

Full size image
Fig. 10
figure 10

Contours of vertical displacement at full load—drained condition (units: m)

Full size image

The load-settlement curves for the selected key nodes are plotted in Figs. 11 and 12 for the undrained and drained conditions, respectively. It can be seen from these two figures that the response is almost linear, and that the maximum amplitude of vertical displacement is located at the middle of the raft. This linear behaviour implies that the loading level for the towers is still below the geotechnical ultimate capacity as expected for such a system in sandy soil.

Fig. 11
figure 11

Load-settlement curves—undrained condition

Full size image
Fig. 12
figure 12

Load-settlement curves—drained condition

Full size image

Figures  13 and 14 present the short-term and long-term settlement profiles along the diagonal of the raft to illustrate the differential settlement. The maximum differential settlements resulted are 8.0 and 10 mm for the undrained and drained conditions, respectively. Figures 12 and 13 indicate that the raft behaves almost as a rigid footing.

Fig. 13
figure 13

Settlement profile through joints 1602–1531—undrained condition

Full size image
Fig. 14
figure 14

Settlement profile through joints 1602–1531—drained condition

Full size image

Stresses in piles

As per the Egyptian code for design and construction of concrete structures 203/2007 [21], the allowable axial compressive stress for piles’ concrete is conservatively estimated to be 4.50 MPa, and the allowable bending stress with medium eccentricity is 5.5 MPa. The distributions of the compressive normal stresses that exceed 4.5 and 5.5 MPa are plotted in Figs. 15 and 16, respectively, whereas the distribution of the tensile stresses is plotted in Fig. 17.

Fig. 15
figure 15

Normal stresses on piles—drained condition—zones with compression stresses exceeding 4500 kPa

Full size image
Fig. 16
figure 16

Normal stresses on piles—drained condition—zones with compression stresses exceeding 5500 kPa

Full size image
Fig. 17
figure 17

Normal stress on piles—drained condition—tension stress zones

Full size image

It can be concluded from Figs. 16 and 17 that the stresses in the real pile shaft section (below raft bottom) have not reached the critical values, since the raft thickness is 3.25 m. The maximum load per pile is 5340 and 3560 kN for towers A and B, respectively.

Contact stresses between the raft and soil

Figure 18 shows the contours of the contact stresses between the raft and soil. This figure implies that the stresses are almost uniform, but increase sharply at the edges. This is a typical behaviour for a rigid footing.

Fig. 18
figure 18

Contact stress contours beneath the raft—drained condition (units: kN/m2)

Full size image

The stress distribution beneath the raft axis of symmetry is plotted in Fig. 19. The average contact stress is about 80 kPa. The vertical in situ stress at the level of the foundation is about 65 kPa. The percentage of total load transferred directly from raft to supporting soil is about 14.5 and 16.5 % for towers A and B, respectively. These results show that a considerable part of the total load was directly transferred from the raft to supporting soil in spite of the use of a large number of piles with conventional factor of safety in sandy soil.

Fig. 19
figure 19

Contact stress distribution beneath the raft axis of symmetry—case of full load—drained condition

Full size image

Conclusions

Based on the results of the numerical investigation presented in this paper, in which a finite-element model has been presented for studying the behaviour of existing conventional piled foundations with raft in direct contact with the ground, a number of conclusions can be drawn as follows:

The analysis of piled–raft foundation is a traditional 3D problem that considers pile–raft–soil interactions. This type of analysis is capable of predicting the distribution of load between raft and piles. However, before performing the 3D finite-element analysis, an essential requirement for such a problem is to perform back analyses of static pile load tests to predict proper pile–soil interface parameters.

The results of the analyses show that although the foundation is primarily designed as a pile group with a conventional factor of safety in sandy soil, a considerable part of the total load was directly transferred to the supporting soil. The percentages of the load transferred by the raft are 14.5 and 16.5 % for towers A and B, respectively.

It is recommended to apply the conventional piled–raft design philosophy to improperly designed pile groups (e.g., in case of unsuccessful pile load test) to avoid the relatively large costs of unnecessary underpinning of foundation. Application of this design philosophy to the case in hand has enabled the construction of tower B to the designed number of stories without underpinning of the foundation.

The proposed methodology considers a conventional factor of safety for piles, and consequently does not violate the existing building codes.

In contrast to the traditional design of pile groups, for piled–raft design, the bending moment at pile–raft connection, which depends on the relative stiffness between raft and piles, shall be taken into consideration in the structural design of the piles.