Introduction

Soil–pile–structure systems are confronted with various and large uncertainties compared to superstructures (for example, see [1–4]). The main sources of uncertainties come from properties (stiffness and damping) of soil itself, soil–pile interaction, pile–soil–pile interaction, layered soil geometrical irregularity due to lack of measurement data, etc. Uncertainties of stiffness and damping of soil deposit seem to be a central concern of many structural designers. The strain dependency of soil properties is investigated through in situ experiments recently [3]. What the structural designers would like to know in the preliminary structural design stage is the upper and lower bounds of earthquake responses of piles and superstructures under the circumstances of these uncertainties.

In this paper, a soil–pile–structure interaction system under an engineering bedrock input ground motion is considered [5–10] and the soil properties (stiffness and damping ratio) are treated as interval parameters (see [11–16]). Interval parameters mean the parameters with uncertain properties. Concrete Young’s modulus is also dealt with as an uncertain parameter in some examples. Then the upper and lower bounds of its earthquake response are evaluated. This problem is a kind of interval analysis problems.

The concept of interval analysis existed many years ago in the field of mathematics and was introduced by Moore [17]. Alefeld and Herzberger [18] subsequently accomplished the pioneering work. They investigated linear interval equation problems, nonlinear interval equation problems and interval eigenvalue analysis problems by enhancing interval arithmetic. Qiu et al. [13] applied the interval arithmetic algorithm to derive the bounds of static structural response by introducing a convergent series expansion of the uncertain structural response. Qiu and Elishakoff [14] extended the interval arithmetic algorithm to interval analysis problems by taking full advantage of the Neumann series expansion of the inverse stiffness matrix. Mullen and Muhanna [19] provided the bounds of the static structural response for all possible loading combinations using the interval arithmetic. After 2000, the interval analysis using Taylor series expansion has been proposed by several researchers [15, 20, 21]. In the early stage, the first-order Taylor series expansion was discussed in the problems of static response and eigenvalue. Chen et al. [15] then introduced the matrix perturbation method using the second-order Taylor series expansion and tried an approximation of the bounds of the objective function without interval arithmetic. It was made clear that the computational demand can be reduced from the number of calculation 2N (N: number of interval parameters) to 2N by neglecting the non-diagonal elements of the Hessian matrix of the objective function without suffering the accuracy. An innovative method for interval analysis for the non-deterministic response has been presented even for large intervals using second-order Taylor series expansion [16]. The possibility has been considered of occurrence of the peak value of the objective function in an inner feasible domain of interval parameters. The critical combination of uncertain structural parameters was determined approximately using the second-order Taylor series expansion.

A response spectrum method due to Kojima et al. [9, 10] is used in this paper for evaluating the maximum seismic pile response of this system (see “Maximum pile response via response spectrum method for structure–pile–soil system subjected to design earthquakes on engineering bedrock surface”). Two scenarios of uncertainty in ground profiles are taken into account (see “Scenario of uncertainty in ground profiles”). This implies that the response variability can change by paying attention to different uncertainty mechanisms. The upper and lower bounds of earthquake responses are computed using the URP (Updated Reference Point) method due to the present authors [16] and the revised new URP method (NURP) (see “New uncertainty analysis method”). A genetic algorithm (GA) is used for investigating the accuracy of the proposed method (see “New uncertainty analysis method”). Although a preliminary and limited investigation has been conducted in Fujita et al. [22], more detailed investigation including a new uncertainty case (case 2 in “Scenario of uncertainty in ground profiles”) and practical applications to actual sites will be presented (see “Application of NURP method to actual ground”).

Maximum pile response via response spectrum method for structure–pile–soil system subjected to design earthquakes on engineering bedrock surface

Modeling of structure–pile–soil system

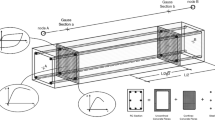
An efficient finite-element model of a structure–pile–soil system as shown in Fig. 1 is used here. To enable the treatment of a non-proportional damping system, a complex-domain response spectrum method is employed in the evaluation of the maximum seismic pile responses of the structure–pile–soil system to the ground motion defined at the engineering bedrock surface. The introduction of an efficient response evaluation method is inevitable because the interval analysis dealing with huge number of uncertain parameter combinations requires much computational task. The efficient finite-element model with the Winkler-type springs for the pile–soil system has been proposed in Nakamura et al. [5, 6] and has been extended to the model including the strain-dependent soil properties [7]. The displacement function of the free-field ground is assumed to be linear (the validity of this assumption is discussed afterward in this section) and that of the pile is assumed to be cubic. To satisfy the deformation compatibility at both sides, the horizontal displacement in this element along the pile element is required to be cubic. Viscous boundaries are incorporated at the bottom of that model and a response spectrum method, developed in Kojima et al. [9], similar to that for the free-field ground [23] is used. The accuracy and reliability of this model and this response spectrum method have been verified through the comparison with recorded pile response under an actual earthquake [7] and with the multi-input model considering nonlinear soil stress–strain relation (see “Comparison with multi-input model including nonlinear horizontal interaction springs”). For better understanding of the readers, the essence of this model is explained briefly in the following.

Fig. 1
figure 1

Finite element model

Full size image

To model the soil–pile interaction, a dynamic Winkler-type spring [24] with frequency dependent damping is introduced. The damping ratios consist of hysteretic one and radiation one [7]. The frequency-dependent damping is transformed into the frequency-independent one evaluated at the fundamental natural frequency of the superstructure. This is essential for the introduction of the response spectrum method. The area of the free-field ground should be determined carefully from the viewpoint of numerical stability. The area of the free-field ground is set to 1.0 × 106 m2 based on the fact that the transfer function amplitude of the free-field ground surface displacement is stable for the value larger than 1.0 × 105 m2 [8]. It is noted that this property of mode isolation between the modes including the vibration of the free-field ground and the vibration of the structure–pile–soil system could cause much difficulty in the mere application of the conventional response spectrum methods.

The strain-dependent nonlinear relations are shown in Fig. 2 for clay and sand which are taken from the Japanese seismic-resistant design code revised in June 2000. To evaluate the strain-dependent nonlinearity of the ground, an equivalent linearization method [23, 25] has been used. In this paper, the convergent equivalent shear modulus \( G_{e} \) and damping ratio \( \beta_{e} \) are used as the nominal values (mean of the smallest and the largest values) in the uncertainty case 1 introduced later (see “Scenario of uncertainty in ground profiles”). The element stiffness matrices \( {\mathbf{K}}_{i} \) for the pile–soil system of i-th layer consist of the element stiffness matrices \( {\mathbf{k}}_{pi} \) for piles, the element stiffness matrices \( {\mathbf{k}}_{Ii} \) for pile–soil interaction springs [26] and the element stiffness matrices \( {\mathbf{k}}_{si} \) for the free-field ground. The element stiffness matrices \( {\mathbf{K}}_{i} \) for the pile–soil system of i-th layer are expressed by

Fig. 2
figure 2

Dependence of shear modulus and damping ratio on strain level [23]

Full size image
$$ {\mathbf{K}}_{i} = {\mathbf{k}}_{pi} + {\mathbf{k}}_{Ii} + {\mathbf{k}}_{si} $$
(1)

The detailed expression can be found in Nakamura et al. [5, 8, 9].

The element damping matrices \( {\mathbf{C}}_{i} \) for the pile–soil system of \( i \)-th layer consist of the element damping matrices \( {\mathbf{c}}_{Ii} \) for the pile–soil interaction dashpot [26] and the element damping matrices \( {\mathbf{c}}_{si} \) for the free-field ground. The element damping matrices \( {\mathbf{C}}_{i} \) for the pile–soil system of \( i \)-th layer are expressed by

$$ {\mathbf{C}}_{i} = {\mathbf{c}}_{Ii} + {\mathbf{c}}_{si} $$
(2)

The system stiffness, damping and mass matrices of the efficient finite-element model are composed of the element stiffness, damping and consistent mass matrices (see [9]) for the pile–soil system of each layer, the element stiffness, damping and mass matrices for superstructure and the element damping matrices consisting of the damping coefficient \( c_{bs} \) and \( c_{bp} \) of the viscous boundary at the bottom of the surface ground and the pile. The damping coefficients \( c_{bs} \) and \( c_{bp} \) are put into the degrees of freedom just above the bedrock in the surface ground and the pile, respectively, and are expressed by

$$ c_{bs} = \rho_{N} V_{sN} A_{s} ,\quad c_{bp} = \rho_{N} V_{sN} A_{p} $$
(3)

where \( \rho_{N} \), \( V_{sN} \) and \( A_{p} \) are the mass density of the engineering bedrock (Nth layer), the shear wave velocity of the engineering bedrock and the cross-section area of the pile, respectively. It is assumed that the angle of rotation of the pile top is zero and the rotation of the pile tip is free.

In this paper, a 10-story building model is considered. The fundamental natural period \( T_{B1} \) is set to 1.0 s for the fixed-base model. The floor mass of the building for a single pile is chosen as 10 × 103 kg and the mass of the foundation for a single pile is set to 30 × 103 kg. All the building models have been simplified into two-mass models (floor masses are transformed into two masses). A cast-in-place reinforced concrete pile is used and its pile diameter is assumed to be 1.5 m. The Young’s modulus of concrete is given as 2.1 × 1010 N/m2 and the concrete mass density is 2.4 × 103 kg/m3.

To investigate the accuracy of the present method, a single pile of diameter = 1.0 m and length = 20 m in a homogeneous semi-infinite ground of shear wave velocity = 100 m/s and damping ratio = 0.05 has been analyzed in Kishida and Takewaki [8]. It has been clarified through the comparison with the thin-layer method [27–29] that the present method has a reasonable accuracy. In addition, the comparison with the continuum model [7] has been made. A two-story shear building model on a surface ground of two soil layers (depth of each soil layer = 10 m, shear wave velocity = 100, 200 m/s from the top, pile diameter = 1.5 m) has been analyzed in Kishida and Takewaki [8]. It has been demonstrated that a fairly good correspondence can be observed in the case of using the Rayleigh damping and this supports clearly the validity of the present sophisticated and efficient FEM model. The comparison of the pile bending moment and shear force is shown in “Appendix 1”.

Another comparison has been made with actual record and the present method has been proven to be accurate enough when taking into account the soil strain-amplitude nonlinearity [7]. Further comparison has also been conducted with a multi-input model taking into account a versatile nonlinear soil constitutive model, i.e. Masing hysteretic rule and Hardin-Drnevich model [9] (see “Comparison with multi-input model including nonlinear horizontal interaction springs”).

Ground models

Surface ground models, referred to as ground model A and B, are employed. The ground model A is a rather soft ground. While, the ground model B is a rather hard ground. The soil profiles of these ground models are shown in Fig. 3 and those are based on the actual grounds data. The SPT (standard penetration test) values of each soil layer are also shown in these figures. The mass densities of surface soil layers and engineering bedrock are 1.8 × 103 and 2.0 × 103 kg/m3. Poisson’s ratio is 0.45.

Fig. 3
figure 3

Profile of shear wave velocity and SPT count: a ground A, b ground B

Full size image

Evaluation of maximum bending moment of pile head via response spectrum method

In this paper, the earthquake response of piles is evaluated using the previously proposed response spectrum method (RSM) [8–10, 30] in terms of complex modal quantities for a structure–pile–soil system subjected to the earthquake ground motion at the engineering bedrock surface. The maximum bending moment at pile head can be expressed by the RSM as

$$ M_{\hbox{max} } = \sqrt {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\left\{ {Z_{s}^{\left( i \right)} \rho_{ss}^{{\left( {ij} \right)}} Z_{s}^{\left( j \right)} + 2Z_{s}^{\left( i \right)} \rho_{sc}^{{\left( {ij} \right)}} Z_{c}^{\left( j \right)} + Z_{c}^{\left( i \right)} \rho_{cc}^{{\left( {ij} \right)}} Z_{c}^{\left( j \right)} } \right\}} } } $$
(4)

where \( Z_{s}^{\left( i \right)} \) and \( Z_{c}^{\left( i \right)} \) represent the bending moment at pile head in the i-th mode for the sine and cosine spectra [9]. \( Z_{s}^{(i)} \) and \( Z_{c}^{(i)} \) are derived by

$$ Z_{s}^{\left( i \right)} = {\text{EI}} \times S_{Ds}^{\left( i \right)} \text{Re} [\nu^{\left( i \right)} \kappa^{(i)} ],\quad Z_{c}^{\left( i \right)} = {\text{EI}} \times S_{Dc}^{\left( i \right)} \text{Re} [\nu^{\left( i \right)} \kappa^{(i)} ] $$
(5)

In Eq. (5), \( EI \), \( S_{Ds}^{(i)} \), \( S_{Dc}^{(i)} \), \( v^{(i)} \) and \( \kappa^{(i)} \) are the bending stiffness of the pile, the mean value of the maxima of the sine spectra, that of the cosine spectra, the i-th complex participation factor and the curvature component at the pile head in the i-th complex eigenmode, respectively. In Eq. (4), \( \rho_{ss}^{(ij)} \) and \( \rho_{cc}^{(ij)} \) are autocorrelation coefficients between the i-th mode and the j-th mode of sine–sine spectra and cosine–cosine spectra, respectively. \( \rho_{sc}^{(ij)} \) is the cross-correlation coefficient between the i-th mode and the j-th mode of sine–cosine spectra [9].

As the design earthquake ground motion at the engineering bedrock surface, the damage-limit (damage initiation) acceleration response spectrum specified in Japanese seismic resistant design code is employed first. In this design spectrum, the structural response needs to be elastic. A comparison of reduction of stiffness and damping ratio of each ground model by the RSM with those by SHAKE under the damage-limit ground motion is shown in Fig. 4. From these figures, it can be observed that the RSM can be applied to evaluate the reduction of equivalent stiffness and damping ratio.

Fig. 4
figure 4

Comparison of reductions of stiffness and equivalent damping ratio derived by RSM with that by SHAKE under damage-limit design ground motion: a stiffness reduction (Ground A), b stiffness reduction (Ground B), c equivalent damping ratio (Ground A), d equivalent damping ratio (Ground B)

Full size image

The same procedure has been applied to the safety-limit level motion and the equivalent stiffness and damping have been evaluated by the response spectrum method.

Comparison with multi-input model including nonlinear horizontal interaction springs

To further investigate the accuracy and reliability of the present response spectrum method, a time-history response analysis using the multi-input model as shown in Fig. 5 has been conducted. In this model, the interaction spring is modeled by the Hardin-Drnevich model (see “Appendix 2”) and the Masing hysteretic rule based on the Masing’s hypothesis for steady-state cyclic hysteretic responses. The damping coefficients of the interaction dashpots have been evaluated by considering the radiation damping component. Figure 6 shows the comparison of the pile bending moments between the present response spectrum method and the multi-input model including nonlinear horizontal interaction springs placed at every 1 m. In the multi-input model, a response-spectrum compatible ground motion (damage-limit level input; Ground A; 2-story model) has been generated at the bedrock and the ground motions at different underground levels (every 1 m) have been produced using the SHAKE program. This procedure has also been conducted for the safety-limit level input (Ground A; 2-story model). It should be kept in mind, while the response spectrum method provides a mean value of the peak responses from an ensemble of ground motions, the multi-input model gives one response result to one input ground motion. Figure 6 indicates that, although the present response spectrum method provides a somewhat different response distribution of pile stresses, especially for the safety-limit level input, the overall properties including the pile-head bending moment can be predicted within an acceptable accuracy.

Fig. 5
figure 5

Multi-input model for accuracy check of the response spectrum method [9]

Full size image
Fig. 6
figure 6

Accuracy check of response spectrum method: a damage limit level, b safety limit level [9]

Full size image

Scenario of uncertainty in ground profiles

There are two kinds of uncertainty in a real world. The first is aleatory uncertainty which is related to unavoidable uncertainty (intrinsic randomness) and the other is epistemic uncertainty which may be able to be reduced in the advancement of research.

In this paper, two uncertainty cases are treated. The first one (case 1) is to consider the variability of the equivalent shear wave velocity and the equivalent damping ratio of soil after the completion of equivalent linearization for the nominal profile. The second one (case 2) is to take into account the variability of the initial shear wave velocity and damping ratio of soil before the equivalent linearization. The first uncertainty may be related to the difference in phase of input ground motions and the variability of dynamic deformation characteristics of soil (effect of confined pressure, etc.). On the other hand, the second uncertainty may be related to the variability of measurements in the field tests and the variability of the transformation from the SPT count into shear wave velocity, etc. However, the variability of the transformation from the SPT count into shear wave velocity may be closely related to case 1 and clear discrimination seems to be difficult. The schematic diagram of these two uncertainty cases is shown in Fig. 7 and the mechanisms of two uncertainty cases are illustrated in Fig. 8. Figure 9 presents the schematic algorithm of the conventional URP method.

Fig. 7
figure 7

Schematic diagram of uncertainty case 1 and uncertainty case 2

Full size image
Fig. 8
figure 8

Schematic diagram of uncertainty case: a case 1, b case 2

Full size image
Fig. 9
figure 9

Schematic algorithm of conventional URP method [16]

Full size image

In this paper, the equivalent shear wave velocity and the equivalent damping ratio are varied \( \pm \)30 % from the nominal one in the uncertainty case 1 and the initial shear wave velocity and the initial damping ratio are varied \( \pm \)30 % from the nominal one in the uncertainty case 2. In addition, when the pile Young’s modulus is uncertain, that is varied \( \pm \)20 % from the nominal one.

Figure 10 shows the upper bound, lower bound and nominal response of the pile bending moment by the conventional URP method in the uncertainty case 2. It can be observed that a large variability exists and the corresponding worst profile is made clear by the URP method.

Fig. 10
figure 10

Upper bound, lower bound and nominal response of pile bending moment by the conventional URP method in uncertainty case 2: a bending moment, b worst profile of shear wave velocity (ratio to nominal), c worst profile of damping ratio (ratio to nominal)

Full size image

Table 1 shows the pile bending moment under the damage limit level input and the safety limit level input in uncertainty cases 1, 2. It can be found that the ratio of the upper bound to the nominal value can become more than six and the ratio in the uncertainty case 2 is larger than that in the uncertainty case 1. This may be due to the fact that the varied strain range used for the equivalent linearization in the uncertainty case 2 is larger than that in the uncertainty case 1. On the other hand, Table 2 presents the comparison of the pile bending moment by the URP method and GA [31]. It can be observed that a large error exists under the safety limit level input (case 2, Ground B). For this purpose, a revised bound evaluation method will be proposed later.

Table 1 Pile bending moment under damage limit level input and safety limit level input in uncertainty cases 1, 2
Full size table
Table 2 Pile bending moment by URP method and GA
Full size table

New uncertainty analysis method

To increase the accuracy and the reliability of the uncertainty analysis, a new method called NURP is proposed here. The essential feature is shown in Fig. 11.

Fig. 11
figure 11

Schematic diagram of new URP method (NURP method)

Full size image

The accuracy check of the conventional URP method and the proposed NURP method by GA (case 2, Safety limit level motion, Ground B) is shown in Fig. 12.

Fig. 12
figure 12

Accuracy check of the conventional URP method and the proposed NURP method by GA (case 2, Safety limit level motion, Ground B): a worst profile of shear wave velocity, b worst profile of damping ratio

Full size image

The comparison of accuracy between the URP and NURP methods is shown in Table 3. It can be found that the accuracy has been increased by the NURP method.

Table 3 Comparison of accuracy between URP and NURP methods
Full size table

Table 4 presents the accuracy of the NURP method in case of uncertainties in the pile Young’s modulus and soil properties. The variability of the pile Young’s modulus is 20 %. It has been made clear that the worst ratio of the pile Young’s modulus to the nominal value is 1.15 in the NURP method and that is 1.2 (upper limit) in GA.

Table 4 Accuracy of the NURP method in case of uncertainties in pile Young’s modulus and soil properties
Full size table

Figure 13 shows the worst profile of shear wave velocity and damping ratio in the accuracy check of the proposed NURP method by GA (case 1, Safety limit level motion, Ground A). Uncertainties in pile Young’s modulus and soil properties have been considered. It can be observed that a fairly good correspondence exists.

Fig. 13
figure 13

Accuracy check of the proposed NURP method by GA in case of uncertainties in pile Young’s modulus and soil properties (Case 1, Safety limit level motion, Ground A), a worst profile of shear wave velocity, b worst profile of damping ratio

Full size image

Application of NURP method to actual ground

To demonstrate the practicality of the proposed NURP method, it has been applied to boring data at 20 sites in Kyoto Prefecture, Japan. The 20 sites (K1–K20) are shown in Fig. 14. In Japan, it is often the case that the transformation from the SPT count into the shear wave velocity is performed. This is because the SPT is standard and the PS log test is limited to high-rise and base-isolated buildings. Three transformation methods due to Imai, Road bridge, Ohta and Goto have been used. These methods are often used in the practical situation in Japan. Figure 15 shows the comparison example of the profiles of the shear wave velocity evaluated by these three methods (at K11, K20). To investigate the variability of the transformation, data analysis has been conducted. As a result, the validity of the variability about 30 % has been confirmed.

Fig. 14
figure 14

Boring sites in Kyoto Prefecture used for uncertainty analysis (https://www.google.co.jp/maps)

Full size image
Fig. 15
figure 15

Shear wave velocity profiles evaluated by three methods: a site K11, b site K20

Full size image

The mean value of the largest value and the smallest value using the above-mentioned three transformation methods in the shear wave velocity and the damping ratio is treated as the nominal value. Then the difference between the maximum (or minimum) and the nominal is dealt with as the varied range.

Figure 16 plots the ratio of the upper bound of the maximum pile bending moment to the nominal value in case 1 and case 2 of uncertainty mechanism under damage limit level (level 1) and safety limit level (level 2) motions. It can be found that the degree of variability of case 2 is larger than that of case 1. Although the uncertainty due to the variability of the transformation from the SPT count into shear wave velocity may be related to the uncertainty case 2 as mentioned above, this procedure has been used only for evaluating the nominal value of the equivalent shear wave velocity and the equivalent damping ratio in the uncertainty case 1.

Fig. 16
figure 16

Ratio of upper bound of maximum pile bending moment to nominal value in case 1 and case 2 of uncertainty mechanism under damage limit level (level 1) and safety limit level (level 2) motions

Full size image

Figure 17 shows the tendency of the worst profile in the shear wave velocity to increase the pile bending moment (uncertainty case 1). The variation of the shear wave velocity to a smaller value in a shallow range and that to a larger value in a deep range seem to attain the worst profile. This combination corresponds to the ‘short pile modeling’.

Fig. 17
figure 17

Tendency of worst profile in shear wave velocity to increase the pile bending moment (case 1, Safety limit level input, Site K14)

Full size image

Figure 18 presents the profiles of worst equivalent shear wave velocities at site K19 and K6. In this example, only the equivalent shear wave velocity and the equivalent damping ratio are treated as uncertain parameters (uncertainty case 1) and the varied range is \( \pm \)30 % from the nominal one which has been evaluated using the procedure explained above in this section. When the equivalent shear wave velocities are almost uniform in the depth direction, the worst combination corresponds to the weak profile of soil stiffness. On the other hand, when the equivalent shear wave velocities are irregular in the depth direction, the worst combination corresponds to the amplification of the irregularity.

Fig. 18
figure 18

Profiles of worst equivalent shear wave velocities: a K19 (small increase from the nominal value: magnification = 1.52), b K6 (large increase from the nominal value: magnification = 3.86)

Full size image

Conclusions

The worst combination of uncertain soil properties to maximize the seismic pile response has been investigated by a revised uncertainty analysis approach. The conclusions are summarized as follows.

  1. 1.

    Under the condition that soil properties (stiffness and damping) are treated as uncertain parameters, the maximum pile bending moment at the pile head in a structure–pile–soil system has been evaluated by the complex-value domain response spectrum method considering the modal correlation. The ground motion has been defined at the engineering bedrock surface. It has been shown that the upper and lower bounds of the bending moment of the pile can be computed effectively using the advanced uncertainty analysis method called the Updated Reference-Point method (URP method) and the revised NURP method.

  2. 2.

    Two different ground models (ground model A as a rather soft ground, ground model B as a rather hard ground) have been investigated to find the worst combination of soil properties for the pile response. It has been confirmed that the variability of the equivalent shear wave velocities even at a deep underground can influence the bending moment at the pile head in the worst combinations of soil parameters.

  3. 3.

    Two uncertainty scenarios have been treated. The first one (case 1) is to consider the variability of equivalent shear wave velocity and equivalent damping ratio of soil after the completion of equivalent linearization for the nominal profile. The second one (case 2) is to take into account the variability of the initial shear wave velocity and damping ratio of soil before the equivalent linearization.

  4. 4.

    The NURP method has been applied to boring data at 20 sites in Kyoto Prefecture, Japan to demonstrate the practical applicability of the NURP method and the validity of the variability range of soil profiles. It has been confirmed that the NURP method is reliable and the 30 % variability range is reasonable. When the equivalent shear wave velocities are almost uniform in the depth direction, the worst combination corresponds to the weak profile of soil stiffness. On the other hand, when the equivalent shear wave velocities are irregular in the depth direction, the worst combination corresponds to the amplification of the irregularity.

  5. 5.

    To investigate the accuracy of the proposed method, the upper bound derived by an anti-optimization approach using a genetic algorithm (MOGA-II [31]) has been compared with those by the URP method and the NURP method. It has been confirmed that the NURP method can be applied to the seismic pile response in terms of the structure–pile–soil system within an acceptable accuracy and the worst variation of soil parameters can be clarified.