Introduction

The mechanics of unsaturated soils started to develop from the 1960s. The first milestone for comprehensive unsaturated soil modeling can be attributed to [1], who have developed the Barcelona basic model (BBM) by extending the modified Cam-Clay model of saturated soils. Then, following the same direction, several works based on the classic Cam Clay model in a critical state framework have been developed (e.g. [2–4]). However, the main drawback of these models is their difficulty to reproduce with accuracy a smooth stress–strain relation at pre-yield and post-yield, pre-peak and post-peak, as well as the volumetric behavior of soils (in particular the smooth transition from contractancy to dilatancy).

One option to improve the limits of classic models is the concept of Bounding surface Plasticity (BSP). This theory, firstly proposed by Dafalias [5] and Dafalias and Herrmann [6] to simulate metal behaviors, was applied by Bardet [7] on saturated sands and later on followed by Gajo and Muirwood [8] as well as by Yu and Khong [9]. The use of the BSP theory to model the behavior of unsaturated soils was originally introduced by Russell and Khalili [10]. These authors also took into account grain breakage, which occurs at high stresses. However, the determination of the model parameters is quite difficult, which prevents its practical application for ordinary loading conditions.

The aim of this paper is to develop a new constitutive model which can remove some short comings of classic elastic–plastic models and to reproduce complex volumetric behaviors by using the BSP theory with a non-associative plastic flow rule, but with a limited number of parameters which are easily measurable.

Essential ideas of BSP theory

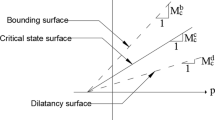
In this section, some general aspects of the bounding surface concept are represented. Contrary to classic plasticity, the BSP theory introduces a non-zero plastic strain rate even inside the bounding surface (analogous but not identical to the classic yield surface), with its amplitude increasing as the current stress point approaches the bounding surface. This is achieved by making the plastic modulus to depend on the distance δ between the current stress point σ′ and an arbitrarily defined image stress point, \( \bar{\varvec{\sigma }}^{\prime } \) located on the Bounding surface (see Fig. 1). This definition leads to a smoothing of the stress–strain curve from small to large strains, reproducing more realistically experimental observations. It exists different way to define the image stress, \( \bar{\varvec{\sigma }}^{\prime } \). Among them, the “radial mapping” method introduced by Dafalias [11] is the simplest and the most widely used. It consists of extrapolating the position vector linking the origin to the current stress until it intersects the image stress on the bounding surface as illustrated in Fig. 1.

Fig. 1
figure 1

Schematic representation of the radial mapping method

Full size image

Model development

The model developed in this study, called the CASMNS model, is based on the CASM-b model [12] for saturated soils: use of the effective stress, same form of the bounding surface, and non-associate law with the same form of plastic potential.

We consider the cylindrical symmetry corresponding to the classical triaxial test. Under this consideration, only two variables are required to define the strain state. In this study, we use the classic Cam Clay variables which are the volumetric strain, noted ε v , and the equivalent deviatoric strain, noted ε q :

$$ \varepsilon_{v} = tr(\varvec{\varepsilon})\;{\text{and}}\;\varepsilon_{q} = \left( {\left( {2/3} \right)\varvec{e}:\varvec{e}} \right)^{1/2} $$
(1)

where \( \varvec{e} =\varvec{\varepsilon}- {\mathbf{1}} \times \varepsilon_{v} /3 \) is the deviatoric strain tensor, 1 is the second order identity tensor, and ε is the total strain tensor which is supposed to be the sum of an elastic and a plastic component:

$$ \varvec{\varepsilon}=\varvec{\varepsilon}^{e} +\varvec{\varepsilon}^{p} $$
(2)

where elastic strain, noted \( \varvec{\varepsilon}^{e} \), and plastic strain, noted \( \varvec{\varepsilon}^{p} \).

Similarly, the stress state can be defined by the mean effective stress, p′ and the equivalent deviatoric stress q:

$$ p^{\prime } = tr\left( {\varvec{\sigma}^{\prime } } \right)/3\;{\text{and}}\;q = \sqrt {(3/2)\varvec{s}:\varvec{s}} $$
(3)

where \( \varvec{s} =\varvec{\sigma}^{\prime } - {\mathbf{1}} \times {p}^{\prime } \) is the deviatoric stress tensor and \( \varvec{\sigma}^{\prime } \) is the effective stress tensor that can be expressed as Dangla and Coussy [13]:

$$ \varvec{\sigma}^{\prime } =\varvec{\sigma}+ \pi {\mathbf{1}} $$
(4)

where σ is the total stress tensor, and π the equivalent pore pressure and 1 is the second order identity tensor. From the several definitions that have been proposed for π (e.g. [13–15]), we chose to follow the expression proposed by Dangla and Coussy:

$$ \pi (s) = sS_{r} + \frac{2}{3}\int_{{S_{r} }}^{1} {s(S)dS} $$
(5)

where s is the suction and Sr is the saturation degree.

Note that this definition is not simply a weighted average of the bulk liquid and gaseous phases, but also accounts for the tangential forces at the liquid–gas interface arising from surface tension effects. Its computation requires information on the soil water retention curve (SWRC), which is the function linking suction s to the degree of water saturation Sr. For the sake of simplicity, the hydraulic hysteresis is neglected here and the following bijective relation proposed by Brooks and Corey [16] is assumed. Note that Sr remains constant equal to unity for suctions below the so-called air entry suction:

$$ S_{r} = \left\{ {\begin{array}{*{20}l} {\left( {\frac{{s_{a} }}{s}} \right)^{\alpha } :s > s_{a} } \hfill \\ {1:s \le s_{a} } \hfill \\ \end{array} } \right.\quad {\text{with}}\quad \alpha < 1 $$
(6)

where sa is the air-entry suction and α is a material constant.

Elastic mechanism

Our main concern here is the plastic behavior. We therefore adopt a simple isotropic logarithmic elastic behavior like Cam Clay to simplify. The strain rates are entirely defined by the stress rate:

$$ \left( {\begin{array}{*{20}c} {d\varepsilon_{v}^{e} } \\ {d\varepsilon_{q}^{e} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {dp^{\prime } /K} \\ {dq/(3G)} \\ \end{array} } \right);\quad K = \frac{{1 + e_{0} }}{\kappa }p^{\prime } ;\quad G = \frac{{3\left( {1 - \nu } \right)}}{{2\left( {1 + \nu } \right)}}K $$
(7)

where K and G are the state-dependent bulk and shear moduli respectively, ν is Poisson ratio and κ is a material constant which governs the elastic moduli, e 0 is the initial void ratio.

Bounding surface and hardening mechanism

The bounding (BS) and the loading surfaces (LS) adopted, of whale-head shape, are described by:

$$ F\left( {\bar{p}^{\prime } ,\bar{q},p_{\pi } \left( {s,\varepsilon_{v}^{p} } \right)} \right) = \left( {\frac{{\bar{q}}}{{M\,\bar{p}^{\prime } }}} \right)^{n} + \frac{1}{\ln r}\ln \left( {\frac{{\bar{p}^{\prime } }}{{p_{\pi } }}} \right) = 0 $$
(8)

As illustrated in Fig. 2, the LS is the homothetic contraction of the BS relative to the origin.

Fig. 2
figure 2

Bounding surface and Loading surface of CASMNS model

Full size image

Since (p′, q) lies on the LS, its image (p′/β, q/β) lies on the BS, giving:

$$ \beta = \frac{{p^{\prime } }}{{p_{\pi } }} \times r^{{\left( {\frac{\eta }{M}} \right)^{n} }} $$
(9)

where β is the scale factor between the BS and the LS β ∊ (0, 1), η = q/p′ is the stress ratio, M is the slope of critical state line, p π is the position of bounding surface summit on the p-axis and r, n are model parameters.

The dependence of p π on suction can be taken into account by an additive term and a multiplicative factor. Owing to insufficiency of experimental data, the simplified expression proposed by Pereira [17] is retained here:

$$ p_{\pi } \left( {s,\varepsilon_{v}^{p} } \right) = \left( {1 + k_{1} \times l(s)} \right)p_{0} \left( {\varepsilon_{v}^{p} } \right) $$
(10)

We also assume that under isotropic virgin compression, the volumetric strain will vary linearly with the logarithm of the mean effective stress with a slope equal to:

$$ \lambda (s) = \left\{ {\begin{array}{*{20}l} {\lambda_{0} - k_{2} \times l(s):s > s_{a} } \hfill \\ {\lambda_{0} :s \le s_{a} } \hfill \\ \end{array} } \right.;\quad l(s) = sS_{r} - s_{a} $$
(11)

The l(s) function in the above equations accounts for the increase of resistance and stiffness with suction. The choice of formulation of this function is particularly important because it determines the shape of the loading surface which then affects the capacity of the model to reproduce wetting collapse. In this study, we assume the relation reported in (11).

The function l(s) is defined in (11) and p 0 is the hardening variable in the case of full saturation, similar to Camclay, verifying:

$$ dp_{0} = \frac{{1 + e_{0} }}{\lambda (0) - \kappa }p_{0} d\varepsilon_{v}^{p} $$
(12)

According to the hardening rule defined by the last two equations, the BS will expand during contractant plastic flow and shrinks during dilatant plastic flow.

Plastic flow rule

It is postulated that the plastic strain rates write:

$$ \left( {\begin{array}{*{20}c} {d\varepsilon_{v}^{p} } \\ {d\varepsilon_{q}^{p} } \\ \end{array} } \right) = d\lambda \left( {\begin{array}{*{20}c} {m_{p} } \\ {m_{q} } \\ \end{array} } \right) $$
(13)

where (m p , m q ) is the unit vector at current stress obtained by normalizing the gradient of a plastic potential g:

$$ \left( {\begin{array}{*{20}c} {m_{p} } \\ {m_{q} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\partial g/\partial p^{\prime } } \\ {\partial g/\partial q} \\ \end{array} } \right) \times \left\| {\left( {\begin{array}{*{20}c} {\partial g/\partial p^{\prime } } \\ {\partial g/\partial q} \\ \end{array} } \right)} \right\|^{ - 1} $$
(14)

In this model, a non-associative flow rule is used, by adopting the plastic potential of Yu [12]:

$$ \begin{aligned} g\left( {p^{\prime } ,q} \right) =\, & mln\left( {1 + (m - 1)\left( {\frac{\eta }{M}} \right)^{n} } \right) \\ & + \,n(m - 1)ln\left( {\frac{{p^{\prime } }}{C}} \right) \\ \end{aligned} $$
(15)

To determine the plastic multiplier, we first introduce the unit vector n:

$$ \begin{aligned} \nabla_{{\bar{\sigma }^{\prime } }} F = & \left( {\frac{\partial F}{{\partial \bar{p}^{\prime } }},\frac{\partial F}{{\partial \bar{q}}},\frac{\partial F}{\partial s}} \right)^{t} ; \\ \varvec{n} =\, & \frac{{\nabla_{{\bar{\sigma }^{\prime } }} F}}{{\left\| {\nabla_{{\bar{\sigma }^{\prime } }} F} \right\|}} = \left( {n_{p} ,n_{q} ,n_{s} } \right)^{t} \\ \end{aligned} $$
(16)

The consistency condition:

$$ dF = \frac{\partial F}{{\partial \bar{p}^{\prime } }}d\bar{p}^{\prime } + \frac{\partial F}{{\partial \bar{q}}}d\bar{q} + \frac{\partial F}{\partial s}ds + \frac{\partial F}{{\partial \varepsilon_{v}^{p} }}d\varepsilon_{v}^{p} = 0 $$
(17)

Combined with the classic assumption that the consistency condition applied to the current stress on the LS and to the image stress on the BS both lead to the same plastic multiplier dλ, allow us to obtain:

$$ d\lambda = \frac{1}{H}\left( {n_{p} dp^{\prime } + n_{q} dq + n_{s} ds} \right) $$
(18)

The plastic multiplier is the sum of two terms:

$$ H = H_{\delta } + H_{b}$$
(19)

The first term is designed to vanish on the BS, when β = 1:

$$ H_{\delta } = \frac{{1 + e_{0} }}{\lambda (s) - \kappa }\frac{{\left( {1 - \beta } \right)^{{}} }}{\beta }\frac{h}{{\left\| {\nabla_{{\bar{\sigma }^{\prime } }} F} \right\|}} $$
(20)

The expression of H b can be found in [18]. The above equations define completely the relation between the total strain and the stress increments.

Determination of material parameters

Altogether, 13 material constants are required to define completely this model. Note that 8 of these parameters can be determined by using experimental data. We used the knowledge of the water retention curve to obtain the parameters α and the air-entry suction s a in Brooks and Corey’s relation. Furthermore, the deformability parameters κ, υ, λ0 can be determined from classic oedometric and triaxial consolidation tests at full saturation. The oedometric test at different controlled suctions has been used to deduce the parameter k1 defining the reduction of compressibility λ (s) with suction. The parameters M and υ can be determined using two triaxial test at different controlled suctions. The remaining parameters: h, m, n, r have to be indirectly determined by successive iteration using results from the triaxial and oedometric tests. Recall that the BBM model requires 12 parameters, taking into account the invariance of CSL in the (p′, q) plane as pointed out by Khalili and Khabbaz [19] and Nuth and Laloui [20]. Comparatively, this model has only one additional parameter while it uses a substantially more complicated plastic driver based on bounding surface plasticity, with a non-associative flow law to achieve a much better prediction on general stress–strain behaviour in general and a more precise description of volumetric behavior in particular.

Examples of application

This section presents a few numerical examples of simulation in order to show the applicability and the quality of the model. Figure 3 shows the flow chart for the implementation of this model in MatLab. In the following paragraphs, this computer code is applied to analyze the behavior of a soil sample subject to different loading paths.

Fig. 3
figure 3

Flow chart for the implementation in MatLab

Full size image

Capacity to reproduce the classic phenomena

As a first example, we consider a series of triaxial compression tests at constant controlled suctions varying from 0.1 to 5 bar. Soil parameters used in this simulation are summarized in Table 1 (Type A).

Table 1 Parameters adopted for the simulations
Full size table

Figure 4a, b show the evolution of deviatoric stress q and volumetric strain ε v with axial strain ε 1. These results show that the model developed is able to simulate correctly complex volumetric behavior (with transition from contractancy to dilatancy), post-peak softening and the increase of stiffness and strength due to suction-increase.

Fig. 4
figure 4

a Deviatoric stress and b volumetric strain versus axial strain of a triaxial test at constant suction

Full size image

The second example uses the same material parameters as shown in Fig. 5a. It considers a more complex loading path (AB: drainage, BC: isotropic compression, CD: imbibition). This example allows testing the capacity of the model to reproduce another fundamental feature of unsaturated soil behaviors, which is the wetting collapse.

Fig. 5
figure 5

a complex loading path, b response of the model in plane q–εv and the collapse phenomenon at a point E

Full size image

Figure 5b shows the result in the plane (s, ε v ). The classic phenomenon of wetting collapse is observed at point E while the volumetric strain changes from dilatant to contractant volumetric behavior.

Comparison with experimental data

Previous two numerical examples show that the model is able to reproduce the classical tendencies which are commonly observed on unsaturated soils. The next step is its validation by experimental data. For that purpose, we used the triaxial tests carried out by Hoang [21] on Hostun S28 sand.

The material parameters of this sand as deduced from the test results are given in Table 1 (Type B). The triaxial tests were performed at constant water contents of 5 and 10 % with confining pressures.

The results of this comparison are shown in Fig. 6a, b in the q–ε 1 plane. A good agreement between the numerical results and experiment data can be observed under any confining pressure and water content (except for the case with w = 10 % and p = 1.5 bar where the difference is slightly more visible).

Fig. 6
figure 6

Triaxial test at a constant water content a w = 5 %, b w = 10 % on sable Hostun S28 ranging from 1 to 2 bar

Full size image

Comparison among BBM, BDNS and CASMNS

To illustrate the main assets of the model developed in this paper, we compared it to other commonly used elasto-plastic models. At first, we compared it with the BDNS model developed by Morvan [22], which is also based on the concept of bounding surface plasticity under a critical state framework with an associate flow rule. The comparison is made based on the experimental data of Russell and Khalili [10]. The material parameters used for the simulations are reported in Table 1 (Type C).

The results in q–ε 1 plane and ε v –ε 1 plane, for three different constant suctions of 0.5, 2 and 4 bar with two different confining pressures of 0.5 and 1 bar are presented in Figs. 7, 8 and 9 respectively.

Fig. 7
figure 7

Deviatoric stress (a) and volumetric strain (b) versus axial strain with a constant suction, s = 0.5 bar

Full size image
Fig. 8
figure 8

Deviatoric stress (a) and volumetric strain (b) with axial strain of a triaxial test at constant suction s = 2 bar

Full size image
Fig. 9
figure 9

Deviatoric stress (a) and volumetric strain (b) with axial strain of a triaxial test at constant suction s = 4 bar

Full size image

They underline that both models can reproduce a post-peak behavior as well as a clear transition from contractant to dilatant behavior in the course of shearing. However, the model developed in this paper, which considers a non-associative flow rule, simulates the volumetric behaviors of sand with a higher precision.

A second comparison is made between the two bounding surface plasticity models (e.g. CASMNS and BDSN) as well as with the BBM model [1], which is the most commonly used model for unsaturated soils.

This second comparison is made based on the experimental data of the triaxial tests at constant suction with a confining pressure of 1 bar, performed by Cui (1993) on Jossigny silt. The material parameters used for the simulations are reported in Table 1 (Type D).The results reported in Fig. 10a, b clearly show the performance of the bounding surface plasticity models. In particular, only the CASMNS model succeeds to reproduce accurately the volumetric behavior of the soil at a high suction of 15 bar.

Fig. 10
figure 10

Deviatoric stress (a) and volumetric strain (b) with axial strain of a triaxial test at constant suction with a confining pressure of 1 bar on Jossygny silt

Full size image

From the preceding results and discussions, it can be observed that the model developed in this study leads to significant improvements compared to other classic elastic–plastic models, at the expense of only a minimum number of additional parameters (same number of parameters as BDNS, and only one more parameter than BBM). The improvement on the smooth transition from pre-peak hardening to post-peak softening is attributed to the use of the Bounding surface plasticity concept, while the use of the non-associate flow rule leads to a better reproduction of the complex volumetric behavior.

Conclusion

A new bounding surface plasticity model is presented in this study. Of fundamental importance in practice, this model developed can be used to describe a wide range of unsaturated soils such as sand, silt, etc. Numerical results performed show that the model can reproduce the essential feature of unsaturated soil behavior including suction induced hardening, the possibility of wetting-collapse. They also underline its abilities to remove some short coming of classic elastic–plastic models, in particular its ability to simulate progressive transition from pre- to post-peak behavior, involving a smooth change of stress–strain variations from pre- to post-yield, as well as complex volumetric behavior.